How to Predict the Efficacy of Free-Product DNAPL Pool Extraction Using 3D High-Precision Numerical Simulations: An Interdisciplinary Test Study in South-Western Sicily (Italy)
Abstract
1. Introduction
2. Study Area
3. Materials and Methods
3.1. Geological and Hydrogeological Investigations
3.2. Hydrochemical Analyses
3.3. Microbiological Analyses: 16S Ribosomal RNA Gene Next-Generation Sequencing (NGS)
3.4. Hydrogeological Parameters of the Numerical Model Using CactusHydro
4. Results
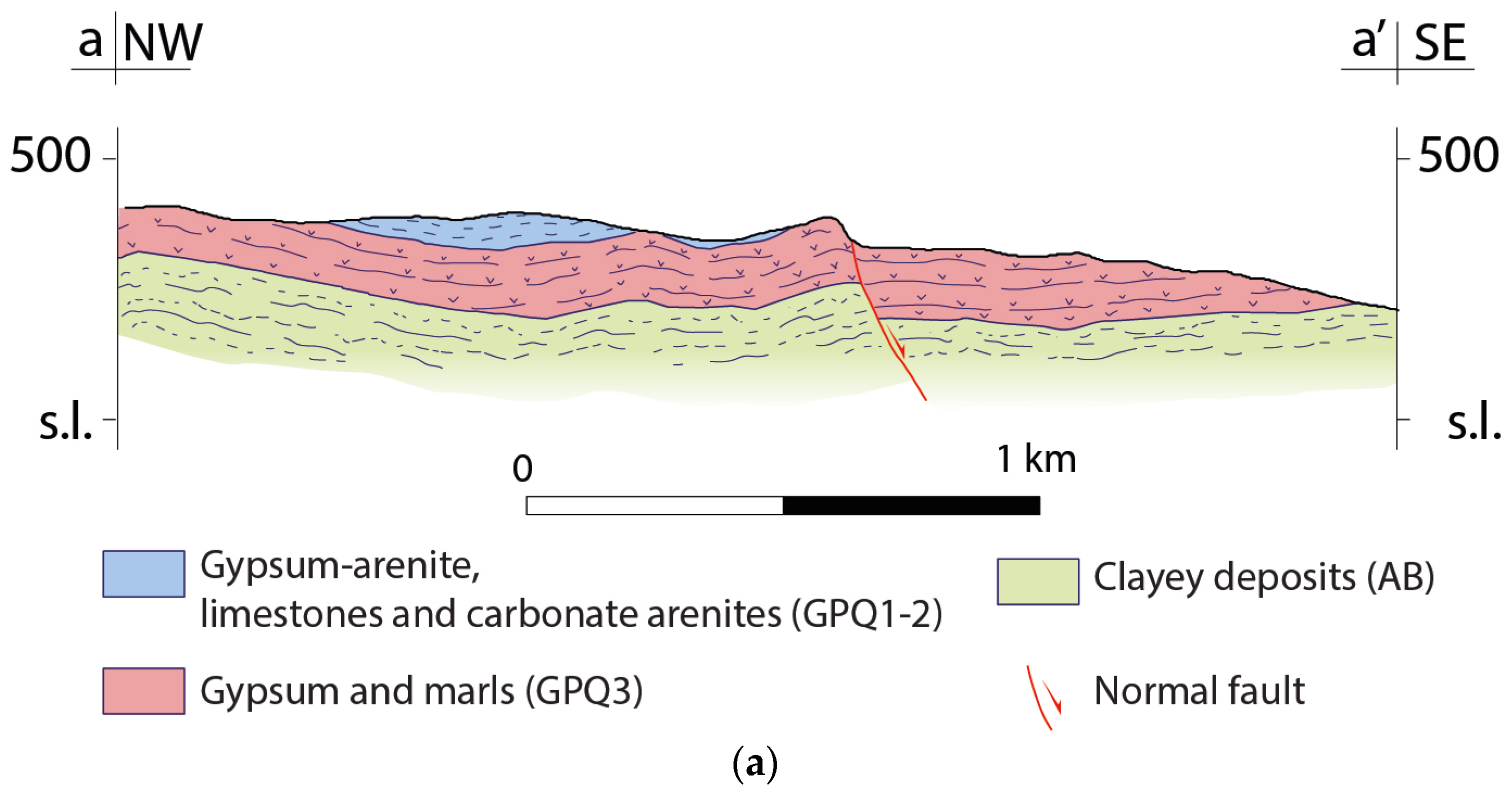
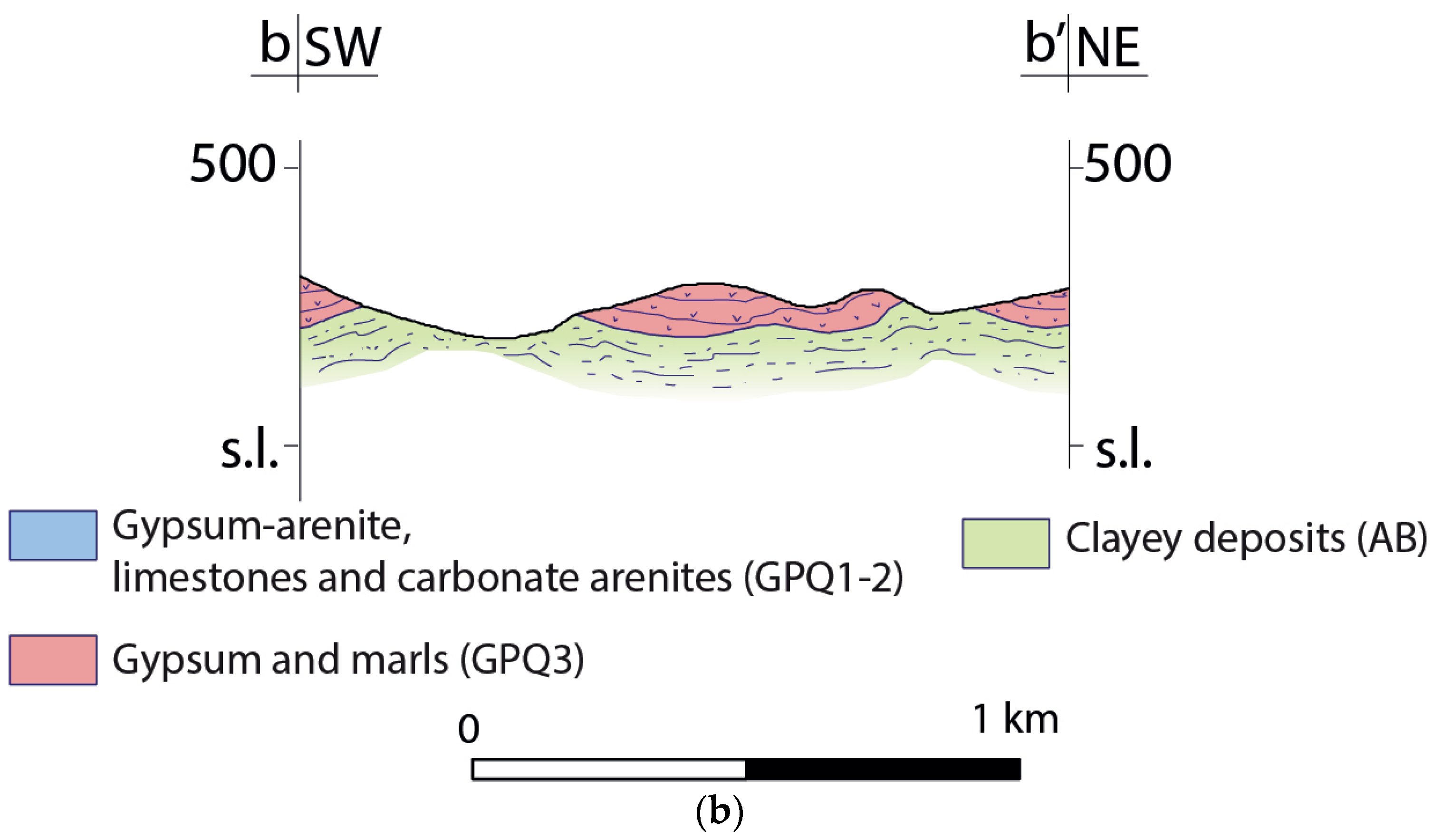
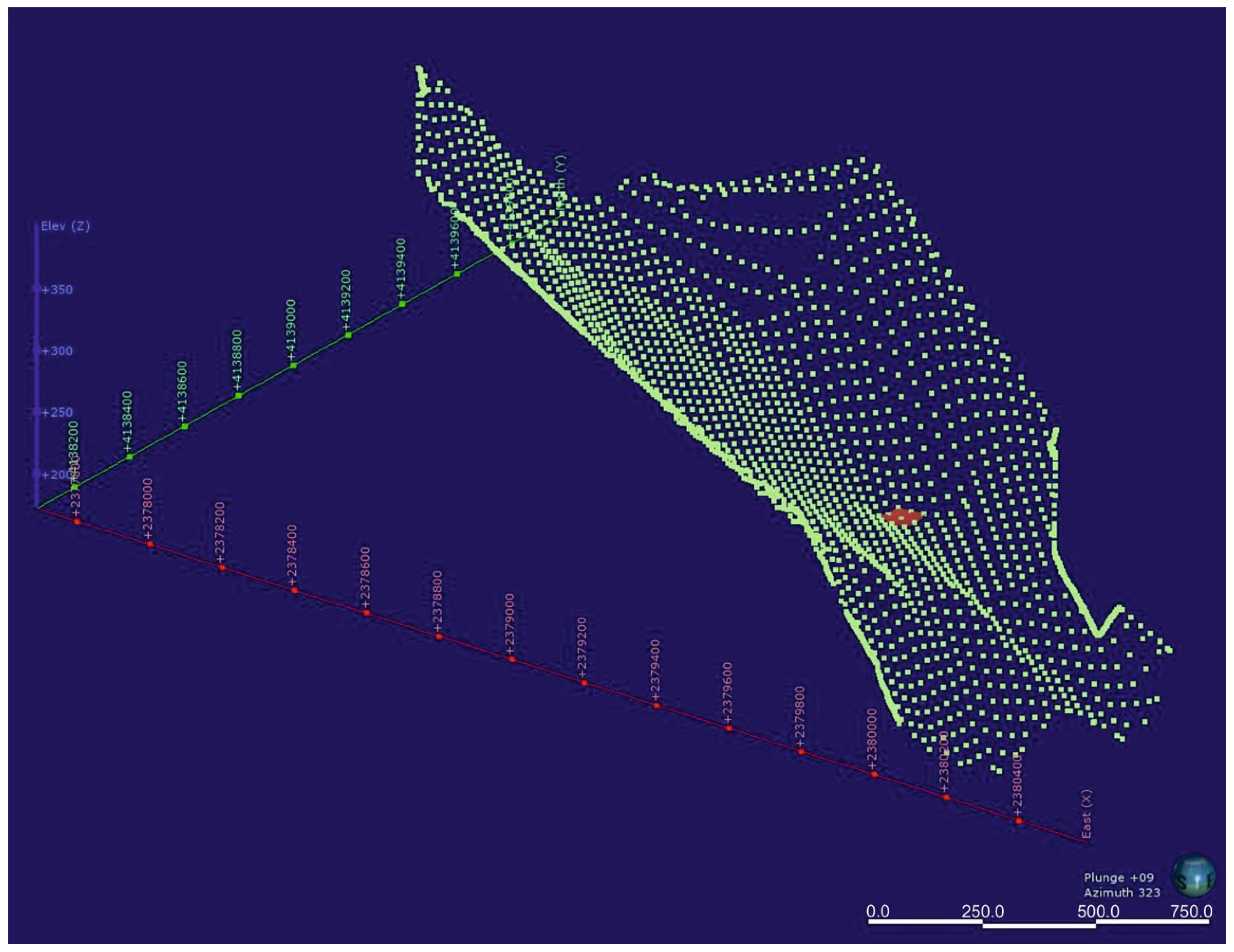
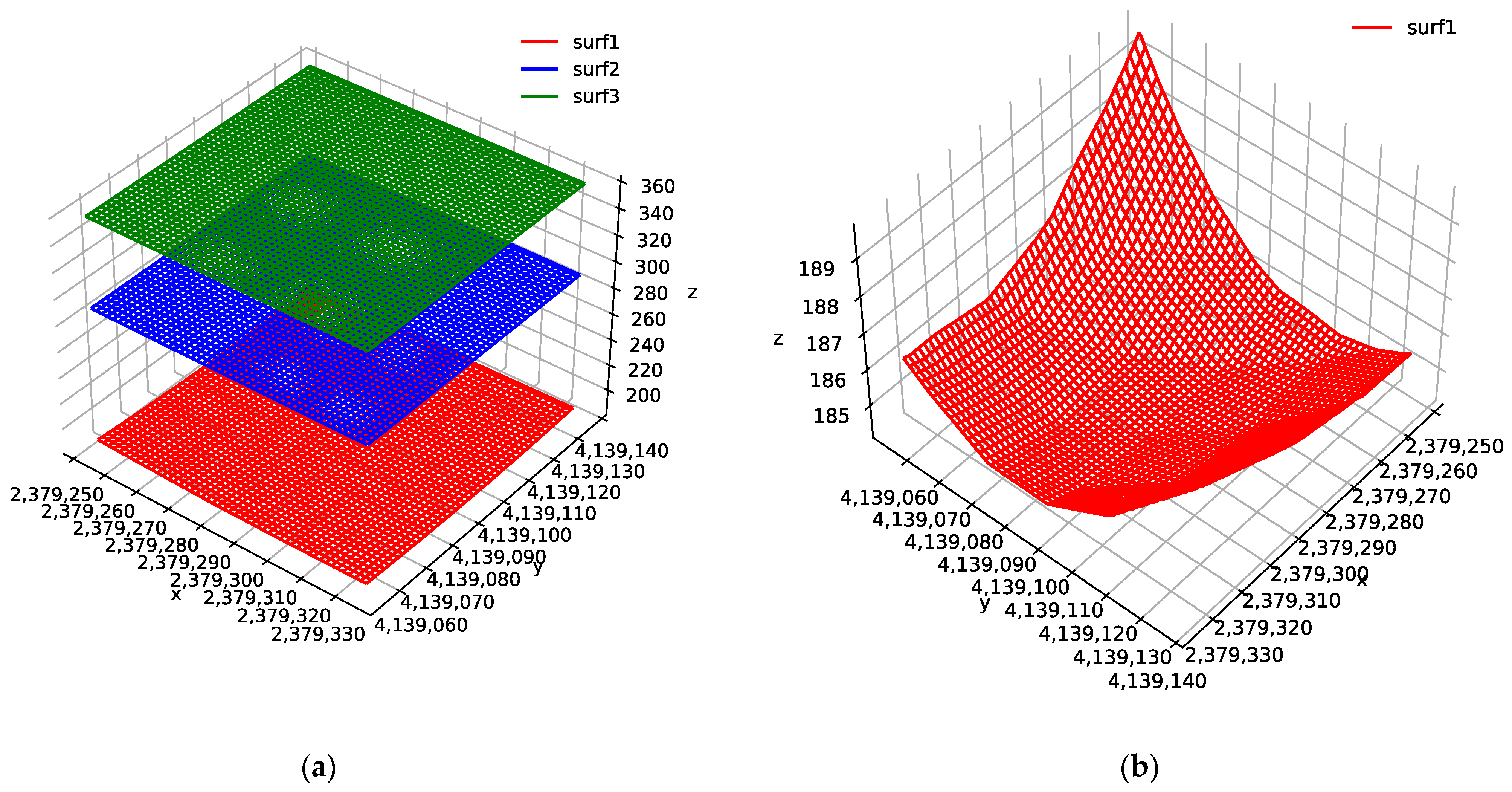
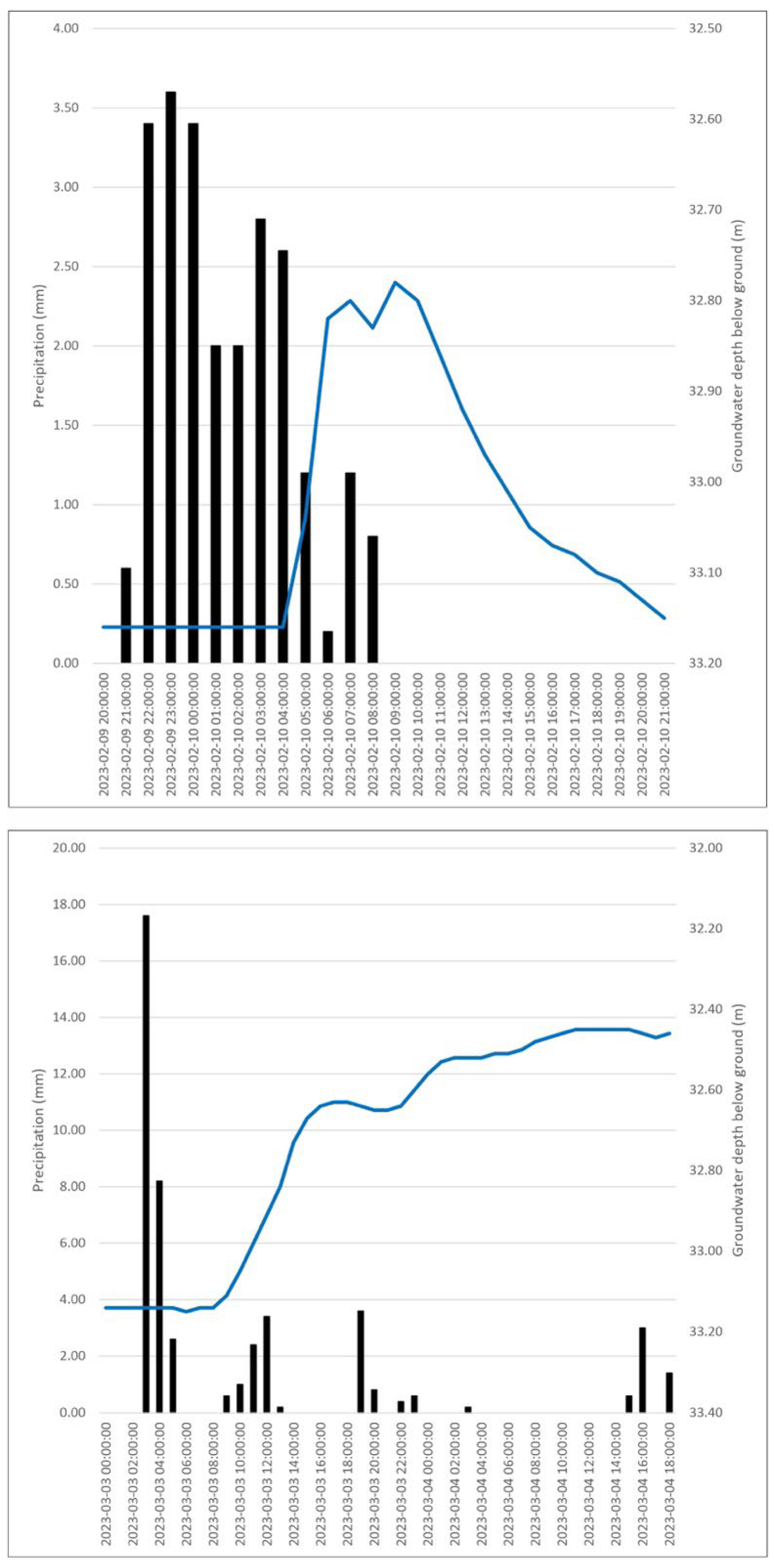
4.1. Morphology of the Bottom Aquitard
4.2. Hydrogeological Model
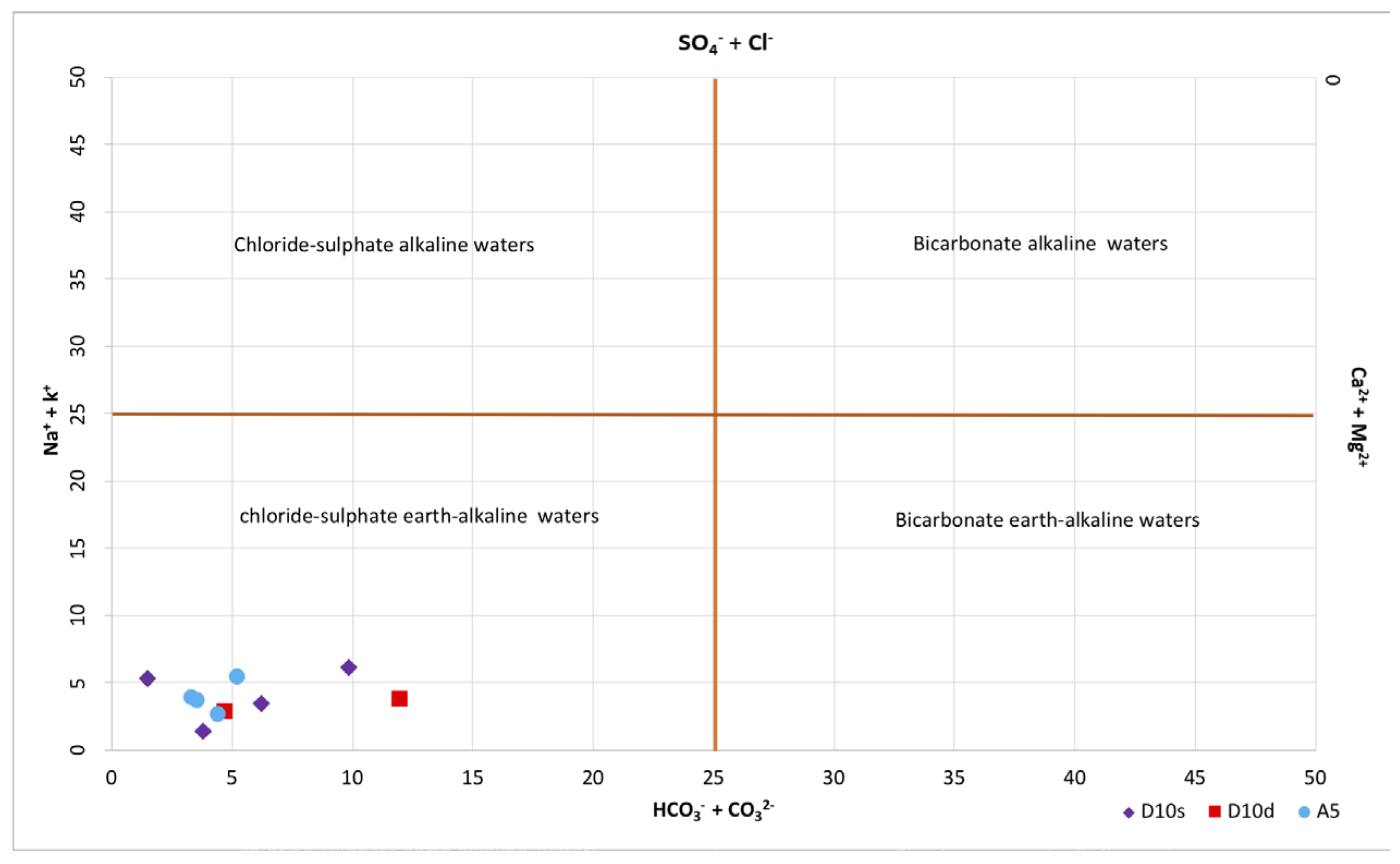
4.3. Hydrochemical Features
4.4. Microbial Communities
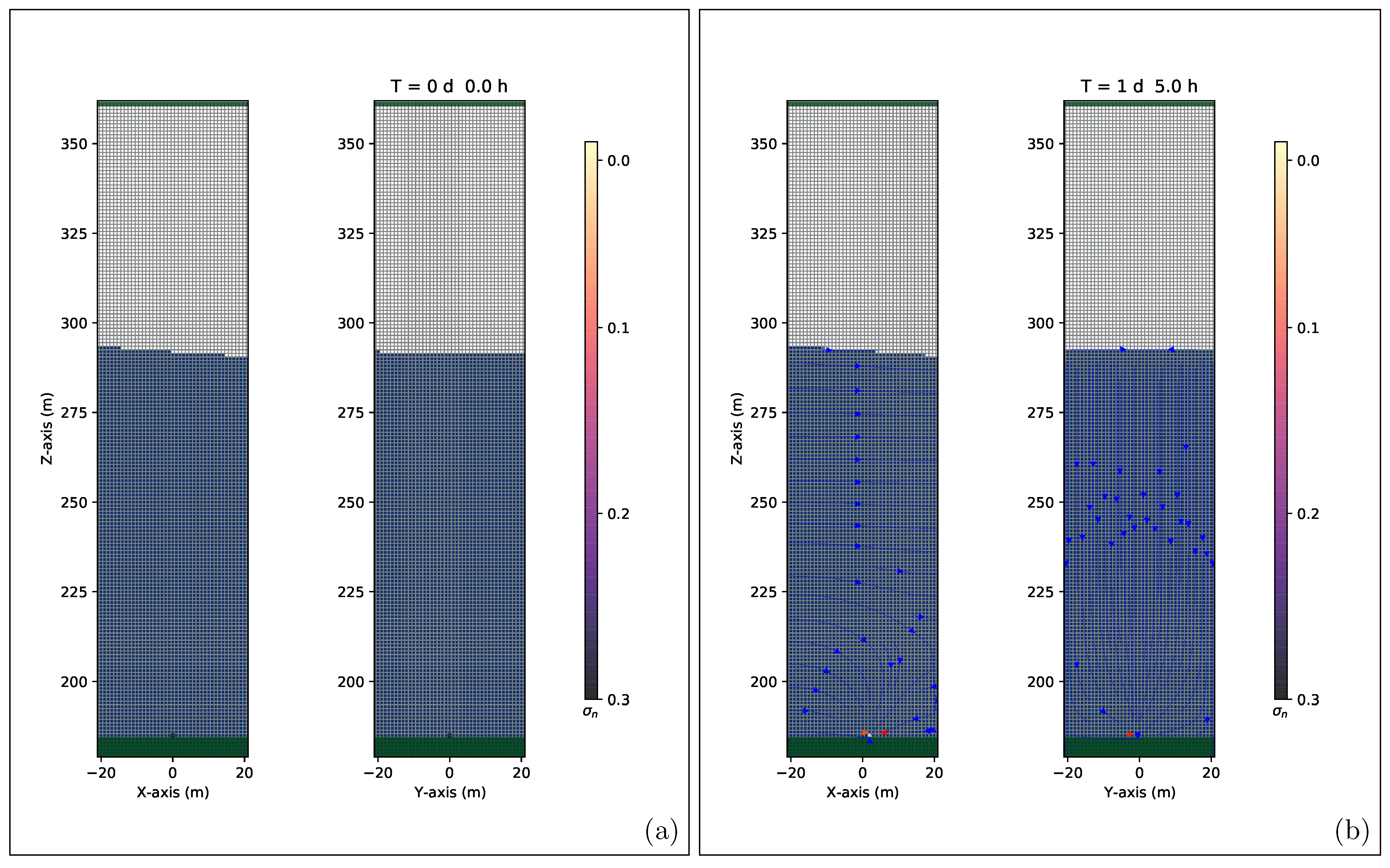
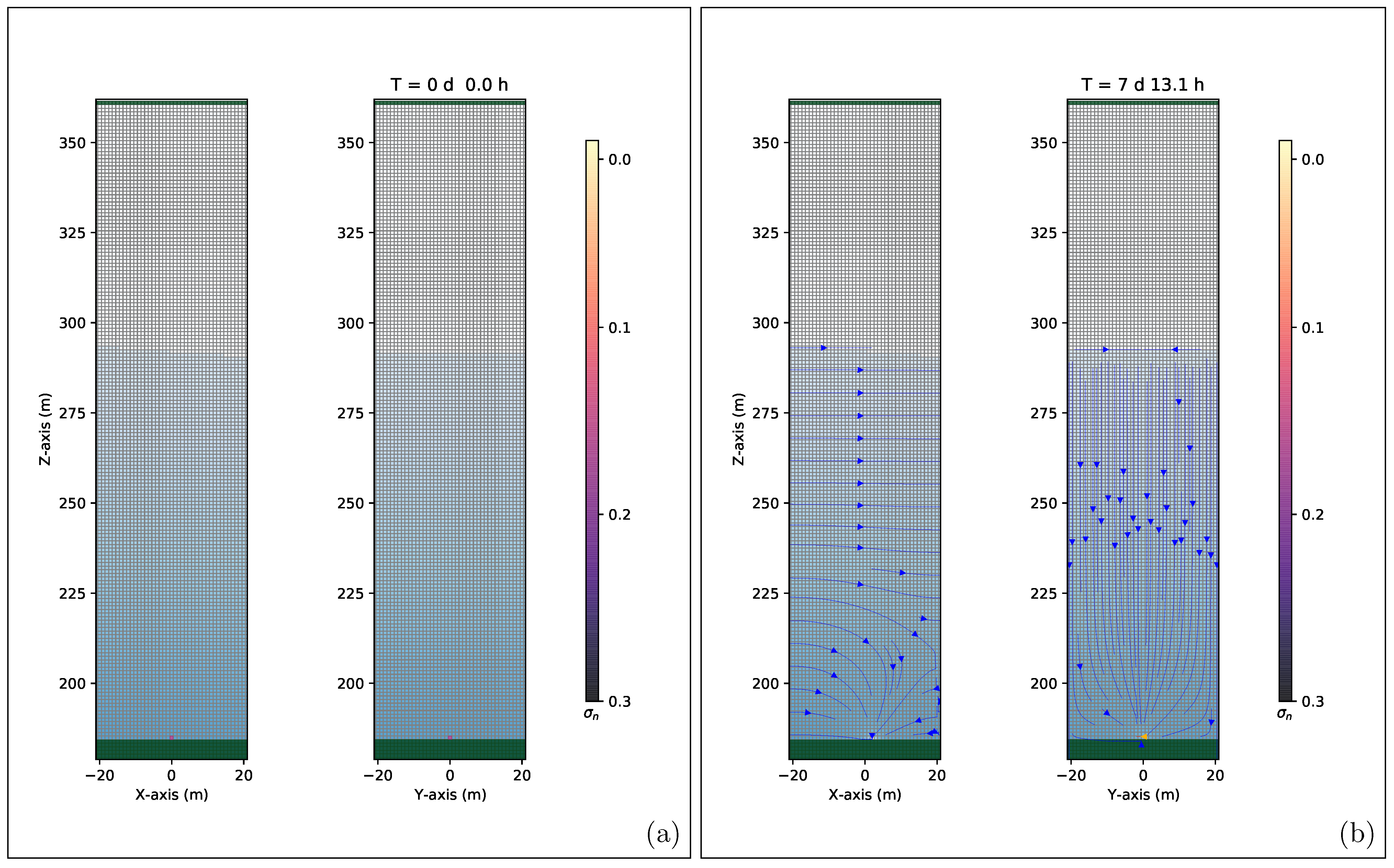
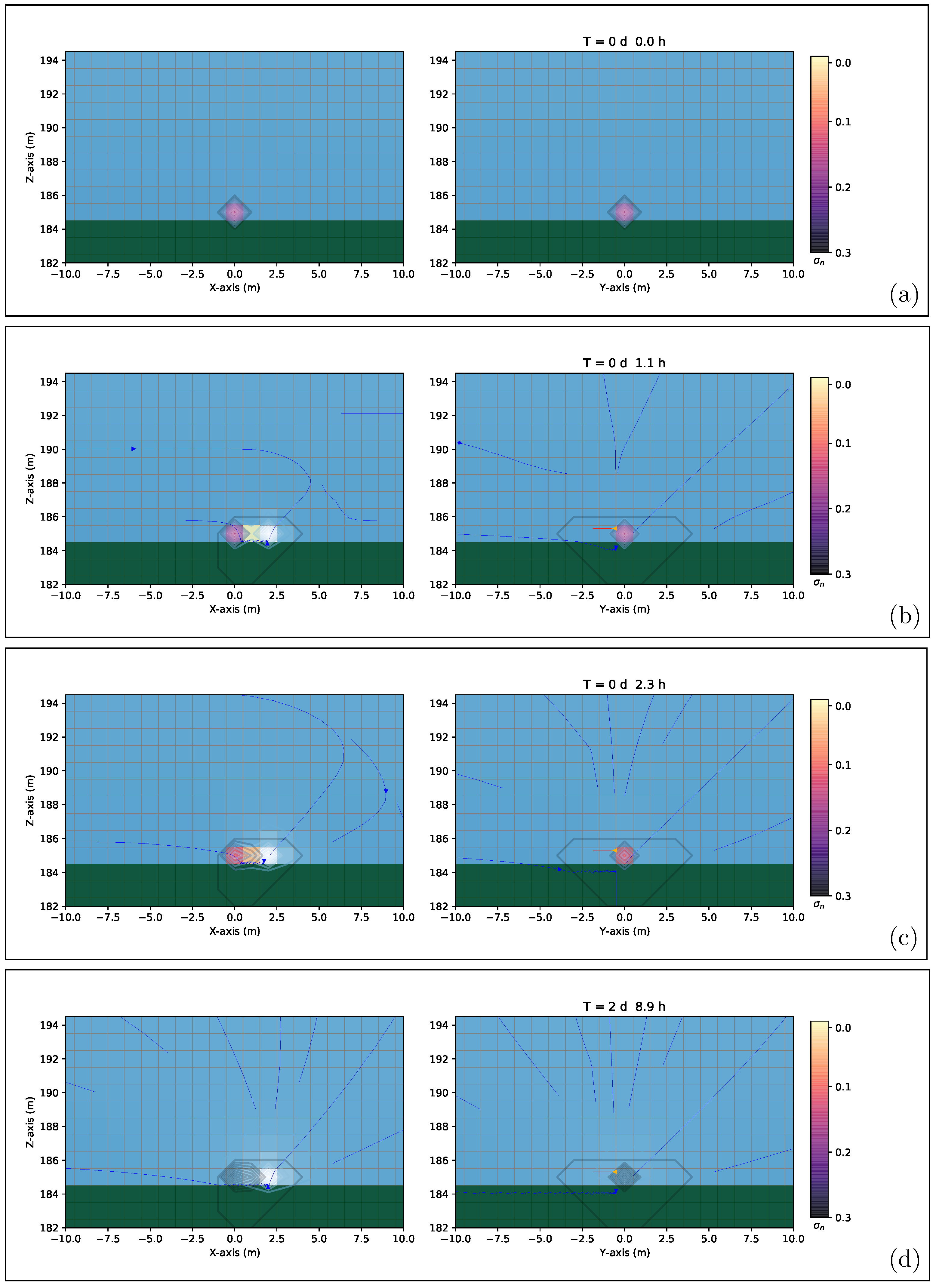
4.5. 3D High-Precision Numerical Simulations Results
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mercer, J.W.; Cohen, R.M. A review of immiscible fluids in the subsurface: Properties, models, characterization and remediation. J. Contam. Hydrol. 1990, 6, 107–163. [Google Scholar] [CrossRef]
- Henschler, D. Toxicity of chlorinated organic compounds: Effects of the introduction of chlorine in organic molecules. Angew. Chem. 1994, 33, 1920–1935. [Google Scholar] [CrossRef]
- Volpe, A.; Del Moro, G.; Rossetti, S.; Tandoi, V.; Lopez, A. Remediation of PCE-contaminated groundwater from an industrial site in southern Italy: A laboratory-scale study. Process Biochem. 2007, 42, 1498–1505. [Google Scholar] [CrossRef]
- Lyman, W.; Reehl, W.; Rosenblatt, D. Handbook of Chemical Properties Estimation Methods-Environmental Behavior of Organic Compound; McGraw-Hill: New York, NY, USA, 1982. [Google Scholar]
- Mackay, D.; Roberts, P.; Cherry, J. Transport of organic contaminants in groundwater. Environ. Sci. Technol. 1985, 19, 384–392. [Google Scholar] [CrossRef] [PubMed]
- Parker, J.C.; Lenhard, R.J.; Kuppusamy, T. A parametric model for constitutive properties governing multi-phase flow in porous media. Water Resour Res. 1987, 23, 618–624. [Google Scholar] [CrossRef]
- Kueper, B.; Frind, E. An overview of immiscible fingering in porous media. J. Contam. Hydrol. 1988, 2, 95–110. [Google Scholar] [CrossRef]
- Kueper, B.; Abbott, W.; Farquhar, G. Experimental observations of multiphase flow in heterogeneous porous media. J. Contam. Hydrol. 1989, 5, 83–95. [Google Scholar] [CrossRef]
- Kueper, B.; Frind, E.O. Two-phase flow in heterogeneous porous media: 2. Model application. Water Resour. Res. 1991, 27, 1059–1070. [Google Scholar] [CrossRef]
- Parker, J. Multiphase flow and transport in porous media. Rev. Geophys. 1989, 27, 311–328. [Google Scholar] [CrossRef]
- Hirata, T.; Muraoka, K. Vertical migration of chlorinated organic compounds in porous media. Water Res. 1988, 22, 481–484. [Google Scholar] [CrossRef]
- Ahmadi, H.; Kilanehei, F.; Nazari-Sharabian, M. Impact of Pumping Rate on Contaminant Transport in Groundwater—A Numerical Study. Hydrology 2021, 8, 103. [Google Scholar] [CrossRef]
- McLaren, R.G.; Sudicky, E.A.; Park, Y.-J.; Illman, W.A. Numerical simulation of DNAPL emissions and remediation in a fractured dolomitic aquifer. J. Contam. Hydrol. 2012, 136, 56–71. [Google Scholar] [CrossRef] [PubMed]
- Guadaño, J.; Gómez, J.; Fernández, J.; Lorenzo, D.; Domínguez, C.M.; Cotillas, S.; García-Cervilla, R.; Santos, A. Remediation of the Alluvial Aquifer of the Sardas Landfill (Sabiñánigo, Huesca) by Surfactant Application. Sustainability 2022, 14, 16576. [Google Scholar] [CrossRef]
- Zhou, J.; Song, B.; Yu, L.; Xie, W.; Lu, X.; Jiang, D.; Kong, L.; Deng, S.; Song, M. Numerical Research on Migration Law of Typical Chlorinated Organic Matter in Shallow Groundwater of Yangtze Delta Region. Water 2023, 15, 1381. [Google Scholar] [CrossRef]
- Zheng, C.; Wang, P.P. MT3DMS: A Modular Three-Dimensional Multispe-cies Transport Model for Simulation of Advection, Dispersion, and Chemical Reactions of Contaminants in Groundwater Systems. In Documentation and User’s Guide; No. SERDP-99-1; U.S. Army Engineer Research and Development Center: Vicksburg, MS, USA, 1999. [Google Scholar]
- Anderson, M.R.; Johnson, R.L.; Pankow, J.K. Dissolution of Dense Chlorinated Solvents into Groundwater. 3. Modeling Contaminant Plumes from Fingers and Pools of Solvent. Environ. Sci. Technol. 1992, 26, 901–908. [Google Scholar] [CrossRef]
- Johnson, R.L.; Pankov, J.F. Dissolution of Dense Chlorinated Solvents into Groundwater. 2. Source Functions for Pools of Solvent. Environ. Sci. Technol. 1992, 26, 896–901. [Google Scholar] [CrossRef]
- Roy, J.W.; Smith, J.E.; Gillham, R.W. Laboratory evidence of natural remobilization of multicomponent DNAPL pools due to dissolution. J. Contam. Hydrol. 2004, 74, 145–161. [Google Scholar] [CrossRef]
- Seagren, E.A.; Rittmann, B.E.; Valocchi, A.J. An experimental investigation of NAPL pool dissolution enhancement by flushing. J. Contam. Hydrol. 1999, 37, 111. [Google Scholar] [CrossRef]
- Chrysikopoulos, C.V.; Voudrias, E.A.; Fyrillas, M.M. Modeling of contaminant transport resulting from dissolution of nonaqueous phase liquid pools in saturated porous media. Transp. Porous Med. 1994, 16, 125–145. [Google Scholar] [CrossRef]
- Chrysikopoulos, C.V. Three-dimensional analytical models of contaminant transport from nonaqueous phase liquid pool dissolution in saturated subsurface formation. Water Resour. Res. 1995, 31, 1137–1145. [Google Scholar] [CrossRef]
- Kenneth, Y.L.; Chrysikopoulos, C.V. Dissolution of a multicomponent of DNAPL pool in an experimental aquifer. J. Hazard. Mater. 2006, B128, 218–226. [Google Scholar]
- Soga, K.; Page, J.W.E.; Illangasekare, T.H. A review of NAPL source zone remediation efficiency and the mass flux approach. J. Hazard. Mater. 2014, 110, 13–27. [Google Scholar] [CrossRef] [PubMed]
- Essaid, H.; Bekins, B.A.; Cozzarelli, I.M. Organic contaminant transport and fate in the subsurface: Evolution of knowledge and understanding. Water Resour. Res. 2015, 51, 4861–4902. [Google Scholar] [CrossRef]
- Praseeja, A.V.; Sajikumar, N. A review on the study of immiscible fluid flow in unsaturated porous media: Modeling and remediation. J. Porous Media 2019, 22, 889–922. [Google Scholar] [CrossRef]
- Ahmed, M.; Saleem, M.R.; Zia, S.; Qamar, S. Central Upwind Scheme for a Compressible Two-Phase Flow Model. PLoS ONE 2015, 10, e0126273. [Google Scholar] [CrossRef] [PubMed]
- Pandare, A.K.; Waltz, J.; Bakosi, J. A reconstructed discontinuous Galerkin method for multi-material hydrodynamics with sharp interfaces. Int. J. Numer. Methods Fluids 2020, 92, 874–889. [Google Scholar] [CrossRef]
- Kuchařík, M.; Liska, R.; Steinberg, S.; Wendroff, B. Optimally-stable second-order accurate difference schemes for non-linear conservation laws in 3D. Appl. Numer. Math. 2006, 56, 589–607. [Google Scholar] [CrossRef]
- Feo, A.; Celico, F. High-resolution shock-capturing numerical simulations of three-phase immiscible fluids from the unsaturated to the saturated zone. Sci. Rep. 2021, 11, 5212. [Google Scholar] [CrossRef]
- Feo, A.; Celico, F. Investigating the migration of immiscible contaminant fluid flow in homogeneous and heterogeneous aquifers with high-precision numerical simulations. PLoS ONE 2022, 17, e0266486. [Google Scholar] [CrossRef]
- Kurganov, A.; Tadmor, E. New high-resolution central scheme for non-linear conservation laws and convection-diffusion equations. J. Comput. Phys. 2000, 160, 241–282. [Google Scholar] [CrossRef]
- Lax, P.; Wendroff, B. Systems of conservation laws. Commun. Pure Appl. Math. 1960, 3, 217–237. [Google Scholar] [CrossRef]
- Hou, T.Y.; LeFloch, P.G. Why nonconservative schemes converge to wrong solutions: Error analysis. Math. Comp. 1994, 62, 497–530. [Google Scholar] [CrossRef]
- Feo, A.; Celico, F.; Zanini, A. Migration of DNAPL in Saturated Porous Media: Validation of High-Resolution Shock-Capturing Numerical Simulations through a Sandbox Experiment. Water 2023, 15, 1471. [Google Scholar] [CrossRef]
- Feo, A.; Pinardi, R.; Scanferla, E.; Celico, F. How to Minimize the Environmental Contamination Caused by Hydrocarbon Releases by Onshore Pipelines: The Key Role of a Three-Dimensional Three-Phase Fluid Flow Numerical Model. Water 2023, 15, 1900. [Google Scholar] [CrossRef]
- Feo, A.; Pinardi, R.; Artoni, A.; Celico, F. Three-Dimensional High-Precision Numerical Simulations of Free-Product DNAPL Extraction in Potential Emergency Scenarios: A Test Study in a PCE-Contaminated Alluvial Aquifer (Parma, Northern Italy). Sustainability 2023, 15, 9166. [Google Scholar] [CrossRef]
- Pinardi, R.; Feo, A.; Ruffini, A.; Celico, F. Purpose-Designed Hydrogeological Maps for Wide Interconnected Surface–Groundwater Systems: The Test Example of Parma Alluvial Aquifer and Taro River Basin (Northern Italy). Hydrology 2023, 10, 127. [Google Scholar] [CrossRef]
- Allen, G.; Goodale, T.; Lanfermann, G.; Radke, T.; Rideout, D.; Thornburg, J. Cactus Users’ Guide. 2011. Available online: http://www.cactuscode.org/documentation/UsersGuide.pdf (accessed on 1 January 2023).
- Cactus Developers. Cactus Computational Toolkit. Available online: http://www.cactuscode.org (accessed on 1 January 2023).
- Goodale, T.; Allen, G.; Lanfermann, G.; Massó, J.; Radke, T.; Seidel, E.; Shalf, J. The Cactus Framework and Toolkit: Design and Applications. In Vector and Parallel Processing—VECPAR’2002, Proceedings of the 5th International Converence, Porto, Portugal, 26–28 June 2002; Lecture Notes in Computer Science; Springer: Berlin, Germany, 2003; Available online: http://edoc.mpg.de/3341 (accessed on 1 January 2023).
- Schnetter, E.; Hawley, S.H.; Hawke, I. Evolutions in 3D numerical relativity using fixed mesh refinement. Class. Quantum Gravity 2004, 21, 1465–1488. [Google Scholar] [CrossRef]
- Schnetter, E.; Diener, P.; Dorband, E.N.; Tiglio, M. A multi-block infrastructure for three-dimensional time-dependent numerical relativity. Class. Quantum Gravity 2006, 23, S553. [Google Scholar] [CrossRef]
- Gugliotta, C.; Gasparo Morticelli, M.; Avellone, G.; Agate, M.; Barchi, M.R.; Albanese, C.; Valenti, V.; Catalano, R. Middle Miocene—Early Pliocene wedge-top basins of North-Western Sicily (Italy). Constraints for the tectonic evolution of a “non-conventional” thrust belt, affected by transpression. J. Geol. Soc. Lond. 2014, 171, 211–226. [Google Scholar] [CrossRef]
- Catalano, R.; Valenti, V.; Albanese, C.; Accaino, F.; Sulli, A.; Tinivella, U.; Gasparo Morticelli, M.; Zanolla, C.; Giustiniani, M. Sicily’s fold/thrust belt and slab rollback: The SI. RI.PRO. seismic crustal transect. J. Geol. Soc. Lond. 2013, 170, 451–464. [Google Scholar]
- Cappadonia, C.; Coratza, P.; Agnesi, V.; Soldati, M. Malta and Sicily joined by geoheritage enhancement and geotourism within the framework of land management and development. Swiss. J. Geosci. 2018, 8, 253. [Google Scholar] [CrossRef]
- Milani, C.; Hevia, A.; Foroni, E.; Duranti, S.; Turroni, F.; Lugli, G.A.; Sanchez, B.; Martín, R.; Gueimonde, M.; van Sinderen, D.; et al. Assessing the Fecal Microbiota: An Optimized Ion Torrent 16S rRNA Gene-Based Analysis Protocol. PLoS ONE 2013, 8, e68739. [Google Scholar] [CrossRef]
- Caporaso, J.G.; Kuczynski, J.; Stombaugh, J.; Bittinger, K.; Bushman, F.D.; Costello, E.K.; Fierer, N.; Gonzalez Peña, A.; Goodrich, J.K.; Gordon, J.I.; et al. QIIME allows analysis of high-throughput community sequencing data. Nat. Methods 2010, 7, 335–336. [Google Scholar] [CrossRef]
- Callahan, B.J.; McMurdie, P.J.; Rosen, M.J.; Han, A.W.; Johnson, A.J.; Holmes, S.P. DADA2: High-resolution sample inference from Illumina amplicon data. Nat. Methods 2016, 13, 581–583. [Google Scholar] [CrossRef]
- Bokulich, N.A.; Kaehler, B.D.; Rideout, J.R.; Dillon, M.; Bolyen, E.; Knight, R.; Huttley, G.A.; Caporaso, G.J. Optimizing taxonomic classification of marker-gene amplicon sequences with QIIME 2′s q2-feature-classifier plugin. Microbiome 2018, 6, 90. [Google Scholar] [CrossRef]
- Quast, C.; Pruesse, E.; Yilmaz, P.; Gerken, J.; Schweer, T.; Yarza, P.; Peplies, J.; Glöckner, F.O. The SILVA ribosomal RNA gene database project: Improved data processing and web-based tools. Nucleic Acids Res. 2012, 41, 590–596. [Google Scholar] [CrossRef] [PubMed]
- Freeze, R.A.; Cherry, J.A. Groundwater Book; Prentice-Hall Inc.: Englewood Cliffs, NJ, USA, 1979. [Google Scholar]
- Van Genuchten, M.T. A closed form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Yu-Shu, W. Multiphase Fluid Flow in Porous and Fractured Reservoirs; Elsevier: Oxford, UK, 2015; p. 243. [Google Scholar]
- Rizzo, P.; Cappadonia, C.; Rotigliano, E.; Iacumin, P.; Sanangelantoni, A.M.; Zerbini, G.; Celico, F. Hydrogeological behaviour and geochemical features of waters in evaporite-bearing low-permeability successions: A case study in Southern Italy. Appl. Sci. 2020, 10, 8177. [Google Scholar] [CrossRef]
- Zaa, C.L.Y.; McLean, J.E.; Dupont, R.R.; Norton, J.M.; Sorensen, D.L. Dechlorinating and iron reducing bacteria distribution in a TCE-contaminated aquifer. Groundw. Monit. Remediat. 2010, 30, 46–57. [Google Scholar] [CrossRef]
- Della-Negra, O.; Chaussonnerie, S.; Fonknechten, N.; Barbance, A.; Muselet, D.; Martin, D.E.; Fouteau, S.; Fischer, C.; Saaidi, P.-L.; Le Paslier, D. Transformation of the recalcitrant pesticide chlordecone by Desulfovibrio sp. 86 with a switch from ring-opening dechlorination to reductive sulfidation activity. Sci. Rep. 2020, 10, 13545. [Google Scholar] [CrossRef]
- Wolterink, A.; Kim, S.; Muusse, M.; Kim, I.S.; Roholl, P.J.; van Ginkel, C.G.; Stams, A.J.M.; Kengen, S.W. Dechloromonas hortensis sp. nov. and strain ASK-1, two novel (per) chlorate-reducing bacteria, and taxonomic description of strain GR-1. Int. J. Syst. Evol. Microbiol. 2005, 55, 2063–2068. [Google Scholar] [CrossRef] [PubMed]

| Parameter | Symbol | Value |
|---|---|---|
| Absolute permeability (max) | ||
| Rock compressibility | ||
| Porosity (max) | ||
| Water viscosity | ||
| Water density | ||
| DNAPL viscosity | ||
| DNAPL density | ||
| Air viscosity | ||
| Air density | ||
| Van Genuchten | ||
| Irreducible wetting phase saturation (min) | ||
| Surface tension of air–water | ||
| Interfacial tension nonaqueous water | ||
| Capillary pressure of air–water at zero saturation | ||
| Capillary pressure of air–nonaqueous phase at zero saturation |
| Parameter | Symbol | Value |
|---|---|---|
| Absolute permeability (min) | ||
| Rock compressibility | ||
| Porosity (min) | ||
| Water viscosity | ||
| Water density | ||
| DNAPL viscosity | ||
| DNAPL density | ||
| Air viscosity | ||
| Air density | ||
| Van Genuchten | ||
| Irreducible wetting phase saturation (max) | ||
| Surface tension of air–water | ||
| Interfacial tension nonaqueous water | ||
| Capillary pressure of air–water at zero saturation | ||
| Capillary pressure of air–nonaqueous phase at zero saturation |
| Average | Median | Min | Max | D.ST. | 25Q | 75Q | 10P | 90P | C.V | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| A5 | T | 20.16 | 20.8 | 16.50 | 23.2 | 2.07 | 19.2 | 21.20 | 17.30 | 21.68 | 971.67 |
| pH | 6.97 | 7.24 | 6.18 | 7.48 | 0.49 | 6.44 | 7.32 | 6.37 | 7.36 | 1426.26 | |
| Eh | 312.67 | 189 | 46.90 | 1572 | 479.08 | 100 | 239.10 | 55.22 | 522.24 | 65.26 | |
| Ec | 3.50 | 2.364 | 0.70 | 9.937 | 2.82 | 1.63 | 4.03 | 1.42 | 6.36 | 124.06 | |
| D10 | T | 19.88 | 20.1 | 16.10 | 22.8 | 1.75 | 19.8 | 20.50 | 18.42 | 20.96 | 1133.66 |
| pH | 7.26 | 7.06 | 6.68 | 8.34 | 0.54 | 6.99 | 7.32 | 6.87 | 7.97 | 1334.70 | |
| Eh | 254.28 | 130.9 | 51.00 | 522.5 | 188.34 | 109.1 | 427.60 | 70.28 | 451.22 | 135.01 | |
| Ec | 3.37 | 3.50 | 1.82 | 5.308 | 1.04 | 2.68 | 3.73 | 2.36 | 4.26 | 322.92 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feo, A.; Lo Medico, F.; Rizzo, P.; Morticelli, M.G.; Pinardi, R.; Rotigliano, E.; Celico, F. How to Predict the Efficacy of Free-Product DNAPL Pool Extraction Using 3D High-Precision Numerical Simulations: An Interdisciplinary Test Study in South-Western Sicily (Italy). Hydrology 2023, 10, 143. https://doi.org/10.3390/hydrology10070143
Feo A, Lo Medico F, Rizzo P, Morticelli MG, Pinardi R, Rotigliano E, Celico F. How to Predict the Efficacy of Free-Product DNAPL Pool Extraction Using 3D High-Precision Numerical Simulations: An Interdisciplinary Test Study in South-Western Sicily (Italy). Hydrology. 2023; 10(7):143. https://doi.org/10.3390/hydrology10070143
Chicago/Turabian StyleFeo, Alessandra, Federica Lo Medico, Pietro Rizzo, Maurizio Gasparo Morticelli, Riccardo Pinardi, Edoardo Rotigliano, and Fulvio Celico. 2023. "How to Predict the Efficacy of Free-Product DNAPL Pool Extraction Using 3D High-Precision Numerical Simulations: An Interdisciplinary Test Study in South-Western Sicily (Italy)" Hydrology 10, no. 7: 143. https://doi.org/10.3390/hydrology10070143
APA StyleFeo, A., Lo Medico, F., Rizzo, P., Morticelli, M. G., Pinardi, R., Rotigliano, E., & Celico, F. (2023). How to Predict the Efficacy of Free-Product DNAPL Pool Extraction Using 3D High-Precision Numerical Simulations: An Interdisciplinary Test Study in South-Western Sicily (Italy). Hydrology, 10(7), 143. https://doi.org/10.3390/hydrology10070143












