Abstract
This study demonstrates an approach to estimate the background value of nitrate as a basis for better groundwater management and protection in areas under long-term human impact. The aim was to determine the ambient background value (ABV) of nitrate in the catchment area of the Velika Gorica well field, a hydrogeologically homogeneous area within the Zagreb aquifer. ABVs are determined using four well-known model-based objective methods (the iterative 2-σ technique, IT; the calculated distribution function, CDF; the cumulative frequency curve, CFC; and the probability plot, PP), while simultaneously testing the reliability of the results of each method. If the results are not statistically significant, data selection is performed. The results show that using data without selection can lead to statistically non-significant ABVs, but with the additional selection of data, a statistically non-significant result became a statistically significant one. In summary, all final ABVs must be statistically significant and determined using as large a data set as possible. Reducing the size of the data set is acceptable only in the case of a statistically non-significant result.
1. Introduction
Groundwater presents the most common and valuable source of drinking and irrigation water in the world [1]. Sustainable management of water and sanitation for the world population is one of the main goals established by the United Nations under the Sustainable Development Goals [2]. A large amount of research has been focused on the evaluation of groundwater quality, which has been diminished by different pollutants [1,3,4,5,6], while others emphasize the importance of implementing measures that will slow down the deterioration of water bodies [7,8,9]. Nitrate pollution of groundwater is one of the main environmental issues worldwide [10,11,12,13,14,15,16,17,18] and nitrate’s increasing trend in natural waters has made it a contaminant of concern [4,19,20]. Burkart and Kolpin [21] have shown that a nitrate concentration greater than 13 mg/L as NO3− in groundwater is a sign of natural groundwater quality degradation due to anthropogenic activities. In order to be sure that groundwater pollution is present, it is important to distinguish between geogenic and anthropogenic influences on groundwater quality by the estimation of geochemical background values that reflect natural processes [22]. Estimating the natural background value in groundwater enables us to recognize the concentration of the geochemical compound that is free from human influence [23]. The Groundwater Directive (2006/118/EC) introduced the term “background value” as “the concentration of a substance or the value of an indicator in a body of groundwater corresponding to no, or only very minor, anthropogenic alterations to undisturbed conditions”. Due to the ubiquitous human influence, which is also reflected in the chemical composition of groundwater, the natural composition of groundwater, especially in shallow aquifers, almost does not exist today. Since, in many parts of the world, human influence on the environment has been present for such a long time that it is futile to try to determine the natural background concentrations of substances in groundwater, Reiman and Garrett [24] devised the concept of the ambient background value (ABV), which describes an immeasurably disturbed and no longer intact background concentration of substances in groundwater. Because background values are location- and scale-dependent, i.e., they change regionally as well as locally [24], it is necessary to divide data sets into homogeneous groups to increase the probability of detecting an environmental problem. Sometimes, it is very difficult to clearly identify the populations related to the background processes as opposed to those reflecting contamination [25,26,27,28]. It has been shown that areas that are unaffected by human activities typically have natural background values of nitrate that do not exceed 5–10 mg/L as NO3− [29].
Many researchers are using approaches based on the analysis of the distribution of many measured data using different statistical methods [30,31,32]. It has been shown that probability density functions can be different in background and anomalous samples, but the main issue is how to recognize these differences with confidence [33]. Although model-based subjective methods of background determination that include the mean plus two standard deviations are the best for data that follow a normal distribution and were frequently used, they are far from ideal when used for regional geochemical data [33]. The problem arises from the fact that the samples represent more than one population or process, resulting in multimodal distribution, where the use of the mean can give overestimated values [34]. On the contrary, model-based objective methods of background determination differ from subjective methods in that the background values and the upper limit of background range, i.e., threshold values, are defined by the data themselves, rather than by an arbitrary decision of the researcher. Recently, model-based objective methods have been gaining more and more importance. They are based on the division of a complete set of measured data into subgroups with characteristic probability density functions that reflect relevant natural geochemical processes and/or pollution events in an area. Background populations can be approximated by normal or lognormal density functions, while different processes have produced an anomalous population that differs from the background [33]. In recent decades, various model-based objective methods (the iterative 2-σ technique, the calculated distribution function, the cumulative frequency curve, and the probability plot) and their combinations have been used worldwide to determine background concentrations and threshold values [29,35,36,37,38,39,40,41]. Furthermore, there are also other statistical approaches. For example, the lithology of aquifers was used to define the natural background values of different chemical parameters in six EU countries [42]. In some cases, natural background values of selected species were estimated by means of the pre-selection and the component separation method [23]. Other studies combined pre-selection methods and statistical approaches [26,43,44,45].
The groundwater of the Zagreb aquifer is threatened due to increasing concentrations of pollutants and decreasing water quantity. Nitrates have been recognized as one of the most common groups of contaminants in the Zagreb aquifer [22], which is designated as a vulnerable area to nitrates, due to agricultural activities, especially on the right bank of the Sava River. Thus far, the elevated nitrate concentrations have been confirmed by various studies [22,46,47], while recent research was focused on the determination of areas with the highest risk for nitrate contamination [48], the definition of nitrate origin [49], the estimation of nitrate trends [50], and the in situ monitoring of multiple soil horizons in Eutric Cambisols at the Velika Gorica site [51]. Furthermore, it has been shown that nitrate concentrations present one of the most heterogeneous pieces of data, which is due to the pronounced anthropogenic influence in different parts of the Zagreb aquifer [52]. The concept of ABVs was implemented by Nakić et al. [25] and Kovač [52] to calculate the ABVs of nitrate in the groundwater of an alluvial aquifer in the Zagreb area. The upper limit of the ABV for the Zagreb aquifer ranged from 4.5 to 10.7 mg/L. Due to the obvious human influence and heterogeneity of the Zagreb aquifer, four different methods (the iterative 2-σ technique, IT; the calculated distribution function, CDF; the cumulative frequency curve, CFC; and the probability plot, PP), which belong to the model-based objective methods, were used to estimate the ABV of nitrate in the catchment area of the Velika Gorica well field, which is located in the southern part of the Zagreb aquifer and complies with the principle of hydrogeological homogeneity. We are referring here to the results of research by a group of authors [53] who revealed that the background concentrations of substances, determined at the level of the regional aquifer, can significantly differ from the background concentrations of the same substances, determined in homogeneous areas within the same aquifer. The importance of applying the principle of homogeneity when determining background concentrations for substances that are sensitive to changes in oxidation-reduction conditions in the subsoil is emphasized by Molinari et al. [43], while Matschullat et al. [40] emphasize that the geochemical background concentration of a chemical substance needs to be determined in spatial conditions that are characterized by homogeneous, mainly climatological, lithological, and pedological features. The objectives of this study are (a) to modify the graphical interpretation of used methods to reduce subjectivity in determining a background value, (b) to show the differences in results when estimating ABVs using all data without selection compared to selected non-normally distributed (NON-ND) data, and (c) to evaluate the reliability of used methods in the anthropogenically influenced area.
2. Study Area
The Zagreb aquifer is situated in the north-western part of the Republic of Croatia along the Sava River, between the Medvednica Mountain in the north and the hills of Vukomeričke Gorice in the south. It is an unconfined aquifer composed of unconsolidated Quaternary sediments consisting mainly of sand, gravel and silt or silty clays and covers an area of approximately 350 km2. The research area is located in the southern part of the Zagreb aquifer (Figure 1). The average annual precipitation for the period 2001 to 2020 is 967 mm. Precipitation is evenly distributed throughout the year, with a monthly average of around 80 mm. The annual average air temperature ranges from 10.5 °C to 12.7 °C, with a minimum in January and a maximum in July (Figure 2).
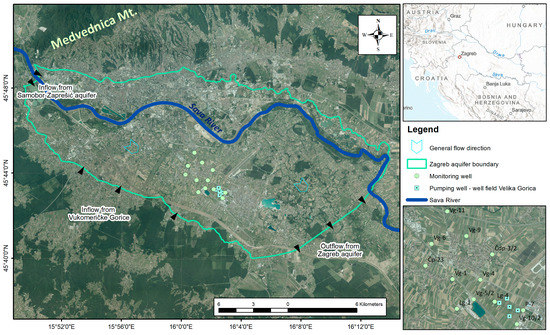
Figure 1.
Research area.
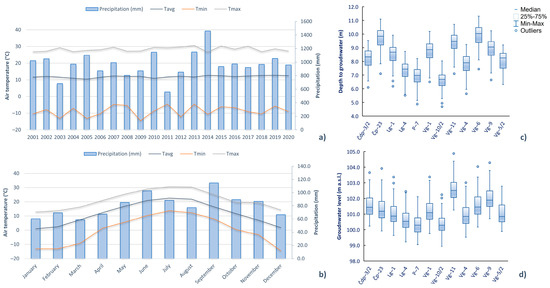
Figure 2.
The annual precipitation (a) and the average monthly precipitation (b) with average, minimum and maximum air temperature; depth to groundwater (c) and groundwater levels (d) for the period 2001 to 2020.
Quaternary sediments were deposited during the Middle and Upper Pleistocene and the Holocene [54]. The shallow layer contains Holocene alluvial deposits of the Sava River, while the deep layer contains Pleistocene lacustrine–marshy deposits [55,56]. The unsaturated zone consists of gravels in the lower part, while the upper part consists mainly of silty to sandy material, interbedded with clay layers in places. The thickness of the unsaturated zone varies from two to eleven meters [57].
The shallow aquifer is in direct hydraulic connection with the Sava River, which is the main source of groundwater recharge [58,59,60,61]. The groundwater level changes mainly due to water level fluctuations of the Sava River, which recharges the aquifer during high water levels, while it discharges the aquifer during low and medium water levels. Other recharge mechanisms include infiltration from precipitation, infiltration from the porous water supply system and the sewage network, but also the water inflow from the Samobor-Zaprešić aquifer in the west and the water inflow across the southern boundary in the Vukomeričke Gorice area [62]. The general groundwater flow direction concurs with the flow direction of the Sava River from west to east (south-east) (Figure 1). The Zagreb aquifer area consists of three major pedological units: Fluvisols, Stagnosols and Eutric Cambisols on the Holocene deposits [63,64].
The Velika Gorica well field is one of the most important well fields in Zagreb County, supplying drinking water to the City of Zagreb and the City of Velika Gorica. The well field consists of five wells drilled to a depth of 39 m to 50 m, drawing water from the shallow aquifer. Near the well field, there are 12 monitoring wells in an area of approximately 9 km2, generally used to monitor groundwater quality in the shallow aquifer. In this small area, the maximum elevation difference is 7 m. The maximum thickness of the unsaturated zone is 9 to 11 m (Figure 2), and most of the land is used for agriculture, mixed with urban areas. Figure 2c,d show that the depths to groundwater and groundwater level fluctuations are similar for all 12 monitoring wells. According to the results of previous research [65,66,67], the groundwater in the influence area of the Velika Gorica well field belongs to the calcium–magnesium–hydrogen carbonate (CaMgHCO3) water type. All this makes the catchment area of the Velika Gorica well field a hydrogeologically homogeneous area relevant for the determination of background values.
3. Materials and Methods
3.1. Available Data Set
The ABV of nitrate was estimated using groundwater chemical data from the national groundwater quality monitoring program of Croatian Waters. Nitrate concentration data from 12 monitoring wells, located in the catchment area of the Velika Gorica well field, have been used for this purpose. Nitrate data sets of the past twenty years (2001–2020) have been analyzed. The data set included three analyses with limit of quantification (LOQ) or limit of detection (LOD) values, one analysis that was not measured and written as “0”, and 135 analyses with unavailable data. Since only four analyses were recorded as “0” or as below the LOQ/LOD values, it was decided that these data would not be used. After data processing, approximately 944 analyses, out of 1083 chemical analyses, were used for background estimation. For the evaluation of the nitrate concentrations in the Sava River and precipitation, 15-year time series data (2001–2015) were used. Data included 627 analyses from the samples of river water (provided by Croatian Waters) and 1225 analyses from the samples of precipitation (provided by Croatian Meteorological and Hydrological Service).
3.2. Description of Methods
In this work, four well-known model-based objective methods were used to estimate the ABV of nitrate.
The iterative 2-σ technique, IT, and the calculated distribution function method, CDF, have been implemented by the Visual Basic (VB) macro entitled BACKGROUND [25], which calculates the background values of chemical parameters and evaluates threshold values that separate background data from anomalous values. The macro integrates these two methods into a widely accessible platform (i.e., Microsoft Excel) and calculates the normal range of background values with 95% confidence. Both methods aim to define the background and threshold by approaching a normal range. The methods process the measured data (i.e., remove values) until a normal distribution is achieved. Thus, what is left in the normally distributed data are the background values and what has been removed are the non-background values [25,40]. The background values are estimated based on data derived from a population, which amounts to a large proportion of the total data set. Statistical methods include the Lilliefors test [68] for testing the normality of data sets and significance of results. If the test statistic D is smaller than the critical value Dcrit, the result is statistically significant, i.e., the determined distribution of the background values corresponds to the normal distribution, which means that the results are acceptable. If the statistic D is greater than the critical value Dcrit, the result is not statistically significant and the obtained background values are overestimated [25]. The advantage of using these two methods is that their application does not require normally or lognormally distributed data, they can be applied to relatively small data sets (n > 30), and they are applicable to unimodal and skewed distributions. Both methods work well only when the generally prevailing background data are used to define the background populations [25]. The IT is suited for the calculation of the threshold value as the outer limit of background variation and considers both the low and high values to define anomalies. The disadvantage of this method is that it cannot be applied to a polymodal distribution. The CDF method is applicable to the polymodal distributions if the data unaffected by human activities are dominant. The method is convenient for use if anthropogenic influences tend to lead to enrichments in natural systems. The lower values should thus be free from anthropogenic influences [40]. The IT and CDF methods differ in that the IT method can also be applied if it is necessary to determine the lower limit of the background value of some pollution indicator. This is the case for dissolved oxygen, which can be an indicator of extreme oxygen consumption due to groundwater pollution [25]. However, research related to the definition of the natural background values of chemical substances is usually focused on the determination of the upper limit of the background value [38,39,41,69,70].
The cumulative frequency curve, CFC, or Lepeltier’s method [71], is a graphical method that analyzes the cumulative sum on a graph with a logarithmic scale. On the graph constructed in this way, a significant deviation from the lognormal distribution is visible as an abrupt change in the graph, i.e., as a point x where the appearance of the elbow is observed, and all values that are less than or equal to x are the result of the cumulative effect of natural processes that cause significant natural variability [40]. In his original work, Lepeltier suggested cumulating high to low values. The advantage of this method is that it enables the identification of meaningful ABVs for relatively small data sets with a minimum of 50 data [71]. A limitation of using this approach is that care must be taken to avoid the temptation to interpret the visual deviations between natural and anthropogenic populations in the lower part of the curve as significant [30]. This method contains an element of subjectivity due to visual detection and is highly dependent on the experience of the researcher [70].
The probability plot, PP, assumes that different processes generate data with different probability distributions and aims to identify several distributions into distinct components and points that separate them, i.e., the threshold values. If there is a partial overlap of background and non-background distributions, then a change in distribution on the PP can be considered as an inflection point [70]. Inflection points can be identified visually as changes in slope [29], or as an intersection of different trend lines [37]. The concentration at the inflection point is defined as the threshold value, below which all measured values of the substance belong to the background concentrations [33,72]. The advantage of this approach is that it enables the identification of multiple populations on the graph. The limitations of using this method are that a minimum of 100 values is needed and the determination of the threshold represents an estimation procedure, subject to random and systematic error [29,33].
In this paper, the inflection points were identified as the intersection of two “linear” segments, as observed in Rahman et al. [37]. The first inflection point separating the first two subsets is assumed to be ABV, while the first population is considered a natural event. Multiple inflection points on the plots may indicate multiple populations of natural or anthropogenic origin contributing to nitrate concentrations in groundwater [37]. To reduce the subjectivity of visual interpretation, subsets were selected to describe the population with the highest possible coefficient of determination. The minimum number of points in a subset was three and was increased by one point each time until the highest possible coefficient of determination was reached.
The first step was to estimate the ABV for data without prior selection to check the reliability of different methods. If one of the selected methods leads to a statistically non-significant result, data selection is required in the second step and re-estimation of the ABV for selected data in the third step. This is based on the fact that the values of a single normally or lognormally distributed population form a straight line on the cumulative probability plots, without the possibility of determining a background value, whereas the values of more mixed populations lead to a curved line with a pronounced inflection point [29]. Data selection was performed using the Lilliefors test [68] by testing normal distribution. TIBCO StatisticaTM (version 13.5.0.17) was utilized to perform the normality tests, while an alpha value of 0.05 was used as the statistical significance level in all data analyses. The Lilliefors test is an adaptation of the Kolmogorov–Smirnov test and uses the same calculations, but the critical value table in the Lilliefors test table is used instead of the Kolmogorov–Smirnov table, which gives the critical value Dcrit. If the test statistic D is less than the critical value Dcrit, the normal distribution cannot be rejected. Under the condition that the test statistic D is greater than the critical value Dcrit, the normal distribution can be rejected.
All final ABVs must be statistically significant and determined using as large as possible a data set. A statistically significant result obtained in the first step is considered acceptable, while, in case of a statistically non-significant result, data selection is required in order to obtain a statistically significant result.
4. Results and Discussion
The descriptive statistics of nitrate concentrations (presented as mg NO3/L) in groundwater in the catchment area of the Velika Gorica well field and Sava River and the precipitation are reported in Table 1. The nitrate concentration of groundwater ranges from 0.2 to 35.7 mg/L, with a mean value of 19.6 mg/L and a median of 19.5 mg/L. It is worth noting that the average value for each monitoring well does not exceed the maximum permissible level for drinking water (50 mg NO3/L), stipulated by EU and Croatian regulations. Nevertheless, these higher concentrations indicate possible natural groundwater quality degradation, considering that, in areas not affected by human activities, the nitrate concentration in groundwater should be much lower [21]. The mean nitrate concentration in the Sava River, as the main source of recharge in the Zagreb aquifer, recorded in the period from 2001 to 2015, is 6.8 mg/L, with the maximum value of 14.6 mg/L. The mean nitrate concentration in precipitation from 2001 to 2015 is 0.8 mg/L, while the maximum measured concentration is 5.2 mg/L. Due to the low nitrate concentrations in precipitation, it can be assumed that precipitation has a very small effect on the nitrate content in the Zagreb aquifer [52]. Furthermore, it has been shown that the local meteoric water line of the Ljubljana area (Slovenia) better describes the stable isotopic composition of groundwater from the Zagreb aquifer than the local meteoric water line of the Zagreb area [22,49,59,73]. This confirms that the Sava River is the main source of recharge of the Zagreb aquifer, since the source of the river water is the precipitation that falls in Slovenia.

Table 1.
Main statistics for nitrate in mg/L = milligram per liter as NO3. SD is standard deviation, CV is coefficient of variation in %, N is number of samples.
First, the ABV of nitrate was estimated in groundwater for data without selection referring to all monitoring wells, using four different methods (Figure 3). The inflection points were determined according to the principle of the highest possible coefficient of determination using the CFC and PP methods. Estimated values vary from 7.1 to 11.8 mg/L. Usage of the IT method resulted in the highest estimate of the background value, while the CDF method gave a non-statistically significant result. As observed in Nakić et al. [25], if D > Dcrit, the result is not statistically significant and the obtained background values are overestimated. Considering that the application of the CDF method gave a noticeable difference in terms of non-statistically significant results, the second step was data selection, performed using the Lilliefors test and re-estimation of the ABV.
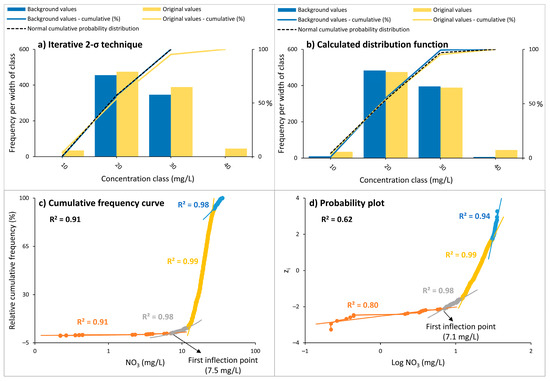
Figure 3.
Four different methods to estimate ABV of nitrate for data without selection: (a) IT: lower background value: 11.8; D < Dcrit, (b) CDF: lower background value: 8.3; D > Dcrit, (c) CFC: background value: 7.5 and (d) PP: background value: 7.1. Arrow indicates first inflection point that separates background and non-background population.
The Lilliefors test was used to test the normality for each well separately (Table 2). This test showed normally distributed data for monitoring wells Vg-11, Vg-4, Vg-6, Vg-9, and Vg-5/2, which are not further considered for the background value estimation procedure in the third step, because, as observed in Panno et al. [29], a single normally or lognormally population forms a straight line on the cumulative probability plots, without the possibility of determining a background value. The data that were not normally distributed (wells Čdp-3/2, Čp-23, Lg-1, Lg-4, P-7, Vg-1 and Vg-10/2) were grouped for further processing as NON-ND data, because it is expected that the cumulative probability plots contain a curved line with at least one inflection point that could indicate the existence of a minimum of two different populations, natural and anthropogenically conditioned. Histograms and normal distribution curves for each well separately are shown in Figure 4.

Table 2.
Lilliefors test of normality. Normally distributed data are bolded (D < Dcrit).
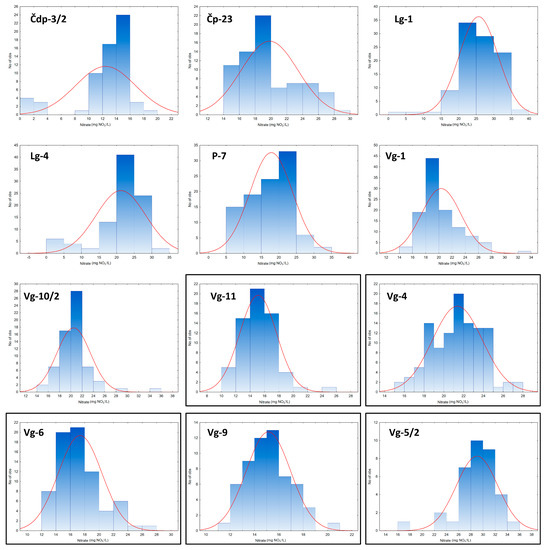
Figure 4.
Histograms and normal distribution curves. Normally distributed data are bolded.
The third step was to re-estimate the ABV of nitrate in groundwater for selected data referring to NON-ND data, using the same methods. The use of selected data resulted in statistically significant results for all methods (Figure 5). It is important to emphasize that the result obtained with data without selection that was not statistically significant became significant.

Figure 5.
Four different methods to estimate ABV of nitrate for selected NON-ND data: (a) IT: lower background value: 13.2; D < Dcrit, (b) CDF: lower background value: 7.2; D < Dcrit, (c) CFC: background value: 7.3 and (d) PP: background value: 6.9. Arrow indicates first inflection point that separates background and non-background population.
Using the IT method again resulted in the highest background value and both results were statistically significant, while the estimated value increased from 11.8 to 13.2. Compared to other methods, IT gave a higher estimation of the nitrate background value because it considers both the low and high values to define anomalies and cannot be applied to a polymodal distribution. The CDF method gave a noticeable difference in terms of non-statistically significant results for data without selection (8.3 mg/L) and statistically significant results for a set of selected data (7.2 mg/L). Although this suggests that the CDF method depends more on which data are used for the calculation with respect to the IT, our results correspond to the results of previous research, where it was shown that it is applicable to polymodal distributions and convenient for use in conditions of anthropogenic activity [40], which are present in the catchment area of the Velika Gorica well field. Results suggest that the usage of CDF is the most applicable when using only NON-ND data, which can be confirmed in the estimation of the statistically significant background value of 7.2 mg/L, unlike the estimate calculated with the all data without selection. Furthermore, Urresti-Estalla et al. [39] suggested that the usage of both IT and CDF methods depends on the nature of the parameter to be estimated as well as the type of frequency distribution curve presented by the data series. From this perspective, the most important criterion to define is whether the low concentration of the parameter that is observed represents a possible indicator of contamination. If not, then CDF should be used instead of the IT only when aquifers are undergoing little pressure.
The usage of lower limits with the first two methods is more convenient in areas under long-term human impacts and corresponds to the usage of the first inflection points from CFCs and PPs [74], which, in the end, makes the results estimated by all methods comparable. The first inflection points observed at plots were directly considered as ABVs, because the first population of the data set was considered to be the consequence of the natural conditions that prevail in the investigated part of the aquifer. The ABV determined by the CFC method decreased from 7.5 to 7.3 mg/L, while the background value determined by the PP method decreased from 7.1 to 6.9 mg/L, for all data and for selected data, respectively. The nitrate concentration showed more than one inflection point on plots, indicating multiple local events of nitrate contamination in groundwater. This is consistent with previous research where it was defined that elevated nitrate concentrations are the result of different sources of contamination, i.e., wastewater and manure [49]. In general, both CFCs and PPs resulted in the extraction of four sets, i.e., populations. Additionally, the aim was also to increase the coefficient of determination of the chosen subset compared to the initial value that was calculated for the entire population. In all cases, the significant improvement in the coefficient of determination was present when dividing entire population into more sub-populations due to different inflection points. However, it must be emphasized that, in our case, CFCs with the entire population had very high values for the coefficient of determination of 0.91 and 0.89 (Figure 3 and Figure 5). This was not the case with PPs, which had starting values for the coefficient of determination of 0.62 and 0.58 (Figure 3 and Figure 5). As observed in Panno et al. [29], the CFC and PP methods can be used in the estimation of nitrate ABVs only when observation wells with non-normally distributed data are included. If these data are not present within the observed data, it is possible that the inflection point will not be recognized.
The study has shown that the CFC and PP methods for data without selection and the CDF method for selected NON-ND data gave consistent and realistic estimations of ABVs that are comparable to nitrate concentrations in the main source of recharge of the Zagreb aquifer, i.e., Sava River [58,59,60,61]. When observing all acceptable (statistically significant) results together, it is evident that all methods, except the IT, gave very similar estimations of nitrate ABVs ranging from 7.1 mg/L to 7.5 mg/L. Preziosi et al. [53] and this research confirmed that the background value of nitrate determined at the level of the Zagreb aquifer [25,52] differs from the background value of nitrate determined in the catchment area of the Velika Gorica well field, a homogeneous area within the same aquifer.
5. Conclusions
The ABVs and threshold values are crucial for identifying groundwater quality and pollution migration. The nitrate concentrations, which are a potential pressure and concern in the Zagreb aquifer, were analyzed. The new approach to estimate the background value of nitrate as a basis for better groundwater management and protection in areas under long-term human impact was applied. The study is based on statistical methodologies developed to separate the natural and anthropogenic populations in monitored concentrations from the national groundwater quality monitoring program of Croatian Waters over a 20-year period. The results show that using data without selection can lead to statistically non-significant results, but, with further data selection, a statistically non-significant result became a statistically significant one. In conclusion, all final results must be statistically significant and determined using as wide as possible a data set. Reducing the size of the data set is acceptable only in the case of statistically non-significant results.
Author Contributions
Conceptualization and methodology, P.B., J.P. and Z.K.; formal analysis and writing—original draft preparation, P.B.; writing—review and editing, J.P., Z.K. and Z.N.; visualization, P.B. and J.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available on request from Croatian Waters and the Croatian Meteorological and Hydrological Service.
Acknowledgments
We would like to thank Croatian Waters and the Croatian Meteorological and Hydrological Service for providing the data. The present research was supported by the Croatian Science Foundation (HRZZ) under the Young Researches’ Career Development Project—Training New Doctoral Students; DOK-2020-01: The use of nitrogen and oxygen stable isotopes in the determination of nitrate origin in the unsaturated and saturated zone of the Velika Gorica well field.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sunitha, V.; Sudharshan Reddy, Y.; Suvarna, B.; Reddy, B.M. Human Health Risk Assessment (HHRA) of Fluoride and Nitrate Using Pollution Index of Groundwater (PIG) in and around Hard Rock Terrain of Cuddapah, A.P. South India. Environ. Chem. Ecotoxicol. 2022, 4, 113–123. [Google Scholar] [CrossRef]
- United Nations. The Sustainable Development Goals Report 2021; United Nations Publications: New York, NY, USA, 2021. [Google Scholar]
- Adimalla, N.; Qian, H.; Nandan, M.J. Groundwater Chemistry Integrating the Pollution Index of Groundwater and Evaluation of Potential Human Health Risk: A Case Study from Hard Rock Terrain of South India. Ecotoxicol. Env. Saf. 2020, 206, 111217. [Google Scholar] [CrossRef] [PubMed]
- Abascal, E.; Gómez-Coma, L.; Ortiz, I.; Ortiz, A. Global Diagnosis of Nitrate Pollution in Groundwater and Review of Removal Technologies. Sci. Total Environ. 2022, 810, 152233. [Google Scholar] [CrossRef]
- Pérez-Indoval, R.; Rodrigo-Ilarri, J.; Cassiraga, E.; Rodrigo-Clavero, M.E. PWC-Based Evaluation of Groundwater Pesticide Pollution in the Júcar River Basin. Sci. Total Environ. 2022, 847, 157386. [Google Scholar] [CrossRef]
- Rezaei, A.; Hassani, H.; Tziritis, E.; Fard Mousavi, S.B.; Jabbari, N. Hydrochemical Characterization and Evaluation of Groundwater Quality in Dalgan Basin, SE Iran. Groundw. Sustain. Dev. 2020, 10, 100353. [Google Scholar] [CrossRef]
- Mekonnen, M.M.; Hoekstra, A.Y. Four Billion People Facing Severe Water Scarcity. Sci. Adv. 2016, 2, e1500323. [Google Scholar] [CrossRef] [PubMed]
- Díaz-Alcaide, S.; Martínez-Santos, P. Review: Advances in Groundwater Potential Mapping. Hydrogeol. J. 2019, 27, 2307–2324. [Google Scholar] [CrossRef]
- Majkić-Dursun, B.; Oros, I.; Oparušić, I.; Petković, A. Assessing Groundwater Quality for Multiuse and Geochemical Evolution in the South Banat Area of Serbia, Pannonian Basin. Pol. J. Env. Stud. 2019, 28, 3269–3278. [Google Scholar] [CrossRef]
- Erisman, J.W.; Galloway, J.N.; Seitzinger, S.; Bleeker, A.; Dise, N.B.; Roxana Petrescu, A.M.; Leach, A.M.; de Vries, W. Consequences of Human Modification of the Global Nitrogen Cycle. Philos. Trans. R. Soc. B Biol. Sci. 2013, 368, 20130116. [Google Scholar] [CrossRef] [PubMed]
- Hosono, T.; Tokunaga, T.; Kagabu, M.; Nakata, H.; Orishikida, T.; Lin, I.T.; Shimada, J. The Use of Δ15N and Δ18O Tracers with an Understanding of Groundwater Flow Dynamics for Evaluating the Origins and Attenuation Mechanisms of Nitrate Pollution. Water Res. 2013, 47, 2661–2675. [Google Scholar] [CrossRef]
- Liu, A.; Ming, J.; Ankumah, R.O. Nitrate Contamination in Private Wells in Rural Alabama, United States. Sci. Total Environ. 2005, 346, 112–120. [Google Scholar] [CrossRef] [PubMed]
- Ma, Z.; Yang, Y.; Lian, X.; Jiang, Y.; Xi, B.; Peng, X.; Yan, K. Identification of Nitrate Sources in Groundwater Using a Stable Isotope and 3DEEM in a Landfill in Northeast China. Sci. Total Environ. 2016, 563–564, 593–599. [Google Scholar] [CrossRef]
- Rockström, J.; Steffen, W.; Noone, K.; Persson, Å.; Chapin, F.S., III; Lambin, E.F.; Lenton, T.M.; Scheffer, M.; Folke, C.; Schellnhuber, H.J.; et al. A Safe Operation Space for Humanity. Nature 2009, 461, 472–475. [Google Scholar] [CrossRef] [PubMed]
- Romanelli, A.; Soto, D.X.; Matiatos, I.; Martínez, D.E.; Esquius, S. A Biological and Nitrate Isotopic Assessment Framework to Understand Eutrophication in Aquatic Ecosystems. Sci. Total Environ. 2020, 715, 136909. [Google Scholar] [CrossRef]
- Xue, D.; de Baets, B.; van Cleemput, O.; Hennessy, C.; Berglund, M.; Boeckx, P. Use of a Bayesian Isotope Mixing Model to Estimate Proportional Contributions of Multiple Nitrate Sources in Surface Water. Environ. Pollut. 2012, 161, 43–49. [Google Scholar] [CrossRef]
- Xue, D.; Botte, J.; de Baets, B.; Accoe, F.; Nestler, A.; Taylor, P.; van Cleemput, O.; Berglund, M.; Boeckx, P. Present Limitations and Future Prospects of Stable Isotope Methods for Nitrate Source Identification in Surface- and Groundwater. Water Res. 2009, 43, 1159–1170. [Google Scholar] [CrossRef] [PubMed]
- Xu, S.; Kang, P.; Sun, Y. A Stable Isotope Approach and Its Application for Identifying Nitrate Source and Transformation Process in Water. Environ. Sci. Pollut. Res. 2016, 23, 1133–1148. [Google Scholar] [CrossRef]
- Fenech, C.; Rock, L.; Nolan, K.; Tobin, J.; Morrissey, A. The Potential for a Suite of Isotope and Chemical Markers to Differentiate Sources of Nitrate Contamination: A Review. Water Res. 2012, 46, 2023–2041. [Google Scholar] [CrossRef]
- Ahada, C.P.S.; Suthar, S. Groundwater Nitrate Contamination and Associated Human Health Risk Assessment in Southern Districts of Punjab, India. Environ. Sci. Pollut. Res. 2018, 25, 25336–25347. [Google Scholar] [CrossRef]
- Burkart, M.R.; Kolpin, D.W. Hydrologic and Land-Use Factors Associated with Herbicides and Nitrate in Near-Surface Aquifers. J. Environ. Qual. 1993, 22, 646–656. [Google Scholar] [CrossRef]
- Nakić, Z.; Ružičić, S.; Posavec, K.; Mileusnić, M.; Parlov, J.; Bačani, A.; Durn, G. Conceptual Model for Groundwater Status and Risk Assessment—Case Study of the Zagreb Aquifer System. Geol. Croat. 2013, 66, 55–77. [Google Scholar] [CrossRef]
- de Caro, M.; Crosta, G.B.; Frattini, P. Hydrogeochemical Characterization and Natural Background Levels in Urbanized Areas: Milan Metropolitan Area (Northern Italy). J. Hydrol. 2017, 547, 455–473. [Google Scholar] [CrossRef]
- Reimann, C.; Garrett, R.G. Geochemical Background—Concept and Reality. Sci. Total Environ. 2005, 350, 12–27. [Google Scholar] [CrossRef] [PubMed]
- Nakić, Z.; Posavec, K.; Bačani, A. A Visual Basic Spreadsheet Macro for Geochemical Background Analysis. Ground Water 2007, 45, 642–647. [Google Scholar] [CrossRef] [PubMed]
- Sellerino, M.; Forte, G.; Ducci, D. Identification of the Natural Background Levels in the Phlaegrean Fields Groundwater Body (Southern Italy). J. Geochem. Explor. 2019, 200, 181–192. [Google Scholar] [CrossRef]
- Cruz, J.; Andrade, C. Natural Background Groundwater Composition in the Azores Archipelago (Portugal): A Hydrogeochemical Study and Threshold Value Determination. Sci. Total Environ. 2015, 520, 127–135. [Google Scholar] [CrossRef] [PubMed]
- Biddau, R.; Cidu, R.; Lorrai, M.; Mulas, M.G. Assessing Background Values of Chloride, Sulfate and Fluoride in Groundwater: A Geochemical-Statistical Approach at a Regional Scale. J. Geochem. Explor. 2017, 181, 243–255. [Google Scholar] [CrossRef]
- Panno, S.; Kelly, W.R.; Martinsek, A.T.; Hackley, K.C. Estimating Background and Threshold Nitrate Concentrations Using Probability Graphs. Ground Water 2006, 44, 697–709. [Google Scholar] [CrossRef]
- Parslow, G.R. Determination of Background and Threshold in Exploration Geochemistry. J. Geochem. Explor. 1974, 3, 319–336. [Google Scholar] [CrossRef]
- Kelly, W.R.; Panno, S.V. Some Considerations in Applying Background Concentrations to Ground Water Studies. Ground Water 2008, 46, 790–792. [Google Scholar] [CrossRef]
- Filzmoser, P.; Garrett, R.G.; Reimann, C. Multivariate Outlier Detection in Exploration Geochemistry. Comput. Geosci. 2005, 31, 579–587. [Google Scholar] [CrossRef]
- Sinclair, A.J. A Fundamental Approach to Threshold Estimation in Exploration Geochemistry: Probability Plots Revisited. J. Geochem. Explor. 1991, 41, 1–22. [Google Scholar] [CrossRef]
- Reimann, C.; Filzmoser, P. Normal and Lognormal Data Distribution in Geochemistry: Death of a Myth. Consequences for the Statistical Treatment of Geochemical and Environmental Data. Environ. Geol. 2000, 39, 1001–1014. [Google Scholar] [CrossRef]
- Geranian, H.; Mokhtari, A.R.; Cohen, D.R. Bivariate Probability Plots: A Method for Delineating Different Populations in Soil Geochemical Data. Sci. Total Environ. 2019, 671, 1047–1055. [Google Scholar] [CrossRef]
- Kim, K.-H.; Yun, S.-T.; Kim, H.-K.; Kim, J.-W. Determination of Natural Backgrounds and Thresholds of Nitrate in South Korean Groundwater Using Model-Based Statistical Approaches. J. Geochem. Explor. 2015, 148, 196–205. [Google Scholar] [CrossRef]
- Rahman, A.; Tiwari, K.K.; Mondal, N.C. Assessment of Hydrochemical Backgrounds and Threshold Values of Groundwater in a Part of Desert Area, Rajasthan, India. Environ. Pollut. 2020, 266, 115150. [Google Scholar] [CrossRef] [PubMed]
- Bulut, O.F.; Duru, B.; Çakmak, Ö.; Günhan, Ö.; Dilek, F.B.; Yetis, U. Determination of Groundwater Threshold Values: A Methodological Approach. J. Clean. Prod. 2020, 253. [Google Scholar] [CrossRef]
- Urresti-Estala, B.; Carrasco-Cantos, F.; Vadillo-Pérez, I.; Jiménez-Gavilán, P. Determination of Background Levels on Water Quality of Groundwater Bodies: A Methodological Proposal Applied to a Mediterranean River Basin (Guadalhorce River, Málaga, Southern Spain). J. Environ. Manag. 2013, 117, 121–130. [Google Scholar] [CrossRef] [PubMed]
- Matschullat, J.; Ottenstein, R.; Reimann, C. Geochemical Background—Can We Calculate It? Environ. Geol. 2000, 39, 990–1000. [Google Scholar] [CrossRef]
- Amiri, V.; Nakhaei, M.; Lak, R.; Li, P. An Integrated Statistical-Graphical Approach for the Appraisal of the Natural Background Levels of Some Major Ions and Potentially Toxic Elements in the Groundwater of Urmia Aquifer, Iran. Environ. Earth Sci. 2021, 80, 432. [Google Scholar] [CrossRef]
- Lions, J.; Devau, N.; Elster, D.; Voutchkova, D.D.; Hansen, B.; Schullehner, J.; Petrović Pantić, T.; Samolov, K.A.; Camps, V.; Arnó, G.; et al. A Broad-Scale Method for Estimating Natural Background Levels of Dissolved Components in Groundwater Based on Lithology and Anthropogenic Pressure. Water 2021, 13, 1531. [Google Scholar] [CrossRef]
- Molinari, A.; Guadagnini, L.; Marcaccio, M.; Guadagnini, A. Natural Background Levels and Threshold Values of Chemical Species in Three Large-Scale Groundwater Bodies in Northern Italy. Sci. Total Environ. 2012, 425, 9–19. [Google Scholar] [CrossRef] [PubMed]
- Parrone, D.; Ghergo, S.; Preziosi, E. A Multi-Method Approach for the Assessment of Natural Background Levels in Groundwater. Sci. Total Environ. 2019, 659, 884–894. [Google Scholar] [CrossRef] [PubMed]
- Preziosi, E.; Parrone, D.; del Bon, A.; Ghergo, S. Natural Background Level Assessment in Groundwaters: Probability Plot versus Pre-Selection Method. J. Geochem. Explor. 2014, 143, 43–53. [Google Scholar] [CrossRef]
- Kovač, Z.; Nakić, Z.; Pavlić, K. Influence of Groundwater Quality Indicators on Nitrate Concentrations in the Zagreb Aquifer System. Geol. Croat. 2017, 70, 93–103. [Google Scholar] [CrossRef]
- Kovač, Z.; Cvetković, M.; Parlov, J. Gaussian Simulation of Nitrate Concentration Distribution in the Zagreb Aquifer. J. Maps 2017, 13, 727–732. [Google Scholar] [CrossRef]
- Huljek, L.; Perković, D.; Kovač, Z. Nitrate Contamination Risk of the Zagreb Aquifer. J. Maps 2019, 15, 570–577. [Google Scholar] [CrossRef]
- Kovač, Z.; Nakić, Z.; Barešić, J.; Parlov, J. Nitrate Origin in the Zagreb Aquifer System. Geofluids 2018, 2018, 2789691. [Google Scholar] [CrossRef]
- Kovač, Z.; Nakić, Z.; Špoljarić, D.; Stanek, D.; Bačani, A. Estimation of Nitrate Trends in the Groundwater of the Zagreb Aquifer. Geosciences 2018, 8, 159. [Google Scholar] [CrossRef]
- Kovač, Z.; Bačani, L.; Ružičić, S.; Parlov, J.; Posavec, K.; Buškulić, P. Using Water Stable Isotopes and Cross-Correlation Analysis to Characterize Infiltration of Precipitation through Unsaturated Zone at the Velika Gorica Site of Zagreb Aquifer. J. Hydrol. Eng. 2023, 28, 04023002. [Google Scholar] [CrossRef]
- Kovač, Z. Podrijetlo nitrata u podzemnoj vodi zagrebačkoga aluvijalnoga vodonosnika (Nitrate Origin in Groundwater of the Zagreb Alluvial Aquifer); University of Zagreb, Faculty of Mining, Geology and Petroleum Engineering: Zagreb, Croatia, 2017. [Google Scholar]
- Preziosi, E.; Giuliano, G.; Vivona, R. Natural Background Levels and Threshold Values Derivation for Naturally As, V and F Rich Groundwater Bodies: A Methodological Case Study in Central Italy. Environ. Earth Sci. 2010, 61, 885–897. [Google Scholar] [CrossRef]
- Velic, J.; Saftic, B. Subsurface Spreading and Facies Characteristics of Middle Pleistocene Deposits between Zaprešić and Samobor. Geološki Vjesn 1991, 44, 69–82. [Google Scholar]
- Velić, J.; Saftić, B.; Malvić, T. Lithologic Composition and Stratigraphy of Quaternary Sediments in the Area of the “Jakuševec” Waste Depository (Zagreb, Northern Croatia). Geol. Croat. 1999, 52, 119–130. [Google Scholar]
- Velić, J.; Durn, G. Alternating Lacustrine-Marsh Sedimentation and Subaerial Exposure Phases during Quaternary: Prečko, Zagreb, Croatia. Geol. Croat. 1993, 46, 71–90. [Google Scholar]
- Ružičić, S.; Mileusnić, M.; Posavec, K. Building Conceptual and Mathematical Model for Water Flow and Solute Transport in the Unsaturated Zone at Kosnica Site. Rud. -Geološko-Naft. Zb. 2012, 25, 21–31. [Google Scholar]
- Posavec, K.; Vukojević, P.; Ratkaj, M.; Bedeniković, T. Cross-Correlation Modelling of Surface Water—Groundwater Interaction Using the Excel Spreadsheet Application. Rud. -Geološko-Naft. Zb. 2017, 32, 25–32. [Google Scholar] [CrossRef]
- Parlov, J.; Kovač, Z.; Nakić, Z.; Barešić, J. Using Water Stable Isotopes for Identifying Groundwater Recharge Sources of the Unconfined Alluvial Zagreb Aquifer (Croatia). Water 2019, 11, 2177. [Google Scholar] [CrossRef]
- Barešić, J.; Parlov, J.; Kovač, Z.; Sironić, A. Use of Nuclear Power Plant Released Tritium as a Groundwater Tracer. Rud. -Geološko-Naft. Zb. 2020, 35, 25–35. [Google Scholar] [CrossRef]
- Kovač, Z.; Barešić, J.; Parlov, J.; Sironić, A. Impact of Hydrological Conditions on the Isotopic Composition of the Sava River in the Area of the Zagreb Aquifer. Water 2022, 14, 2263. [Google Scholar] [CrossRef]
- Posavec, K. Identifikacija i prognoza minimalnih razina podzemne vode zagrebackoga aluvijalnog vodonosnika modelima recesijskih krivulja (Identification and Prediction of Minimum Ground Water Levels of Zagreb Alluvial Aquifer Using Recession Curve Models); University of Zagreb, Faculty of Mining, Geology and Petroleum Engineering: Zagreb, Croatia, 2006. [Google Scholar]
- Bogunović, M.; Vidaček, Ž.; Husnjak, S.; Sraka, M. Inventory of Soils in Croatia. Agric. Conspec. Sci. 1998, 63, 105–112. [Google Scholar]
- Ružičić, S. Model Transporta Potencijalno Toksičnih Elemenata Kroz Nesaturiranu Zonu na Području Regionalnoga Vodocrpilišta Kosnica (Transport Model of Potentially Toxic Elements through Unsaturated Zone at Regional Wellfield Kosnica); Faculty of Mining, Geology and Petroleum Engineering, University of Zagreb: Zagreb, Croatia, 2013. [Google Scholar]
- Nakić, Z.; Horvat, S.; Bačani, A. Statistical Indicators of Groundwater Geochemical Characteristics in a Quaternary Aquifer from the Mala Mlaka Well Field Catchment Area (Zagreb, Croatia). Geol. Croat. 2005, 58, 87–99. [Google Scholar] [CrossRef]
- Vlahović, T.; Bačani, A.; Posavec, K. Hydrogeochemical Stratification of the Unconfined Samobor Aquifer (Zagreb, Croatia). Environ. Geol. 2009, 57, 1707–1722. [Google Scholar] [CrossRef]
- Buškulić, P.; Parlov, J. Hydrogeochemical Facies of Groundwater in the Influence Area of the Velika Gorica Well Field. In Proceedings of the Mathematical Methods and Terminology in Geology 2022, 4th Croatian Scientific Congress about Geomathematics and Terminology in Geology; Malvić, T., Ivšinović, J., Eds.; University of Zagreb, Faculty of Mining, Geology and Petroleum Engineering: Zagreb, Croatia, 2022; pp. 1–196. [Google Scholar]
- Lilliefors, H.W. On the Kolmogorov-Smirnov Test for Normality with Mean and Variance Unknown. J. Am. Stat. Assoc. 1967, 62, 399–402. [Google Scholar] [CrossRef]
- de Lima Rodrigues, A.S.; Malafaia, G.; Costa, A.T.; Nalini Junior, H.A. Background Values for Chemical Elements in Sediments of the Gualaxo Do Norte River Basin, MG, Brazil. Rev. De Ciências Ambient. —RCA 2013, 7, 15–32. [Google Scholar] [CrossRef]
- Nakić, Z.; Kovač, Z.; Parlov, J.; Perković, D. Ambient Background Values of Selected Chemical Substances in Four Groundwater Bodies in the Pannonian Region of Croatia. Water 2020, 12, 2671. [Google Scholar] [CrossRef]
- Lepeltier, C. A Simplified Statistical Treatment of Geochemical Data by Graphical Representation. Econ. Geol. 1969, 64, 538–550. [Google Scholar] [CrossRef]
- Nakić, Z.; Posavec, K.; Parlov, J. Model-Based Objective Methods for the Estimation of Groundwater Geo- Chemical Background. Aqua Mundi 2010, 1, 65–72. [Google Scholar] [CrossRef]
- Marković, T.; Brkić, Ž.; Larva, O. Using Hydrochemical Data and Modelling to Enhance the Knowledge of Groundwater Flow and Quality in an Alluvial Aquifer of Zagreb, Croatia. Sci. Total Environ. 2013, 458–460, 508–516. [Google Scholar] [CrossRef]
- Rahman, A.; Mondal, N.C.; Tiwari, K.K. Anthropogenic Nitrate in Groundwater and Its Health Risks in the View of Background Concentration in a Semi Arid Area of Rajasthan, India. Sci. Rep. 2021, 11, 9279. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).