Uncertainty and Global Sensitivity Analysis of a Membrane Biogas Upgrading Process Using the COCO Simulator
Abstract
1. Introduction
1.1. Uncertainty and Global Sensitivity Analysis
1.2. CAPE-OPEN Process Simulators
1.3. Scope of This Work
2. Materials and Methods
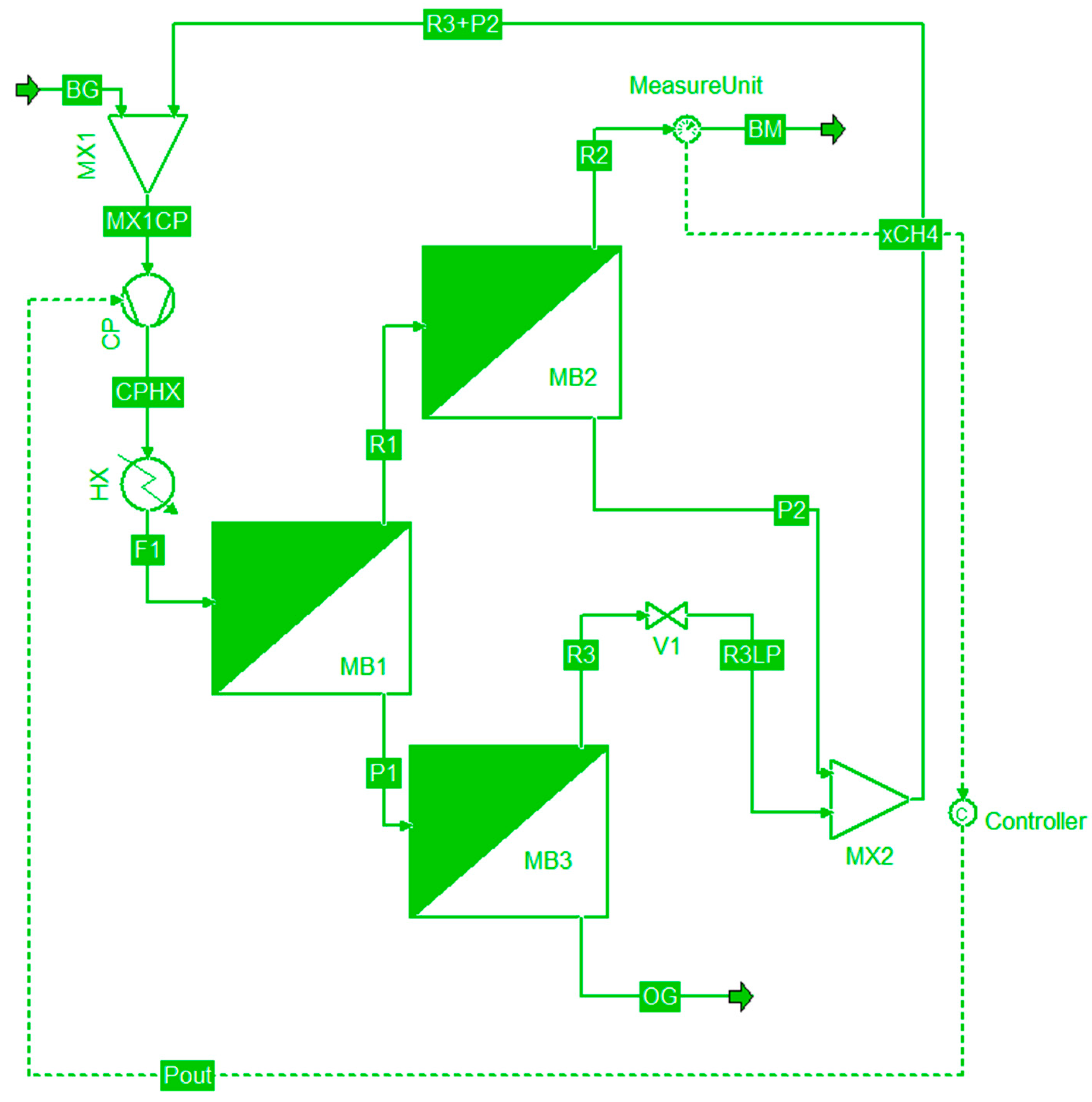
2.1. Case Study
2.2. Deterministic Simulation of the Process in COCO
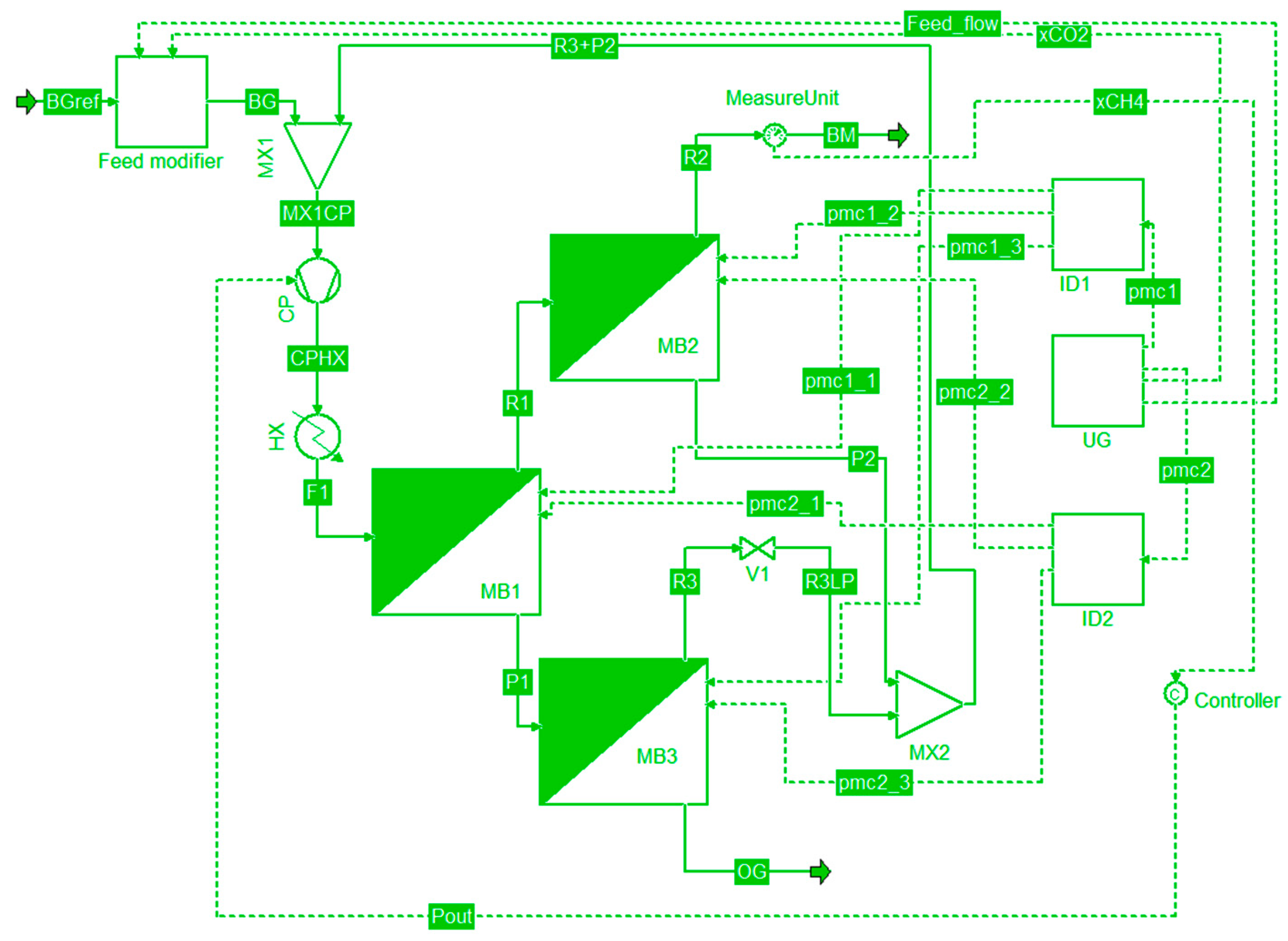
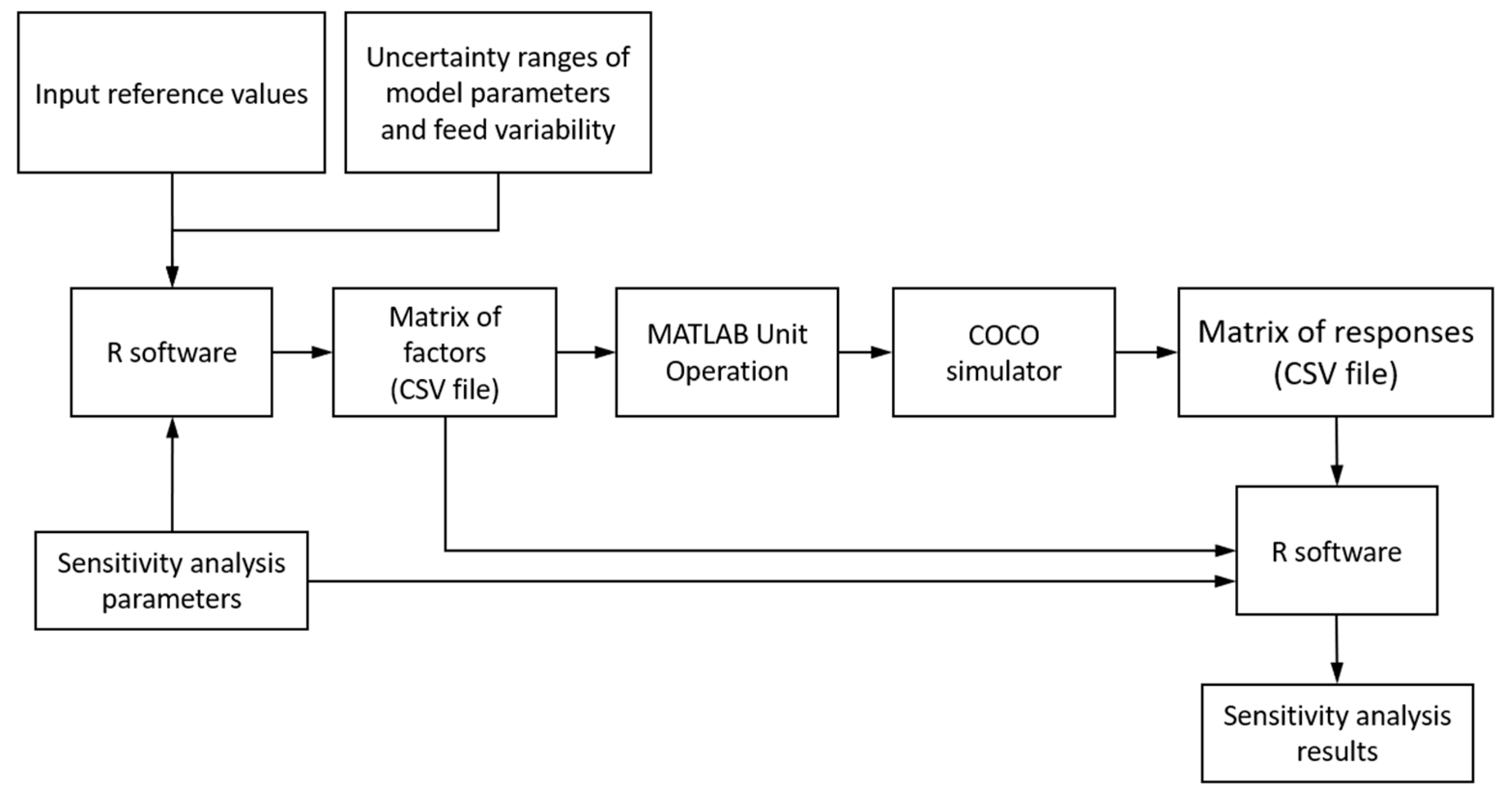
2.3. Application of Uncertainty and Sensitivity Methodology
2.3.1. Characterization of the Uncertainty Sources
2.3.2. Response Variables Studied
2.3.3. User Module for Uncertainties
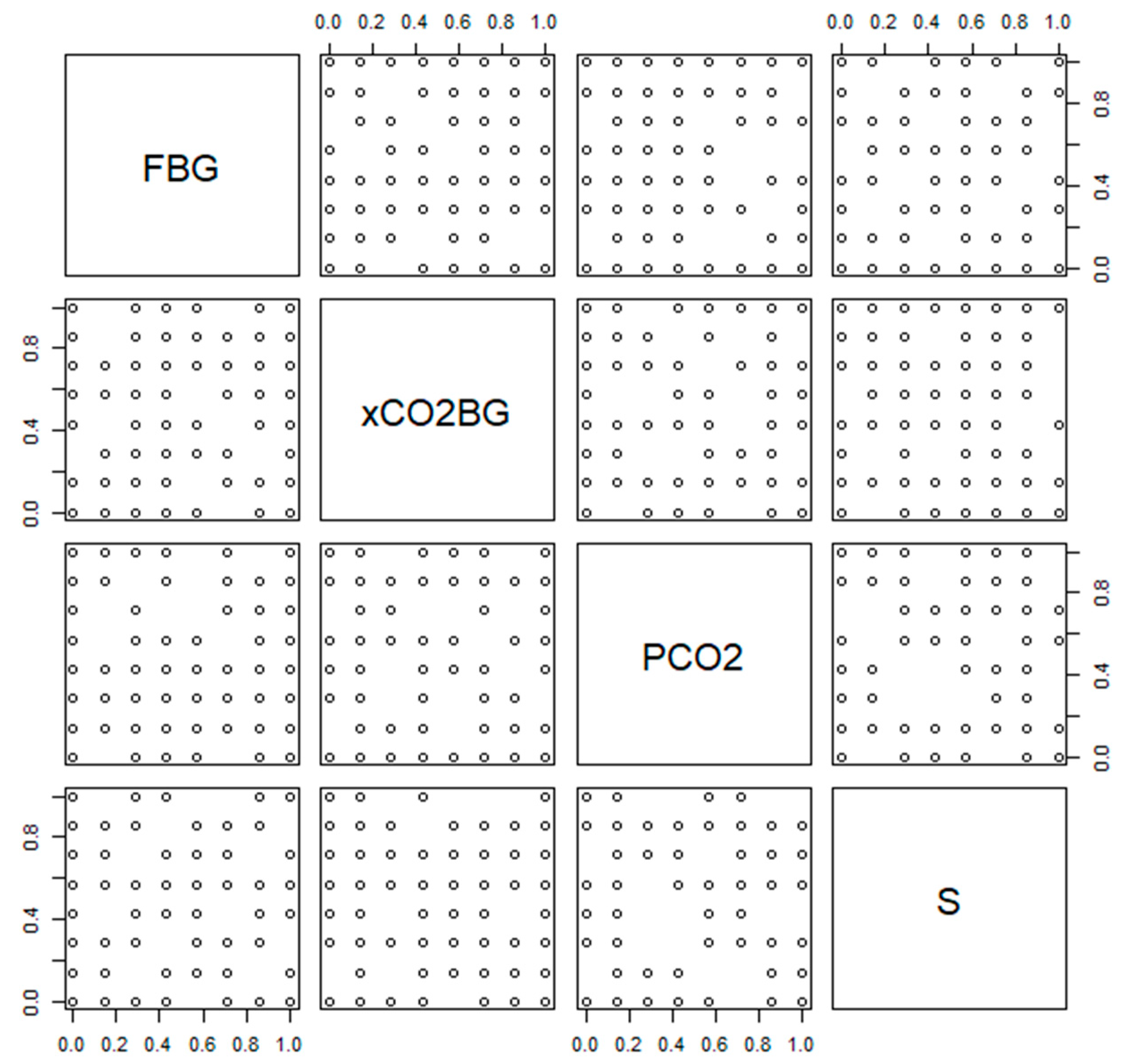
2.3.4. Morris’ Analysis of Global Sensitivity
2.3.5. Determination of Sobol’ Indices
2.3.6. Uncertainty Analysis for Determination of Tolerance Limits
3. Results
3.1. Deterministic Simulation Results
3.2. Sensitivity Analysis
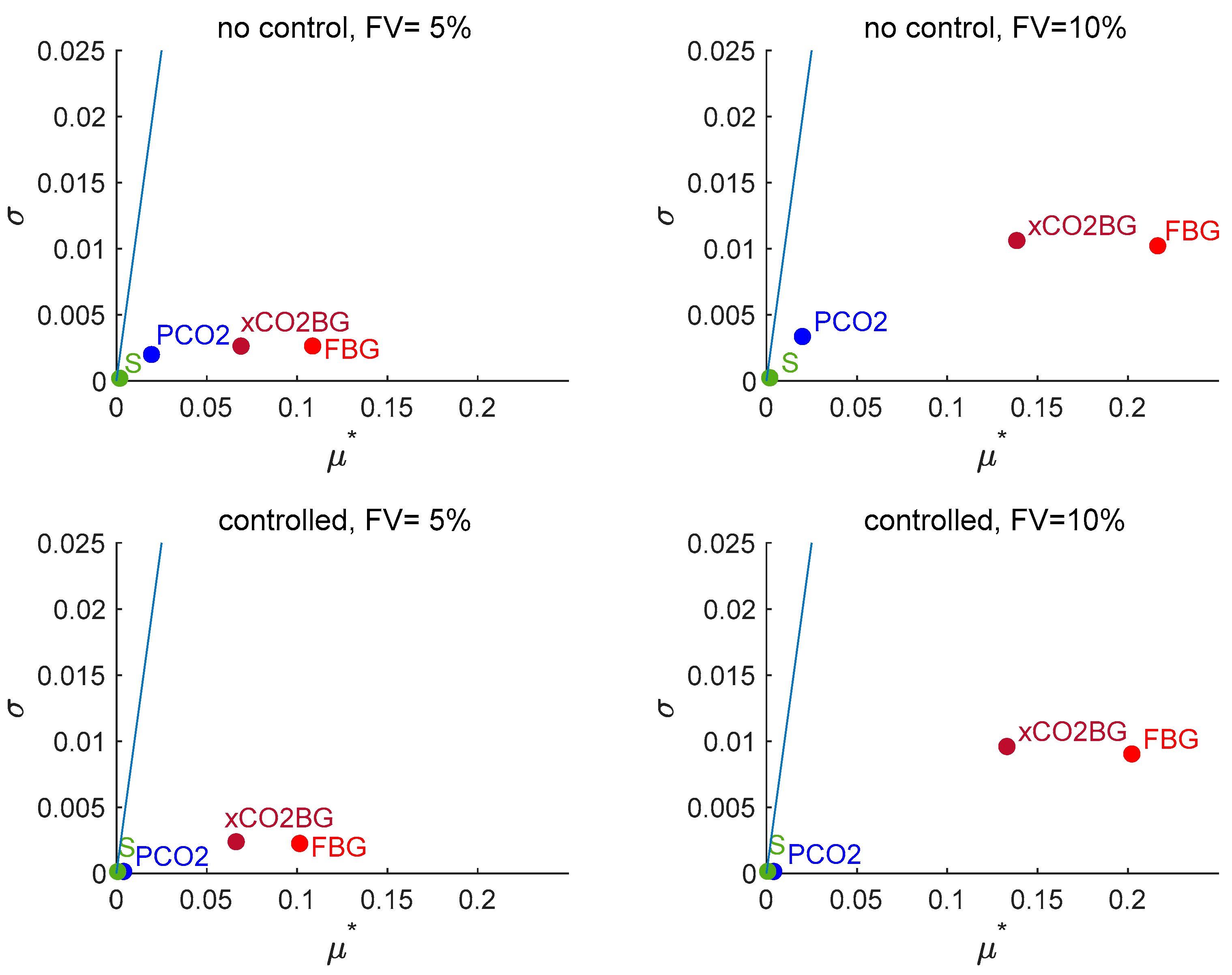
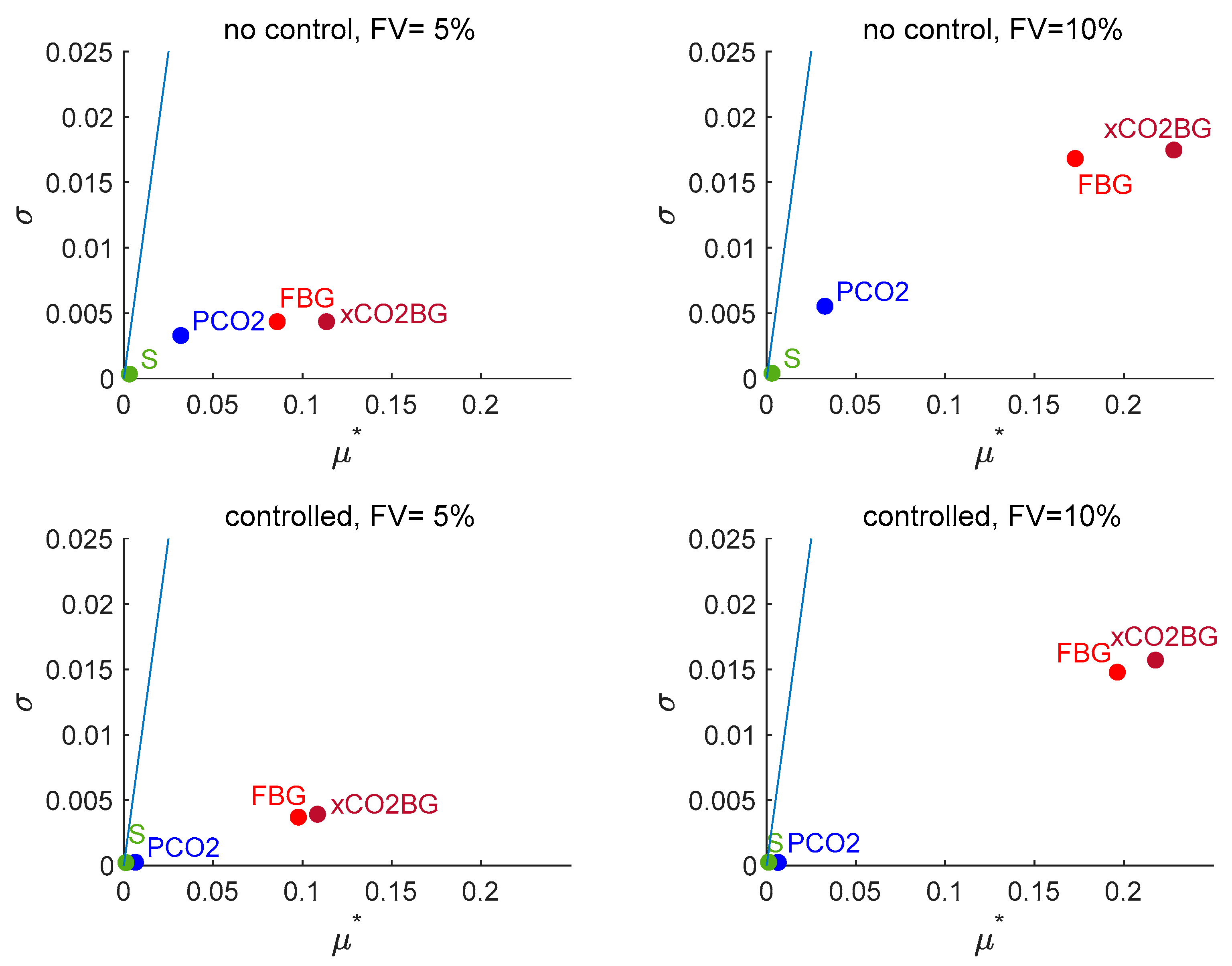
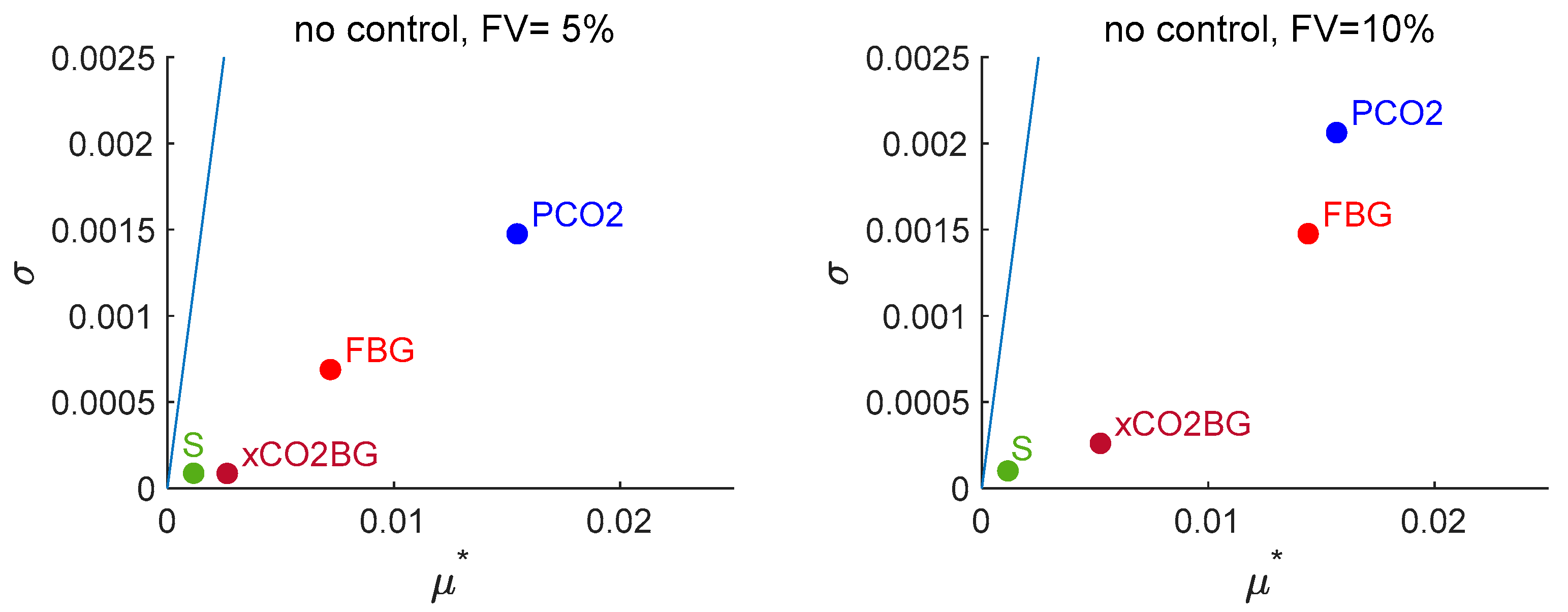
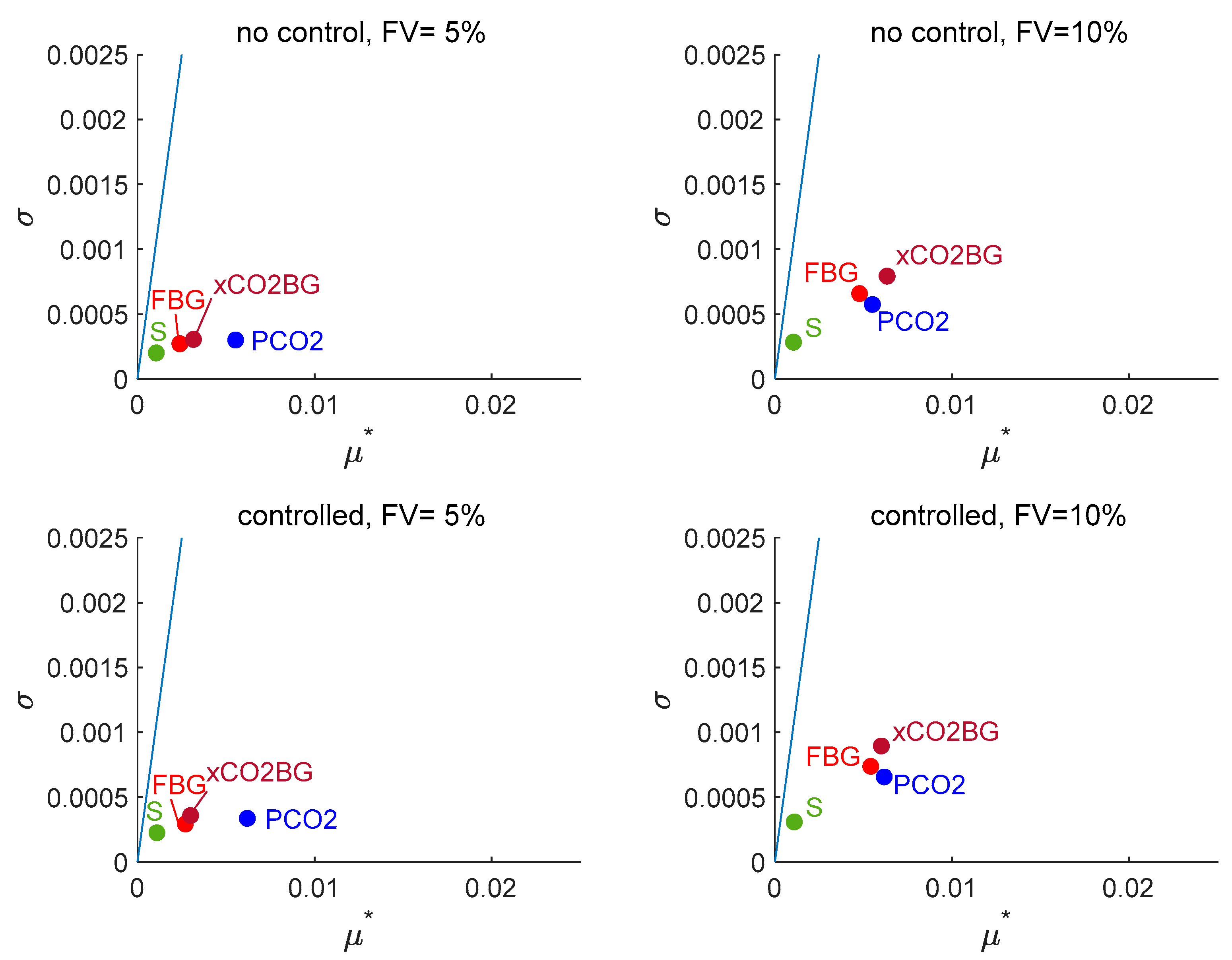
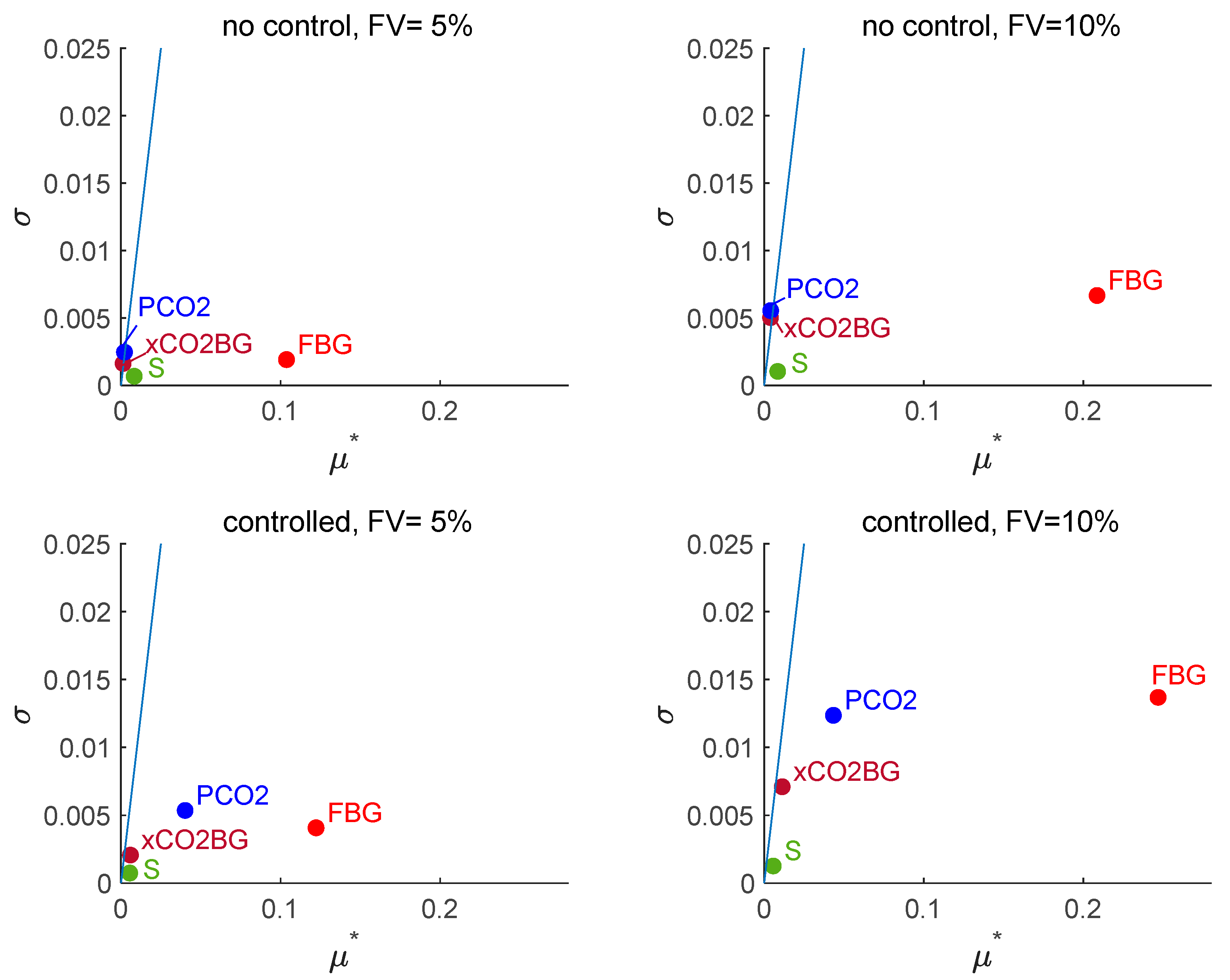
3.2.1. Morris Sensitivity Analysis
3.2.2. Sobol’ Indices for Each Factor Across the System Responses
3.3. Determination of Tolerance Limits of the Responses
4. Discussion
| Reference | Application Domain | K | N | Main Outcomes |
|---|---|---|---|---|
| This work | Biogas upgrading (membrane separation, COCO simulator) | 4 | 150 | Relative impact of feed and membrane parameter uncertainties studied on product streams and process utilities |
| Bhati et al. [42] | Perovskite manufacturing | 12 | - | Material factors contribute the most to the cost of all manufacturing capacities |
| Sangregorio-Soto et al. [43] | Continuous microalgae culture | 9 | - | Practical use of combining Morris assessment and Sobol’ index using several dynamic models to study the biomass response |
| Kuncheekanna et al. [44] | CO2 capture by absorption (testing of sensitivity methods) | 8 | 1000 | Sobol’ indices share ranking capabilities similar to those of the Borgonovo and Morris methods |
| Barahmand et al. [45] | Anaerobic digestion (ADM1-like bioprocess model) | 48 | - | Impact of biological parameters uncertainties on methane yield |
| Öner et al. [46] | Pharmaceutical crystallization | 10 | 140 | Morris analysis identified the most influential parameter in process performance |
| Sepúlveda et al. [47] | Mineral processing (process improvement) | 12 | - | Global sensitivity analysis is useful to study separation circuits; Morris method is recommended because of its low computation requirements |
| Mery et al. [48] | Water treatment life cycle assessment (LCA) | 18 | - | Morris assessment and LCA are helpful in engineering design choices |
| Ruano et al. [49] | Wastewater treatment plant (fuzzy control) | 17 | 1000 | Improved method to determine the optimal number of repetitions of the Morris method |
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CAPE | Computer Assisted Process Engineering |
| COCO | CAPE-OPEN to CAPE-OPEN Compliant Steady-State Simulator Environment |
| COFE | CAPE-OPEN Flowsheet Environment |
| FV | Feed Variability |
| LTL | Lower Tolerance Limit |
| RLG | Relative Lower-Bound Gap |
| Sc. | Scenario |
| RUG | Relative Upper-Bound Gap |
| UTL | Upper Tolerance Limit |
Appendix A

References
- Soize, C. Uncertainty Quantification, 1st ed.; Springer: Cham, Switzerland, 2017; Volume 23. [Google Scholar] [CrossRef]
- Saltelli, A.; Tarantola, S.; Campolongo, F.; Ratto, M. Global Sensitivity Analysis for Importance Assessment. In Sensitivity Analysis in Practice; Wiley: Hoboken, NJ, USA, 2004; pp. 31–61. [Google Scholar] [CrossRef]
- Al-Douri, A.; Kazantzi, V.; Currie-Gregg, N.; El-Halwagi, M.M. Integrating Uncertainty Quantification in Reliability, Availability, and Maintainability (RAM) Analysis in the Conceptual and Preliminary Stages of Chemical Process Design. Chem. Eng. Res. Des. 2021, 167, 281–291. [Google Scholar] [CrossRef]
- Barahmand, Z.; Samarakoon, G. Sensitivity Analysis and Anaerobic Digestion Modeling: A Scoping Review. Fermentation 2022, 8, 624. [Google Scholar] [CrossRef]
- Li, Q.; Wan, H.; Zhao, Z.; Liu, F. Robust Batch-to-Batch Optimization with Global Sensitivity Analysis for Microbial Fermentation Processes under Model-Plant Mismatch. Chem. Eng. Sci. 2025, 301, 120658. [Google Scholar] [CrossRef]
- Yliruka, M.; Moret, S.; Shah, N. Detail or Uncertainty? Applying Global Sensitivity Analysis to Strike a Balance in Energy System Models. Comput. Chem. Eng. 2023, 177, 108287. [Google Scholar] [CrossRef]
- Oyegoke, T. COCO, a Process Simulator: Methane Oxidation Simulation & Its Agreement with Commercial Simulator’s Predictions. Chem. Prod. Process Model. 2023, 18, 995–1004. [Google Scholar] [CrossRef]
- Amsterchem COCO. Cape Open to Cape Open Simulation Environment. Available online: https://www.amsterchem.com/coco.html (accessed on 1 May 2025).
- Andreasen, A.; van Baten, J. Techno-Economic Analysis and Optimization of Gray and Green Methanol Synthesis Using Flowsheet Automation and Surrogate Modeling. Energy Fuels 2025, 39, 3359–3374. [Google Scholar] [CrossRef]
- Krone, D.; Esche, E.; Skiborowski, M.; Repke, J.U. Optimization-Based Process Synthesis by Phenomena-Based Building Blocks and an MINLP Framework Featuring Structural Screening. Comput. Chem. Eng. 2025, 194, 108955. [Google Scholar] [CrossRef]
- Alqaheem, Y.; Alobaid, M. Development of a Membrane Process in CAPE-OPEN to CAPE-OPEN (COCO) Simulator for Carbon Dioxide Separation. Results Eng. 2024, 22, 102239. [Google Scholar] [CrossRef]
- Bisotti, F.; Gilardi, M.; Berglihn, O.T.; Tschentscher, R.; Hansen, L.D.; Horn, S.J.; Várnai, A.; Wittgens, B. From Laboratory Scale to Innovative Spruce-Based Biorefinery. Note I: Conceptual Process Design and Simulation. Comput. Aided Chem. Eng. 2024, 53, 2449–2454. [Google Scholar] [CrossRef]
- Tangsathitkulchai, C.; Punsuwan, N.; Weerachanchai, P. Simulation of Batch Slow Pyrolysis of Biomass Materials Using the Process-Flow-Diagram COCO Simulator. Processes 2019, 7, 775. [Google Scholar] [CrossRef]
- Iarikov, D.D.; Ted Oyama, S. Review of CO2/CH4 Separation Membranes. Membr. Sci. Technol. 2011, 14, 91–115. [Google Scholar] [CrossRef]
- Tomczak, W.; Gryta, M.; Daniluk, M.; Żak, S. Biogas Upgrading Using a Single-Membrane System: A Review. Membranes 2024, 14, 80. [Google Scholar] [CrossRef]
- Janusz-Cygan, A.; Jaschik, J.; Tańczyk, M. Upgrading Biogas from Small Agricultural Sources into Biomethane by Membrane Separation. Membranes 2021, 11, 938. [Google Scholar] [CrossRef]
- Vrbová, V.; Ciahotný, K. Upgrading Biogas to Biomethane Using Membrane Separation. Energy Fuels 2017, 31, 9393–9401. [Google Scholar] [CrossRef]
- Kim, S.J.; Song, Y.; Binns, M.; Yeo, J.G.; Kim, J.K. Process-Integrated Optimization and Techno-Economic Analysis of Membrane System for Biogas Upgrading: Effect of Membrane Performance from an Economic Perspective. J. Membr. Sci. 2025, 713, 123286. [Google Scholar] [CrossRef]
- Azadi Tabar, M.; Maghsoudi, H.; Denayer, J.F.M. Hybrid Membrane-Vacuum Pressure Swing Adsorption: Low-Cost Technology for Simultaneous Biomethane and Carbon Dioxide Production from Biogas. Bioresour. Technol. 2025, 422, 132241. [Google Scholar] [CrossRef] [PubMed]
- Abejón, R.; Casado-Coterillo, C.; Garea, A. Techno-Economic Optimization of Multistage Membrane Processes with Innovative Hollow Fiber Modules for the Production of High-Purity CO2 and CH4 from Different Sources. Ind. Eng. Chem. Res. 2022, 61, 8149–8165. [Google Scholar] [CrossRef] [PubMed]
- Deng, L.; Hägg, M.B. Techno-Economic Evaluation of Biogas Upgrading Process Using CO2 Facilitated Transport Membrane. Int. J. Greenh. Gas Control 2010, 4, 638–646. [Google Scholar] [CrossRef]
- Zito, P.F.; Brunetti, A.; Barbieri, G. Multi-Step Membrane Process for Biogas Upgrading. J. Membr. Sci. 2022, 652, 120454. [Google Scholar] [CrossRef]
- Ungerank, M.; Baumgarten, G.; Priske, M.; Roegl, H. Process for Separation of Gases 2012. Patent WO 2012/00727, 5 January 2012. [Google Scholar]
- Scholz, M. Membrane Based Biogas Upgrading Processes. Ph.D. Thesis, Rheinisch-Westfälische Technische Hochschule Aachen University, Aachen, Germany, 2013. [Google Scholar]
- Böttcher, N.; Taron, J.; Kolditz, O.; Liedl, R.; Park, C.-H. Comparison of Equations of State for Carbon Dioxide for Numerical Simulations. In Proceedings of the ModelCARE2011, Leipzig, Germany, 18–22 September 2011; IAHS Press: Oxfordshire, UK, 2011; Volume 355. [Google Scholar]
- Guerrero Piña, J.C.; Alpízar, D.; Murillo, P.; Carpio-Chaves, M.; Pereira-Reyes, R.; Vega-Baudrit, J.; Villarreal, C. Advances in Mixed-Matrix Membranes for Biorefining of Biogas from Anaerobic Digestion. Front. Chem. 2024, 12, 1393696. [Google Scholar] [CrossRef]
- Weiland, P. Biogas Production: Current State and Perspectives. Appl. Microbiol. Biotechnol. 2010, 85, 849–860. [Google Scholar] [CrossRef]
- Petersson, A.; Wellinger, A. Biogas Upgrading Technologies-Developments and Innovations. Technical Report in IEA Bioenergy Task 37-Energy from Biogas and Landfill. Available online: https://task37.ieabioenergy.com/technical-reports/ (accessed on 20 August 2025).
- Li, Y.; Chen, D.; He, X. Preparation and Characterization of Polyvinylalcohol/Polysulfone Composite Membranes for Enhanced CO2/N2 Separation. Polymers 2023, 15, 124. [Google Scholar] [CrossRef] [PubMed]
- Kadirkhan, F.; Sean, G.P.; Ismail, A.F.; Wan Mustapa, W.N.F.; Halim, M.H.M.; Kian, S.W.; Yean, Y.S. CO2 Plasticization Resistance Membrane for Natural Gas Sweetening Process: Defining Optimum Operating Conditions for Stable Operation. Polymers 2022, 14, 4537. [Google Scholar] [CrossRef]
- Haider, S.; Lie, J.A.; Lindbråthen, A.; Hägg, M.B. Pilot–Scale Production of Carbon Hollow Fiber Membranes from Regenerated Cellulose Precursor-Part II: Carbonization Procedure. Membranes 2018, 8, 97. [Google Scholar] [CrossRef]
- Adewole, J.K.; Ahmad, A.L.; Ismail, S.; Leo, C.P. Current Challenges in Membrane Separation of CO2 from Natural Gas: A Review. Int. J. Greenh. Gas Control 2013, 17, 46–65. [Google Scholar] [CrossRef]
- Ansaloni, L.; Minelli, M.; Baschetti, M.G.; Sarti, G.C. Effects of Thermal Treatment and Physical Aging on the Gas Transport Properties in Matrimid®. Oil Gas Sci. Technol.-Rev. IFP Energ. Nouv. 2015, 70, 367–379. [Google Scholar] [CrossRef][Green Version]
- Robeson, L.M. The Upper Bound Revisited. J. Membr. Sci. 2008, 320, 390–400. [Google Scholar] [CrossRef]
- Iooss, B.; Da Veiga, S.; Janon, A.; Pujol, G. Sensitivity: Global Sensitivity Analysis of Model Outputs and Importance Measures, R Package Version 1.30.1; R Foundation for Statistical Computing; R Core Team: Vienna, Austria, 2024. [Google Scholar] [CrossRef]
- Marelli, S.; Sudret, B. UQLab: A Framework for Uncertainty Quantification in MATLAB. In Proceedings of the 2nd International Conference on Vulnerability and Risk Analysis and Management (ICVRAM 2014), Liverpool, UK, 13–16 July 2014; pp. 2554–2563. [Google Scholar] [CrossRef]
- Marelli, S.; Sudret, B. UQLab User Manual—Polynomial Chaos Expansions; Report UQLab-V2.1-104, Chair of Risk, Safety and Uncertainty Quantification; ETH Zurich: Zurich, Switzerland, 2024; Available online: https://www.uqlab.com/pce-user-manual (accessed on 20 August 2025).
- Zhang, B.Y.; Ni, Y.Q. A Novel Sparse Polynomial Chaos Expansion Technique with High Adaptiveness for Surrogate Modelling. Appl. Math. Model. 2023, 121, 562–585. [Google Scholar] [CrossRef]
- Porter, N.W. Wilks’ Formula Applied to Computational Tools: A Practical Discussion and Verification. Ann. Nucl. Energy 2019, 133, 129–137. [Google Scholar] [CrossRef]
- Bhati, N.; Dyson, P.J.; Nazeeruddin, M.K.; Maréchal, F. Techno-Economic Analysis Framework for Perovskite Solar Module Production at Various Manufacturing Capacities. Renew. Energy 2026, 256, 123752. [Google Scholar] [CrossRef]
- Sangregorio-Soto, V.; Garzón-Castro, C.L.; Mazzanti, G. Input Significance Ranking of Microalgae Continuous Culture Models. J. Chem. Technol. Biotechnol. 2023, 98, 1608–1619. [Google Scholar] [CrossRef]
- Kuncheekanna, V.N.; Jakobsen, J.P. Exploring Global Uncertainty Quantification and Sensitivity Analysis Methodologies: CO2 Capture Absorber Model with MEA Solvent as a Test Case. Chem. Eng. Res. Des. 2023, 200, 107–133. [Google Scholar] [CrossRef]
- Barahmand, Z. Comprehensive Local Sensitivity Analysis of the ADM1-Based Anaerobic Digestion Process. In The WIT Transactions on Ecology and the Environment; WIT Press: Southampton, UK, 2022; Volume 258, pp. 235–246. [Google Scholar] [CrossRef]
- Öner, M.; Stocks, S.M.; Sin, G. Comprehensive Sensitivity Analysis and Process Risk Assessment of Large Scale Pharmaceutical Crystallization Processes. Comput. Chem. Eng. 2020, 135, 106746. [Google Scholar] [CrossRef]
- Sepúlveda, F.D.; Cisternas, L.A.; Gálvez, E.D. The Use of Global Sensitivity Analysis for Improving Processes: Applications to Mineral Processing. Comput. Chem. Eng. 2014, 66, 221–232. [Google Scholar] [CrossRef]
- Mery, Y.; Tiruta-Barna, L.; Benetto, E.; Baudin, I. An Integrated “Process Modelling-Life Cycle Assessment” Tool for the Assessment and Design of Water Treatment Processes. Int. J. Life Cycle Assess. 2013, 18, 1062–1070. [Google Scholar] [CrossRef]
- Ruano, M.V.; Ribes, J.; Seco, A.; Ferrer, J. An Improved Sampling Strategy Based on Trajectory Design for Application of the Morris Method to Systems with Many Input Factors. Environ. Model. Softw. 2012, 37, 103–109. [Google Scholar] [CrossRef]
- Florio, C.; Fiorentino, G.; Corcelli, F.; Ulgiati, S.; Dumontet, S.; Güsewell, J.; Eltrop, L. A Life Cycle Assessment of Biomethane Production from Waste Feedstock through Different Upgrading Technologies. Energies 2019, 12, 718. [Google Scholar] [CrossRef]
- Da Conceicao, M.; Nemetz, L.; Rivero, J.; Hornbostel, K.; Lipscomb, G. Gas Separation Membrane Module Modeling: A Comprehensive Review. Membranes 2023, 13, 639. [Google Scholar] [CrossRef]
- Merkel, T.C.; Lin, H.; Wei, X.; Baker, R. Power Plant Post-Combustion Carbon Dioxide Capture: An Opportunity for Membranes. J. Membr. Sci. 2010, 359, 126–139. [Google Scholar] [CrossRef]

| Parameter Description | Nominal Value |
|---|---|
| Feed flow | 6692 mol/h |
| Mole fraction of CH4 in the feed | 0.6 |
| Mole fraction of CO2 in the feed | 0.4 |
| CO2/CH4 selectivity | 60 |
| CO2 permeance | 60 GPU |
| Retentate pressure (stage 2) | 16.0 bar |
| Permeate pressure (stage 1) | 3.3 bar |
| Permeate pressure (stages 2 and 3) | 1.0 bar |
| Area stage 1 | 167 m2 |
| Area stage 2 | 164 m2 |
| Area stage 3 | 254 m2 |
| Parameter | Description | Reference Value | Variation |
|---|---|---|---|
| FBG | Flow of biogas | 6692 mol/h | ±5%, ±10% of reference |
| xCO2BG | CO2 molar fraction of biogas | 40% | ±5%, ±10% |
| PCO2 | CO2 membrane permeance | 60 GPU | ±10% |
| S | CO2/CO4 selectivity | Equation (1) applied to 60 | ±5% |
| Response Variable | Definition |
|---|---|
| FBM | Molar flow of the upgraded biomethane (retentate of unit MB2) |
| xCH4BM | CH4 fraction of the upgraded biomethane |
| FOG | Molar flow of the off-gas stream (permeate of unit MB3) |
| xCO2G | CO2 fraction of the off-gas stream |
| EDC | Energy demand of compressor CP |
| HDX | Heat duty of heat exchanger HX |
| Response | Non-Controlled Scenario | Controlled Scenario |
|---|---|---|
| FBM | 4163 mol/h | 4154 mol/h |
| FOG | 2529 mol/h | 2538 mol/h |
| xCH4BM | 0.9579 | 0.9600 |
| xCO4OG | 0.9890 | 0.9891 |
| EDC | 29.95 kW | 30.12 kW |
| HDX | −29.78 kW | −29.97 kW |
| EDC/FBG | 16.11 kJ/mol | 16.21 kJ/mol |
| HDX/FBG | −16.02 kJ/mol | −16.12 kJ/mol |
| Response | Factor | Sobol’ Indices (Scenario NC) | Sobol’ Indices (Scenario C) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Si-5 | ST-5 | Si-10 | ST-10 | Si-5 | ST-5 | Si-10 | ST-10 | ||
| FBM | FBG | 0.700 | 0.700 | 0.711 | 0.712 | 0.703 | 0.703 | 0.703 | 0.704 |
| xCO2BG | 0.278 | 0.279 | 0.282 | 0.284 | 0.296 | 0.296 | 0.296 | 0.297 | |
| PCO2 | 0.021 | 0.021 | 0.005 | 0.006 | 0.001 | 0.001 | 0.000 | 0.000 | |
| S | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| FOG | FBG | 0.348 | 0.348 | 0.359 | 0.362 | 0.446 | 0.447 | 0.446 | 0.448 |
| xCO2BG | 0.605 | 0.606 | 0.626 | 0.628 | 0.551 | 0.552 | 0.551 | 0.553 | |
| PCO2 | 0.046 | 0.046 | 0.012 | 0.012 | 0.002 | 0.002 | 0.001 | 0.001 | |
| S | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| xCH4BM | FBG | 0.175 | 0.176 | 0.437 | 0.440 | ||||
| xCO2BG | 0.024 | 0.024 | 0.059 | 0.059 | |||||
| PCO2 | 0.795 | 0.797 | 0.498 | 0.501 | |||||
| S | 0.005 | 0.005 | 0.003 | 0.003 | |||||
| xCO2OG | FBG | 0.120 | 0.121 | 0.241 | 0.243 | 0.130 | 0.131 | 0.277 | 0.280 |
| xCO2BG | 0.208 | 0.209 | 0.420 | 0.422 | 0.161 | 0.162 | 0.343 | 0.346 | |
| PCO2 | 0.647 | 0.649 | 0.323 | 0.327 | 0.686 | 0.688 | 0.364 | 0.368 | |
| S | 0.023 | 0.023 | 0.011 | 0.012 | 0.021 | 0.021 | 0.011 | 0.012 | |
| EDC | FBG | 0.993 | 0.994 | 0.998 | 0.998 | 0.902 | 0.903 | 0.970 | 0.971 |
| xCO2BG | 0.000 | 0.000 | 0.000 | 0.000 | 0.002 | 0.003 | 0.002 | 0.002 | |
| PCO2 | 0.000 | 0.000 | 0.000 | 0.000 | 0.093 | 0.093 | 0.026 | 0.027 | |
| S | 0.006 | 0.006 | 0.002 | 0.002 | 0.002 | 0.002 | 0.000 | 0.000 | |
| HDX | FBG | 0.993 | 0.993 | 0.998 | 0.998 | 0.891 | 0.891 | 0.967 | 0.968 |
| xCO2BG | 0.000 | 0.000 | 0.000 | 0.001 | 0.002 | 0.002 | 0.002 | 0.002 | |
| PCO2 | 0.000 | 0.001 | 0.000 | 0.000 | 0.105 | 0.106 | 0.030 | 0.031 | |
| S | 0.006 | 0.006 | 0.002 | 0.002 | 0.002 | 0.002 | 0.000 | 0.000 | |
| Response | Units | Sc. | FV | Mean | LTL | UTL | RLG 1 | RUG 2 | CV 3 |
|---|---|---|---|---|---|---|---|---|---|
| FBM | mol/h | NC | ±5% | 4161 | 3829 | 4502 | 7.98% | 8.19% | 3.75% |
| NC | ±10% | 4159 | 3510 | 4812 | 15.61% | 15.70% | 7.45% | ||
| C | ±5% | 4151 | 3837 | 4438 | 7.57% | 6.93% | 3.50% | ||
| C | ±10% | 4148 | 3532 | 4731 | 14.86% | 14.06% | 7.01% | ||
| FOG | mol/h | NC | ±5% | 2525 | 2305 | 2753 | 8.72% | 9.03% | 4.20% |
| NC | ±10% | 2521 | 2116 | 2974 | 16.05% | 17.98% | 8.25% | ||
| C | ±5% | 2535 | 2325 | 2761 | 8.30% | 8.91% | 4.21% | ||
| C | ±10% | 2532 | 2119 | 2991 | 16.28% | 18.14% | 8.41% | ||
| xCH4BM | – | NC | ±5% | 0.958 | 0.947 | 0.966 | 1.17% | 0.84% | 0.45% |
| NC | ±10% | 0.958 | 0.943 | 0.968 | 1.58% | 1.11% | 0.59% | ||
| xCO2OG | – | NC | ±5% | 0.989 | 0.985 | 0.993 | 0.41% | 0.41% | 0.19% |
| NC | ±10% | 0.989 | 0.982 | 0.994 | 0.64% | 0.58% | 0.27% | ||
| C | ±5% | 0.989 | 0.985 | 0.993 | 0.45% | 0.44% | 0.20% | ||
| C | ±10% | 0.989 | 0.982 | 0.995 | 0.67% | 0.60% | 0.29% | ||
| EDC | kW | NC | ±5% | 29.94 | 28.39 | 31.47 | 5.19% | 5.12% | 3.04% |
| NC | ±10% | 29.92 | 26.91 | 32.97 | 10.09% | 10.16% | 6.08% | ||
| C | ±5% | 30.12 | 28.15 | 32.45 | 6.54% | 7.72% | 3.70% | ||
| C | ±10% | 30.11 | 26.63 | 34.27 | 11.57% | 13.80% | 7.22% | ||
| HDX | kW | NC | ±5% | 29.77 | 28.22 | 31.30 | 5.21% | 5.14% | 3.05% |
| NC | ±10% | 29.76 | 26.74 | 32.80 | 10.13% | 10.24% | 6.10% | ||
| C | ±5% | 29.97 | 27.95 | 32.35 | 6.72% | 7.94% | 3.77% | ||
| C | ±10% | 29.96 | 26.42 | 34.18 | 11.82% | 14.09% | 7.33% | ||
| EDC/FBG | kJ/mol | NC | ±5% | 16.12 | 16.03 | 16.21 | 0.56% | 0.53% | 0.27% |
| NC | ±10% | 16.13 | 16.00 | 16.26 | 0.78% | 0.85% | 0.35% | ||
| C | ±5% | 16.22 | 15.84 | 16.69 | 2.33% | 2.89% | 1.23% | ||
| C | ±10% | 16.22 | 15.65 | 16.88 | 3.49% | 4.06% | 1.70% | ||
| HDX/FBG | kJ/mol | NC | ±5% | 16.03 | 15.94 | 16.12 | 0.55% | 0.57% | 0.28% |
| NC | ±10% | 16.04 | 15.91 | 16.19 | 0.76% | 0.96% | 0.37% | ||
| C | ±5% | 16.13 | 15.73 | 16.63 | 2.49% | 3.10% | 1.32% | ||
| C | ±10% | 16.13 | 15.54 | 16.83 | 3.70% | 4.33% | 1.82% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gozálvez-Zafrilla, J.M.; Santafé-Moros, A. Uncertainty and Global Sensitivity Analysis of a Membrane Biogas Upgrading Process Using the COCO Simulator. ChemEngineering 2025, 9, 94. https://doi.org/10.3390/chemengineering9050094
Gozálvez-Zafrilla JM, Santafé-Moros A. Uncertainty and Global Sensitivity Analysis of a Membrane Biogas Upgrading Process Using the COCO Simulator. ChemEngineering. 2025; 9(5):94. https://doi.org/10.3390/chemengineering9050094
Chicago/Turabian StyleGozálvez-Zafrilla, José M., and Asunción Santafé-Moros. 2025. "Uncertainty and Global Sensitivity Analysis of a Membrane Biogas Upgrading Process Using the COCO Simulator" ChemEngineering 9, no. 5: 94. https://doi.org/10.3390/chemengineering9050094
APA StyleGozálvez-Zafrilla, J. M., & Santafé-Moros, A. (2025). Uncertainty and Global Sensitivity Analysis of a Membrane Biogas Upgrading Process Using the COCO Simulator. ChemEngineering, 9(5), 94. https://doi.org/10.3390/chemengineering9050094








