Graph Neural Networks for Sustainable Energy: Predicting Adsorption in Aromatic Molecules
Abstract
1. Introduction
- Preparing specialized datasets by performing an ensemble extraction on existing data and segregating aromatic molecules (Section 3.1);
- Implementing and comparing fine-tuning strategies, including full model retraining and partial updates where key model components are systematically frozen (Section 3.2.2);
- Analyzing the role of model components to understand how Interaction and Output Blocks contribute to domain adaptation;
- Evaluating the impact of data diversity by augmenting the training set with chemically related, out-of-domain molecules.
2. Background
2.1. Adsorption Energy
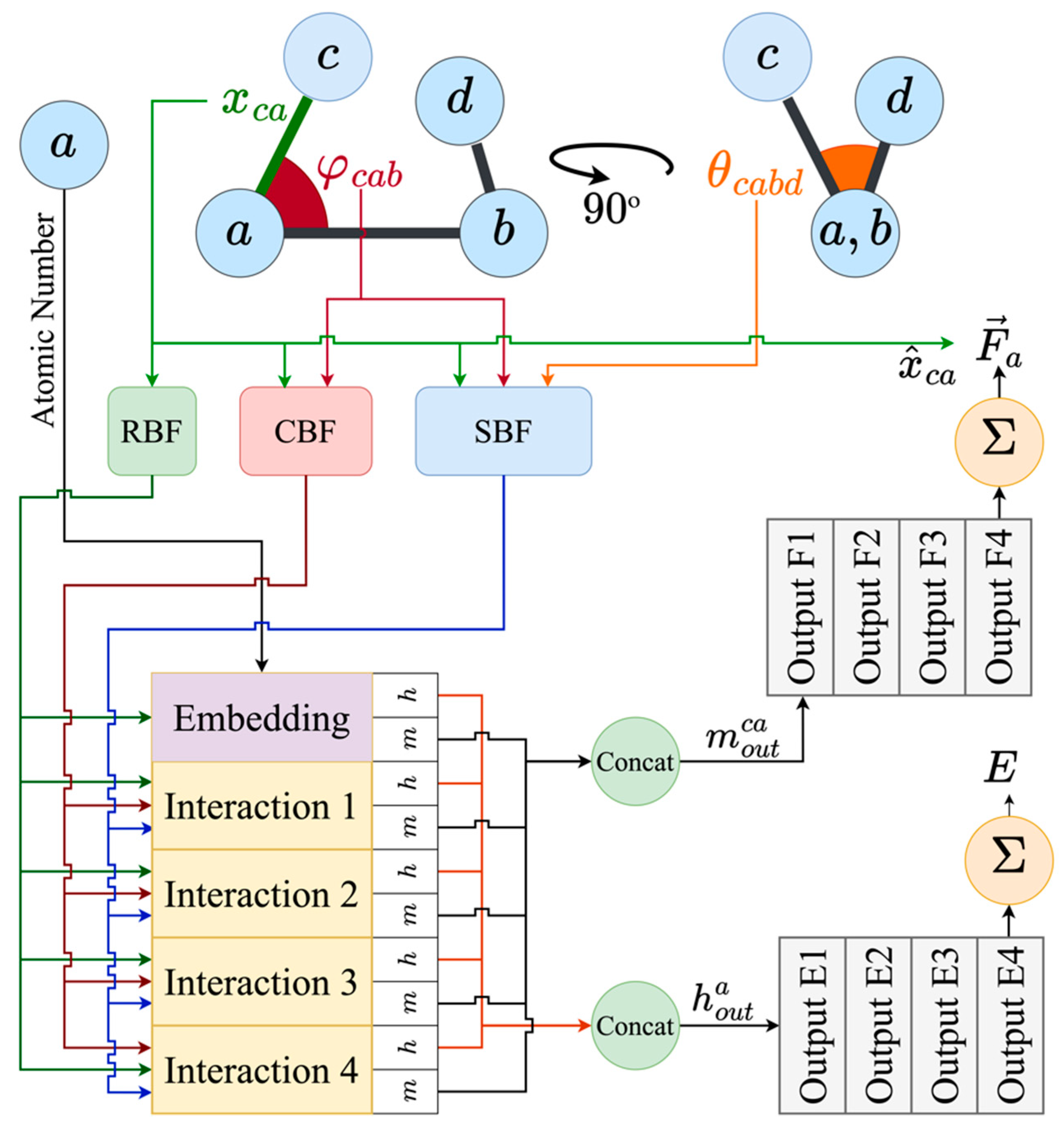
2.2. Equivariant GNNS for Adsorption Energy Prediction
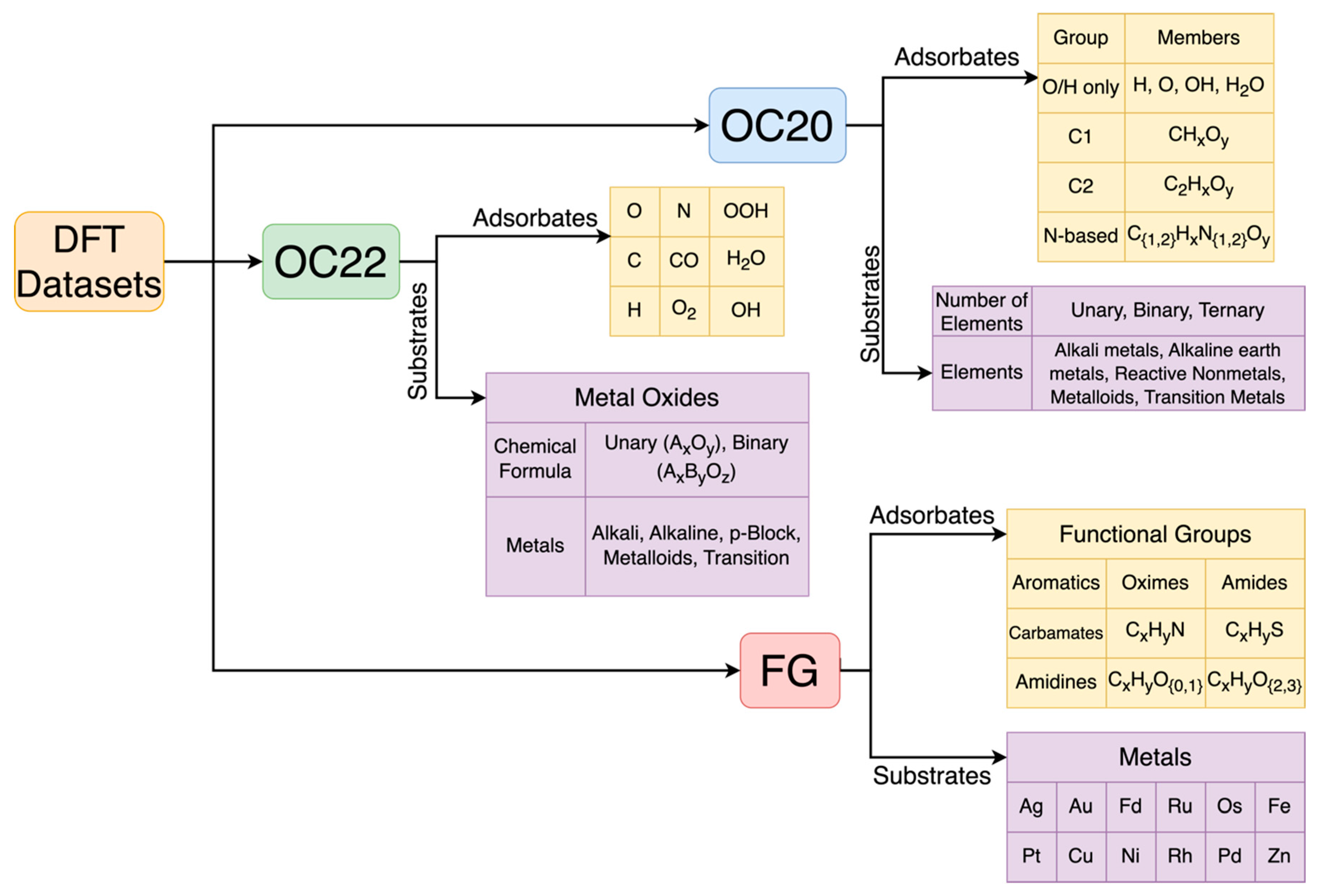
2.3. DFT Datasets
2.3.1. Open Catalyst Datasets (OC20 and OC22)
2.3.2. FG Dataset
2.4. Challenges in Applying GNNs to Predict Adsorption Energies for Large Molecules
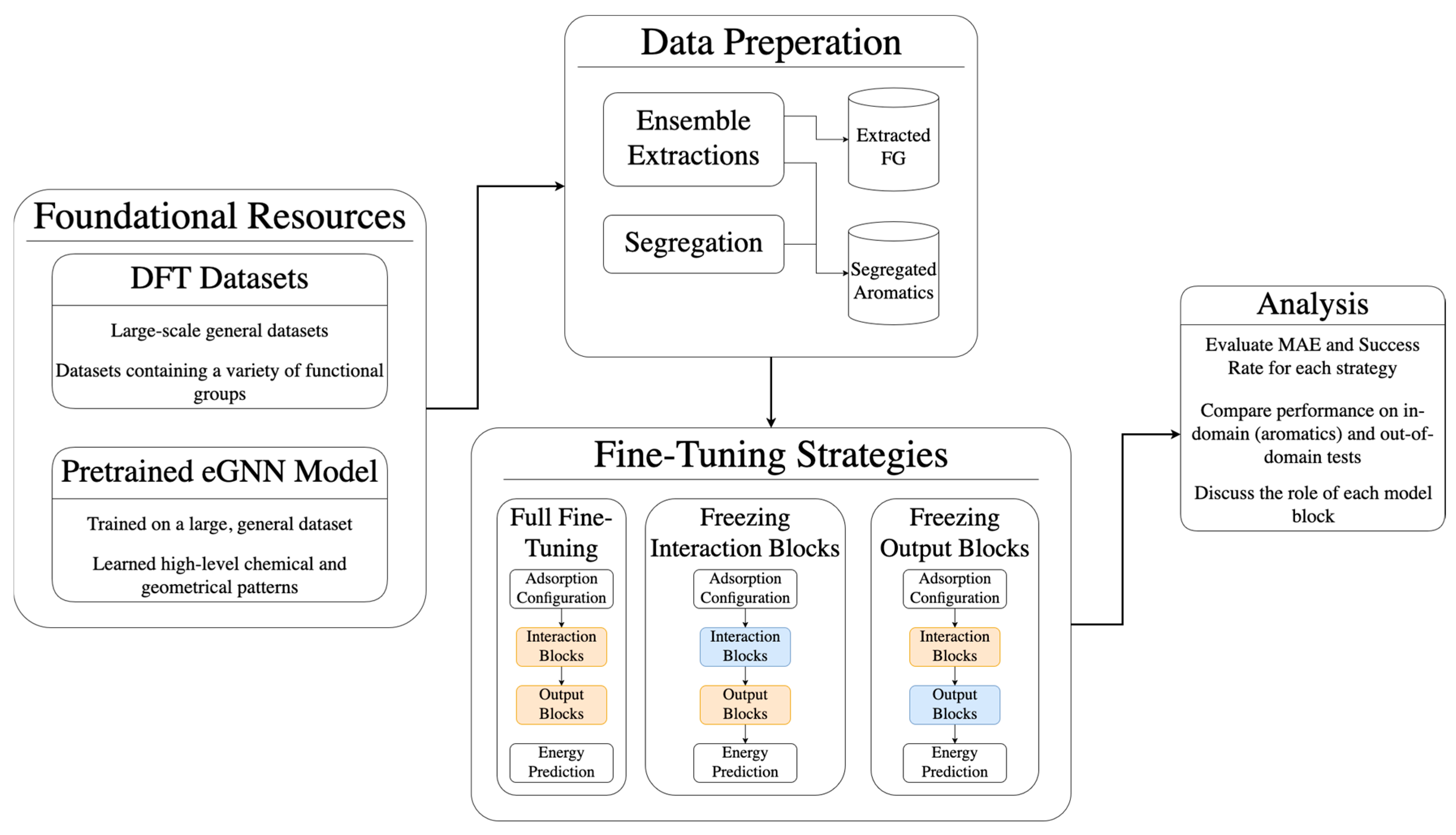
3. Methods
3.1. Processing the Dataset
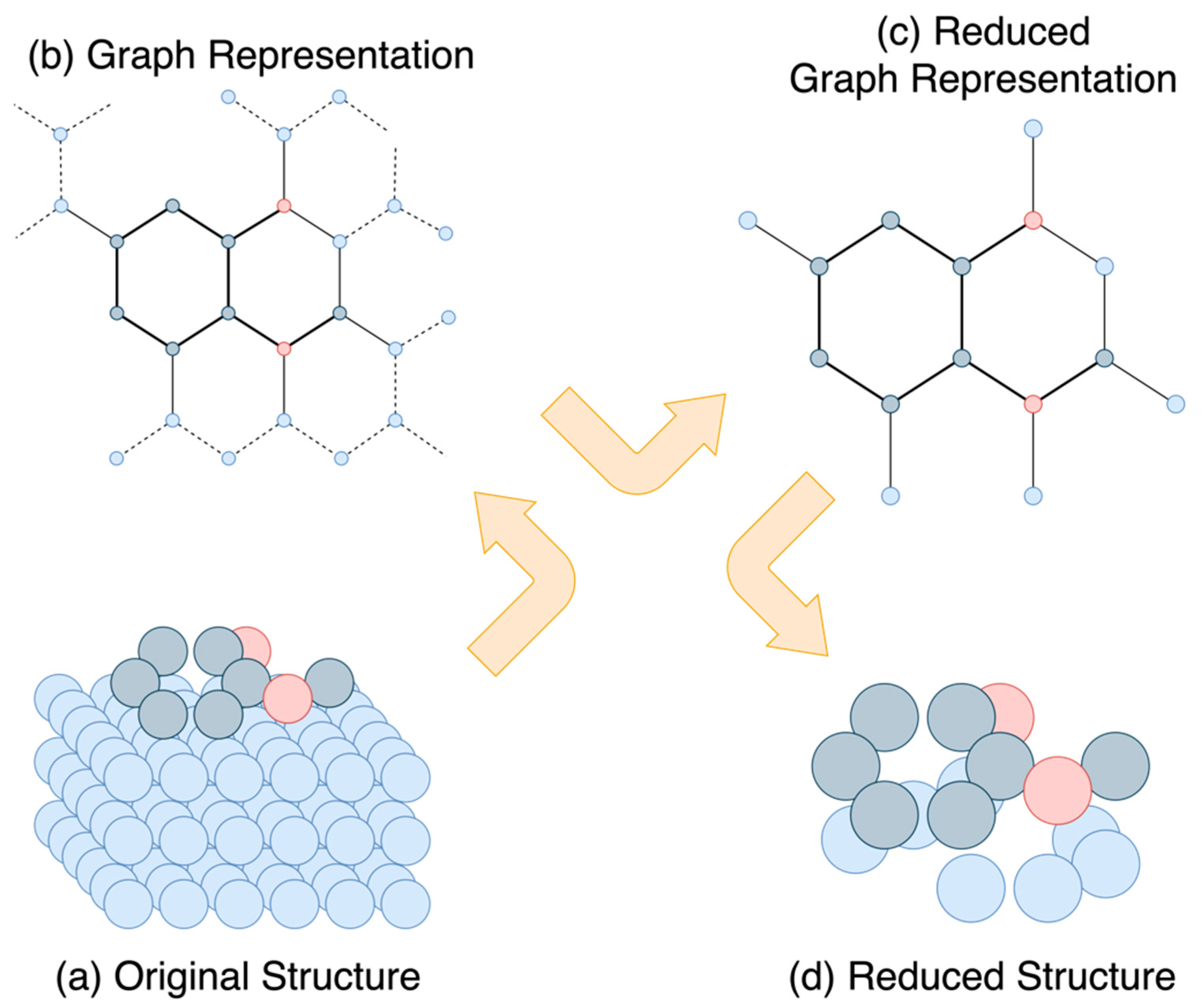
3.1.1. Ensemble Extraction
3.1.2. Segregating the Functional Groups
3.2. Fine-Tuning Details
3.2.1. The Pretrained Model
3.2.2. Fine-Tuning Strategies
3.2.3. Evaluation Metrics
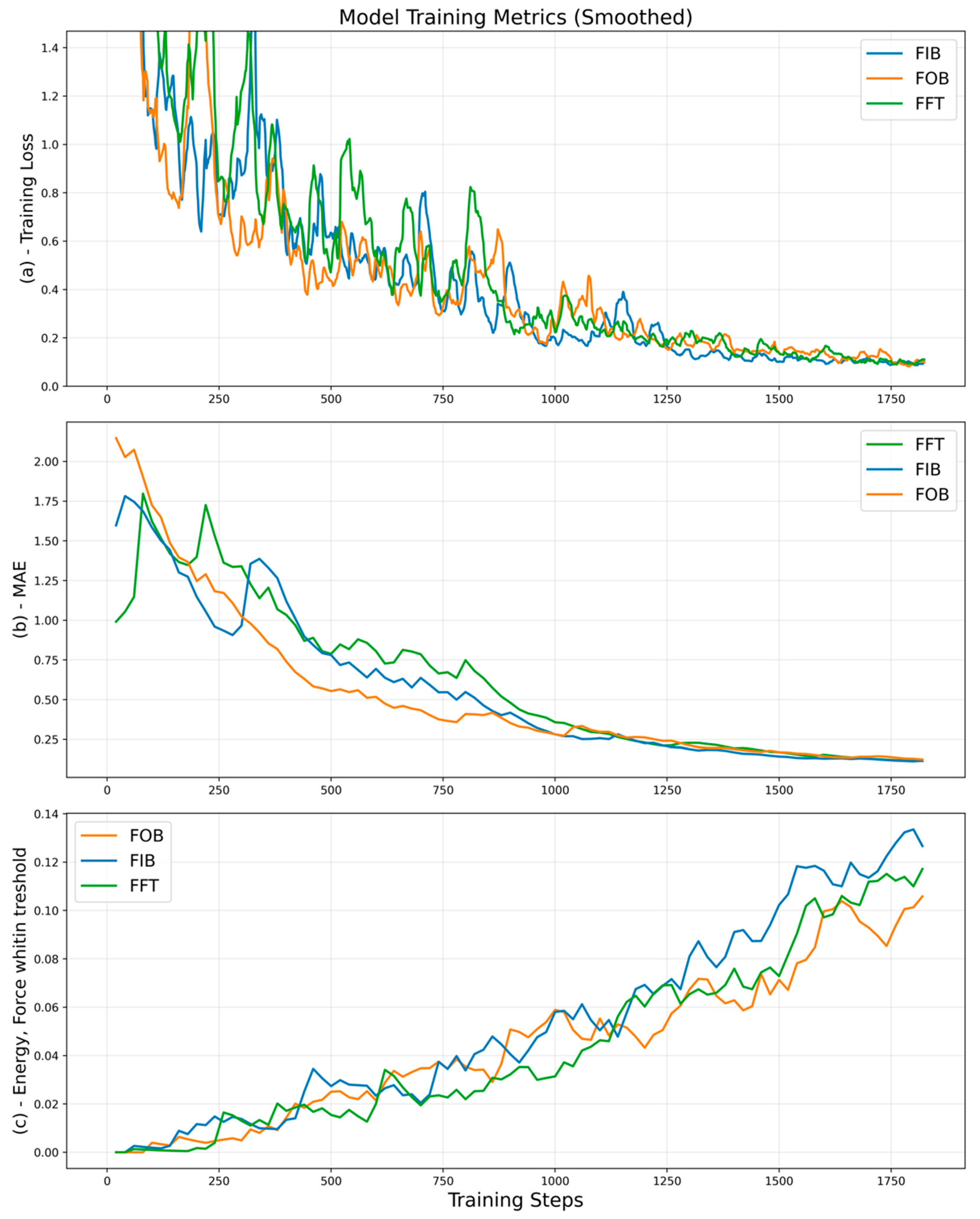
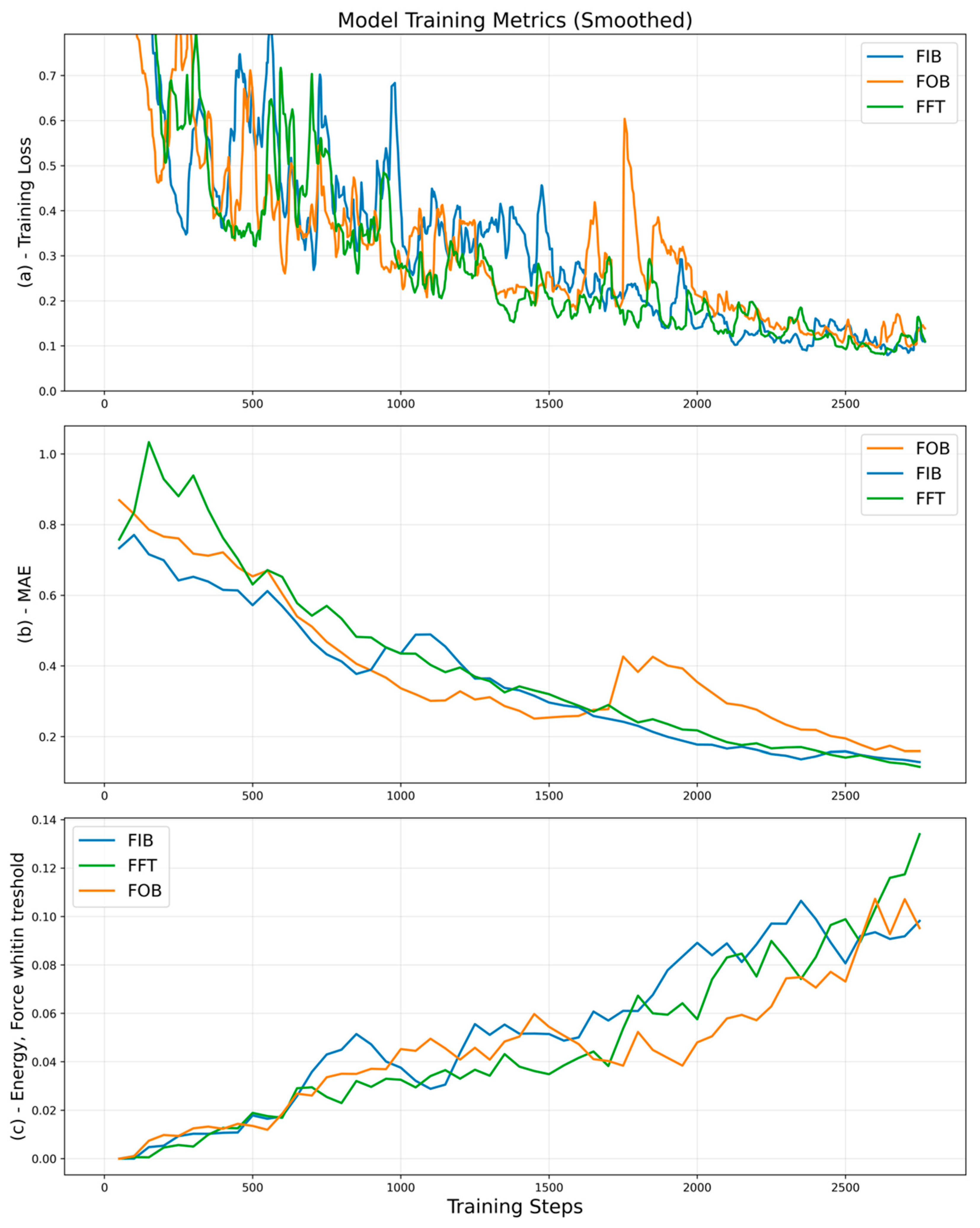
4. Results and Discussions
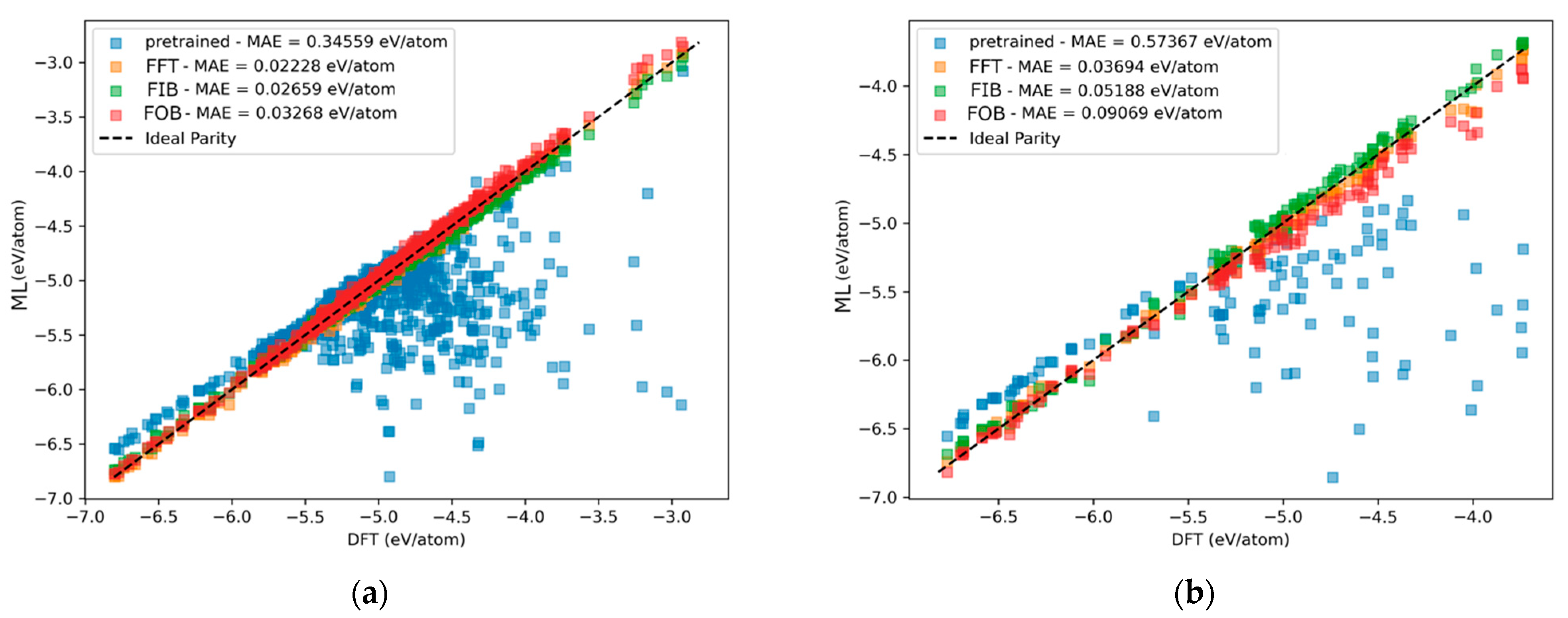
4.1. Comparing Data Diversity
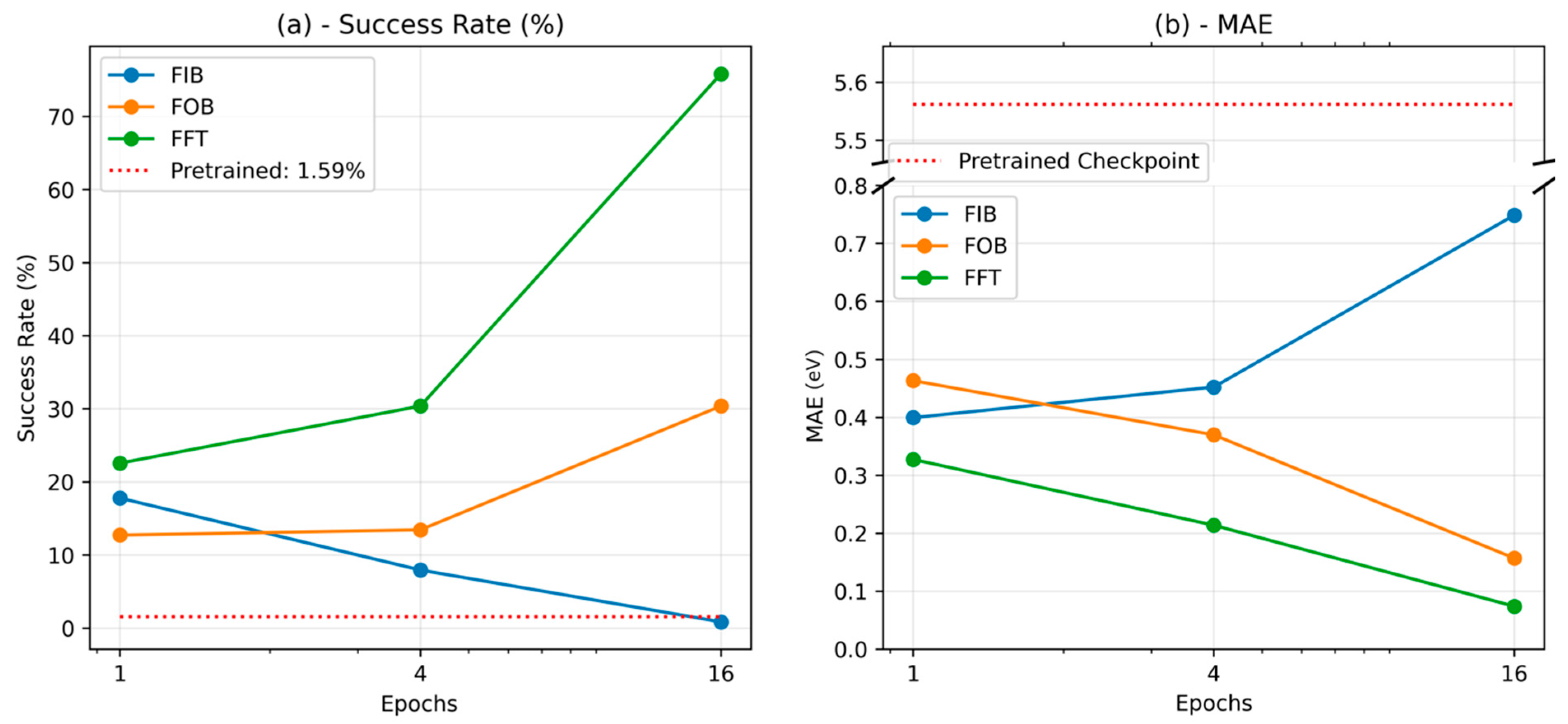
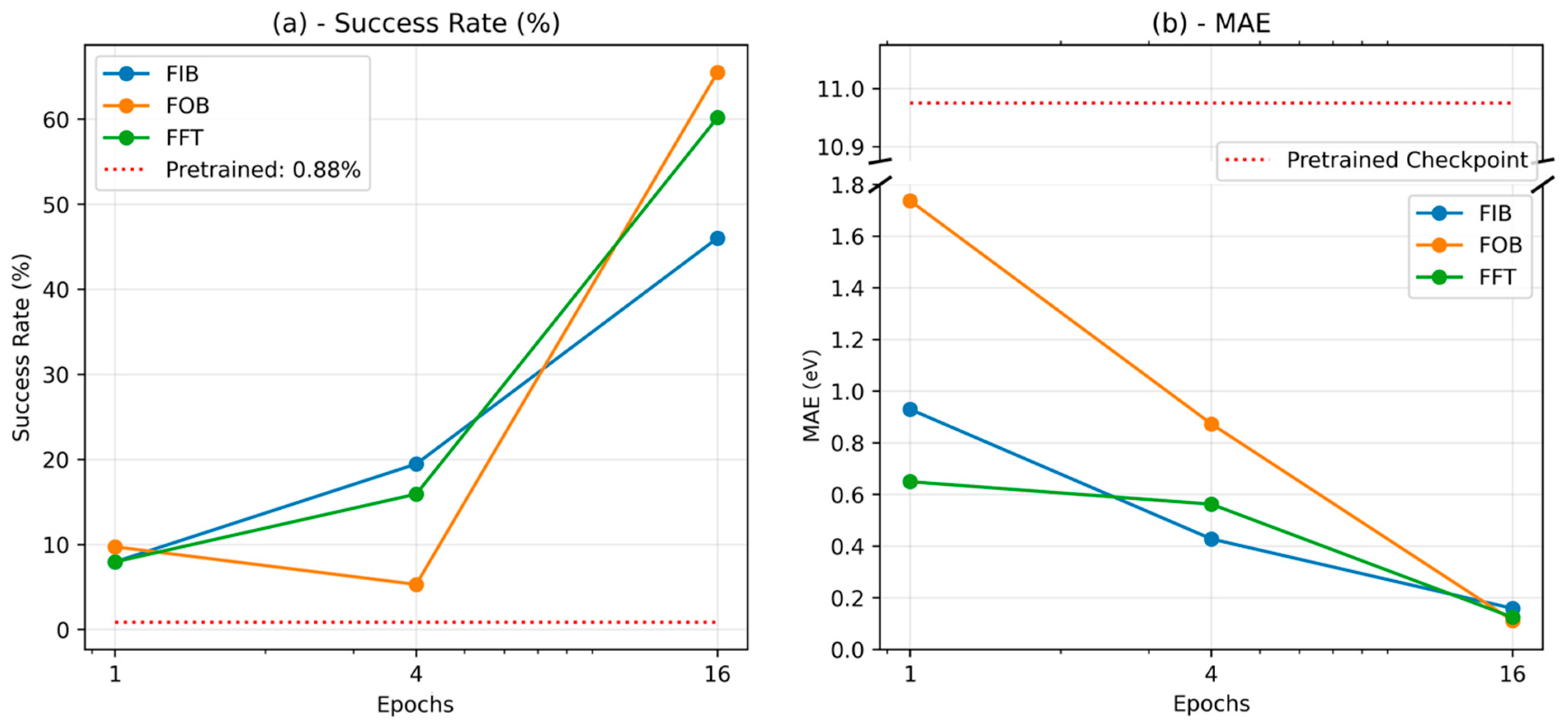
4.2. Comparing Fine-Tuning Strategies
4.3. Implications
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Advances in Fine-Tuning GNNs
Appendix A.2. Equivariant GNNs
Appendix A.3. Details on the Architecture of GemNet-OC
| Module | Layer Name | Type | Neurons (in→out) |
|---|---|---|---|
| Embedding Init | atom_emb.embeddings | Embedding | (83 elements → 256-dim vector) |
| edge_emb.dense.linear | Linear + SiLU | 640 → 512 | |
| Basis Embedding (Quadruplet) | mlp_rbf_qint.linear | Linear | 128 → 16 |
| mlp_cbf_qint | Basis Embedding | (implicit) | |
| mlp_sbf_qint | Basis Embedding | (implicit) | |
| Basis Embedding (Atom–Edge Interaction) | mlp_rbf_aeint.linear | Linear | 128 → 16 |
| mlp_cbf_aeint | Basis Embedding | (implicit) | |
| mlp_rbf_eaint.linear | Linear | 128 → 16 | |
| mlp_cbf_eaint | Basis Embedding | (implicit) | |
| mlp_rbf_aint | Basis Embedding | (implicit) | |
| Basis Embedding (Triplet) | mlp_rbf_tint.linear | Linear | 128 → 16 |
| mlp_cbf_tint | Basis Embedding | (implicit) | |
| Misc/Basis Embedding | mlp_rbf_h.linear | Linear | 128 → 16 |
| mlp_rbf_out.linear | Linear | 128 → 16 |
| Module | Layer Name | Type | Neurons (in→out) |
|---|---|---|---|
| Core Update (edge) | dense_ca.linear | Linear + SiLU | 512 → 512 |
| Triplet Interaction (trip_interaction) | dense_ba.linear | Linear + SiLU | 512 → 512 |
| mlp_rbf.linear | Linear | 16 → 512 | |
| mlp_cbf.bilinear.linear | Efficient Bilinear | 1024 → 64 | |
| down_projection.linear | Linear + SiLU | 512 → 64 | |
| up_projection_ca.linear | Linear + SiLU | 64 → 512 | |
| up_projection_ac.linear | Linear + SiLU | 64 → 512 | |
| Quadruplet Interaction (quad_interaction) | dense_db.linear | Linear + SiLU | 512 → 512 |
| mlp_rbf.linear | Linear | 16 → 512 | |
| mlp_cbf.linear | Linear | 16 → 32 | |
| mlp_sbf.bilinear.linear | Efficient Bilinear | 1024 → 32 | |
| down_projection.linear | Linear + SiLU | 512 → 32 | |
| up_projection_ca.linear | Linear + SiLU | 32 → 512 | |
| up_projection_ac.linear | Linear + SiLU | 32 → 512 | |
| Atom–Edge Interaction (atom_edge_interaction) | dense_ba.linear | Linear + SiLU | 256 → 256 |
| mlp_rbf.linear | Linear | 16 → 256 | |
| mlp_cbf.bilinear.linear | Efficient Bilinear | 1024 → 64 | |
| down_projection.linear | Linear + SiLU | 256 → 64 | |
| up_projection_ca.linear | Linear + SiLU | 64 → 512 | |
| up_projection_ac.linear | Linear + SiLU | 64 → 512 | |
| Edge–Atom Interaction (edge_atom_interaction) | dense_ba.linear | Linear + SiLU | 512 → 512 |
| mlp_rbf.linear | Linear | 16 → 512 | |
| mlp_cbf.bilinear.linear | Efficient Bilinear | 1024 → 64 | |
| down_projection.linear | Linear + SiLU | 512 → 64 | |
| up_projection_ca.linear | Linear + SiLU | 64 → 256 | |
| Atom–Atom Interaction (atom_interaction) | bilinear.linear | Bilinear | 1024 → 64 |
| down_projection.linear | Linear + SiLU | 256 → 64 | |
| up_projection.linear | Linear + SiLU | 64 → 256 | |
| Edge Residual Stack (before skip ×2) | Residual Layers (Edge) | 512 → 512 ×2 per Residual | |
| Atom Residual Stack (atom_emb_layers ×2) | Residual Layers (Atom) | 256 → 256 ×2 per Residual | |
| Atom Update (atom_update) | dense_rbf.linear | Linear | 16 → 512 |
| layers[0].linear | Linear + SiLU | 512 → 256 | |
| layers[1–3] | Residual (2× Linear each) | 256 → 256 ×2 per Residual | |
| Post-Concat. Layer | concat_layer.dense.linear | Linear + SiLU | 1024 → 512 |
| Final Residual Layer | residual_m[0] | Residual (2× Linear) | 512 → 512 ×2 |
| Module | Layer Name | Type | Neurons (in→out) |
|---|---|---|---|
| Output Block | dense_rbf.linear | Linear | 16 → 512 |
| layers[0].linear | Linear + SiLU | 512 → 256 | |
| layers[1–3] | Residual (2× Linear each) | 256 → 256 ×2 per Residual | |
| Energy Head (per block) | seq_energy_pre[0].linear | Linear + SiLU | 512 → 256 |
| seq_energy_pre[1–3] | Residual (2× Linear each) | 256 → 256 ×2 per Residual | |
| seq_energy2[0–2] | Residual (2× Linear each) | 256 → 256 ×2 per Residual | |
| Force Prediction Head | dense_rbf_F.linear | Linear | 16 → 512 |
| seq_forces[0–2] | Residual (2× Linear each) | 512 → 512 ×2 per Residual |
| Module | Layer Name | Type | Neurons (in→out) |
|---|---|---|---|
| Global Output MLP | out_mlp_E[0].linear | Linear + SiLU | 1280 → 256 |
| out_mlp_E[1–2] | Residual (2× Linear each) | 256 → 256 ×2 per Residual | |
| Final Energy Output | out_energy.linear | Linear | 256 → 1 |
| Global Force MLP | out_mlp_F[0].linear | Linear + SiLU | 2560 → 512 |
| out_mlp_F[1–2] | Residual (2× Linear each) | 512 → 512 ×2 per Residual | |
| Final Force Output | out_forces.linear | Linear | 512 → 1 |
Appendix B
References
- Liggio, J.J.; Li, S.M.; Hayden, K.; Taha, Y.M.; Stroud, C.; Darlington, A.; Drollette, B.D.; Gordon, M.; Lee, P.; Liu, P.; et al. Oil sands operations as a large source of secondary organic aerosols. Nature 2016, 534, 91–94. [Google Scholar] [CrossRef] [PubMed]
- Mullins, O.C. The Asphaltenes. Annu. Rev. Anal. Chem. 2011, 4, 393–418. [Google Scholar] [CrossRef]
- Torres, A.; Suárez, J.A.; Remesal, E.R.; Márquez, A.M.; Sanz, J.F.; Cañibano, C.R. Adsorption of Prototypical Asphaltenes on Silica: First-Principles DFT Simulations Including Dispersion Corrections. J. Phys. Chem. B 2018, 122, 618–624. [Google Scholar] [CrossRef]
- Fan, S.; Wang, H.; Wang, P.; Jiao, W.; Wang, S.; Qin, Z.; Dong, M.; Wang, J.; Fan, W. Formation and evolution of the coke precursors on the zeolite catalyst in the conversion of methanol to olefins. Chem. Catal. 2024, 4, 100927. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, H.B.; Zhou, D.; Liu, B. Adsorption Energy in Oxygen Electrocatalysis. Chem. Rev. 2022, 122, 17028–17072. [Google Scholar] [CrossRef]
- Nørskov, J.K.; Rossmeisl, J.; Logadottir, A.; Lindqvist, L.; Kitchin, J.R.; Bligaard, T.; Jónsson, H. Origin of the overpotential for oxygen reduction at a fuel-cell cathode. J. Phys. Chem. B 2004, 108, 17886–17892. [Google Scholar] [CrossRef]
- Chandrakumar, K.R.S.; Ghosh, S.K. Alkali-Metal-Induced Enhancement of Hydrogen Adsorption in C60 Fullerene: An ab Initio Study. Nano Lett. 2008, 8, 13–19. [Google Scholar] [CrossRef]
- Pablo-García, S.; Morandi, S.; Vargas-Hernández, R.A.; Jorner, K.; Ivković, Ž.; López, N.; Aspuru-Guzik, A. Fast evaluation of the adsorption energy of organic molecules on metals via graph neural networks. Nat. Comput. Sci. 2023, 3, 433–442. [Google Scholar] [CrossRef]
- Ehrlich, S.; Moellmann, J.; Grimme, S. Dispersion-Corrected Density Functional Theory for Aromatic Interactions in Complex Systems. Acc. Chem. Res. 2013, 46, 916–926. [Google Scholar] [CrossRef]
- Lan, J.; Palizhati, A.; Shuaibi, M.; Wood, B.M.; Wander, B.; Das, A.; Uyttendaele, M.; Zitnick, C.L.; Ulissi, Z.W. AdsorbML: A leap in efficiency for adsorption energy calculations using generalizable machine learning potentials. npj Comput. Mater. 2023, 9, 172. [Google Scholar] [CrossRef]
- Liao, Y.-L.; Smidt, T. Equiformer: Equivariant Graph Attention Transformer for 3D Atomistic Graphs. arXiv 2022, arXiv:2206.11990. [Google Scholar]
- Gasteiger, J.; Giri, S.; Margraf, J.T.; Günnemann, S. Fast and Uncertainty-Aware Directional Message Passing for Non-Equilibrium. arXiv 2020, arXiv:2011.14115. [Google Scholar]
- Unke, O.T.; Meuwly, M. PhysNet: A Neural Network for Predicting Energies, Forces, Dipole Moments, and Partial Charges. J. Chem. Theory Comput. 2019, 15, 3678–3693. [Google Scholar] [CrossRef]
- Jiao, Z.; Mao, Y.; Lu, R.; Liu, Y.; Guo, L.; Wang, Z. Fine-Tuning Graph Neural Networks via Active Learning: Unlocking the Potential of Graph Neural Networks Trained on Nonaqueous Systems for Aqueous CO2 Reduction. J. Chem. Theory Comput. 2025, 21, 3176–3186. [Google Scholar] [CrossRef]
- Falk, J.; Bonati, L.; Novelli, P.; Parrinello, M.; Pontil, M. Transfer learning for atomistic simulations using GNNs and kernel mean embeddings. arXiv 2023, arXiv:2306.01589. [Google Scholar]
- Liao, Y.-L.; Wood, B.; Das, A.; Smidt, T. EquiformerV2: Improved Equivariant Transformer for Scaling to Higher-Degree Representations. arXiv 2023, arXiv:2306.12059. [Google Scholar]
- Schütt, K.T.; Unke, O.T.; Gastegger, M. Equivariant message passing for the prediction of tensorial properties and molecular spectra. arXiv 2021, arXiv:2102.03150. [Google Scholar] [CrossRef]
- Chanussot, L.; Das, A.; Goyal, S.; Lavril, T.; Shuaibi, M.; Riviere, M.; Tran, K.; Heras-Domingo, J.; Ho, C.; Hu, W.; et al. 2020 (OC20) Dataset and Community Challenges. ACS Catal. 2021, 11, 6059–6072. [Google Scholar] [CrossRef]
- Facebookresearch. Fairchem. 2020. Available online: https://Github.Com/Facebookresearch/Fairchem (accessed on 15 March 2025).
- Sriram, A.; Choi, S.; Yu, X.; Brabson, L.M.; Das, A.; Ulissi, Z.; Uyttendaele, M.; Medford, A.J.; Sholl, D.S. The Open DAC 2023 Dataset and Challenges for Sorbent Discovery in Direct Air Capture. ACS Cent. Sci. 2024, 10, 923–941. [Google Scholar] [CrossRef]
- Lee, Y.; Chen, A.S.; Tajwar, F.; Kumar, A.; Yao, H.; Liang, P.; Finn, C. Surgical Fine-Tuning Improves Adaptation to Distribution Shifts. arXiv 2022, arXiv:2210.11466. [Google Scholar]
- Peterson, A.A. Global optimization of adsorbate-surface structures while preserving molecular identity. Top. Catal. 2014, 57, 40–53. [Google Scholar] [CrossRef]
- Montoya, J.H.; Persson, K.A. A high-throughput framework for determining adsorption energies on solid surfaces. npj Comput. Mater. 2017, 3, 14. [Google Scholar] [CrossRef]
- Jung, H.; Sauerland, L.; Stocker, S.; Reuter, K.; Margraf, J.T. Machine-learning driven global optimization of surface adsorbate geometries. npj Comput. Mater. 2023, 9, 114. [Google Scholar] [CrossRef]
- Gilmer, J.; Schoenholz, S.S.; Riley, P.F.; Vinyals, O.; Dahl, G.E. Neural Message Passing for Quantum Chemistry. arXiv 2017, arXiv:1704.01212. [Google Scholar] [CrossRef]
- Kong, J.-G.; Zhao, K.-L.; Li, J.; Li, Q.-X.; Liu, Y.; Zhang, R.; Zhu, J.-J.; Chang, K. Self-supervised Representations and Node Embedding Graph Neural Networks for Accurate and Multi-scale Analysis of Materials. arXiv 2022, arXiv:2211.03563. [Google Scholar] [CrossRef]
- Gutiérrez-Gómez, L.; Delvenne, J.C. Unsupervised network embeddings with node identity awareness. Appl. Netw. Sci. 2019, 4, 82. [Google Scholar] [CrossRef]
- Gasteiger, J.; Groß, J.; Günnemann, S. Directional Message Passing for Molecular Graphs. arXiv 2020, arXiv:2003.03123. [Google Scholar]
- Tran, R.; Lan, J.; Shuaibi, M.; Wood, B.M.; Goyal, S.; Das, A.; Heras-Domingo, J.; Kolluru, A.; Rizvi, A.; Shoghi, N.; et al. The Open Catalyst 2022 (OC22) Dataset and Challenges for Oxide Electrocatalysts. ACS Catal. 2023, 13, 3066–3084. [Google Scholar] [CrossRef]
- Gasteiger, J.; Shuaibi, M.; Sriram, A.; Günnemann, S.; Ulissi, Z.; Zitnick, C.L.; Das, A. GemNet-OC: Developing Graph Neural Networks for Large and Diverse Molecular Simulation Datasets. arXiv 2022, arXiv:2204.02782. [Google Scholar]
- Gasteiger, J.; Becker, F.; Günnemann, S. GemNet: Universal Directional Graph Neural Networks for Molecules. arXiv 2021, arXiv:2106.08903. [Google Scholar]
- Yan, Z.; Zhang, H.; Piramuthu, R.; Jagadeesh, V.; DeCoste, D.; Di, W.; Yu, Y. HD-CNN: Hierarchical Deep Convolutional Neural Networks for Large Scale Visual Recognition. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 2740–2748. [Google Scholar]
- Liu, J.-m.; Yang, M.-h.; Xiang, Y. Hierarchical features learning with convolutional neural networks based on aircraft recognition on images from remote sensing image. In Proceedings of the 2016 IEEE International Conference on Consumer Electronics-China (ICCE-China), Shenzhen, China, 19–21 December 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, M.; Kitchin, J.R. Neural network embeddings based similarity search method for atomistic systems. Digit. Discov. 2022, 1, 636–644. [Google Scholar] [CrossRef]
- Kolluru, A.; Shuaibi, M.; Palizhati, A.; Shoghi, N.; Das, A.; Wood, B.; Zitnick, C.L.; Kitchin, J.R.; Ulissi, Z.W. Open Challenges in Developing Generalizable Large-Scale Machine-Learning Models for Catalyst Discovery. ACS Catal. 2022, 12, 8572–8581. [Google Scholar] [CrossRef]
- Schaarschmidt, M.; Riviere, M.; Ganose, A.M.; Spencer, J.S.; Gaunt, A.L.; Kirkpatrick, J.; Axelrod, S.; Battaglia, P.W.; Godwin, J. Learned Force Fields Are Ready for Ground State Catalyst Discovery. arXiv 2022, arXiv:2209.12466. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Wimmer, P.; Mehnert, J.; Condurache, A.P. Dimensionality reduced training by pruning and freezing parts of a deep neural network: A survey. Artif. Intell. Rev. 2023, 56, 14257–14295. [Google Scholar] [CrossRef]
- Miao, Z.; Zhao, M. Weight-freezing: A motor imagery inspired regularization approach for EEG classification. Biomed. Signal Process. Control 2025, 100, 107015. [Google Scholar] [CrossRef]
- Macchietto, S.; Hewitt, G.F.; Coletti, F.; Crittenden, B.D.; Dugwell, D.R.; Galindo, A.; Jackson, G.; Kandiyoti, R.; Kazarian, S.G.; Luckham, P.F.; et al. Fouling in Crude Oil Preheat Trains: A Systematic Solution to an Old Problem. Heat Transf. Eng. 2011, 32, 197–215. [Google Scholar] [CrossRef]
- Sdanghi, G.; Canevesi, R.L.S.; Celzard, A.; Thommes, M.; Fierro, V. Characterization of Carbon Materials for Hydrogen Storage and Compression. C 2020, 6, 46. [Google Scholar] [CrossRef]
- Thomas, N.; Smidt, T.; Kearnes, S.; Yang, L.; Li, L.; Kohlhoff, K.; Riley, P. Tensor field networks: Rotation- and translation-equivariant neural networks for 3D point clouds. arXiv 2018, arXiv:1802.08219. [Google Scholar] [CrossRef]
- Schütt, K.T.; Sauceda, H.E.; Kindermans, P.-J.; Tkatchenko, A.; Müller, K.-R. SchNet—A deep learning architecture for molecules and materials. J. Chem. Phys. 2018, 148, 241722. [Google Scholar] [CrossRef]
| Strategy | Frozen Blocks | Trainable Blocks (Number of Trainable Parameters) | Total Number of Trainable Parameters (Fraction of the Model’s Total Parameters) |
|---|---|---|---|
| Freezing the Interaction Blocks (FIB) | Interaction | Basis Functions (12,288) | 18,466,304 (~0.45) |
| Atom and Edge Embeddings (21,248 + 327,680) | |||
| Outputs (5 × 3,031,040) | |||
| Energy and Force MLPs (2,949,888) | |||
| Freezing the Output Blocks (FOB) | Output | Basis Functions (12,288) | 26,066,528 (~0.63) |
| Atom and Edge Embeddings (21,248 + 327,680) | |||
| Interactions (4 × 5,688,856) | |||
| Energy and Force MLPs (2,949,888) | |||
| Full Fine-Tuning (FFT) | - | Basis Functions (12,288) | 41,221,728 (1.0) |
| Atom and Edge Embeddings (21,248 + 327,680) | |||
| Interactions (4 × 5,688,856) | |||
| Outputs (5 × 3,031,040) |
| Segregated Aromatics | Extracted FG | |||
|---|---|---|---|---|
| Model | Success Rate (%) | MAE (eV) | Success Rate (%) | MAE (eV) |
| Pretrained GemNet-OC | 0.88 | 10.975 | 1.59 | 5.562 |
| GemNet-OC fine-tuned on Extracted FG | 70.80 | 0.084 | 75.83 | 0.074 |
| GemNet-OC fine-tuned on Segregated Aromatics | 60.18 | 0.125 | 23.15 | 0.456 |
| GAME-Net trained on Extracted FG | - | 0.34 | - | 0.18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Parashkooh, H.I.; Jian, C. Graph Neural Networks for Sustainable Energy: Predicting Adsorption in Aromatic Molecules. ChemEngineering 2025, 9, 85. https://doi.org/10.3390/chemengineering9040085
Parashkooh HI, Jian C. Graph Neural Networks for Sustainable Energy: Predicting Adsorption in Aromatic Molecules. ChemEngineering. 2025; 9(4):85. https://doi.org/10.3390/chemengineering9040085
Chicago/Turabian StyleParashkooh, Hasan Imani, and Cuiying Jian. 2025. "Graph Neural Networks for Sustainable Energy: Predicting Adsorption in Aromatic Molecules" ChemEngineering 9, no. 4: 85. https://doi.org/10.3390/chemengineering9040085
APA StyleParashkooh, H. I., & Jian, C. (2025). Graph Neural Networks for Sustainable Energy: Predicting Adsorption in Aromatic Molecules. ChemEngineering, 9(4), 85. https://doi.org/10.3390/chemengineering9040085






