Vanillin Quantum–Classical Photodynamics and Photostatic Optical Spectra
Abstract
1. Introduction
2. Materials and Methods
3. Results
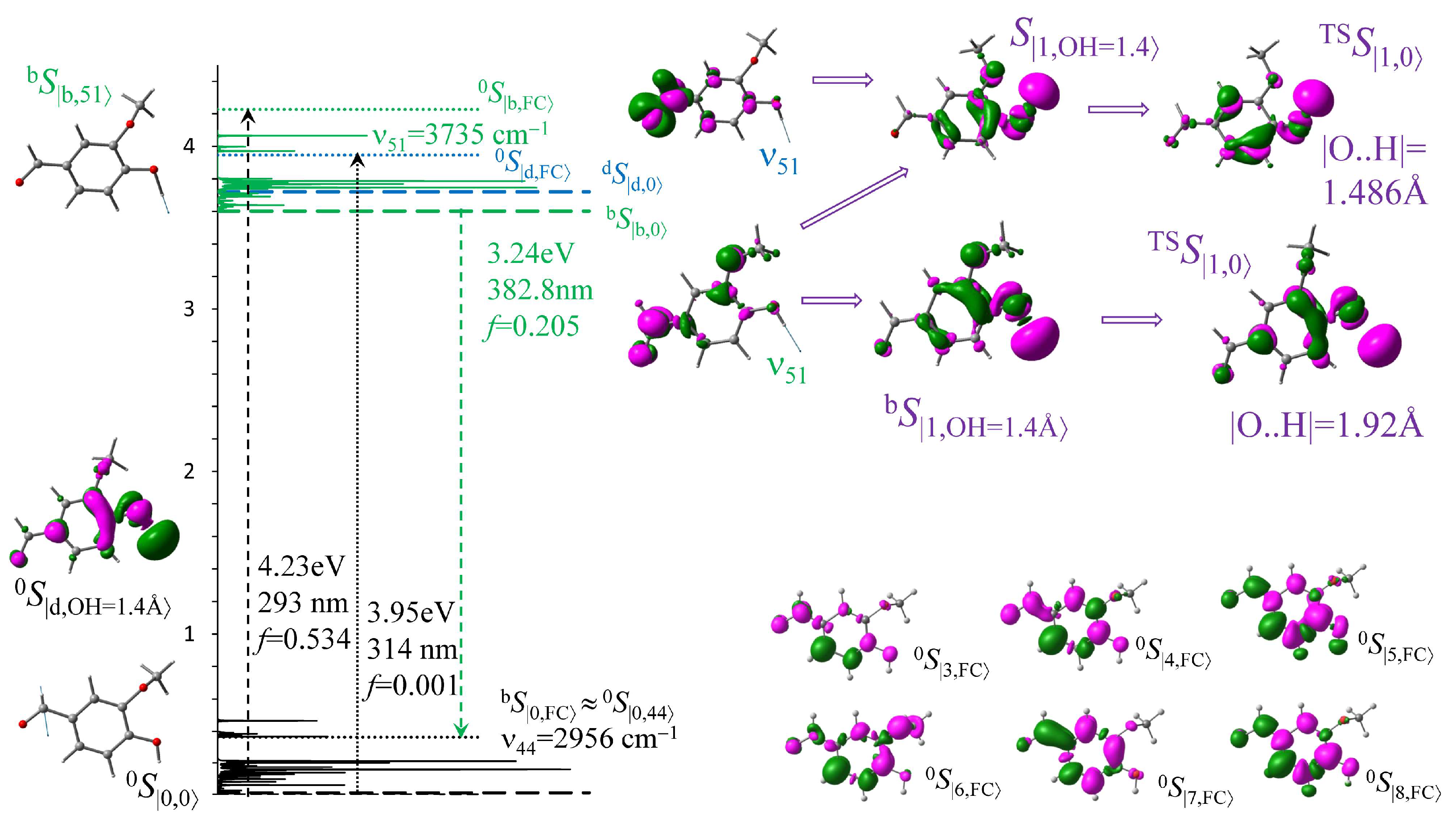
3.1. Vertical Electronic Transitions and IR Spectra
3.2. Statistical Absorption and Fluorescence Spectra
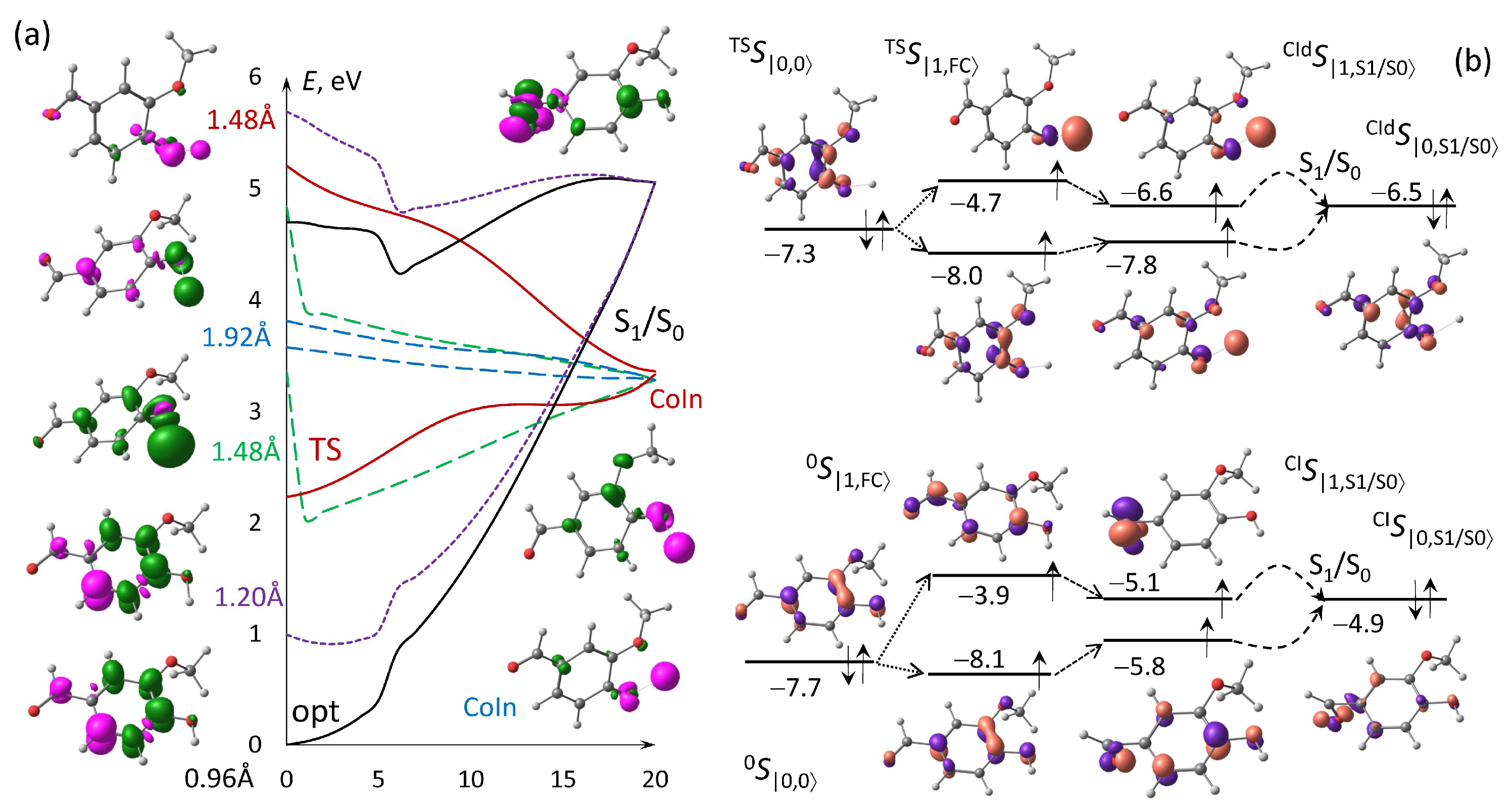
3.3. Conical Intersection Searching for Photo-Predissociation
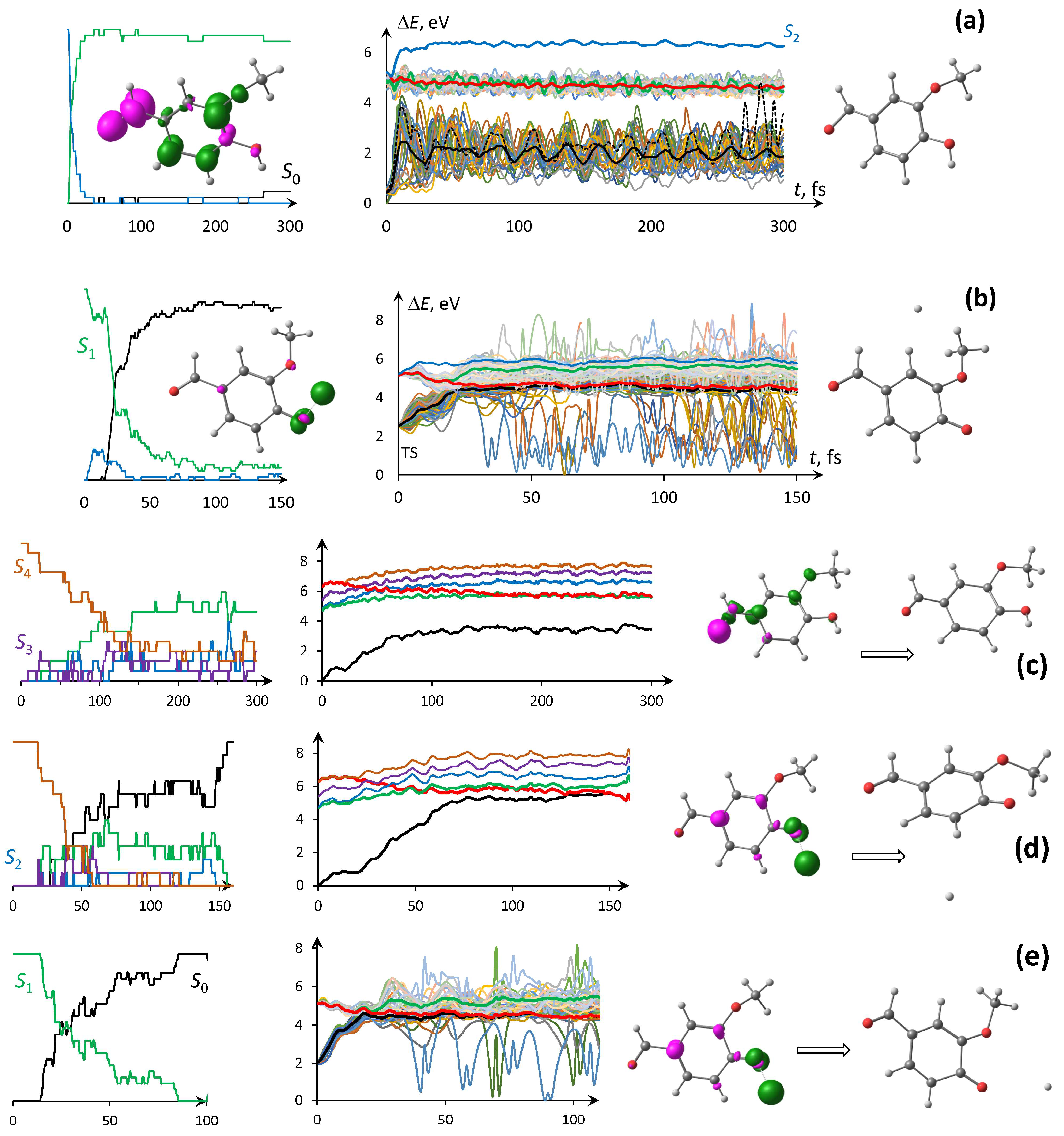
3.4. Photodynamic PES Trajectories Through NAMD
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| VNL | Vanillin |
| CoIn | Conical intersection |
| QCMD | Quantum–classical molecular dynamic |
| SMD PCM | Solvation model of polarizable continuum model |
| NAMD | Nonadiabatic molecular dynamics |
| LR-MRSF | Linear response mixed-reference spin–flip |
| TD-DFT | Time-dependent density functional theory |
| eQCMD | Extended statistical quantum-mechanical/molecular dynamic |
| MO | Molecular orbital |
| TSH | Trajectory surface hopping |
| ESPF | Embedding electrostatic potential fitting |
| VEE | Vertical electronic excitation |
| EDD | Electron density differences |
| PES | Potential energy surfaces |
| DMO | Dyson molecular orbitals |
| SBC | Spherical boundary conditions |
References
- Go, B.R.; Lyu, Y.; Ji, Y.; Li, Y.J.; Huang, D.D.; Li, X.; Nah, T.; Lam, C.H.; Chan, C.K. Aqueous Secondary Organic Aerosol Formation from the Direct Photosensitized Oxidation of Vanillin in the Absence and Presence of Ammonium Nitrate. Atmos. Chem. Phys. 2022, 22, 273–293. [Google Scholar] [CrossRef]
- Al-Hunaiti, A.; Mohaidat, Q.; Bsoul, I.; Mahmood, S.; Taher, D.; Hussein, T. Synthesis and Characterization of Novel Phyto-Mediated Catalyst, and Its Application for a Selective Oxidation of (VAL) into Vanillin under Visible Light. Catalysts 2020, 10, 839. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, Q.; Ren, X.; Xie, J.; Chang, N.; Zhang, Q. Novel Photobase Generators Mediated Thiol-Epoxy “Click” Reaction for Self-Healing, Degradable and Recyclable Photoresist Based on Bio-Vanillin and Eugenol. Chem. Eng. J. 2025, 503, 158304. [Google Scholar] [CrossRef]
- Loisel, G.; Mekic, M.; Liu, S.; Song, W.; Jiang, B.; Wang, Y.; Deng, H.; Gligorovski, S. Ionic Strength Effect on the Formation of Organonitrate Compounds through Photochemical Degradation of Vanillin in Liquid Water of Aerosols. Atmos. Environ. 2021, 246, 118140. [Google Scholar] [CrossRef]
- Carena, L.; Zoppi, B.; Sordello, F.; Fabbri, D.; Minella, M.; Minero, C. Phototransformation of Vanillin in Artificial Snow by Direct Photolysis and Mediated by Nitrite. Environ. Sci. Technol. 2023, 57, 8785–8795. [Google Scholar] [CrossRef] [PubMed]
- Arya, S.S.; Rookes, J.E.; Cahill, D.M.; Lenka, S.K. Vanillin: A Review on the Therapeutic Prospects of a Popular Flavouring Molecule. Adv. Tradit. Med. 2021, 21, 1–17. [Google Scholar] [CrossRef]
- Liu, B.; Lim, C.-H.; Miyake, G.M. Light-Driven Intermolecular Charge Transfer Induced Reactivity of Ethynylbenziodoxol(on)e and Phenols. J. Am. Chem. Soc. 2018, 140, 12829–12835. [Google Scholar] [CrossRef]
- Kusaka, R.; Nihonyanagi, S.; Tahara, T. The Photochemical Reaction of Phenol Becomes Ultrafast at the Air–Water Interface. Nat. Chem. 2021, 13, 306–311. [Google Scholar] [CrossRef]
- Ishiyama, T.; Tahara, T.; Morita, A. Why the Photochemical Reaction of Phenol Becomes Ultrafast at the Air–Water Interface: The Effect of Surface Hydration. J. Am. Chem. Soc. 2022, 144, 6321–6325. [Google Scholar] [CrossRef]
- Pomogaev, V.; Bocharnikova, E.; Tchaikovskaya, O.; Avramov, P. Phenol Photostatic Spectra and Quantum-Classical Photodynamic Deprotonation. Int. J. Quantum Chem. 2024, 124, e27504. [Google Scholar] [CrossRef]
- Pomogaev, V.; Bocharnikova, E.; Avramov, P.; Tchaikovskaya, O. P-Cresol Quantum-Classical Photodynamics, Photostatic UV, IR and Raman Spectra. J. Mol. Struct. 2025, 1344, 142986. [Google Scholar] [CrossRef]
- Vusovich, O.V.; Lapin, I.N.; Svetlichnyi, V.A.; Sul’timova, N.B.; Tchaikovskaya, O.N. Comparison of Vanillin and Isovanillin Photolysis in Aqueous Solutions. Russ. Phys. J. 2014, 56, 1287–1291. [Google Scholar] [CrossRef]
- Huix-Rotllant, M.; Schwinn, K.; Pomogaev, V.; Farmani, M.; Ferré, N.; Lee, S.; Choi, C.H. Photochemistry of Thymine in Solution and DNA Revealed by an Electrostatic Embedding QM/MM Combined with Mixed-Reference Spin-Flip TDDFT. J. Chem. Theory Comput. 2023, 19, 147–156. [Google Scholar] [CrossRef]
- Pomogaev, V.A.; Sadiq, S.; Filatov, M.; Choi, C.H. Modeling of Photochemical Conversions on Nonadiabatic Molecular Dynamics Trajectories; Izvestiya Vuzov. Fizika: Tomsk, Russia, 2023; Volume 66, pp. 25–33. [Google Scholar]
- Pomogaev, V.; Pomogaeva, A.; Avramov, P.; Jalkanen, K.J.; Kachin, S. Thermo-Dynamical Contours of Electronic-Vibrational Spectra Simulated Using the Statistical Quantum–Mechanical Methods. Theor. Chem. Acc. 2011, 130, 609–632. [Google Scholar] [CrossRef]
- Pomogaev, V.A.; Ramazanov, R.R.; Ruud, K.; Artyukhov, V.Y. Insight into the Fluorescence Quenching of Trp214 at HSA by the Dimetridazole Ligand from Simulation. J. Photochem. Photobiol. A Chem. 2018, 254, 86–100. [Google Scholar] [CrossRef]
- Zuehlsdorff, T.J.; Shedge, S.V.; Lu, S.-Y.; Hong, H.; Aguirre, V.P.; Shi, L.; Isborn, C.M. Vibronic and Environmental Effects in Simulations of Optical Spectroscopy. Annu. Rev. Phys. Chem. 2021, 72, 165–188. [Google Scholar] [CrossRef]
- Kubenko, V.G.; Pomogaev, V.A.; Buglak, A.A.; Kononov, A.I. Photophysics of 5,6,7,8-Tetrahydrobiopterin on a Femtosecond Time-Scale. J. Photochem. Photobiol. B Biol. 2025, 265, 113134. [Google Scholar] [CrossRef]
- Huix-Rotllant, M.; Ferré, N. Analytic Energy, Gradient, and Hessian of Electrostatic Embedding QM/MM Based on Electrostatic Potential-Fitted Atomic Charges Scaling Linearly with the MM Subsystem Size. J. Chem. Theory Comput. 2021, 17, 538–548. [Google Scholar] [CrossRef]
- Alías-Rodríguez, M.; Bonfrate, S.; Park, W.; Ferré, N.; Choi, C.H.; Huix-Rotllant, M. Solvent Effects and pH Dependence of the X-Ray Absorption Spectra of Proline from Electrostatic Embedding Quantum Mechanics/Molecular Mechanics and Mixed-Reference Spin-Flip Time-Dependent Density-Functional Theory. J. Phys. Chem. A 2023, 127, 10382–10392. [Google Scholar] [CrossRef]
- Park, W.; Shen, J.; Lee, S.; Piecuch, P.; Filatov, M.; Choi, C.H. Internal Conversion between Bright (11 Bu+) and Dark (21 Ag−) States in s-Trans-Butadiene and s-Trans-Hexatriene. J. Phys. Chem. Lett. 2021, 12, 9720–9729. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.; Kim, E.E.; Nakata, H.; Lee, S.; Choi, C.H. Efficient Implementations of Analytic Energy Gradient for Mixed-Reference Spin-Flip Time-Dependent Density Functional Theory (MRSF-TDDFT). J. Chem. Phys. 2019, 150, 184111. [Google Scholar] [CrossRef] [PubMed]
- Sadiq, S.; Park, W.; Mironov, V.; Lee, S.; Filatov (Gulak), M.; Choi, C.H. Prototropically Controlled Dynamics of Cytosine Photodecay. J. Phys. Chem. Lett. 2023, 14, 791–797. [Google Scholar] [CrossRef] [PubMed]
- Shostak, S.; Park, W.; Oh, J.; Kim, J.; Lee, S.; Nam, H.; Filatov, M.; Kim, D.; Choi, C.H. Ultrafast Excited State Aromatization in Dihydroazulene. J. Am. Chem. Soc. 2023, 145, 1638–1648. [Google Scholar] [CrossRef] [PubMed]
- Lee, I.S.; Ha, J.; Han, D.; Kim, T.I.; Moon, S.W.; Min, S.K. PyUNIxMD: A Python-Based Excited State Molecular Dynamics Package. J. Comput. Chem. 2021, 42, 1755–1766. [Google Scholar] [CrossRef]
- Accomasso, D.; Jankowska, J. Quantum-Classical Simulations Reveal the Photoisomerization Mechanism of a Prototypical First-Generation Molecular Motor. Chem. A Eur. J. 2025, 31, e202403768. [Google Scholar] [CrossRef]
- Park, W.; Lee, S.; Huix-Rotllant, M.; Filatov, M.; Choi, C.H. Impact of the Dynamic Electron Correlation on the Unusually Long Excited-State Lifetime of Thymine. J. Phys. Chem. Lett. 2021, 12, 4339–4346. [Google Scholar] [CrossRef]
- Park, W.; Komarov, K.; Lee, S.; Choi, C.H. Mixed-Reference Spin-Flip Time-Dependent Density Functional Theory: Multireference Advantages with the Practicality of Linear Response Theory. J. Phys. Chem. Lett. 2023, 14, 8896–8908. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Petersson, G.A.; Al-Laham, M.A. A Complete Basis Set Model Chemistry. II. Open-shell Systems and the Total Energies of the First-row Atoms. J. Chem. Phys. 1991, 94, 6081–6090. [Google Scholar] [CrossRef]
- Rassolov, V.A.; Ratner, M.A.; Pople, J.A.; Redfern, P.C.; Curtiss, L.A. 6-31G* Basis Set for Third-row Atoms. J. Comput. Chem. 2001, 22, 976–984. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian, 16, Revision C.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Becke, A.D. A New Mixing of Hartree-Fock and Local Density-Functional Theories. J. Chem. Phys. 1993, 98, 1372–1377. [Google Scholar] [CrossRef]
- Petersson, G.A.; Bennett, A.; Tensfeldt, T.G.; Al-Laham, M.A.; Shirley, W.A.; Mantzaris, J. A Complete Basis Set Model Chemistry. I. The Total Energies of Closed-Shell Atoms and Hydrides of the First-Row Elements. J. Chem. Phys. 1988, 89, 2193–2218. [Google Scholar] [CrossRef]
- Barbatti, M.; Bondanza, M.; Crespo-Otero, R.; Demoulin, B.; Dral, P.O.; Granucci, G.; Kossoski, F.; Lischka, H.; Mennucci, B.; Mukherjee, S.; et al. Newton-X Platform: New Software Developments for Surface Hopping and Nuclear Ensembles. J. Chem. Theory Comput. 2022, 18, 6851–6865. [Google Scholar] [CrossRef] [PubMed]
- Toldo, J.M.; Telles do Casal, M.; Ventura, E.; Andrade do Monte, S.; Barbatti, M. Surface Hopping Modeling of Charge and Energy Transfer in Complex Environments. Phys. Chem. Chem. Phys. 2023, 25, 8293–8316. [Google Scholar] [CrossRef] [PubMed]
- Shu, Y.; Zhang, L.; Chen, X.; Sun, S.; Huang, Y.; Truhlar, D.G. Nonadiabatic Dynamics Algorithms with Only Potential Energies and Gradients: Curvature-Driven Coherent Switching with Decay of Mixing and Curvature-Driven Trajectory Surface Hopping. J. Chem. Theory Comput. 2022, 18, 1320–1328. [Google Scholar] [CrossRef]
- Liu, X.-Y.; Chen, W.-K.; Fang, W.-H.; Cui, G. Nonadiabatic Dynamics Simulations for Photoinduced Processes in Molecules and Semiconductors: Methodologies and Applications. J. Chem. Theory Comput. 2023, 19, 8491–8522. [Google Scholar] [CrossRef]
- Crespo-Otero, R.; Barbatti, M. Recent Advances and Perspectives on Nonadiabatic Mixed Quantum–Classical Dynamics. Chem. Rev. 2018, 118, 7026–7068. [Google Scholar] [CrossRef]
- Zhang, L.; Ullah, A.; Pinheiro Jr, M.; Dral, P.O.; Barbatti, M. Excited-State Dynamics with Machine Learning. In Quantum Chemistry in the Age of Machine Learning; Elsevier: Amsterdam, The Netherlands, 2023; pp. 329–353. ISBN 978-0-323-90049-2. [Google Scholar]
- Ferré, N.; Filatov, M.; Huix-Rotllant, M. (Eds.) Density-Functional Methods for Excited States; Topics in Current Chemistry; Springer International Publishing: Cham, Switzerland, 2016; Volume 368, ISBN 978-3-319-22080-2. [Google Scholar]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef]
- Martínez, L.; Andrade, R.; Birgin, E.G.; Martínez, J.M. P ACKMOL: A Package for Building Initial Configurations for Molecular Dynamics Simulations. J. Comput. Chem. 2009, 30, 2157–2164. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Maxwell, D.S.; Tirado-Rives, J. Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236. [Google Scholar] [CrossRef]
- Pomogaev, V.; Pomogaeva, A.; Aoki, Y. Absorption Spectra of Estradiol and Tryptophan Constructed by the Statistical and Elongation Methods. J. Phys. Chem. A 2009, 113, 1429–1433. [Google Scholar] [CrossRef]
- Ortiz, J.V. Dyson-Orbital Concepts for Description of Electrons in Molecules. J. Chem. Phys. 2020, 153, 070902. [Google Scholar] [CrossRef]
- Filatov, M.; Lee, S.; Nakata, H.; Choi, C.H. Computation of Molecular Electron Affinities Using an Ensemble Density Functional Theory Method. J. Phys. Chem. A 2020, 124, 7795–7804. [Google Scholar] [CrossRef]
- Pomogaev, V.; Lee, S.; Shaik, S.; Filatov, M.; Choi, C.H. Exploring Dyson’s Orbitals and Their Electron Binding Energies for Conceptualizing Excited States from Response Methodology. J. Phys. Chem. Lett. 2021, 12, 9963–9972. [Google Scholar] [CrossRef]
- Gordon, M.S. GAMESS. Available online: https://www.msg.chem.iastate.edu/gamess/ (accessed on 30 September 2023).
- Schmidt, M.W.; Baldridge, K.K.; Boatz, J.A.; Elbert, S.T.; Gordon, M.S.; Jensen, J.H.; Koseki, S.; Matsunaga, N.; Nguyen, K.A.; Su, S.; et al. General Atomic and Molecular Electronic Structure System. J. Comput. Chem. 1993, 14, 1347–1363. [Google Scholar] [CrossRef]
- Ponder, J.W. TINKER: Software Tools for Molecular Design, Version 8.10.1. 2021. Available online: http://dasher.wustl.edu/tinker/ (accessed on 25 November 2022).
- Chemcraft—Graphical Software for Visualization of Quantum Chemistry Computations Version 1.8, Build 682. Available online: https://www.chemcraftprog.com (accessed on 15 July 2025).
- Žagar, E.; Grdadolnik, J. An Infrared Spectroscopic Study of H-Bond Network in Hyperbranched Polyester Polyol. J. Mol. Struct. 2003, 658, 143–152. [Google Scholar] [CrossRef]

| VNLsbcWM Last Frame | VNLespf3WM | VNLqm3WM | VNL@SMD | |||||
|---|---|---|---|---|---|---|---|---|
| Sd | 308.5 (0.001) | 0.93|2→0′〉 | 323.2 (0.000) | 0.95|1→0′〉 | 313.6 (0.000) | 0.65|3→0′〉 | 312.5 (0.000) | 0.82|2→0′〉 |
| 0.22|2→0′〉 | 0.13|1→0′〉 | |||||||
| Sb | 285.0 (0.071) | 0.53|0→0′〉 | 272.3 (0.114) | 0.65|0→0′〉 | 276.01 (0.151) | 0.72|1→0′〉 | 283.3 (0.161) | 0.77|0→0′〉 |
| 0.38|1→0′〉 | 0.25|2→0′〉 | 0.12|4→0′〉 | 0.12|1→0′〉 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pomogaev, V.; Tchaikovskaya, O. Vanillin Quantum–Classical Photodynamics and Photostatic Optical Spectra. ChemEngineering 2025, 9, 76. https://doi.org/10.3390/chemengineering9040076
Pomogaev V, Tchaikovskaya O. Vanillin Quantum–Classical Photodynamics and Photostatic Optical Spectra. ChemEngineering. 2025; 9(4):76. https://doi.org/10.3390/chemengineering9040076
Chicago/Turabian StylePomogaev, Vladimir, and Olga Tchaikovskaya. 2025. "Vanillin Quantum–Classical Photodynamics and Photostatic Optical Spectra" ChemEngineering 9, no. 4: 76. https://doi.org/10.3390/chemengineering9040076
APA StylePomogaev, V., & Tchaikovskaya, O. (2025). Vanillin Quantum–Classical Photodynamics and Photostatic Optical Spectra. ChemEngineering, 9(4), 76. https://doi.org/10.3390/chemengineering9040076






