Abstract
Solid–liquid separation plays a decisive role in various industrial applications particularly in the treatment and purification of suspensions. Solid bowl centrifuges, such as the decanter centrifuge, are commonly employed in these processes as they operate continuously and enable high throughputs with short processing times. However, predicting the separation performance of solid bowl centrifuges proves to be challenging due to dynamic phenomena within the apparatus, such as particle settling, sediment build-up, consolidation and sediment transport. In practice, design considerations and the dimensioning of the apparatus rely on analytical models and the manufacturer’s expertise. Computational Fluid Dynamics (CFD) offers a way to deepen our understanding of these devices by allowing detailed examination of flow phenomena and their influence on the separation processes. This study utilizes the open-source software OpenFOAM to simulate multiphase flow in a laboratory-scale decanter centrifuge, solving individual transport equations for each particle size class. The basis is the characterization of the material through targeted laboratory experiments to derive material functions that describe the hindered settling and the sediment consolidation. Furthermore, experiments on a laboratory decanter served as validation. The results demonstrate the solver’s capability to replicate clarification and classification within the apparatus. Furthermore, the solver supports the definition of geometries tailored to specific separation tasks. This research demonstrates the potential of CFD for a better understanding of complex centrifuge processes and for optimizing their design to improve performance.
1. Introduction
Essential basic operations in process engineering are clarification and classification [1]. The former means that the particles are separated as completely as possible so that the liquid is free of particles, the latter means the separation of a disperse mixture of solids into individual fractions according to certain criteria, such as particle size or particle density. Clarification and classification are used primarily in the mining [2,3] and recycling [4] industries but play also an important role in the food [5], pharmaceutical [6] and chemical [7] industries. For example, an optimal clarification process is particularly important when purity and quality play a major role, such as in the production and purification of active ingredients. An example from the chemical industry is given for classification: precipitation or crystallization methods enable particles to be generated, but there is no guarantee that their size does not exceed or fall below a certain threshold. To prevent disturbances in the downstream processes, it is necessary to separate oversize (desliming) and undersize particles (degritting). If the separation criterion is the particle size, sieving and filtration as well as centrifugation are the most common methods used on an industrial scale to classify particles in a liquid phase [8]. Sieves solely enable to classify particles with a size 2 [8,9]. In some cases, two or more subsequent sieving steps may be required, which causes a higher product loss. Filters and membranes [10,11,12] enable the classification of fine dispersed particles. But, their use for classification requires the avoidance of cake formation (fouling), which is why cross-flow filtration is often used. Nevertheless, fine particles accumulate on the filter or membrane, leading to the clogging of the pores (blinding). Therefore, regular cleaning and the replacement of filters and membranes are essential.
Hydrocyclones allow the classification [13,14,15] of suspensions with a solids volume fraction 10 . They offer the advantage of a comparatively simple design without rotating parts and a continuous operation. Due to the tangential inflow of the suspension and the cylindrical–conical design, a potential vortex is formed. The outer vortex (primary vortex) discharges the coarse particles, while the inner vortex (secondary vortex) discharges the finer particles. However, the throughput is limited because, as the particle size decreases, the diameter of the apparatus also decreases, and thus the pressure drop increases [16].
Centrifuges are a preferred tool for the separation of fine dispersed particles in the micrometer and submicrometer range (≤ 10 ) as well as in the case of small density differences between solids and fluid due to the high centrifugal forces they may achieve [1]. Next to tubular centrifuges [8,17,18,19,20,21] and disk stack centrifuges [22,23], decanter centrifuges [24,25] are used to clarify and classify particles.
Decanter centrifuges are continuously operating centrifuges and offer the advantage that they can handle both slightly and highly concentrated suspensions [22,26]. In addition to thickening and clarification, decanter centrifuges are also used to classify solid particles [3,25]. Gleiß [27] has developed a compartment model to predict the separation behavior of decanter centrifuges in real time. In addition to the solids fraction in centrate and concentrate, it also predicts the separation efficiency. Based on the work of Gleiß [27], Menesklou [3] has continued to develop the model and demonstrates its scale-up capability. By coupling with other process models, it is also possible to map an entire process chain [28]. While the compartment model by Gleiß [27] assumes the flow as a plug-flow velocity profile, Bai et al. [25] have developed a physical model for the description of solid–liquid separation and particle size classification that takes into account flow characteristics, such as back flow, in the apparatus based on the experimental work of Faust [29] and Madsen [30]. Published experimental data [27,31,32] were used for validation [25]. The model allows the modeling of the separation process as well as the investigation of the influence of different process parameters on the solids recovery [33]. In comparison to the compartment model by Gleiß [27], however, Bai et al. [25] do not take the compression of the sediment into account.
In contrast to reduced-order models, CFD simulations allow the calculation of the flow conditions in an entailed manner. Hammerich [34] has integrated a distribution algorithm, which takes into account the material behavior such as sedimentation, consolidation and the rheological flow behavior of the suspension and the sediment, for simulating tubular centrifuges. This solver enables the investigation of sediment formation while taking into account the consolidation and rheological behavior of the sediment. Additionally, residence time behavior is calculated using this method, providing insights into changes in flow conditions. Hammerich [34] varied the number of particle classes, considering at least one and at most 11 particle size classes to investigate their influence on sediment formation and its structure. Five classes represented the best compromise between computational time and accuracy for the investigation of the sediment behavior. The validation ensued by matching the sediment shape from experiment and simulation. However, the design of the solver requires structured meshes, which makes the transfer to complex apparatuses difficult or even impossible.
Baust et al. [35,36] have also developed a resolved simulation model that allows the investigation of the separation behavior and the flow behavior in centrifuges. In contrast to the approach of Hammerich [34], it is based on the work of Bürger and Concha [37] and uses the flux density function to model the material behavior. The necessary material functions are derived from laboratory-scale experiments [38]. This work presents an extension of the existing simulation model to include a particle size distribution. The first step was to characterize the material, a limestone–water suspension. For this purpose, the hindered settling function was derived from sinking velocity distributions. This function depends on the solids volume fraction, as well as on the particle size, as revealed by laboratory experiments, which is also taken into account in the material function. Furthermore, the effective solids stress was determined by examining individual sediment layers from experiments conducted with a beaker centrifuge. The validation involves experiments with the beaker centrifuge and with a laboratory centrifuge demonstrating the simulation’s accurate reproduction of the experimental data. In summary, the solver enables the simulation of classification processes. Additionally, the outlook demonstrates the solver’s capability to support the design or selection of optimal geometries for specific separation tasks.
2. Materials and Methods
This chapter gives an overview of the numerical methodology, the extension of the simulation model and the experimental methods to determine the material functions. In contrast to concentrated suspensions, where small distances between particles lead to uniform sedimentation, segregation at lower concentrations is decisive for classification [39]. These segregation effects affect the separation performance of centrifuges.
2.1. Numerical Setup
The implementation of this method took place in the open-source software OpenFOAM (v2212, OpenCFD Ltd., Bracknell, UK) and is based on the solver pimpleFoam, which is a solver for incompressible, turbulent flow of Newtonian fluids and enables mesh motion. The solid particles and the liquid are combined into one single mixed phase [35]. The simulation methodology is based on the following assumptions:
- A1
- Neglect of the gas phase;
- A2
- Same shape and density of all particles;
- A3
- Incompressibility of the particles and the fluid;
- A4
- No mass transfer between the components;
- A5
- Model the interactions between the disperse and the continuous phase by an additional transport equation for the solids volume fraction;
- A6
- Neglect of wall effects.
The CFD-solver calculates the Navier–Stokes equations that mathematically express the conservation of mass
and the momentum
and describe the temporal and spatial development of the mixtures’ velocity , so they are temporally and spatially resolved. The variable t stands for the time, p is the pressure, the density and the kinematic viscosity of the mixture. Most of the methods based on the Euler–Euler method solely accept a discrete particle size distribution. Therefore, each considered particle size corresponds to its own particle size class i.
The transport equation (Equation (3)) describes for each particle class the accumulation of the solids volume fraction , which depends on the convective flow as mixing phase as well as on the sedimentation and on the compression of the forming sediment. In this case, the solids volume fraction corresponds to the sum of all particle size fractions and thus describes the ratio between the total particle volume to the total volume .
The variable r stands for the radius, is the angular velocity, g is the acceleration due to gravity, and and for the density of the solid and the liquid phase. The vectors and are unit vectors, where is parallel to the axis of rotation and is orthogonal to and thus acts in the direction of the acceleration force. The equation to describe the transport of the solids volume fraction for a monodisperse particle system was proposed by Garrido et al. [40]. Berres and Bürger [41] extended this expression to describe the separation behavior of polydisperse particle systems also for batch centrifugation. The factor stabilizes the equation [35] and assumes values between 0 and 1. It depends on the gel point , which marks the transition between suspension () and sediment (). Therefore, is described by a sigmoid function and takes values between 0 and 1 to ensure numerical stability at the transition between slurry and sediment [35]. The two remaining functions and represent the material functions for the sedimentation behavior and the compressive behavior of the sediment.
The flux density function
was introduced by Kynch [42] and is defined as the product of the settling velocity and the solids volume fraction . According to Stokes [43], the settling velocity of one single, spherical particle with the diameter x depends on the density difference of the liquid and the solids, the liquid’s viscosity and the acceleration due to gravity g.
However, this approach is solely valid for creeping flow, infinite diluted systems and for Newtonian fluids. With an increase in the solids volume fraction, the momentum exchange between solids and liquid increases, which leads to a hindrance during sedimentation. The hindered settling function is defined as the ratio of the actual settling velocity in relation to the settling velocity according to Stokes [43].
Richardson and Zaki [44] describe the hindered settling function of high-concentrated suspensions (zone sedimentation) solely as a function of the solids volume fraction.
With creeping flow and assuming monodispersity, the exponent has the value . In practice, particle systems are often not monodisperse and are represented by a particle size distribution to take into account polydispersity. Moreover, the particle shape often deviates from the shape of a sphere. Michaels and Bolger [45] provide an extension of the approach of Richardson and Zaki [44] by adding the maximum solids volume fraction of the suspension and the empirical parameters and .
The formation and structure of the sediment depends on the properties of the disperse phase such as particle size, particle shape and interparticle interactions. The compressive behavior of the sediment may be described by the compression resistance as a function of the solids volume fraction. Green et al. [46] describe the consolidation behavior by a power approach.
The parameters and are empirical values. The influence of individual particle classes on the compression resistance is not taken into account by this model.
The solids volume fraction affects the viscosity of the suspension and the sediment and provides a link back to the current, Equation (2). The rheological behavior of the suspension and the sediment may have a decisive influence on the separation result [34]. At the transition from suspension to sediment, the flow behavior changes abruptly. The particle contacts within the formed sediment result in the sediment being able to absorb and transmit additional forces and stresses compared to a suspension [47]. Newtonian fluids exhibit linear viscous flow behavior, meaning that the shear stress is proportional to the strain rate .
The proportional constant is the dynamic viscosity . To describe the flow behavior of suspensions, which cannot be calculated directly from the individual components, the relative viscosity is used, which is defined as the ratio of the dynamic viscosity of the suspension to the viscosity of the pure liquid [48].
The literature contains various approaches [48,49,50,51] for modeling the influence of the solids volume fraction on the flow behavior through the relative viscosity. To characterize the rheological properties of the slurry, the Quemda approach [50] was used.
This method relates the relative viscosity to the ratio of the solids volume fraction to the maximum packing density . A common method for describing the flow behavior of sediments is the Herschel–Bulkley approach [52]
with the consistency K and the flow index as adjustment parameters [47]. The parameter is the the yield locus of the sediment. A decrease in viscosity with increasing shear rate indicates shear thinning or pseudo plastic flow behavior (), while an increase in viscosity with increasing shear rate indicates shear thickening or dilatant flow behavior (). If , the fluid is a so-called Bingham plastic [53]. It has a yield point and a linear flow behavior like a Newtonian fluid. According to the solver structure of OpenFOAM, the kinematic viscosity , which is the quotient of the dynamic viscosity and the density, is modeled within the developed framework.
Here, Equation (13) is used to model the suspension and Equation (14) to model the sediment.
2.2. Experimental Setup
Various laboratory instruments allow the characterization of the suspension that consists of water and limestone Mikhard (Provencale SA, Brignoles, France) with a mean diameter of and a density of 2700 kg3m−1. The particle size distribution was measured with a laser diffraction spectrometer based on HELOS technology (Sympatec, Clausthal-Zellerfeld, Germany), which covers a measuring range from 20 nm to 20 µm. A LIQXI wet dosing unit directs the sample into a flow cell to dilute the suspensions to a suitable concentration. The laser diffraction sensor contains a blue light source and additional multi-element photodetectors for the detection of forward, wide-angle and backward scattered light signals. For each sample, at least five consecutive measurements were performed, whereby the measured light signal was corrected with the signal of a reference measurement without particles [54,55].
Measurements of the settling velocity distribution of the particle system as a function of the solids volume fraction provided the basis for the determination of the hindered settling function (Equation (7)). The analytical centrifuge LUMiSizer (LUM GmbH, Berlin, Germany) allows us to measure the settling behavior of real particle systems on a small scale [56]. The cuvettes are placed horizontally in the LUMiSizer and irradiated lengthwise with monochromatic light of constant wavelength during centrifugation. The light transmitted through the cuvette is detected by a charge-coupled device (CCD) sensor and converted into the extinction using the Bouguer–Beer–Lambert law. The analytical centrifuge uses the STEP technology (Space and Time resolved Extinction Profiles) to evaluate spatially and temporally resolved changes in the extinction profiles and thus enables the determination of particle velocity distributions.
Compressible sediments exhibit a correlation between the effective solids stress and the solids volume fraction. The consolidation due to the acting centrifugal force was investigated with the help of a cutting device developed by Reinach [57]. First, the suspension was centrifuged until the state of equilibrium with regard to sediment compression was reached. The experiment lasted 90 . The base of the sediment beaker is movable, which allowed the defined removal of discrete sediment layers. The solids volume fraction of each layer was determined gravimetrically. Reinach [57] exploited the equilibrium state in each sediment layer i to calculate the compression resistance. In addition to centrifugal force and buoyancy force, the layers above press on the layer below, which in turn presses on layers below. The cross-sectional area A of the sediment is constant, hence the respective pressures are summed up instead of the forces. According to Reinach [57], the compression resistance of the particle network of the layer, which was present in layer i during centrifugation, was calculated as follows:
The variable r refers to the radial position starting from the axis of rotation of the beaker centrifuge, is the solid mass of the respective layer. The index j indicates the layers above the considered layer i.
Validation experiments and numerical investigations were carried out with the MD-80 decanter centrifuge from Lemitec GmbH (Berlin, Germany). Decanter centrifuges basically consist of a cylindrical–conical bowl containing a screw conveyor (Figure 1). The suspension flows centrally into the apparatus, is pre-accelerated and enters the bowl chamber through openings in the screw body. The solid particles accumulate on the inner wall of the bowl due to the rotating bowl and the resulting centrifugal force and form the sediment. The screw’s differential rotation transports the sediment towards the cone and out of the device. At the same time, the centrate flows in the opposite direction via a liquid weir out of the apparatus. The Lemitec centrifuge works according to the counter-flow principle. The centrifuge has an overall length of 315 , with a cylindrical part of 172 and a conical part of 143 . For the simulation, the wall thickness of the flights were assumed to be 2 . The bowl diameter measures 80 , the cone angle is 7°. In relation to the internal wall radius of the bowl, the centrifuge provides a maximum centrifugal acceleration of 4400 g. The pond depth is adjustable by means of different weir disks.
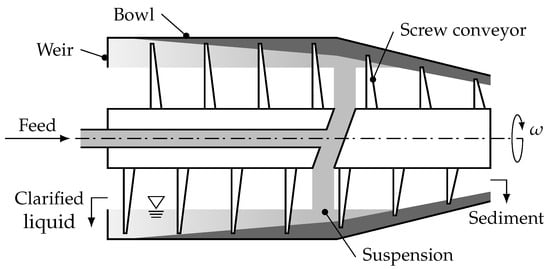
Figure 1.
Schematic description of a decanter centrifuge.
2.3. Computational Geometries and Discretization
Before simulating the decanter centrifuge, the beaker centrifuge experiments were simulated to test the functionality of the solver. The numerical representation of the sedimentation as well as the sediment formation and consolidation in the beaker solely takes place in the direction of the acting centrifugal force. The geometry has a spatial extension of 7 , which corresponds to the filling level, and is divided into 700 cells. This corresponds to a cell size of 1 , which is about the same as the measurement accuracy from the experiments. There is no spatial discretization in the other two directions.
The mesh for the laboratory decanter centrifuge is based on the experience gained in previous work [35,36]. The decanter centrifuge mesh consists of about 1,200,000 cells in the form of structured hexahedrons. In terms of accuracy and computing time, this mesh refinement is a good compromise. The gap between the tip of the screw and the bowl was not resolved. The weir has a height of 10 . The overflow above the weir is reduced to 4 , which is half the height of the overflow in the previous work. In addition, the grid cells were refined by a factor of two above the weir. The flow in the decanter centrifuge was assumed to be the rotation of a rigid body. The differential velocity between the screw and the bowl was resolved by the dynamic mesh. In the applied approach, the gas phase was neglected. At the beginning of the simulation, the apparatus was filled with pure liquid. The inlet velocity was defined according to the volumetric flow rate, which was evenly distributed over four openings in the screw body. The solids volume fraction of the slurry was assumed to be constant at the inlet. At the outlet, the pressure was specified. The no-slip boundary condition (Dirichlet) applies to the velocity and the Neumann boundary condition to the pressure at the walls. A list of all boundary conditions and the results of the mesh independence study can be found in the Appendix A according to the previous work of Baust et al. [36].
In decanter centrifuges, a complex three-dimensional flow is formed [22,36], which is not the best prerequisite for the settling of solids. In a conventional conveyor, the liquid to be clarified flows along the helix structure formed by the flights. The liquid velocity is much higher than it would be if it were to flow directly in the axial direction instead. To enhance the clarification effect, modern screw conveyors are equipped with windows in their flights, allowing for an axial flow of the clarified liquid [26]. To investigate this effect two additional geometries were created based on the original decanter geometry using the the ANSYS DesignModeler software Ansys 2020 R1, Ansys, Inc., Canonsburg, PA, USA. Figure 2 shows the different designs for the screw flight. In contrast to the conventional solid helical flight (a), the other two designs have windows. The windows in case (b) are merely lower than the set weir height. Additionally, the windows in case (c) become larger from turn to turn towards the weir, as illustrated (Figure 2) in a slightly more extreme form. In the final winding, thus the height measures only 4 . In all cases are no windows in the conical part of the cylinder. The characteristics of the mesh were set analogous to those of the original mesh. Likewise, the initial and boundary conditions were chosen to be the same.
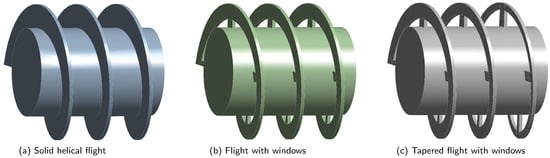
Figure 2.
Simplified illustration of the screw geometry variation.
The flow geometry and two mesh fragments of the modified screw geometry with windows (b) from Figure 2 is shown in Figure 3 as an example. The mesh had to be cut several times and divided into different segments to achieve a structured mesh of uniform hexahedrons. Challenges included the beginning and the end of the flights, the windows, the inlets and the transition between the cylindrical and conical part of the apparatus. Accordingly, the cutting planes correspond to the bridges between the windows, as seen in the enlarged view on the left, and to the transition between the conical and cylindrical parts, as seen on the right. Additional cutting planes were necessary in the area of the inlet. The two enlargements show that windows are only present in the cylindrical part of the apparatus and that no windows are present in the inlet area and in the cone. This is due to the turbulence in the inlet zone and the sediment transport up the cone by the screw.
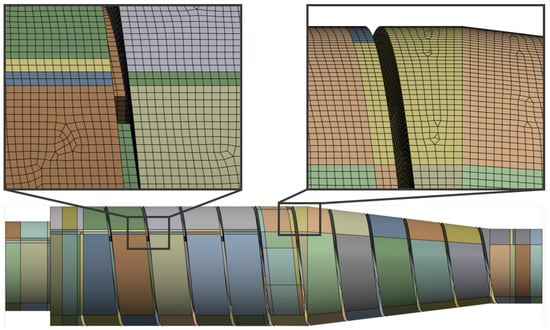
Figure 3.
Mesh of the decanter centrifuge generated with ANSYS DesignModeler. To obtain a structured mesh consisting of hexahedrons, the geometry was divided into 368 segments. As an example, two sections of the mesh are shown enlarged. The magnification factor is about six.
The developed simulation method only allows the consideration of a discrete particle size distribution. Therefore, each considered particle size corresponds to a specific particle size class. In this context, it can be assumed that a higher number of particle size classes leads to more accurate simulation results with a simultaneous increase in computing time. Thus, it is crucial for a computationally efficient simulation method to find a compromise in the number of considered particle classes. Figure 4 shows the discretization of the particle size distribution of the investigated limestone particles. The solid line represents the particle size distribution measured using laser diffraction. The points mark the particle sizes of the discretization. For the simulation with merely one particle size (a), the mean particle size was taken. Furthermore, the particle size was discretized with three (b), five (c), ten (d) and twenty (f) particle size classes. In all discretizations, each particle size class has the same mass fraction of the particle system. Consequently, the width of the individual particle classes is equally distributed. The distribution in (e) is an exception. Here, the distribution was also discretized by ten particle classes. However, the particle classes did not have the same mass fractions. Instead, starting from the mean particle size , the number of supporting points increases exponentially both in the direction towards smaller particle sizes and towards larger particle sizes. For example, the next smaller grid point corresponds to half of the next larger supporting point for the supporting points below the . Above the , the reverse applies accordingly.
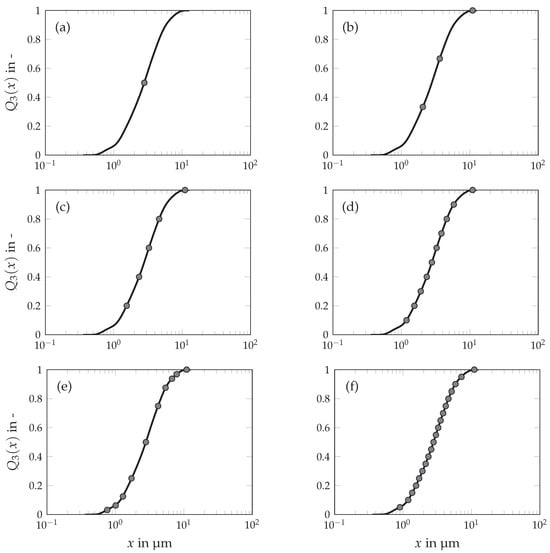
Figure 4.
Discretization of the particle size distribution of limestone, by one (a), three (b), five (c), ten (d,e) and twenty (f) particle classes.
3. Results and Discussion
The advantage of the presented solver lies in the combination of CFD simulation with the material-specific functions, which enables the simulation of the classification in complex apparatuses, such as decanter centrifuges. Based on the material functions derived from laboratory experiments and their simulation, the final step is the simulation of the classification in the centrifuge.
3.1. Determination of the Material Functions
To evaluate the effect of classification in decanter centrifuges, the first step was the determination of suitable material functions. The hindered settling function relates settling velocity distribution at different solids volume fractions to the Stokes’ settling velocity (Equation (7)). For this purpose, the settling velocities are measured with the LUMiSizer, and the particle size distribution is measured with the Helos. Figure 5 shows the hindered settling function exemplary for the , and of limestone, where the measuring points as well as the material model (dashed lines) are shown. With rising solids volume fraction the hindrance of the particles among each other increases and the settling velocity decreases. At the same time, the distance between the curves is found to be larger at low solids volume fractions and decreases with rising solids volume fraction. This behavior may be explained due to the sedimentation of the particles according to their size at low concentrations and the formation of a sedimentation front caused by the increasing hindrance at higher solids volume fractions. The course of the hindered settling function may be described for all particle size classes with one function that depends on the solids volume fraction and the corresponding particle size x.
For and , Equation (17) corresponds to the Richardson–Zaki [44] approach (Equation (8)). Michaels–Bolger [45] presented another approach (Equation (9)) to describe hindered settling using , , and as empirical parameters. Just like the Richardson–Zaki model, the Michaels–Bolger model is independent of the particle size. All models based on these approaches, such as the dynamic models of Gleiß et al. [27] and Menesklou [3], show no dependence of the hindered settling function on the particle size, so that remains constant. However, the studied limestone particle system exhibited a different behavior. In addition to the dependence on the solids volume fraction, there is a further dependence on the particle size x, which is accounted for by the prefactor . To model the hindered settling behavior, has been replaced by the parameters and in the Michaels–Bolger model. The parameter is assumed to be 1. The remaining empirical parameters show the following values for the investigated material: , 1.3 × 10−4 and .
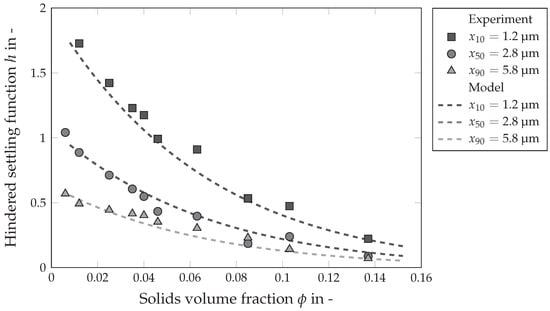
Figure 5.
Influence of the solids volume fraction on the hindered settling velocity for different particle size classes of a limestone–water suspension.
Another important material function is the consolidation function. It describes the sediment build-up and consolidation behavior. Figure 6 shows the effective solids stress of the investigated limestone-water suspension, showing both the measuring points and the model (dashed line). The lower layers in the sediment have a denser packing with lower porosity, as expected, because the layers above press on the layers below. In contrast, the upper layers have a correspondingly low solids volume fraction. The compression behavior is described by the potency approach according to Green et al. [46] (Equation (10)). The parameters take the values and . The gel point is at .
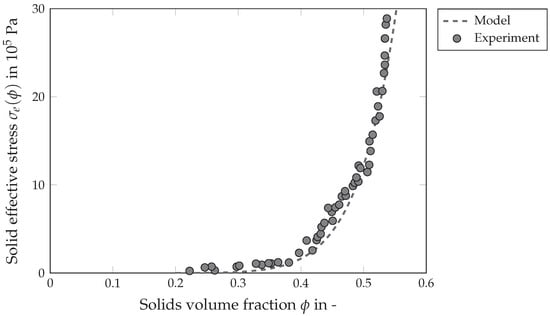
Figure 6.
Solids effective stress as a function of the solids volume fraction for the product limestone.
Table 1 gives an overview of all material parameters. The values for the hindered settling function and the effective solid stress were determined experimentally. In this case, the validation takes place by measuring the solids volume fraction and the particle size distribution. Sampling from the inside of the centrifuge was impossible due to the geometry of the centrifuge itself, with its rotating bowl and screw. For this reason, the parameters for the rheological behavior of the sediment were assumed values as in Baust et al. [36].

Table 1.
Overview of the used material characteristics.
In general, the physical behavior is modeled using material functions, but this does not provide a complete picture of what happens in the apparatus. The processes inside centrifuges are very complex and direct measurement is often not possible due to their geometry. However, different approaches can be found in the literature: Hammerich [34] has simulated tubular centrifuges and derived material parameters for the rheological behavior from experiments with a modified shear cell that allows the measurement of liquid-saturated sediments. The validation was performed by comparing the simulation with tubular centrifuge experiments, where the sediment was formed on half-shells. After the separation process, the shells were removed from the centrifuge together with the sediment and the sediment surface was measured with a laser. A quite elaborate method for investigating the separation behavior in centrifuges while the process is in progress is offered by the wireless electrical resistance detector (WERD) [58,59]. Kurnianto Prayitno et al. [24,60] used the WERD method to investigate hindered settling behavior as well as the formation of sediment in the apparatus and derived model equations describing the separation behavior.
3.2. Influence of the Number of Transported Particle Classes
To evaluate the influence of the number of particle size classes, the batch centrifugation tests were simulated first. For this purpose, a slurry was centrifuged in a beaker centrifuge. After reaching the state of equilibrium, the sediment was removed and divided into individual layers. The particle size distribution was then determined for each layer. The number of particle size classes plays an important role. For this reason, the number of particle classes was varied in the simulation of the beaker centrifuge. Figure 7 shows the cumulative distribution of particle size in two different sediment layers, layer 2 (blue) and layer 7 (orange). In total, the sediment was divided into eight layers, each approximately 1 thick, with layer 1 being the top layer and layer 8 the bottom layer. The dashed line represents the distribution measured in the experiment. The markers indicate the simulation data with varying numbers of particle classes: The square stands for three, the circle for five, the triangle for ten and the rhombus for twenty particle size classes. The initial suspension had a solids volume fraction of 8 and was centrifuged at a rotational speed of 2000 rpm until equilibrium was reached. Regardless of the number of particle size classes, all simulations reproduce the trend of the experimental data well, whereby the deviations between the simulation and the experimental data are smaller for layer 7 than for layer 2. As the number of particle size classes increases, the supporting points lie on top of each other. A slight shift to the right towards larger particles can be recognized for the simulation of three particle size classes in layer 7. In contrast, the simulation with an inhomogeneous distribution of ten particle size classes exhibits the highest deviation for the upper layer (layer 2). This steeper distribution leads to larger deviations, especially for smaller and larger fractions. It is possible that the close proximity of the larger particle size classes on the one hand and the smaller particle size classes on the other leads to the greater hindrance of these coarse and fine fractions.
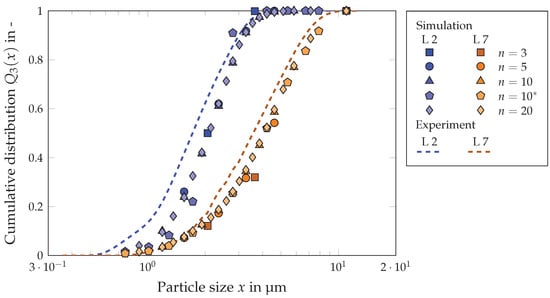
Figure 7.
Influence of the number of particle size classes on the sediment structure in the beaker centrifuge: The solids volume fraction of the suspension was , the rotational speed was min−1. The asterisk (*) indicates a non-homogeneously discretized distribution according to Figure 4e.
Figure 8 shows the validation of the simulation method for the batch centrifugation by comparing the cumulative distribution of the particle size of the experiment with the distribution of the simulation. The black solid line depicts the particle size distribution of the slurry, the dashed lines the distributions from the experiments measured with the laser diffraction spectrometer. The markings represent the discrete distributions of the simulation, whereby the distribution was mapped by ten particle size classes. The different shades of gray indicate the individual layers. Again, the sediment was segmented into eight layers, each approximately 1 thick, with the topmost layer labeled as layer 1 and the bottommost as layer 8. The lightest shade represents layer 1, while the darkest shade corresponds to layer 8. The slurry had a solids volume fraction of 8 . The rotational speed during the experiment was 2000 rpm, which corresponds to a C-value of 1160 g. The experimental and simulated data exhibit the expected segregation pattern consistent with the results obtained from the hindered settling function (Figure 5): an increasing segregation (swarm sedimentation) with a decreasing solids volume fraction was already evident in the experiments for material characterization. Accordingly, smaller particles are present in the top layer. The average particle size in the experiment is , in the simulation . In contrast, larger particles appear in the lowest layer. Here, the mean particle size is in the experiment and in the simulation. For the simulation, the values for the mean particle size were interpolated linearly. Below , there are slight deviations. This deviation may be explained by an inaccuracy of the measurement precision in the range of very fine particles. In laser diffraction, the particle size is determined from the measured change in the intensity of the scattered light as a function of the scattering angle. This means that large particles scatter light at small angles (Fraunhofer diffraction), while small particles scatter light at large angles (Mie scattering). However, if the particle shape deviates from the spherical shape, the jagged particle shape with its additional edges and surfaces causes more diffuse scattering patterns. This complicates the interpretation and the evaluation and it is possible that smaller particles are detected than are actually present. According to Li et al. [61], laser diffraction analysis might underestimate the particle size by up to 10 to 20%.
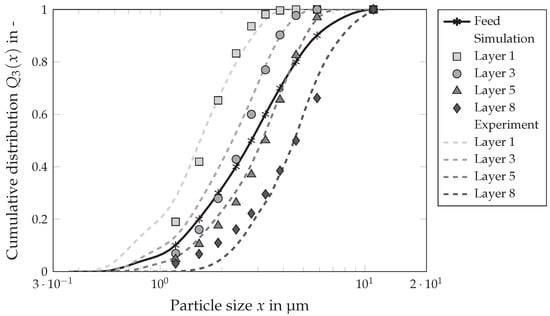
Figure 8.
Particle size distribution in the individual sediment layers: The solids volume fraction of the suspension was , the rotational speed was min−1. Ten particle size classes were used for the discretization.
The next step was the investigation of the influence of the number of particle size classes for the decanter centrifuge. In Figure 9, the cumulative distribution of the particle size is depicted for the centrate (blue) and the sediment (orange). The dashed line corresponds to the distribution observed in the experimental data. The simulation results with different numbers of particle classes are represented by markers: a square for three, a circle for five, a triangle for ten, and a rhombus for twenty particle size classes. The inlet solids volume fraction remained constant at , the rotational speed was 3000 rpm, the differential velocity was 5 rpm, and the volumetric flow rate was consistently 24 Lh−1. It is recognizable that both the centrate and the sediment can be represented through the simulation. As observed in the simulation of the beaker centrifuge, the accuracy increases with a greater number of particle size classes. However, the most significant deviation is evident in the simulation with ten unevenly distributed particle size classes. An improved representation of centrate and sediment was expected due to the increased number of support points in that region. The simulation data solely fall within the size range of the experimental data but do not accurately reflect their trend. Similar to the beaker centrifuge, the distribution curve is much steeper. It is therefore not advisable to divide the particle size classes unevenly. Also notable is the significant deviation of the smallest support point for the centrate in the division into twenty particle size classes. For the smaller fractions, the chosen measurement method may not be optimal and a more precise resolution may be required.
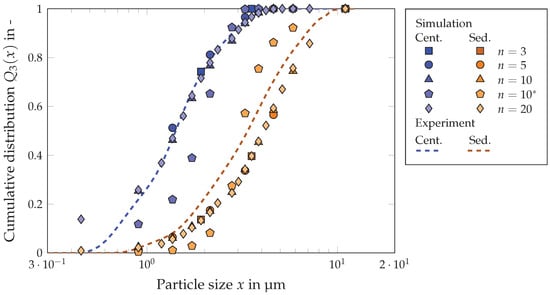
Figure 9.
Influence of the number n of particle size classes on the particle size distribution in the centrate and the sediment: the solids volume fraction of the feed suspension was , the volume flow rate was Lh−1 and the rotational speed was min−1. The asterisk (*) indicates a non-homogeneously discretized distribution according to Figure 4e.
Figure 10 illustrates the impact of the number of particle size classes on computation time for two types of centrifuges: a beaker centrifuge, characterized by a non-complex flow behavior, and a decanter centrifuge, where both the complex flow through CFD and the solution of transport equations for solids volume fraction are simulated. Represented on the Y-axes are the normalized computation times for both centrifuges, defined as the ratio of the required computation time to the simulated time. This measure reveals the additional time needed for the simulation to calculate one second in real time. The blue Y-axis and the bars show the data for the beaker centrifuge, the orange-colored data for the decanter centrifuge. The beaker centrifuge simulations were performed on a workstation with an Intel Core i7-8700 processor (Intel Deutschland GmbH, Neubiberg, Germany). The challenge of achieving a physical simulation time of 60 and more for the decanter simulations was passed by running OpenFOAM in parallel on the bwUniCluster, the shared high-performance computing system of Baden-Württemberg’s universities and universities of applied sciences. Each simulation ran on a node with 40 cores. The processor was an Intel Xeon Gold 6230. The findings from the diagram indicate that the number of particle size classes has a more significant impact on computation time for the beaker centrifuge compared to the decanter. In the simulation of the beaker centrifuge, the computational time for simulating five particle size classes is 1.3 times that required for a single particle size class, with the simulation of 10 particle size classes extending to 1.7 times the duration, and the simulation of 20 particle size classes significantly increasing to 2.4 times the duration. Regarding the decanter centrifuge, a noteworthy allocation of computation time appears directed towards flow calculations. In this context, the disparity between simulating 10 and 20 particle size classes relative to a single class is merely 13% and 20%, respectively. More than 120 have been simulated for the decanter centrifuge. The simulated time for the beaker centrifuge corresponds to the actual test time. Nevertheless, owing to the time necessary to attain a steady state within the continuous apparatus, the absolute difference is not negligible. Hence, simulations of the decanter centrifuge were executed employing ten particle size scales.
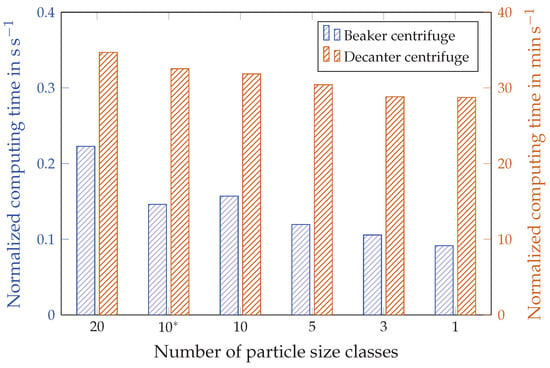
Figure 10.
Required computation time for the simulation of the beaker centrifuge and the decanter centrifuge depending on the number of particle size classes. The asterisk (*) indicates a non-homogeneously discretized distribution according to Figure 4e.
3.3. Mechanical Dewatering and Clarification
Important separation tasks of decanter centrifuges are the clarification and dewatering of suspensions. Figure 11 shows the comparison of the simulation and experimental results for the solids volume fraction of the centrate and the sediment. In the results presented, the solids volume fraction at the inlet was constant at , the differential velocity was 5 rpm, and the volumetric flow rate was constant at 24 Lh−1. Shown in orange is the dependence of the solids volume fraction in the sediment and in blue is the solids volume fraction in the centrate on the rotational speed. The axes are scaled differently accordingly. Furthermore, triangular markers indicate the simulation results, while circles indicate the experimental results. As expected, the solids fraction in the sediment increases with the rising rotational speed. At the same time, the solids fraction in the centrate decreases. The reason for this is that with higher speeds, increasingly smaller particles are separated. In addition, a higher centrifugal force acts on the sediment, which is why it is compressed more. The simulation reproduces the experimental data well with the deviations being highest at 1000 rpm. In total, the simulation tends to underestimate the solids volume fractions in the sediment determined in the experiment. This may be related to additional shear compression in the apparatus [47,62] which was not taken into account in the material characterization. At lower speeds, the simulation overestimates solids volume fraction in the centrate. The simplifications made for the simulation may be responsible for the deviations in the centrate. For example, the gas phase was neglected and the overflow from the liquid weir was set at a constant level and also designed more generously. On the one hand, it was necessary to ensure that there were enough cells to map the outlet with sufficient accuracy. On the other hand, these cells should not be too small to avoid increasing the computing time.
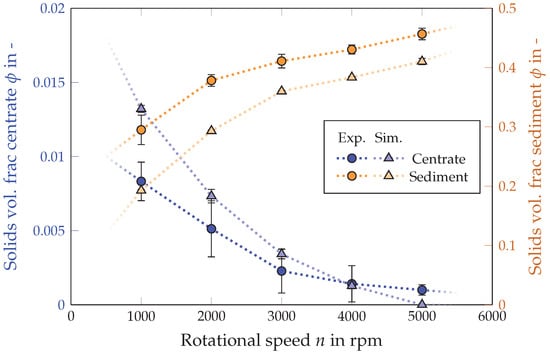
Figure 11.
Solids volume fraction of the centrate (blue) and the sediment (orange) at a volumetric flow rate of 36 Lh−1 with varying rotational speed: Comparison of simulation and experiment.
3.4. Simulation of the Classification Process
Another important task is classification, for which decanter centrifuges are also used. The decisive factors here are how long the particles remain in the apparatus and how fast they sediment. In addition, the solids volume concentration of the suspension should be reduced so that the particles do not hinder each other excessively during sedimentation. Figure 12 shows the influence of the rotational speed on the particle size distribution in the centrate. The markers indicate the simulation results, the dashed lines represent the experimentally measured distributions. The different shades of gray indicate the influence of the rotational speed. The solids volume fraction at the inlet was 2 , the volume flow and the differential speed were constant at 36 Lh−1 and 5 rpm. As expected, the particle size distribution shifts towards smaller particles as the rotational speed increases. This means that more particles were separated. Overall, the simulation matches the experimental data. The deviations between simulation and experiment are consistent with the results regarding the solids volume fraction in centrate and sediment. There is a tendency for the particle size distribution to shift to the right towards larger particle sizes at lower rotational speeds and to the left towards smaller particle sizes at higher rotational speeds. It is also noticeable that with increasing rotational speed and the associated shift of the particle size distribution to the left, the lowest support point moves further upwards. For 1000 and 2000 rpm, it is still below 20%, for 4000 and 5000 rpm, just above 40%. For higher accuracy, it is recommended to simulate with more particle size classes for future simulations.
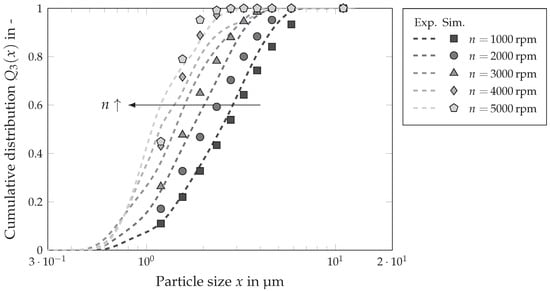
Figure 12.
Influence of the rotational speed n on the particle size distribution of the centrate: The solids volume fraction of the feed suspension was , the volume flow rate was Lh−1 and the rotational speed varies between 1000 rpm and 5000 rpm.
In addition to the rotational speed, the residence time plays an important role in the separation in decanter centrifuges. Figure 13 shows the influence of the volume flow rate on the particle size distribution in the centrate. Again, the dashed line represents the experimental data and the markers refer to the simulation data. The different shades of gray indicate the different volume flow rates. The solids volume fraction at the inlet was 2 , the rotational speed and the differential speed were constant at 3000 rpm and 5 rpm. The simulation data reproduces the experimental data well. The lower the volume flow rate, the higher the residence time in the apparatus. This means that the particles have a longer time to sediment and smaller particles may also be separated. Both the experimental and the simulation data show this behavior, which can be seen in the diagram by the shift of the particle size distribution to the left with decreasing volume flow rate. As with the speed, it is also evident for the volume flow that the fixed definition of particle size classes may pose a disadvantage in the classification simulation. At a volume flow rate of 24 Lh−1, the lowest support point is just over 40%. Consequently, the simulation of the classification is limited to a certain extent by the number of particle size classes.
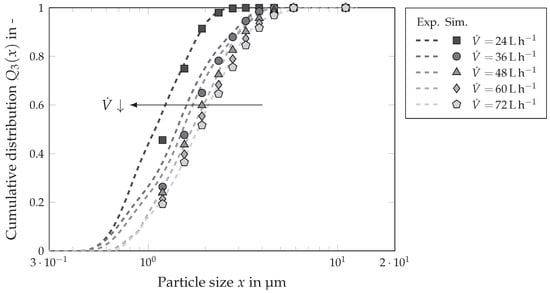
Figure 13.
Influence of the rotational speed n on the particle size distribution of the centrate: The solids volume fraction of the feed suspension was , the rotational speed was rpm and the volume flow rate varies between 24 Lh−1 and 72 Lh−1.
The flow through the decanter centrifuge classifies the particle system along the screw channel in the direction of the overflow weir. Depending on the separation process, for example clarification or classification, it is possible to determine the required length of the cylindrical part of the centrifuge using the CFD simulations. Figure 14 illustrates the particle size distribution in different segments of the apparatus. The inlet winding corresponds to segment 1, the following winding to segment 2, and so on until after the last turn (segment 6) before the clarified liquid (centrate) exits the decanter centrifuge via the weir. In the simulation, the solids volume fraction was set at 2 , the rotational speed at 5000 rpm, the differential speed at 5 rpm and the volumetric flow rate at 36 Lh−1. It is clearly evident that the suspension becomes clearer as the number of turns passed increases, as shown by the shift of the particle size distribution to the left. Notably, the diagram reveals that a substantial portion of particle separation occurs within the first three segments. The efficiency of particle separation decreases in the later segments, with the majority of separation processes taking place in the early segments. This is confirmed by the relative distance between the distributions. After each segment, fewer particles are separated progressively.
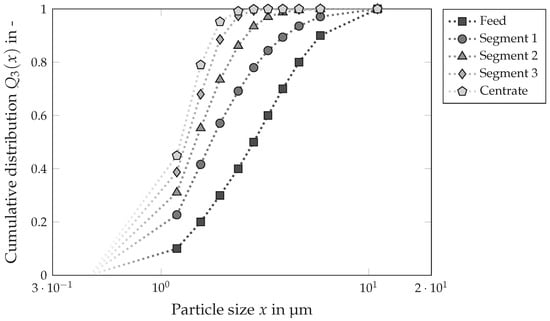
Figure 14.
Particle size distribution of the centrate in different segments in the decanter centrifuge: The solids volume fraction of the feed suspension was , the volume flow rate was Lh−1 and the rotational speed was .
3.5. Outlook: Geometry Optimization
The extension of the solver by taking into account entire particle size distributions enables the resolution of various separation problems, such as clarification or classification. Accordingly, the CFD solver may now be used to optimize the geometry of the apparatus or its components. The conventional conveyor, for example, has a helical flight without openings. For clarification, an alternative to the solid flight is a screw flight with windows, which allows the clarified liquid to flow axially from the inlet zone to the centrate outlet [26].
Figure 15 shows the distribution of solids in the apparatus for different geometry designs of the flights. The geometry in (a) and (b) has a conventional solid flight, while (c) has windows and (d) additionally has a tapered flight height towards the weir. In the cases (b), (c) and (d) the rotational speed is 2000 rpm, in case (a) 4000 rpm. It is discernible that a substantial proportion of the solids are deposited directly in the inlet region and in the immediately following segments. In the cases of the solid flight, the stirring effect, as described in the literature [22,36], is also evident, which complicates the separation of fine particles or may even result in the re-suspension of particles already deposited. The openings in the screw flight allow the expected axial flow of the suspension to be clarified. In addition, the flow design counteracts strong vortex formation in the screw segment and prevents re-suspension of already deposited particles. In both cases (c) and (d), a clear phase is distinctly visible (blue color shading). It is also noticeable that the effect intensifies in the case of tapered flight (d). The reason for this lies in the slower axial flow rate caused by the increasing flow cross-section in the case of the tapered flight, which leads to a stabilization of the flow and at the same time better separation of the particles. In all cases, it can be observed that a deflection of the flow occurs immediately at the centrate discharge, near the weir. Consequently, particles located below the weir are entrained in the reverse direction and discharged with the centrate. To prevent this, the installation of a baffle protruding a few millimeters into the processing chamber orthogonally to the weir could be advantageous. This serves to constrain the vortex. For the cases (c) and (d), a continuous centrate removal along the entire cylindrical section could be considered, possibly through an additional axial channel with a series of integrated perforations.
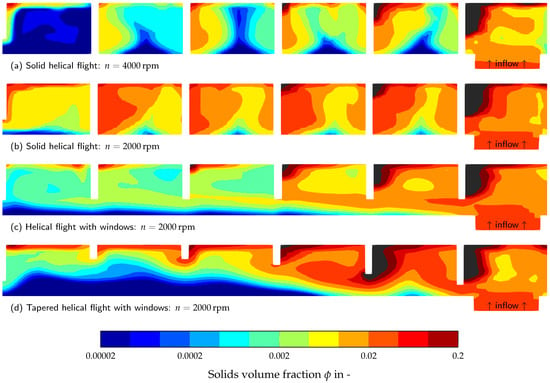
Figure 15.
Solid distribution in the cylindrical section of the decanter centrifuge with various flight designs. The color scale indicates the solids volume fraction in the apparatus. The sediment () is shown in gray.
Depending on the centrifuge’s application, the evaluation of the separation efficiency is not solely influenced by the particle size distribution, but also by the solids volume fraction in the centrate and the sediment. To quantify the visual results, both the separation efficiency and the sharpness of separation were analyzed. The separation efficiency, crucial for clarification, is defined as the ratio of the mass of solids separated in the centrifuge to the initial mass of solids in the feed. Figure 16 shows the separation efficiency as a function of the rotational speed for different geometries at a constant volume flow rate of 36 Lh−1, constant differential speed of 5 rpm and an initial solids volume fraction of 2 . It is apparent that with a higher rotational speed, the separation efficiency rises for all three geometries. Simultaneously, it is noticeable that the modified flights significantly enhance the separation performance. For example, approximately the same separation efficiency is achieved at 1000 rpm as with the conventional flight at 2000 rpm or a slightly better one at 2000 rpm than at 4000 rpm with the solid flight. Furthermore, the tapered flight seems to perform slightly worse at lower rotational speeds than the flight with windows only. However, as indicated by Figure 15, the re-suspension of already separated particles at the weir plate plays a crucial role, and enhanced clarification could be achieved by implementing an additional continuous axial discharge for the centrate.
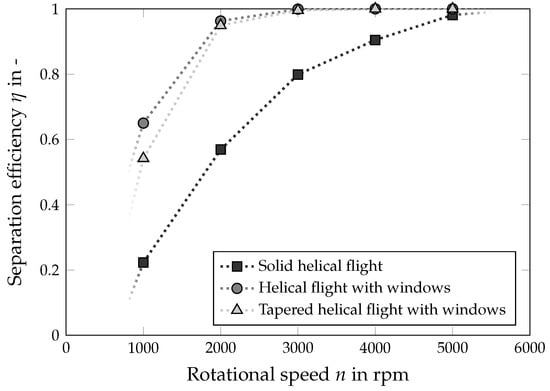
Figure 16.
Separation efficiency for different flight designs of the screw: The solids volume fraction of the feed suspension was , the volume flow rate was Lh−1.
The same applies to the separation sharpness , a measure for classification defined as the ratio of to of the grade efficiency, thereby describing the steepness of the grade efficiency curve [63]. A value of signifies an ideal and perfectly sharp separation, which is not achievable in practice. According to Löffler [64], the selectivity of a technical separation is in the size range of and for a sharp technical separation, it is in the size range of . In the case of the modified geometries, the separation is so effective that practically all particles have been removed, making it impossible to determine a separation sharpness. In the case of the solid helical flight, a sharpness of separation of 0.37 is achieved at 1000 rpm, while at rotational speeds of 2000, 3000, and 4000 rpm the sharpness of separation remains approximately constant at 0.74. Just as the separation efficiency can be enhanced by integrating windows in the flights, so can the separation sharpness. For instance, the separation sharpness is around 0.71 at 1000 rpm.
4. Conclusions and Outlook
This work is concerned with the clarification and classification in centrifuges using the example of the decanter centrifuge. To achieve this, a solver was extended by additional transport equations in order to take particle size classes into account. Experiments with a beaker centrifuge and a laboratory decanter are used for validation.
The first step involved an examination of the present material concerning its sedimentation and consolidation behavior. The hindered settling function describes the influence of solids volume fraction on the settling behavior of particles in a suspension. Measurements of settling velocity distributions as a function of the solids volume fraction, and particle size measurements via laser diffraction served as the basis for determining sedimentation hindrance. The approach originating from Michales and Bolger [45] was extended by introducing the particle size, enabling the calculation of an individual hindrance factor for each particle size class. It is noticeable that, with increasing solids volume fraction, the profiles of the individual graphs for the respective particle size classes converge. For the determination of the effective solids stress, sediments were segmented into individual layers, and based on the method of Reinach [57], the compression resistance was determined as a function of the solids volume fraction. The effective solids stress could be described using the power approach by Green et al. [46].
Furthermore, it was investigated how many particle classes are necessary to describe the deposition accurately enough. Initially, the batch experiments used to determine the consolidation function were simulated, whereby the particle size distribution in the different layers was extracted and compared with the experimental results. As expected, the accuracy improves with an increasing number of particle size classes. The simulation results from the decanter centrifuge confirmed this outcome. A look at the computing time reveals that solving the additional transport equations for the particle size classes has a relatively minor impact on overall computation time. Instead, the calculation of the flow seems to constitute the majority. However, the absolute computation time is not negligible, leading to the selection of ten particle size classes for subsequent simulations.
By expanding the solver to include the capability of resolving particle size classes, it is now feasible to investigate clarification and classification in separation devices. As anticipated, rising rotational speeds lead to a decrease in the solids volume fraction in the centrate and an increase in the sediment. The simulated results align well with the experimental findings. Differences, such as the deviations of the solids volume fraction in the sediment, can be explained by the neglected shear compaction. Furthermore, the particle size distributions of the centrate were examined by varying the rotational speed and the volumetric flow rate. With rising rotational speed, the cumulative particle size distribution shifts to the left towards smaller particle sizes, since increasingly finer particles are also separated. In contrast, a higher volume flow rate results in a reduction in the residence time, causing less fine particles to be separated. Again, the simulated results are in good agreement with the experimental results. However, there is also a limitation due to the small number of particle size classes when the volume flow rate decreases or the rotational speed increases in the simulation of the centrate (Figure 12 and Figure 13). Consequently, it may be concluded that the number of particle size classes depends to a certain extent on the process parameters, which makes an additional sensitivity study necessary, starting with the extreme case of low volume flow rate and high rotational speed for decanter centrifuges.
Furthermore, the extension of the solver enables the ideal choice or design of the apparatus geometry for the respective process. As an example, the screw conveyor was modified by adding windows to the flight which corresponds to the design features of many newer centrifuges. The windows enable an axial flow of the centrate and, as demonstrated, contribute to improved clarification.
In summary, the expansion of the solver now enables the simulation of all essential separation tasks in centrifuges, such as thickening, clarification, or classification. Simulating individual particle size classes requires comparatively little time, rendering the solver efficient and making it conceivable to simulate larger apparatuses on the pilot or industrial scales. Moreover, the solver can be utilized to choose or design the optimal geometry required for a specific separation task.
Author Contributions
Conceptualization, H.K.B.; methodology, H.K.B.; validation H.K.B.; formal analysis H.K.B.; investigation, H.K.B.; software H.K.B.; visualization, H.K.B.; writing—original draft preparation, H.K.B.; writing—review and editing, H.K.B., M.G. and H.N.; resources, H.N.; supervision, M.G. and H.N.; project administration, H.K.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Acknowledgments
The authors would like to thank all students and colleagues who have contributed to the successful completion of this work. Furthermore, they acknowledge support by the state of Baden-Württemberg through bwHPC and by the KIT-Publication Fund of the Karlsruhe Institute of Technology.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Mesh Characteristics
Table A1 lists all the boundary conditions used in the several simulations.

Table A1.
Boundary conditions of the simulation.
Table A1.
Boundary conditions of the simulation.
| Inlet | Outlet | Rotating Walls | Stationary Walls | |
|---|---|---|---|---|
| flowRateInletVelocity | zeroGradient | movingWallVelocity | noSlip | |
| p | fixedFluxPressure | fixedValue | fixedFluxPressure | fixedFluxPressure |
| fixedvalue | zeroGradient | zeroGradient | zeroGradient | |
| zeroGradient | zeroGradient | zeroGradient | zeroGradient | |
| zeroGradient | zeroGradient | zeroGradient | zeroGradient |
To ensure that the resolution of the mesh was sufficiently accurate, the cell size of the mesh was reduced and the simulation results were compared. The mesh size became 600,000, 1,200,000 and 2,400,000 cell elements using cell sizes of , and , respectively. In addition, mesh quality characteristics were checked: none of the meshes had a maximum skewness greater than 0.85 and orthogonality was never less than 0.18. The criteria used to investigate mesh independence were the velocity distribution and the sediment structure in the screw channel. Figure A1 shows the results of the mesh independence study. It shows that the cell size mesh deviates significantly from finer meshes due to the larger cells and thus different sediment distribution. The velocity profile deviates by 21% from the finest resolution and the solids volume fraction deviates by 34%. However, the profiles for the axial velocity component and the solids volume fraction are well represented by the 0.8 mm mesh. The deviations are only 2% and 3%, respectively. For this reason, the simulations were performed using the mesh. A more detailed description of the grid study can be found in Baust et al. [36].
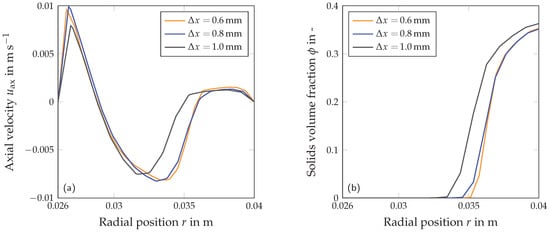
Figure A1.
Mesh independence study: (a) the axial velocity component and (b) the solids volume fraction are plotted against the radial position r in the screw channel [36].
References
- Müller, F. Wet Classification in the Fines Range < 10 μm. Chem. Eng. Technol. 2010, 33, 1419–1426. [Google Scholar]
- Whitworth, A.J.; Forbes, E.; Verster, I.; Jokovic, V.; Awatey, B.; Parbhakar-Fox, A. Review on advances in mineral processing technologies suitable for critical metal recovery from mining and processing wastes. Clean. Eng. Technol. 2022, 7, 100451. [Google Scholar] [CrossRef]
- Menesklou, P. Entwicklung Eines Hybriden Simulationsmodells zur Optimierung des Betriebsverhaltens von Dekantierzentrifugen. Ph.D. Thesis, Karlsruhe Institute of Technology (KIT), Karlsruhe, Germany, 2022. (In German). [Google Scholar]
- Lahtela, V.; Hamod, H.; Kärki, T. Assessment of critical factors in waste electrical and electronic equipment (WEEE) plastics on the recyclability: A case study in Finland. Sci. Total Environ. 2022, 830, 155627. [Google Scholar] [CrossRef]
- Haller, N.; Kulozik, U.; Haller, N.; Kulozik, U. Separation of Whey Protein Aggregates by Means of Continuous Centrifugation. Food Bioprocess Technol. 2019, 12, 1052–1067. [Google Scholar] [CrossRef]
- Padilla-Zamudio, A.; Guerrero-Germán, P.; Tejeda-Mansir, A. Plasmid DNA primary recovery from E. coli lysates by depth bed microfiltration. Bioprocess Biosyst. Eng. 2015, 38, 1091–1096. [Google Scholar] [CrossRef]
- Summerhays, R.; Gaspar, A. Thickening, Filtration and Clarification in the Phosphoric Acid Industry. Procedia Eng. 2016, 138, 164–173. [Google Scholar] [CrossRef]
- Spelter, L.E.J. Abtrennung und Klassierung Kolloidaler Partikel in Zentrifugen: Experimenteller Nachweis und Modellierung der Sedimentation in halbkontinuierlichen Vollmantelzentrifuge. Ph.D. Thesis, Karlsruhe Institute of Technology (KIT), Karlsruhe, Germany, 2012. (In German). [Google Scholar]
- Starrett, J.B.; Galvin, K.P. Application of inclined channels in the hydrodynamic classification of minerals by particle size. Miner. Eng. 2023, 195, 108002. [Google Scholar] [CrossRef]
- Lösch, P.; Nikolaus, K.; Antonyuk, S. Classification of Fine Particles Using the Hydrodynamic Forces in the Boundary Layer of a Membrane. Chem. Ing. Tech. 2019, 91, 1656–1662. [Google Scholar] [CrossRef]
- Wu, N.; Wyart, Y.; Rose, J.; Angeletti, B.; Moulin, P. Application of membrane processes in fractionation of elements in river water. Water Sci. Technol. 2015, 72, 2277–2290. [Google Scholar] [CrossRef]
- Wu, N.; Wyart, Y.; Liu, Y.; Rose, J.; Moulin, P. An overview of solid/liquid separation methods and size fractionation techniques for engineered nanomaterials in aquatic environment. Environ. Technol. Rev. 2013, 2, 55–70. [Google Scholar] [CrossRef]
- Zhang, C.; Shuaishuai, L. Study on the separation mechanism of coal and gangue particles during coal slime classification in a hydrocyclone. Powder Technol. 2023, 424, 118566. [Google Scholar] [CrossRef]
- Zhao, Q.; Cui, B.; Ji, A.; Song, T.; Shen, Y. Experimental and numerical study of the effect of particle size distribution on hydrocyclone classification. Adv. Powder Technol. 2024, 35, 104398. [Google Scholar] [CrossRef]
- Khatri, N.; Singh, M.; Pokhriyal, S.; Rene, E.R. Computational fluid dynamics modelling of primary sludge classification in an activated sludge process based wastewater treatment plant: Simulating the hydrodynamic behaviour and experimental verification of the classification efficiency. Chem. Eng. J. 2023, 464, 142475. [Google Scholar] [CrossRef]
- Neesse, T.; Dueck, J.; Schwemmer, H.; Farghaly, M. Using a high pressure hydrocyclone for solids classification in the submicron range. Miner. Eng. 2015, 71, 85–88. [Google Scholar] [CrossRef]
- Yamamoto, T.; Shinya, T.; Fukui, K.; Yoshida, H. Classification of particles by centrifugal separator and analysis of the fluid behavior. Adv. Powder Technol. 2011, 22, 294–299. [Google Scholar] [CrossRef]
- Konrath, M. Klassierung von Feinstpartikeln Mittels Schnelldrehender Sedimentationszentrifugen. Ph.D. Thesis, Karlsruhe Institute of Technology (KIT), Karlsruhe, Germany, 2016. (In German). [Google Scholar]
- Kumar, A.; Subramanian, V.K.; Velaga, S.; Kodandaraman, J.; Sujatha, P.N.; Baskaran, R.; Kumar, S.; Ananda Rao, B.M. Performance evaluation of a tubular bowl centrifuge by using laser obscuration method as an online measurement tool. Sep. Sci. Technol. 2020, 55, 1839–1851. [Google Scholar] [CrossRef]
- Winkler, M.; Rhein, F.; Nirschl, H.; Gleiss, M. Real-Time Modeling of Volume and Form Dependent Nanoparticle Fractionation in Tubular Centrifuges. Nanomaterials 2022, 12, 3161. [Google Scholar] [CrossRef]
- Sinn, T.; Menesklou, P.; Nirschl, H.; Gleiß, M. Further developments of a dynamic real-time model of a tubular centrifuge fed with multi-component dispersions for application in fractionation for Direct Recycling of lithium-ion batteries. Chem. Eng. Sci. 2023, 277, 118858. [Google Scholar] [CrossRef]
- Stahl, W.H. Fest-Flüssig-Trennung. 2, Industrie-Zentrifugen; Maschinen- & Verfahrenstechnik, DrM Press: Männedorf, Switzerland, 2004. (In German) [Google Scholar]
- Wang, Y.; Forssberg, E.; Li, J.; Pan, Z. Continuous ultra-fine classification in a disc stack nozzle centrifuge – effects of g-forces and disc geometry. China Particuology 2003, 1, 70–75. [Google Scholar] [CrossRef]
- Kurnianto Prayitno, Y.A.; Sejati, P.A.; Zhao, T.; Iso, Y.; Kawashima, D.; Takei, M. In situ measurement of hindered settling function in decanter centrifuge by periodic segmentation technique in wireless electrical resistance detector (psWERD). Adv. Powder Technol. 2021, 33, 103370. [Google Scholar] [CrossRef]
- Bai, C.; Park, H.; Wang, L. Modelling solid-liquid separation and particle size classification in decanter centrifuges. Sep. Purif. Technol. 2021, 263, 118408. [Google Scholar] [CrossRef]
- Records, A.; Sutherland, K. Decanter Centrifuge Handbook; Elsevier Science Ltd.: Oxford, UK, 2001. [Google Scholar]
- Gleiß, M.; Hammerich, S.; Kespe, M.; Nirschl, H. Application of the dynamic flow sheet simulation concept to the solid-liquid separation: Separation of stabilized slurries in continuous centrifuges. Chem. Eng. Sci. 2017, 163, 167–178. [Google Scholar] [CrossRef]
- Skorych, V.; Buchholz, M.; Dosta, M.; Baust, H.K.; Gleiß, M.; Haus, J.; Weis, D.; Hammerich, S.; Kiedorf, G.; Asprion, N.; et al. Use of Multiscale Data-Driven Surrogate Models for Flowsheet Simulation of an Industrial Zeolite Production Process. Processes 2022, 10, 2140. [Google Scholar] [CrossRef]
- Faust, T.; Gösele, W. Untersuchungen zur Klärwirkung von Dekantierzentrifugen. Chem. Ing. Tech. 1985, 8, 698–699. (In German) [Google Scholar] [CrossRef]
- Madsen, B. Flow and sedimentation in decanter centrifuge. Int. Chem. Eng. Symp. Ser. 1993, 7, 263–266. [Google Scholar]
- Hou, T.H. Evaluation of separator performance by number-size distribution data. Powder Technol. 1985, 41, 99–104. [Google Scholar] [CrossRef]
- Pinkerton, A.P.; Klima, M.S. Evaluation of a solid-bowl centrifuge for ultrafine size separations. Miner. Metall. Process. 2001, 18, 162–166. [Google Scholar] [CrossRef]
- Bai, C.; Park, H.; Wang, L. A Model–Based Parametric Study of Centrifugal Dewatering of Mineral Slurries. Minerals 2022, 12, 1288. [Google Scholar] [CrossRef]
- Hammerich, S. Numerische Simulation des Fest-Flüssig-Trennprozesses in Vollmantelzentrifugen. Ph.D. Thesis, Karlsruhe Institute of Technology (KIT), Karlsruhe, Germany, 2020. (In German). [Google Scholar]
- Baust, H.K.; Hammerich, S.; König, H.; Nirschl, H.; Gleiß, M. A Resolved Simulation Approach to Investigate the Separation Behavior in Solid Bowl Centrifuges Using Material Functions. Separations 2022, 9, 248. [Google Scholar] [CrossRef]
- Baust, H.K.; Hammerich, S.; König, H.; Nirschl, H.; Gleiß, M. Resolved simulation of the clarification and dewatering in decanter centrifuges. Processes 2024, 12, 9. [Google Scholar] [CrossRef]
- Bürger, R.; Concha, F. Settling velocities of particulate systems: 12. Batch centrifugation of flocculated suspensions. Int. J. Miner. Process. 2001, 63, 115–145. [Google Scholar] [CrossRef]
- Zhai, O.; Baust, H.; Gleiß, M.; Nirschl, H. Model-based Scale Up of Solid Bowl Centrifuges Using Experimentally Determined Material Functions. Chem. Ing. Tech. 2023, 95, 189–198. [Google Scholar] [CrossRef]
- Bickert, G. Sedimentation Feinster Suspendierter Partikeln im Zentrifugalfeld. Ph.D. Thesis, University of Karlsruhe (TH), Karlsruhe, Germany, 1997. (In German). [Google Scholar]
- Garrido, P.; Concha, F.; Bürger, R. Settling velocities of particulate systems: 14. Unified model of sedimentation, centrifugation and filtration of flocculated suspensions. Int. J. Miner. Process. 2003, 72, 57–74. [Google Scholar] [CrossRef]
- Berres, S.; Bürger, R. On gravity and centrifugal settling of polydisperse suspensions forming compressible sediments. Int. J. Solids Struct. 2003, 40, 4965–4987. [Google Scholar] [CrossRef]
- Kynch, G.J. A theory of sedimentation. Trans. Faraday Soc. 1952, 48, 166–176. [Google Scholar] [CrossRef]
- Stokes, G.G. On the effect of internal friction of fluids on the motion of pendulums. Trans. Camb. Philos. Soc. 1851, 9, 8–106. [Google Scholar]
- Richardson, J.F.; Zaki, W.N. The sedimentation of a suspension of uniform spheres under conditions of viscous flow. Chem. Eng. Sci. 1954, 3, 65–73. [Google Scholar] [CrossRef]
- Michaels, A.S.; Bolger, J.C. Settling rates and sediment volumes of flucculated Kaolin suspensions. Ind. Eng. Chem. Fundam. 1961, 1, 24–33. [Google Scholar] [CrossRef]
- Green, M.D.; Eberl, M.; Landman, K.A. Compressive yield stress of flocculated suspensions: Determination via experiment. AIChE J. 1996, 42, 2308–2318. [Google Scholar] [CrossRef]
- Erk, A.; Luda, B. Influencing Sludge Compression in Solid-Bowl Centrifuges. Chem. Eng. Technol. 2004, 27, 1089–1093. [Google Scholar] [CrossRef]
- Hochstein, B. Rheologie von Kugel-und Fasersuspensionen Mit Viskoelastischen Matrixflüssigkeiten. Ph.D. Thesis, University of Karlsruhe (TH), Karlsruhe, Germany, 1997. (In German). [Google Scholar]
- Einstein, A. Eine neue Bestimmung der Moleküldimensionen. Ann. Phys. 1906, 324, 289–306. [Google Scholar] [CrossRef]
- Quemada, D. Rheology of concentrated disperse systems and minimum energy dissipation principle. Rheol. Acta 1977, 16, 82–94. [Google Scholar] [CrossRef]
- Krieger, I.M.; Dougherty, T.J. A mechanism for non-Newtonian flow in suspensions of rigid spheres. Trans. Soc. Rheol. 1959, 3, 137–152. [Google Scholar] [CrossRef]
- Herschel, W.H.; Bulkley, R. Measurement of Consistency as Applied to Rubber-Benzine Solutions. Proc. Am. Soc. Test. Mater. 1926, 26, 621–633. [Google Scholar]
- Bingham, E.C. An investigation of the laws of plastic flow. Bull. Bur. Stand. 1916, 13, 309–353. [Google Scholar] [CrossRef]
- Wolf, A.; Flegler, A.; Prieschl, J.; Stuebinger, T.; Witt, W.; Seiser, F.; Vinnay, T.; Sinn, T.; Gleiß, M.; Nirschl, H.; et al. Centrifugation based separation of lithium iron phosphate (LFP) and carbon black for lithium-ion battery recycling. Chem. Eng. Process. Process Intensif. 2021, 160, 108310. [Google Scholar] [CrossRef]
- Seiser, F.; Stübinger, T.; Witt, W.; Flegler, A.; Mandel, K.; Sinn, T.; Gleiß, M.; Nirschl, H.; Vinnay, T. AUTOKLASS—Automatische Klassierung von Partikeln aus Dispersionen zur Rohstoffrückgewinnung: Schlussbericht; Carl Padberg Zentrifugenbau GmbH: Lahr, Germany, 2021. (In German) [Google Scholar]
- Detloff, T.; Sobisch, T.; Lerche, D. Particle size distribution by space or time dependent extinction profiles obtained by analytical centrifugation (concentrated systems). Powder Technol. 2007, 174, 50–55. [Google Scholar] [CrossRef]
- Reinach, H. Gleichgewicht und Kinetik der Pressentfeuchtung im Zentrifugalfeld einer Becherzentrifuge und in Einer Stempelpresse, Dargestellt an Einem Stark Kompressiblem Schlamm. Ph.D. Thesis, University of Karlsruhe (TH), Karlsruhe, Germany, 1992. (In German). [Google Scholar]
- Atagi, Y.; Zhao, T.; Iso, Y.; Takei, M. Real-Time Imaging of Particles Distribution in Centrifugal Particles-Liquid Two-Phase Fields by Wireless Electrical Resistance Tomography (WERT) System. IEEE Access 2019, 7, 12705–12713. [Google Scholar] [CrossRef]
- Zhao, T.; Iso, Y.; Ikeda, R.; Okawa, K.; Takei, M. Real-time measurement of particle volume fraction in centrifugal fields by wireless electrical resistance detector. Flow Meas. Instrum. 2019, 65, 90–97. [Google Scholar] [CrossRef]
- Kurnianto Prayitno, Y.A.; Zhao, T.; Iso, Y.; Takei, M. In situ measurement of sludge thickness in high-centrifugal force by optimized particle resistance normalization for wireless electrical resistance detector (WERD). Meas. Sci. Technol. 2020, 32, 034001. [Google Scholar] [CrossRef]
- Li, H.; Li, J.; Bodycomb, J.; Patience, G.S. Experimental Methods in Chemical Engineering: Particle Size Distribution by Laser Diffraction-PSD. Can. J. Chem. Eng. 2019, 97, 1974–1981. [Google Scholar] [CrossRef]
- Buscall, R.; Mills, P.D.A.; Stewart, R.F.; Sutton, D.; White, L.R.; Yates, G.E. The rheology of strongly-flocculated suspensions. J. Non-Newton. Fluid Mech. 1987, 24, 183–202. [Google Scholar] [CrossRef]
- Eder, T. Probleme der Trennschärfe. In Aufbereitungstechnik 2; 1961. (In German) [Google Scholar]
- Löffler, F.; Raasch, J. Grundlagen der Mechanischen Verfahrenstechnik; Vieweg+Teubner: Braunschw, Germany, 1992. (In German) [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).