Abstract
We report a detailed investigation of the vibrational modes, structure, and dynamics of glutathione (GSH) solutions using ultrasonic relaxation spectroscopy, FT-IR vibrational spectroscopy, and electronic absorption measurements. The experimental data were analyzed using density functional theory (DFT) and molecular docking calculations. Three distinct Debye-type relaxation processes can be observed in the acoustic spectra, which are assigned to conformational changes between GSH conformers, the self-association of GSH, and protonation processes. The standard volume changes for each process were estimated both experimentally and theoretically, revealing a close resemblance among them. The higher the effect of the relaxation process in the structure, the greater the induced volume changes. From the temperature dependence of specific acoustic parameters, the thermodynamic characteristics of each process were determined. The experimental FT-IR spectra were compared with the corresponding theoretically predicted vibrational spectra, revealing that the GSH dimers and extended conformers dominate the structure of GSH solutions in the high-concentration region. The absorption spectra in the ultraviolet region confirmed the gradual aggregation mechanism that takes place in the aqueous GSH solutions. The results of the present study were discussed and analyzed in the framework of the current phenomenological status of the field.
1. Introduction
Glutathione (GSH) is a well known tripeptide with the following molecular formula: C10H17N3O6S. It consists of a glutamic acid attached through its side chain to the terminal N atom of cysteinylglycine and derivative of thiol and L-cysteine. It contains a rather unusual peptide linkage between the amine group belonging to cysteine and the carboxyl group belonging to the glutamate side chain [1]. Glutathione is present in most living cells, from bacteria to mammals, and as an antioxidant, it helps protect cells from reactive oxygen species such as free radicals and peroxides [1,2]. It is used scientifically as a measure of cellular toxicity. The IUPAC name of GSH is (2S)-2-Amino-5-({(2R)-1-[(carboxymethyl)amino]-1-oxo-3-sulfanylpropan-2-yl}amino)-5-oxopentanoic acid. The γ-bond between the glutamic acid and cysteine amino acids provides peculiar characteristics, including GSH’s property to be insusceptible to proteolysis. Additionally, the presence of the thiol-containing cysteine residue awards GSH with redox catalytic properties [3].
The minimization of the amount of GSH in the human body has been accepted as a common strategy in the treatment of aggressive and metastatic cancers, as it enhances the sensitivity of cancer cells to chemotherapy with toxic drugs and to the application of radiation [4,5,6]. On the other hand, several other diseases, including cardiovascular diseases [7], stroke [8], HIV/AIDS [9], diabetes [10], and brain disorders such as Alzheimer’s disease [11], Parkinson’s disease [12], and schizophrenia [13], are linked with the minimization of GSH and a parallel oxidative stress. Recently, it has been reported that the defensive glutathione antioxidant ability in the human body decreases linearly after the age of 45, causing several diseases that are associated with age [14]. Thus, it is of crucial importance to provide methodologies aiming to reinstate the glutathione amount in the body despite its low-partition coefficient and high-degradation rate via catalytic pathways including bacterial and epithelial GGT [15]. All these processes that are related to GSH bioavailability are based on the physicochemical and structural properties of glutathione, and, in essence, the atomic arrangement at short- and intermediate-range length scales is the decisive factor for tuning the physicochemical properties of GSH.
In this paper, we report on the structural aspects of GSH aqueous solutions and their concentration and temperature dependence. Ultrasonic relaxation spectroscopy, Fourier-transform infrared spectroscopy, and electronic absorption measurements were used for this purpose. Ultrasonic relaxation spectroscopy covers the 104 to 1010 Hz frequency region and can provide information for processes with relaxation times in wide time scales that range from 10−5 to 10−11 s, corresponding to intermediate-range length scales [16,17,18]. One the other hand, vibrational spectroscopy may provide information about the vibrational dynamics in short-range order with time scales between 10−12 and 10−14 s [19,20,21]. Combining these spectroscopic tools with a so-wide time scale has been shown to be a powerful and effective tool to describe the dynamics of a molecular system without any kind of restrictions concerning the type of the relaxation processes involved. Density functional theory (DFT) calculations and molecular docking methodologies were applied to theoretically evaluate the possibility of conformational changes, self-association, and protonation processes. The associated volume changes due to these processes were also estimated and compared with the experimental findings. In fact, all the above findings can be practically attributed to alterations in network rigidity due to variations in bonding interactions at the molecular level.
2. Materials and Methods
2.1. Solution Preparation
Crystalline glutathione as a white powder in a reduced form (Merck, purity > 99%) was used as received to prepare a series of aqueous solutions under ambient conditions and continuous stirring utilizing triply distilled water. The resulting solutions, corresponding to molar concentrations of 1, 2, 3, 4, 5, 7.5, and 10 mM, were clear and colorless. The final volume of each solution was 5 mL. Special attention was paid to acquiring all measurements from fresh solutions to ensure the absence of GSH degradation. Two more dense aqueous GSH solutions with 3.2 and 6.76% w/v were prepared for the IR absorption measurements. Because of the relatively great amount of GSH in dense solutions, the solid occupies a considerable volume of the final solution. As a result, the use of Molarity units is incorrect since the final volume is different from the quantity of the added solvent. Therefore, the usage of the percent weight per volume concentration (% w/v) leads to greater accuracy.
The mass density and pH of each solution were measured using a temperature-controlled cell (DMA 40, Anton Paar, Ashland, VA, USA) with an accuracy of ±0.0001 g/cm3 and a pH meter (Crison (Woodville North, Australia), micropH 2002) at 20 °C. The resolution of the pH measurements was 0.01, and the accuracy was ±0.03 units.
2.2. Infrared and Electronic Absorption Measurements
The infrared spectra of the two more dense solutions corresponding to 3.2 and 6.76% w/v were measured in the mid-IR spectral region, namely in the 4000 to 370 cm−1 spectral region, in transmittance mode under isobaric conditions by means of a compact FT/IR-4700 spectrometer (JASCO International Co., Ltd., Tokyo, Japan). The liquid sample was placed between two KBr pellets of ~1 mm thickness in sandwich mode. Dry potassium bromide powder of spectroscopic grade was used to prepare the pellets. The spectrometer was equipped with a stable 45° Michelson sealed interferometer with a corner cube mirror, auto-alignment, and DSP control. The spectral resolution of all measurements was fixed at 2 cm−1. The signal-to-noise ratio was estimated to be equal to 35,000:1. The light source was a standard high-intensity ceramic source. The signal was detected using a DLATGS detector with Peltier-type cooling. The spectrum of an “empty” KBr pellet was recorded as a background to account for atmospheric vapor compensation and KBr absorption [22].
The electronic absorption spectra of all solutions were recorded at 20 °C by means of the UV-1600 PC series double beam spectrophotometer (VWR International, Radnor, PA, USA) operating from 190 to 700 nm with a spectral resolution of 0.5 nm. The pathlength was fixed at 1 cm for all measurements. The quartz cell was thermostated with an accuracy of ±0.01 °C. More details about the measurement procedures can be found in [23].
2.3. Acoustic Absorption and Velocity Measurements
A set of wide-band piezoelectric elements was used to measure the sound absorption coefficient in parallel-path pulse mode as a function of concentration and temperature. The first transducer sends the acoustic wave to the sample, while the second one detects the transmitted signal after the sample. The distance between the two piezoelectric elements, namely the acoustic path, was fixed at 1 cm. The transmitting transducer was triggered by a sinusoidal burst of specific frequency. A repetition rate of 5 ms was adequate for avoiding coincidence between the next pulse and the echoes. All signals were monitored in the time domain by means of a digital oscilloscope (Tektronix, TBS 1202B, Tektronix, Beaverton, OR, USA). The excess sound absorption coefficient αexcess(f) as a function of frequency, which is attributed to solute, is calculated by subtracting the absorption of the solvent from that of the solution. The so-called pulse–echo overlap technique was utilized for the speed of sound measurements. The sound absorption of the solvent (water) in the frequency range covered in this work was found to be constant and thus non-relaxing. All acoustic absorption and sound speed measurements were performed in a temperature range of 10–35 °C with a constant step of 5 °C. The temperature during measurement taking was controlled within ±0.01 °C. The accuracy of the experimental sound absorption and velocity were ±5% and ±0.01%, respectively. In order to test and calibrate our apparatus, we performed a series of sound velocity and attenuation measurements for several non-relaxing reference liquids, including water, castor oil, glycerin, benzene, etc., and the results are presented in [24]. The agreement between our experimental values of both velocity and sound attenuation coefficients and the corresponding literature values is adequate, indicating that our setup is reliable for precisely measuring the velocity and attenuation of ultrasound in neat liquids and solutions. More details about the experimental setup and the measurement protocols can be found elsewhere [24,25,26]. In a relaxation process, molecules may occupy two or more inner energy levels. By applying an external ultrasonic field, the propagation of the soundwave disturbs the equilibrium distribution of the molecules between these energy levels. For relatively low values of the soundwave frequency, the time between two successive cycles is long enough for the energy transfer from the ultrasonic wave to the internal degrees of freedom. As the ultrasonic frequency increases, a time delay is observed between the variation in the temperature and pressure of the wave and the restoration of the internal equilibrium. This phenomenon can be detected experimentally by measuring the ultrasound absorption coefficient a as a function of ultrasound frequency f as a saddle point of the α/f2 ratio for a characteristic relaxation frequency fr in the a/f2 vs. f plot.
2.4. Density Functional Theory (DFT) Calculations
The structure and the vibrational spectroscopic properties of the GSH molecule were estimated by employing a density functional theory (DFT) methodology combined with the 6-311G (d,p) basis set. All calculations were carried out in vacuum after applying tight optimization criteria without adjusting force constants utilizing Gaussian 09 suite of programs [27]. The calculated vibrational frequencies were corrected with the corresponding scaling factor.
2.5. Molecular Docking Calculations
Molecular docking calculations were carried out in AutoDock software (version 4.2, Scripps Research, San Diego, CA, USA). To elucidate the self-aggregation process, one molecule of glutathione was used as the receptor, and a second one was used as the ligand. The structure of glutathione’s molecule was optimized using the B3LYP/6-311G (d,p) basis set, and the optimized structure was used in the molecular docking analysis. The receptor was placed in the center of a simulation box with dimensions 25 Å × 25 Å × 25 Å while the ligand was moving freely within its boundaries. The grid spacing was fixed at its default value, 0.375 Å, which is adequate considering the size of glutathione’s molecule [28]. The number of rotating bonds for the ligand was set at the maximum. Charges were assigned by means of Gasteiger charges that model the electrostatic potential of the molecule through summation over the atomic electron densities in the molecule. The best poses were selected after an evaluation carried out by using the Lamarckian genetic algorithm (LGA) [29]. Following the above procedure, we obtained the structure of the glutathione self-aggregate. The structure of the so-obtained dimer was subsequently subjected to optimization with the same basis set before the calculation of the theoretical IR spectra and additional physicochemical properties, including molecular volume.
2.6. Conformational Search and Clustering Procedures
The possible conformers of glutathione were found by applying the OPLS force field considering water as a solvent and the Mixed torsional/Low-mode sampling method. For each rotatable bond, 100 steps were permitted, while the energy difference between the conformers was set, as usual, at 5.02 kcal/mol [30]. The probability of a torsion rotation to molecule translation was set at 0.5. The elimination of similar conformers was performed based on atom distance deviation. Conformers with a distance between their atoms smaller than 0.5 Å were considered as similar and thus eliminated. The minimization of the conformers’ energy was achieved using the Conjugate Gradient (CG) methodology with maximum iterations of 2500 and 0.05 convergence threshold. The total number of conformers generated by this protocol was estimated to be equal to 134. All calculations were performed in GROMACS molecular dynamics package [31].
Conformer clustering was based on the calculation of the root-mean-square deviation of atomic positions (RMSD) matrix, which is the measure of the average distance between the atoms that are usually the backbone atoms, using the atomic coordinates for each conformer. As a linkage method, centroid-based clustering was implemented. The criterion to select an optimal number of clusters is the Kelley index, which levels the clusters’ spread at a particular level with the number of clusters at this level. According to the Kelley index, 13 clusters were found. In a dendrogram at the left side was the closed conformer of glutathione, and on the right side was the open conformer of glutathione [32].
3. Results and Discussion
3.1. Relaxation Processes Occurring in GSH Aqueous Solutions
The characteristics of its molecular structure are the drivers of GSH’s participation in a variety of structural and dynamical processes, including (i) conformational changes due to its inherent flexibility, (ii) molecular self-aggregation reactions upon the dilution of GSH in aqueous solutions in the low-concentration region, and (iii) protonation and deprotonation reactions due to the presence of the two carboxylic acids, the amine, and the thiol groups. The overall structure of the GSH molecule includes eight coordination sites comprising two carboxyl-, one amino-, two carbonyl-, two amide-, and one thiol-functional groups. The integration of density functional theory (DFT), molecular dynamics, and molecular docking calculations is a strong aspect of the present study. Initially, the optimized structure and the corresponding vibrational spectroscopic properties of the GSH molecule were estimated in a vacuum environment by employing a density functional theory (DFT) methodology. The estimation and clustering of all possible conformers of GSH was performed by applying the OPLS force field in GROMACS molecular dynamics software (version 4.6), considering water as a solvent and the Mixed torsional/Low-mode sampling method, while the minimization of the conformers’ energy was achieved using the Conjugate Gradient (CG) methodology. Conformer clustering was based on the calculation of the root-mean-square deviation of atomic positions (RMSD) matrix. Progress in achieving a comprehensive understanding of the self-aggregation of the GSH molecules was achieved by carrying out molecular docking calculations. The optimized structure, several physicochemical properties (including molecular volume), and the corresponding vibrational properties of the glutathione self-aggregate were subsequently evaluated with the same density functional theory (DFT) methodology.
The theoretical investigation of the possible conformations of glutathione performed in this work revealed that GSH may exist in an extended and in a folded form, with the extended conformer tending to be more energetically favored. Both the folded and extended conformations of GSH are presented in Figure 1a and have been experimentally evidenced [33]. Furthermore, it was found that the dominating conformation in a neutral environment is the one with the maximum distance between the thiol group and the amine and carboxylate of the Glutamic acid (Glu) residue. Each of the two peptide bonds that are near the Cysteine (Cys) residue is in trans-configuration relative to the thiol-functional group [34,35]. In general, the equilibrium reaction between the folded and extended GSH conformers can be written as:
where (GSH)* indicates one possible GSH conformer.
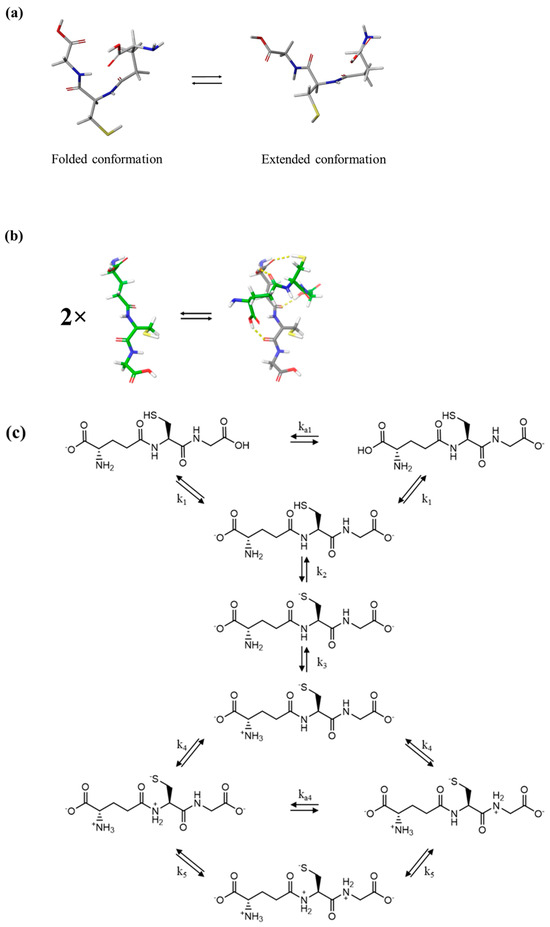
Figure 1.
(a) The two conformation isomers (left: folded isomer; right: extended isomer) observed in GSH. The extended isomer was confirmed to be the most stable by DFT calculations. (b) Left: the optimized molecular structure of a GSH monomer. Right: the formed dimer as estimated from the molecular docking study of self–aggregation. The two monomers that formed the dimer are designated by gray and green carbon atoms to facilitate a better observation of the docking regions. The dimer was confirmed as being suitably stable by DFT calculations. (c) Possible tautomers of the reduced GSH in aqueous solutions of various pH. Tautomers differ from each other by a dissociation step with a distinct dissociation constant. The tautomers on the left are favored in solutions with low pH.
When GSH is subjected to intracellularly or chemically oxidative stress, it is transformed to an oxidized glutathione dimer (GSSG) through a disulfide S-S bond. The GSSG is converted back into GSH only when the enzyme glutathione reductase is used. The GSH-to-GSSG oxidation is of crucial importance for almost all key intercellular reactions that involve GSH. In an aqueous environment, this reaction occurs only when an oxidizing agent is engaged. Despite the fact that GSH is stable in the solid state for at least 5 years when stored at 4 °C, it appears very unstable in aqueous solutions [36]. When aqueous solutions are exposed to air, the reduced glutathione converts to its disulfide dimer, forming oxidized glutathione (GSSG).
Our theoretical molecular docking study indicated that a glutathione dimer is formed by hydrogen bonds, while the sulfur atoms of the two GSH monomeric units are far away from one another. As an input in the molecular docking calculations, we used an optimized structure of the glutathione molecule, which is presented in the left side of Figure 1b. The output of the calculation was the GSH dimer shown in the right side of Figure 1b. The two monomers interact with each other, forming four new bonds. Indeed, as shown in Figure 1b, two new hydrogen bonds are formed between the hydroxyl of the glutamic acid of the one monomer with the oxygen atom of the glutamic acid and with the hydrogen atom of the sulfur group of cysteine of the other monomer. A third hydrogen bond is formed between the oxygen of the cysteine of the one monomer and the hydroxyl group of the glutamic acid of the other monomeric unit. Finally, the fourth hydrogen bond is formed between the hydroxyl group of glycine of the one monomer with the oxygen of glutamic acid of the other monomer.
The self-aggregation reaction leading to the formation of a GSH dimer is expected to occur in the low-concentration region and can be written as:
GSH and (GSH)n denote the monomeric and aggregate units, respectively, and the aggregation number is equal to n = 2. Trimers and tetramers, with n = 3 and 4, respectively, may also be formed; however, these higher aggregates are hardly present in the highly dilute solutions explored in this study. The binding free energy for the dimerization reaction was evaluated theoretically and found to be equal to −3.44 kcal/mol. The self-assembling of glutathione in an aqueous environment was recently studied using an ultrasonically induced birefringence method [37].
For high GSH concentrations, solvent (water) and GSH molecules interact, forming mixed water–GSH aggregates. This association reaction can be written as follows:
where (H2O)m and GSH∙(H2O)m represent the water clathrates and the mixed water–GSH aggregate, both of the which are formed by hydrogen bonding.
The molecular structure of the reduced glutathione, which is characterized by various biological donor atoms and its inherent flexibility, allows for the presence of several possible tautomers of glutathione in an aqueous environment. The relative population of these tautomers is strongly affected by the pH of the solution. The structures of tautomers of the reduced glutathione, with its eight coordination sites, are shown in Figure 1c. The protonation and deprotonation of the two carboxylic acids, the amine, and the thiol groups take place upon the dissolution of GSH in water. For the corresponding dissociation steps and the relevant dissociation constants ka,i, i = 1, 2, 3, and 4.
3.2. Effect of Concentration on the Relaxation Behavior
The absorption a of high-frequency soundwaves in solutions has two main contributions, namely non-relaxing and the relaxing contributions. The viscosity- and thermal-based losses of the sound energy are the non-relaxing contributions and are thus independent of the ultrasound frequency f. These losses account for a smaller portion of the ultrasonic absorption. The dynamic chemical equilibria present in neat liquids and solutions contribute, to a great degree, to the sound absorption at the corresponding relaxation frequencies or resonant frequencies fr that characterize the inherent chemical equilibria of the system. Figure 2 shows the excess ultrasonic absorption a/f2 curves as a function of frequency for all concentrations studied at 20 °C. The absorption coefficient of the solvent (water) is measured near ~20 × 10−17 s2/cm and frequency independent. The contribution of the solvent is subtracted from the measured absorption coefficient of the solutions. If the system contains more than one sound-absorbing chemical equilibria, the frequency reduced sound absorption a/f2 data can be fitted in the frequency domain using the well-known Debye-type equation:
where k = 1, 2, … denotes the maximum number of relaxation processes that the system exhibits, Ai is the relaxation amplitude of the i-th relaxation process, and B is the non-relaxing background sound absorption ratio in the high-frequency limit . Each relaxation process modeled by Equation (4) is shown as a sigmoidal excess over the non-relaxing background sound absorption in the semi-log a/f2 vs. f plot. The characteristic relaxation frequency fr is the frequency that corresponds to the sagmatic point of the sigmoidal function in this representation. Additional relaxation frequencies are observed as extra sagmatic points in the sigmoidal function with distinct values.
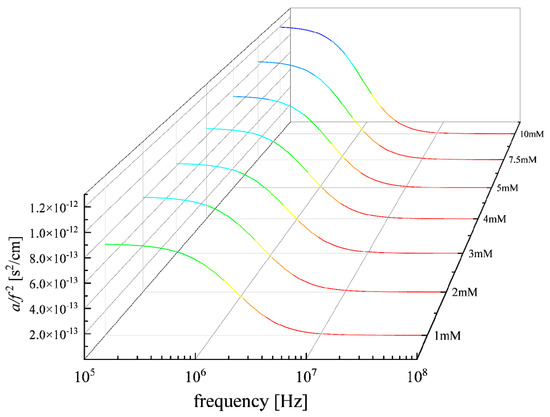
Figure 2.
Excess ultrasonic absorption a/f2 as a function of frequency for all concentrations studied at 20 °C. Continuous lines correspond to Debye-type relaxation curves after the fitting procedure described in the text.
In the case of glutathione aqueous solutions, three distinct relaxation processes were detected in the MHz frequency range studied in this work. The three individual processes were quantitatively estimated by the Levenberg–Marquardt’s fitting method, and representative results are presented in Figure 3a for a solution corresponding to 1 mM concentration. To investigate the presence of distinct relaxation frequencies, we normalized the y-axis values from zero to one, and the resulting spectra are shown in Figure 3b. The presence of three relaxation processes is clearly evidenced.
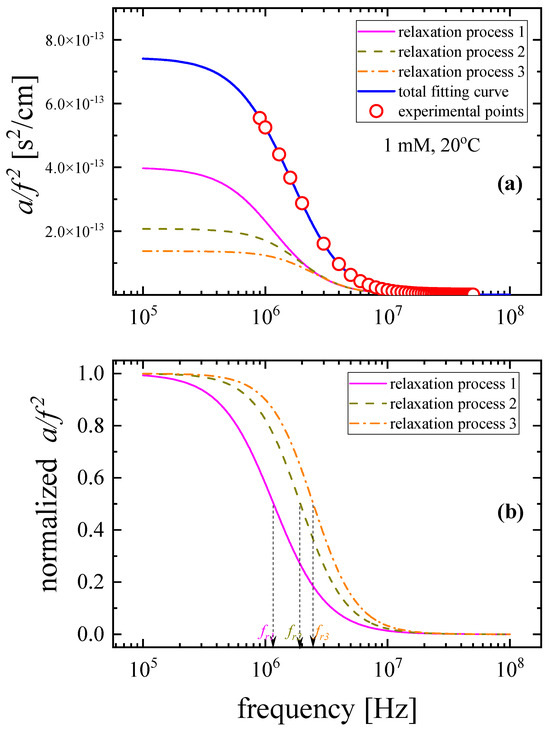
Figure 3.
(a) Excess ultrasonic absorption as a function of frequency for a solution corresponding to a concentration of 1 mM. Open symbols denote the experimental values, and solid lines correspond to the total fitting and the individual curves related with the three relaxation processes, respectively. (b) Normalized excess ultrasonic absorption spectra in the same frequency range. The three distinct relaxation frequencies are detectable as sagmatic points in the sigmoidal Debye-type profiles.
Figure 4a,b illustrate the concentration dependences of the characteristic frequency and amplitude of the relaxation processes that were detected in the acoustic spectra. The and free fitting parameters received from the non-linear least-mean-square fitting procedure are summarized in Table 1.
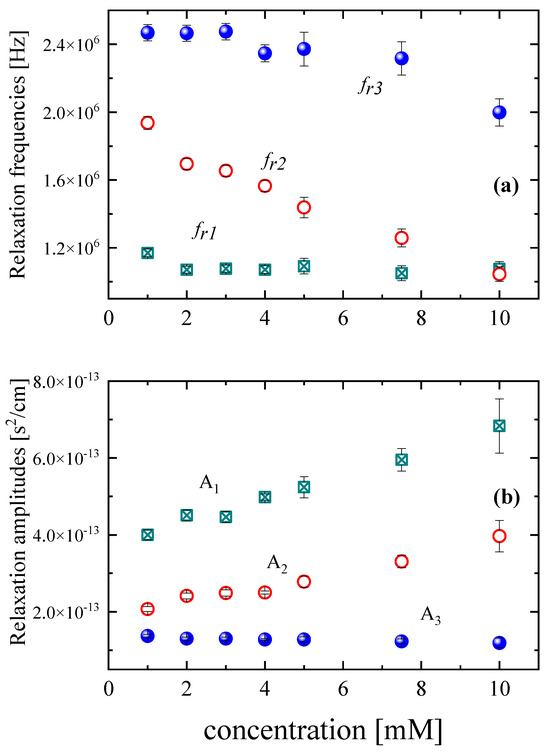
Figure 4.
Concentration dependences of the relaxation frequencies (a) and amplitudes (b).

Table 1.
Relaxation parameters for all GSH solutions at 20 °C.
Starting from the lower-frequency mechanism, it seems that the relaxation frequency fr1 appears almost constant with solution concentration, while the corresponding amplitude increases monotonically. This behavior is typical of a unimolecular reaction, such as the reported conformational change between the folded and extended GSH conformers and the reaction formulated in Equation (1). Previously conducted Raman and NMR spectroscopic studies evidenced these conformational changes [33,34,35]. In general, the relaxation processes observed in molecular systems such as glutathione aqueous solutions can be categorized into thermal and structural processes. Thermal relaxation mechanisms are usually observed in systems where fluctuations in the ultrasonic wave perturb a chemical intra-molecular equilibrium, such as the one detected here between the folded and extended GSH conformers, which involves intra-molecular rotational rearrangements through translational and vibrational coupling. The second relaxation process detected in the acoustic spectra is characterized by an increase in the relaxation amplitude and a red shift in the characteristic frequency. This process is attributed to the aggregation reaction of glutathione, which was recently experimentally evidenced using an ultrasonically induced birefringence technique [37]. The increase in the relaxation amplitude indicates that the aggregation mechanism is enhanced with increasing solution concentration. The third process identified in the acoustic spectra appears at higher frequencies and is attributed to the proton transfer reactions between possible tautomers of the reduced GSH in aqueous solutions of various pH. Tautomers differ from each other by a dissociation step with a distinct dissociation constant, as presented in Figure 1c. In a more acidic environment, i.e., one with a low pH value, the tautomers on the left of Figure 1c are favored. The amplitude of this relaxation mechanism remains almost constant with solution concentration, revealing that this process is relatively insensitive to concentration, while the opposite is true for the acidity of the solutions. In our case and at 20 °C, pH varies between 3.37 at 1 mM and 2.74 at 10 mM. This variation is minor, and it does not seem to strongly affect the amplitude of the relaxation assigned to protonation and deprotonation reactions. The second and the third relaxation processes are classified into structural processes, since they involve intermolecular rearrangements that are frequently associated with large volume changes between different equilibrium states. In general, structural processes are linked with shear (structural) viscosity and have been observed to prevail in strongly associated liquids consisting of polar molecules interacting through hydrogen bonding [38,39].
The standard volume change for the conformational change, the association–dissociation reaction, and the protonation and deprotonation reactions can be directly evaluated based on the experimental maximum excess absorption per wavelength , the solution density ρ, the sound velocity u, the absolute temperature T, the gas constant R, and the concentration term Γ from the following equation [40,41]:
The maximum value of the absorption per wavelength is a function of the relaxation frequency fr, the relaxation amplitude A, and the sound velocity u, which can be calculated as follows:
The reciprocal of the concentration term can be estimated as [42]:
where j represents the number of the species involved in the chemical reaction, while cj and Δνj are the molar concentrations corresponding at equilibrium and the difference in the stoichiometric coefficients of the reactants and products, respectively.
Considering the conformational changes represented in Equation (1) as a first-order reaction, the equilibrium kinetics are described by a relaxation time, which is given by the following [43,44,45]:
Subscript 1 denotes relaxation process 1, which is assigned to the equilibrium reaction between the folded and extended GSH conformers. and represent the probabilities of the forward and backward transition, respectively, and . Furthermore, the equilibrium constant is:
The corresponding concentration term for this case will be:
Concentrations and are the concentrations at the equilibrium state. The equilibrium constant was estimated to be equal to .
For the association–dissociation reaction presented in Equation (2), considering the mechanism in one mean stage, the kinetics can be described as [46,47]:
This equation expresses the relation between the relaxation time and the reactant concentration [GSH] at the equilibrium state. and are the forward and backward rate constants, respectively. The interaction between the GSH and water molecules are expected at frequencies well above 70 MHz; thus, the second detected relaxation process is attributed to the association–dissociation reaction described by Equation (2). To determine the aggregation number, we tested different values on n. The value n = 2 was found to provide the least error of plots of as a function of . Values higher than 2 resulted in continuously increasing errors, which means that the most favorable aggregation number is n = 2, and GSH dimers were revealed as the most thermodynamically favorable. Afterwards, the forward and backward rate constant values were estimated to be equal to and , respectively. The corresponding concentration term for this case is given by the following:
Concerning the charge transfer reaction, the possible tautomers of the reduced GSH in aqueous solutions of various pH that are presented in Figure 1c can be described as:
Tautomers Gi with i = 1, 2, 3, 4, and 5 are presented in Figure 1c starting from left to right and differ from each other by a dissociation step with a distinct dissociation constant. Tautomers on the left are favored in solutions with low pH. The corresponding concentration term for this case will be:
Since our experiments were performed at 20 °C and pH varied between 3.37 and 2.74 for 1–10 mM, the last two terms in Equation (14) can be eliminated, meaning that we have the following:
From Equations (10), (12), and (15), we were able to calculate the corresponding concentration term for each relaxation mechanism, and subsequently, we evaluated the standard volume changes for each process as a function of GSH concentration at 20 °C. The results are presented in Figure 5. The solid, dotted, and dash-dotted lines correspond to the theoretically estimated isentropic standard volume changes corresponding to each relaxation process, calculated by means of the B3LYP/6-311G (d,p) basis set. The theoretical volume changes were found to be close to the experimentally determined volume changes, even though the calculation was performed in a vacuum environment free of potential intermolecular interactions. The volume changes due to the dimerization of GSH (structural relaxation) are affected by concentration to a greater extent compared to the volume changes due to the conformational variations between rotational isomers (thermal relaxation). Structural relaxation is expected to have a much stronger impact on the structure than thermal relaxation, and the higher the structural effect, the greater the volume change will be.
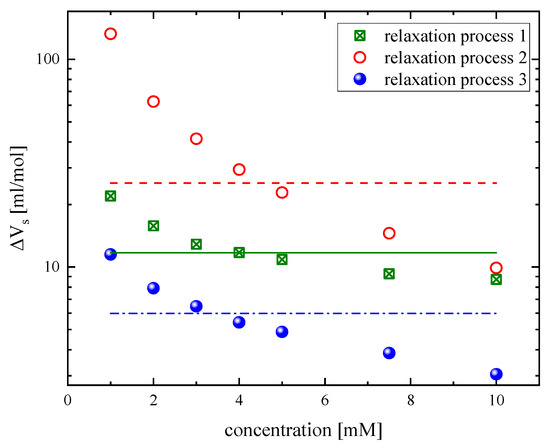
Figure 5.
Standard volume changes for the conformational changes (relaxation process 1), the association–dissociation reaction (relaxation process 2), and the protonation and deprotonation reactions (relaxation process 3) as a function of GSH concentration at 20 °C. The solid, dotted, and dash-dotted lines correspond to the theoretically estimated standard volume changes corresponding to each relaxation process. See the main text for details about the calculation procedure.
3.3. Effect of Temperature on the Relaxation Behavior
The frequency dependence of the excess ultrasonic absorption a/f2 is presented in Figure 6 for a 5 mM solution and for all temperatures studied. The continuous lines represent the Debye-type relaxation curves modeled by Equation (4). The observed reduction in the ultrasonic absorption ratio a/f2 of glutathione with increasing ultrasonic frequency in the 10 to 35 °C temperature range is characteristic of relaxational behavior.
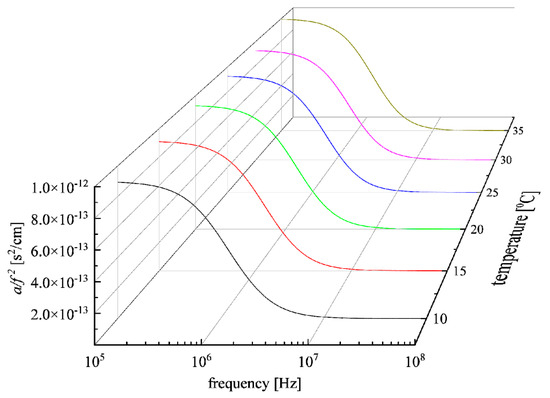
Figure 6.
Excess ultrasonic absorption a/f2 as a function of frequency for a solution with concentration 5 mM for all temperatures studied. The continuous lines correspond to the Debye-type relaxation curves for each temperature.
The and free fitting parameters obtained from the non-linear least-mean-square fitting procedure for each temperature are illustrated in Figure 7(a) and (b), respectively, and summarized in Table 2. The relaxation frequencies for all processes increase linearly with temperature, though with different slopes. On the other hand, relaxation amplitudes A1 and A2 exhibit a slight increase, while amplitude A3 decreases with temperature.
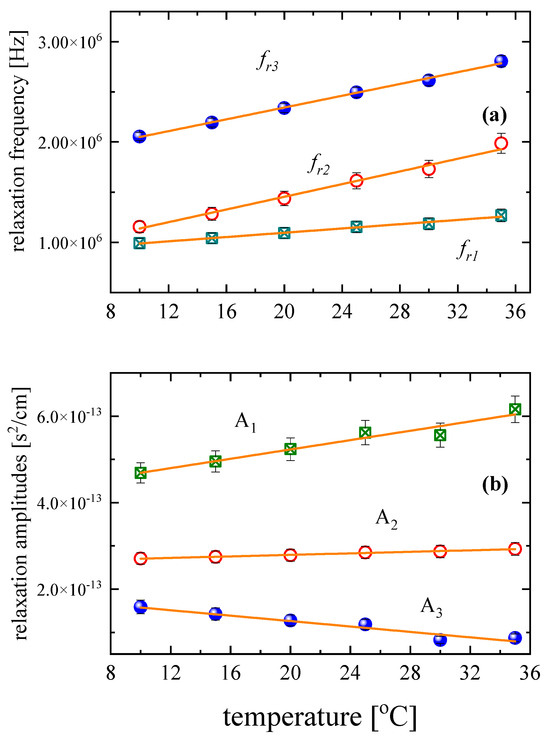
Figure 7.
Temperature dependence of the characteristic ultrasonic relaxation frequencies (a) and amplitudes of relaxation (b).

Table 2.
Relaxation parameters of a GSH solution (5 mM concentration) for all temperatures studied.
From the temperature dependence of the characteristic frequency of the relaxation process, the activation enthalpy, entropy, and free energy can be estimated in the context of Eyring’s rate theory [43,44,45]:
is the activation free energy of the i-th process, while kB and h denote the Boltzmann and Planck constants, respectively. The variation in as a function of reciprocal temperature is presented in Figure 8 for all relaxation processes. The results reveal a clear linear dependency with a negative slope, as expected. The activation enthalpy for each relaxation mechanism was estimated directly from the slope of this graph using the following equation:
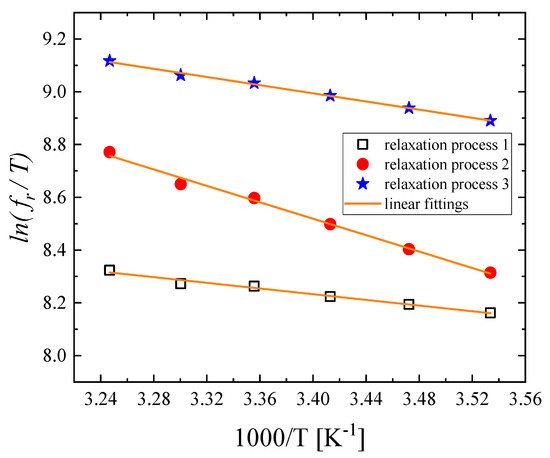
Figure 8.
Variation in as a function of reciprocal temperature for all relaxation processes.
And the activation entropy of the i-th process is estimated from the intercept of each line.
For the conformational changes (relaxation process 1), the activation enthalpy, entropy, and free energy were found to be equal to , , and , respectively. For the aggregation reaction (relaxation process 2), the activation enthalpy, entropy, and free energy were found to be equal to , , and , respectively. Finally, for the protonation–deprotonation reactions (relaxation process 3), the activation enthalpy, entropy, and free energy were found to be equal to , , and , respectively. The linear dependency that can be observed in Figure 8 supports our assumption that the entropy and the entropy change for each process are almost constant in the temperature range studied here. Another interesting finding is that the entropy change’s contribution to the free energy change is small for all relaxation mechanisms.
From the maximum value of the absorption per wavelength , the absolute temperature and the sound velocity, we may evaluate the enthalpy difference for a relaxation process through using the following equation [42,43,44,45]:
In the above equation, parameters V, Θ, and J are the molar volume, the thermal expansion coefficient, and the unit conversion factor (J = 4.187 J/cal). The rest of the symbols, CP and ρ, denote the specific heat per unit mass at constant pressure and the solution mass density, respectively. From Equation (18) we can obtain the following:
The variation in with reciprocal temperature for the relaxation processes attributed to conformational changes (process 1) is presented in Figure 9. Also, in this case, the observed linear dependency is in line with our assumption that the enthalpy and the entropy difference for the specific relaxation process is constant and temperature independent, at least in the temperature range studied. The derivation of Equation (18) has been reported in [24]. This equation is valid only when the equilibrium constant is well below unity and the volume change ΔV associated with the relaxation mechanism is negligible compared to the corresponding enthalpy change ΔH0. These assumptions are valid only for the relaxation process related to the conformational changes. From the slop of the versus plot (Figure 9), we can estimate the enthalpy difference between the extended conformer and the folded conformer, which was estimated to be equal to ΔH0 = 3.23 ± 0.28 kcal/mol.
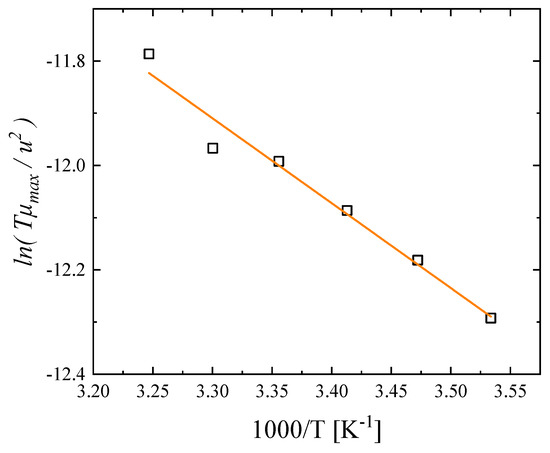
Figure 9.
Reciprocal temperature dependence of for the relaxation process attributed to conformational changes (process 1).
3.4. Probing Molecular Structure and Conformation based on Vibrational and Electronic Properties
To further elucidate the mechanisms that affect the structure of GSH upon dilution at the molecular level, we recorded the IR vibrational spectra of representative relatively dense solutions corresponding to concentrations of 3.2 and 6.76% w/v. These spectra are presented in Figure 10. In the same figure, the theoretically predicted IR spectra corresponding to the GSH monomer, dimer, extended conformer, and folded conformer in the vapor phase are also shown. The main bands observed in the IR spectra of GSH aqueous solutions and their assignments are summarized in Table 3. Starting from the high frequencies, the broad spectral envelope located at 3250–3628 cm−1 is attributed to –OH, NH, and NH2 functional groups. The bands near ~3020 and ~2523 cm−1 are assigned to C–H stretching modes and a –SH functional group. Finally, the bands near ~1712 and ~1598 cm−1 are attributed to –C=O of the acid and amide groups, respectively. We will focus our attention on the 1700–1500 cm−1 spectral region. The GSH dimer and the extended conformer are expected to dominate the structure of the GSH solutions in this relatively denser concentration region. Due to the inherent flexibility of GSH, when dissolved in water, it does not remain in a regular state, causing variations in the conformations and in the hydrogen bonding network. On the other hand, due to the small size of the water molecules and their ability to provide and accept protons, these molecules form bridging hydrogen bonds with GSH and break down the folded conformers. The conformational flexibility of GSH means that GSH can shift between the extended and the folded conformations; nevertheless, it mostly stays in the extended conformation in aqueous environment. Indeed, our comparison reveals that the four bands in the region 1685–1620 cm−1 and the band at ~1508 cm−1 of the theoretically predicted IR spectrum of the GSH dimer almost coincide with the ~1650 cm−1 band and the shoulder band at 1520 cm−1 of the experimental spectra, respectively. Furthermore, the bands observed in the theoretically predicted spectrum of the extended conformer between 1684 and 1645 cm−1 also coincide with the experimental bands of the GSH solutions in the same spectral range. The comparison between experimental FT-IR spectra and theoretical predictions is a key aspect of this study. Quantum chemical calculations allowed us to confirm the proposed structures and allowed for an in-depth understanding of the electronic structures. The theoretical results also showed good agreement with the experimental findings. DFT calculations were carried out to elucidate the influence of the structural modification on the spectroscopic properties and to provide insights into the factors controlling the observed relaxation phenomena. The extent of the spectral similarities was evaluated in a quantitative manner by the correlation coefficients for the selected spectral data. Pearson-type correlations were calculated for the absorbance values corresponding to different spectra for each wavenumber. Every point of the scatter matrix corresponds to a specific wavenumber in the IR spectra. The points that are included in the confidence eclipse correspond to correlations above 95%. This methodology revealed that most of the points were inside the confidence eclipse, which is indicative of the spectral similarity between the experimental and theoretical FT-IR spectra. The agreement between the theoretical findings and the experimental IR spectra is adequate, and any observed discrepancies can be understood by considering that the calculation was performed in vacuum without the presence of any intermolecular interactions. Definitely, the FT-IR spectroscopy proved sensitive to changes in the chemical structures of molecules and to molecular conformation.
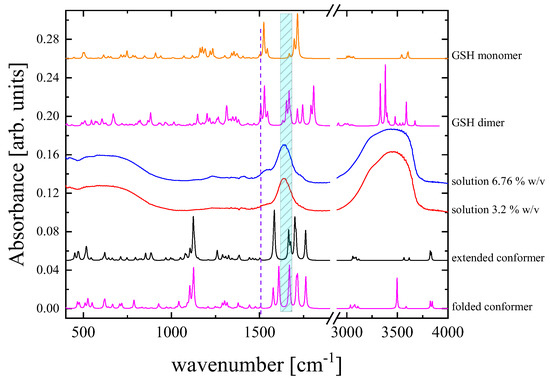
Figure 10.
Experimental IR absorbance spectra of aqueous GSH solutions with 3.2 and 6.76% w/v. The calculated IR spectra of the GSH monomer, dimer, extended conformer, and folded conformer are also shown for a direct comparison.

Table 3.
Vibrational frequencies and assignments for the GSH solution (5 mM concentration) for all temperatures studied.
The ultraviolet absorption spectrum of glutathione in water is presented in Figure 11a. We can observe an absorption band near ~203 nm in the spectra of glutathione, which is assigned to the electronic transition from the HOMO state to the LUMO, LUMO+1, and LUMO+2 states. Two additional bands can also be detected near ~232 and ~225 nm, depending on the solution concentration, and these bands are related to various the electronic transitions of the glutathione molecule instead of the dissociation of peptide bonds [48]. Figure 11b,c illustrate absorbance and the wavelength values corresponding to the maximum of the broad band as a function of concentration. Both spectral parameters seem to follow a monotonous increasing trend. It is interesting to note that above 4 mM concentration, the variation in the Amax follows a linear dependency with Pearson’s r = 0.99835. A sudden change near 4 mM was also observed in the concentration dependency of the structural (shear) viscosity, density, specific conductivity, sound velocity, isentropic compressibility, and pH. This behavior is associated with the gradual aggregation mechanism that takes place in aqueous GSH solutions [37].
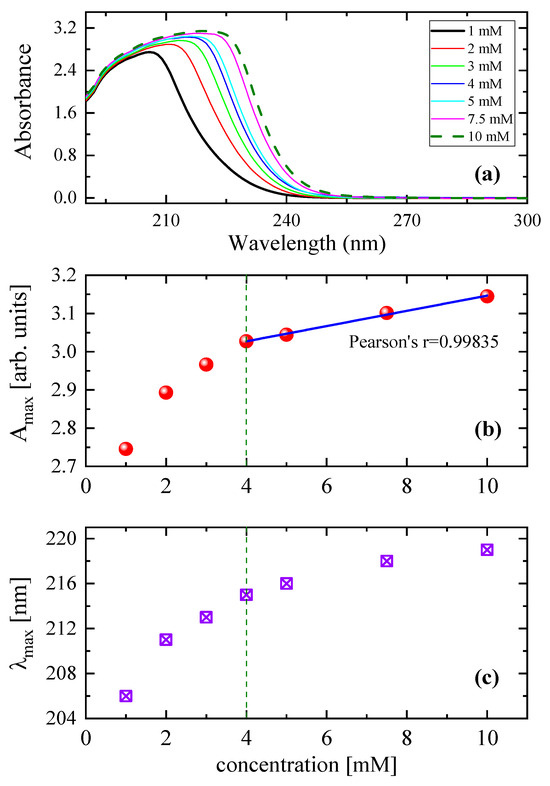
Figure 11.
(a) UV-Vis absorption spectra of GSH aqueous solutions at 20 °C for all concentrations studied. Absorbance (b) and wavelength (c) values corresponding to the maximum of the broad band as a function of concentration.
The findings of the present work contribute to the current understanding of GSH solution dynamics and structure. Although many theories and experiments were used to study GSH, the hydrogen bonding network and the correlative conformations of GSH in aqueous solutions are seldom involved. To gain a deeper insight into the GSH–water system, we employed theoretical calculations and various spectroscopic techniques. The competitive formation of GSH–hydrogen bonding interactions in aqueous solutions leads to hydrogen bonding networks and the distribution of conformations that may play an important role in the activity of GSH under physiological conditions. Our theoretical calculations revealed that GSH is highly flexible in aqueous solutions, which is in agreement with the structural model proposed in the literature. The GSH molecules shift from the extended to the folded conformation when dissolved in water, revealing a good proton donor and acceptor ability. On the other hand, water molecules may form hydrogen bonds with GSH molecules, forming more stable clusters. Consequently, water molecules act as a structure breaker for the folded conformation. This insight is expected to provide a better understanding of the detected relaxation phenomena.
4. Conclusions
Ultrasonic relaxation and FT-IR spectroscopy, combined with electronic absorption measurements, were used to describe the dynamics of GSH solutions and elucidate associated relaxation processes. DFT and molecular docking calculations were performed to theoretically examine the presence of possible conformational changes, self-association, and protonation processes. Three distinct Debye-type relaxation processes can be observed in the acoustic spectra. The process observed in the lower frequency is assigned to the conformational changes between the folded and extended GSH conformers. The second relaxation process detected in the acoustic spectra is attributed to the aggregation reaction of glutathione, while the third process identified in the spectra appears in the higher-frequency region and is related to the proton transfer reactions between possible tautomers of GSH reduced in aqueous solutions, depending on the acidity of the solution. The standard volume changes for each process were evaluated experimentally and found to be close to the theoretically predicted values. The volume changes due to structural relaxation (dimerization of GSH) are higher than the volume changes due to thermal relaxation (conformational variations between rotational isomers). Higher structural alterations induce greater volume changes. The activation enthalpy, entropy, and free energy were estimated for the conformational changes, the aggregation reaction, and the protonation–deprotonation reactions, respectively. The enthalpy difference could be accurately estimated only for the conformational changes. The experimental FT-IR spectra corresponding to dense solutions are dominated by the presence of vibrational bands characteristic of GSH dimers and extended conformers. The ultraviolet absorption spectra of glutathione in water revealed the gradual aggregation mechanism that takes place in aqueous GSH solutions.
Author Contributions
Conceptualization, A.G.K.; methodology, A.G.K.; quantum mechanical calculations, A.T. and P.S.; molecular docking calculations, C.K.; validation, A.G.K.; investigation, A.T., P.S., C.K. and A.G.K.; writing—original draft preparation, A.G.K.; writing—review and editing, A.G.K.; review and editing, A.T., P.S. and C.K.; supervision, A.G.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data will be made available on request.
Acknowledgments
This work was carried out in fulfilment of the requirements for the Ph.D. thesis of A. Tryfon according to the curriculum of the Department of Chemistry, University of Ioannina, under the supervision of A. G. Kalampounias.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Hunter, G.; Eagles, A. Glutathione: A critical study. J. Biol. Chem. 1927, 72, 147–166. [Google Scholar] [CrossRef]
- Hamilton, C.J.; Arbach, M.; Groom, M. Beyond Glutathione: Different Low Molecular Weight Thiols as Mediators of Redox Regulation and Other Metabolic Functions in Lower Organisms. In Recent Advances in Redox Active Plant and Microbial Products; Jacob, C., Kirsch, G., Slusarenko, A., Winyard, P., Burkholz, T., Eds.; Springer: Dordrecht, The Netherlands, 2014; Volume 11, pp. 291–320. [Google Scholar]
- Gaucher, C.; Boudier, A.; Bonetti, J.; Clarot, I.; Leroy, P.; Parent, M. Glutathione: Antioxidant Properties Dedicated to Nanotechnologies. Antioxidants 2018, 7, 62. [Google Scholar] [CrossRef]
- Estrela, J.; Obrador, E.; Navarro, J.; Delavega, M.; Pellicer, J. Elimination of Ehrlich tumours by ATP-induced growth inhibition, glutathione depletion and X-rays. Nat. Med. 1995, 1, 84–88. [Google Scholar] [CrossRef]
- Mena, S.; Benlloch, M.; Ortega, A.; Carretero, J.; Obrador, E.; Asensi, M.; Petschen, I.; Brown, B.D.; Estrela, J.M. Bcl-2 and glutathione depletion sensitizes B16 melanoma to combination therapy and eliminates metastatic disease. Clin. Cancer Res. 2007, 13, 2658–2666. [Google Scholar] [CrossRef]
- Rocha, C.R.R.; Garcia, C.C.M.; Vieira, D.B.; Quinet, A.; de Andrade-Lima, L.C.; Munford, V.; Belizário, J.E.; Menck, C.F.M. Glutathione depletion sensitizes cisplatin- and temozolomide-resistant glioma cells in vitro and in vivo. Cell Death Dis. 2014, 5, e1505. [Google Scholar] [CrossRef]
- Vargas, F.; Rodríguez-Gómez, I.; Pérez-Abud, R.; Vargas Tendero, P.; Baca, Y.; Wangensteen, R. Cardiovascular and renal manifestations of glutathione depletion induced by buthionine sulfoximine. Am. J. Hypertens. 2012, 25, 629–635. [Google Scholar] [CrossRef]
- Anderson, M.F.; Nilsson, M.; Eriksson, P.S.; Sims, N.R. Glutathione monoethyl ester provides neuroprotection in a rat model of stroke. Neurosci. Lett. 2004, 354, 163–165. [Google Scholar] [CrossRef]
- Herzenberg, L.A.; De Rosa, S.C.; Dubs, J.G.; Roederer, M.; Anderson, M.T.; Ela, S.W.; Deresinski, S.C.; Herzenberg, L.A. Glutathione deficiency is associated with impaired survival in HIV disease. Proc. Natl. Acad. Sci. USA 1997, 94, 1967–1972. [Google Scholar] [CrossRef]
- Lagman, M.; Ly, J.; Saing, T.; Kaur Singh, M.; Vera Tudela, E.; Morris, D.; Chi, P.-T.; Ochoa, C.; Sathananthan, A.; Venketaraman, V. Investigating the causes for decreased levels of glutathione in individuals with type II diabetes. PLoS ONE 2015, 10, e0118436. [Google Scholar] [CrossRef]
- Martin, H.L.; Teismann, P. Glutathione—A review on its role and significance in Parkinson’s disease. FASEB J. 2009, 23, 3263–3272. [Google Scholar] [CrossRef]
- Pocernich, C.B.; Butterfield, D.A. Elevation of glutathione as a therapeutic strategy in Alzheimer disease. Biochim. Biophys. Acta 2009, 1822, 625–630. [Google Scholar] [CrossRef]
- Gu, F.; Chauhan, V.; Chauhan, A. Glutathione redox imbalance in brain disorders. Curr. Opin. Clin. Nutr. Metab. Care 2015, 18, 89–95. [Google Scholar] [CrossRef]
- Jones, D.P.; Mody, V.C.; Carlson, J.L.; Lynn, M.J.; Sternberg, P. Redox analysis of human plasma allows separation of pro-oxidant events of aging from decline in antioxidant defenses. Free Radic. Biol. Med. 2002, 33, 1290–1300. [Google Scholar] [CrossRef]
- Witschi, A.; Reddy, S.; Stofer, B.; Lauterburg, B.H. The systemic availability of oral glutathione. Eur. J. Clin. Pharmacol. 1992, 43, 667–669. [Google Scholar] [CrossRef]
- Siafarika, P.; Papanikolaou, M.G.; Kabanos, T.A.; Kalampounias, A.G. Probing the equilibrium between mono- and di-nuclear nickel(II)-diamidate {[NiII(DQPD)]x, x = 1, 2} complexes in chloroform solutions by combining acoustic and vibrational spectroscopies and molecular orbital calculations. Chem. Phys. 2021, 549, 111279. [Google Scholar] [CrossRef]
- Tsigoias, S.; Kouderis, C.; Mylona-Kosmas, A.; Boghosian, S.; Kalampounias, A.G. Proton-transfer in 1,1,3,3 tetramethyl guanidine by means of ultrasonic relaxation and Raman spectroscopies and molecular orbital calculations. Spectrochim. Acta A Mol. Biomol. Spectrosc. 2020, 229, 117958. [Google Scholar] [CrossRef]
- Siafarika, P.; Kouderis, C.; Kalampounias, A.G. Non-Debye segmental relaxation of poly-N-vinyl-carbazole in dilute solution. Mol. Phys. 2021, 119, e1802075. [Google Scholar] [CrossRef]
- Kalampounias, A.G.; Kirillov, S.A.; Steffen, W.; Yannopoulos, S.N. Raman spectra and microscopic dynamics of bulk and confined salol. J. Mol. Struct. 2003, 651–653, 475–483. [Google Scholar] [CrossRef]
- Kalampounias, A.G. Dilution effect on the vibrational frequency and vibrational relaxation of PbCl2–KCl ionic liquids. J. Mol. Liq. 2015, 202, 68–74. [Google Scholar] [CrossRef]
- Kalampounias, A.G.; Tsilomelekis, G.; Boghosian, S. Unraveling the role of microenvironment and hydrodynamic forces on the vibrational relaxation rates of pyridine–water complexes. J. Mol. Liq. 2014, 198, 299–306. [Google Scholar] [CrossRef]
- Latsis, G.K.; Banti, C.N.; Kourkoumelis, N.; Papatriantafyllopoulou, C.; Panagiotou, N.; Tasiopoulos, A.; Douvalis, A.; Kalampounias, A.G.; Bakas, T.; Hadjikakou, S.K. Poly Organotin Acetates against DNA with Possible Implementation on Human Breast Cancer. Int. J. Mol. Sci. 2018, 19, 2055. [Google Scholar] [CrossRef]
- Kalampounias, A.G.; Papatheodorou, G.N. Ligand Field States and Vibrational Modes of Solid and Molten Elpasolite: Cs2NaHoCl6. Z. Naturforsch. 2007, 62, 169–175. [Google Scholar] [CrossRef]
- Stogiannidis, G.; Tsigoias, S.; Kalampounias, A.G. Conformational energy barriers in methyl acetate—Ethanol solutions: A temperature-dependent ultrasonic relaxation study and molecular orbital calculations. J. Mol. Liq. 2020, 302, 112519. [Google Scholar] [CrossRef]
- Kalampounias, A.G. Exploring conformational change profile of n-propyl ester of formic acid by combining ultrasonic relaxation spectroscopy and molecular orbital calculations. J. Mol. Struct. 2020, 1212, 128146. [Google Scholar] [CrossRef]
- Kouderis, C.; Siafarika, P.; Kalampounias, A.G. Disentangling proton-transfer and segmental motion relaxations in poly-vinyl-alcohol aqueous solutions by means of ultrasonic relaxation spectroscopy. Polymer 2021, 217, 123479. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; et al. Gaussian 09, Revision A.02; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Kouderis, C.; Tsigoias, S.; Siafarika, P.; Kalampounias, A.G. The Effect of Alkali Iodide Salts in the Inclusion Process of Phenolphthalein in β-Cyclodextrin: A Spectroscopic and Theoretical Study. Molecules 2023, 28, 1147. [Google Scholar] [CrossRef]
- Morris, G.M.; Goodsell, D.S.; Halliday, R.S.; Huey, R.; Hart, W.E.; Belew, R.K.; Olson, A.J. Automated docking using a Lamarckian genetic algorithm and an empirical binding free energy function. J. Comput. Chem. 1998, 19, 1639–1662. [Google Scholar] [CrossRef]
- Gürsoy, O.; Smieško, M. Searching for bioactive conformations of drug-like ligands with current force fields: How good are we? J. Cheminform. 2017, 9, 29. [Google Scholar] [CrossRef]
- Van Der Spoel, D.; Lindahl, E.; Hess, B.; Groenhof, G.; Mark, A.E.; Berendsen, H.J.C. GROMACS: Fast, flexible, and free. J. Comput. Chem. 2005, 26, 1701–1718. [Google Scholar] [CrossRef]
- Shao, J.; Tanner, S.W.; Thompson, N.; Cheatham, T.E. Clustering Molecular Dynamics Trajectories: 1. Characterizing the Performance of Different Clustering Algorithms. J. Chem. Theory Comput. 2007, 3, 2312–2334. [Google Scholar] [CrossRef]
- Singh, G.; Dogra, S.D.; Kaur, S.; Tripathi, S.K.; Prakash, S.; Rai, B.; Saini, G.S.S. Structure and vibrations of glutathione studied by vibrational spectroscopy and density functional theory. Spectrochim. Acta A Mol. Biomol. Spectrosc. 2015, 149, 505–515. [Google Scholar] [CrossRef]
- Fujiwara, S.; Formicka-Koziowska, G.; Kozlowski, H. Conformational Study of Glutathione by NMR. Bull. Chem. Soc. Jpn. 1977, 50, 3131–3135. [Google Scholar] [CrossRef]
- Lampela, O.; Juffer, A.H.; Rauk, A. Conformational Analysis of Glutathione in Aqueous Solution with Molecular Dynamics. J. Phys. Chem. A 2003, 107, 9208–9220. [Google Scholar] [CrossRef]
- Stevens, R.; Stevens, L.; Price, N.C. The stabilities of various thiol compounds used in protein purifications. Biochem. Educ. 1983, 11, 70. [Google Scholar] [CrossRef]
- Tryfon, A.; Siafarika, P.; Kouderis, C.; Kalampounias, A.G. Self-assembling of glutathione in aqueous environment: A combined experimental and theoretical study. J. Mol. Liq. 2023, 390, 122957. [Google Scholar] [CrossRef]
- Tsigoias, S.; Papanikolaou, M.G.; Kabanos, T.A.; Kalampounias, A.G. Structure and dynamics of aqueous norspermidine solutions: An in situ ultrasonic relaxation spectroscopic study. J. Phys. Condens. Matter 2021, 33, 495104. [Google Scholar] [CrossRef]
- Risva, M.; Tsigoias, S.; Boghosian, S.; Kaziannis, S.; Kalampounias, A.G. Exploring the influence of urea on the proton-transfer reaction in aqueous amine solutions with Raman and ultrasonic relaxation spectroscopy. Mol. Phys. 2023, 121, e2163314. [Google Scholar] [CrossRef]
- Nishikawa, S.; Yasunaga, T.; Takahashi, K. Kinetic studies of fast reactions in aqueous solutions of amylamine by means of ultrasonic absorption. Bull. Chem. Soc. Jpn. 1973, 46, 2992–2997. [Google Scholar] [CrossRef]
- Kouderis, C.; Siafarika, P.; Kalampounias, A.G. Molecular relaxation dynamics and self-association of dexamethasone sodium phosphate solutions. Chem. Pap. 2021, 75, 6115–6125. [Google Scholar] [CrossRef]
- Kaatze, U.; Hushcha, T.O.; Eggers, F. Ultrasonic broadband spectrometry of liquids a research tool in pure and applied chemistry and chemical physics. J. Solut. Chem. 2000, 29, 299–368. [Google Scholar] [CrossRef]
- Herzfeld, K.F.; Litovitz, T.A. Absorption and Dispersion of Ultrasonic Waves, 1st ed.; Academic Press: New York, NY, USA, 1959. [Google Scholar]
- Ensminger, D.; Bond, L.J. Ultrasonics: Fundamentals, Technologies, and Applications, 3rd ed.; CRC Press: New York, NY, USA, 2011. [Google Scholar]
- Blandamer, M.J. Introduction to Chemical Ultrasonics; Academic Press: New York, NY, USA, 1973. [Google Scholar]
- Nishikawa, S.; Haraguchi, H.; Fukuyama, Y. Effect of ether oxygen on proton transfer and aggregation reactions of amines in water by ultrasonic absorption method. Bull. Chem. Soc. Jpn. 1991, 64, 1274–1282. [Google Scholar] [CrossRef]
- Nishikawa, S.; Kamimura, E. Dynamic characteristic of amitriptyline in water by ultrasonic relaxation method and molecular orbital calculation. J. Phys. Chem. A 2011, 115, 535–539. [Google Scholar] [CrossRef]
- Beaven, G.H.; Holiday, E.R. Ultraviolet Absorption Spectra of Proteins and Amino Acids. Adv. Protein Chem. 1952, 7, 319–386. [Google Scholar] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).