Abstract
This study aims to approximate the optimum sulfate content of cement, applying maximization of compressive strength as a criterion for cement produced in industrial mills. The design includes tests on four types of cement containing up to three main components and belonging to three strength classes. We developed relationships correlating to 7- and 28-day strength with the sulfate and clinker content of the cement (CL), as well as the clinker mineral composition (tricalcium silicate, C3S, tricalcium aluminate, C3A). We correlated strength with the ratio %SO3/CL and the molecular ratios MSO3/C3S and MSO3/C3A. The data processing stage proved that artificial neural networks (ANNs) fit the results’ distribution better than a parabolic function, providing reliable models. The optimal %SO3/CL value for 7- and 28-day strength was 2.85 and 3.00, respectively. Concerning the ratios of SO3 at the mineral phases for 28-day strength, the best values were MSO3/C3S = 0.132–0.135 and MSO3/C3A = 1.55. We implemented some of the ANNs to gain a wide interval of input variables’ values. Thus, the approximations of SO3 optimum using ANNs had a relatively broad application in daily plant quality control, at least as a guide for experimental design. Finally, we investigated the impact of SO3 uncertainty on the 28-day strength variance using the error propagation method.
Keywords:
sulfates; cement; strength; clinker; optimization; artificial neural networks; model; uncertainty 1. Introduction
The most critical properties characterizing the performance of cement are early and typical compressive strength and setting time. Calcium sulfate addition affects these characteristics by simultaneously acting as a modifier and a regulator of their values []. The cement must contain clinker and calcium sulfate, while the standards permit the usage of other components, like limestone, pozzolans, fly ash, and slag. Gypsum is the primary source of sulfates (SO3) composed mainly of calcium sulfate dihydrate (CASO4.2H2O or Cs.2H) and a small content of anhydrite (CaSO4 or Cs). During cement grinding, elevated temperatures partially dehydrate gypsum into hemihydrate form or bassanite (CaSO4.0.5H2O or Cs.0.5H) []. Copeland et al. [] and a recent systematic review [] clarify the solubility of the three phases of CaSO4.
Clinker is mainly composed of four mineral phases: tricalcium silicate (3CaO ∙ SiO2 or C3S), dicalcium silicate (2CaO ∙ SiO2 or C2S), tricalcium aluminate (3CaO ∙ Al2O3 or C3A), and tetra calcium aluminoferrite (4CaO ∙ Al2O3 ∙ Fe2O3 or C4AF). Bogue established the mathematical formulae for calculating the four clinker compounds as a function of the percentages of the four basic oxides CaO, SiO2, Al2O3, Fe2O3, or C, S, A, F, as well as the free lime CaOf [] (pp. 245–250).
The reactions of these four mineral components with water (H) give rise to various compounds, in which the dominant phases are calcium silicate hydrates (C-S-H) and calcium hydroxide (CH). Equations (5) and (6) express generalized forms of the hydration reactions of C3S and C2S, including some small decimal numbers m and n [].
Gypsum addition also obstructs the fast exothermic reaction of C3A by forming ettringite (C3A.3Cs.32H), according to Equation (7).
Ettringite formation regulates uncontrolled C3A hydration, preventing flash set during concrete production, transfer, and placement [,,]. Conversely, adding too much gypsum leads to a drop in strength and detrimental expansion of concrete and mortar, meaning there is a sulfate optimum. Cement standards, such as EN 197-1:2011 [] and ASTM C150 [], prohibit sulfates above a certain level per type of cement, though they do not suggest an optimal value because that figure depends on the various physical, chemical, and mechanical properties of cement and clinker produced in the specific conditions of each production unit. Furthermore, the property to be optimized impacts the location of the optimum. Some standards, such as ASTM C563-16 [], define a method for determining the optimal SO3, albeit only for a particular property of cement, i.e., 1-day compressive strength.
Historically, determining the optimal sulfates in cement was subjected to intensive and continuous research. In recent years, a primary goal of the cement industry was the reduction in its carbon footprint by decreasing CO2 emissions in clinker production and clinker consumption per ton of product. Optimizing the composition of raw materials for clinker production can achieve the above goal [,]. Optimizing SO3 is essential for reducing clinker incorporation into the cement while retaining or improving product performance. Lerch [] conducted the first thorough study of sulfate optimization in cement past and mortar. According to the researcher, the optimal sulfate content in cement is closely related to hydration heat, length changes of mortar specimens cured in water, alkalis, C3A content, and cement fineness. Fincan [] mentions that Lerch was a pioneer and inspired many studies on sulfate optimization in cement and cementitious systems.
Several researchers investigated the impact of SO3 on the hydration of the clinker mineral phases [,,,,,,,,,]. Bentur [] found that gypsum influenced the quantity and quality of the hydrated products by accelerating the hydration process and, at the same time, lowering the intrinsic strength of the gel. He interpreted the effect of gypsum on strength in terms of its influence on the extent of hydration and the chemical composition of the gel. Soroka et al. [] concluded that gypsum accelerates the rate of hydration when its addition is below the optimum SO3 content. Nevertheless, if the gypsum added exceeds the optimal level, considerable obstruction occurs. The authors did not observe any effect of the SO3 content on the density of the hydration products and pore-size distribution. They pointed out that further study is required to explain the impact of SO3 on strength. On the contrary, Sersale et al. [] found that gypsum addition modified the microstructure of Portland cement mortars. They correlated these modifications with the mechanical behavior of cement mortars by examining Portland cement with sulfate content ranging between 1.5 and 4.5%. A SO3 content of 2–3.5% promotes a shifting in the pore size distribution to lower values, ranging between 100 and 1000 Å, and a variation in total porosity. They concluded that this issue is likely the main factor governing the influence of SO3 on the compressive strength of Portland cement. Gunay [], in his thesis, studied the influence of aluminates hydration in the presence of calcium sulfate on C3S hydration and its consequences on cement optimum sulfate. He observed the SO3 optimum when the hydration of C3S, during the accelerated period, takes place simultaneously or slightly before the exothermic peak due to the dissolution of C3A and the precipitation of mono-substituted Al2O3 and Fe2O3 (AFm). He concluded that the presence of AFm during the accelerated period of C3S hydration would be the cause of the observed modification of the microstructure of the cement paste: the porosity increases with the addition of calcium sulfate, though the assembly of hydrates is denser. This effect of the sulfate level is the source of the optimal compressive strength observed by Gunay. Zunino et al. [] investigated the influence of sulfate addition on hydration kinetics and the C-S-H morphology of C3S and C3S/C3A systems at an early age. Adding gypsum changed the needle length of C-S-H and increased the nucleation density. In C3S/C3A systems, they did not observe any difference in C-S-H morphology before and after the aluminate peak. Andrade Neto et al. [] studied the hydration and interactions between pure and doped C3S and C3A in the presence of different calcium sulfates. Except for sulfates of gypsum, Miller et al. [], Taylor [], and Horkoss et al. [] investigated the importance of the amount and phases of SO3 incorporated into the clinker. Mohammed et al. [] optimized the SO3 content of a CEM I cement via grinding clinker with a ball mill until a fineness of 3270 cm2/g was achieved, before preparing mixes with ground gypsum ranging from 0 to 9%. According to their results, the water demanded for normal consistency, setting times, compressive strength, the heat of hydration, swelling, drying shrinkage, and hydration degree are adversely affected by gypsum addition above or below the optimal. For this cement, which was composed only of clinker and gypsum, they found that the optimal sulfate for 2-, 7-, and 28-day strength was 3%.
Nowadays, with the reduction in CO2 emissions being imperative, composite types of cement constitute the bulk of the products of the cement industry, rendering the optimization of sulfates in such cement more relevant. During the last few decades, numerous researchers conducted deep research investigating the optimal sulfate content of cement containing supplementary cementitious materials (SCM) [,,,,,,]. Yamashita et al. [] investigated the influence of limestone powder (LSP) on the optimum SO3 for Portland cement samples with different Al2O3 contents, which was not negligible. Analyses showed that if SO3 is less than optimal, an increase in sulfate promotes hydration in C3A and increases compressive strength. In the presence of higher SO3 content, excess formation of expansive ettringite introduced more pores, and compressive strength decreased. After adding LSP, a lower sulfate content was adequate to obtain the maximum compressive strength. Liu et al. [] examined the effect of gypsum content on cementitious mixtures containing limestone, fly ash, and slag by studying several properties: initial and final setting time, past fluidity, water demand, and strength. Adu-Amankwah et al. [] conducted detailed research into the consequence of sulfate additions on hydration and the performance of ternary slag–limestone composite cement using complementary techniques. Their results showed that the presence of sulfate influenced the early-age reaction kinetics of the clinker phases and supplementary cementitious materials. These changes impacted the total porosity and cement strength in opposing ways: porosity was reduced with increasing ettringite fraction, while the lower water content of the C-S-H reduced the space-filling capacity of the C-S-H. Han et al. [] investigated the effect of gypsum on the properties of composite binders containing high-volume slag and iron tailing powder using multiple measuring techniques. They concluded that although incorporating gypsum promoted early hydration of cement and slag, it limited their further hydration at later ages. Added gypsum formed a large amount of ettringite and densified early-age pore structure, though it coarsened later-age pore structure. Fiscan [] optimized sulfate in cement–slag blends based on calorimetry and early strength results, investigating the influence of fineness, C3A, C4AF of cement, and the Al2O3 content of slag on the optimum SO3. Niemuth [] examined the effect of fly ash on the optimum sulfate content in Portland cement, providing experimental data on strength development and heat release during early hydration for cement–fly ash systems with different SO3 levels. He demonstrated that some fly ash samples achieve their sulfate demand. When a cement contains these samples, there is effectively an increase in the optimal SO3 level compared to the corresponding CEM I Portland cement. In his research into the optimal SO3 content of Portland and pozzolanic cement types, Tsamatsoulis et al. [] reached the same conclusion.
Increasingly, cement manufacturers use grinding aids/strength improvers to reduce energy consumption and improve cement quality. According to Magistri et al. [], hydration in the presence of such additives proceeds differently than in cement produced without them, remarkably improving cement properties. Hirsch et al. [] examined the impact of triethanolamine (TEA) on the sulfate balance of Portland cement with mixed sulfate carriers (Cs.2H, Cs.0.5H, CS). Their results indicated that TEA influenced the balance of sulfate and aluminate-containing clinker phases. These effects were closely related to the types and amounts of the sulfate carriers present in the cement. The very practical, from a process point of view, research of Recchi et al. [] investigates the influences of the type (Cs.2H, Cs.0.5H, Cs) and amount of calcium sulfate on the reactivity of TEA and tri-isopropanolamine (TIPA) strength improvers, which are today’s most widely used alkanolamines. TEA is an early compressive strength enhancer, while TIPA increases the late strengths. The authors concluded that if the sulfate carrier is bassanite, the early strength increase obtained with the addition of TEA is more evident due to the higher solubility of Cs.0.5H. On the other hand, TIPA is significantly less efficient at increasing late strength when bassanite is the source of SO3, i.e., Cs.0.5H is not preferable when the objective of ΤIPA use is to enhance 28-day strength. Andrade Neto et al. [] recently conducted a detailed review of the effect of SO3 on cement hydration, noticing that despite many years of research, questions regarding sulfate optimization remain. Further investigation into the influence of clinker and CaSO4 characteristics using different supplementary cementitious materials and chemical admixtures is needed.
Some researchers provided or applied equations correlating optimal SO3 with the cement’s chemical and physical characteristics. For achieving maximum 28-day strength with C3A, K2O, Na2O, and fineness of cement, Schade et al. [] presented three equations (Haskell, Jawed and Skalny, and Ost). They utilized the third equation to perform a design of experiments (DoE) to model the sulfate amounts in ultra-finely ground and fast-hardening clinker. Kurdowski [] reported four equations for approximating the optimal SO3 content (Ost, Lerch, Jirku, and Haskell), before noticing that these empirical equations have limited accuracy, even if they include the main factors affecting the optimum gypsum addition. He considered that using experimentation to determine the most convenient sulfate addition is the best approach. Andrade Neto et al. [] summarized the laboratory methods for determining the correct SO3 content in conjunction with their advantages and disadvantages. From an industrial perspective, strength measurement is the most utilized method, since compressive strength is a key performance criterion for producers and customers. ASTM C563-16 [] describes the determination of approximate optimum SO3 for maximum compressive strength by measuring the change in this property of cement mortar as a result of substituting calcium sulfate for a portion of the cement. The standard suggests a parabolic equation between strength and sulfate that optimally fits the experimental points when assuming a symmetric distribution. The optimal SO3 approximation corresponds to the value providing the vertex of the parabola. The standard clearly states that in cases of a skewed function of the strength versus sulfate to the right or left of the peak, an asymmetric distribution function may provide a better fit. Niemuth [], Tsamatsoulis [], and Fincan [] applied the parabolic formula in their attempts to find an adequate approximation of SO3 optimal content. Tsamatsoulis [], when trying to determine a unified function for several cement types with variable clinker content, used the ratio of sulfate amount to clinker percent (%SO3/CL) as an independent variable.
This study aims to approximate the optimal SO3 content of cement using the maximization of compressive strength as a criterion for cement produced in industrial mills. The experimental design includes tests on four types of cement containing up to three main components, except gypsum, and belonging to three strength classes. We developed several relationships correlating the 7- and 28-day strengths of the sulfate and clinker content of the cement and the clinker mineral composition. We normalized the results to obtain unique functions for all experimental data, using an approach similar to the method presented in []. This study proved that a shallow artificial neural network [,] fits the data distribution better than a parabolic function. Finally, we focused on the impact of SO3 uncertainty on the 28-day strength variance using the error propagation method. The structure of the paper is as follows: Section 2 includes the sampling procedure, experimental methods, and test results; Section 3 describes the implemented algorithms for data processing, including a detailed discussion of each set of results; and, finally, Section 4 summarizes the main conclusions of this research.
2. Materials and Methods
In this study, we chose to optimize the sulfate amount of the basic cement types produced according to EN 197: 2011 [] in the Halyps cement plant, using the compressive strength criterion as a guide. Table 1 shows the CEM types investigated and the norm requirements as regards composition and strength limits. The nominal composition did not contain the gypsum. The producer was responsible for adjusting its content by respecting the maximum SO3 limit, which was 4% for CEM I 52.5 N and 3.5% for the other three CEM types. We observed that the research covered a wide range of Portland (CEM I, CEM II) and pozzolanic (CEM IV) types. The study was, therefore, general for the cement products of this specific cement plant. The optimal value of cement sulfate depended on various factors, which were summarized by Andrade Neto et al. [] as follows: (a) clinker mineralogy (C3S, C3A) and alkali content, as well as cement and clinker fineness; (b) form of SO3 carriers (Cs.2H, Cs.0.5H, Cs or alkali sulfates), as well as mineral or chemical gypsum; (c) intergrinding or separate grinding of clinker and gypsum; (d) content and type of SCM; (e) grinding aid/strength improver type; (f) hydration age; (g) water/binder ratio; and (h) curing conditions. Using the standard EN 196-1 [] to create mortars, we attempted to find the SO3 contents for maximum 7- and 28-day strength and examined the optimum position as a function of hydration age, fulfilling the conditions (f)–(h).

Table 1.
CEM types tested.
The goal of the experimentation was to obtain cement samples as close as possible to industrially produced cement in terms of fineness, chemical characteristics, forms of the sulfate carriers, and interaction of the grinding aid with the solids. Grinding in the Halyps cement plant was performed through co-grinding the raw materials in closed-circuit mills equipped with high-performance separators and co-feeding a 28-day strength enhancer into the mill feed. In an earlier study [], we found that for a step change in gypsum, the mill circuit required around 1 h to reach the steady state regarding SO3. For each CEM type, by operating the mill in automatic mode and after stabilizing the circuit around the operating set points and the desired fineness, we suddenly decreased the gypsum to 2%. There was no change in the percentage of clinker, while another material increased in proportion (limestone or pozzolan). Sampling of around 20 kg of the final product followed after 1.5 h. The second step was an increase in gypsum to 7.5% and a proportional decrease in limestone or pozzolan to maintain the %clinker constant. Further sampling took place 1.5 h after this change. During this process, with an operation kept as constant as possible, the laboratory sampled clinker at the mill inlet. In this way, the lab created two samples of industrial cement with low and high gypsum for each CEM type. Mixing them in proper proportions yielded samples with suitable SO3 values usable to correlate strength and sulfate. The industrial tests of the four CEM types were realized within two months to allow the clinker composition to incorporate the actual production variances.
The samples’ analysis comprised several mechanical, physical, and chemical tests: (i) fineness with air-jet sieving and specific surface with Blaine apparatus, using EN 196-6 []; (ii) loss on ignition (LOI), insoluble residue (InsRes), and oxides analysis via XRF by applying EN 196-2 []; (iii) laser particle size analysis; (iv) compressive strength measurement using EN 196-1; and (v) clinker and cement phases using XRD. Halyps lab conducted the analyses (i)–(iv), while the Devnya Cement lab performed the XRD analysis.
2.1. Clinker and Raw Materials Analysis
Aside from the experiment illustration, clinker, gypsum, limestone, and pozzolan analyses used during the test are necessary for estimating the CEM composition. Table 2 demonstrates the XRF and XRD analyses of the four clinkers. The mean values of the loss on ignition and insoluble residue were equal to 0.3. Equation (8) presents the molecular ratio between SO3 and alkalies, i.e., MSO3.

Table 2.
Clinker XRF and XRD analyses.
Table 2 presents the mean values and standard deviations of SO3, C3S, and MSO3. The corresponding annual values for 2022 of the Halyps clinker were as follows: SO3 = 0.86 ± 0.25, C3S = 64.7 ± 2.5, and MSO3 = 0.88 ± 0.24; these results mean that the variance in the four clinkers’ properties covers a significant amount of the actual variability in the plant clinker in terms of quality. The mineral phases measured via XRD differ from those computed with Bogue formulae, though the C3S values fit relatively well. XRD did not detect anhydrite and langbeinite because the MSO3 < 1. Table 3 presents the average analysis of the three raw materials. Assuming that CaO, MgO, SO3, and LOI exist in gypsum in the form of calcium and magnesium carbonates, gypsum dihydrate, and anhydrite, we computed these four components by solving the corresponding linear system. The results show that gypsum is mainly dihydrate, containing a small percentage of anhydrite.

Table 3.
Raw materials analyses.
2.2. Cement Analyses
The laboratories conducted chemical, physical, and mechanical tests on the cement samples to reliably correlate the variables and minimize uncertainties. Table 4 provides both the chemical analysis of the eight samples taken for the CEM types under investigation and the gypsum phases within the cement measured via XRD. We also took advantage of the automatic recording of process data in the plant database to find the cement temperature at the mill outlet for each of the eight tests. Table 4 shows the mean value of this temperature (TCEM) for each of the eight tests. Although the detection of gypsum phases via XRD could be approximated, the main conclusion was that hemihydrate was null or negligible. This issue arose because the cement temperature at the mill outlet never reached 100 °C, as dihydrate starts to dehydrate to Cs.0.5H []. Krause et al. [] experimentally found that the transformation of gypsum into hemihydrate could take place at a temperature of 50 °C. However, our industrial results do not verify these findings.

Table 4.
Chemical analysis of cement samples.
Table 5 shows the fineness measurements of these samples expressed as %residues in 40, 32, and 20 microns (R40, R32, R20) and obtained via air-jet sieving and Blaine. All samples had 100% passing in the 90 microns sieve (R90 = 0). The same table demonstrates several fineness modules obtained via laser particle size analysis: diameters of 50%, 90%, and 10% passing (D50, D90, D10), as well as percentages between 32 and 3 microns (P32–R3).

Table 5.
Fineness of cement samples.
The solution of a linear system, as given in Equations (9)–(12) and expressing the mass balances, provided the dry cement composition of all samples using chemical analysis of cement, clinker, and raw materials. This estimation avoided the uncertainties of the mill feeders where the raw materials had a certain percentage of moisture.
CL, G, Lim, and Pz are the clinker, gypsum, limestone, and pozzolan percentages With SO3 X, LOIX, and InsResX, we denoted the sulfate, loss on ignition, and insoluble residue of the material X (X = CL, G, Lim, Pz, CEM). Solving the system of (9)–(11) produced the composition of CEM I 52.5 N and CEM II A-L 42.5 N. The calculation of the Pz requires the solution of the system (9)–(12) for CEM II B-M(P-L) 32.5 N. For the CEM IV(P) 32.5 N with high pozzolan content, our algorithm used three additional equations that expressed the mass balances of SiO2, Al2O3, and CaO. The composition results from the error minimization between the actual and calculated chemical analysis of cement were realized using the Generalized Reduced Gradient non-linear regression method. The lab conducted a chemical analysis, except for the eight samples, of the residues at 40, 32, and 20 microns of each of them. By determining the composition of the total sample and the material retained in each sieve, we calculated the %constituents of the material that passes through that sieve. The above approach made it feasible to calculate the composition in each fraction and investigate the grindability of the materials during co-grinding. Table 6 depicts the %components of the samples and passings through the three mentioned sieves and the residues of each material in the three sieves. Equations (13) and (14) provide these values.

Table 6.
Compositions of cement samples and passing in each sieve and materials’ residues.
The j indexes from 1 to 3 correspond to the sieves at 40, 32, and 20 microns, while the k indexes 1 to 4 correspond to the four materials (clinker, gypsum, limestone, pozzolan). Rj is the residue of a sample at the sieve j, and RMk,j is the residue of material k at the sieve j. CompSamplek is the percentage of the component k within the sample, while CompResk,j and CompPassk,j are the percentages of the component k in the residue and passing in the sieve j.
These results indicate the higher grindability of gypsum and limestone compared to the other compounds. We observed that clinker and pozzolan had similar grindability. Therefore, approximating the optimal SO3 content using industrially produced cement in a closed-circuit mill was crucial. It was difficult to obtain the same particle size per constituent and the distribution of the grinding aid via grinding in an open circuit lab apparatus or interblending the previously ground materials. Tang et al. [] concluded that when testing to determine the optimum sulfate content, it was significant to co-grind the calcium sulfate with clinker because co-grinding resulted in lower sulfate demand than interblending. Thus, the results obtained via the latter method would not be representative.
2.3. Cement Samples Mixing and Related Tests
The lab mixed the cement samples of low and high gypsum to create new samples at regular and proper intervals of SO3 values. Complete chemical analysis of these samples, composition calculation—as described in Section 2.2—mortars preparation, and measuring the 7- and 28-day compressive strengths followed.
Table 7 depicts the proportions of low and high gypsum samples, the SO3 and %Clinker values, the %ratio of sulfates to clinker (%SO3/CL), and the 7- and 28-day compressive strengths of each mix for the four CEM types investigated. SO3 values stem from XRF measurement, while %Clinker results stem from composition calculation.

Table 7.
Cement analysis and compressive strength.
In Appendix A, we provide a list of raw materials suppliers and the manufacturers of the main equipment used.
3. Data Processing and Results
3.1. Correlation of Strength with Sulfates and Clinker Content
The results of Table 7 indicate that the 7- and 28-day strengths depend strongly on the %Clinker and SO3 values. Cement fineness, the clinker’s mineral composition, supplementary cementitious materials, and the kind and dosage of strength enhancer also impact compressive strength. The results shown in Table 5 show that the fineness at 40 microns was similar for samples of 2 and 7.5% gypsum for each CEM type. Therefore, the same method would apply to the prepared mixes. Furthermore, we used the same type and dosage of strength improver for all CEM types, which enhances the 28-day strength. As the SO3 value used to obtain maximum strength depends on the clinker content, we used the ratio %SO3/CL–SO3/CL as an independent variable. Our algorithm used the following dimensionless 7- and 28-day strengths to normalize the results for all CEM types.
At age X, StrX is the compressive strength for a given SO3/CL, MaxStrX is the maximum strength of the cement type, RelStrX is the relative strength for a value of SO3/CL, and X = 7 or 28. Figure 1a,b depict the relative 7- and 28-day strengths as a function of SO3/CL, proving that a single distribution can describe the results of the four CEM types.
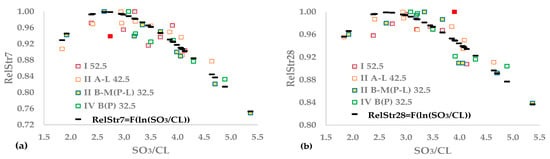
Figure 1.
Functions between SO3/CL and (a) RelStr7 or (b) RelStr28.
The initial processing stage was applied to the parabolic Equations (17) and (18) to correlate the 7- and 28-day relative strengths with SO3/CL: SO3/CL was the independent variable for the first equation, resulting in a symmetric curve around the maximum, and ln(SO3/CL) was the independent variable for the second equation, taking into account the asymmetry of these experimental data. Equations (19) and (20) calculate the optimum SO3/CL of (17) and (18). For the optimal value, RelStrX(SO3/CLopt) shall be equal to 1. Constraint (21) guarantees the above values.
The optimal coefficients of (17) and (18) were estimated through minimizing the residual error, with the Generalized Reduced Gradient algorithm used at this stage. For each model, Equations (22) and (23) provide the residual error, sRes, and coefficient of determination, R2, respectively. Our algorithm used the error, sOpt, which is given in Equation (24), to assess whether a model satisfactorily approximates the sulfate optimum.
M is the number of the experimental points RelStrX(I) for X = 7 or 28 and I = 1 to M, while RelStrXCalc(I) are the corresponding computed values for each model. sExp is the standard deviation of the population of RelStrX, and k represents the degrees of freedom of the applied equation. The number of variables in (18) and (19) is three; however, k = 2 since both models are subject to the constraint (22). Nopt is the count of RelStrX that is greater or equal to 0.99. Table 8 demonstrates the optimal coefficients Ai, Bi, with i = 0, 1, or 2, as well as the SO3/CLOpt, sRes, sExp, sOpt, and R2 for each model. The algorithm permits up to 1 outlier out of the 33 experimental points when the absolute difference between actual and computed values is higher than 2sRes.

Table 8.
Coefficients and statistics of parabolic model.
Table 8 results show that using the logarithm of SO3/CL as an independent variable covers a part of the data asymmetry. In both the 7- and 28-day strengths, the logarithmic model has a higher R2 than the symmetric parabolic equation and more effectively approximates the maximum strength values that show smaller sOpt values. In Figure 1a,b, black dashes indicate calculated values using the asymmetric equation, and red points depict outliers. For 7-day strength, optimum SO3/CL = 2.67 seems reasonable, though it is probably found to the left of the closest approximation. In Figure 1b, all points with RelStr28 ≥ 0.99 are found to the right of the best approximation. Therefore, there is an underestimation of the optimal value, and a better model is necessary. We implemented shallow neural networks (ANN) with one hidden layer to overcome this discrepancy.
The input vector X contains the SO3/CL values, and the output vectors RelStrX are the 7- and 28-day relative strengths. The dimension of the vectors is M. Equation (25) provides the respecting normalized variable XN, where XMIN and XMAX are the minimum and maximum values of the SO3/CL. The output vectors are already normalized because their values continuously belong to the interval [0, 1]. The hidden layer has NN nodes using the sigmoid equation as an activation function, which were provided in Equation (26). Equation (27) gives the input ZJ to each node, where W0J and W1J are the biases and the synaptic weights between the input and the hidden layer, respectively. Finally, Equation (28) calculates the values of RelStrXCalc, where VJ are the synaptic weights between the hidden layer and the output.
Through the Generalized Reduced Gradient algorithm, we estimated the synaptic weights of Equations (27) and (28) by minimizing the residual error of Equation (22), sResJ, for all experimental data. The minimum sRes occurs when the number of nodes in the hidden layer NN = 2. Therefore, the continuous ANN function results in the Formulae (29), where Xn is a continuous variable belonging to the interval [XMIN, XMAX]. The numerical optimization problem contains two constraints for the optimal Xn: the value of the ANN function for this point should be close to 1, and the derivative should be close to 0. Equation (30) expresses these two constraints. The freedom degrees in Equation (22) are k = 6 − 2 = 4 due to these constraints.
Table 9 demonstrates the synaptic weights and statistics of the two ANNs, while Figure 2a,b illustrates the fitting of the ANNs results to the experimental data. Applying neural networks with one hidden layer and two nodes improves all statistics compared to logarithmic equations. For the 28-day relative strength, the improvements are 5.5% for sRes, 2.6% for R2, and 91.2% for sOpt, i.e., the ANNs more effectively approximate both the shape of the experimental curve and the optimum SO3. The same conclusion emerges from Figure 2a,b. The optimal SO3/CL increases with the age of the mortar (SO3/CL28-day > SO3/CL7-day), which confirms the previous studies’ findings [,,,].

Table 9.
Synaptic weights and statistics of ANNs.
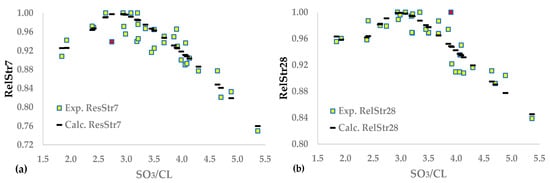
Figure 2.
Neural network functions between SO3/CL and (a) RelStr7 or (b) RelStr28.
The residual errors shown in Table 9, which were computed using all experimental data, are training errors, strain. To estimate the test error (sTest), as well as due to the limited number of data (M = 33), we applied the following procedure for the 28-day ANN: (a) the training set contains M-1 datasets, and the remaining set is used for testing; (b) the non-linear regression technique calculates the optimal parameters of the training set and its sRes; (c) we compute the value of the test set using these synaptic weights, the input value, and Equation (29); (d) the difference between the experimental and the calculated test value is the error, sT, of the test; (e) the algorithm considers all possible combinations of training and test sets, resulting in M datasets of both types; and (f) Equation (31) provides the training and test errors, taking into account the error of each dataset.
The algorithm for the 28-day relative strength gives the following results: sTrain = 0.0167, and sTest = 0.0172. The coefficient of determination, R2, of the test set is 0.813. By applying the same procedure to the logarithmic model, the R2 of the test set is 0.793, proving that the implementation of ANNs causes a significant improvement in all investigated statistics.
3.2. Correlation of Strength with Sulfates and Clinker Mineral Phases
According to the literature, a function exists between the SO3 optimum and the C3S and C3A of clinker [,,,,,,,]. Figure 3a,b shows the relationship between the 28-day relative strength and the ratio of either (a) moles SO3/moles C3A (MSO3/C3A) or (b) moles SO3/moles C3S (MSO3/C3S), in a similar way to the method shown in Figure 1a,b. The correlation includes the mineral phases of the clinker contained in the cement, which is initially computed via the Bogue formula and shown in Table 2. Equations (32) calculate the two mentioned molecular ratios, where MWSO3 = 80, MWC3A = 270, and MWC3S = 228 are the molecular weights of SO3, C3A, and C3S, respectively.
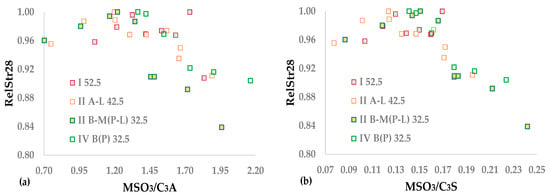
Figure 3.
Functions between (a) MSO3/C3A and (b) MSO3/C3S and RelStr28.
Figure 3a,b show that a single distribution can describe the results of the four CEM types. However, the scattering of the points is higher than that observed in Figure 1b because the two independent inputs combine three measured or calculated variables, resulting in a higher level of uncertainty. The two plots are not symmetrical around their maximum values. Thus, the ANN model, which was successfully applied in Section 3.1, is appropriate. The algorithm implements the set of Equations (25)–(30) where the vector X is either the vector of MSO3/C3A or MSO3/C3S, while Xnopt corresponds to the optimal position of each variable. Table 10 shows the synaptic weights and statistics of the two ANNs correlating RelStr28, with the mineral phases of the clinker calculated using XRF analysis and the Bogue formulae.

Table 10.
Synaptic weights and statistics of ANNs using C3A and C3S as inputs (Bogue formulae).
The algorithm permits up to 2 outliers out of the 33 experimental points because of the higher uncertainty of the input variables, compared to the ANN correlating RelStr28 and SO3/CL. Figure 4a,b depicts the fitting of the ANNs results to the experimental data. FANN(MSO3/C3A) presents a low R2, and the model is unreliable. In contrast, FANN(MSO3/C3S) has satisfactory statistics close to those of FANN(SO3/CL). Furthermore, the two outliers (red points) of Figure 4b are at a distance of ~3sRes from the calculated points.
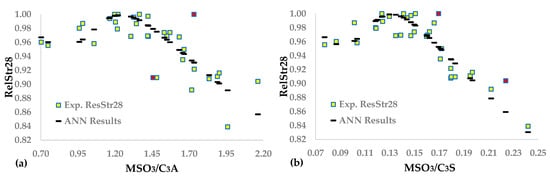
Figure 4.
Neural network functions between (a) MSO3/C3A and (b) MSO3/C3S and RelStr28.
We repeated the procedure that uses the mineral constituents directly determined via XRD to investigate the accuracy of data fitting and the position of the optimum sulfates. We implemented all ANNs, except for total C3AXRD and C3SXRD, as well as M1 C3SXRD, which is more reactive, according to the literature [,]. Table 2 shows the values of these phases measured via XRD, and Equation (33) calculates the corresponding three molecular ratios.
Table 11 demonstrates the synaptic weights and the statistics of the three ANNs correlating RelStr28, with the mineral phases of the clinker determined via XRD analyses.

Table 11.
Synaptic weights and statistics of ANNs using C3AXRD, C3SXRD, and M1C3SXRD.
Figure 5a–c depicts the experimental and calculated data using the three ANNs. Comparing the coefficients of determination of FANN(MSO3/C3AXRD) and FANN(MSO3/C3A), we observed that the R2 of the former model is much higher than that of the latter model, before concluding that determining C3A via XRD results in adequate data fitting and reliable approximation of the optimal sulfates. FAA(MSO3/C3SXRD) and FAA(MSO3/C3S) fit both similarly and satisfactorily to experimental data, and their optimal molecular ratio of SO3 to mineral phase is roughly the same. The R2 of FANN(MSO3/M1C3SXRD) is relatively low, though the sOpt is sufficiently reasonable. Therefore, the corresponding optimal molecular ratio could be an initial approximation of the optimum SO3.
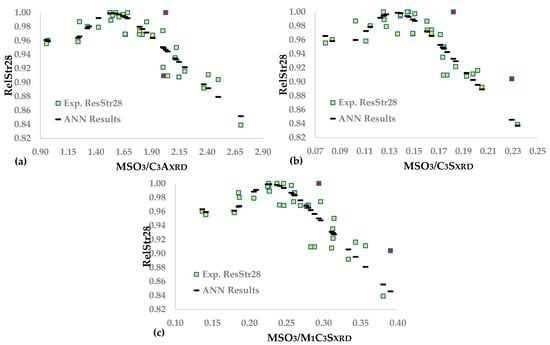
Figure 5.
Neural network functions between following models: (a) MSO3/C3AXRD; (b) MSO3/C3SXRD; (c) MSO3/M1C3SXRD and RelStr28.
3.3. Correlation of Strengh with Sulfates and Clinker Content under Selected Size
In Section 3.1, we investigated the function between compressive strength and the factor %SO3/CL, considering the total clinker content of each cement sample. We tried to evaluate whether some finer part of the clinker improved the relationship between the RelStr28 and the variable SO3/CL because it contributed substantially to the 28-day strength, thus applying the subsequent procedure.
- (a)
- We considered the %clinker content to be passing a size (40 μ, 32 μ), CLPassj, as given in Equation (34). The symbols j, CompPass1,j, and Rj are the same in Formulas (13) and (34). The upper part of Table 5 shows the values of CompPass1,j for the samples of low and high gypsum and the four CEM types.
- (b)
- CLLj and CLHj denote the %clinker passing the sieve j for the low and high gypsum samples. We used the linear combination (35) to calculate the %clinker passing, CLPj, for each mix of percentages P and 100-P of low and high gypsum samples. Table 7 provides these proportions for all CEM types.
- (c)
- We attempted two correlations using CLP1 and CLP2 at 40 μ and 32 μ. Equation (36) provides the two independent variables of the two ANN functions.
Table 12 provides the synaptic weights and statistics of the two functions between RelStr28 and clinker content under 40 μ and 32 μ, while Figure 6a,b depicts the fitting of the ANNs results to the experimental data. The calculation permits up to two outliers because the independent variables arise from more chemical analyses and physical measurements (sieving) than SO3/CL, resulting in higher uncertainty.

Table 12.
Synaptic weights and statistics of ANNs.
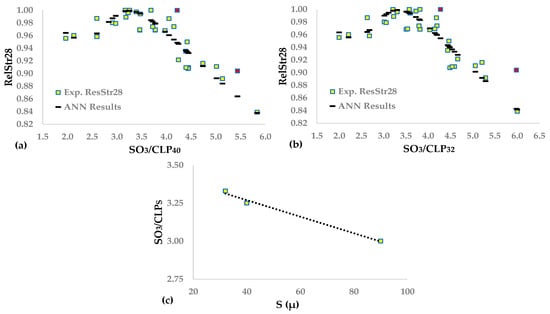
Figure 6.
Neural network functions between (a) SO3/CLP40, (b) SO3/CLP32, and RelStr28. (c) Function between SO3/PCLS and sieve opening size S.
We derived the following conclusions by comparing Table 11 and Table 12 and Figure 2b and Figure 6a,b.
- (a)
- The total clinker content of the cement is the %clinker in a sieve where the passing is 100%, e.g., 90 microns, as well as SO3/CL = SO3/CLP90. Thus, the three ratios, i.e., SO3/CL90, SO3/CLP40, and SO3/CLP32, express the clinker content of cement under some sieve.
- (b)
- There is an approximate linear increase in the optimal ratio SO3/CLPS when the sieve size, S, decreases from 90 μ to 32 μ, as shown in Figure 6c.
- (c)
- FAA(SO3/CL) and FAA(SO3/CLP40) have a similarly good fit to the experimental data, though the second ANN has a higher R2, making it probably preferable.
- (d)
- FAA(SO3/CLP32) seems to be the worst model. Its sOpt is higher than those the other two models, and despite accepting two outliers, the R2 is the same as that of FAA(SO3/CL).
- (e)
- Based on this model, one could conclude that cement hydration in 28 days proceeds to create clinker grains coarser that are than 32 microns, meaning that FAA(SO3/CL) and FAA(SO3/CLP40) provide a more accurate fitting to the data and a closer approximation to the optimal SO3.
- (f)
- The fraction between 3 and 32 microns is critical in achieving maximum 28-day strength, according to Celic []. Table 5 results show that P32-R3 ranges between 59.4 and 66.9%. The literature [] states that the optimum fraction is 70%. If the CEM types studied had such P32–R3, the relationship between RelStr28 and CLP32 might improve.
3.4. Summary of Results
Table 13 summarizes the optimal sulfate ratios for ANNs with R2 ≥ 0.82. As sRes is around 0.016 for all ANNs, as well as to achieve an estimation of the confidence interval of each optimum, we considered the ratios to the left and right of the optimal value, where ResStr28 = 0.98. A second check concerned the compatibility of the optimal sulfates calculated from the six ANNs for each CEM type. The algorithm used Table 2, Table 6 and Table 7 and Equation (35) to determine the average C3S, C3SXRD, and C3AXRD and the average percentages of Clinker, CLP1, and CLP2 for each CEM type. Next, it calculated the optimal SO3 content per model and CEM type. Table 13 shows these results.

Table 13.
Summary of results and optimal SO3 (%) of ANNs.
Table 13 shows that the low and high ratios for RelStr28 = 0.98 are not symmetrical around the optimum because the distributions are asymmetrical. The six models closely approximated the SO3 optimum, providing roughly the same value per CEM type. Therefore, the ANNs are reliable for the studied clinker mineralogy and cement fineness.
3.5. Uncertainty Analysis
All developed models indicate that SO3 content affects compressive strength. Approximating the optimal location is critical to cement plant quality control. In this context, the SO3 variance can impact the strength variance. An analytical error propagation model can facilitate a quantitative correlation between these variances. The variance of y, σy2, of an analytical function y = f(x1, x2, …, xn) can be determined using those of independent variables xi, σi2 when applying Equation (37).
We implemented the error propagation equation for the models RelStr28 = FANN(SO3/CL) and RelStr28 = FANN(MSO3/C3S). The independent variables of the first model were the SO3 content, the clinker fraction CL = %Clinker/100, and laboratory reproducibility in 28-day strength measurement, σR. The second model used the C3S content as an additional input. Equation (38) gives the derivatives of (29).
If Xn = SO3/CL, the partial derivatives of SO3 and CL are:
Otherwise, if Xn = MSO3/C3S, the derivatives of the three variables are:
Equations (41) and (42) give the 28-day strength variances, σ2Str28, of the two models.
We applied the error propagation equations for CEM II A-L 42.5 N, with MaxStr28 = 54 MPa, CL = 0.775, and C3S = 64.7%, while also assuming the following values for the input standard deviations: σCL = 0.02, σC3S = 2, σR = 0.02, SO3 of cement from 2% to 3% with a step of 0.1%, and σSO3 from 0.05% to 0.3%, increasing in steps of 0.05%. Figure 7a,b show the standard deviation σStr28 as a function of SO3 and σSO3 for the two models investigated.
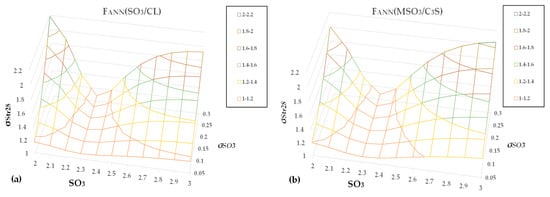
Figure 7.
σStr28 as a function of SO3 and σSO3 for models (a) FANN(SO3/CL) and (b) FANN(MSO3/C3S).
The two figures lead to the following remarks.
- (a)
- The shape of the functions is similar for both models, making the joint conclusions more reliable.
- (b)
- If the location of the SO3 target is near the optimum value and realized independently of the SO3 standard deviation, the 28-day strength variance remains low. Therefore, an adequate approximation of the optimal sulfate achieves two goals: maximum strength and reduced strength variance, regardless of SO3 variation.
- (c)
- As the SO3 value differs from the optimum value, an increase in SO3 variance leads to a deterioration of strength variability. For SO3 = 2.9%, an increase in σSO3 from 0.05 to 0.2 causes an increase in σStr28 from 1.2 to 1.5 for the first model and from 1.3 to 1.6 for the second model.
- (d)
- The above remarks necessitate an automatic controller that regulates SO3 using gypsum dosing to achieve the SO3 target with minimum variance, like the model presented in the literature [].
- (e)
- In Figure 7a,b, the surfaces are not symmetrical around the optimal line σSO3 = f(SO3opt), where SO3opt denotes the optimal sulfate. The left side slope is steeper than the right, meaning that if SO3 < SO3opt, the deterioration in σStr28 variance is more substantial than in SO3 > SO3opt.
4. Conclusions
This study attempts to approximate the optimal sulfate content of cement exclusively using cement manufactured in closed-circuit industrial mills. The advantage of this technique is that the obtained samples have the same properties (fineness, composition, forms of the sulfate carriers, and interaction of the grinding aid with the solids) as those of the cement produced. Additionally, the particle distribution of each component within each sample results from the actual production process, which is almost impossible to accomplish via grinding in a laboratory mill. The experimental design includes physical, chemical, and mechanical tests on four CEM types containing up to three main components, except gypsum, and the raw materials. The sampling was realized within two months to allow the clinker mineral composition to incorporate actual production variations. The plant laboratory took two samples of low and high gypsum for each CEM type by keeping constant the clinker content, before mixing the samples in conventional proportions to obtain new samples with a gradual increase in SO3. After air jet sieving, XRF analysis provided the chemical composition of the specimens and their residues at each sieve size. The solution of a system of equations provides the %components of the above. The main conclusions of this study are as follows.
- (1)
- A unique curve can express the function between relative compressive strength and the ratio between sulfate and clinker content—SO3/CL—for all CEM types. This conclusion holds for both the total clinker and the clinker passing the 40 μ and 32 μ sieves of cement. A parabolic equation between relative compressive strength and SO3/CL can fit the experimental data. Using the logarithm of SO3/CL as an independent variable, the equation provides a better R2 than the simple parabola because it covers a part of the data asymmetry. However, the logarithmic model underestimates the optimal SO3/CL position for both 7- and 28-day strength.
- (2)
- A shallow ANN with one hidden layer and two nodes provides a better R2 in training and test sets, as well as a closer approximation of the optimal SO3/CL than the simple second-order models. The numerical algorithm for determining the synaptic weights comprises two constraints for the maximum value and its derivative. The optimal SO3/CL is 2.85 for the 7-day strength and 3.0 for the 28-day strength.
- (3)
- The ANN using the clinker passing at 40 μ in the sulfate to clinker ratio, SO3/CLP40, gives equivalently reliable results to the first fundamental ANN with SO3/CLP40Opt = 3.25. The corresponding ANN using the clinker passing through a 32 μ sieve seems to be the worst among the three ANNs for the particle distributions of cement samples investigated with SO3/CLP32Opt = 3.33. SO3/CL = SO3/CLP90 because all cement specimens were finer than 90 μ. The three optimal sulfate-to-clinker ratios are in good linear agreement with the sieves’ grid size.
- (4)
- The clinker content of the four CEM types varies from 58 to 90%, covering most of modern cement production. The above result means that the implemented ANNs and their approximation to optimal SO3 can have a relatively broad application, at least as a guide for an experimental design.
- (5)
- Our research investigated the well-known functions between SO3, C3S, and C3A computed with Bogue formulae and direct measurement via XRD. We expressed the ratio of SO3 using each mineral phase as a molecular ratio, and we developed the corresponding ANN models between 28-day compressive strength and these variables.
- (6)
- Determination of C3A via XRD results in adequate data fitting and reliable approximation of the optimal sulfates. The optimal MSO3/C3AXRD is 1.55, though the C3A range is short for the series of clinkers examined.
- (7)
- The ANNs using MSO3/C3SXRD and MSO3/C3S fit both similarly and satisfactorily to experimental data, and their optimal molecular ratio of SO3 to mineral phase is roughly the same, being 0.135 and 0.132, respectively. The clinkers’ C3S ranged from 61 to 68, covering the majority of good reactivity clinkers manufactured nowadays. The above result means that the developed ANNs and the corresponding approximation of optimum sulfate could have a relatively general implementation. The attempt to correlate 28-day strength with M1 C3S, which is measured via XRD, did not perform as well as previous models.
- (8)
- Particular focus was also given to the impact of SO3 uncertainty on the 28-day strength variance using the error propagation method. One of the main conclusions is that an adequate approximation to the optimal sulfate achieves two goals: maximum strength and reduced strength variance. An automatic controller regulating SO3 using gypsum dosing to achieve the SO3 target with minimum variance is also necessary. Therefore, if a cement plant operates the cement mills, with the SO3 target being close to optimum, and regulates sulfates with an automatic controller, it can gain significant improvement in the products’ quality.
This research proposes some technical novelties concerning a procedure used to approximate the SO3 optimum on an industrial scale, the tools to obtain it, and optimal ratios of sulfate to several characteristics of cement and clinker. We suggest the exclusive use of industrial cement samples of several CEM types with low and high gypsum and their convenient mixing. Using relative strength and the ratio of SO3 to a quality parameter, e.g., %clinker, C3S, etc., normalizes the results, allowing them to appear in a single curve. The developed algorithm successfully used neural networks to fit and reliably predict the results. According to the authors’ knowledge, it is hard to find application of ANNs for SO3 optimization in the literature. We provide approximations of optimum SO3 as a function of clinker content, %clinker passing through some sieves, C3S, and C3A. We calculated some of these functions for a wide interval of input variables’ values. Thus, these approximations could have a relatively broad application in daily plant quality control, at least as a guide for experimental design.
The research into the correlation between optimum SO3 and some main cement characteristics could continue for the relationship between optimal sulfate and cement fineness, using samples of products manufactured in industrial closed-circuit mills.
Author Contributions
Conceptualization, D.C.T.; methodology, D.C.T. and C.A.K.; software, D.C.T. (developed in Excel and C#); validation, D.C.T. and C.A.K.; formal analysis, D.C.T.; investigation, C.A.K. and D.V.T.; writing—original draft preparation, D.C.T.; writing—review and editing, D.C.T.; supervision, D.C.T.; project administration, D.C.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data and results presented in this paper are available upon request from the authors.
Acknowledgments
The authors are grateful to N. Chankova, Quality Manager at Devnya Cement AD, for providing the XRD analyses of the samples. The authors are also grateful to reviewers for their constructive comments, which helped to improve the present paper.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
List of the companies supplying raw materials and main measuring devices
- Materials
- Clinker and cement: Halyps Building Materials, S. A., Aspropyrgos, Greece.
- Raw materials suppliers
- Pozzolan: Aegean Perlites S. A., Nissiros, Greece.
- Gypsum: George Zervakis S.A.—Gypsum Mines of Eastern Crete, Sitia, Greece.
- Limestone: Aragonitis Quarry, Aspropyrgos, Greece.
- Grinding Aid: GCP Applied Technologies, Milan, Italy.
- Measuring instruments
- XRF analyzer: Malvern-Panalytical, Almelo, the Netherlands.
- XRD analyzer: Malvern-Panalytical, Almelo, the Netherlands.
- Press, mixer, jolting apparatus, molds: Toni Technik, Berlin, Germany.
- Air jet sieving apparatus and sieves: Hosokawa Alpine, Augsburg, Germany.
- Laser particle size analyzer: Cilas, Orléans, France.
- Labs performing the tests
- The laboratory of Devnya Cement AD (Devnya, Bulgaria) performed the XRD analyses. The laboratory of Halyps Building Materials S.A. (Aspropyrgos, Greece) performed the sampling and all remaining physical, chemical, and mechanical tests.
References
- Lee, F.M. The Chemistry of Cement and Concrete, 3rd ed.; Chemical Publishing Company Inc.: New York, NY, USA, 1971; pp. 180–181, 297–298, 303, 308–310. [Google Scholar]
- Knappert, J.; Treiber, K.; Seemann, S. Gypsum dehydration potential and mean residence time of a stirred media mill during ultra-fine grinding of cement clinker and gypsum. ZKG Cem. Lime Gypsum 2022, 2. Available online: https://www.zkg.de/en/artikel/zkg_Gypsum_dehydration_potential_and_mean_residence_time_of_a_stirred_media-3749114.html (accessed on 7 April 2023).
- Copeland, L.E.; Kantro, D.L. Chemistry of Hydration of Portland Cement at Ordinary Temperature. In The Chemistry of Cements, 2nd ed.; Taylor, H.F.W., Ed.; Academic Press Inc.: London, UK, 1972; Volume 1, pp. 313–370. [Google Scholar]
- Taherdangkoo, R.; Tian, M.; Sadighi, A.; Meng, T.; Yang, H.; Butscher, C. Experimental Data on Solubility of the Two Calcium Sulfates Gypsum and Anhydrite in Aqueous Solutions. Data 2022, 7, 140. [Google Scholar] [CrossRef]
- Bogue, R.H. The Chemistry of the Portland Cement, 2nd ed.; Reinhold Publishing Corporation: London, UK, 1955; pp. 245–250. [Google Scholar]
- Mindess, S.; Young, J.F.; Darwin, D. Concrete, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2003. [Google Scholar]
- Niemuth, M. Effect of Fly Ash on the Optimum Sulfate of Portland Cement. Ph.D. Thesis, Purdue University, West Lafayette, IA, USA, December 2012; p. 68. Available online: https://www.researchgate.net/publication/266077758_Effect_of_Fly_Ash_on_Optimum_Sulfate_of_Portland_Cement (accessed on 7 April 2023).
- Evans, K.A. The Optimum Sulphate Content in Portland Cement. p. 3. Available online: https://tspace.library.utoronto.ca/bitstream/1807/11621/1/MQ29389.pdf (accessed on 7 April 2023).
- CEN/TC 51, EN 197-1:2011; Cement. Part 1: Composition, Specifications and Conformity Criteria for Common Cements. CEN: Brussels, Belgium, 2011; pp. 10–15.
- ASTM C150/C150M-22; Standard Specification for Portland Cement. ASTM International: West Conshohocken, PA, USA, 2022.
- ASTM C563-16; Standard Guide for Approximation of Optimum SO3 in Hydraulic Cement Using Compressive Strength. ASTM International: West Conshohocken, PA, USA, 2016.
- Khudyakova, T.M.; Kolesnikova, O.G.; Zhanikulov, N.N.; Botabaev, N.E.; Kenzhibaeva, G.S.; Iztleuov, G.M.; Suigenbaeva, A.Z.; Kutzhanova, A.N.; Ashirbaev, H.A.; Kolesnikova, V.A. Low-Basicity Cement, Problems and Advantages of its Utilization. Refract. Ind. Ceram. 2021, 62, 369–374. [Google Scholar] [CrossRef]
- Kolesnikova, O.; Vasilyeva, N.; Kolesnikov, A.; Zolkin, A. Optimization of raw mix using technogenic waste to produce cement clinker. Mining Inf. Anal. Bull. 2022, 10–11, 103–115. [Google Scholar] [CrossRef]
- Lerch, W. The Influence of Gypsum on the Hydration and Properties of Portland Cement Pastes. Proc. Am. Soc. Test. Mater. 1946, 46, 1252–1291. [Google Scholar]
- Fincan, M. Sulfate Optimization in the Cement-Slag Blended System Based on Calorimetry and Strength Studies. Ph.D. Thesis, University of South Florida, Tampa, FL, USA, 2021; p. 2. Available online: https://digitalcommons.usf.edu/cgi/viewcontent.cgi?article=9967&context=etd (accessed on 7 April 2023).
- Bentur, A. Effect of Gypsum on the Hydration and Strength of C3S Pastes. J. Am. Ceram. Soc. 1976, 59, 210–213. [Google Scholar] [CrossRef]
- Jelenić, I.; Panović, A.; Halle, R.; Gaćeša, T. Effect of gypsum on the hydration and strength development of commercial portland cements containing alkali sulfates. Cem. Concr. Res. 1977, 7, 239–245. [Google Scholar] [CrossRef]
- Soroka, I.; Abayneh, M. Effect of gypsum on properties and internal structure of PC paste. Cem. Concr. Res. 1986, 16, 495–504. [Google Scholar] [CrossRef]
- Sersale, R.; Cioffi, R.; Frigione, G.; Zenone, F. Relationship between gypsum content, porosity and strength in cement. I. Effect of SO3 on the physical microstructure of Portland cement mortars. Cem. Concr. Res. 1991, 21, 120–126. [Google Scholar] [CrossRef]
- Tennis, P.D.; Jennigs, H.M. A model for two types of calcium silicate hydrate in the microstructure of Portland cement pastes. Cem. Concr. Res. 2000, 30, 855–863. [Google Scholar] [CrossRef]
- Jansen, D.; Goetz-Neunhoeffer, F.; Stabler, C.; Neubauer, J. A remastered external standard method applied to the quantification of early OPC hydration. Cem. Concr. Res. 2011, 41, 602–608. [Google Scholar] [CrossRef]
- Gunay, S.A.A. Influence of Aluminates Phases Hydration in Presence of Calcium Sulfate on Silicates Phases Hydration: Consequences on Cement Optimum Sulfate. Ph.D. Thesis, University of Bourgogne, Bourgogne, France, 2012. Available online: https://theses.hal.science/tel-00767768 (accessed on 7 April 2023).
- Termkhajornkit, P.; Vu, Q.H.; Barbarulo, R.; Daronnat, S.; Chanvillard, G. Dependence of compressive strength on phase assemblage in cement pastes: Beyond gel–space ratio—Experimental evidence and micromechanical modeling. Cem. Concr. Res. 2014, 56, 1–11. [Google Scholar] [CrossRef]
- Zunino, F.; Scrivener, K. The influence of sulfate addition on hydration kinetics and C-S-H morphology of C3S and C3S/C3A systems. Cem. Concr. Res. 2022, 160, 106930. [Google Scholar] [CrossRef]
- Andrade Neto, J.S.; de Matos, P.R.; De la Torre, A.G.; Campos, C.E.M.; Torres, S.M.; Monteiro, P.J.M.; Kirchheim, A.P. Hydration and interactions between pure and doped C3S and C3A in the presence of different calcium sulfates. Cem. Concr. Res. 2022, 159, 106893. [Google Scholar] [CrossRef]
- Miller, F.M.; Tang, F.J. The distribution of sulfur in present-day clinkers of variable sulfur content. Cem. Concr. Res. 1996, 26, 1821–1829. [Google Scholar] [CrossRef]
- Taylor, H.F.W. Distribution of sulfate between phases in Portland cement clinkers. Cem. Concr. Res. 1999, 29, 1173–1179. [Google Scholar] [CrossRef]
- Horkoss, S.; Lteif, R.; Rizk, T. Influence of the clinker SO3 on the cement characteristics. Cem. Concr. Res. 2011, 41, 913–919. [Google Scholar] [CrossRef]
- Mohammed, S.; Safiullah, O. Optimization of the SO3 content of an Algerian Portland cement: Study on the effect of various amounts of gypsum on cement properties. Constr. Build. Mater. 2018, 164, 262–370. [Google Scholar] [CrossRef]
- Yamashita, H.; Yamada, K.; Hirao, H.; Hoshino, S. Influence of Limestone Powder on the Optimum Gypsum Content for Portland Cement with Different Alumina Content. Available online: https://www.researchgate.net/publication/285554157_Influence_of_Limestone_Powder_on_the_Optimum_Gypsum_Content_for_Portland_Cement_with_Different_Alumina_Content (accessed on 7 April 2023).
- Irassar, E.F.; Violini, D.; Rahhal, V.F.; Milanesi, C.; Trezza, M.A.; Bonavetti, V.L. Influence of limestone content, gypsum content and fineness on early age properties of Portland limestone cement produced by inter-grinding. Cem. Concr. Compos. 2011, 33, 192–200. [Google Scholar] [CrossRef]
- Liu, F.; Lan, M.Z. Effects of Gypsum on Cementitious Systems with Different Mineral Mixtures. Available online: https://www.researchgate.net/publication/269647645_Effects_of_Gypsum_on_Cementitious_Systems_with_Different_Mineral_Mixtures (accessed on 7 April 2023).
- Adu-Amankwah, S.; Black, L.; Skocek, J.; Ben Haha, M.; Zajac, M. Effect of sulfate additions on hydration and performance of ternary slag-limestone composite cements. Constr. Build. Mater. 2018, 164, 451–462. [Google Scholar] [CrossRef]
- Han, F.; Zhou, Y.; Zhang, Z. Effect of gypsum on the properties of composite binder containing high- volume slag and iron tailing powder. Constr. Build. Mater. 2020, 252, 119023. [Google Scholar] [CrossRef]
- Tsamatsoulis, D.; Nikolakakos, N. Optimizing the Sulphates Content of Cement Using Multivariable Modelling and Uncertainty Analysis. Chem. Biochem. Eng. Q. 2013, 27, 133–144. Available online: http://silverstripe.fkit.hr/cabeq/assets/Uploads/Cabeq-2013-02-03.pdf (accessed on 19 June 2023).
- Al Salaheen, M.; Alaloul, W.S.; Malkawi, A.B.; de Brito, J.; Alzubi, K.M.; Al-Sabaeei, A.M.; Alnarabiji, M.S. Modelling and Optimization for Mortar Compressive Strength Incorporating Heat-Treated Fly Oil Shale Ash as an Effective Supplementary Cementitious Material Using Response. Materials 2022, 15, 6538. [Google Scholar] [CrossRef]
- Magistri, M.; Lo Presti, A.; Salvioni, D. Limestone and Fly Ash Blended Cements: Correlation between Durability, Performances and Particle Size Distribution. Available online: http://civmin.utoronto.ca/wp-content/uploads/2019/05/28.pdf (accessed on 7 April 2023).
- Hirch, T.; Lu, Z.; Stepan, D. Impact of triethanolamine on the sulfate balance of Portland cements with mixed sulfate carriers. J. Am. Ceram. Soc. 2021, 104, 4829–4842. [Google Scholar] [CrossRef]
- Recchi, P.; Magistri, M.; Lo Presti, A.; Cerulli, T. Influences of the Type and Amount of Calcium Sulphate on the Reactivity of Alkanolamine-Based Set Accelerators/Strength Improvers. Available online: http://cadd.mapei.com/wp-content/uploads/2011/07/2011-07-ICCC-Recchi-et-al_influence-of-calcium-sulphates.pdf (accessed on 7 April 2023).
- Andrade Neto, J.S.; De la Torre, A.G.; Kirchheim, A.P. Effects of sulfates on the hydration of Portland cement—A review. Constr. Build. Mater. 2021, 279, 122428. [Google Scholar] [CrossRef]
- Schade, T.; Middendorf, B. Use of Design of Experiments (DoE) to Model the Sulphate Agent Amount of (Ultra) Finely Ground and Fast Hardening Portland Cement Clinker. Materials 2021, 14, 5573. [Google Scholar] [CrossRef]
- Kurdowski, W. Cement and Concrete Chemistry; Springer Science & Business Media: New York, NY, USA, 2014; pp. 217–218. [Google Scholar]
- Escobar, C.A.; Morales-Menendez, R. Process-Monitoring-for-Quality—A Model Selection Criterion for Shallow Neural Networks. Available online: https://www.academia.edu/86483788/Process_monitoring_for_quality_A_model_selection_criterion (accessed on 7 April 2023).
- Tsamatsoulis, D. Prediction of Cement Compressive Strength by Combining Dynamic Models of Neural Networks. Chem. Biochem. Eng. Q. 2021, 35, 295–318. [Google Scholar] [CrossRef]
- CEN/TC 51, EN 196-1:2016; Methods of Testing Cement—Part 1: Determination of Strength. CEN Management Centre: Brussels, Belgium, 2016.
- Tsamatsoulis, D. Simulation of Cement Grinding Process for Optimal Control of SO3 Content. Chem. Biochem. Eng. Q. 2014, 28, 13–25. Available online: https://hrcak.srce.hr/en/clanak/174265 (accessed on 19 June 2023).
- CEN/TC 51, EN 196-6:2010; Methods of Testing Cement—Part 6: Determination of Fineness. CEN Management Centre: Brussels, Belgium, 2010.
- CEN/TC 51, EN 196-2:2013; Methods of Testing Cement—Part 2: Chemical Analysis of Cement. CEN Management Centre: Brussels, Belgium, 2013.
- Pritzel, C.; Emami, M.; Afflerbach, S.; Killian, M.; Trettin, R. Formation of α-Hemihydrate Inside of a Gypsum Crystal during the Dehydration Process. Crystals 2022, 12, 1780. [Google Scholar] [CrossRef]
- Krause, F.; Renner, B.; Coppens, F.; Dewanckele, J.; Schwotzer, M. Reactivity of Gypsum-Based Materials Subjected to Thermal Load: Investigation of Reaction Mechanisms. Materials 2020, 13, 1427. [Google Scholar] [CrossRef]
- Tang, F.J.; Gartner, E.M. Influence of sulfate source on Portland cement hydration. Adv. Cem. Res. 1988, 1, 67–74. [Google Scholar] [CrossRef]
- Staněk, T.; Sulovský, P. The influence of the alite polymorphism on the strength of the Portland cement. Cem. Concr. Res. 2002, 32, 1169–1175. [Google Scholar] [CrossRef]
- Celic, I.B. The effects of particle size distribution and surface area upon cement strength development. Powder Technol. 2009, 188, 272–276. [Google Scholar] [CrossRef]
- Rapid Laboratory Particle Size Analysis of Cements Using Laser Diffraction. Available online: https://www.bettersizeinstruments.com/uploads/file/rapid-laboratory-particle-size-analysis-of-cements-using-laser-diffraction.pdf (accessed on 7 April 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).