Numerical Study of Dry Reforming of Methane in Packed and Fluidized Beds: Effects of Key Operating Parameters
Abstract
1. Introduction
- The catalyst moving in liquified form has enhanced the continuous operation process, which gives flexibility in temperature control and smoothly responds to changes in operation;
- Improvements in gas and solid mixing have led to isothermal operations free of cold and hot spots;
- More contact between the catalyst and reactant gases increases the conversion, mass, and heat rates;
- Lower pressure drop;
- Suitable for large-scale operation.
2. Numerical Simulation
2.1. CFD Model and Simulation Setup
2.1.1. Gas-Species Transport Equations
| |
| (3) | |
| |
| (4) | |
| |
| (5) | |
| |
| (6) | |
| |
| (7) | |
| |
| (8) | |
| |
| (9) | |
2.1.2. Equations of Energy Conservation
2.2. Reaction Kinetics
3. Results and Discussion
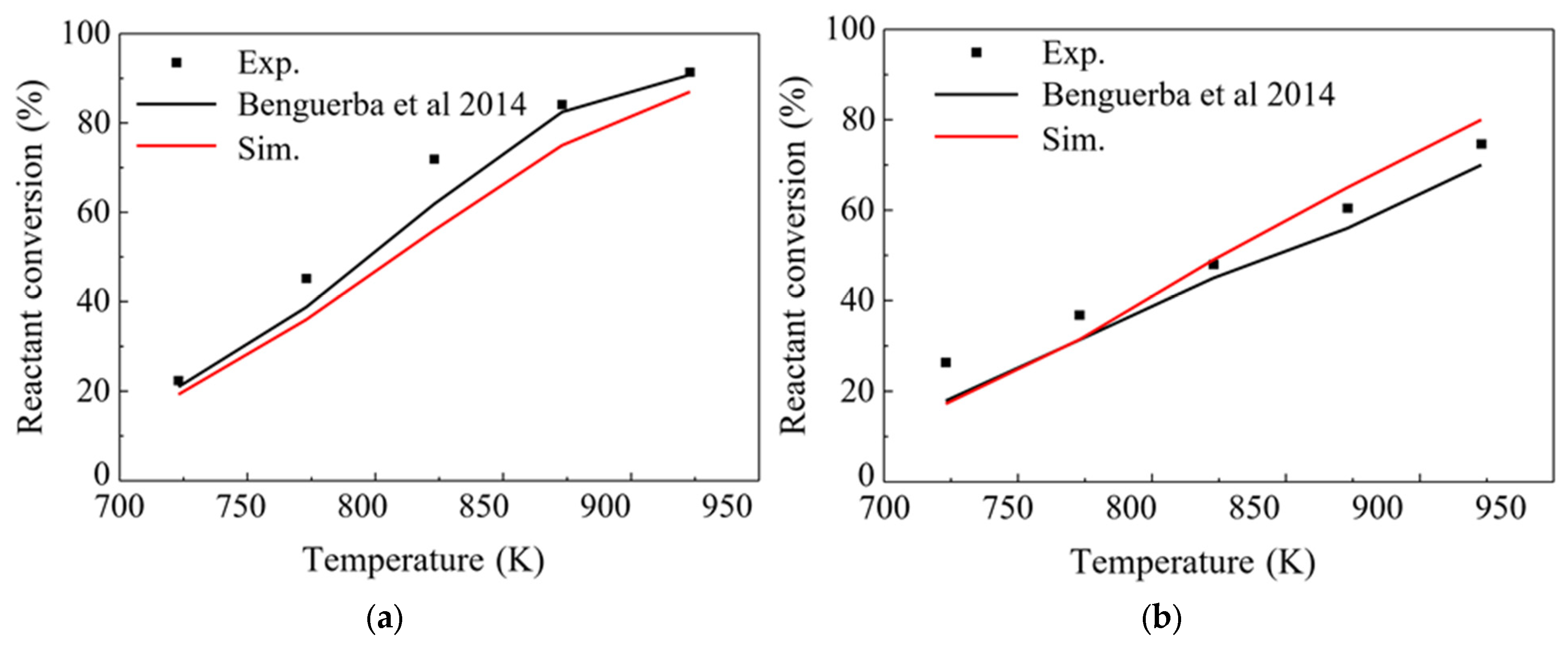
3.1. Model Validation of Packed Bed
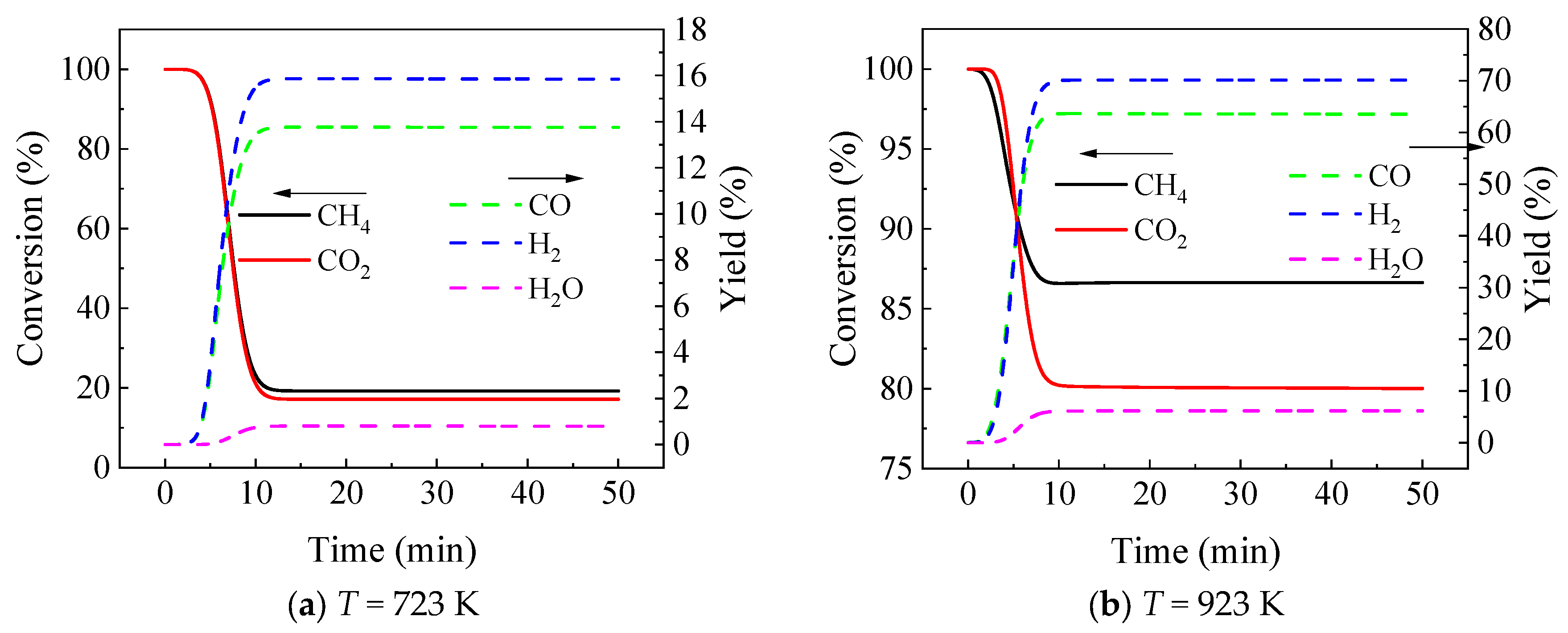
3.2. Effect of Temperature
3.3. Effect of Components
3.4. Coke Formation
3.5. Comparison of Conversion in Packed and Fluidized Beds
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fan, M.-S.; Abdullah, A.Z.; Bhatia, S. Catalytic Technology for Carbon Dioxide Reforming of Methane to Synthesis Gas. ChemCatChem 2009, 1, 192–208. [Google Scholar] [CrossRef]
- Wang, S.; Lu, G.Q.; Millar, G.J. Carbon Dioxide Reforming of Methane To Produce Synthesis Gas over Metal-Supported Catalysts: State of the Art. Energy Fuels 1996, 10, 896–904. [Google Scholar] [CrossRef]
- Sazali, N. Emerging technologies by hydrogen: A review. Int. J. Hydrogen Energy 2020, 45, 18753–18771. [Google Scholar] [CrossRef]
- Noh, Y.S.; Lee, K.-Y.; Moon, D.J. Hydrogen production by steam reforming of methane over nickel based structured catalysts supported on calcium aluminate modified SiC. Int. J. Hydrogen Energy 2019, 44, 21010–21019. [Google Scholar] [CrossRef]
- Hilliard, S. Water Splitting Photoelectrocatalysis: The Conception and Construction of a Photoelectrocatalytic Water Splitting Cell. Doctoral Dissertation, Université Pierre et Marie Curie-Paris VI, Paris, France, 2016. [Google Scholar]
- Turner, J.A. Sustainable hydrogen production. Science 2004, 305, 972–974. [Google Scholar] [CrossRef]
- Bahzad, H.; Shah, N.; Dowell, N.M.; Boot-Handford, M.; Soltani, S.M.; Ho, M.; Fennell, P.S. Development and techno-economic analyses of a novel hydrogen production process via chemical looping. Int. J. Hydrogen Energy 2019, 44, 21251–21263. [Google Scholar] [CrossRef]
- Gangadharan, P.; Kanchi, K.C.; Lou, H.H. Evaluation of the economic and environmental impact of combining dry reforming with steam reforming of methane. Chem. Eng. Res. Des. 2012, 90, 1956–1968. [Google Scholar] [CrossRef]
- Şener, A.N.; Günay, M.E.; Leba, A.; Yıldırım, R. Statistical review of dry reforming of methane literature using decision tree and artificial neural network analysis. Catal. Today 2018, 299, 289–302. [Google Scholar] [CrossRef]
- Al-Fatesh, A.S.; Naeem, M.A.; Fakeeha, A.H.; Abasaeed, A.E. Role of La2O3 as Promoter and Support in Ni/γ-Al2O3 Catalysts for Dry Reforming of Methane. Chin. J. Chem. Eng. 2014, 22, 28–37. [Google Scholar] [CrossRef]
- Aramouni, N.A.K.; Touma, J.G.; Tarboush, B.A.; Zeaiter, J.; Ahmad, M.N. Catalyst design for dry reforming of methane: Analysis review. Renew. Sustain. Energy Rev. 2018, 82, 2570–2585. [Google Scholar] [CrossRef]
- Arora, S.; Prasad, R. An overview on dry reforming of methane: Strategies to reduce carbonaceous deactivation of catalysts. RSC Adv. 2016, 6, 108668–108688. [Google Scholar] [CrossRef]
- Bang, S.; Hong, E.; Baek, S.W.; Shin, C.-H. Effect of acidity on Ni catalysts supported on P-modified Al2O3 for dry reforming of methane. Catal. Today 2018, 303, 100–105. [Google Scholar] [CrossRef]
- Chen, X.; Sheng, Z.; Murata, S.; Zen, S.; Kim, H.-H.; Nozaki, T. CH4 dry reforming in fluidized-bed plasma reactor enabling enhanced plasma-catalyst coupling. J. CO2 Util. 2021, 54, 101771. [Google Scholar] [CrossRef]
- Fujitsuka, H.; Kobayashi, T.; Tago, T. Development of Silicalite-1-encapsulated Ni nanoparticle catalyst from amorphous silica-coated Ni for dry reforming of methane: Achieving coke formation suppression and high thermal stability. J. CO2 Util. 2021, 53, 101707. [Google Scholar] [CrossRef]
- Pakhare, D.; Spivey, J. A review of dry (CO2) reforming of methane over noble metal catalysts. Chem. Soc. Rev. 2014, 43, 7813–7837. [Google Scholar] [CrossRef]
- Yusuf, M.; Farooqi, A.S.; Alam, M.A.; Keong, L.K.; Hellgardt, K.; Abdullah, B. Response surface optimization of syngas production from greenhouse gases via DRM over high performance Ni–W catalyst. Int. J. Hydrogen Energy 2021, 47, 31058–31071. [Google Scholar] [CrossRef]
- Zambrano, D.; Soler, J.; Herguido, J.; Menéndez, M. Kinetic Study of Dry Reforming of Methane Over Ni–Ce/Al2O3 Catalyst with Deactivation. Top. Catal. 2019, 62, 456–466. [Google Scholar] [CrossRef]
- Wang, J. Continuum theory for dense gas-solid flow: A state-of-the-art review. Chem. Eng. Sci. 2020, 215, 115428. [Google Scholar] [CrossRef]
- Parker, J.; LaMarche, K.; Chen, W.; Williams, K.; Stamato, H.; Thibault, S. CFD simulations for prediction of scaling effects in pharmaceutical fluidized bed processors at three scales. Powder Technol. 2013, 235, 115–120. [Google Scholar] [CrossRef]
- Zhang, Y.; Lan, X.; Gao, J. Modeling of gas-solid flow in a CFB riser based on computational particle fluid dynamics. Pet. Sci. 2012, 9, 535–543. [Google Scholar] [CrossRef]
- Abbasi, A.; Islam, M.A.; Ege, P.E.; de Lasa, H.I. CPFD flow pattern simulation in downer reactors. AIChE J. 2013, 59, 1635–1647. [Google Scholar] [CrossRef]
- Chen, X.; Wang, J. A comparison of two-fluid model, dense discrete particle model and CFD-DEM method for modeling impinging gas–solid flows. Powder Technol. 2014, 254, 94–102. [Google Scholar] [CrossRef]
- Andrews, M.J.; O’Rourke, P.J. The multiphase particle-in-cell (MP-PIC) method for dense particulate flows. Int. J. Multiph. Flow 1996, 22, 379–402. [Google Scholar] [CrossRef]
- Zhao, P.; O’Rourke, P.J.; Snider, D. Three-dimensional simulation of liquid injection, film formation and transport, in fluidized beds. Particuology 2009, 7, 337–346. [Google Scholar] [CrossRef]
- Snider, D.; Banerjee, S. Heterogeneous gas chemistry in the CPFD Eulerian–Lagrangian numerical scheme (ozone decomposition). Powder Technol. 2010, 199, 100–106. [Google Scholar] [CrossRef]
- Karimipour, S.; Pugsley, T. Application of the particle in cell approach for the simulation of bubbling fluidized beds of Geldart A particles. Powder Technol. 2012, 220, 63–69. [Google Scholar] [CrossRef]
- Abbasi, A.; Ege, P.E.; de Lasa, H.I. CPFD simulation of a fast fluidized bed steam coal gasifier feeding section. Chem. Eng. J. 2011, 174, 341–350. [Google Scholar] [CrossRef]
- Chen, C.; Werther, J.; Heinrich, S.; Qi, H.-Y.; Hartge, E.-U. CPFD simulation of circulating fluidized bed risers. Powder Technol. 2013, 235, 238–247. [Google Scholar] [CrossRef]
- Berrouk, A.S.; Pornsilph, C.; Bale, S.S.; Du, Y.; Nandakumar, K. Simulation of a Large-Scale FCC Riser Using a Combination of MP-PIC and Four-Lump Oil-Cracking Kinetic Models. Energy Fuels 2017, 31, 4758–4770. [Google Scholar] [CrossRef]
- Oloruntoba, A.; Zhang, Y.; Xiao, H. Study on effect of gas distributor in fluidized bed reactors by hydrodynamics-reaction-coupled simulations. Chem. Eng. Res. Des. 2022, 177, 431–447. [Google Scholar] [CrossRef]
- Oloruntoba, A.; Zhang, Y.; Xiao, H. Hydrodynamics-reaction-coupled simulations in a low-scale batch FCC regenerator: Comparison between an annular and a free-bubbling fluidized beds. Powder Technol. 2022, 407, 117608. [Google Scholar] [CrossRef]
- Xiao, H.; Zhang, Y.; Wang, J. Virtual error quantification of cross-correlation algorithm for solids velocity measurement in different gas fluidization regimes. Chem. Eng. Sci. 2021, 246, 117013. [Google Scholar] [CrossRef]
- Xiao, H.; Zhang, Y.; Wang, J. Correlating measurement qualities of cross-correlation based solids velocimetry with solids convection-mixing competing mechanism in different gas fluidization regimes. Chem. Eng. Sci. 2022, 253, 117602. [Google Scholar] [CrossRef]
- Yates, J.; Lettieri, P. Fluidized-Bed Reactors: Processes and Operating Conditions; Springer: Cham, Switzerland, 2016; Volume 26. [Google Scholar]
- Enos, J.L. Petroleum, Progress and Profits: A History of Process Innovation; MIT Press: Cambridge, MA, USA, 1962. [Google Scholar]
- CPFD Software. Available online: https://cpfd-software.com/ (accessed on 12 January 2023).
- Snider, D.M. Three fundamental granular flow experiments and CPFD predictions. Powder Technol. 2007, 176, 36–46. [Google Scholar] [CrossRef]
- Snider, D.M. An Incompressible Three-Dimensional Multiphase Particle-in-Cell Model for Dense Particle Flows. J. Comput. Phys. 2001, 170, 523–549. [Google Scholar] [CrossRef]
- Benguerba, Y.; Dehimi, L.; Virginie, M.; Dumas, C.; Ernst, B. Modelling of methane dry reforming over Ni/Al2O3 catalyst in a fixed-bed catalytic reactor. React. Kinet. Mech. Catal. 2014, 114, 109–119. [Google Scholar] [CrossRef]
- Durán, P.; Sanz-Martínez, A.; Soler, J.; Menéndez, M.; Herguido, J. Pure hydrogen from biogas: Intensified methane dry reforming in a two-zone fluidized bed reactor using permselective membranes. Chem. Eng. J. 2019, 370, 772–781. [Google Scholar] [CrossRef]
- Wen, C.-Y. Mechanics of Fluidization. In Chemical Engineering Progress Symposium Series; American Institute of Chemical Engineers: New York, NY, USA, 1966. [Google Scholar]
- Yang, N.; Wang, W.; Ge, W.; Li, J. CFD simulation of concurrent-up gas–solid flow in circulating fluidized beds with structure-dependent drag coefficient. Chem. Eng. J. 2003, 96, 71–80. [Google Scholar] [CrossRef]
- Wehinger, G.D.; Eppinger, T.; Kraume, M. Detailed numerical simulations of catalytic fixed-bed reactors: Heterogeneous dry reforming of methane. Chem. Eng. Sci. 2015, 122, 197–209. [Google Scholar] [CrossRef]
- Wehinger, G.D.; Eppinger, T.; Kraume, M. Evaluating Catalytic Fixed-Bed Reactors for Dry Reforming of Methane with Detailed CFD. Chem. Ing. Tech. 2015, 87, 734–745. [Google Scholar] [CrossRef]
- Wehinger, G.D.; Kraume, M.; Berg, V.; Korup, O.; Mette, K.; Schlögl, R.; Behrens, M.; Horn, R. Investigating dry reforming of methane with spatial reactor profiles and particle-resolved CFD simulations. AIChE J. 2016, 62, 4436–4452. [Google Scholar] [CrossRef]
- Karst, F.; Maestri, M.; Freund, H.; Sundmacher, K. Reduction of microkinetic reaction models for reactor optimization exemplified for hydrogen production from methane. Chem. Eng. J. 2015, 281, 981–994. [Google Scholar] [CrossRef]
- Olsbye, U.; Wurzel, T.; Mleczko, L. Kinetic and Reaction Engineering Studies of Dry Reforming of Methane over a Ni/La/Al2O3 Catalyst. Ind. Eng. Chem. Res. 1997, 36, 5180–5188. [Google Scholar] [CrossRef]
- Wurzel, T.; Malcus, S.; Mleczko, L. Reaction engineering investigations of CO2 reforming in a fluidized-bed reactor. Chem. Eng. Sci. 2000, 55, 3955–3966. [Google Scholar] [CrossRef]
- Yin, L.; Wang, S.; Lu, H.; Ding, J.; Mostofi, R.; Hao, Z. Simulation of effect of catalyst particle cluster on dry methane reforming in circulating fluidized beds. Chem. Eng. J. 2007, 131, 123–134. [Google Scholar] [CrossRef]
- Abbas, S.Z.; Dupont, V.; Mahmud, T. Kinetics study and modelling of steam methane reforming process over a NiO/Al2O3 catalyst in an adiabatic packed bed reactor. Int. J. Hydrogen Energy 2017, 42, 2889–2903. [Google Scholar] [CrossRef]
- de la Cruz-Flores, V.G.; Martinez-Hernandez, A.; Gracia-Pinilla, M.A. Deactivation of Ni-SiO2 catalysts that are synthetized via a modified direct synthesis method during the dry reforming of methane. Appl. Catal. A Gen. 2020, 594, 117455. [Google Scholar] [CrossRef]
- Mark, M.F.; Maier, W.F.; Mark, F. Reaction kinetics of the CO2 reforming of methane. Chem. Eng. Technol. 1997, 20, 361–370. [Google Scholar] [CrossRef]
- Benguerba, Y.; Dehimi, L.; Virginie, M.; Dumas, C.; Ernst, B. Numerical investigation of the optimal operative conditions for the dry reforming reaction in a fixed-bed reactor: Role of the carbon deposition and gasification reactions. React. Kinet. Mech. Catal. 2015, 115, 483–497. [Google Scholar] [CrossRef]
- Chen, S.; Zaffran, J.; Yang, B. Dry reforming of methane over the cobalt catalyst: Theoretical insights into the reaction kinetics and mechanism for catalyst deactivation. Appl. Catal. B Environ. 2020, 270, 118859. [Google Scholar] [CrossRef]
- Nikoo, M.K.; Amin, N.A.S. Thermodynamic analysis of carbon dioxide reforming of methane in view of solid carbon formation. Fuel Process. Technol. 2011, 92, 678–691. [Google Scholar] [CrossRef]
- Niu, J.; Liland, S.E.; Yang, J.; Rout, K.R.; Ran, J.; Chen, D. Effect of oxide additives on the hydrotalcite derived Ni catalysts for CO2 reforming of methane. Chem. Eng. J. 2019, 377, 119763. [Google Scholar] [CrossRef]
- Kumar, M.; Srivastava, V.C. Simulation of a Fluidized-Bed Reactor for Dimethyl Ether Synthesis. Chem. Eng. Technol. 2010, 33, 1967–1978. [Google Scholar] [CrossRef]
- Prasad, P.; Elnashaie, S.S.E.H. Novel Circulating Fluidized-Bed Membrane Reformer for the Efficient Production of Ultraclean Fuels from Hydrocarbons. Ind. Eng. Chem. Res. 2002, 41, 6518–6527. [Google Scholar] [CrossRef]
- Jing, Q.; Lou, H.; Mo, L.; Zheng, X. Comparative study between fluidized bed and fixed bed reactors in methane reforming with CO2 and O2 to produce syngas. Energy Convers. Manag. 2006, 47, 459–469. [Google Scholar] [CrossRef]
- Thiemsakul, D.; Kamsuwan, C.; Piemjaiswang, R.; Piumsomboon, P.; Chalermsinsuwan, B. Computational fluid dynamics simulation of internally circulating fluidized bed reactor for dry reforming of methane. Energy Rep. 2022, 8, 817–824. [Google Scholar] [CrossRef]
- Xiao, H.; Zhang, Y.; Hua, Y.; Oloruntoba, A. Quantitative comparison of measurement quality of cross-correlation based particle velocity instruments in different gas fluidization regimes. Adv. Powder Technol. 2021, 32, 3915–3926. [Google Scholar] [CrossRef]
- Aguedal, L.; Semmar, D.; Berrouk, A.S.; Azzi, A.; Oualli, H. 3D vortex structure investigation using large eddy simulation of flow around a rotary oscillating circular cylinder. Eur. J. Mech.-B Fluids 2018, 71, 113–125. [Google Scholar] [CrossRef]
- Abrahamsen, A.R.; Geldart, D. Behavior of gas-fluidized beds of fine powder part I: Homogeneous expansion. Powder Technol. 1980, 26, 35–46. [Google Scholar] [CrossRef]
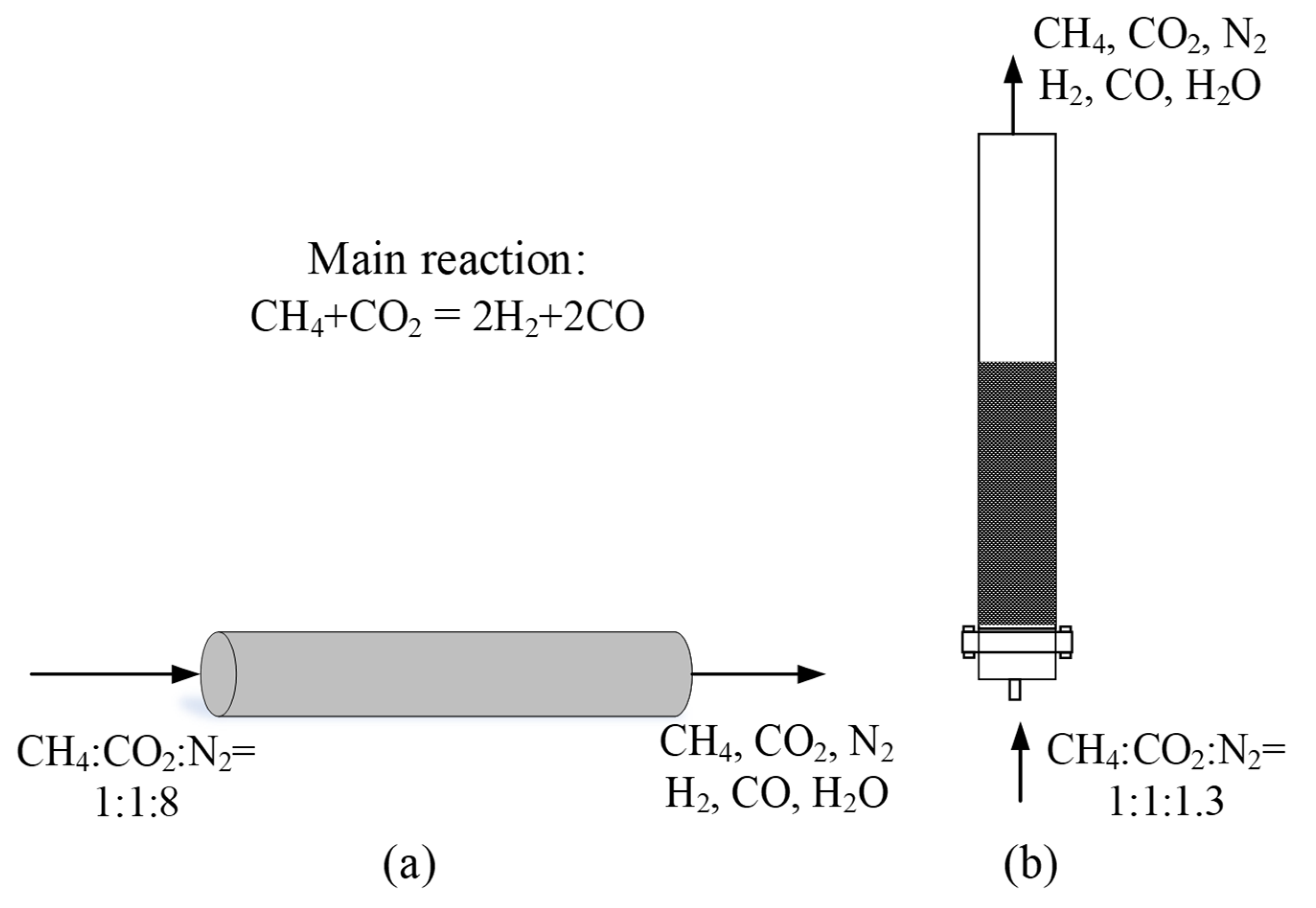
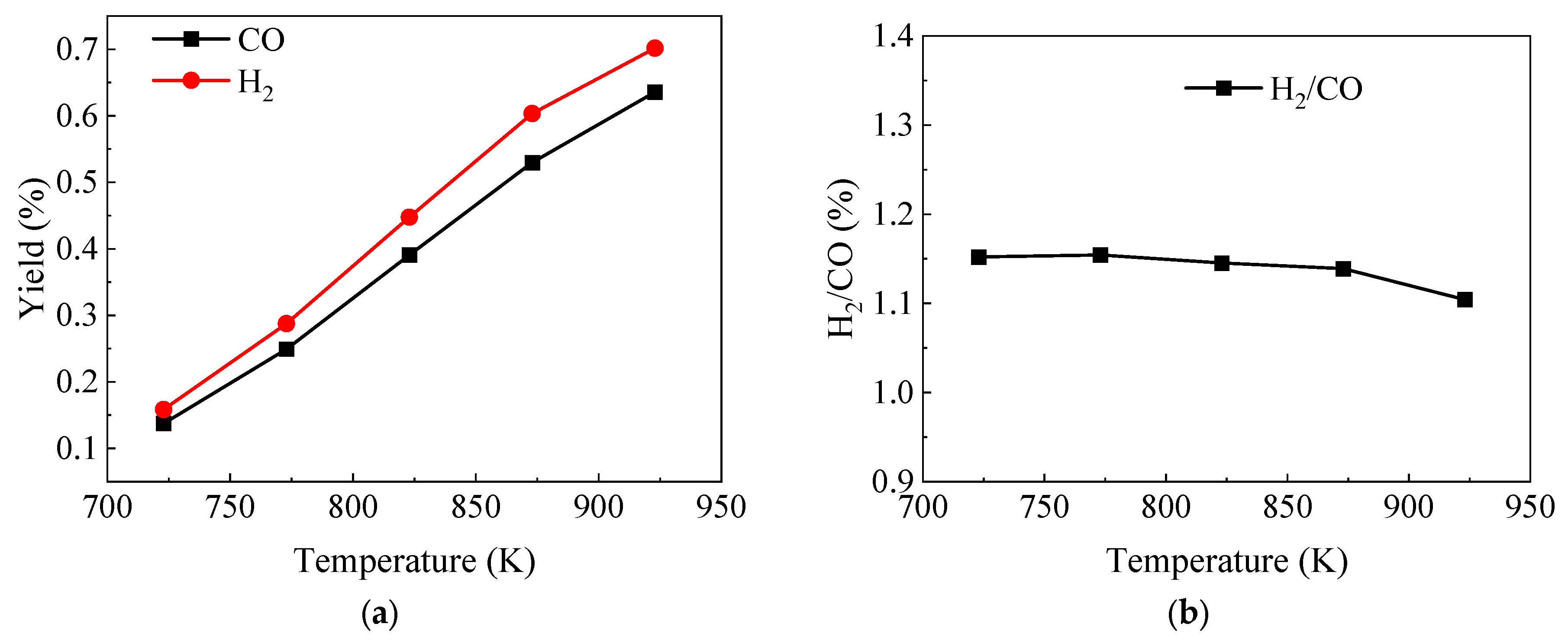

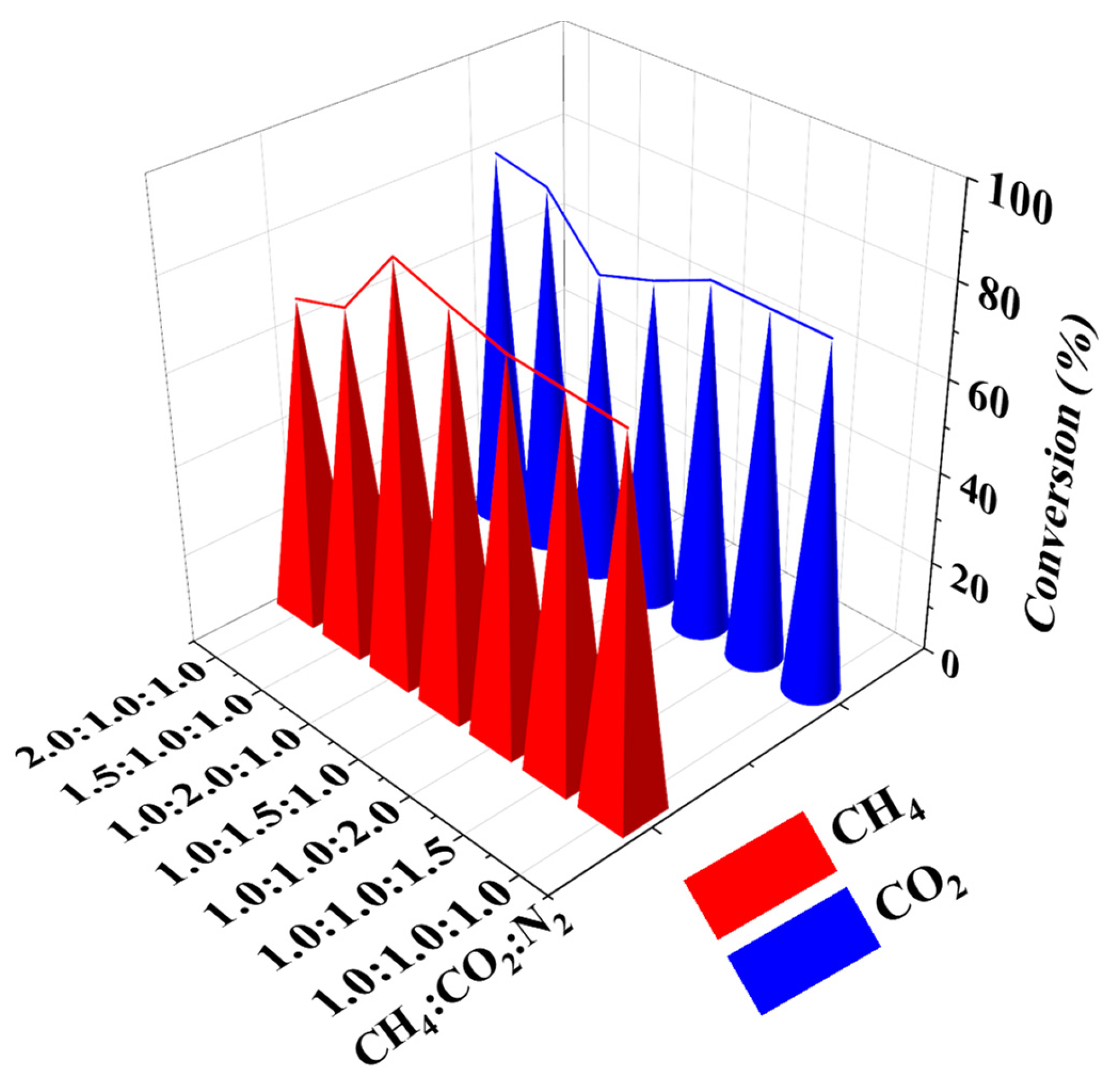

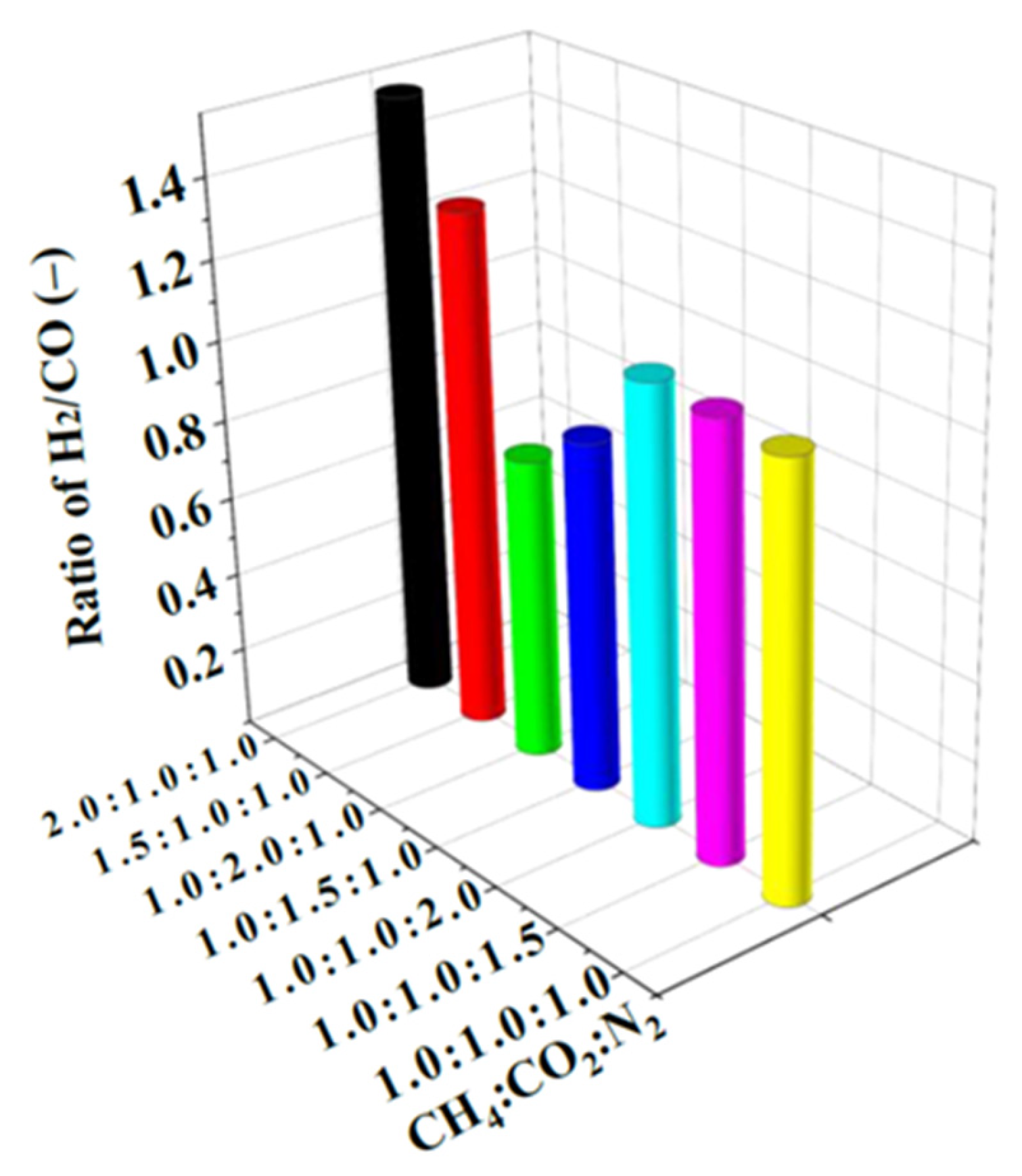

| (a) | (b) | ||
|---|---|---|---|
| Parameters | Value | Parameters | Value |
| Operating pressure, P (Pa) | 101,325 | Operating pressure, P (Pa) | 101,325 |
| Operating temperature, T (K) | 723–923 | Operating temperature, T (K) | 773 |
| Gas density, ρg (kg/m3) | 1.2 | Gas density, ρg (kg/m3) | 0.456 |
| Gas viscosity, μ (Pa·s) | 1.8 × 10−5 | Gas viscosity, μ (Pa·s) | 3.62 × 10−5 |
| Particle density, ρp (kg/m3) | 1500 | Particle density, ρp (kg/m3) | 1250 |
| Average particle diameter, (mm) | 0.32 | Particle diameter, dp (μm) | 106–180 |
| Particle volume fraction at close pack | 0.6 | Particle volume fraction at close pack | 0.2 |
| CH4/CO2 feed ratio | 1:1 | CH4/CO2 feed ratio | 1:1 |
| CH4/N2 feed ratio | 1:8 | CH4/N2 feed ratio | 1:1.3 |
| Diameter, D (m) | 0.008 | Diameter, D (m) | 0.03 |
| Length, L (m) | 0.22 | Length, L (m) | 0.03 |
| Inlet flow rate, mL/min | 52.2 | Column height, H (m) | 0.3 |
| Drag model | WenYu-Ergun [42] | Static bed height, Hs (m) | 0.15 |
| - | Superficial gas Ug velocity, (m/s) | 0.0064–0.15 | |
| Drag model | EMMS [43] | ||
| Bed | P (bar) | Ug (m/s) | T (K) | CH4:CO2:N2 (Mole) | XCH4, Exp. | XCH4, Sim. | Coke Content (gc/gcat/min/103) |
|---|---|---|---|---|---|---|---|
| Packed bed | 1.0 | 0.005 | 773.0 | 1:1:1.3 | - | 26.6% | 2.30 |
| Bubbling fluidized bed | 1.0 | 0.006 | 773.0 | 1:1:1.3 | 21.0% | 29.7% | 1.92 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Otaibi, F.; Xiao, H.; Berrouk, A.S.; Polychronopoulou, K. Numerical Study of Dry Reforming of Methane in Packed and Fluidized Beds: Effects of Key Operating Parameters. ChemEngineering 2023, 7, 57. https://doi.org/10.3390/chemengineering7030057
Al-Otaibi F, Xiao H, Berrouk AS, Polychronopoulou K. Numerical Study of Dry Reforming of Methane in Packed and Fluidized Beds: Effects of Key Operating Parameters. ChemEngineering. 2023; 7(3):57. https://doi.org/10.3390/chemengineering7030057
Chicago/Turabian StyleAl-Otaibi, Fahad, Hongliang Xiao, Abdallah S. Berrouk, and Kyriaki Polychronopoulou. 2023. "Numerical Study of Dry Reforming of Methane in Packed and Fluidized Beds: Effects of Key Operating Parameters" ChemEngineering 7, no. 3: 57. https://doi.org/10.3390/chemengineering7030057
APA StyleAl-Otaibi, F., Xiao, H., Berrouk, A. S., & Polychronopoulou, K. (2023). Numerical Study of Dry Reforming of Methane in Packed and Fluidized Beds: Effects of Key Operating Parameters. ChemEngineering, 7(3), 57. https://doi.org/10.3390/chemengineering7030057