Invertase Immobilization on Magnetite Nanoparticles for Efficient Fructooligosaccharide Generation: A Comprehensive Kinetic Analysis and Reactor Design Strategy
Abstract
1. Introduction
2. Modeling Approach
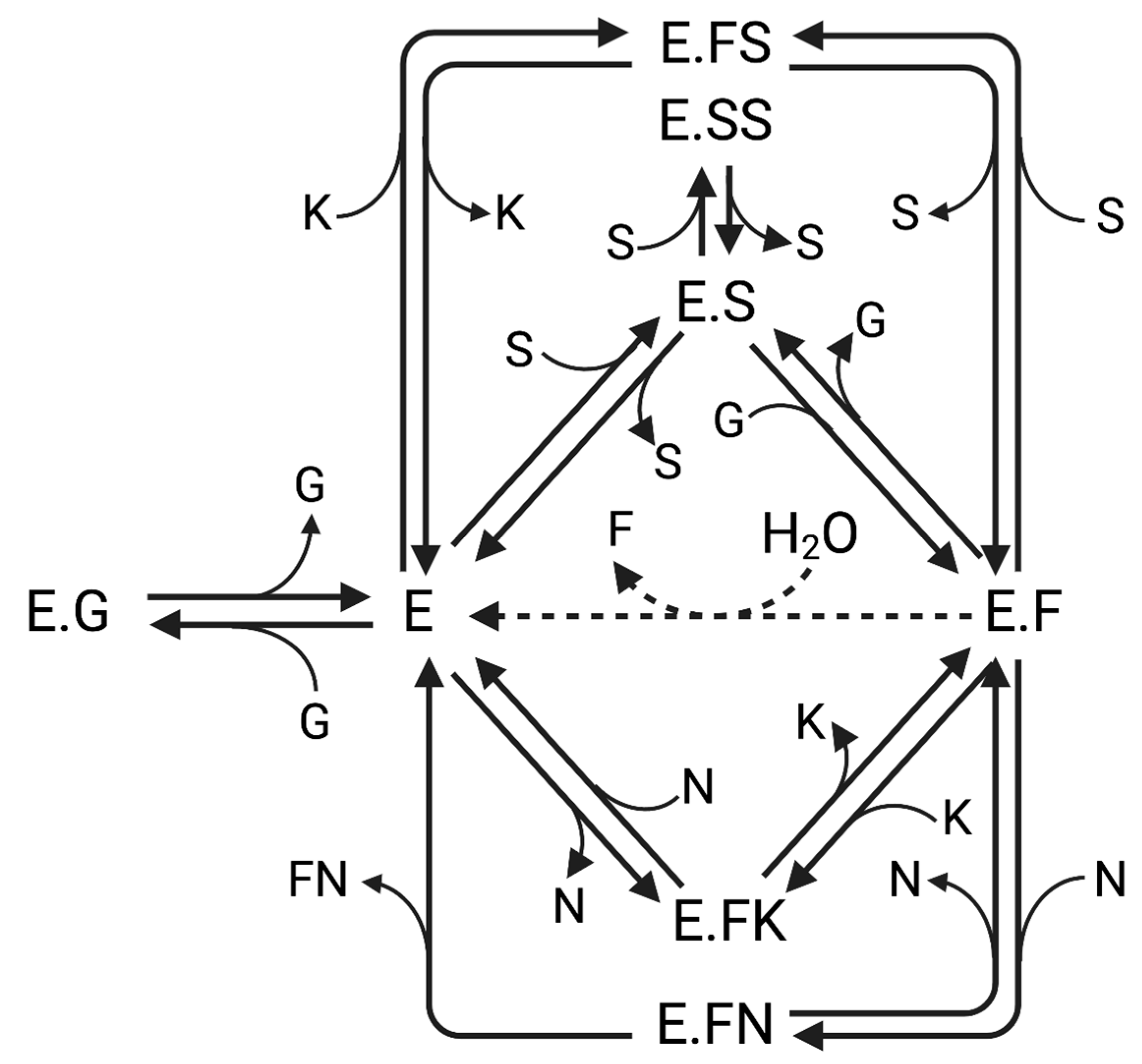
2.1. Hydrolysis and Transfructosylation Reaction Modeling
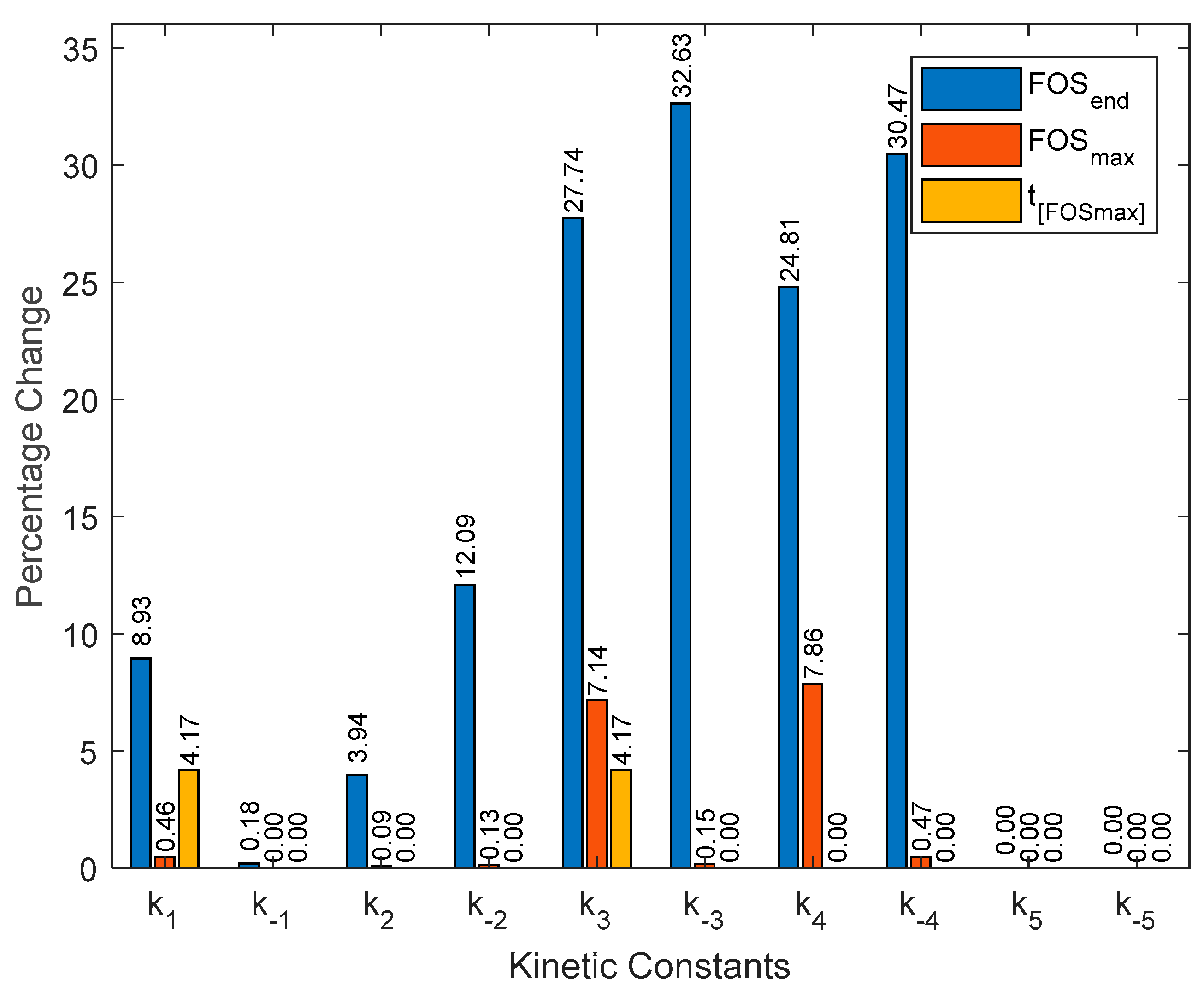
2.2. Kinetic Parameters Sensitivity Analysis
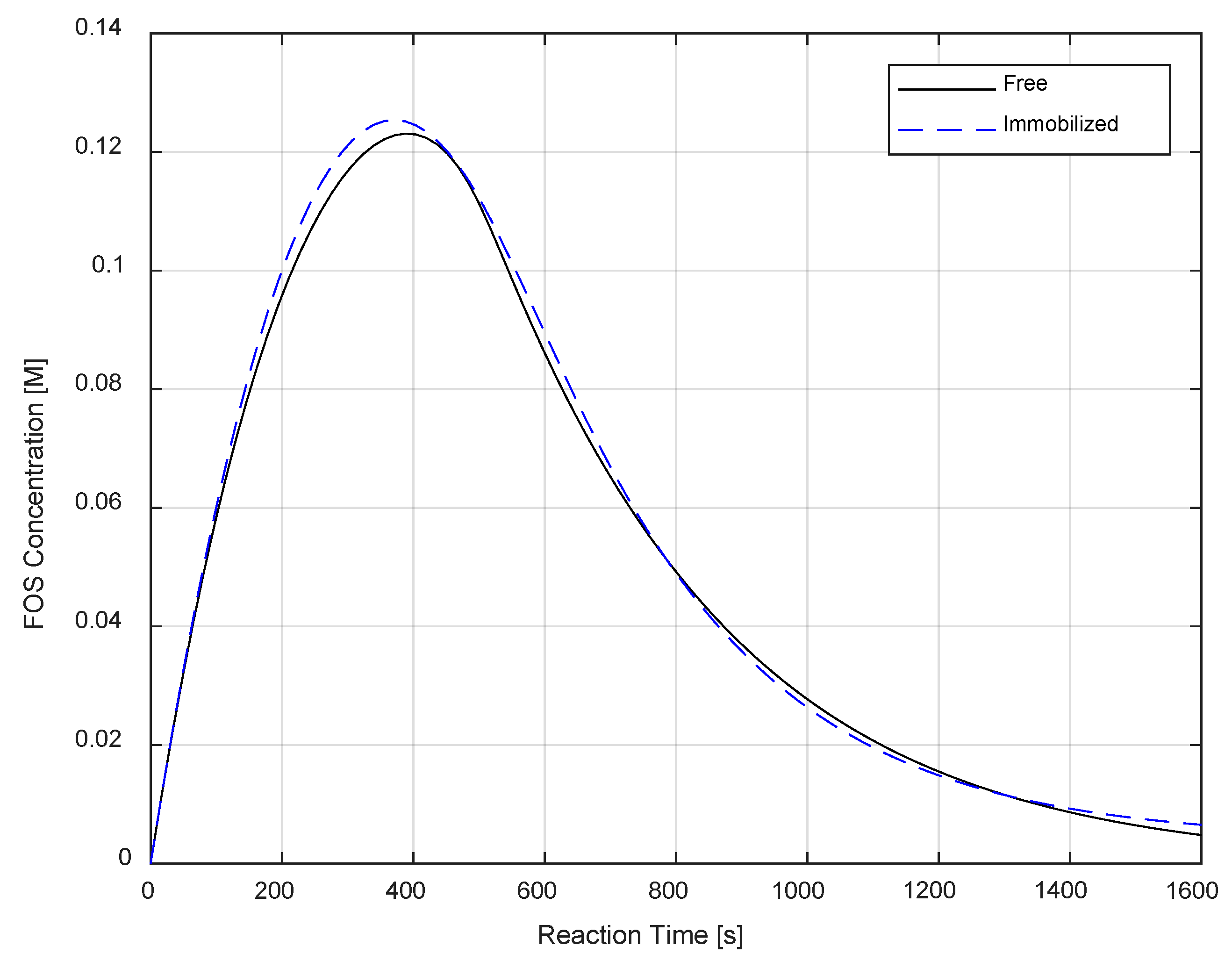
2.3. Immobilized Kinetic Parameter Estimation
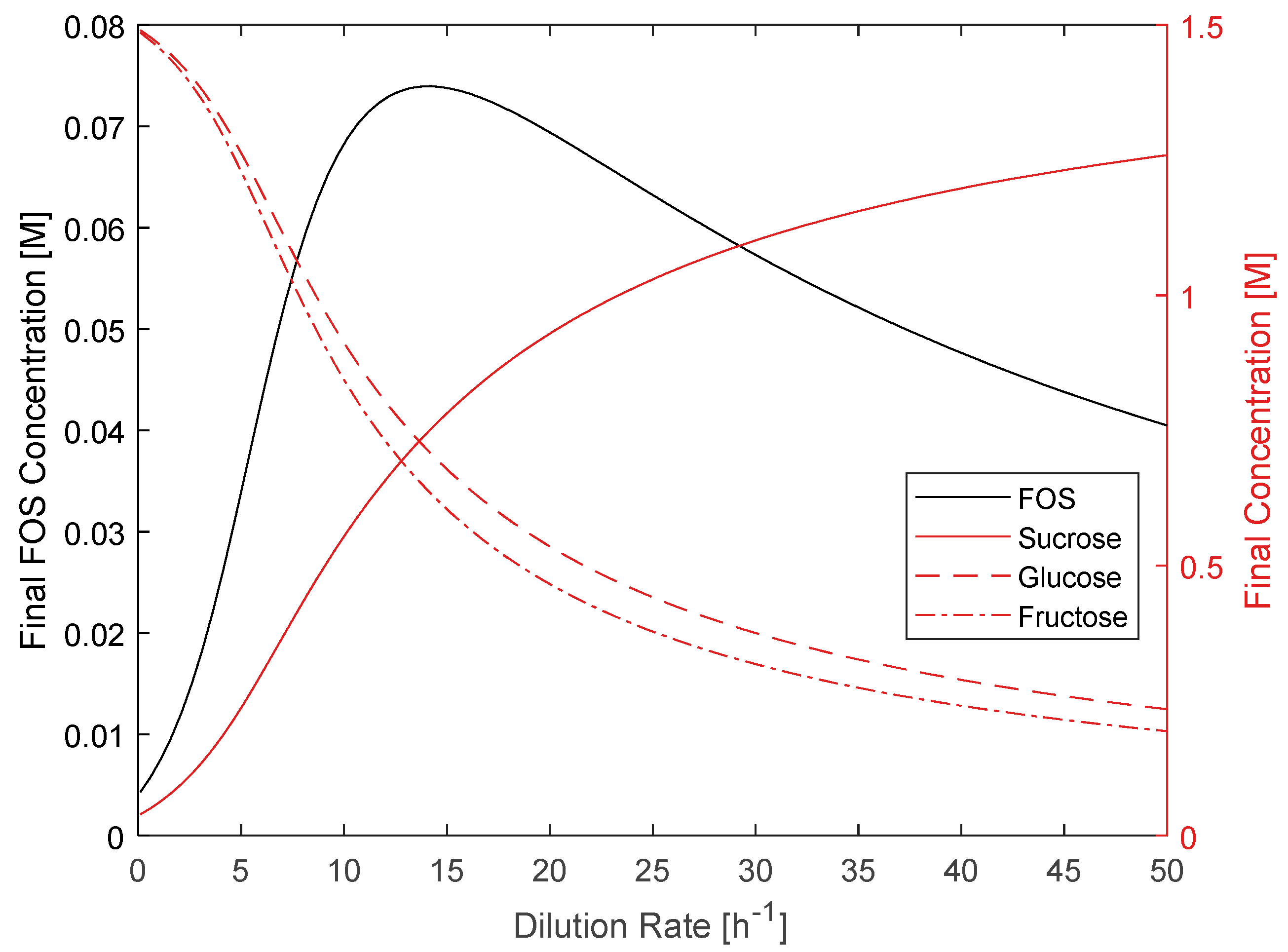
2.4. CSTR Modeling
2.5. Glucose Inhibition Modeling
2.6. Glucose Inhibition: Batch Model
2.7. Glucose Inhibition: CSTR Model
3. Results and discussion
3.1. Hydrolysis and Transfructosylation Reaction
3.2. Kinetic Parameters Sensitivity Analysis
3.3. Immobilized Kinetic Parameter Estimation
3.4. CSTR Modeling
3.5. Glucose Inhibition Modeling
3.5.1. Glucose Inhibition: Batch Model
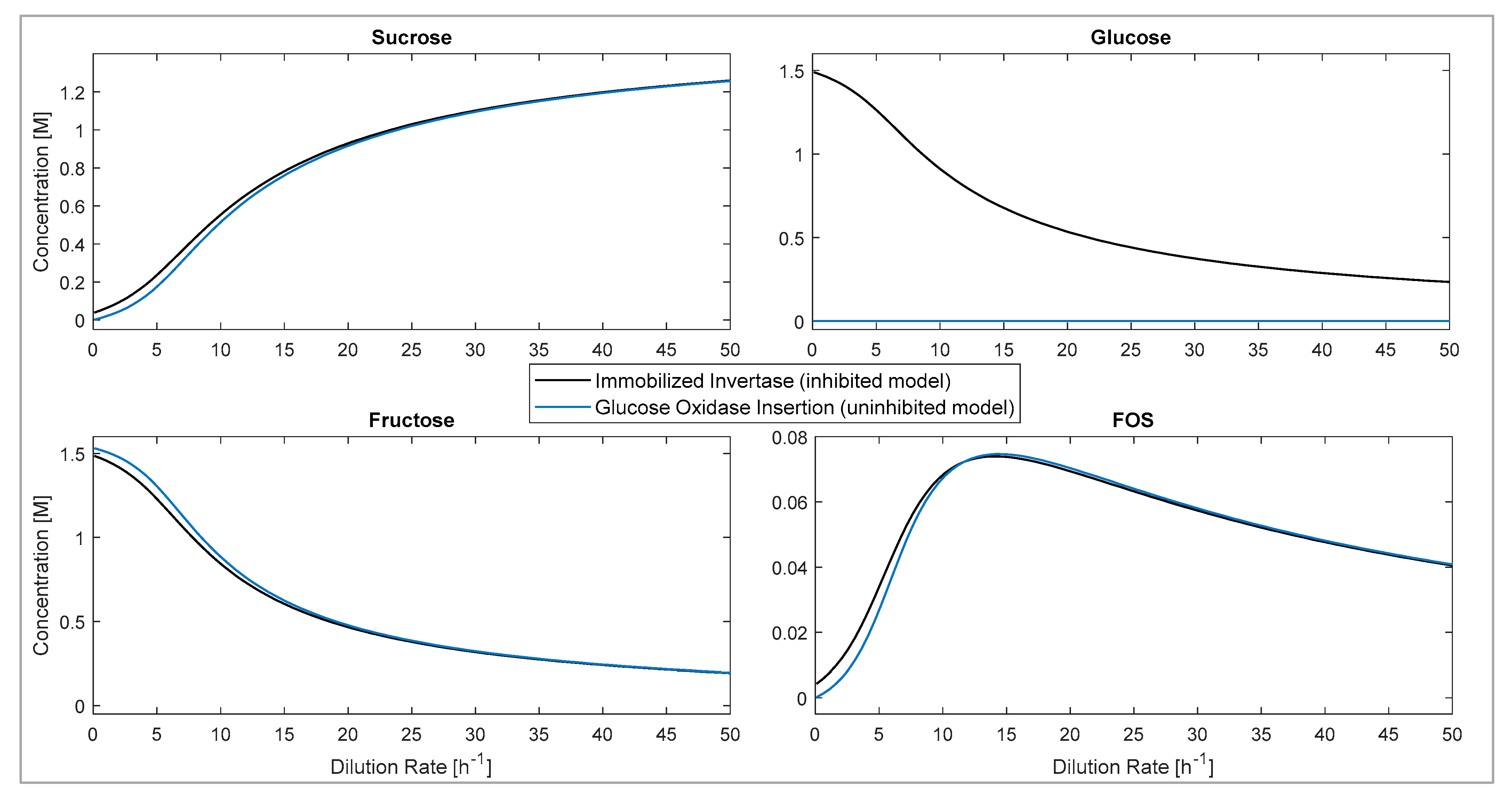
3.5.2. Glucose Inhibition: CSTR Model
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Khandekar, D.C.; Palai, T.; Agarwal, A.; Bhattacharya, P.K. Kinetics of sucrose conversion to fructo-oligosaccharides using enzyme (invertase) under free condition. Bioprocess Biosyst. Eng. 2014, 37, 2529–2537. [Google Scholar] [CrossRef] [PubMed]
- Chen, G.; Li, C.; Chen, K. Fructooligosaccharides: A Review on Their Mechanisms of Action and Effects. In Studies in Natural Products Chemistry; Elsevier: Amsterdam, The Netherlands, 2016; Volume 48, ISBN 9780444636027. [Google Scholar]
- Lafraya, Á.; Sanz-Aparicio, J.; Polaina, J.; Marín-Navarro, J. Fructo-oligosaccharide synthesis by mutant versions of Saccharomyces cerevisiae invertase. Appl. Environ. Microbiol. 2011, 77, 6148–6157. [Google Scholar] [CrossRef] [PubMed]
- Kulshrestha, S.; Tyagi, P.; Sindhi, V.; Yadavilli, K.S. Invertase and its applications—A brief review. J. Pharm. Res. 2013, 7, 792–797. [Google Scholar] [CrossRef]
- Veana, F.; Flores-Gallegos, A.C.; Gonzalez-Montemayor, A.M.; Michel-Michel, M.; Lopez-Lopez, L.; Aguilar-Zarate, P.; Ascacio-Valdés, J.A.; Rodríguez-Herrera, R. Invertase: An enzyme with importance in confectionery food industry. In Enzymes in Food Technology; Springer: Singapore, 2018; pp. 187–212. [Google Scholar] [CrossRef]
- Vega, R.; Zuniga-Hansen, M.E. A new mechanism and kinetic model for the enzymatic synthesis of short-chain fructooligosaccharides from sucrose. Biochem. Eng. J. 2014, 82, 158–165. [Google Scholar] [CrossRef]
- Avigad, G.; Dey, P.M. Carbohydrate Metabolism: Storage Carbohydrates; Academics Press: San Diego, CA, USA, 1997; ISBN 0122146743. [Google Scholar]
- Michel, M.R.; Rodríguez-Jasso, R.M.; Aguilar, C.N.; Gonzalez-Herrera, S.M.; Flores-Gallegos, A.C.; Rodríguez-Herrera, R. Fructosyltransferase Sources, Production. In Probiotics and Prebiotics in Human Nutrition and Health; InTech: Rijeka, Croatia, 2016. [Google Scholar] [CrossRef]
- Gupta, M.N.; Kaloti, M.; Kapoor, M.; Solanki, K. Nanomaterials as matrices for enzyme immobilization. Artif. Cells Blood Substit. Biotechnol. 2011, 39, 98–109. [Google Scholar] [CrossRef]
- Walker, J.M.; Ditor, S.E.E. Immobilization of Enzymes and Cells, 2nd ed.; Guisan, J.M., Ed.; Humana Press: Madrid, Spain, 2006; ISBN 1588292908. [Google Scholar]
- Robinson, P.K. Enzymes: Principles and biotechnological applications. Essays Biochem. 2015, 59, 1–41. [Google Scholar] [CrossRef]
- Tischer, W.; Kasche, V. Immobilized enzymes: Crystals or carriers? Trends Biotechnol. 1999, 17, 326–335. [Google Scholar] [CrossRef]
- Valerio, S.G.; Alves, J.S.; Klein, M.P.; Rodrigues, R.C.; Hertz, P.F. High operational stability of invertase from Saccharomyces cerevisiae immobilized on chitosan nanoparticles. Carbohydr. Polym. 2013, 92, 462–468. [Google Scholar] [CrossRef]
- Cabrera, M.P.; Assis, C.R.D.; Neri, D.F.M.; Pereira, C.F.; Soria, F.; Carvalho, L.B. High sucrolytic activity by invertase immobilized onto magnetic diatomaceous earth nanoparticles. Biotechnol. Rep. 2017, 14, 38–46. [Google Scholar] [CrossRef]
- Donadelli, J.A.; García Einschlag, F.S.; Laurenti, E.; Magnacca, G.; Carlos, L. Soybean peroxidase immobilized onto silica-coated superparamagnetic iron oxide nanoparticles: Effect of silica layer on the enzymatic activity. Colloids Surf. B Biointerfaces 2018, 161, 654–661. [Google Scholar] [CrossRef]
- Minteer, S.D. Enzyme Stabilization and Immobilization. Methods Mol. Biol. 2011, 679, 230. [Google Scholar] [CrossRef]
- Fortes, C.C.S.; Daniel-da-Silva, A.L.; Xavier, A.M.R.B.; Tavares, A.P.M. Optimization of enzyme immobilization on functionalized magnetic nanoparticles for laccase biocatalytic reactions. Chem. Eng. Process. Process Intensif. 2017, 117, 1–8. [Google Scholar] [CrossRef]
- Ramírez-acosta, C.M.; Cifuentes, J.; Castellanos, M.C.; Moreno, R.J.; Muñoz-camargo, C.; Cruz, J.C.; Reyes, L.H. Ph-responsive, cell-penetrating, core/shell magnetite/silver nanoparticles for the delivery of plasmids: Preparation, characterization, and preliminary in vitro evaluation. Pharmaceutics 2020, 12, 561. [Google Scholar] [CrossRef] [PubMed]
- Torres-Vanegas, J.D.; Cifuentes, J.; Puentes, P.R.; Quezada, V.; Garcia-Brand, A.J.; Cruz, J.C.; Reyes, L.H. Assessing cellular internalization and endosomal escape abilities of novel BUFII-Graphene oxide nanobioconjugates. Front. Chem. 2022, 10, 974218. [Google Scholar] [CrossRef]
- Gonzalez-Melo, C.; Garcia-Brand, A.J.; Quezada, V.; Reyes, L.H.; Muñoz-Camargo, C.; Cruz, J.C. Highly efficient synthesis of type B gelatin and low molecular weight chitosan nanoparticles: Potential applications as bioactive molecule carriers and cell-penetrating agents. Polymers 2021, 13, 4078. [Google Scholar] [CrossRef]
- Ramírez-Acosta, C.M.; Cifuentes, J.; Cruz, J.C.; Reyes, L.H. Patchy Core/Shell, Magnetite/Silver Nanoparticles via Green and Facile Synthesis: Routes to Assure Biocompatibility. Nanomaterials 2020, 10, 1857. [Google Scholar] [CrossRef]
- Popescu, R.C.; Andronescu, E.; Vasile, B.S. Recent advances in magnetite nanoparticle functionalization for nanomedicine. Nanomaterials 2019, 9, 1791. [Google Scholar] [CrossRef]
- Can, K.; Ozmen, M.; Ersoz, M. Immobilization of albumin on aminosilane modified superparamagnetic magnetite nanoparticles and its characterization. Colloids Surf. B Biointerfaces 2009, 71, 154–159. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, H.H.; Kim, M. An Overview of Techniques in Enzyme Immobilization. Appl. Sci. Converg. Technol. 2017, 26, 157–163. [Google Scholar] [CrossRef]
- Gürsel, A.; Alkan, S.; Toppare, L.; Yaǧci, Y. Immobilization of invertase and glucose oxidase in conducting H-type polysiloxane/polypyrrole block copolymers. React. Funct. Polym. 2003, 57, 57–65. [Google Scholar] [CrossRef]
- Cirpan, A.; Alkan, S.; Toppare, L.; Hepuzer, Y.; Yagci, Y. Immobilization of invertase in conducting copolymers of 3-methylthienyl methacrylate. Bioelectrochemistry 2003, 59, 29–33. [Google Scholar] [CrossRef] [PubMed]
- Waifalkar, P.P.; Parit, S.B.; Chougale, A.D.; Sahoo, S.C.; Patil, P.S.; Patil, P.B. Immobilization of invertase on chitosan coated γ-Fe2O3 magnetic nanoparticles to facilitate magnetic separation. J. Colloid Interface Sci. 2016, 482, 159–164. [Google Scholar] [CrossRef] [PubMed]
- Vargas, G.A.R.; Cuellar, J.C.R. Sucrose hydrolysis by invertase of Saccharomyces cerevisiae immobilized on cobalt ferrite magnetic nanoparticles. Acta Agron. 2019, 68, 115–125. [Google Scholar] [CrossRef]
- de Souza Soares, A.; Augusto, P.E.D.; Júnior, B.R.D.C.L.; Nogueira, C.A.; Vieira, É.N.R.; de Barros, F.A.R.; Stringheta, P.C.; Ramos, A.M. Ultrasound assisted enzymatic hydrolysis of sucrose catalyzed by invertase: Investigation on substrate, enzyme and kinetics parameters. Lwt 2019, 107, 164–170. [Google Scholar] [CrossRef]
- Vu, T.K.H.; Le, V.V.M. Biochemical studies on the immobilization of the enzyme invertase (EC.3.2.1.26) in alginate gel and its kinetics. Int. Food Res. J. 2008, 15, 73–78. [Google Scholar]
- Azodi, M.; Falamaki, C.; Mohsenifar, A. Sucrose hydrolysis by invertase immobilized on functionalized porous silicon. J. Mol. Catal. B Enzym. 2011, 69, 154–160. [Google Scholar] [CrossRef]
- Szymańska, K.; Pudło, W.; Mrowiec-Białoń, J.; Czardybon, A.; Kocurek, J.; Jarzȩbski, A.B. Immobilization of invertase on silica monoliths with hierarchical pore structure to obtain continuous flow enzymatic microreactors of high performance. Microporous Mesoporous Mater. 2013, 170, 75–82. [Google Scholar] [CrossRef]
- Alvarado-Huallanco, M.B.; Maugeri Filho, F. Kinetic studies and modelling of the production of fructooligosaccharides by fructosyltransferase from Rhodotorula sp. Catal. Sci. Technol. 2011, 1, 1043–1050. [Google Scholar] [CrossRef]
- Kim, M.H.; In, M.J.; Cha, H.J.; Yoo, Y.J. An empirical rate equation for the fructooligosaccharide-producing reaction catalyzed by β-fructofuranosidase. J. Ferment. Bioeng. 1996, 82, 458–463. [Google Scholar] [CrossRef]
- Yun, J.W.; Kim, D.H.; Kim, K.W. Theoretical calculation of the sugar concentrations during enzymatic production of fructooligosaccharides. Biotechnol. Tech. 1996, 10, 871–874. [Google Scholar] [CrossRef]
- Lee, W.C.; Chiang, C.J.; Tsai, P.Y. Kinetic modeling of fructo-oligosaccharide production catalyzed by immobilized β-fructofuranosidase. Ind. Eng. Chem. Res. 1999, 38, 2564–2570. [Google Scholar] [CrossRef]
- Shuler, M.; Kargi, F.; DeLisa, M. Bioprocess Engineering: Basic Concepts; Prentice Hall: Hoboken, NJ, USA, 1992; Volume 22. [Google Scholar]
- MathWorks (2023) Solve Stiff ODEs, MATLAB & Simulink. Available online: https://www.mathworks.com/help/matlab/math/solve-stiff-odes.html (accessed on 8 May 2023).
- Garcia-Galan, C.; Berenguer-Murcia, Á.; Fernandez-Lafuente, R.; Rodrigues, R.C. Potential of different enzyme immobilization strategies to improve enzyme performance. Adv. Synth. Catal. 2011, 353, 2885–2904. [Google Scholar] [CrossRef]
- Tao, Z.; Raffel, R.A.; Souid, A.K.; Goodisman, J. Kinetic studies on enzyme-catalyzed reactions: Oxidation of glucose, decomposition of hydrogen peroxide and their combination. Biophys. J. 2009, 96, 2977–2988. [Google Scholar] [CrossRef] [PubMed]
- Gibson, Q.H.; Swoboda, B.E.P.; Massey, V. Kinetics of Action of Glucose. J. Biol. Chem. 1964, 239, 3927–3934. [Google Scholar] [CrossRef]
- Chastang, T.; Pozzobon, V.; Taidi, B.; Courot, E.; Clément, C.; Pareau, D. Resveratrol production by grapevine cells in fed-batch bioreactor: Experiments and modelling. Biochem. Eng. J. 2018, 131, 9–16. [Google Scholar] [CrossRef]
- Cruz, A.J.G.; Silva, A.S.; Araujo, M.L.G.C.; Giordano, R.C.; Hokka, C.O. Modelling and optimization of the cephalosporin C production bioprocess in a fed-batch bioreactor with invert sugar as substrate. Chem. Eng. Sci. 1999, 54, 3137–3142. [Google Scholar] [CrossRef]
- Germec, M.; Turhan, I. Kinetic modeling and sensitivity analysis of inulinase production in large-scale stirred tank bioreactor with sugar beet molasses-based medium. Biochem. Eng. J. 2021, 176, 108201. [Google Scholar] [CrossRef]
- de Moura, F.A.; Macagnan, F.T.; da Silva, L.P. Oligosaccharide production by hydrolysis of polysaccharides: A review. Int. J. Food Sci. Technol. 2015, 50, 275–281. [Google Scholar] [CrossRef]
- Zi, Z. Sensitivity analysis approaches applied to systems biology models. IET Syst. Biol. 2011, 5, 336–346. [Google Scholar] [CrossRef]
- Marino, S.; Hogue, I.B.; Ray, C.J.; Kirschner, D.E. A methodology for performing global uncertainty and sensitivity analysis in systems biology. J. Theor. Biol. 2008, 254, 178–196. [Google Scholar] [CrossRef]
- Ayhan, F.; Ayhan, H.; Pişkin, E.; Tanyolac, A. Optimization of urease immobilization onto non-porous HEMA incorporated poly (EGDMA) microbeads and estimation of kinetic parameters. Bioresour. Technol. 2002, 81, 131–140. [Google Scholar] [CrossRef] [PubMed]
- Carrara, C.R.; Rubiolo, A.C. Determination of kinetics parameters for free and immobilized β-galactosidase. Process Biochem. 1996, 31, 243–248. [Google Scholar] [CrossRef]
- Li, C.; Lin, J.; Gao, L.; Lin, H.; Lin, J. Modeling and simulation of enzymatic gluconic acid production using immobilized enzyme and CSTR–PFTR circulation reaction system. Biotechnol. Lett. 2018, 40, 649–657. [Google Scholar] [CrossRef] [PubMed]
- Santos-Moriano, P.; Woodley, J.M.; Plou, F.J. Continuous production of chitooligosaccharides by an immobilized enzyme in a dual-reactor system. J. Mol. Catal. B Enzym. 2016, 133, 211–217. [Google Scholar] [CrossRef]
- IwAsAKI, K.; Inoue, M.; MATsUBARA, Y. Continuous hydrolysis of pectate by immobilized endo-polygalacturonase in a continuously stirred tank reactor. Biosci. Biotechnol. Biochem. 1998, 62, 262–267. [Google Scholar] [CrossRef]
- Wapshott-Stehli, H.L.; Grunden, A.M. In situ H2O2 generation methods in the context of enzyme biocatalysis. Enzyme Microb. Technol. 2021, 145, 109744. [Google Scholar] [CrossRef]
- Freakley, S.J.; Kochius, S.; van Marwijk, J.; Fenner, C.; Lewis, R.J.; Baldenius, K.; Marais, S.S.; Opperman, D.J.; Harrison, S.T.L.; Alcalde, M.; et al. A chemo-enzymatic oxidation cascade to activate C–H bonds with in situ generated H2O2. Nat. Commun. 2019, 10, 4178. [Google Scholar] [CrossRef]



| Parameters | Free | Immobilized |
|---|---|---|
| 1525.72 | 1485.41 | |
| 0.04 | 195.75 | |
| 100.20 | 109.80 | |
| 26.02 | 4.46 | |
| 13.57 | 11.26 | |
| 43.20 | 35.16 | |
| 1.96 | 1.91 | |
| 80.10 | 81.41 | |
| 0.00 | ||
| 7.79 | 7.80 |
| Parameters | Value [41] |
|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Polanía Melo, D.; Hernández Bravo, A.; Cruz, J.C.; Reyes, L.H. Invertase Immobilization on Magnetite Nanoparticles for Efficient Fructooligosaccharide Generation: A Comprehensive Kinetic Analysis and Reactor Design Strategy. ChemEngineering 2023, 7, 55. https://doi.org/10.3390/chemengineering7030055
Polanía Melo D, Hernández Bravo A, Cruz JC, Reyes LH. Invertase Immobilization on Magnetite Nanoparticles for Efficient Fructooligosaccharide Generation: A Comprehensive Kinetic Analysis and Reactor Design Strategy. ChemEngineering. 2023; 7(3):55. https://doi.org/10.3390/chemengineering7030055
Chicago/Turabian StylePolanía Melo, David, Andrés Hernández Bravo, Juan C. Cruz, and Luis H. Reyes. 2023. "Invertase Immobilization on Magnetite Nanoparticles for Efficient Fructooligosaccharide Generation: A Comprehensive Kinetic Analysis and Reactor Design Strategy" ChemEngineering 7, no. 3: 55. https://doi.org/10.3390/chemengineering7030055
APA StylePolanía Melo, D., Hernández Bravo, A., Cruz, J. C., & Reyes, L. H. (2023). Invertase Immobilization on Magnetite Nanoparticles for Efficient Fructooligosaccharide Generation: A Comprehensive Kinetic Analysis and Reactor Design Strategy. ChemEngineering, 7(3), 55. https://doi.org/10.3390/chemengineering7030055








