Mathematical Modelling of Muña Leaf Drying (Minthostachys mollis) for Determination of the Diffusion Coefficient, Enthalpy, and Gibbs Free Energy
Abstract
1. Introduction
2. Materials and Methods
2.1. Raw Material
2.2. Raw Material Conditioning
2.3. Drying Process
2.4. Mathematical Models
2.5. Activation Energy and Thermodynamic Properties
2.6. Statistical Analysis
3. Results and Discussion
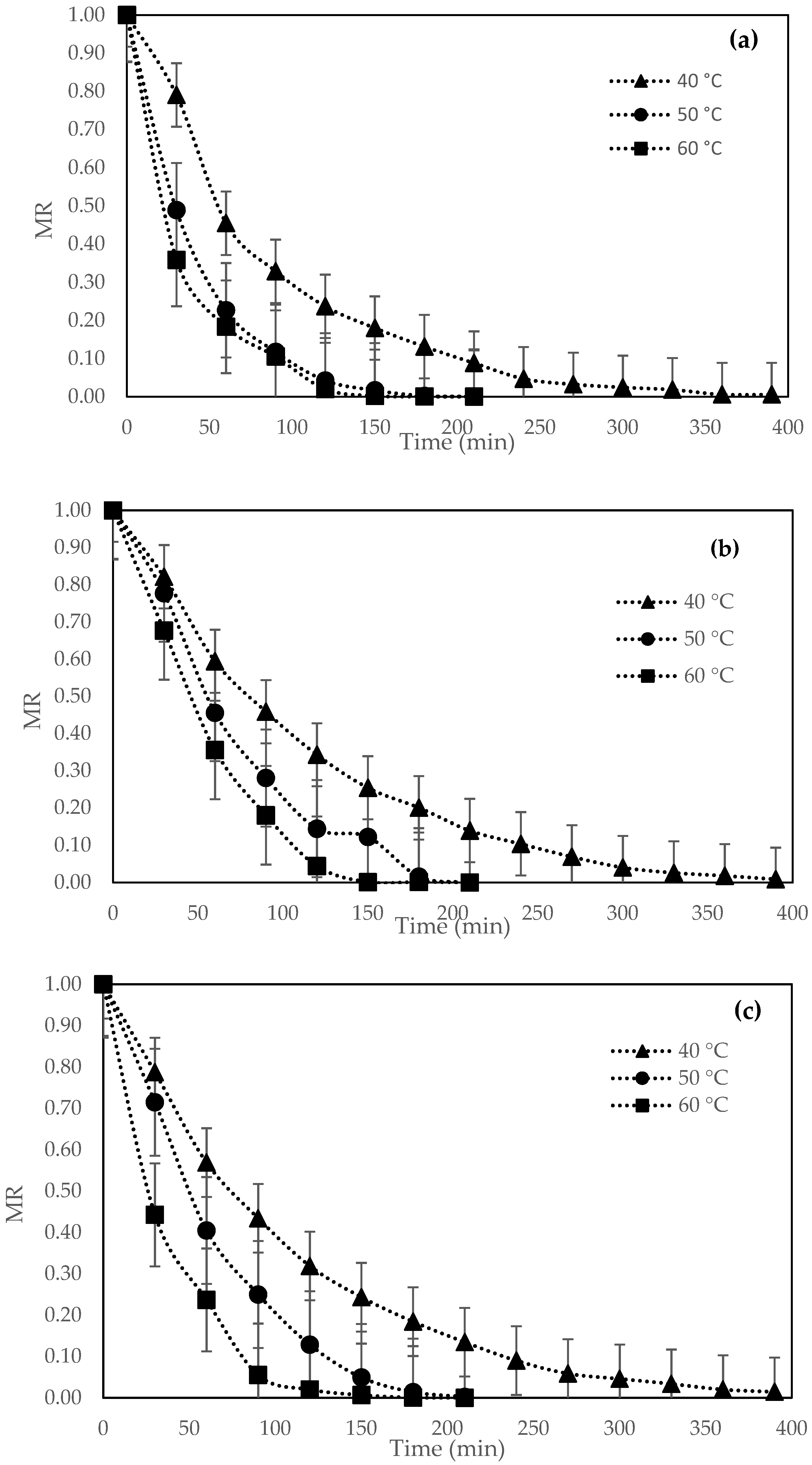
3.1. Drying Kinetic Curves
3.2. Mathematical Modeling of Drying Kinetics
3.3. Diffusion Coefficient, Thermodynamic Properties and Activation Energy
3.3.1. Water Diffusion Coefficient
3.3.2. Thermodynamic Properties
3.3.3. Activation Energy
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cano, C.; Bonilla, P.; Roque, M.; Ruiz, J. Actividad antimicótica in vitro y metabolitos del aceite esencial de las hojas de Minthostachys mollis (muña). Revista Peruana Medicina Experimental Y Salud Pública 2008, 25, 298–301. [Google Scholar]
- PromPerú—Comisión De Promoción Del Perú Para La Exportación Y El Turismo. Súper Muña. 2021. Available online: https://peru.info/es-pe/superfoods/detalle/super-muna (accessed on 15 August 2022).
- Dalia, P.P.; Park, J.S.; Moscoso, M.R.; Salazar-Granara, A. Diferencias en la presencia de alcaloides y fenoles de cinco muestras de muña de expendio informal procedentes de mercados populares en Lima-Perú. Horizonte Médico. Horiz. Médico 2018, 18, 25–29. [Google Scholar]
- Aguirre Tipismana, L.G. Consumo De Plantas Medicinales En Usuarios Del Centro Integral Del Adulto Mayor De La Molina. USMP. 2017. Available online: https://repositorio.usmp.edu.pe/handle/20.500.12727/4398 (accessed on 25 August 2022).
- Instituto Nacional De Estadística E Informática–Perú (INEI). Estimaciones Y Proyecciones De Población, 1950–2050. Boletín De Análisis Demográfico, N° 36, 2017. Available online: http://190.102.131.45/epidemiologia/pdf/interes_2.pdf (accessed on 10 July 2022).
- Roersch, C. Medicinal plants in the Dominican Republic and their possible role in public health care. In Proceedings of the XXIX International Horticultural Congress on Horticulture: Sustaining Lives, Livelihoods and Landscapes (IHC2014): V World Congress on Medicinal and Aromatic Plants and International Symposium on Plants, as Factories of Natural Substances, Edible and Essential Oils, Brisbane, Australia, 17 August 2014; Volume 1125, pp. 249–254. [Google Scholar]
- Fuertes, C.; Murguía, Y. Estudio comparativo del aceite esencial de Minthostachys mollis (Kunth) Griseb “muña” de tres regiones peruanas por cromatografía de gases y espectrometría de masas. Rev. Cienc. E Investig. 2001, 4, 23–39. [Google Scholar] [CrossRef]
- Lemus-Mondaca, R.; Vega-Gálvez, A.; Moraga, N.O.; Astudillo, S. Dehydration of S tevia rebaudiana Bertoni Leaves: Kinetics, Modeling and Energy Features. J. Food Process. Preserv. 2015, 39, 508–520. [Google Scholar] [CrossRef]
- Dorneles, L.D.N.S.; Goneli, A.L.D.; Cardoso, C.A.L.; da Silva, C.B.; Hauth, M.R.; Oba, G.C.; Schoeninger, V. Effect of air temperature and velocity on drying kinetics and essential oil composition of Piper umbellatum L. leaves. Ind. Crops Prod. 2019, 142, 111846. [Google Scholar] [CrossRef]
- Przeor, M.; Flaczyk, E.; Beszterda, M.; Szymandera-Buszka, K.E.; Piechocka, J.; Kmiecik, D.; Szczepaniak, O.; Kobus-cisowska, J.; Jarzębski, M.; Tylewicz, U. Air-drying temperature changes the content of the phenolic acids and flavonols in white mulberry (Morus alba L.) leaves. Ciência Rural 2019, 49. [Google Scholar] [CrossRef]
- Khodja, Y.K.; Dahmoune, F.; Madani, K.; Khettal, B. Conventional method and microwave drying kinetics of Laurus nobilis leaves: Effects on phenolic compounds and antioxidant activity. Braz. J. Food Technol. 2020, 23. [Google Scholar] [CrossRef]
- Bosco, D.; Roche, L.A.; Della Rocca, P.A.; Mascheroni, R.H. Osmodehidrocongelación de batata fortificada con zinc y calcio. Innotec 2018, 23–31. [Google Scholar] [CrossRef]
- Fernando, J.A.K.M.; Amarasinghe, A.D.U.S. Drying kinetics and mathematical modeling of hot air drying of coconut coir pith. SpringerPlus 2016, 5, 807. [Google Scholar] [CrossRef]
- Babu, A.K.; Kumaresan, G.; Raj, V.A.A.; Velraj, R. Review of leaf drying: Mechanism and influencing parameters, drying methods, nutrient preservation, and mathematical models. Renew. Sustain. Energy Rev. 2018, 90, 536–556. [Google Scholar] [CrossRef]
- Rocha, R.P.D.; Melo, E.D.C.; Corbín, J.B.; Berbert, P.A.; Donzeles, S.M.; Tabar, J.A. Cinética del secado de tomillo. Rev. Bras. Eng. Agrícola E Ambient. 2012, 16, 675–683. [Google Scholar] [CrossRef]
- Bahammou, Y.; Tagnamas, Z.; Lamharrar, A.; Idlimam, A. Thin-layer solar drying characteristics of Moroccan horehound leaves (Marrubium vulgare L.) under natural and forced convection solar drying. Sol. Energy 2019, 188, 958–969. [Google Scholar] [CrossRef]
- Jideani, V.A.; Mpotokwana, S.M. Modeling of water absorption of Botswana bambara varieties using Peleg’s equation. J. Food Eng. 2009, 92, 182–188. [Google Scholar] [CrossRef]
- Martins, E.A.; Lage, E.Z.; Goneli, A.L.; Hartmann Filho, C.P.; Lopes, J.G. Cinética de secagem de folhas de timbó (Serjania marginata Casar). Rev. Bras. Eng. Agrícola E Ambient. 2015, 19, 238–244. [Google Scholar] [CrossRef]
- Silva, L.A.; Resende, O.; Virgolino, Z.Z.; Bessa, J.F.V.; Morais, W.A.; Vidal, V.M. Cinética de secagem e difusividade efetiva em folhas de jenipapo (Genipa americana L.). Rev. Bras. De Plantas Med. 2015, 17, 953–963. [Google Scholar] [CrossRef]
- Gasparin, P.P.; Christ, D.; Coelho, S.R.M. Secagem de folhas Mentha piperita em leito fixo utilizando diferentes temperaturas e velocidades de ar. Rev. Ciênc. Agron. 2017, 48, 242–250. [Google Scholar]
- Bensebia, O.; Allia, K. Drying and extraction kinetics of rosemary leaves: Experiments and modeling. J. Essent. Oil-Bear. Plants 2015, 18, 99–111. [Google Scholar] [CrossRef]
- Da Silva, N.C.B.; dos Santos, S.G.; da Silva, D.P.; Silva, I.L.; Rodovalho, R.S. Drying kinetics and thermodynamic properties of boldo (Plectranthus barbatus Andrews) leaves. Científica 2019, 47, 1–7. [Google Scholar] [CrossRef]
- Quequeto, W.D.; Siqueira, V.C.; Mabasso, G.A.; Isquierdo, E.P.; Leite, R.A.; Ferraz, L.R.; Hoscher, R.H.; Schoeninger, V.; Jordan, R.A.; Goneli, A.L.D.; et al. Mathematical modeling of thin-layer drying kinetics of Piper aduncum L. leaves. J. Agric. Sci. 2019, 11, 225–235. [Google Scholar] [CrossRef]
- Martins, E.A.; Goneli, A.L.; Goncalves, A.A.; Hartmann Filho, C.P.; Siqueira, V.C.; Oba, G.C. Drying kinetics of blackberry leaves. Rev. Bras. Eng. Agrícola E Ambient. 2018, 22, 570–576. [Google Scholar] [CrossRef]
- Eneighe, S.A.; Dzelagha, F.B.; Nde, D.B. Production of an herbal green tea from ambang (Xymalos monospora) leaves: Influence of drying method and temperature on the drying kinetics and tea quality. J. Food Sci. Technol. 2020, 57, 3381–3389. [Google Scholar] [CrossRef]
- Doymaz, I. Thin-layer drying behaviour of mint leaves. J. Food Eng. 2006, 74, 370–375. [Google Scholar] [CrossRef]
- Kaya, A.; Aydın, O. An experimental study on drying kinetics of some herbal leaves. Energy Convers. Manag. 2009, 50, 118–124. [Google Scholar] [CrossRef]
- Doymaz, İ.; Tugrul, N.; Pala, M. Drying characteristics of dill and parsley leaves. J. Food Eng. 2006, 77, 559–565. [Google Scholar] [CrossRef]
- Moreira, R.; Chenlo, F.; Torres, M.D.; Vallejo, N. Thermodynamic analysis of experimental sorption isotherms of loquat and quince fruits. J. Food Eng. 2008, 88, 514–521. [Google Scholar] [CrossRef]

| Model Name | Model Equation | Equation |
|---|---|---|
| Page | MR = exp (−k·tn) | (1) |
| Modified Page | MR = exp (−k·t)n | (2) |
| Midilli | MR = a·exp (−k·tn) + b·t | (3) |
| Lewis | MR = exp (−k·t) | (4) |
| Wang and Singh | MR = 1 + (a·t) + (b·t2) | (5) |
| Logarithmic | MR = a·exp (-k·t) + c | (6) |
| Peleg | MR = (1 − t)/(k1 + (k2·t2)) | (7) |
| Henderson and Pabis | MR = a·exp (−k·t) | (8) |
| Moisture ratio | MR = (wt − we)/(wo − we) | (9) |
| Sample | Model | Statistics | Parameters | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| r2 | SSE | MSE | RMSE | ||||||||||
| SB | Midilli | 0.425 | 5.269 | 0.258 | 0.499 | a | 1.085 | B | 7.473 | k | −57.716 | n | −5.971 |
| Logarithmic | 0.994 | 4.117 | 0.274 | 0.524 | a | 0.575 | C | 1.563 | k | 0.012 | |||
| Page | 0.924 | 0.073 | 0.004 | 0.062 | k | 51.380 | N | 51.380 | |||||
| Modified Page | 0.521 | 0.003 | 0.000 | 0.014 | k | 2.618 | N | −1.036 | |||||
| Henderson and Pabis | 0.700 | 0.131 | 0.009 | 0.093 | a | 1.908 | K | 0.001 | |||||
| Wang and Singh | 0.597 | 4.117 | 0.257 | 0.507 | a | 0.006 | B | 0.000 | |||||
| Peleg | 0.659 | 2.616 | 0.174 | 0.418 | k1 | 0.473 | k2 | −0.606 | |||||
| Lewis | 0.465 | 0.233 | 0.016 | 0.125 | k | −0.001 | |||||||
| Fick’s second law | 0.923 | 0.0523 | 0.073 | 0.042 | Deff | 3.182 × 10−10 | |||||||
| BAA | Midilli | 0.963 | 0.114 | 0.006 | 0.078 | a | −0.585 | B | 20.399 | k | −24.721 | n | −3.494 |
| Logarithmic | 0.998 | 0.001 | 0.000 | 0.007 | a | 0.578 | C | 1.555 | k | 0.009 | |||
| Page | 0.405 | 46.497 | 3.100 | 1.761 | k | 51.380 | N | 51.380 | |||||
| Modified Page | 0.627 | 4.539 | 0.303 | 0.550 | k | 2.618 | n | −1.028 | |||||
| Henderson and Pabis | 0.806 | 0.089 | 0.006 | 0.077 | a | 0.001 | k | 1.959 | |||||
| Wang and Singh | 0.556 | 2.768 | 0.185 | 0.430 | a | 0.006 | b | 0.000 | |||||
| Peleg | 0.381 | 0.284 | 0.019 | 0.138 | k1 | 0.474 | k2 | −0.595 | |||||
| Lewis | 0.704 | 4.539 | 0.284 | 0.533 | k | −0.001 | |||||||
| Fick’s second law | 0.921 | 0.146 | 0.0352 | 0.077 | Deff | 3.098 × 10−10 | |||||||
| B60 | Midilli | 0.969 | 0.114 | 0.006 | 0.078 | a | −0.449 | b | 27.008 | k | −50.981 | n | −5.544 |
| Logarithmic | 0.999 | 0.000 | 0.000 | 0.005 | a | 0.578 | c | 1.553 | k | 0.009 | |||
| Page | 0.433 | 45.937 | 3.062 | 1.750 | k | 5.682 | n | 5.682 | |||||
| Modified Page | 0.604 | 4.419 | 0.295 | 0.543 | k | 2.618 | n | −1.031 | |||||
| Henderson and Pabis | 0.790 | 0.096 | 0.006 | 0.080 | a | 1.946 | k | 0.001 | |||||
| Wang and Singh | 0.572 | 2.719 | 0.181 | 0.426 | a | 0.006 | b | 0.000 | |||||
| Peleg | 0.409 | 0.270 | 0.018 | 0.134 | k1 | 0.473 | k2 | −0.599 | |||||
| Lewis | 0.688 | 4.419 | 0.276 | 0.526 | k | −0.001 | |||||||
| Fick’s second law | 0.944 | 0.029 | 0.230 | 0.012 | Deff | 3.075 × 10−10 | |||||||
| Sample | Model | Statistics | Parameters | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| r2 | SSE | MSE | RMSE | ||||||||||
| SB | Midilli | 0.792 | 0.058 | 0.010 | 0.088 | a | 16.218 | b | −1.564 | k | −13.986 | n | −3.666 |
| Logarithmic | 1.000 | 0.000 | 0.000 | 0.003 | a | 0.561 | c | 1.572 | k | 0.024 | |||
| Page | 0.772 | 22.841 | 3.263 | 1.806 | k | 43.649 | n | 43.649 | |||||
| Modified Page | 0.545 | 4.616 | 0.474 | 0.674 | k | 2.618 | n | −0.885 | |||||
| Henderson and Pabis | 0.698 | 0.085 | 0.012 | 0.110 | a | 0.001 | k | 1.937 | |||||
| Wang and Singh | 0.772 | 1.738 | 0.248 | 0.498 | a | 0.011 | b | 0.000 | |||||
| Peleg | 0.958 | 5.656 | 0.808 | 0.899 | k1 | −8.129 | k2 | −0.538 | |||||
| Lewis | 0.589 | 2.474 | 0.309 | 0.556 | k | −0.003 | |||||||
| Fick’s second law | 0.872 | 1.496 | 0.262 | 0.991 | Deff | 6.195 × 10−10 | |||||||
| BAA | Midilli | 0.849 | 0.051 | 0.007 | 0.081 | a | 0.330 | b | −17.883 | k | −12.486 | n | −1.413 |
| Logarithmic | 0.990 | 0.003 | 0.001 | 0.024 | a | 0.012 | c | 1.528 | k | 0.012 | |||
| Page | 0.506 | 24.891 | 3.556 | 1.886 | k | 42.657 | n | 42.657 | |||||
| Modified Page | 0.753 | 5.520 | 0.566 | 0.737 | k | 2.618 | n | −0.858 | |||||
| Henderson and Pabis | 0.885 | 0.039 | 0.006 | 0.074 | a | 0.001 | k | 2.059 | |||||
| Wang and Singh | 0.486 | 2.008 | 0.287 | 0.536 | a | 0.013 | b | 0.000 | |||||
| Peleg | 0.484 | 0.174 | 0.025 | 0.158 | k1 | 0.467 | k2 | −0.583 | |||||
| Lewis | 0.789 | 3.101 | 0.388 | 0.623 | k | −0.003 | |||||||
| Fick’s second law | 0.898 | 0.957 | 0.168 | 0.205 | Deff | 4.646 × 10−10 | |||||||
| B60 | Midilli | 0.809 | 0.061 | 0.008 | 0.088 | a | 1.273 | b | −0.459 | k | −15.893 | n | −2.460 |
| Logarithmic | 0.995 | 0.002 | 0.000 | 0.017 | a | 0.613 | c | 1.545 | k | 0.013 | |||
| Page | 0.561 | 24.426 | 3.489 | 1.868 | k | 6.561 | n | 6.561 | |||||
| Modified Page | 0.714 | 5.312 | 0.546 | 0.724 | k | 2.618 | n | −0.865 | |||||
| Henderson and Pabis | 0.856 | 0.046 | 0.007 | 0.081 | a | 0.001 | k | 2.033 | |||||
| Wang and Singh | 0.567 | 1.955 | 0.279 | 0.528 | a | 0.012 | b | 0.000 | |||||
| Peleg | 0.539 | 0.148 | 0.021 | 0.145 | k1 | 0.468 | k2 | −0.588 | |||||
| Lewis | 0.752 | 2.955 | 0.369 | 0.608 | k | −0.003 | |||||||
| Fick’s second law | 0.866 | 0.649 | 0.109 | 0.352 | Deff | 4.459 × 10−10 | |||||||
| Sample | Model | Statistics | Parameters | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| r2 | SSE | MSE | RMSE | ||||||||||
| SB | Midilli | 0.628 | 0.098 | 0.016 | 0.123 | a | 0.020 | b | −16.572 | k | −19.213 | n | −1.645 |
| Logarithmic | 0.995 | 0.001 | 0.000 | 0.016 | a | 0.558 | c | 1.570 | k | 0.031 | |||
| Page | 0.868 | 19.703 | 3.284 | 1.812 | k | 21.007 | n | 21.007 | |||||
| Modified Page | 0.521 | 4.015 | 0.478 | 0.677 | k | 2.618 | n | −0.833 | |||||
| Henderson and Pabis | 0.672 | 0.087 | 0.014 | 0.120 | a | 0.002 | k | 2.064 | |||||
| Wang and Singh | 0.786 | 1.587 | 0.265 | 0.514 | a | 0.012 | b | 0.000 | |||||
| Peleg | 0.854 | 0.039 | 0.006 | 0.080 | k1 | 0.470 | k2 | −0.615 | |||||
| Lewis | 0.567 | 2.193 | 0.313 | 0.560 | k | −0.003 | |||||||
| Fick’s second law | 0.931 | 0.037 | 0.0246 | 0.084 | Deff | 7.744 × 10−10 | |||||||
| BAA | Midilli | 0.976 | 0.007 | 0.002 | 0.041 | a | 0.002 | b | −15.807 | k | −31.810 | n | −2.262 |
| Logarithmic | 0.997 | 0.001 | 0.000 | 0.013 | a | 0.569 | c | 1.565 | k | 0.026 | |||
| Page | 0.801 | 20.030 | 3.338 | 1.827 | k | 88.354 | n | 88.354 | |||||
| Modified Page | 0.565 | 4.153 | 0.495 | 0.688 | k | 2.618 | n | −0.852 | |||||
| Henderson and Pabis | 0.713 | 0.079 | 0.013 | 0.114 | a | 0.001 | k | 1.950 | |||||
| Wang and Singh | 0.798 | 1.653 | 0.275 | 0.525 | a | 0.012 | b | 0.000 | |||||
| Peleg | 0.968 | 5.599 | 0.933 | 0.966 | k1 | −8.479 | k2 | −0.530 | |||||
| Lewis | 0.602 | 2.291 | 0.327 | 0.572 | k | −0.003 | |||||||
| Fick’s second law | 0.946 | 0.358 | 0.029 | 0.071 | Deff | 7.357 × 10−10 | |||||||
| B60 | Midilli | 0.859 | 0.042 | 0.007 | 0.081 | a | 0.628 | b | 0.521 | k | −14.952 | n | −2.068 |
| Logarithmic | 0.988 | 0.004 | 0.001 | 0.027 | a | 0.636 | c | 1.524 | k | 0.012 | |||
| Page | 0.840 | 22.004 | 3.667 | 1.915 | k | 21.007 | n | 21.007 | |||||
| Modified Page | 0.776 | 5.014 | 0.596 | 0.756 | k | 2.618 | n | −0.833 | |||||
| Henderson and Pabis | 0.893 | 0.032 | 0.005 | 0.073 | a | 0.002 | k | 2.064 | |||||
| Wang and Singh | 0.505 | 1.869 | 0.312 | 0.558 | a | 0.015 | b | 0.000 | |||||
| Peleg | 0.789 | 5.922 | 0.987 | 0.994 | k1 | −7.390 | k2 | −0.514 | |||||
| Lewis | 0.798 | 2.838 | 0.405 | 0.637 | k | −0.003 | |||||||
| Fick’s second law | 0.969 | 0.682 | 0.032 | 0.458 | Deff | 7.583 × 10−10 | |||||||
| Sample | Temperature (°C) | Effective Diffusivity (Deff × 10−10 m2/s) | Δh (kJ/mol) | Δs (kJ/mol × K) | ΔG (kJ/mol) | Activation Energy (kJ/mol) | R2 |
|---|---|---|---|---|---|---|---|
| SB | 40 | 3.182 ± 0.049 | 37.332 | −0.229 | 109.288 | 39.935 | 0.929 |
| 50 | 6.195 ± 0.040 | 37.249 | −0.230 | 111.587 | |||
| 60 | 7.744 ± 0.012 | 37.166 | −0.230 | 113.889 | |||
| BAA | 40 | 3.098 ± 0.162 | 37.329 | −0.228 | 108.955 | 39.315 | 0.992 |
| 50 | 4.646 ± 0.854 | 36.992 | −0.229 | 111.252 | |||
| 60 | 7.357 ± 0.014 | 36.909 | −0.230 | 113.487 | |||
| B60 | 40 | 3.075 ± 0.035 | 37.075 | −0.229 | 108.957 | 39.678 | 0.922 |
| 50 | 4.459 ± 0.475 | 36.984 | −0.229 | 111.305 | |||
| 60 | 7.583 ± 0.014 | 36.709 | −0.230 | 113.551 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Silva-Paz, R.J.; Mateo-Mendoza, D.K.; Eccoña-Sota, A. Mathematical Modelling of Muña Leaf Drying (Minthostachys mollis) for Determination of the Diffusion Coefficient, Enthalpy, and Gibbs Free Energy. ChemEngineering 2023, 7, 49. https://doi.org/10.3390/chemengineering7030049
Silva-Paz RJ, Mateo-Mendoza DK, Eccoña-Sota A. Mathematical Modelling of Muña Leaf Drying (Minthostachys mollis) for Determination of the Diffusion Coefficient, Enthalpy, and Gibbs Free Energy. ChemEngineering. 2023; 7(3):49. https://doi.org/10.3390/chemengineering7030049
Chicago/Turabian StyleSilva-Paz, Reynaldo J., Dante K. Mateo-Mendoza, and Amparo Eccoña-Sota. 2023. "Mathematical Modelling of Muña Leaf Drying (Minthostachys mollis) for Determination of the Diffusion Coefficient, Enthalpy, and Gibbs Free Energy" ChemEngineering 7, no. 3: 49. https://doi.org/10.3390/chemengineering7030049
APA StyleSilva-Paz, R. J., Mateo-Mendoza, D. K., & Eccoña-Sota, A. (2023). Mathematical Modelling of Muña Leaf Drying (Minthostachys mollis) for Determination of the Diffusion Coefficient, Enthalpy, and Gibbs Free Energy. ChemEngineering, 7(3), 49. https://doi.org/10.3390/chemengineering7030049






