Low-Cost Eddy-Resolving Simulation in the Near-Field of an Annular Swirling Jet for Spray Drying Applications
Abstract
1. Introduction
2. Numerical Methods and Turbulence Modeling
2.1. Governing Equations
2.2. Turbulence Modeling
2.2.1. The SST Model
2.2.2. Detached-Eddy Simulation
2.2.3. The SST-DES Model
2.2.4. SST-Delayed DES Model
2.2.5. SST-SAS Model
2.3. Numerical Schemes and Methods
Pressure-Velocity Coupling
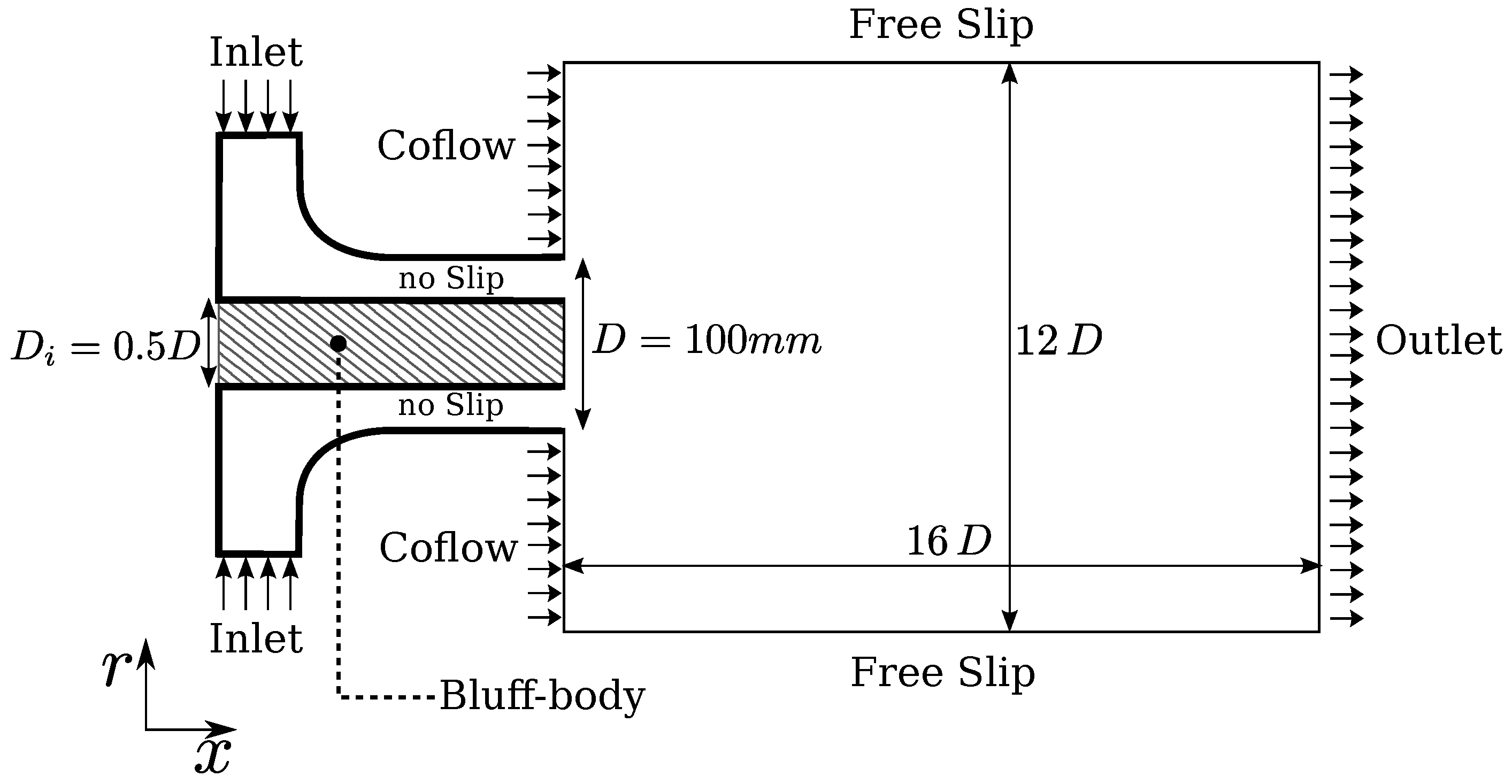
3. Computational Configuration
3.1. Flow Configuration
3.2. Computational Domain
3.3. Boundary Conditions
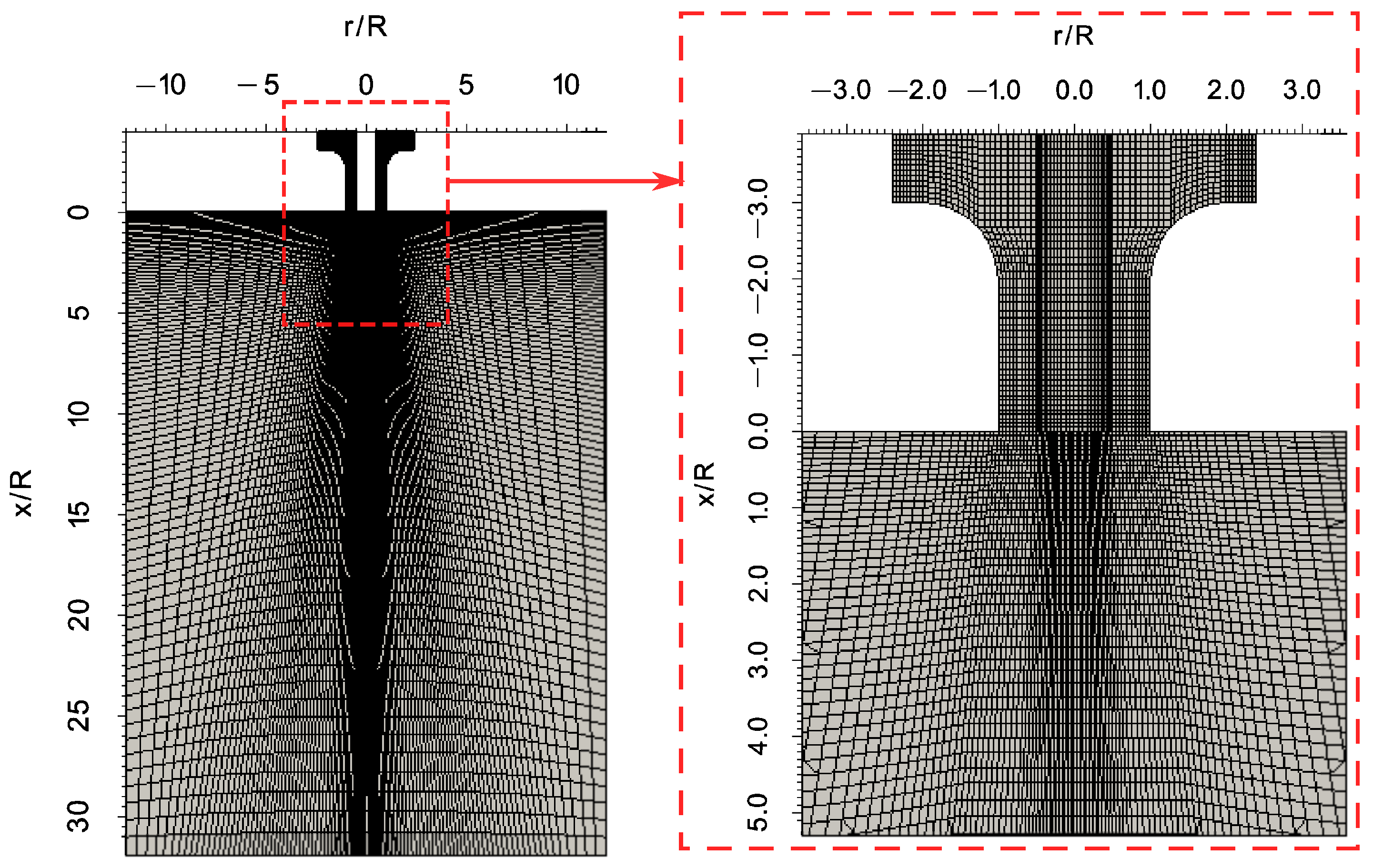
3.4. Grid
4. Study Cases and Methodology
5. Results and Discussion
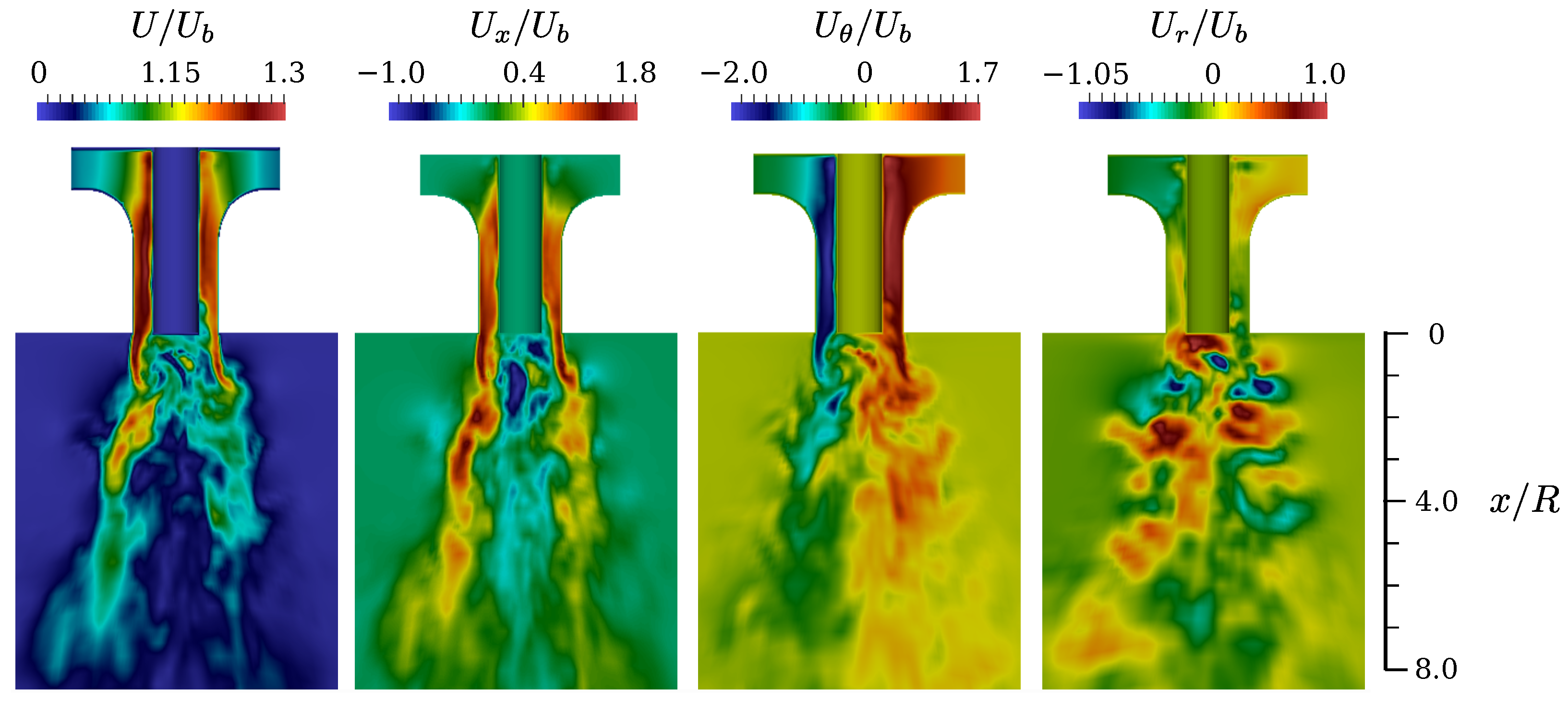
5.1. Description of the Flow Field
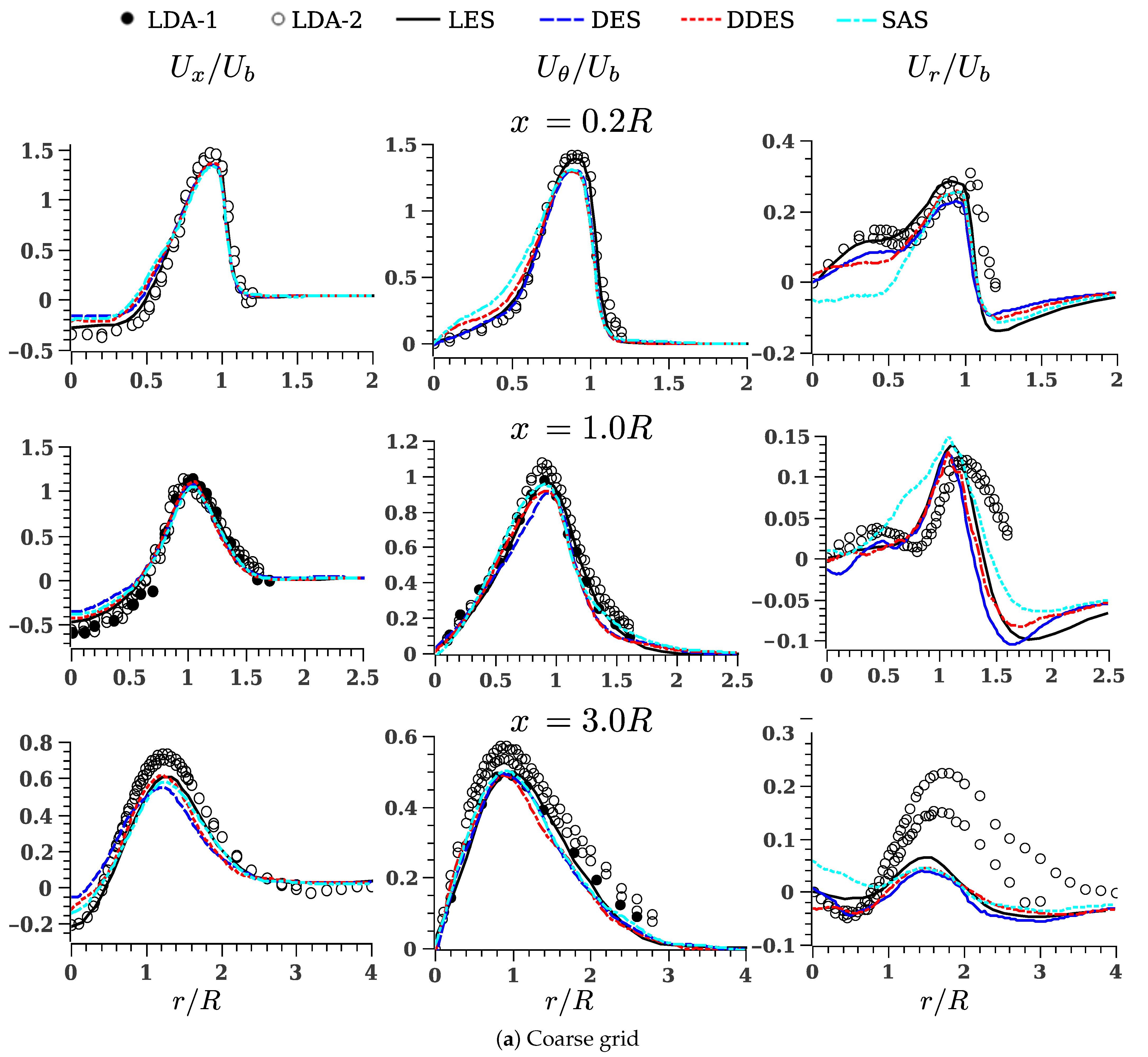
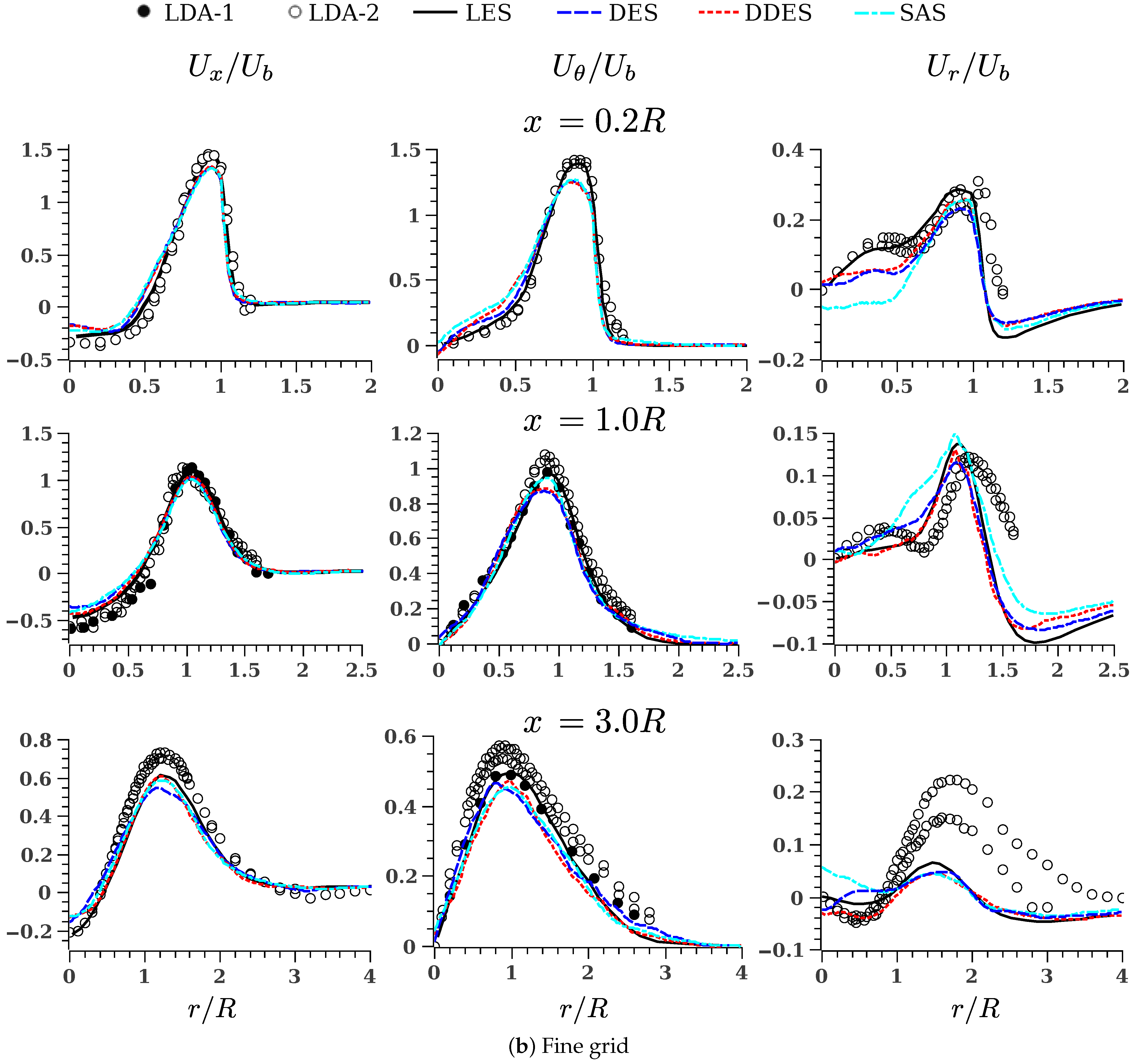
- For the axial velocity contours (), the central recirculation region and the high velocity jet are easily differentiated. In this particular case, large-scale detached turbulent structures are detected at
- For the tangential velocity contours (), the swirling structure of the jet is clearly noticed. The energy of the swirling flow decays farther from the inlet. Tangential back-flow is also recognized in the outer mixing regions. Differences are also detected in shape and magnitude of the instantaneous tangential flow structures around the symmetry axis.
- For the radial velocity contours (), an alternating behavior of is detected. While little variation on this velocity component is observed inside the inlet diffuser, an alternating pattern in is quickly developed just in the very near-field ().
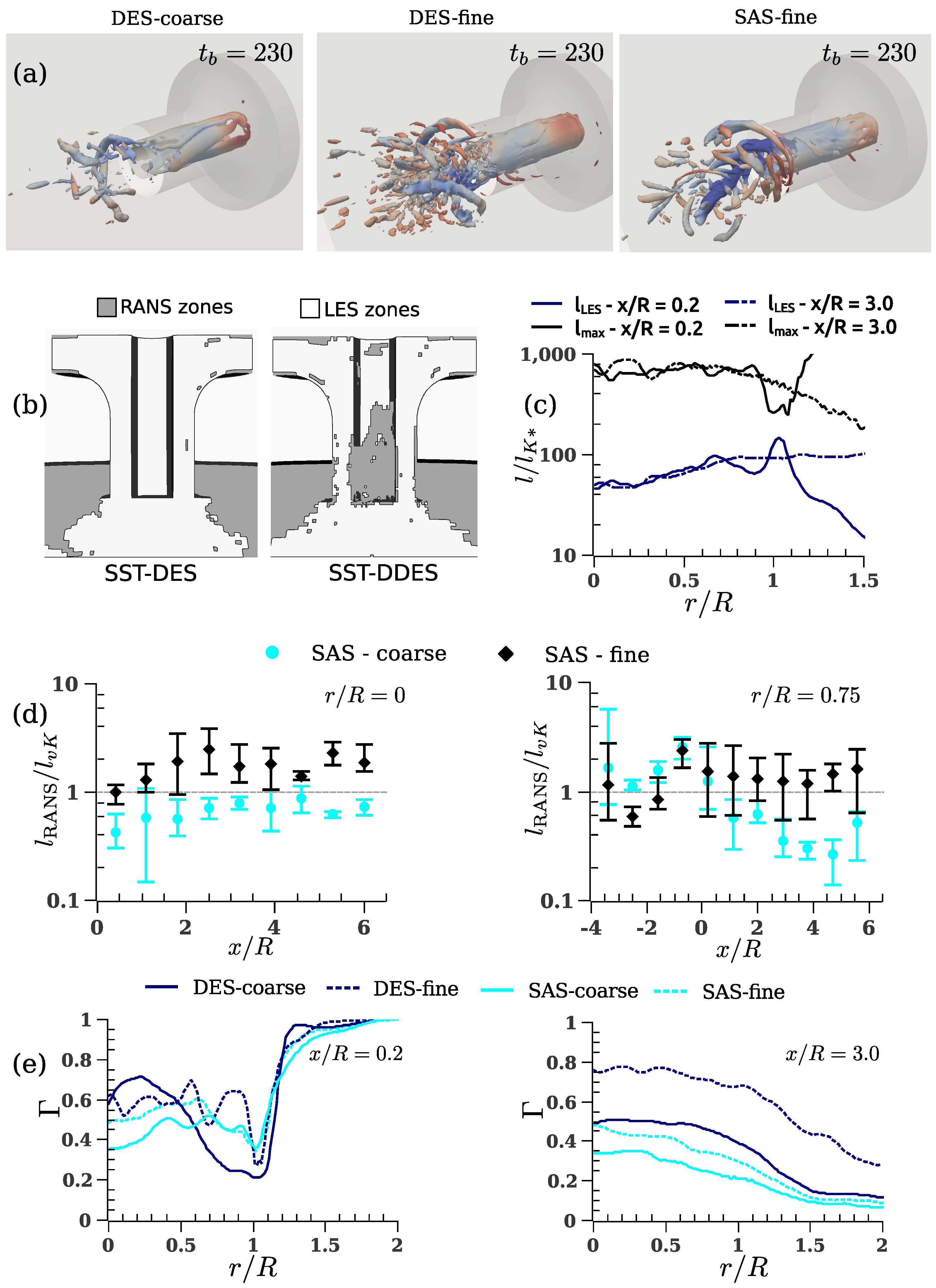
5.2. Grid Size and Turbulence-Resolving Capabilities
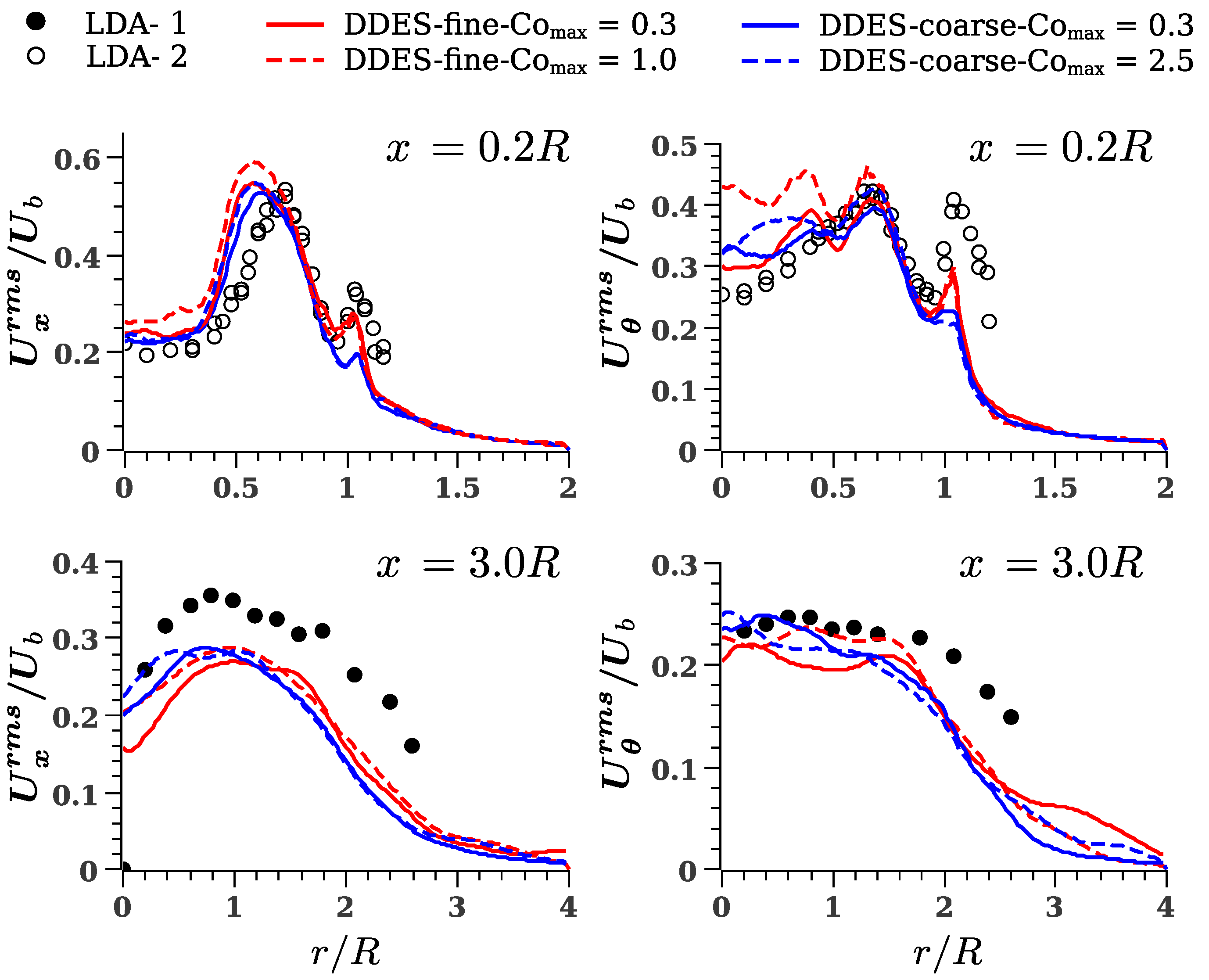
5.3. Mean Velocity Profiles: Comparison with Experimental and LES Data
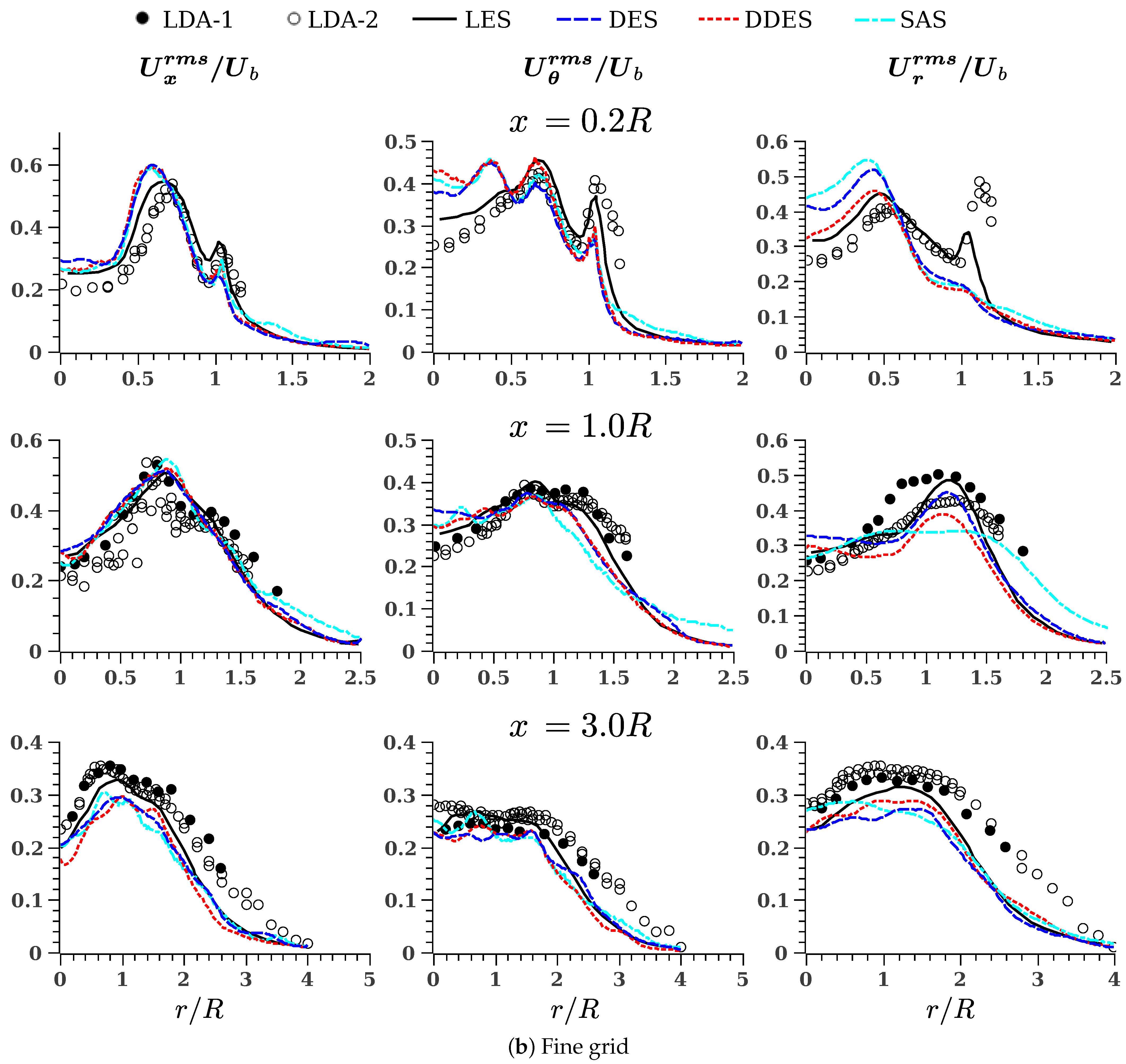
5.4. Fluctuations: Comparison with Experimental and LES Data
5.5. Quantitative Differences: Error Calculation
5.5.1. Error Criteria
5.5.2. Global MAE
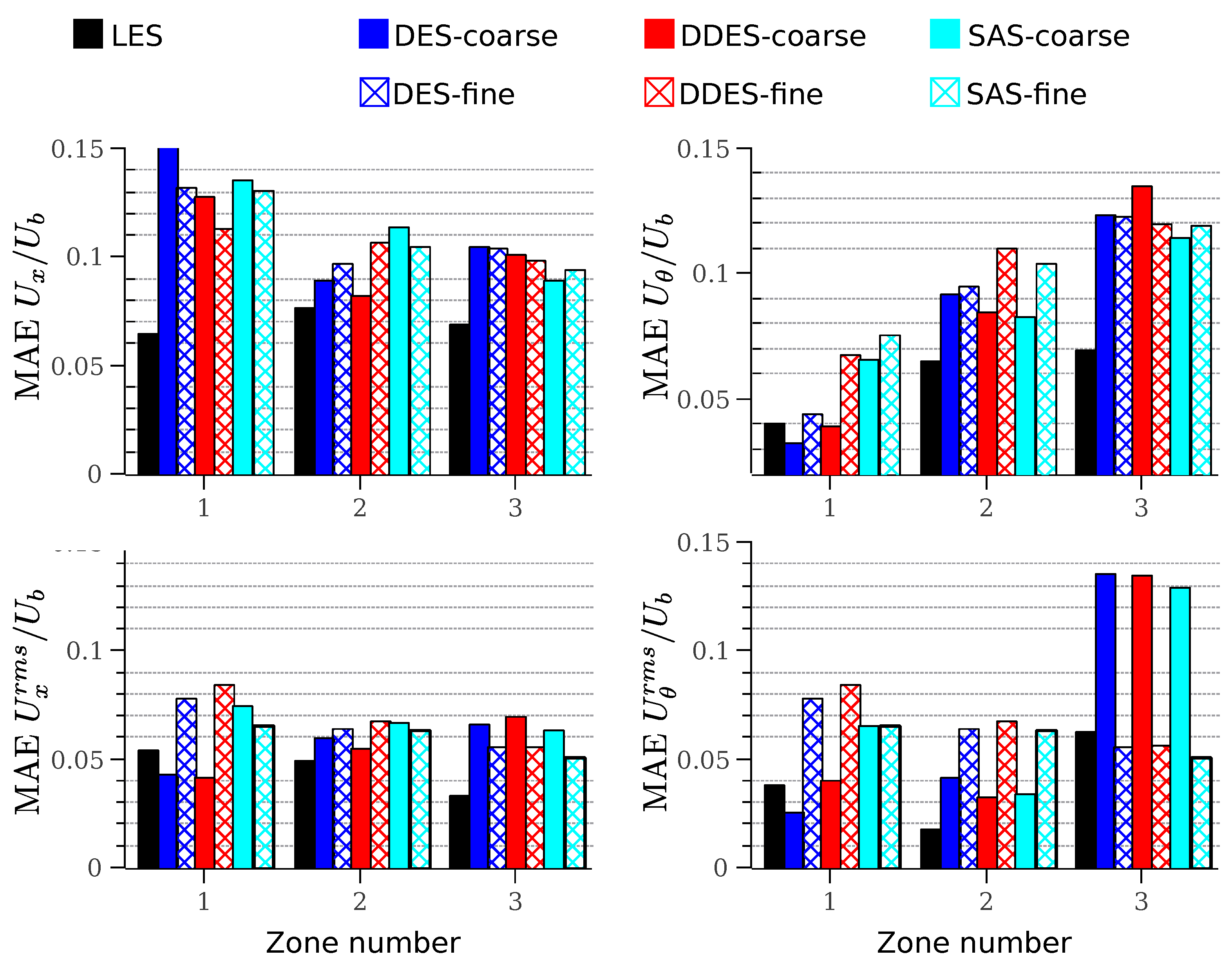
5.5.3. MAE per Jet Zones
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chterev, I.; Foley, C.; Foti, D.; Kostka, S.; Caswell, A.; Jiang, N.; Lynch, A.; Noble, D.; Menon, S.; Seitzman, J.; et al. Flame and flow topologies in an annular swirling flow. Combust. Sci. Technol. 2014, 186, 1041–1074. [Google Scholar] [CrossRef]
- Danlos, A.; Lalizel, G.; Patte-Rouland, B. Experimental characterization of the initial zone of an annular jet with a very large diameter ratio. Exp. Fluids 2013, 54, 1–17. [Google Scholar] [CrossRef][Green Version]
- García-Villalba, M.; Fröhlich, J. LES of a free annular swirling jet–Dependence of coherent structures on a pilot jet and the level of swirl. Int. J. Heat Fluid Flow 2006, 27, 911–923. [Google Scholar] [CrossRef]
- Ko, N.; Chan, W. Similarity in the initial region of annular jets: Three configurations. J. Fluid Mech. 1978, 84, 641–656. [Google Scholar] [CrossRef]
- Langrish, T.; Williams, J.; Fletcher, D. Simulation of the effects of inlet swirl on gas flow patterns in a pilot-scale spray dryer. Chem. Eng. Res. Des. 2004, 82, 821–833. [Google Scholar] [CrossRef]
- Masters, K. Spray Drying Handbook; Longman Scientific & Technical: Harlow, UK, 1991; ISBN 9780470217436. [Google Scholar]
- Lampa, A.; Fritsching, U. Large Eddy Simulation of the spray formation in confinements. Int. J. Heat Fluid Flow 2013, 43, 26–34. [Google Scholar] [CrossRef]
- Gicquel, L.Y.; Staffelbach, G.; Poinsot, T. Large eddy simulations of gaseous flames in gas turbine combustion chambers. Prog. Energy Combust. Sci. 2012, 38, 782–817. [Google Scholar] [CrossRef]
- Pitsch, H. Large-eddy simulation of turbulent combustion. Annu. Rev. Fluid Mech. 2006, 38, 453–482. [Google Scholar] [CrossRef]
- Apte, S.V.; Mahesh, K.; Moin, P.; Oefelein, J.C. Large-eddy simulation of swirling particle-laden flows in a coaxial-jet combustor. Int. J. Multiph. Flow 2003, 29, 1311–1331. [Google Scholar] [CrossRef]
- Jakirlic, S.; Hanjalic, K.; Tropea, C. Modeling rotating and swirling turbulent flows: A perpetual challenge. AIAA J. 2002, 40, 1984–1996. [Google Scholar] [CrossRef]
- Lampa, A.; Fritsching, U. Analysis of confined spray processes for powder production. In Proceedings of the ICLASS 2012 12th Triennial International Conference on Liquid Atomization and Spray Systems, Heidelberg, Germany, 2–6 September 2012. [Google Scholar]
- Fletcher, D.; Langrish, T. Scale-adaptive simulation (SAS) modelling of a pilot-scale spray dryer. Chem. Eng. Res. Des. 2009, 87, 1371–1378. [Google Scholar] [CrossRef]
- Francia, V.; Martín, L.; Bayly, A.; Simmons, M. Deposition and wear of deposits in swirl spray dryers: The equilibrium exchange rate and the wall-borne residence time. Procedia Eng. 2015, 102, 831–840. [Google Scholar] [CrossRef]
- Kieviet, F.; Van Raaij, J.; De Moor, P.; Kerkhof, P. Measurement and modelling of the air flow pattern in a pilot-plant spray dryer. Chem. Eng. Res. Des. 1997, 75, 321–328. [Google Scholar] [CrossRef]
- Jongsma, F.; Innings, F.; Olsson, M.; Carlsson, F. Large eddy simulation of unsteady turbulent flow in a semi-industrial size spray dryer. Dairy Sci. Technol. 2013, 93, 373–386. [Google Scholar] [CrossRef]
- Jasak, H.; Luo, J.; Kaluderčić, B.; Gosman, A.; Echtle, H.; Liang, Z.; Wirbeleit, F.; Wierse, M.; Rips, S.; Werner, A.; et al. Rapid CFD simulation of internal combustion engines. SAE Technical Paper. SAE Trans. 1999, 108, 1694–1703. [Google Scholar] [CrossRef]
- Fröhlich, J.; von Terzi, D. Hybrid LES/RANS methods for the simulation of turbulent flows. Prog. Aerosp. Sci. 2008, 44, 349–377. [Google Scholar] [CrossRef]
- Fureby, C. Towards the use of large eddy simulation in engineering. Prog. Aerosp. Sci. 2008, 44, 381–396. [Google Scholar] [CrossRef]
- Menter, F.; Kuntz, M.; Langtry, R. Ten years of industrial experience with the SST turbulence model. In Proceedings of the 4th International Symposium on Turbulence, Heat and Mass Transfer, Antalya, Turkey, 12–17 October 2003; Volume 4, pp. 625–632. [Google Scholar]
- Zhiyin, Y. Large-eddy simulation: Past, present and the future. Chin. J. Aeronaut. 2015, 28, 11–24. [Google Scholar] [CrossRef]
- Javadi, A.; Nilsson, H. A comparative study of scale-adaptive and large-eddy simulations of highly swirling turbulent flow through an abrupt expansion. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2014; Volume 22, p. 022017. [Google Scholar] [CrossRef]
- Javadi, A.; Nilsson, H. LES and DES of strongly swirling turbulent flow through a suddenly expanding circular pipe. Comput. Fluids 2015, 107, 301–313. [Google Scholar] [CrossRef]
- Paik, J.; Sotiropoulos, F. Numerical simulation of strongly swirling turbulent flows through an abrupt expansion. Int. J. Heat Fluid Flow 2010, 31, 390–400. [Google Scholar] [CrossRef]
- Mansouri, Z.; Boushaki, T. Investigation of large-scale structures of annular swirling jet in a non-premixed burner using delayed detached eddy simulation. Int. J. Heat Fluid Flow 2019, 77, 217–231. [Google Scholar] [CrossRef]
- Gimbun, J.; Muhammad, N.I.S.; Law, W.P. Unsteady RANS and detached eddy simulation of the multiphase flow in a co-current spray drying. Chin. J. Chem. Eng. 2015, 23, 1421–1428. [Google Scholar] [CrossRef]
- Noor, M.; Jolius, G. Detached eddy simulation (DES) of co-current spray dryer. Int. J. Technol. Manag. 2013, 2, 17–22. [Google Scholar]
- Anandharamakrishnan, C. Computational Fluid Dynamics Applications in Food Processing; Springer: New York, NY, USA, 2013. [Google Scholar] [CrossRef]
- Mujumdar, A.; Huang, L.; Chen, X. An overview of the recent advances in spray-drying. Dairy Sci. Technol. 2010, 90, 211–224. [Google Scholar] [CrossRef]
- Büchner, H.; Petsch, O. Experimental investigation of instabilities in turbulent premixed flames. In Proceedings of the 1st International Workshop on Unsteady Combustion, Karlsruhe, Germany, 8–9 July 2004. [Google Scholar]
- Hillemanns, R. Das Strömungs-und Reaktionsfeld sowie Stabilisierungseigenschaften von Drallflammen unter dem Einfluss der inneren Rezirkulationszone. Ph.D. Thesis, Universitaet Karlsruhe, Karlsruhe, Germany, 1988. [Google Scholar]
- García-Villalba, M.; Fröhlich, J.; Rodi, W. Identification and analysis of coherent structures in the near field of a turbulent unconfined annular swirling jet using large eddy simulation. Phys. Fluids 2006, 18, 055103. [Google Scholar] [CrossRef]
- Jin, Y.; Chen, X.D. A three-dimensional numerical study of the gas/particle interactions in an industrial-scale spray dryer for milk powder production. Dry. Technol. 2009, 27, 1018–1027. [Google Scholar] [CrossRef]
- Menter, F. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Jubaer, H.; Afshar, S.; Xiao, J.; Chen, X.D.; Selomulya, C.; Woo, M.W. On the effect of turbulence models on CFD simulations of a counter-current spray drying process. Chem. Eng. Res. Des. 2019, 141, 592–607. [Google Scholar] [CrossRef]
- Travin, A.K.; Shur, M.L.; Spalart, P.R.; Strelets, M.K. Improvement of delayed detached-eddy simulation for LES with wall modelling. In Proceedings of the European Conference on Computational Fluid Dynamics ECCOMAS CFD, Egmond aan Zee, The Netherlands, 5–8 September 2006. [Google Scholar]
- Strelets, M. Detached eddy simulation of massively separated flows. In Proceedings of the 39th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2001; p. 879. [Google Scholar] [CrossRef]
- Gritskevich, M.S.; Garbaruk, A.V.; Schütze, J.; Menter, F.R. Development of DDES and IDDES formulations for the k-ω shear stress transport model. Flow Turbul. Combust. 2012, 88, 431–449. [Google Scholar] [CrossRef]
- Egorov, Y.; Menter, F. Development and application of SST-SAS turbulence model in the DESIDER project. In Advances in Hybrid RANS-LES Modelling; Springer: Berlin/Heidelberg, Germany, 2008; pp. 261–270. [Google Scholar] [CrossRef]
- Travin, A.; Shur, M.; Strelets, M.; Spalart, P. Physical and numerical upgrades in the detached-eddy simulation of complex turbulent flows. In Advances in LES of Complex Flows; Springer: Berlin/Heidelberg, Germany, 2002; pp. 239–254. [Google Scholar] [CrossRef]
- Jasak, H. Error analysis and estimation for the finite volume method with applications to fluid flows. Ph.D Thesis, University of London, London, UK, 1996. [Google Scholar]
- Holzmann, T. Mathematics, Numerics, Derivations and OpenFOAM®, Holzmann CFD. Available online: https://www.researchgate.net/publication/307546712_Mathematics_Numerics_Derivations_and_OpenFOAMR (accessed on 5 September 2021).
- García-Villalba, M.; Fröhlich, J.; Rodi, W. On inflow boundary conditions for large eddy simulation of turbulent swirling jets. In Proceedings of the 21st Int. Congress of Theoretical and Applied Mechanics, Warsaw, Poland, 15–21 August 2004. [Google Scholar]
- Anandharamakrishnan, C.; Gimbun, J.; Stapley, A.G.F.; Rielly, C.D. A study of particle histories during spray drying using computational fluid dynamic simulations. Dry. Technol. 2010, 28, 566–576. [Google Scholar] [CrossRef][Green Version]
- Keshani, S.; Montazeri, M.H.; Daud, W.R.W.; Nourouzi, M.M. CFD modeling of air flow on wall deposition in different spray dryer geometries. Dry. Technol. 2015, 33, 784–795. [Google Scholar] [CrossRef]
- Saleh, S.; Nahi Saleh, S. Transient simulation of air flow in a co-current spray dryer. In Proceedings of the European Drying Conference–EuroDrying, Palma, Spain, 26–28 October 2011; pp. 26–28. [Google Scholar]
- Benavides-Morán, A.; Cubillos, A.; Gómez, A. Spray drying experiments and CFD simulation of guava juice formulation. Dry. Technol. 2020, 39, 450–465. [Google Scholar] [CrossRef]
- Moukalled, F.; Mangani, L.; Darwish, M. Temporal Discretization: The Transient Term. In The Finite Volume Method in Computational Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 2016; pp. 489–533. [Google Scholar] [CrossRef]
- Kalaushina, E.; Smirnovsky, A.; Brovin, D.; Kolesnik, E. Large Eddy Simulation of turbulent circular jet using OpenFOAM. In Proceedings of the 2019 Ivannikov Ispras Open Conference (ISPRAS), Moscow, Russia, 5–6 December 2019; pp. 97–102. [Google Scholar]
- Pope, S.B. Ten questions concerning the large-eddy simulation of turbulent flows. New J. Phys. 2004, 6, 35. [Google Scholar] [CrossRef]
- Woo, M.W.; Huang, L.X.; Mujumdar, A.S.; Daud, W.R.W. CFD Simulation of Spray Dryers; Number 1; National University of Singapore: Singapore, 2010; Chapter 1; pp. 1–36. [Google Scholar]
- Zheng, W.; Yan, C.; Liu, H.; Luo, D. Comparative assessment of SAS and DES turbulence modeling for massively separated flows. Acta Mech. Sin. 2016, 32, 12–21. [Google Scholar] [CrossRef]
- Gimbun, J.; Rielly, C.D.; Nagy, Z.K.; Derksen, J.J. Detached eddy simulation on the turbulent flow in a stirred tank. AIChE J. 2012, 58, 3224–3241. [Google Scholar] [CrossRef]
- Sommerfeld, M.; Qiu, H.H. Detailed measurements in a swirling particulate two-phase flow by a phase-Doppler anemometer. Int. J. Heat Fluid Flow 1991, 12, 20–28. [Google Scholar] [CrossRef]
- Ochowiak, M.; Krupińska, A.; Włodarczak, S.; Matuszak, M.; Markowska, M.; Janczarek, M.; Szulc, T. The Two-Phase Conical Swirl Atomizers: Spray Characteristics. Energies 2020, 13, 3416. [Google Scholar] [CrossRef]



| Direction | ||||
|---|---|---|---|---|
| Grid | Elements | |||
| Coarse | 278,000 | 90 | 60 | 45 |
| Fine | 1,000,000 | 144 | 88 | 72 |
| Grid | Coarse | Fine | ||||
|---|---|---|---|---|---|---|
| Case name | 1c | 2c | 3c | 1f | 2f | 3f |
| Turbulence (SST) | DES | DDES | SAS | DES | DDES | SAS |
| Courant number (max.) | ||||||
| Swirl number | ||||||
| Bulk velocity | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gutiérrez Suárez, J.A.; Gómez Mejía, A.; Galeano Urueña, C.H. Low-Cost Eddy-Resolving Simulation in the Near-Field of an Annular Swirling Jet for Spray Drying Applications. ChemEngineering 2021, 5, 80. https://doi.org/10.3390/chemengineering5040080
Gutiérrez Suárez JA, Gómez Mejía A, Galeano Urueña CH. Low-Cost Eddy-Resolving Simulation in the Near-Field of an Annular Swirling Jet for Spray Drying Applications. ChemEngineering. 2021; 5(4):80. https://doi.org/10.3390/chemengineering5040080
Chicago/Turabian StyleGutiérrez Suárez, Jairo Andrés, Alexánder Gómez Mejía, and Carlos Humberto Galeano Urueña. 2021. "Low-Cost Eddy-Resolving Simulation in the Near-Field of an Annular Swirling Jet for Spray Drying Applications" ChemEngineering 5, no. 4: 80. https://doi.org/10.3390/chemengineering5040080
APA StyleGutiérrez Suárez, J. A., Gómez Mejía, A., & Galeano Urueña, C. H. (2021). Low-Cost Eddy-Resolving Simulation in the Near-Field of an Annular Swirling Jet for Spray Drying Applications. ChemEngineering, 5(4), 80. https://doi.org/10.3390/chemengineering5040080






