Methanol–Water Purification Control Using Multi-Loop PI Controllers Based on Linear Set Point and Disturbance Models
Abstract
1. Introduction
2. Methods
2.1. Data Collection
2.2. Creating the Disturbance Model through System Identification
2.3. Controller Pairing
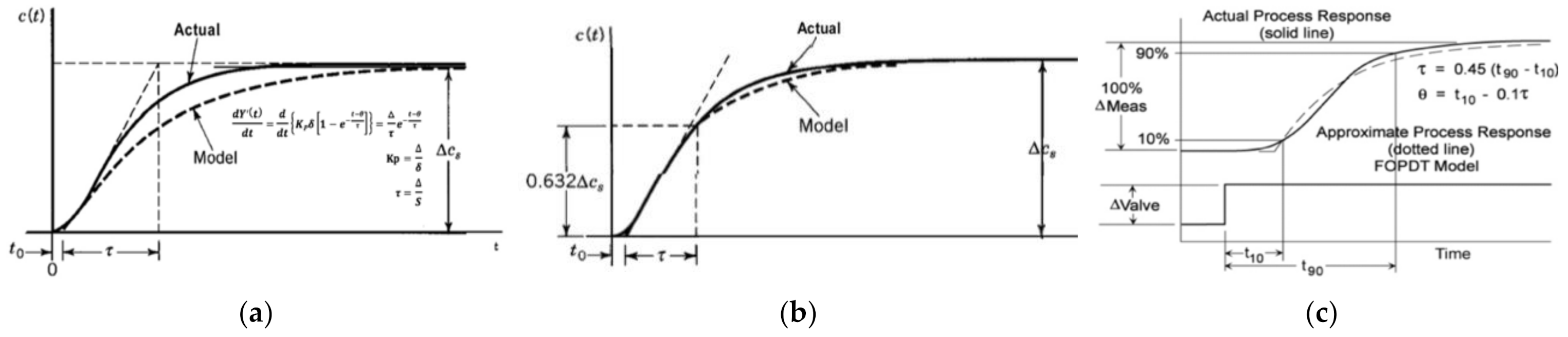
2.4. Controller Tuning
- -
- There are changes in output if the error is not zero. Because of its design, even in small error situations, this controller will eradicate errors.
- -
- The reset time (𝜏i) ensures that the output returns to the set stage.
- Calculating initial PI parameter values;
- BLT de-tuning:
- Assume factor F with a typical range of 1.5 < F < 4;
- Calculate new values of the controller’s parameter, where the detune controller gain is Kci, and the detune reset time is 𝛕ii:
- Determine the log modulus function (Lc) using a multivariable Nyquist plot (W):
- Reassume the F factor until the bode plot of W is stable, indicators are stated in Table 6 below.
2.5. Performance Evaluation
3. Results and Discussion
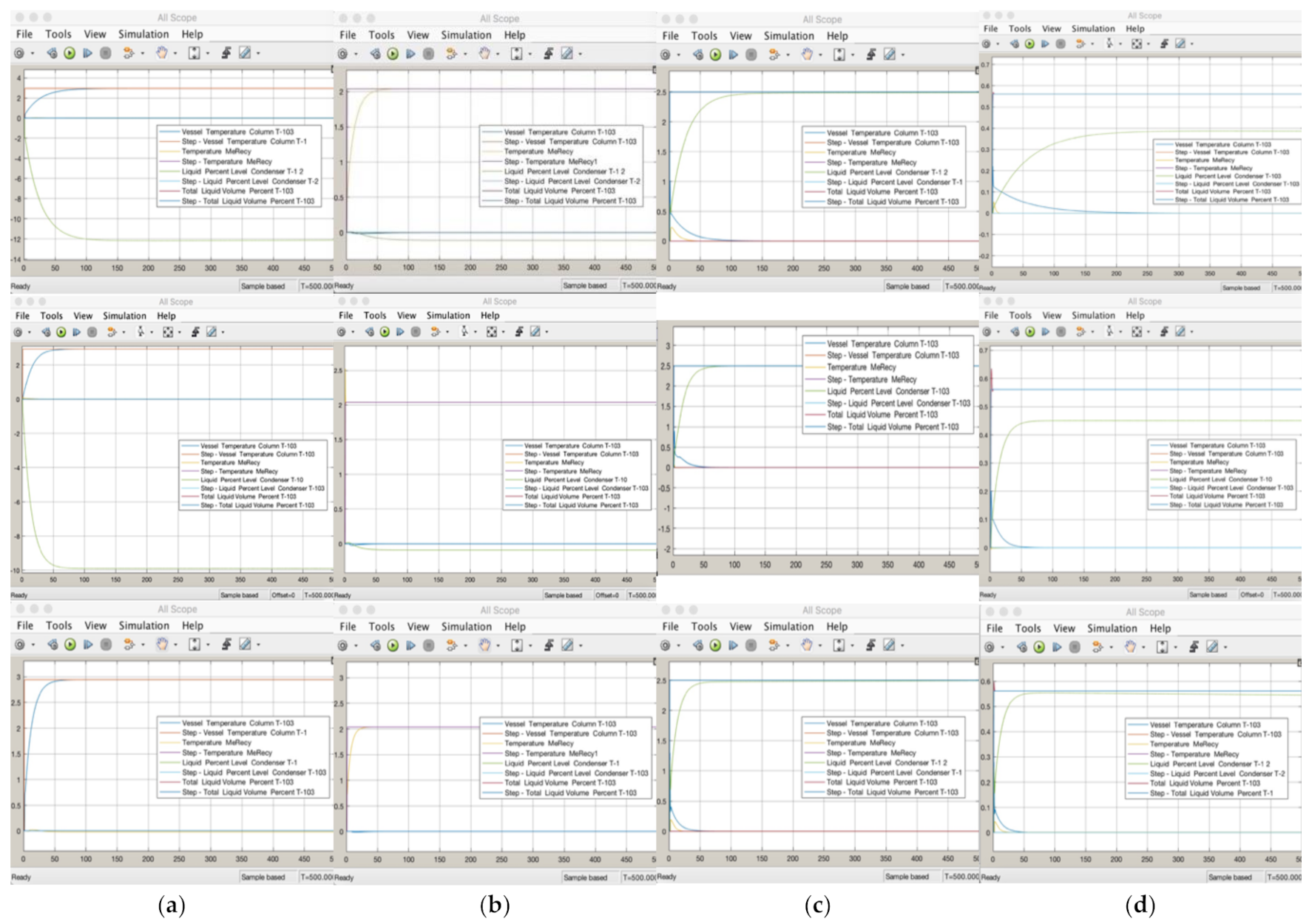
3.1. Disturbance Model
3.2. Controller Pairing
| RGA11 = | RGA21 = | RGA31 = | RGA41 = |
| 0.2452 | 15.8404 | 265.6956 | 0.1637 |
| RGA12 = | RGA22 = | RGA32 = | RGA42 = |
| 0.0555 | 0.6979 | −4.7820 | 0.1538 |
| RGA13 = | RGA23 = | RGA33 = | RGA43 = |
| −0.7833 | −50.8558 | −851.0568 | 0.2304 |
| RGA14 = | RGA24 = | RGA34 = | RGA44 = |
| −0.0915 | −6.7712 | −111.6737 | 1.0274 |
3.3. Multiloop PI Controller Tuning
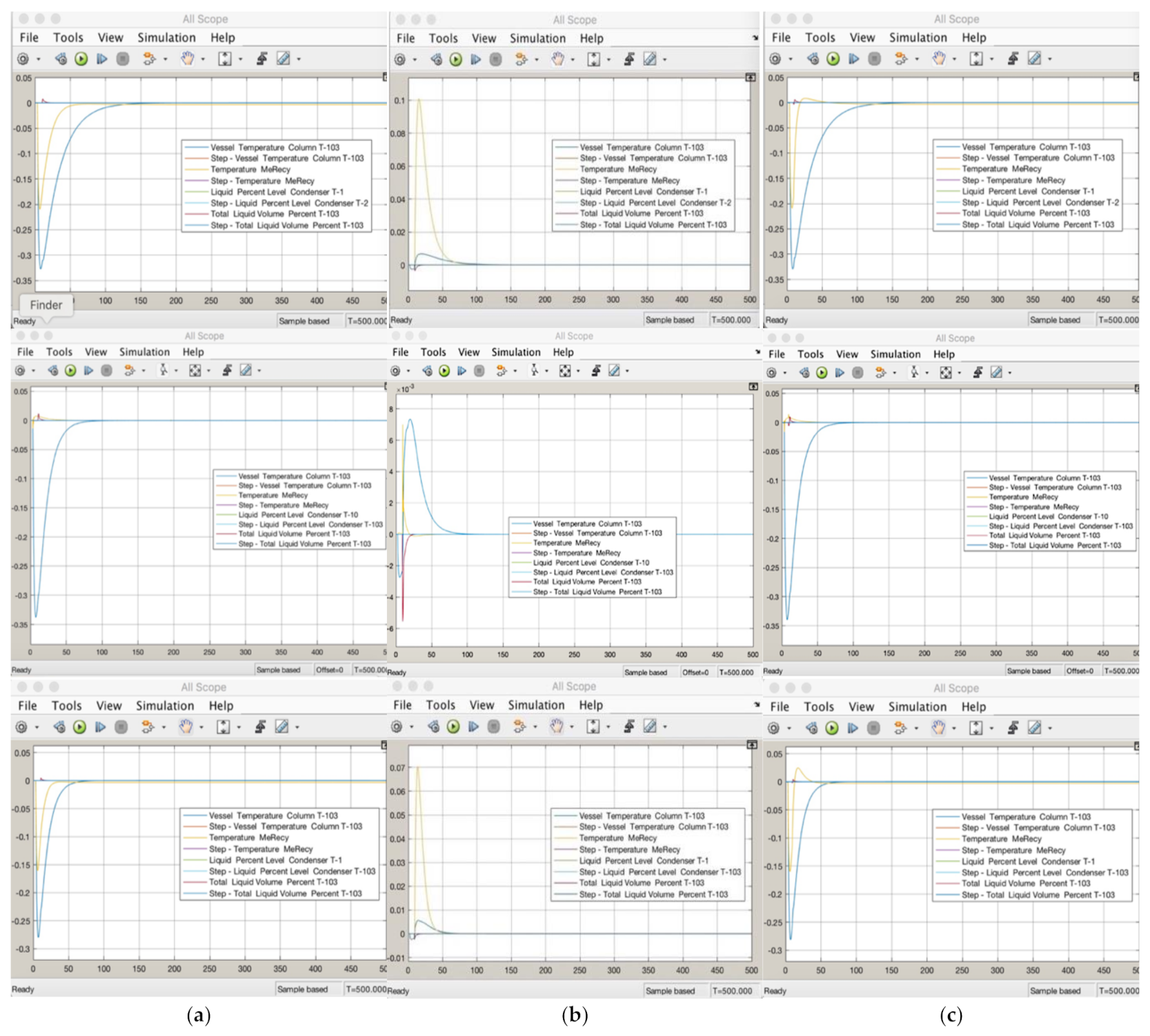
3.4. Performance Test
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ministry of Energy and Mineral Resources Republic of Indonesia. Handbook of Energy & Economic Statistics of Indonesia; Head of Center for Data and Information Technology on Energy and Mineral Resources: Jakarta, Indonesia, 2018.
- Musalaiah, M.; Engineer, T.C.; Peddintaiah, K. A Theoretical Study on Dimethyl Ether: An Alternative Fuel for Future Generations. Int. Res. J. Eng. Technol. (IRJET) 2016, 3, 238–243. [Google Scholar]
- Takeishi, K. Dimethyl ether (DME): A clean fuel/energy for the 21st century and the low carbon society. Int. J. Energy Environ. 2016, 10, 238–242. [Google Scholar]
- Falco, M.D. Dimethyl Ether (DME) Production; University UCBM: Rome, Italy, 2017. [Google Scholar]
- Solichin, A.; Sari, M.; Rahmiyati, W.Y. Production of DME from Syngas (for Oxygenates in Diesel Oil and Blending LPG): Plant Design Report; Department of Chemical Engineering, Faculty of Engineering, Universitas Indonesia: Depok, Indonesia, 2011. [Google Scholar]
- Atef, G.; Almadani, A.; Noaman, S. Manufacturing of DME from Methanol; King Fahd University of Petroleum & Minerals: Dhahran, Saudi Arabia, 2015. [Google Scholar] [CrossRef]
- Dieterich, V.; Buttler, A.; Hanel, A.; Spliethoff, H.; Fendt, S. Power-to-liquid via synthesis of methanol, DME or Fischer–Tropsch-fuels: A review. R. Soc. Chem. 2020, 13, 3207–3252. [Google Scholar] [CrossRef]
- Khaleel, A. Methanol Dehydration to Dimethyl Ether over Highly Porous Xerogel Alumina Catalyst: Flow Rate Effect. Fuel Process Technol. 2010, 91, 1505–1509. [Google Scholar] [CrossRef]
- Dyrda, K.M.; Wilke, V.; Haas-Santo, K.; Dittmeyer, R. Experimental Investigation of the Gas/Liquid Phase Separation Using a Membrane-Based Micro Contactor. ChemEngineering 2018, 2, 55. [Google Scholar] [CrossRef]
- Liptak, B. Instrument Engineer’s Handbook: Process Control; CRC Taylor & Francis: Boca Raton, FL, USA, 2012. [Google Scholar] [CrossRef]
- Marlin, T. Process Control: Designing Processes and Control System for Dynamic Performance, 2nd ed.; McGraw Hill: Singapore, 2015; ISBN 9780070393622. [Google Scholar]
- Wahid, A.; Gunawan, T.A. Pengendalian Proses Purifikasi DME dan Metanol pada Pabrik DME dari Gas Sintesis. Sinergi 2015, 19, 57–66. [Google Scholar] [CrossRef][Green Version]
- Wahid, A.; Brillianto, Z.H. Multivariable Model Predictive Control (4 × 4) of Methanol Water Separation in Dimethyl Ether Production. AIP Conf. Proc. 2015, 2255, 030055. [Google Scholar] [CrossRef]
- Nandong, J. Decentralized Control Systems; Curtin University: Curtin, Malaysia, 2020. [Google Scholar] [CrossRef]
- Vu Truong, N.; Lee, M. Optimal Design of Multi-loop PI Controllers for Enhanced Disturbance Rejection in Multivariable Processes; School of Chemical Engineering and Technology Yeungnam University: Gyeoungbuk, Korea, 2007; Available online: http://psdc.yu.ac.kr (accessed on 22 July 2020).
- Biyanto, T.; Sordi, N.; Sehamat, N.; Zabiri, H. PID Multivariable Tuning System Using BLT Method for Distillation Column; IOP Publishing: Tokyo, Japan, 2018. [Google Scholar] [CrossRef]
- Farsi, M. Dynamic Modeling and Controllability Analysis of DME Production in an Isothermal Fixed Bed Reactor; Department of Chemical Engineering, School of Chemical and Petroleum Engineering, Shiraz University: Shiraz, Iran, 2015. [Google Scholar] [CrossRef][Green Version]
- Huang, H.; Jeng, J.; Chiang, C.; Pan, W. A Direct Method for Multi-Loop PI/PID Controller Design; Department of Chemical Engineering, National Taiwan University: Taipei, China, 2003. [Google Scholar] [CrossRef]
- Kumar, R.; Anand, S.; Khulbey, A.; Jha, A.N. Design of Fractional Order Controller for Wood-Berry Distillation Column; Department of Instrumentation and Control Engineering, Netaji Subhas University of Technology: New Delhi, India, 2020; ISBN 9781728169163. [Google Scholar]
- Kalpana, R.; Harukumar, K.; Senthukumar, J.; Balasubramanian, G.; Gour, A. Multivariable Static Output Feedback Control of a Binary Distillation Column Using Linear Matrix Inequalities and Genetic Algorithm; School of Electrical and Electronics Engineering, Sastra University: Thanjavur, India, 2017. [Google Scholar] [CrossRef]
- Kalhoro, A.; Memon, S. Design of Multivariable PID Controllers: A Comparative Study; Department of Electronic Engineering, Mehran University: Jamshoro, Pakistan, 2021. [Google Scholar] [CrossRef]
- Alawad, N.; Muter, A. Optimal Control of Model Reduction Binary Distillation Column; Department of Computer Engineering, Faculty of Engineering, Mustansiriyah University: Baghdad, Iraq, 2021. [Google Scholar] [CrossRef]
- Ogunnaike, B.A.; Ray, W.H. Multivarianle Design Controller Design for Linear Systems Having Multiple Time Delays; Department of Chemical Engineering, University of Winconsin: Madison, WI, USA, 1979. [Google Scholar]
- Smith, C. Digital Computer Process Control; Intext: Scranton, PA, USA, 1972; ISBN 0700224017/9780700224012. [Google Scholar]
- Camacho, E.F.; Bordons, C. Model Predictive Control, 2nd ed.; Springer: London, UK, 2007; ISBN 9780857293985. [Google Scholar]
- Vazquez, F.; Morilla, F. Tuning Decentralized PID Controllers for MIMO Systems with Decouplers. In Proceedings of the 15th Triennial World Congress, Barcelona, Spain, 21–26 July 2002. [Google Scholar] [CrossRef]
- Krishna, G.H.; Kiranmayi, R.; Rathaiah, M. Control System Design for 3 × 3 Processes Based on Effective Transfer Function and Fractional Order Filter. Int. J. Eng. Adv. Technol. (IJEAT) 2019, 8, 637–642. [Google Scholar]
- Chau, P.C. Chemical Process Control: A First Course with MATLAB; University of California: San Diego, CA, USA, 2001. [Google Scholar] [CrossRef]
- Wahid, A.; Tanuwijaya, R. Pemilihan Metode Penyetelan Pengendali PI pada Pengendalian Pabrik Regasifikasi LNG Menggunakan Metode Skor. In Proceedings of the Seminar Nasional Teknik Kimia UNPAR, Bandung, Indonesia, 19 November 2015. [Google Scholar]
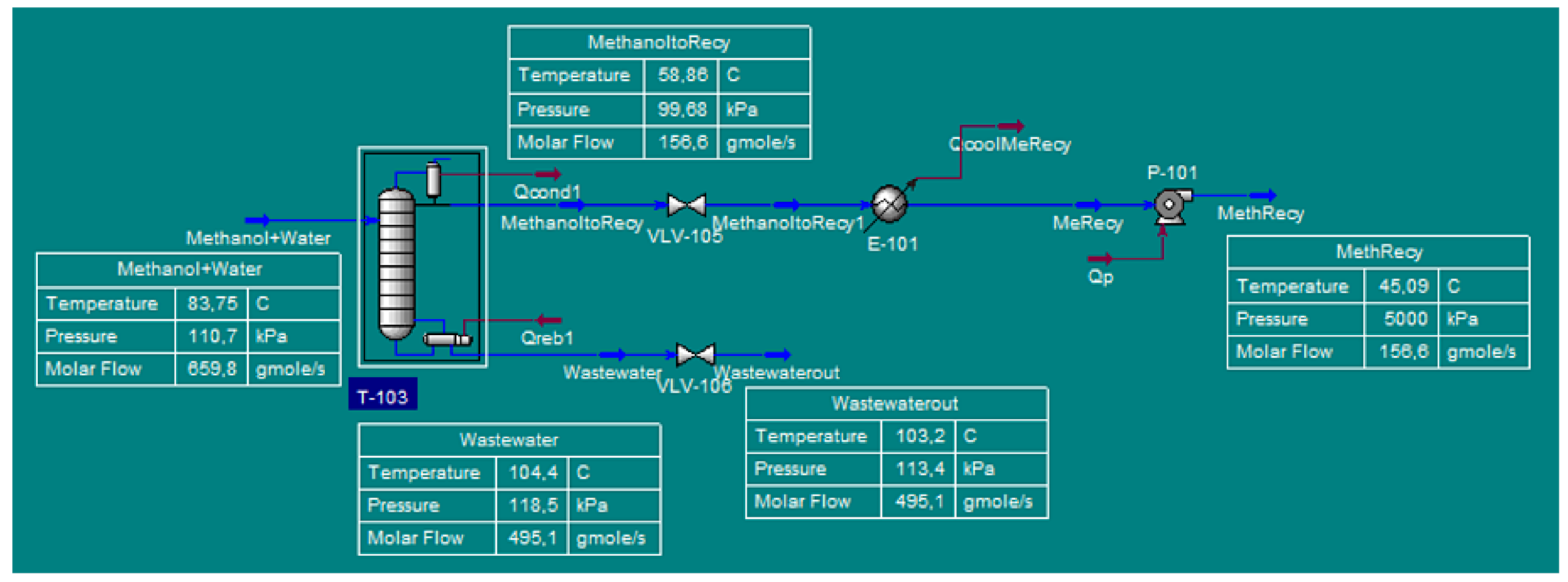


| Unit | Code | Objectives | Initial | Final |
|---|---|---|---|---|
| Cooler | E-101 | Cools methanol distillates | 240 ℉ | 110 ℉ |
| Pump | P-101 | To increase the recycle flow pressure | 200 kPa | 3500 kPa |
| Process Parameters | T-103 |
|---|---|
| Number of Stages | 30 |
| Condenser Pressure | 14.69 psia |
| Reboiler Pressure | 14.69 psia |
| Stream Inlet Stage | 19 |
| No | Unit Process | Controller Type | Controlled Variable | Manipulated Variable | Set Point | Actuator | Disturbance |
|---|---|---|---|---|---|---|---|
| 1 | Condenser T-103 | Temperature control | Temperature | Heat flow | 58.81 °C | Control Valve Qcond1 | Changes in the inlet feed (methanol + water) temperature and molar flow |
| 2 | Cooler E-101 | Heat flow | 40.75 °C | Control Valve QcoolMeRecy | |||
| 3 | Condenser T-103 | Level control | Column Level | Methanol to recycle Flow | 49.96% | Actuator Desired Position VLV- 105 | |
| 4 | Column T-103 | Wastewater flow | 11.22% | Actuator Desired Position VLV- 106 |
| λ | Possible Pairing |
|---|---|
| λmn < 0 | Unstable interactions |
| λmn = 1 | No interaction exists |
| λmn = 0.5 | Strong interactions |
| λmn > 1 | Interactions in the opposite direction of the variables, and stronger as value increases |
| λmn < 1 | Interactions in the same direction of the variables, and stronger as the value decreases |
| Λ | Possible Pairing |
|---|---|
| No interaction. The controller design is a SISO system. | |
| Strong interaction if 𝛿 is close to 1; weak interaction if 𝛿 << 1. |
| Stable | Marginally Stable | Unstable |
|---|---|---|
| Phase over frequency > gain cross over frequency | Phase over frequency = gain cross over frequency | Phase over frequency < gain cross over frequency |
| Gain margin > 1 | Gain margin = 1 | Gain margin < 1 |
| Phase margin = positive | Phase margin = 0 | Phase margin = negative |
| Disturbance | Variable Process | |||
|---|---|---|---|---|
| CV1 | CV2 | CV3 | CV4 | |
| Inlet Flow | ||||
| Inlet Temperature | ||||
| Controlled Variable (CV) | Controller Parameter | Big Log-Modulus Tuning | Fine Tuning | Wahid and Gunawan (2015) | |
|---|---|---|---|---|---|
| 1 | Vessel Temperature of Condenser T-103 | P | 0.67 | 0.24 | 1 |
| I | 0.33 | 1.64 | 0.5 | ||
| 2 | MeRecy Temperature | P | 0.67 | 4.90 | 1 |
| I | 0.33 | 42.41 | 0.5 | ||
| 3 | Liquid Percent Level of Condenser T-103 | P | 0.01 | −67.01 | 0.01 |
| I | 2.16 | 6.75 × 10−19 | 1.80 | ||
| 4 | Total Liquid Volume Percent of T-103 | P | 9.00 | 3.49 | 13.50 |
| I | 1.59 | 3.56 | 2.38 | ||
| CV | Set Point | Increase 5% | Delta (Δ) |
|---|---|---|---|
| 1 | 58.81 ℃ | 61.75 ℃ | 2.94 |
| 2 | 40.75 ℃ | 42.79 ℃ | 2.04 |
| 3 | 49.96% | 52.46% | 2.5 |
| 4 | 11.22% | 11.78% | 0.56 |
| Disturbance | |||
| Feed Temperature | 81.74 °C | 85.83 °C | 4.09 |
| Feed Flow | 659.8 gmol/s | 692.72 gmol/s | 32.98 |
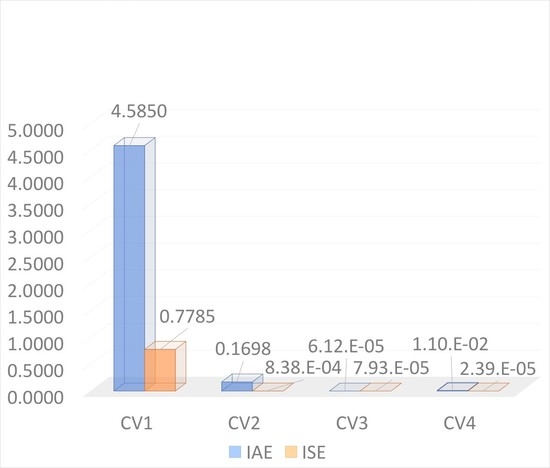
| CV | IAE | Improvement | |||||
|---|---|---|---|---|---|---|---|
| MMPC (Wahid and Brillianto 2020) | Multi-Loop PI | Multi-Loop PI | |||||
| Big Log-Modulus Tuning | Wahid & Gunawan (2015) | Fine-Tuning | Big Log-Modulus Tuning | Wahid & Gunawan (2015) | Fine-Tuning | ||
| Feed Temperature Disturbance | |||||||
| 1 | 3.70 × 101 | 1.05 × 101 | 4.71 | 6.65 | 71.58% | 87.27% | 82.01% |
| 2 | 7.96 × 101 | 1.24 | 2.98 × 10 | 1.62 × 10−1 | 98.45% | 96.26% | 99.80% |
| 3 | 6.18 | 6.26 × 10−9 | 6.84 × 102 | 7.93 × 10−5 | 100.00% | −1.10 × 104% | 100.00% |
| 4 | 2.04 × 102 | 2.47 × 10−2 | 1.10 × 10−2 | 2.82 × 10−2 | 99.99% | 99.99% | 99.97% |
| Feed Flow Disturbance | |||||||
| 1 | 3.75 × 101 | 3.11 × 10−1 | 1.53 × 10−1 | 2.09 × 10−1 | 99.17% | 99.59% | 99.44% |
| 2 | 1.55 × 102 | 4.97 × 10−1 | 9.20 × 10−1 | 1.18 × 10−2 | 99.68% | 99.41% | 99.99% |
| 3 | 3.32 | 1.46 × 10−6 | 1.62 × 101 | 1.87 × 10−6 | 100.00% | −385.80% | 100.00% |
| 4 | 7.41 × 101 | 1.16 × 10−2 | 5.15 × 10−3 | 1.33 × 10−2 | 99.98% | 99.99% | 99.98% |
| Feed Flow and Temperature Disturbance | |||||||
| 1 | 2.24 × 101 | 1.02 × 101 | 4.59 | 6.48 | 54.19% | 79.49% | 71.02% |
| 2 | 1.64 × 102 | 1.47 | 2.66 | 1.70 × 10−1 | 99.11% | 98.38% | 99.90% |
| 3 | 1.24 × 101 | 6.12 × 10−5 | 6.69 × 102 | 7.74 × 10−5 | 100.00% | −5.31 × 103% | 100.00% |
| 4 | 2.04 × 102 | 2.47 × 10−2 | 1.10 × 10−2 | 2.82 × 10−2 | 99.98% | 99.99% | 99.98% |
| CV | ISE | Improvement | |||||
|---|---|---|---|---|---|---|---|
| MMPC (Wahid and Brillianto 2020) | Multi-Loop PI | Multi-Loop PI | |||||
| Big Log-Modulus Tuning | Wahid & Gunawan (2015) | Fine-Tuning | Big Log-Modulus Tuning | Wahid & Gunawan (2015) | Fine-Tuning | ||
| Feed Temperature Disturbance | |||||||
| 1 | 2.30 × 101 | 2.03 | 8.01 × 10−1 | 1.41 | 91.20% | 96.52% | 93.89% |
| 2 | 1.06 × 102 | 9.90 × 10−2 | 1.58 × 10−1 | 7.03 × 10−4 | 99.91% | 99.85% | 100.00% |
| 3 | 6.41 × 10−1 | 8.31 × 10−5 | 9.53 × 102 | 1.29 × 10−4 | 99.99% | −1.49 × 105% | 99.98% |
| 4 | 6.94 × 102 | 1.01 × 10−4 | 2.39 × 10−5 | 1.63 × 10−4 | 100.00% | 100.00% | 100.00% |
| Feed Flow Disturbance | |||||||
| 1 | 6.62 × 101 | 1.33 × 10−3 | 5.47 × 10−4 | 1.02 × 10−3 | 100.00% | 100.00% | 100.00% |
| 2 | 4.43 × 102 | 2.17 × 10−2 | 4.20 × 10−1 | 1.62 × 10−5 | 100.00% | 99.91% | 100.00% |
| 3 | 7.68 × 10−1 | 4.66 × 10−8 | 5.41 × 10−1 | 7.31 × 10−8 | 100.00% | 29.57% | 100.00% |
| 4 | 9.64 × 101 | 2.23 × 10−5 | 5.35 × 10−6 | 3.70 × 10−5 | 100.00% | 100.00% | 100.00% |
| Feed Flow and Temperature Disturbance | |||||||
| 1 | 2.68 × 101 | 1.95 | 7.79 × 10−1 | 1.36 | 92.71% | 97.09% | 94.91% |
| 2 | 3.85 × 102 | 1.08 × 10−1 | 1.29 × 10−1 | 8.38 × 10−4 | 99.97% | 99.97% | 100.00% |
| 3 | 1.83 | 7.93 × 10−5 | 9.10 × 102 | 1.22 × 10−4 | 100.00% | −4.96 × 104% | 99.99% |
| 4 | 6.94 × 102 | 1.01 × 10−4 | 2.39 × 10−5 | 1.63 × 10−4 | 100.00% | 100.00% | 100.00% |
| CV | IAE | Improvement | |||||
|---|---|---|---|---|---|---|---|
| MMPC (Wahid and Brillianto 2020) | Multi-Loop PI | Multi-Loop PI | |||||
| Big Log-Modulus Tuning | Wahid & Gunawan (2015) | Fine-Tuning | Big Log-Modulus Tuning | Wahid & Gunawan (2015) | Fine-Tuning | ||
| CV1 Setpoint Change | |||||||
| 1 | 1.81 × 102 | 6.61 × 101 | 2.96 × 101 | 4.17 × 101 | 63.51% | 83.66% | 77.02% |
| 2 | 4.28 | 8.97 | 9.26 | 1.04 | −109.63% | −116.24% | 75.70% |
| 3 | 4.36 | 4.08 × 103 | 4.16 × 103 | 4.82 × 103 | −93,386.24% | −9.53 × 104% | −1.10 × 105% |
| 4 | 2.00 × 10−2 | 2.29 × 10−3 | 1.37 × 10−3 | 1.65 × 10−2 | 88.54% | 93.16% | 17.70% |
| CV2 Setpoint Change | |||||||
| 1 | 4.10 × 10−1 | 7.34 × 10−1 | 3.28 × 10−1 | 4.60 × 10−1 | −79.02% | 19.95% | −12.15% |
| 2 | 5.64 × 101 | 1.83 × 101 | 8.20 | 2.71 × 10−1 | 67.48% | 85.46% | 99.52% |
| 3 | 3.20 × 10−1 | 3.59 × 101 | 3.73 × 101 | 4.35 × 101 | −11,112.50% | −11,546.88% | −13,493.75% |
| 4 | 2.00 × 10−2 | 1.68 × 10−4 | 8.12 × 10−5 | 6.45 × 10−4 | 99.16% | 99.59% | 96.78% |
| CV | IAE | Improvement | |||||
|---|---|---|---|---|---|---|---|
| MMPC (Wahid and Brillianto 2020) | Multi-Loop PI | Multi-Loop PI | |||||
| Big Log-Modulus Tuning | Wahid & Gunawan (2015) | Fine-Tuning | Big Log-Modulus Tuning | Wahid & Gunawan (2015) | Fine-Tuning | ||
| CV3 Setpoint Change | |||||||
| 1 | 7.32 | 7.51 | 5.80 | 6.97 | −2.60% | 20.71% | 4.77% |
| 2 | 4.67 | 9.21 × 10−1 | 2.20 | 3.80 × 10−1 | 80.29% | 52.89% | 91.86% |
| 3 | 5.59 × 101 | 4.16 × 102 | 3.92 × 102 | 1.34 × 103 | −643.43% | −601.59% | −2301.22% |
| 4 | 5.00 × 10−2 | 1.43 × 10−1 | 4.61 × 10−1 | 1.27 | −185.20% | −821.40% | −2430.00% |
| CV4 Setpoint Change | |||||||
| 1 | 5.20 × 10−1 | 7.19 | 1.31 | 1.84 | −1282.31% | −151.15% | −254.42% |
| 2 | 5.30 × 10−1 | 2.98 × 10−1 | 7.42 × 10−1 | 4.31 × 10−2 | 43.70% | −39.91% | 91.87% |
| 3 | 5.79 | 1.73 × 102 | 1.89 × 102 | 2.19 × 102 | −2886.18% | −3.17 × 103% | −3.68 × 103% |
| 4 | 5.74 × 101 | 1.42 × 10−1 | 1.03 × 10−1 | 2.84 × 10−1 | 99.75% | 99.82% | 99.51% |
| CV | ISE | Improvement | |||||
|---|---|---|---|---|---|---|---|
| MMPC (Wahid and Brillianto 2020) | Multi-Loop PI | Multi-Loop PI | |||||
| Big Log-Modulus Tuning | Wahid & Gunawan (2015) | Fine-Tuning | Big Log-Modulus Tuning | Wahid & Gunawan (2015) | Fine-Tuning | ||
| CV1 Setpoint Change | |||||||
| 1 | 4.35 × 102 | 8.90 × 101 | 3.92 × 101 | 6.42 × 101 | 79.54% | 90.99% | 85.23% |
| 2 | 4.00 × 10−2 | 1.72 × 10−1 | 1.77 × 10−1 | 3.37 × 10−2 | −328.75% | −343.50% | 15.80% |
| 3 | 6.00 × 10−2 | 3.39 × 104 | 3.49 × 104 | 4.71 × 104 | −5.65 × 107% | −5.82 × 107% | −7.84 × 107% |
| 4 | 5.36 × 10−7 | 9.18 × 10−8 | 4.40 × 10−8 | 9.48 × 10−6 | 82.88% | 91.79% | −1669.03% |
| CV2 Setpoint Change | |||||||
| 1 | 5.00 × 10−4 | 7.45 × 10−3 | 3.07 × 10−3 | 6.63 × 10−3 | −1389.60% | −514.60% | −1226.20% |
| 2 | 7.11 × 101 | 1.44 × 101 | 5.94 | 2.49 × 10−1 | 79.68% | 91.6425% | 99.65% |
| 3 | 2.00 × 10−4 | 2.73 | 2.88 | 3.91 | −1.37 × 106% | −1.44 × 106% | −1.95 × 106% |
| 4 | 8.30 × 10−7 | 4.43 × 10−9 | 3.29 × 10−9 | 2.17 × 10−7 | 99.47% | 99.60% | 73.86% |
| CV3 Setpoint Change | |||||||
| 1 | 1.00 × 10−2 | 4.86 × 10−1 | 1.85 | 1.90 | −4759% | −18,370.00% | −18,930.00% |
| 2 | 6.00 × 10−2 | 7.18 × 10−3 | 1.70 × 10−1 | 7.38 × 10−2 | 88.04% | −182.83% | −23.00% |
| 3 | 3.10 × 101 | 3.71 × 102 | 3.19 × 102 | 1.22 × 103 | −1099.23% | −930.68% | −3845.75% |
| 4 | 5.80 × 10−6 | 4.27 × 10−2 | 5.69 × 10−1 | 1.59 | −7.36 × 105% | −9.82 × 106% | −2.73 × 107% |
| CV4 Setpoint Change | |||||||
| 1 | 4.00 × 10−4 | 4.79 × 10−1 | 9.19 × 10−2 | 1.35 × 10−1 | −1.20 × 105% | −2.29 × 104% | −3.37 × 104% |
| 2 | 5.00 × 10−4 | 6.56 × 10−3 | 9.32 × 10−3 | 6.75 × 10−5 | −1.21 × 103% | −1764.80% | 86.51% |
| 3 | 1.30 × 10−1 | 6.29 × 101 | 7.23 × 101 | 9.73 × 101 | −48,30% | −5.55 × 104% | −7.47 × 104% |
| 4 | 2.50 × 101 | 4.20 × 10−2 | 2.80 × 10−2 | 7.99 × 10−2 | 99.83% | 99.89% | 99.68% |
| Controlled Variable (CV) | Tuning Method | P | I | |
|---|---|---|---|---|
| 1 | Vessel Temperature of Condenser T-103 | WG | 0.67 | 0.33 |
| 2 | MeRecy Temperature | FT | 4.90 | 42.41 |
| 3 | Liquid Percent Level of Condenser T-103 | BLT | 0.01 | 2.16 |
| 4 | Total Liquid Volume Percent of T-103 | WG | 13.50 | 2.38 |
| CV | IAE | Improvement | ISE | Improvement | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| MMPC (Wahid & Brillianto 2020) | Multi-Loop | MMPC (Wahid & Brillianto 2020) | Multi-Loop | ||||||||
| Tuning Method | Simulink | Unisim | Simulink | Unisim | Simulink | Unisim | Simulink | Unisim | |||
| CV1 Setpoint Change | |||||||||||
| 1 | 1.81 × 102 | WG | 2.96 × 101 | 2.08 × 10−3 | 83.66% | 100.00% | 4.35 × 102 | 3.92 × 101 | 2.65 × 10−4 | 90.99% | 100.00% |
| 2 | 4.28 | FT | 1.04 | 1.15 × 10−2 | 75.70% | 99.73% | 4.00 × 10−2 | 3.37 × 10−2 | 1.92 × 10−4 | 15.80% | 99.52% |
| 3 | 4.36 | BLT | 4.08 × 103 | 1.34 × 10−2 | −93,386.24% | 99.69% | 6.00 × 10−2 | 3.39 × 104 | 1.83 × 10−4 | −5.65 × 107% | 99.69% |
| 4 | 2.00 × 10−2 | WG | 1.37 × 10−3 | 1.37 × 10−3 | 93.16% | 93.16% | 5.36 × 10−7 | 4.40 × 10−8 | 2.89 × 10−7 | 91.79% | 46.18% |
| CV2 Setpoint Change | |||||||||||
| 1 | 4.10 × 10−1 | WG | 3.28 × 10−1 | 1.27 × 10−2 | 19.95% | 96.91% | 5.00 × 10−4 | 3.07 × 10−3 | 2.45 × 10−4 | −514.60% | 51.05% |
| 2 | 5.64 × 101 | FT | 2.71 × 10−1 | 2.76 × 10−1 | 99.52% | 99.51% | 7.11 × 101 | 2.49 × 10−1 | 6.43 × 10−1 | 99.65% | 99.10% |
| 3 | 3.20 × 10−1 | BLT | 3.59 × 101 | 3.25 × 10−3 | −11,112.50% | 98.99% | 2.00 × 10−4 | 2.73 | 1.48 × 10−5 | −1.37 × 106% | 92.59% |
| 4 | 2.00 × 10−2 | WG | 8.12 × 10−5 | 1.36 × 10−3 | 99.59% | 93.22% | 8.30 × 10−7 | 3.29 × 10−9 | 2.78 × 10−7 | 99.60% | 66.51% |
| CV3 Setpoint Change | |||||||||||
| 1 | 7.32 | WG | 5.80 | 1.25 × 10−2 | 20.71% | 99.83% | 1.00 × 10−2 | 1.85 | 2.40 × 10−4 | −18370.00% | 97.60% |
| 2 | 4.67 | FT | 3.80 × 10−1 | 1.11 × 10−2 | 91.86% | 99.76% | 6.00 × 10−2 | 7.38 × 10−2 | 1.83 × 10−4 | −23.00% | 99.70% |
| 3 | 5.59 × 101 | BLT | 4.16 × 102 | 2.66 × 10−3 | −643.43% | 100.00% | 3.10 × 101 | 3.71 × 102 | 1.47 × 10−5 | −1099.23% | 100.00% |
| 4 | 5.00 × 10−2 | WG | 4.61 × 10−1 | 8.26 × 10−4 | −821.40% | 98.35% | 5.80 × 10−6 | 5.69 × 10−1 | 1.10 × 10−6 | −9.82 × 106% | 81.06% |
| CV4 Setpoint Change | |||||||||||
| 1 | 5.20 × 10−1 | WG | 1.31 | 1.28 × 10−2 | −151.15% | 97.53% | 4.00 × 10−4 | 9.19 × 10−2 | 2.51 × 10−4 | −2.29 × 104% | 37.25% |
| 2 | 5.30 × 10−1 | FT | 4.31 × 10−2 | 1.14 × 10−2 | 91.87% | 97.84% | 5.00 × 10−4 | 6.75 × 10−5 | 1.91 × 10−4 | 86.51% | 61.80% |
| 3 | 5.79 | BLT | 1.73 × 102 | 3.26 × 10−3 | −2886.18% | 99.94% | 1.30 × 10−1 | 6.29 × 101 | 1.50 × 10−5 | −4.83 × 104% | 99.99% |
| 4 | 5.74 × 101 | WG | 1.03 × 10−1 | 4.04 × 10−4 | 99.82% | 100.00% | 2.50 × 101 | 2.80 × 10−2 | 2.83 × 10−7 | 99.89% | 100.00% |
| Feed Temperature Disturbance | |||||||||||
| 1 | 3.70 × 101 | WG | 4.71 | 1.61 × 10−1 | 87.27% | 99.56% | 2.30 × 101 | 8.01 × 10−1 | 2.78 × 10−2 | 96.52% | 99.88% |
| 2 | 7.96 × 101 | FT | 1.62 × 10−1 | 1.07 × 10−2 | 99.80% | 99.99% | 1.06 × 102 | 7.03 × 10−4 | 1.14 × 10−4 | 100.00% | 100.00% |
| 3 | 6.18 | BLT | 6.26 × 10−9 | 9.44 × 10−3 | 100.00% | 99.85% | 6.41 × 10−1 | 8.31 × 10−5 | 9.06 × 10−5 | 99.99% | 99.99% |
| 4 | 2.04 × 102 | WG | 1.10 × 10−2 | 2.52 × 10−3 | 99.99% | 100.00% | 6.94 × 102 | 2.39 × 10−5 | 1.17 × 10−5 | 100.00% | 100.00% |
| Feed Flow Disturbance | |||||||||||
| 1 | 3.75 × 101 | WG | 1.53 × 10−1 | 1.67 × 10−1 | 99.59% | 99.56% | 6.62 × 101 | 5.47 × 10−4 | 4.22 × 10−5 | 100.00% | 100.00% |
| 2 | 1.55 × 102 | FT | 1.18 × 10−2 | 1.38 × 10−2 | 99.99% | 99.99% | 4.43 × 102 | 1.62 × 10−5 | 1.15 × 10−4 | 100.00% | 100.00% |
| 3 | 3.32 | BLT | 1.46 × 10−6 | 7.36 × 10−4 | 100.00% | 99.98% | 7.68 × 10−1 | 4.66 × 10−8 | 6.73 × 10−7 | 100.00% | 100.00% |
| 4 | 7.41 × 101 | WG | 5.15 × 10−3 | 9.42 × 10−3 | 99.99% | 99.99% | 9.64 × 101 | 5.35 × 10−6 | 9.45 × 10−5 | 100.00% | 100.00% |
| Feed Flow and Temperature Disturbance | |||||||||||
| 1 | 2.24 × 101 | WG | 4.59 | 1.70 × 10−1 | 79.49% | 99.24% | 2.68 × 101 | 7.79 × 10−1 | 3.01 × 10−2 | 97.09% | 99.89% |
| 2 | 1.64 × 102 | FT | 1.70 × 10−1 | 1.14 × 10−2 | 99.90% | 99.99% | 3.85 × 102 | 8.38 × 10−4 | 1.14 × 10−4 | 100.00% | 100.00% |
| 3 | 1.24 × 101 | BLT | 6.12 × 10−5 | 3.42 × 10−3 | 100.00% | 99.97% | 1.83 | 7.93 × 10−5 | 2.96 × 10−5 | 100.00% | 100.00% |
| 4 | 2.04 × 102 | WG | 1.10 × 10−2 | 3.27 × 10−2 | 99.99% | 99.98% | 6.94 × 102 | 2.39 × 10−5 | 1.43 × 10−3 | 100.00% | 100.00% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wahid, A.; Rikimata, M. Methanol–Water Purification Control Using Multi-Loop PI Controllers Based on Linear Set Point and Disturbance Models. ChemEngineering 2021, 5, 70. https://doi.org/10.3390/chemengineering5040070
Wahid A, Rikimata M. Methanol–Water Purification Control Using Multi-Loop PI Controllers Based on Linear Set Point and Disturbance Models. ChemEngineering. 2021; 5(4):70. https://doi.org/10.3390/chemengineering5040070
Chicago/Turabian StyleWahid, Abdul, and Monica Rikimata. 2021. "Methanol–Water Purification Control Using Multi-Loop PI Controllers Based on Linear Set Point and Disturbance Models" ChemEngineering 5, no. 4: 70. https://doi.org/10.3390/chemengineering5040070
APA StyleWahid, A., & Rikimata, M. (2021). Methanol–Water Purification Control Using Multi-Loop PI Controllers Based on Linear Set Point and Disturbance Models. ChemEngineering, 5(4), 70. https://doi.org/10.3390/chemengineering5040070