A Simplified Framework for Modelling Viscoelastic Fluids in Discrete Multiphysics
Abstract
:1. Introduction
2. Viscoelastic Behaviour and Standard Models
3. SPH Formulation
4. Proposed Modelling Technique
5. Numerical Experiments
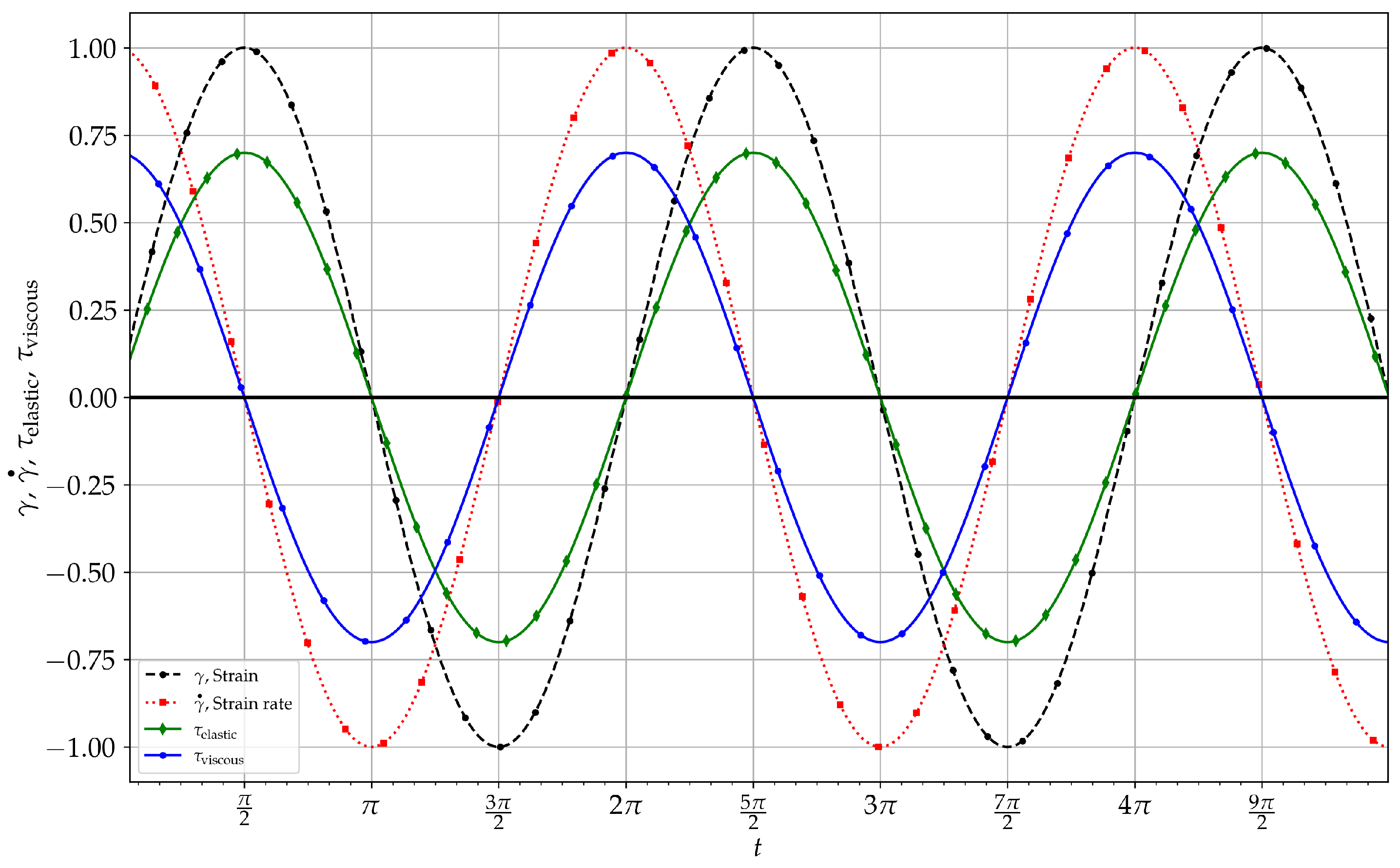
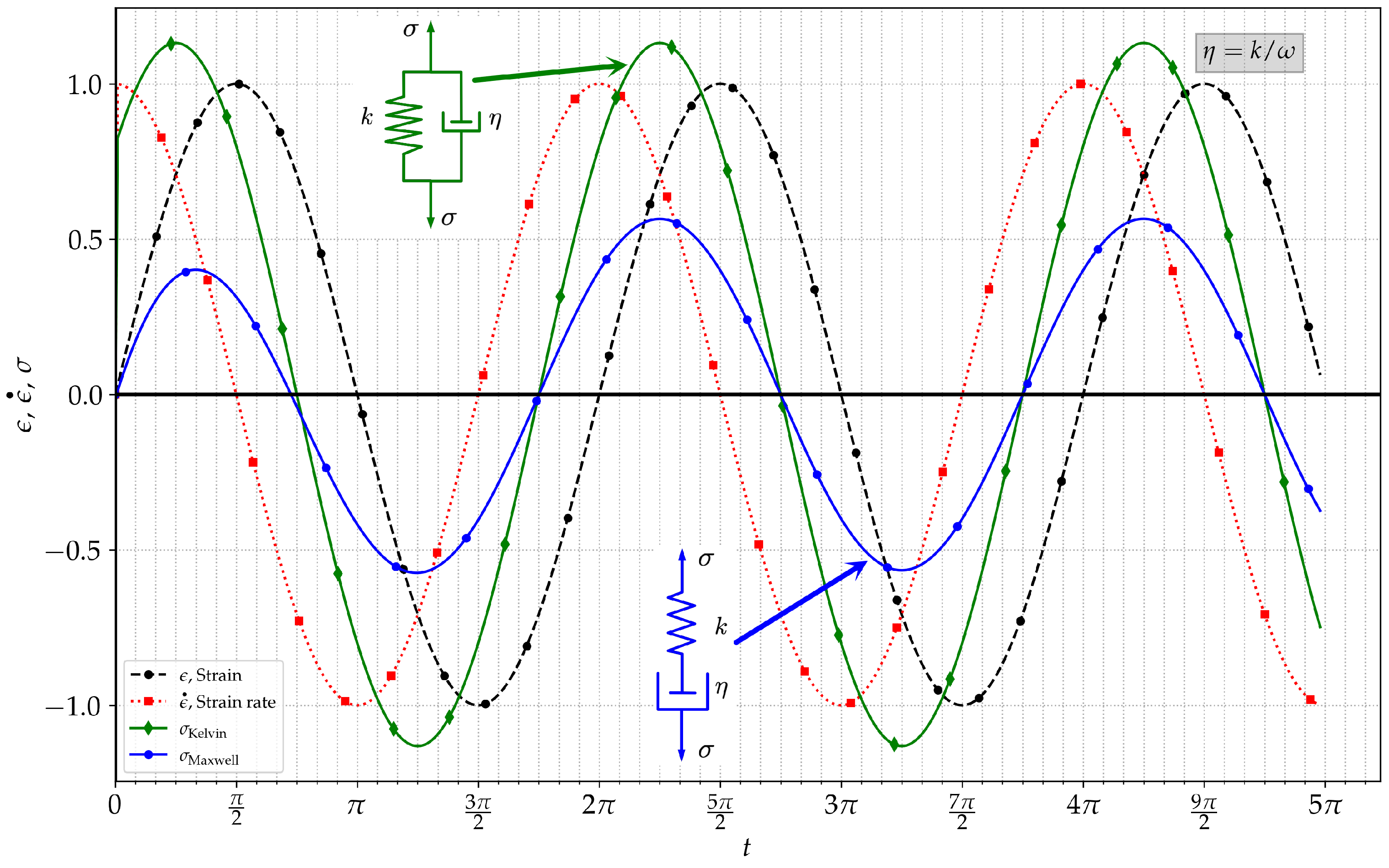
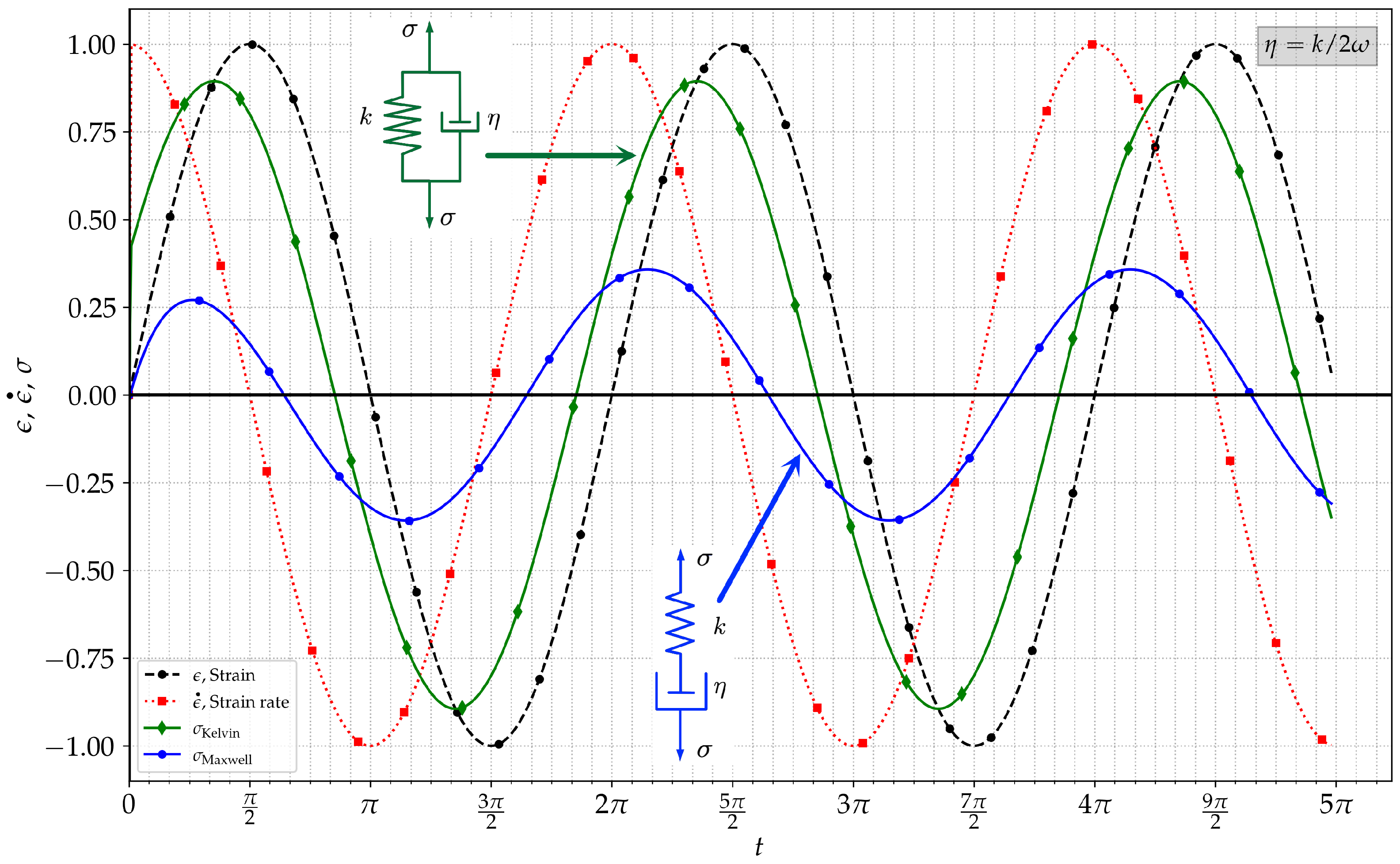
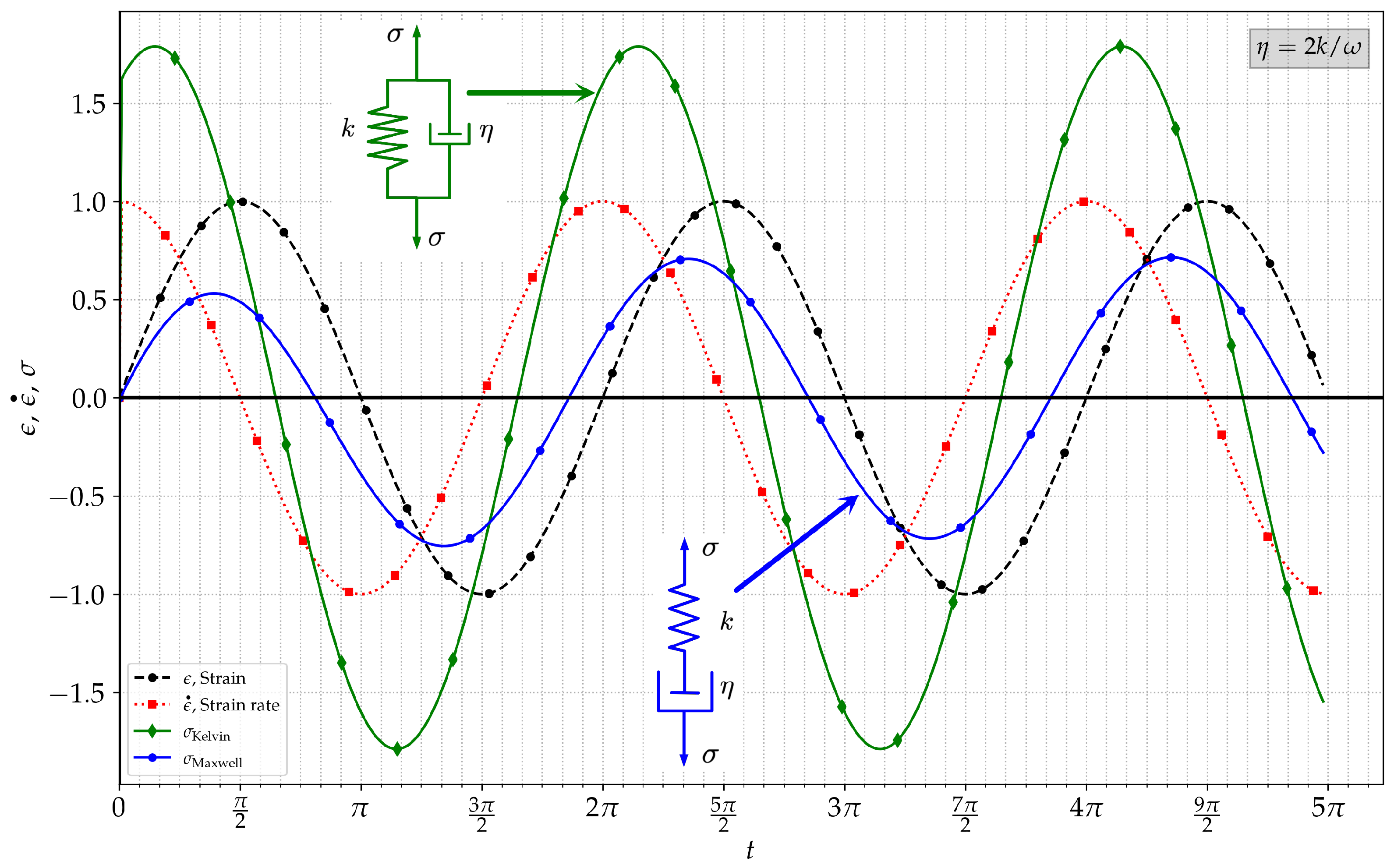
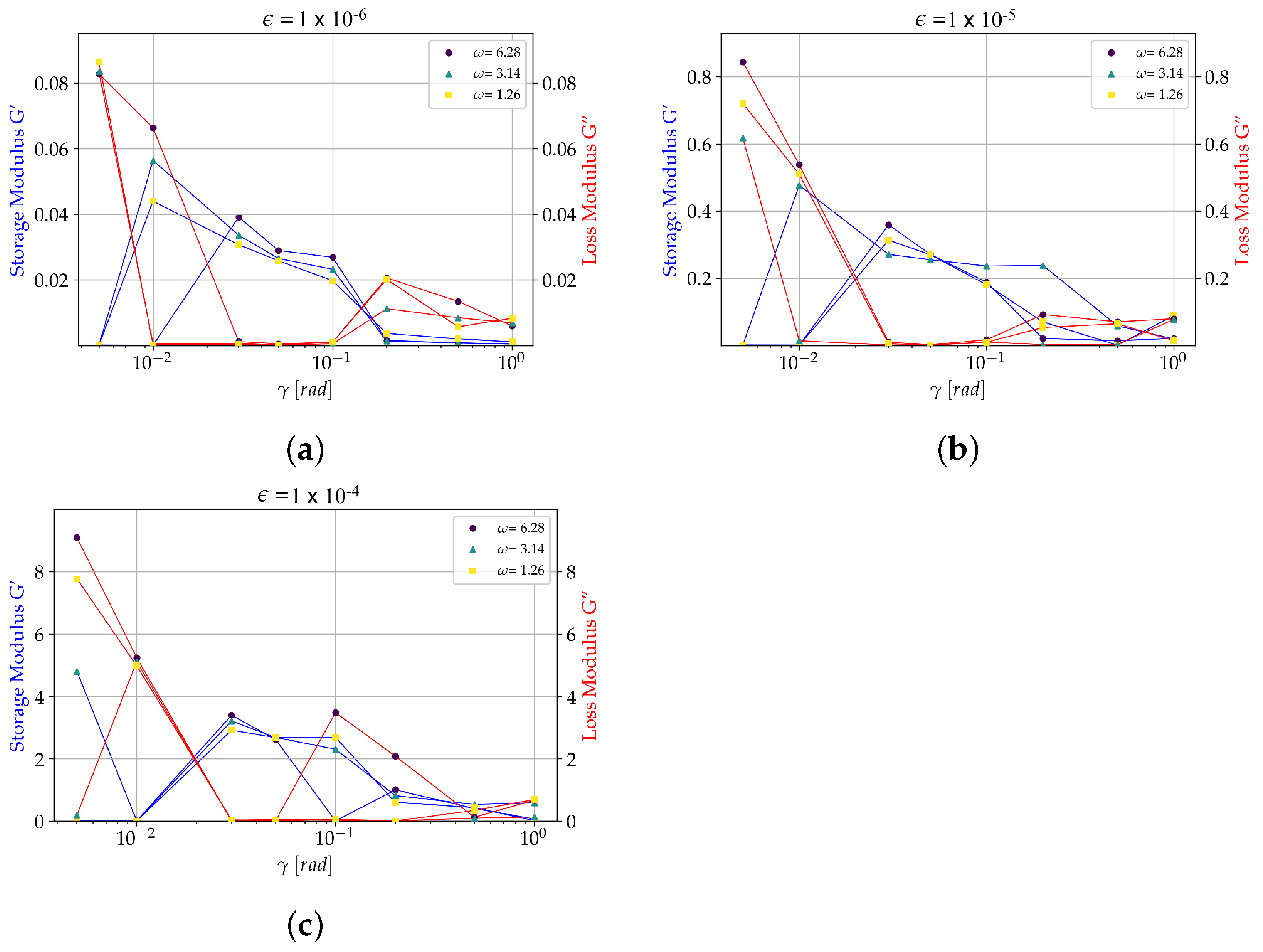
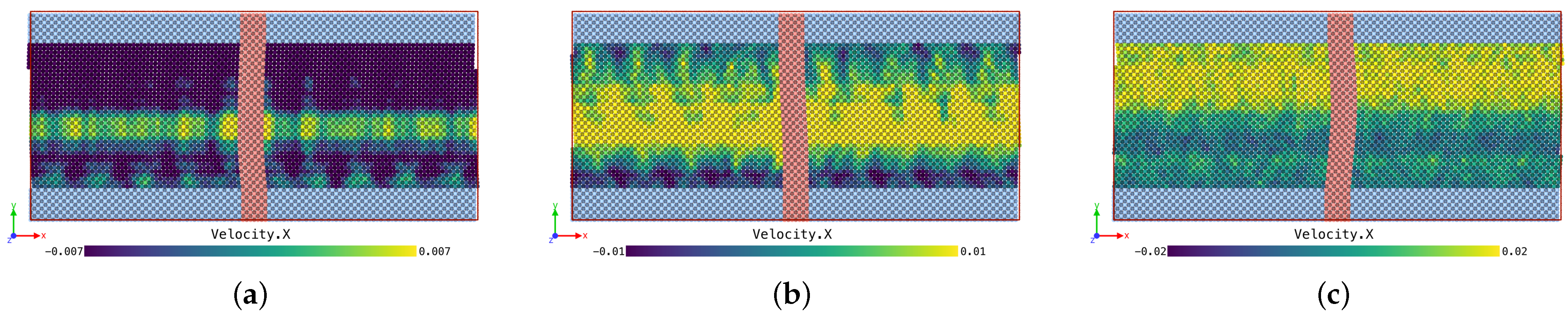
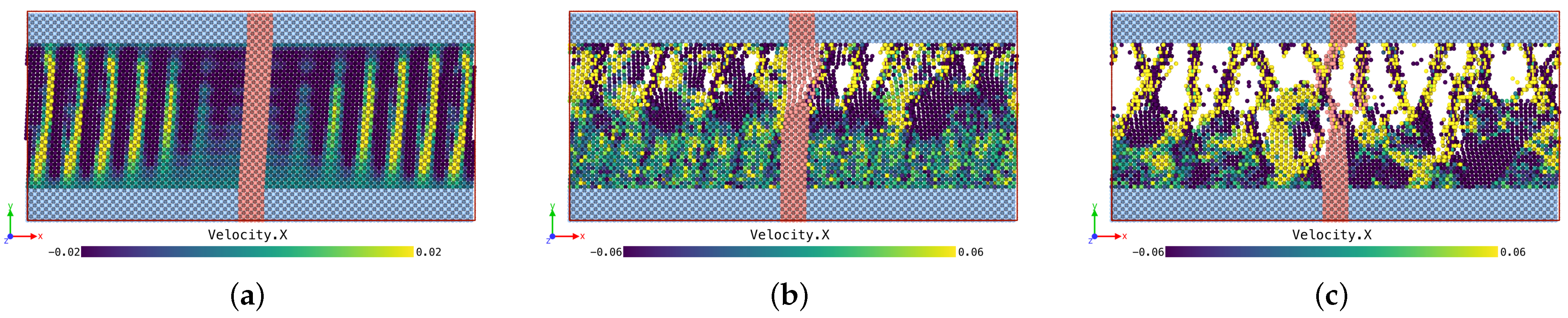
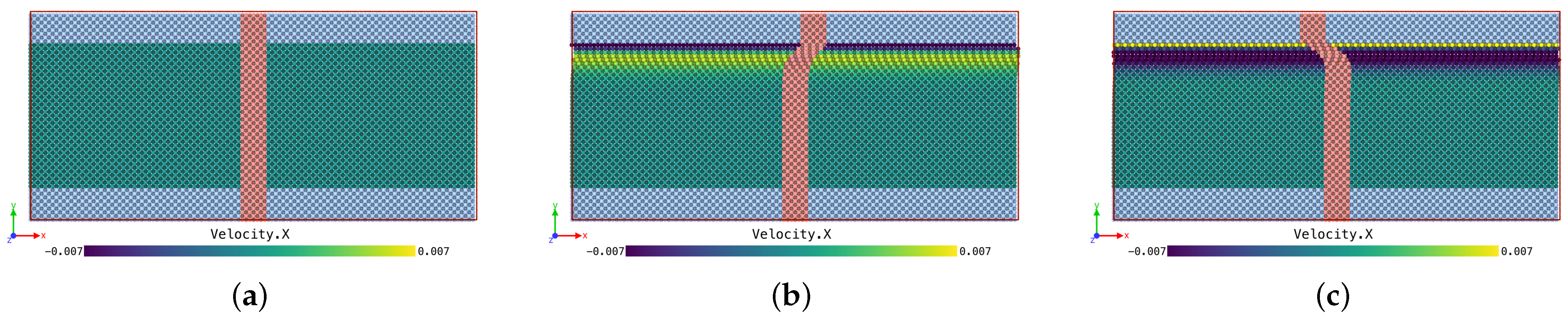
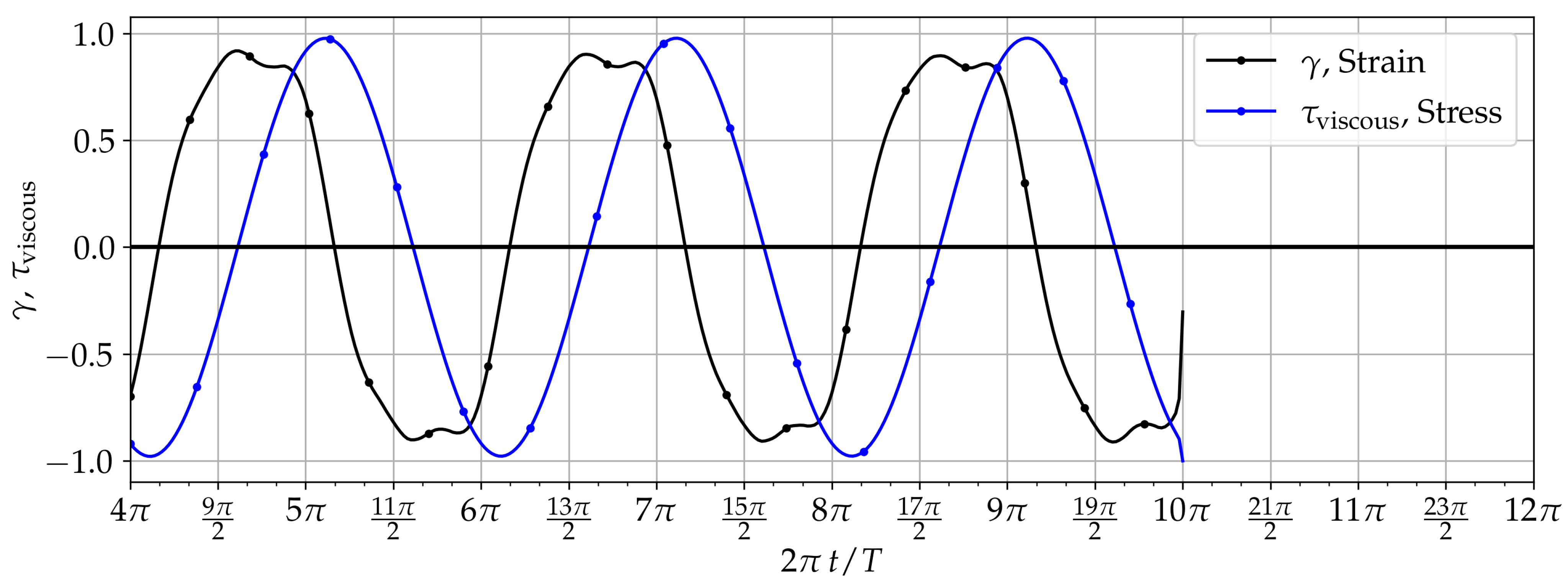
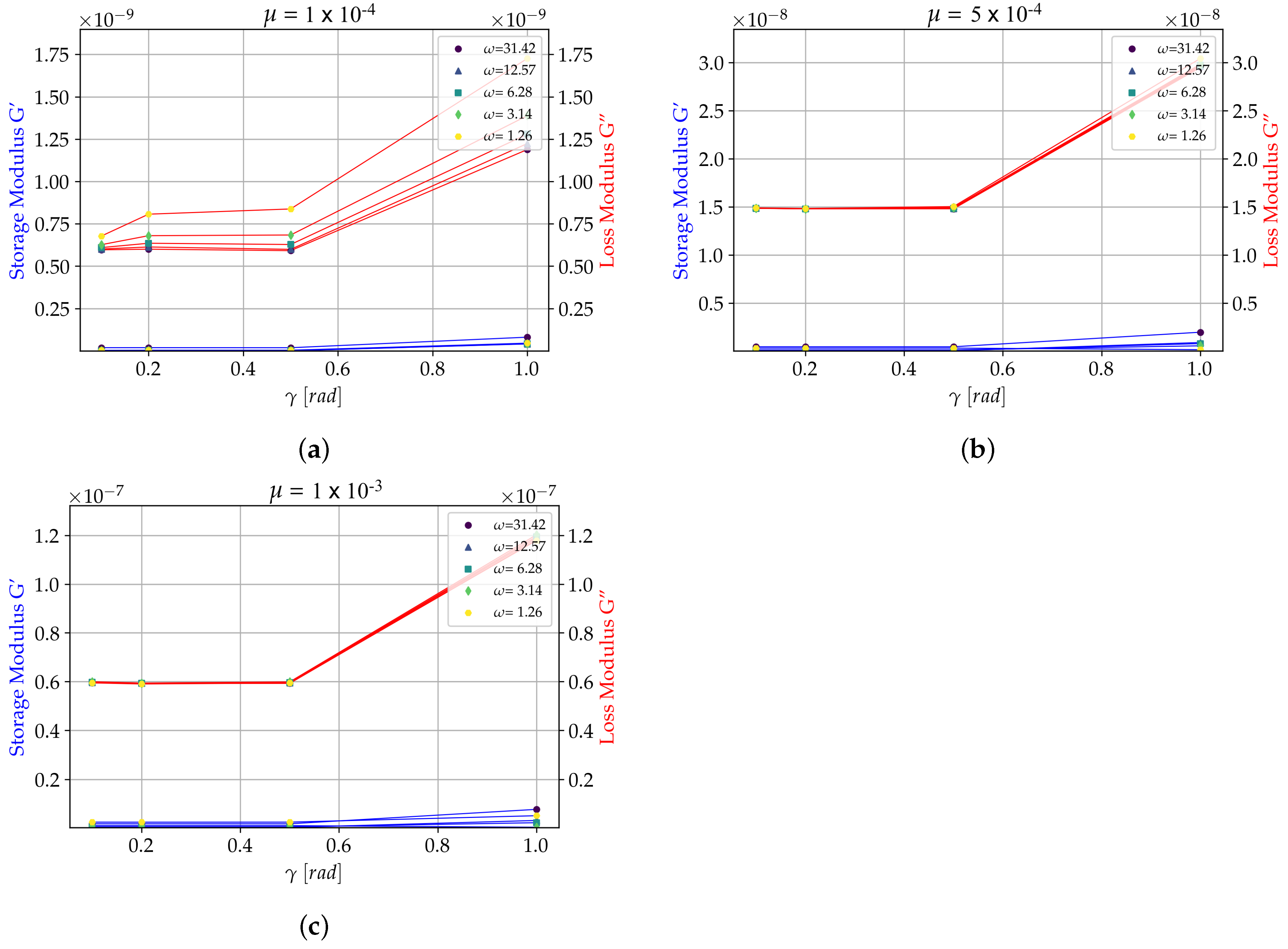
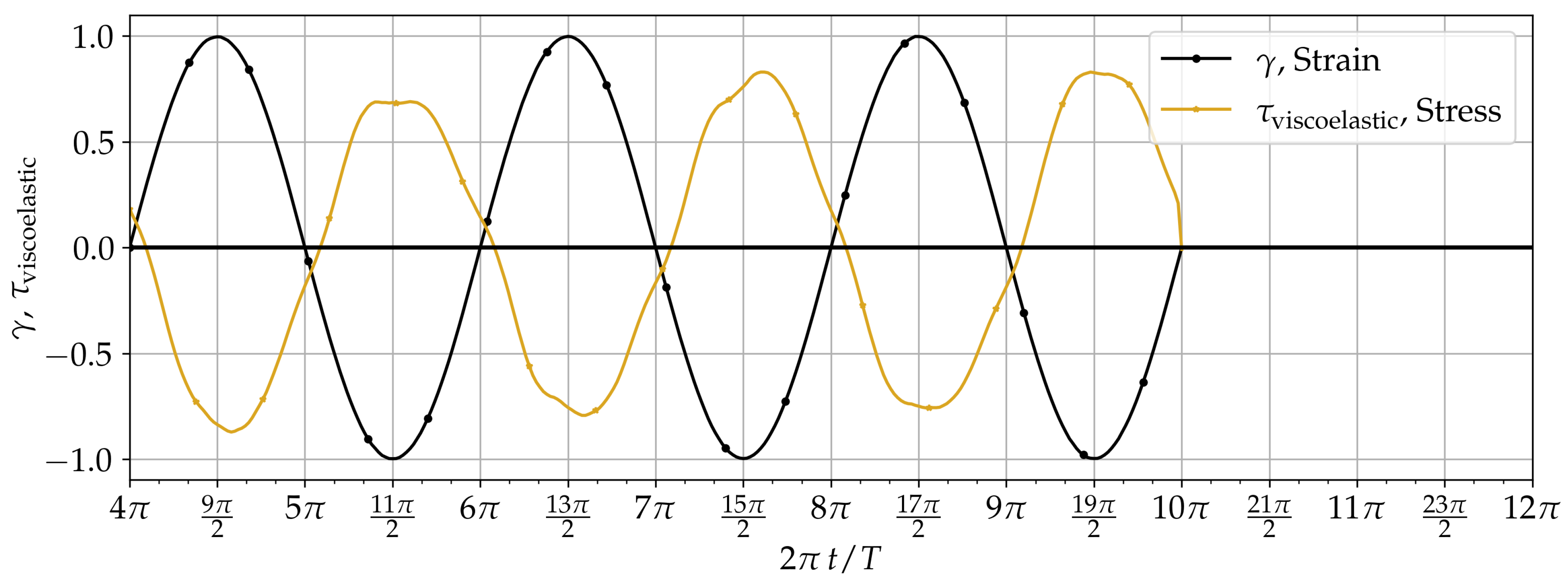
5.1. Dynamic Response to Oscillating Shear
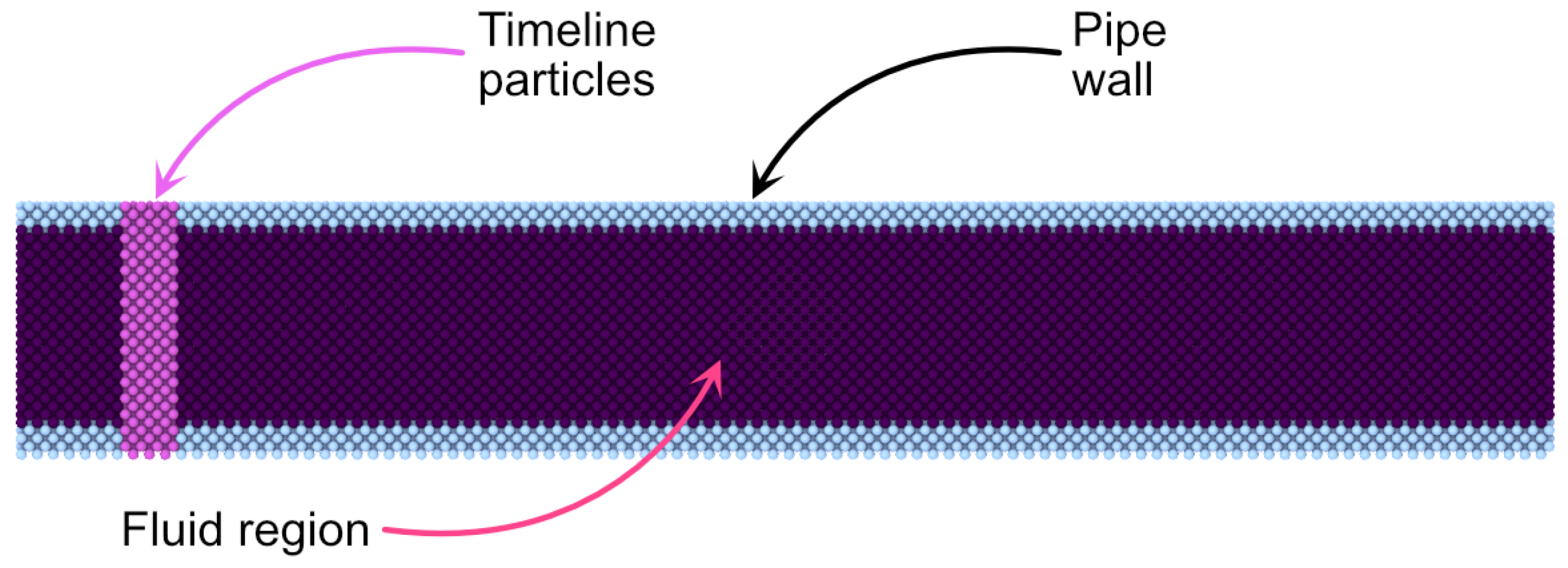
5.2. Viscoelastic Flows in Cylindrical Pipes
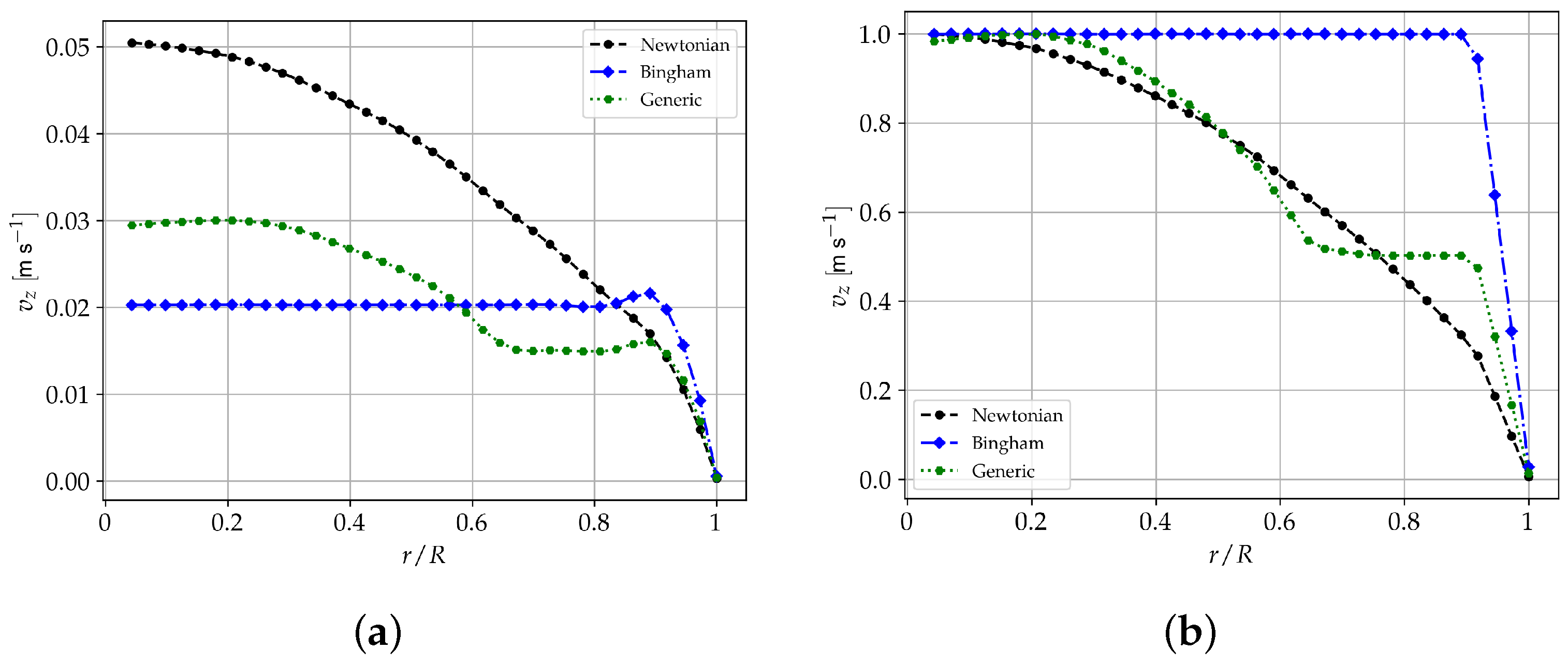
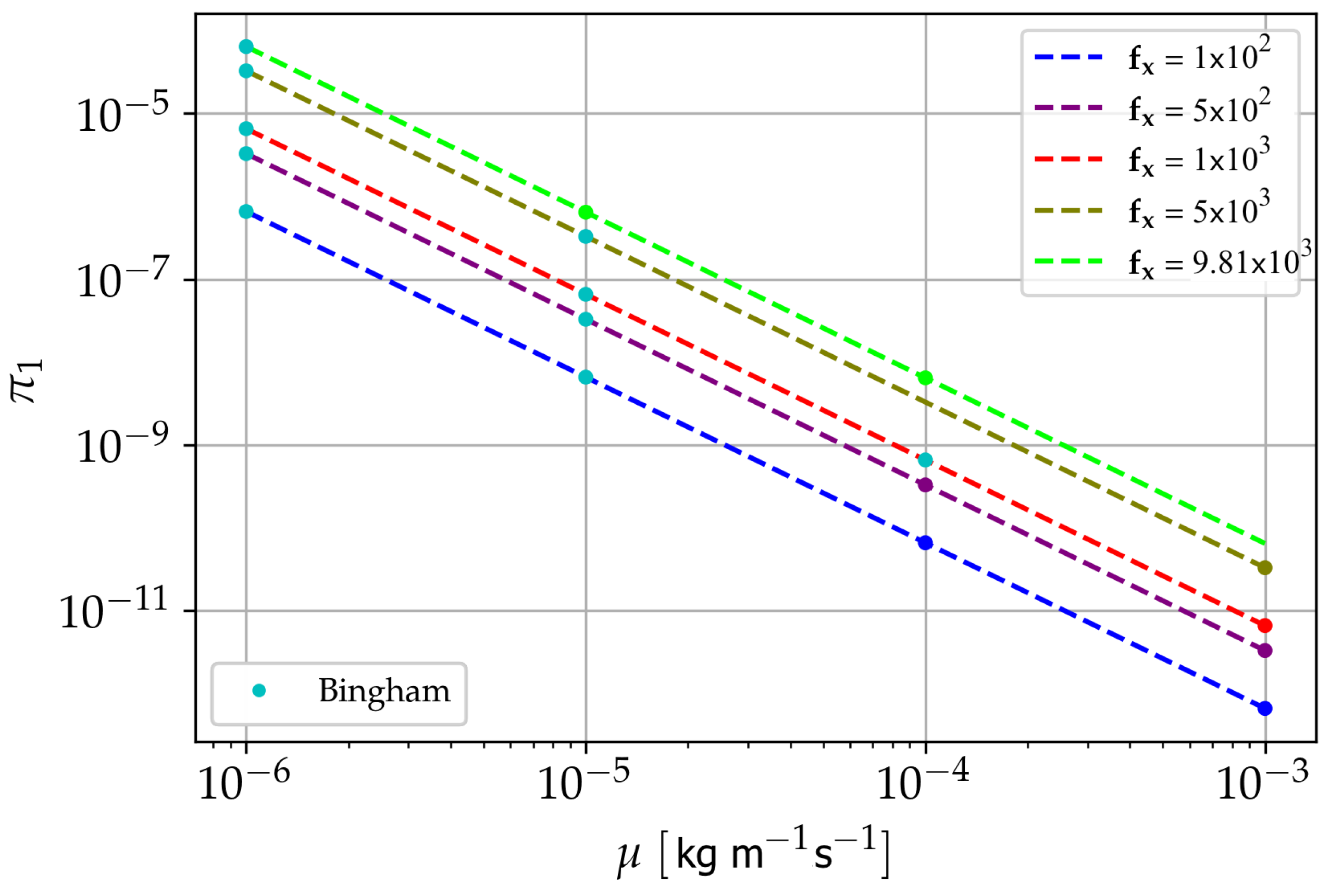
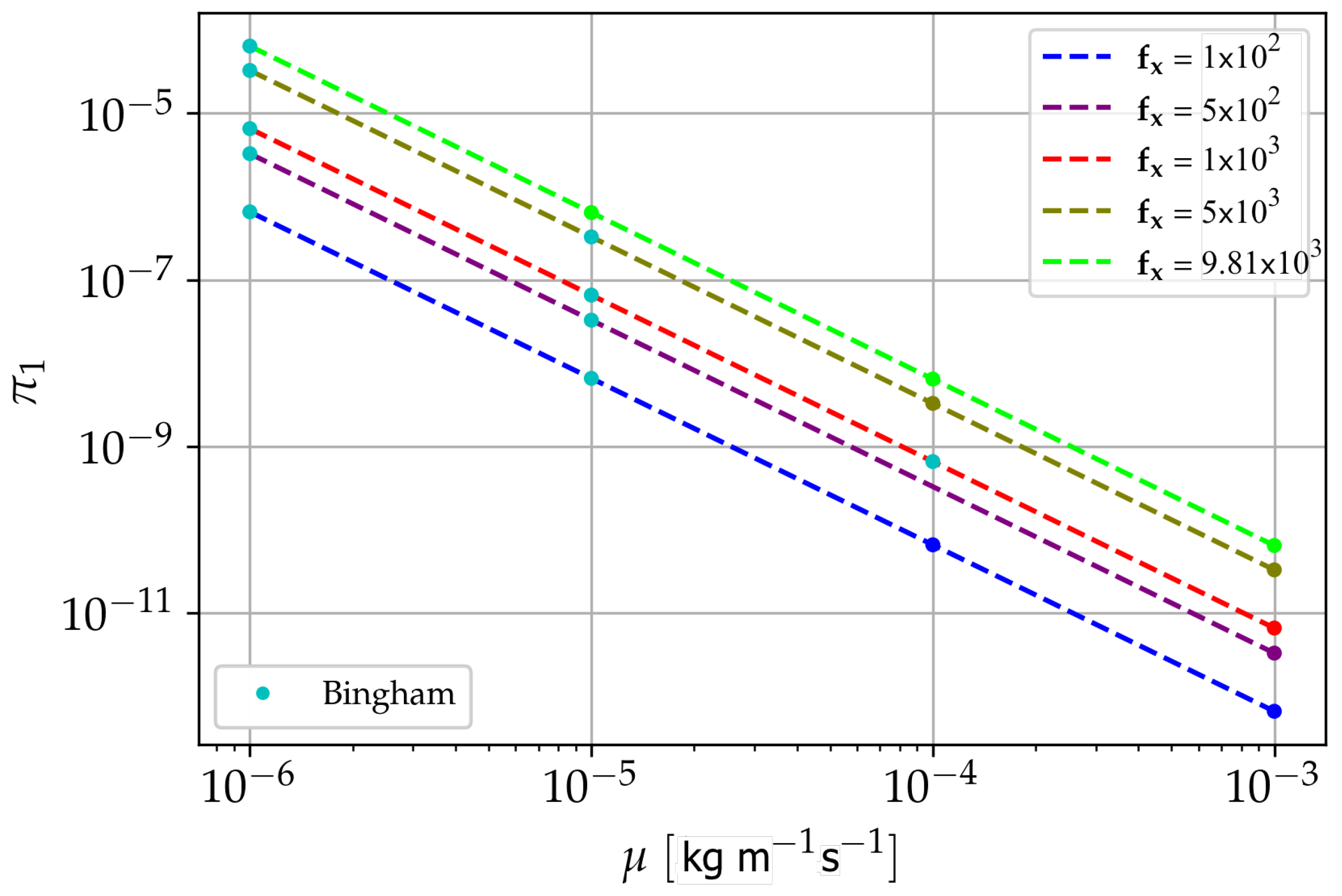
5.2.1. Bingham Flows: Velocity Profiles and Yield Stress
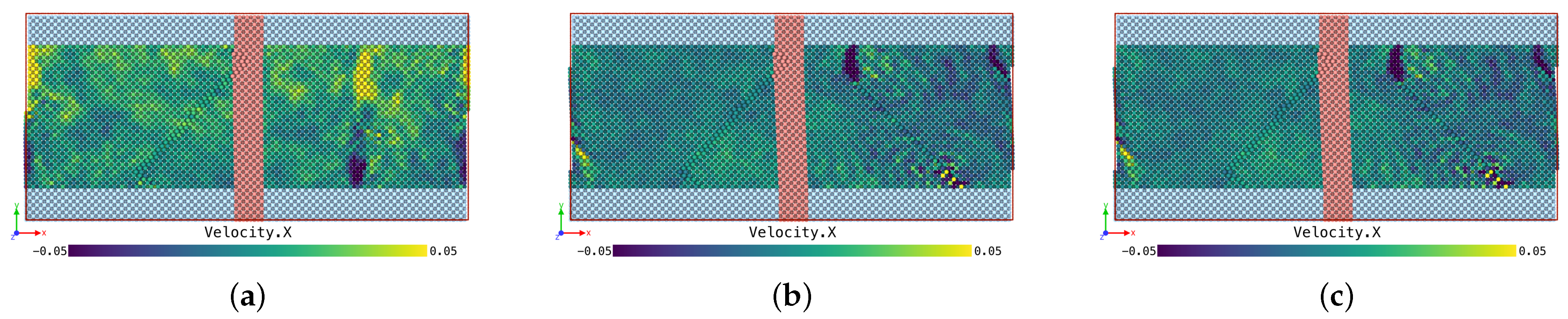
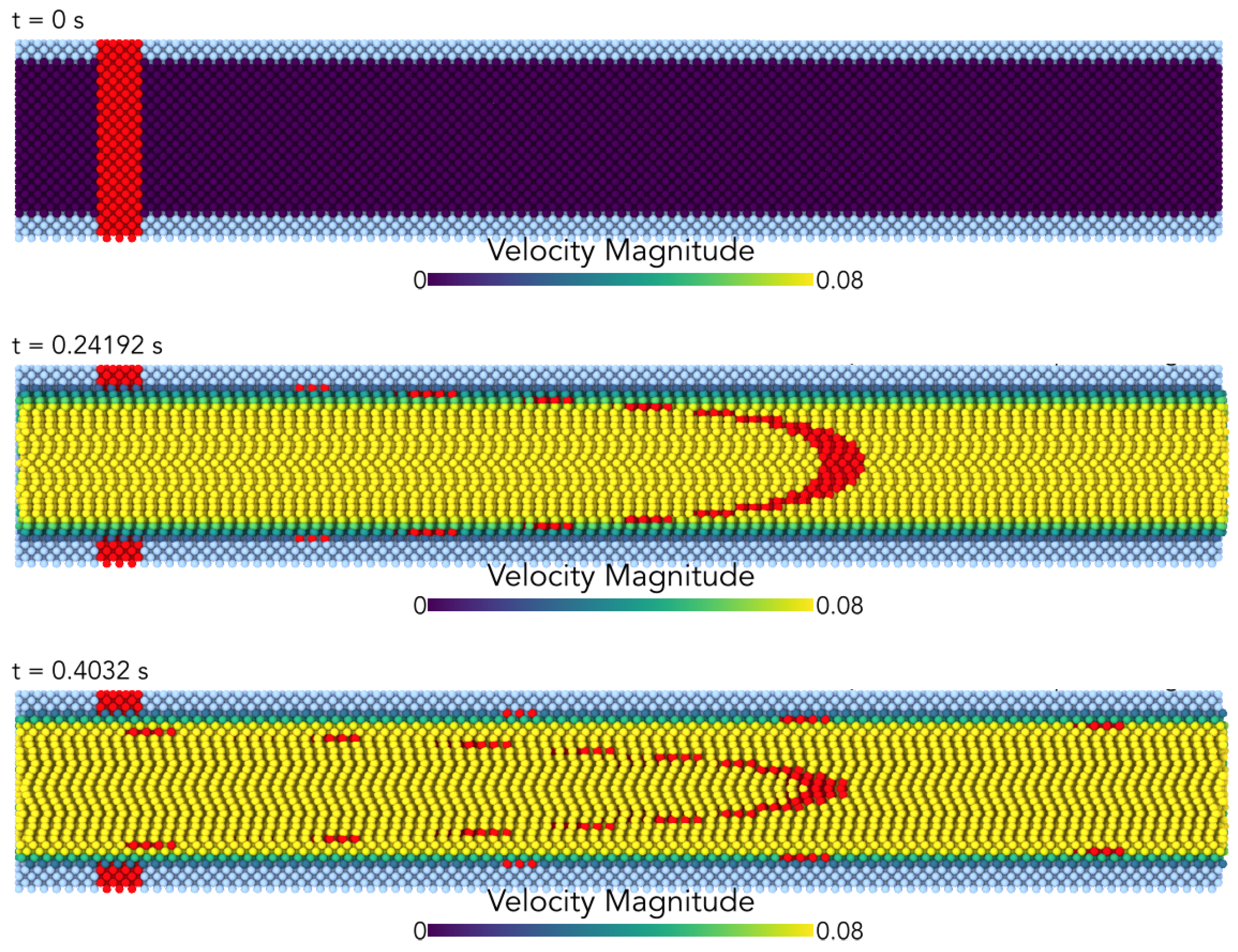
5.2.2. Pipe Flow-Numerical Experiments
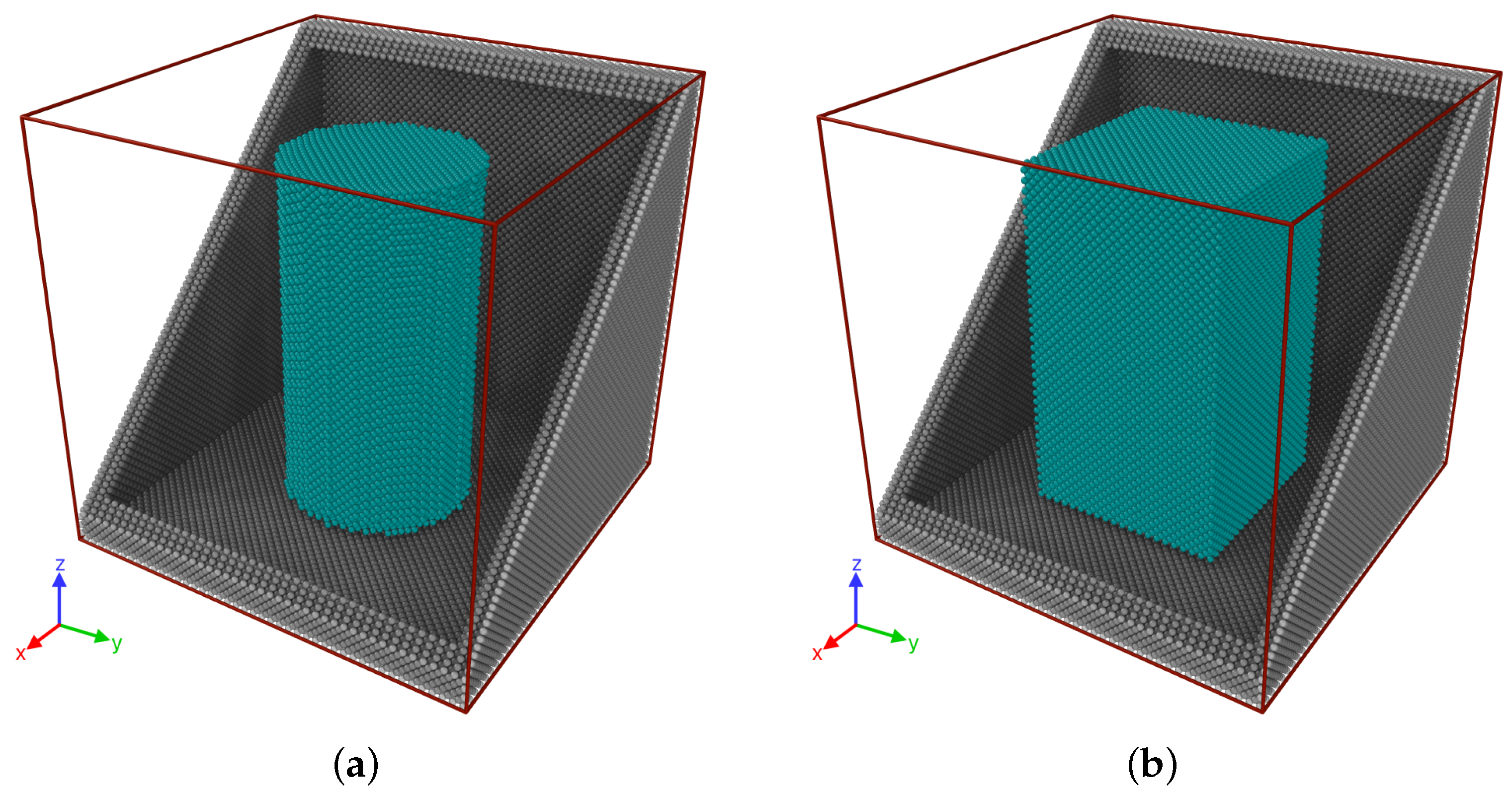
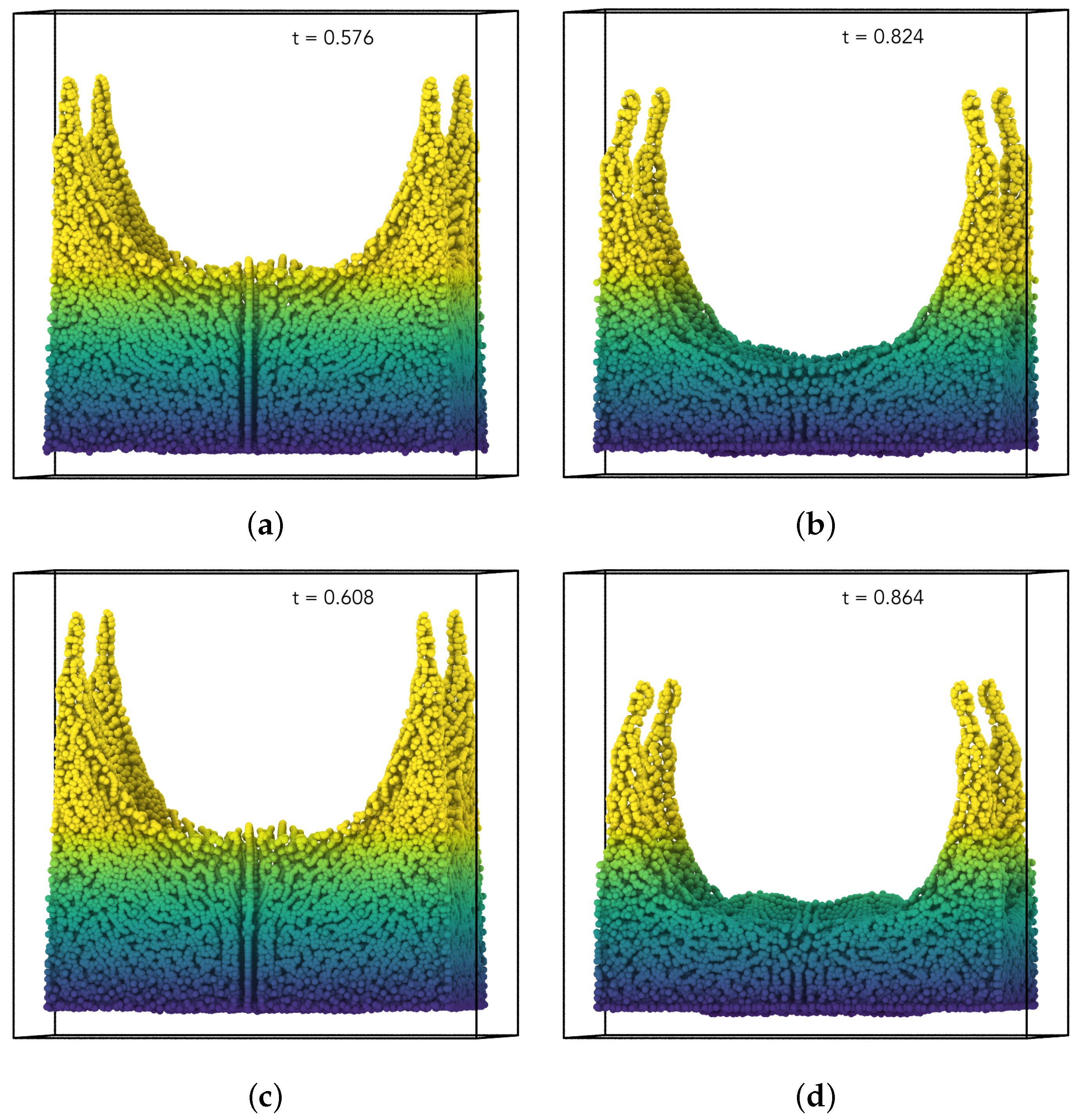
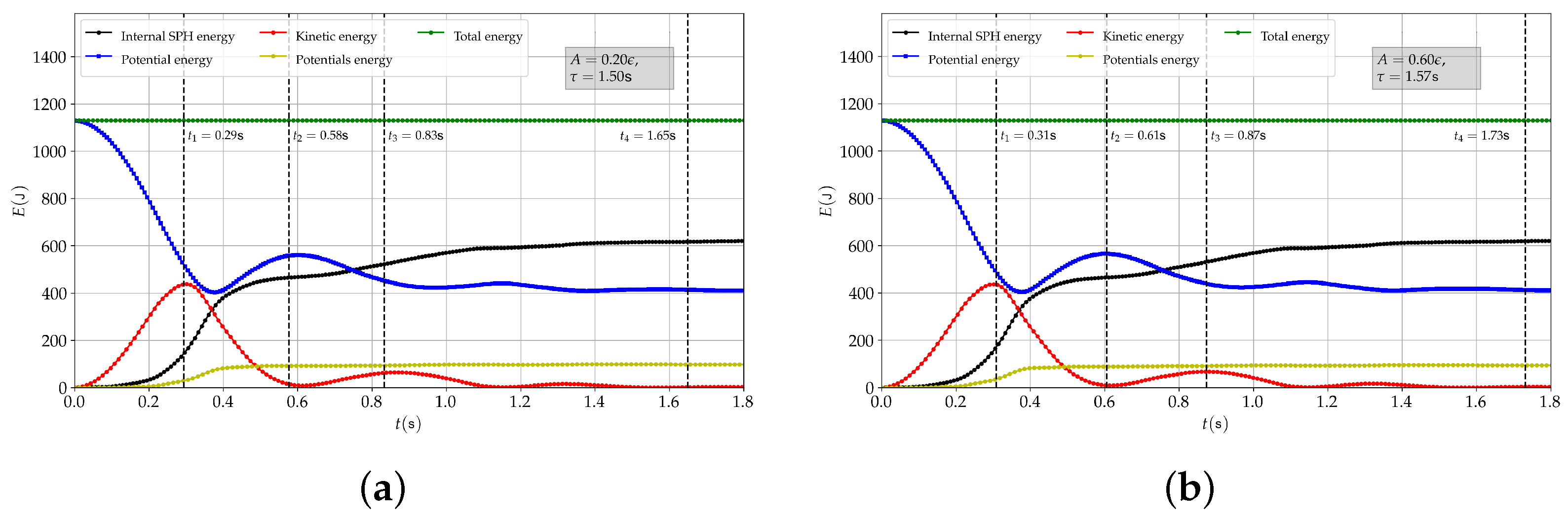
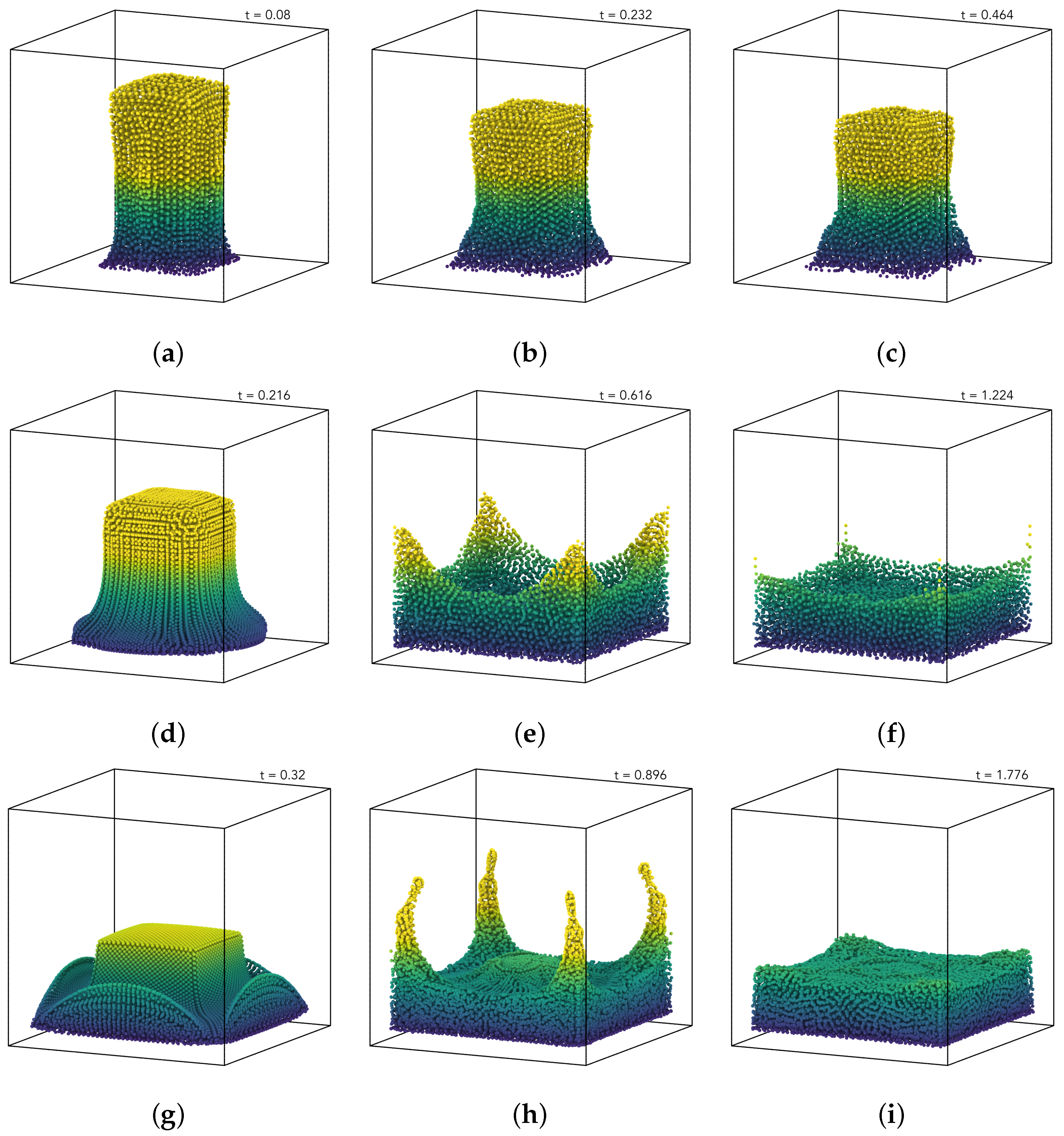
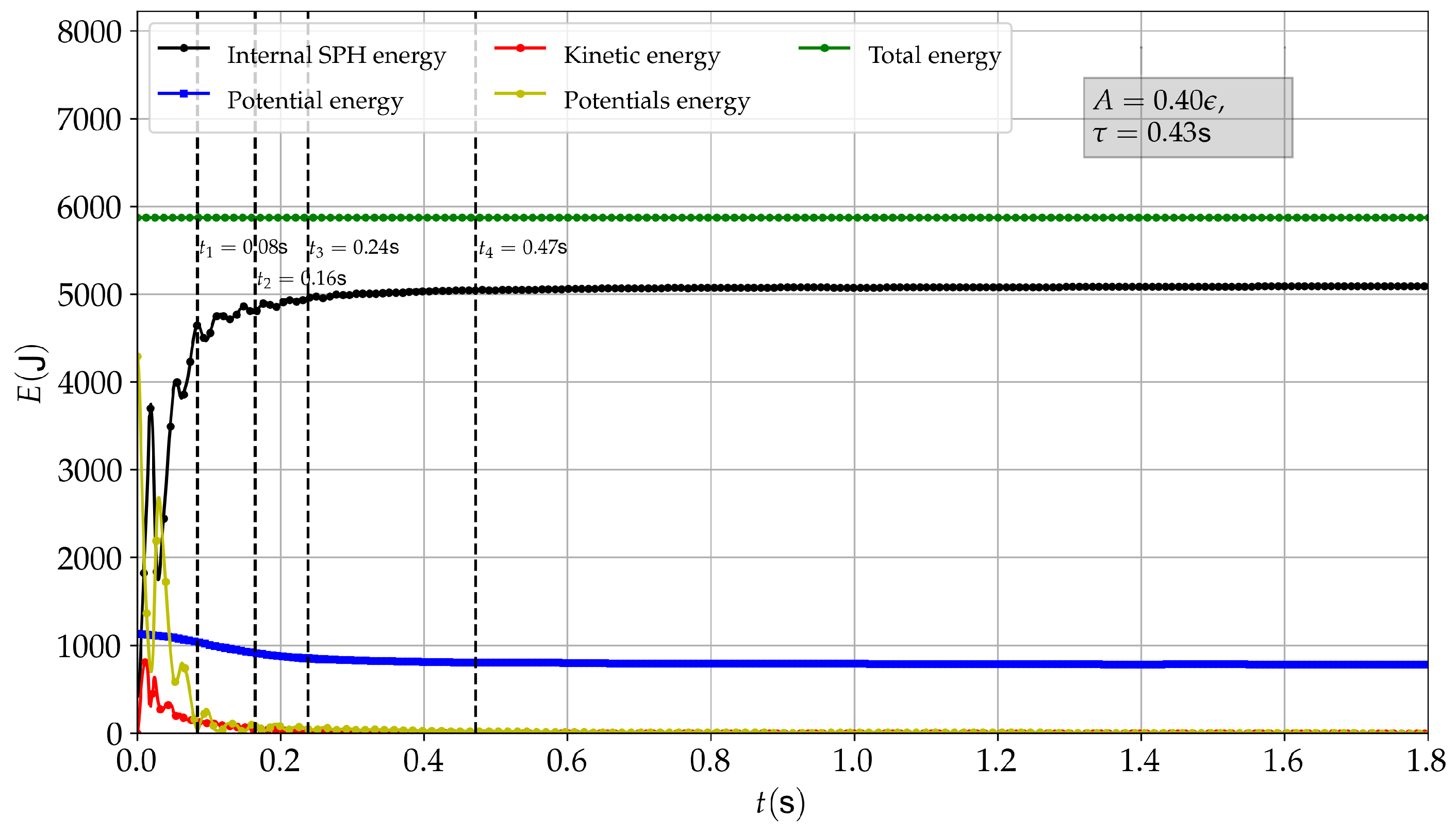
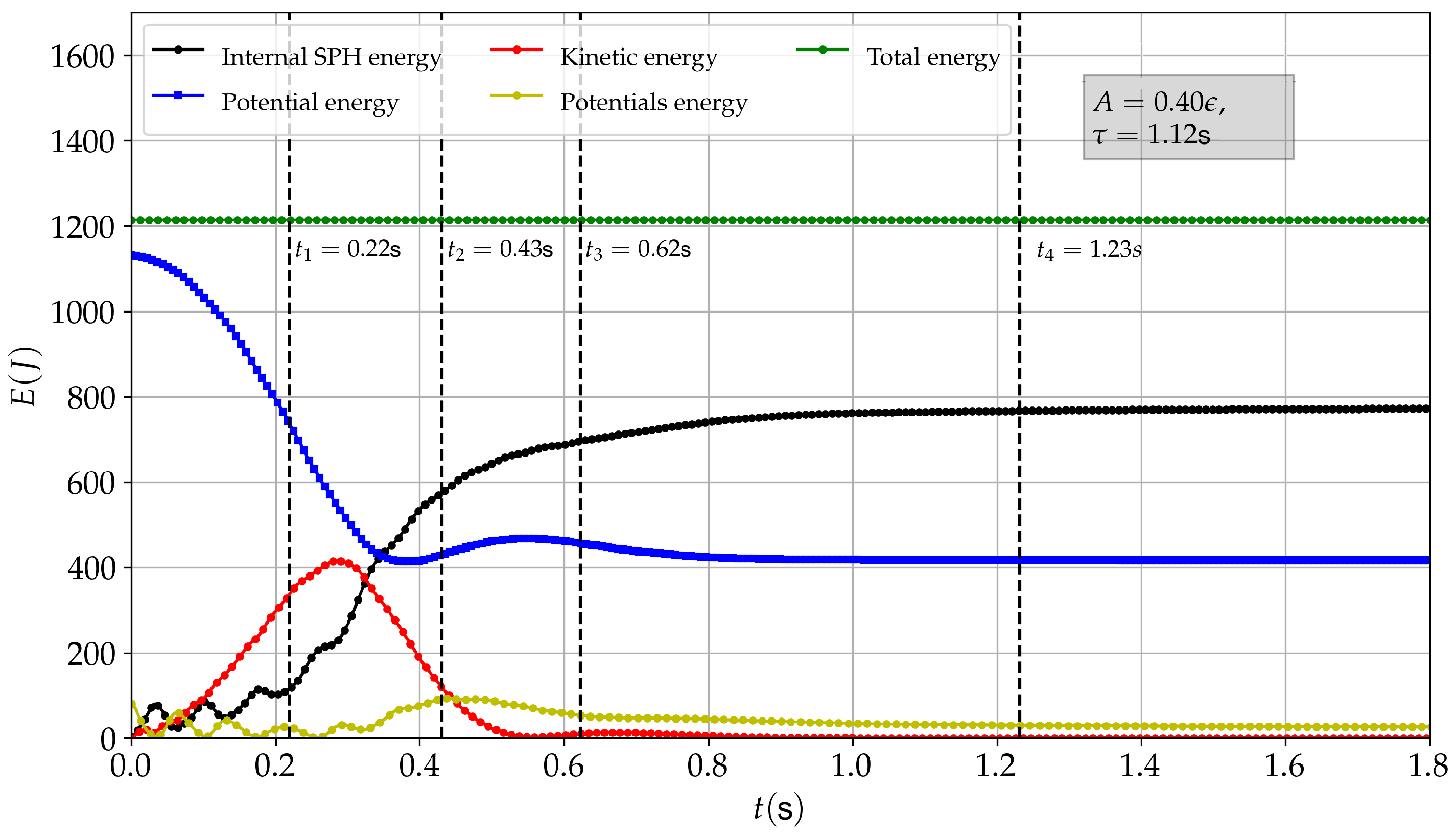
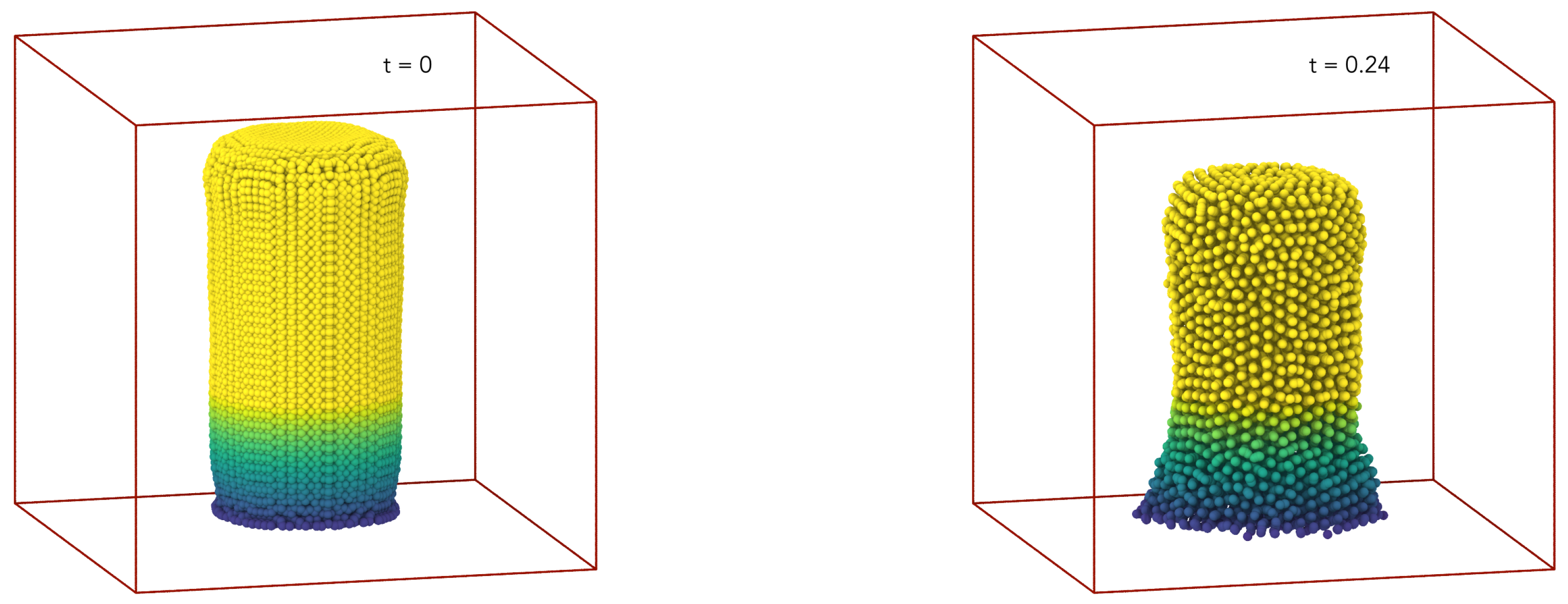
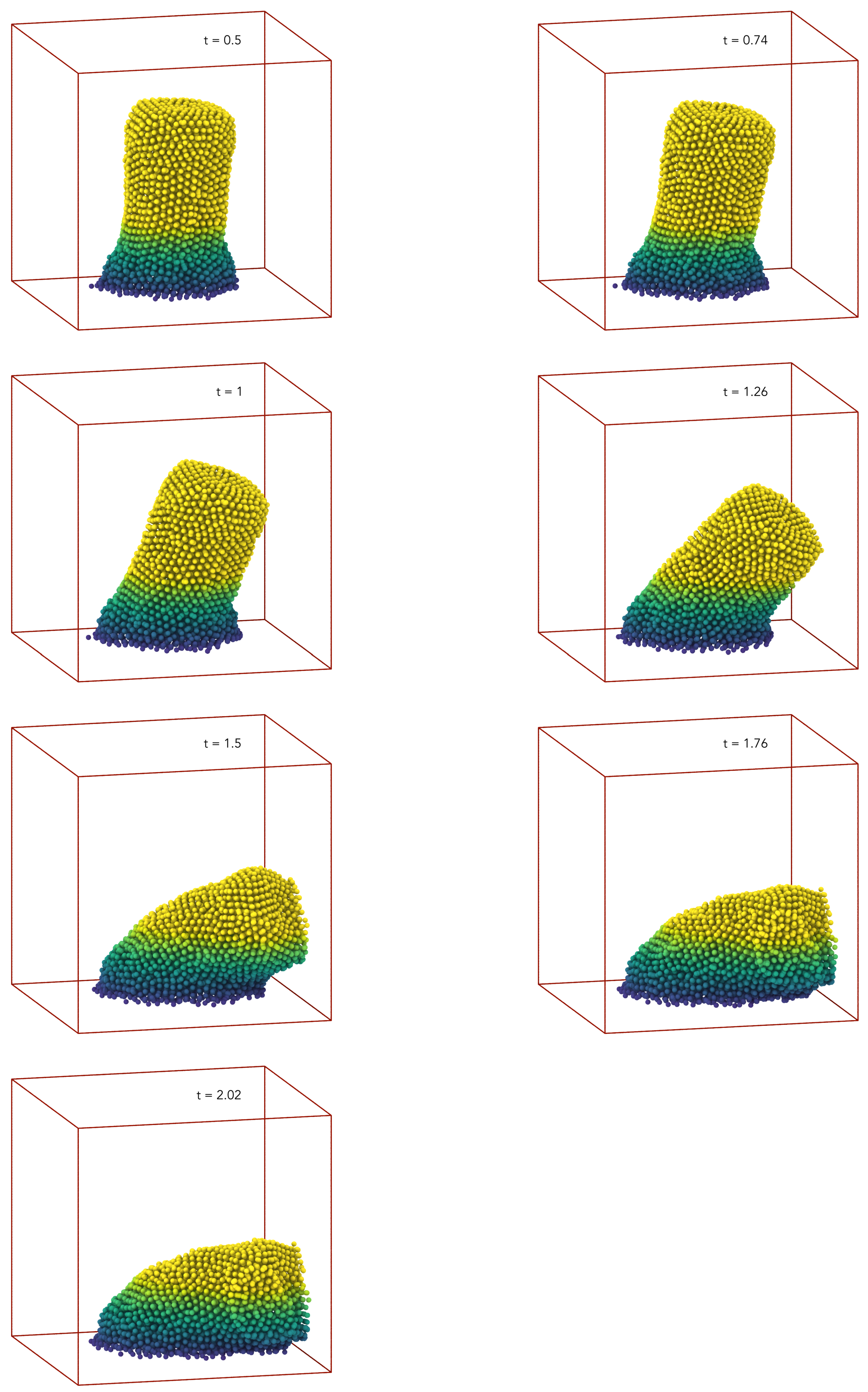
5.3. Column Collapse Due to Gravitational Potential
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Stamper, R.L.; Lieberman, M.F.; Drake, M.V. Secondary open angle glaucoma. In Becker-Shaffer’s Diagnosis and Therapy of the Glaucomas; Elsevier: Edinburgh, UK, 2009; pp. 266–293. [Google Scholar] [CrossRef]
- Yang, K.H. Material Laws and Properties. In Basic Finite Element Method as Applied to Injury Biomechanics; Associated Press: London, UK, 2018; pp. 231–256. [Google Scholar] [CrossRef]
- Chandran, N.; Sarathchandran, C.; Thomas, S. Introduction to rheology. In Rheology of Polymer Blends and Nanocomposites; Springer: Dordrecht, The Netherlands, 2009; pp. 1–17. [Google Scholar] [CrossRef]
- Ferry, J.D. Viscoelastic Properties of Polymers; John Wiley & Sons: New York, NY, USA, 1980. [Google Scholar]
- Nowick, A. Anelastic Relaxation in Crystalline Solids; Academic Press: New York, NY, USA, 1972. [Google Scholar]
- Lakes, R.S. Viscoelastic measurement techniques. Rev. Sci. Instrum. 2004, 75, 797–810. [Google Scholar] [CrossRef] [Green Version]
- Ardakani, H.A.; Mitsoulis, E.; Hatzikiriakos, S.G. Thixotropic flow of toothpaste through extrusion dies. J. Non-Newton. Fluid Mech. 2011, 166, 1262–1271. [Google Scholar] [CrossRef]
- Mitsoulis, E.; Khalfalla, Y.; Benyounis, K. Polymer Film Casting: Modeling. In Reference Module in Materials Science and Materials Engineering; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar] [CrossRef]
- Tabilo-Munizaga, G.; Barbosa-Cánovas, G.V. Rheology for the food industry. J. Food Eng. 2005, 67, 147–156. [Google Scholar] [CrossRef]
- Myhan, R.; Białobrzewski, I.; Markowski, M. An approach to modeling the rheological properties of food materials. J. Food Eng. 2012, 111, 351–359. [Google Scholar] [CrossRef]
- Derkach, S.R.; Krägel, J.; Miller, R. Methods of measuring rheological properties of interfacial layers (Experimental methods of 2D rheology). Colloid J. 2009, 71, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Denn, M.M. Issues in Viscoelastic Fluid Mechanics. Annu. Rev. Fluid Mech. 1990, 22, 13–32. [Google Scholar] [CrossRef]
- Shariff, M.H.B.M.; Bustamante, R.; Merodio, J. Rate type constitutive equations for fiber reinforced nonlinearly vicoelastic solids using spectral invariants. Mech. Res. Commun. 2017, 84, 60–64. [Google Scholar] [CrossRef]
- Jha, N.K.; Reinoso, J.; Dehghani, H.; Merodio, J. Constitutive modeling framework for residually stressed viscoelastic solids at finite strains. Mech. Res. Commun. 2019, 95, 79–84. [Google Scholar] [CrossRef]
- Drozdov, A.D.; Kolmanovskii, V.B. Constitutive Models of Viscoelastic Materials. In Stability in Viscoelasticity; Academic Press, Elsevier: Amsterdam, The Netherlands, 1994; pp. 1–132. [Google Scholar] [CrossRef]
- Wineman, A. Nonlinear Viscoelastic Solids—A Review. Math. Mech. Solids 2009, 14, 300–366. [Google Scholar] [CrossRef]
- Balbi, V.; Shearer, T.; Parnell, W.J. A modified formulation of quasi-linear viscoelasticity for transversely isotropic materials under finite deformation. Proc. R. Soc. Math. Phys. Eng. Sci. 2018, 474, 20180231. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Capilnasiu, A.; Nordsletten, D. Comparative Analysis of Nonlinear Viscoelastic Models across Common Biomechanical Experiments. J. Elast. 2021, 1–36. [Google Scholar] [CrossRef]
- Mackay, A.T.; Phillips, T.N. On the derivation of macroscopic models for compressible viscoelastic fluids using the generalized bracket framework. J. Non-Newton. Fluid Mech. 2019, 266, 59–71. [Google Scholar] [CrossRef]
- Clavet, S.; Beaudoin, P.; Poulin, P. Particle-based viscoelastic fluid simulation. In Proceedings of the 2005 ACM SIGGRAPH/Eurographics symposium on Computer Animation-SCA’05, Los Angeles, CA, USA, 29–31 July 2005; ACM Press: New York, NY, USA, 2005. [Google Scholar] [CrossRef]
- Westervoß, P.; Turek, S.; Damanik, H.; Ouazzi, A. The Tensor Diffusion approach for simulating viscoelastic fluids. J. Non-Newton. Fluid Mech. 2020, 286, 104431. [Google Scholar] [CrossRef]
- Rajagopal, K.R.; Srinivasa, A.R. A Gibbs-potential-based formulation for obtaining the response functions for a class of viscoelastic materials. Proc. R. Soc. Math. Phys. Eng. Sci. 2011, 467, 39–58. [Google Scholar] [CrossRef]
- Goktekin, T.G.; Bargteil, A.W.; O’Brien, J.F. A method for animating viscoelastic fluids. ACM Trans. Graph. 2004, 23, 463–468. [Google Scholar] [CrossRef] [Green Version]
- Chang, Y.; Bao, K.; Liu, Y.; Zhu, J.; Wu, E. A particle-based method for viscoelastic fluids animation. In Proceedings of the 16th ACM Symposium on Virtual Reality Software and Technology-VRST’09, Kyoto, Japan, 18–20 November 2009; ACM Press: New York, NY, USA, 2009; pp. 111–117. [Google Scholar] [CrossRef]
- Takamatsu, K.; Kanai, T. A fast and practical method for animating particle-based viscoelastic fluids. Int. J. Virtual Real. 2011, 10, 29–35. [Google Scholar] [CrossRef]
- Alexiadis, A. A smoothed particle hydrodynamics and coarse-grained molecular dynamics hybrid technique for modelling elastic particles and breakable capsules under various flow conditions. Int. J. Numer. Methods Eng. 2014, 100, 713–719. [Google Scholar] [CrossRef]
- Alexiadis, A. A new Framework for Modelling the Dynamics and the Breakage of Capsules, Vesicles and Cells in Fluid Flow. Procedia IUTAM 2015, 16, 80–88. [Google Scholar] [CrossRef] [Green Version]
- Alexiadis, A. The Discrete Multi-Hybrid System for the Simulation of Solid-Liquid Flows. PLoS ONE 2015, 10, e0124678. [Google Scholar] [CrossRef] [Green Version]
- Mohammed, A.M.; Ariane, M.; Alexiadis, A. Using Discrete Multiphysics Modelling to Assess the Effect of Calcification on Hemodynamic and Mechanical Deformation of Aortic Valve. ChemEngineering 2020, 4, 48. [Google Scholar] [CrossRef]
- Schütt, M.; Stamatopoulos, K.; Simmons, M.; Batchelor, H.; Alexiadis, A. Modelling and simulation of the hydrodynamics and mixing profiles in the human proximal colon using Discrete Multiphysics. Comput. Biol. Med. 2020, 121, 103819. [Google Scholar] [CrossRef]
- Sahputra, I.H.; Alexiadis, A.; Adams, M.J. A Coarse Grained Model for Viscoelastic Solids in Discrete Multiphysics Simulations. ChemEngineering 2020, 4, 30. [Google Scholar] [CrossRef]
- Chhabra, R.P.; Richardson, J.F. Non-Newtonian Flow in the Process Industries: Fundamentals and Engineering Applications; Butterworth-Heinemann: Oxford, MS, USA, 1999. [Google Scholar]
- Mai-Duy, N.; Phan-Thien, N. Understanding Viscoelasticity; Springer International Publishing AG: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Flügge, W. Viscoelasticity; Springer: Berlin/Heidelberg, Germany, 1975. [Google Scholar]
- Bonfanti, A.; Kaplan, J.L.; Charras, G.; Kabla, A. Fractional viscoelastic models for power-law materials. Soft Matter 2020, 16, 6002–6020. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Xu, Y.; Li, J. Stationary probability densities of generalized Maxwell-type viscoelastic systems under combined harmonic and Gaussian white noise excitations. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 1–9. [Google Scholar] [CrossRef]
- Epaarachchi, J.A. The effect of viscoelasticity on fatigue behaviour of polymer matrix composites. In Creep and Fatigue in Polymer Matrix Composites; Woodhead Publishing Limited: Cambridge, UK, 2011; pp. 492–513. [Google Scholar] [CrossRef]
- Renaud, F.; Dion, J.L.; Chevallier, G.; Tawfiq, I.; Lemaire, R. A new identification method of viscoelastic behavior: Application to the generalized Maxwell model. Mech. Syst. Signal Process. 2011, 25, 991–1010. [Google Scholar] [CrossRef] [Green Version]
- Qi, H.; Xu, M. Unsteady flow of viscoelastic fluid with fractional Maxwell model in a channel. Mech. Res. Commun. 2007, 34, 210–212. [Google Scholar] [CrossRef]
- Lewandowski, R.; Chorążyczewski, B. Identification of the parameters of the Kelvin–Voigt and the Maxwell fractional models, used to modeling of viscoelastic dampers. Comput. Struct. 2010, 88, 1–17. [Google Scholar] [CrossRef]
- Marynowski, K.; Kapitaniak, T. Kelvin–Voigt versus Bürgers internal damping in modeling of axially moving viscoelastic web. Int. J. Non-Linear Mech. 2002, 37, 1147–1161. [Google Scholar] [CrossRef]
- Gingold, R.A.; Monaghan, J.J. Smoothed particle hydrodynamics: Theory and application to non-spherical stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–389. [Google Scholar] [CrossRef]
- Lucy, L.B. A numerical approach to the testing of the fission hypothesis. Astron. J. 1977, 82, 1013. [Google Scholar] [CrossRef]
- Monaghan, J.J.; Gingold, R.A. Shock simulation by the particle method SPH. J. Comput. Phys. 1983, 52, 374–389. [Google Scholar] [CrossRef]
- Ganzenmuller, G.C.; Steinhauser, M.O.; Liedekerke, P.V. The implementation of Smooth Particle Hydrodynamics in LAMMPS. Liedekerke Kathol. Univ. Leuven 2011, 1, 1–26. [Google Scholar]
- Liu, M.B.; Liu, G.R. Smoothed Particle Hydrodynamics (SPH): An Overview and Recent Developments. Arch. Comput. Methods Eng. 2010, 17, 25–76. [Google Scholar] [CrossRef] [Green Version]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- LAMMPS. LAMMPS Molecular Dynamics Simulator. Available online: https://www.lammps.org/index.html (accessed on 1 August 2021).
- Morris, J.P.; Fox, P.J.; Zhu, Y. Modeling Low Reynolds Number Incompressible Flows Using SPH. J. Comput. Phys. 1997, 136, 214–226. [Google Scholar] [CrossRef]
- Lattanzio, J.C.; Monaghan, J.J.; Monaghan, H.; Schwarz, M.P. Controlling Penetration. SIAM J. Sci. Stat. Comput. 1986, 7, 591–598. [Google Scholar] [CrossRef]
- Albano, A.; Alexiadis, A. Interaction of Shock Waves with Discrete Gas Inhomogeneities: A Smoothed Particle Hydrodynamics Approach. Appl. Sci. 2019, 9, 5435. [Google Scholar] [CrossRef] [Green Version]
- Albano, A.; le Guillou, E.; Danzé, A.; Moulitsas, I.; Sahputra, I.H.; Rahmat, A.; Duque-Daza, C.A.; Shang, X.; Ching Ng, K.; Ariane, M.; et al. How to Modify LAMMPS: From the Prospective of a Particle Method Researcher. ChemEngineering 2021, 5, 30. [Google Scholar] [CrossRef]
- Ellero, M.; Kröger, M.; Hess, S. Viscoelastic flows studied by smoothed particle dynamics. J. Non–Newton. Fluid Mech. 2002, 105, 35–51. [Google Scholar] [CrossRef]
- Pazdniakou, A.; Adler, P.M. Lattice Spring Models. Transp. Porous Media 2012, 93, 243–262. [Google Scholar] [CrossRef]
- Cooke, I.R.; Kremer, K.; Deserno, M. Tunable generic model for fluid bilayer membranes. Phys. Rev. E 2005, 72, 011506. [Google Scholar] [CrossRef] [Green Version]
- Frasca, P.; Harper, R.; Katz, L. Strain and frequency dependence of shear storage modulus for human single osteons and cortical bone microsamples—Size and hydration effects. J. Biomech. 1981, 14, 679–690. [Google Scholar] [CrossRef]
- Mason, T.G.; Weitz, D.A. Optical Measurements of Frequency-Dependent Linear Viscoelastic Moduli of Complex Fluids. Phys. Rev. Lett. 1995, 74, 1250–1253. [Google Scholar] [CrossRef]
- Xu, X.; Gupta, N. Determining elastic modulus from dynamic mechanical analysis: A general model based on loss modulus data. Materialia 2018, 4, 221–226. [Google Scholar] [CrossRef]
- Cruchaga, M.A.; Celentano, D.J.; Tezduyar, T.E. Collapse of a liquid column: Numerical simulation and experimental validation. Comput. Mech. 2007, 39, 453–476. [Google Scholar] [CrossRef]
- Cruchaga, M.A.; Celentano, D.J.; Tezduyar, T.E. Computational Modeling of the Collapse of a Liquid Column Over an Obstacle and Experimental Validation. J. Appl. Mech. Trans. ASME 2009, 76, 021202. [Google Scholar] [CrossRef]
- Greaves, D.M. Simulation of viscous water column collapse using adapting hierarchical grids. Int. J. Numer. Methods Fluids 2006, 50, 693–711. [Google Scholar] [CrossRef]
- Ariane, M.; Kassinos, S.; Velaga, S.; Alexiadis, A. Discrete multi-physics simulations of diffusive and convective mass transfer in boundary layers containing motile cilia in lungs. Comput. Biol. Med. 2018, 95, 34–42. [Google Scholar] [CrossRef]

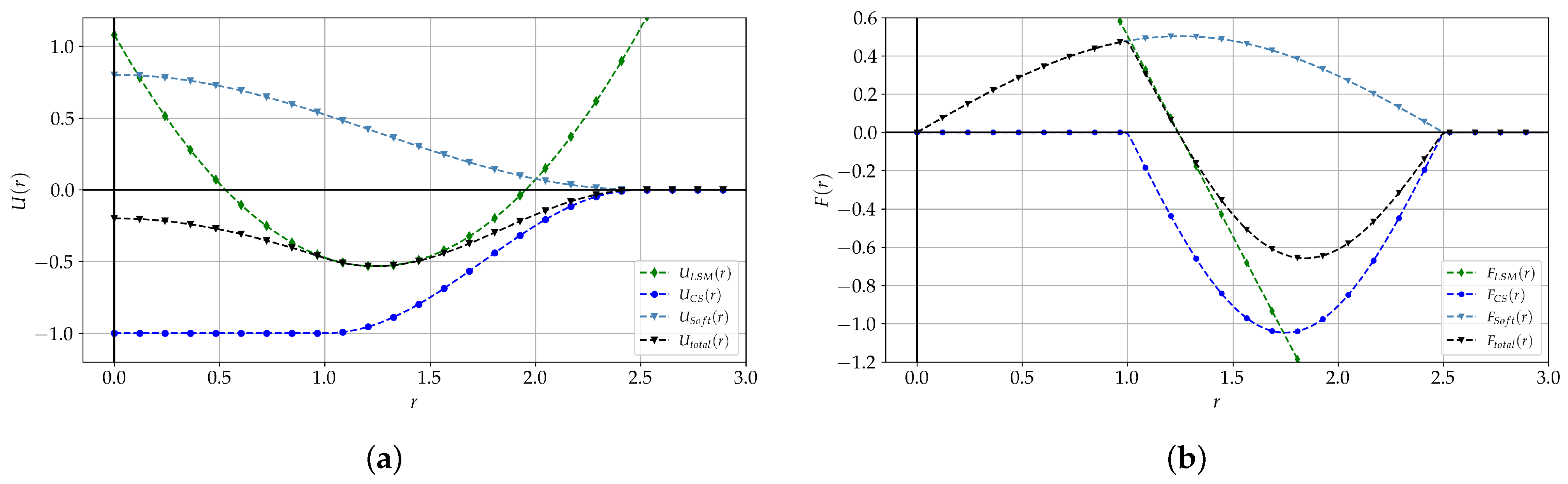









| BCC Lattice | FCC Lattice | |
|---|---|---|
| Activation distance-attractive potential | ||
| Cutoff distance-attractive potential | ||
| Cutoff distance-repulsive potential | ||
| Prefactor-repulsive potential |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duque-Daza, C.; Alexiadis, A. A Simplified Framework for Modelling Viscoelastic Fluids in Discrete Multiphysics. ChemEngineering 2021, 5, 61. https://doi.org/10.3390/chemengineering5030061
Duque-Daza C, Alexiadis A. A Simplified Framework for Modelling Viscoelastic Fluids in Discrete Multiphysics. ChemEngineering. 2021; 5(3):61. https://doi.org/10.3390/chemengineering5030061
Chicago/Turabian StyleDuque-Daza, Carlos, and Alessio Alexiadis. 2021. "A Simplified Framework for Modelling Viscoelastic Fluids in Discrete Multiphysics" ChemEngineering 5, no. 3: 61. https://doi.org/10.3390/chemengineering5030061
APA StyleDuque-Daza, C., & Alexiadis, A. (2021). A Simplified Framework for Modelling Viscoelastic Fluids in Discrete Multiphysics. ChemEngineering, 5(3), 61. https://doi.org/10.3390/chemengineering5030061