Fluid-Structure Interaction in Coronary Stents: A Discrete Multiphysics Approach
Abstract
1. Introduction
2. Methods
2.1. Discrete Multiphysics
2.2. Smooth Particle Hydrodynamics (SPH)
2.3. Lattice Spring Model (LSM)
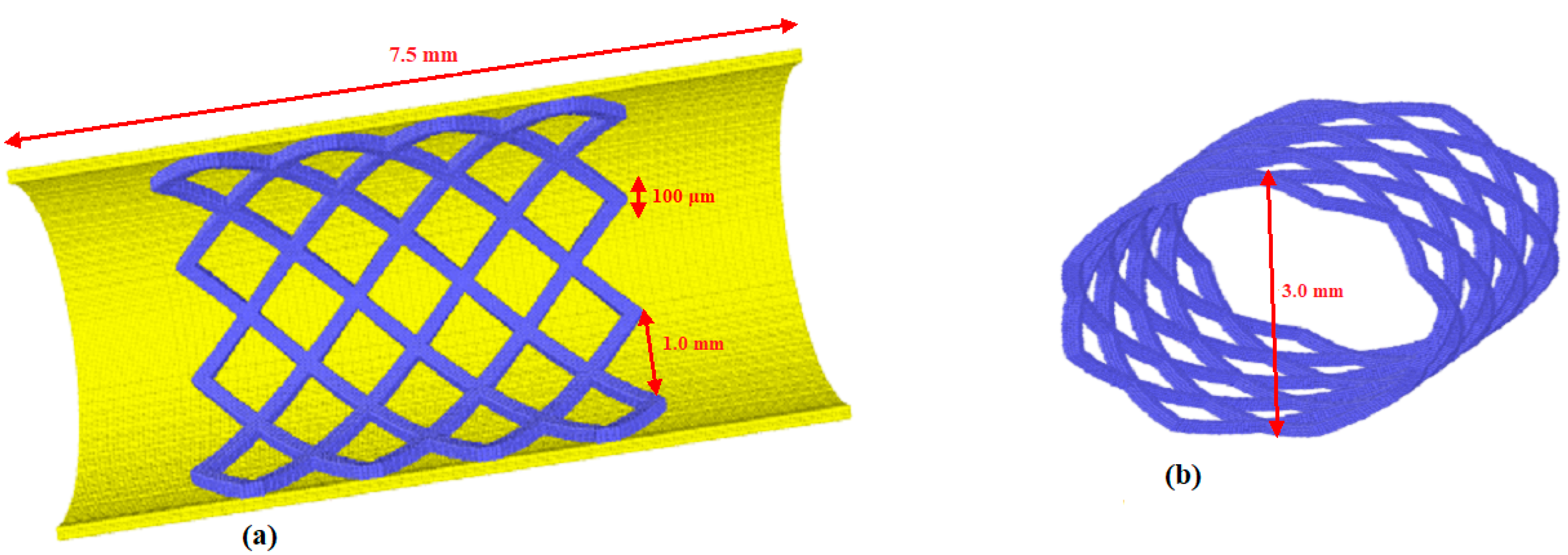
3. Model and Geometry
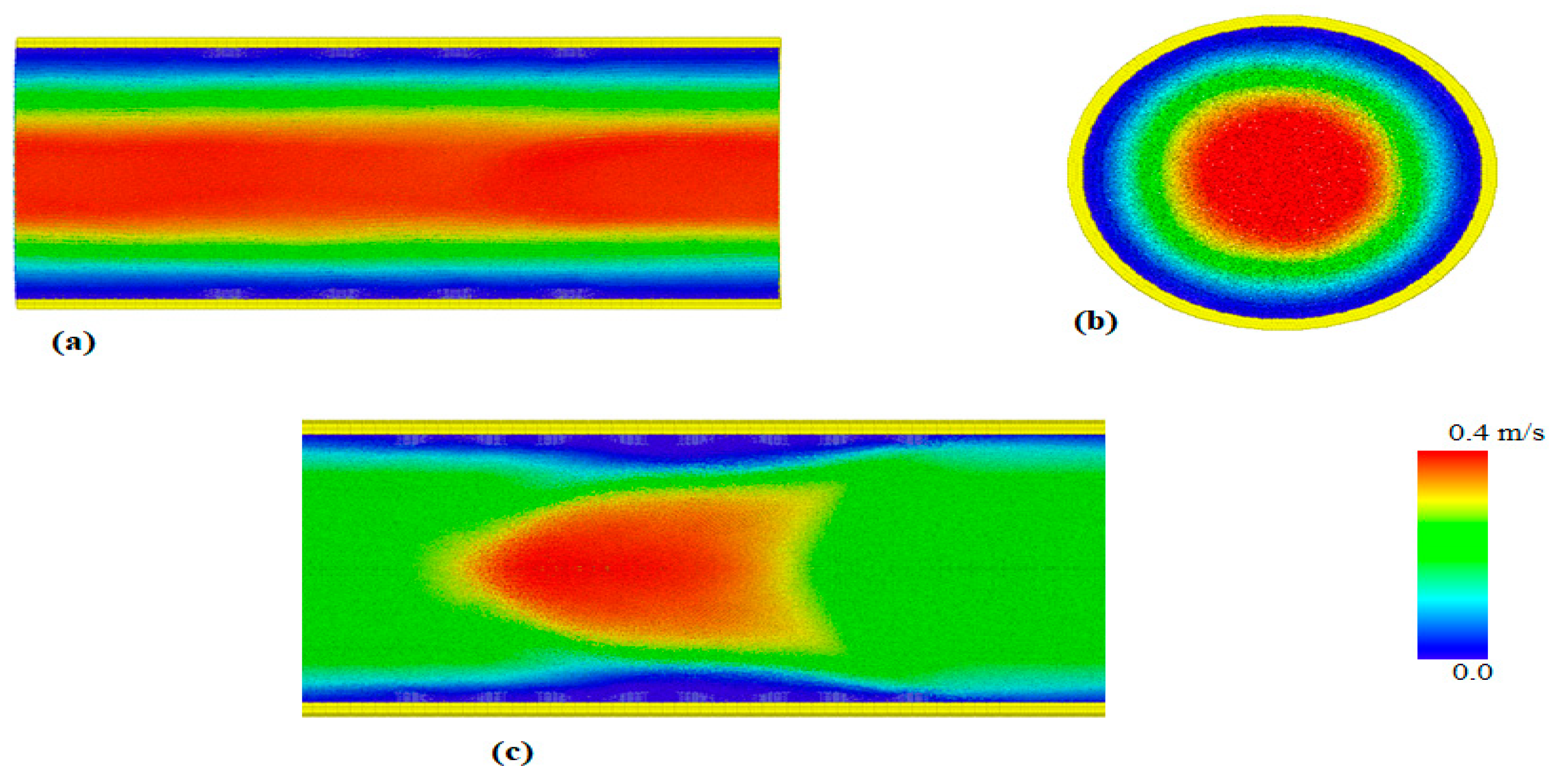
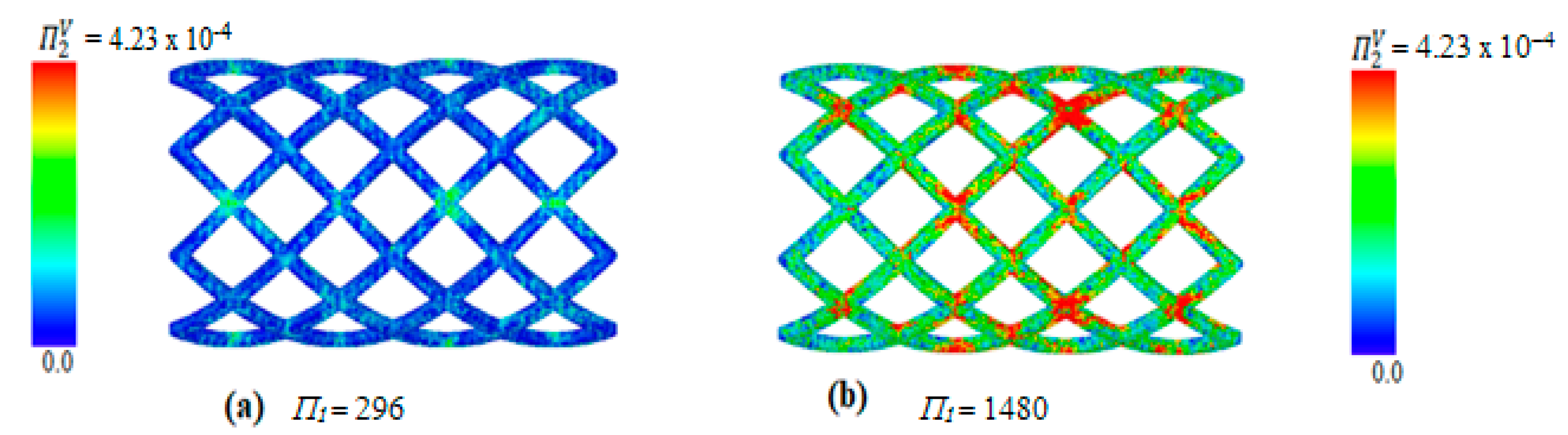
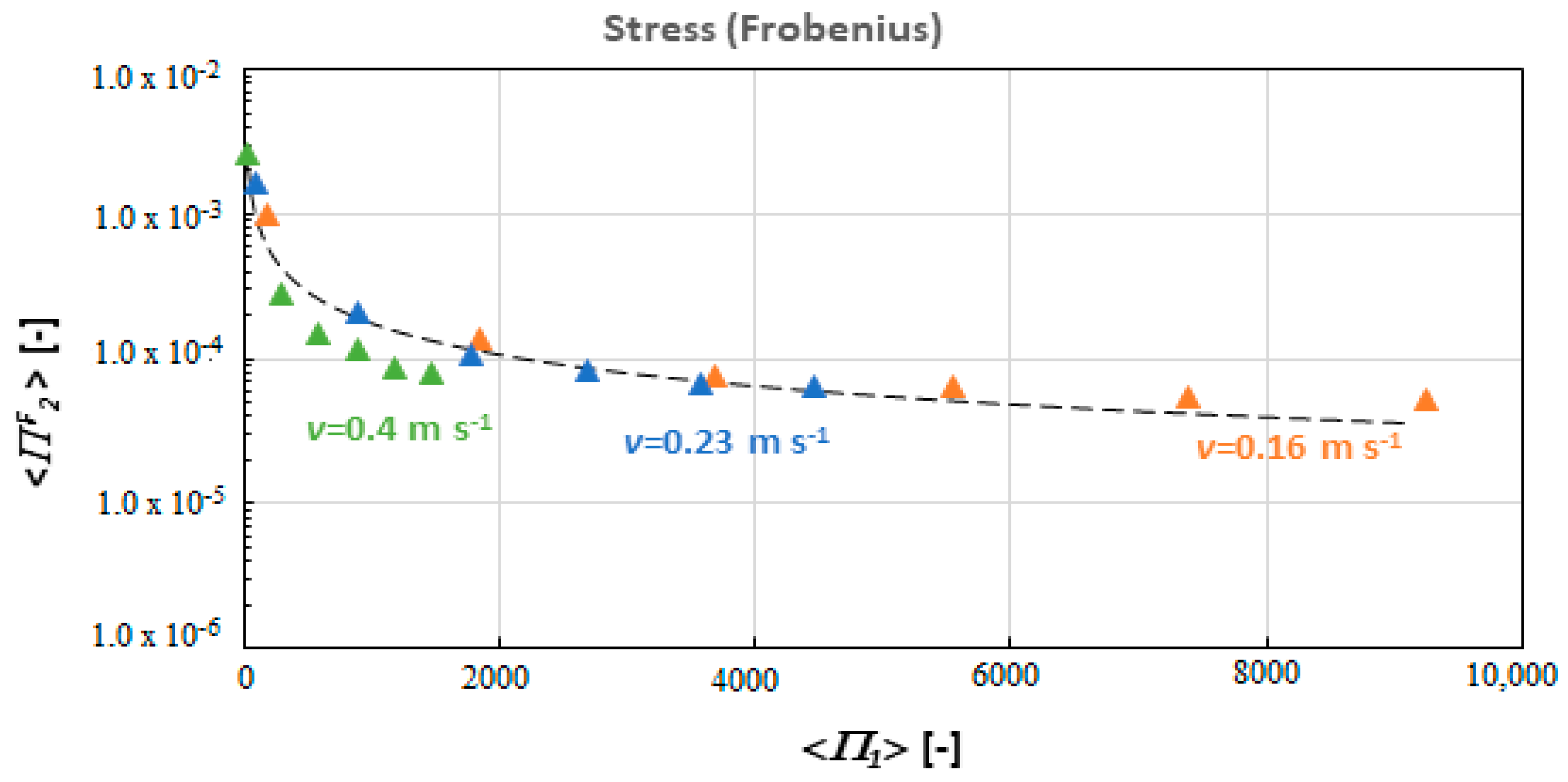
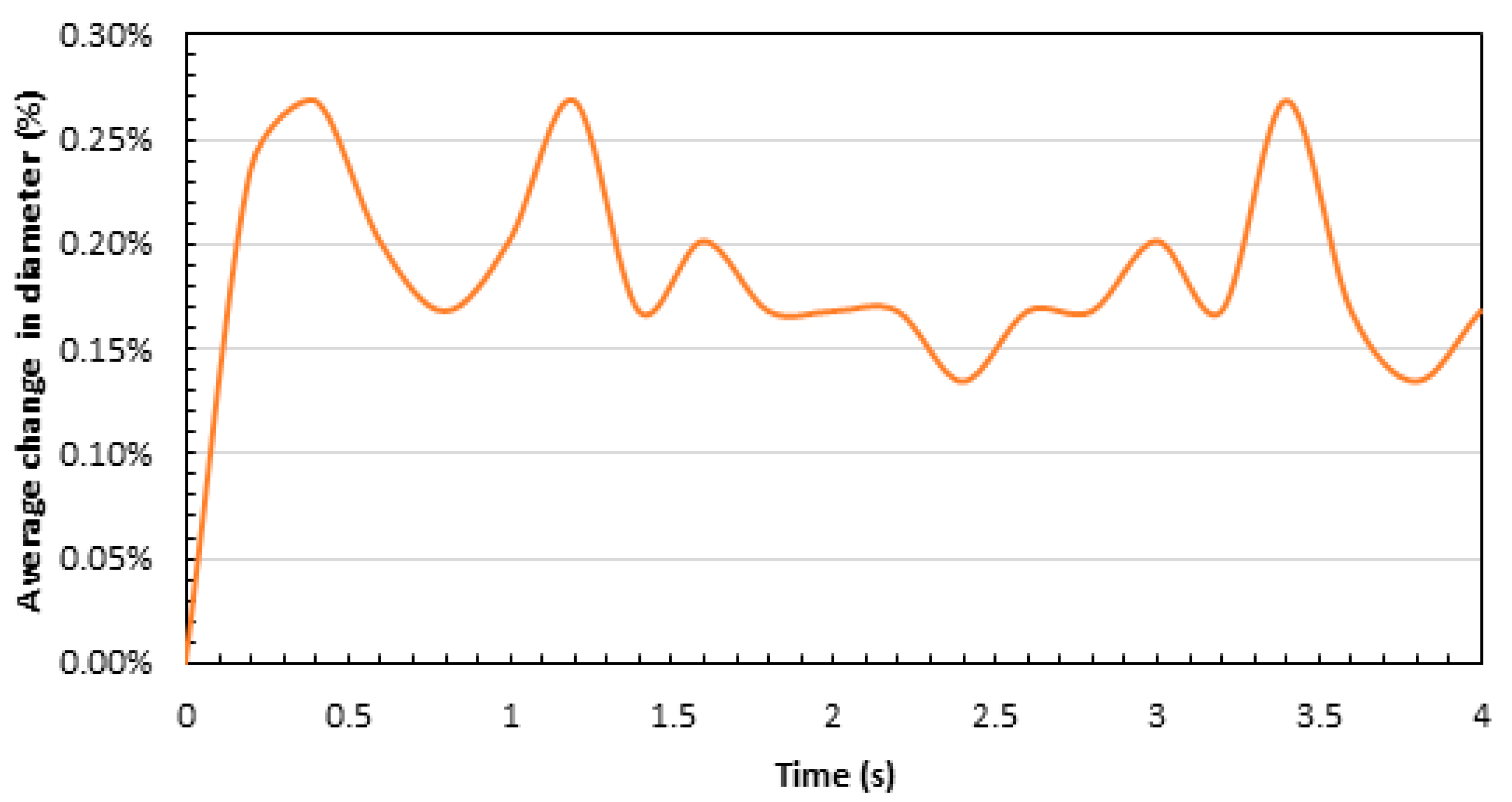
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Brown, J.C.; Gerhardt, T.E.; Kwon, E. Risk Factors for Coronary Artery Disease. In StatPearls; StatPearls Publishing: Treasure Island, FL, USA, 2021. [Google Scholar]
- Kolodgie, F.D.; Nakazawa, G.; Sangiorgi, G.; Ladich, E.; Burke, A.P.; Virmani, R. Pathology of Atherosclerosis and Stenting. Neuroimaging Clin. N. Am. 2007, 17, 285–301. [Google Scholar] [CrossRef] [PubMed]
- Evju, Ø.; Mardal, K.-A. On the Assumption of Laminar Flow in Physiological Flows: Cerebral Aneurysms as an Illustrative Example. In Modeling the Heart and the Circulatory System; Quarteroni, A., Ed.; MS&A.; Springer International Publishing: Cham, Germany, 2015; Volume 14, pp. 177–195. ISBN 978-3-319-05229-8. [Google Scholar]
- Otsuka, F.; Yasuda, S.; Noguchi, T.; Ishibashi-Ueda, H. Pathology of Coronary Atherosclerosis and Thrombosis. Cardiovasc. Diagn. Ther. 2016, 6, 396–408. [Google Scholar] [CrossRef]
- Griffith, M.D.; Leweke, T.; Thompson, M.C.; Hourigan, K. Effect of Small Asymmetries on Axisymmetric Stenotic Flow. J. Fluid Mech. 2013, 721, R1. [Google Scholar] [CrossRef]
- Jain, K. Transition to Turbulence in an Oscillatory Flow through Stenosis. Biomech. Model. Mechanobiol. 2020, 19, 113–131. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, S.A.; Giddens, D.P. Pulsatile Poststenotic Flow Studies with Laser Doppler Anemometry. J. Biomech. 1984, 17, 695–705. [Google Scholar] [CrossRef]
- Di Venuta, I.; Boghi, A.; Gori, F. Three-Dimensional Numerical Simulation of a Failed Coronary Stent Implant at Different Degrees of Residual Stenosis. Part I: Fluid Dynamics and Shear Stress on the Vascular Wall. Numer. Heat Transf. Part A Appl. 2017, 71, 638–652. [Google Scholar] [CrossRef]
- Pant, S.; Bressloff, N.W.; Limbert, G. Geometry Parameterization and Multidisciplinary Constrained Optimization of Coronary Stents. Biomech. Model. Mechanobiol. 2012, 11, 61–82. [Google Scholar] [CrossRef]
- Hsiao, H.-M.; Lee, K.-H.; Liao, Y.-C.; Cheng, Y.-C. Hemodynamic Simulation of Intra-Stent Blood Flow. Procedia Eng. 2012, 36, 128–136. [Google Scholar] [CrossRef]
- Wei, L.; Chen, Q.; Li, Z. Influences of Plaque Eccentricity and Composition on the Stent–Plaque–Artery Interaction during Stent Implantation. Biomech. Model. Mechanobiol. 2019, 18, 45–56. [Google Scholar] [CrossRef]
- Colombo, A.; Stankovic, G.; Moses, J.W. Selection of Coronary Stents. J. Am. Coll. Cardiol. 2002, 40, 1021–1033. [Google Scholar] [CrossRef]
- Balossino, R.; Gervaso, F.; Migliavacca, F.; Dubini, G. Effects of Different Stent Designs on Local Hemodynamics in Stented Arteries. J. Biomech. 2008, 41, 1053–1061. [Google Scholar] [CrossRef]
- Duraiswamy, N.; Jayachandran, B.; Byrne, J.; Moore, J.E.; Schoephoerster, R.T. Spatial Distribution of Platelet Deposition in Stented Arterial Models under Physiologic Flow. Ann. Biomed. Eng. 2005, 33, 1767–1777. [Google Scholar] [CrossRef] [PubMed]
- Pant, S.; Bressloff, N.W.; Forrester, A.I.J.; Curzen, N. The Influence of Strut-Connectors in Stented Vessels: A Comparison of Pulsatile Flow Through Five Coronary Stents. Ann. Biomed. Eng. 2010, 38, 1893–1907. [Google Scholar] [CrossRef] [PubMed]
- Finet, G.; Rioufol, G. Coronary Stent Longitudinal Deformation by Compression: Is This a New Global Stent Failure, a Specific Failure of a Particular Stent Design or Simply an Angiographic Detection of an Exceptional PCI Complication? EuroIntervention 2012, 8, 177–181. [Google Scholar] [CrossRef] [PubMed]
- Choudhury, T.R.; Al-Saigh, S.; Burley, S.; Li, L.; Shakhshir, N.; Mirhosseini, N.; Wang, T.; Arnous, S.; Khan, M.A.; Mamas, M.A.; et al. Longitudinal Deformation Bench Testing Using a Coronary Artery Model: A New Standard? Open Heart 2017, 4, e000537. [Google Scholar] [CrossRef] [PubMed]
- Ding, H.; Zhang, Y.; Liu, Y.; Shi, C.; Nie, Z.; Liu, H.; Gu, Y. Analysis of Vascular Mechanical Characteristics after Coronary Degradable Stent Implantation. BioMed Res. Int. 2019, 2019, 8265374. [Google Scholar] [CrossRef]
- Chinikar, M.; Sadeghipour, P. Coronary Stent Fracture: A Recently Appreciated Phenomenon with Clinical Relevance. Curr. Cardiol. Rev. 2014, 10, 349–354. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Alqahtani, A.; Suwaidi, J.; Mohsen, M. Stent Fracture: How Frequently Is It Recognized? Heart Views 2013, 14, 72. [Google Scholar] [CrossRef] [PubMed]
- Faik, I.; Mongrain, R.; Leask, R.L.; Rodes-Cabau, J.; Larose, E.; Bertrand, O. Time-Dependent 3D Simulations of the Hemodynamics in a Stented Coronary Artery. Biomed. Mater. 2007, 2, S28–S37. [Google Scholar] [CrossRef]
- Caiazzo, A.; Evans, D.; Falcone, J.-L.; Hegewald, J.; Lorenz, E.; Stahl, B.; Wang, D.; Bernsdorf, J.; Chopard, B.; Gunn, J.; et al. A Complex Automata Approach for In-Stent Restenosis: Two-Dimensional Multiscale Modelling and Simulations. J. Comput. Sci. 2011, 2, 9–17. [Google Scholar] [CrossRef]
- Beier, S.; Ormiston, J.; Webster, M.; Cater, J.; Norris, S.; Medrano-Gracia, P.; Young, A.; Cowan, B. Hemodynamics in Idealized Stented Coronary Arteries: Important Stent Design Considerations. Ann. Biomed. Eng. 2016, 44, 315–329. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Yang, J.; Huang, N.; Uhl, C.; Zhou, Y.; Liu, Y. Mechanical Response of Cardiovascular Stents under Vascular Dynamic Bending. Biomed. Eng. Online 2016, 15, 21. [Google Scholar] [CrossRef] [PubMed]
- Wei, L.; Leo, H.L.; Chen, Q.; Li, Z. Structural and Hemodynamic Analyses of Different Stent Structures in Curved and Stenotic Coronary Artery. Front. Bioeng. Biotechnol. 2019, 7, 366. [Google Scholar] [CrossRef] [PubMed]
- Alexiadis, A. A Smoothed Particle Hydrodynamics and Coarse-Grained Molecular Dynamics Hybrid Technique for Modelling Elastic Particles and Breakable Capsules under Various Flow Conditions: SPH-CGMD HYBRID. Int. J. Numer. Meth. Eng. 2014, 100, 713–719. [Google Scholar] [CrossRef]
- Schütt, M.; Stamatopoulos, K.; Simmons, M.J.H.; Batchelor, H.K.; Alexiadis, A. Modelling and Simulation of the Hydrodynamics and Mixing Profiles in the Human Proximal Colon Using Discrete Multiphysics. Comput. Biol. Med. 2020, 121, 103819. [Google Scholar] [CrossRef]
- Ariane, M.; Kassinos, S.; Velaga, S.; Alexiadis, A. Discrete Multi-Physics Simulations of Diffusive and Convective Mass Transfer in Boundary Layers Containing Motile Cilia in Lungs. Comput. Biol. Med. 2018, 95, 34–42. [Google Scholar] [CrossRef] [PubMed]
- Mohammed, A.M.; Ariane, M.; Alexiadis, A. Using Discrete Multiphysics Modelling to Assess the Effect of Calcification on Hemodynamic and Mechanical Deformation of Aortic Valve. ChemEngineering 2020, 4, 48. [Google Scholar] [CrossRef]
- Ariane, M.; Wen, W.; Vigolo, D.; Brill, A.; Nash, F.G.B.; Barigou, M.; Alexiadis, A. Modelling and Simulation of Flow and Agglomeration in Deep Veins Valves Using Discrete Multi Physics. Comput. Biol. Med. 2017, 89, 96–103. [Google Scholar] [CrossRef]
- Ariane, M.; Vigolo, D.; Brill, A.; Nash, F.G.B.; Barigou, M.; Alexiadis, A. Using Discrete Multi-Physics for Studying the Dynamics of Emboli in Flexible Venous Valves. Comput. Fluids 2018, 166, 57–63. [Google Scholar] [CrossRef]
- Albano, A.; Alexiadis, A. A Smoothed Particle Hydrodynamics Study of the Collapse for a Cylindrical Cavity. PLoS ONE 2020, 15, e0239830. [Google Scholar] [CrossRef]
- Albano, A.; Alexiadis, A. Non-Symmetrical Collapse of an Empty Cylindrical Cavity Studied with Smoothed Particle Hydrodynamics. Appl. Sci. 2021, 11, 3500. [Google Scholar] [CrossRef]
- Liu, W.; Wu, C.-Y. Modelling Complex Particle–Fluid Flow with a Discrete Element Method Coupled with Lattice Boltzmann Methods (DEM-LBM). ChemEngineering 2020, 4, 55. [Google Scholar] [CrossRef]
- Ng, K.C.; Alexiadis, A.; Chen, H.; Sheu, T.W.H. A Coupled Smoothed Particle Hydrodynamics-Volume Compensated Particle Method (SPH-VCPM) for Fluid Structure Interaction (FSI) Modelling. Ocean Eng. 2020, 218, 107923. [Google Scholar] [CrossRef]
- Sahputra, I.H.; Alexiadis, A.; Adams, M.J. A Coarse Grained Model for Viscoelastic Solids in Discrete Multiphysics Simulations. ChemEngineering 2020, 4, 30. [Google Scholar] [CrossRef]
- Ruiz-Riancho, I.N.; Alexiadis, A.; Zhang, Z.; Garcia Hernandez, A. A Discrete Multi-Physics Model to Simulate Fluid Structure Interaction and Breakage of Capsules Filled with Liquid under Coaxial Load. Processes 2021, 9, 354. [Google Scholar] [CrossRef]
- Sanfilippo, D.; Ghiassi, B.; Alexiadis, A.; Hernandez, A.G. Combined Peridynamics and Discrete Multiphysics to Study the Effects of Air Voids and Freeze-Thaw on the Mechanical Properties of Asphalt. Materials 2021, 14, 1579. [Google Scholar] [CrossRef] [PubMed]
- Alexiadis, A. Deep Multiphysics and Particle–Neuron Duality: A Computational Framework Coupling (Discrete) Multiphysics and Deep Learning. Appl. Sci. 2019, 9, 5369. [Google Scholar] [CrossRef]
- Alexiadis, A.; Simmons, M.J.H.; Stamatopoulos, K.; Batchelor, H.K.; Moulitsas, I. The Duality between Particle Methods and Artificial Neural Networks. Sci. Rep. 2020, 10, 16247. [Google Scholar] [CrossRef]
- Liu, G.R.; Liu, M.B. Smoothed Particle Hydrodynamics: A Meshfree Particle Method; World Scientific: Singapore, 2003; ISBN 978-981-238-456-0. [Google Scholar]
- Kot, M.; Nagahashi, H.; Szymczak, P. Elastic Moduli of Simple Mass Spring Models. Vis. Comput. 2015, 31, 1339–1350. [Google Scholar] [CrossRef]
- Kot, M. Mass Spring Models of Amorphous Solids. ChemEngineering 2021, 5, 3. [Google Scholar] [CrossRef]
- Monaghan, J.J. Smoothed Particle Hydrodynamics. Annu. Rev. Astron. Astrophys. 1992, 30, 543–574. [Google Scholar] [CrossRef]
- Morris, J.P.; Fox, P.J.; Zhu, Y. Modeling Low Reynolds Number Incompressible Flows Using SPH. J. Comput. Phys. 1997, 136, 214–226. [Google Scholar] [CrossRef]
- Pazdniakou, A.; Adler, P.M. Lattice Spring Models. Transp. Porous Med. 2012, 93, 243–262. [Google Scholar] [CrossRef]
- Wall, J.G.; Podbielska, H.; Wawrzyńska, M. (Eds.) Functionalized Cardiovascular Stents; Woodhead Publishing Series in Biomaterials; Elsevier: Amsterdam, The Netherlands; Woodhead Publishing: Duxford, UK; Cambridge, MA, USA, 2018; ISBN 978-0-08-100496-8. [Google Scholar]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Ku, D.N. Blood Flow in Arteries. Annu. Rev. Fluid Mech. 1997, 29, 399–434. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and Analysis of Atomistic Simulation Data with OVITO–the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Alexiadis, A. The Discrete Multi-Hybrid System for the Simulation of Solid-Liquid Flows. PLoS ONE 2015, 10, e0124678. [Google Scholar] [CrossRef]
- Vrints, C.J.; Claeys, M.J.; Bosmans, J.; Conraads, V.; Snoeck, J.P. Effect of Stenting on Coronary Flow Velocity Reserve: Comparison of Coil and Tubular Stents. Heart 1999, 82, 465–470. [Google Scholar] [CrossRef] [PubMed]
- Wiesent, L.; Schultheiß, U.; Schmid, C.; Schratzenstaller, T.; Nonn, A. Experimentally Validated Simulation of Coronary Stents Considering Different Dogboning Ratios and Asymmetric Stent Positioning. PLoS ONE 2019, 14, e0224026. [Google Scholar] [CrossRef]
- Huo, Y.; Kassab, G.S. Pulsatile Blood Flow in the Entire Coronary Arterial Tree: Theory and Experiment. Am. J. Physiol. Heart Circ. Physiol. 2006, 291, H1074–H1087. [Google Scholar] [CrossRef]
- Cheung, Y. Systemic Circulation. In Paediatric Cardiology; Elsevier: Amsterdam, The Netherlands, 2010; pp. 91–116. ISBN 978-0-7020-3064-2. [Google Scholar]


| SPH | |
|---|---|
| Number of SPH fluid particles | 1,609,452 |
| Mass of each particle (fluid) | 3.41 × 10−12 kg |
| Length L | 7.5 × 10−3 m |
| Diameter D | 3.0 × 10−3 m |
| Particle spacing l | 3.33 × 10−5 m |
| Smoothing length h | 7.5 × 10−5 m |
| Local acceleration term g0 | 0.47138–1.25 m s−2 |
| Fluid Density ρ | 1056 kg m−3 |
| Viscosity μ | 0.0035 Pa∙s |
| Sound speed c0 | 4 m s−1 |
| Alpha α | 0.1–0.25 [-] |
| Time step Δt | 1 × 10−7 s |
| LSM | |
| Number of SPH stent particles | 46,336 |
| Number of SPH wall particles | 207,016 |
| Mass of each particle of the stent (Solid) | 3.41 × 10−12 kg |
| Mass of each particle of the wall (Solid) | 6.0 × 10−12 kg |
| Stent thickness | 1.0 × 10−4 m |
| Elastic constant k | 0.5−25 kg s−2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohammed, A.M.; Ariane, M.; Alexiadis, A. Fluid-Structure Interaction in Coronary Stents: A Discrete Multiphysics Approach. ChemEngineering 2021, 5, 60. https://doi.org/10.3390/chemengineering5030060
Mohammed AM, Ariane M, Alexiadis A. Fluid-Structure Interaction in Coronary Stents: A Discrete Multiphysics Approach. ChemEngineering. 2021; 5(3):60. https://doi.org/10.3390/chemengineering5030060
Chicago/Turabian StyleMohammed, Adamu Musa, Mostapha Ariane, and Alessio Alexiadis. 2021. "Fluid-Structure Interaction in Coronary Stents: A Discrete Multiphysics Approach" ChemEngineering 5, no. 3: 60. https://doi.org/10.3390/chemengineering5030060
APA StyleMohammed, A. M., Ariane, M., & Alexiadis, A. (2021). Fluid-Structure Interaction in Coronary Stents: A Discrete Multiphysics Approach. ChemEngineering, 5(3), 60. https://doi.org/10.3390/chemengineering5030060







