Influence of Pressure, Velocity and Fluid Material on Heat Transport in Structured Open-Cell Foam Reactors Investigated Using CFD Simulations
Abstract
1. Introduction
2. Materials and Methods
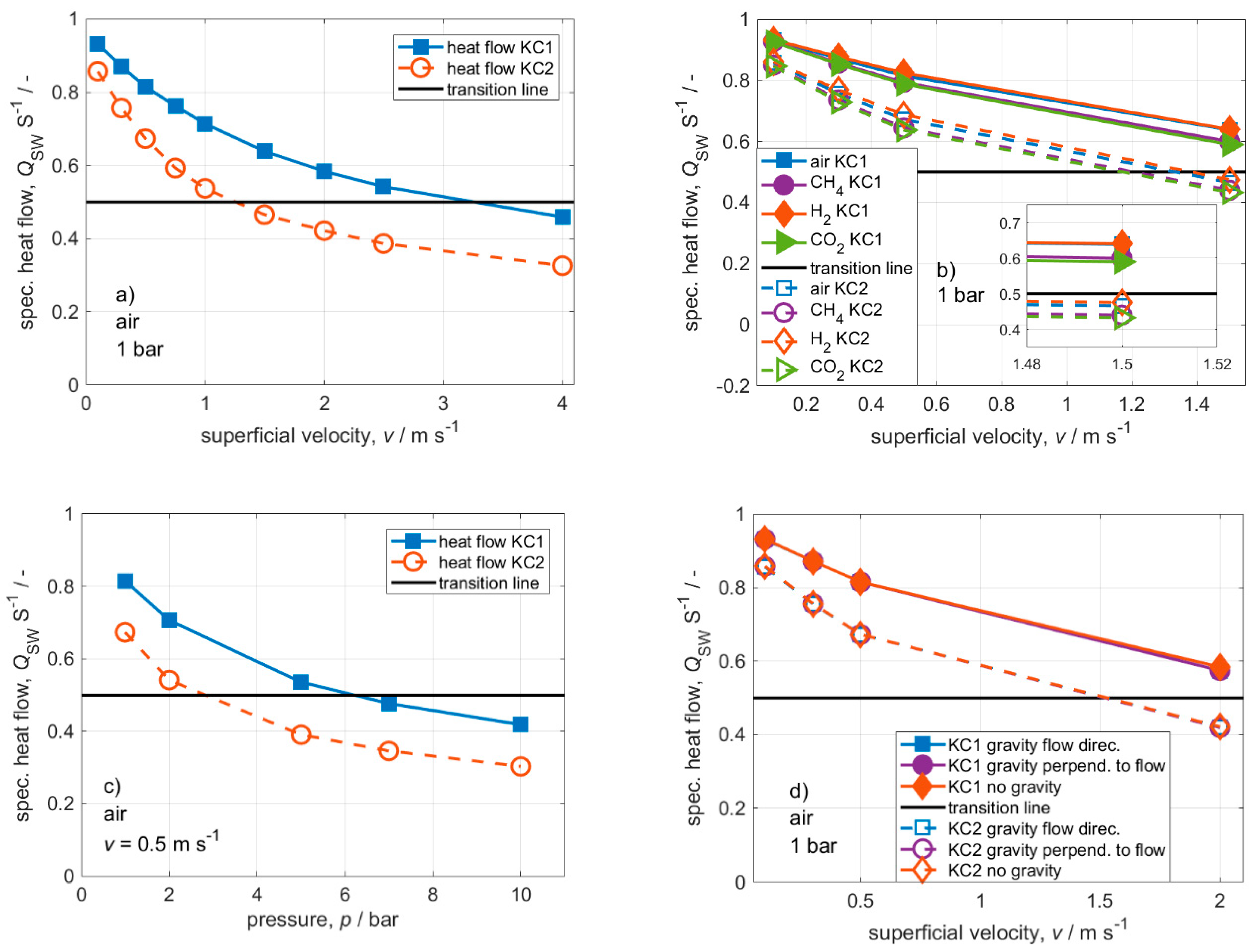
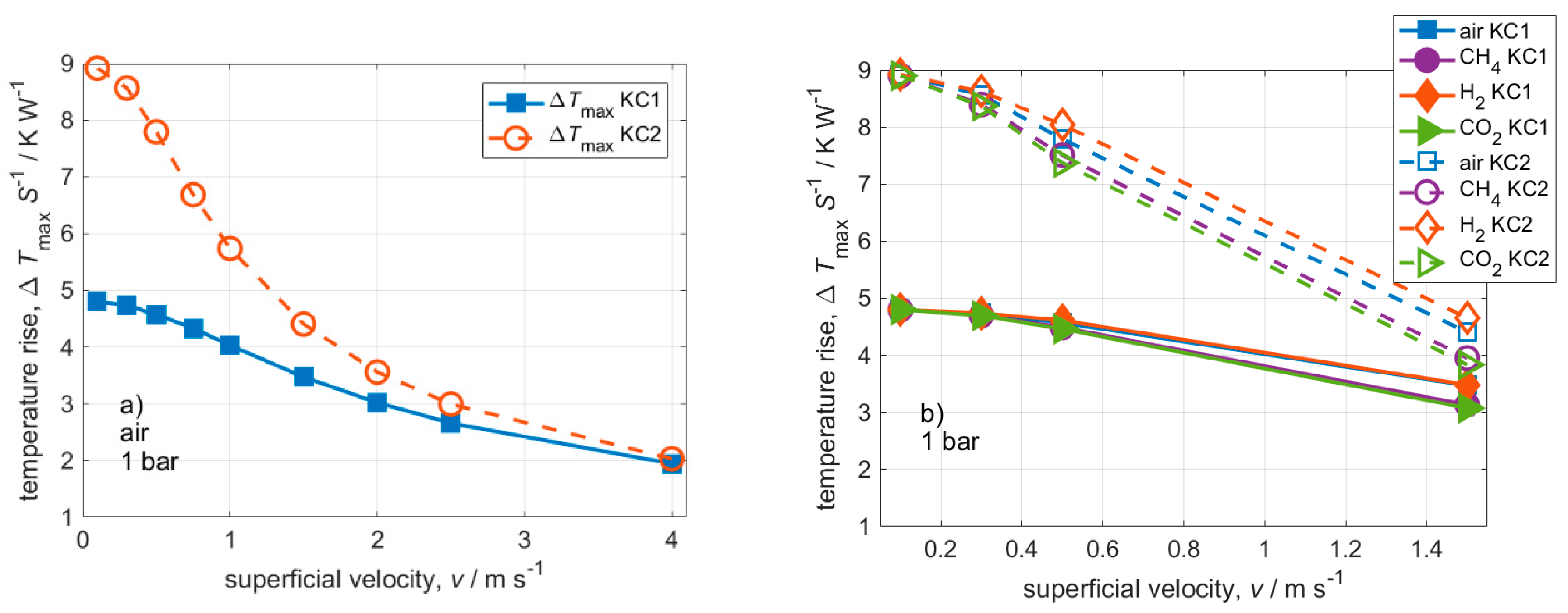
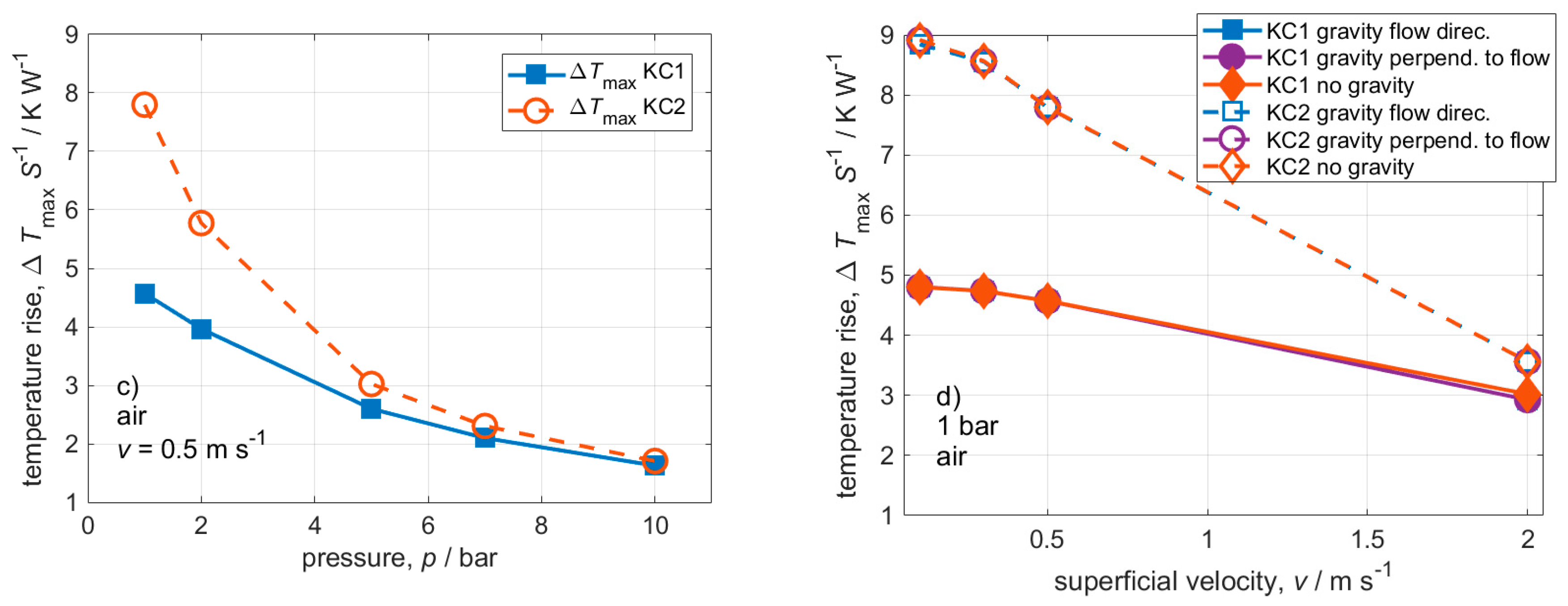
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Latin | |
| cp | isobaric heat capacity, J kg−1 K−1 |
| dc | cell diameter, m |
| ds | strut diameter, m |
| g | gravitational acceleration, 9.81 m s−2 |
| Q | heat flow, W |
| QSF | heat flow solid to fluid, W |
| QSW | heat flow solid to wall, W |
| h | specific enthalpy, J kg−1 |
| p | pressure, Pa |
| S | total heat source intensity, W |
| Sv | specific surface area, m−1 |
| T | temperature, K |
| Tw | wall temperature, K |
| Tmax | maximum temperature, K |
| U | velocity, m s−1 |
| v | superficial velocity, m s−1 |
| Greek | |
| εO | open porosity, - |
| μ | dynamic viscosity, Pa s |
| λ | thermal conductivity, W m−1 K−1 |
| ρ | density, kg m−3 |
Appendix A. Depiction of Volume Meshes

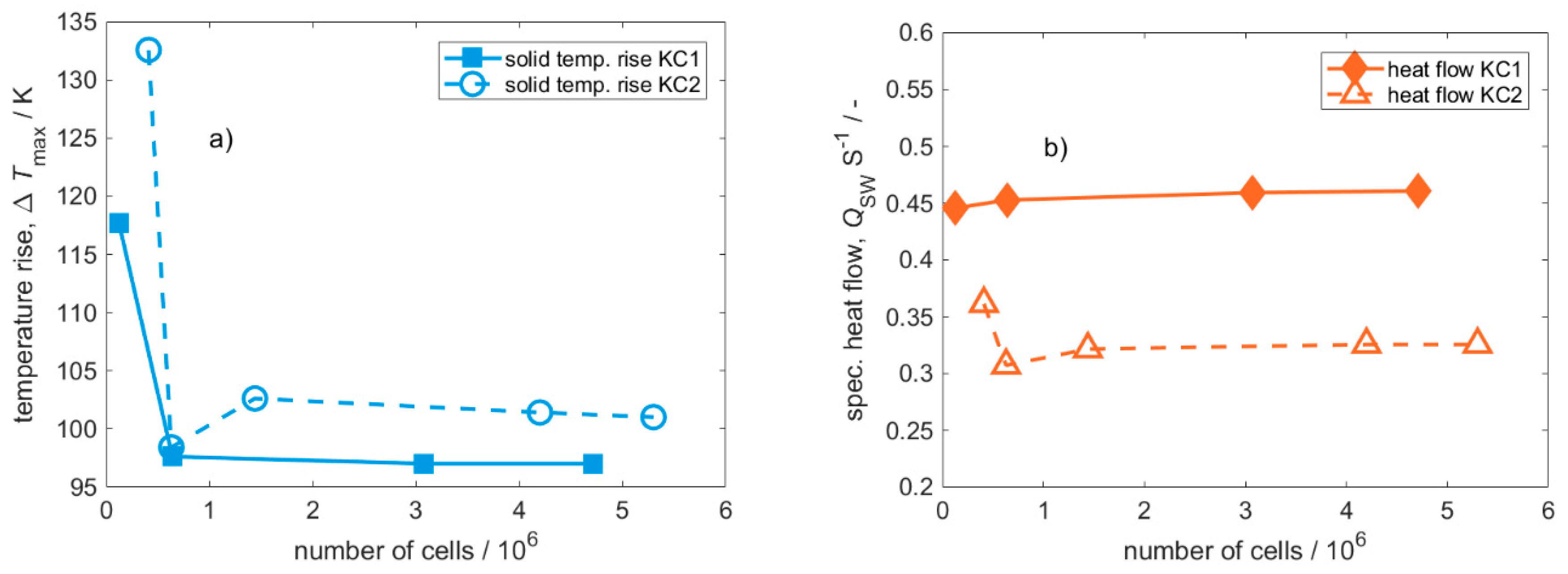
Appendix B. Grid Independence Study
References
- Kiewidt, L.; Thöming, J. Multiscale modelling of monolithic sponges as catalyst carrier for the methanation of carbon dioxide. Chem. Eng. Sci. X 2019, 2, 100016. [Google Scholar] [CrossRef]
- Stiegler, T.; Meltzer, K.; Tremel, A.; Baldauf, M.; Wasserscheid, P.; Albert, J. Development of a Structured Reactor System for CO2 Methanation under Dynamic Operating Conditions. Energy Technol. 2019, 7, 1900047. [Google Scholar] [CrossRef]
- Gräf, I.; Ladenburger, G.; Kraushaar-Czarnetzki, B. Heat transport in catalytic sponge packings in the presence of an exothermal reaction: Characterization by 2D modeling of experiments. Chem. Eng. J. 2016, 287, 425–435. [Google Scholar] [CrossRef]
- Vogt, C.; Monai, M.; Kramer, G.J.; Weckhuysen, B.M. The renaissance of the Sabatier reaction and its applications on Earth and in space. Nat. Catal. 2019, 2, 188–197. [Google Scholar] [CrossRef]
- Kalz, K.F.; Kraehnert, R.; Dvoyashkin, M.; Dittmeyer, R.; Gläser, R.; Krewer, U.; Reuter, K.; Grunwaldt, J.D. Future Challenges in Heterogeneous Catalysis: Understanding Catalysts under Dynamic Reaction Conditions. ChemCatChem 2017, 9, 17–29. [Google Scholar] [CrossRef]
- Rönsch, S.; Schneider, J.; Matthischke, S.; Schlüter, M.; Götz, M.; Lefebvre, J.; Prabhakaran, P.; Bajohr, S. Review on methanation—From fundamentals to current projects. Fuel 2016, 166, 276–296. [Google Scholar] [CrossRef]
- Kiewidt, L.; Thöming, J. Predicting optimal temperature profiles in single-stage fixed-bed reactors for CO2-methanation. Chem. Eng. Sci. 2015, 132, 59–71. [Google Scholar] [CrossRef]
- Kiewidt, L.; Thöming, J. Pareto-optimal design and assessment of monolithic sponges as catalyst carriers for exothermic reactions. Chem. Eng. J. 2019, 359, 496–504. [Google Scholar] [CrossRef]
- Gräf, I.; Rühl, A.K.; Kraushaar-Czarnetzki, B. Experimental study of heat transport in catalytic sponge packings by monitoring spatial temperature profiles in a cooled-wall reactor. Chem. Eng. J. 2014, 244, 234–242. [Google Scholar] [CrossRef]
- Dixon, A.G.; Partopour, B. Computational Fluid Dynamics for Fixed Bed Reactor Design. Annu. Rev. Chem. Biomol. Eng. 2020, 11, 109–130. [Google Scholar] [CrossRef] [PubMed]
- Bracconi, M.; Ambrosetti, M.; Maestri, M.; Groppi, G.; Tronconi, E. A fundamental analysis of the influence of the geometrical properties on the effective thermal conductivity of open-cell foams. Chem. Eng. Process. Process Intensif. 2018, 129, 181–189. [Google Scholar] [CrossRef]
- Ranut, P.; Nobile, E.; Mancini, L. High resolution X-ray microtomography-based CFD simulation for the characterization of flow permeability and effective thermal conductivity of aluminum metal foams. Exp. Therm. Fluid Sci. 2015, 67, 30–36. [Google Scholar] [CrossRef]
- Iasiello, M.; Bianco, N.; Chiu, W.K.S.; Naso, V. Anisotropic convective heat transfer in open-cell metal foams: Assessment and correlations. Int. J. Heat Mass Transf. 2020, 154, 119682. [Google Scholar] [CrossRef]
- Della Torre, A.; Montenegro, G.; Onorati, A.; Tabor, G. CFD characterization of pressure drop and heat transfer inside porous substrates. Energy Procedia 2015, 81, 836–845. [Google Scholar] [CrossRef]
- Sinn, C.; Kranz, F.; Wentrup, J.; Thöming, J.; Wehinger, G.D.; Pesch, G.R. CFD Simulations of Radiative Heat Transport in Open-Cell Foam Catalytic Reactors. Catalysts 2020, 10, 716. [Google Scholar] [CrossRef]
- Zafari, M.; Panjepour, M.; Emami, M.D.; Meratian, M. Microtomography-based numerical simulation of fluid flow and heat transfer in open cell metal foams. Appl. Therm. Eng. 2015, 80, 347–354. [Google Scholar] [CrossRef]
- Wu, Z.; Caliot, C.; Flamant, G.; Wang, Z. Numerical simulation of convective heat transfer between air flow and ceramic foams to optimise volumetric solar air receiver performances. Int. J. Heat Mass Transf. 2011, 54, 1527–1537. [Google Scholar] [CrossRef]
- Razza, S.; Heidig, T.; Bianchi, E.; Groppi, G.; Schwieger, W.; Tronconi, E.; Freund, H. Heat transfer performance of structured catalytic reactors packed with metal foam supports: Influence of wall coupling. Catal. Today 2016, 273, 187–195. [Google Scholar] [CrossRef]
- Sinn, C.; Pesch, G.R.; Thöming, J.; Kiewidt, L. Coupled conjugate heat transfer and heat production in open-cell ceramic foams investigated using CFD. Int. J. Heat Mass Transf. 2019, 139, 600–612. [Google Scholar] [CrossRef]
- Ambrosio, G.; Bianco, N.; Chiu, W.K.S.; Iasiello, M.; Naso, V.; Oliviero, M. The effect of open-cell metal foams strut shape on convection heat transfer and pressure drop. Appl. Therm. Eng. 2016, 103, 333–343. [Google Scholar] [CrossRef]
- Bianchi, E.; Schwieger, W.; Freund, H. Assessment of Periodic Open Cellular Structures for Enhanced Heat Conduction in Catalytic Fixed-Bed Reactors. Adv. Eng. Mater. 2016, 18, 608–614. [Google Scholar] [CrossRef]
- Diani, A.; Bodla, K.K.; Rossetto, L.; Garimella, S.V. Numerical investigation of pressure drop and heat transfer through reconstructed metal foams and comparison against experiments. Int. J. Heat Mass Transf. 2015, 88, 508–515. [Google Scholar] [CrossRef]
- Du, S.; Tong, Z.X.; Zhang, H.H.; He, Y.L. Tomography-based determination of Nusselt number correlation for the porous volumetric solar receiver with different geometrical parameters. Renew. Energy 2019, 135, 711–718. [Google Scholar] [CrossRef]
- Aguirre, A.; Chandra, V.; Peters, E.A.J.F.; Kuipers, J.A.M.; Neira D’Angelo, M.F. Open-cell foams as catalysts support: A systematic analysis of the mass transfer limitations. Chem. Eng. J. 2020, 393, 124656. [Google Scholar] [CrossRef]
- Dong, Y.; Korup, O.; Gerdts, J.; Roldán Cuenya, B.; Horn, R. Microtomography-based CFD modeling of a fixed-bed reactor with an open-cell foam monolith and experimental verification by reactor profile measurements. Chem. Eng. J. 2018, 353, 176–188. [Google Scholar] [CrossRef]
- Della Torre, A.; Lucci, F.; Montenegro, G.; Onorati, A.; Dimopoulos Eggenschwiler, P.; Tronconi, E.; Groppi, G. CFD modeling of catalytic reactions in open-cell foam substrates. Comput. Chem. Eng. 2016, 92, 55–63. [Google Scholar] [CrossRef]
- Wehinger, G.D.; Heitmann, H.; Kraume, M. An artificial structure modeler for 3D CFD simulations of catalytic foams. Chem. Eng. J. 2016, 284, 543–556. [Google Scholar] [CrossRef]
- Bracconi, M.; Ambrosetti, M.; Maestri, M.; Groppi, G.; Tronconi, E. A fundamental investigation of gas/solid mass transfer in open-cell foams using a combined experimental and CFD approach. Chem. Eng. J. 2018, 352, 558–571. [Google Scholar] [CrossRef]
- Frey, M.; Bengaouer, A.; Geffraye, G.; Edouard, D.; Roger, A.C. Aluminum Open Cell Foams as Efficient Supports for Carbon Dioxide Methanation Catalysts: Pilot-Scale Reaction Results. Energy Technol. 2017, 5, 2078–2085. [Google Scholar] [CrossRef]
- Montenegro Camacho, Y.S.; Bensaid, S.; Lorentzou, S.; Vlachos, N.; Pantoleontos, G.; Konstandopoulos, A.; Luneau, M.; Meunier, F.C.; Guilhaume, N.; Schuurman, Y.; et al. Development of a robust and efficient biogas processor for hydrogen production. Part 2: Experimental campaign. Int. J. Hydrogen Energy 2018, 43, 161–177. [Google Scholar] [CrossRef]
- Bianchi, E.; Groppi, G.; Schwieger, W.; Tronconi, E.; Freund, H. Numerical simulation of heat transfer in the near-wall region of tubular reactors packed with metal open-cell foams. Chem. Eng. J. 2015, 264, 268–279. [Google Scholar] [CrossRef]
- Nie, Z.; Lin, Y.; Tong, Q. Modeling structures of open cell foams. Comput. Mater. Sci. 2017, 131, 160–169. [Google Scholar] [CrossRef]
- STAR-CCM+. Available online: https://www.plm.automation.siemens.com/global/en/products/simcenter/STAR-CCM.html (accessed on 6 October 2020).
- Wehinger, G.D. Radiation Matters in Fixed-Bed CFD Simulations. Chemie-Ingenieur-Technik 2019, 91, 583–591. [Google Scholar] [CrossRef]
- Iasiello, M.; Cunsolo, S.; Bianco, N.; Chiu, W.K.S.; Naso, V. Developing thermal flow in open-cell foams. Int. J. Therm. Sci. 2017, 111, 129–137. [Google Scholar] [CrossRef]
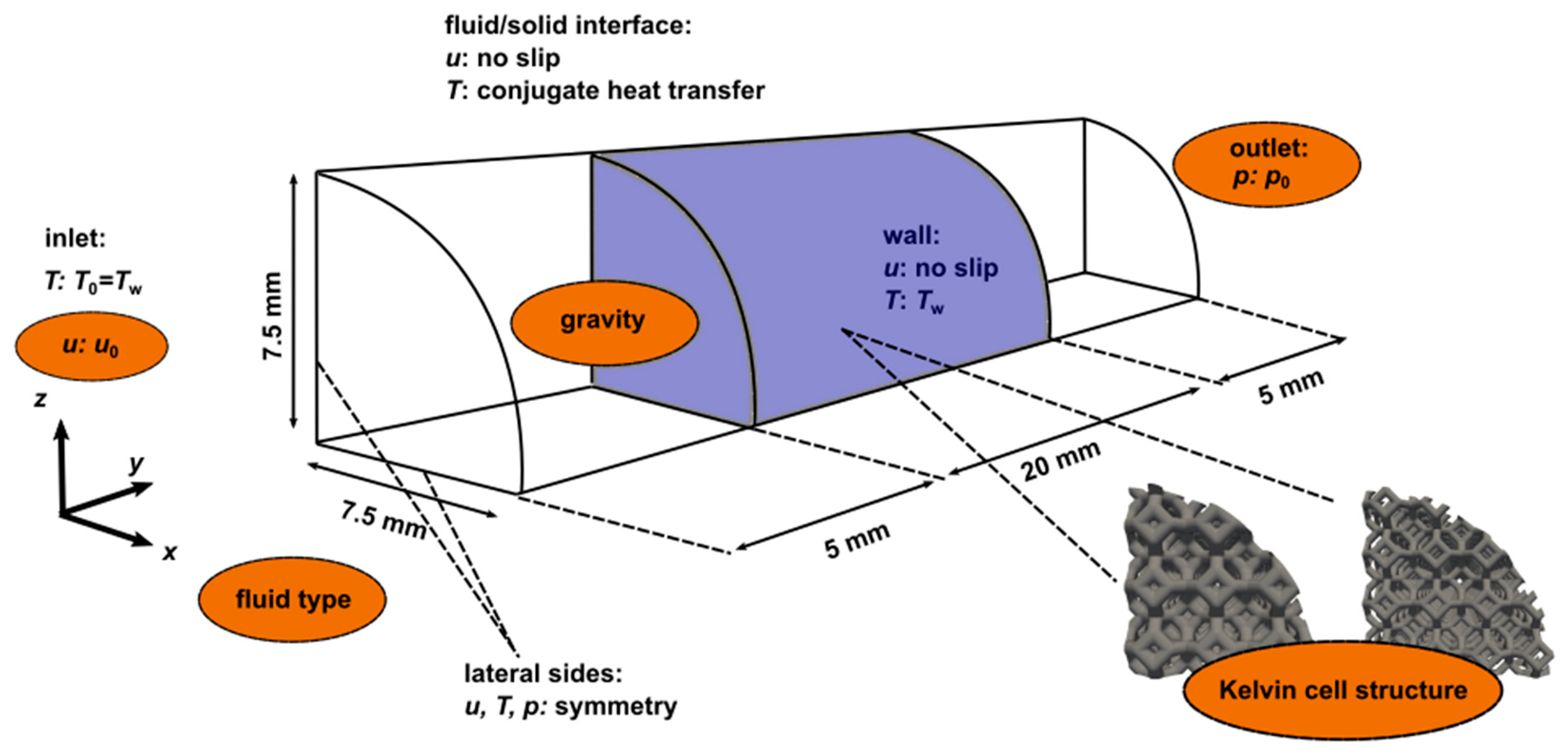
| Parameter, Symbol. | Kelvin Cell 1 (KC1) | Kelvin Cell 2 (KC2) |
|---|---|---|
| open porosity, εO | 0.724 | 0.845 |
| specific surface area, SV | 1467.8 m−1 | 1518.9 m−1 |
| cell diameter, dc | 1.924 mm | 1.733 mm |
| strut diameter, ds | 0.591 mm | 0.35 mm |
| Property | Assumption | |
|---|---|---|
| Fluid dynamic viscosity | µ | Sutherland equation |
| Fluid heat capacity | cp,f | polynomial |
| Fluid thermal conductivity | λf | Sutherland equation |
| Fluid density Superficial velocity | δf v | ideal gas law const. (0.1–4 m s−1) |
| Pore Reynolds number (air) Wall/inlet temperature Outlet pressure | Tw = Tin p | const. (0.3–76) const. (500 K) const. (1–10 bar) |
| Solid heat capacity | cp,s | const. (1000 J kg−1 K−1). |
| Solid thermal conductivity | λs | const. (5 W m−1 K−1) |
| Solid density Solid heat source | δs S | const. (3950 kg m−3) const. (total: 12.5 W) |
| Gravitational acceleration | considered | |
| Turbulence Radiation | Realizable k-ε RANS (All y+ wall-treatment) neglected [15] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sinn, C.; Wentrup, J.; Thöming, J.; Pesch, G.R. Influence of Pressure, Velocity and Fluid Material on Heat Transport in Structured Open-Cell Foam Reactors Investigated Using CFD Simulations. ChemEngineering 2020, 4, 61. https://doi.org/10.3390/chemengineering4040061
Sinn C, Wentrup J, Thöming J, Pesch GR. Influence of Pressure, Velocity and Fluid Material on Heat Transport in Structured Open-Cell Foam Reactors Investigated Using CFD Simulations. ChemEngineering. 2020; 4(4):61. https://doi.org/10.3390/chemengineering4040061
Chicago/Turabian StyleSinn, Christoph, Jonas Wentrup, Jorg Thöming, and Georg R. Pesch. 2020. "Influence of Pressure, Velocity and Fluid Material on Heat Transport in Structured Open-Cell Foam Reactors Investigated Using CFD Simulations" ChemEngineering 4, no. 4: 61. https://doi.org/10.3390/chemengineering4040061
APA StyleSinn, C., Wentrup, J., Thöming, J., & Pesch, G. R. (2020). Influence of Pressure, Velocity and Fluid Material on Heat Transport in Structured Open-Cell Foam Reactors Investigated Using CFD Simulations. ChemEngineering, 4(4), 61. https://doi.org/10.3390/chemengineering4040061





