Development of a Pressure Stable Inline Droplet Generator with Live Droplet Size Measurement
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
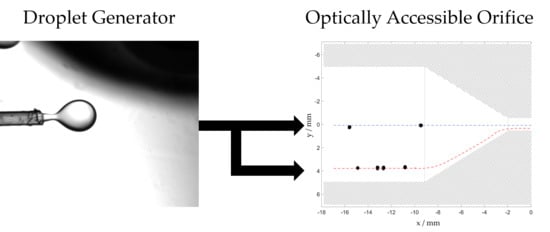
2.2. Experimental Setup
2.3. Image Processing
3. Results
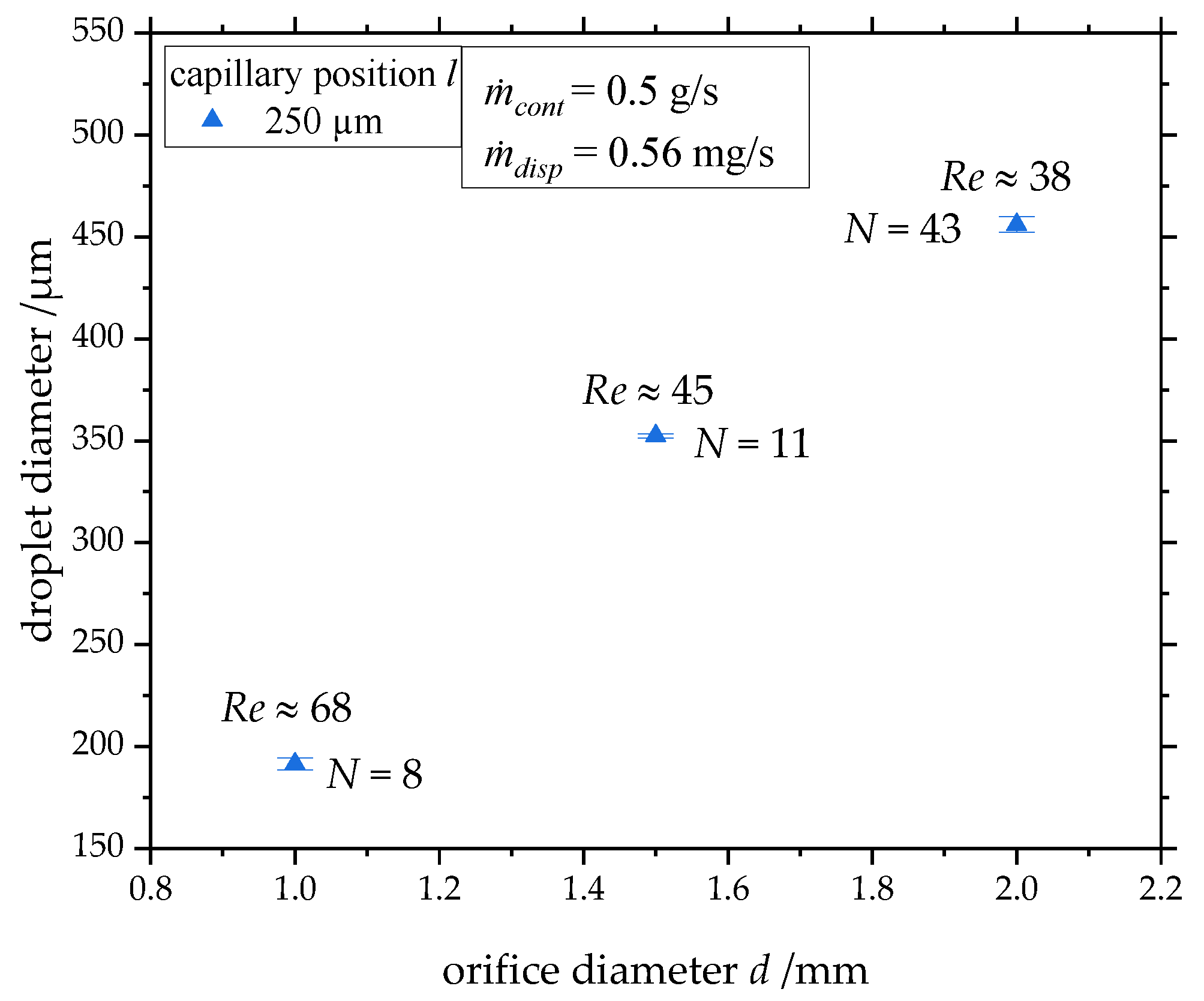
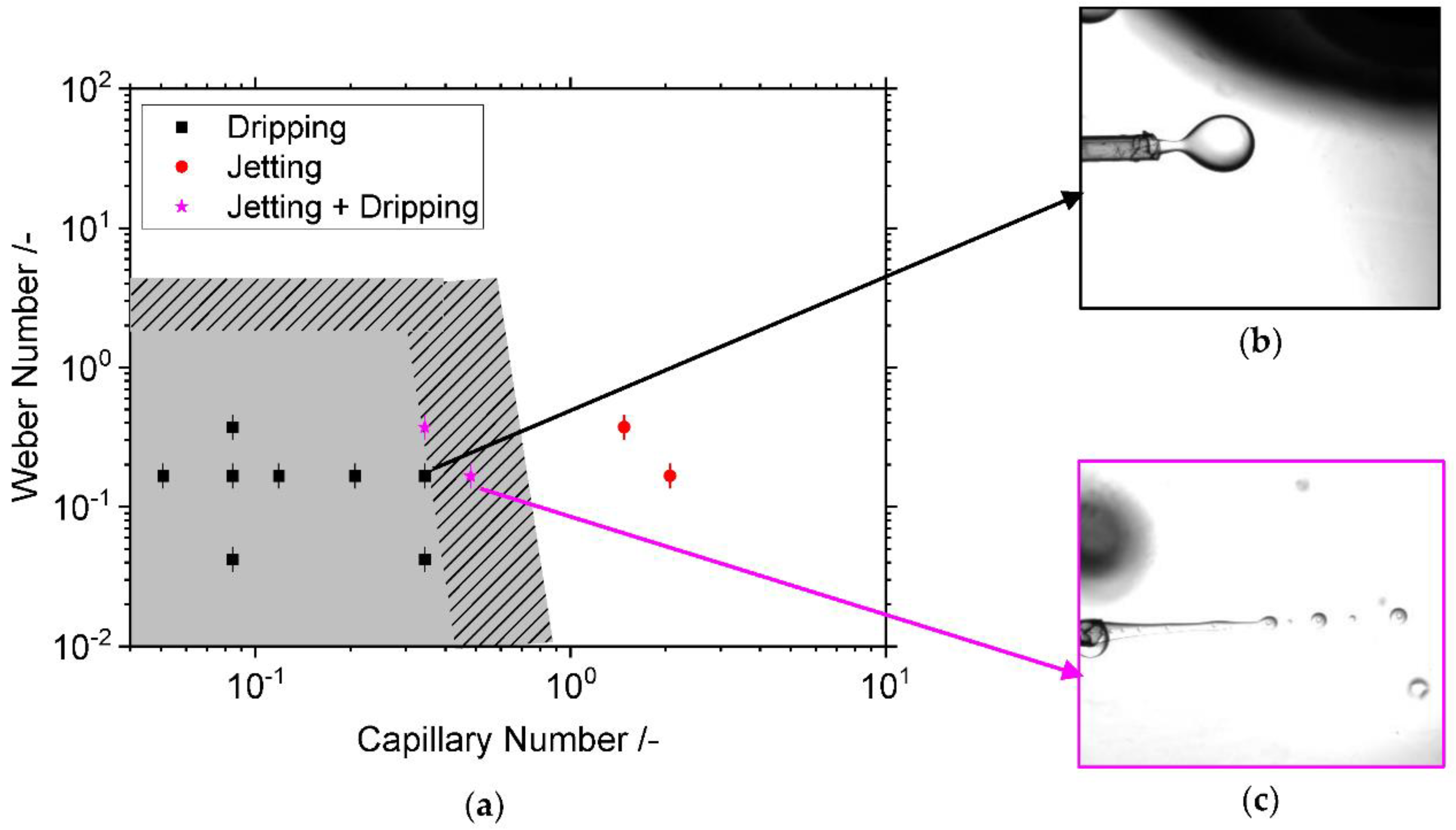
3.1. Influence of the Capillary’s Geometry and Position
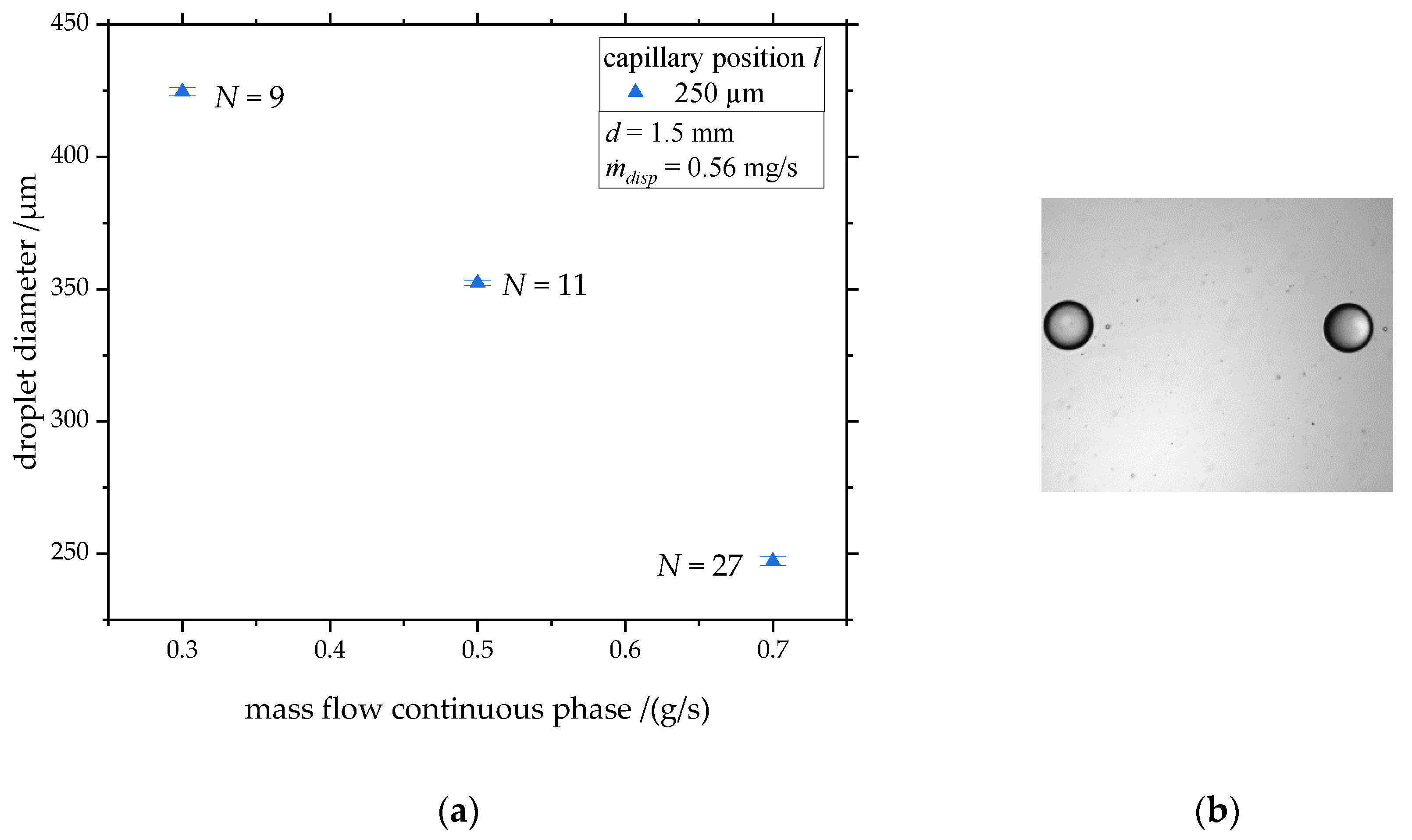
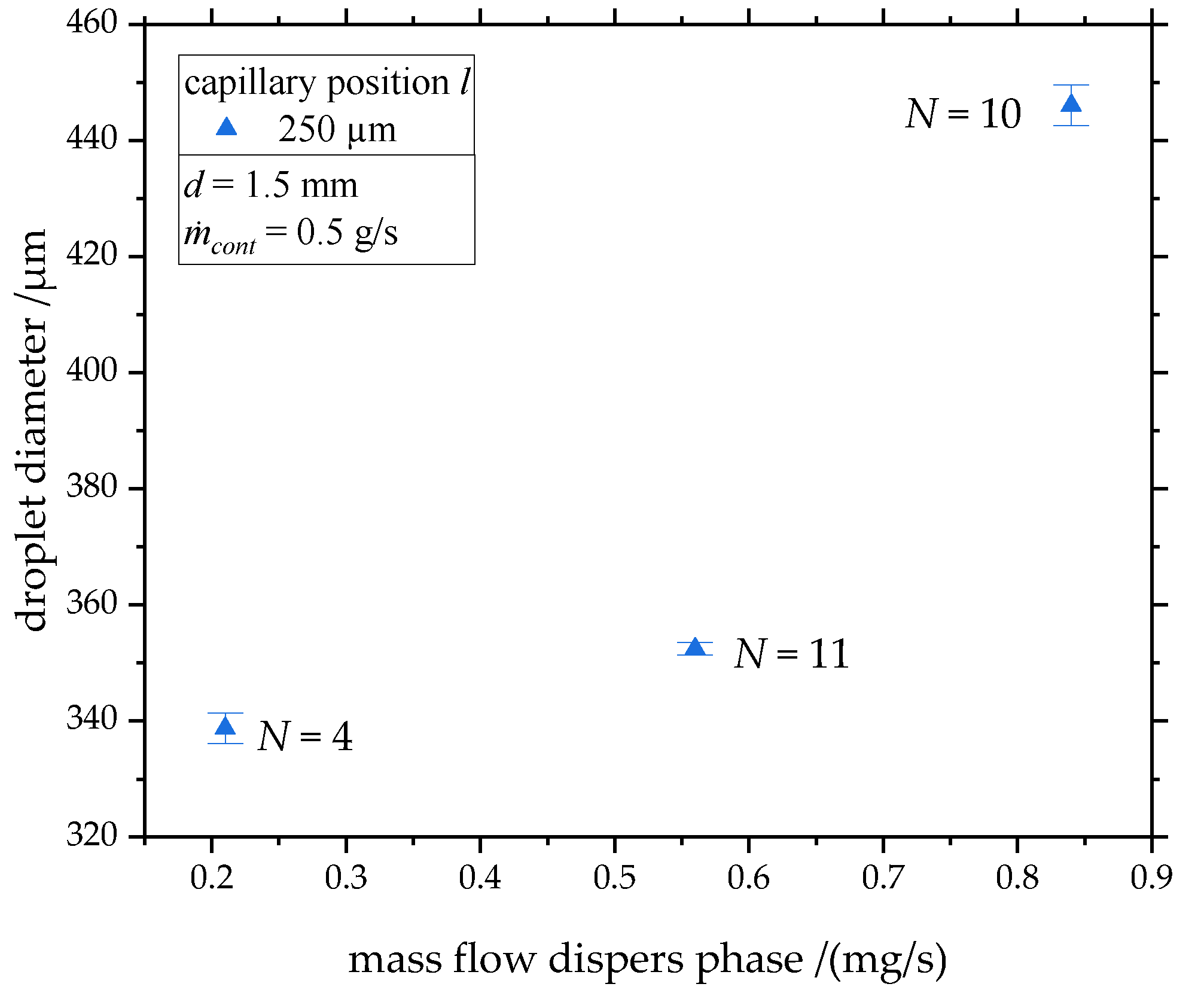
3.2. Influence of Continuous and Disperse Phase Mass Flow
3.3. Reinjection of the Produced Emulsion in Front of a Scaled Disruption Unit
4. Discussion
- Orifice diameter : Due to production inaccuracies, no even jet was formed if the orifice diameter was smaller than 1 mm, resulting in larger droplets.
- Limit of the disperse phase fraction: The disperse phase fraction is connected to the flow conditions in the droplet generator, resulting in decreasing disperse phase fractions when increasing the total mass flow over the optically accessible disruption unit. This limitation can be solved by numbering up the capillary tips.
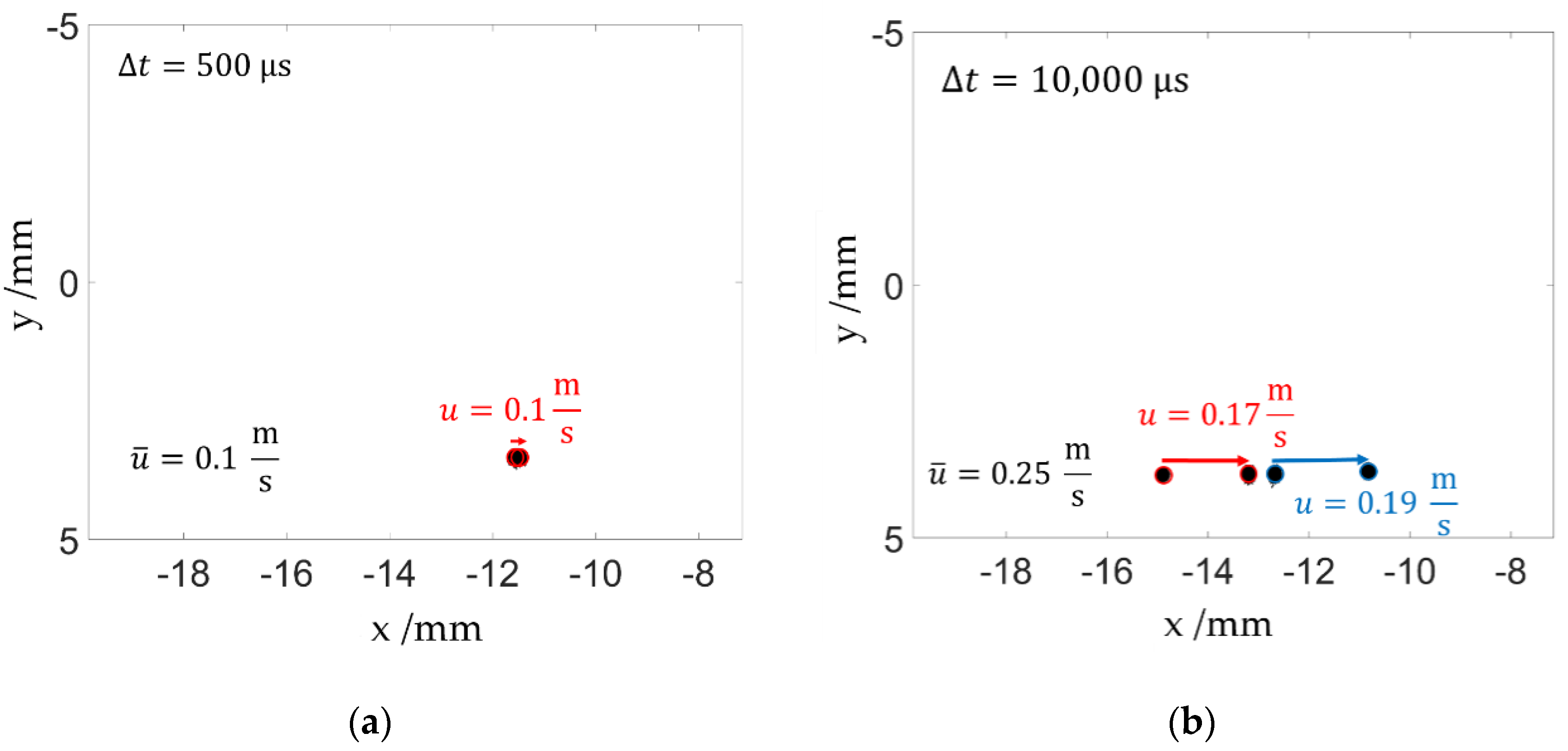
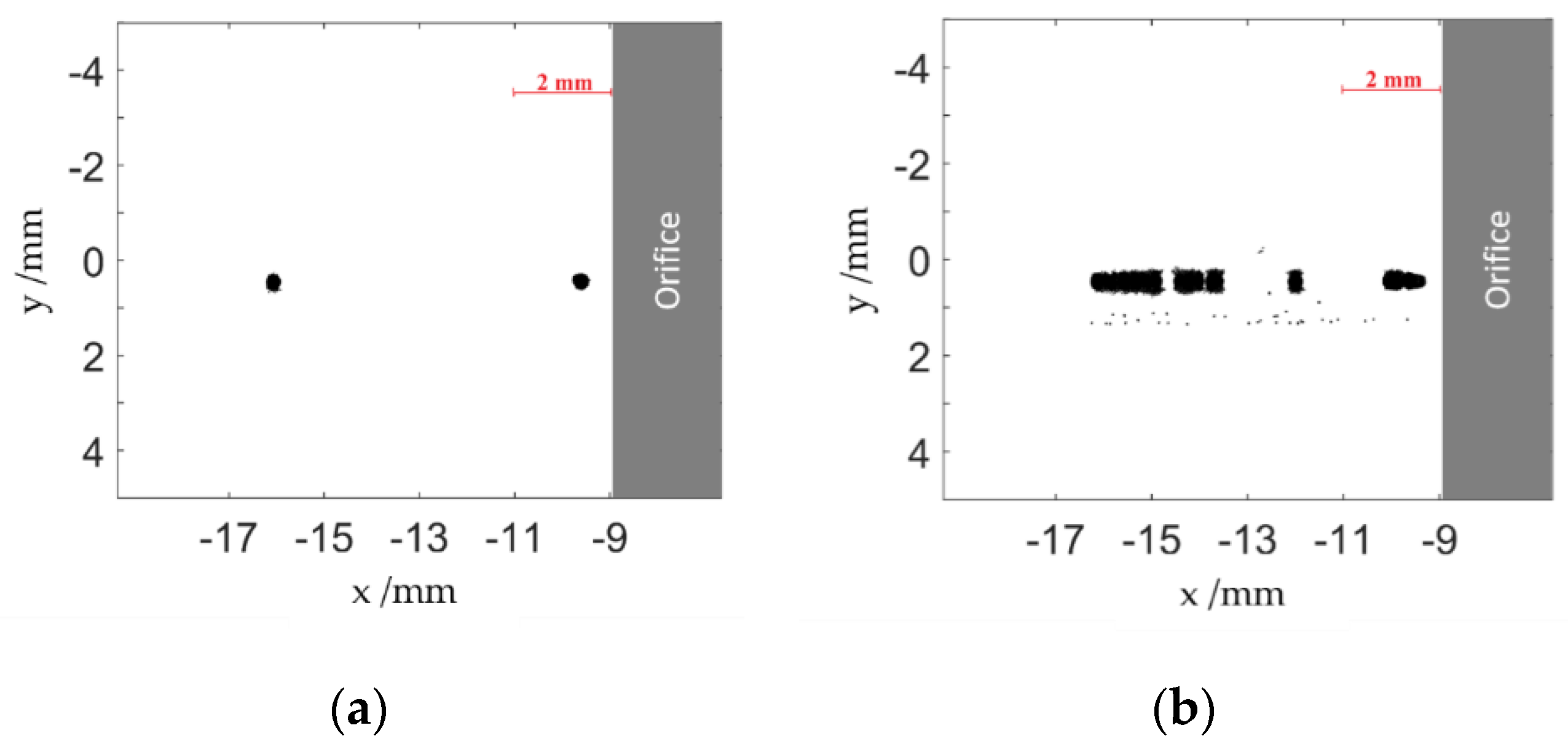
- Droplet velocity does not reach the velocity of the surrounding fluid: The droplets do not completely accelerate to the velocity of the continuous phase at higher velocities in the inlet channel of the disruption unit. This may result in lower stresses on the droplets. It is expected, however, that this influence is moderate as the fluid is accelerated by a factor of 100 in the disruption unit which should eliminate the velocity deviation of the droplets.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gaulin, A. Appareil et Procédé pour la Stabilisation du Lait. Patent Brecet 295,596, 23 May 1899. [Google Scholar]
- Walstra, P. Formation of Emulsions. In P. Becher: Encyclopedia of Emulsion Technology, Volume 1 Basic Theory; Mieth, G., Ed.; Marcel Dekker: New York, NY, USA, 1983. [Google Scholar]
- Schuchmann, H.P. Advances in Hydrodynamic Pressure Processing for Enhancing Emulsification and Dispersion. In Innovative Food Processing Technologies: Extraction, Separation, Component Modification and Process Intensification, 1st ed.; Knoerzer, K., Juliano, P., Smithers, G., Eds.; Woodhead Publishing: Sawston, UK, 2016; pp. 387–412. ISBN 978-0-08-100294-0. [Google Scholar]
- Walstra, P.; Smulders, P.E.A. Chapter 2. Emulsion Formation. In Modern Aspects of Emulsion Science; Binks, B.P., Ed.; Royal Society of Chemistry: Cambridge, UK, 1998; pp. 56–99. ISBN 978-0-85404-439-9. [Google Scholar]
- Schlender, M.; Minke, K.; Spiegel, B.; Schuchmann, H.P. High-pressure double stage homogenization processes: Influences of plant setup on oil droplet size. Chem. Eng. Sci. 2015, 131, 162–171. [Google Scholar] [CrossRef]
- Bisten, A.; Rudolf, D.; Karbstein, H.P. Comparison of flow patterns and droplet deformations of modified sharp-edged and conical orifices during high-pressure homogenisation using µPIV. Microfluid. Nanofluid. 2018, 22, 607. [Google Scholar] [CrossRef]
- Innings, F.; Trägårdh, C. Visualization of the Drop Deformation and Break-Up Process in a High Pressure Homogenizer. Chem. Eng. Technol. 2005, 28, 882–891. [Google Scholar] [CrossRef]
- Innings, F.; Fuchs, L.; Trägårdh, C. Theoretical and experimental analyses of drop deformation and break-up in a scale model of a high-pressure homogenizer. J. Food Eng. 2011, 103, 21–28. [Google Scholar] [CrossRef]
- Kelemen, K.; Gepperth, S.; Koch, R.; Bauer, H.-J.; Schuchmann, H.P. On the visualization of droplet deformation and breakup during high-pressure homogenization. Microfluid. Nanofluid. 2015, 19, 1139–1158. [Google Scholar] [CrossRef]
- Wieth, L.; Kelemen, K.; Braun, S.; Koch, R.; Bauer, H.-J.; Schuchmann, H.P. Smoothed Particle Hydrodynamics (SPH) simulation of a high-pressure homogenization process. Microfluid. Nanofluid. 2016, 20, 5011. [Google Scholar] [CrossRef]
- Håkansson, A. Scale-down failed—Dissimilarities between high-pressure homogenizers of different scales due to failed mechanistic matching. J. Food Eng. 2017, 195, 31–39. [Google Scholar] [CrossRef]
- Håkansson, A.; Innings, F.; Revstedt, J.; Trägårdh, C.; Bergenståhl, B. Estimation of turbulent fragmenting forces in a high-pressure homogenizer from computational fluid dynamics. Chem. Eng. Sci. 2012, 75, 309–317. [Google Scholar] [CrossRef]
- Håkansson, A.; Innings, F.; Trägårdh, C.; Bergenståhl, B. A high-pressure homogenization emulsification model—Improved emulsifier transport and hydrodynamic coupling. Chem. Eng. Sci. 2013, 91, 44–53. [Google Scholar] [CrossRef]
- Håkansson, A.; Trägårdh, C.; Bergenståhl, B. Dynamic simulation of emulsion formation in a high pressure homogenizer. Chem. Eng. Sci. 2009, 64, 2915–2925. [Google Scholar] [CrossRef]
- Håkansson, A.; Trägårdh, C.; Bergenståhl, B. Studying the effects of adsorption, recoalescence and fragmentation in a high pressure homogenizer using a dynamic simulation model. Food Hydrocoll. 2009, 23, 1177–1183. [Google Scholar] [CrossRef]
- Håkansson, A. Emulsion Formation by Homogenization: Current Understanding and Future Perspectives. Annu. Rev. Food Sci. Technol. 2019, 10, 239–258. [Google Scholar] [CrossRef] [PubMed]
- Håkansson, A. On the validity of different methods to estimate breakup frequency from single drop experiments. Chem. Eng. Sci. 2020, 115908. [Google Scholar] [CrossRef]
- Taylor, G.I. The formation of emulsions in definable fields of flow. Proc. R. Soc. A 1934, 146, 501–523. [Google Scholar]
- Grace, H.P. dispersion phenomena in high viscosity immiscible fluid systems and application of static mixers as dispersion devices in such systems. Chem. Eng. Commun. 1982, 14, 225–277. [Google Scholar] [CrossRef]
- Rayleigh, L. On The Instability of Jets. Proc. Lond. Math. Soc. 1878, 1, 4–13. [Google Scholar] [CrossRef] [Green Version]
- Tomotika, S. On the instability of a cylindrical thread of a viscous liquid surrounded by another viscous fluid. Proc. R. Soc. Lond. A 1935, 150, 322–337. [Google Scholar] [CrossRef]
- Kelemen, K.; Crowther, F.E.; Cierpka, C.; Hecht, L.L.; Kähler, C.J.; Schuchmann, H.P. Investigations on the characterization of laminar and transitional flow conditions after high pressure homogenization orifices. Microfluid. Nanofluid. 2015, 18, 599–612. [Google Scholar] [CrossRef]
- Håkansson, A.; Fuchs, L.; Innings, F.; Revstedt, J.; Trägårdh, C.; Bergenståhl, B. High resolution experimental measurement of turbulent flow field in a high pressure homogenizer model and its implications on turbulent drop fragmentation. Chem. Eng. Sci. 2011, 66, 1790–1801. [Google Scholar] [CrossRef]
- Innings, F.; Trägårdh, C. Analysis of the flow field in a high-pressure homogenizer. Exp. Therm. Fluid Sci. 2007, 32, 345–354. [Google Scholar] [CrossRef]
- Walzel, P. Advanteges and Limits in large Scale Modeling of Atomizers. In Proceedings of the 2nd International Conference on Liquid Atomization and Spray Systems: ICLASS-‘82, Madison, WI, USA, 20–24 June 1982; Crosby, E.J., Ed.; Department of Chemical Engineering-University of Wisconsin: Madison, WI, USA, 1982; pp. 187–194. [Google Scholar]
- Kolb, G.; Wagner, G.; Ulrich, J. Untersuchungen zum Aufbruch von Einzeltropfen in Dispergiereinheiten zur Emulsionsherstellung. Chem. Ing. Tech. 2001, 73, 80–83. [Google Scholar] [CrossRef]
- Budde, C.; Schaffner, D.; Walzel, P. Drop Breakup in Liquid-Liquid Dispersions at an Orifice Plate Observed in a Large-Scale Model. Chem. Eng. Technol. 2002, 25, 1164–1167. [Google Scholar] [CrossRef]
- Christopher, G.F.; Anna, S.L. Microfluidic methods for generating continuous droplet streams. J. Phys. D Appl. Phys. 2007, 40, R319–R336. [Google Scholar] [CrossRef]
- Vladisavljević, G.T.; Kobayashi, I.; Nakajima, M. Production of uniform droplets using membrane, microchannel and microfluidic emulsification devices. Microfluid. Nanofluid. 2012, 13, 151–178. [Google Scholar] [CrossRef] [Green Version]
- Utada, A.S.; Fernandez-Nieves, A.; Stone, H.A.; Weitz, D.A. Dripping to jetting transitions in coflowing liquid streams. Phys. Rev. Lett. 2007, 99, 94502. [Google Scholar] [CrossRef]
- Umbanhowar, P.B.; Prasad, V.; Weitz, D.A. Monodisperse Emulsion Generation via Drop Break off in a Coflowing Stream. Langmuir 2000, 16, 347–351. [Google Scholar] [CrossRef]
- Rayleigh, L., VI. On the capillary phenomena of jets. Proc. R. Soc. Lond. 1879, 29, 71–97. [Google Scholar] [CrossRef]
- Cramer, C.; Fischer, P.; Windhab, E.J. Drop formation in a co-flowing ambient fluid. Chem. Eng. Sci. 2004, 59, 3045–3058. [Google Scholar] [CrossRef]
- Duxenneuner, M.R. Visualization, Design, and Scaling of Drop Generation in Coflow Processes; ETH Zurich: Zürich, Switzerland, 2009. [Google Scholar]
- Zhang, D.F.; Stone, H.A. Drop formation in viscous flows at a vertical capillary tube. Phys. Fluids 1997, 9, 2234–2242. [Google Scholar] [CrossRef] [Green Version]
- Utada, A.S.; Chu, L.-Y.; Fernandez-Nieves, A.; Link, D.R.; Holtze, C.; Weitz, D.A. Dripping, Jetting, Drops, and Wetting: The Magic of Microfluidics. Mrs Bull. 2007, 32, 702–708. [Google Scholar] [CrossRef] [Green Version]





| 1148.55 | |
| 920 | |
| 15.5 | |
| 0.00942 | |
| 0.02947 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Preiss, F.J.; Dagenbach, T.; Fischer, M.; Karbstein, H.P. Development of a Pressure Stable Inline Droplet Generator with Live Droplet Size Measurement. ChemEngineering 2020, 4, 60. https://doi.org/10.3390/chemengineering4040060
Preiss FJ, Dagenbach T, Fischer M, Karbstein HP. Development of a Pressure Stable Inline Droplet Generator with Live Droplet Size Measurement. ChemEngineering. 2020; 4(4):60. https://doi.org/10.3390/chemengineering4040060
Chicago/Turabian StylePreiss, Felix Johannes, Teresa Dagenbach, Markus Fischer, and Heike Petra Karbstein. 2020. "Development of a Pressure Stable Inline Droplet Generator with Live Droplet Size Measurement" ChemEngineering 4, no. 4: 60. https://doi.org/10.3390/chemengineering4040060
APA StylePreiss, F. J., Dagenbach, T., Fischer, M., & Karbstein, H. P. (2020). Development of a Pressure Stable Inline Droplet Generator with Live Droplet Size Measurement. ChemEngineering, 4(4), 60. https://doi.org/10.3390/chemengineering4040060