3-D Multi-Tubular Reactor Model Development for the Oxidative Dehydrogenation of Butene to 1,3-Butadiene
Abstract
1. Introduction
2. Model Development
2.1. Mass Conservation
2.2. Momentum Conservation
Turbulent Modeling
2.3. Reaction Kinetics
2.4. Energy Equations
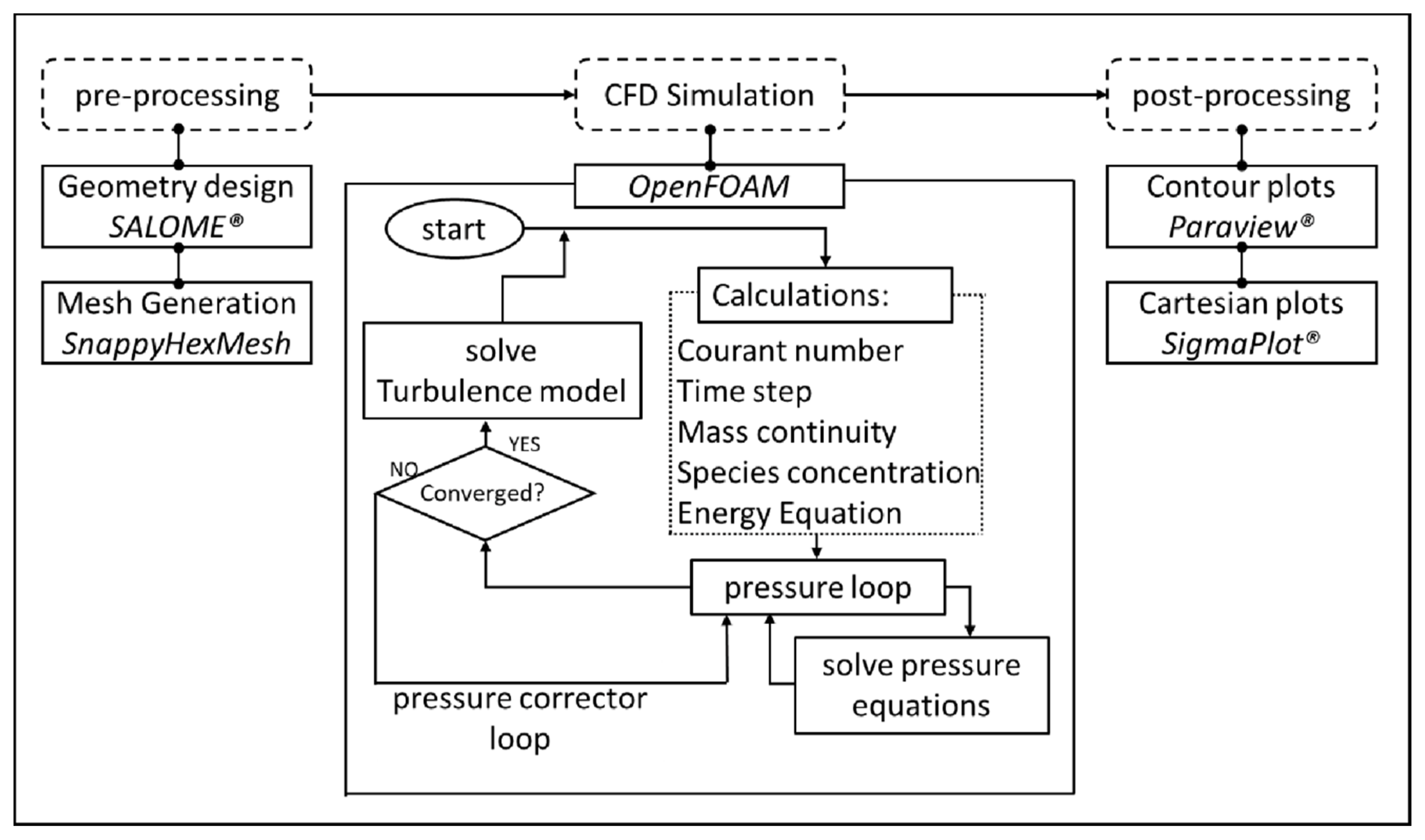
3. Computational Fluid Dynamics (CFD) Simulation Methods
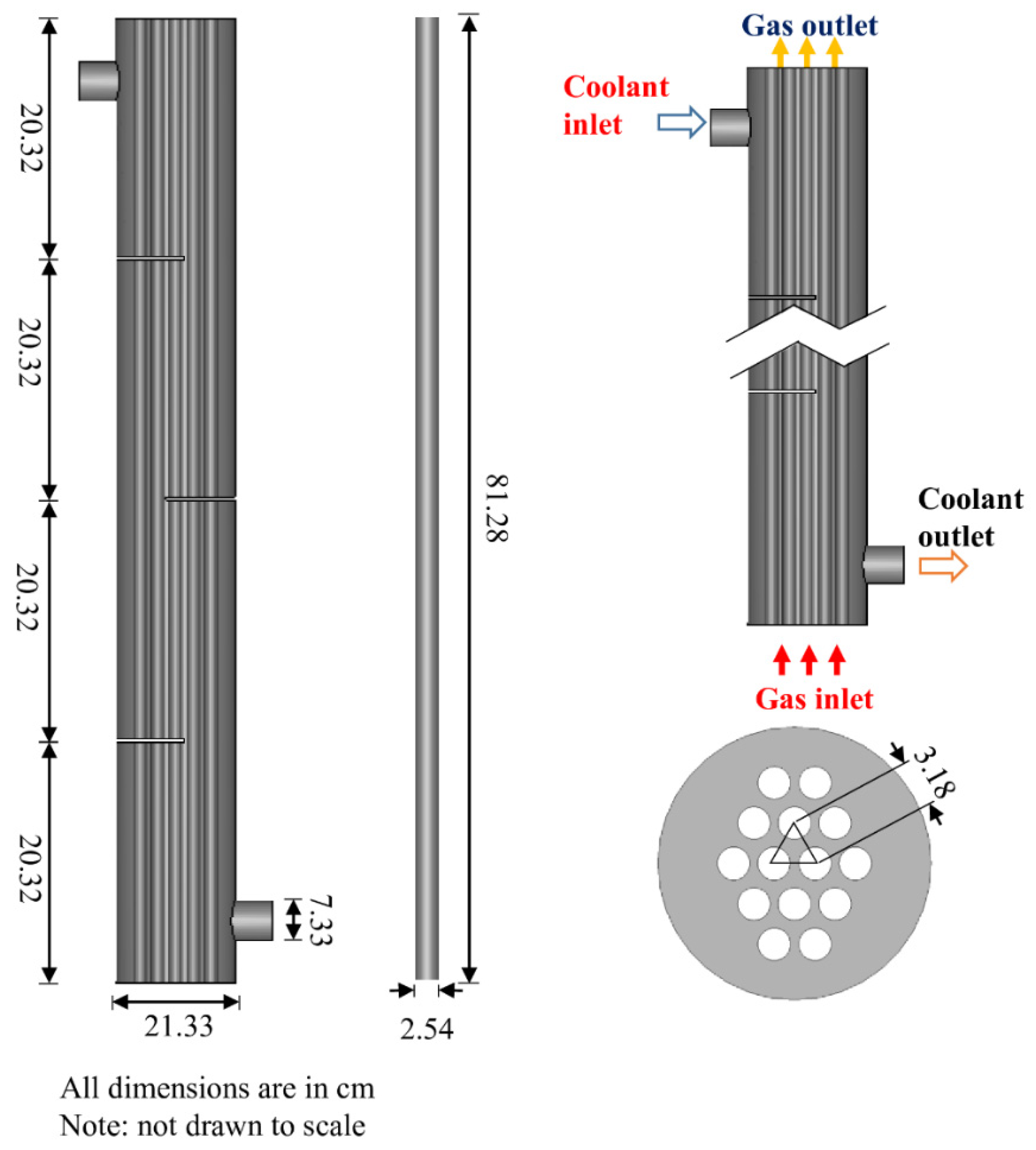
3.1. Geometry and Mesh Generation
3.1.1. Geometric Description of the Multi-Tubular Reactor
3.1.2. Mesh Generation
3.2. Model Parameters Used in the Computational Fluid Dynamics (CFD) Model
3.3. Solution Strategy
4. Results and Discussion
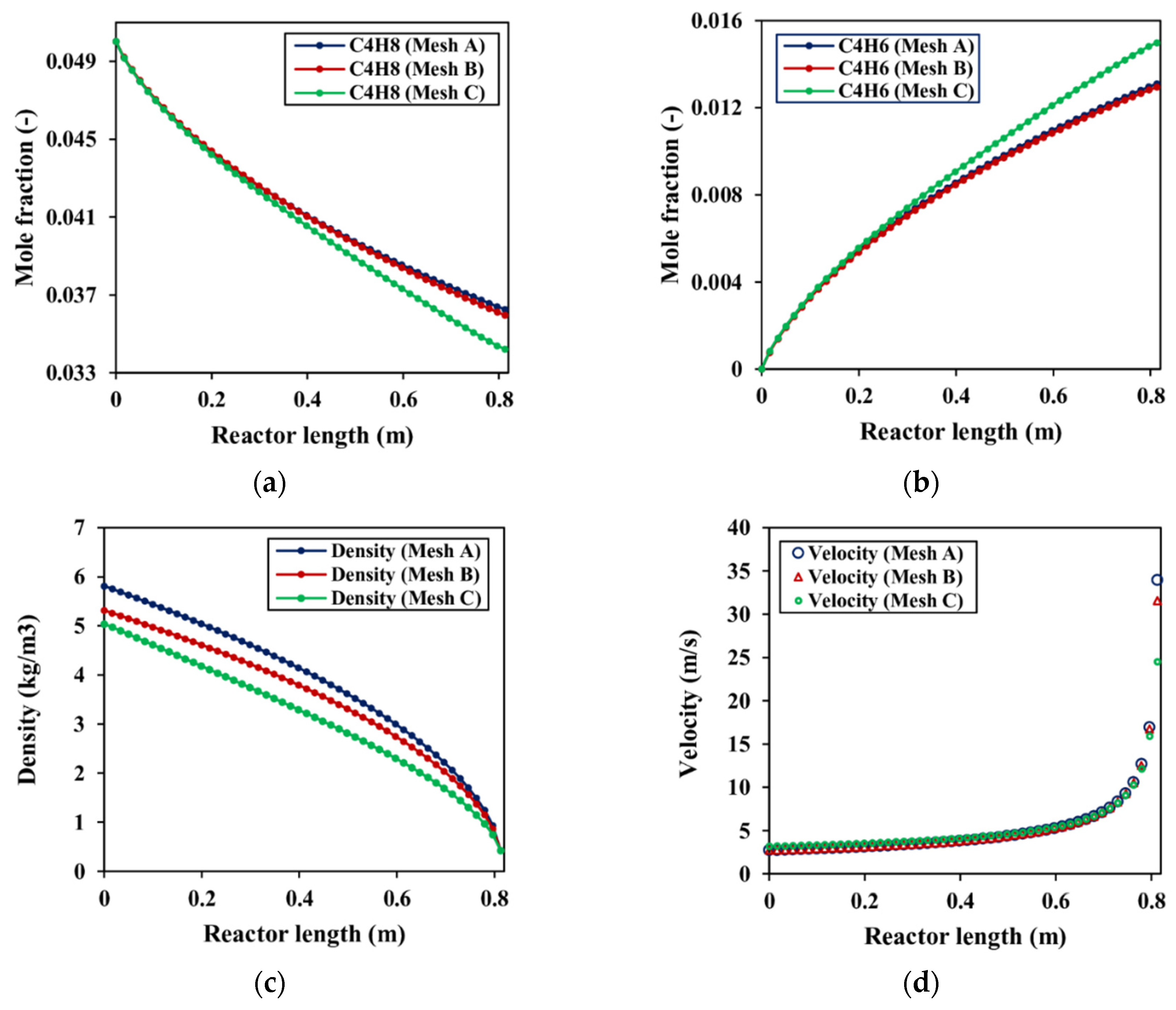
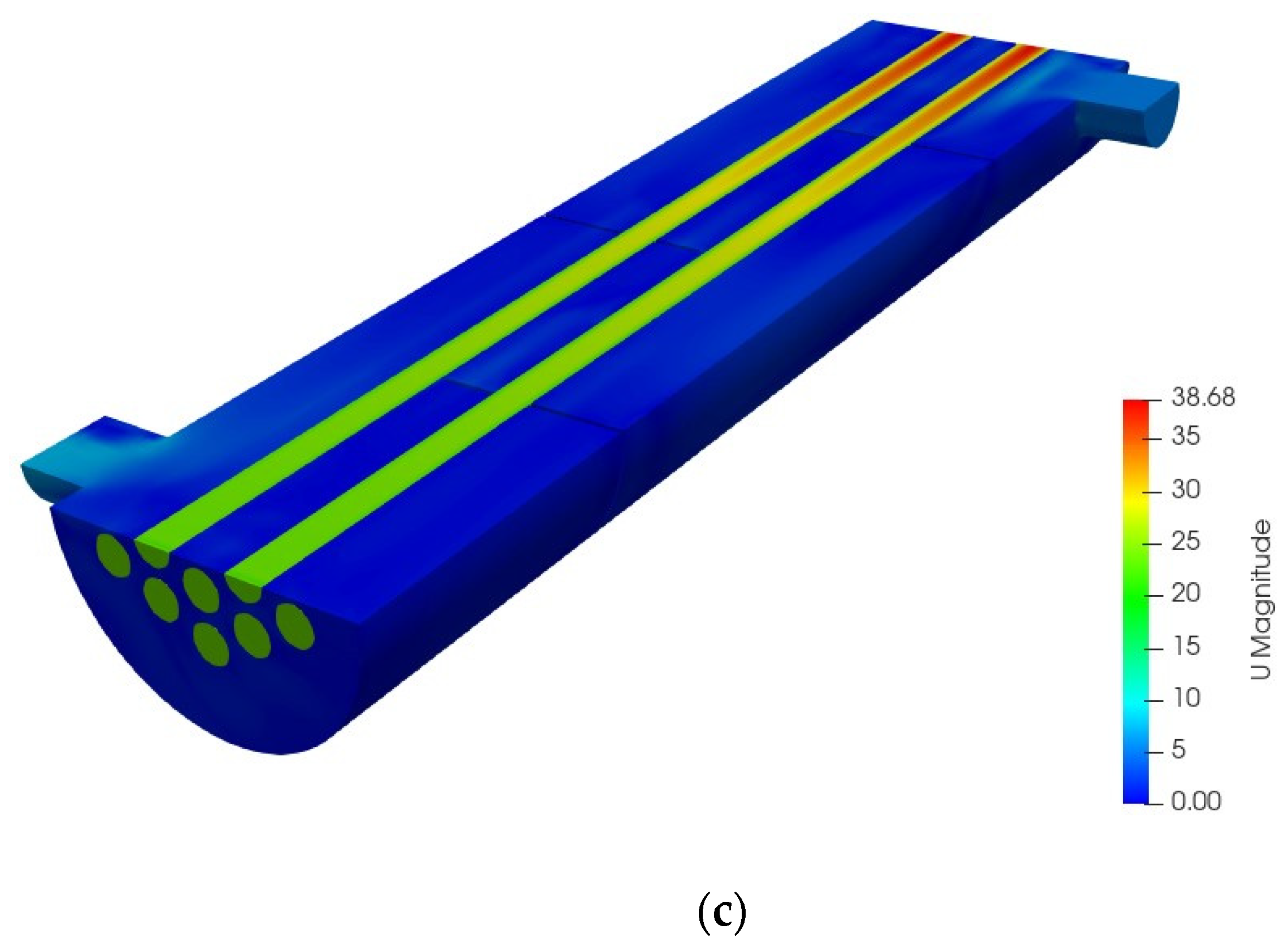
4.1. Mesh Independence Test
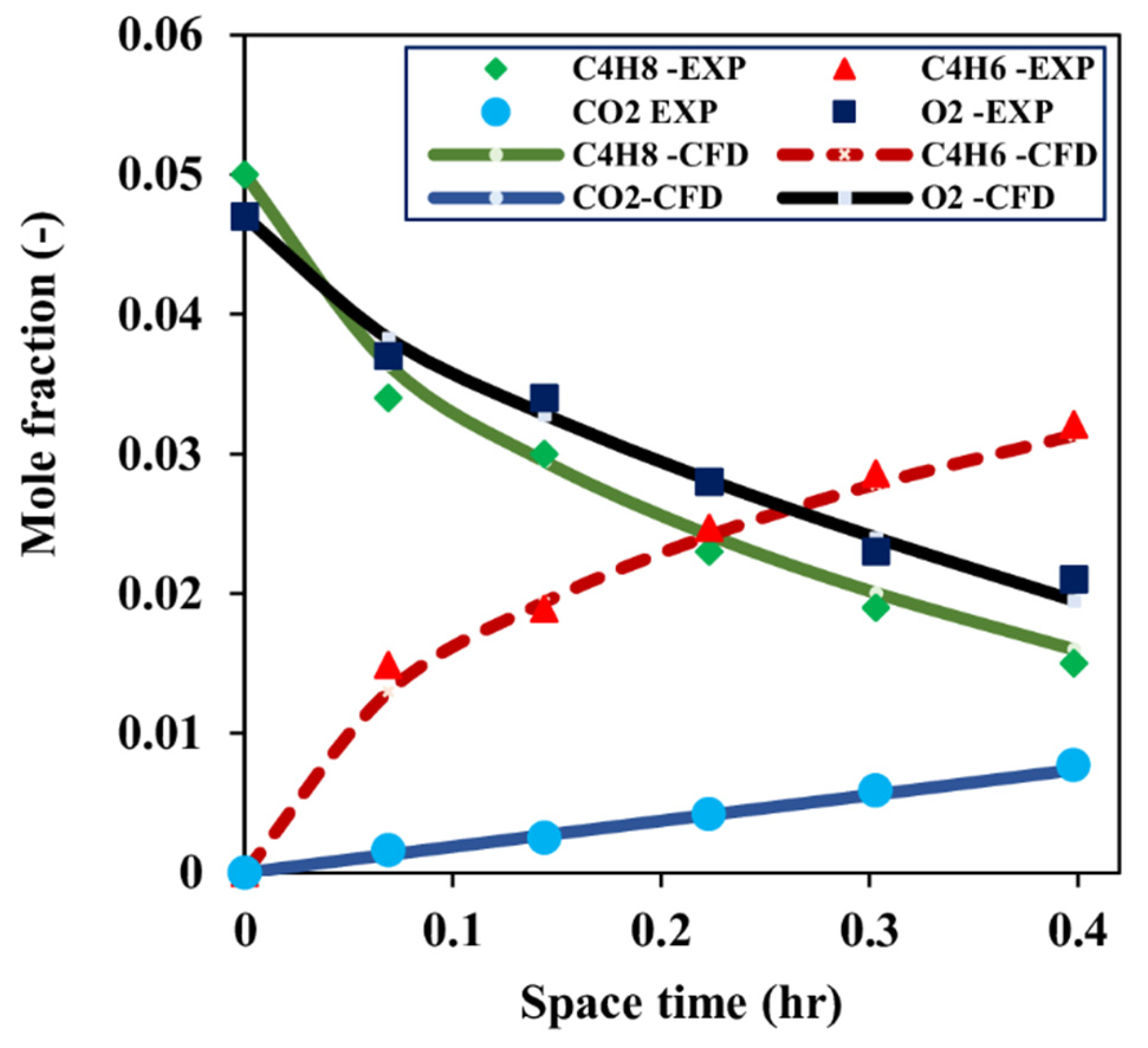
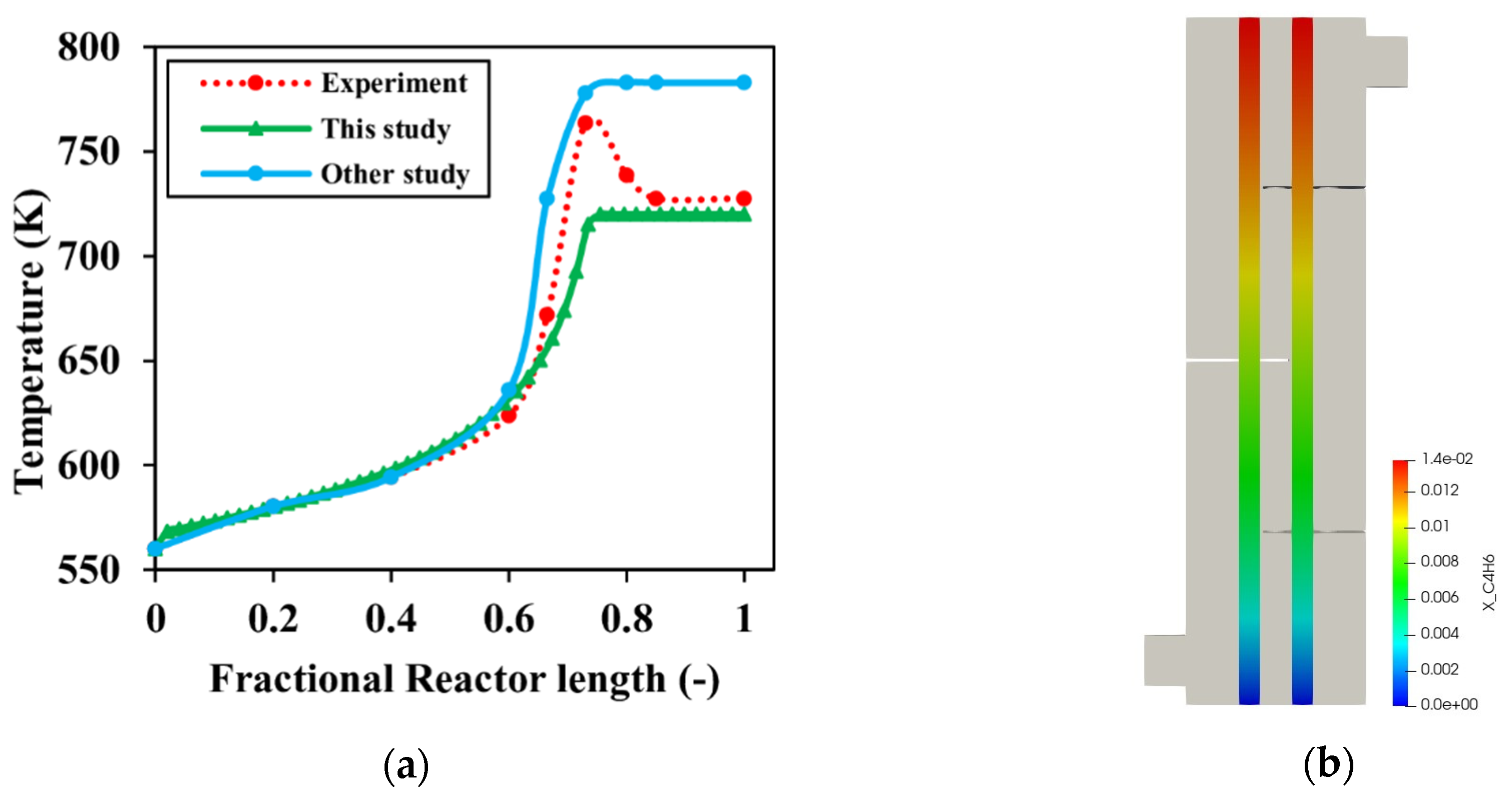
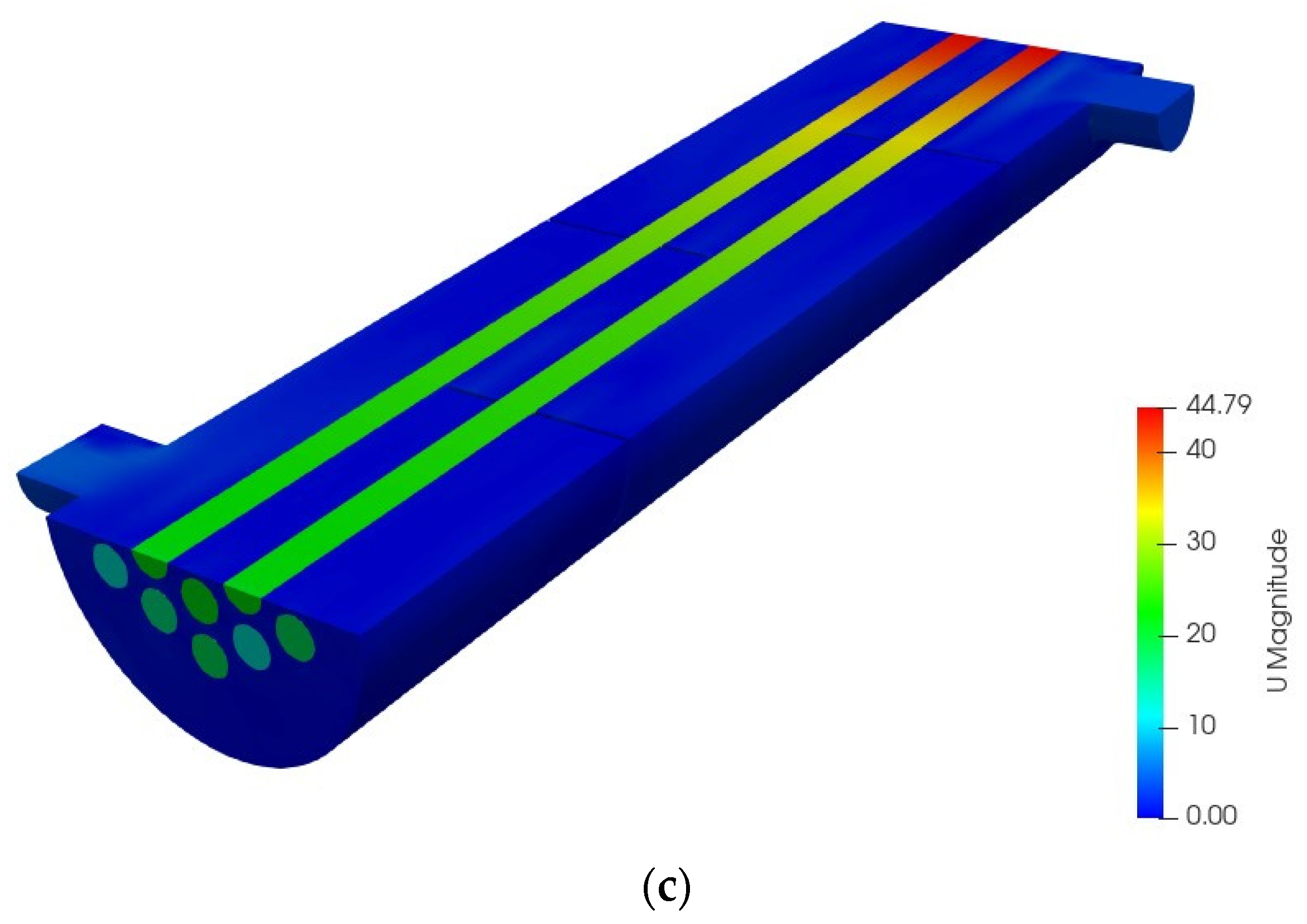
4.2. 3D Model Validation and Analysis
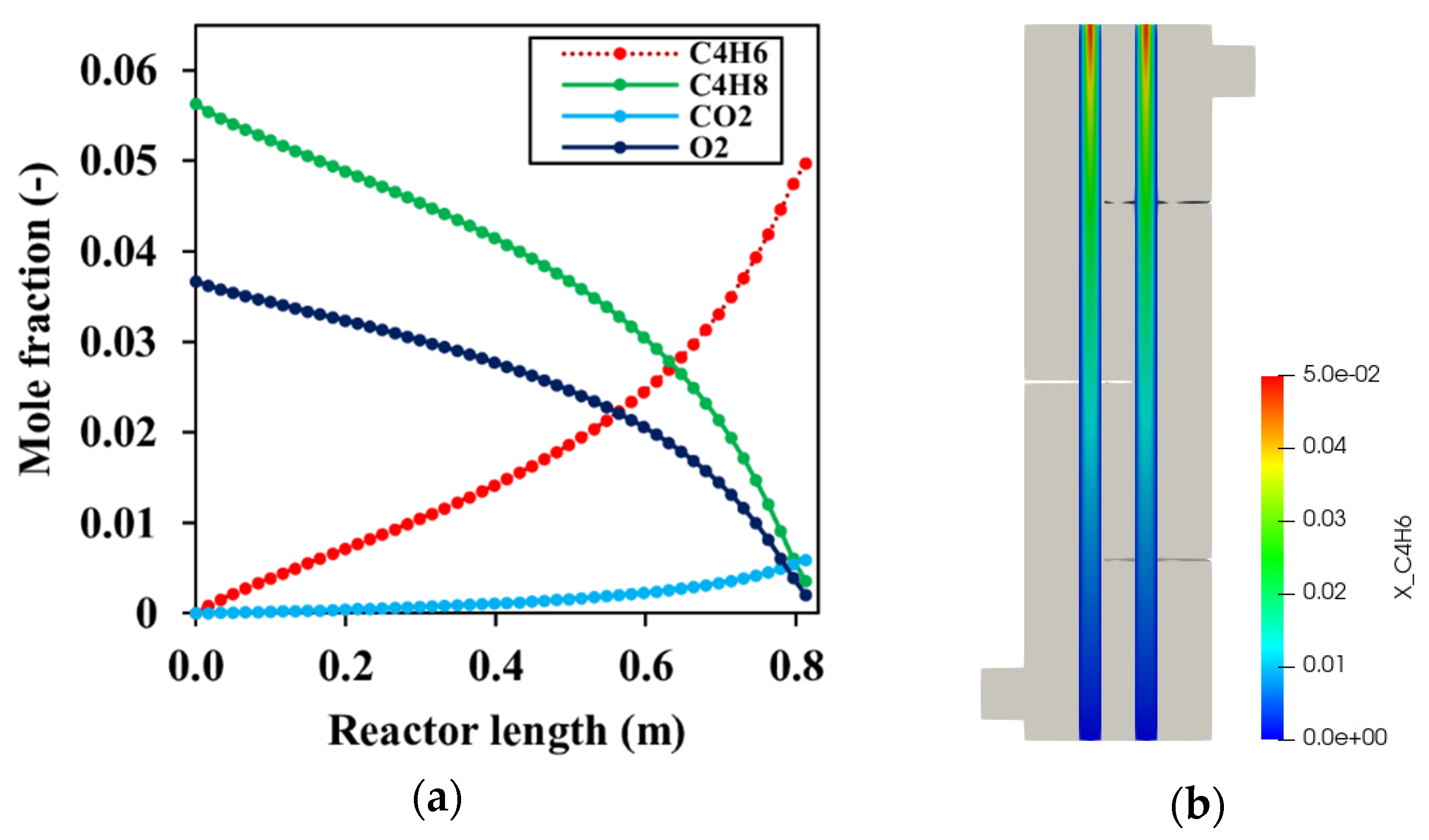
4.3. Parametric Study
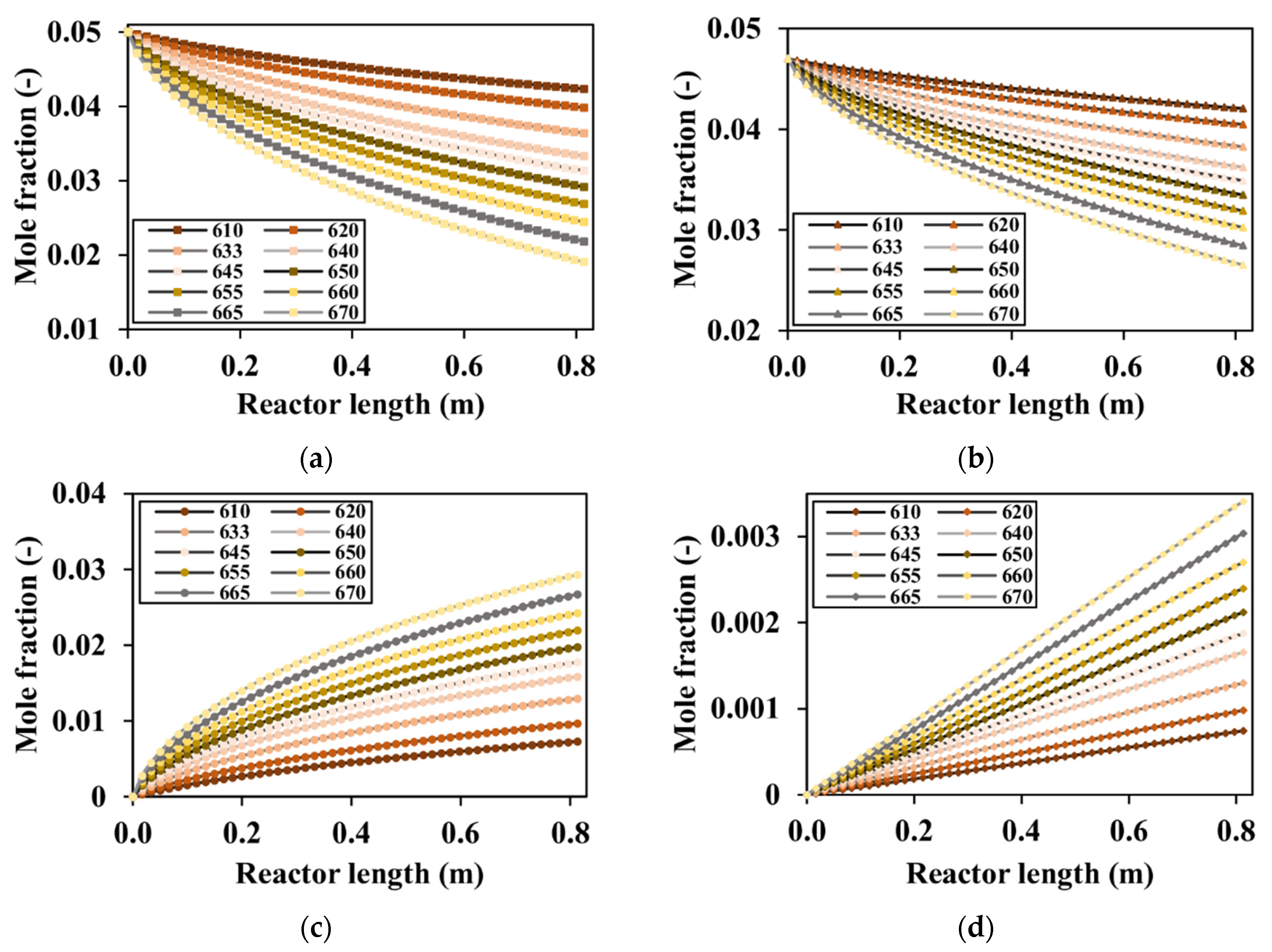
4.3.1. Effect of Thermal Conditions
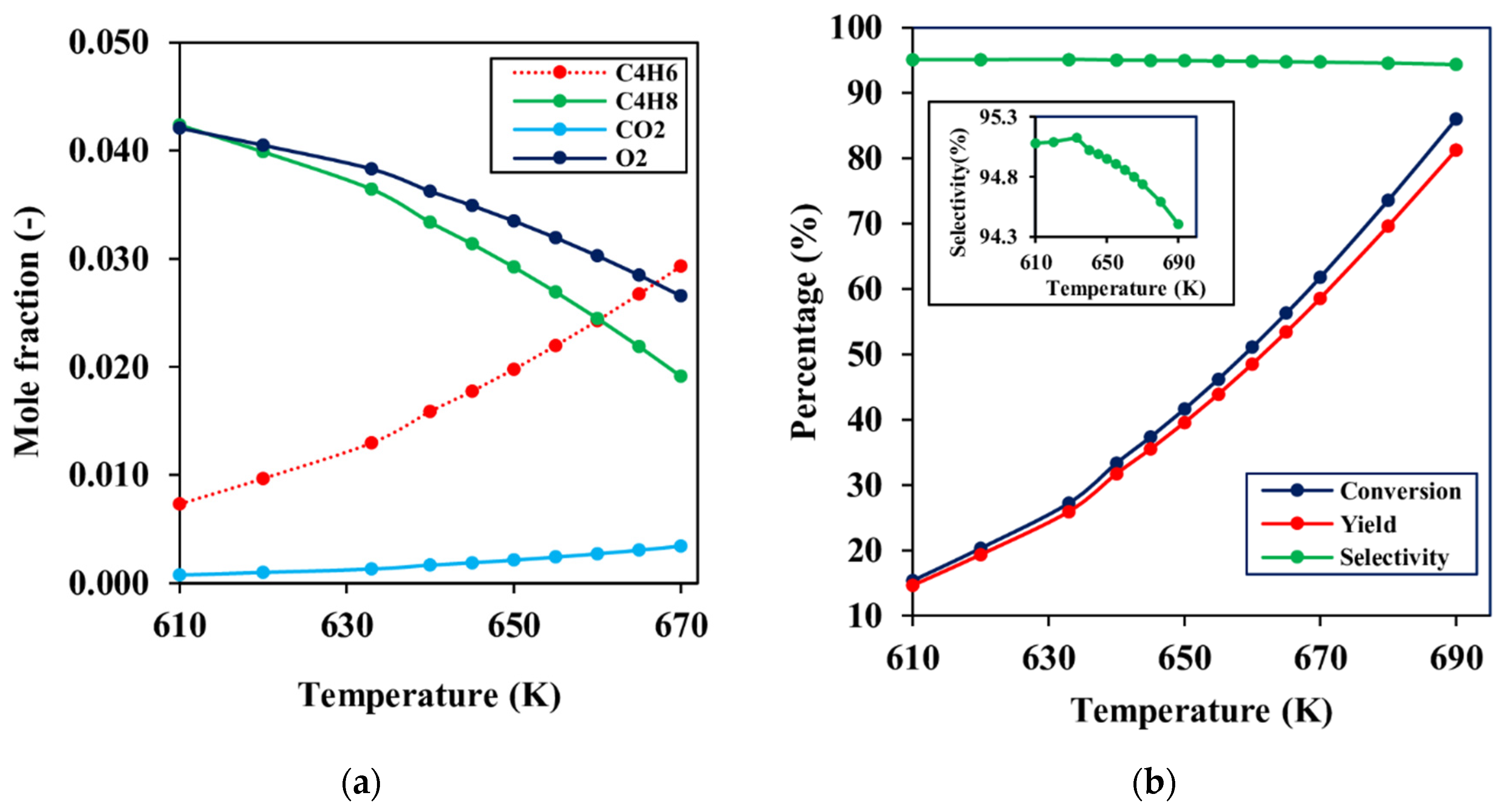
4.3.2. Effect of Temperature
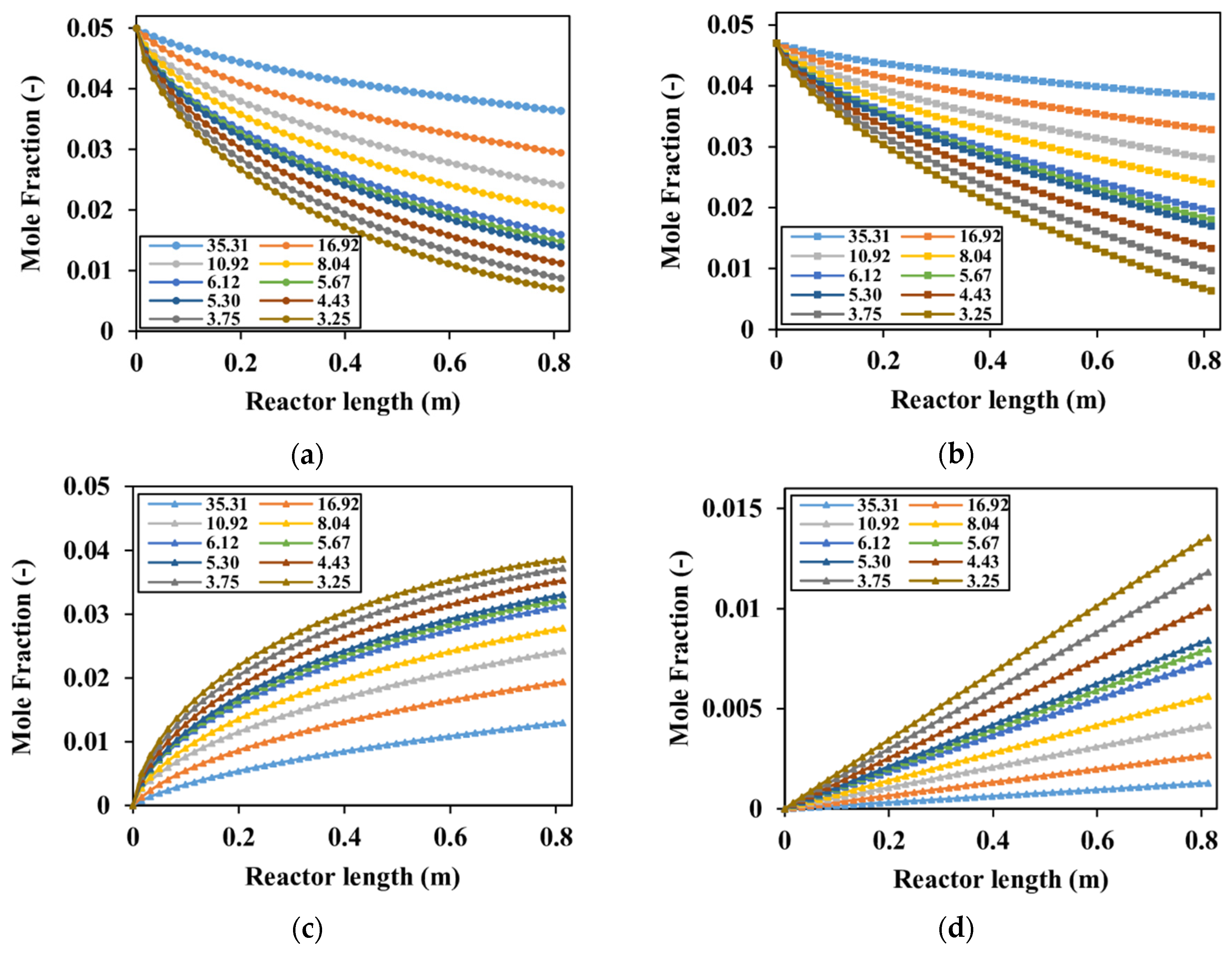
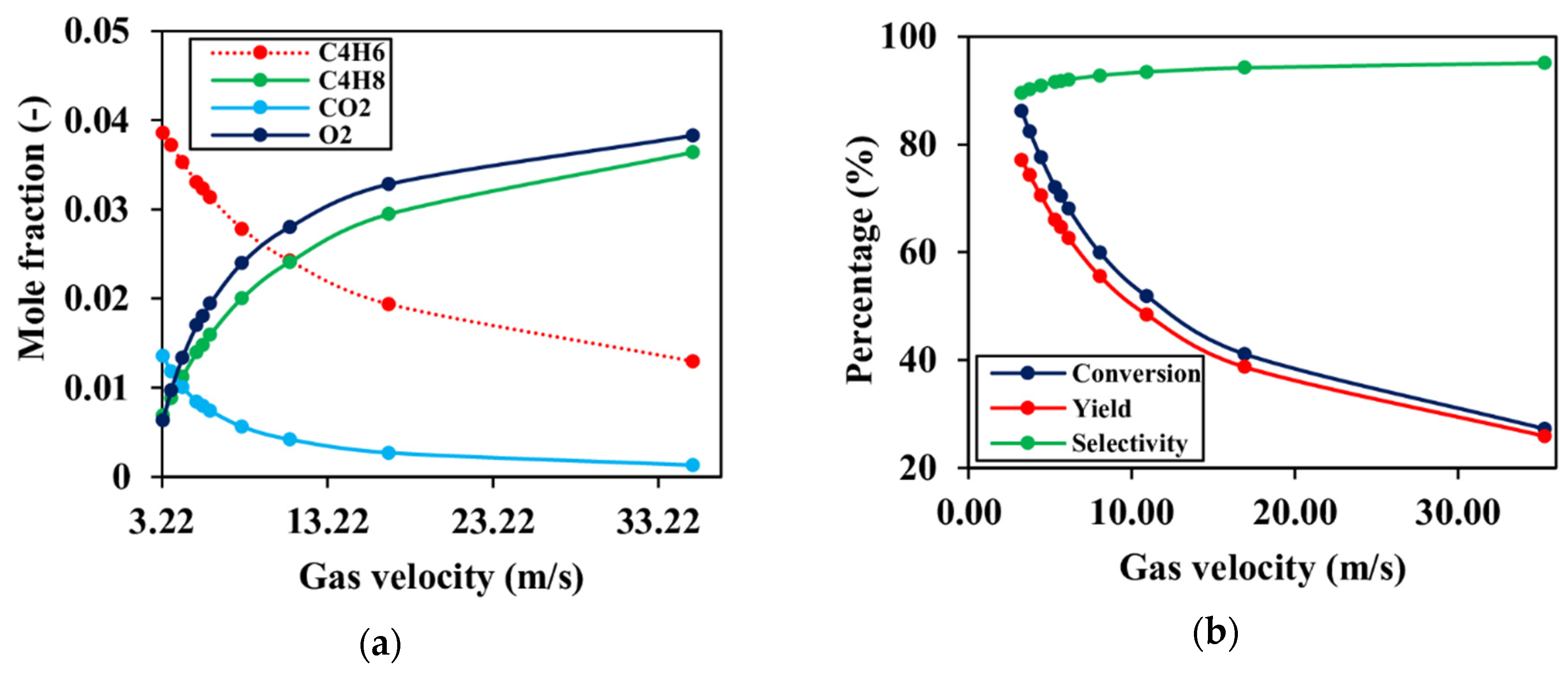
4.3.3. Effect of Gas Velocity
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Rischard, J.; Antinori, C.; Maier, L.; Deutschmann, O. Oxidative dehydrogenation of n-butane to butadiene with Mo-V-MgO catalysts in a two-zone fluidized bed reactor. Appl. Catal. A Gen. 2016, 511, 23–30. [Google Scholar] [CrossRef]
- White, W.C. Butadiene production process overview. Chem. Biol. Interact. 2007, 166, 10–14. [Google Scholar] [CrossRef] [PubMed]
- Qi, Y.; Liu, Z.; Liu, S.; Cui, L.; Dai, Q.; He, J.; Dong, W.; Bai, C. Synthesis of 1,3-butadiene and its 2-substituted monomers for synthetic rubbers. Catalysts 2019, 9, 97. [Google Scholar] [CrossRef]
- Yoshimura, Y.; Kijima, N.; Hayakawa, T.; Murata, K.; Suzuki, K.; Mizukami, F.; Matano, K.; Konishi, T.; Oikawa, T.; Saito, M.; et al. Catalytic cracking of naphtha to light olefins. Catal. Surv. Japan 2001, 4, 157–167. [Google Scholar] [CrossRef]
- Yan, W.; Kouk, Q.Y.; Luo, J.; Liu, Y.; Borgna, A. Catalytic oxidative dehydrogenation of 1-butene to 1,3-butadiene using CO2. Catal. Commun. 2014, 46, 208–212. [Google Scholar] [CrossRef]
- Ren, T.; Patel, M.; Blok, K. Olefins from conventional and heavy feedstocks: Energy use in steam cracking and alternative processes. Energy 2006, 31, 425–451. [Google Scholar] [CrossRef]
- Hong, E.; Park, J.H.; Shin, C.H. Oxidative Dehydrogenation of n-Butenes to 1,3-Butadiene over Bismuth Molybdate and Ferrite Catalysts: A Review. Catal. Surv. Asia 2016, 20, 23–33. [Google Scholar] [CrossRef]
- Bhasin, M.M.; McCain, J.H.; Vora, B.V.; Imai, T.; Pujadó, P.R. Dehydrogenation and oxydehydrogenation of paraffins to olefins. Appl. Catal. A Gen. 2001, 221, 397–419. [Google Scholar] [CrossRef]
- Herguido, J.; Menendez, M.; Santamarıa, J. Oxidative Dehydrogenation of n -Butane in a Two-Zone Fluidized-Bed Reactor. Ind. Eng. Chem. Res. 1999, 38, 90–97. [Google Scholar] [CrossRef]
- Schäfer, R.; Noack, M.; Kölsch, P.; Stöhr, M.; Caro, J. Comparison of different catalysts in the membrane-supported dehydrogenation of propane. Catal. Today 2003, 82, 15–23. [Google Scholar] [CrossRef]
- Park, S.; Lee, Y.; Kim, G.; Hwang, S. Production of butene and butadiene by oxidative dehydrogenation of butane over carbon nanomaterial catalysts. Korean J. Chem. Eng. 2016, 33, 3417–3424. [Google Scholar] [CrossRef]
- Callejas, C.; Soler, J.; Herguido, J.; Menéndez, M.; Santamaría, J. Catalytic dehydrogenation of n-butane in a fluidized bed reactor with separate coking and regeneration zones. Stud. Surf. Sci. Catal. 2000, 130, 2717–2722. [Google Scholar] [CrossRef]
- Vajda, S.; Pellin, M.J.; Greeley, J.P.; Marshall, C.L.; Curtiss, L.A.; Ballentine, G.A.; Elam, J.W.; Catillon-Mucherie, S.; Redfern, P.C.; Mehmood, F.; et al. Subnanometre platinum clusters as highly active and selective catalysts for the oxidative dehydrogenation of propane. Nat. Mater. 2009, 8, 213–216. [Google Scholar] [CrossRef]
- Rischard, J.; Franz, R.; Antinori, C.; Deutschmann, O. Oxidative dehydrogenation of butenes over Bi-Mo and Mo-V based catalysts in a two-zone fluidized bed reactor. AIChE J. 2017, 63, 43–50. [Google Scholar] [CrossRef]
- Elkhalifa, E.A.; Friedrich, H.B. Magnesium oxide as a catalyst for the dehydrogenation of n-octane. Arab. J. Chem. 2018, 11, 1154–1159. [Google Scholar] [CrossRef]
- Xingan, W.; Huiqin, L. Comparison of the technology of oxidative dehydrogenation in a fluidized-bed reactor with those of other reactors for butadiene. Ind. Eng. Chem. Res. 1996, 35, 2570–2575. [Google Scholar] [CrossRef]
- Hiwale, R.; Smith, R.; Hwang, S. A novel methodology for the modeling of CO2 absorption in monoethanolamine (MEA) using discrimination of rival kinetics. J. Ind. Eng. Chem. 2015, 25, 78–88. [Google Scholar] [CrossRef]
- Sterrett, J.S.; Mcllvried, H.G. Kinetics of the Oxidative Dehydrogenation of Butene to Butadiene over a Ferrite Catalyst. Ind. Eng. Chem. Process. Des. Dev. 1974, 13, 54–59. [Google Scholar] [CrossRef]
- Ding, X.J.; Xiao, D.L.; Wang, X.L.; Liu, S.L. The redox model of the kinetics for the oxidative dehydrogenation over the ferrite catalyst. J. Mol. Catal. 1988, 2, 25–30. [Google Scholar]
- Téllez, C.; Menéndez, M.; Santamaría, J. Kinetic study of the oxidative dehydrogenation of butane on V/MgO catalysts. J. Catal. 1999, 183, 210–221. [Google Scholar] [CrossRef]
- Ajayi, B.P.; Abussaud, B.; Jermy, R.; Al Khattaf, S. Kinetic modelling of n-butane dehydrogenation over CrOxVOx/MCM-41 catalyst in a fixed bed reactor. Prog. React. Kinet. Mech. 2014, 39, 341–353. [Google Scholar] [CrossRef]
- Madaan, N.; Haufe, R.; Shiju, N.R.; Rothenberg, G. Oxidative Dehydrogenation of n-Butane: Activity and Kinetics over VOx/Al2O3 Catalysts. Top. Catal. 2014, 57, 1400–1406. [Google Scholar] [CrossRef]
- Tanimu, A.; Jaenicke, S.; Alhooshani, K. Heterogeneous catalysis in continuous flow microreactors: A review of methods and applications. Chem. Eng. J. 2017, 327, 792–821. [Google Scholar] [CrossRef]
- Tanimu, G.; Abussaud, B.A.; Asaoka, S.; Alasiri, H. Kinetic Study on n-Butane Oxidative Dehydrogenation over the (Ni, Fe, Co)-Bi-O/Î-Al2O3 Catalyst. Ind. Eng. Chem. Res. 2020, 59, 2773–2780. [Google Scholar] [CrossRef]
- Mendoza, J.A.; Hwang, S. Tubular reactor design for the oxidative dehydrogenation of butene using computational fluid dynamics (CFD) modeling. Korean J. Chem. Eng. 2018, 35, 2157–2163. [Google Scholar] [CrossRef]
- De Smet, C.R.H.; De Croon, M.H.J.M.; Berger, R.J.; Marin, G.B.; Schouten, J.C. Design of adiabatic fixed-bed reactors for the partial oxidation of methane to synthesis gas. Application to production of methanol and hydrogen-for-fuel-cells. Chem. Eng. Sci. 2001, 56, 4849–4861. [Google Scholar] [CrossRef]
- Soler, J.; Téllez, C.; Herguido, J.; Menéndez, M.; Santamaría, J. Modelling of a two-zone fluidised bed reactor for the oxidative dehydrogenation of n-butane. Powder Technol. 2001, 120, 88–96. [Google Scholar] [CrossRef]
- Hukkanen, E.J.; Rangitsch, M.J.; Witt, P.M. Non-adiabatic multitubular fixed-bed catalytic reactor model coupled with shell-side coolant CFD model. Ind. Eng. Chem. Res. 2013, 52, 15437–15446. [Google Scholar] [CrossRef]
- Huang, K.; Lin, S.; Wang, J.; Luo, Z. Numerical evaluation on the intraparticle transfer in butylene oxidative dehydrogenation fixed-bed reactor over ferrite catalysts. J. Ind. Eng. Chem. 2015, 29, 172–184. [Google Scholar] [CrossRef]
- Dixon, A.G.; Nijemeisland, M. CFD as a design tool for fixed-bed reactors. Ind. Eng. Chem. Res. 2001, 40, 5246–5254. [Google Scholar] [CrossRef]
- Chen, X.; Dai, J.; Luo, Z. CFD modeling using heterogeneous reaction kinetics for catalytic dehydrogenation syngas reactions in a fixed-bed reactor. Particuology 2013, 11, 703–714. [Google Scholar] [CrossRef]
- Fattahi, M.; Kazemeini, M.; Khorasheh, F.; Darvishi, A.; Rashidi, A.M. Fixed-bed multi-tubular reactors for oxidative dehydrogenation in ethylene process. Chem. Eng. Technol. 2013, 36, 1691–1700. [Google Scholar] [CrossRef]
- Launder, B.E.; Spalding, D.B. The numerical computation of turbulent flows. Comput. Methods Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar] [CrossRef]
- Byrne, R.C. TEMA Standards of the Tubular Exchanger, 9th ed.; Tubular Exchanger Manufacturers Association, INC.: New York, NY, USA, 2007; pp. 298–300. [Google Scholar]
- Gbadago, D.Q.; Oh, H.T.; Oh, D.H.; Lee, C.H.; Oh, M. CFD simulation of a packed bed industrial absorber with interbed liquid distributors. Int. J. Greenh. Gas. Control. 2020. [Google Scholar] [CrossRef]
- Worstell, J. Adiabatic Fixed-Bed Reactors: Practical Guides in Chemical Engineering; Butterworth-Heinemann: Texas, TX, USA, 2014. [Google Scholar]



| Parameter | Unit | Value |
|---|---|---|
| A1 | kmol/kgcat-s | 1.66 × 109 |
| A2 | kmol/kgcat-s | 6.69 × 103 |
| E1 | J/mol | 139745.6 |
| E2 | J/mol | 87027.2 |
| KB | atm−1 | 0 |
| KBD | atm−1 | 285 |
| atm−1 | 415 | |
| atm−1 | 1800 | |
| n | - | 0.142 |
| Parameters | Unit | Value |
|---|---|---|
| Shell diameter | cm | 21.33 |
| Shell length | cm | 81.28 |
| Tube diameter | cm | 2.54 |
| Tube length | cm | 81.28 |
| Tube pitch | cm | 3.18 |
| Tube pattern | - | 30°-triangular |
| Number of tubes | - | 14 |
| Nozzle diameter | cm | 7.33 |
| Nozzle length | cm | 5.6 |
| Baffle spacing | cm | 20.32 |
| Baffle thickness | cm | 0.37 |
| Number of baffles | - | 3 |
| Parameters | Unit | Value |
|---|---|---|
| Operating pressure | atm | 1 |
| Gas inlet temperature | K | 633 |
| Gas velocity | m/s | variant |
| Coolant inlet temperature | K | 300 |
| Coolant velocity | m/s | 1 |
| Inlet mole compositions | ||
| Butene (C4H8) | - | 0.05 |
| Oxygen (O2) | - | 0.047 |
| Steam (H2O) | - | 0.717 |
| Nitrogen (N2) | - | 0.186 |
| Butadiene (C4H6) | - | 0 |
| Carbon dioxide (CO2) | - | 0 |
| Bulk density of catalyst | kg/m3 | 7393.92 |
| Porosity | - | 0.35 |
| Actual catalyst density | kg/m3 | 4806.05 |
| k | m2/s2 | 0.00375 |
| ε | m2/s3 | 0.012 |
| Boundary field | Gas inlet | Coolant inlet | Gas outlet | Coolant outlet | Wall |
|---|---|---|---|---|---|
| Gas velocity | fixedValue | fixedValue | zeroGradient | zeroGradient | noSlip |
| Coolant velocity | fixedValue | fixedValue | zeroGradient | zeroGradient | noSlip |
| Pressure | fixedFlux Pressure | fixedFlux Pressure | totalPressure | totalPressure | fixedFlux Pressure |
| Temperature | fixedValue | fixedValue | inletOutlet | inletOutlet | zeroGradient |
| Species concentration | fixedValue | fixedValue | inletOutlet | inletOutlet | zeroGradient |
| Epsilon | fixedValue | fixedValue | zeroGradient | zeroGradient | epsilonWall Function |
| K | fixedValue | fixedValue | zeroGradient | zeroGradient | kqRWall Function |
| Term | Keyword | Description | Scheme |
|---|---|---|---|
| Convection | divSchemes | Discretizing the divergence, | Gauss limitedLinear V 1 |
| Gradient | gradSchemes | Discretizing the gradient, | Gauss linear 1 |
| Diffusion | laplacianSchemes | Discretizing the Laplacian, | Gauss linear orthogonal |
| Time derivative | ddtSchemes | Discretizing first and second-order term derivatives, | Euler |
| Others | interpolationSchemes snGradSchemes | Cell to face interpolations Component of gradient normal to a cell face | linear orthogonal |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moon, J.; Gbadago, D.Q.; Hwang, S. 3-D Multi-Tubular Reactor Model Development for the Oxidative Dehydrogenation of Butene to 1,3-Butadiene. ChemEngineering 2020, 4, 46. https://doi.org/10.3390/chemengineering4030046
Moon J, Gbadago DQ, Hwang S. 3-D Multi-Tubular Reactor Model Development for the Oxidative Dehydrogenation of Butene to 1,3-Butadiene. ChemEngineering. 2020; 4(3):46. https://doi.org/10.3390/chemengineering4030046
Chicago/Turabian StyleMoon, Jiyoung, Dela Quarme Gbadago, and Sungwon Hwang. 2020. "3-D Multi-Tubular Reactor Model Development for the Oxidative Dehydrogenation of Butene to 1,3-Butadiene" ChemEngineering 4, no. 3: 46. https://doi.org/10.3390/chemengineering4030046
APA StyleMoon, J., Gbadago, D. Q., & Hwang, S. (2020). 3-D Multi-Tubular Reactor Model Development for the Oxidative Dehydrogenation of Butene to 1,3-Butadiene. ChemEngineering, 4(3), 46. https://doi.org/10.3390/chemengineering4030046





