An Assessment of Drag Models in Eulerian–Eulerian CFD Simulation of Gas–Solid Flow Hydrodynamics in Circulating Fluidized Bed Riser
Abstract
1. Introduction
2. Simulation System
3. CFD Model
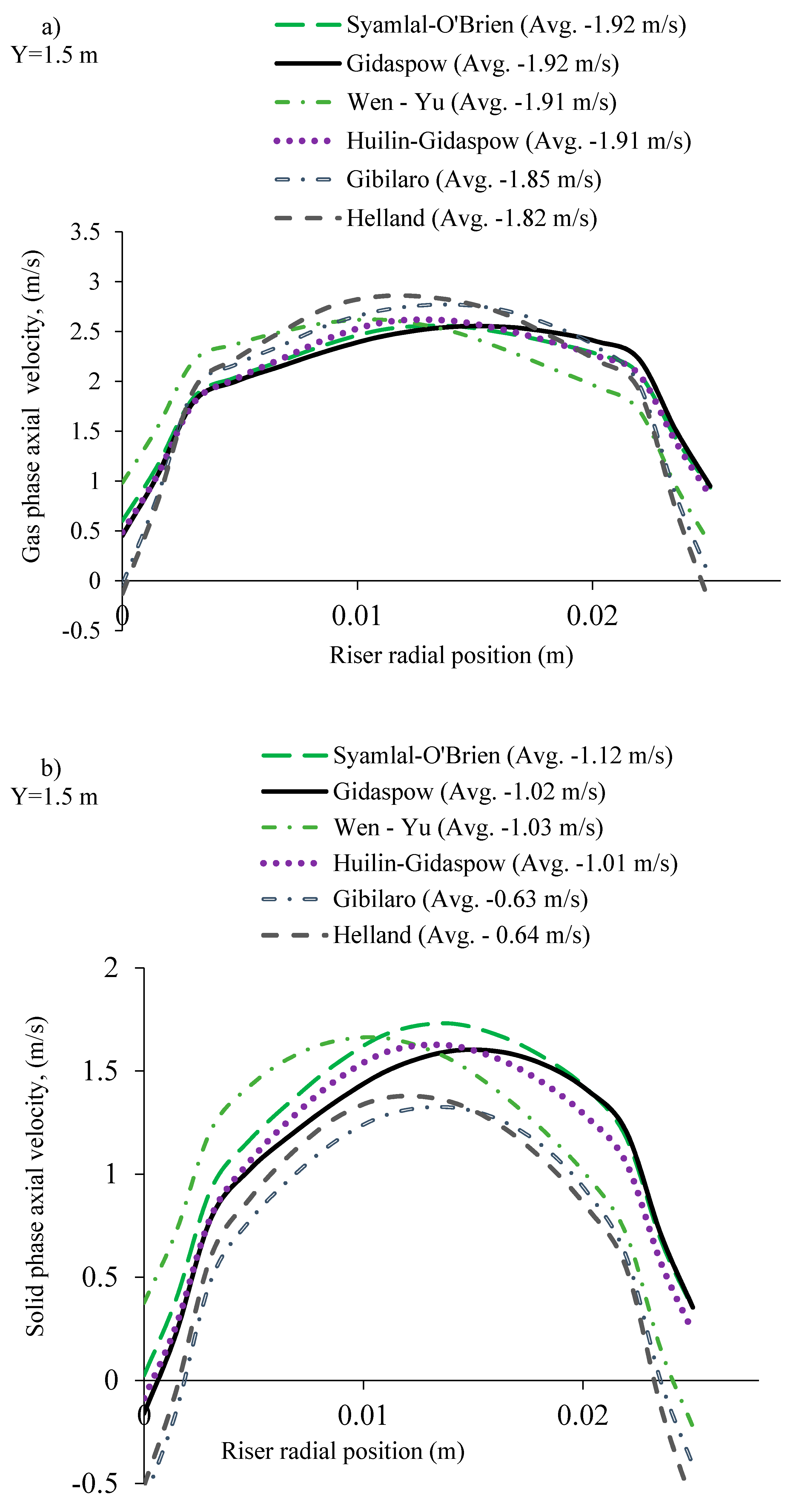
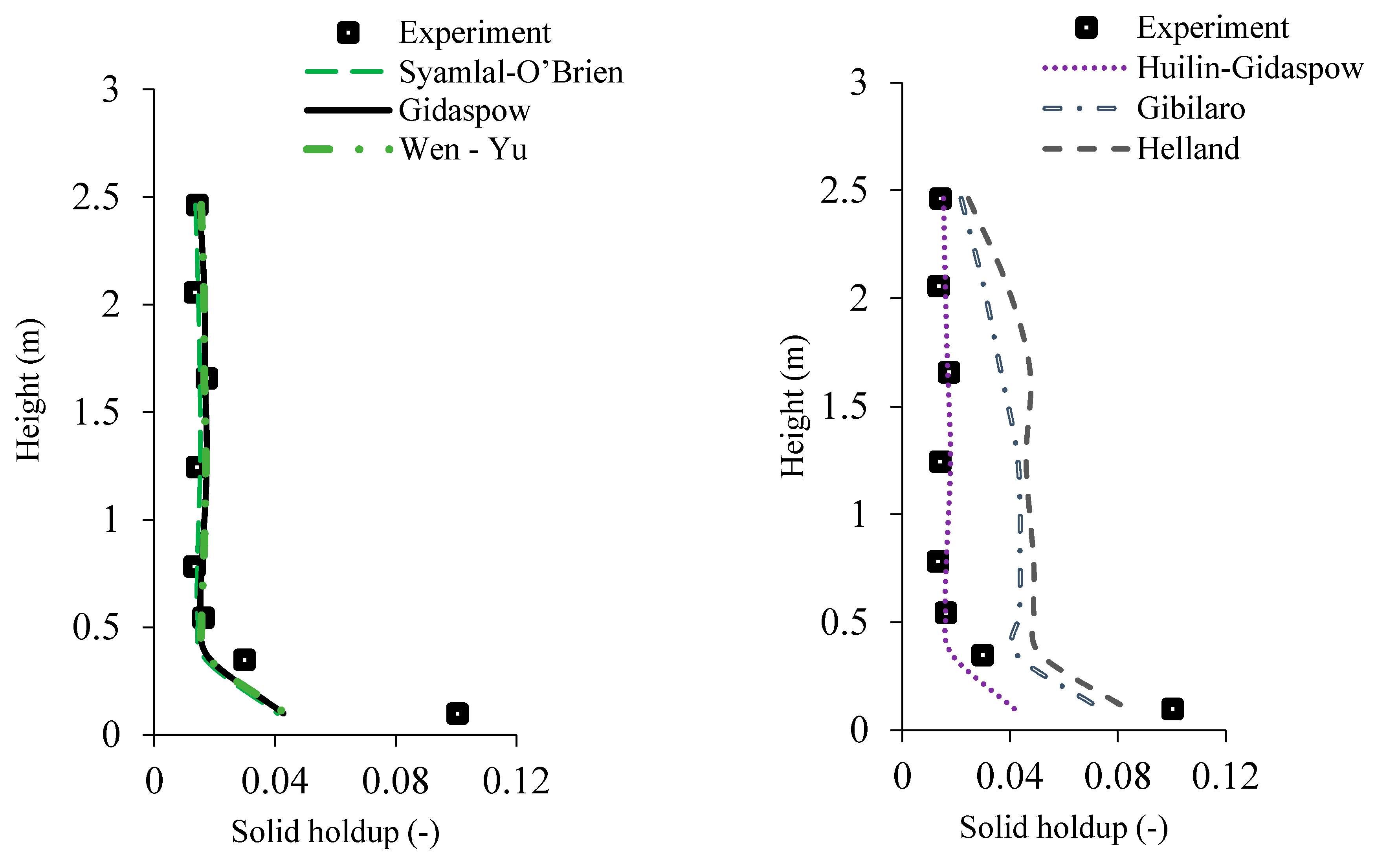
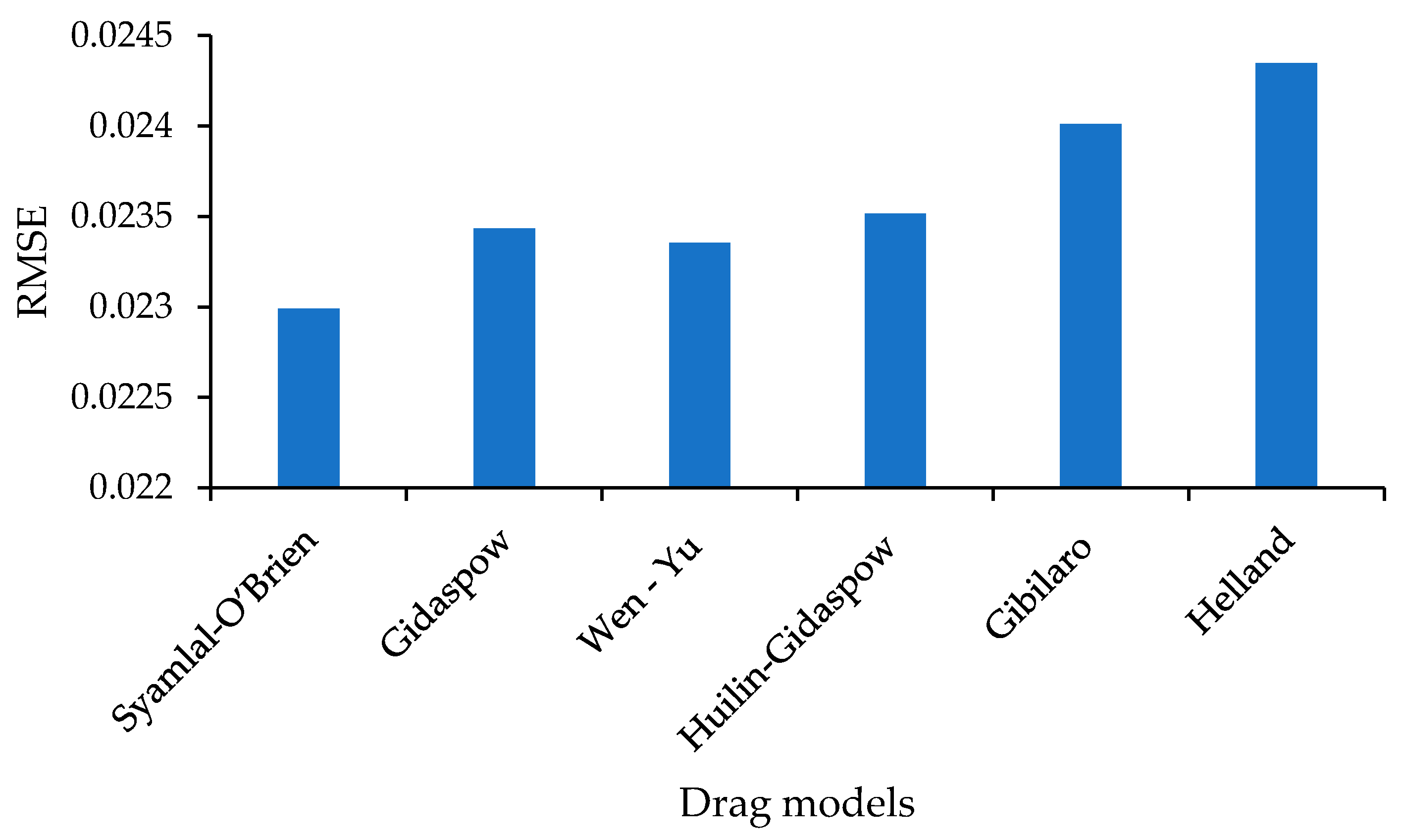
4. Result and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| CD | Dimensionless drag coefficient |
| dp | Solid particle mean diameter (μm) |
| D | CFB riser diameter (m) |
| ess | Particle–particle restitution coefficient |
| ew | Particle–wall restitution coefficient |
| Gs | Solid flux (kg/m2s) |
| g | Gravitational acceleration (m/s2) |
| g0,ss | Radial distribution function |
| H | CFB riser height (m) |
| kθs | Diffusion coefficient for granular energy (kg/m s) |
| pi | Pressure (Pa) |
| qs | Granular temperature flux at the wall |
| Rei | Reynolds number |
| Ug | Superficial gas velocity (m/s) |
| particle slip velocity parallel to the wall | |
| νi | Velocity (m/s) |
| Greek Symbols | |
| αi | Phase i, volume fraction |
| αs,max | Solid volume fraction at maximum packing |
| γθs | Collisional dissipation of energy (kg/m3s) |
| θi | Granular temperature (m2/s2) |
| λs | Solid phase bulk viscosity (kg/s/m) |
| μi | Shear viscosity (kg/s/m) |
| ρi | Phase i, density (kg/m3) |
| τi | Stress tensor for phase i, (Pa) |
| Kgs | Gas–solid phase interphase momentum exchange coefficient, (kg/m3s) |
| φ | Specularity coefficient |
| Φgs | Transfer rate of energy (kg/m3s) |
| Subscripts | |
| col | collisional |
| fr | frictional |
| g | gas phase |
| kin | kinetic |
| s | solid phase |
| ss | solid-solid |
| w | wall |
| Abbreviation | |
| 2D | Two-dimensional |
| CFD | Computational fluid dynamics |
| CFB | Circulating fluidized bed |
| SIMPLE | semi-implicit method for pressure-linked equations |
| TFM | Two-fluid model |
| RMSE | Root mean square error |
Appendix A
| References | Reactor Size H-Height (m) D-Diameter (m) | Flow Conditions Ug–Superficial gas velocity (m/s) Gs–Solid circulation rate (kg/m2s) | Solid Material Properties and Type ρs–Particle Density (kg/m3) ds–Mean Particle Diameter (μm) | Drag Models Used (Comments) |
|---|---|---|---|---|
| Upadhyay and Park (2015) [16] | H: 3 m D: 0.025 m | Ug–2.0 m/s Gs – 39.15, 51.05, 73.21 kg/m2s | Silica sand ρs–2525 kg/m3 ds–130 μm | Gidaspow drag [16] |
| Almuttahar and Taghipour (2008) [37] | H: 6.1 m D: 0.076 m | Ug–8, 6, 4, 8, 8, 4 m/s (Case 1~6) Gs–455, 355, 325, 254, 555, 94 kg/m2s (Case 1~6) | FCC particle ρs–1600 kg/m3 ds–70 μm | Syamlal-O’Brien [17] |
| Almuttahar and Taghipour (2008) [38] | H: 6.1 m D: 0.0762 m | Ug–8.0 m/s Gs–453 kg/m3 | FCC particle ρs–1600 kg/m3 ds–70 μm | Syamlal-O’Brien [17] |
| Neri and Gidaspow, (2000) [39] | H: 6.58 m D: 0.075 m | Ug–2.61 m/s Gs–20.4 kg/m2s | FCC particle ρs–1654 kg/m3 ds–75 μm | Gidaspow drag [17] |
| Chalermsinsuwan et al. (2009) [40] | H: 14.2 m D: 0.2 m | Ug–5.2 m/s Gs–489 kg/m2s Ug–3.25 m/s Gs–98.80 kg/m2s | FCC ρs–1712 kg/m3 ds–76 μm | EMMS |
| Jin et al. (2010) [36] | H: 5.12 m D: 0.06 m | Ug–9.8, 8.6, 10.7 m/s Gs–546, 364 kg/m2s | Geldart B ρs–2580 kg/m3 ds–385 μm | Syamlal-O’Biren [17] |
| Wilde et al. (2003) [41] | H: 14.434 m D: 1.56 m | Ug–3.36 m/s Gs–2.6 kg/m2s | Geldart A ρs–1550 kg/m3 ds–60 μm | Gidaspow [16] |
| Koksal and Hamdullahpur (2005) [42] | H: 7.6 m D: 0.23 m | FCC Ug–3,5 m/s Gs–18,33 kg/m2s Silica sand Ug–5 m/s Gs–8 kg/m2s | Silica sand (Geldart B) ρs–2650 kg/m3 ds–250 μm FCC ρs–1600 kg/m3 ds–60 μm | Wen-Yu [15] |
| Shah et al. (2011) [28] | Low solid flux: H: 10.5 m D:0.09 m High solid flux: H: 14.2 m D: 0.2 m | Low solid flux: Ug–1.52 m/s Gs–14.3 kg/m2s High solid flux: Ug–5.2 m/s Gs–489 kg/m2s | FCC Low solid flux: ρs–930 kg/m3 ds–54 μm High solid flux: ρs–1712 kg/m3 ds–76μm | EMMS (Best prediction) Gidaspow [16] |
| Benyahia et al. (2005) [43] | H: 1.42 m D: 0.0142 m | Ug–14.85 m/s Gs–15 kg/m2s | Glass bead ρs–2500 kg/m3 ds–70 μm | Syamlal O’Brien [17] |
| Vaishali et al. (2007) [29] | H: 7.9 m D: 0.152 m | Fast Fluidization (FF) Ug–3.2 m/s Gs–26.6 kg/m2s Dilute Phase Transport (DPT) Ug–3.9, 4.5 m/s Gs–33.7, 36.8 kg/m2s | Scandium coated with Parylene polymer ρs–2550 kg/m3 ds–150 μm | Wen-Yu [15] Syamlal-O’Brien [17] (Best prediction) |
| Cloete et al. (2011) [44] | Periodic section: H: 0.8 m D: 0.076 m | Ug–3.5 m/s Gs–100 kg/m2s | FCCρs–1500 kg/m3 ds–67 μm | Syamlal-O’Brien [17] |
| Li et al. (2020) [45] | Transport section: H: 3 m D: 0.51 m Enlarged section: H: 0.152 m D: 0.635 m | Ug–1.6 m/s Gs–4.64 kg/m2s | Iron-based oxygen carriers (Geldart D) ρs–2500 kg/m3 ds–1500 μm | Gidaspow [16] |
| Li et al. (2014) [46] | Square riser section: H: 9.14 m Cross sectional dimension: 0.146 * 0.146 m Circular NETL B22 CFB riser: H: 16.8 m D: 0.305 m Circular Malcus et al.’s CFB riser: H: 7 m D: 0.14 m | Square riser section: Ug–5.5 m/s Gs–40 kg/m2s Circular NETL B22 CFB riser: Ug–5.14 m/s Gs–9.26, 40 kg/m2s Ug–7.58 m/s Gs–14 kg/s Circular Malcus et al.’s CFB riser: Ug–4.7 m/s Gs–302 kg/m2s | Square riser section: Sand particle ρs–2640 kg/m3 ds–213 μm Circular NETL B22 CFB riser: Glass beads ρs–2425 kg/m3 ds–59 μm High-density polyethylene (HDPE) beads ρs–863 kg/m3 ds–800 μm Circular Malcus et al.’s CFB riser: FCC ρs–1740 kg/m3 ds–89 μm | Gidaspow [16] |
| Wang et al. (2010) [30] | H: 10 m D: 0.076 m | Ug – 8 m/s Gs – 300, 500 kg/m2s | Geldart A ρs–1500 kg/m3 ds–67 μm | Syamlal-O’Brien [17] (Best prediction) Wen-Yu [15] Gidaspow model |
| Zhang et al. (2015) [31] | H: 17 m D: 0.102 m | Case-1: Ug – 8.6 m/s Gs – 530 kg/m2s Case-2: Ug – 8.6 m/s Gs – 530 kg/m2s | Geldart B ρs–2951 kg/m3 ds–89 μm | EMMS/Matrix (Best prediction) Gidaspow model |
| Zhang et al. (2015) [32] | H: 18.3 m D: 0.1 m | Ug–8.6, 8.0, 4.0 m/s Gs–171, 627, 635, 869, 209, 823, 857, 1045 kg/m2s | Geldart B Case-1: ρs–2951 kg/m3 ds–89 μm Case-2: ρs–2620 kg/m3 ds–154 μm Case-3 ρs–2620 kg/m3 ds–154 μm | EMMS (Best prediction) Gidaspow [19] |
Appendix B
B.1. Continuity Equation and Momentum Conservation Equation: i = gas phase (g), j = solid phase (s)
- Continuity equation:
B.2. Momentum Conservation Equation
- Momentum equation:
B.3. Kinetic Theory of Granular Flow (KTGF)
- Solid phase granular temperature equation:= Generation of energy by the solid phase stress tensor
- Solid phase pressure:where, g0,ss radial distribution function
- Solid bulk viscosity:
- Solid phase shear viscosity:
B.4. Shear Stress and Collision Energy at the Wall
References
- Kunii, D.; Levenspiel, O. Fluidization Engineering, 2nd ed.; Butterworth-Heinemann Inc.: Boston, MA, USA, 1991. [Google Scholar]
- Berruti, F.; Pugsley, T.S.; Godfroy, L.; Chaouki, J.; Patience, G.S. Hydrodynamics of circulating fluidized bed risers: A review. Can. J. Chem. Eng. 1995, 73, 579–602. [Google Scholar] [CrossRef]
- Knowlton, T.M.; Grace, J.R.; Avidan, A.A. Circulating Fluidized Beds; Blackie Academic & Professional: London, UK, 1997. [Google Scholar]
- Naren, P.R.; Lali, A.M.; Ranade, V.V. Evaluating EMMS model for simulating high solid flux risers. Chem. Eng. Res. Des. 2007, 85, 1188–1202. [Google Scholar] [CrossRef]
- Abgrall, R. On essentially non-oscillatory schemes on unstructured meshes: Analysis and implementation. J. Comput. Phys. 1994, 114, 45–58. [Google Scholar] [CrossRef]
- Durlofsky, L.J.; Engquist, B.; Osher, S. Triangle based adaptive stencils for the solution of hyperbolic conservation laws. J. Comput. Phys. 1992, 98, 64–73. [Google Scholar] [CrossRef]
- Liu, X.D.; Osher, S.; Chan, T. Weighted essentially non-oscillatory schemes. J. Comput. Phys. 1994, 115, 200–212. [Google Scholar] [CrossRef]
- Cockburn, B.; Shu, C.W. Runge–Kutta discontinuous galerkin methods for convection-dominated problems. J. Comput. Phys. 2001, 16, 173–261. [Google Scholar]
- Liu, Y.; Zhang, W.; Jiang, Y.; Ye, Z. A high-order finite volume method on unstructured grids using RBF reconstruction. Comput. Math. Appl. 2016, 72, 1096–1117. [Google Scholar] [CrossRef]
- Liu, H.; Xu, K.; Zhu, T.; Ye, W. Multiple temperature kinetic model and its applications to micro-scale gas flows. Comput. Fluids 2012, 67, 115–122. [Google Scholar] [CrossRef]
- Zhu, T.; Ye, W. Theoretical and numerical studies of noncontinuum gas-phase heat conduction in micro/nano devices. Numer. Heat Tranf. B-Fundam. 2010, 57, 203–226. [Google Scholar] [CrossRef]
- Karpinska, A.M.; Bridgeman, J. CFD-aided modelling of activated sludge systems—A critical review. Water Res. 2016, 88, 861–879. [Google Scholar] [CrossRef]
- Wang, J. Continuum theory for dense gas-solid flow: A state-of-the-art review. Chem. Eng. Sci. 2019, 215, 115428. [Google Scholar] [CrossRef]
- Ding, J.; Gidaspow, D. A bubbling fluidization model using kinetic theory of granular flow. AICHE J. 1990, 36, 523–538. [Google Scholar] [CrossRef]
- Kuipers, J.A.M.; Van Duin, K.J.; Van Beckum, F.P.H.; Van Swaaij, W.P.M. A numerical model of gas-fluidized beds. Chem. Eng. Sci. 1992, 47, 1913–1924. [Google Scholar] [CrossRef]
- Upadhyay, M.; Park, J.H. CFD simulation via conventional Two-Fluid Model of a circulating fluidized bed riser: Influence of models and model parameters on hydrodynamic behavior. Powder Technol. 2015, 272, 260–268. [Google Scholar] [CrossRef]
- Tsuji, Y.; Kawaguchi, T.; Tanaka, T. Discrete particle simulation of two-dimensional fluidized bed. Powder Technol. 1993, 77, 79–87. [Google Scholar] [CrossRef]
- Deen, N.G.; Annaland, M.V.S.; Van der Hoef, M.A.; Kuipers, J.A.M. Review of discrete particle modeling of fluidized beds. Chem. Eng. Sci. 2007, 62, 28–44. [Google Scholar] [CrossRef]
- Andrews, M.J.; O’Rourke, P.J. The multiphase particle-in-cell (MP-PIC) method for dense particulate flows. Int. J. Multiph. Flow 1996, 22, 379–402. [Google Scholar] [CrossRef]
- Upadhyay, M.; Park, H.C.; Hwang, J.G.; Choi, H.S.; Jang, H.N.; Seo, Y.C. Computational particle-fluid dynamics simulation of gas-solid flow in a circulating fluidized bed with air or O2/CO2 as fluidizing gas. Powder Technol. 2017, 318, 350–362. [Google Scholar] [CrossRef]
- Shah, M.T.; Utikar, R.P.; Pareek, V.K.; Tade, M.O.; Evans, G.M. Effect of closure models on Eulerian–Eulerian gas–solid flow predictions in riser. Powder Technol. 2015, 269, 247–258. [Google Scholar] [CrossRef]
- Ranade, V.V. Computational Flow Modeling for Chemical Reactor Engineering; Academic Press: London, UK, 2001; pp. 19–20. [Google Scholar]
- Agrawal, K.; Loezos, P.N.; Syamlal, M.; Sundaresan, S. The role of meso-scale structures in rapid gas–solid flows. J. Fluid Mech. 2001, 445, 151–185. [Google Scholar] [CrossRef]
- Wen, C.Y. Mechanics of fluidization. Chem. Eng. Prog. Symp. Ser. 1966, 62, 100–111. [Google Scholar]
- Gidaspow, D.; Bezburuah, R.; Ding, J. Hydrodynamics of circulating fluidized beds: Kinetic theory approach (No. CONF-920502-1). In Fluidization VII: Proceedings of the 7th Engineering Foundation Conference on Fluidization; Engineering Foundation: Gold Coast, Australia, 1992; pp. 75–82. [Google Scholar]
- Syamlal, M.; O’Brien, T.J. Computer simulation of bubbles in a fluidized bed. AIChE Symp. Ser. 1989, 85, 22–31. [Google Scholar]
- Ergun, S. Fluid flow through packed columns. Chem. Eng. Prog. 1952, 48, 89–94. [Google Scholar]
- Shah, M.T.; Utikar, R.P.; Tade, M.O.; Pareek, V.K. Hydrodynamics of an FCC riser using energy minimization multiscale drag model. Chem. Eng. J. 2011, 168, 812–821. [Google Scholar] [CrossRef]
- Vaishali, S.; Roy, S.; Bhusarapu, S.; Al-Dahhan, M.H.; Dudukovic, M.P. Numerical simulation of gas–solid dynamics in a circulating fluidized-bed riser with Geldart group B particles. Ind. Eng. Chem. Res. 2007, 46, 8620–8628. [Google Scholar] [CrossRef]
- Wang, X.; Jin, B.; Zhong, W.; Xiao, R. Modeling on the hydrodynamics of a high-flux circulating fluidized bed with Geldart Group A particles by kinetic theory of granular flow. Energy Fuels 2010, 24, 1242–1259. [Google Scholar] [CrossRef]
- Zhang, Y.; Lei, F.; Wang, S.; Xiang, X.; Xiao, Y. A numerical study of gas–solid flow hydrodynamics in a riser under dense suspension upflow regime. Powder Technol. 2015, 280, 227–2383. [Google Scholar] [CrossRef]
- Zhang, Y.; Lei, F.; Xiao, Y. The influence of pressure and temperature on gas-solid hydrodynamics for Geldart B particles in a high-density CFB riser. Powder Technol. 2018, 327, 17–28. [Google Scholar] [CrossRef]
- Huilin, L.; Gidaspow, D. Hydrodynamics of binary fluidization in a riser: CFD simulation using two granular temperatures. Chem. Eng. Sci. 2003, 58, 3777–3792. [Google Scholar] [CrossRef]
- Gibilaro, L.G.; Di Felice, R.; Waldram, S.P.; Foscolo, P.U. Generalized friction factor and drag coefficient correlations for fluid-particle interactions. Chem. Eng. Sci. 1985, 40, 1817–1823. [Google Scholar] [CrossRef]
- Helland, E.; Bournot, H.; Occelli, R.; Tadrist, L. Drag reduction and cluster formation in a circulating fluidised bed. Chem. Eng. Sci. 2007, 62, 148–158. [Google Scholar] [CrossRef]
- Jin, B.; Wang, X.; Zhong, W.; Tao, H.; Ren, B.; Xiao, R. Modeling on high-flux circulating fluidized bed with Geldart Group B particles by kinetic theory of granular flow. Energy Fuels 2010, 24, 3159–3172. [Google Scholar] [CrossRef]
- Almuttahar, A.; Taghipour, F. Computational fluid dynamics of a circulating fluidized bed under various fluidization conditions. Chem. Eng. Sci. 2008, 63, 1696–1709. [Google Scholar] [CrossRef]
- Almuttahar, A.; Taghipour, F. Computational fluid dynamics of high density circulating fluidized bed riser: Study of modeling parameters. Powder Technol. 2008, 185, 11–23. [Google Scholar] [CrossRef]
- Neri, A.; Gidaspow, D. Riser hydrodynamics: Simulation using kinetic theory. AIChE J. 2000, 46, 52–67. [Google Scholar] [CrossRef]
- Chalermsinsuwan, B.; Piumsomboon, P.; Gidaspow, D. Kinetic theory based computation of psri riser: Part i-estimate of mass transfer coefficient. Chem. Eng. Sci. 2009, 64, 1195–1211. [Google Scholar] [CrossRef]
- Juray, D.W.; Guy, B.M.; Geraldine, J.H. The effects of abrupt T-outlets in a riser: 3D simulation using the kinetic theory of granular flow. Chem. Eng. Sci. 2003, 58, 877–888. [Google Scholar]
- Koksal, M.; Hamdullahpur, F. CFD simulation of the gas–solid flow in the riser of a circulating fluidized bed with secondary air injection. Chem. Eng. Commun. 2005, 192, 1151–1179. [Google Scholar] [CrossRef]
- Benyahia, S.; Syamlal, M.; O’Brien, T.J. Evaluation of boundary conditions used to model dilute, turbulent gas/solids flows in a pipe. Powder Technol. 2005, 156, 62–72. [Google Scholar] [CrossRef]
- Cloete, S.; Amini, S.; Johansen, S.T. A fine resolution parametric study on the numerical simulation of gas–solid flows in a periodic riser section. Powder Technol. 2011, 205, 103–111. [Google Scholar] [CrossRef]
- Li, S.; Shen, Y. Numerical study of gas-solid flow behaviors in the air reactor of coal-direct chemical looping combustion with Geldart D particles. Powder Technol. 2020, 361, 74–86. [Google Scholar] [CrossRef]
- Li, T.; Pannala, S.; Shahnam, M. CFD simulations of circulating fluidized bed risers, part II, evaluation of differences between 2D and 3D simulations. Powder Technol. 2014, 254, 115–124. [Google Scholar] [CrossRef]
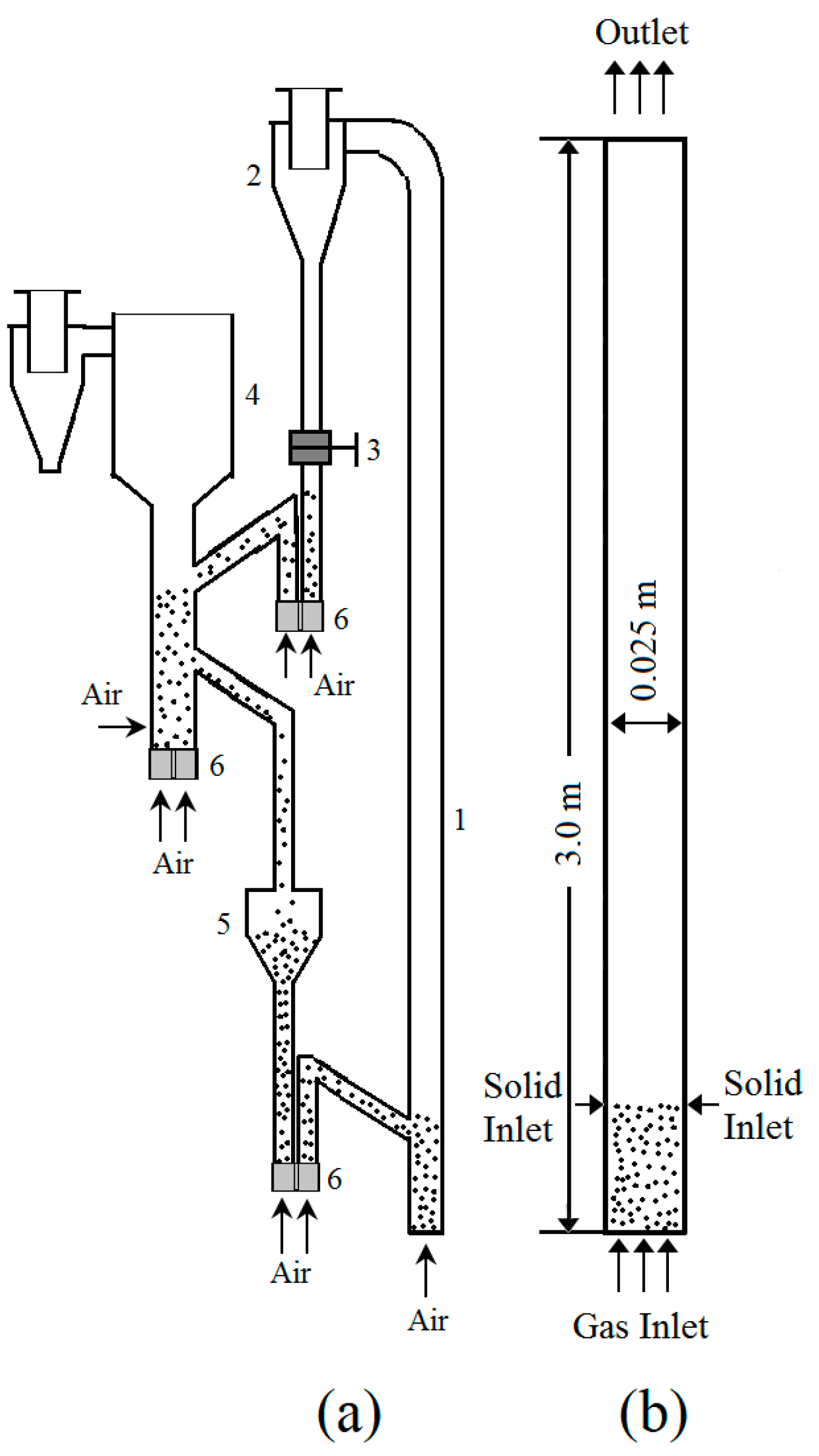
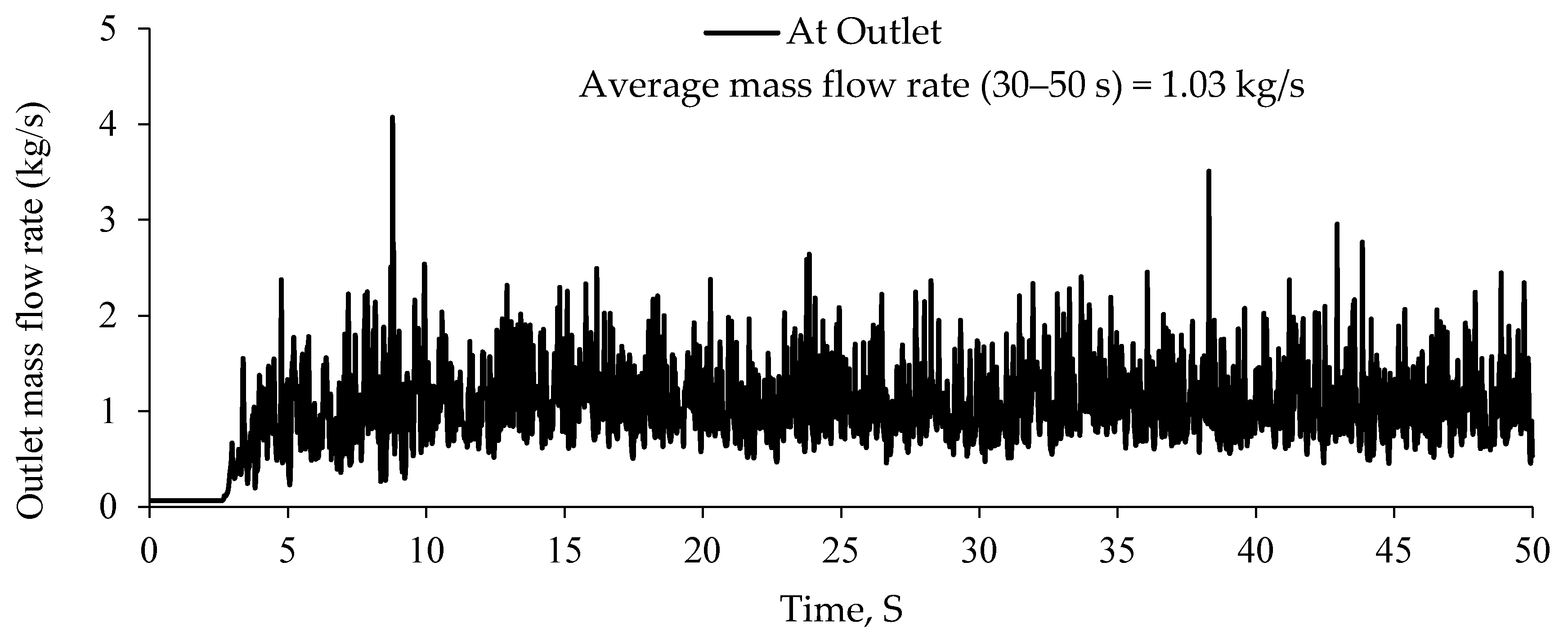
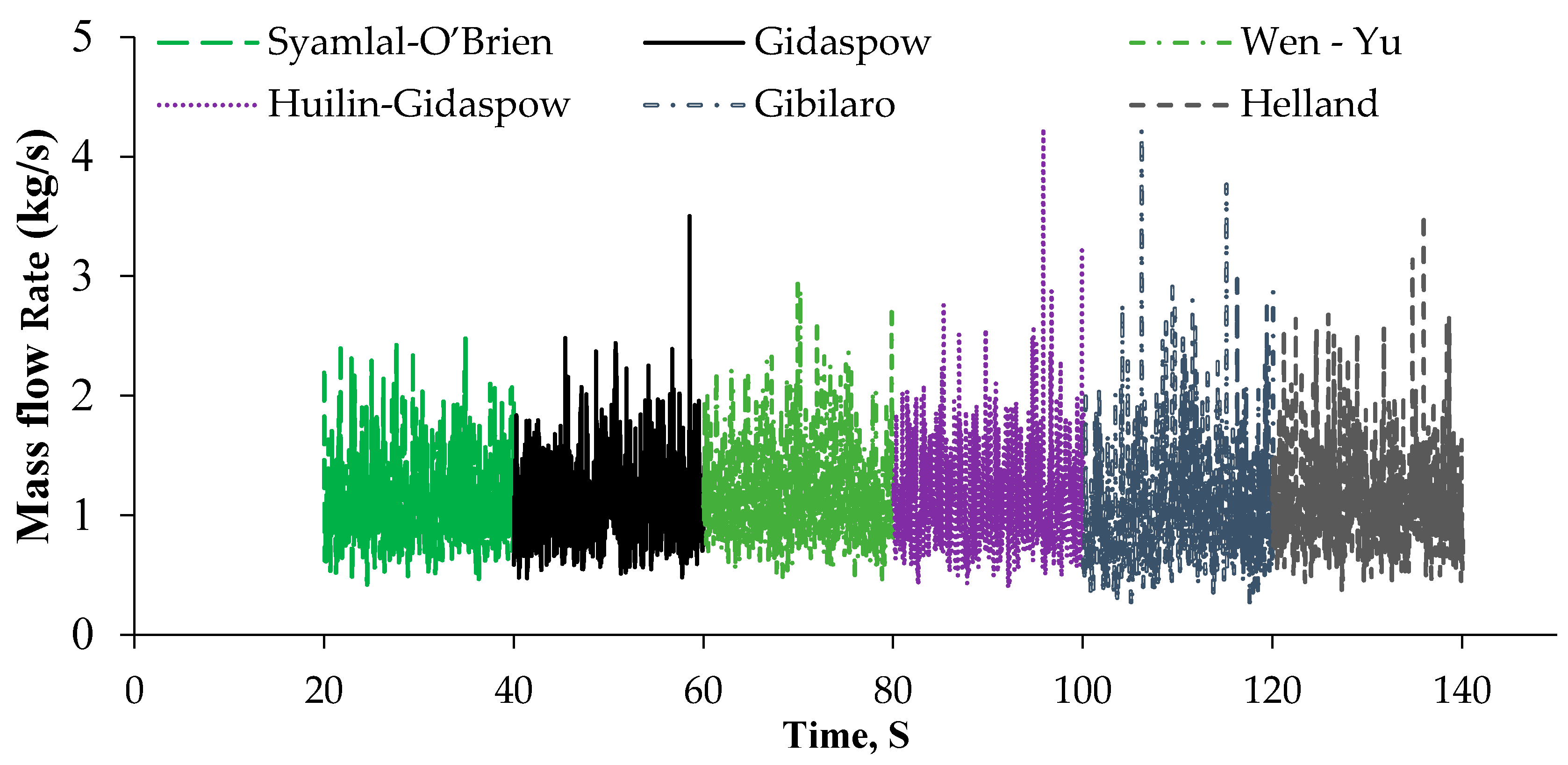
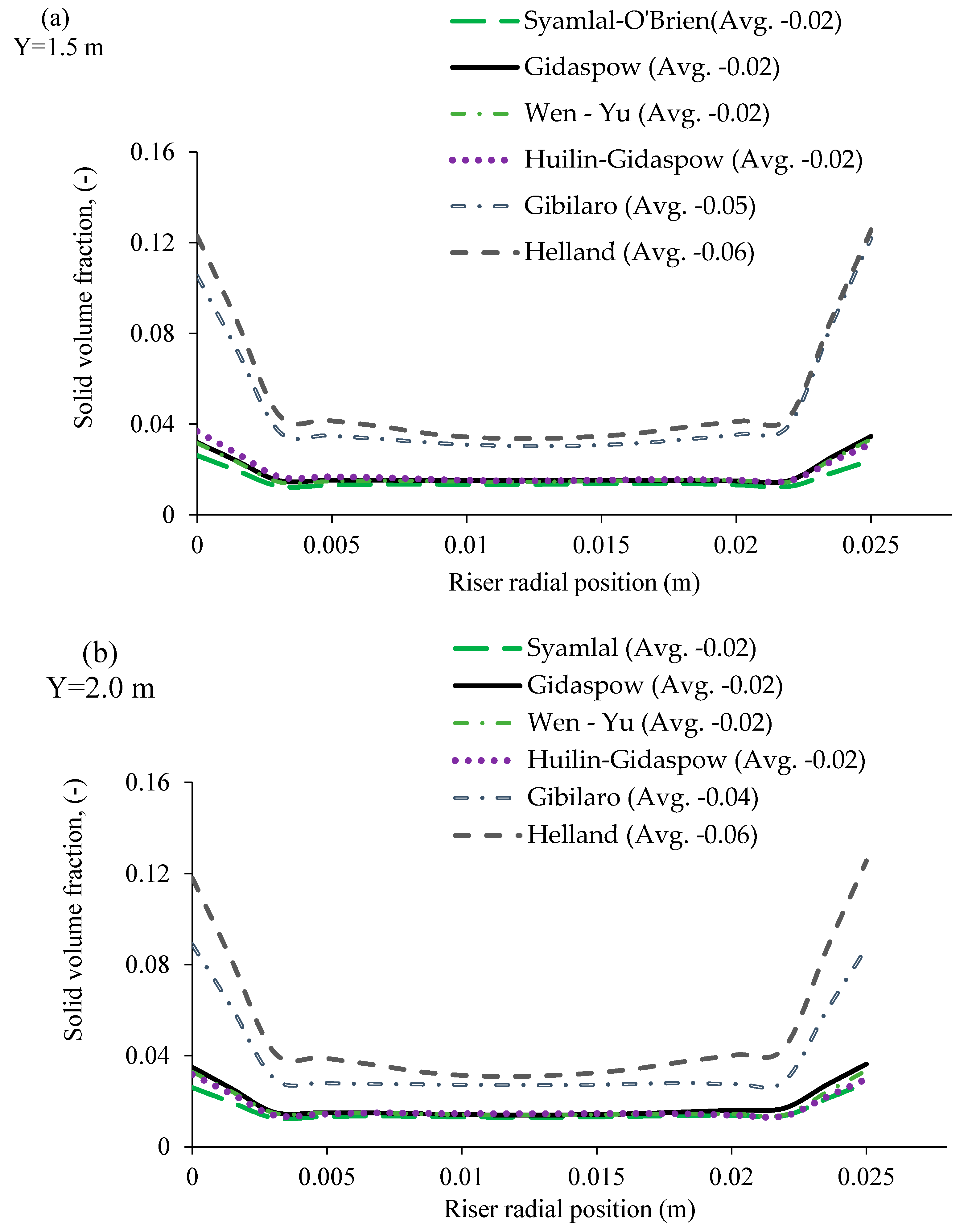
| Description | Value |
|---|---|
| CFB riser: | |
| Diameter, D | 0.025 m |
| Height, H | 3.0 m |
| Fluidizing media properties: | |
| Gas density, ρg | 1.225 kg/m3 |
| Solid phase density, ρs | 2525 kg/m3 |
| Particle mean diameter, dp | 130 μm |
| Flow condition: | |
| Superficial gas velocity, Ug | 2 m/s |
| Solid particle flux, Gs | 39.14 kg/m2s |
| Particle–Wall and Particle–Particle Interactions Parameter Value: | ||
|---|---|---|
| Specularity coefficient (φ) | - | 0.0001 |
| Particle–wall restitution coefficient (ew) | - | 0.9 |
| Particle–particle restitution coefficient (ess) | - | 0.9 |
| Packing limit (αs,max) | - | 0.63 |
| Transient solver calculation and convergence criteria: | ||
| Time step (s) | - | 0.0005 |
| Convergence criteria | - | 10−3 |
| Maximum iterations per time step | - | 50 |
| Discretization schemes settings: | ||
| Momentum | - | 1st order upwind |
| Volume fraction | - | 1st order upwind |
| Transient formulation | - | 1st order implicit |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Upadhyay, M.; Kim, A.; Kim, H.; Lim, D.; Lim, H. An Assessment of Drag Models in Eulerian–Eulerian CFD Simulation of Gas–Solid Flow Hydrodynamics in Circulating Fluidized Bed Riser. ChemEngineering 2020, 4, 37. https://doi.org/10.3390/chemengineering4020037
Upadhyay M, Kim A, Kim H, Lim D, Lim H. An Assessment of Drag Models in Eulerian–Eulerian CFD Simulation of Gas–Solid Flow Hydrodynamics in Circulating Fluidized Bed Riser. ChemEngineering. 2020; 4(2):37. https://doi.org/10.3390/chemengineering4020037
Chicago/Turabian StyleUpadhyay, Mukesh, Ayeon Kim, Heehyang Kim, Dongjun Lim, and Hankwon Lim. 2020. "An Assessment of Drag Models in Eulerian–Eulerian CFD Simulation of Gas–Solid Flow Hydrodynamics in Circulating Fluidized Bed Riser" ChemEngineering 4, no. 2: 37. https://doi.org/10.3390/chemengineering4020037
APA StyleUpadhyay, M., Kim, A., Kim, H., Lim, D., & Lim, H. (2020). An Assessment of Drag Models in Eulerian–Eulerian CFD Simulation of Gas–Solid Flow Hydrodynamics in Circulating Fluidized Bed Riser. ChemEngineering, 4(2), 37. https://doi.org/10.3390/chemengineering4020037




