Parametric Sensitivity of CSTBRs for Lactobacillus casei: Normalized Sensitivity Analysis

Abstract

In this paper, a sensitivity analysis of a continuous stirred tank bioreactor (CSTBR) was conducted to determine a parametrically sensitive regime. The growth of a lactic acid bacterium, namely, Lactobacillus casei, in a pH-controlled CSTBR was considered as a process model. Normalized objective sensitivities of the minimum pH were determined with respect to input parameters. A generalized criterion for sensitivity was defined for determining the parametric range of three input variables, i.e., dilution rate base stream (θ), base concentration (R), and initial pH (pH₀) for maintaining optimal pH range in the reactor. The system exhibits sensitive behavior for θ, R, and pH₀, from 0.095 to 0.295, 0 to 0.865, and 4.42 to 4.77, respectively. The critical values of θ, R, and pH₀ are 0.0195, 0.48, and 4.6, respectively. The mathematical model can also be used to determine a parametrically sensitive regime for other important parameters, namely, temperature, the concentration of metabolites, and other byproducts. The mathematical tool can also be used in bioreactor design and the improvement of control strategies.

1. Introduction

Continuous stirred tank reactors are the most widely used reactors for continuous and large scale production in many industries due to their high flexibility. For the production of bioenergy vectors (e.g., biogas, biohydrogen, bioethanol) continuous type systems are also preferred. The reactors used for bioprocesses are termed as continuous stirred type bioreactors (CSTBR).

The biochemical processes in CSTBR can be mathematically described as a set of ordinary differential equations, which explicitly or implicitly provide the relationship between the system behavior and input parameters. The system behavior is defined by the output or dependent variables that change in time or space. Whereas input parameters contain the physicochemical parameters, the initial conditions, and operating conditions of the system. When the output variables of a system change drastically with a small variation of input parameters, the specific range of that input parameter is called parametric sensitivity region of the system. Once a biochemical system undergoes through this parametric sensitivity region, its performance becomes unpredictable because outputs change sharply with a small variation of the input variable. For all chemical and biological processes, there exists a parametric range within which a process becomes unstable and unreliable, where even small variations in parameters abruptly change the performance. Thus, it is important to investigate a change in the behavior of a system with respect to any change in parameters. Such a study is called parametric sensitivity analysis [1]. In the context of chemical reactors, Bilous and Amundson [2] first introduced this concept of parametric sensitivity and runaway (where the system becomes unstable).

However, the parametric sensitivity studies for bioprocesses in CSTBR are limited. It is essential to have sufficient information on the kinetics of microbial growth and product output for better control and optimization of CSTBRs.

Many research articles are available on parametric sensitivity in non-isothermal and non-adiabatic chemical reactors [3,4] that discuss the occurrence of multiple steady states. These studies are suitable to predict a priori criteria for parametric sensitivity based upon which any possible steady-state regime of the reactor can be identified. On the other hand, research on the nonlinear dynamics behavior of CSTBRs is limited due to the complex mechanism of microbial growth and generation of secondary metabolic products. Moreover, in many cases, the influence of operating conditions on microbial growth which directly affect CSTBR operation is not adequately understood.

In CSTBRs, the growth of microorganisms is subjected to vary due to the influence of some operating variables, such as temperature, dissolved oxygen, and pH value [5,6,7,8]. Among these variables, pH plays a vital role in exerting a significant impact on various aspects of bioprocesses where fermentation is involved. The microbial cultures have an optimum pH range which is the most favorable condition for their growth [9,10]. The product that is produced in a process can be either an acid or a base, pH; therefore, pH is also a critical output variable. If the pH value of the microbial growth medium goes beyond the optimum pH range, the microbial growth could be hindered. Some comprehensive studies have been reported on the occurrence of multiple steady states for CSTBRs and other similar bioreactors [11,12].

Dutta et al. [12] investigated the parametric sensitivity of pH using a generalized sensitivity criterion proposed by Morbidelli and Verma [3,13] in a batch type bioreactor used for a phenol degradation system. However, information on the parametric sensitivity of CSTBRs is not widely available in the literature. Das et al. [14] defined a criterion, denoted as “pH-runaway” condition of CSTBR, which stated, pH-sensitive microorganisms stop growing when pH of the growth medium goes beyond its optimum range, and CSTBR operation becomes vulnerable. In their study, growth of lactic acid bacteria (LAB), namely, Pediococcus acidilactici with a continuous NaOH dosing for maintaining the pH system, was studied in a CSTBR. The parametric sensitivity of pH was observed in both unique and multiple steady-state conditions for a particular set of input variables. However, the parametric range of input variables that simultaneously affect the CSTBR operation cannot be predicted by their model. Moreover, a generalized criterion for sensitivity, independent of the topology of pH contour for recognizing the extent of parameters, where a CSTBR exhibits sensitive behavior, is not available in the literature.

Therefore, the focus of this study is to develop a mathematical model of CSTBR and derive an expression for normalized sensitivity function to determine parameter space and the critical value of input parameters where the system becomes unstable. The general methodology presented here can be modified to study the influence of other variables on microbial growth and can be used as a useful tool to design control strategies in CSTBRs.

2. Methodology

In this paper, the CSTBR bioprocess model of Das et al. [14] is adapted to describe the kinetics within the reactor. In order to to obtain kinetic constants relating to this study, batch experiments were performed and a calibrated model was used to conduct sensitivity analysis and highlight the sensitive parameter range and values for the considered variables.

The influence of pH on microbial growth was examined experimentally in a number of batch experiments. A lactic acid bacterium (LAB), Lactobacillus casei, was selected for these experiments. The initial pH of the reaction medium was varied to determine the impact of pH on the microbial growth rate. The data obtained from these batch experiments identified the optimum range of pH for the growth of LAB. From the data, the kinetic constants for the microbial growth model were also obtained.

By using the necessary knowledge on the kinetic parameters of microbial growth, including their dependence on pH, a model of CSTBR operation was developed. The mathematical model is capable of predicting time-dependent changes in the concentration of substrate, biomass, lactic acid, salt, and pH. The reactor pH is kept constant by assuming a continuous flow of the alkaline stream. The model is then used to analyze normalized sensitivity with respect to input variables; initial system pH, the dilution rate of the alkaline stream, and its concentration where pH-minimum (the lowest value of pH attain for a set of input variable) is an objective function. The sensitivity of the pH-minimum with respect to the vector of input parameters is investigated, along with the determination of critical values of input parameters where a “pH-runaway” condition occurs. Finally, the sensitivity analysis identified a parameter space, where pH becomes simultaneously sensitive to small changes in input parameters. The following objectives were achieved in order to fulfill the overall aim of the paper.

◦

Perform batch experiments using a lactic acid bacterium, Lactobacillus casei, to find out the optimum pH for microbial growth and other growth associated kinetic parameters;

◦

Derive a generalized criterion for sensitivity by obtaining an objective sensitivity function for pH with respect to input variables;

◦

Predict the critical value of input parameters and parameter space where the system becomes unstable and exhibits sensitive behavior.

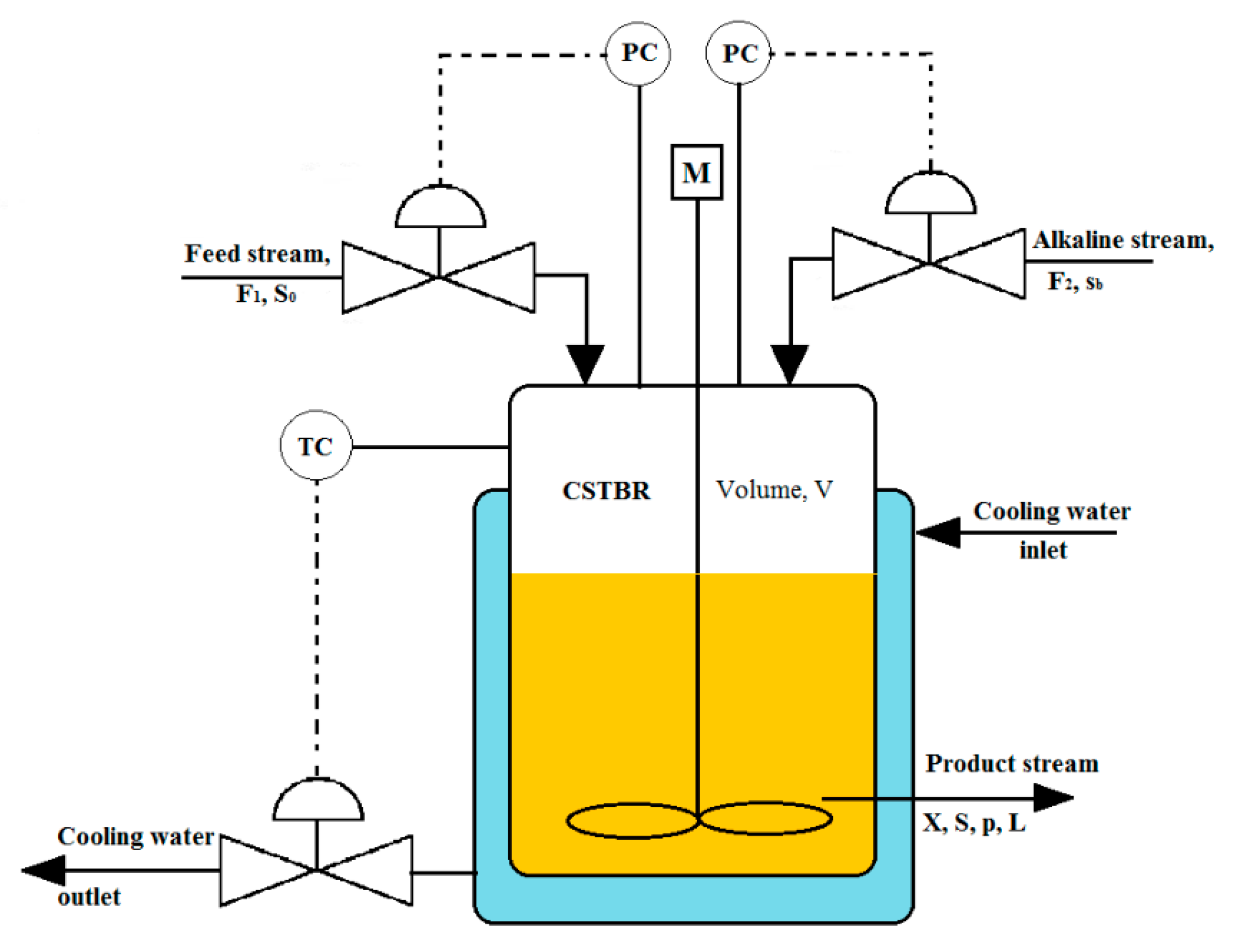
2.1. Experimental Analysis

The details of the materials and equipment used for the batch experiments are provided in

Table 1. Details of materials and equipment used for the batch study.

Microorganism	Lactobacillus casei (NCIM 5303) (Procured from the National Chemical Laboratory, Pune, India [18])
Chemicals for DNS method (Merck Specialties Private Limited, India)	3,5-dinitro salicylic acid, sodium hydroxide, sodium potassium tartrate
Equipment	A BOD incubator shaker (G. B. Enterprises, Kolkata, India); Autoclave (G. B. Enterprises, Kolkata, India) Centrifuge (Plasto Craft Industries Pvt. Ltd., India); Fermenter (B. Braun Biotech International); Peristaltic pump (Enertech Electronics Pvt. Ltd., India); UV-visible spectrophotometer (Varian, India); Shimadzu Corporation Reverse Phase HPLC (Model no: CBM-Ro A); pH meter (Sartorius, PB-11).

. A probiotic bacterium, Lactobacillus casei (LAB), is chosen, which is commonly used in dairy and pharmaceutical industries [15,16]. LAB is a gram-positive and facultative anaerobic bacterium. The pure stock culture was maintained separately at 37 °C in de Man Rogosa and Sharpe (MRS) medium for 18 h. After 18 h, the stock culture was kept at 4 °C. For the batch experiment, the composition of MRS medium is modified, and the composition of modified MRS (mMRS) is provided in

Table 2. Man Rogosa and Sharpe (MRS) composition in 100 mL solution.

Components	Amount (g)
Peptone	1.0
Beef extract	0.8
Yeast extract	0.4
Glucose	2.0
Sodium acetate trihydrate	0.5
Polysorbate 80 (also known as Tween 80)	0.1
Dipotassium hydrogen phosphate 0.2	0.2
Triammonium citrate	0.2
Magnesium sulfate heptahydrate	0.02
Manganese sulfate tetrahydrate	0.05

.

2.1.1. Modified MRS Culture Preparation

The mMRS was prepared by varying the glucose concentration from 10 gL⁻¹ to 50 gL⁻¹. The pH of each glucose concentration was varied from 5 to 8, using 2N HCl and 2M NaOH. In order to make the prepared mMRS media sterile, it was autoclaved at 121 °C for 15 min.

2.1.2. Batch Experiment

The incubating batch experiments were performed in 150 mL Erlenmeyer flasks using 50 mL modified MRS (mMRS) media. The temperature for all experiments was maintained at 37 °C. The experiment was started by adding 1% inoculum of LAB in mMRS media of 50 mL volume for every initial pH and glucose concentration. The flasks were then agitated at 60 rpm at 37 °C for 24 h. The carbon source (glucose) concentration was varied from 10.0 gL⁻¹ to 50.0 gL⁻¹. At each glucose concentration, experiments were conducted by varying initial pH in the range of 5.0 to 8.0. The microbial growth kinetics were studied for 24 h. Each experimental run was repeated three times to confirm the statistical accuracy of the results.

2.1.3. Assessment

Samples were withdrawn at an interval of 2 h during incubation. After centrifuging at 10,000 rpm, the supernatant was passed through a 0.22-micron filter for analyzing lactic acid concentration with the help of HPLC (Agilent 1260 series Agilent Technologies India Pvt Ltd., New Delhi, India). The mobile phase was 5 mM sulphuric acid with a flow rate of 0.6 mL/min at 35 °C, and the stationary phase was a Hypersil gold column. The cell biomass concentration of each sample was analyzed using a spectrophotometer (Perkin Elmer LAMBDA 850+ UV/Vis, India) at a wavelength of 600 nm. Cell dry weight was measured by withdrawing 5 mL of sample and centrifuging it at 10,000 rpm for 20 min. The supernatant is collected separately, and the pellet is dried at 100 °C to construct a standard calibration curve of cell biomass vs. optical density. The collected supernatant was also analyzed to determine the reduced sugar concentration using the dinitrosalicylic (DNS) acid reagent through spectrophotometry at 540 nm [5,17].

2.2. Theoretical Analysis

2.2.1. Kinetics Modeling

The most popular and simplest model, the Monod model, which describes the microbial reaction of microbial growth within a single substrate, was considered. The Monod equation is as follows:

$$\mathsf{\mu }=\frac{{\mathsf{\mu }}_{\max }\mathrm{S}}{{\mathrm{K}}_{\mathrm{S}}+\mathrm{S}},$$

(1)

where,

• μ specific microbial growth rate, (h⁻¹)
• μ_max maximum specific microbial growth rate, (h⁻¹)
• K_S substrate saturation constant (Monod constant) (gL⁻¹)
• S substrate (glucose) concentration (gL⁻¹)

Kinetic parameters of the Monod model were determined using the initial specific growth rate at each initial glucose concentration obtained at each initial pH. Equation (1) can be linearized in the form of Equation (2) to find out the kinetic parameters (μ_max and K_s) by making double reciprocal plots of μ versus S at each initial pH.

$$\frac{1}{\mathsf{\mu }}=\frac{{\mathrm{K}}_{\mathrm{S}}}{{\mathsf{\mu }}_{\max }\mathrm{S}}+\frac{1}{{\mathsf{\mu }}_{\max }}.$$

(2)

Regression analysis can be used to find the best fit for a straight line on a plot of 1/μ vs. 1/S, and the values of μ_max and K_S are determined. The variation of μ_max with initial pH would determine an optimum value of pH at which μ_max is maximum, thus, describing optimum conditions for the microbial growth. By plotting the values of normalized μ_max, i.e., μ_max,N vs. initial pH, a second-order correlation, similar to that obtained by Lallai et al. [19] and Datta et al. [12], is then obtained, as given in Equation (3)

$${\mathsf{\mu }}_{\max ,\mathrm{N}}=\left(\mathrm{A}+\mathrm{B}·\mathrm{pH}+\mathrm{C}·{\mathrm{pH}}^2\right),$$

(3)

where

$${\mathsf{\mu }}_{\max ,\mathrm{N}}=\frac{{\mathsf{\mu }}_{\max }}{{\mathsf{\mu }}_{\max ,\mathrm{opt}}},$$

(4)

where, μ_max,opt, μ_max at optimum pH.

Therefore, Equation (1) can be written as

$$\mathsf{\mu }=\frac{{\mathsf{\mu }}_{\max ,\mathrm{opt}}\left(\mathrm{A}+\mathrm{B}·\mathrm{pH}+\mathrm{C}·{\mathrm{pH}}^2\right)\mathrm{S}}{{\mathrm{K}}_{\mathrm{S}}+\mathrm{S}}.$$

(5)

This correlation defines the influence of pH on the specific microbial growth rate. A, B, and C are the second-order polynomial constants, and their values can be determined by nonlinear regression analysis of the experimental data. The mathematical model is used to design bioreactors and offer the necessary information to adopt control strategies for reactor operations. The mathematical model is based on conservation equations of mass or molar balance for each component in the process and simulates the kinetics of the bioprocess in a reactor. For quantitative prediction, the kinetic constants may be obtained experimentally.

2.2.2. Mathematical Modeling of CSTBRs

A continuous stirred tank bioreactor (CSTBR) as described by Das et al. [14] in which the feed conditions contain the glucose at a flow rate of F₁ (Lh⁻¹) and the glucose concentration of glucose is S₀ (gL⁻¹) was considered in this present study. The feed condition is sterile, which indicates that the feed is not containing any microbial cell. An alkaline stream containing aqueous NaOH fed to the bioreactor at a flow rate of F₂ (Lh⁻¹) and the concentration of NaOH is s_b (M) for controlling pH of the reaction medium. The volume of the bioreactor is V (L), and X (gL⁻¹) and S (gL⁻¹) are the cell and substrate (glucose) concentrations in the output stream, respectively. The detailed reaction scheme is shown in Figure 1.

The primary biochemical reaction in the CSTBR is described in Equation (6),

$$\mathrm{X}+\mathrm{Glucose}\to \mathrm{nX}+{\mathrm{CH}}_3\mathrm{CH}\left(\mathrm{OH}\right)\mathrm{COOH}\left(\mathrm{Lactic}\mathrm{acid}\right)+\mathrm{Caseicin}.$$

(6)

In the above biochemical reaction, bacterial cell, X is growing by utilizing glucose as a substrate, and the main byproduct is lactic acid. The optimum pH for microbial growth is maintained by continuously feeding the alkaline stream (NaOH) to the CSTBR. The acid-neutralizing reaction is taking place, as shown in Equation (7).

$${\mathrm{CH}}_3\mathrm{CH}\left(\mathrm{OH}\right)\mathrm{COOH}+\mathrm{NaOH}\to {\mathrm{CH}}_3\mathrm{CH}\left(\mathrm{OH}\right)\mathrm{COONa}+{\mathrm{H}}_2\mathrm{O}.$$

(7)

By knowing the concentration of NaOH and the salt (sodium lactate), the pH of the solution medium can be calculated using the Henderson–Hasselbalch equation [20] as shown in Equation (8).

$$\mathrm{pH}={\mathrm{pK}}_{\mathrm{a}}+\log \frac{{\mathrm{s}}_{\mathrm{A}}}{\mathrm{p}},$$

(8)

where,

• K_i  the equilibrium dissociation constant for lactic acid
• s_A  molar concentration of sodium lactate (M)
• p  molar concentrations of lactic acid (M)

The unsteady-state mass, molar, and pH balance are established in the following manner:

The mass balances are given by

$$\frac{\mathrm{dX}}{\mathrm{dt}}=\left(\mathsf{\mu }-\mathrm{D}-{\mathrm{D}}_1\right)\mathrm{X},$$

(9)

$$\frac{\mathrm{dS}}{\mathrm{dt}}=\mathrm{D}\left({\mathrm{S}}_0-\mathrm{S}\right)-{\mathrm{D}}_1\mathrm{S}-\frac{1}{{\mathrm{Y}}_{\raisebox{1ex}{$\mathrm{X}$}\!\left/ \!\raisebox{-1ex}{$\mathrm{S}$}\right.}}\mathsf{\mu }\mathrm{X},$$

(10)

where,

• D = F₁/V, dilution rate of the glucose feed stream (h⁻¹)
• D₁ = F₂/V, dilution rate of the alkaline stream (h⁻¹)
• Y_X/S yield coefficient for cell (g.g⁻¹)
• t time (h)

The Mole Balances are given as

$$\frac{\mathrm{dp}}{\mathrm{dt}}=-\mathrm{Dp}+\frac{{\mathrm{Y}}_{\raisebox{1ex}{$\mathrm{p}$}\!\left/ \!\raisebox{-1ex}{$\mathrm{X}$}\right.}\mathsf{\mu }\mathrm{X}}{{\mathrm{M}}_{\mathrm{a}}}-{\mathrm{D}}_1\left({\mathrm{s}}_{\mathrm{b}}+\mathrm{p}\right),$$

(11)

$$\frac{{\mathrm{ds}}_{\mathrm{A}}}{\mathrm{dt}}={\mathrm{D}}_1\left({\mathrm{s}}_{\mathrm{b}}-{\mathrm{s}}_{\mathrm{A}}\right)-{\mathrm{Ds}}_{\mathrm{A}},$$

(12)

where,

Y_p/S yield coefficient for product (g.g⁻¹)

M_a Molecular weight of lactic acid (g.mol⁻¹)

The pH balance is obtained by differentiating Equation (8), and given as

$$\frac{\mathrm{dpH}}{\mathrm{dt}}=\frac{1}{{\mathrm{s}}_{\mathrm{A}}}\frac{{\mathrm{ds}}_{\mathrm{A}}}{\mathrm{dt}}-\frac{1}{\mathrm{p}}\frac{\mathrm{dp}}{\mathrm{dt}}.$$

(13)

The mass and molar balances were suitably transformed into the dimensionless form using the variables described in

Table 3. Definitions of the dimensionless variable used in the model.

Parameter	Definition	Parameter	Definition
α	$\mathrm{X}/\left({\mathrm{S}}_0{\mathrm{Y}}_{\raisebox{1ex}{$\mathrm{X}$}\!\left/ \!\raisebox{-1ex}{$\mathrm{S}$}\right.}\right)$	U	$\mathsf{\mu }/\mathrm{D}$
β	$\mathrm{S}/{\mathrm{S}}_0$	θ	${\mathrm{D}}_1/\mathrm{D}$
z	${\mathrm{pM}}_{\mathrm{a}}/\left({\mathrm{S}}_0{\mathrm{Y}}_{\raisebox{1ex}{$\mathrm{p}$}\!\left/ \!\raisebox{-1ex}{$\mathrm{S}$}\right.}\right)$	m	${\mathsf{\mu }}_{\max }/\mathrm{D}$
R	${\mathrm{s}}_{\mathrm{b}}{\mathrm{M}}_{\mathrm{b}}/{\mathrm{S}}_0$	n	${\mathrm{K}}_{\mathrm{S}}/{\mathrm{S}}_0$
L	${\mathrm{s}}_{\mathrm{a}}{\mathrm{M}}_{\mathrm{c}}/{\mathrm{S}}_0$	b	$\mathrm{B}.{\mathrm{pH}}_0$
γ	$\mathrm{pH}/{\mathrm{pH}}_0$	c	$\mathrm{C}.{\mathrm{pH}}_0^2$
τ	$\mathrm{tD}$	M1	${\mathrm{M}}_{\mathrm{a}}{\mathrm{Y}}_{\raisebox{1ex}{$\mathrm{p}$}\!\left/ \!\raisebox{-1ex}{$\mathrm{S}$}\right.}/{\mathrm{M}}_{\mathrm{b}}$
M2	${\mathrm{M}}_{\mathrm{c}}/{\mathrm{M}}_{\mathrm{b}}$

.

Therefore, the model equations in the non-dimensional form are as follows:

$$\frac{\mathrm{d}\mathsf{\alpha }}{\mathrm{d}\mathsf{\tau }}=\left(\mathrm{U}-\mathsf{\theta }-1\right)\mathsf{\alpha },$$

(14)

$$\frac{\mathrm{d}\mathsf{\beta }}{\mathrm{d}\mathsf{\tau }}=\left(1-\mathsf{\beta }\right)-\mathrm{U}.\mathsf{\alpha }-\mathsf{\theta }.\mathsf{\beta },$$

(15)

$$\frac{\mathrm{dz}}{\mathrm{d}\mathsf{\tau }}=-\mathrm{z}+\mathrm{U}.\mathsf{\alpha }-\mathsf{\theta }\left({\mathrm{M}}_1\mathrm{R}+\mathrm{z}\right),$$

(16)

$$\frac{\mathrm{dL}}{\mathrm{d}\mathsf{\tau }}=\left({\mathrm{M}}_2\mathrm{R}-\mathrm{L}\right)\mathsf{\theta }-\mathrm{L},$$

(17)

$$\frac{\mathrm{d}\mathsf{\gamma }}{\mathrm{d}\mathsf{\tau }}=\frac{1}{{\mathrm{pH}}_0}\left[\frac{1}{\mathrm{L}}\frac{\mathrm{dL}}{\mathrm{d}\mathsf{\tau }}-\frac{1}{\mathrm{z}}\frac{\mathrm{dz}}{\mathrm{d}\mathsf{\tau }}\right].$$

(18)

On the other hand, the non-dimensional expression for the specific growth rate can be expressed as

$$\mathrm{U}=\frac{\mathrm{m}\mathsf{\beta }}{\mathrm{n}+\mathsf{\beta }}\mathrm{I},$$

(19)

where,

$$\mathrm{I}=\mathrm{A}+\mathrm{B}.\mathsf{\gamma }+\mathrm{C}.{\mathsf{\gamma }}^2.$$

(20)

The differential Equations (14)–(18) can be solved numerically using the 4th order Runge–Kutta method using the following initial conditions. At

$$\mathsf{\tau }=0;\mathsf{\gamma }=1;\mathsf{\alpha }={\mathsf{\alpha }}_0;\mathsf{\beta }={\mathsf{\beta }}_0;\mathrm{z}={\mathrm{z}}_0;\mathrm{L}={\mathrm{L}}_0.$$

(21)

2.2.3. Sensitivity Analysis

For analyzing the pH-sensitivity, the method adopted by Morbedelli and Varma [3,13] and Dutta et al. [12] is considered. In this case, the governing equations for pH and the substrate concentration are written by dividing Equation (18) by Equation (15)

$$\frac{\mathrm{d}\mathsf{\gamma }}{\mathrm{d}\mathsf{\beta }}=\frac{\frac{\mathrm{R}·\mathsf{\theta }}{{\mathrm{pH}}_0}\left[\frac{{\mathrm{M}}_2}{\mathrm{L}}+\frac{{\mathrm{M}}_1}{\mathrm{z}}-\frac{\mathrm{U}·\mathsf{\alpha }}{\mathrm{z}·\mathrm{R}·\mathsf{\theta }}\right]}{1-\mathrm{U}.\mathsf{\alpha }-\left(1+\mathsf{\theta }\right)\mathsf{\beta }}=\mathrm{g}\left(\mathsf{\varphi },\mathsf{\alpha },\mathsf{\beta },\mathrm{z},\mathrm{L},\mathsf{\gamma }\right),$$

(22)

where ϕ is the vector of input parameters, namely, initial system pH (pH₀), the dilution rate of the alkaline stream (θ), and its concentration (R). Similarly, dividing Equations (14), (16), and (17) by Equation (15), the following equations are obtained as below.

$$\frac{\mathrm{d}\mathsf{\alpha }}{\mathrm{d}\mathsf{\beta }}=\frac{\mathrm{U}.\mathsf{\alpha }-\left(1+\mathsf{\theta }\right)\mathsf{\alpha }}{1-\mathrm{U}.\mathsf{\alpha }-\left(1+\mathsf{\theta }\right)\mathsf{\beta }},$$

(23)

$$\frac{\mathrm{dz}}{\mathrm{d}\mathsf{\beta }}=\frac{\mathrm{U}.\mathsf{\alpha }-\left(1+\mathsf{\theta }\right).\mathrm{z}-{\mathrm{M}}_1.\mathsf{\theta }.\mathrm{R}}{1-\mathrm{U}.\mathsf{\alpha }-\left(1+\mathsf{\theta }\right)\mathsf{\beta }},$$

(24)

$$\frac{\mathrm{dL}}{\mathrm{d}\mathsf{\beta }}=\frac{{\mathrm{M}}_2.\mathsf{\theta }.\mathrm{R}-\left(1+\mathsf{\theta }\right).\mathrm{L}}{1-\mathrm{U}.\mathsf{\alpha }-\left(1+\mathsf{\theta }\right)\mathsf{\beta }}.$$

(25)

With the following initial conditions,

$$\mathrm{pH}={\mathrm{pH}}_0;\mathsf{\alpha }={\mathsf{\alpha }}_0;\mathrm{z}={\mathrm{z}}_0\mathrm{and}\mathrm{L}={\mathrm{L}}_0;\mathsf{\beta }={\mathsf{\beta }}_0.$$

(26)

By differentiating Equation (22) with respect to parameter ϕ, the expression for first-order local sensitivity s_ϕ can be evaluated as

$$\frac{{\mathrm{ds}}_{\mathsf{\varphi }}}{\mathrm{d}\mathsf{\beta }}=\frac{\mathrm{dg}}{\mathrm{d}\mathsf{\varphi }}+\frac{\mathrm{dg}}{\mathrm{d}\mathsf{\gamma }}.{\mathrm{s}}_{\mathsf{\varphi }}.$$

(27)

The adjoined equation from Equation (27) takes the following form:

$$\frac{{\mathrm{dp}}_{\mathsf{\beta }}}{\mathrm{d}\mathsf{\beta }}=\mathrm{H}.{\mathrm{p}}_{\mathsf{\beta }}\mathrm{for}\mathsf{\beta }\in \left({\mathsf{\beta }}_{0,}{\mathsf{\beta }}^{*}\right),$$

(28)

where,

$$\mathrm{H}=-\frac{\mathrm{dg}}{\mathrm{d}\mathsf{\gamma }}$$

(29)

and

$${\mathrm{p}}_{\mathsf{\beta }}=\frac{{\overline{\mathrm{s}}}_{\mathsf{\varphi }}\left(\mathsf{\beta }\right)}{{\overline{\mathrm{s}}}_{\mathsf{\varphi }}\left(0\right)}.$$

(30)

Furthermore, β₀ indicates the value of initial substrate concentration (dimensionless), whereas β^* indicates the substrate concentration in the reactor at which γ = γ_min. The initial conditions of Equation (28) are

$$\mathrm{At},\mathsf{\beta }={\mathsf{\beta }}_0;\mathsf{\rho }=1;{\mathrm{s}}_{\mathsf{\varphi }}\left(0\right)=\frac{\mathrm{d}\mathsf{\gamma }}{\mathrm{d}{\mathsf{\varphi }}_{\mathrm{i}}}=0,$$

(31)

where, ϕ_i is one element of the parameter vector, ϕ.

2.2.4. Calculation of Sensitivities

The normalized objective sensitivities can be evaluated as follows:

• Equations (22)–(25) and (28) are solved simultaneously with the help of initial conditions given in Equations (26) and (31) until the γ reaches its minimum value. The corresponding values of ρ_β^* and β* wre determined;
• ${\overline{\mathrm{s}}}_{\mathsf{\varphi }}$(0) given by Equation (30) was calculated using the value of ρ_β* with the help of the following equation:

  $${\overline{\mathrm{s}}}_{\mathsf{\varphi }}\left(0\right)=\frac{{\overline{\mathrm{s}}}_{\mathsf{\varphi }}\left({\mathsf{\beta }}^{*}\right)}{{\mathsf{\rho }}_{{\mathsf{\beta }}^{*}}}=\frac{1}{{\mathsf{\rho }}_{{\mathsf{\beta }}^{*}}};$$

  (32)
• The objective sensitivity is then evaluated by solving the following equation:

  $${\mathrm{s}}_{{\mathsf{\varphi }}_{\mathrm{i}}}^{*}={\mathrm{s}}_{{\mathsf{\varphi }}_{\mathrm{i}}}\left(0\right).{\overline{\mathrm{s}}}_{\mathsf{\varphi }}\left(0\right)+{{\displaystyle \int }}_{{\mathsf{\beta }}_0}^{{\mathsf{\beta }}^{*}}{\mathsf{\sigma }}_{\mathrm{i}}.{\overline{\mathrm{s}}}_{\mathsf{\varphi }}\left(\mathsf{\beta }\right)\mathrm{d}\mathsf{\beta },$$

  (33)

  where,

  $${\mathsf{\sigma }}_{\mathrm{i}}=\frac{\partial \mathrm{g}}{\partial {\mathsf{\varphi }}_{\mathrm{i}}}\mathrm{for}\mathsf{\beta }\in \left({\mathsf{\beta }}_{0,}1\right).$$

  (34)

The expressions for σ_i and corresponding values for each ϕ_i are provided in

Table 4. Expressions of σ_i for various parameters ϕ_i, as defined in equation (33).

ϕi	σi
pH0	$\frac{\mathrm{R}.\mathsf{\theta }\left[\frac{{\mathrm{M}}_2}{\mathrm{L}}+\frac{{\mathrm{M}}_1}{\mathrm{z}}-\frac{\mathrm{U}·\mathsf{\alpha }}{\mathrm{z}·\mathrm{R}·\mathsf{\theta }}\right]}{{\mathrm{pH}}_0^2\left[\mathrm{U}.\mathsf{\alpha }+\left(1+\mathsf{\theta }\right)\mathsf{\beta }-1\right]}$
θ	$\frac{\mathrm{R}.\mathsf{\theta }.\mathsf{\beta }\left[\frac{{\mathrm{M}}_2}{\mathrm{L}}+\frac{{\mathrm{M}}_1}{\mathrm{z}}-\frac{\mathrm{U}·\mathsf{\alpha }}{\mathrm{z}·\mathrm{R}·\mathsf{\theta }}\right]}{{\mathrm{pH}}_0{\left[\mathrm{U}.\mathsf{\alpha }+\left(1+\mathsf{\theta }\right)\mathsf{\beta }-1\right]}^2}-\frac{\mathrm{R}\left[\frac{{\mathrm{M}}_2}{\mathrm{L}}+\frac{{\mathrm{M}}_1}{\mathrm{z}}-\frac{\mathrm{U}·\mathsf{\alpha }}{\mathrm{z}·\mathrm{R}·\mathsf{\theta }}\right]}{{\mathrm{pH}}_0\left[\mathrm{U}.\mathsf{\alpha }+\left(1+\mathsf{\theta }\right)\mathsf{\beta }-1\right]}-\frac{\mathrm{U}·\mathsf{\alpha }}{\mathsf{\theta }.\mathrm{z}.{\mathrm{pH}}_0\left[\mathrm{U}.\mathsf{\alpha }+\left(1+\mathsf{\theta }\right)\mathsf{\beta }-1\right]}$
R	$-\frac{\mathsf{\theta }\left[\frac{{\mathrm{M}}_2}{\mathrm{L}}+\frac{{\mathrm{M}}_1}{\mathrm{z}}-\frac{\mathrm{U}·\mathsf{\alpha }}{\mathrm{z}·\mathrm{R}·\mathsf{\theta }}\right]}{{\mathrm{pH}}_0\left[\mathrm{U}.\mathsf{\alpha }+\left(1+\mathsf{\theta }\right)\mathsf{\beta }-1\right]}-\frac{\mathrm{U}·\mathsf{\alpha }}{\mathrm{R}.\mathrm{z}.{\mathrm{pH}}_0\left[\mathrm{U}.\mathsf{\alpha }+\left(1+\mathsf{\theta }\right)\mathsf{\beta }-1\right]}$

.

3. Results

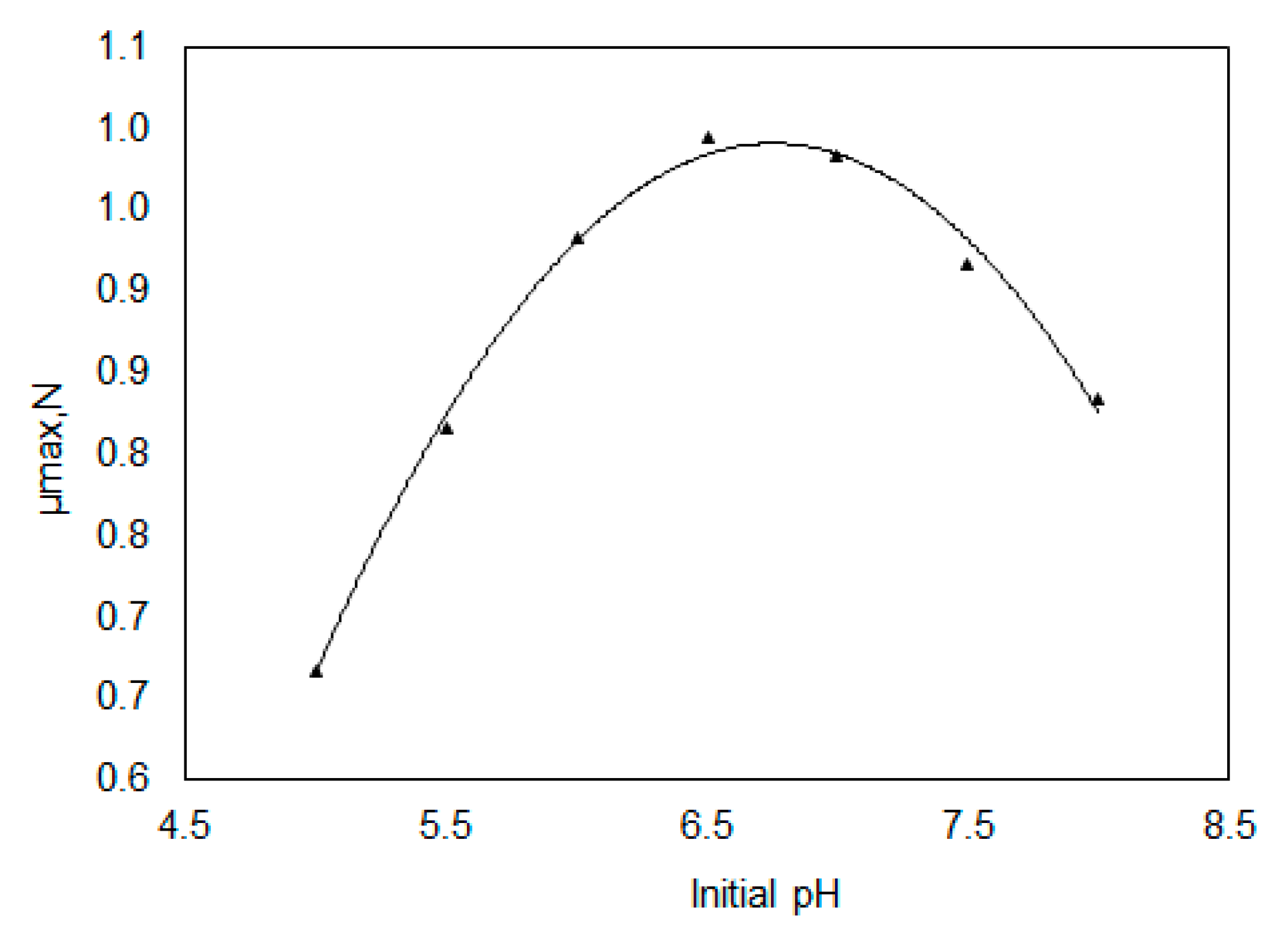
3.1. Determination of Kinetic Parameters of Lactobacillus Casei in Batch Culture

At each initial pH, the maximum specific growth rate (µ_max) and substrate saturation constant (K_S) are determined using Equation (2). The values of normalized µ_max, i.e., µ_max.N are plotted as a function of initial pH, is shown in Figure 2. As observed from Figure 2, at pH = 6.75, (µ_max) reaches the maximum value, which is considered as the optimum pH for the microbial growth.

The maximum specific growth rate (µ_max) at optimum pH is denoted as µ_{max, opt}. A second-order correlation is obtained, as specified in Equation (3). The different values of the constants of Equation (3) and other kinetic constants evaluated from the experiments are provided in

Table 5. Values of kinetic parameters.

Kinetic Parameter	Value
µmax,opt (h−1)	0.6
KS (gL−1)	0.08144
YX/S (gg−1)	0.238
Yp/X (gg−1)	3.36
Yp/S (gg−1)	0.8
A	−3.8507
B	1.434
C	−0.1062

.

3.2. pH Sensitivity of a Continuous Stirred Tank Bioreactor

The main objective of this analysis is to determine the parametric range of input variables at which the CSTBR system becomes vulnerable. The system behavior is demonstrated in terms of normalized objective sensitivities coefficients as a function of input parameters. The mathematical model of the system consists of the Equations (22)–(25), (28), and (33). The Equations (22)–(25) and (28) were simultaneously solved using Runga–Kutta 4th order method, and Equation (33) is solved using the trapezoidal numerical integration method. The results are illustrated in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11. Figure 3, Figure 4 and Figure 5 show normalized objective sensitivities of the pH-minimum, S(γ*, ϕ_i), as a function of the input parameters, i.e., dimensionless dilution rate of base feed stream (θ), the dimensionless concentration of base, (R) and initial pH (pH₀) of the system.

In Figure 3, S (γ*, θ), S (γ*, R), and S (γ*, pH₀) are plotted against the dimensionless dilution rate of the base feed stream (θ). In this mathematical operation, the input parameter (θ) was varied in the range of 0 to 1, where the values of other input parameters pH₀ and R were kept constant at 6.75 and 0.8, respectively. As the value of θ reached 0.095, the system started showing sensitivity behavior, and S (γ*, θ) and S (γ*, R) started increasing, whereas S (γ*, pH₀) started decreasing. At θ = 0.0195, the values of sensitivity functions attained their maxima (for S (γ*, θ) and S (γ*, R)) and minima (S (γ*, pH₀)). Further, for the increment of θ, the sensitivity functions S (γ*, θ) and S (γ*, R) were decreasing, and S (γ*, pH0) was increasing. This trend became near to 0 when θ reached a value of 0.295 and the system was again nonsensitive with respect to input parameter (θ). Therefore, the parameter range of θ is between 0.095 and 0.295, where the system becomes simultaneously sensitive. The value of θ at which the sensitivity functions attain their maxima and minima are defined as the critical value of θ.

Figure 4 shows the plots of S(γ*,θ), S(γ*,R), and S(γ*,pH₀) versus the concentration of the base stream, (R). In this case, the dimensionless base stream concentration was varied in the range of 1 to 4 in order to observe the system behavior in terms of sensitivity functions S(γ*,θ), S(γ*,R), and S(γ*,pH₀), where the values of θ and pH₀ were kept constant at 0.3 and 6.75, respectively. The system starts showing sensitivity behavior, and S(γ*,θ) and S(γ*,R) started increasing, whereas S(γ*,pH₀) started decreasing from the beginning. This trend of the increment (for S(γ*,θ) and S(γ*,R)) descent (for S(γ*,pH₀) was observed until R reached its value of 0.48. At this R = 0.48, sensitivity functions attained their maxima (for S(γ*,θ) and S(γ*,R)) and minima (S(γ*,pH₀)) and became near to 0 when R reached a value of 0.865. The system was again nonsensitive with respect to input parameter R at this stage. Therefore, the parameter range of R is between 0 and 0.865, where the system becomes simultaneously sensitive. The critical value of the dimensionless base stream concentration R_C is 0.48.

The system behavior is also investigated in terms of sensitivity functions as a function of the initial pH (pH₀) of the system. The sensitivity functions S(γ*,θ), S(γ*,R), and S(γ*,pH₀) with respect to pH₀ are shown in Figure 5. Here, the pH₀ was varied in the range of 4 to 6 to observe the system behavior in terms of sensitivity functions S(γ*,θ), S(γ*,R), and S(γ*,pH₀), where the values of θ and R were kept constant at 0.5 and 8, respectively. The system did not show any sensitivity for pH₀ from 4 to 4.42. As the value of pH₀ crossed 4.42, it started showing sensitivity behavior, and S(γ*,θ) and S(γ*,R) started increasing, whereas S(γ*,pH₀) started decreasing. This movement of the increment (for S(γ*,θ) and S(γ*,R)) descent (for S(γ*,pH₀) was observed until pH₀ reached its value of 4.6. At this pH₀ = 4.6, sensitivity functions attained their maxima (for S(γ*,θ) and S(γ*,R)) and minima (S(γ*,pH₀)) and became near to 0 when pH₀ reached a value of 4.765. The system was again nonsensitive with respect to input parameter pH₀ at this stage. Therefore, the parameter range of pH₀ is between 4.42 and 4.765, where the system becomes simultaneously sensitive. The critical value of the initial system pH, pH₀ is 4.6.

Figure 6 and Figure 7 show the nature of normalized objective sensitivity as a function of θ with the variation of R and pH₀, which is the combined effects of R and pH₀ on sensitivity function S(γ*, θ). The dimensionless input variables θ and R were varied to observe the behavior of CSTBR in terms of the sensitivity coefficient, S(γ*, θ) with constant pH₀, which is presented in Figure 6. In this case, the range of θ and R was varied from 0 to 1 and 0 to 4, respectively. The parametric zone where the system found sensitivity is provided in

Table 6. Different critical values of input parameters (from Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11).

Sensitivity Coefficients S(γ*, ϕi)	Variable Parameters (Critical Values)		Sensitive Zone of Input Variables		Fixed Parameters
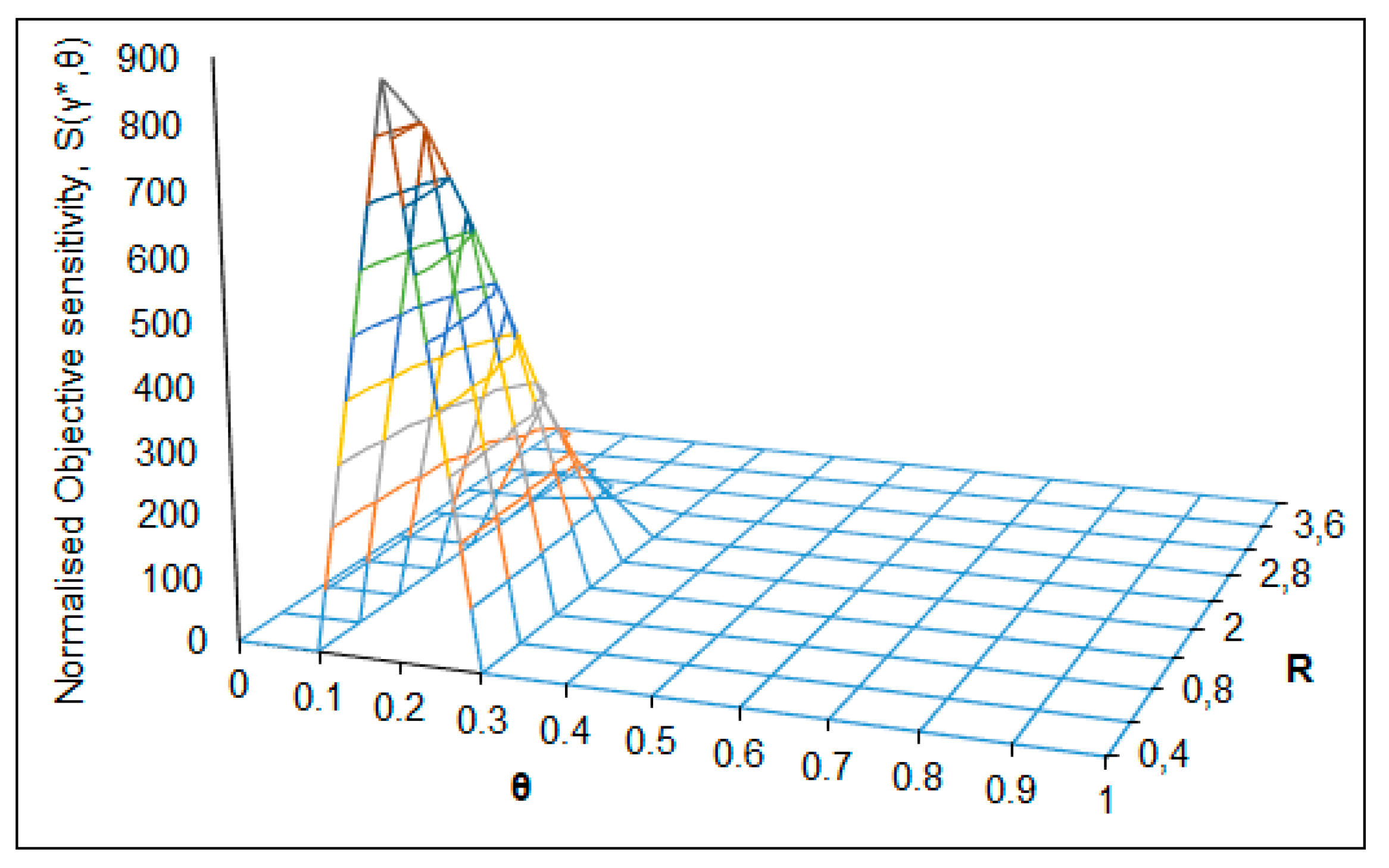
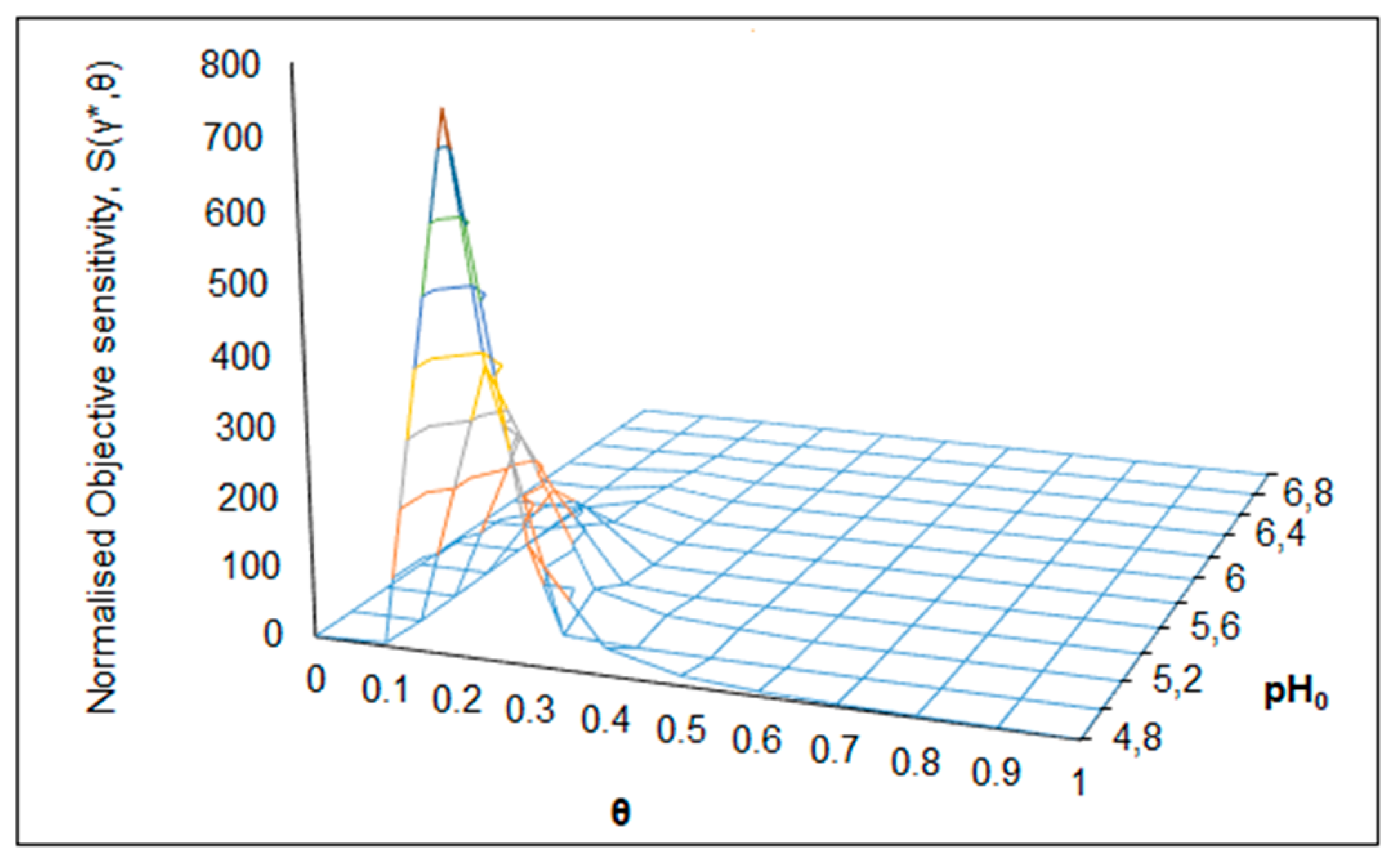
S(γ*,θ) = 885 (Figure 6)	θC = 0.2	RC = 0.4	θ → 0.1–0.3	R → 0–2.4	pH0 = 6.75
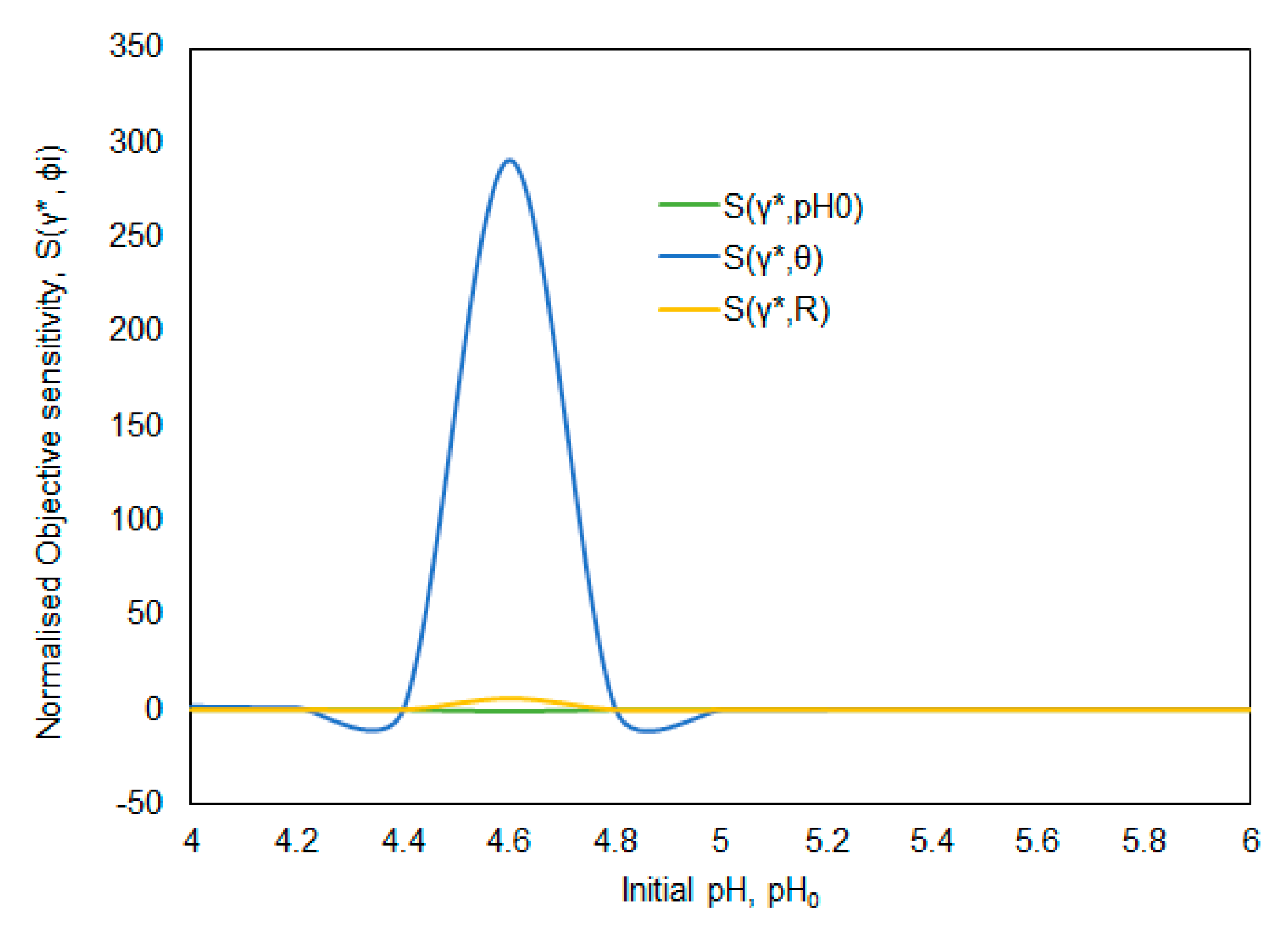
S(γ*,θ) = 735 (Figure 7)	θC = 0.2	pH0C = 4.8	θ → 0.1–0.3	pH0 → 4.8–6.0	R = 0.2
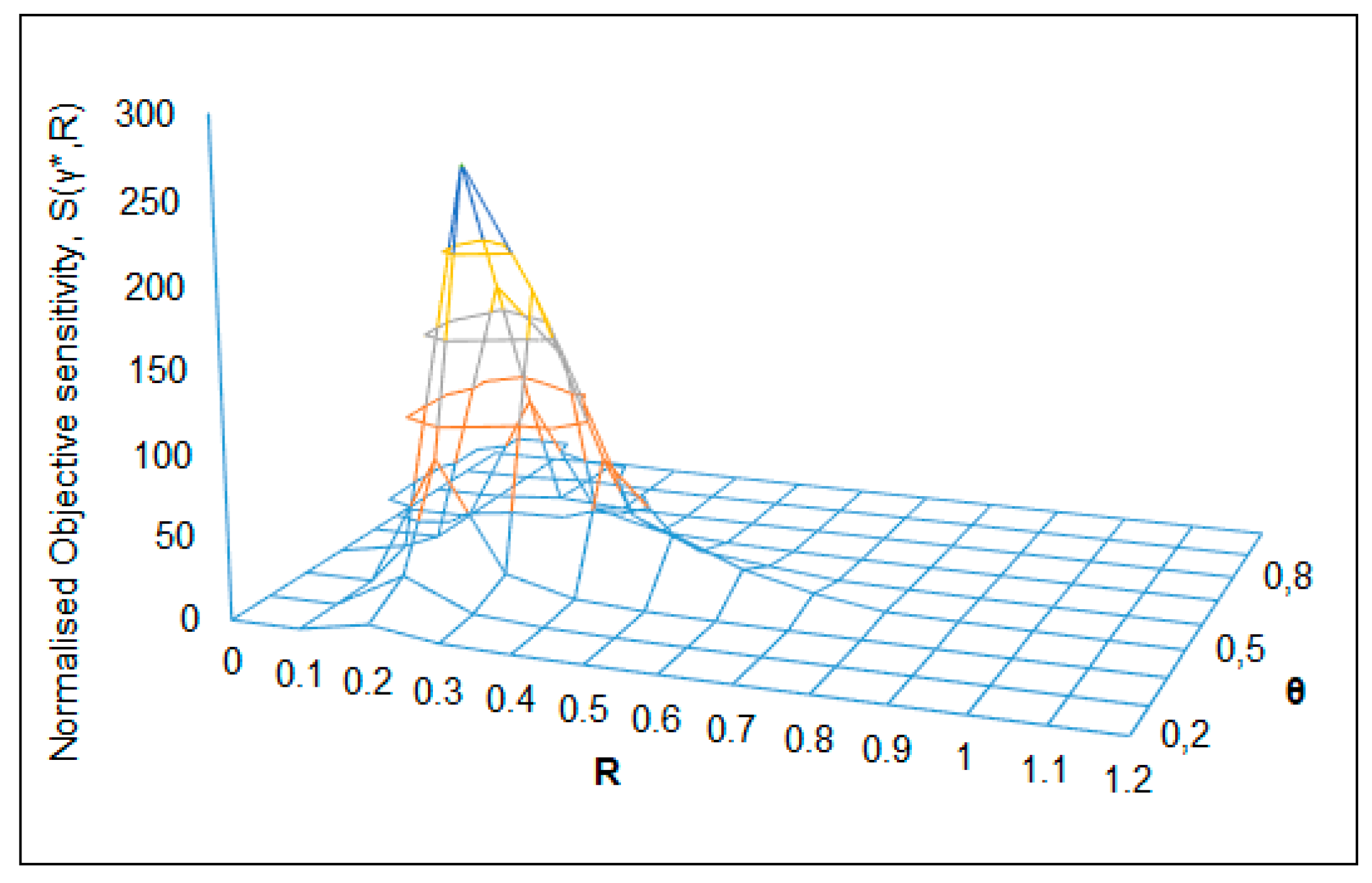
S(γ*,R) = 285 (Figure 8)	RC = 0.2	θC = 0.5	R → 0.1–0.75	θ → 0.05–0.7	pH0 = 6.5
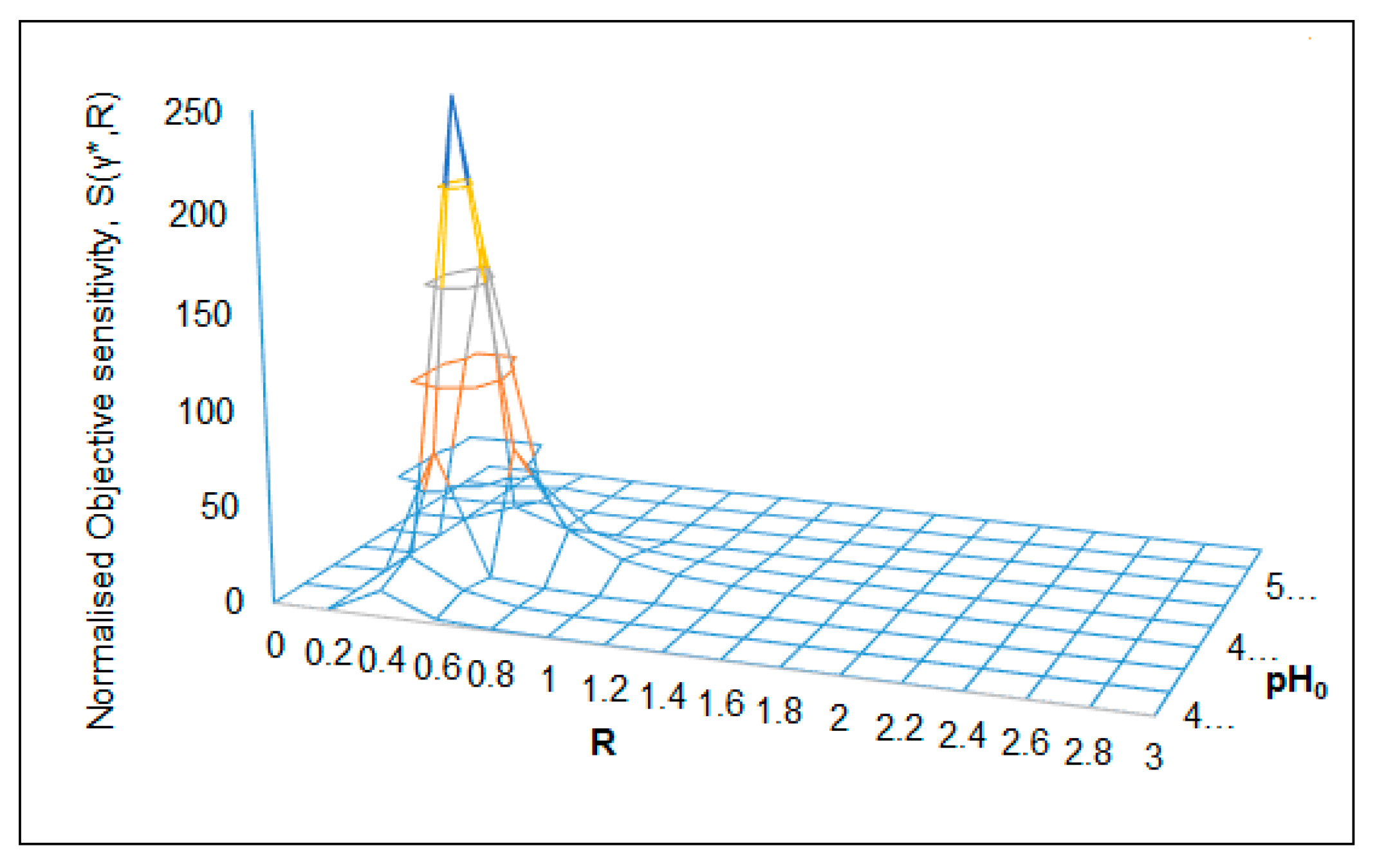
S(γ*,R) = 245 (Figure 9)	RC = 0.4	pH0C = 4.6	R → 0.2–1.4	pH0 → 4.2–4.6	θ = 0.3
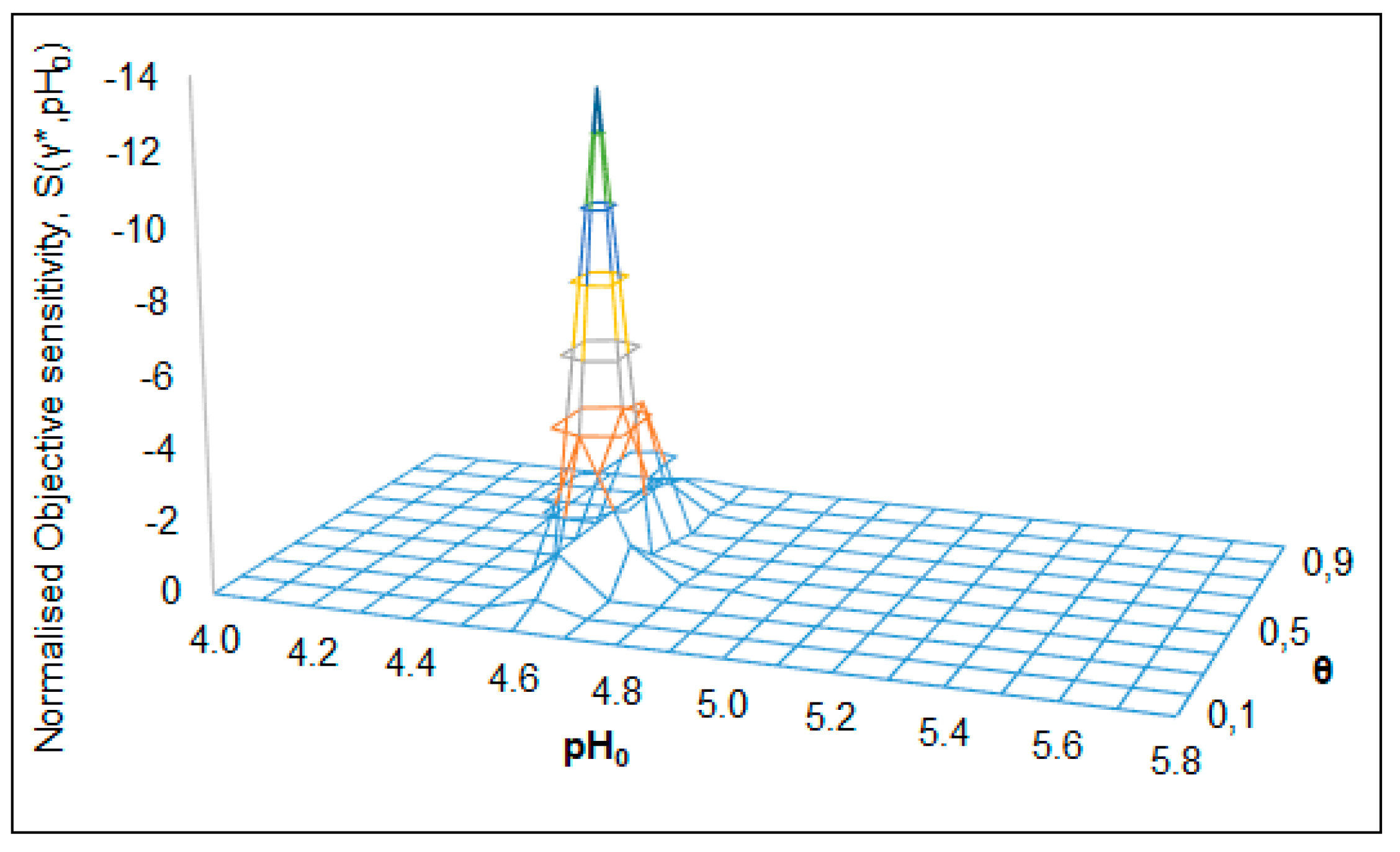
S(γ*,pH0) = –7.8 (Figure 10)	pH0 = 4.6	RC = 0.8	pH0 → 4.5–4.8	R → 0.4–2.0	θ = 0.7
S(γ*,pH0) = –13.8 (Figure 11)	pH0C = 4.6	θC = 0.5	pH0 → 4.45–4.85	θ → 0.25–0.75	R = 0.8

. The sensitive function, S(γ*, θ), reached a maximum with a magnitude of 885 and the corresponding critical value of input variables is determined. The critical values of θ and R are provided in Table 6.

The behavior of CSTBR is presented in Figure 7 in terms of the sensitivity coefficient, S(γ*, θ). Figure 7 shows the variation of S(γ*, θ) with respect to the initial pH (pH₀) and θ. With a fixed value of R = 0.2, the θ and pH₀ were varied from 0 to 1 and 4.8 to 7.0, respectively. The sensitive zone for CSTBR operation for θ is 0.1 to 0.3, and for pH₀ the range is between 4.8 and 6. The sensitive function, S(γ*, θ), reached a maximum with a value of 735, and the corresponding critical values of input variables pH₀ and θ are determined. Table 6 provides the critical values of θ and pH₀ for this case.

The nature of normalized objective sensitivity as a function of R with the variation of θ and pH₀ have shown in Figure 8 and Figure 9 to find out the influence of θ and pH₀ on the sensitivity function, S(γ*, R). Figure 8 shows the critical value of R and θ at a constant initial pH, pH₀ = 6.5, when S(γ*, R) attains its maximum. The system does not show any sensitive behavior when θ goes beyond 0.7 and R = 0.75. The details of the input range and critical values of input parameters are given in Table 6.

A similar trend occurred when pH₀ and R were the input variables. In this case, the range of R and pH₀ were varied from 0 to 3 and from 4 to 5, respectively. The influence of input parameters on sensitivity function S(γ*, R) are illustrated in Figure 9. The maximum value of sensitivity function S(γ*,R) is 245, and the corresponding critical values of R and pH₀ are provided in Table 6. The determined sensitive region for CSTBR with respect to R and pH₀ is 0.2 to 1.4 and 4.2 to 4.6, respectively.

The behavior of normalized objective sensitivity as a function of pH₀, S(γ*, pH₀) with the variation of R and θ are shown in Figure 10 and Figure 11. The influences of R and pH₀ on S(γ*, pH₀) at a fixed value of θ = 0.7 are presented in Figure 10. From the figure, it can be observed that the sensitivity function S(γ*, pH₀) exhibit sensitive behavior in a negative direction. The S(γ*, pH₀) reached its lowest value of −7.8 when the R and pH₀ values are at 0.8 and 4.6, respectively. The sensitive region and critical values of input variables are presented in Table 6.

Similar behavior of sensitivity function, S(γ*, pH₀), was observed when pH₀ and θ were varied from 4 to 5.4 and 0 to 3, respectively, keeping R constant at 0.8. From the observation, it is found that the S(γ*, pH₀) reached its lowest value of −13.8 when the θ and pH₀ are at 0.5 and 4.6, respectively. The plot of normalized objective sensitivity S(γ*, pH₀) as a function of parameters R and θ is presented in Figure 11. The sensitive zone and the critical values of pH₀ and θ corresponding to S(γ*,pH₀) are provided in Table 6.

4. Discussions

The influence of initial pH on microbial growth is observed in the present study through batch experiments. From the results, it is observed that initially, when the experiments conducted within the initial pH range of 5.5 to 7.5, the microbial growth is not significantly affected. Therefore, the optimum value of pH is found to be within that range of 5.5 to 7.5, which is 6.75. However, as the initial pH went below or above that particular range, a considerable change in the microbial growth rate is observed. Therefore, the effects of pH on microbial growth are pragmatically observed.

On the other hand, from the sensitivity analysis of CSTBRs, it is found that the selected input parameters have significant influence for reactor operation. This analytical study provides a good insight at what extend these selected parameters can hinder the CSTBR operation. From Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11, it is observed that there is a zone where the system showed its undesirable behavior in terms of sensitivity coefficients. The magnitude of the input parameters pH₀, θ, and R at which the normalized objective sensitivity attain their maxima or minima are termed as critical values. The critical values of pH_0C, θ_C, and R_C provide the boundary separating the stable pH system from an unstable pH system sometimes defined as the pH-runaway condition [14]. The magnitude of S(γ*,θ), S(γ*,R), and S(γ*,pH₀) at critical points show that the influence of initial pH (pH₀) has less impact on the sensitivity behavior compared to other input parameters, namely, R and θ.

Positive values of the objective normalized sensitivity of the pH-minimum with respect to input parameters θ and R indicate that the pH-minimum increases as the magnitude of these parameter increase. The negative value of objective normalized sensitivity of the pH-minimum with respect to pH₀ indicates that the pH-minimum increases as pH₀ decreases. Thus, if the sensitivity is positive, the transition from a stable pH system to pH-runaway behavior occurs as this parameter is increased. In contrast, if the sensitivity is negative, the same transition occurs when the corresponding parameter is decreased.

5. Conclusions

This paper presents the behavior of a CSTBR using lactic acid bacteria, namely, L. casei, through parametric sensitivity analysis. From the batch experiments, one can certainly observe that the microbial growth profoundly depends on the system pH. The parametric range of inputs for maintaining optimal pH range conductive for the microbial growth during reactor operation is determined. The impact of input parameters, which are directly involved in maintaining the pH of the system, is observed by determining normalized objective sensitivity of pH. A generalized criterion of sensitivity, i.e., a specific range of input parameters at which the CSTBR becomes sensitive. In the present study, pH was selected as the objective function for determining the generalized criteria. The sensitivity analysis was conducted with respect to three dimensionless input variables, dilution rate θ; base concentration, R, and initial pH, pH₀. The sensitive operating zone for CSTBR was determined in terms of sensitivity function, S(γ*,ϕ_i), with respect to three selected input parameters. From the investigation, the sensitive zone of input parameters is from 0.095 to 0.295 for θ, from 0 to 0.865 for R, and from 4.42 to 4.765 for pH₀. Whereas, the critical values of input parameters θ, R, and pH₀ are 0.0195, 0.48, and 4.6, respectively. From this investigation, it can be concluded that the methodology implemented in the present study to define a generalized criterion to determine a parametrically sensitive regime can also be applied for any other output parameters, namely, temperature, the concentration of metabolites, and other byproducts. Thus, this mathematical model can be used as a design tool to predict CSTBR behavior and to develop control systems for the CSTBR operations.