A Numerical Implementation of the Soret Effect in Drying Processes
Abstract
:1. Introduction
2. Methods
2.1. Linear Nonequilibrium Thermodynamic Derivation
2.2. Drying System
2.3. Thermodynamic Forces for a n-Component Drying System
2.4. Heat and Mass Flux for a Binary Drying System
3. Results
3.1. Drying System and Model
3.2. Implementation of the Drying Model
3.2.1. Flux Equations
3.2.2. Soret Effect
3.2.3. Governing Equations
3.2.4. Boundary and Initial Conditions
3.2.5. Numerical Implementation
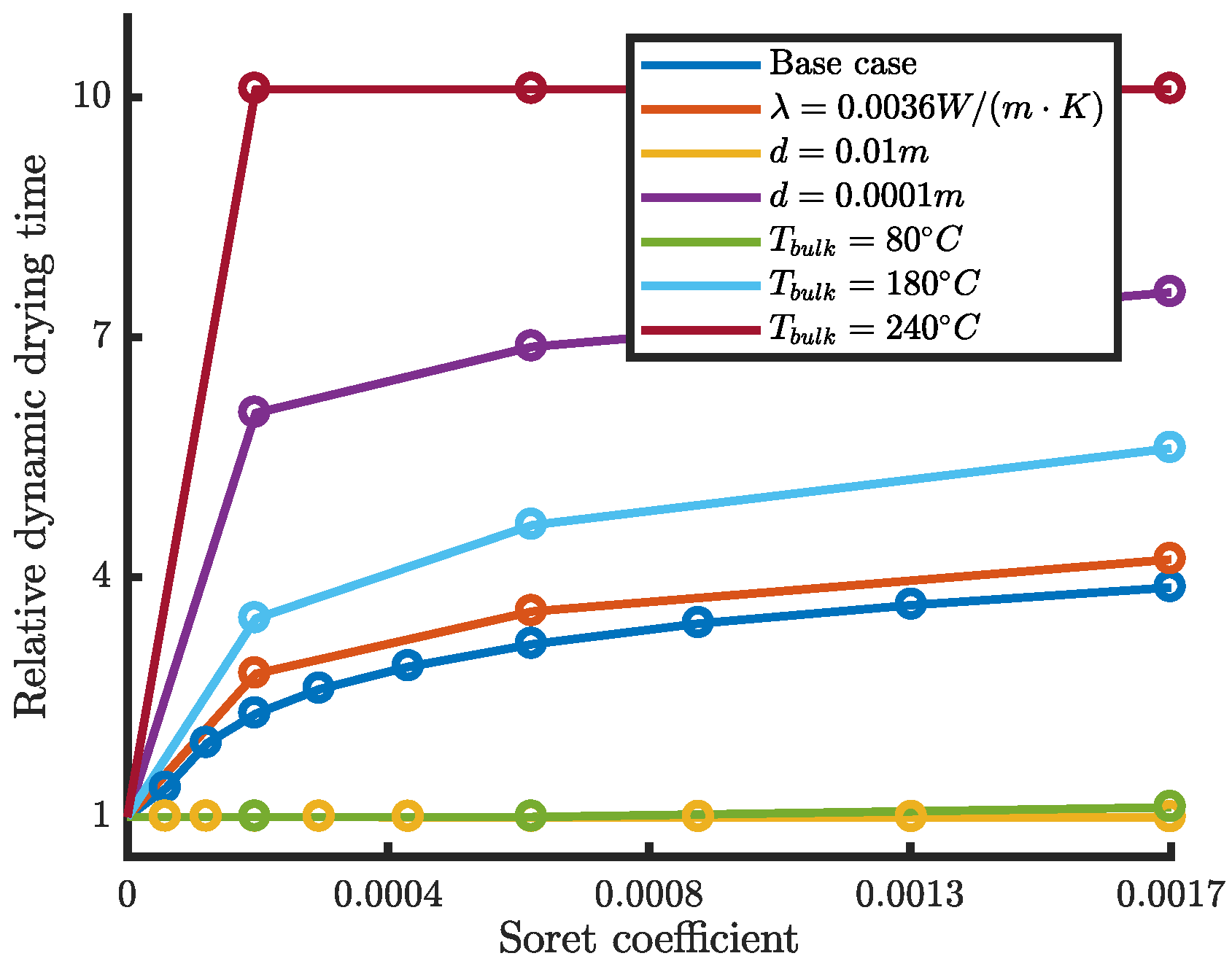
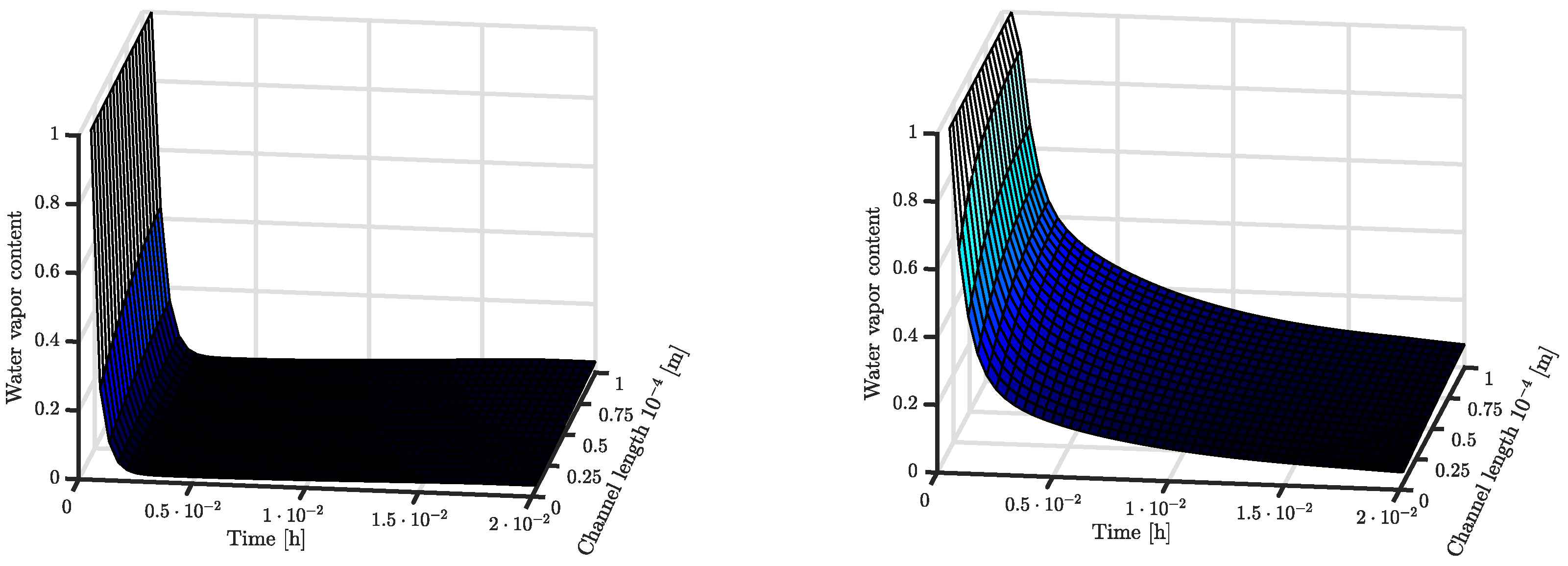
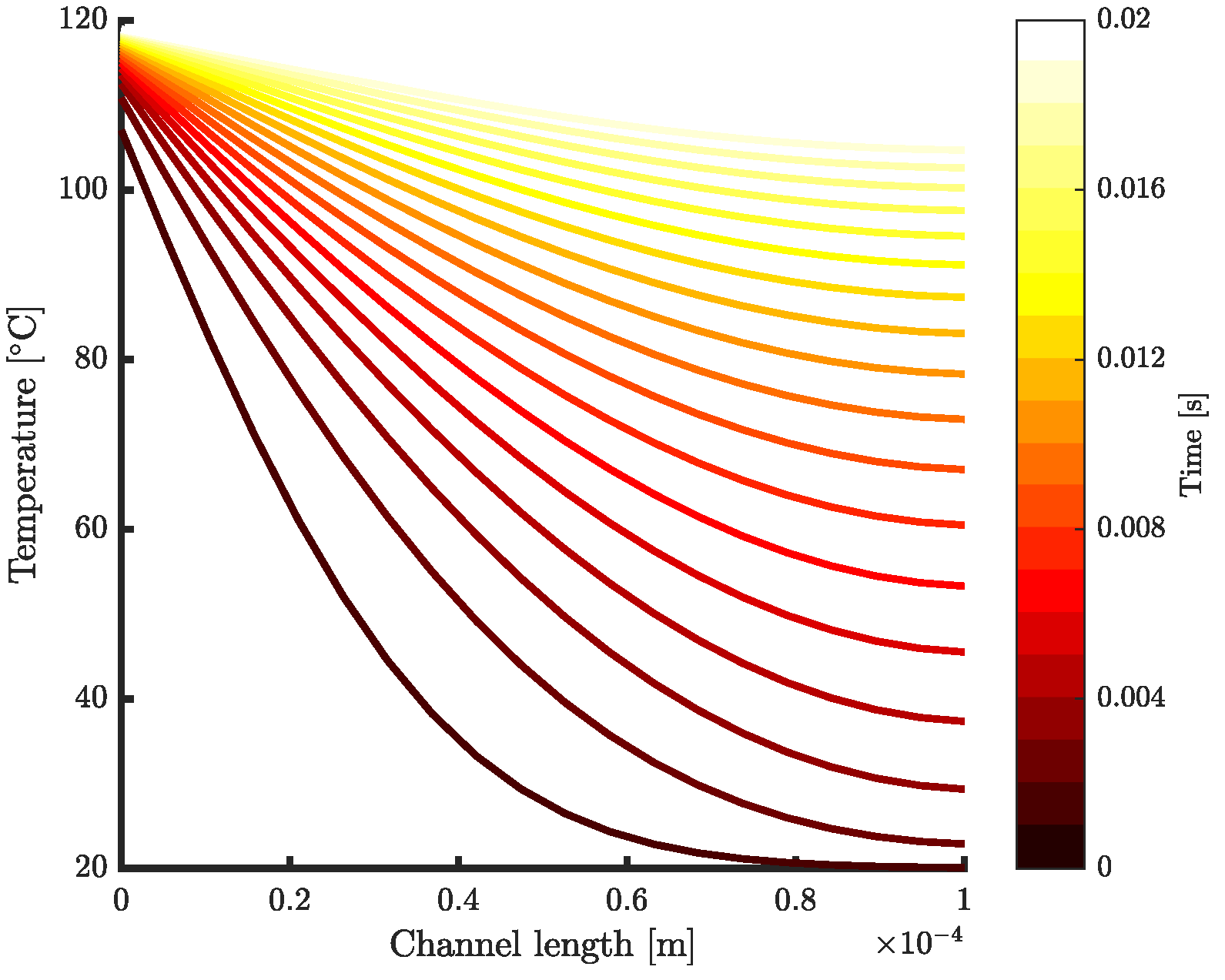
3.3. Simulation Results
4. Discussion
Author Contributions
Acknowledgments
Conflicts of Interest
Nomenclature
| Latin letters | ||
| unit tensor with mass fraction | - | |
| a | thermal diffusivity | |
| affinity of a chemical reaction | ||
| C | concentration | mol/m |
| heat capacity | J/(molK) | |
| d | particle size (radius) | m |
| D | molar diffusion constant | m/s |
| molar diffusion constant of water in air | m/s | |
| thermodiffusion coefficient | m/s | |
| mass force | - | |
| mass flux | kg/(ms) | |
| general flux | - | |
| chemical reaction rate of component j | mol/(sm) | |
| heat flux | W/m | |
| conduction energy flux | W/m | |
| mass transfer coefficient | m/s | |
| L | length | m |
| m | mass | kg |
| M | molar mass | kg/mol |
| n | amount of substance | mol |
| Nussel number | - | |
| P | pressure | Pa |
| Prantl number | - | |
| R | universal gas constant | J/(molK) |
| Reynold number | - | |
| Soret coefficient | - | |
| s | molar entropy | J/(molK) |
| t | time | s |
| T | temperature | C or K |
| u | molar internal energy | J/mol |
| v | molarvolume | m |
| mole fraction | - | |
| moisture Content of component i | kg/kg | |
| indicator gas-phase moisture content | kg/kg | |
| relative moisture content | - | |
| Greek letters | ||
| heat transfer coefficient | W/(mK) | |
| factor | - | |
| boundary layer thickness | m | |
| thermodynamic force | - | |
| entropy production | - | |
| mass fraction | kg/kg | |
| chemical potential | - | |
| kinematic viscosity | ||
| thermal conductivity | W/(mK) | |
| phenomenological constant | - | |
| latent heat | j/mol | |
| density of dry material | mol/m or kg/m | |
| density of fluid | kg/m | |
| porosity | m/m | |
| dissipation function | - | |
| shear stress | Pa | |
| kinetic energy | J | |
| Sub- and superscripts | ||
| diss | dissipative | |
| g | gas/vapour phase | |
| i | component i | |
| l | liquid phase | |
| M | mass | |
| n | amout of components | |
| Q | heat | |
| q | heat | |
| T | at constant temperature | |
| tot | total | |
| v | vapour phase | |
| VL | vapour liquid interface | |
| W | water | |
| ∞ | bulk | |
References
- Takamte, G.; Edoun, M.; Monkam, L.; Kuitche, A.; Kamga, R. Numerical Simulation of Convective Drying of Mangoes (mangifera Indica L.) Under Variable Thermal Conditions. Inter. J. Therm. Technol. 2013, 3, 48–52. [Google Scholar]
- Keey, R.B. Drying Principles and Practice, 1st ed.; Pergamon Press: Oxford, NY, USA, 1972; p. xix. 358p. [Google Scholar]
- Kowalski, S.J. Thermodynamics of Viscoelastic Materials Under Drying; Springer: Berlin/Heidelberg, Germany, 2003; pp. 80–95. [Google Scholar] [CrossRef]
- de Groot, S.R.; Mazur, P. Non–Equilibrium Thermodynamics; Dover Publications: New York, NY, USA, 1984; ISBN 9780486647418. [Google Scholar]
- Demirel, Y. Chapter 3—Fundamentals of Nonequilibrium Thermodynamics. In Nonequilibrium Thermodynamics; Elsevier: Amsterdam, The Netherlands, 2014; pp. 119–176. [Google Scholar] [CrossRef]
- Kirschner, I.; Molnár, P. Relation between Curie’s principle and Onsager’s reciprocity. Acta Phys. Hung. 1989, 66, 277–287. [Google Scholar] [CrossRef]
- Chen, X.D.; Putranto, A. Modelling Drying Processes: A Reaction Engineering Approach; Cambridge University Press: Cambridge, UK, 2010; Volume 9781107012103, pp. 1–214. [Google Scholar] [CrossRef]
- Luikov, A.V. Systems of differential equations of heat and mass transfer in capillary-porous bodies (review). Inter. J. Heat Mass Transf. 1975, 18, 1–14. [Google Scholar] [CrossRef]
- Nadi, F.; Rahimi, G.H.; Younsi, R.; Tavakoli, T.; Hamidi-Esfahani, Z. Numerical Simulation of Vacuum Drying by Luikov’s Equations. Dry. Technol. 2012, 30, 197–206. [Google Scholar] [CrossRef]
- Cussler, E.L. Diffusion Mass Transfer in a Fluid System; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar] [CrossRef]
- Kowalski, S.J. Characterization of drying processes. In Thermomechanics of Drying Processes; Springer: Berlin/Heidelberg, Germany, 2003; Volume 8, pp. 24–30. [Google Scholar] [CrossRef]
- Saghir, M.Z.; Jiang, C.G.; Chacha, M.; Yan, Y.; Khawaja, M.; Pan, S. 9—Thermodiffusion in Porous Media. In Transport Phenomena in Porous Media III; Pergamon: Oxford, UK, 2005. [Google Scholar] [CrossRef]
- Luikov, A.V. Heat and Mass Transfer in Capillary-Porous Bodies. In Advances in Heat Transfer; Elsevier Science: Amsterdam, The Netherlands, 1964; pp. 123–184. [Google Scholar]
- Avramidis, S.; Hatzikiriakos, S.G.; Siau, J.F. An irreversible thermodynamics model for unsteady-state nonisothermal moisture diffusion in wood. Wood Sci. Technol. 1994, 28, 349–358. [Google Scholar] [CrossRef]
- Kempers, L.J. A comprehensive thermodynamic theory of the soret effect in a multicomponent gas, liquid, or solid. J. Chem. Phys. 2001, 115, 6330–6341. [Google Scholar] [CrossRef]
- Chase, M.W., Jr. NIST-JANAF Themochemical Tables, Fourth Edition. J. Phys. Chem. Ref. Data Monogr. 1998, 9, 1–1951. [Google Scholar]
- Chen, X.D. Moisture diffusivity in food and biological materials. Dry. Technol. 2007, 25, 1203–1213. [Google Scholar] [CrossRef]
- Berechnungsmethoden für Stoffeigenschaften. In VDI-Wärmeatlas; Springer: Berlin/Heidelberg, Germany, 1997; pp. 129–510. [CrossRef]
- Easteal, A.J.; Price, W.E.; Woolf, L.A. Diaphragm cell for high-temperature diffusion measurements. Tracer diffusion coefficients for water to 363 K. J. Chem. Soc. Faraday Trans. Phys. Chem. Condens. Phases 1989, 85, 1091–1097. [Google Scholar] [CrossRef]
- Handscomb, C.S.; Kraft, M.; Bayly, A.E. A new model for the drying of droplets containing suspended solids. Chem. Eng. Sci. 2009, 64, 628–637. [Google Scholar] [CrossRef]
- Schmidt-Hansberg, B.; Klein, M.F.; Peters, K.; Buss, F.; Pfeifer, J.; Walheim, S.; Colsmann, A.; Lemmer, U.; Scharfer, P.; Schabel, W. In situ monitoring the drying kinetics of knife coated polymer-fullerene films for organic solar cells. J. Appl. Phys. 2009, 106. [Google Scholar] [CrossRef]
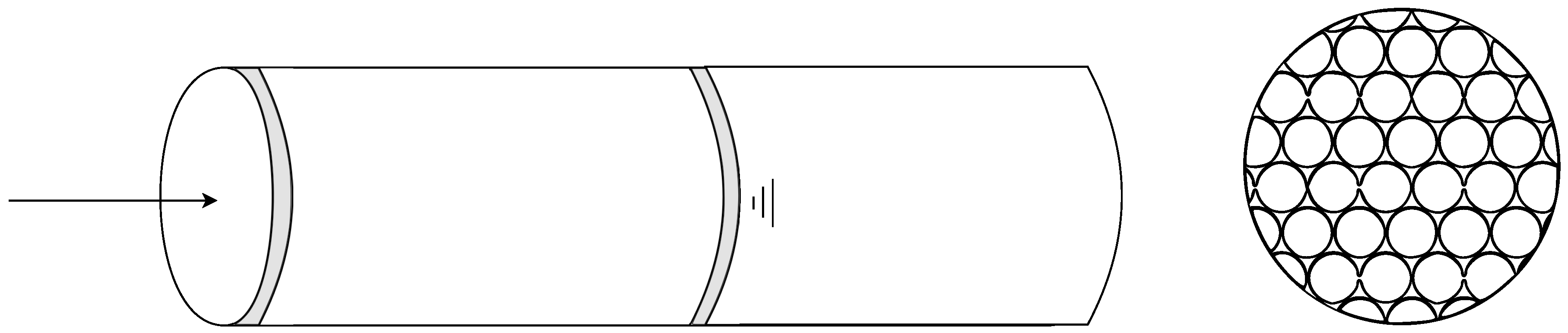
| Drying region: | 2nd and 3rd region proposed by Keey [2], where moisture transport changes from liquid to vapour phase diffusion |
| Macro model: | A sphere made of horizontally arranged parallel tubular channels packed in a primitive cubic system |
| Channel model: | Hollow tubular channels with impermeable walls, the channel is radially and tangentially symmetric |
| Drying process: | Evaporation of water at a receding gas–liquid interface at the button of the channel, gas-phase diffusion from the gas–liquid interface to the channel opening and convection to the bulk |
| Constants | Description | Units | Value |
|---|---|---|---|
| Bulk moisture content | - | 0 | |
| Bulk temperature | K | 393 | |
| P | System Pressure | Pa | 1 × 105 |
| Heat capacity of water | 73 [18] | ||
| Vaporization Enthalpy of water | 2400 [18] | ||
| Density of air | 1 [18] | ||
| Density of liquid water | 1000 [18] | ||
| D | Moisture diffusion coefficient | 2.5 × 10−5 [2] | |
| Liquid water Diffusion coefficient | 1 × 10−9 [19] | ||
| R | Universal gas constant | 8.314 | |
| Molar mass water | 18 × 10−3 | ||
| Molar mass air | 0.028 | ||
| Heat conductivity | 0.0012 [18] |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Häussling Löwgren, B.; Bergmann, J.; Alves-Filho, O. A Numerical Implementation of the Soret Effect in Drying Processes. ChemEngineering 2020, 4, 13. https://doi.org/10.3390/chemengineering4010013
Häussling Löwgren B, Bergmann J, Alves-Filho O. A Numerical Implementation of the Soret Effect in Drying Processes. ChemEngineering. 2020; 4(1):13. https://doi.org/10.3390/chemengineering4010013
Chicago/Turabian StyleHäussling Löwgren, Bartolomeus, Julius Bergmann, and Odilio Alves-Filho. 2020. "A Numerical Implementation of the Soret Effect in Drying Processes" ChemEngineering 4, no. 1: 13. https://doi.org/10.3390/chemengineering4010013
APA StyleHäussling Löwgren, B., Bergmann, J., & Alves-Filho, O. (2020). A Numerical Implementation of the Soret Effect in Drying Processes. ChemEngineering, 4(1), 13. https://doi.org/10.3390/chemengineering4010013




