Predictive Modeling of Corrosion in Al/Mg Dissimilar Joint
Abstract
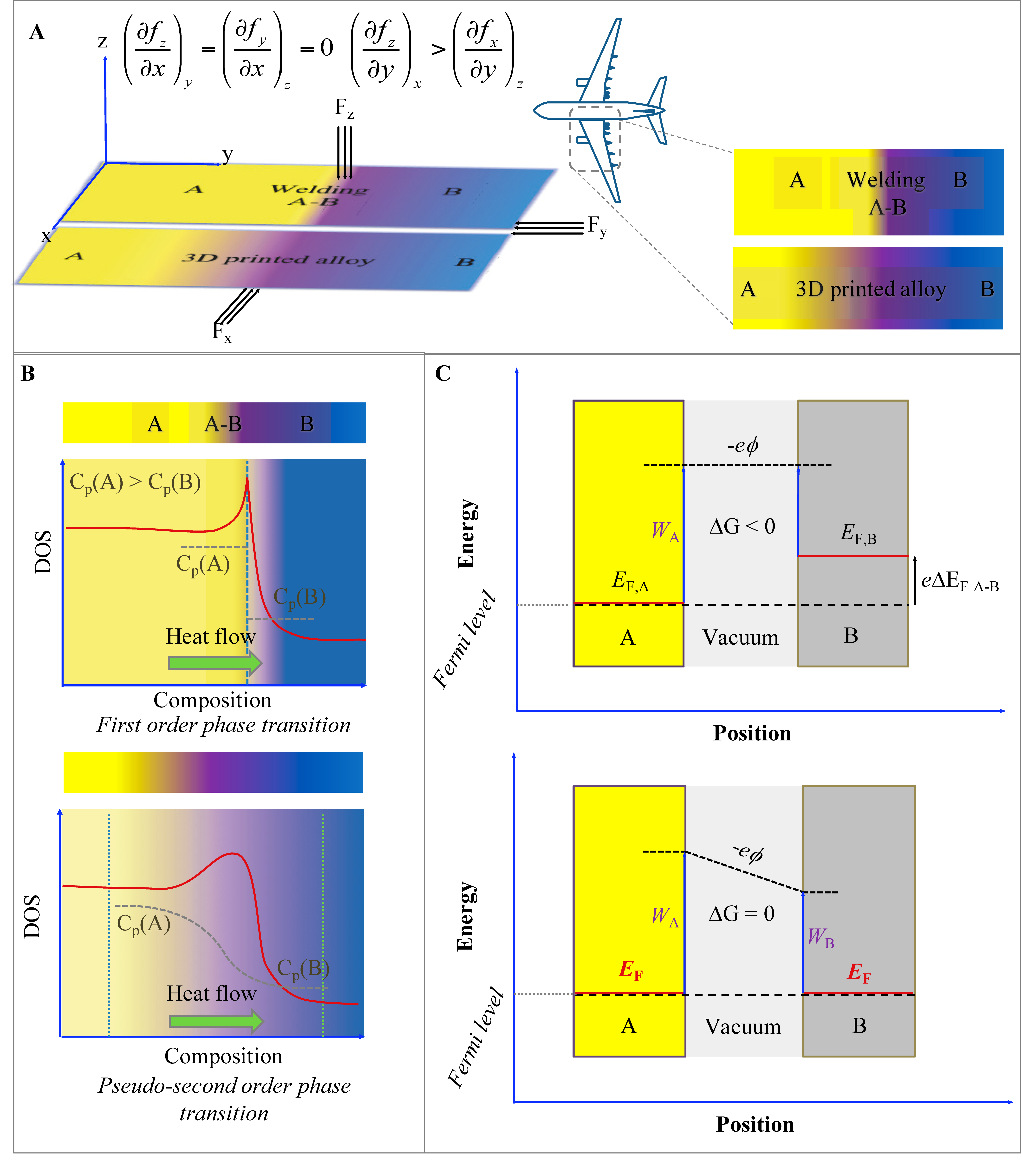
1. Introduction
2. Computational Details
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wang, S.; Ma, Q.; Li, Y. Characterization of microstructure, mechanical properties and corrosion resistance of dissimilar welded joint between 2205 duplex stainless steel and 16MnR. Mater. Des. 2011, 32, 831–837. [Google Scholar] [CrossRef]
- Bosch, R.W.; Bogaerts, W.F. A theoretical study of AC-induced corrosion considering diffusion phenomena. Corros. Sci. 1998, 40, 323–336. [Google Scholar] [CrossRef]
- Melchers, R.E. Mathematical modelling of the diffusion controlled phase in marine immersion corrosion of mild steel. Corros. Sci. 2003, 45, 923–940. [Google Scholar] [CrossRef]
- Gu, B.; Luo, J.; Mao, X. Hydrogen-facilitated anodic dissolution-type stress corrosion cracking of pipeline steels in near-neutral pH solution. Corros. Eng. 1999, 55, 96–106. [Google Scholar] [CrossRef]
- Celis, J.P.; Ponthiaux, P.; Wenger, F. Tribo-corrosion of materials: Interplay between chemical, electrochemical, and mechanical reactivity of surfaces. Wear 2006, 261, 939–946. [Google Scholar] [CrossRef]
- Könönen, M.H.O.; Lavonius, E.T.; Kivilahti, J.K. SEM observations on stress corrosion cracking of commercially pure titanium in a topical fluoride solution. Dent. Mater. 1995, 11, 269–272. [Google Scholar] [CrossRef]
- Ramezanianpour, A.A.; Zolfagharnasab, A.; Zadeh, F.B.; Estahbanati, S.H.; Boushehri, R.; Pourebrahimi, M.R.; Ramezanianpour, A.M. Effect of supplementary cementing materials on concrete resistance against sulfuric acid attack. In High Tech Concrete: Where Technology and Engineering Meet—Proceedings of the 2017 Fib Symposium; Springer International Publishing: Basel, Switzerland, 2017; pp. 2290–2298. [Google Scholar]
- Boushehri, R.; Hasanpour Estahbanati, S.; Ghasemi-Fare, O. Controlling Frost Heaving in Ballast Railway Tracks Using Low Enthalpy Geothermal Energy. In Proceedings of the Transportation Research Board 98th Annual Meeting, Washington, DC, USA, 13–17 January 2019. [Google Scholar]
- Winzer, N.; Atrens, A.; Song, G.; Ghali, E.; Dietzel, W.; Kainer, K.U.; Hort, N.; Blawert, C. A critical review of the Stress Corrosion Cracking (SCC) of magnesium alloys. Adv. Eng. Mater. 2005, 7, 659–693. [Google Scholar] [CrossRef]
- Dubi, Y.; Di Ventra, M. Colloquium: Heat flow and thermoelectricity in atomic and molecular junctions. Rev. Mod. Phys. 2011, 83, 131–155. [Google Scholar] [CrossRef]
- Azad, E.; Peik, B.; Abbasi, B.; Abbasi, B. A numerical simulation of thermo-mechanical behavior of a single fracture in porous rock. In Proceedings of the 52nd U.S. Rock Mechanics/Geomechanics Symposium, Seattle, WA, USA, 17–20 June 2018. [Google Scholar]
- Binder, K. Theory of first-order phase transitions. Rep. Prog. Phys. 1987, 50, 783–859. [Google Scholar] [CrossRef]
- Zhang, C.; Ma, J. Simulation via direct computation of partition functions. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2007, 76, 036708. [Google Scholar] [CrossRef]
- Irikura, K.K. Anharmonic partition functions for polyatomic thermochemistry. J. Chem. Thermodyn. 2014, 73, 183–189. [Google Scholar] [CrossRef]
- Abed, W.M.; Domingues, A.F.; Poole, R.J.; Dennis, D.J.C. Heat transfer enhancement in a cross-slot micro-geometry. Int. J. Therm. Sci. 2017, 121, 249–265. [Google Scholar] [CrossRef]
- Lutich, A.A.; Gaponenko, S.V.; Gaponenko, N.V.; Molchan, I.S.; Sokol, V.A.; Parkhutik, V. Anisotropic light scattering in nanoporous materials: A photon density of states effect. Nano Lett. 2004, 4, 1755–1758. [Google Scholar] [CrossRef]
- Tata, B.V.R.; Joshi, R.G.; Gupta, D.K.; Brijitta, J.; Raj, B. Crystalline arrays of submicron-sized particles through colloidal route. Curr. Sci. 2012, 103, 1175–1184. [Google Scholar]
- Hellawell, A.; Lu, S.Z. The mechanism of silicon modification in aluminum-silicon alloys: Impurity induced twinning. Metall. Mater. Trans. A 1987, 18, 1721–1733. [Google Scholar]
- Brown, R.; Sprowls, D.; Shumaker, M. The Resistance of Wrought High Strength Aluminum Alloys to Stress Corrosion Cracking. Stress Corrosion Cracking of Metals—A State of the Art. ASTM Int. 2009. [Google Scholar] [CrossRef]
- Sanders, R.E. Technology innovation in aluminum products. JOM 2001, 53, 21–25. [Google Scholar] [CrossRef]
- Tsangaraki-Kaplanoglou, I.; Theohari, S.; Dimogerontakis, T.; Wang, Y.M.; Kuo, H.H.; Kia, S. Effect of alloy types on the anodizing process of aluminum. Surf. Coat. Technol. 2006, 200, 2634–2641. [Google Scholar] [CrossRef]
- Liang, J.S.Y.; Su, J.C. Residual stress modeling in orthogonal machining. CIRP Ann. Manuf. Technol. 2007, 56, 65–68. [Google Scholar] [CrossRef]
- Sane, S.P.; Dickinson, M.H. The control of flight force by a flapping wing: Lift and drag production. J. Exp. Biol. 2001, 204, 2607–2626. [Google Scholar]
- Kerschen, G.; Golinval, J.C.; Vakakis, A.F.; Bergman, L.A. The method of proper orthogonal decomposition for dynamical characterization and order reduction of mechanical systems: An overview. Nonlinear Dyn. 2005, 41, 147–169. [Google Scholar] [CrossRef]
- Foolad, F.; Blankenau, P.; Kilic, A.; Allen, R.G.; Huntington, J.L.; Erickson, T.A.; Ozturk, D.; Morton, C.G.; Ortega, S.; Ratcliffe, I.; et al. Comparison of the Automatically Calibrated Google Evapotranspiration Application—EEFlux and the Manually Calibrated METRIC Application. Preprints 2018. [Google Scholar] [CrossRef]
- Foolad, F.; Franz, T.E.; Wang, T.; Gibson, J.; Kilic, A.; Allen, R.G.; Suyker, A. Feasibility analysis of using inverse modeling for estimating field-scale evapotranspiration in maize and soybean fields from soil water content monitoring networks. Hydrol. Earth Syst. Sci. 2017, 21, 1263–1277. [Google Scholar] [CrossRef]
- Soleymani, F.; Rezaei, S.M.; Sharifi, S.; Zareinejad, M. Position control of a servo-pneumatic actuator using generalized Maxwell-Slip friction model. In Proceedings of the 4th RSI International Conference on Robotics and Mechatronics(ICORM 2016), Tehran, Iran, 26–28 October 2016; pp. 246–251. [Google Scholar]
- Hasson, D.F.; Crowe, C.R. Materials for Marine Systems and Structures Treatise on Materials Science and Technology; Academic Press: Cambridge, MA, USA, 2013; p. 28. [Google Scholar]
- Kirubakaran, A.; Jain, S.; Nema, R.K. A review on fuel cell technologies and power electronic interface. Renew. Sustain. Energy Rev. 2009, 13, 2430–2440. [Google Scholar] [CrossRef]
- Mohammadrezaei, V.; Ebrahimi, M.; Beyramabadi, S.A. Study of the effect of molecular cluster size alanine concentrations in water by using the activity coefficient method and density functional theory. Bulg. Chem. Commun. 2017, 49, 147–151. [Google Scholar]
- Mohammadrezaei, V.; Ebrahimi, M.; Beyramabadi, S.A. Calculation of concentration of alanine in water using the activity coefficient model and ab initio model. Bulg. Chem. Commun. 2017, 49, 106–108. [Google Scholar]
- Canneaux, S.; Bohr, F.; Henon, E. KiSThelP: A program to predict thermodynamic properties and rate constants from quantum chemistry results. J. Comput. Chem. 2014, 35, 82–93. [Google Scholar] [CrossRef]
- Chakraborty, P.; Ma, T.; Zahiri, A.H.; Cao, L.; Wang, Y. Carbon-Based Materials for Thermoelectrics. Adv. Condens. Matter Phys. 2018, 2018, 3898479. [Google Scholar] [CrossRef]
- Mohammadi Nasab, A.; Wang, D.; Chen, Z.; Shan, W. Buckling shape transition of an embedded thin elastic rod after failure of surrounding elastic medium. Extrem. Mech. Lett. 2017, 15, 51–56. [Google Scholar] [CrossRef]
- Sharifi, S.; Rezaei, S.M.; Tivay, A.; Soleymani, F.; Zareinejad, M. Multi-class fault detection in electro-hydraulic servo systems using support vector machines. In Proceedings of the 4th RSI International Conference on Robotics and Mechatronics(ICROM 2016), Tehran, Iran, 26–28 October 2016; pp. 252–257. [Google Scholar]
- Bisquert, J.; Fabregat-Santiago, F.; Mora-Seró, I.; Garcia-Belmonte, G.; Barea, E.M.; Palomares, E. A review of recent results on electrochemical determination of the density of electronic states of nanostructured metal-oxide semiconductors and organic hole conductors. Inorg. Chim. Acta 2008, 361, 684–698. [Google Scholar] [CrossRef]
- Reiss, H. The Fermi level and the redox potential. J. Phys. Chem. 1985, 89, 3783–3791. [Google Scholar] [CrossRef]
- Bergveld, P.; Hendrikse, J.; Olthuis, W. Theory and application of the material work function for chemical on the field principle. Meas. Sci. Technol. 1998, 9, 1801–1808. [Google Scholar] [CrossRef]
- Jin, Y.; Liu, M.; Zhang, C.; Leygraf, C.; Wen, L.; Pan, J. First-Principle Calculation of Volta Potential of Intermetallic Particles in Aluminum Alloys and Practical Implications. J. Electrochem. Soc. 2017, 164, C465–C473. [Google Scholar] [CrossRef]
- Rohwerder, M.; Turcu, F. High-resolution Kelvin probe microscopy in corrosion science: Scanning Kelvin probe force microscopy (SKPFM) versus classical scanning Kelvin probe (SKP). Electrochim. Acta 2007, 53, 290–299. [Google Scholar] [CrossRef]
- Elahifard, M.R.; Behjatmanesh-Ardakani, R.; Ahmadvand, S.; Abbasi, B.; Abbasi, B. A mechanistic study of photo-oxidation of phenol and AB92 by AgBr/TiO2. Res. Chem. Intermed. 2019, 1–12. [Google Scholar] [CrossRef]
- Elahifard, M.R.; Ahmadvand, S.; Mirzanejad, A. Effects of Ni-doping on the photo-catalytic activity of TiO2 anatase and rutile: Simulation and experiment. Mater. Sci. Semicond. Process. 2018, 84, 10–16. [Google Scholar] [CrossRef]
- Emami-Meibodi, M.; Elahifard, M.R. Modeling investigation on the thermal conductivity of saturated vapor. Fluid Phase Equilibria 2018, 474, 14–19. [Google Scholar] [CrossRef]
- Farsad, M.; Elahifard, M.R.; Behjatmanesh-Ardakani, R. Full-potential DFT study of CO dissociation on Fe–Cu cluster. Theor. Chem. Acc. 2018, 137, 142. [Google Scholar] [CrossRef]
- Heydari, H.; Elahifard, M.R.; Behjatmanesh-Ardakani, R. Role of oxygen vacancy in the adsorption and dissociation of the water molecule on the surfaces of pure and Ni-doped rutile (110): A periodic full-potential DFT study. Surf. Sci. 2019, 679, 218–224. [Google Scholar] [CrossRef]
- Ren, X.; Tkatchenko, A.; Rinke, P.; Scheffler, M. Beyond the Random-Phase Approximation for the Electron Correlation Energy: The Importance of Single Excitations. Phys. Rev. Lett. 2011, 106, 153003. [Google Scholar] [CrossRef]
- Perdew, J.; Burke, K.; Wang, Y. Generalized gradient approximation for the exchange-correlation hole of a many-electron system. Phys. Rev. B 1996, 54, 16533–16539. [Google Scholar] [CrossRef]
- Perdew, J.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metalamorphous-semiconductor transition in germanium. Phys. Rev. B 1994, 49, 14251–14269. [Google Scholar] [CrossRef]
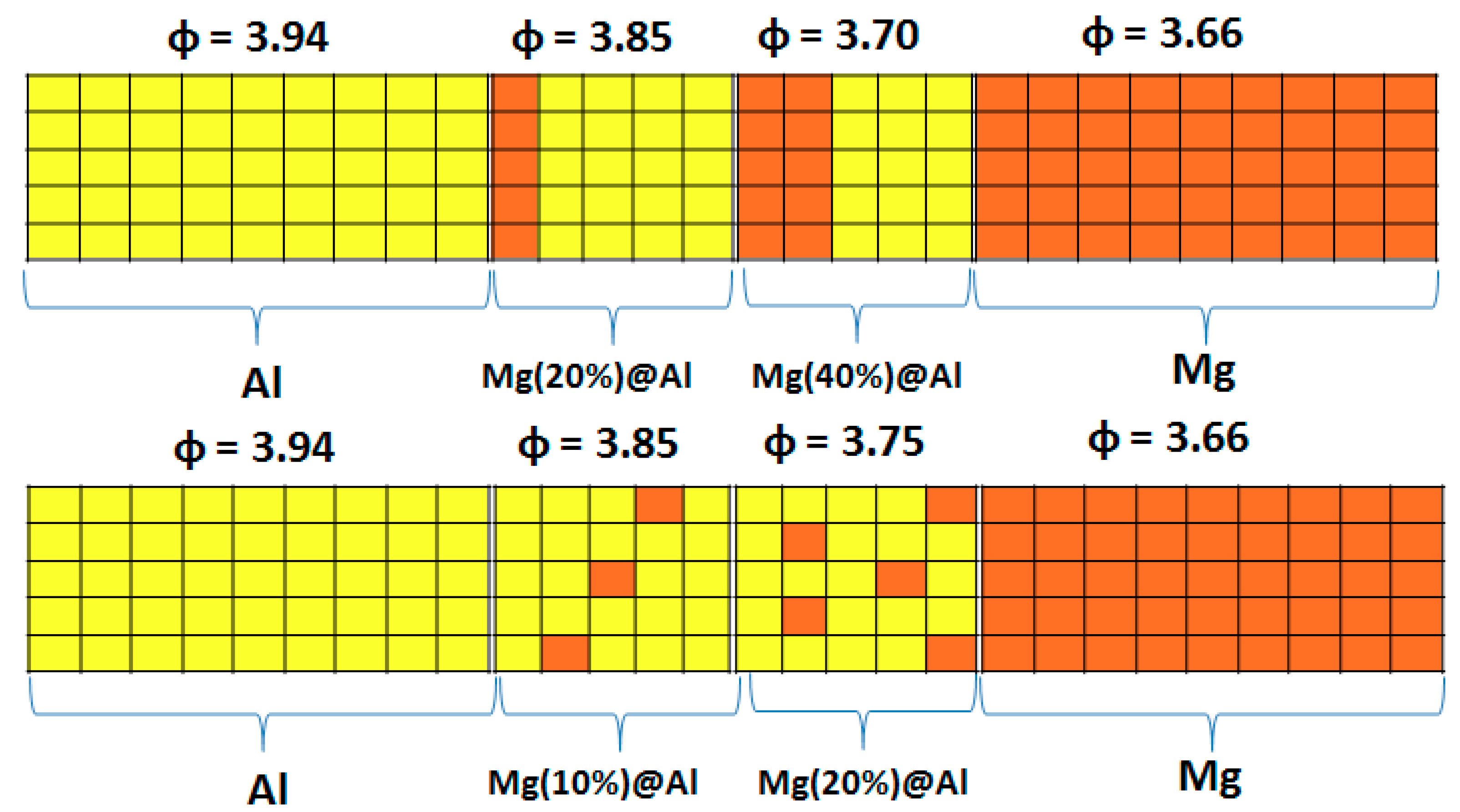
| Work Function | Mg | Al |
|---|---|---|
| Work function (surface) | 3.69 | 3.94 |
| Work function (nanolayer) | 3.66 | 3.94 |
| Work function (experiment) | 3.68 | 4.08 |
| Vertical Cuts |  |  |  |  |
|---|---|---|---|---|
| Structure |  |  | 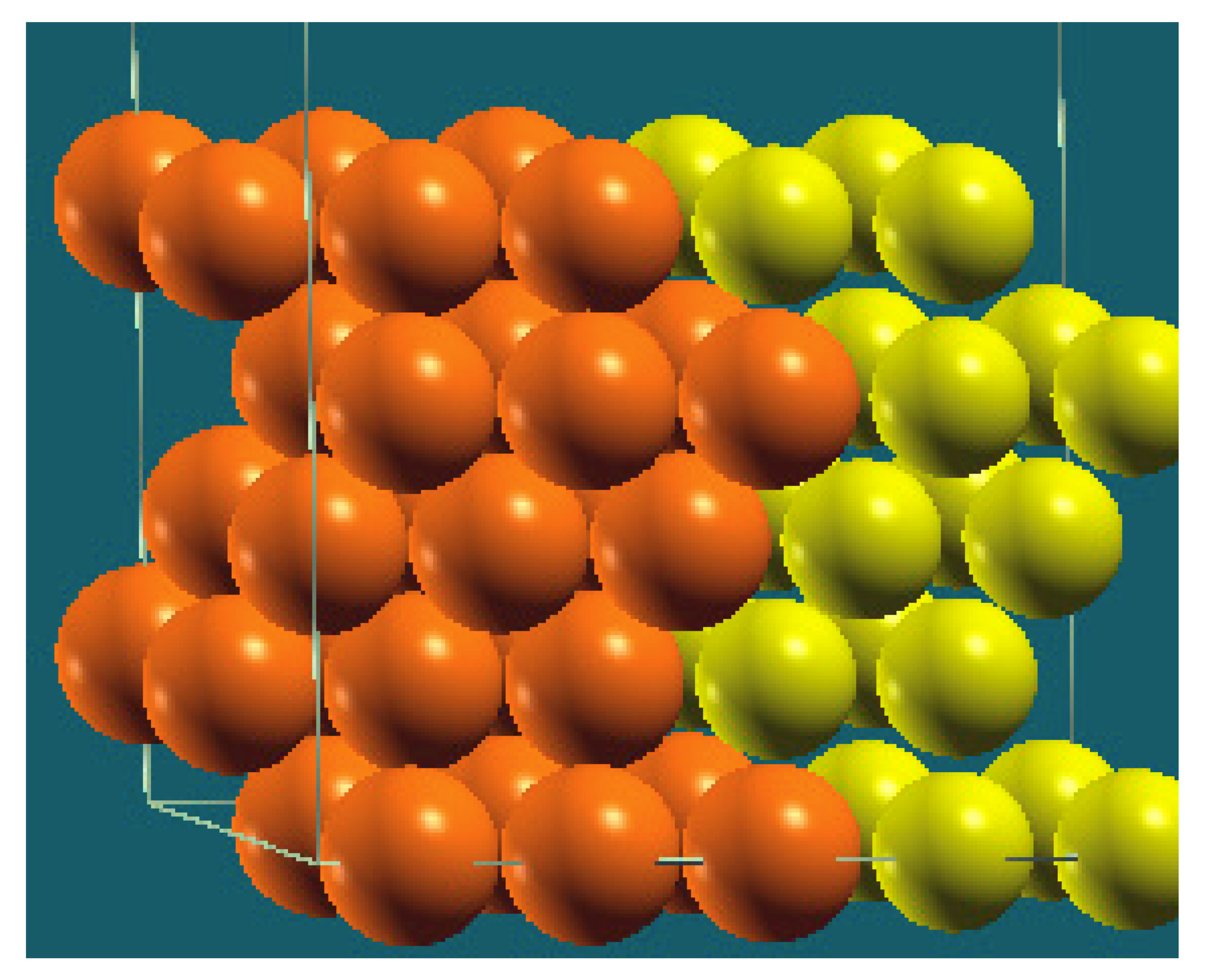 | 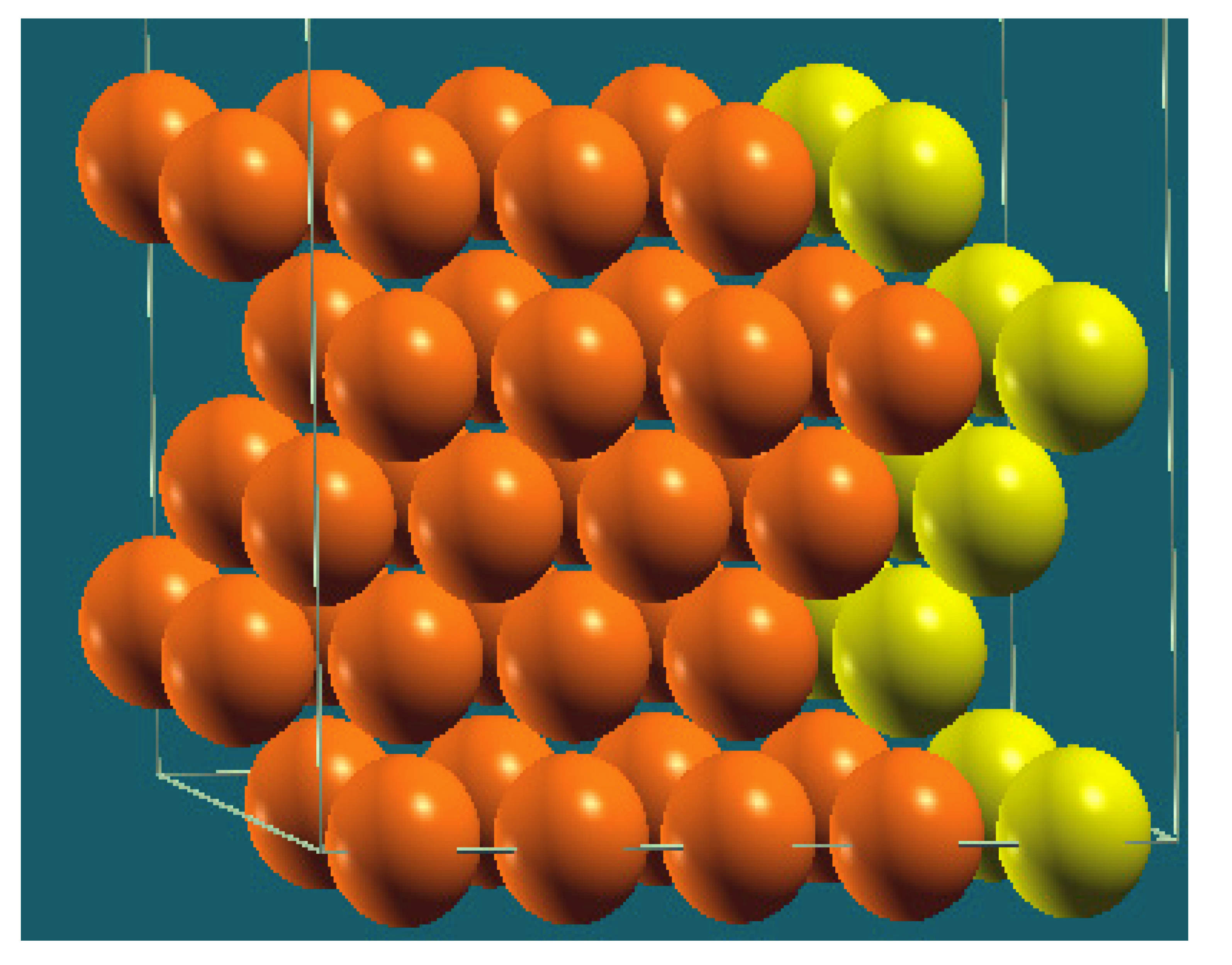 |
| Percentage of Mg atoms (red balls) | 20 | 40 | 60 | 80 |
| Work function of the top layer (surface) | 3.85 | 3.70 | 3.68 | 3.62 |
| Work function of the bottom layer (surface, eV) | 3.84 | 3.72 | 3.71 | 3.65 |
| Energy (eV) | −319,262.69 | −307,680.11 | −296,098.15 | −284,516.63 |
| Work function of the top layer (nanolayer, eV) | 3.83 | 3.69 | 3.68 | 3.60 |
| Work function of the bottom layer (nanolayer, eV) | 3.83 | 3.69 | 3.68 | 3.60 |
| Energy (eV) | −325,054.31 | −319,263.12 | −313,472.16 | −307,681.56 |
| Horizontal Cuts | 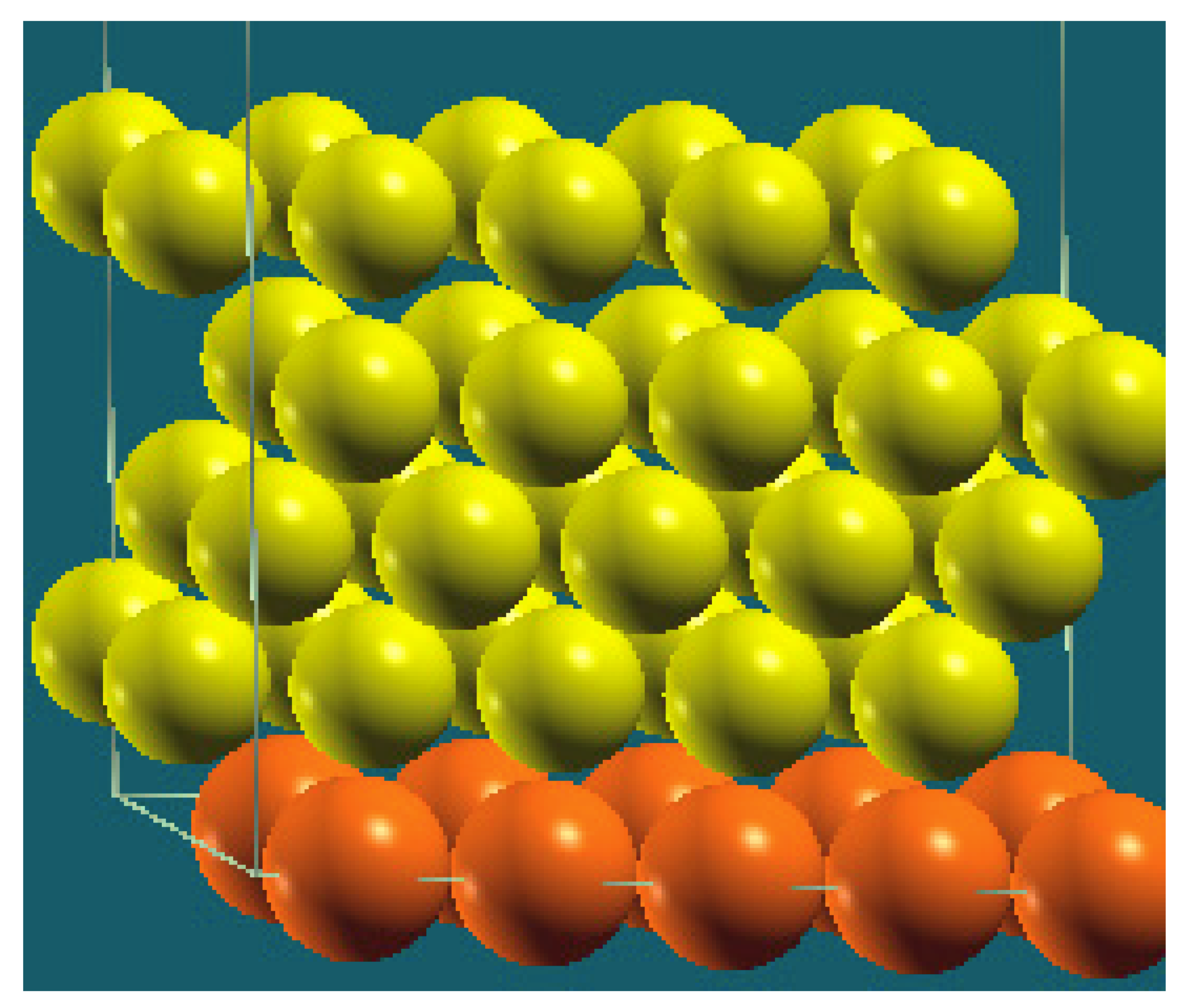 | 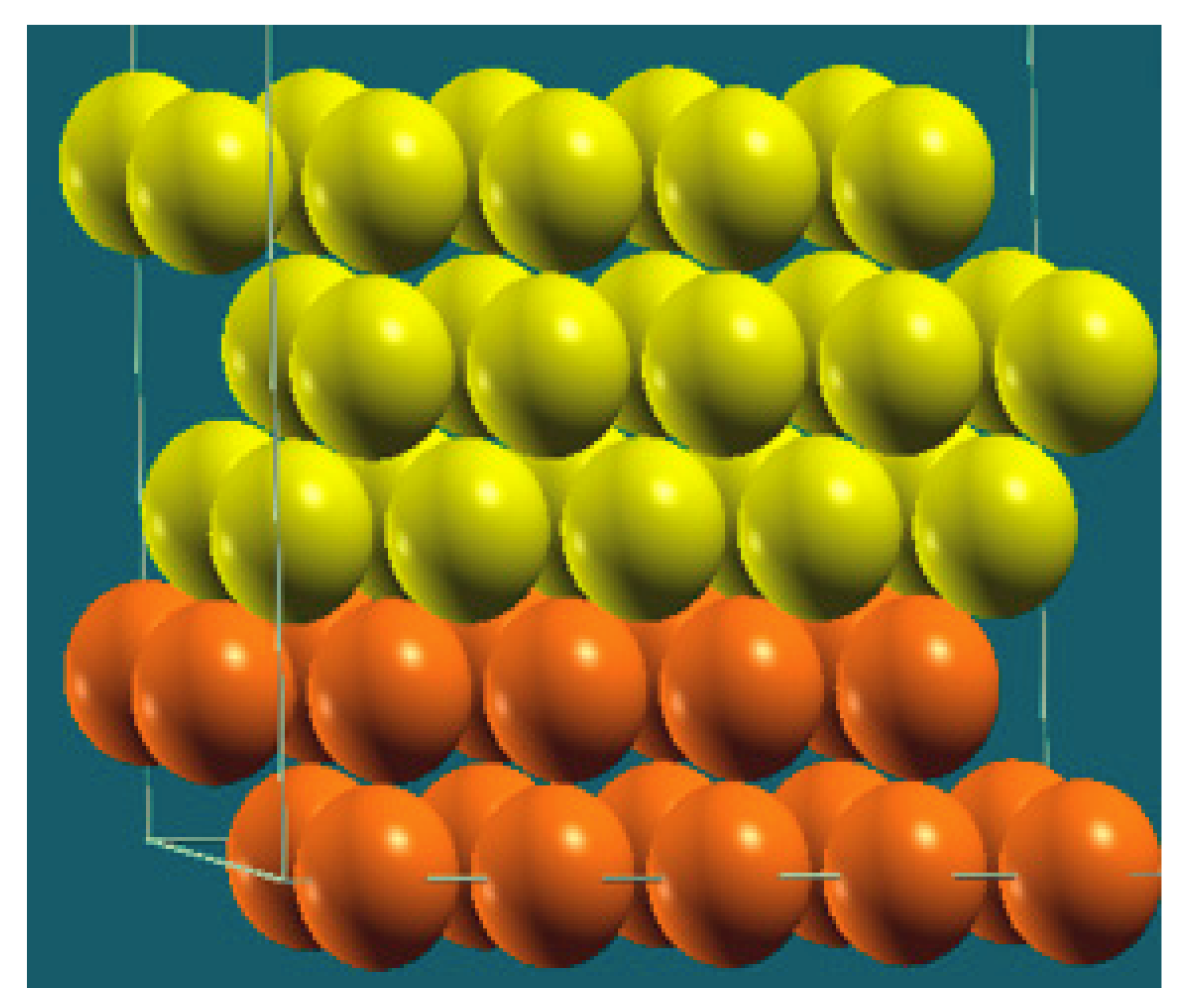 | 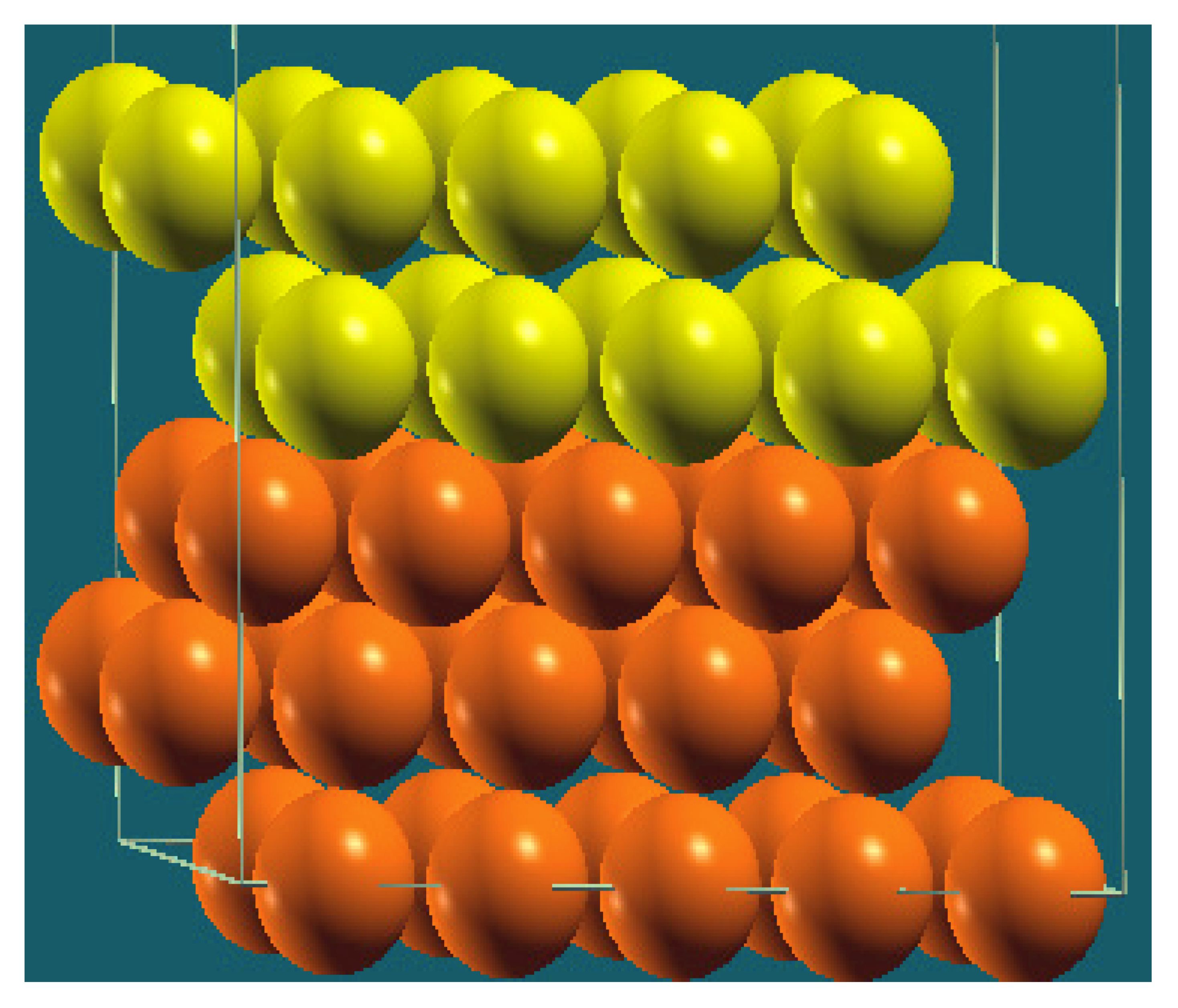 | 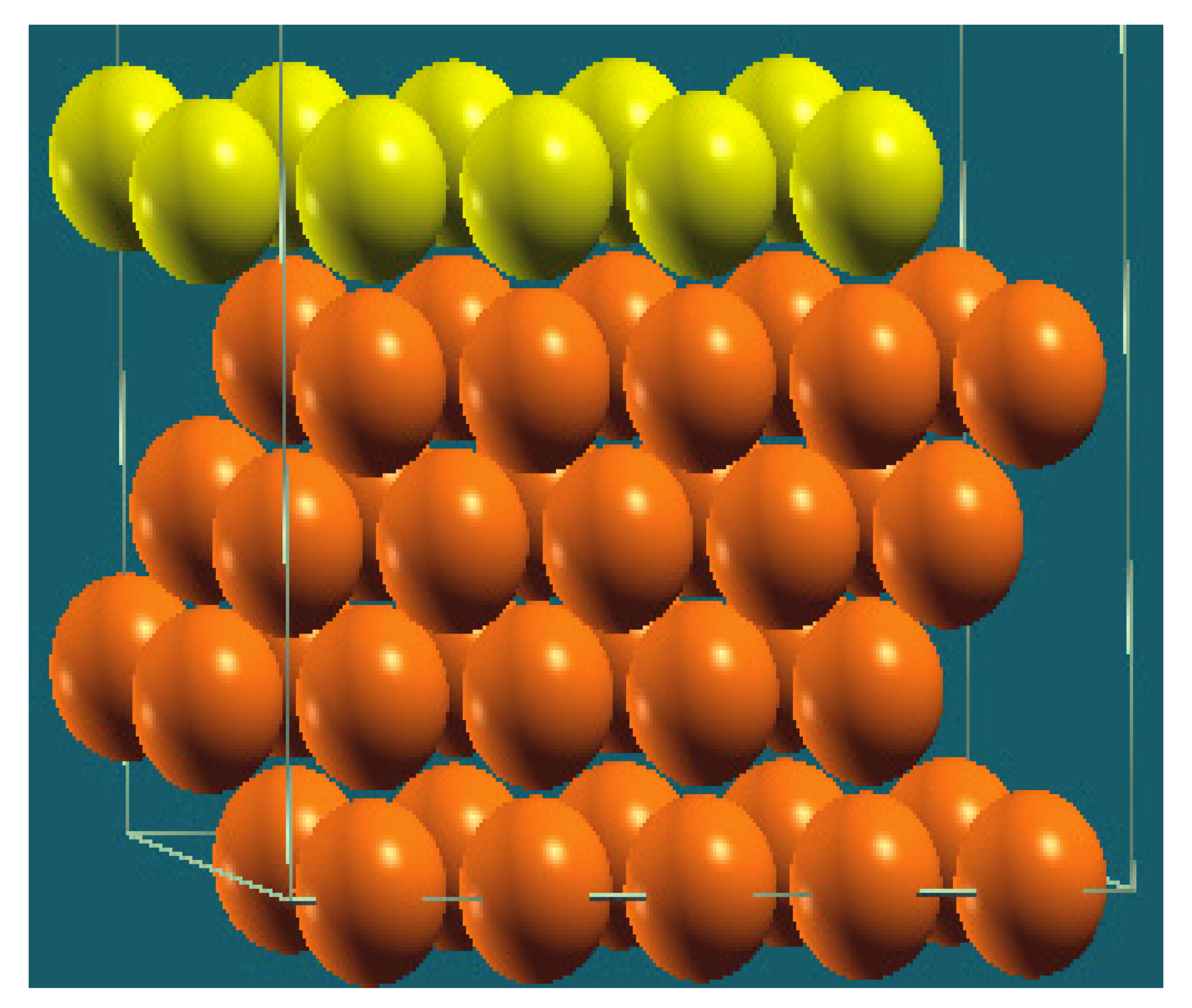 |
|---|---|---|---|---|
| Percentage | 20 | 40 | 60 | 80 |
| Work function of the top layer (surface) | 3.69 | 3.50 | 3.65 | 3.68 |
| Work function of the bottom layer (surface, eV) | 3.99 | 3.97 | 4.09 | 4.07 |
| Energy (eV) | −319,262.63 | −307,679.54 | −296,096.01 | −284,513.94 |
| Work function of the top layer (nanolayer, eV) | 3.69 | 3.47 | 3.57 | 3.61 |
| Work function of the bottom layer (nanolayer, eV) | 3.99 | 3.95 | 4.06 | 4.02 |
| Energy (eV) | −319,262.63 | 307,679.66 | 296,097.09 | 284,514.93 |
| Homogenous | 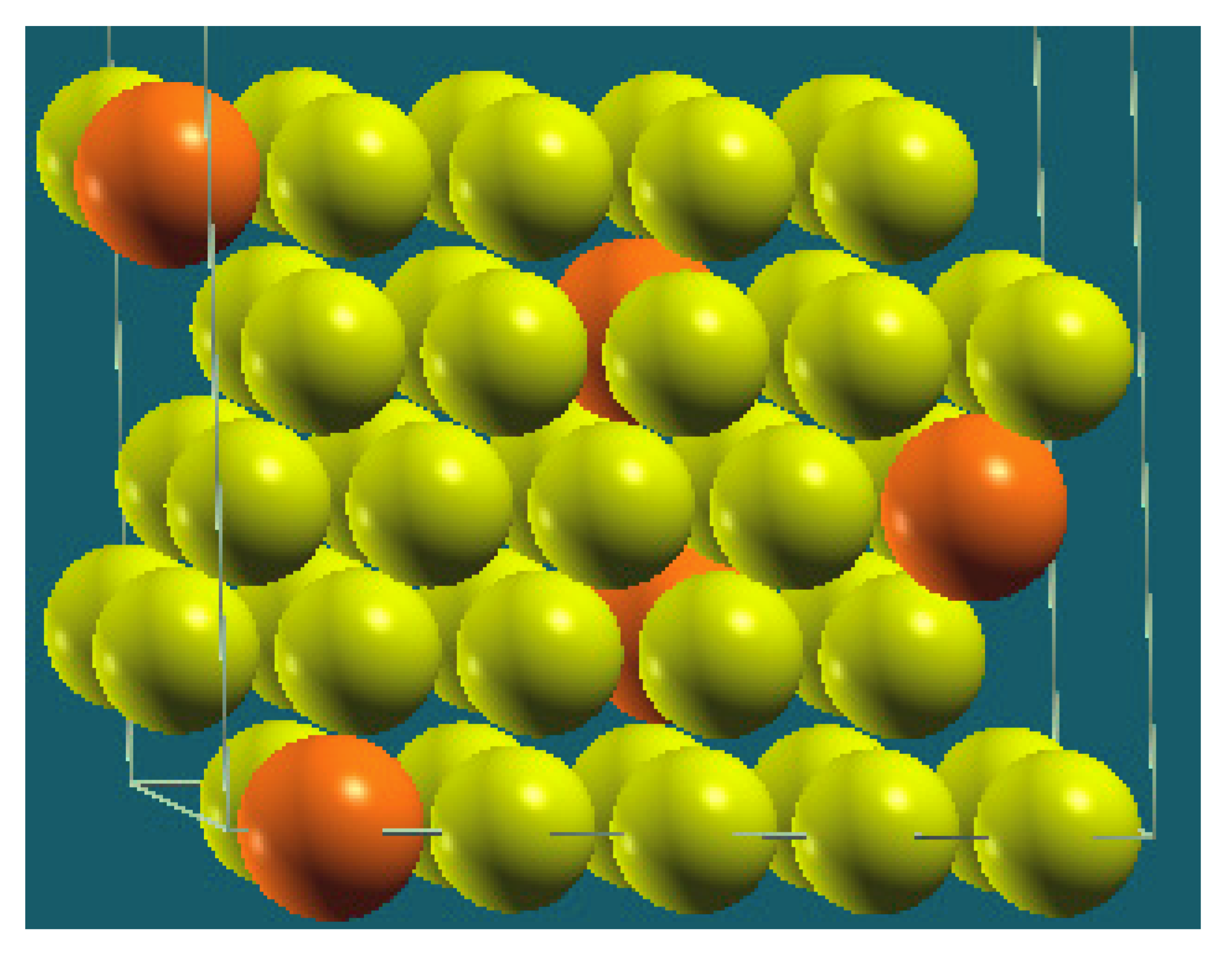 |  |  | 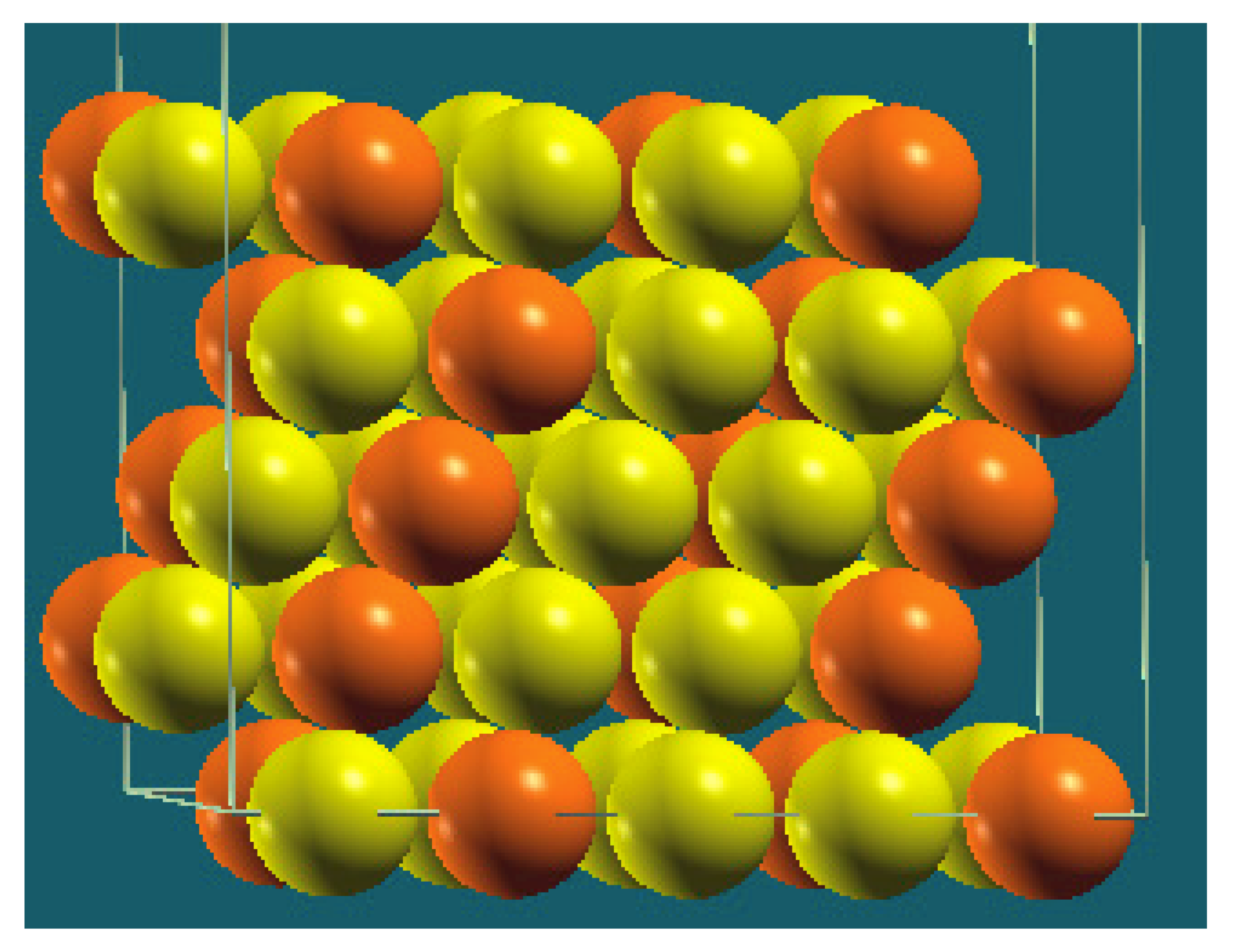 |
|---|---|---|---|---|
| Percentage | 10 | 20 | 30 | 40 |
| Work function of the top layer (surface) | 3.85 | 3.75 | 3.65 | 3.66 |
| Work function of the bottom layer (surface, eV) | 3.85 | 3.75 | 3.65 | 3.67 |
| Energy (eV) | −325,054.22 | −319,262.96 | −313,471.94 | −307,681.31 |
| Work function of the top layer (nanolayer, eV) | 3.84 | 3.75 | 3.65 | 3.68 |
| Work function of the bottom layer (nanolayer, eV) | 3.85 | 3.75 | 3.65 | 3.68 |
| Energy (eV) | −325,054.31 | −319,263.12 | −313,472.16 | −307,681.56 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmadvand, S.; Elahifard, M.; Peik, B.; Behjatmanesh-Ardakani, R.; Abbasi, B.; Abbasi, B. Predictive Modeling of Corrosion in Al/Mg Dissimilar Joint. ChemEngineering 2019, 3, 70. https://doi.org/10.3390/chemengineering3030070
Ahmadvand S, Elahifard M, Peik B, Behjatmanesh-Ardakani R, Abbasi B, Abbasi B. Predictive Modeling of Corrosion in Al/Mg Dissimilar Joint. ChemEngineering. 2019; 3(3):70. https://doi.org/10.3390/chemengineering3030070
Chicago/Turabian StyleAhmadvand, Seyedsaied, Mohammadreza Elahifard, Bijan Peik, Reza Behjatmanesh-Ardakani, Behrooz Abbasi, and Bahman Abbasi. 2019. "Predictive Modeling of Corrosion in Al/Mg Dissimilar Joint" ChemEngineering 3, no. 3: 70. https://doi.org/10.3390/chemengineering3030070
APA StyleAhmadvand, S., Elahifard, M., Peik, B., Behjatmanesh-Ardakani, R., Abbasi, B., & Abbasi, B. (2019). Predictive Modeling of Corrosion in Al/Mg Dissimilar Joint. ChemEngineering, 3(3), 70. https://doi.org/10.3390/chemengineering3030070





