Effect of Water Saturation on H2 and CO Solubility in Hydrocarbons
Abstract
:1. Introduction
2. Background
2.1. Empirical Solubility Correlations
2.2. Activity Coefficients for Water Hydrocarbon Mixtures
2.3. Equation of State Studies of Water-Hydrocarbon Mixtures
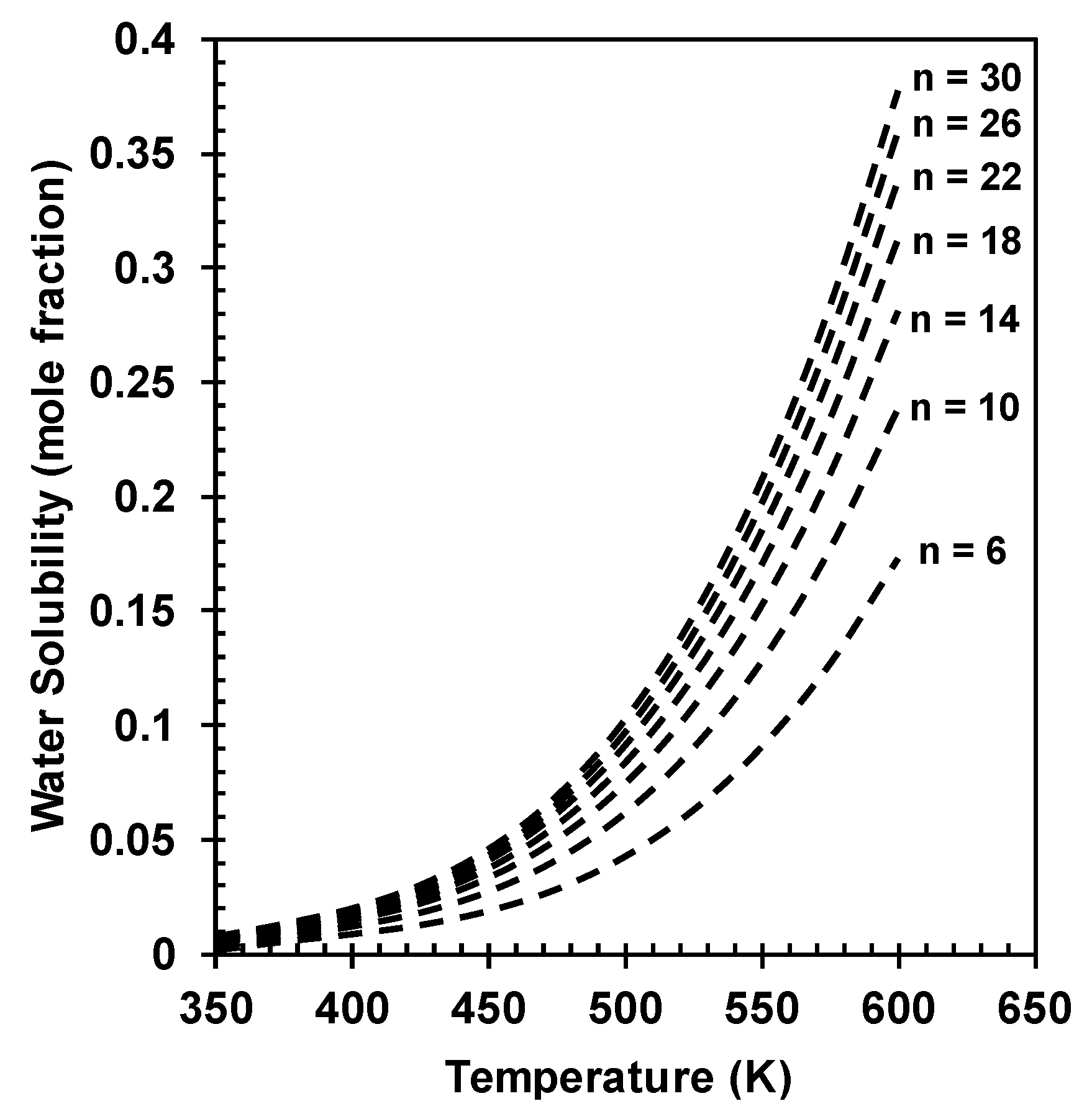
3. Calculating Water Solubility in Hydrocarbons
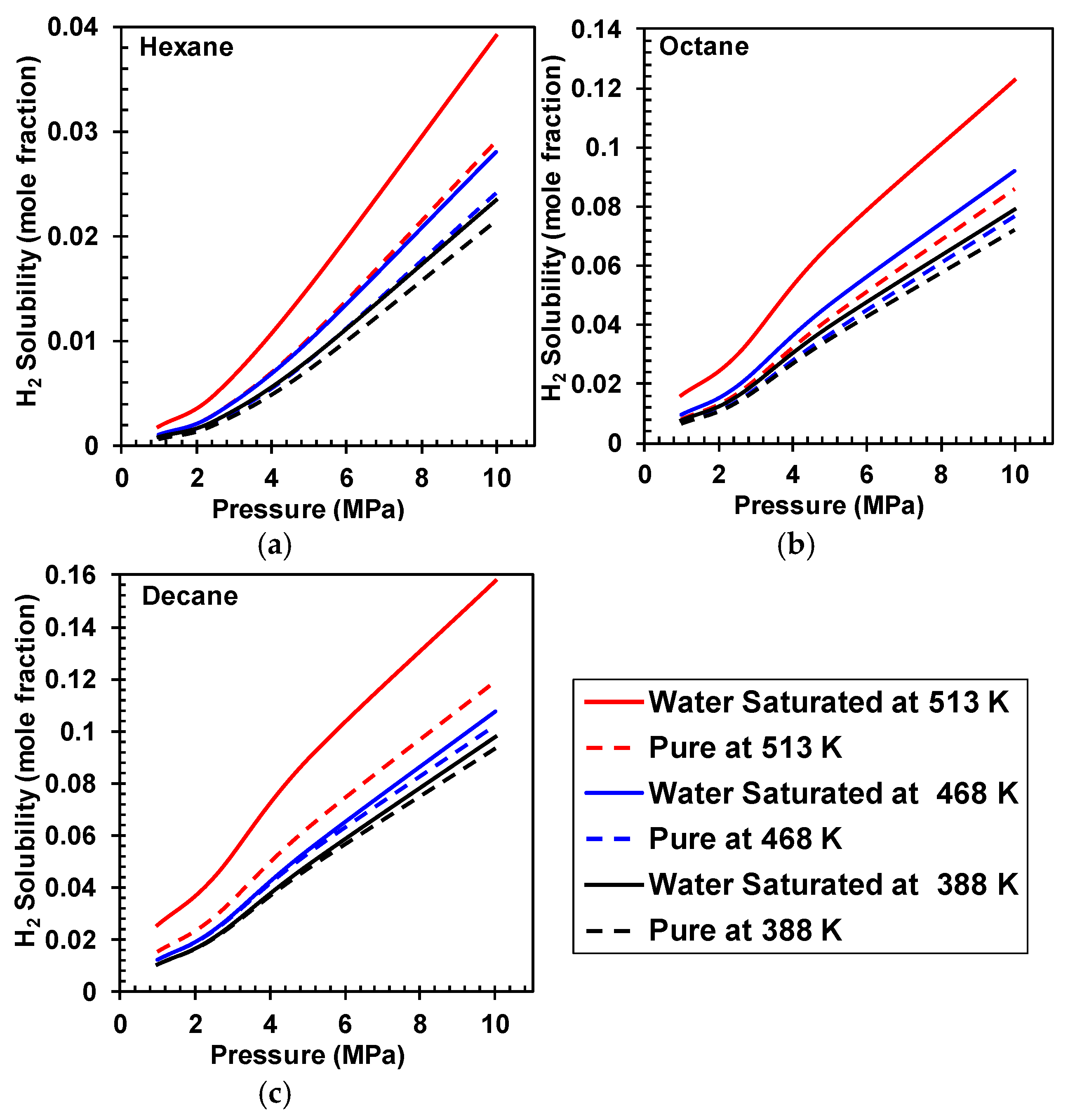
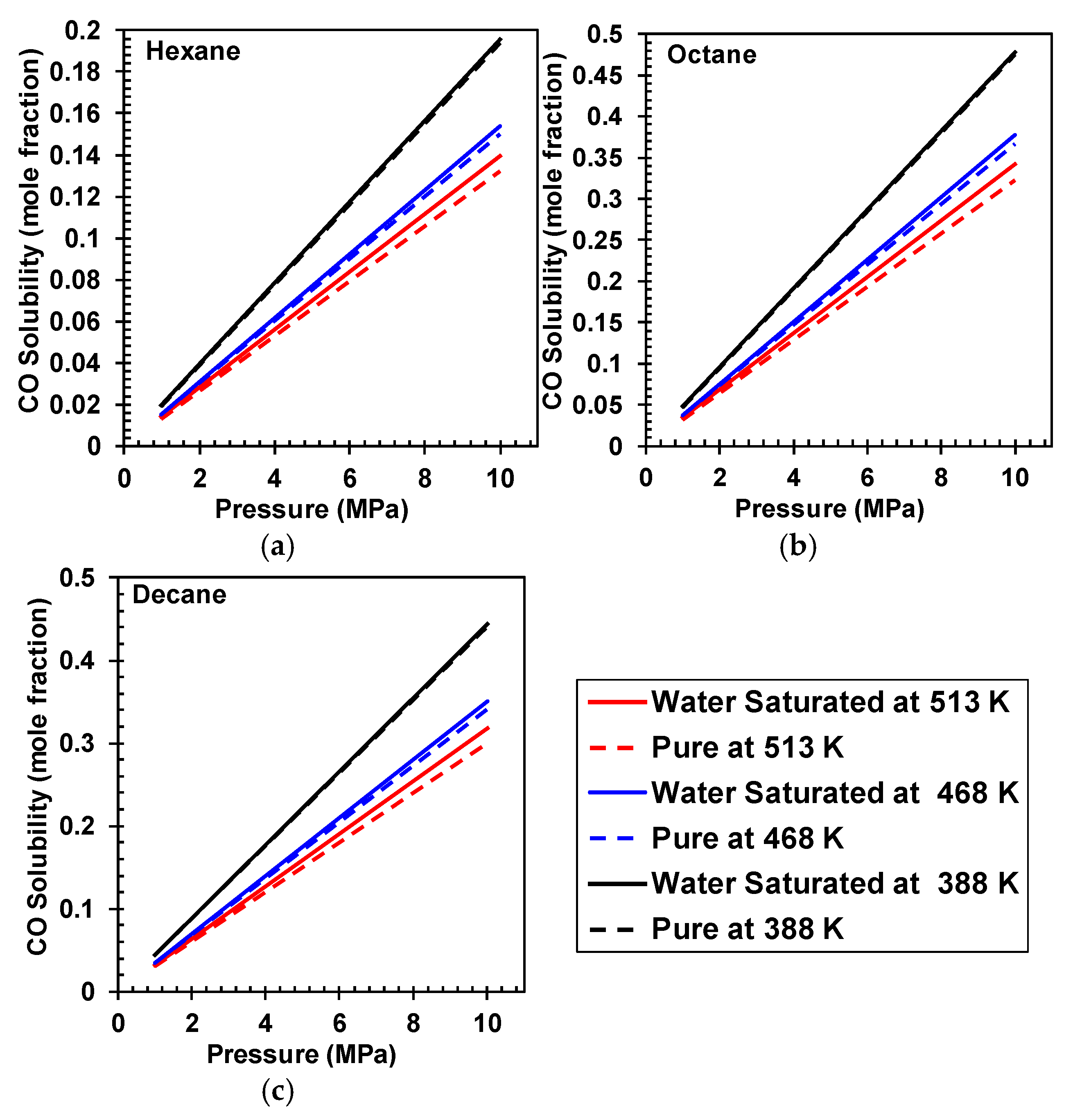
4. H2 and CO Solubilities in Pure and Water-Saturated Hydrocarbons
5. Concluding Remarks
Funding
Conflicts of Interest
References
- Karandikar, B.M.; Morsi, B.I.; Shah, Y.T.; Carr, N.L. Effect of water on the solubilities and mass transfer coefficients of gases in a heavy fraction of fischer-tropsch products. Can. J. Chem. Eng. 1987, 65, 973–981. [Google Scholar] [CrossRef]
- Karandikar, B.; Morsi, B.; Shah, Y.; Carr, N. Effect of water on the solubility and mass transfer coefficients of CO and H2 in a Fischer-Tropsch liquid. Chem. Eng. 1986, 33, 157–168. [Google Scholar] [CrossRef]
- Lindenberg, A. Sur une relation simple entre le volume moléculaire et la solubilité dans leau des hydrocarbures et dérivés halogénés. C. R. Hebd. Seances De L Acad. Des Sci. 1956, 243, 2057–2060. [Google Scholar]
- McAuliffe, C. Solubility in Water of Paraffin, Cycloparaffin, Olefin, Acetylene, Cycloolefin, and Aromatic Hydrocarbons1. J. Phys. Chem. 1966, 70, 1267–1275. [Google Scholar] [CrossRef]
- Klevens, H. The The Effect of Added Hydrocarbons upon Critical Concentrations of Soap and Detergent Solutions. J. Phys. Chem. 1950, 54, 1012–1016. [Google Scholar] [CrossRef]
- Irmann, F. Eine einfache Korrelation zwischen Wasserlöslichkeit und Struktur von Kohlenwasserstoffen und Halogenkohlenwasserstoffen. Chemie Ingenieur Technik 1965, 37, 789–798. [Google Scholar] [CrossRef]
- Hermann, R.B. Theory of Hydrophobic Bonding. 2. Correlation of Hydrocarbon Solubility in Water with Solvent Cavity Surface-Area. J. Phys. Chem. 1972, 76, 2754–2759. [Google Scholar] [CrossRef]
- Amidon, G.; Yalkowsky, S.; Anik, S.; Valvani, S. Solubility of nonelectrolytes in polar solvents. V. Estimation of the solubility of aliphatic monofunctional compounds in water using a molecular surface area approach. J. Phys. Chem. 1975, 79, 2239–2246. [Google Scholar] [CrossRef]
- Schatzberg, P. Solubilities of water in several normal alkanes from C7 to C161. J. Phys. Chem. 1963, 67, 776–779. [Google Scholar] [CrossRef]
- Ambrose, D.; Patel, N.C. The correlation and estimation of vapour pressures IV. Extrapolation of vapour pressures and estimation of critical pressures by the principle of corresponding states using two reference fluids with non-spherical molecules. J. Chem. Thermodyn. 1984, 16, 459–468. [Google Scholar] [CrossRef]
- Hubbard, J. Electron Correlations in Narrow Energy Bands. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1963, 276, 238–257. [Google Scholar]
- Tsonopoulos, C.; Wilson, G.M. High-temperature mutual solubilities of hydrocarbons and water. Part I: Benzene, cyclohexane and n-hexane. AIChE J. 1983, 29, 990–999. [Google Scholar] [CrossRef]
- Heidman, J.L.; Tsonopoulos, C.; Brady, C.J.; Wilson, G.M. High-temperature mutual solubilities of hydrocarbons and water. Part II: Ethylbenzene, ethylcyclohexane, and n-octane. AIChE J. 1985, 31, 376–384. [Google Scholar] [CrossRef]
- Brady, C.J.; Cunningham, J.R.; Wilson, G.M. RR-62: Water-Hydrocarbon Liquid-Liquid-Vapor Equilibrium Measurements in 530 Degrees F; Wiltec Research Co.: Provo, UT, USA, 1982. [Google Scholar]
- Deal, C.; Derr, E. Selectivity and solvency in aromatics recovery. Ind. Eng. Chem. Process Des. Dev. 1964, 3, 394–399. [Google Scholar] [CrossRef]
- Deal, C.H.; Derr, E.L. Group contributions in mixtures. Ind. Eng. Chem. 1968, 60, 28–38. [Google Scholar] [CrossRef]
- Tsonopoulos, C.; Prausnitz, J.M. Activity coefficients of aromatic solutes in dilute aqueous solutions. Ind. Eng. Chem. Fundam. 1971, 10, 593–600. [Google Scholar] [CrossRef]
- Spahl, R.; Luft, G. Einfluß von Molmasse und Molekülverzweigungen auf das Entmischungsverhalten von Ethylen/Polyethylen-Systemen unter Hochdruck. Berichte der Bunsengesellschaft für physikalische Chemie 1982, 86, 621–625. [Google Scholar] [CrossRef]
- Hu, Y.; Azevedo, E.; Lüdecke, D.; Prausnitz, J. Thermodynamics of associated solutions: Henry’s constants for nonpolar solutes in water. Fluid Phase Equilib. 1984, 17, 303–321. [Google Scholar] [CrossRef]
- Black, C.; Joris, G.G.; Taylor, A.H.S. The Solubility of Water in Hydrocarbons. J. Chem. Phys. 1948, 16, 537–543. [Google Scholar] [CrossRef]
- Hildebrand, J.H. Solubility of Water in Hydrocarbons. J. Chem. Phys. 1949, 17, 1346–1347. [Google Scholar] [CrossRef]
- Li, C.C.; McKetta, J.J. Vapor-Liquid Equilibrium in the Propylene-Water System. J. Chem. Eng. Data 1963, 8, 271–275. [Google Scholar] [CrossRef]
- West, E.W.; Erbar, J.H. Three Phase Equilibrium Calculations. In Proceedings of the Fifty-Second Annual GPA Convention, 1973. [Google Scholar]
- Heidemann, R.A. Three-phase equilibria using equations of state. AIChE J. 1974, 20, 847–855. [Google Scholar] [CrossRef]
- Reid, R.C.; Prausnitz, J.M.; Sherwood, T.K. The Properties of Gases and Liquids; McGraw-Hill Education: New York, NY, USA, 1977. [Google Scholar]
- Ambrose, D. Thermodynamic properties of organic oxygen compounds XLIX. The vapour pressure of solid acetic acid. J. Chem. Thermodyn. 1979, 11, 183–185. [Google Scholar] [CrossRef]
- Leet, W.A. Fluid-phase equilibria in mixtures of water and heavy hydrocarbons at elevated temperatures and pressures. Ph.D. Thesis, Purdue University, West Lafayette, IN, USA, 1986. [Google Scholar]
- Huron, M.J.; Vidal, J. New Mixing Rules in Simple Equations of State for Representing Vapor-Liquid-Equilibria of Strongly Non-Ideal Mixtures. Fluid Phase Equilib. 1979, 3, 255–271. [Google Scholar] [CrossRef]
- Mathias, P.M.; Copeman, T.W. Extension of the Peng-Robinson equation of state to complex mixtures: Evaluation of the various forms of the local composition concept. Fluid Phase Equilib. 1983, 13, 91–108. [Google Scholar] [CrossRef]
- Mollerup, J. Correlation of Thermodynamic Properties of Mixtures Using A Random-Mixture Reference State. Fluid Phase Equilib. 1983, 15, 189–207. [Google Scholar] [CrossRef]
- Whiting, W.B.; Prausnitz, J.M. Equations of state for strongly nonideal fluid mixtures: Application of local compositions toward density-dependent mixing rules. Fluid Phase Equilib. 1982, 9, 119–147. [Google Scholar] [CrossRef]
- Dimitrelis, D.; Prausnitz, J.M. Comparison of 2 Hard-Sphere Reference Systems for Perturbation Theories for Mixtures. Fluid Phase Equilib. 1986, 31, 1–21. [Google Scholar] [CrossRef]
- Wagner, W.; Pruß, A. The IAPWS Formulation 1995 for the Thermodynamic Properties of Ordinary Water Substance for General and Scientific Use. J. Phys. Chem. Ref. Data 2002, 31, 387–535. [Google Scholar] [CrossRef]
- Sanchez, I.; Rodgers, P. Solubility of gases in polymers. Pure Appl. Chem. 1990, 62, 2107–2114. [Google Scholar] [CrossRef]
- Haschets, C.W.C.; Shine, A.D.A.; Secor, R.M.R. Prediction of water solubilities in hydrocarbons and polyethylene at elevated temperatures and pressures. Ind. Eng. Chem. Res. 1994, 33, 1040–1046. [Google Scholar] [CrossRef]
- National Institute of Standards and Technology (NIST). National Institute of Standards and Technology Property Database; NIST: Gaithersburg, MD, USA, 2015. [Google Scholar]
- Maączyński, A.; Góral, M.; Wiśniewska-Gocłowska, B.; Skrzecz, A.; Shaw, D. Mutual solubilities of water and alkanes. Monatshefte für Chemie/Chem. Mon. 2003, 134, 633–653. [Google Scholar] [CrossRef]
- Span, R.; Wagner, W. A new equation of state for carbon dioxide covering the fluid region from the triple-point temperature to 1100 K at pressures up to 800 MPa. J. Phys. Chem. Ref. Data 1996, 25, 1509. [Google Scholar] [CrossRef]
- Leachman, J.W.; Jacobsen, R.T.; Penoncello, S.G.; Lemmon, E.W. Fundamental Equations of State for Parahydrogen, Normal Hydrogen, and Orthohydrogen. J. Phys. Chem. Ref. Data 2009, 38, 721. [Google Scholar] [CrossRef]
- Kerley, G.I.; Abdallah, J., Jr. Theoretical equations of state for molecular fluids: Nitrogen, oxygen, and carbon monoxide. J. Chem. Phys. 1980, 73, 5337–5350. [Google Scholar] [CrossRef]
| Component | r | |||
|---|---|---|---|---|
| n-hexane | 775 | 298 | 476 | 8.37 |
| n-octane | 815 | 307 | 502 | 10.34 |
| n-decane | 837 | 305 | 530 | 11.75 |
| Water | 1105 | 2690 | 623 | 8.46 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Basha, O.M. Effect of Water Saturation on H2 and CO Solubility in Hydrocarbons. ChemEngineering 2019, 3, 21. https://doi.org/10.3390/chemengineering3010021
Basha OM. Effect of Water Saturation on H2 and CO Solubility in Hydrocarbons. ChemEngineering. 2019; 3(1):21. https://doi.org/10.3390/chemengineering3010021
Chicago/Turabian StyleBasha, Omar M. 2019. "Effect of Water Saturation on H2 and CO Solubility in Hydrocarbons" ChemEngineering 3, no. 1: 21. https://doi.org/10.3390/chemengineering3010021
APA StyleBasha, O. M. (2019). Effect of Water Saturation on H2 and CO Solubility in Hydrocarbons. ChemEngineering, 3(1), 21. https://doi.org/10.3390/chemengineering3010021




