Thermodynamic Assessment of the Suitability of the Limiting Selectivity to Screen Ionic Liquid Entrainers for Homogeneous Extractive Distillation Processes
Abstract
:1. Introduction
2. Theory
2.1. Binary System
2.2. Adding IL as Entrainer
2.3. Using Limiting Selectivity
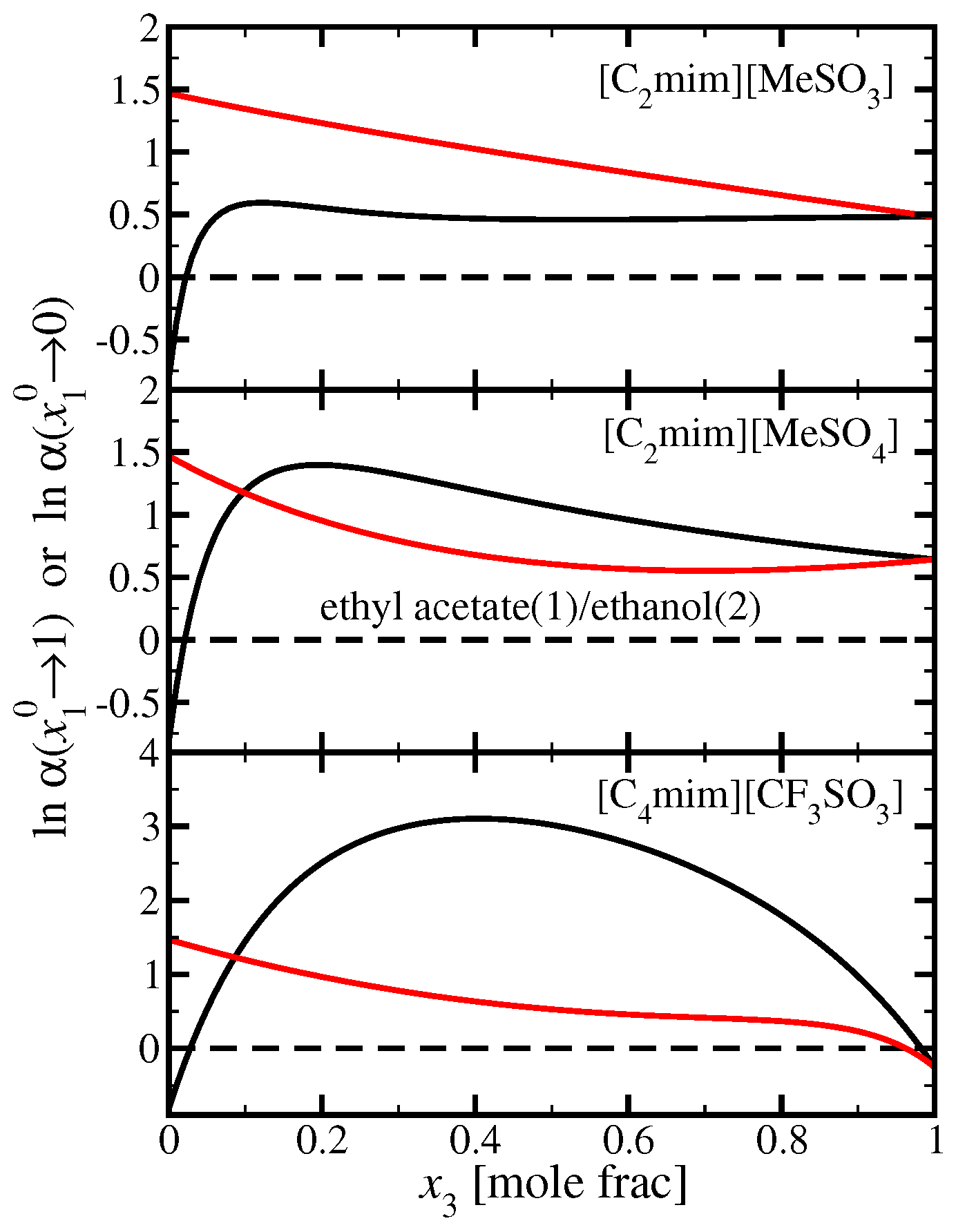
3. Application
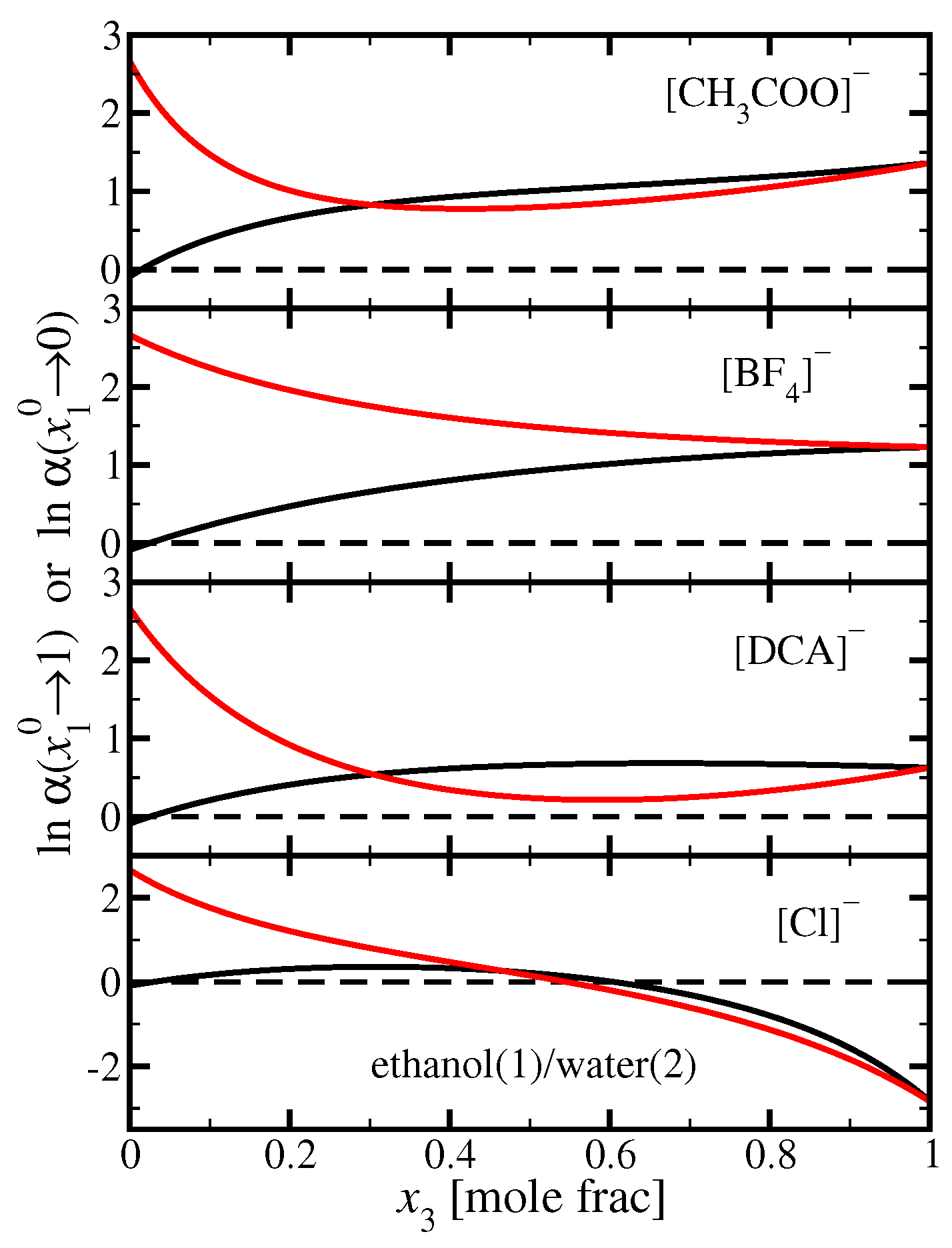
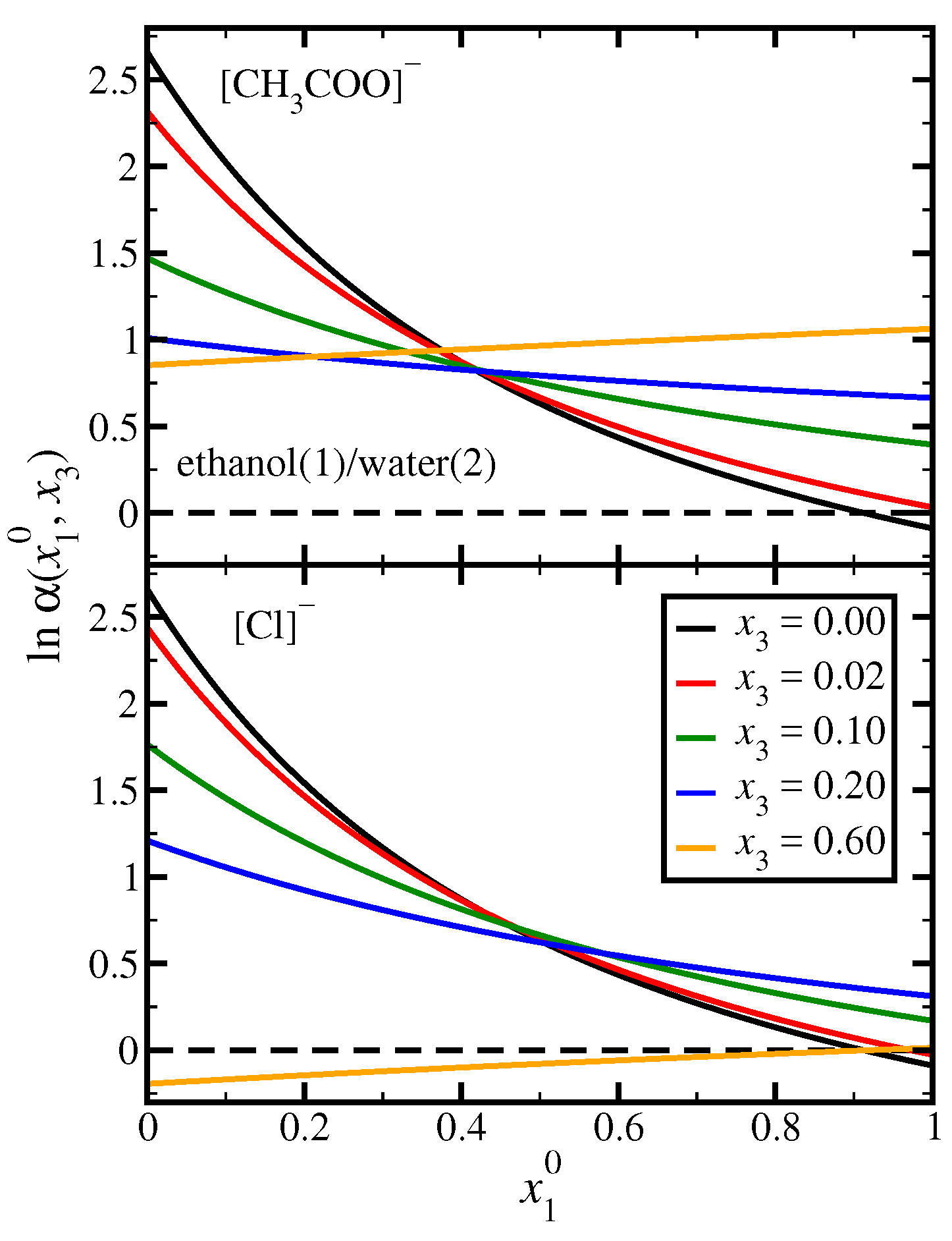
3.1. Ethanol(1)/Water(2)
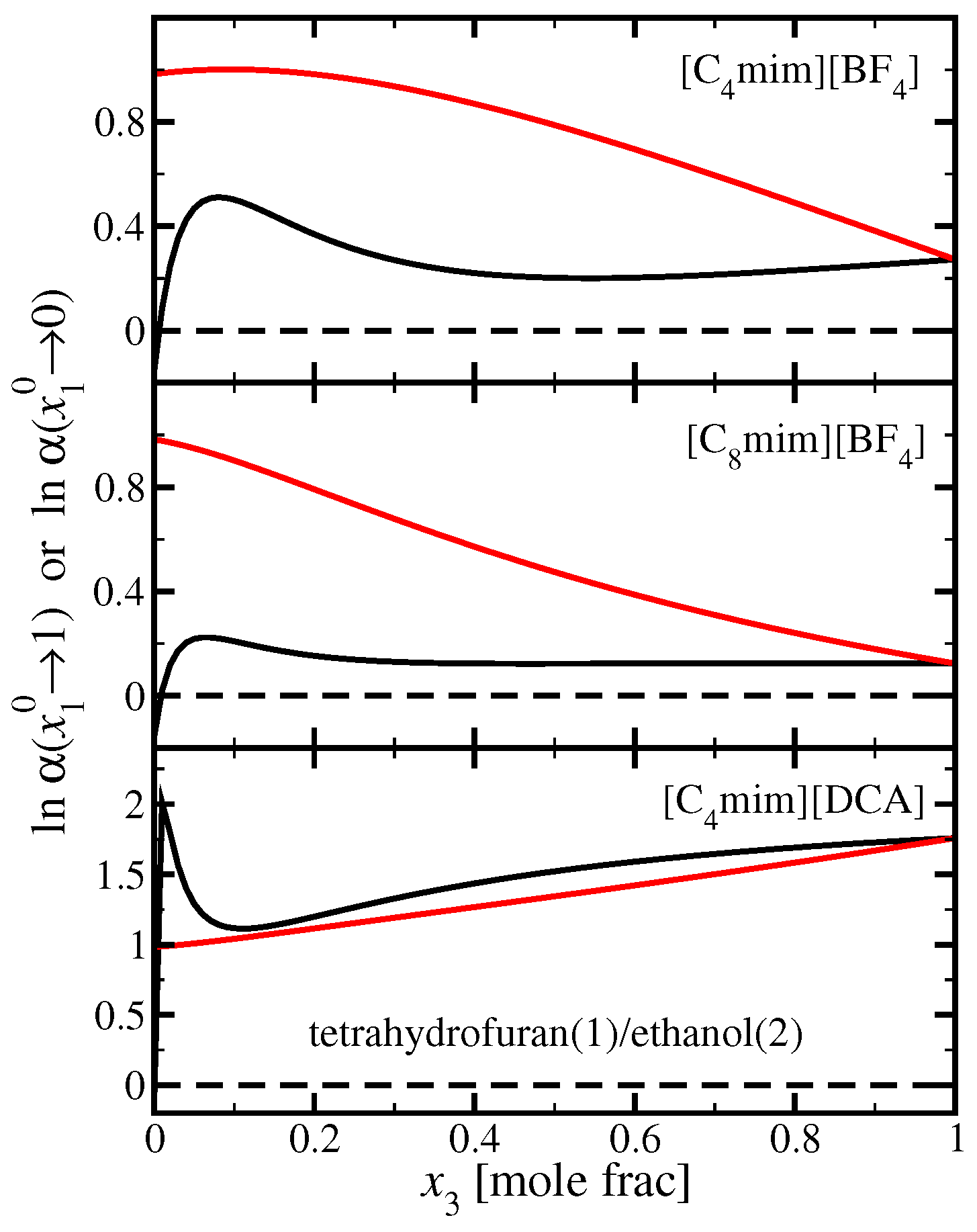
3.2. Tetrahydrofuran(1)/Ethanol(2)
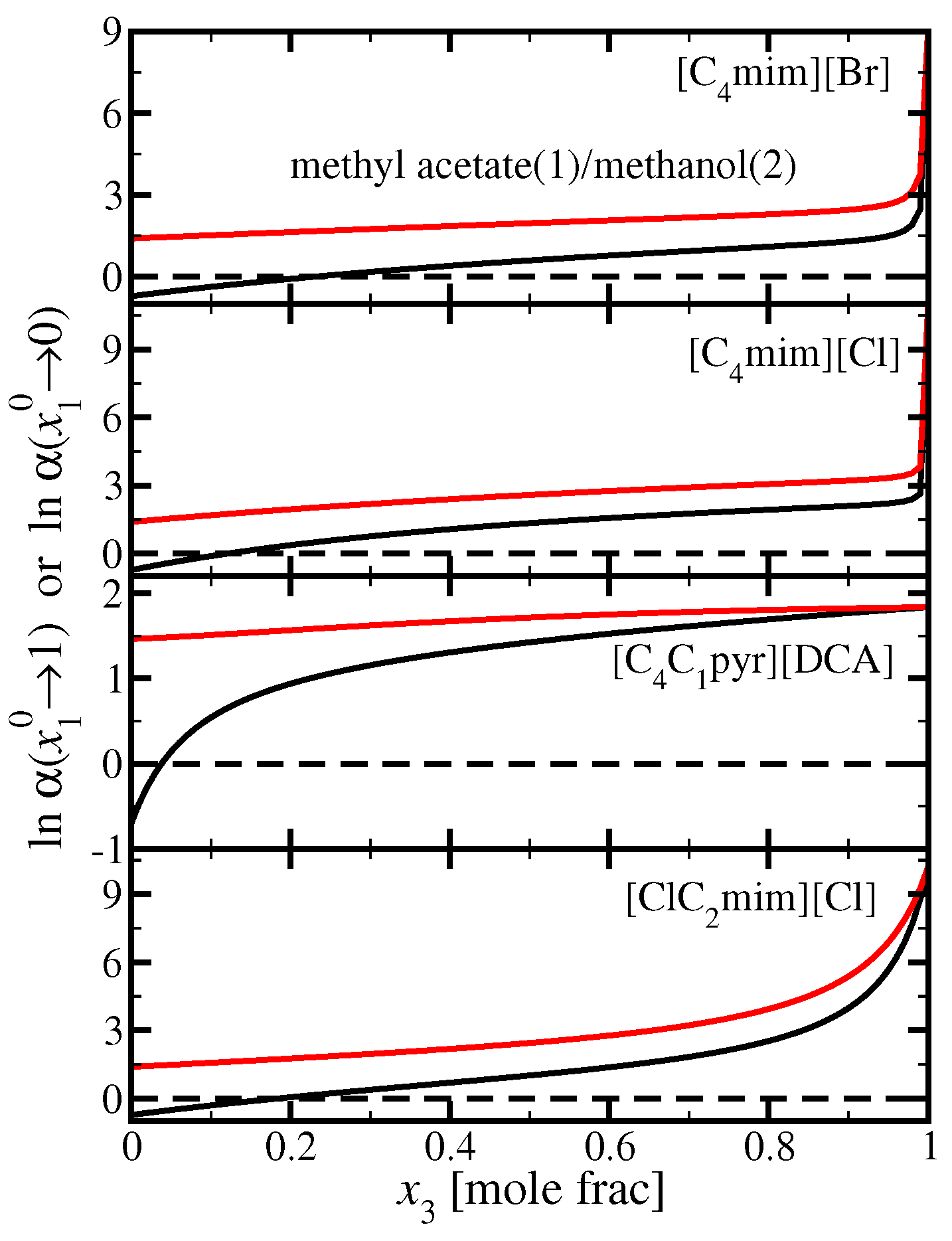
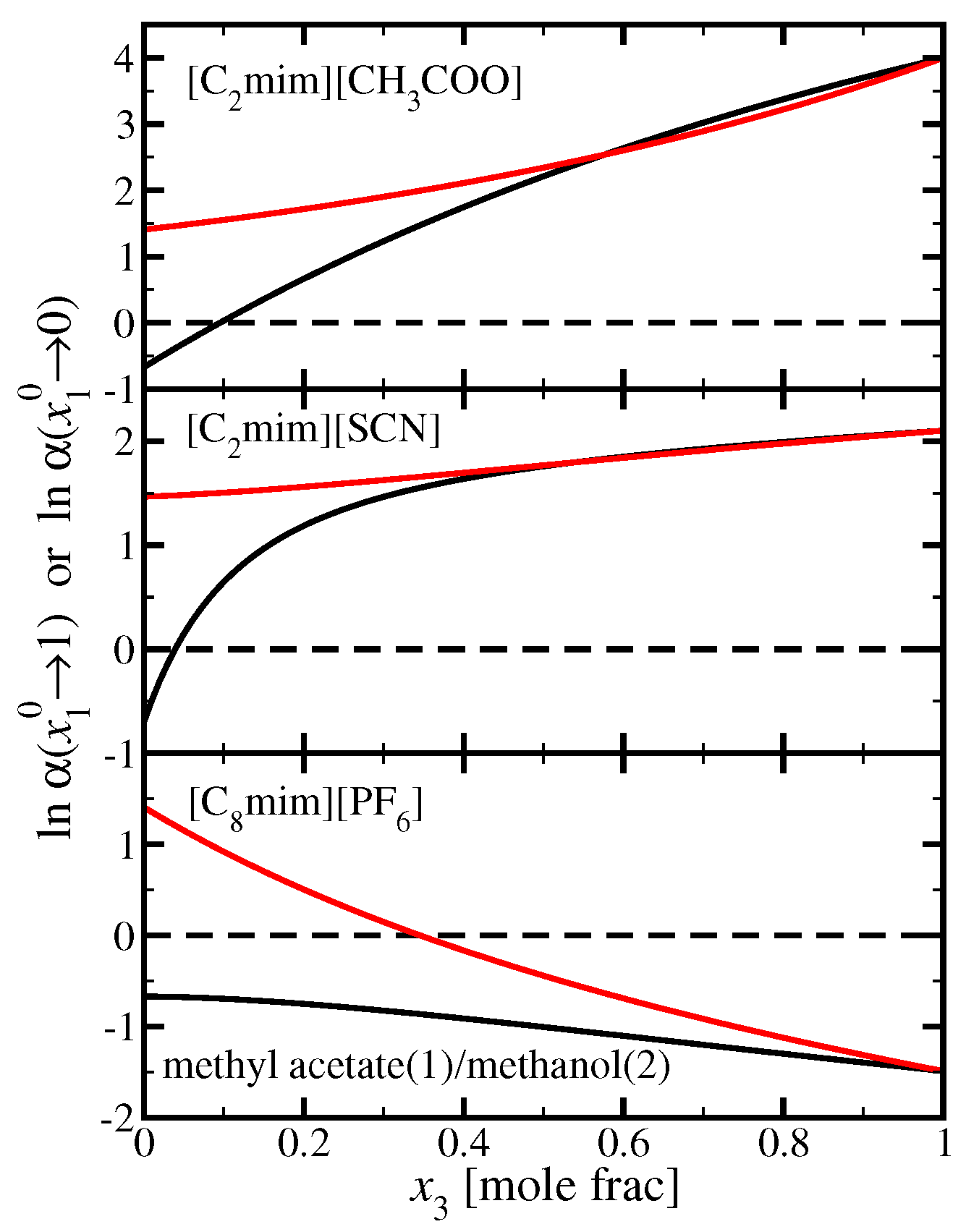
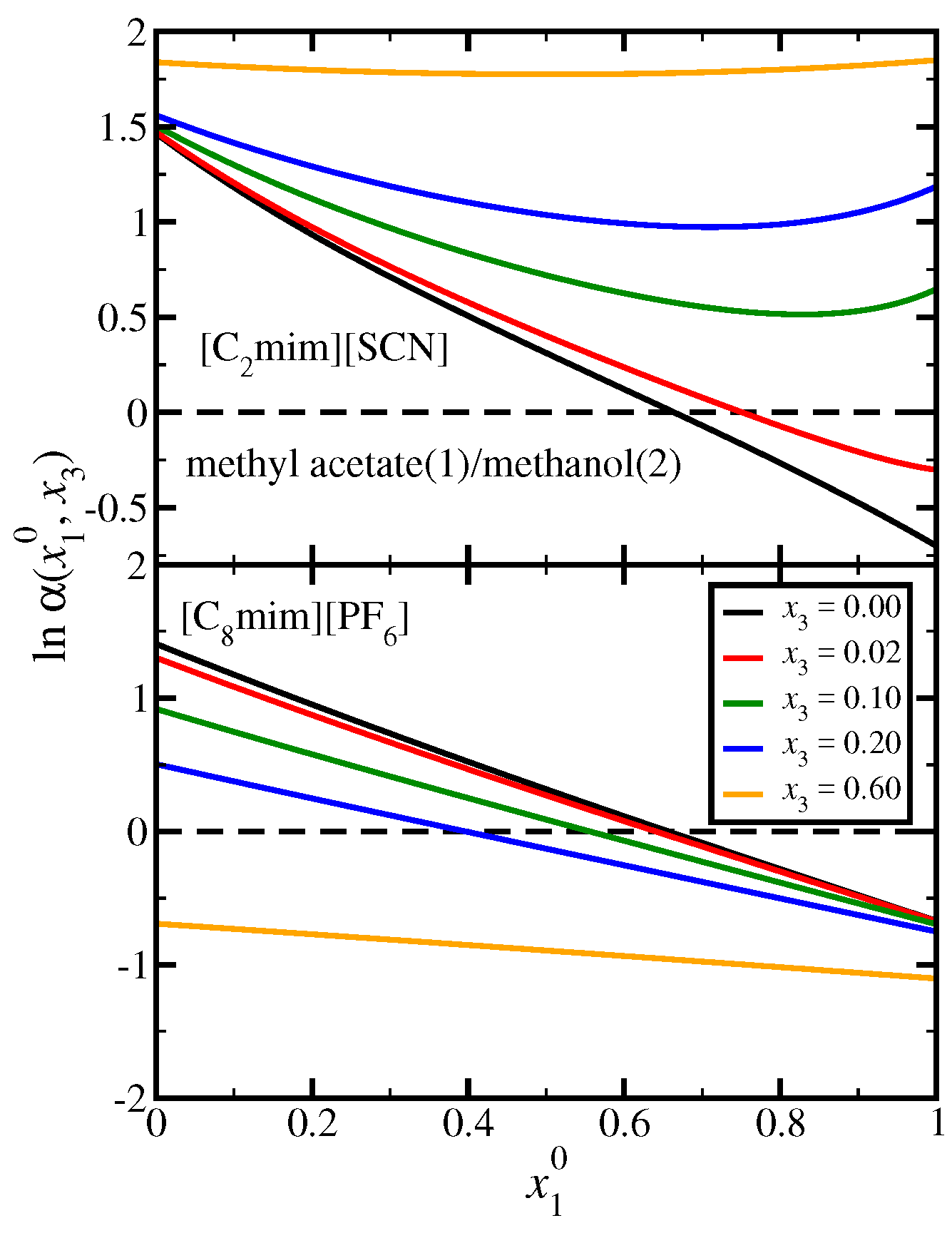
3.3. Methyl Acetate(1)/Methanol(2)
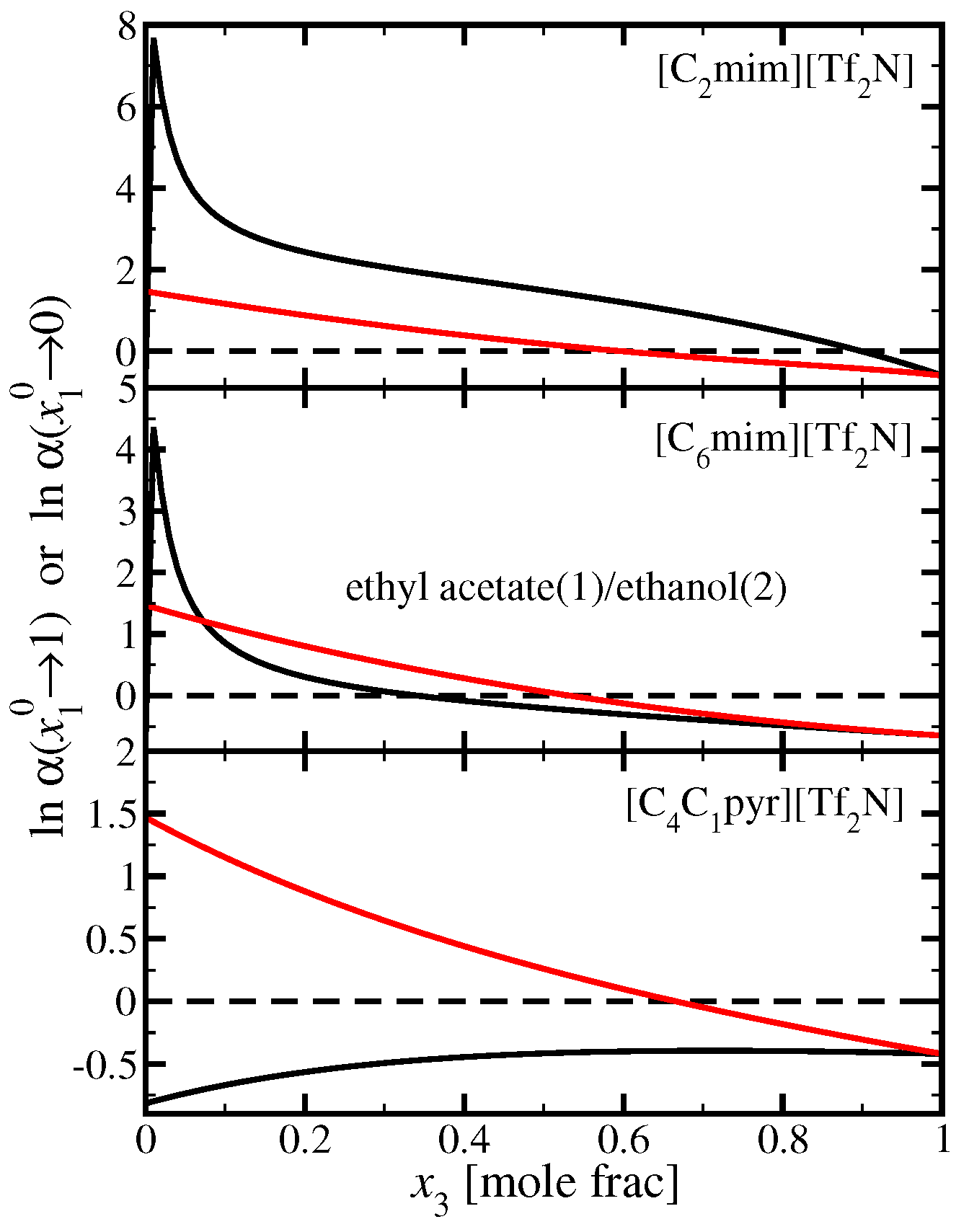
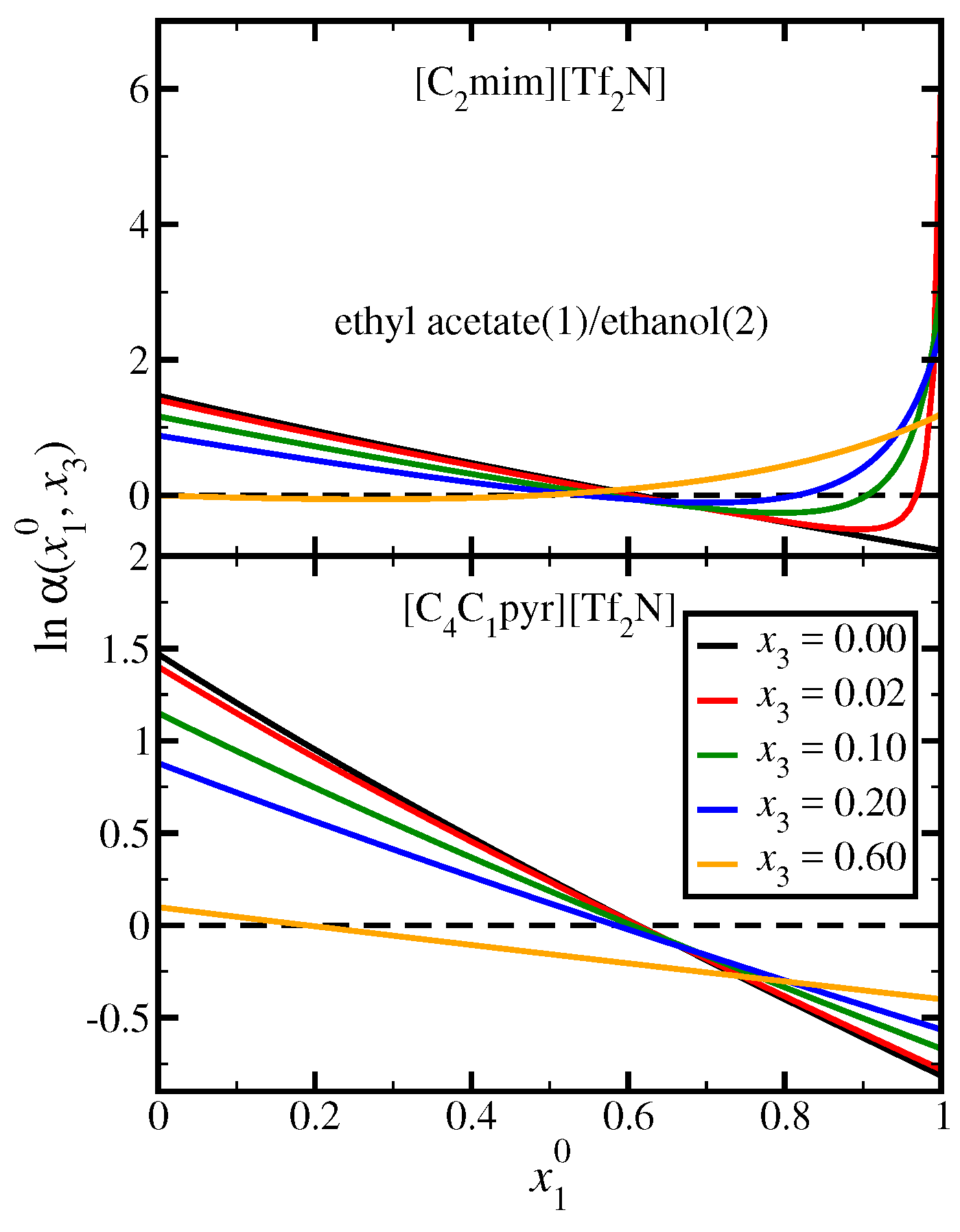
3.4. Ethyl Acetate(1)/Ethanol(2)
4. Summary and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wankat, P.C. Separation Process Engineering: Includes Mass Transfer, 3rd ed.; Pearson Education, Inc.: Upper Saddle River, NJ, USA, 2012. [Google Scholar]
- Kumar, R.; Prausnitz, J.M.; King, C.J. Process Design Considerations for Extractive Distillation: Separation of Propylene-Propane. In Extractive and Azeotropic Distillation; American Chemical Society: Washington, DC, USA, 1972; Chapter 2; pp. 16–34. [Google Scholar]
- Tassios, D.P. Rapid Screening of Extractive Distillation Solvents. In Extractive and Azeotropic Distillation; American Chemical Society: Washington, DC, USA, 1972; Chapter 4; pp. 46–63. [Google Scholar]
- Basios, J.C.; Soares, M.E.; Medina, A.G. Selection of Solvents for Extractive Distillation. A Data Bank for Activity Coefficients at large Dilution. Ind. Eng. Chem. Process Des. Dev. 1985, 24, 420–426. [Google Scholar]
- Zhu, Z.; Geng, X.; He, W.; Chen, C.; Wang, Y.; Gao, J. Computer-Aided Screening of Ionic Liquids As Entrainers for Separating Methyl Acetate and Methanol via Extractive Distillation. Ind. Eng. Chem. Res. 2018, 57, 9656–9664. [Google Scholar] [CrossRef]
- Paduszyński, K. In Silico Calculation of large Dilution Activity Coefficients of Molecular Solutes in Ionic Liquids: Critical Review of Current Methods and New Models Based on Three Machine Learning Algorithms. J. Chem. Inf. Model 2016, 56, 1420–1437. [Google Scholar] [CrossRef] [PubMed]
- Lazzaroni, M.J.; Bush, D.; Eckert, C.A.; Frank, T.C.; Gupta, S.; Olson, J.D. Revision of MOSCED Parameters and Extension to Solid Solubility Calculations. Ind. Eng. Chem. Res. 2005, 44, 4075–4083. [Google Scholar] [CrossRef]
- Angell, C.A.; Ansari, Y.; Zhao, Z. Ionic Liquids: Past, present, and future. Faraday Discuss. 2012, 154, 9–27. [Google Scholar] [CrossRef] [PubMed]
- Brennecke, J.F.; Maginn, E.J. Ionic Liquids: Innovative Fluids for Chemical Processing. AIChE J. 2001, 47, 2384–2389. [Google Scholar] [CrossRef]
- Dhanalakshmi, J.; Sai, P.S.T.; Balakrishnan, A.R. Study of Ionic Liquids as Entrainers for the Separation of Methyl Acetate-Methanol and Ethyl Acetate-Ethanol Systems Using the COSMO-RS Model. Ind. Eng. Chem. Res. 2013, 52, 16396–16405. [Google Scholar] [CrossRef]
- Ge, Y.; Zhang, L.; Yuan, X.; Geng, W.; Ji, J. Selection of ionic liquids as entrainers for separation of (water + ethanol). J. Chem. Thermodyn. 2008, 40, 1248–1252. [Google Scholar] [CrossRef]
- Cao, L.; Liu, P.; Wang, B.; Li, Q. Vapor-liquid equilibria for tetrahydrofuran + ethanol system containing three different ionic liquids at 101.3 kPa. Fluid Phase Equilib. 2014, 372, 49–55. [Google Scholar] [CrossRef]
- Zhang, Z.; Hu, A.; Zhang, T.; Zhang, Q.; Sun, M.; Sun, D.; Li, W. Separation of methyl acetate + methanol azeotropic mixture using ionic liquids as entrainers. Fluid Phase Equilib. 2015, 401, 1–8. [Google Scholar] [CrossRef]
- Dohnal, V.; Baránková, E.; Blahut, A. Separation of methyl acetate + methanol azeotropic mixture using ionic liquids as entrainers. Chem. Eng. J. 2014, 237, 199–208. [Google Scholar] [CrossRef]
- Chai, J.; Cui, X.; Zhang, Y.; Li, R.; Feng, T. Vapor-Liquid Equilibrium and Liquid-Liquid Equilibrium of Methyl Acetate + Methanol + 1-Ethyl-3-methylimidazolium Acetate. J. Chem. Eng. Data 2011, 56, 282–287. [Google Scholar]
- Chai, J.; Cui, X.; Zhang, Y.; Li, R.; Feng, T. Isobaric Vapor-Liquid Equilibrium for Methanol + Methyl Acetate + 1-Octyl-3-methylimidazolium Hexafluorophosphate at 101.3 kPa. J. Chem. Eng. Data 2011, 56, 2884–2888. [Google Scholar]
- Andreatta, A.E.; Charnley, M.P.; Brennecke, J.F. Using Ionic Liquids to Break the Ethanol-Ethyl Acetate Azeotrope. ACS Sustain. Chem. Eng. 2015, 3, 3435–3444. [Google Scholar] [CrossRef]
- Lei, Z.; Dai, C.; Zhu, J.; Chen, B. Extractive Distillation with Ionic Liquids: A Review. AIChE J. 2014, 60, 3312–3329. [Google Scholar] [CrossRef]
- Jongmans, M.T.G.; Schuur, B.; de Haan, A.B. Ionic Liquid Screening for Ethylbenzene/Styrene Separation by Extractive Distillation. Ind. Eng. Chem. Res. 2011, 50, 10800–10810. [Google Scholar] [CrossRef]
- Song, Z.; Zhou, T.; Qi, Z.; Sundmacher, K. Systematic Method for Screening Ionic Liquids as Extraction Solvents Exemplified by an Extractive Desulfurization Process. ACS Sustain. Chem. Eng. 2017, 5, 3382–3389. [Google Scholar] [CrossRef]
- Navarro, P.; Larriba, M.; Delgado-Mellado, N.; Ayuso, M.; Romero, M.; García, J.; Rodríguez, F. Experimental screening towards developing ionic liquid-based extractive distillation in the dearomatization of refinery streams. Sep. Purif. Technol. 2018, 201, 268–275. [Google Scholar] [CrossRef]
- Zhu, Z.; Ri, Y.; Li, M.; Jia, H.; Wang, Y.; Wang, Y. Extractive distillation for ethanol dehydration using imidazolium-based ionic liquids as solvents. Chem. Eng. Process. Process Intensif. 2016, 109, 190–198. [Google Scholar] [CrossRef]
- Kulajanpeng, K.; Suriyapraphadilok, U.; Gani, R. Systematic screening methodology and energy efficient design of ionic liquid-based separation processes. J. Clean. Prod. 2016, 11, 93–107. [Google Scholar] [CrossRef]
- Ley, R.T.; Paluch, A.S. Understanding the large solubility of lidocaine in 1-n-butyl-3-methylimidazolium based ionic liquids using molecular simulation. J. Chem. Phys. 2016, 144, 084501. [Google Scholar] [CrossRef] [PubMed]
- Caudle, M.R.; Cox, C.E.; Ley, R.T.; Paluch, A.S. A molecular study of the wastewater contaminants atenolol and atrazine in 1-n-butyl-3-methylimidazolium based ionic liquids for potential treatment applications. Mol. Phys. 2017, 115, 1264–1273. [Google Scholar] [CrossRef]
- Paluch, A.S.; Lourenço, T.C.; Han, F.; Costa, L.T. Understanding the Solubility of Acetaminophen in 1-n-Alkyl-3-methylimidazolium-Based Ionic Liquids Using Molecular Simulation. J. Phys. Chem. B 2016, 120, 3360–3369. [Google Scholar] [CrossRef] [PubMed]
- Granberg, R.A.; Rasmuson, A.C. Solubility of Paracetamol in Binary and Ternary Mixtures of Water + Acetone + Toluene. J. Chem. Eng. Data 2000, 45, 478–483. [Google Scholar] [CrossRef]
- Prausnitz, J.M.; Lichtenthaler, R.N.; de Azevedo, E.G. Molecular Thermodynamics of Fluid-Phase Equilibria, 2nd ed.; Prentice-Hall, Inc.: Englewood Cliffs, NJ, USA, 1986. [Google Scholar]
- Brandani, V. Use of large-Dilution Activity Coefficients for Predicting Azeotrope Formation at Constant Temperature and Partial Miscibility in Binary Liquid Mixtures. Ind. Eng. Chem. Fundam. 1974, 13, 154–156. [Google Scholar] [CrossRef]
- Larson, R.E.; Hostetler, R.P.; Edwards, B.H. Calculus, 6th ed.; Houghton Mifflin Company: New York, NY, USA, 1998. [Google Scholar]
- Tsirlin, A.; Sukin, I.A.; Balunov, A.; Schwalbe, K. The Rule of Temperature Coefficients for Selection of Optimal Separation Sequence for Multicomponent Mixtures in Thermal Systems. J. Non-Equilib. Thermodyn. 2017, 42, 359–369. [Google Scholar] [CrossRef]
- Momoh, S.O. Assessing the Accuracy of Selectivity as a Basis for Solvent Screening in Extractive Distillation Processes. Sep. Sci. Technol. 1991, 26, 729–742. [Google Scholar] [CrossRef]
- Kister, H.Z. Distillation Design; McGraw Hill, Inc.: New York, NY, USA, 1992. [Google Scholar]
- Shulgin, I.; Fischer, K.; Gmehling, J. Classification of Homogeneous Binary Azeotropes. Ind. Eng. Chem. Res. 2001, 40, 2742–2747. [Google Scholar] [CrossRef]
- Missen, R.W. On Criteria for Occurence of Azeotropes in Isothermal and Isobaric Binary Systems. Can. J. Chem. Eng. 2005, 83, 667–674. [Google Scholar] [CrossRef]
- Missen, R.W. On Determination of Azeotropic Coordinates from gE for Binary Isothermal and Isobaric Systems. Can. J. Chem. Eng. 2006, 84, 316–321. [Google Scholar] [CrossRef]
- Earle, M.J.; Esperança, J.M.S.S.; Gilea, M.A.; Canongia Lopes, J.N.; Rebelo, L.P.N.; Magee, J.W.; Seddon, K.R.; Widegren, J.A. The distillation and volatility of ionic liquids. Nature 2006, 439, 831–834. [Google Scholar] [CrossRef] [PubMed]
- Rai, N.; Maginn, E.J. Vapor-Liquid Coexistence and Critical Behavior of Ionic Liquids via Molecular Simulation. J. Phys. Chem. Lett. 2011, 2, 1439–1443. [Google Scholar] [CrossRef]
- Rai, N.; Maginn, E.J. Critical behaviour and vapour-liquid coexistence of 1-alkyl-3-methylimidazolium bis(trifluoromethylsulfonyl)amide ionic liquids via Monte Carlo simulations. Faraday Discuss. 2012, 154, 53–69. [Google Scholar] [CrossRef] [PubMed]
- Rane, K.S.; Errington, J.R. Saturation Properties of 1-Alkyl-3-methylimidazolium Based Ionic Liquids. J. Phys. Chem. B 2014, 118, 8734–8743. [Google Scholar] [CrossRef] [PubMed]
- Yaws, C.L.; Narasimhan, P.K.; Gabbula, C. Yaws’ Handbook of Antoine Coefficients for Vapor Pressure (2nd Electronic Edition); Knovel: New York, NY, USA, 2009. [Google Scholar]
| IL Anion | Equation (17) | Ref. |
|---|---|---|
| [CHCOO] | 0.0144 | 0.0144 |
| [BF] | 0.0249 | 0.0249 |
| [DCA] | 0.0255 | 0.0255 |
| [Cl] | 0.0288 | 0.0289 |
| IL Anion | Equation (17) | Ref. |
|---|---|---|
| [Cmim][BF] | 0.0065 | 0.0061 |
| [Cmim][BF] | 0.0089 | 0.0087 |
| [Cmim][DCA] | 0.0007 | 0.0007 |
| IL Anion | Equation (17) | Ref. |
|---|---|---|
| [Cmim][Br] | 0.2307 | 0.2308 |
| [Cmim][Cl] | 0.1203 | 0.1203 |
| [Cmim][CHCOO] | 0.0953 | 0.0953 |
| [Cmim][SCN] | 0.0391 | 0.0398 |
| [CCpyr][DCA] | 0.0381 | 0.0419 |
| [ClCmim][Cl] | 0.1823 | 0.1823 |
| [Cmim][PF] | 0.3455 | 0.3456 |
| IL Anion | Equation (17) | Ref. |
|---|---|---|
| [Cmim][CFSO] | 0.0288 | 0.0595 |
| [CCpyr][TfN] | 0.6659 | 0.6659 |
| [Cmim][MeSO] | 0.0226 | 0.0468 |
| [Cmim][MeSO] | 0.0208 | 0.0511 |
| [Cmim][TfN] | 0.0010 | 0.3775 |
| [Cmim][TfN] | 0.0016 | 0.5324 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paluch, A.S.; Dhakal, P. Thermodynamic Assessment of the Suitability of the Limiting Selectivity to Screen Ionic Liquid Entrainers for Homogeneous Extractive Distillation Processes. ChemEngineering 2018, 2, 54. https://doi.org/10.3390/chemengineering2040054
Paluch AS, Dhakal P. Thermodynamic Assessment of the Suitability of the Limiting Selectivity to Screen Ionic Liquid Entrainers for Homogeneous Extractive Distillation Processes. ChemEngineering. 2018; 2(4):54. https://doi.org/10.3390/chemengineering2040054
Chicago/Turabian StylePaluch, Andrew S., and Pratik Dhakal. 2018. "Thermodynamic Assessment of the Suitability of the Limiting Selectivity to Screen Ionic Liquid Entrainers for Homogeneous Extractive Distillation Processes" ChemEngineering 2, no. 4: 54. https://doi.org/10.3390/chemengineering2040054
APA StylePaluch, A. S., & Dhakal, P. (2018). Thermodynamic Assessment of the Suitability of the Limiting Selectivity to Screen Ionic Liquid Entrainers for Homogeneous Extractive Distillation Processes. ChemEngineering, 2(4), 54. https://doi.org/10.3390/chemengineering2040054






