Ultrasonic Power to Enhance Limestone Dissolution in the Wet Flue Gas Desulfurization Process. Modeling and Results from Stepwise Titration Experiments
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
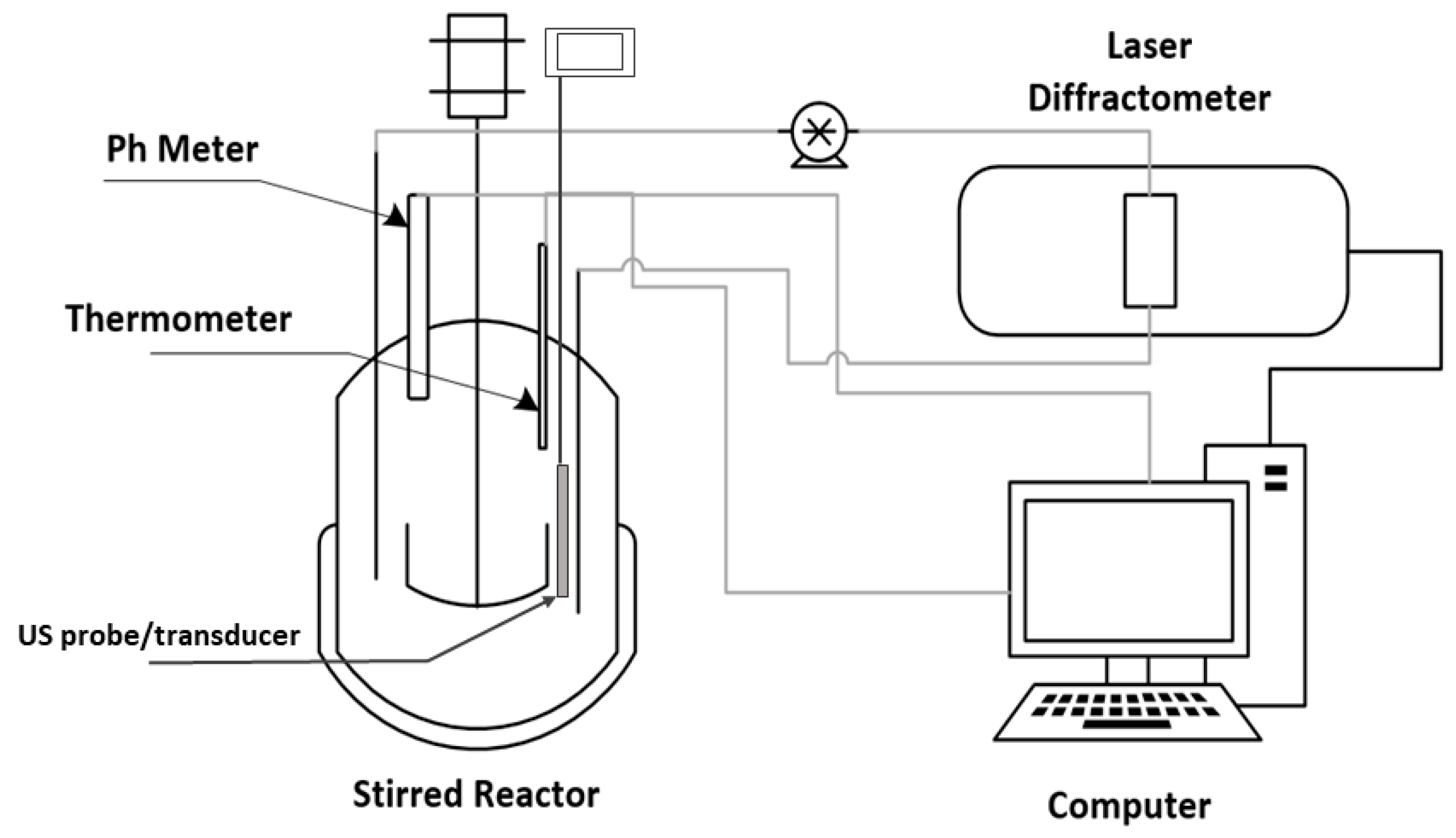
2.2. Experimental Setup
2.3. Procedure
2.3.1. PSD and pH Measurements
2.3.2. Z-Potential Measurements Sample Preparation
2.3.3. Z-potential Measurements
2.4. Theory/Calculation
3. Results
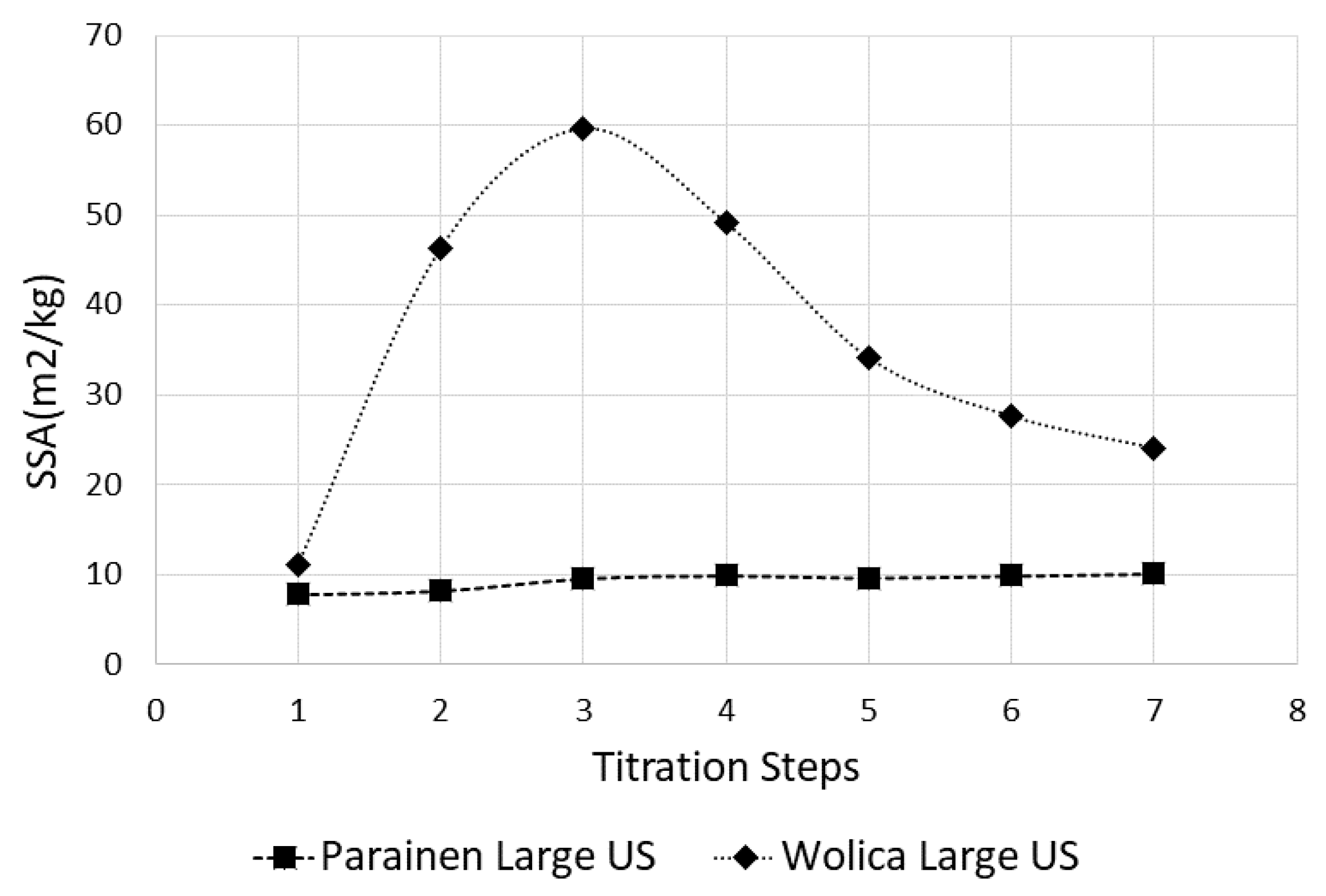
3.1. Limestone Characterization
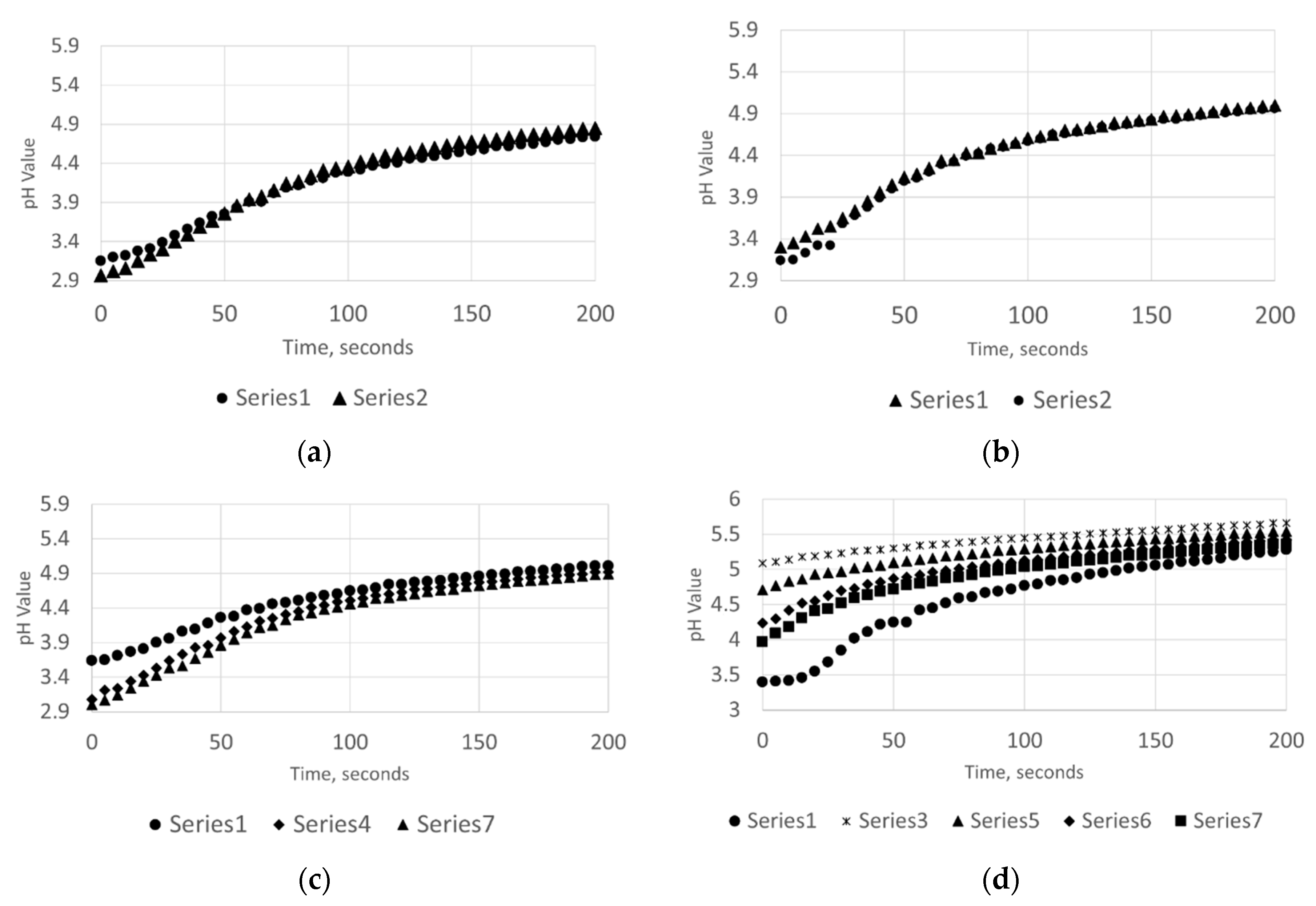
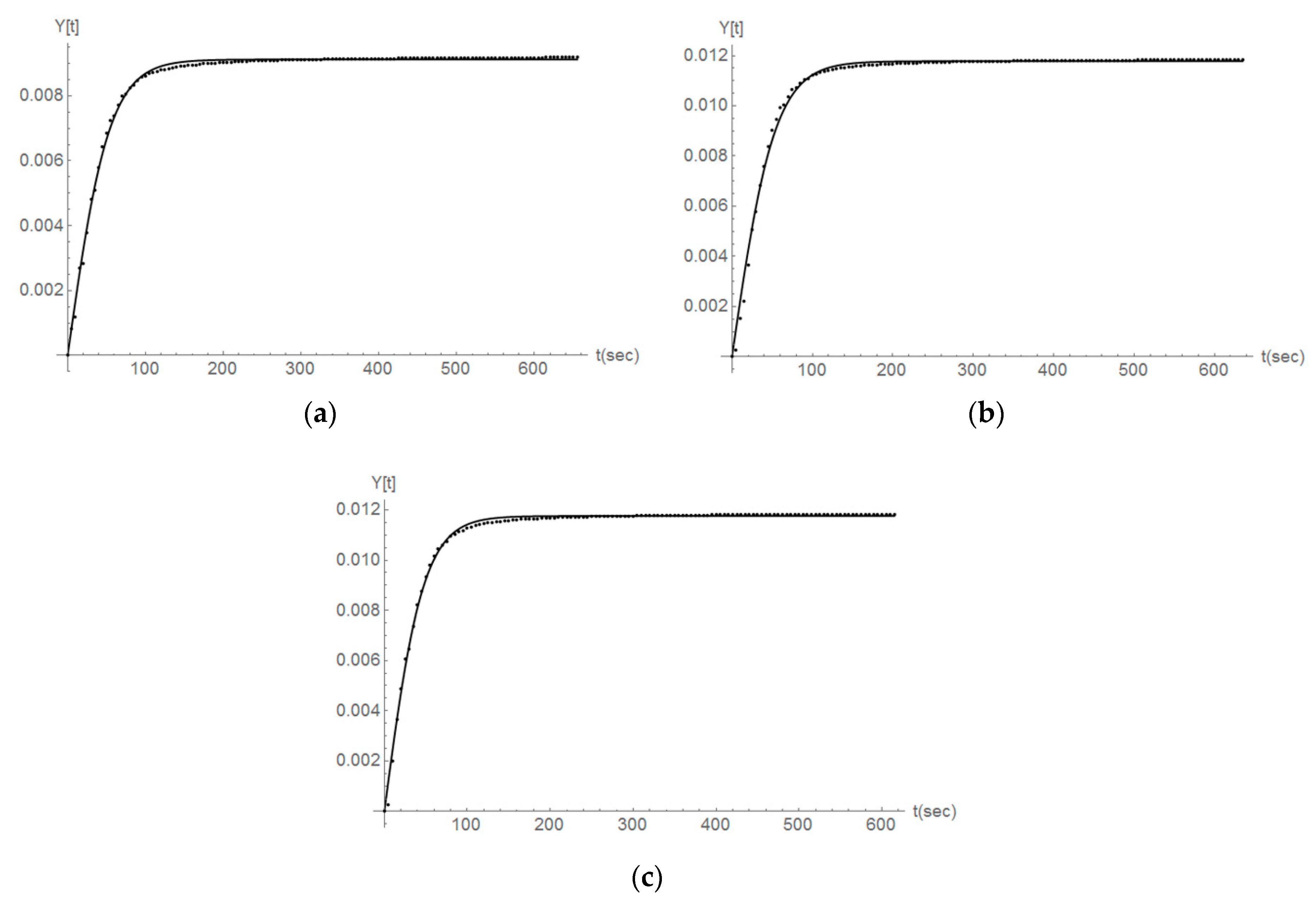
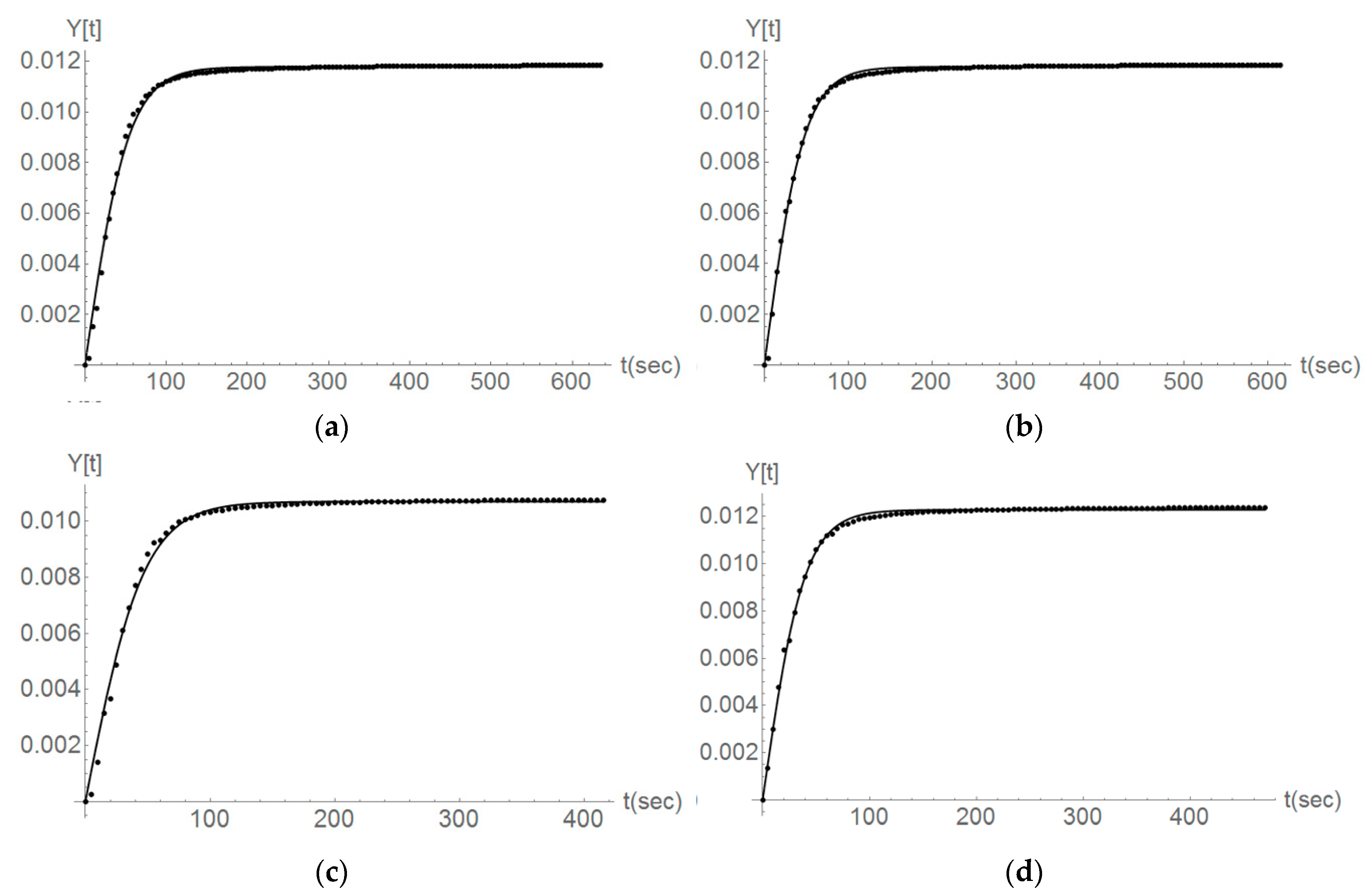
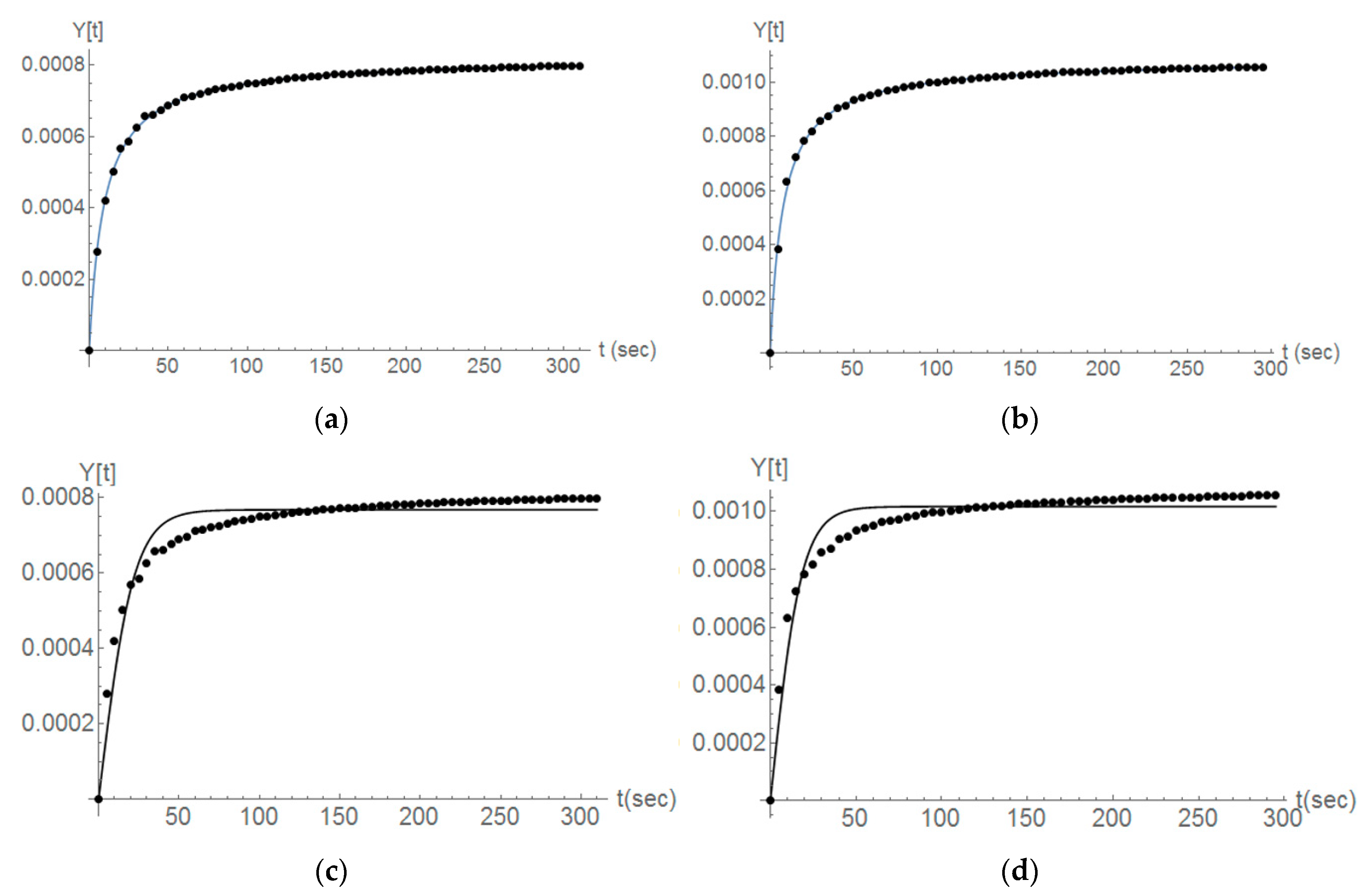
3.2. Dissolution Rate
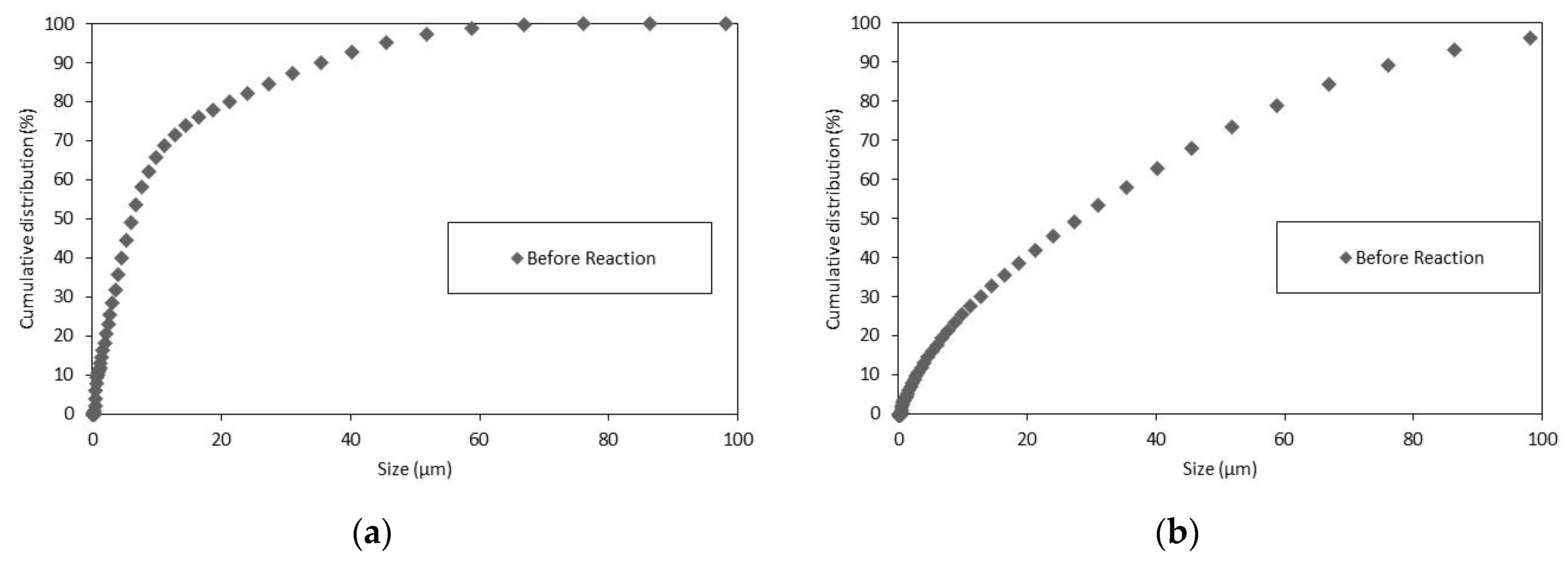
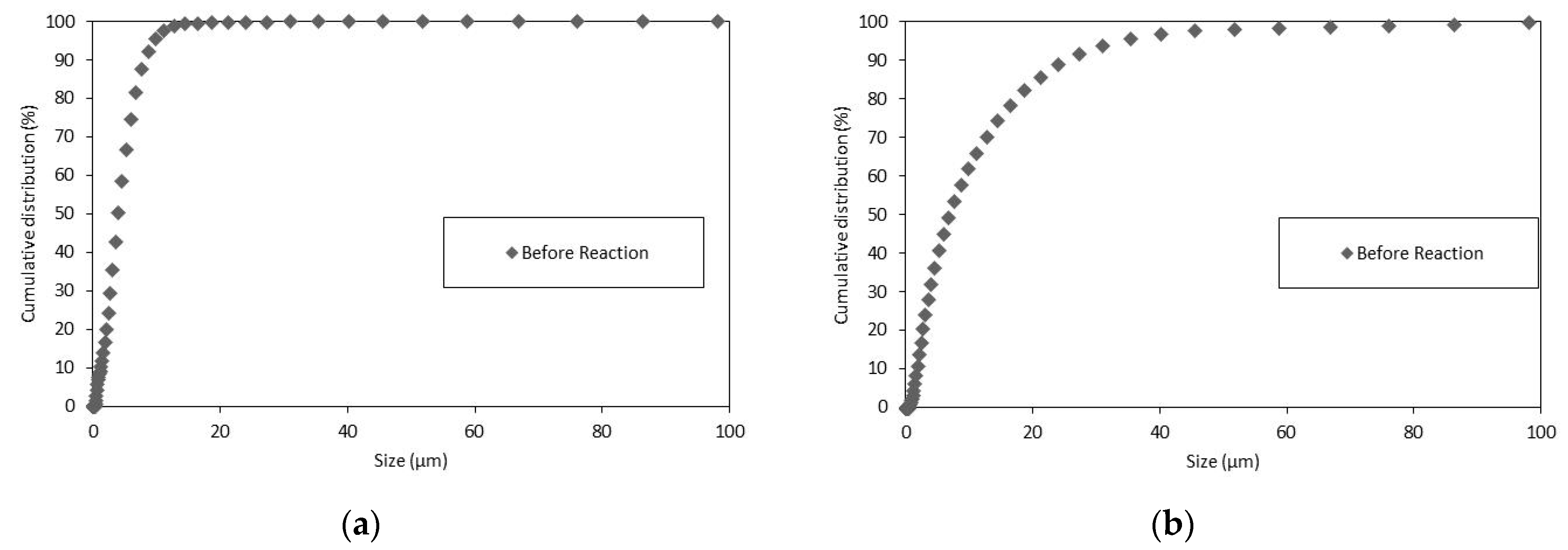
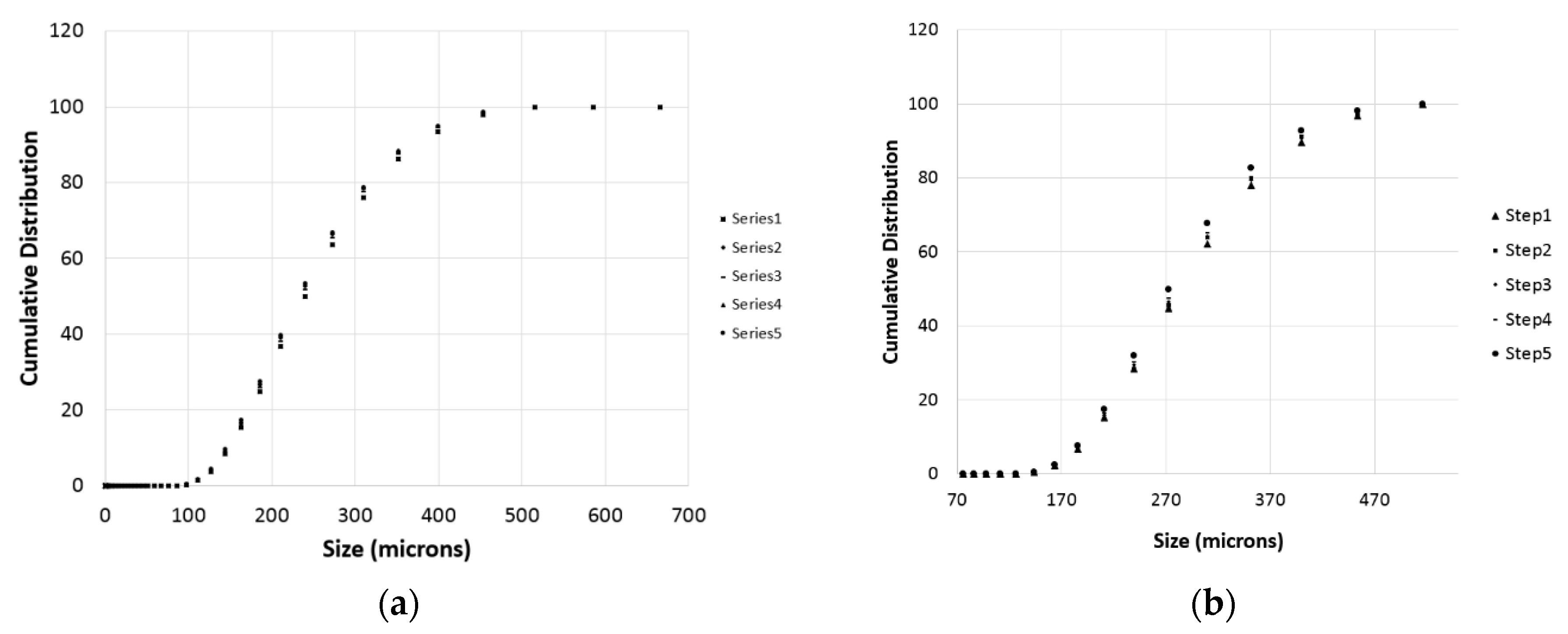
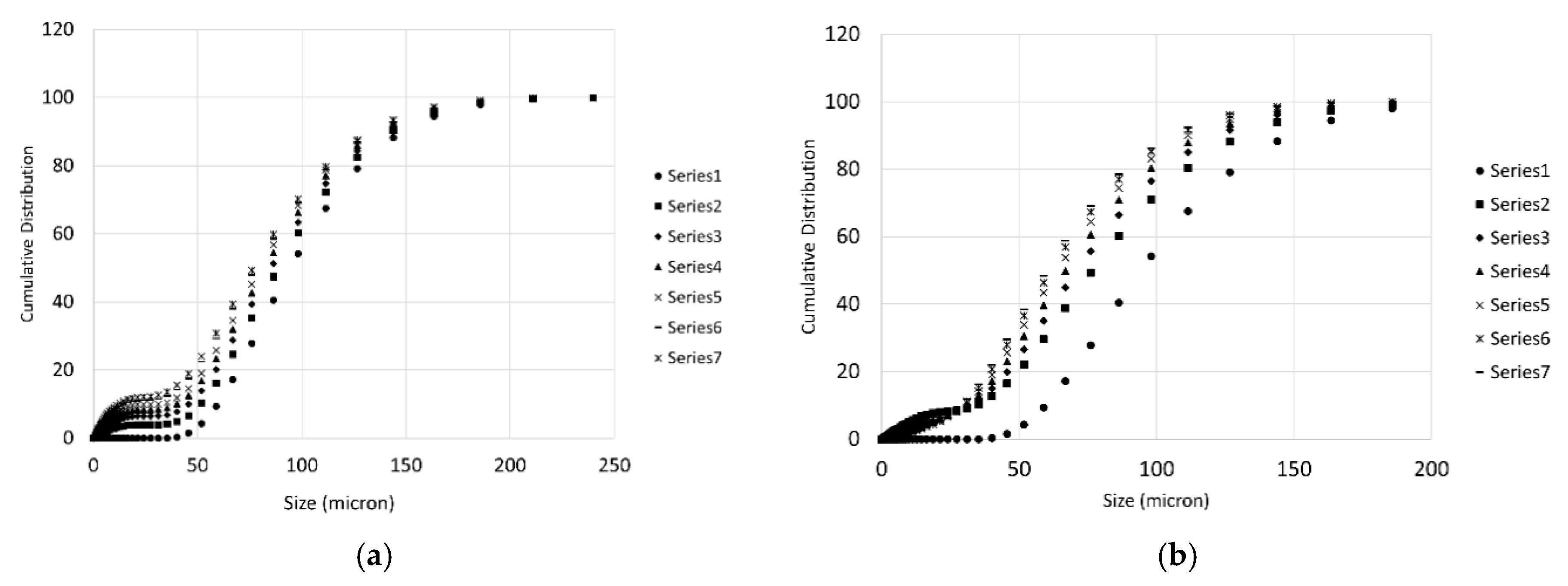
3.3. Particle Size Distributions
4. Discussion
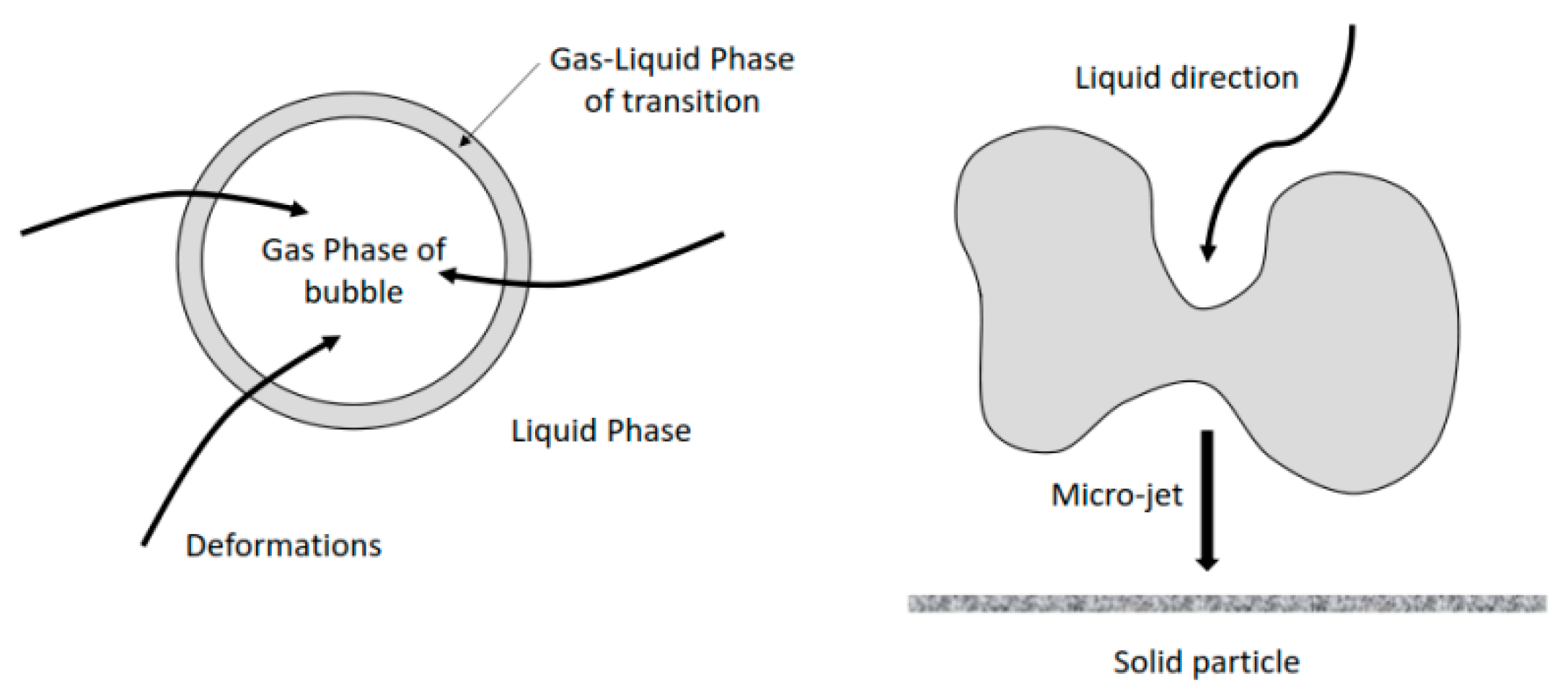
4.1. Effects of Ultrasound on Specific Surface Area determination
4.2. Mathematical Modelling
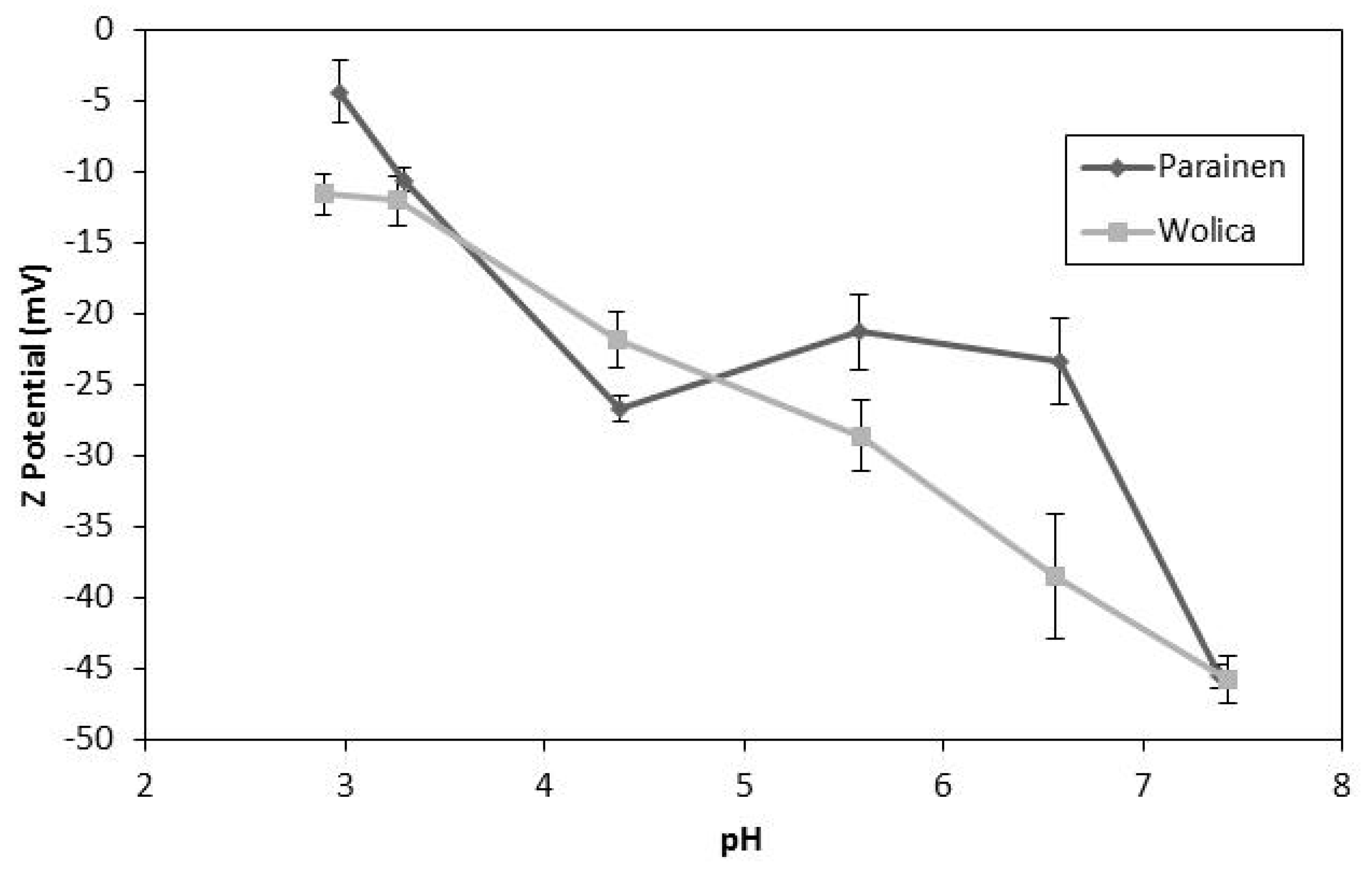
4.3. Effect of Surface Interactions on Limestone Dissolution
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- McGranahan, G.; Murray, F. Air Pollution and Health in Rapidly Developing Countries; Routledge: Abingdon, UK, 2003; ISBN 1-85383-966-3. [Google Scholar]
- De Blasio, C.; Carletti, C.; Lundell, A.; Visuri, V.-V.; Kokkonen, T.; Westerlund, T.; Fabritius, T.; Järvinen, M. Employing a step-wise titration method under semi-slow reaction regime for evaluating the reactivity of limestone and dolomite in acidic environment. Miner. Eng. 2016, 86, 43–58. [Google Scholar] [CrossRef]
- U.S. Energy Information Administration. US EIA November 2017 Monthly Energy Review; EIA: Washington, DC, USA, 2017.
- Del Valle-Zermeño, R.; Formosa, J.; Chimenos, J.M. Wet flue gas desulfurization using alkaline agents. Rev. Chem. Eng. 2015, 31. [Google Scholar] [CrossRef]
- De Gisi, S.; Molino, A.; Notarnicola, M. Enhancing the recovery of gypsum in limestone-based wet flue gas desulfurization with high energy ball milling process: A feasibility study. Process Saf. Environ. Prot. 2017, 109, 117–129. [Google Scholar] [CrossRef]
- Guelli, U.; Souza, S.M.A.; Santos, F.B.F.; Ulson de Souza, A.A.; Vidal Barrero, F. Limestone dissolution in flue gas desulfurization—experimental and numerical study. J. Chem. Technol. Biotechnol. 2010, 85, 1208–1214. [Google Scholar] [CrossRef]
- Stultz, S.C.; Kitto, J.B. Steam: It’s Generation and Use, 40th ed.; Babcock & Wilcox: Barberton, OH, USA, 1992. [Google Scholar]
- Hrastel, I.; Gerbec, M.; Stergaršek, A. Technology optimization of wet flue gas desulfurization process. Chem. Eng. Technol. 2007, 30, 220–233. [Google Scholar] [CrossRef]
- Carletti, C.; De Blasio, C.; Mäkilä, E.; Salonen, J.; Westerlund, T. Optimization of a Wet Flue Gas Desulfurization Scrubber through Mathematical Modeling of Limestone Dissolution Experiments. Ind. Eng. Chem. Res. 2015, 54, 9783–9797. [Google Scholar] [CrossRef]
- De Blasio, C.; Carletti, C.; Westerlund, T.; Järvinen, M. On modeling the dissolution of sedimentary rocks in acidic environments. An overview of selected mathematical methods with presentation of a case study. J. Math. Chem. 2013, 51, 2120–2143. [Google Scholar] [CrossRef]
- Pepe, F. Dissolution of Finely Ground Limestone Particles in Acidic Solutions. Ind. Eng. Chem. Res. 2001, 40, 5378–5385. [Google Scholar] [CrossRef]
- De Blasio, C.; Mäkilä, E.; Westerlund, T. Use of carbonate rocks for flue gas desulfurization: Reactive dissolution of limestone particles. Appl. Energy 2012, 90, 175–181. [Google Scholar] [CrossRef]
- Toprac, A.J.; Rochelle, G.T. Limestone dissolution in stack gas desulfurization. A mass-transfer model is shown to predict the the measured dissolution rates with less than 30% error. Environ. Progress 1982, 1, 52–58. [Google Scholar] [CrossRef]
- Lund, K.; Fogler, H.S.; McCune, C.C. Acidization—I. The dissolution of dolomite in hydrochloric acid. Chem. Eng. Sci. 1973, 28, 691–700. [Google Scholar] [CrossRef]
- Altun, N.E. Assessment of marble waste utilization as an alternative sorbent to limestone for SO2 control. Fuel Process. Technol. 2014, 128, 461–470. [Google Scholar] [CrossRef]
- Bjerle, I.; Rochelle, G.T. Limestone dissolution from a plane surface. Chem. Eng. Sci. 1984, 39, 183–185. [Google Scholar] [CrossRef]
- Sun, B.; Zhou, Q.; Chen, X.; Xu, T.; Hui, S. Effect of particle size in a limestone–hydrochloric acid reaction system. J. Hazard. Mater. 2010, 179, 400–408. [Google Scholar] [CrossRef] [PubMed]
- Dou, B.; Pan, W.; Jin, Q.; Wang, W.; Li, Y. Prediction of SO2 removal efficiency for wet Flue Gas Desulfurization. Energy Convers. Manag. 2009, 50, 2547–2553. [Google Scholar] [CrossRef]
- Siagi, Z.O.; Mbarawa, M. Dissolution rate of South African calcium-based materials at constant pH. J. Hazard. Mater. 2009, 163, 678–682. [Google Scholar] [CrossRef] [PubMed]
- Wallin, M.; Bjerle, I. A mass transfer model for limestone dissolution from a rotating cylinder. Chem. Eng. Sci. 1989, 44, 61–67. [Google Scholar] [CrossRef]
- Plummer, L.N.; Wigley, T.M.L.; Parkhurst, D.L. The kinetics of calcite dissolution in CO2-water systems at 5 degrees to 60 degrees C and 0.0 to 1.0 atm CO2. Am. J. Sci. 1978, 278, 179–216. [Google Scholar] [CrossRef]
- Fusi, L.; Monti, A.; Primicerio, M. Determining calcium carbonate neutralization kinetics from experimental laboratory data. J. Math. Chem. 2012, 50, 2492–2511. [Google Scholar] [CrossRef]
- Jafari, R.; Tanguy, P.A.; Chaouki, J. Characterization of minimum impeller speed for suspension of solids in liquid at high solid concentration, using gamma-ray densitometry. Int. J. Chem. Eng. 2012, 2012, 945314. [Google Scholar] [CrossRef]
- Hosseini, S.; Patel, D.; Ein-Mozaffari, F.; Mehrvar, M. Study of solid- liquid mixing in agitated tanks through computational fluid dynamics modeling. Ind. Eng. Chem. Res. 2010, 49, 4426–4435. [Google Scholar] [CrossRef]
- Levenspiel, O. Chemical Reaction Engineering, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1999. [Google Scholar]
- Barton, P.; Vatanatham, T. Kinetics of limestone neutralization of acid waters. Environ. Sci. Technol. 1976, 10, 262–266. [Google Scholar] [CrossRef] [PubMed]
- Chou, L.E.I.; Garrels, R.M.; Wollast, R. Comparative study of the kinetics and mechanisms of dissolution of carbonate minerals. Chem. Geol. 1989, 78, 269–282. [Google Scholar] [CrossRef]
- Tosun, I. Modelling in Transport Phenomena, a Conceptual Approach; Elsevier: Amsterdam, The Netherlands, 2002; ISBN 0444510524. [Google Scholar]
- Shengyu, L.; Wende, X.; Pei, L.; Zhixiang, Y. Feasibility Study of New Limestone Flue Gas Desulfurization Process. Clean Soil Air Water 2008, 36, 482–487. [Google Scholar] [CrossRef]
- Andritz Group. Andritz Air Pollution Control Is a Global Supplier of Systems for Flue Gas Cleaning Solutions Worldwide; Andritz: Graz, Austria, 2018. [Google Scholar]
- Babcock & Wilcox Power Generation Group. Inhibited Oxidation Wet Flue Gas Desulfurization; Babcock & Wilcox Power Generation Group: Barberton, OH, USA, 2012. [Google Scholar]
- Okur, H.; Tekin, T.; Ozer, A.K.; Bayramoglu, M. Effect of ultrasound on the dissolution of colemanite in H2SO4. Hydrometallurgy 2002, 67, 79–86. [Google Scholar] [CrossRef]
- Hagenson, L.C.; Doraiswamy, L.K. Comparison of the effects of ultrasound and mechanical agitation on a reacting solid-liquid system. Chem. Eng. Sci. 1998, 53, 131–148. [Google Scholar] [CrossRef]
- Grénman, H.; Murzina, E.; Rönnholm, M.; Eränen, K.; Mikkola, J.-P.; Lahtinen, M.; Salmi, T.; Murzin, D.Y. Enhancement of solid dissolution by ultrasound. Chem. Eng. Process. 2007, 46, 862–869. [Google Scholar] [CrossRef]
- Thompson, L.H.; Doraiswamy, L.K. Sonochemistry: Science and Engineering. Ind. Eng. Chem. Res. 1999, 38, 1215–1249. [Google Scholar] [CrossRef]
- Suslick, K.S. Sonochemistry. Science 1990, 247, 1439–1445. [Google Scholar] [CrossRef] [PubMed]
- Martin, D.J.; Wells, I.T.P.; Goodwin, C.R. Physics of ultrasound. Anaesth. Intensiv. Care Med. 2015, 16, 132–135. [Google Scholar] [CrossRef]
- De Blasio, C. Reactive Dissolution of Sedimentary Rocks in Flue Gas Desulfurization. Modeling and Experimental Investigation; Painosalama: Turku, Finland, 2010; ISBN 978-952-12-2482-9. [Google Scholar]
- Järvinen, L.; Leiro, J.A.; Bjondahl, F.; Carletti, C.; Eklund, O. XPS and SEM study of calcite bearing rock powders in the case of reactivity measurement with HCl solution. Surf. Interface Anal. 2012, 44, 519–528. [Google Scholar] [CrossRef]
- Carletti, C.; Grénman, H.; De Blasio, C.; Mäkilä, E.; Salonen, J.; Murzin, D.Y.; Salmi, T.; Westerlund, T. Revisiting the dissolution kinetics of limestone–experimental analysis and modeling. J. Chem. Technol. Biotechnol. 2016, 91, 1517–1531. [Google Scholar] [CrossRef]
- Molerus, O.; Latzel, W. Suspension of solid particles in agitated vessels—II. Archimedes numbers >40, reliable prediction of minimum stirrer angular velocities. Chem. Eng. Sci. 1987, 42, 1431–1437. [Google Scholar] [CrossRef]
- Carletti, C.; De Blasio, C.; Miceli, M.; Pirone, R.; Westerlund, T. Ultrasonic enhanced limestone dissolution: Experimental and mathematical modeling. Chem. Eng. Process. 2017, 118, 26–36. [Google Scholar] [CrossRef]
- Kaszuba, M.; Corbett, J.; Watson, F.M.; Jones, A. High-concentration zeta potential measurements using light-scattering techniques. Philos. Trans. Math. Phys. Eng. Sci. 2010, 368, 4439–4451. [Google Scholar] [CrossRef] [PubMed]
- Hudson, J.L.; Rochelle, G.T. Flue Gas Desulfurization; ACS Symposium Series: Washington, DC, USA, 1982; ISBN 978-0-8412-0722-6. [Google Scholar]
- Boudreau, B.P. Diagenetic Models and Their Implementation: Modelling Transport and Reactions in Aquatic Sediments; Springer: Berlin, Germany, 1997. [Google Scholar]
- Chen, D. Applications of ultrasound in water and wastewater treatment. In Handbook on Application of Ultrasound: Sonochemistry for Sustainability; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Pang, Y.L.; Abdullah, A.Z.; Bhatia, S. Review on sonochemical methods in the presence of catalysts and chemical additives for treatment of organic pollutants in wastewater. Desalination 2011, 277, 1–14. [Google Scholar] [CrossRef]
- Pinton, G.F.; Trahey, G.E. Modeling of shock wave propagation in large amplitude ultrasound. Ultrason. Imaging 2008, 30, 44–60. [Google Scholar] [CrossRef] [PubMed]
- Prédali, J.-J.; Cases, J.-M. Zeta potential of magnesian carbonates in inorganic electrolytes. J. Colloid Interface Sci. 1973, 45, 449–458. [Google Scholar] [CrossRef]
- Moulin, P.; Roques, H. Zeta potential measurement of calcium carbonate. J. Colloid Interface Sci. 2003, 261, 115–126. [Google Scholar] [CrossRef]
- Carletti, C. New Aspects in Limestone Dissolution for Wet Flue Gas Desulfurization; Åbo Akademi University: Åbo, Finland, 2015. [Google Scholar]
- Iyer, R.S.; Stanmore, B.R.; Pullammanappallil, P.C. The role of the diffuse double layer in leaching of calcium from the surface of flyash particles. Colloids Surf. Physicochem. Eng. Asp. 2001, 177, 69–74. [Google Scholar] [CrossRef]
- Pokrovsky, O.S.; Schott, J. Surface chemistry and dissolution kinetics of divalent metal carbonates. Environ. Sci. Technol. 2002, 36, 426–432. [Google Scholar] [CrossRef] [PubMed]
- Farooq, U.; Tweheyo, M.T.; Sjøblom, J.; Øye, G. Surface characterization of model, outcrop, and reservoir samples in low salinity aqueous solutions. J. Dispers. Sci. Technol. 2011, 32, 519–531. [Google Scholar] [CrossRef]


| Wolica Samples | Parainen Samples |
|---|---|
| WL 1.7–2 g | PL 2–3 g |
| WL US 0.9–2 g | PL US 2–4 g |
| WS 1–1.5 g | PS 2 g |
| WS US 0.8 g | PS US 1.9–2.5 g |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Blasio, C.; Carletti, C.; Salonen, J.; Björklund-Sänkiaho, M. Ultrasonic Power to Enhance Limestone Dissolution in the Wet Flue Gas Desulfurization Process. Modeling and Results from Stepwise Titration Experiments. ChemEngineering 2018, 2, 53. https://doi.org/10.3390/chemengineering2040053
De Blasio C, Carletti C, Salonen J, Björklund-Sänkiaho M. Ultrasonic Power to Enhance Limestone Dissolution in the Wet Flue Gas Desulfurization Process. Modeling and Results from Stepwise Titration Experiments. ChemEngineering. 2018; 2(4):53. https://doi.org/10.3390/chemengineering2040053
Chicago/Turabian StyleDe Blasio, Cataldo, Claudio Carletti, Jarno Salonen, and Margareta Björklund-Sänkiaho. 2018. "Ultrasonic Power to Enhance Limestone Dissolution in the Wet Flue Gas Desulfurization Process. Modeling and Results from Stepwise Titration Experiments" ChemEngineering 2, no. 4: 53. https://doi.org/10.3390/chemengineering2040053
APA StyleDe Blasio, C., Carletti, C., Salonen, J., & Björklund-Sänkiaho, M. (2018). Ultrasonic Power to Enhance Limestone Dissolution in the Wet Flue Gas Desulfurization Process. Modeling and Results from Stepwise Titration Experiments. ChemEngineering, 2(4), 53. https://doi.org/10.3390/chemengineering2040053