CFD Simulation of Ethanol Steam Reforming System for Hydrogen Production
Abstract
1. Introduction
1.1. Mechanism of Steam Ethanol Reforming Process
1.2. Ethanol Burner Steam Reformer
- (1)
- Convection
- (2)
- Radiation
- (3)
- Conduction
1.2.2 Convection
1.2.3 Radiative Heat Transfer
1.2.4 Conduction Heat Transfer
2. Materials and Methods
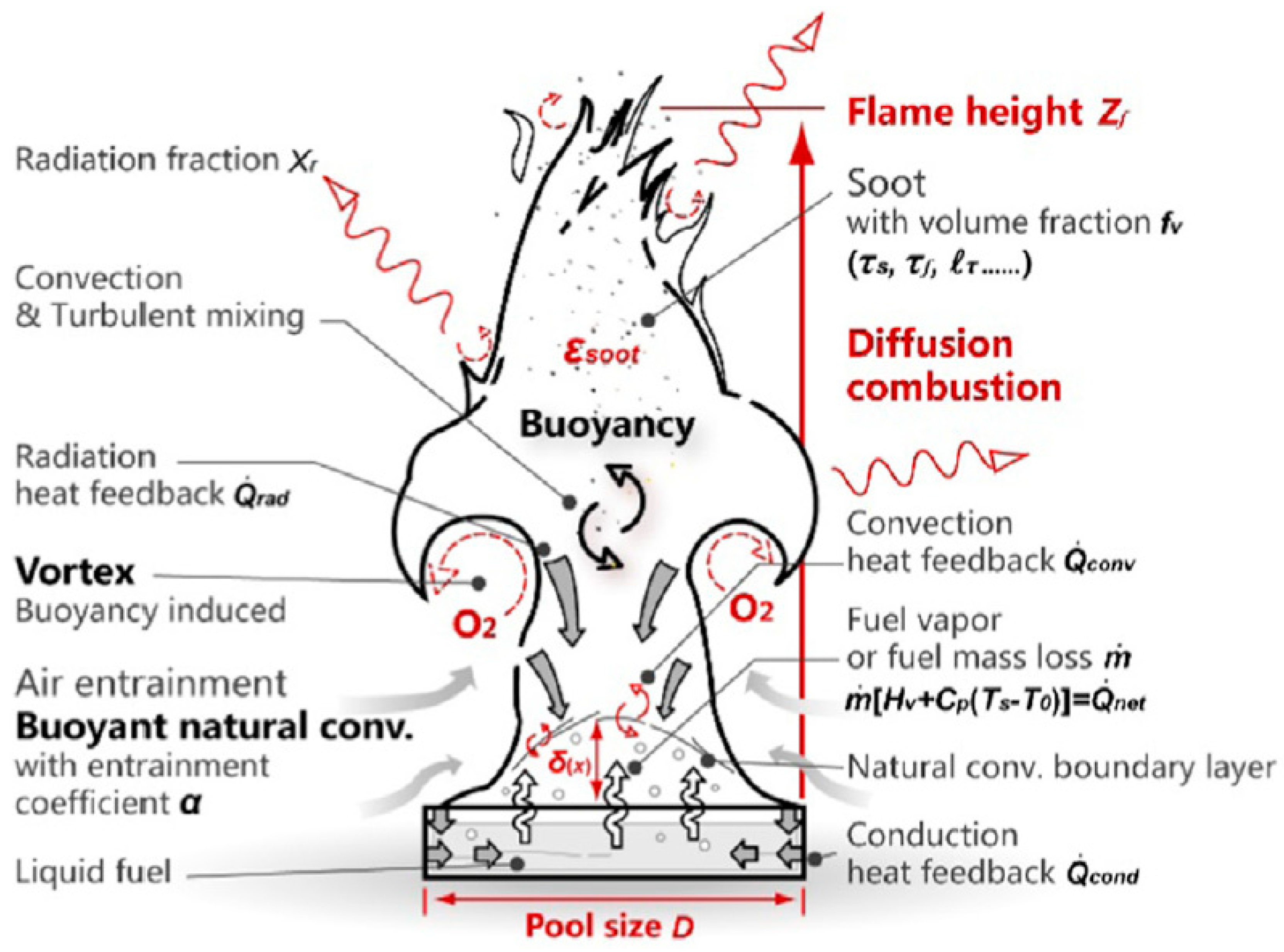
2.1. Fire Dynamic Simulation Modeling of the Burner
2.2. Governing Equations of FDS Software
2.2.1. Mass and Species Transport
2.2.2. Momentum Transport
2.2.3. LES
2.2.4. Energy Transport
2.2.5. Equation of State
2.2.6. FDS Modelling of the Ethanol Burner
- (1)
- The thermal diffusivity of the ethanol is low (the ratio between the thermal conductivity and the heat capacity multiplied by the density). Therefore, the heat front penetrates within a short distance inside the ethanol pool.
- (2)
- The radiative heat flux is attenuated inside the liquid phase.
- (3)
- The internal flow inside the liquid can be neglected (natural convection). Therefore, the convective heat transfer inside the ethanol liquid pool can be neglected.
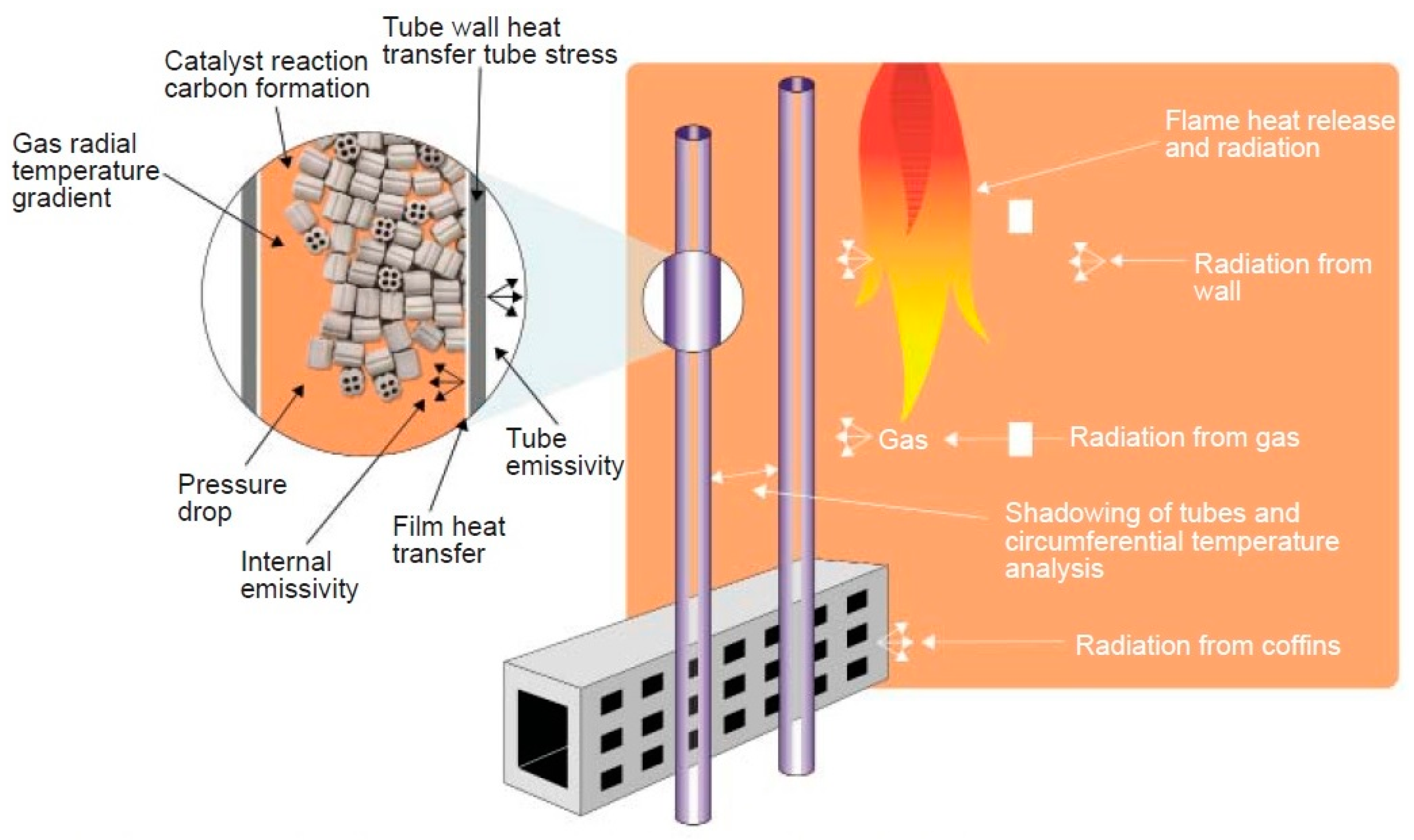
2.3. Multiphysics Analysis of the Reformer Model
2.3.1. Model Kinetics—Reformer Bed
2.3.2. Fluid Flow—Reformer Bed
2.3.3. Energy Transport—Reformer Bed
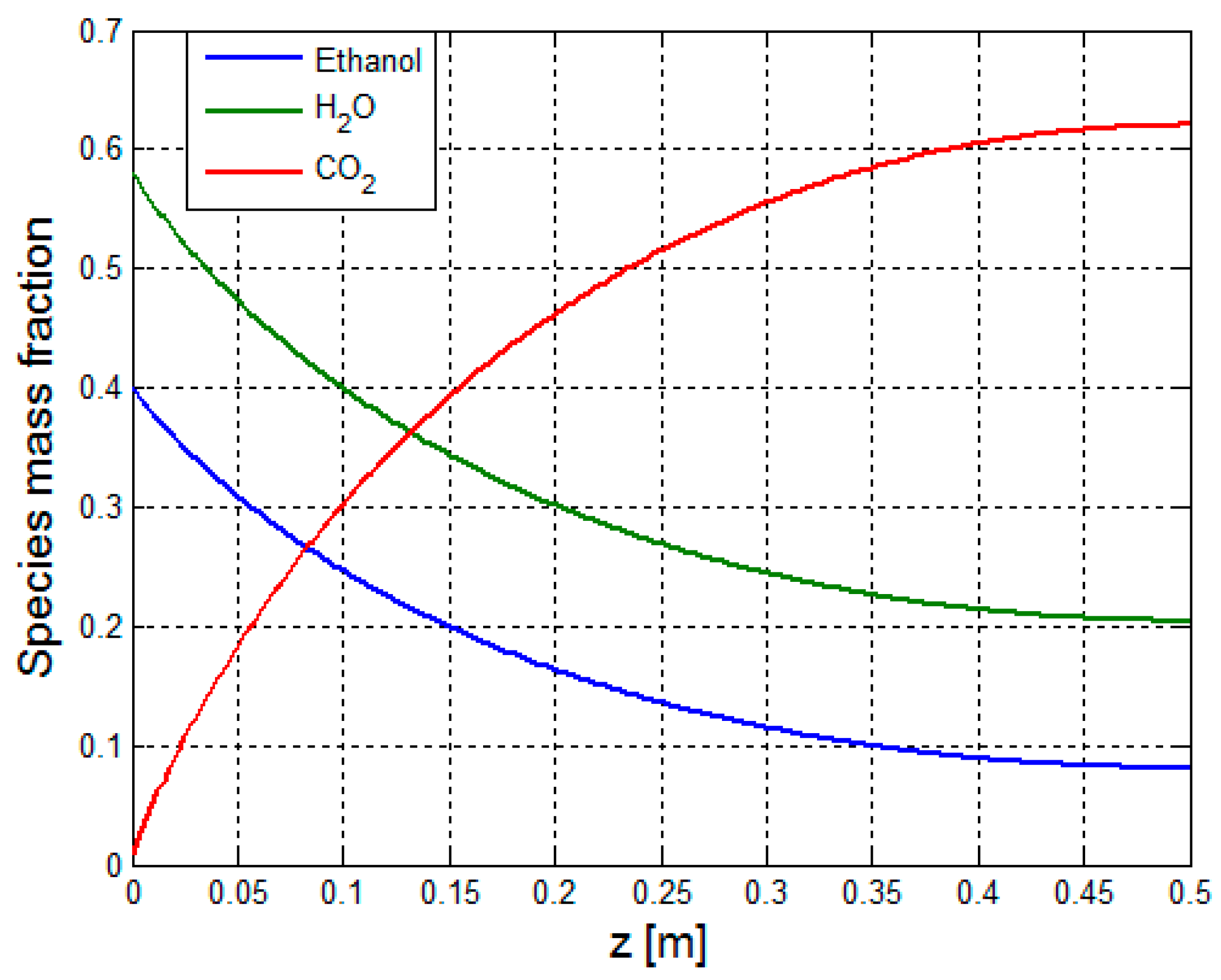
2.3.4. Mass Transport—Reformer Bed
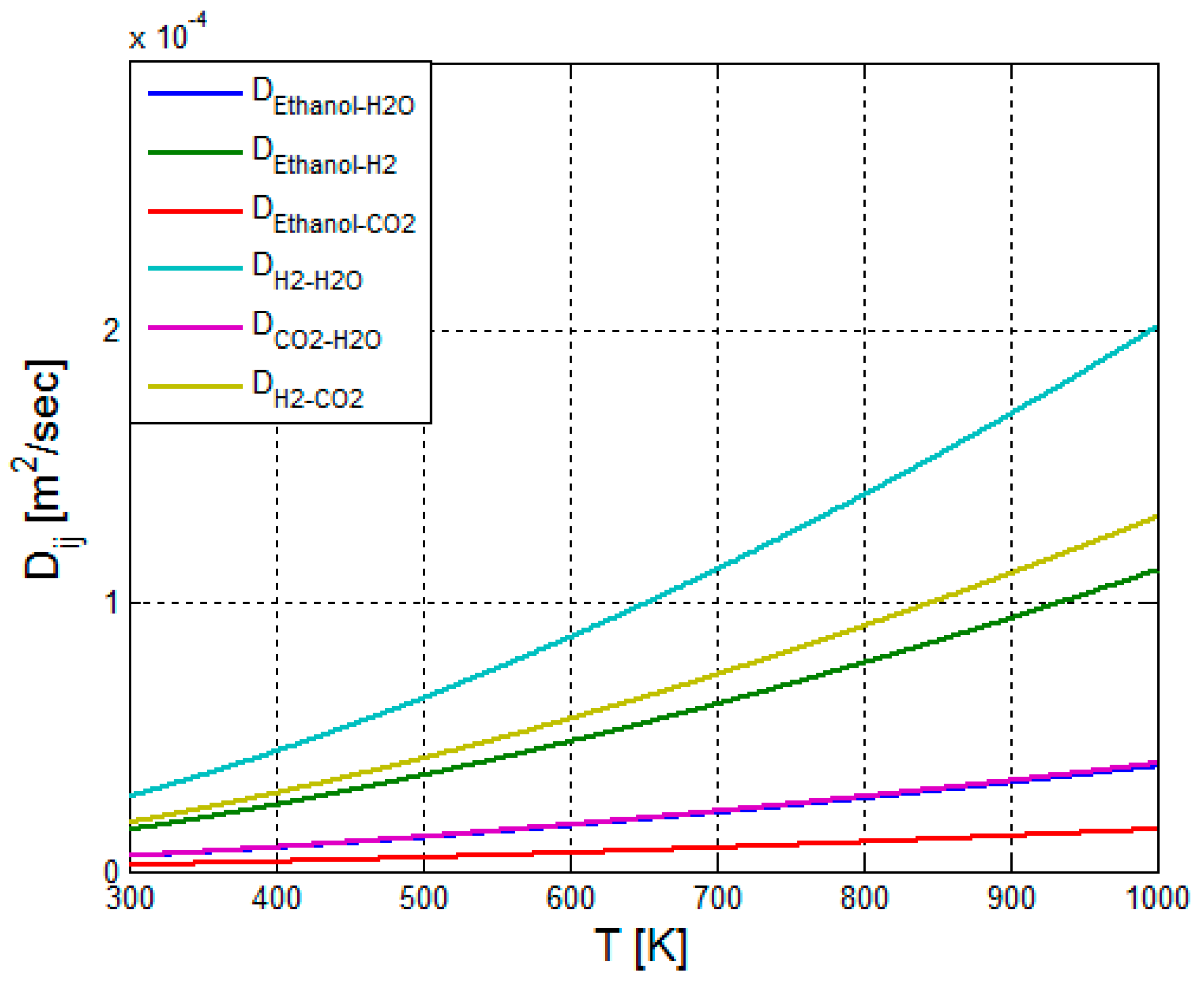
2.3.5. Calculation of the Binary Diffusion Coefficients—Reformer Bed
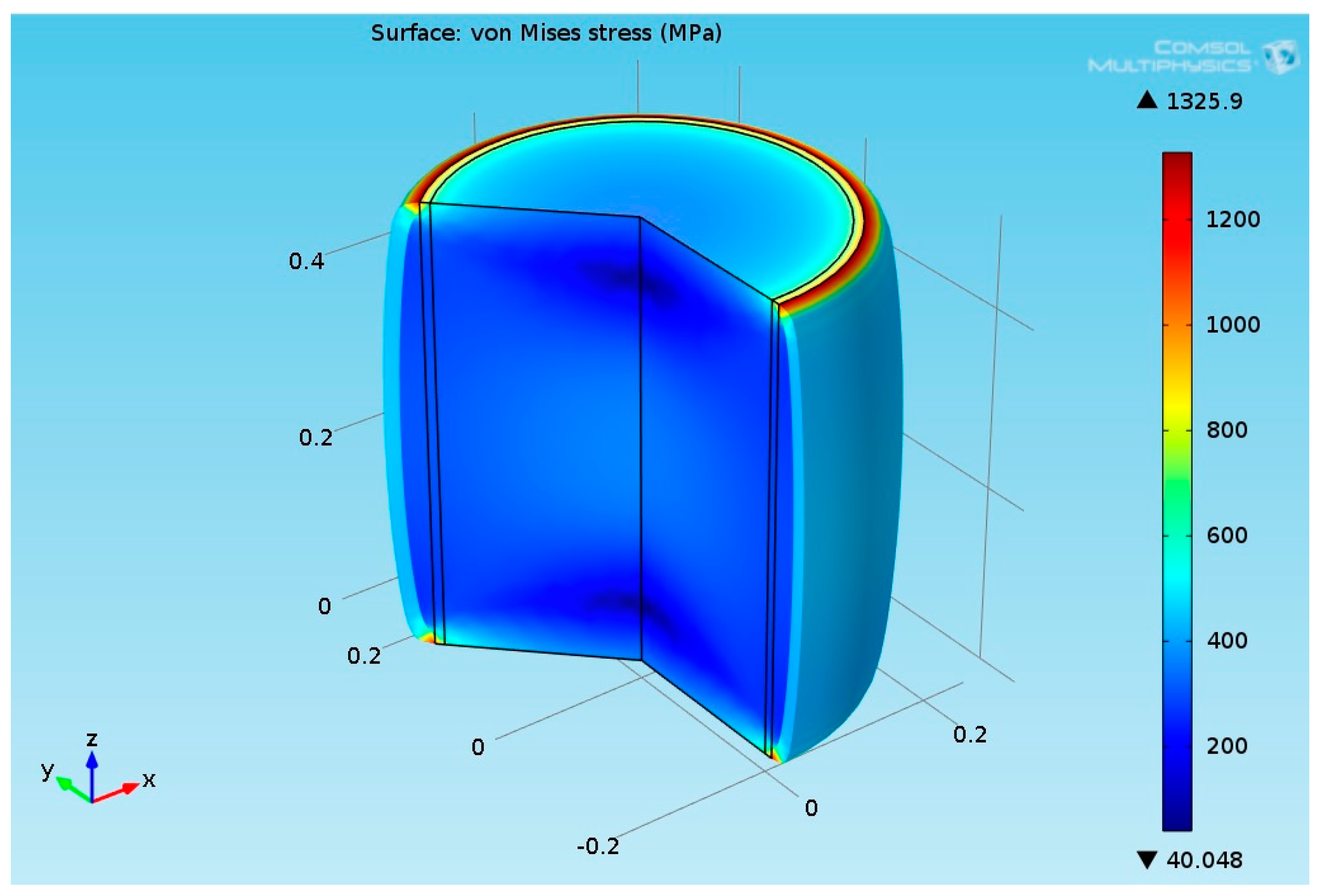
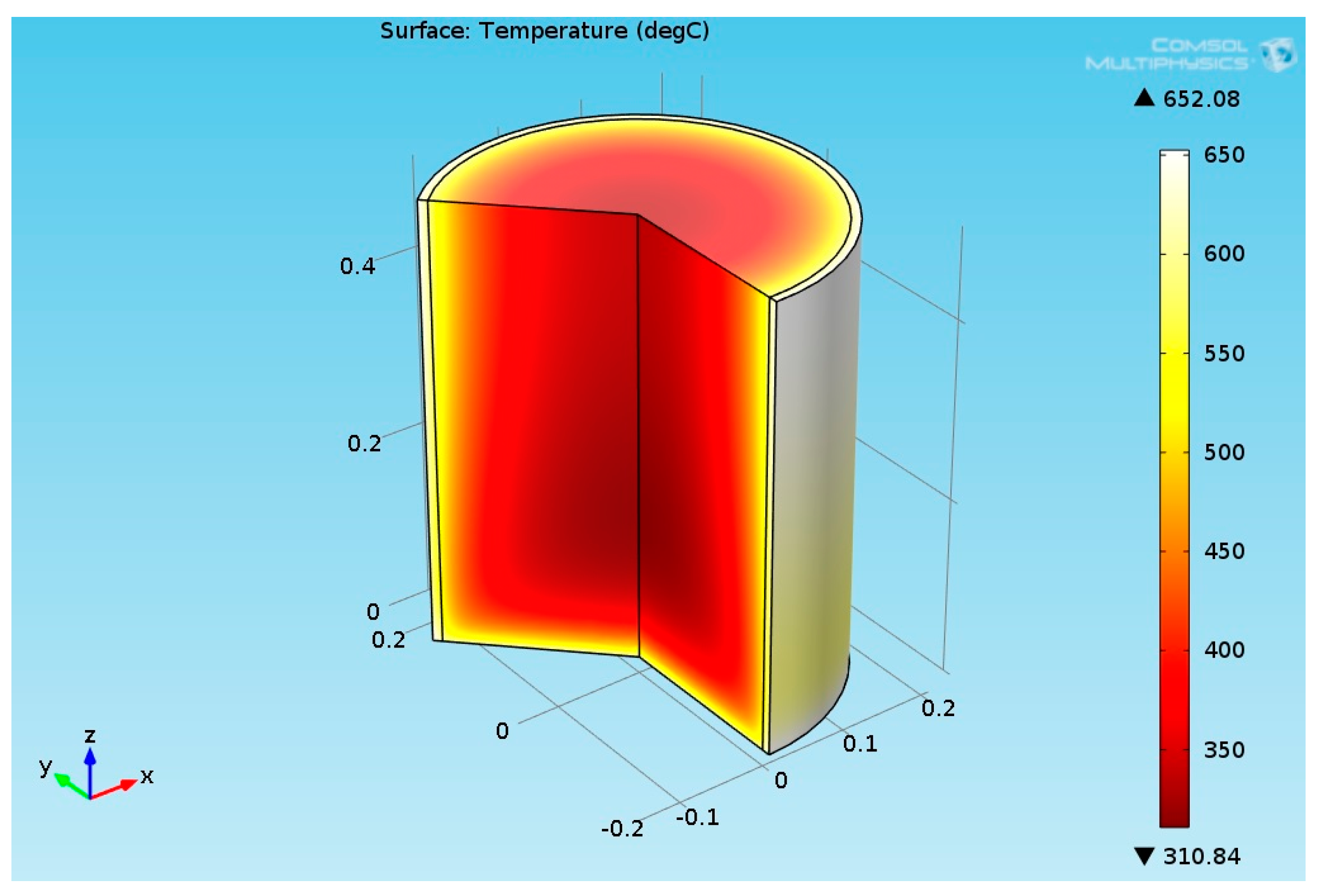
2.3.6. Structural Analysis—Reformer Bed and Steel Tube
3. Results
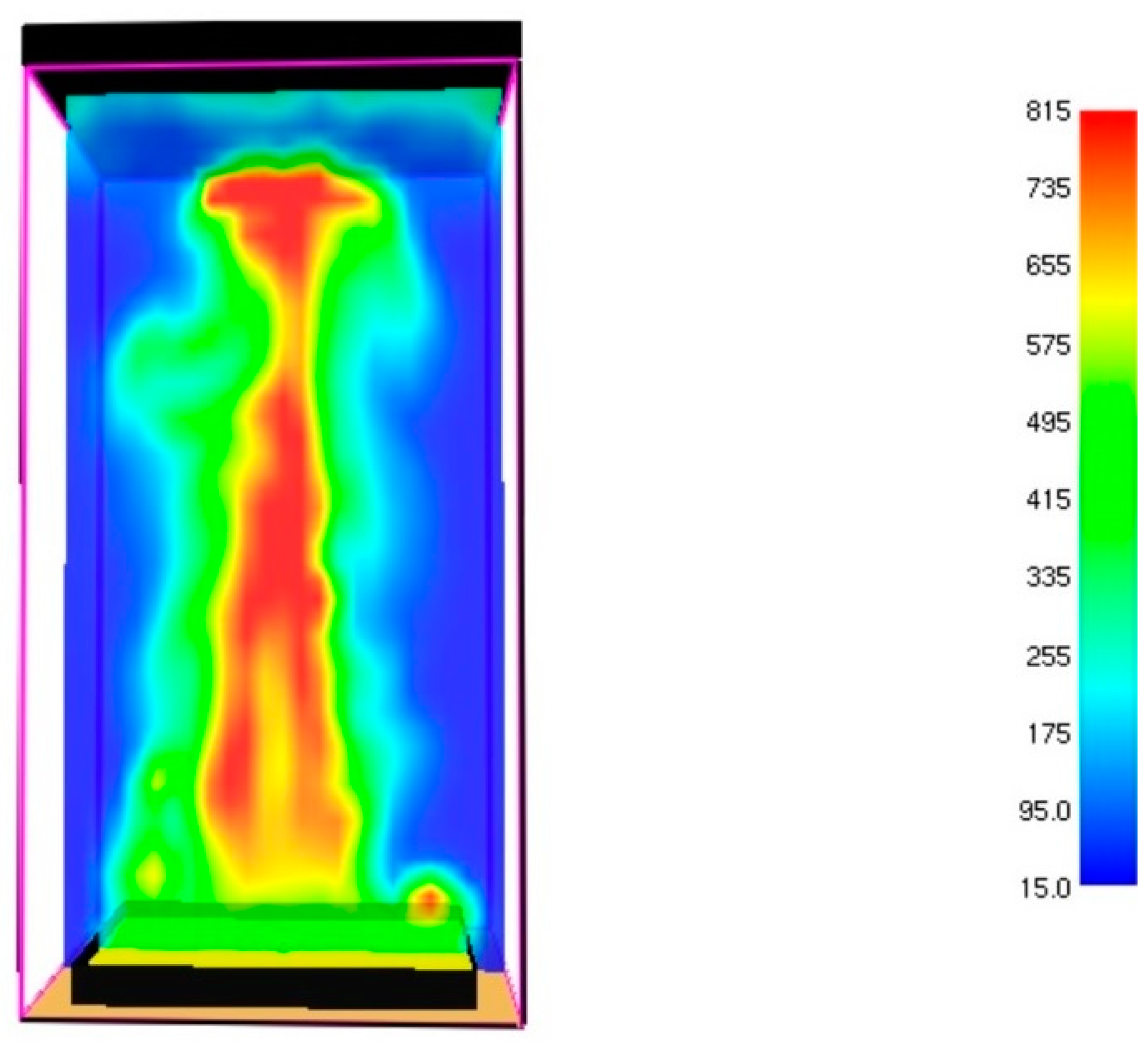
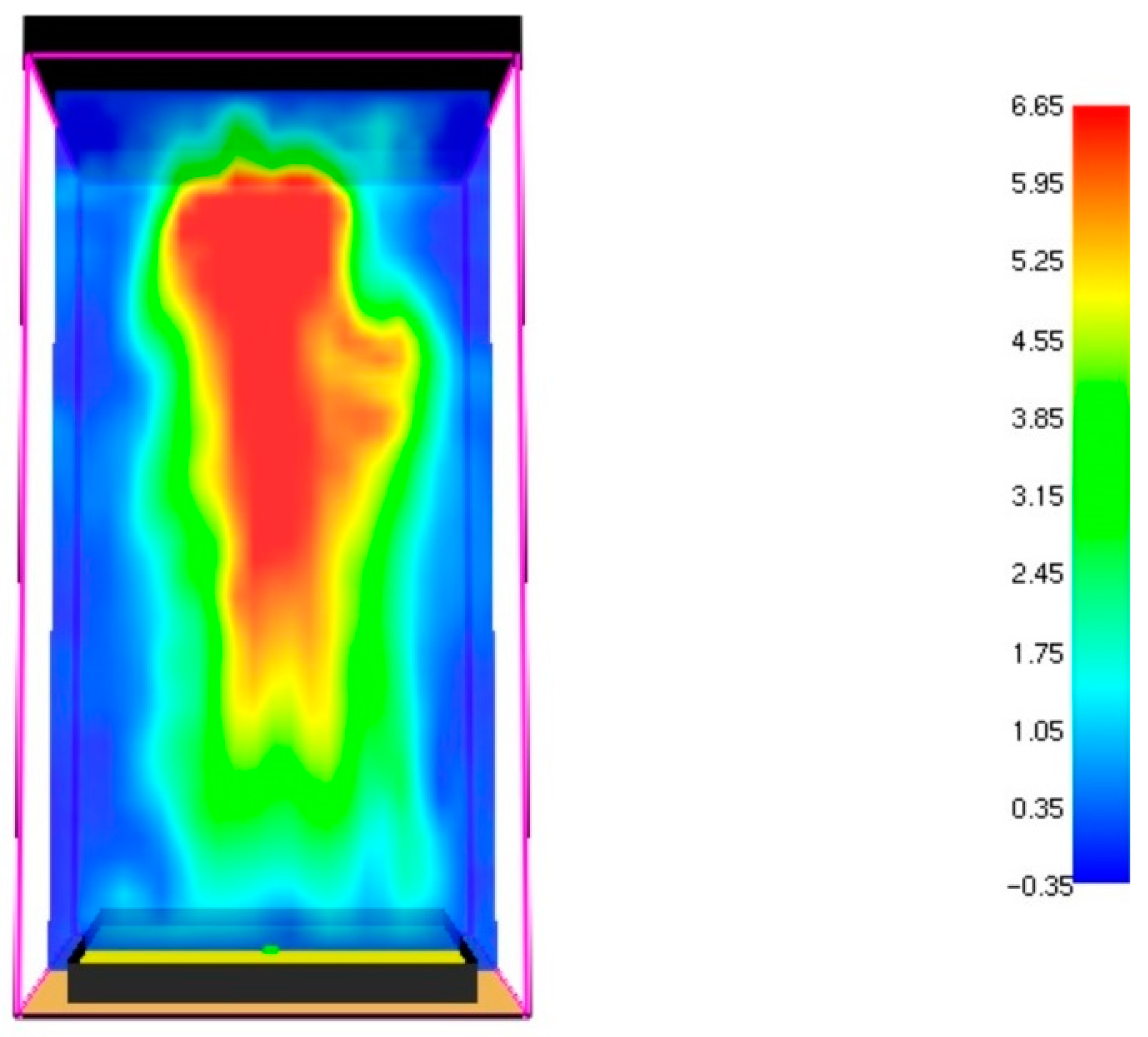
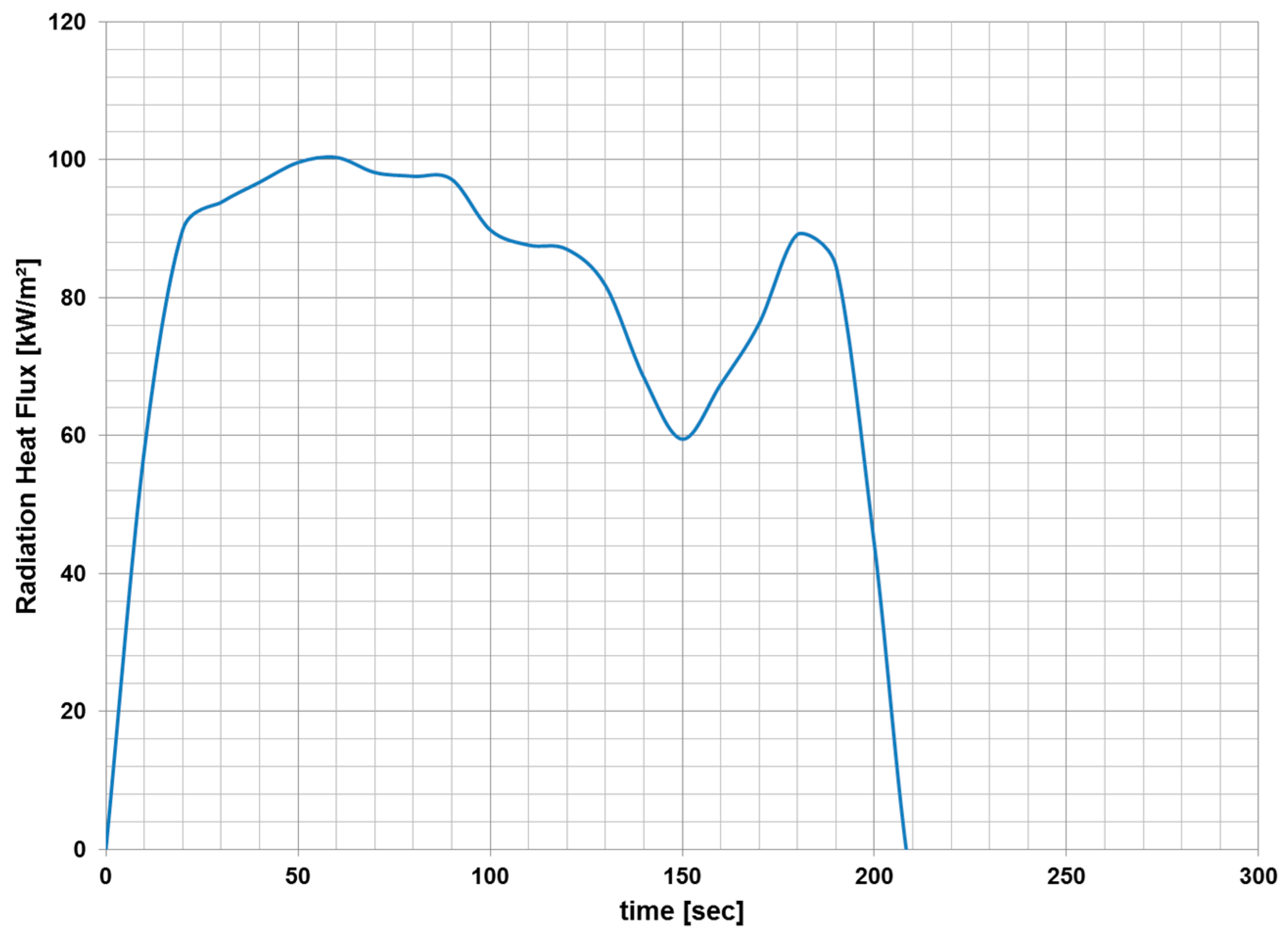
3.1. Fire Dynamics Simulator Software Results
3.2. Multi-Physics Analysis of the Operation of the Ethanol Steam Reformer
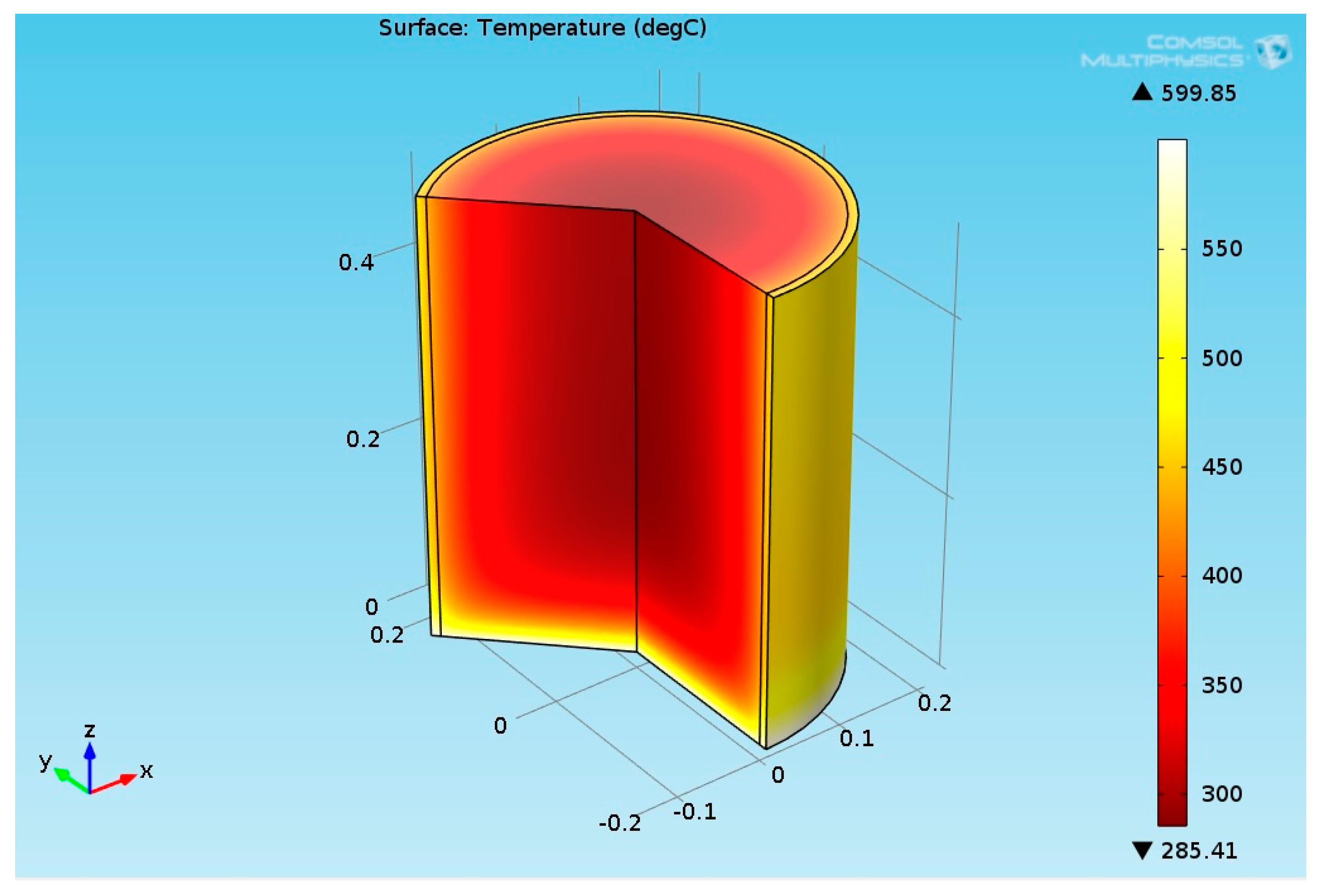
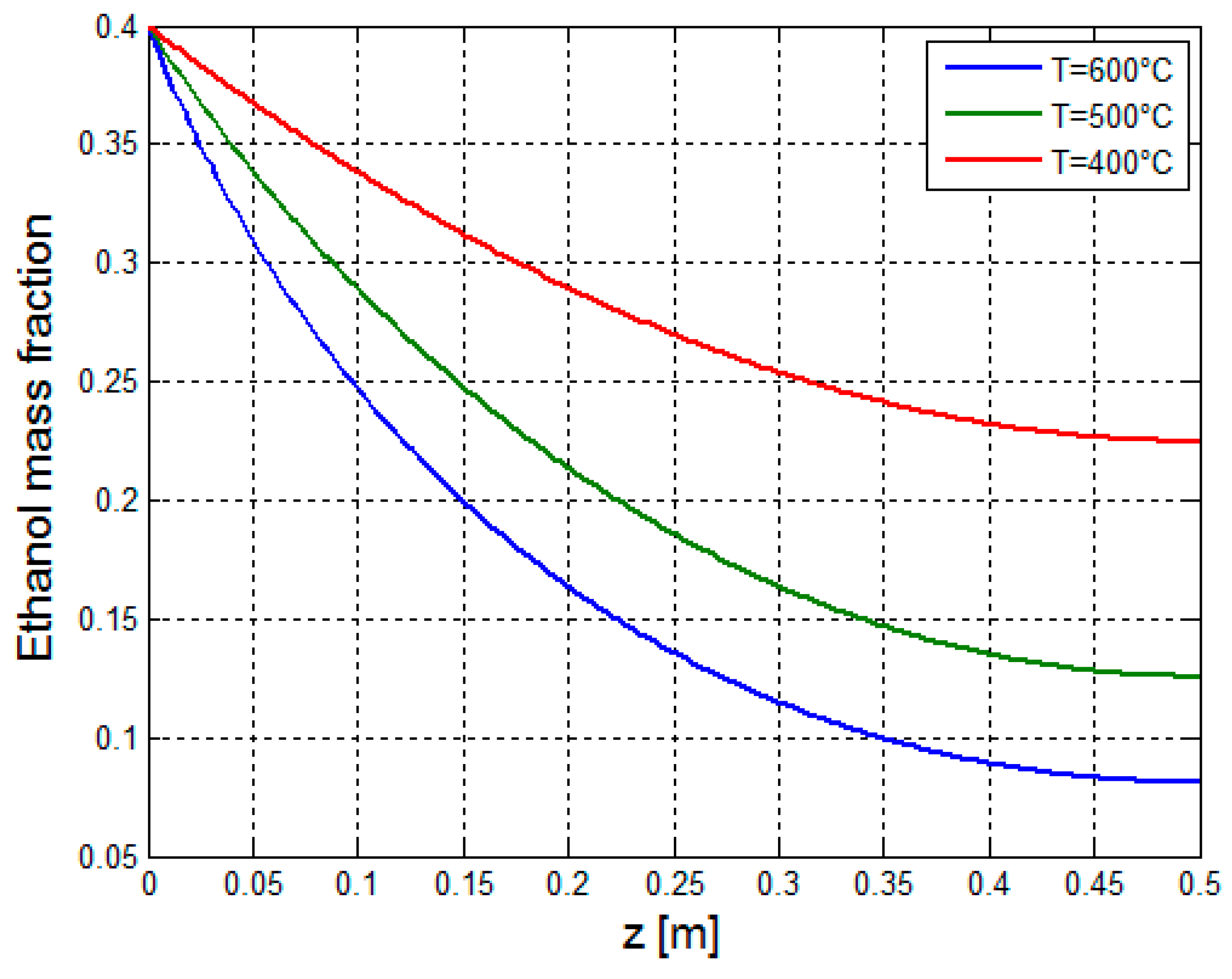
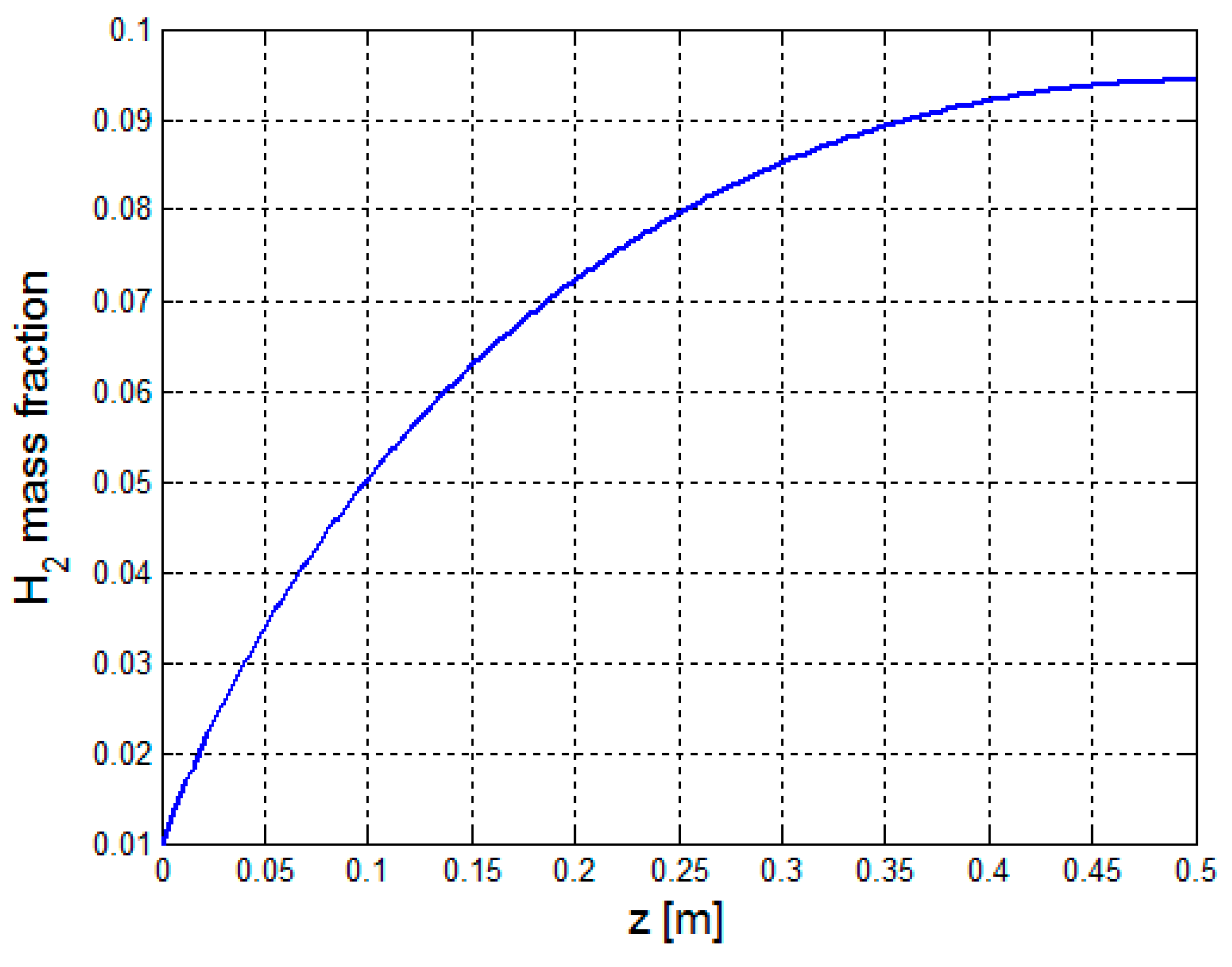
3.2.1. Multiphysics Results for Low Heat Flux Input
3.2.2. Multiphysics Results for High Heat Flux Input
4. Discussion
5. Conclusions
Funding
Conflicts of Interest
References
- Poran, A.; Tartakovsky, L. Performance and emissions of a direct injection internal combustion engine devised for joint operation with a high-pressure thermochemical recuperation system. Energy 2017, 124, 214–226. [Google Scholar] [CrossRef]
- Akande, A.; Aboudheir, A.; Idem, R.; Dalai, A. Kinetic modeling of hydrogen production by the catalytic reforming of crude ethanol over a co-precipitated Ni-Al2O3 catalyst in a packed bed tubular reactor. Int. J. Hydrogen Energy 2006, 31, 1707–1715. [Google Scholar] [CrossRef]
- Marino, F.; Boveri, M.; Baronetti, G.; Laborde, M. Hydrogen production from steam reforming of bioethanol using Cu/Ni/K/γ-Al2O3 catalysts. Effect of Ni. Int. J. Hydrogen Energy 2001, 26, 665–668. [Google Scholar] [CrossRef]
- Bineli, A.R.; Tasić, M.B. Catalytic Steam Reforming of Ethanol for Hydrogen Production: Brief Status. Chem. Ind. Chem. Eng. Q. 2016, 22, 327–332. [Google Scholar] [CrossRef]
- Akande, A.J. Production of Hydrogen by Reforming of Crude Ethanol. Master’s Thesis, University of Saskatchewan, Saskatoon, SK, Canada, 2005. [Google Scholar]
- Athanasios, N.F.; Kondaridesm, D.I. Production of hydrogen for fuel cells by reformation of biomass-derived ethanol. Catal. Today 2002, 75, 145–155. [Google Scholar]
- Klouz, V.; Fierro, V.; Denton, P.; Katz, H.; Lisse, J.P.; Bouvot-mauduit, S.; Mirodatos, C. Ethanol reforming for hydrogen production in a hybrid electric vehicle: Process optimization. J. Power Sources 2002, 105, 26–34. [Google Scholar] [CrossRef]
- Uriz, I.; Arzamendi, G.; López, E.; Llorca, J.; Gandía, L.M. Computational fluid dynamics simulation of ethanol steam reforming in catalytic wall micro channels. Chem. Eng. J. 2011, 167, 603–609. [Google Scholar] [CrossRef]
- Uriz, I.; Arzamendi, G.; Diéguez, P.M.; Gandía, L.M. Computational fluid dynamics as a tool for designing hydrogen energy technologies. In Renewable Hydrogen Technologies: Production, Purification, Storage, Applications and Safety; Elsevier: Oxford, UK, 2013; Chapter 17; pp. 401–435. [Google Scholar]
- Lao, L.; Aguirre, A.; Tran, A.; Wu, Z.; Durand, H.; Christofides, P.D. CFD modeling and control of a steam methane reforming reactor. Chem. Eng. Sci. 2016, 148, 78–92. [Google Scholar] [CrossRef]
- Lewis, B.; Von Elbe, G. Combustion Flames and Explosion of Gases, 2nd ed.; Academic Press Inc.: New York, NY, USA; London, UK, 1961. [Google Scholar]
- Diéguez, P.M.; López-San, M.J.; Idareta, I.; Uriz, I.; Arzamendi, G.G.; Luis, M. Hydrogen Hazards and Risks Analysis through CFD Simulations. In Renewable Hydrogen Technologies: Production, Purification, Storage, Applications and Safety; Elsevier: Oxford, UK, 2013; Chapter 18; pp. 437–452. [Google Scholar]
- Tartakosky, L.; Sheintoch, M. Fuel Reforming in Internal Combustion Engines. Prog. Energy Combust. Sci. 2018, 67, 88–114. [Google Scholar] [CrossRef]
- European Industrial Gases Association AISBL. Combustion Safety for Steam Reformer Operation; IGC Doc 172/12/E; European Industrial Gases Association AISBL: Brussels, Belgium, 2012. [Google Scholar]
- Olafadehan, O.A.; Ayoola, A.A.; Akintunde, O.O.; Adeniyi, V.O. Mechanistic Kinetic Models for Steam Reforming of Concentrated Crude Ethanol on Ni/Al2O3 Catalyst. J. Eng. Sci. Technol. 2015, 10, 633–653. [Google Scholar] [CrossRef]
- Loock, S.; Ernst, W.S.; Thomsen, S.G.; Jensen, M.F. Improving Carbon Efficiency in an Auto-Thermal Methane Reforming Plant with Gas Heated Heat Exchange Reforming technology. In Proceedings of the 7th World Congress of Chemical Engineering, Glasgow, UK, 10–14 July 2005. [Google Scholar]
- Carlsson, M. Carbon Formation in Steam Reforming and Effect of Potassium Promotion. Johnson Matthey Technol. Rev. 2015, 59, 313–318. [Google Scholar] [CrossRef]
- Heywood, J.B. Internal Combustion Engine Fundamentals; McGraw-Hill Book Company: New York, NY, USA, 1988. [Google Scholar]
- McGrattan, K. Fire Dynamics Simulator (Version 5)—Technical Reference Guide Volume 1: Mathematical Model; NIST Special Publication 1018; National Institute of Standards and Technology U.S. Department of Commerce: Gaithersburg, MD, USA, 2010.
- McGrattan, K.; Forney, G.P. Fire Dynamics Simulator (Version 5)—User’s Guide; NIST Special Publication 1019; National Institute of Standards and Technology U.S. Department of Commerce: Gaithersburg, MD, USA, 2010.
- McGrattan, K. Numerical Simulation of the Caldecott Tunnel Fire, April 1982; NISTIR 7231; National Institute of Standards and Technology U.S. Department of Commerce: Gaithersburg, MD, USA, 2005.
- Hu, L. A review of physics and correlations of pool fire behavior in wind and future challenges. Fire Saf. J. 2017, 91, 41–55. [Google Scholar] [CrossRef]
- Hamins, A.; Kashiwagi, T.; Bruch, R.R.; Toten, G.E. Fire Resistance of Industrial Fluids, ASTM STP 1284; Toten, G.E., Reichel, J.E., Eds.; American Society for Testing and Materials: Philadelphia, PA, USA, 1995. [Google Scholar]
- Thermo-Physical Properties of Ethanol. Available online: https://www.thermalfluidscentral.org/encyclopedia/index.php/Thermophysical_Properties:_Ethanol (accessed on 8 June 2018).
- De-Souza, Z.G.M.; Moraes, F.F. Parametric Study of Hydrogen Production from Ethanol Steam Reforming in Membrane Micro-reactor. Braz. J. Chem. Eng. 2013, 30, 355–367. [Google Scholar] [CrossRef]
- Neufeld, P.D.; Jansen, A.R.; Aziz, R.A. Empirical equations to calculate 16 of the transport collision integrals Ω(l,s)* for the Lennard-Jones (1216–) potential. J. Chem. Phys. 1972, 57, 1100–1102. [Google Scholar] [CrossRef]
- Perry, R.H.; Green, D.W.; Maloney, J.O. Perry’s Chemical Engineers’ Handbook, 7th ed.; McGraw Hill: New York, NY, USA, 1997. [Google Scholar]
- Kubota Metal Corporation. Fahramet Division, Alloy Data Sheet, Heat Resistant Alloy HK40; Kubota Metal Corporation: Orillia, ON, Canada, April 1991. [Google Scholar]
- Steel Founders’ Society of America. Steel Casting Handbook; Supplement 9, High Alloy Data Sheets Heat Series; Steel Founders’ Society of America: Crystal Lake, IL, USA, 2004. [Google Scholar]
- Van Echo, J.A.; Roach, D.B.; Hall, A.M. Short Time Tensile and Long-Time Creep Rupture Properties of the HK-40 Alloy and Type 310 Stainless Steel at Temperature to 2000 °C. ASME J. Basic Eng. Trans. 1967, 89, 465–478. [Google Scholar] [CrossRef]


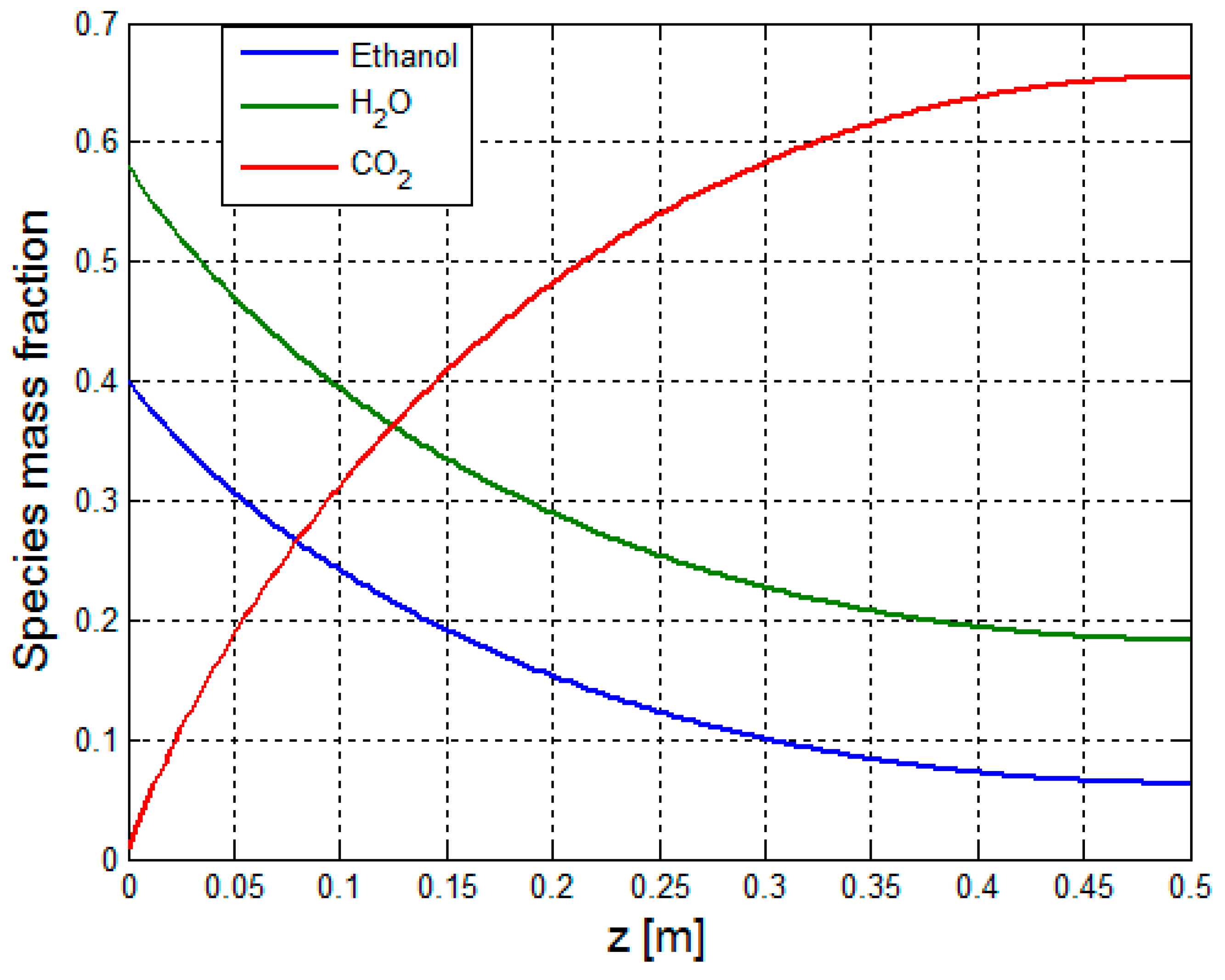
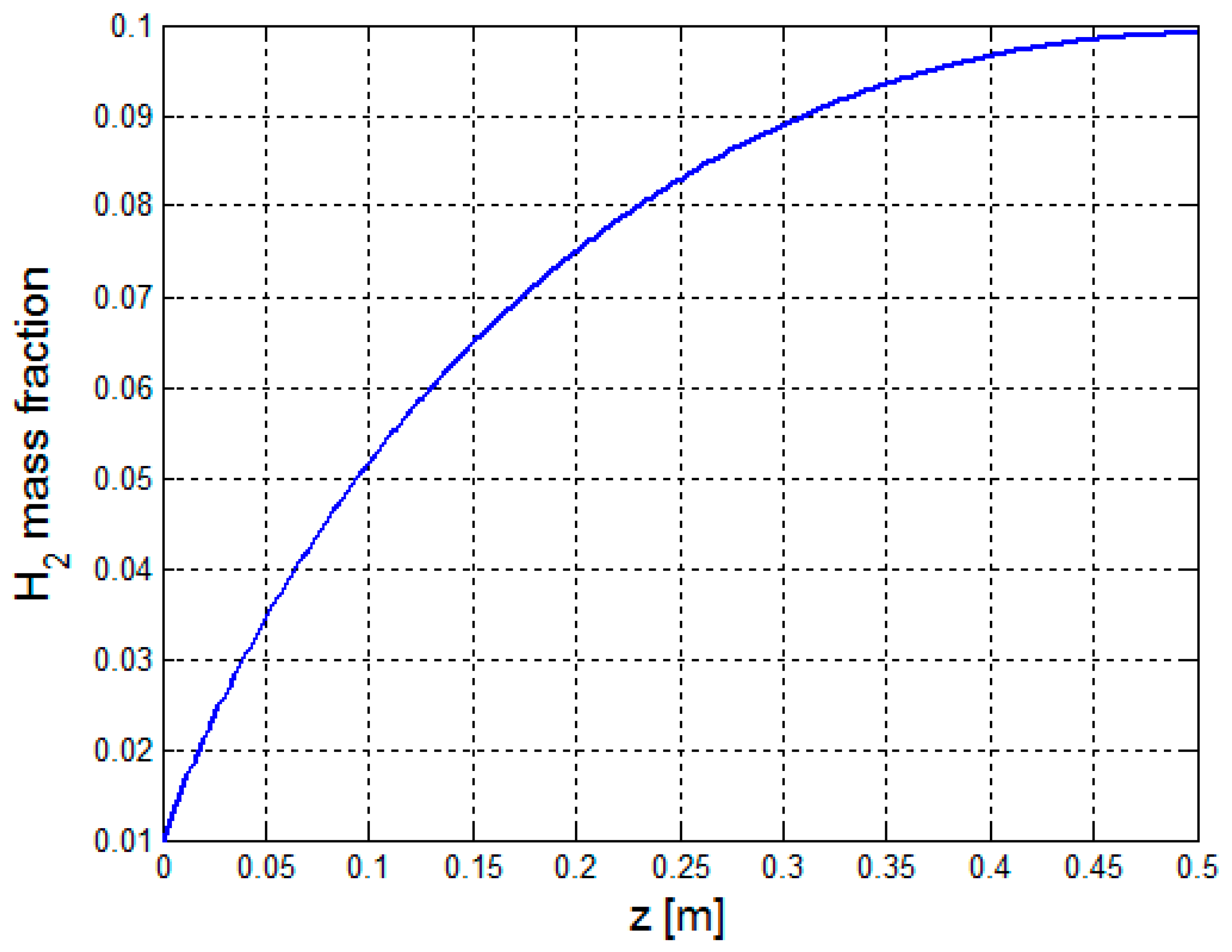


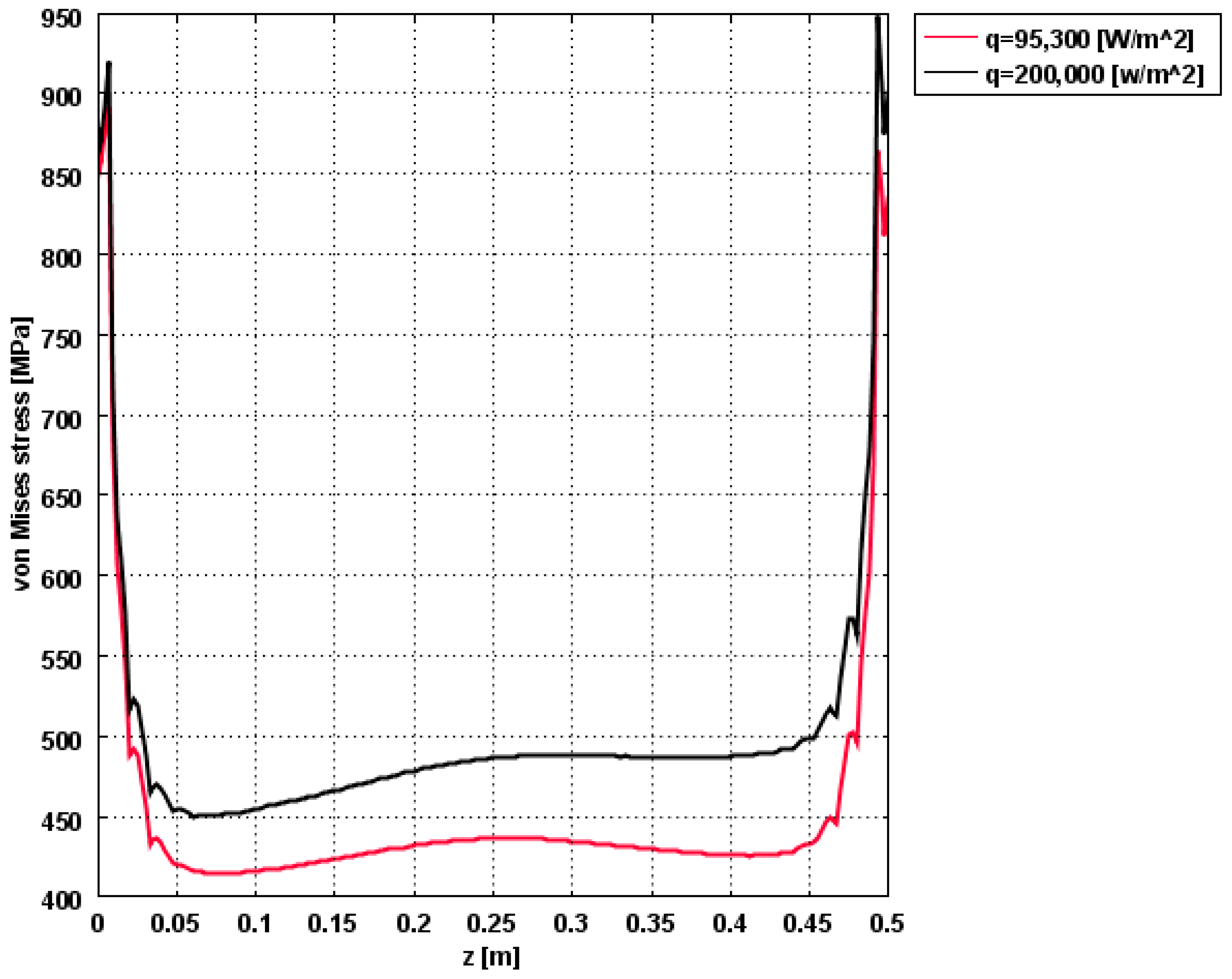
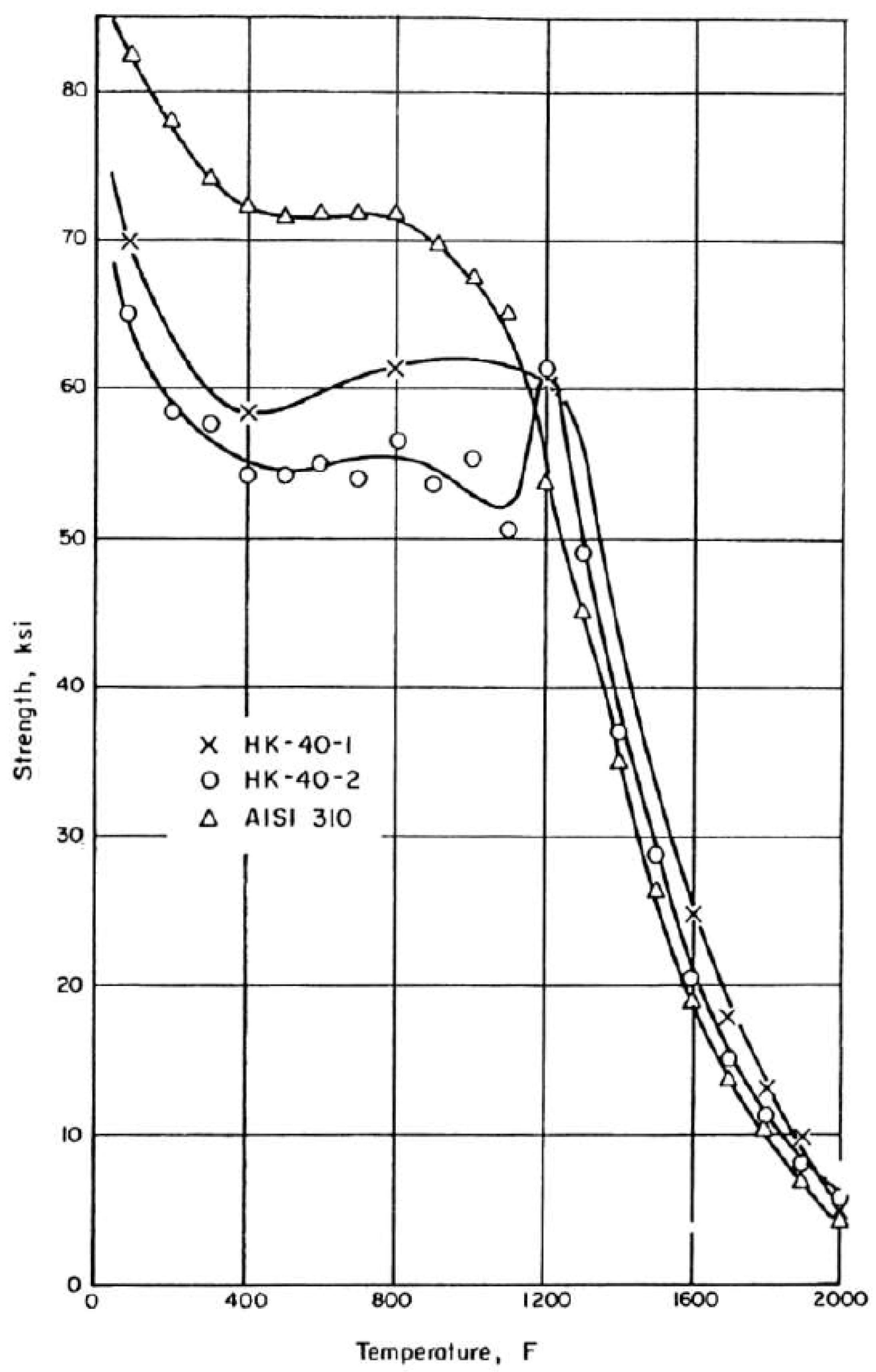

| Material Property | Value |
|---|---|
| rho | 3960 (kg/m3) |
| Cp | 880 (J/(kg·°C)) |
| k | 33 (w/(m·°C)) |
| Lennard-Jones Collision Diameter | (Angstroms) |
| Ethanol | 4.455 |
| H2O | 2.655 |
| CH4 | 3.882 |
| CO | 3.590 |
| CO2 | 3.996 |
| H2 | 2.968 |
| Maximum Attractive Energy between Two molecules | (K) |
| Ethanol | 391.0 |
| H2O | 363.0 |
| CH4 | 136.5 |
| CO | 110.3 |
| CO2 | 190.0 |
| H2 | 33.3 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Davidy, A. CFD Simulation of Ethanol Steam Reforming System for Hydrogen Production. ChemEngineering 2018, 2, 34. https://doi.org/10.3390/chemengineering2030034
Davidy A. CFD Simulation of Ethanol Steam Reforming System for Hydrogen Production. ChemEngineering. 2018; 2(3):34. https://doi.org/10.3390/chemengineering2030034
Chicago/Turabian StyleDavidy, Alon. 2018. "CFD Simulation of Ethanol Steam Reforming System for Hydrogen Production" ChemEngineering 2, no. 3: 34. https://doi.org/10.3390/chemengineering2030034
APA StyleDavidy, A. (2018). CFD Simulation of Ethanol Steam Reforming System for Hydrogen Production. ChemEngineering, 2(3), 34. https://doi.org/10.3390/chemengineering2030034




