Exergy Evaluation of Desalination Processes
Abstract
:1. Introduction
2. Energy, Entropy, and Exergy Relationship
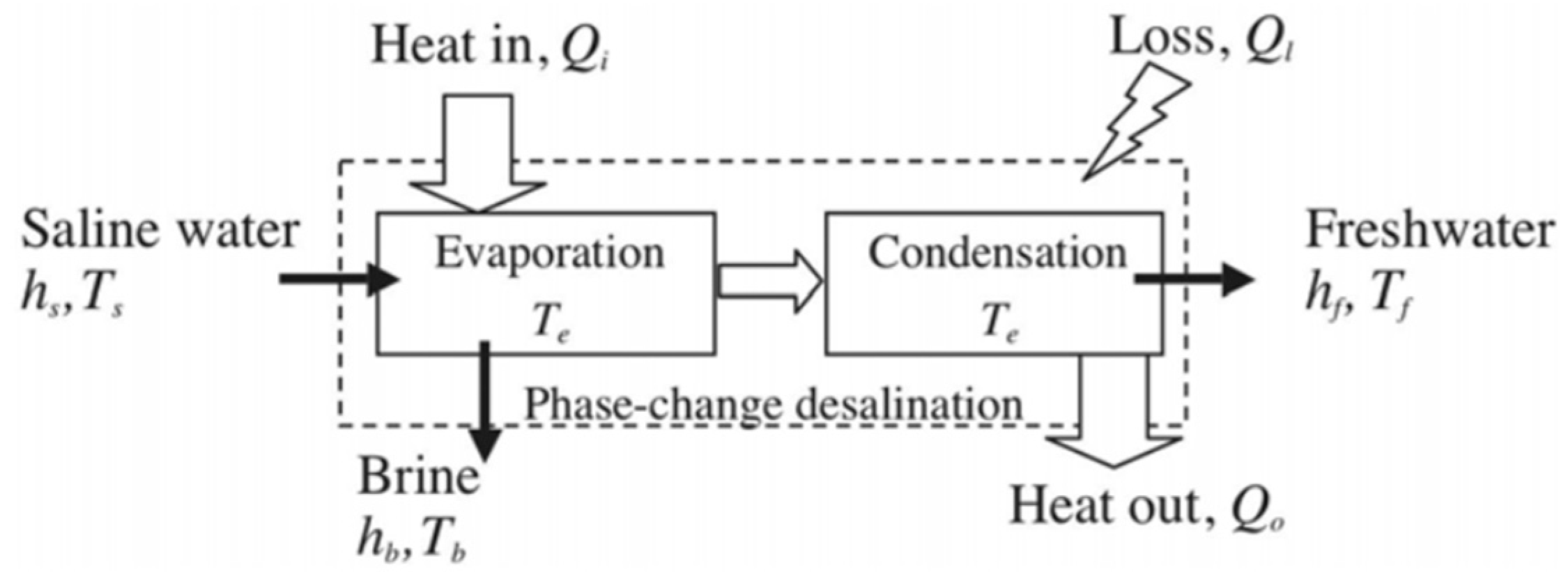
3. Desalination Processes and Operation Principles
4. Energy and Exergy Analysis of Desalination Processes
4.1. First Law of Thermodynamics
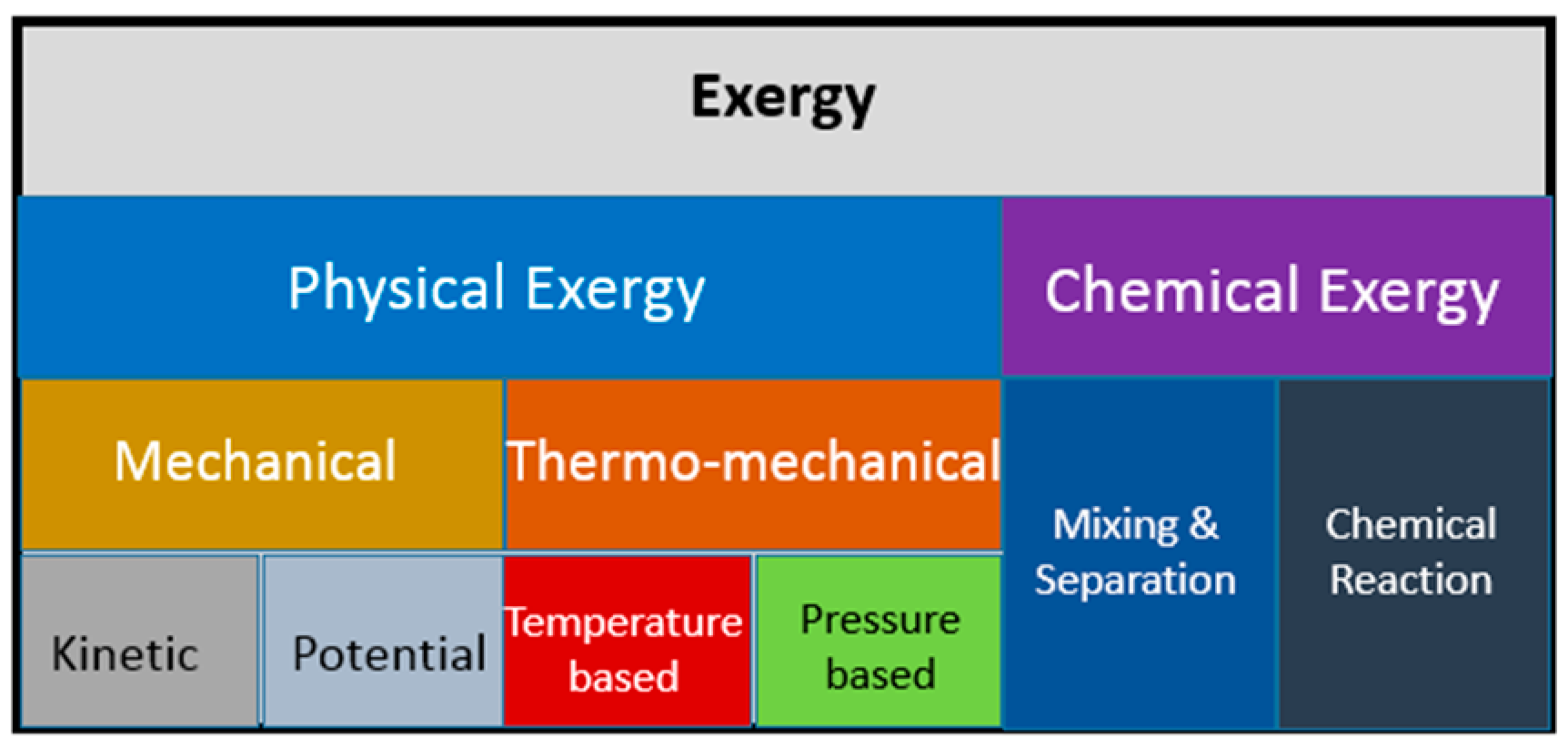
4.2. Exergy of Energy Flows
4.3. Exergy Analysis
4.4. Why Exergy Analysis in Desalination Processes
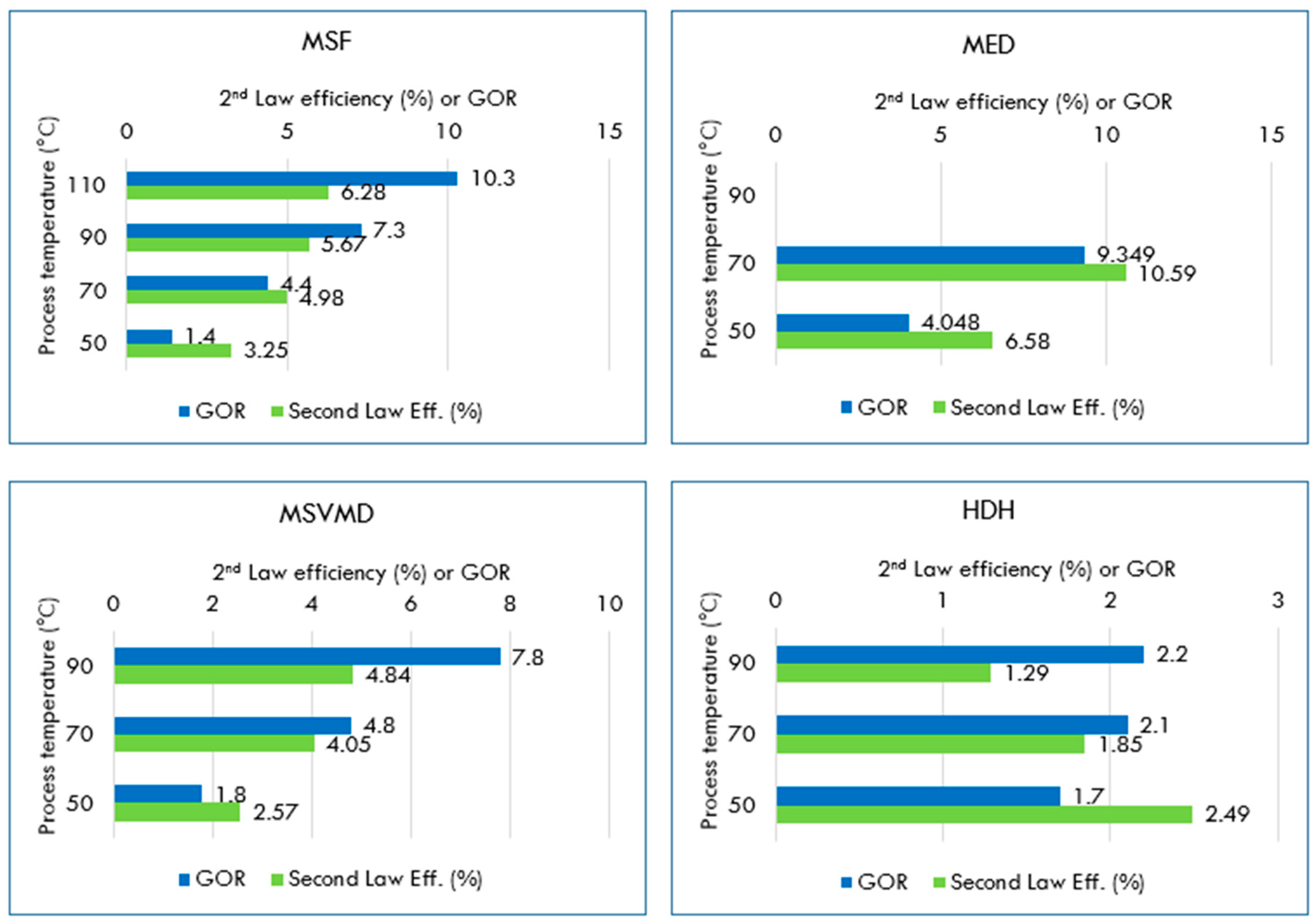
5. Case Studies for Desalination Exergy Performance Analysis
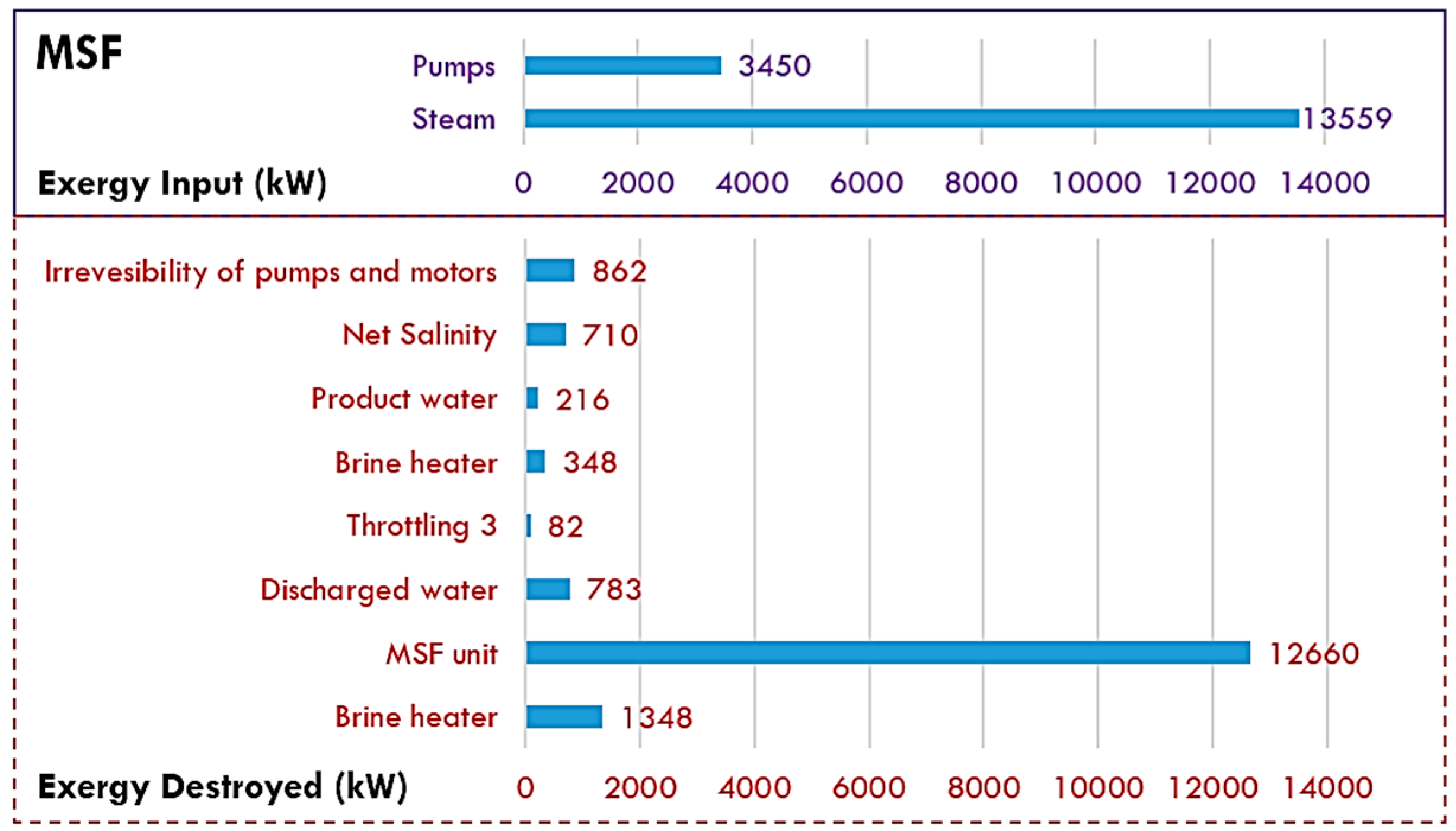
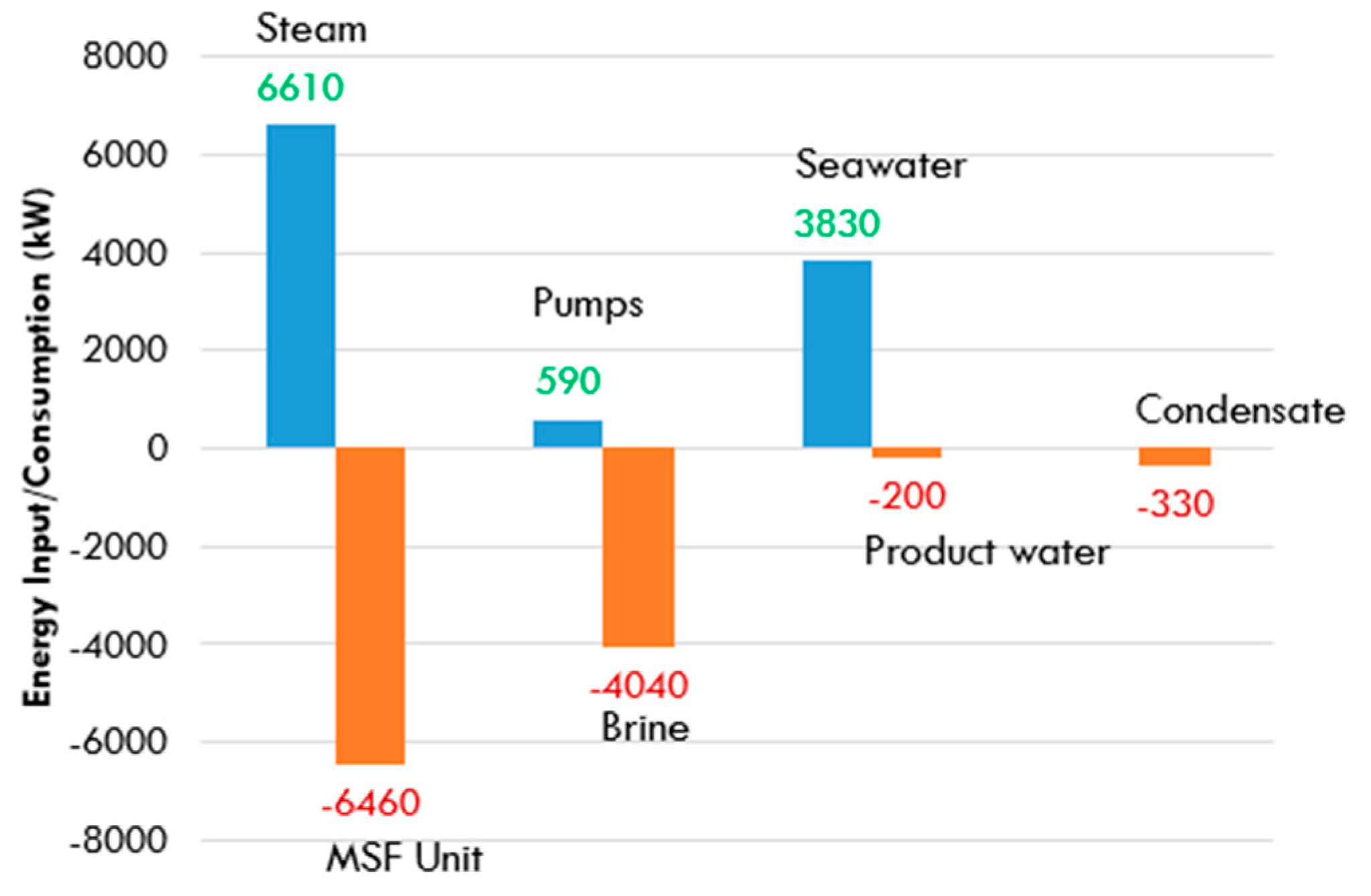
5.1. MSF Desalination
5.2. Multi-Effect Distillation (MED) or Evaporation (MEE) Process
5.2.1. Exergy Evaluation of MED Process
5.2.2. MED-TVC Process
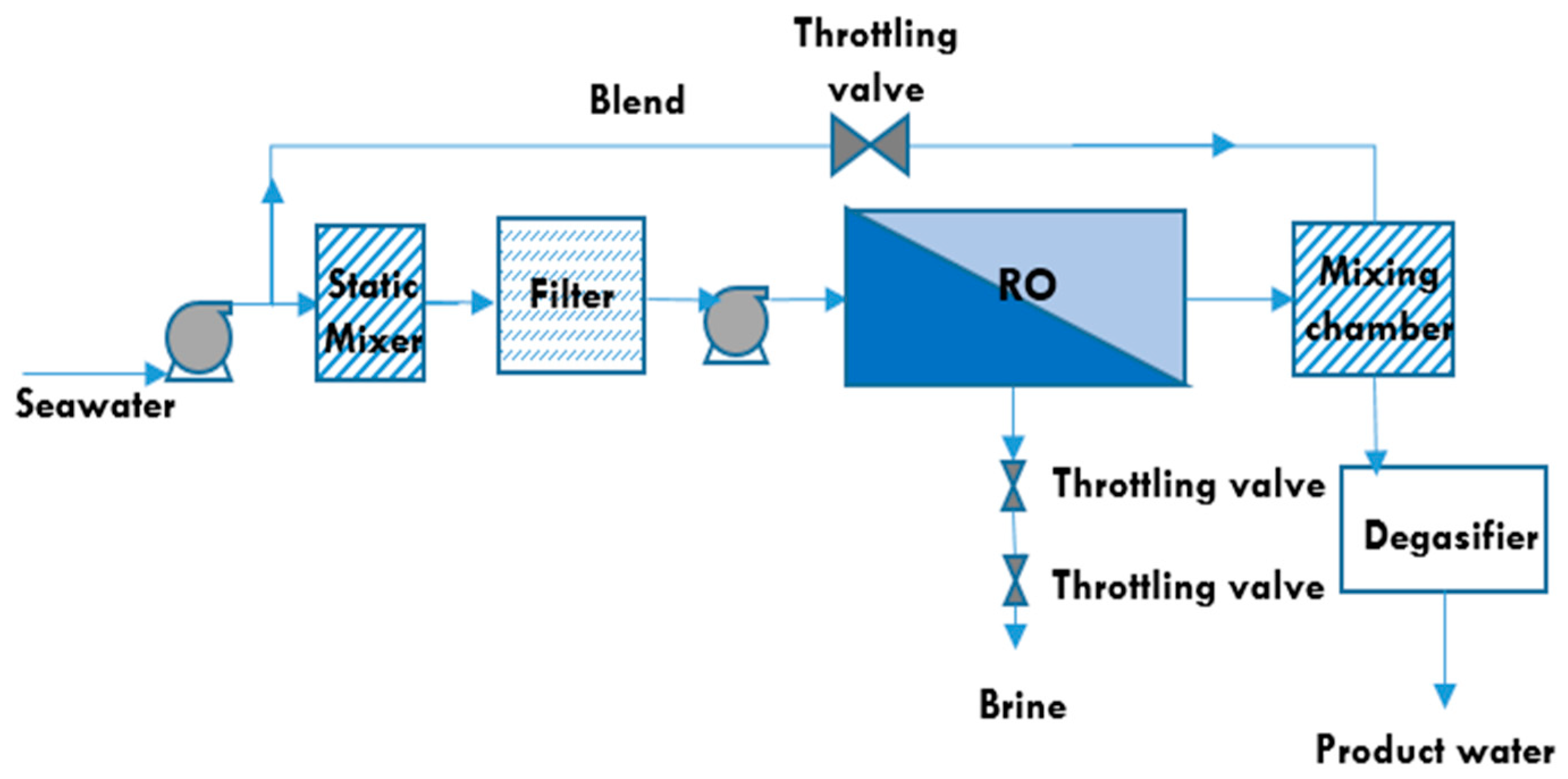
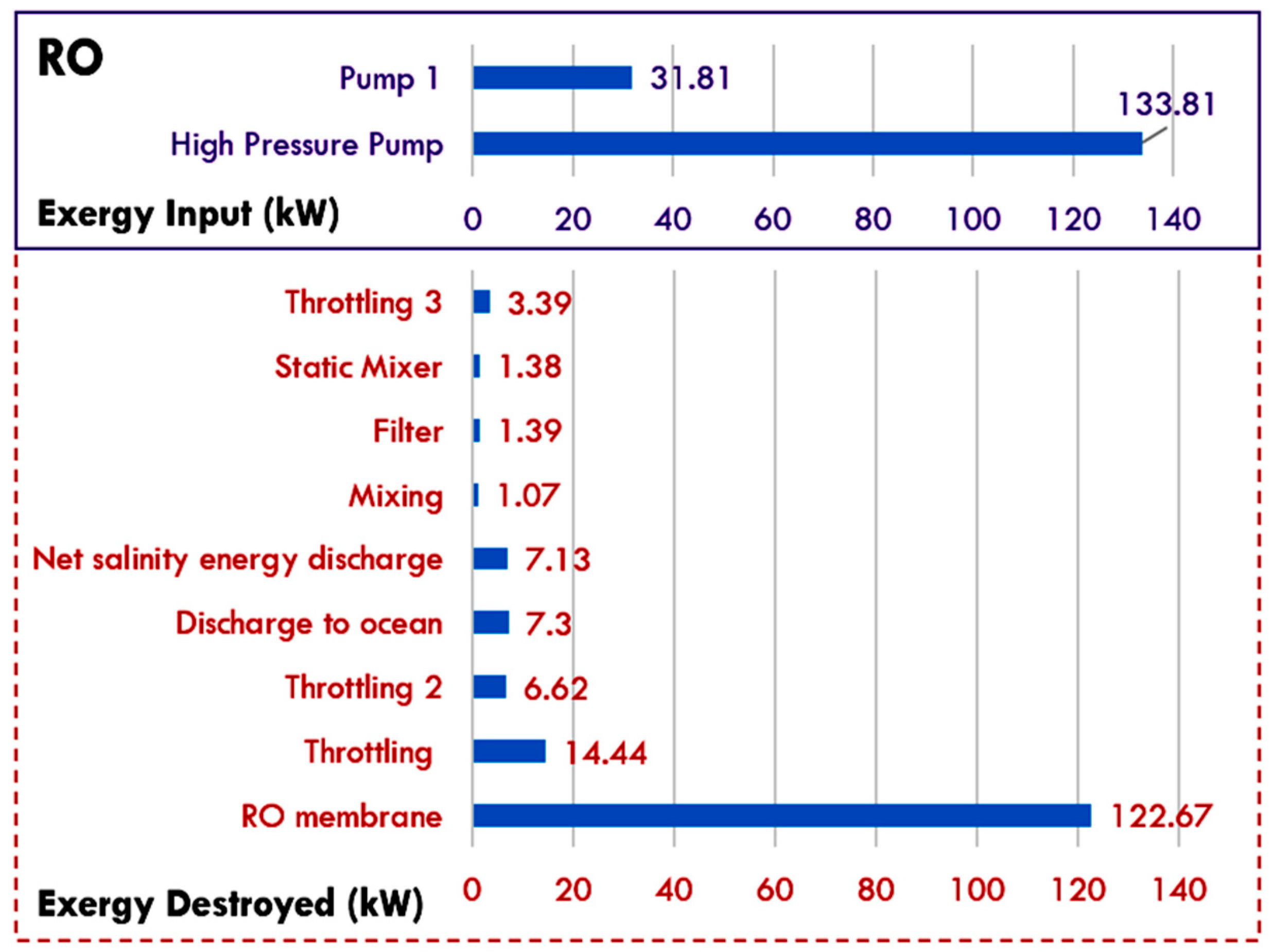
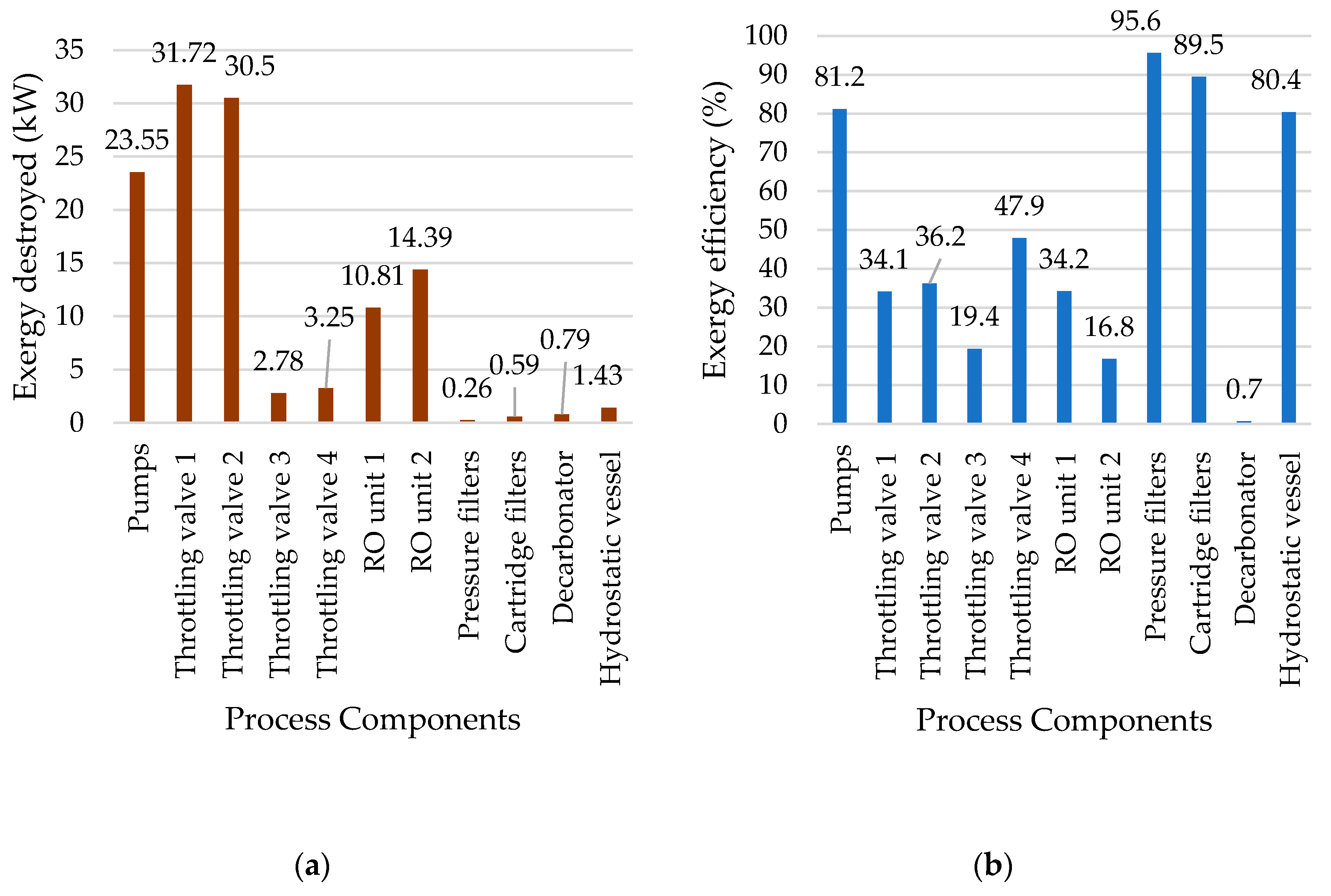
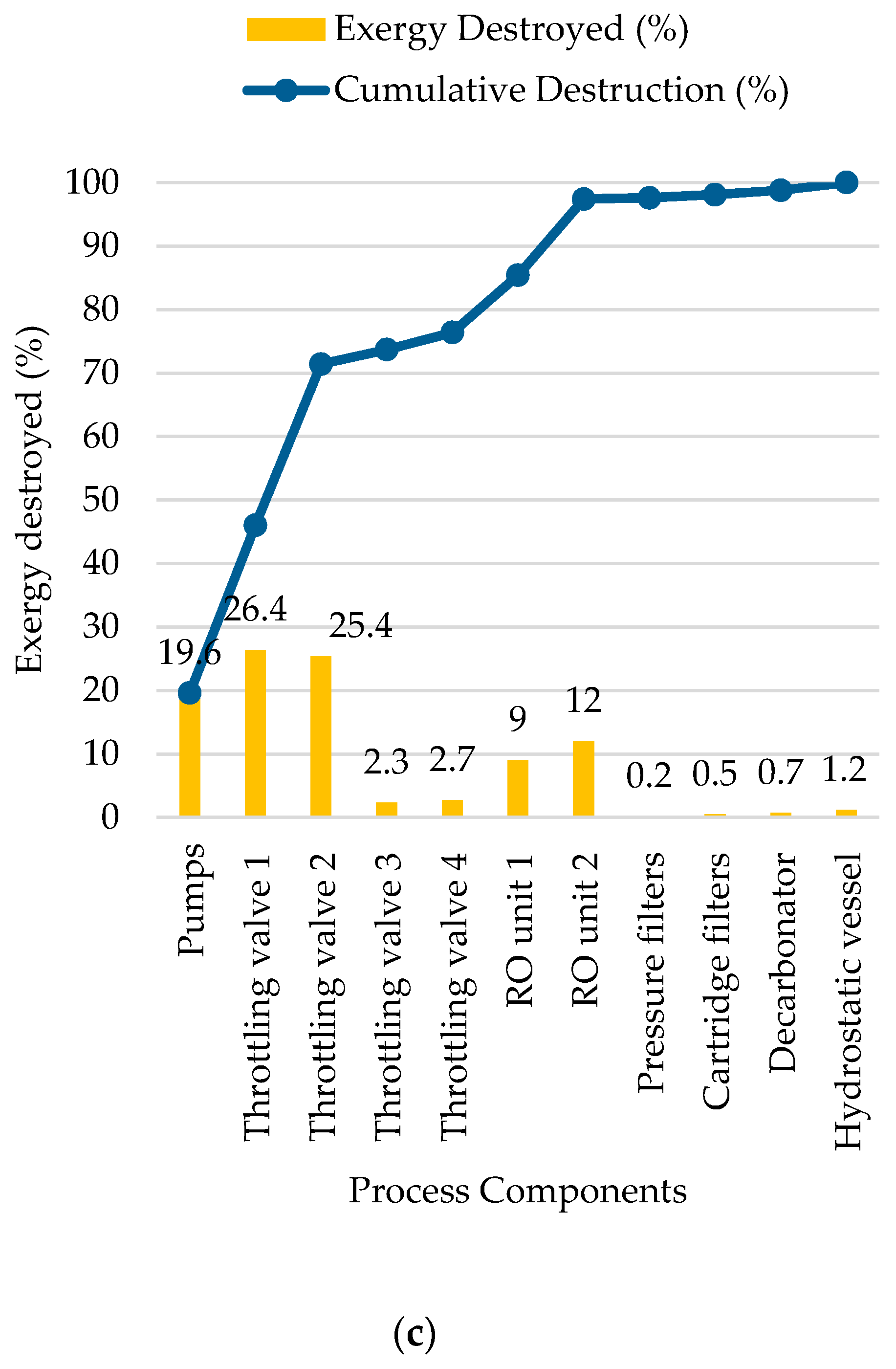
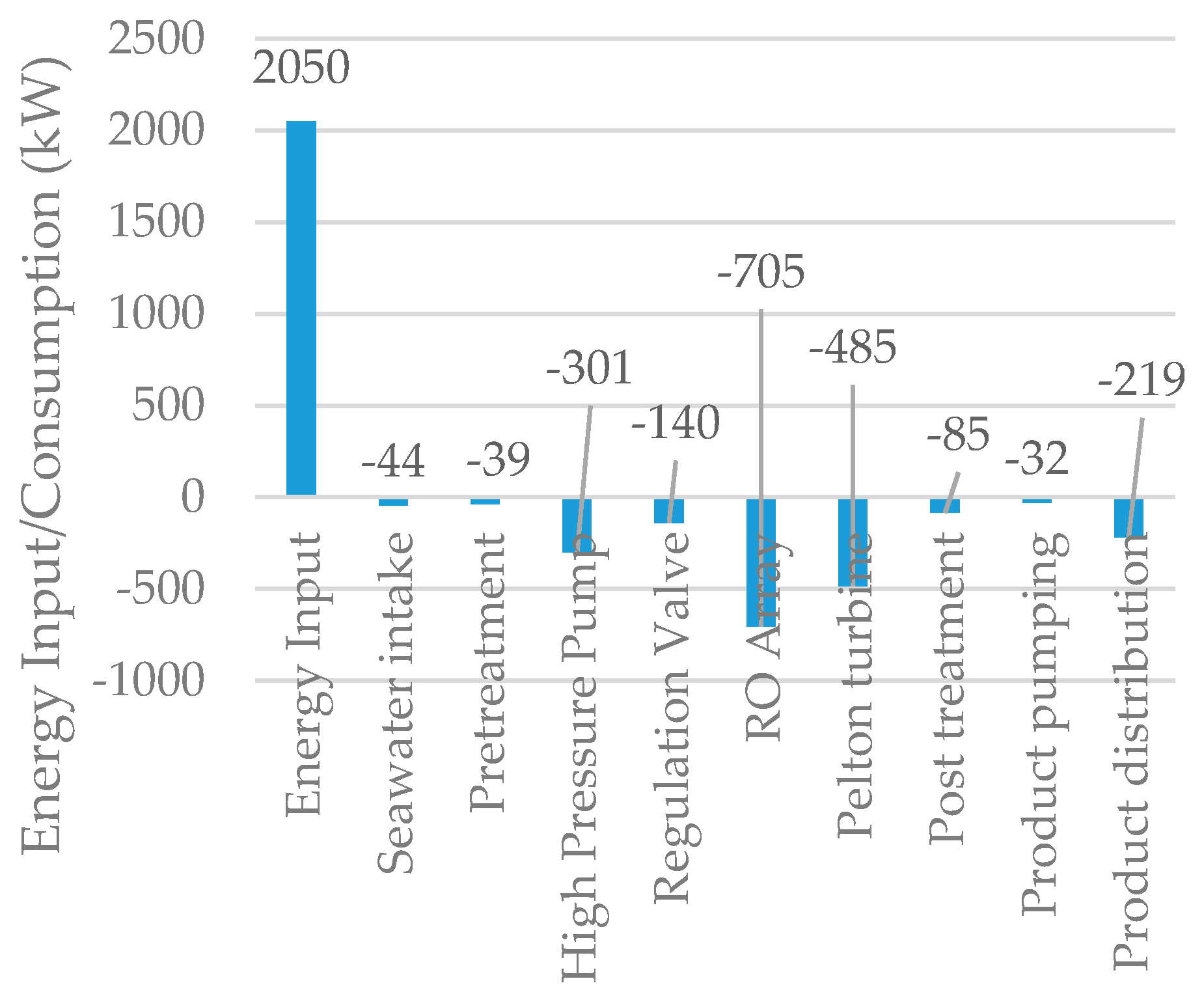
5.3. Reverse Osmosis Membrane Process
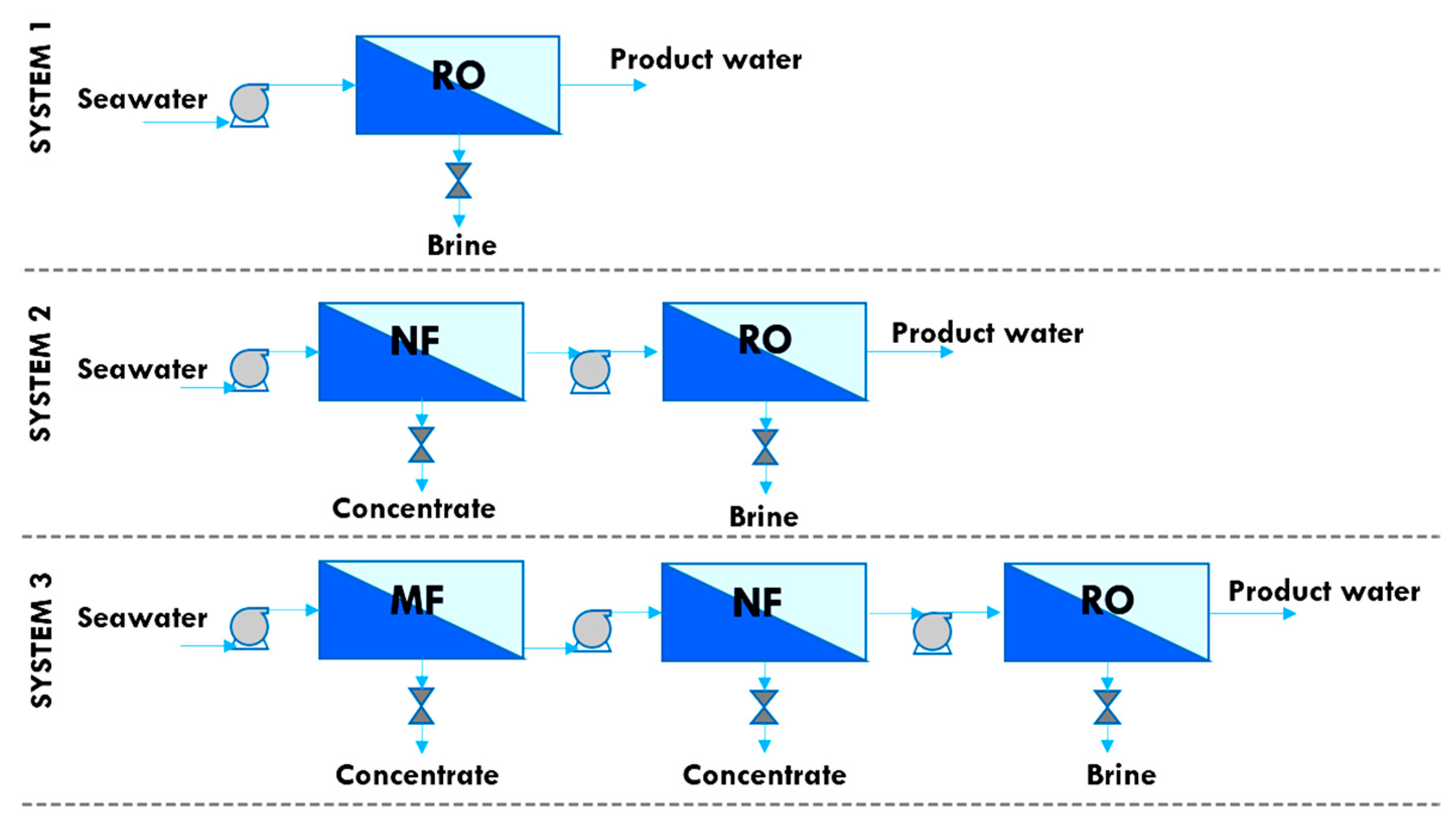
5.4. Integrated Membrane Systems
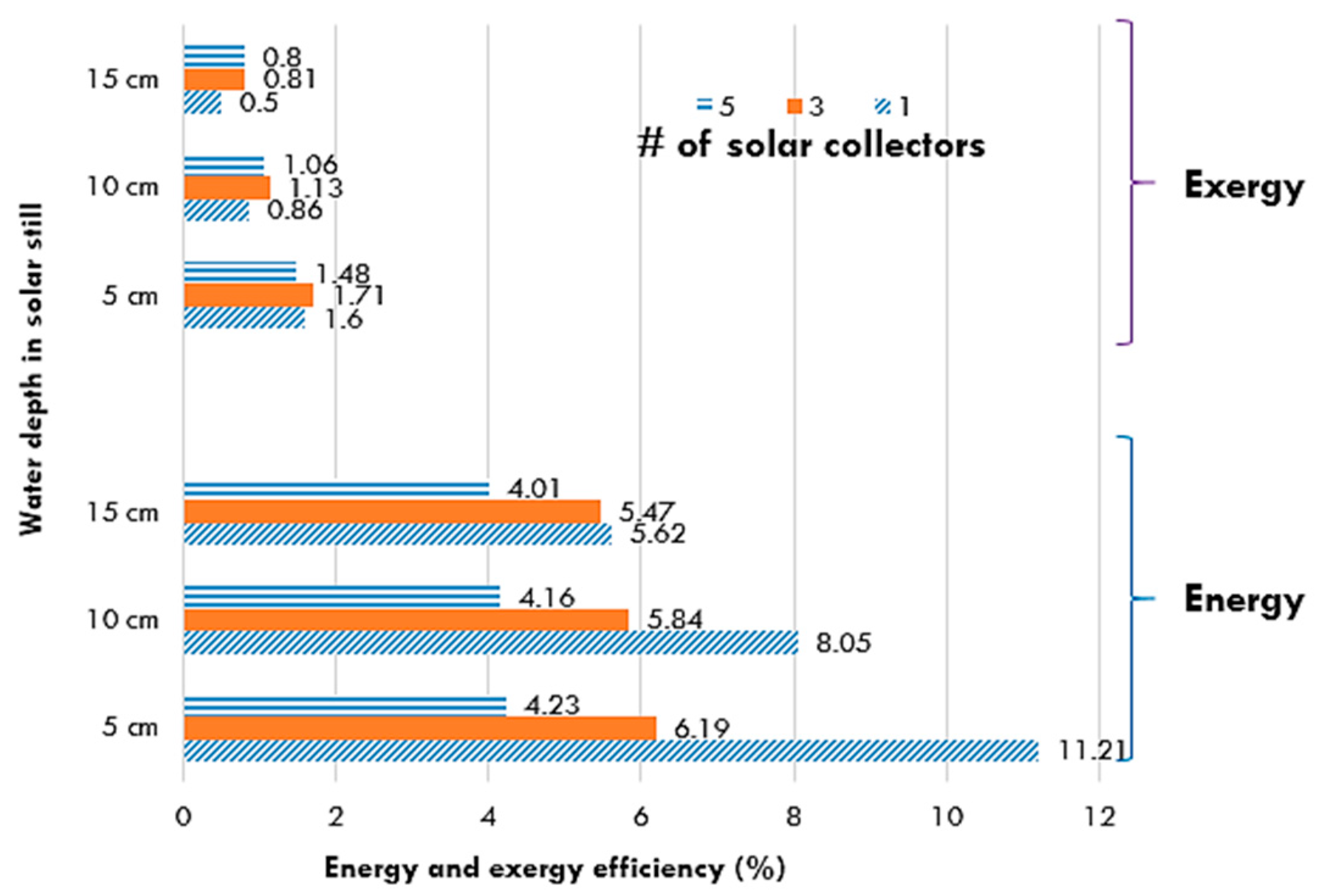
5.5. Solar Stills
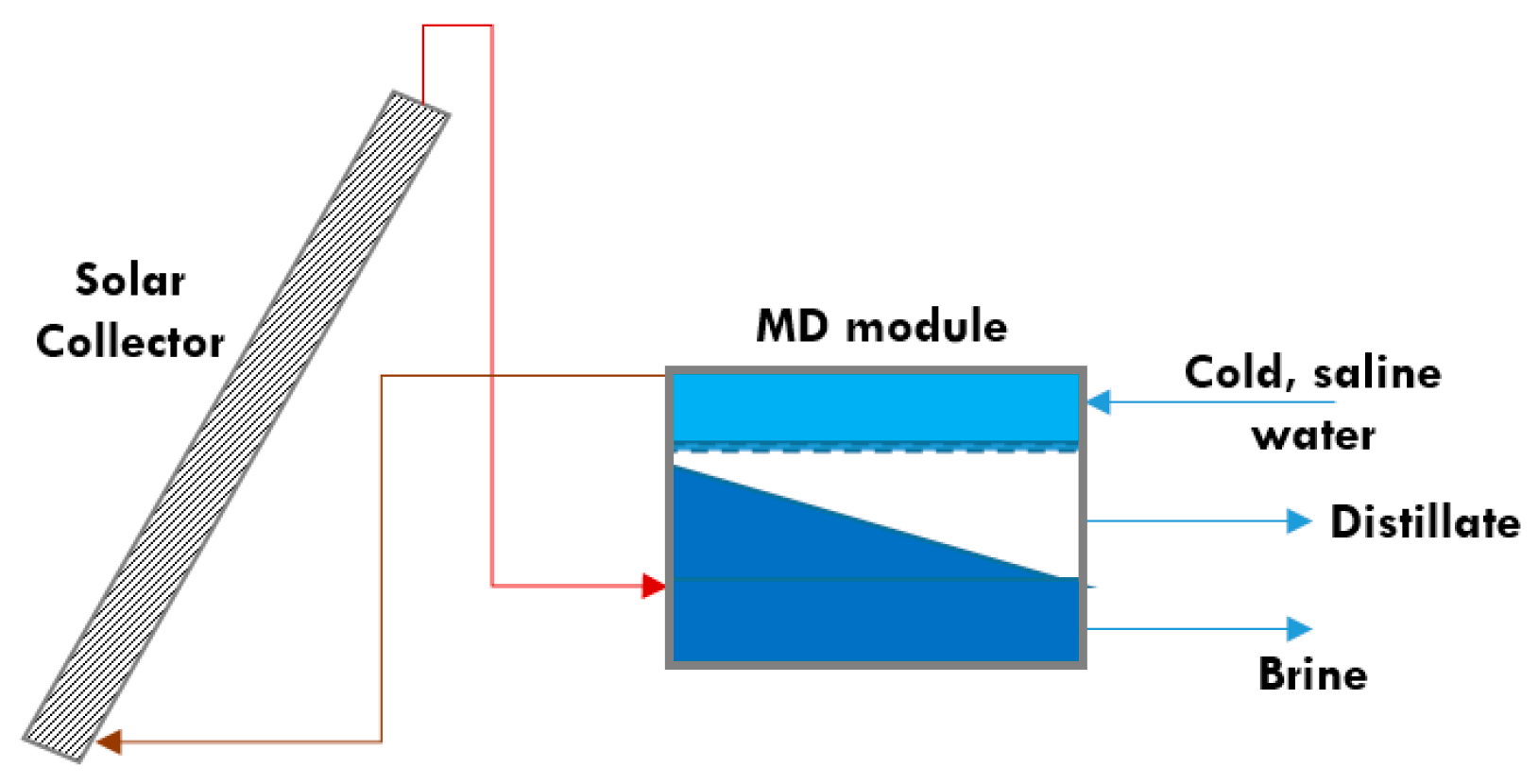
5.6. Membrane Distillation
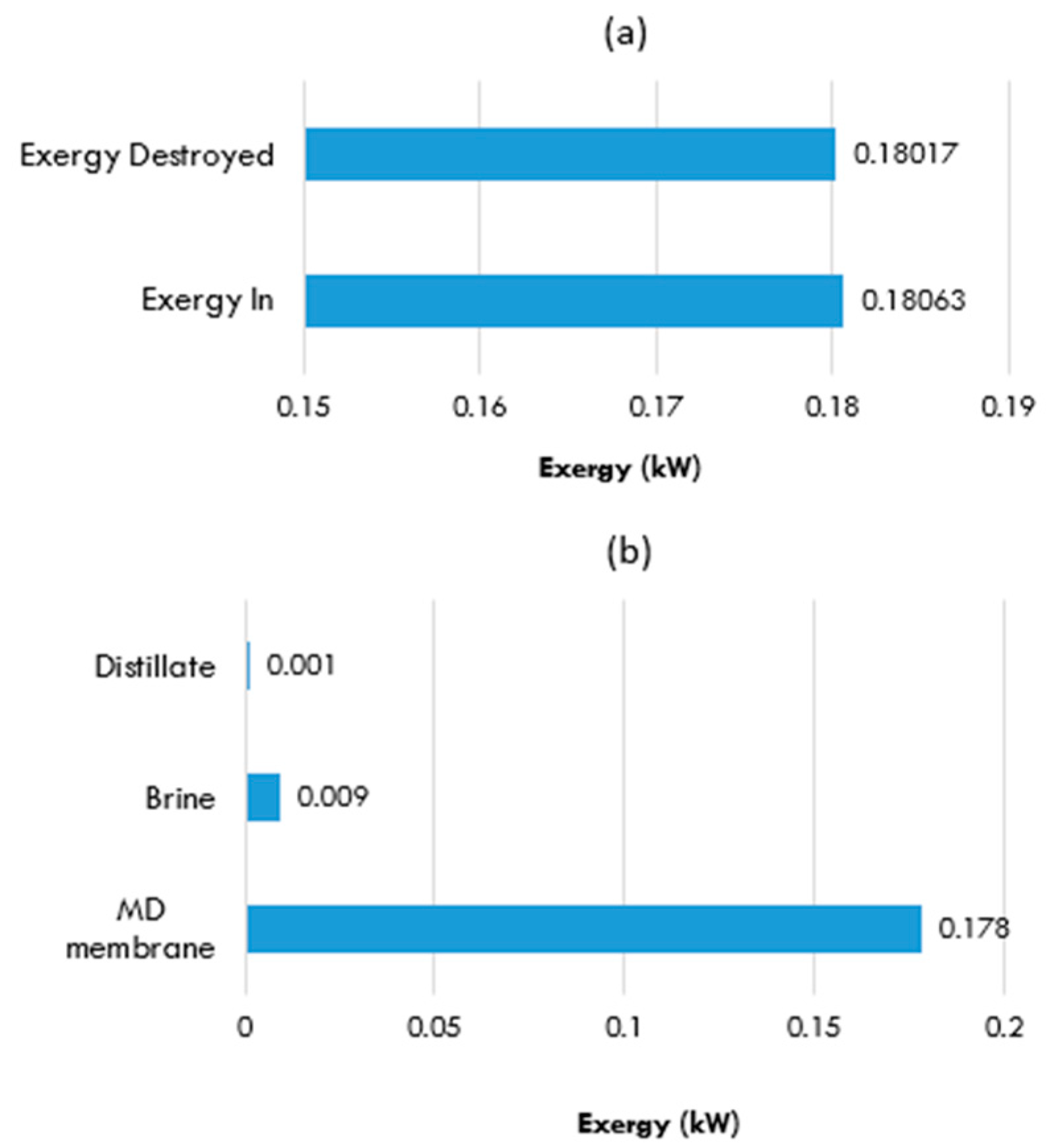
5.6.1. MD Unit without a Heat Exchanger
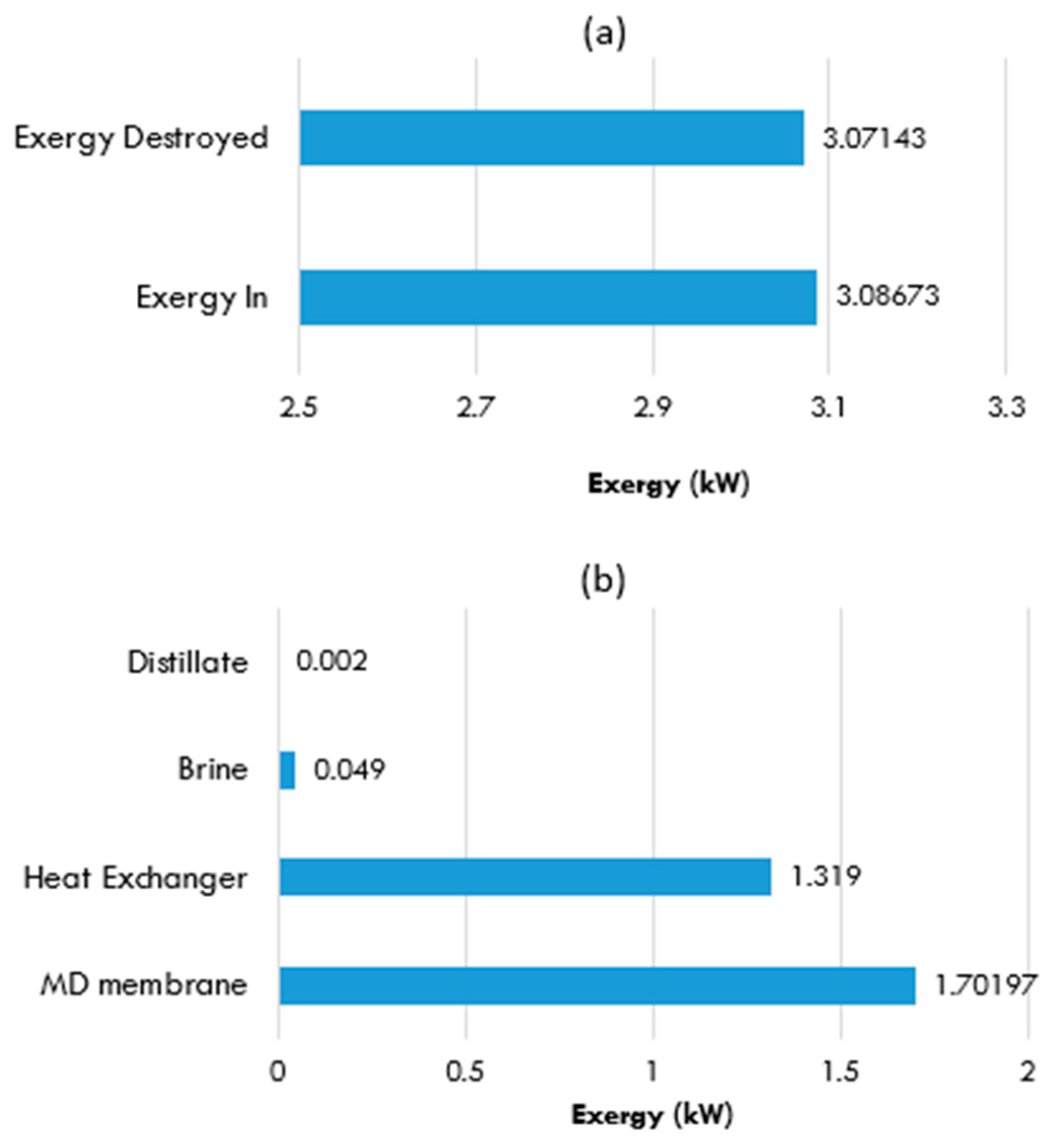
5.6.2. MD Unit with a Heat Exchanger
5.7. Other Configurations
6. Entropy Generation in Desalination Processes
7. Desalination Exergy Costs (Thermoeconomics)
8. Concluding Remarks
Acknowledgments
Conflicts of Interest
Nomenclature
| A | surface area (m2) |
| cp | specific heat of ideal gas at constant pressure (kJ kg−1 K−1) |
| Δ | temperature difference (K) |
| E, ex | exergy (kJ) |
| Ė | exergy flow rate (kW) |
| h | specific enthalpy (kJ kg−1) |
| m | mass flow rate (kg h−1) |
| p | pressure (atm.) |
| Q | heat energy (kJ) |
| total heat transfer rate (kW) | |
| s | specific entropy (kJ kg−1 K−1) |
| T | absolute temperature or temperature (K) |
| To | reference temperature (K) |
| U | heat transfer rate (kJh−1m−2) |
| W | net work transfer rate (kW) |
| w | seawater concentration (kg kg−1) |
| Greeks | |
| Ψ | exergetic efficiency (%) |
| μ | chemical exergy (kJ kg−1) |
| η | thermal efficiency (%) |
| Subscripts | |
| b | brine |
| D | destruction |
| e | exit, specific exergy |
| eff | efficiency |
| ex | exergy |
| f | freshwater |
| hv | heat of vaporization (latent heat) |
| i | inlet |
| in | input, supply |
| o | surroundings |
| s | saline water stream, sun |
| th | thermal |
| v | vapor |
| w | withdrawal stream |
References
- Gude, V.G.; Nirmalakhandan, N.; Deng, S. Renewable and sustainable approaches for desalination. Renew. Sustain. Energy Rev. 2010, 14, 2641–2654. [Google Scholar] [CrossRef]
- Gude, V.G. Energy storage for desalination processes powered by renewable energy and waste heat sources. Appl. Energy 2015, 137, 877–898. [Google Scholar] [CrossRef]
- Gude, V.G. Desalination of deep groundwater aquifers for freshwater supplies—Challenges and strategies. Groundw. Sustain. Dev. 2018, 6, 87–92. [Google Scholar] [CrossRef]
- Gude, V.G. Desalination and sustainability—An appraisal and current perspective. Water Res. 2016, 89, 87–106. [Google Scholar] [CrossRef] [PubMed]
- Gude, V.G. Desalination and water reuse to address global water scarcity. Rev. Environ. Sci. Bio/Technol. 2017, 16, 591–609. [Google Scholar] [CrossRef]
- Kotas, T.J. The Exergy Method of Thermal Plant Analysis; Elsevier: New York, NY, USA, 2013. [Google Scholar]
- Sandnes, B. Exergy Efficient Production, Storage and Distribution of Solar Energy. Ph.D. Thesis, University of Oslo, Oslo, Norway, 2003. [Google Scholar]
- Hepbasli, A. A key review on exergetic analysis and assessment of renewable energy resources for a sustainable future. Renew. Sustain. Energy Rev. 2008, 12, 593–661. [Google Scholar] [CrossRef]
- Gude, V.G.; Nirmalakhandan, N.; Deng, S.; Maganti, A. Desalination at low temperatures: An exergy analysis. Desalin. Water Treat. 2012, 40, 272–281. [Google Scholar] [CrossRef]
- Drioli, E.; Laganà, F.; Criscuoli, A.; Barbieri, G. Integrated membrane operations in desalination processes. Desalination 1999, 122, 141–145. [Google Scholar] [CrossRef]
- Mehdizadeh, H. Membrane desalination plants from an energy–exergy viewpoint. Desalination 2006, 191, 200–209. [Google Scholar] [CrossRef]
- Martínez, A.; Uche, J.; Rubio, C.; Carrasquer, B. Exergy cost of water supply and water treatment technologies. Desalin. Water Treat. 2010, 24, 123–131. [Google Scholar] [CrossRef]
- Mabrouk, A.N.A.; Nafey, A.S.; Fath, H.E. Steam, electricity and water costs evaluation of power desalination co-generation plants. Desalin. Water Treat. 2010, 22, 56–64. [Google Scholar] [CrossRef]
- Göǧüş, Y.A.; Çamdalı, Ü.; Kavsaoğlu, M.Ş. Exergy balance of a general system with variation of environmental conditions and some applications. Energy 2002, 27, 625–646. [Google Scholar] [CrossRef]
- Nisan, S. Utilisation of the exergy method for the cost evaluation of integrated nuclear desalination systems. Desalin. Water Treat. 2009, 8, 225–235. [Google Scholar] [CrossRef]
- Narayan, G.P.; Sharqawy, M.H.; Lienhard, V.J.H.; Zubair, S.M. Thermodynamic analysis of humidification dehumidification desalination cycles. Desalin. Water Treat. 2010, 16, 339–353. [Google Scholar] [CrossRef] [Green Version]
- Ucar, A.; Inallı, M. Thermal and exergy analysis of solar air collectors with passive augmentation techniques. Int. Commun. Heat Mass Transf. 2006, 33, 1281–1290. [Google Scholar] [CrossRef]
- Mistry, K.H.; Lienhard, J.H.; Zubair, S.M. Effect of entropy generation on the performance of humidification-dehumidification desalination cycles. Int. J. Therm. Sci. 2010, 49, 1837–1847. [Google Scholar] [CrossRef] [Green Version]
- Molinari, R.; Gagliardi, R.; Drioli, E. Methodology for estimating saving of primary energy with membrane operations in industrial processes. Desalination 1995, 100, 125–137. [Google Scholar] [CrossRef]
- Gude, V.G.; Nirmalakhandan, N.; Deng, S. Desalination using solar energy: Towards sustainability. Energy 2011, 36, 78–85. [Google Scholar] [CrossRef]
- Gundersen, T. An Introduction to the Concept of Exergy and Energy Quality; Lecture Notes; Norwegian University of Science and Technology: Trondheim, Norway, 2011. [Google Scholar]
- Sciubba, E.; Wall, G. A brief commented history of exergy from the beginnings to 2004. Int. J. Thermodyn. 2007, 10, 1–26. [Google Scholar]
- Sharqawy, M.H.; Zubair, S.M. On exergy calculations of seawater with applications in desalination systems. Int. J. Therm. Sci. 2011, 50, 187–196. [Google Scholar] [CrossRef] [Green Version]
- Bejan, A.; Tsatsaronis, G.; Moran, M.J. Thermal Design and Optimization; John Wiley & Sons: Hoboken, NJ, USA, 1996. [Google Scholar]
- Petela, R. Exergy of undiluted thermal radiation. Sol. Energy 2003, 74, 469–488. [Google Scholar] [CrossRef]
- Ng, K.C.; Shahzad, M.W.; Son, H.S.; Hamed, O.A. An exergy approach to efficiency evaluation of desalination. Appl. Phys. Lett. 2017, 110, 184101. [Google Scholar] [CrossRef]
- Carrasquer, B.; Martínez-Gracia, A.; Uche, J. Exergy costs analysis of water desalination and purification techniques by transfer functions. Energy Convers. Manag. 2016, 126, 51–59. [Google Scholar] [CrossRef]
- Spiegler, K.S.; El-Sayed, Y. The energetics of desalination processes. Desalination 2001, 134, 109–128. [Google Scholar] [CrossRef]
- Kahraman, N.; Cengel, Y.A. Exergy analysis of a MSF distillation plant. Energy Convers. Manag. 2005, 46, 2625–2636. [Google Scholar] [CrossRef]
- Ersayin, E.; Ozgener, L. Performance analysis of combined cycle power plants: A case study. Renew. Sustain. Energy Rev. 2015, 43, 832–842. [Google Scholar] [CrossRef]
- Nafey, A.S.; Fath, H.E.S.; Mabrouk, A.A. Exergy and thermoeconomic evaluation of MSF process using a new visual package. Desalination 2006, 201, 224–240. [Google Scholar] [CrossRef]
- Najafi, B.; Shirazi, A.; Aminyavari, M.; Rinaldi, F.; Taylor, R.A. Exergetic, economic and environmental analyses and multi-objective optimization of an SOFC-gas turbine hybrid cycle coupled with an MSF desalination system. Desalination 2014, 334, 46–59. [Google Scholar] [CrossRef]
- Al-Weshahi, M.A.; Anderson, A.; Tian, G. Exergy efficiency enhancement of MSF desalination by heat recovery from hot distillate water stages. Appl. Therm. Eng. 2013, 53, 226–233. [Google Scholar] [CrossRef]
- Al-Sulaiman, F.A.; Ismail, B. Exergy analysis of major recirculating multi-stage flash desalting plants in Saudi Arabia. Desalination 1995, 103, 265–270. [Google Scholar] [CrossRef]
- García-Rodríguez, L.; Gómez-Camacho, C. Exergy analysis of the SOL-14 plant (Plataforma Solar de Almeria, Spain). Desalination 2001, 137, 251–258. [Google Scholar] [CrossRef]
- Nafey, A.S.; Fath, H.E.S.; Mabrouk, A.A. Thermo-economic investigation of multi effect evaporation (MEE) and hybrid multi effect evaporation—Multi stage flash (MEE-MSF) systems. Desalination 2006, 201, 241–254. [Google Scholar] [CrossRef]
- Ng, K.C.; Thu, K.; Oh, S.J.; Ang, L.; Shahzad, M.W.; Ismail, A.B. Recent developments in thermally-driven seawater desalination: Energy efficiency improvement by hybridization of the MED and AD cycles. Desalination 2015, 356, 255–270. [Google Scholar] [CrossRef]
- Sayyaadi, H.; Saffari, A.; Mahmoodian, A. Various approaches in optimization of multi effects distillation desalination systems using a hybrid meta-heuristic optimization tool. Desalination 2010, 254, 138–148. [Google Scholar] [CrossRef]
- Hamed, O.A. Thermoeconomic analysis of combined power cycle integrated with MSF/SWRO desalination plant. Desalin. Water Treat. 2016, 57, 26552–26561. [Google Scholar] [CrossRef]
- Hamed, O.A.; Zamamiri, A.M.; Aly, S.; Lior, N. Thermal performance and exergy analysis of a thermal vapor compression desalination system. Energy Convers. Manag. 1996, 37, 379–387. [Google Scholar] [CrossRef]
- Al-Najem, N.M.; Darwish, M.A.; Youssef, F.A. Thermovapor compression desalters: Energy and availability—Analysis of single-and multi-effect systems. Desalination 1997, 110, 223–238. [Google Scholar] [CrossRef]
- Alasfour, F.N.; Darwish, M.A.; Amer, A.B. Thermal analysis of ME—TVC+ MEE desalination systems. Desalination 2005, 174, 39–61. [Google Scholar] [CrossRef]
- Choi, H.S.; Lee, T.J.; Kim, Y.G.; Song, S.L. Performance improvement of multiple-effect distiller with thermal vapor compression system by exergy analysis. Desalination 2005, 182, 239–249. [Google Scholar] [CrossRef]
- Samaké, O.; Galanis, N.; Sorin, M. Thermodynamic study of multi-effect thermal vapour-compression desalination systems. Energy 2014, 72, 69–79. [Google Scholar] [CrossRef]
- Esfahani, I.J.; Ataei, A.; Shetty, V.; Oh, T.; Park, J.H.; Yoo, C. Modeling and genetic algorithm-based multi-objective optimization of the MED-TVC desalination system. Desalination 2012, 292, 87–104. [Google Scholar] [CrossRef]
- Eshoul, N.M.; Agnew, B.; Mnider, A.M. Parametric study of mult-effect desalination with thermal vapour compression plant. In Proceedings of the 2016 7th International Renewable Energy Congress (IREC), Hammamet, Tunisia, 22–24 March 2016; pp. 1–6. [Google Scholar]
- Carballo, J.A.; Bonilla, J.; Roca, L.; De la Calle, A.; Palenzuela, P.; Alarcón-Padilla, D.C. Optimal operating conditions analysis for a multi-effect distillation plant according to energetic and exergetic criteria. Desalination 2018, 435, 70–76. [Google Scholar] [CrossRef]
- Piacentino, A. Application of advanced thermodynamics, thermoeconomics and exergy costing to a Multiple Effect Distillation plant: In-depth analysis of cost formation process. Desalination 2015, 371, 88–103. [Google Scholar] [CrossRef]
- Nafey, A.S.; Fath, H.E.S.; Mabrouk, A.A. Thermoeconomic design of a multi-effect evaporation mechanical vapor compression (MEE–MVC) desalination process. Desalination 2008, 230, 1–15. [Google Scholar] [CrossRef]
- Mabrouk, A.A.; Nafey, A.S.; Fath, H.E.S. Thermoeconomic analysis of some existing desalination processes. Desalination 2007, 205, 354–373. [Google Scholar] [CrossRef]
- Catrini, P.; Cipollina, A.; Micale, G.; Piacentino, A.; Tamburini, A. Exergy analysis and thermoeconomic cost accounting of a Combined Heat and Power steam cycle integrated with a Multi Effect Distillation-Thermal Vapour Compression desalination plant. Energy Convers. Manag. 2017, 149, 950–965. [Google Scholar] [CrossRef]
- Mokhtari, H.; Sepahvand, M. Thermoeconomic and exergy analysis in using hybrid systems (GT+ MED+ RO) for desalination of brackish water in Persian Gulf. Desalination 2016, 399, 1–15. [Google Scholar] [CrossRef]
- Cerci, Y. Exergy analysis of a reverse osmosis desalination plant in California. Desalination 2002, 142, 257–266. [Google Scholar] [CrossRef]
- Aljundi, I.H. Second-law analysis of a reverse osmosis plant in Jordan. Desalination 2009, 239, 207–215. [Google Scholar] [CrossRef]
- Romero-Ternero, V.; García-Rodríguez, L.; Gómez-Camacho, C. Exergy analysis of a seawater reverse osmosis plant. Desalination 2005, 175, 197–207. [Google Scholar] [CrossRef]
- Macedonio, F.; Curcio, E.; Drioli, E. Integrated membrane systems for seawater desalination: Energetic and exergetic analysis, economic evaluation, experimental study. Desalination 2007, 203, 260–276. [Google Scholar] [CrossRef]
- Ameri, M.; Eshaghi, M.S. A novel configuration of reverse osmosis, humidification–dehumidification and flat plate collector: Modeling and exergy analysis. Appl. Therm. Eng. 2016, 103, 855–873. [Google Scholar] [CrossRef]
- El-Emam, R.S.; Dincer, I. Thermodynamic and thermoeconomic analyses of seawater reverse osmosis desalination plant with energy recovery. Energy 2014, 64, 154–163. [Google Scholar] [CrossRef]
- Drioli, E.; Curcio, E.; Di Profio, G.; Macedonio, F.; Criscuoli, A. Integrating membrane contactors technology and pressure-driven membrane operations for seawater desalination: Energy, exergy and costs analysis. Chem. Eng. Res. Des. 2006, 84, 209–220. [Google Scholar] [CrossRef]
- Torchia-Nunez, J.C.; Porta-Gandara, M.A.; Cervantes-de Gortari, J.G. Exergy analysis of a passive solar still. Renew. Energy 2008, 33, 608–616. [Google Scholar] [CrossRef]
- Sow, O.; Siroux, M.; Desmet, B. Energetic and exergetic analysis of a triple-effect distiller driven by solar energy. Desalination 2005, 174, 277–286. [Google Scholar] [CrossRef]
- Gude, V.G.; Nirmalakhandan, N.; Deng, S. Integrated PV-thermal system for desalination and power production. Desalin. Water Treat. 2011, 36, 129–140. [Google Scholar] [CrossRef]
- Gude, V.G.; Nirmalakhandan, N.; Deng, S.; Maganti, A. Low temperature desalination using solar collectors augmented by thermal energy storage. Appl. Energy 2012, 91, 466–474. [Google Scholar] [CrossRef]
- Ibrahim, A.G.; Dincer, I. A solar desalination system: Exergetic performance assessment. Energy Convers. Manag. 2015, 101, 379–392. [Google Scholar] [CrossRef]
- Al-Kharabsheh, S.; Goswami, D.Y. Analysis of an innovative water desalination system using low-grade solar heat. Desalination 2003, 2003, 323–332. [Google Scholar] [CrossRef]
- Gude, V.G.; Nirmalakhandan, N. Desalination using low-grade heat sources. ASCE J. Energy Eng. 2008, 134, 95–101. [Google Scholar] [CrossRef]
- Gude, V.G.; Nirmalakhandan, N. Combined desalination and solar-assisted air-conditioning system. Energy Convers. Manag. 2008, 49, 3326–3330. [Google Scholar] [CrossRef]
- Gude, V.G.; Nirmalakhandan, N.; Deng, S. Sustainable low temperature desalination: A case for renewable energy. J. Renew. Sustain. Energy 2011, 3, 043108. [Google Scholar] [CrossRef]
- Tiwari, G.N.; Dimri, V.; Chel, A. Parametric study of an active and passive solar distillation system: Energy and exergy analysis. Desalination 2009, 242, 1–18. [Google Scholar] [CrossRef]
- Dwivedi, V.K.; Tiwari, G.N. Annual energy and exergy analysis of single and double slope passive solar stills. Trends Appl. Sci. Res. 2008, 3, 225–241. [Google Scholar]
- Ranjan, K.R.; Kaushik, S.C.; Panwar, N.L. Energy and exergy analysis of passive solar distillation systems. Int. J. Low-Carbon Technol. 2016, 11, 211–221. [Google Scholar] [CrossRef]
- Asbik, M.; Ansari, O.; Bah, A.; Zari, N.; Mimet, A.; El-Ghetany, H. Exergy analysis of solar desalination still combined with heat storage system using phase change material (PCM). Desalination 2016, 381, 26–37. [Google Scholar] [CrossRef]
- Kianifar, A.; Heris, S.Z.; Mahian, O. Exergy and economic analysis of a pyramid-shaped solar water purification system: Active and passive cases. Energy 2012, 38, 31–36. [Google Scholar] [CrossRef]
- Kaushik, S.C.; Ranjan, K.R.; Panwar, N.L. Optimum exergy efficiency of single-effect ideal passive solar stills. Energy Effic. 2013, 6, 595–606. [Google Scholar] [CrossRef]
- Zoori, H.A.; Tabrizi, F.F.; Sarhaddi, F.; Heshmatnezhad, F. Comparison between energy and exergy efficiencies in a weir type cascade solar still. Desalination 2013, 325, 113–121. [Google Scholar] [CrossRef]
- Dehghan, A.A.; Afshari, A.; Rahbar, N. Thermal modeling and exergetic analysis of a thermoelectric assisted solar still. Sol. Energy 2015, 115, 277–288. [Google Scholar] [CrossRef]
- Ranjan, K.R.; Kaushik, S.C. Exergy analysis of the active solar distillation systems integrated with solar ponds. Clean Technol. Environ. Policy 2014, 16, 791–805. [Google Scholar] [CrossRef]
- Gude, V.G.; Mummaneni, A.; Nirmalakhandan, N. Emergy, energy and exergy analysis of a solar powered low temperature desalination system. Desalin. Water Treat. 2017, 74, 21–34. [Google Scholar] [CrossRef]
- Gude, V.G.; Nirmalakhandan, N. Desalination at low temperatures and low pressures. Desalination 2009, 244, 239–247. [Google Scholar] [CrossRef]
- Gude, V.G.; Nirmalakhandan, N.; Deng, S.; Maganti, A. Feasibility study of a new two-stage low temperature desalination process. Energy Convers. Manag. 2012, 56, 192–198. [Google Scholar] [CrossRef]
- Yarlagadda, S.; Gude, V.G.; Camacho, L.M.; Pinappu, S.; Deng, S. Potable water recovery from As, U, and F contaminated ground waters by direct contact membrane distillation process. J. Hazard. Mater. 2011, 192, 1388–1394. [Google Scholar] [CrossRef] [PubMed]
- Yarlagadda, S.; Camacho, L.M.; Gude, V.G.; Wei, Z.; Deng, S. Membrane distillation for desalination and other separations. Recent Pat. Chem. Eng. 2009, 2, 128–158. [Google Scholar] [CrossRef]
- Qtaishat, M.R.; Banat, F. Desalination by solar powered membrane distillation systems. Desalination 2013, 308, 186–197. [Google Scholar] [CrossRef]
- Saffarini, R.B.; Summers, E.K.; Arafat, H.A. Economic evaluation of stand-alone solar powered membrane distillation systems. Desalination 2012, 299, 55–62. [Google Scholar] [CrossRef]
- Banat, F.; Jwaied, N.; Rommel, M.; Koschikowski, J.; Wieghaus, M. Desalination by a “compact SMADES” autonomous solarpowered membrane distillation unit. Desalination 2007, 217, 29–37. [Google Scholar] [CrossRef]
- Banat, F.; Jwaied, N. Exergy analysis of desalination by solar-powered membrane distillation units. Desalination 2008, 230, 27–40. [Google Scholar] [CrossRef]
- Banat, F.; Jwaied, N.; Rommel, M.; Koschikowski, J.; Wieghaus, M. Performance evaluation of the “large SMADES” autonomous desalination solar-driven membrane distillation plant in Aqaba, Jordan. Desalination 2007, 217, 17–28. [Google Scholar] [CrossRef]
- Chow, T.T.; Pei, G.; Fong, K.F.; Lin, Z.; Chan, A.L.S.; Ji, J. Energy and exergy analysis of photovoltaic–thermal collector with and without glass cover. Appl. Energy 2009, 86, 310–316. [Google Scholar] [CrossRef]
- Al-Obaidani, S.; Curcio, E.; Macedonio, F.; Di Profio, G.; Al-Hinai, H.; Drioli, E. Potential of membrane distillation in seawater desalination: Thermal efficiency, sensitivity study and cost estimation. J. Membr. Sci. 2008, 323, 85–98. [Google Scholar] [CrossRef]
- Woldemariam, D.; Martin, A.; Santarelli, M. Exergy analysis of air-gap membrane distillation systems for water purification applications. Appl. Sci. 2017, 7, 301. [Google Scholar] [CrossRef]
- Miladi, R.; Frikha, N.; Gabsi, S. Exergy analysis of a solar-powered vacuum membrane distillation unit using two models. Energy 2017, 120, 872–883. [Google Scholar] [CrossRef]
- Alarcón-Padilla, D.C.; García-Rodríguez, L. Application of absorption heat pumps to multi-effect distillation: A case study of solar desalination. Desalination 2007, 212, 294–302. [Google Scholar] [CrossRef]
- Mistry, K.H.; Lienhard, J.H. Generalized least energy of separation for desalination and other chemical separation processes. Entropy 2013, 15, 2046–2080. [Google Scholar] [CrossRef]
- Mistry, K.H.; McGovern, R.K.; Thiel, G.P.; Summers, E.K.; Zubair, S.M.; Lienhard, V.J.H. Entropy generation analysis of desalination technologies. Entropy 2011, 13, 1829–1864. [Google Scholar] [CrossRef] [Green Version]
- Warsinger, D.M.; Mistry, K.H.; Nayar, K.G.; Chung, H.W.; Lienhard, V.J.H. Entropy generation of desalination powered by variable temperature waste heat. Entropy 2015, 17, 7530–7566. [Google Scholar] [CrossRef]
- Uche, J.; Serra, L.; Valero, A. Exergy costs and inefficiency diagnosis of a dual-purpose power and desalination plant. J. Energy Resour. Technol. 2006, 128, 186–193. [Google Scholar] [CrossRef]
- Sayyaadi, H.; Saffari, A. Thermoeconomic optimization of multi effect distillation desalination systems. Appl. Energy 2010, 87, 1122–1133. [Google Scholar] [CrossRef]
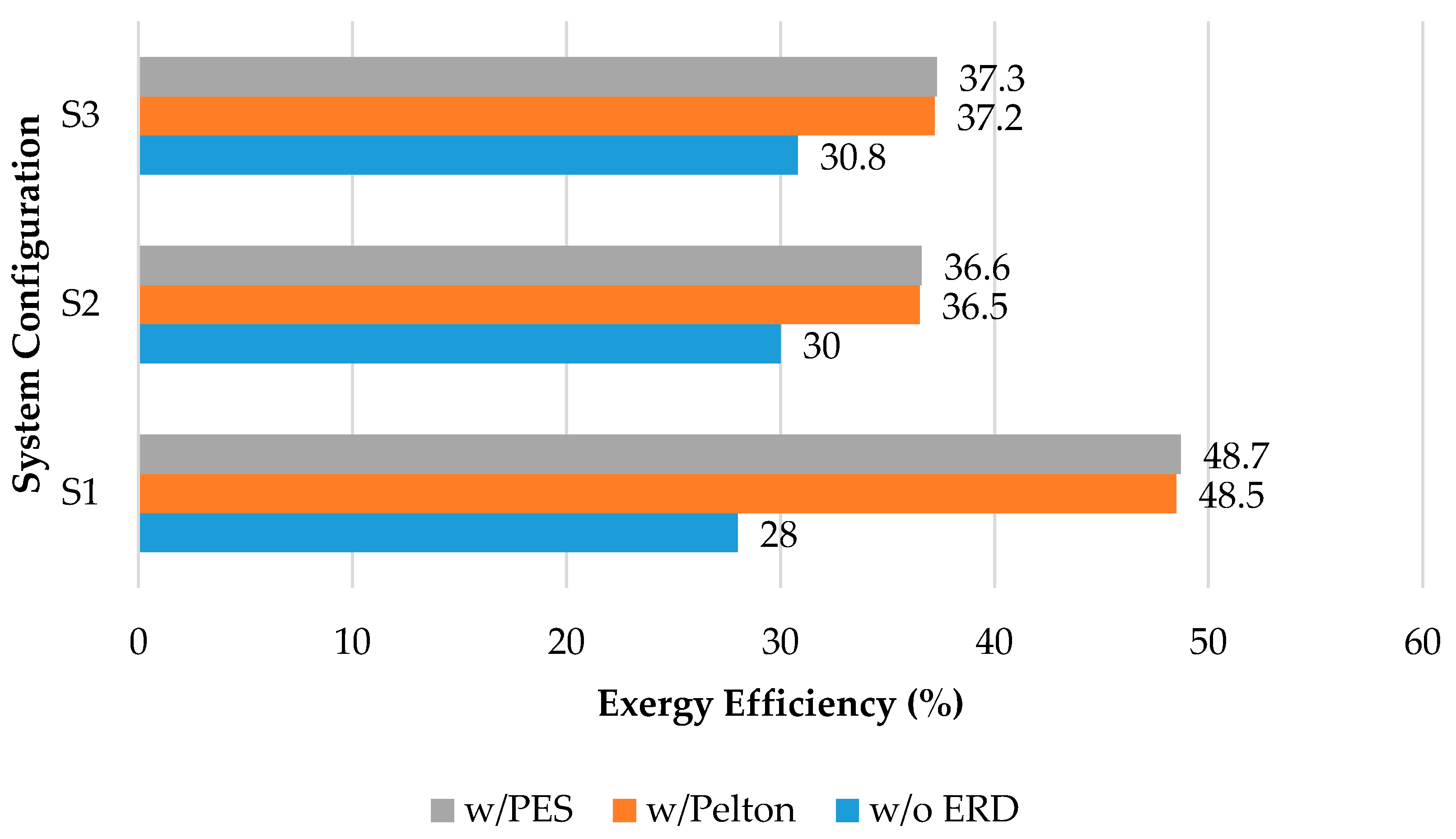

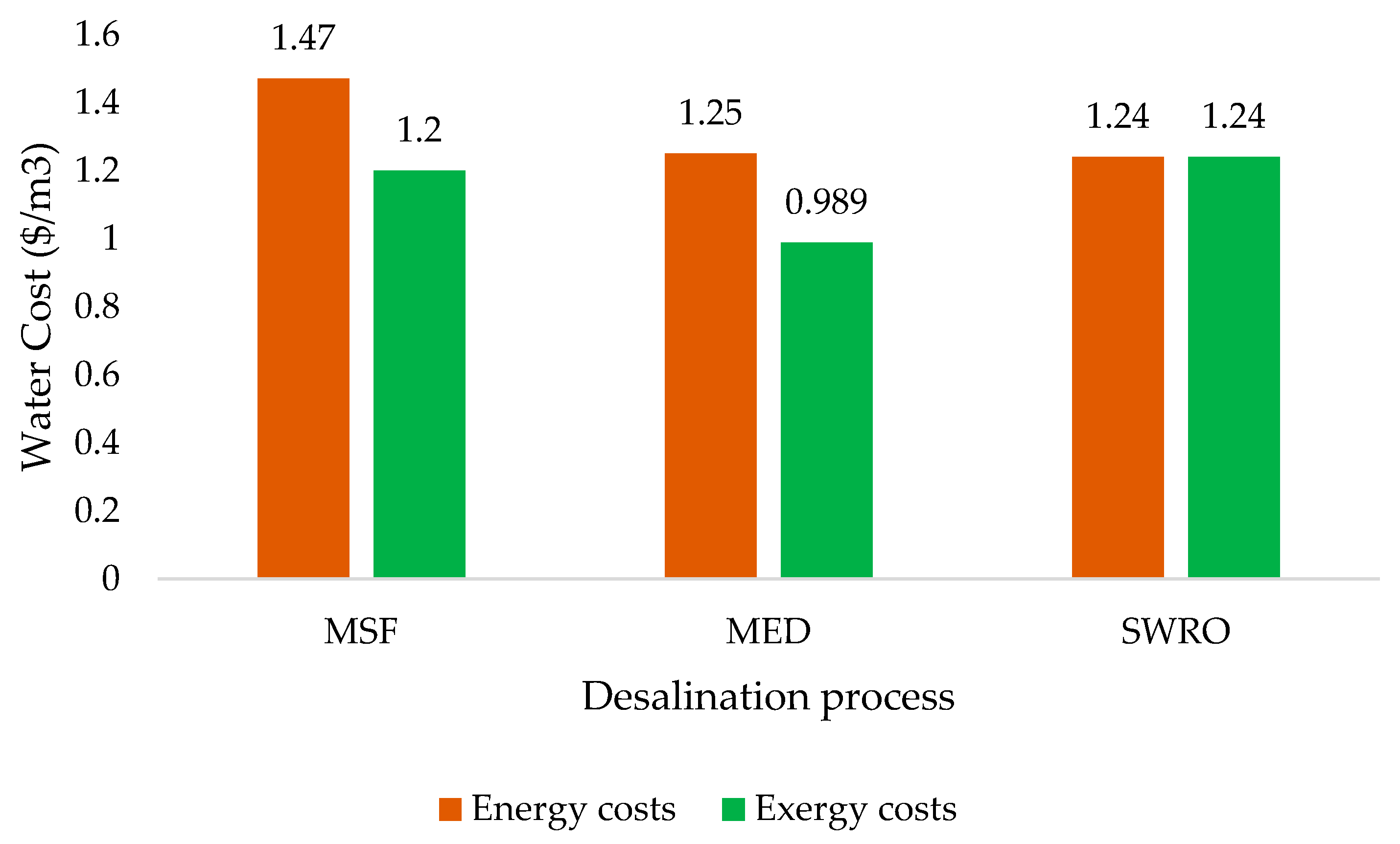
| Type of Energy Flow | Specific Energy | Specific Exergy |
|---|---|---|
| Kinetic | 0.5 V2 | 0.5 V2 |
| Potential | gΔz | gΔz |
| Heat | q | |
| Mechanical | w | w |
| Electrical | ItΔV | ItΔV |
| Chemical, pure substance | ΔgG | μ − μ0 + RT0ln(c/c0) |
| Radiation | I |
| Process | Exergy Destruction | Basis for Calculation | |
|---|---|---|---|
| kWh/ton | J/mol | ||
| Reverse osmosis | 0.98 | 63.8 | 35 atm excess pressure at 25 °C |
| Electrodialysis | 12.87 | 834 | 0.8 Voltage per membrane pair at 25 °C |
| Vapor compression | 2.77 | 179 | Compression unit temp. 60.75 °C; ΔT = 1.5 °C |
| Multi-effect evaporation | 2.83 | 183 | Average temperature of 50.75 °C; ΔT = 1.5 °C |
| Multi-stage flash desalination | 4.89 | 316.5 | Average temperature of 71.5 °C; ΔT = 3 °C |
| Process | Description | Performance | Ref. |
|---|---|---|---|
| Solid oxide fuel cell–gas turbine (SOFC–GT) hybrid system integrated with a multi stage flash (MSF) desalination unit. | Heuristic optimization method, namely, multi-objective genetic algorithm (MOGA). | Maximum achievable exergy efficiency of 46.7% with optimal design. | [32] |
| Desalination capacity—256 m3/day; performance ratio of 8.8 | MSF system exergy efficiency—3.49% | ||
| MSF with heat recovery from hot distillate water stages | IPSEpro software was used. Capacity—91,200 m3/day; # of stages 19 (16 heat recovery + 3 heat rejection) with a performance ratio of 8.43 | Overall exergy efficiency—5.8% | [33] |
| Exergy destroyed: | |||
| heat recovery stages—55.0% | |||
| brine heater—17.0% | |||
| heat rejection stages—10.0% | |||
| pumps—4.3% | |||
| brine streams disposal—14.0% | |||
| With heat recovery—14.0% | |||
| Recirculating MSF plants in Saudi Arabia, namely, Al-Khobar II, Al-Jubail II, and Shuaibah | Quantitative assessment of MSF desalination plants. | TBT—Exergy efficiency | [34] |
| Al-Khobar II: Capacity—194,200 m3/day; # of stages—16 (10 identical units) | 87 °C—4.61% | ||
| 106 °C—5.21% | |||
| 115 °C—5.35% | |||
| Al-Jubail II: Capacity—940,000 m3/day; # of stages—22 (40 identical units) | 90.6 °C—10.02% | ||
| 90.8 °C—10.38% | |||
| 112.8 °C—7.61% | |||
| Shuaibah: Capacity—181,818 m3/day; # of stages—19 (10 identical units) | 76.5 °C—3.57% | ||
| 90.0 °C—1.78% | |||
| 101.5 °C—1.12% |
| Process | Description | Performance | Ref. |
|---|---|---|---|
| MEE-MVC | Capacity—5000 m3/day; feed temperature—27 °C; compressor—60 °C; heating steam—70 °C # of evaporators—1–6 | Exergy efficiency: | [49] |
| 1 effect (3.8%); | |||
| 2 effects (5.8%); | |||
| 3 effects (6.6%); | |||
| 4 effects (7.5%); | |||
| 6 effects (no change) | |||
| Capacity—1500 m3/day; feed temperature—27 °C; compressor—60 °C; heating steam—70 °C # of evaporators—1–6 | Exergy efficiency: | ||
| 1 effect (3.8%); | |||
| 2 effects (5.8%); | |||
| 3 effects (6.6%); | |||
| 4 effects (7.5%); | |||
| 6 effects (8.4%); | |||
| 8 effects (no change) | |||
| Capacity—3750 m3/day; feed temperature—21 °C; Evaporator 1–65 °C; Evaporator 2–60 °C Evaporator surface area—2670 m2 | Exergy efficiency | ||
| With make-up steam—4.34% | |||
| Without make-up steam—5.75% | |||
| MEE-TVC | Capacity—1200 m3/day; feed temperature and TDS—27 °C and 45,000 mg/L; # of evaporators and surface area—2 and 2160 m2 | Exergy efficiency—2.2% | [50] |
| Capacity—5000 m3/day; feed temperature and TDS—27 °C and 45,000 mg/L; # of evaporators and surface area—2 and 8978 m2 | Exergy efficiency—2.1% | ||
| MEE-MVC | Capacity—1500 m3/day; feed temperature and TDS—27 °C and 45,000 mg/L; # of evaporators and surface area—2 and 3866 m2 | Exergy efficiency—5.8% | |
| Capacity—5000 m3/day; feed temperature and TDS—27 °C and 45,000 mg/L; # of evaporators and surface area—2 and 12848 m2 | Exergy efficiency—5.8% | ||
| MED-TVC | Capacity—5000 m3/day; forward feed type, 12 effects combined with TVC at the last effect. Exergy efficiency at different steam extraction pressures: Pa = 4890 kPa, Pb = 2800 kPa, Pc = 1480 kPa, Pd = 700 kPa and Pe = 290 kPa | Exergy efficiencies: | [51] |
| Pa—4.9% | |||
| Pb—5.0% | |||
| Pc—5.1% | |||
| Pd—6.0% | |||
| Pe—7.1% | |||
| Combined CHP-MED-TVC | Capacity—5000 m3/day; forward feed type, 12 effects combined with TVC at the last effect; # of MED units: 0–4. Exergy efficiency at different steam extraction pressures: Pa = 4890 kPa, Pb = 2800 kPa, Pc = 1480 kPa, Pd = 700 kPa and Pe = 290 kPa | Exergy efficiencies: | |
| Pa (4-0)—2.5–3.8% | |||
| Pb (4-0)—2.6–3.8% | |||
| Pc (4-0)—2.8–3.8% | |||
| Pd (4-0)—2.9–3.8% | |||
| Pe (4-0)—3.0–3.8% | |||
| Gas Turbine + MED + RO | Capacity—16874 m3/day; Power production—10 MW. Power—water generation unit consisting of compressor, gas turbine (GT), combustion chamber (CC), Air compressor (AC), high recovery steam generation (HRSG), MED and RO | Exergy Destruction: | [52] |
| AC—2.0% | |||
| CC—14.0% | |||
| GT—1.5% | |||
| HRSG—5.9% | |||
| MED—3.9% | |||
| RO—0.5% |
| System 1 | System 2 | System 3 | |
|---|---|---|---|
| Process description | Direct RO | NF pretreatment + RO | MF + NF pretreatment + RO |
| Brine flow rate, m3/h | 629.9 | 504.5 | 531.9 |
| Brine concentration, g/L | 57.6 | 71.9 | 68.0 |
| Fresh water flow rate, m3/h | 421.2 | 547.0 | 517.6 |
| Fresh water concentration, g/L | 0.34 | 0.27 | 0.27 |
| Fresh water recovery, % | 40.1 | 52.0 | 49.2 |
| Process | Capacity, m3/day | Exergy Efficiency, % | Reference |
|---|---|---|---|
| RO | 7250 | 4.3 | [53] |
| RO | 2850 | 0.7 | [57] |
| SWRO | 7586 | 5.8 | [58] |
| MF-NF-RO | 12,408 | 30.9 | [59] |
| Desalination Device | Description | Performance | Ref. |
|---|---|---|---|
| Passive solar still | Exergy analysis of individual compounds | Collector—12.9% | [60] |
| Brine—6.0% | |||
| Solar still—5.0% | |||
| Passive solar still | Single and Double slope solar still | Thermal Efficiency | [70] |
| Single—22.6–31.3% | |||
| Double—25.4–34.3% | |||
| Exergy Efficiency | |||
| Single—0.18–1.25% | |||
| Double—0.13–1.16% | |||
| Passive solar still | Wind and insulation effects | Max. exergy efficiency—9.48% | [71] |
| Daily Avg. exergy efficiency—4.93% | |||
| Exergy saved by Insulation—7.71% | |||
| Active solar still | Evaporator maintained under vacuum with an air-cooled condenser | A 12% increase in basin absorptivity increased distillate by 27%, energy utilization by 25%, and exergy efficiency by 39%. | [64] |
| Effect of absorptivity of basin and heat loss reduction from basin walls | A 75% reduction in basin heat losses increased distillate production by 87% and exergy performance by 152%. | ||
| Solar still with energy storage | Phase change material thermal storage | Daytime exergy efficiency < 5% | [72] |
| Nighttime exergy efficiency > 80% | |||
| Pyramid-shaped solar still | Comparison of summer and winter conditions, effect of water depth | No significant difference. Higher exergy efficiency at a lower water depth (4–8 cm) | [73] |
| Single-effect horizontal basin-type passive solar stills | Thermodynamic model development | Ultimate energy efficiency 80.0% | [74] |
| Optimum exergy efficiency 21.1% | |||
| Weir type cascade solar still | Computer simulation package, effect of brine flow rate | Inlet brine flow rate of 0.065 kg/min—10.5% | [75] |
| Inlet brine flow rate of 0.2 kg/min—3.14% | |||
| High brine inlet flow rate—3.8–7.34% | |||
| Thermoelectric assisted solar still | Dynamic thermodynamic modeling study | Energy efficiency—19.8% | [76] |
| Exergy efficiency—0.95% | |||
| Exergy destruction in thermo-electric module—63.4% | |||
| Active solar still | Solar still integrated with solar pond | Energy efficiency—38.6% | [77] |
| Exergy efficiency—2.7% |
| Process | Capacity, m3/day | Exergy Efficiency, % | Reference |
|---|---|---|---|
| MD on RO retentate | 22,344 | 19.1–21.9 | [59] |
| MD | 0.31 | 0.3 | [86] |
| DCMD with HR | 24,000 | 28.3 | [89] |
| DCMD without HR | 24,000 | 25.6 | [89] |
| AGMD (Xzero) | 0.22–0.73 | 8.54–19.32 | [89] |
| AGMD (Elixir500) | 0.1–0.17 | 18.3–26.5 | [90] |
| Solar powered VMD | 43 | 3.25 | [91] |
| Solar powered VMD | 43 | 0.18 | [91] |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gude, V.G. Exergy Evaluation of Desalination Processes. ChemEngineering 2018, 2, 28. https://doi.org/10.3390/chemengineering2020028
Gude VG. Exergy Evaluation of Desalination Processes. ChemEngineering. 2018; 2(2):28. https://doi.org/10.3390/chemengineering2020028
Chicago/Turabian StyleGude, Veera Gnaneswar. 2018. "Exergy Evaluation of Desalination Processes" ChemEngineering 2, no. 2: 28. https://doi.org/10.3390/chemengineering2020028
APA StyleGude, V. G. (2018). Exergy Evaluation of Desalination Processes. ChemEngineering, 2(2), 28. https://doi.org/10.3390/chemengineering2020028





