Two-Phase Bubble Columns: A Comprehensive Review
Abstract
1. Introduction
2. Bubble Column Fluid-Dynamics
2.1. The Flow Regimes and the Flow Regime Tranistions in Bubble Columns
2.1.1. The Flow Regimes in Bubble Columns
2.1.2. The Flow Regime Transitions
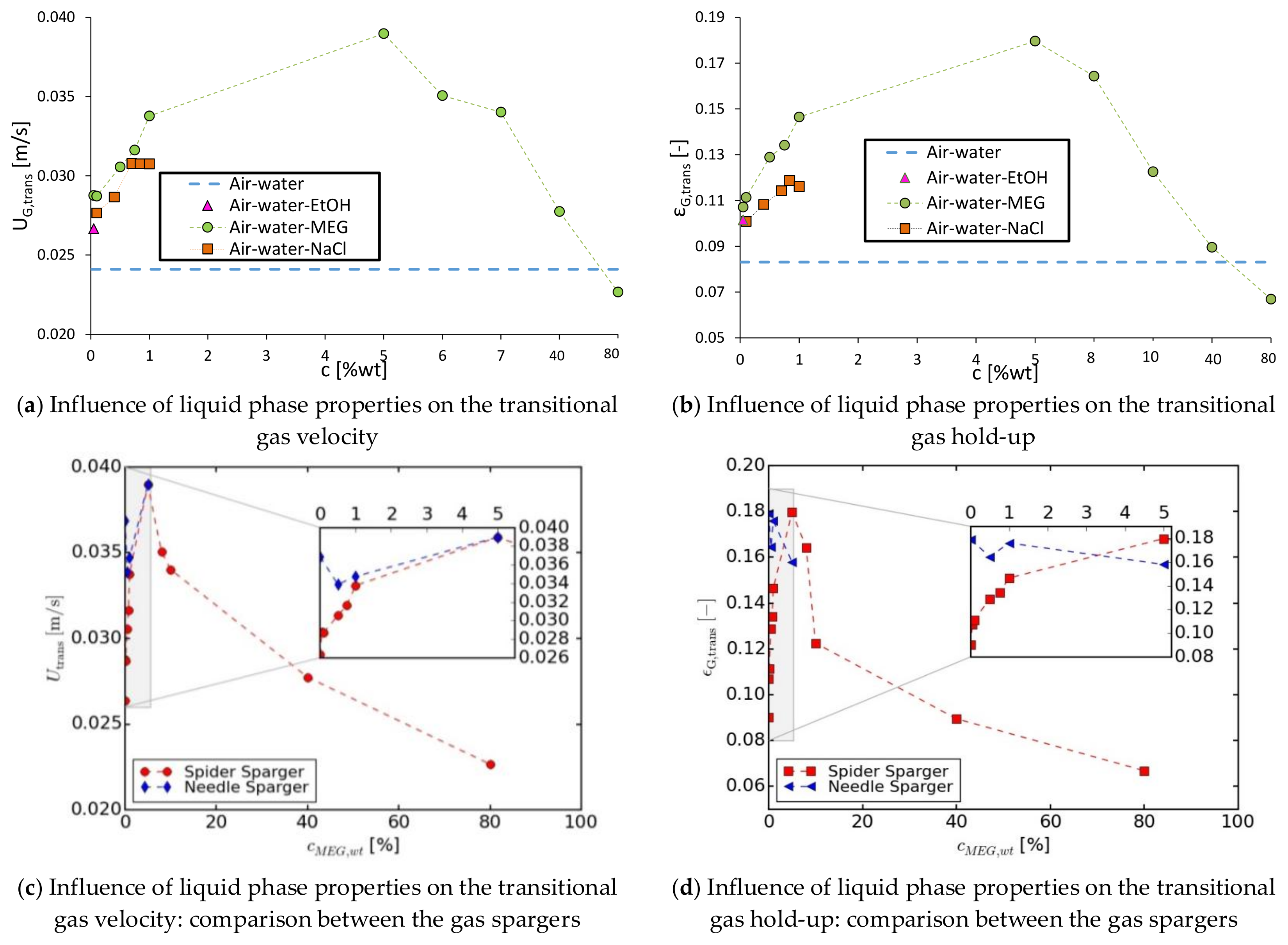
Influence of the Bubble Column Design
Influence of the Bubble Column Operation Mode
Influence of the Liquid Phase Viscosity
Influence of the Active Compounds: Inorganic Compounds (“positive surfactants”)
Influence of the Active Compounds: Organic Compounds (“negative surfactants”)
Pressure and Temperature
2.1.3. The Flow Regime Maps
2.2. The Gas Hold-Up
2.2.1. Influence of the Bubble Column Operation
Superficial Gas Velocity and Gas Holdup Curve Structure
Superficial Liquid Velocity
2.2.2. Influence of the Bubble Column Design
Column Size
Aspect Ratio
Gas Sparger
2.2.3. Influence of the Liquid Properties
Viscous Media
Active Compounds
Inorganic Compounds
Organic Compounds
2.2.4. Influence of Gas Properties
2.2.5. Influence of the Pressure and Temperature
Pressure
Temperature
2.2.6. Gas Hold-Up Correlations
Scheme of Correlations by Lockett and Kirkpatrick
Scheme of Correlations Based on εG: From Hugmark towards Reilly et al.
Scheme of Correlations Based on εG/(1 − εG)4: The Akita and Toshida Scheme
Scheme of Correlations for Newtonian and Non-Newtonian Liquid Phases
Scheme of Correlations of Syeda et al.
Scheme of Correlations for Bubble Column Scaling-Up
2.3. The Bubble Size Distribution and Shapes
- the Eötvös number:
- the Morton number (defined only by the properties of the phases):
- the Reynolds number:
- the Weber number:
2.3.1. Influence of the Bubble Column Design and Operation
Superficial Gas Velocity
Gas Sparger Design
2.3.2. Influence of the Liquid Properties
Viscous Media
Active Compounds
Influence of the Gas Properties
2.3.3. Influence of the Pressure and Temperature
Pressure
Temperature
2.4. Local Flow Properties
2.5. Interfacial Area
2.6. The Mass Transfer
2.6.1. Physical Phenomena and Approaches
Influence of the Bubble Column Design
Influence of the Bubble Column Operating Conditions
Influence of the Liquid and Gas Phase Properties
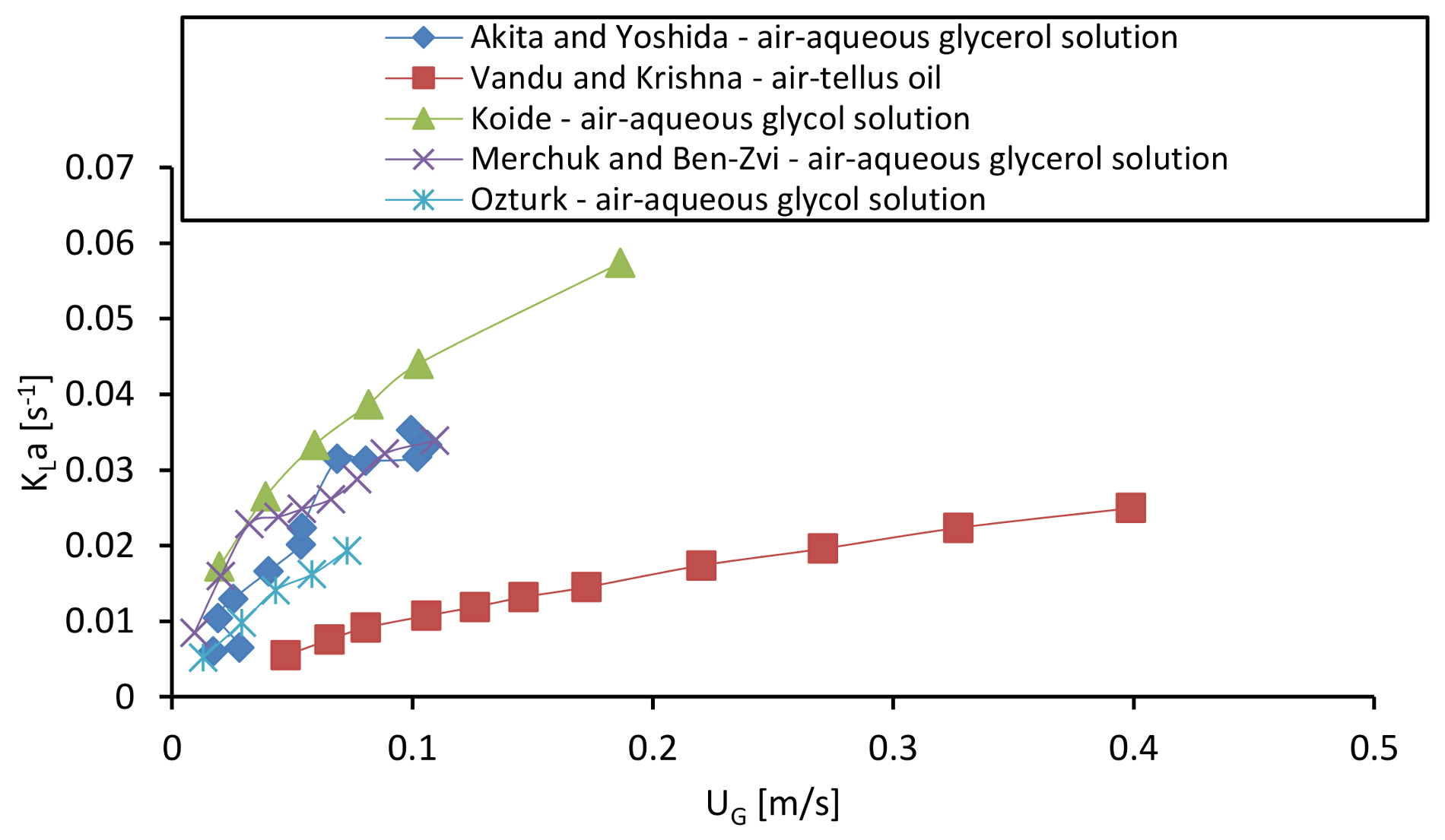
2.6.2. The Mass Transfer Correlations
3. The Experimental Techniques
3.1. The Flow Regimes
3.2. The Gas Hold-Up
3.3. The Bubble Size Distribution and Shape
3.4. The Local Flow Properties
3.5. The Mass Transfer
4. The Modeling Approaches
4.1. The Eulerian Multi-Fluid Approach
4.2. A Focus on the Population Balance Modeling
4.2.1. The Approach
4.2.2. The Governing Equations
Bubble Coalescence Phenomena and Modeling
- collision between two bubbles trapping a liquid film;
- drainage of the liquid film;
- film rupture and coalescence.
Bubble Break-Up Phenomena and Modeling
5. Conclusions, Guidelines and Outlooks
5.1. Summary of the Literature Survey
5.2. Guidelines
- Different studies have investigated, in the few last decades, either local or global fluid dynamics properties; unfortunately, the studies concerning both local and global fluid dynamics properties are still limited in number. In this respect, experimental studies should always provide a multi-scale evaluation of bubble column fluid dynamics (i.e., by studying, at least, both gas hold-up and bubble size distribution);
- Experimental studies should always provide detailed information concerning the main bubble column design criteria (as listed in Section 2.3.2) in order to relate the experimental results to the geometrical scale of the bubble column (i.e., “large-diameter”, “small-diameter”, “coarse gas sparger”, fine gas sparger”, etc.); in particular, information on non-dimensional bubble column diameters, aspect ratios and gas sparger openings should be always provided
- In comparisons involving the flow regime transition, detailed information concerning the flow regime transition criteria should be specified; in addition, authors should carefully evaluate if the flow regime transition method is suitable with the applied definition of flow regime transition;
- When presenting a numerical approach, sensitivity studies on (a) interfacial closures; (b) time and (c) space discretization should be always be performed;
- The modeling approach of the dispersed phase (i.e., mono-dispersed, bi-dispersed, PBM) should always be related to the prevailing flow regime observed in the bubble column;
5.3. Outlooks
- Proposing a precise mathematical description of the flow regime transitions, as listed and described in Section 2.2.2. This approach should take into account the role of instabilities in flow regime transitions, to support the mathematical description of the boundaries of the flow regimes; in particular, this approach should be applied to develop a comprehensive flow regime map;
- Performing comprehensive and multi-scale experimental studies to propose complete datasets for large-scale bubble columns (viz. gas holdup, bubble size distributions and shape data, and local flow properties); such datasets would provide a valuable basis to validate numerical approaches for scaling-up purposes;
- Understanding the influence of interfacial properties on the “bubble-scale” and clarifying how the “bubble-scale” influences the “reactor-scale”;
- Proposing a unified theory to explain all the dual effects observed in the literature (e.g., viscous liquid phases, organic compounds, inorganic compounds, etc.);
- Performing experimental studies concerning the influences of the operating conditions and phase properties on bubble shape in dense bubbly flow conditions; in this regard, approaches for studying the three-dimensional bubble shape should be developed;
- Performing a comprehensive comparison of the experimental techniques for both the global and the local fluid dynamic properties;
- Extending the validation of the “baseline” approaches, to establish a common numerical framework for both small scale and large scale bubble columns; the validation should consider both the local and the global fluid dynamics properties in bubble columns;
- Extending the validation of numerical approaches to model the mass transfer phenomena in bubble columns;
- Extending the validation of the numerical approaches to the heterogeneous flow regime.
Author Contributions
Conflicts of Interest
Nomenclature
| Aspect ratio | |
| Eötvös number | |
| Morton number | |
| Reynolds number | |
| Weber number | |
| Frothing parameters |
| AR | Aspect Ratio |
| BSD | Bubble Size Distribution |
| CMC | Carboxymethyl cellulose |
| DNS | Direct numerical simulations |
| EtOH | Ethanol |
| HZDR | Helmholtz–Zentrum Dresden–Rossendorf |
| MEG | Monoethylene glycol |
| NaCl | Sodium chloride |
| PBE | Population Balance Equation |
| PBM | Population Balance Model |
| PoliMi | Politecnico di Milano |
| RANS | Reynolds-averaged Navier–Stokes |
| RSM | Reynolds Stress Models |
| Local velocity | [m/s] | |
| a | Major axis of the bubble | [m] |
| ai | Interfacial area | [1/mm] |
| B | Retarded Hamaker constant | [J m] |
| c | Molar concentration | [mol/L] |
| C | Parameter in Equation (31) | [-] |
| c* | Equilibrium concentration | [mol/L] |
| cEtOH,wt | Mass concentration of EtOH | [%] |
| cMEG,wt | Mass concentration of MEG | [%] |
| ct | Molar transition concentration of NaCl | [mol/L] |
| cwt | Mass concentration | [kg/L] |
| D*H | Non-dimensional diameter (Equation (1)) | [-] |
| D*H,Cr | Critical non-dimensional diameter | [-] |
| dbmax | Maximum stable bubble size | [mm] |
| dc | Diameter of the bubble column | [m] |
| deq | Bubble equivalent diameter | [mm] |
| DH | Hydraulic diameter | [m] |
| do | Gas sparger holes diameter | [mm] |
| e | Parameter in Equation (7) | [-] |
| E | Bubble aspect ratio | [-] |
| f | Function | [-] |
| FD | Drag force | [kg/m2 s2] |
| FL | Lift force | [kg/m2 s2] |
| FTD | Turbulent dispersion force | [kg/m2 s2] |
| FVM | Virtual mass force | [kg/m2 s2] |
| FWL | Wall force | [kg/m2 s2] |
| g | Acceleration due to gravity | [m/s2] |
| h | Height along the bubble column | [m] |
| H0 | Height of the free surface before aeration | [m] |
| Hc | Height of the bubble column | [m] |
| HD | Height of the free surface after aeration | [m] |
| K | Consistency index | [Pa s] |
| ki (i = 1, 2) | Coefficients in the aspect ratio correlation (Equation (44)) | [-] |
| kL | Volumetric mass transfer coefficient | [m/s] |
| MI | Momentum exchanges | [kg/m2 s2] |
| n* | Dimensionless concentration (Equation (2)) | [-] |
| P | Probability density function in Equation (70) | [-] |
| Pv | Vapor pressure in Equation (9) | [Pa] |
| rb | Bubble radius in Equation (2) | [mm] |
| Rb | Gas constant | [J/mol K] |
| S | Total source/sink term in the population balance equation | [m3/s] |
| Sb | Source/sink term due to break-up | [m3/s] |
| Sc | Source/sink term due to coalescence | [m3/s] |
| Sm | Source/sink term due to mass transfer | [m3/s] |
| Sp | Source/sink term due to pressure change | [m3/s] |
| Sph | Source/sink term due to phase change | [m3/s] |
| Sr | Source/sink term due to reaction | [m3/s] |
| t | Time | [s] |
| T | Temperature | [K] |
| tG | Mean residence time of the dispersed phase | [s] |
| u | Mean rise velocity | [m/s] |
| U | Superficial velocity | [m/s] |
| U* | Dimensionaless gas velocity | [-] |
| ub | Local velocity of bubble volumes | [m/s] |
| ubr | Bubble rising velocity in Equation (26) | [m/s] |
| V | Volume | [m3] |
| Vb | Bubble volume in population balance equations | [m3] |
| zi (i = 1, …, 5) | Coefficients in the aspect ratio correlation (Equation (44)) | [-] |
| Void fraction in the Eulerian–Eulerian constitutive equations | [-] | |
| Shear rate | [1/s] | |
| Viscous and Reynolds stresses | [kg/m s2] | |
| β | Coefficient in Equations (6) and (7) | [-] |
| γ | Coefficient in Equation (6) | [-] |
| Γ | Coalescence rate | [m3/s] |
| ε | Hold-up | [-] |
| ε | Parameter in Equation (12) | [-] |
| μ | Dynamic viscosity | [kg/m s] |
| μa | Apparent dynamic viscosity | [kg/m s] |
| μeff | Effective viscosity | [kg/m s] |
| ν | Bubble terminal velocity | [m/s] |
| νL | Bubble terminal velocity | [m2/s] |
| ρ | Density | [kg/m3] |
| σ | Surface tension | [N/m] |
| τ | Time scale | [1/s] |
| χ | Kinematic surface tension | [m3/s] |
| Ω | Break-up rate | [m3/s] |
| c | Parameter related to the bubble column |
| coalescence induced bubbles | Coalescence induced bubbles |
| cr | Critical parameter |
| G | Gas phase |
| j | j-th dispersed phase in governing equations |
| k | k-th continuous phase in governing equations |
| L | Liquid phase |
| Local | Local parameter |
| non-coalescence induced bubbles | Non-coalescence induced bubbles |
| swarm | Swarm parameter |
| trans | Transition point (it refers at the homogeneous flow regime) |
| trans,I | First transition point (end of the homogeneous flow regime, defined when considering both the first and the second regime transitions) |
| trans,II | Second transition point (end of the transition flow regime, defined when considering both the first and the second regime transitions) |
| wt | Mass concentration |
| z | Generic phase in governing equations |
| → | Vector quantity |
References
- Leonard, C.; Ferrasse, J.H.; Boutin, O.; Lefevre, S.; Viand, A. Bubble column reactors for high pressures and high temperatures operation. Chem. Eng. Res. Des. 2015, 100, 391–421. [Google Scholar] [CrossRef]
- Rollbusch, P.; Bothe, M.; Becker, M.; Ludwig, M.; Grünewald, M.; Schlüter, M.; Franke, R. Bubble columns operated under industrially relevant conditions–Current understanding of design parameters. Chem. Eng. Sci. 2015, 126, 660–678. [Google Scholar] [CrossRef]
- Deckwer, W.D. Bubble Column Reactors; John Wiley & Sons Ltd.: Chichester, UK, 1992. [Google Scholar]
- Zehner, P.; Kraume, M. Bubble Columns. In Ullmann’s Encyclopedia of Industrial Chemistry; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2005. [Google Scholar]
- Kikukawa, H. Physical and transport properties governing bubble column operations. Int. J. Multiph. Flow 2017, 93, 115–129. [Google Scholar] [CrossRef]
- Sasaki, S.; Hayashi, K.; Tomiyama, A. Effects of liquid height on gas holdup in air–water bubble column. Exp. Therm. Fluid Sci. 2016, 72, 67–74. [Google Scholar] [CrossRef]
- Besagni, G.; Inzoli, F.; De Guido, G.; Pellegrini, L.A. Experimental investigation on the influence of ethanol on bubble column hydrodynamics. Chem. Eng. Res. Des. 2016, 1112, 1–15. [Google Scholar] [CrossRef]
- Zahradník, J.; Fialová, M.; Ruzicka, M.; Drahoš, J.; Kastanek, F.; Thomas, N.H. Duality of the gas-liquid flow regimes in bubble column reactors. Chem. Eng. Sci. 1997, 52, 3811–3826. [Google Scholar] [CrossRef]
- Lucas, D.; Rzehak, R.; Krepper, E.; Ziegenhein, T.; Liao, Y.; Kriebitzsch, S.; Apanasevich, P. A strategy for the qualification of multi-fluid approacheds for nuclear reactor safety. Nucl. Eng. Des. 2015. [Google Scholar] [CrossRef]
- Ziegenhein, T.; Rzehak, R.; Lucas, D. Transient simulation for large scale flow in bubble columns. Chem. Eng. Sci. 2015, 122, 1–13. [Google Scholar] [CrossRef]
- Besagni, G.; Inzoli, F.; De Guido, G.; Pellegrini, L.A. The dual effect of viscosity on bubble column hydrodynamics. Chem. Eng. Sci. 2017, 158, 509–538. [Google Scholar] [CrossRef]
- Besagni, G.; Inzoli, F. The effect of liquid phase properties on bubble column fluid dynamics: Gas holdup, flow regime transition, bubble size distributions and shapes, interfacial areas and foaming phenomena. Chem. Eng. Sci. 2017, 170, 270–296. [Google Scholar] [CrossRef]
- Mudde, R.F.; Harteveld, W.K.; van den Akker, H.E.A. Uniform Flow in Bubble Columns. Ind. Eng. Chem. Res. 2009, 48, 148–158. [Google Scholar] [CrossRef]
- Besagni, G.; Gallazzini, L.; Inzoli, F. Effect of gas sparger design on bubble column hydrodynamics using pure and binary liquid phases. Chem. Eng. Sci. 2018, 176, 116–126. [Google Scholar] [CrossRef]
- Takagi, S.; Matsumoto, Y. Surfactant effects on bubble motion and bubbly flows. Annu. Rev. Fluid Mech. 2011, 43, 615–636. [Google Scholar] [CrossRef]
- Takagi, S.; Ogasawara, T.; Matsumoto, Y. The effects of surfactant on the multiscale structure of bubbly flows. Philos. Trans. R. Sci. A Math. Phys. Eng. Sci. 2008, 366, 2117–2129. [Google Scholar] [CrossRef] [PubMed]
- Beinhauer, R. Dynamic Measurement of the Relative Gas Contents in Bubble Columns by Means of X-ray Absorption; TU Berlin: Berlin, Germany, 1971. [Google Scholar]
- Schumpe, A.; Grund, G. The Gas Disengagement Technique for Studying Gas Holdup Structure in Bubble Columns. Can. J. Chem. Eng. 1986, 64, 891–896. [Google Scholar] [CrossRef]
- Krishna, R.; Urseanu, M.I.; Dreher, A.J. Gas hold-up in bubble columns: Influence of alcohol addition versus operation at elevated pressures. Chem. Eng. Process. Process Intensif. 2000, 39, 371–378. [Google Scholar] [CrossRef]
- Krishna, R.; Dreher, A.J.; Urseanu, M.I. Influence of alcohol addition on gas hold-up in bubble columns: Development of a scale up model. Int. Commun. Heat Mass Transf. 2000, 27, 465–472. [Google Scholar] [CrossRef]
- Montoya, G.; Lucas, D.; Baglietto, E.; Liao, Y. A review on mechanisms and models for the churn-turbulent flow regime. Chem. Eng. Sci. 2016, 141, 86–103. [Google Scholar] [CrossRef]
- Kitscha, J.; Kocamustafaogullari, G. Breakup criteria for fluid particles. Int. J. Multiph. Flow 1989, 15, 573–588. [Google Scholar] [CrossRef]
- Brooks, C.S.; Paranjape, S.S.; Ozar, B.; Hibiki, T.; Ishii, M. Two-group drift-flux model for closure of the modified two-fluid model. Int. J. Heat Fluid Flow 2012, 37, 196–208. [Google Scholar] [CrossRef]
- Shah, Y.T.; Kelkar, B.G.; Godbole, S.P.; Deckwer, W.D. Design parameters estimations for bubble column reactors. AIChE J. 1982, 28, 353–379. [Google Scholar] [CrossRef]
- Deckwer, W.-D.; Field, R.W. Bubble Column Reactors; Wiley: New York, NY, USA, 1992; Volume 200. [Google Scholar]
- Nedeltchev, S.; Shaikh, A. A new method for identification of the main transition velocities in multiphase reactors based on information entropy theory. Chem. Eng. Sci. 2013, 100, 2–14. [Google Scholar] [CrossRef]
- Nedeltchev, S. New methods for flow regime identification in bubble columns and fluidized beds. Chem. Eng. Sci. 2015, 137, 436–446. [Google Scholar] [CrossRef]
- Besagni, G.; Di Pasquali, A.; Gallazzini, L.; Gottardi, E.; Colombo, L.P.M.; Inzoli, F. The effect of aspect ratio in counter-current gas-liquid bubble columns: Experimental results and gas holdup correlations. Int. J. Multiph. Flow 2017, 94, 53–78. [Google Scholar] [CrossRef]
- Sarrafi, A.; Müller-Steinhagen, H.; Smith, J.M.; Jamialahmadi, M. Gas holdup in homogeneous and heterogeneous gas—liquid bubble column reactors. Can. J. Chem. Eng. 1999, 77, 11–21. [Google Scholar] [CrossRef]
- Ohki, Y.; Inoue, H. Longitudinal mixing of the liquid phase in bubble columns. Chem. Eng. Sci. 1970, 25, 1–16. [Google Scholar] [CrossRef]
- Ruzicka, M.C.; Drahoš, J.; Fialova, M.; Thomas, N.H. Effect of bubble column dimensions on flow regime transition. Chem. Eng. Sci. 2001, 56, 6117–6124. [Google Scholar] [CrossRef]
- Al-Oufi, F.M.; Rielly, C.D.; Cumming, I.W. An experimental study of gas void fraction in dilute alcohol solutions in annular gap bubble columns using a four-point conductivity probe. Chem. Eng. Sci. 2011, 66, 5739–5748. [Google Scholar] [CrossRef]
- Al-Oufi, F.M.; Cumming, I.W.; Rielly, C.D. Destabilisation of homogeneous bubbly flow in an annular gap bubble column. Can. J. Chem. Eng. 2010, 88, 482–490. [Google Scholar] [CrossRef]
- Besagni, G.; Inzoli, F. Influence of internals on counter-current bubble column hydrodynamics: Holdup, flow regime transition and local flow properties. Chem. Eng. Sci. 2016, 145, 162–180. [Google Scholar] [CrossRef]
- Xue, J.; Al-Dahhan, M.; Dudukovic, M.P.; Mudde, R.F. Bubble velocity, size, and interfacial area measurements in a bubble column by four-point optical probe. AIChE J. 2008, 54, 350–363. [Google Scholar] [CrossRef]
- Mohagheghian, S.; Elbing, B.R. Characterization of Bubble Size Distributions within a Bubble Column. Fluids 2018, 3, 13. [Google Scholar] [CrossRef]
- Besagni, G.; Gallazzini, L.; Inzoli, F. On the scale-up criteria for bubble columns. Petroleum 2017. [Google Scholar] [CrossRef]
- Passos, A.D.; Voulgaropoulos, V.P.; Paras, S.V.; Mouza, A.A. The effect of surfactant addition on the performance of a bubble column containing a non-Newtonian liquid. Chem. Eng. Res. Des. 2015, 95, 93–104. [Google Scholar] [CrossRef]
- Anastasiou, A.D.; Passos, A.D.; Mouza, A.A. Bubble columns with fine pore sparger and non-Newtonian liquid phase: Prediction of gas holdup. Chem. Eng. Sci. 2013, 98, 331–338. [Google Scholar] [CrossRef]
- Poulsen, B.R.; Iversen, J.J.L. Membrane sparger in bubble column, airlift, and combined membrane–ring sparger bioreactors. Biotechnol. Bioeng. 1999, 64, 452–458. [Google Scholar] [CrossRef]
- Garnier, C.; Lance, M.; Marié, J.L. Measurement of local flow characteristics in buoyancy-driven bubbly flow at high void fraction. Exp. Therm. Fluid Sci. 2002, 26, 811–815. [Google Scholar] [CrossRef]
- Ruzicka, M.C.; Zahradník, J.; Drahoš, J.; Thomas, N.H. Homogeneous–heterogeneous regime transition in bubble columns. Chem. Eng. Sci. 2001, 56, 4609–4626. [Google Scholar] [CrossRef]
- Zahradnik, J.; Kaštanek, F. Gas holdup in uniformly aerated bubble column reactors. Chem. Eng. Commun. 1979, 3, 413–429. [Google Scholar] [CrossRef]
- Thorat, B.N.; Joshi, J.B. Regime transition in bubble columns: Experimental and predictions. Exp. Therm. Fluid Sci. 2004, 28, 423–430. [Google Scholar] [CrossRef]
- Şal, S.; Gül, Ö.F.; Özdemir, M. The effect of sparger geometry on gas holdup and regime transition points in a bubble column equipped with perforated plate spargers. Chem. Eng. Process. Process Intensif. 2013, 70, 259–266. [Google Scholar] [CrossRef]
- Besagni, G.; Inzoli, F. Comprehensive experimental investigation of counter-current bubble column hydrodynamics: Holdup, flow regime transition, bubble size distributions and local flow properties. Chem. Eng. Sci. 2016, 146, 259–290. [Google Scholar] [CrossRef]
- Akita, K.; Yoshida, F. Gas Holdup and Volumetric Mass Transfer Coefficient in Bubble Columns. Effects of Liquid Properties. Ind. Eng. Chem. Process Des. Dev. 1973, 12, 76–80. [Google Scholar] [CrossRef]
- Jin, H.; Yang, S.; He, G.; Wang, M.; Williams, R.A. The effect of gas-liquid counter-current operation on gas hold-up in bubble columns using electrical resistance tomography. J. Chem. Technol. Biotechnol. 2010, 85, 1278–1283. [Google Scholar] [CrossRef]
- Otake, T.; Tone, S.; Shinohara, K. Gas holdup in the bubble column with cocurrent and countercurrent gas-liquid flow. J. Chem. Eng. Jpn. 1981, 338–340. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Yamazaki, Y. Characteristics of Counter current Gas-Liquid Two-Phase Flow in Vertical Tubes. J. Nucl. Eng. Des. Sci. Technol. 1982, 19, 985–996. [Google Scholar] [CrossRef]
- Besagni, G.; Guédon, G.; Inzoli, F. Experimental investigation of counter current air-water flow in a large diameter vertical pipe with inners. J. Phys. Conf. Ser. 2014, 547, 012024. [Google Scholar] [CrossRef]
- Besagni, G.; Guédon, G.R.; Inzoli, F. Annular Gap Bubble Column: Experimental Investigation and Computational Fluid Dynamics Modeling. J. Fluids Eng. 2016, 138, 011302. [Google Scholar] [CrossRef]
- Besagni, G.; Inzoli, F. Bubble size distributions and shapes in annular gap bubble column. Exp. Therm. Fluid Sci. 2016, 4, 27–48. [Google Scholar] [CrossRef]
- De Guido, G.; Besagni, G.; Inzoli, F.; Pellegrini, L.A. New gas holdup data in large counter-current bubble columns. In Proceedings of the ICMF-2016–9th International Conference on Multiphase Flow, Florence, Italy, 22–27 May 2016. [Google Scholar]
- Trivedi, R.; Renganathan, T.; Krishnaiah, K. Hydrodynamics of countercurrent bubble column: Experiments and predictions. Chem. Eng. J. 2018, 338, 636–650. [Google Scholar] [CrossRef]
- Wilkinson, P.M.; Spek, A.P.; van Dierendonck, L.L. Design Parameters Estimation for Scale-Up of High-Pressure Bubble Columns. AIChE J. 1992, 38, 544–554. [Google Scholar] [CrossRef]
- Yang, J.H.; Yang, J.-I.; Kim, H.-J.; Chun, D.H.; Lee, H.-T.; Jung, H. Two regime transitions to pseudo-homogeneous and heterogeneous bubble flow for various liquid viscosities. Chem. Eng. Process. Process Intensif. 2010, 49, 1044–1050. [Google Scholar] [CrossRef]
- Lange, V.; Azzopardi, B.J.; Licence, P. Hydrodynamics of ionic liquids in bubble columns. In Ionic Liquids-New Aspects for the Future; InTechOpen: London, UK, 2013. [Google Scholar] [CrossRef]
- Kuncová, G.; Zahradník, J. Gas holdup and bubble frequency in a bubble column reactor containing viscous saccharose solutions. Chem. Eng. Process. Process Intensif. 1995, 34, 25–34. [Google Scholar] [CrossRef]
- Ruzicka, M.C.; Drahoš, J.; Mena, P.C.; Teixeira, J.A. Effect of viscosity on homogeneous–heterogeneous flow regime transition in bubble columns. Chem. Eng. J. 2003, 96, 15–22. [Google Scholar] [CrossRef]
- Olivieri, G.; Elena Russo, M.; Simeone, M.; Marzocchella, A.; Salatino, P. Effects of viscosity and relaxation time on the hydrodynamics of gas–liquid systems. Chem. Eng. Sci. 2011, 66, 3392–3399. [Google Scholar] [CrossRef]
- Rabha, S.; Schubert, M.; Hampel, U. Regime transition in viscous and pseudo viscous systems: A comparative study. AIChE J. 2014, 60, 3079–3090. [Google Scholar] [CrossRef]
- Marrucci, G.; Nicodemo, L. Coalescence of gas bubbles in aqueous solutions of inorganic electrolytes. Chem. Eng. Sci. 1967, 22, 1257–1265. [Google Scholar] [CrossRef]
- Keitel, G.; Onken, U. Inhibition of bubble coalescence by solutes in air/water dispersions. Chem. Eng. Sci. 1982, 37, 1635–1638. [Google Scholar] [CrossRef]
- Firouzi, M.; Howes, T.; Nguyen, A.V. A quantitative review of the transition salt concentration for inhibiting bubble coalescence. Adv. Colloid Interface Sci. 2015, 222, 305–318. [Google Scholar] [CrossRef] [PubMed]
- Craig, V.S.J.; Ninham, B.W.; Pashley, R.M. The effect of electrolytes on bubble coalescence in water. J. Phys. Chem. 1993, 97, 10192–10197. [Google Scholar] [CrossRef]
- Deschenes, L.A.; Barrett, J.; Muller, L.J.; Fourkas, J.T.; Mohanty, U. Inhibition of Bubble Coalescence in Aqueous Solutions. 1. Electrolytes. J. Phys. Chem. B 1998, 102, 5115–5119. [Google Scholar] [CrossRef]
- Weissenborn, P.K.; Pugh, R.J. Surface Tension of Aqueous Solutions of Electrolytes: Relationship with Ion Hydration, Oxygen Solubility, and Bubble Coalescence. J. Colloid Interface Sci. 1996, 184, 550–563. [Google Scholar] [CrossRef] [PubMed]
- Orvalho, S.; Ruzicka, M.C.; Drahos, J. Bubble Column with Electrolytes: Gas Holdup and Flow Regimes. Ind. Eng. Chem. Res. 2009, 48, 8237–8243. [Google Scholar] [CrossRef]
- Ruzicka, M.C.; Vecer, M.M.; Orvalho, S.; Drahoš, J. Effect of surfactant on homogeneous regime stability in bubble column. Chem. Eng. Sci. 2008, 63, 951–967. [Google Scholar] [CrossRef]
- Zahradník, J.; Fialová, M.; Linek, V. The effect of surface-active additives on bubble coalescence in aqueous media. Chem. Eng. Sci. 1999, 54, 4757–4766. [Google Scholar] [CrossRef]
- Prince, M.J.; Blanch, H.W. Transition electrolyte concentrations for bubble coalescence. AIChE J. 1990, 36, 1425–1429. [Google Scholar] [CrossRef]
- Lessard, R.R.; Zieminski, S.A. Bubble Coalescence and Gas Transfer in Aqueous Electrolytic Solutions. Ind. Eng. Chem. Fundam. 1971, 10, 260–269. [Google Scholar] [CrossRef]
- Nguyen, P.T.; Hampton, M.A.; Nguyen, A.V.; Birkett, G.R. The influence of gas velocity, salt type and concentration on transition concentration for bubble coalescence inhibition and gas holdup. Chem. Eng. Res. Des. 2012, 90, 33–39. [Google Scholar] [CrossRef]
- Besagni, G.; Inzoli, F. Influence of electrolyte concentration on holdup, flow regime transition and local flow properties in a large scale bubble column. J. Phys. Conf. Ser. 2015, 655, 012039. [Google Scholar] [CrossRef]
- Ribeiro, C.P., Jr.; Mewes, D. The influence of electrolytes on gas hold-up and regime transition in bubble columns. Chem. Eng. Sci. 2007, 62, 4501–4509. [Google Scholar] [CrossRef]
- Kelkar, B.G.; Phulgaonkar, S.R.; Shah, Y.T. The effect of electrolyte solutions on hydrodynamic and backmixing characteristics in bubble columnns. Chem. Eng. J. 1983, 27, 125–133. [Google Scholar] [CrossRef]
- Grover, G.S.; Rode, C.V.; Chaudhari, R.V. Effect of temperature on flow regimes and gas hold-up in a bubble column. Can. J. Chem. Eng. 1986, 64, 501–504. [Google Scholar] [CrossRef]
- Jamialahmadi, M.; Müller-Steinhagen, H. Effect of alcohol, organic acid and potassium chloride concentration on bubble size, bubble rise velocity and gas hold-up in bubble columns. Chem. Eng. J. 1992, 50, 47–56. [Google Scholar] [CrossRef]
- Hikita, H.; Asai, S.; Tanigawa, K.; Segawa, K.; Kitao, M. Gas hold-up in bubble columns. Chem. Eng. J. 1980, 20, 59–67. [Google Scholar] [CrossRef]
- Albijanić, B.; Havran, V.; Petrović, D.L.; Durić, M.; Tekić, M.N. Hydrodynamics and mass transfer in a draft tube airlift reactor with dilute alcohol solutions. AIChE J. 2007, 53, 2897–2904. [Google Scholar] [CrossRef]
- Krishna, R.; Ellenberger, J.; Maretto, C. Flow regime transition in bubble columns. Int. Commun. Heat Mass Transf. 1999, 26, 467–475. [Google Scholar] [CrossRef]
- Dargar, P.; Macchi, A. Effect of surface-active agents on the phase holdups of three-phase fluidized beds. Chem. Eng. Process. Process Intensif. 2006, 45, 764–772. [Google Scholar] [CrossRef]
- Clark, K.N. The effect of high pressure and temperature on phase distributions in a bubble column. Chem. Eng. Sci. 1990, 45, 2301–2307. [Google Scholar] [CrossRef]
- Cui, Z. Hydrodynamics in a Bubble Column at Elevated Pressures and Turbulence Energy Distribution in Bubbling Gas-Liquid and Gas-Liquid-Solid Flow Systems; The Ohio State University: Columbus, OH, USA, 2005. [Google Scholar]
- Hashemi, S.; Macchi, A.; Servio, P. Gas–liquid mass transfer in a slurry bubble column operated at gas hydrate forming conditions. Chem. Eng. Sci. 2009, 64, 3709–3716. [Google Scholar] [CrossRef]
- Kang, Y.; Cho, Y.J.; Woo, K.J.; Kim, K.I.; Kim, S.D. Bubble properties and pressure fluctuations in pressurized bubble columns. Chem. Eng. Sci. 2000, 55, 411–419. [Google Scholar] [CrossRef]
- Kemoun, A.; Cheng Ong, B.; Gupta, P.; Al-Dahhan, M.H.; Dudukovic, M.P. Gas holdup in bubble columns at elevated pressure via computed tomography. Int. J. Multiph. Flow 2001, 27, 929–946. [Google Scholar] [CrossRef]
- Krishna, R.; Wilkinson, P.M.; Van Dierendonck, L.L. A model for gas holdup in bubble columns incorporating the influence of gas density on flow regime transitions. Chem. Eng. Sci. 1991, 46, 2491–2496. [Google Scholar] [CrossRef]
- Kumar, S.; Munshi, P.; Khanna, A. High Pressure Experiments and Simulations in Cocurrent Bubble Columns. Procedia Eng. 2012, 42, 842–853. [Google Scholar] [CrossRef][Green Version]
- Letzel, H.M.; Schouten, J.C.; van den Bleek, C.M.; Krishna, R. Influence of elevated pressure on the stability of bubbly flows. Chem. Eng. Sci. 1997, 52, 3733–3739. [Google Scholar] [CrossRef]
- Letzel, M.H.; Schouten, J.C.; van den Bleek, C.M.; Krishna, R. Effect of gas density on large-bubble holdup in bubble column reactors. AIChE J. 1998, 44, 2333–2336. [Google Scholar] [CrossRef]
- Lin, T.J.; Juang, R.C.; Chen, C.C. Characterizations of flow regime transitions in a high-pressure bubble column by chaotic time series analysis of pressure fluctuation signals. Chem. Eng. Sci. 2001, 56, 6241–6247. [Google Scholar] [CrossRef]
- Reilly, I.; Scott, D.; Debruijn, T.; MacIntyre, D. The role of gas phase momentum in determining gas holdup and hydrodynamic flow regimes in bubble column operations. Can. J. Chem. Eng. 1994, 72, 3–12. [Google Scholar] [CrossRef]
- Shaikh, A.; Al-Dahhan, M. Characterization of the hydrodynamic flow regime in bubble columns via computed tomography. Flow Meas. Instrum. 2005, 16, 91–98. [Google Scholar] [CrossRef]
- Han, L.; Al-Dahhan, M.H. Gas–liquid mass transfer in a high pressure bubble column reactor with different sparger designs. Chem. Eng. Sci. 2007, 62, 131–139. [Google Scholar] [CrossRef]
- Fan, L.S.; Yang, G.Q.; Lee, D.J.; Tsuchiya, K.; Luo, X. Some aspects of high-pressure phenomena of bubbles in liquids and liquid–solid suspensions. Chem. Eng. Sci. 1999, 54, 4681–4709. [Google Scholar] [CrossRef]
- Wilkinson, P.M.; Dierendonck, L.L.V. Pressure and gas density effects on bubble break-up and gas hold-up in bubble columns. Chem. Eng. Sci. 1990, 45, 2309–2315. [Google Scholar] [CrossRef]
- Lott, F.; Kelder, H.; Teitelbaum, H. A transition from Kelvin–Helmholtz instabilities to propagating wave instabilities. Phys. Fluids A Fluid Dyn. 1992, 4, 1990–1997. [Google Scholar] [CrossRef]
- Bukur, D.B.; Petrovic, D.; Daly, J.G. Flow regime transitions in a bubble column with a paraffin wax as the liquid medium. Ind. Eng. Chem. Res. 1987, 26, 1087–1092. [Google Scholar] [CrossRef]
- Lin, T.J.; Tsuchiya, K.; Fan, L.-S. On the measurements of regime transition in high-pressure bubble columns. Can. J. Chem. Eng. 1999, 77, 370–374. [Google Scholar] [CrossRef]
- Shaikh, A.; Al-Dahhan Muthanna, H. A Review on Flow Regime Transition in Bubble Columns. Int. J. Chem. React. Eng. 2007, 5. [Google Scholar] [CrossRef]
- Zhang, J.P.; Grace, J.R.; Epstein, N.; Lim, K.S. Flow regime identification in gas-liquid flow and three-phase fluidized beds. Chem. Eng. Sci. 1997, 52, 3979–3992. [Google Scholar] [CrossRef]
- Wu, B.; Firouzi, M.; Mitchell, T.; Rufford, T.E.; Leonardi, C.; Towler, B. A critical review of flow maps for gas-liquid flows in vertical pipes and annuli. Chem. Eng. J. 2017, 326, 350–377. [Google Scholar] [CrossRef]
- Fair, J.R.; Lambright, A.J.; Andersen, J.W. Heat Transfer and Gas Holdup in a Sparged Contactor. Ind. Eng. Chem. Process Des. Dev. 1962, 1, 33–36. [Google Scholar] [CrossRef]
- Gopal, J.S.; Sharma, M.M. Mass transfer characteristics of low H/D bubble columns. Can. J. Chem. Eng. 1983, 61, 517–526. [Google Scholar] [CrossRef]
- Sada, E.; Katoh, S.; Yoshii, H.; Yamanishi, T.; Nakanishi, A. Performance of the gas bubble column in molten salt systems. Ind. Eng. Chem. Process Des. Dev. 1984, 23, 151–154. [Google Scholar] [CrossRef]
- Reilly, I.G.; Scott, D.S.; De Bruijn, T.; Jain, A.; Piskorz, J. A correlation for gas holdup in turbulent coalescing bubble columns. Can. J. Chem. Eng. 1986, 64, 705–717. [Google Scholar] [CrossRef]
- Kawase, Y.; Moo-Young, M. Influence of antifoam agents on gas hold-up and mass transfer in bubble columns with non-newtonian fluids. Appl. Microbiol. Biotechnol. 1987, 27, 159–167. [Google Scholar] [CrossRef]
- Ying, D.H.; Moujaes, S.; Sivasubramanian, R.; Givens, E. Gas/Slurry Flow in Coal-Liquefaction Processes (Fluid Dynamics in 3-Phase-Flow Column); Quarterly Technical Progress Report, 1 January–31 March 1981; Air Products and Chemicals, Inc.: Allentown, PA, USA, 1981. [Google Scholar]
- Thorat, B.N.; Shevade, A.V.; Bhilegaonkar, K.N.; Aglawe, R.H.; Parasu Veera, U.; Thakre, S.S.; Pandit, A.B.; Sawant, S.B.; Joshi, J.B. Effect of Sparger Design and Height to Diameter Ratio on Fractional Gas Hold-up in Bubble Columns. Chem. Eng. Res. Des. 1998, 76, 823–834. [Google Scholar] [CrossRef]
- Yoshida, F.; Akita, K. Performance of gas bubble columns: Volumetric liquid-phase mass transfer coefficient and gas holdup. AIChE J. 1965, 11, 9–13. [Google Scholar] [CrossRef]
- Voigt, J.; Schügerl, K. Absorption of oxygen in countercurrent multistage bubble columns—I Aqueous solutions with low viscosity. Chem. Eng. Sci. 1979, 34, 1221–1229. [Google Scholar] [CrossRef]
- Rollbusch, P.; Becker, M.; Ludwig, M.; Bieberle, A.; Grünewald, M.; Hampel, U.; Franke, R. Experimental investigation of the influence of column scale, gas density and liquid properties on gas holdup in bubble columns. Int. J. Multiph. Flow 2015, 75, 88–106. [Google Scholar] [CrossRef]
- Sangnimnuan, A.; Prasad, G.N.; Agnew, J.B. Gas hold-up and backmixing in a bubble-column reactor under coal-hydroliquefaction conditions. Chem. Eng. Commun. 1984, 25, 193–212. [Google Scholar] [CrossRef]
- de Bruijn, T.J.W.; Chase, J.D.; Dawson, W.H. Gas holdup in a two-phase vertical tubular reactor at high pressure. Can. J. Chem. Eng. 1988, 66, 330–333. [Google Scholar] [CrossRef]
- Lau, R.; Peng, W.; Velazquez-Vargas, L.G.; Yang, G.Q.; Fan, L.S. Gas-Liquid Mass Transfer in High-Pressure Bubble Columns. Ind. Eng. Chem. Res. 2004, 43, 1302–1311. [Google Scholar] [CrossRef]
- Yang, G.Q.; Fan, L.S. Axial liquid mixing in high-pressure bubble columns. AIChE J. 2003, 49, 1995–2008. [Google Scholar] [CrossRef]
- Shawaqfeh, A.T. Gas holdup and liquid axial dispersion under slug flow conditions in gas–liquid bubble column. Chem. Eng. Process. Process Intensif. 2003, 42, 767–775. [Google Scholar] [CrossRef]
- Hills, J.H. The operation of a bubble column at high throughputs: I. Gas holdup measurements. Chem. Eng. J. 1976, 12, 89–99. [Google Scholar] [CrossRef]
- Baawain, M.S.; El-Din, M.G.; Smith, D.W. Artificial neural networks modeling of ozone bubble columns: Mass transfer coefficient, gas hold-up, and bubble size. Ozone Sci. Eng. 2007, 29, 343–352. [Google Scholar] [CrossRef]
- Chaumat, H.; Billet-Duquenne, A.M.; Augier, F.; Mathieu, C.; Delmas, H. Mass transfer in bubble column for industrial conditions—Effects of organic medium, gas and liquid flow rates and column design. Chem. Eng. Sci. 2005, 60, 5930–5936. [Google Scholar] [CrossRef]
- Jin, H.; Yang, S.; Wang, M.; Williams, R.A. Measurement of gas holdup profiles in a gas liquid cocurrent bubble column using electrical resistance tomography. Flow Meas. Instrum. 2007, 18, 191–196. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, R.A.; Munshi, P.; Khanna, A. Gas Hold-up in Three Phase Co-current Bubble Columns. Procedia Eng. 2012, 42, 782–794. [Google Scholar] [CrossRef]
- Pjontek, D.; Parisien, V.; Macchi, A. Bubble characteristics measured using a monofibre optical probe in a bubble column and freeboard region under high gas holdup conditions. Chem. Eng. Sci. 2014, 111, 153–169. [Google Scholar] [CrossRef]
- Shah, M.; Kiss, A.A.; Zondervan, E.; Van Der Schaaf, J.; De Haan, A.B. Gas holdup, axial dispersion, and mass transfer studies in bubble columns. Ind. Eng. Chem. Res. 2012, 51, 14268–14278. [Google Scholar] [CrossRef]
- Simonnet, M.; Gentric, C.; Olmos, E.; Midoux, N. Experimental determination of the drag coefficient in a swarm of bubbles. Chem. Eng. Sci. 2007, 62, 858–866. [Google Scholar] [CrossRef]
- Biń, A.K.; Duczmal, B.; Machniewski, P. Hydrodynamics and ozone mass transfer in a tall bubble column. Chem. Eng. Sci. 2001, 56, 6233–6240. [Google Scholar] [CrossRef]
- Krishna, R.; Ellenberger, J. Gas holdup in bubble column reactors operating in the churn-turbulent flow regime. AIChE J. 1996, 42, 2627–2634. [Google Scholar] [CrossRef]
- Krishna, R.; Baten, J.M.v.; Urseanu, M.I. Scale Effects on the Hydrodynamics of Bubble Columns Operating in the Homogeneous Flow Regime. Chem. Eng. Technol. 2001, 24, 451–458. [Google Scholar] [CrossRef]
- Urseanu, M.I.; Guit, R.P.M.; Stankiewicz, A.; van Kranenburg, G.; Lommen, J.H.G.M. Influence of operating pressure on the gas hold-up in bubble columns for high viscous media. Chem. Eng. Sci. 2003, 58, 697–704. [Google Scholar] [CrossRef]
- Behkish, A.; Lemoine, R.; Sehabiague, L.; Oukaci, R.; Morsi, B.I. Gas holdup and bubble size behavior in a large-scale slurry bubble column reactor operating with an organic liquid under elevated pressures and temperatures. Chem. Eng. J. 2007, 128, 69–84. [Google Scholar] [CrossRef]
- Hughmark, G.A. Holdup and Mass Transfer in Bubble Columns. Ind. Eng. Chem. Process Des. Dev. 1967, 6, 218–220. [Google Scholar] [CrossRef]
- Kato, Y.; Nishiwaki, A.; Fukuda, T.; Tanaka, S. The behavior of suspended solid particles and liquid in bubble columns. J. Chem. Eng. Jpn. 1972, 5, 112–118. [Google Scholar] [CrossRef]
- Koide, K.; Morooka, S.; Ueyama, K.; Matsuura, A.; Yamashita, F.; Iwamoto, S.; Kato, Y.; Inoue, H.; Shigeta, M.; Suzuki, S.; et al. Behavior of bubbles in large scale bubble column. J. Chem. Eng. Jpn. 1979, 12, 98–104. [Google Scholar] [CrossRef][Green Version]
- Deckwer, W.-D.; Louisi, Y.; Zaidi, A.; Ralek, M. Hydrodynamic Properties of the Fischer-Tropsch Slurry Process. Ind. Eng. Chem. Process Des. Dev. 1980, 19, 699–708. [Google Scholar] [CrossRef]
- Nottenkamper, R.; Steiff, A.; Weinspach, P. Experimental investigation of hydrodynamics of bubble columns. Ger. Chem. Eng. 1983, 6, 147–155. [Google Scholar]
- Koide, K.; Takazawa, A.; Komura, M.; Matsunaga, H. Gas holdup and volumetric liquid-phase mass transfer coefficient in solid-suspended bubble columns. J. Chem. Eng. Jpn. 1984, 17, 459–466. [Google Scholar] [CrossRef]
- Lemoine, R.; Behkish, A.; Sehabiague, L.; Heintz, Y.J.; Oukaci, R.; Morsi, B.I. An algorithm for predicting the hydrodynamic and mass transfer parameters in bubble column and slurry bubble column reactors. Fuel Process. Technol. 2008, 89, 322–343. [Google Scholar] [CrossRef]
- Kantarci, N.; Borak, F.; Ulgen, K.O. Bubble column reactors. Process Biochem. 2005, 40, 2263–2283. [Google Scholar] [CrossRef]
- Forret, A.; Schweitzer, J.M.; Gauthier, T.; Krishna, R.; Schweich, D. Influence of scale on the hydrodynamics of bubble column reactors: An experimental study in columns of 0.1, 0.4 and 1 m diameters. Chem. Eng. Sci. 2003, 58, 719–724. [Google Scholar] [CrossRef]
- Patil, V.K.; Joshi, J.B.; Sharma, M.M. Sectionalised bubble column: Gas hold-up and wall side solid—Liquid mass transfer coefficient. Can. J. Chem. Eng. 1984, 62, 228–232. [Google Scholar] [CrossRef]
- Kastanek, F.; Zahradnik, J.; Kratochvil, J.; Cermak, J. Modeling of large-scale bubble column reactors for non-ideal gas–liquid systems. Front. Chem. React. Eng. 1984, 1, 330–344. [Google Scholar]
- Sasaki, S.; Uchida, K.; Hayashi, K.; Tomiyama, A. Effects of column diameter and liquid height on gas holdup in air-water bubble columns. Exp. Therm. Fluid Sci. 2017, 82, 359–366. [Google Scholar] [CrossRef]
- Besagni, G.; Guédon, G.R.; Inzoli, F. Computational fluid-dynamic modeling of the mono-dispersed homogeneous flow regime in bubble columns. Nuclear Eng. Des. 2018, 331, 222–237. [Google Scholar] [CrossRef]
- Reith, T.; Renken, S.; Israël, B.A. Gas hold-up and axial mixing in the fluid phase of bubble columns. Chem. Eng. Sci. 1968, 23, 619–629. [Google Scholar] [CrossRef]
- Krishna, R.; Sie, S.T. Design and scale-up of the Fischer–Tropsch bubble column slurry reactor. Fuel Process. Technol. 2000, 64, 73–105. [Google Scholar] [CrossRef]
- Bouaifi, M.; Hebrard, G.; Bastoul, D.; Roustan, M. A comparative study of gas hold-up, bubble size, interfacial area and mass transfer coefficients in stirred gas–liquid reactors and bubble columns. Chem. Eng. Process. Process Intensif. 2001, 40, 97–111. [Google Scholar] [CrossRef]
- Parasu Veera, U.; Joshi, J.B. Measurement of Gas Hold-up Profiles in Bubble Column by Gamma Ray Tomography: Effect of Liquid Phase Properties. Chem. Eng. Res. Des. 2000, 78, 425–434. [Google Scholar] [CrossRef]
- Eissa, S.H.; Schügerl, K. Holdup and backmixing investigations in cocurrent and countercurrent bubble columns. Chem. Eng. Sci. 1975, 30, 1251–1256. [Google Scholar] [CrossRef]
- Khare, A.S.; Joshi, J.B. Effect of fine particles on gas hold-up in three-phase sparged reactors. Chem. Eng. J. 1990, 44, 11–25. [Google Scholar] [CrossRef]
- Godbole, S.P.; Honath, M.F.; Shah, Y.T. Holdup structure in highly viscous Newtonian and non-Newtonian liquids in bubble columns. Chem. Eng. Commun. 1982, 16, 119–134. [Google Scholar] [CrossRef]
- Bach, H.F.; Pilhofer, T. Variation of Gas Holdup in Bubble Columns With Physical Properties of Liquids and Operating Parameters of Columns. Ger. Chem. Eng. 1978, 1, 270–275. [Google Scholar]
- Hwang, S.-J.; Cheng, Y.-L. Gas holdup and liquid velocity in three-phase internal-loop airlift reactors. Chem. Eng. Sci. 1997, 52, 3949–3960. [Google Scholar] [CrossRef]
- Ruthiya Keshav, C.; van der Schaaf, J.; Kuster Ben, F.M.; Schouten Jaap, C. Influence of Particles and Electrolyte on Gas Hold-Up and Mass Transfer in a Slurry Bubble Column. Int. J. Chem. React. Eng. 2006, 4. [Google Scholar] [CrossRef]
- Kluytmans, J.H.J.; Kuster, B.F.M.; Schouten, J.C. Gas Holdup in a Slurry Bubble Column: Influence of Electrolyte and Carbon Particles. Ind. Eng. Chem. Res. 2001, 40, 5326–5333. [Google Scholar] [CrossRef]
- Kellermann, H.; Jüttner, K.; Kreysa, G. Dynamic modelling of gas hold-up in different electrolyte systems. J. Appl. Electrochem. 1998, 28, 311–319. [Google Scholar] [CrossRef]
- Zahradnik, J.; Fialova, M.; Kastanek, F.; Green, K.; Thomas, N. The effect of electrolytes on bubble coalescence and gas holdup in bubble column reactors. Chem. Eng. Res. Des. 1995, 73, 341–346. [Google Scholar]
- Zahradník, J.; Kuncová, G.; Fialová, M. The effect of surface active additives on bubble coalescence and gas holdup in viscous aerated batches. Chem. Eng. Sci. 1999, 54, 2401–2408. [Google Scholar] [CrossRef]
- Kelkar, B.G.; Godbole, S.P.; Honath, M.F.; Shah, Y.T.; Carr, N.L.; Deckwer, W.D. Effect of addition of alcohols on gas holdup and backmixing in bubble columns. AIChE J. 1983, 29, 361–369. [Google Scholar] [CrossRef]
- Shah, Y.T.; Joseph, S.; Smith, D.N.; Ruether, J.A. On the behavior of the gas phase in a bubble column with ethanol-water mixtures. Ind. Eng. Chem. Process Des. Dev. 1985, 24, 1140–1148. [Google Scholar] [CrossRef]
- Besagni, G.; Inzoli, F. The effect of electrolyte concentration on counter-current gas–liquid bubble column fluid dynamics: Gas holdup, flow regime transition and bubble size distributions. Chem. Eng. Res. Des. 2017, 118, 170–193. [Google Scholar] [CrossRef]
- Hur, Y.G.; Yang, J.H.; Jung, H.; Lee, K.Y. Continuous alcohol addition in vaporized form and its effect on bubble behavior in a bubble column. Chem. Eng. Res. Des. 2014, 92, 804–811. [Google Scholar] [CrossRef]
- Guo, K.; Wang, T.; Yang, G.; Wang, J. Distinctly different bubble behaviors in a bubble column with pure liquids and alcohol solutions. J. Chem. Technol. Biotechnol. 2016. [Google Scholar] [CrossRef]
- Syeda, S.R.; Afacan, A.; Chuang, K.T. Prediction of gas hold-up in a bubble column filled with pure and binary liquids. Can. J. Chem. Eng. 2002, 80, 44–50. [Google Scholar] [CrossRef]
- Bhaga, D.; Pruden, B.B.; Weber, M.E. Gas holdup in a bubble column containing organic liquid mixtures. Can. J. Chem. Eng. 1971, 49, 417–420. [Google Scholar] [CrossRef]
- Andrew, S. Frothing in two-component liquid mixtures. In Proceedings of the International Symposium on Distillation, Brighton, UK, 8–10 September 1969; pp. 73–78. [Google Scholar]
- Hecht, K.; Bey, O.; Ettmüller, J.; Graefen, P.; Friehmelt, R.; Nilles, M. Effect of Gas Density on Gas Holdup in Bubble Columns. Chem. Ing. Tech. 2015, 87, 762–772. [Google Scholar] [CrossRef]
- Jordan, U.; Schumpe, A. The gas density effect on mass transfer in bubble columns with organic liquids. Chem. Eng. Sci. 2001, 56, 6267–6272. [Google Scholar] [CrossRef]
- Letzel, H.M.; Schouten, J.C.; Krishna, R.; van den Bleek, C.M. Gas holdup and mass transfer in bubble column reactors operated at elevated pressure. Chem. Eng. Sci. 1999, 54, 2237–2246. [Google Scholar] [CrossRef]
- Shulman, H.L.; Molstad, M.C. Gas-Bubble Columns for Gas-Liquid Contacting. Ind. Eng. Chem. 1950, 42, 1058–1070. [Google Scholar] [CrossRef]
- Koetsier, W.T.; Van Swaaij, W.P.M.; Van der Most, M. Maximum hold-up in bubble columns. J. Chem. Eng. Jpn. 1976, 9, 332–333. [Google Scholar] [CrossRef]
- öztürk, S.S.; Schumpe, A.; Deckwer, W.D. Organic liquids in a bubble column: Holdups and mass transfer coefficients. AIChE J. 1987, 33, 1473–1480. [Google Scholar] [CrossRef]
- Behkish, A.; Lemoine, R.; Oukaci, R.; Morsi, B.I. Novel correlations for gas holdup in large-scale slurry bubble column reactors operating under elevated pressures and temperatures. Chem. Eng. J. 2006, 115, 157–171. [Google Scholar] [CrossRef]
- Dewes, I.; Schumpe, A. Gas density effect on mass transfer in the slurry bubble column. Chem. Eng. Sci. 1997, 52, 4105–4109. [Google Scholar] [CrossRef]
- Idogawa, K.; Ikeda, K.; Fukuda, T.; Morooka, S. Behavior of bubbles of the air-water system in a column under high pressure. Int. Chem. Eng. 1986, 26, 468–474. [Google Scholar]
- Ishiyama, H.; Isokawa, Y.; Sawai, J.; Kojima, H. Hydrodynamics in a small size pressurized bubble column. Chem. Eng. Sci. 2001, 56, 6273–6278. [Google Scholar] [CrossRef]
- Jiang, P.; Lin, T.J.; Luo, X.; Fan, L.S. Flow visualization of high pressure (21 MPa) bubble column: Bubble characteristics. Chem. Eng. Res. Des. 1995, 73, 269–274. [Google Scholar]
- Kang, Y.; Cho, Y.J.; Woo, K.J.; Kim, S.D. Diagnosis of bubble distribution and mass transfer in pressurized bubble columns with viscous liquid medium. Chem. Eng. Sci. 1999, 54, 4887–4893. [Google Scholar] [CrossRef]
- Lin, T.J.; Tsuchiya, K.; Fan, L.S. Bubble Flow Characteristics in Bubble Columns at Elevated Pressure and Temperature. AIChE J. 1998, 44, 545–560. [Google Scholar] [CrossRef]
- Luo, X.; Lee, D.J.; Lau, R.; Yang, G.; Fan, L.-S. Maximum stable bubble size and gas holdup in high-pressure slurry bubble columns. AIChE J. 1999, 45, 665–680. [Google Scholar] [CrossRef]
- Maalej, S.; Benadda, B.; Otterbein, M. Interfacial area and volumetric mass transfer coefficient in a bubble reactor at elevated pressures. Chem. Eng. Sci. 2003, 58, 2365–2376. [Google Scholar] [CrossRef]
- Schäfer, R.; Merten, C.; Eigenberger, G. Bubble size distributions in a bubble column reactor under industrial conditions. Exp. Therm. Fluid Sci. 2002, 26, 595–604. [Google Scholar] [CrossRef]
- Therning, P.; Rasmuson, A. Liquid dispersion, gas holdup and frictional pressure drop in a packed bubble column at elevated pressures. Chem. Eng. J. 2001, 81, 331–335. [Google Scholar] [CrossRef]
- Oyevaar, M.; Bos, R.; Westerterp, K. Interfacial areas and gas hold-ups in gas—Liquid contactors at elevated pressures from 0.1 to 8.0 MPa. Chem. Eng. Sci. 1991, 46, 1217–1231. [Google Scholar] [CrossRef]
- Lorenz, O.; Schumpe, A.; Ekambara, K.; Joshi, J.B. Liquid phase axial mixing in bubble columns operated at high pressures. Chem. Eng. Sci. 2005, 60, 3573–3586. [Google Scholar] [CrossRef]
- Pohorecki, R.; Moniuk, W.; Zdrójkowski, A.; Bielski, P. Hydrodynamics of a pilot plant bubble column under elevated temperature and pressure. Chem. Eng. Sci. 2001, 56, 1167–1174. [Google Scholar] [CrossRef]
- Soong, Y.; Harke, F.W.; Gamwo, I.K.; Schehl, R.R.; Zarochak, M.F. Hydrodynamic study in a slurry-bubble-column reactor. Catal. Today 1997, 35, 427–434. [Google Scholar] [CrossRef]
- Kölbel, H.; Klötzer, D.; Hammer, H. Zur Reaktionstechnik von Blasensäulen-Reaktoren mit suspendiertem Katalysator bei erhöhtem Druck. Chem. Ing. Tech. 1971, 43, 103–111. [Google Scholar] [CrossRef]
- Yang, W.; Wang, J.; Jin, Y. Mass transfer characteristics of syngas components in slurry system at industrial conditions. Chem. Eng. Technol. 2001, 24, 651–657. [Google Scholar] [CrossRef]
- Lockett, M.; Kirkpatrick, R. Ideal bubbly flow and actual flow in bubble columns. Trans. Inst. Chem. Eng 1975, 53, 267–273. [Google Scholar]
- Mashelkar, R. Bubble columns. Br. Chem. Eng. 1970, 15, 1297. [Google Scholar]
- Kato, Y.; Nishiwaki, A. Longitudinal dispersion coefficient of a liquid in a bubble column. Int. Chem. Eng. 1972, 12, 182–187. [Google Scholar] [CrossRef][Green Version]
- Hikita, H.; Kikukawa, H. Liquid-phase mixing in bubble columns: Effect of liquid properties. Chem. Eng. J. 1974, 8, 191–197. [Google Scholar] [CrossRef]
- Gestrich, W.; Rähse, W. Der relative Gasgehalt von Blasenschichten. Chem. Ing. Tech. 1975, 47, 8–13. [Google Scholar] [CrossRef]
- Kumar, A.; Degaleesan, T.E.; Laddha, G.S.; Hoelscher, H.E. Bubble swarm characteristics in bubble columns. Can. J. Chem. Eng. 1976, 54, 503–508. [Google Scholar] [CrossRef]
- Friedel, L.; Herbrechtsmeier, P.; Steiner, R. Mean gas holdup in downflow bubble columns. Ger. Chem. Eng. 1980, 3, 342. [Google Scholar]
- Elgozali, A.; Linek, V.; Fialová, M.; Wein, O.; Zahradník, J. Influence of viscosity and surface tension on performance of gas–liquid contactors with ejector type gas distributor. Chem. Eng. Sci. 2002, 57, 2987–2994. [Google Scholar] [CrossRef]
- Mersmann, A. Design and scale-up of bubble and spray columns. Ger. Chem. Eng. 1978, 1, 1–11. [Google Scholar]
- Santus, D.; Salvagno, N. Purificazione di Gas Naturale da Composti Acidi Mediante Assorbimento Fisico Downhole. Master’s Thesis, Politecnico di Milano, Milan, Italy, 2014. [Google Scholar]
- Riquarts, H.-P.; Pilhofer, T. Modell des heterogenen Strömungszustandes in Blasensäulen. Verfahrenstechnik 1978, 12, 77–80. [Google Scholar]
- Iordache, O.M.; Muntean, O.I. Stochastic approach to the hydrodynamics of gas-liquid dispersions. Ind. Eng. Chem. Fundam. 1981, 20, 204–207. [Google Scholar] [CrossRef]
- Schumpe, A.; Deckwer, W.D. Viscous media in tower bioreactors: Hydrodynamic characteristics and mass transfer properties. Bioprocess Eng. 1987, 2, 79–94. [Google Scholar] [CrossRef]
- Kawase, Y.; Moo-Young, M. Theoretical prediction of gas hold-up in bubble columns with Newtonian and non-Newtonian fluids. Ind. Eng. Chem. Res. 1987, 26, 933–937. [Google Scholar] [CrossRef]
- Schumpe, A.; Deckwer, W.D. Gas holdups, specific interfacial areas, and mass transfer coefficients of aerated carboxymethyl cellulose solutions in a bubble column. Ind. Eng. Chem. Process Des. Dev. 1982, 21, 706–711. [Google Scholar] [CrossRef]
- Viswanathan, K.; Rao, D.S. Inviscid liquid circulation in bubble columns. Chem. Eng. Commun. 1984, 25, 133–155. [Google Scholar] [CrossRef]
- Kawase, Y.; Moo-Young, M. Influence of non-Newtonian flow behaviour on mass transfer in bubble columns with and without draft tubes. Chem. Eng. Commun. 1986, 40, 67–83. [Google Scholar] [CrossRef]
- Kataoka, H.; Takeuchi, H.; Nakao, K.; Yagi, H.; Tadaki, T.; Otake, T.; Miyauchi, T.; Washimi, K.; Watanabe, K.; Yoshida, F. Mass transfer in a large bubble column. J. Chem. Eng. Jpn. 1979, 12, 105–110. [Google Scholar] [CrossRef][Green Version]
- Zou, R.; Jiang, X.; Li, B.; Zu, Y.; Zhang, L. Studies on gas holdup in a bubble column operated at elevated temperatures. Ind. Eng. Chem. Res. 1988, 27, 1910–1916. [Google Scholar] [CrossRef]
- Kawase, Y.; Umeno, S.; Kumagai, T. The prediction of gas hold-up in bubble column reactors: Newtonian and non-newtonian fluids. Chem. Eng. J. 1992, 50, 1–7. [Google Scholar] [CrossRef]
- Besagni, G.; Inzoli, F. Novel gas holdup and regime transition correlation for two-phase bubble columns. J. Phys. Conf. Ser. 2017, 923, 012011. [Google Scholar] [CrossRef]
- Gaddis, E.S.; Vogelpohl, A. Bubble formation in quiescent liquids under constant flow conditions. Chem. Eng. Sci. 1986, 41, 97–105. [Google Scholar] [CrossRef]
- Risso, F. Agitation, Mixing, and Transfers Induced by Bubbles. Annu. Rev. Fluid Mech. 2018, 50, 25–48. [Google Scholar] [CrossRef]
- Liao, Y.; Lucas, D. A literature review of theoretical models for drop and bubble breakup in turbulent dispersions. Chem. Eng. Sci. 2009, 64, 3389–3406. [Google Scholar] [CrossRef]
- Liao, Y.; Lucas, D. A literature review on mechanisms and models for the coalescence process of fluid particles. Chem. Eng. Sci. 2010, 65, 2851–2864. [Google Scholar] [CrossRef]
- Haberman, W.L.; Morton, R.K.; Basin, D.W.T.M. An Experimental Investigation of the Drag and Shape of Air Bubbles Rising in Various Liquids; Haberman, W.L., Morton, R.K., Eds.; David W. Taylor Model Basin: Washington, DC, USA, 1953. [Google Scholar] [CrossRef]
- Clift, R.; Grace, J.R.; Weber, M.E. Bubbles, Drops, and Particles; Dover Publications, Inc.: Mineola, NY, USA, 1978. [Google Scholar]
- Chao, B.T. Motion of Spherical Gas Bubbles in a Viscous Liquid at Large Reynolds Numbers. Phys. Fluids 1962, 5, 69–79. [Google Scholar] [CrossRef]
- Celata, G.P.; Cumo, M.; D’Annibale, F.; Di Marco, P.; Tomiyama, A.; Zovini, C. Effect of gas injection mode and purity of liquid on bubble rising in two-component systems. Exp. Therm. Fluid Sci. 2006, 31, 37–53. [Google Scholar] [CrossRef]
- Celata, G.P.; Cumo, M.; D’Annibale, F.; Tomiyama, A. The wake effect on bubble rising velocity in one-component systems. Int. J. Multiph. Flow 2004, 30, 939–961. [Google Scholar] [CrossRef]
- Celata, G.P.; D’Annibale, F.; Di Marco, P.; Memoli, G.; Tomiyama, A. Measurements of rising velocity of a small bubble in a stagnant fluid in one- and two-component systems. Exp. Therm. Fluid Sci. 2007, 31, 609–623. [Google Scholar] [CrossRef]
- Okawa, T.; Tanaka, T.; Kataoka, I.; Mori, M. Temperature effect on single bubble rise characteristics in stagnant distilled water. Int. J. Heat Mass Transf. 2003, 46, 903–913. [Google Scholar] [CrossRef]
- Wellek, R.M.; Agrawal, A.K.; Skelland, A.H.P. Shape of liquid drops moving in liquid media. AIChE J. 1966, 12, 854–862. [Google Scholar] [CrossRef]
- Moore, D.W. The rise of a gas bubble in a viscous liquid. J. Fluid Mech. 1959, 6, 113–130. [Google Scholar] [CrossRef]
- Taylor, T.D.; Acrivos, A. On the deformation and drag of a falling viscous drop at low Reynolds number. J. Fluid Mech. 1964, 18, 466–476. [Google Scholar] [CrossRef]
- Tadaki, T.; Maeda, S. On the shape and velocity of single air bubbles rising in various liquids. Kagaku Kogaku 1961, 25, 254–264. [Google Scholar] [CrossRef]
- Bozzano, G.; Dente, M. Shape and terminal velocity of single bubble motion: A novel approach. Comput. Chem. Eng. 2001, 25, 571–576. [Google Scholar] [CrossRef]
- Aoyama, S.; Hayashi, K.; Hosokawa, S.; Tomiyama, A. Shapes of ellipsoidal bubbles in infinite stagnant liquids. Int. J. Multiph. Flow 2016, 79, 23–30. [Google Scholar] [CrossRef]
- Besagni, G.; Brazzale, P.; Fiocca, A.; Inzoli, F. Estimation of bubble size distributions and shapes in two-phase bubble column using image analysis and optical probes. Flow Meas. Instrum. 2016. [Google Scholar] [CrossRef]
- Besagni, G.; Inzoli, F.; Ziegenhein, T.; Hessenkemper, H.; Lucas, D. Bubble aspect ratio in dense bubbly flows: Experimental studies in low Morton-number systems. J. Phys. Conf. Ser. 2017, 923, 012014. [Google Scholar] [CrossRef]
- Ziegenhein, T.; Lucas, D. Observations on bubble shapes in bubble columns under different flow conditions. Exp. Therm. Fluid Sci. 2017, 85, 248–256. [Google Scholar] [CrossRef]
- Chilekar, V.P.; van der Schaaf, J.; Kuster, B.F.M.; Tinge, J.T.; Schouten, J.C. Influence of elevated pressure and particle lyophobicity on hydrodynamics and gas–liquid mass transfer in slurry bubble columns. AIChE J. 2010, 56, 584–596. [Google Scholar] [CrossRef]
- Ferreira, A.; Cardoso, P.; Teixeira, J.A.; Rocha, F. pH influence on oxygen mass transfer coefficient in a bubble column. Individual characterization of kL and a. Chem. Eng. Sci. 2013, 100, 145–152. [Google Scholar] [CrossRef][Green Version]
- García-Abuín, A.; Gómez-Díaz, D.; Losada, M.; Navaza, J.M. Bubble column gas–liquid interfacial area in a polymer+surfactant+water system. Chem. Eng. Sci. 2012, 75, 334–341. [Google Scholar] [CrossRef]
- García-Abuín, A.; Gómez-Díaz, D.; Navaza, J.M.; Vidal-Tato, I. CO2 capture by aqueous solutions of glucosamine in a bubble column reactor. Chem. Eng. J. 2010, 162, 37–42. [Google Scholar] [CrossRef]
- Lau, R.; Lee, P.H.V.; Chen, T. Mass transfer studies in shallow bubble column reactors. Chem. Eng. Process. Process Intensif. 2012, 62, 18–25. [Google Scholar] [CrossRef]
- Majumder, S.K.; Kundu, G.; Mukherjee, D. Bubble size distribution and gas–liquid interfacial area in a modified downflow bubble column. Chem. Eng. J. 2006, 122, 1–10. [Google Scholar] [CrossRef]
- Muroyama, K.; Imai, K.; Oka, Y.; Hayashi, J.I. Mass transfer properties in a bubble column associated with micro-bubble dispersions. Chem. Eng. Sci. 2013, 100, 464–473. [Google Scholar] [CrossRef]
- Smith, J.S.; Burns, L.F.; Valsaraj, K.T.; Thibodeaux, L.J. Bubble Column Reactors for Wastewater Treatment. 2. The Effect of Sparger Design on Sublation Column Hydrodynamics in the Homogeneous Flow Regime. Ind. Eng. Chem. Res. 1996, 35, 1700–1710. [Google Scholar] [CrossRef]
- Pohorecki, R.; Moniuk, W.; Zdrójkowski, A. Hydrodynamics of a bubble column under elevated pressure. Chem. Eng. Sci. 1999, 54, 5187–5193. [Google Scholar] [CrossRef]
- Rubia, M.D.L.; García-Abuín, A.; Gómez-Díaz, D.; Navaza, J.M. Interfacial area and mass transfer in carbon dioxide absorption in TEA aqueous solutions in a bubble column reactor. Chem. Eng. Process. Process Intensif. 2010, 49, 852–858. [Google Scholar] [CrossRef]
- Lau, Y.M.; Sujatha, K.T.; Gaeini, M.; Deen, N.G.; Kuipers, J.A.M. Experimental study of the bubble size distribution in a pseudo-2D bubble column. Chem. Eng. Sci. 2013, 98, 203–211. [Google Scholar] [CrossRef]
- Hernandez-Aguilar, J.R.; Coleman, R.G.; Gomez, C.O.; Finch, J.A. A comparison between capillary and imaging techniques for sizing bubbles in flotation systems. Miner. Eng. 2004, 17, 53–61. [Google Scholar] [CrossRef]
- Wongsuchoto, P.; Charinpanitkul, T.; Pavasant, P. Bubble size distribution and gas–liquid mass transfer in airlift contactors. Chem. Eng. J. 2003, 92, 81–90. [Google Scholar] [CrossRef]
- Parthasarathy, R.; Ahmed, N. Bubble Size Distribution in a Gas Sparged Vessel Agitated by a Rushton Turbine. Ind. Eng. Chem. Res. 1994, 33, 703–711. [Google Scholar] [CrossRef]
- Lu, J.; Biswas, S.; Tryggvason, G. A DNS study of laminar bubbly flows in a vertical channel. Int. J. Multiph. Flow 2006, 32, 643–660. [Google Scholar] [CrossRef]
- Lu, J.; Tryggvason, G. Effect of bubble size in turbulent bubbly downflow in a vertical channel. Chem. Eng. Sci. 2007, 62, 3008–3018. [Google Scholar] [CrossRef]
- Lu, J.; Tryggvason, G. Dynamics of nearly spherical bubbles in a turbulent channel upflow. J. Fluid Mech. 2013, 732, 166–189. [Google Scholar] [CrossRef]
- Ziegenhein, T.; Lucas, D. On sampling bias in multiphase flows: Particle image velocimetry in bubbly flows. Flow Meas. Instrum. 2016, 48, 36–41. [Google Scholar] [CrossRef]
- Ziegenhein, T.; Zalucky, J.; Rzehak, R.; Lucas, D. On the hydrodynamics of airlift reactors, Part I: Experiments. Chem. Eng. Sci. 2016, 150, 54–65. [Google Scholar] [CrossRef]
- Ziegenhein, T.; Garcon, M.; Lucas, D. Particle tracking using micro bubbles in bubbly flows. Chem. Eng. Sci. 2016, 153, 155–164. [Google Scholar] [CrossRef]
- Kulkarni, A.A.; Joshi, J.B. Bubble Formation and Bubble Rise Velocity in Gas−Liquid Systems: A Review. Ind. Eng. Chem. Res. 2005, 44, 5873–5931. [Google Scholar] [CrossRef]
- Camarasa, E.; Vial, C.; Poncin, S.; Wild, G.; Midoux, N.; Bouillard, J. Influence of coalescence behaviour of the liquid and of gas sparging on hydrodynamics and bubble characteristics in a bubble column. Chem. Eng. Process. Process Intensif. 1999, 38, 329–344. [Google Scholar] [CrossRef]
- Polli, M.; Stanislao, M.D.; Bagatin, R.; Bakr, E.A.; Masi, M. Bubble size distribution in the sparger region of bubble columns. Chem. Eng. Sci. 2002, 57, 197–205. [Google Scholar] [CrossRef]
- Miyahara, T.; Tanaka, A. Size of bubbles generated from porous plates. J. Chem. Eng. Jpn. 1997, 30, 353–355. [Google Scholar] [CrossRef]
- Koide, K.; Kato, S.; Tanaka, Y.; Kubota, H. Bubbles generated from porous plates. J. Chem. Eng. Jpn. 1968, 1, 51–56. [Google Scholar] [CrossRef]
- Hur, Y.G.; Yang, J.H.; Jung, H.; Park, S.B. Origin of regime transition to turbulent flow in bubble column: Orifice- and column-induced transitions. Int. J. Multiph. Flow 2013, 50, 89–97. [Google Scholar] [CrossRef]
- Kazakis, N.A.; Mouza, A.A.; Paras, S.V. Experimental study of bubble formation at metal porous spargers: Effect of liquid properties and sparger characteristics on the initial bubble size distribution. Chem. Eng. J. 2008, 137, 265–281. [Google Scholar] [CrossRef]
- Manoharan, S.; Jog, M.A.; Manglik, R.M. Effects of Liquid Viscosity on Bubble Growth From Submerged Orifice Plates. Am. Soc. Mech. Eng. 2017. [Google Scholar] [CrossRef]
- Zhang, C.; Fu, T.; Zhu, C.; Jiang, S.; Ma, Y.; Li, H.Z. Dynamics of bubble formation in highly viscous liquids in a flow-focusing device. Chem. Eng. Sci. 2017, 172, 278–285. [Google Scholar] [CrossRef]
- Abbassi, W.; Besbes, S.; El Hajem, M.; Ben Aissia, H.; Champagne, J.Y.; Jay, J. Influence of operating conditions and liquid phase viscosity with volume of fluid method on bubble formation process. Eur. J. Mech.-B/Fluids 2017, 65, 284–298. [Google Scholar] [CrossRef]
- Philip, J.; Proctor, J.M.; Niranjan, K.; Davidson, J.F. Gas hold-up and liquid circulation in internal loop reactors containing highly viscous newtonian and non-newtonian liquids. Chem. Eng. Sci. 1990, 45, 651–664. [Google Scholar] [CrossRef]
- Xu, X.; Zhang, J.; Liu, F.; Wang, X.; Wei, W.; Liu, Z. Rising behavior of single bubble in infinite stagnant non-Newtonian liquids. Int. J. Multiph. Flow 2017, 95, 84–90. [Google Scholar] [CrossRef]
- Laupsien, D.; Cockx, A.; Line, A. Bubble Plume Oscillations in Viscous Fluids. Chem. Eng. Technol. 2017, 40, 1484–1493. [Google Scholar] [CrossRef]
- Sahu, K.C. A review on rising bubble dynamics in viscosity-stratified fluids. Sādhanā 2017, 42, 575–583. [Google Scholar]
- Zenit, R.; Feng, J.J. Hydrodynamic Interactions Among Bubbles, Drops, and Particles in Non-Newtonian Liquids. Annu. Rev. Fluid Mech. 2018, 50, 505–534. [Google Scholar] [CrossRef]
- Orvalho, S.; Ruzicka, M.C.; Olivieri, G.; Marzocchella, A. Bubble coalescence: Effect of bubble approach velocity and liquid viscosity. Chem. Eng. Sci. 2015, 134, 205–216. [Google Scholar] [CrossRef]
- Sun, W.; Zhu, C.; Fu, T.; Yang, H.; Ma, Y.; Li, H. The minimum in-line coalescence height of bubbles in non-Newtonian fluid. Int. J. Multiph. Flow 2017, 92, 161–170. [Google Scholar] [CrossRef]
- Gumulya, M.; Joshi, J.B.; Utikar, R.P.; Evans, G.M.; Pareek, V. Bubbles in viscous liquids: Time dependent behaviour and wake characteristics. Chem. Eng. Sci. 2016, 144, 298–309. [Google Scholar] [CrossRef]
- Keitel, G.; Onken, U. The effect of solutes on bubble size in air-water dispersions. Chem. Eng. Commun. 1982, 17, 85–98. [Google Scholar] [CrossRef]
- Machon, V.; Pacek, A.W.; Nienow, A.W. Bubble Sizes in Electrolyte and Alcohol Solutions in a Turbulent Stirred Vessel. Chem. Eng. Res. Des. 1997, 75, 339–348. [Google Scholar] [CrossRef]
- Lin, T.-J.; Fan, L.-S. Heat transfer and bubble characteristics from a nozzle in high-pressure bubble columns. Chem. Eng. Sci. 1999, 54, 4853–4859. [Google Scholar] [CrossRef]
- Ishibashi, H.; Onozaki, M.; Kobayashi, M.; Hayashi, J.I.; Itoh, H.; Chiba, T. Gas holdup in slurry bubble column reactors of a 150 t/d coal liquefaction pilot plant process. Fuel 2001, 80, 655–664. [Google Scholar] [CrossRef]
- Kováts, P.; Thévenin, D.; Zähringer, K. Characterizing fluid dynamics in a bubble column aimed for the determination of reactive mass transfer. Heat Mass Transf. 2018, 54, 453–461. [Google Scholar] [CrossRef]
- Hills, J. Radial non-uniformity of velocity and voidage in a bubble column. Trans. Inst. Chem. Eng 1974, 52, 1–9. [Google Scholar]
- Joshi, J.B.; Parasu, V.U.; Prasad, C.V.; Phanikumar, D.V.; Thakre, S.S.; Thorat, B.N. Gas holdu-up structure in bubble column reactors. PINSA 1998, 64, 441–567. [Google Scholar]
- Tomiyama, A.; Tamai, H.; Zun, I.; Hosokawa, S. Transverse migration of single bubbles in simple shear flows. Chem. Eng. Sci. 2002, 57, 1849–1858. [Google Scholar] [CrossRef]
- Lucas, D.; Prasser, H.M.; Manera, A. Influence of the lift force on the stability of a bubble column. Chem. Eng. Sci. 2005, 60, 3609–3619. [Google Scholar] [CrossRef]
- Wu, Y.; Cheng Ong, B.; Al-Dahhan, M.H. Predictions of radial gas holdup profiles in bubble column reactors. Chem. Eng. Sci. 2001, 56, 1207–1210. [Google Scholar] [CrossRef]
- Nassos, G.P.; Bankoff, S.G. Slip velocity ratios in an air-water system under steady-state and transient conditions. Chem. Eng. Sci. 1967, 22, 661–668. [Google Scholar] [CrossRef]
- Ueyama, K.; Miyauchi, T. Properties of recirculating turbulent two phase flow in gas bubble columns. AIChE J. 1979, 25, 258–266. [Google Scholar] [CrossRef]
- Luo, H.; Svendsen, H.F. Turbulent circulation in bubble columns from eddy viscosity distributions of single-phase pipe flow. Can. J. Chem. Eng. 1991, 69, 1389–1394. [Google Scholar] [CrossRef]
- Van Dierendonck, L.; Fortuin, J.; Venderbos, D. The specific contact area in gas-liquid reactors. In Proceedings of the 4th European Symposium on Chemical Reactor Engineering, Brussels, Belgium, 9 September 1968; pp. 205–215. [Google Scholar]
- Gestrich, W.; Krauss, W. Die spezifische Phasengrenzfläche in Blasenschichten. Chem. Ing. Tech. 1975, 47, 360–367. [Google Scholar] [CrossRef]
- Akita, K.; Yoshida, F. Bubble Size, Interfacial Area, and Liquid-Phase Mass Transfer Coefficient in Bubble Columns. Ind. Eng. Chem. Process Des. Dev. 1974, 13, 84–91. [Google Scholar] [CrossRef]
- Martín, M.; Montes, F.J.; Galán, M.A. Physical explanation of the empirical coefficients of gas–liquid mass transfer equations. Chem. Eng. Sci. 2009, 64, 410–425. [Google Scholar] [CrossRef]
- Deckwer, W.D.; Schumpe, A. Improved tools for bubble column reactor design and scale-up. Chem. Eng. Sci. 1993, 48, 889–911. [Google Scholar] [CrossRef]
- Nedeltchev, S.; Jordan, U.; Schumpe, A. Correction of the penetration theory based on mass-transfer data from bubble columns operated in the homogeneous regime under high pressure. Chem. Eng. Sci. 2007, 62, 6263–6273. [Google Scholar] [CrossRef]
- Wang, T.; Wang, J. Numerical simulations of gas–liquid mass transfer in bubble columns with a CFD–PBM coupled model. Chem. Eng. Sci. 2007, 62, 7107–7118. [Google Scholar] [CrossRef]
- Krauβ, M.; Rzehak, R. Reactive absorption of CO2 in NaOH: Detailed study of enhancement factor models. Chem. Eng. Sci. 2017, 166, 193–209. [Google Scholar] [CrossRef]
- Rzehak, R.; Krepper, E. Euler-Euler simulation of mass-transfer in bubbly flows. Chem. Eng. Sci. 2016, 155, 459–468. [Google Scholar] [CrossRef]
- Vik, C.B.; Solsvik, J.; Hillestad, M.; Jakobsen, H.A. A multifluid-PBE model for simulation of mass transfer limited processes operated in bubble columns. Comput. Chem. Eng. 2018, 110, 115–139. [Google Scholar] [CrossRef]
- Lemoine, R.; Morsi, B.I. An algorithm for predicting the hydrodynamic and mass transfer parameters in agitated reactors. Chem. Eng. J. 2005, 114, 9–31. [Google Scholar] [CrossRef]
- Sauer, T.; Hempel, D.-C. Fluid dynamics and mass transfer in a bubble column with suspended particles. Chem. Eng. Technol. 1987, 10, 180–189. [Google Scholar] [CrossRef]
- Lochiel, A.C.; Calderbank, P.H. Mass transfer in the continuous phase around axisymmetric bodies of revolution. Chem. Eng. Sci. 1964, 19, 471–484. [Google Scholar] [CrossRef]
- Nedeltchev, S.; Nigam, K.D.P.; Schumpe, A. Prediction of mass transfer coefficients in a slurry bubble column based on the geometrical characteristics of bubbles. Chem. Eng. Sci. 2014, 106, 119–125. [Google Scholar] [CrossRef]
- Nedeltchev, S. Theoretical prediction of mass transfer coefficients in both gas–liquid and slurry bubble columns. Chem. Eng. Sci. 2017, 157, 169–181. [Google Scholar] [CrossRef]
- Higbie, R. The rate of absorption of a pure gas into a still liquid during short periods of exposure. Trans. AIChE 1935, 31, 365–389. [Google Scholar]
- Calderbank, P.H.; Moo-Young, M.B. The continuous phase heat and mass-transfer properties of dispersions. Chem. Eng. Sci. 1961, 16, 39–54. [Google Scholar] [CrossRef]
- Calderbank, P.H.; Johnson, D.S.L.; Loudon, J. Mechanics and mass transfer of single bubbles in free rise through some Newtonian and non-Newtonian liquids. Chem. Eng. Sci. 1970, 25, 235–256. [Google Scholar] [CrossRef]
- Weber, M.E. The effect of surface active agents on mass transfer from spherical cap bubbles. Chem. Eng. Sci. 1975, 30, 1507–1510. [Google Scholar] [CrossRef]
- Kawase, Y.; Halard, B.; Moo-Young, M. Theoretical prediction of volumetric mass transfer coefficients in bubble columns for Newtonian and non-Newtonian fluids. Chem. Eng. Sci. 1987, 42, 1609–1617. [Google Scholar] [CrossRef]
- Schumpe, A.; Serpemen, Y.; Deckwer, W.D. Effective application of bubble columns. Ger. Chem. Eng. 1979, 2, 234–241. [Google Scholar]
- Vandu, C.O.; Krishna, R. Influence of scale on the volumetric mass transfer coefficients in bubble columns. Chem. Eng. Process. Process Intensif. 2004, 43, 575–579. [Google Scholar] [CrossRef]
- Deckwer, W.D.; Burckhart, R.; Zoll, G. Mixing and mass transfer in tall bubble columns. Chem. Eng. Sci. 1974, 29, 2177–2188. [Google Scholar] [CrossRef]
- Hikita, H.; Asai, S.; Tanigawa, K.; Segawa, K.; Kitao, M. The volumetric liquid-phase mass transfer coefficient in bubble columns. Chem. Eng. J. 1981, 22, 61–69. [Google Scholar] [CrossRef]
- Merchuk, J.C.; Ben-Zvi, S. A novel approach to the correlation of mass transfer rates in bubble columns with non-Newtonian liquids. Chem. Eng. Sci. 1992, 47, 3517–3523. [Google Scholar] [CrossRef]
- Dudley, J. Mass transfer in bubble columns: A comparison of correlations. Water Res. 1995, 29, 1129–1138. [Google Scholar] [CrossRef]
- Deckwer, W.; Schumpe, A. Bubble columns—The state of the art and current trends. Int. Chem. Eng. 1987, 27, 405–422. [Google Scholar]
- Nakanoh, M.; Yoshida, F. Gas Absorption by Newtonian and Non-Newtonian Liquids in a Bubble Column. Ind. Eng. Chem. Process. Des. Dev. 1980, 19, 190–195. [Google Scholar] [CrossRef]
- Suh, I.S.; Schumpe, A.; Deckwer, W.D.; Kulicke, W.M. Gas-liquid mass transfer in the bubble column with viscoelastic liquid. Can. J. Chem. Eng. 1991, 69, 506–512. [Google Scholar] [CrossRef]
- Zhao, M.; Niranjan, K.; Davidson, J.F. Mass transfer to viscous liquids in bubble columns and air-lift reactors: Influence of baffles. Chem. Eng. Sci. 1994, 49, 2359–2369. [Google Scholar] [CrossRef]
- Boyer, C.; Duquenne, A.-M.; Wild, G. Measuring techniques in gas–liquid and gas–liquid–solid reactors. Chem. Eng. Sci. 2002, 57, 3185–3215. [Google Scholar] [CrossRef]
- Jakobsen, H.A. Chemical reactor modeling: Multiphase reactive flow. In Multiphase Reactive Flows; Springer: Berlin, Germany, 2014. [Google Scholar]
- Zuber, N.; Findlay, J.A. Average Volumetric Concentration in Two-Phase Flow Systems. J. Heat Transf. 1965, 87, 453–468. [Google Scholar] [CrossRef]
- Gourich, B.; Vial, C.; Essadki, A.H.; Allam, F.; Belhaj Soulami, M.; Ziyad, M. Identification of flow regimes and transition points in a bubble column through analysis of differential pressure signal—Influence of the coalescence behavior of the liquid phase. Chem. Eng. Process. Process Intensif. 2006, 45, 214–223. [Google Scholar] [CrossRef]
- Wallis, G.B. One-Dimensional Two-Phase Flow; McGraw-Hill: New York, NY, USA, 1969. [Google Scholar]
- Vial, C.; Camarasa, E.; Poncin, S.; Wild, G.; Midoux, N.; Bouillard, J. Study of hydrodynamic behaviour in bubble columns and external loop airlift reactors through analysis of pressure fluctuations. Chem. Eng. Sci. 2000, 55, 2957–2973. [Google Scholar] [CrossRef]
- Fan, L.T.; Kang, Y.; Neogi, D.; Yashima, M. Fractal analysis of fluidized particle behavior in liquid-solid fluidized beds. AIChE J. 1993, 39, 513–517. [Google Scholar] [CrossRef]
- Ellis, N.; Briens, L.A.; Grace, J.R.; Bi, H.T.; Lim, C.J. Characterization of dynamic behaviour in gas–solid turbulent fluidized bed using chaos and wavelet analyses. Chem. Eng. J. 2003, 96, 105–116. [Google Scholar] [CrossRef]
- Lu, X.; Li, H. Wavelet analysis of pressure fluctuation signals in a bubbling fluidized bed. Chem. Eng. J. 1999, 75, 113–119. [Google Scholar] [CrossRef]
- Drahoš, J.; Bradka, F.; Punčochář, M. Fractal behaviour of pressure fluctuations in a bubble column. Chem. Eng. Sci. 1992, 47, 4069–4075. [Google Scholar] [CrossRef]
- Briens, C.L.; Briens, L.A.; Hay, J.; Hudson, C.; Margaritis, A. Hurst’s Analysis to Detect Minimum Fluidization and Gas Maldistribution in Fluidized Beds. AIChE J. 1997, 43, 1904–1908. [Google Scholar] [CrossRef]
- Bai, D.; Bi, H.T.; Grace, J.R. Chaotic Behavior of Fluidized Beds Based on Pressure and Voidage Fluctuations. AIChE J. 1997, 43, 1357–1361. [Google Scholar] [CrossRef]
- Marzocchella, A.; Zijerveld, R.C.; Schouten, J.C.; Van Den Bleek, C.M. Chaotic Behavior of Gas-Solids Flow in the Riser of a Laboratory-Scale Circulating Fluidized Bed. AIChE J. 1997, 43, 1458–1468. [Google Scholar] [CrossRef]
- van den Bleek, C.M.; Schouten, J.C. Deterministic chaos: A new tool in fluidized bed design and operation. Chem. Eng. J. BioChem. Eng. J. 1993, 53, 75–87. [Google Scholar] [CrossRef]
- Ajbar, A.; Al-Masry, W.; Ali, E. Prediction of flow regimes transitions in bubble columns using passive acoustic measurements. Chem. Eng. Process. Process Intensif. 2009, 48, 101–110. [Google Scholar] [CrossRef]
- Cassanello, M.; Larachi, F.; Kemoun, A.; Al-Dahhan, M.H.; Dudukovic, M.P. Inferring liquid chaotic dynamics in bubble columns using CARPT. Chem. Eng. Sci. 2001, 56, 6125–6134. [Google Scholar] [CrossRef]
- Kikuchi, R.; Yano, T.; Tsutsumi, A.; Yoshida, K.; Punchochar, M.; Drahos, J. Diagnosis of chaotic dynamics of bubble motion in a bubble column. Chem. Eng. Sci. 1997, 52, 3741–3745. [Google Scholar] [CrossRef]
- Letzel, H.M.; Schouten, J.C.; Krishna, R.; van den Bleek, C.M. Characterization of regimes and regime transitions in bubble columns by chaos analysis of pressure signals. Chem. Eng. Sci. 1997, 52, 4447–4459. [Google Scholar] [CrossRef]
- Lin, T.J.; Juang, R.C.; Chen, Y.C.; Chen, C.C. Predictions of flow transitions in a bubble column by chaotic time series analysis of pressure fluctuation signals. Chem. Eng. Sci. 2001, 56, 1057–1065. [Google Scholar] [CrossRef]
- Nedeltchev, S.; Kumar, S.B.; Dudukovic, M.P. Flow regime identification in a bubble column based on both Kolmogorov entropy and quality of mixedness derived from CARPT data. Can. J. Chem. Eng. 2003, 81, 367–374. [Google Scholar] [CrossRef]
- Nedeltchev, S.; Shaikh, A.; Al-Dahhan, M. Flow regime identification in a bubble column based on both statistical and chaotic parameters applied to computed tomography data. Chem. Eng. Technol. 2006, 29, 1054–1060. [Google Scholar] [CrossRef]
- Tchowa Medjiade, W.; Rosenbaum Alvaro, A.; Schumpe, A. Flow regime transitions in a bubble column. Chem. Eng. Sci. 2017, 170, 263–269. [Google Scholar] [CrossRef]
- Zhong, W.; Wang, X.; Qianjun, L.I.; Jin, B.; Zhang, M.; Xiao, R.; Huang, Y. Analysis on chaotic nature of a pressurized spout-fluid bed by information theory based shannon entropy. Can. J. Chem. Eng. 2009, 87, 220–227. [Google Scholar] [CrossRef]
- Kang, Y.; Woo, K.J.; Ko, M.H.; Cho, Y.J.; Kim, S.D. Particle Flow Behavior in Three-Phase Fluidized Beds. Korean J. Chem. Eng. 1999, 16, 784–788. [Google Scholar] [CrossRef]
- Shiea, M.; Mostoufi, N.; Sotudeh-Gharebagh, R. Comprehensive study of regime transitions throughout a bubble column using resistivity probe. Chem. Eng. Sci. 2013, 100, 15–22. [Google Scholar] [CrossRef]
- Rodrigues, R.T.; Rubio, J. New basis for measuring the size distribution of bubbles. Miner. Eng. 2003, 16, 757–765. [Google Scholar] [CrossRef]
- Busciglio, A.; Grisafi, F.; Scargiali, F.; Brucato, A. On the measurement of local gas hold-up and interfacial area in gas–liquid contactors via light sheet and image analysis. Chem. Eng. Sci. 2010, 65, 3699–3708. [Google Scholar] [CrossRef]
- Xu, C.; Shepard, T. Digital Image Processing Algorithm for Determination and Measurement of In-Focus Spherical Bubbles. In Proceedings of the ASME 2014 4th Joint US-European Fluids Engineering Division Summer Meeting collocated with the ASME 2014 12th International Conference on Nanochannels, Microchannels, and Minichannels, Chicago, IL, USA, 3–7 August 2014; pp. V01BT22A002–V001BT022A002. [Google Scholar]
- Lau, Y.M.; Möller, F.; Hampel, U.; Schubert, M. Ultrafast X-ray tomographic imaging of multiphase flow in bubble columns–Part 2: Characterisation of bubbles in the dense regime. Int. J. Multiph. Flow 2018. [Google Scholar] [CrossRef]
- Lau, Y.M.; Hampel, U.; Schubert, M. Ultrafast X-ray tomographic imaging of multiphase flow in bubble columns–Part 1: Image processing and reconstruction comparison. Int. J. Multiph. Flow 2018. [Google Scholar] [CrossRef]
- Azizi, S.; Yadav, A.; Lau, Y.M.; Hampel, U.; Roy, S.; Schubert, M. On the experimental investigation of gas-liquid flow in bubble columns using ultrafast X-ray tomography and radioactive particle tracking. Chem. Eng. Sci. 2017, 170, 320–331. [Google Scholar] [CrossRef]
- Adetunji, O.; Rawatlal, R. Estimation of bubble column hydrodynamics: Image-based measurement method. Flow Meas. Instrum. 2017, 53, 4–17. [Google Scholar] [CrossRef]
- Guan, X.; Yang, N. Bubble properties measurement in bubble columns: From homogeneous to heterogeneous regime. Chem. Eng. Res. Des. 2017, 127, 103–112. [Google Scholar] [CrossRef]
- Hernandez-Alvarado, F.; Kalaga, D.V.; Turney, D.; Banerjee, S.; Joshi, J.B.; Kawaji, M. Void fraction, bubble size and interfacial area measurements in co-current downflow bubble column reactor with microbubble dispersion. Chem. Eng. Sci. 2017, 168, 403–413. [Google Scholar] [CrossRef]
- Nedeltchev, S.; Hampel, U.; Schubert, M. Extraction of information and reconstruction entropies from ultrafast X-ray tomography data in a bubble column. Chem. Eng. Sci. 2017, 170, 225–233. [Google Scholar] [CrossRef]
- Murgan, I.; Bunea, F.; Ciocan, G.D. Experimental PIV and LIF characterization of a bubble column flow. Flow Meas. Instrum. 2017, 54, 224–235. [Google Scholar] [CrossRef]
- Möller, F.; Seiler, T.; Lau, Y.M.; Weber, M.; Weber, M.; Hampel, U.; Schubert, M. Performance comparison between different sparger plate orifice patterns: Hydrodynamic investigation using ultrafast X-ray tomography. Chem. Eng. J. 2017, 316, 857–871. [Google Scholar] [CrossRef]
- Wen, J.; Sun, Q.; Sun, Z.; Gu, H. An improved image processing technique for determination of volume and surface area of rising bubble. Int. J. Multiph. Flow 2018. [Google Scholar] [CrossRef]
- Zaruba, A.; Krepper, E.; Prasser, H.M.; Schleicher, E. Measurement of bubble velocity profiles and turbulent diffusion coefficients of the gaseous phase in rectangular bubble column using image processing. Exp. Therm. Fluid Sci. 2005, 29, 851–860. [Google Scholar] [CrossRef]
- Karn, A.; Ellis, C.; Arndt, R.; Hong, J. An integrative image measurement technique for dense bubbly flows with a wide size distribution. Chem. Eng. Sci. 2015, 122, 240–249. [Google Scholar] [CrossRef]
- Rodríguez-Rodríguez, J.; Martínez-Bazán, C.; Montañes, J.L. A novel particle tracking and break-up detection algorithm: Application to the turbulent break-up of bubbles. Meas. Sci. Technol. 2003, 14, 1328. [Google Scholar] [CrossRef]
- Lecuona, A.; Sosa, P.A.; Rodríguez, P.A.; Zequeira, R.I. Volumetric characterization of dispersed two-phase flows by digital image analysis. Meas. Sci. Technol. 2000, 11, 1152. [Google Scholar] [CrossRef]
- Bian, Y.; Dong, F.; Zhang, W.; Wang, H.; Tan, C.; Zhang, Z. 3D reconstruction of single rising bubble in water using digital image processing and characteristic matrix. Particuology 2013, 11, 170–183. [Google Scholar] [CrossRef]
- Sahagian, D.L.; Proussevitch, A.A. 3D particle size distributions from 2D observations: Stereology for natural applications. J. Volcanol. Geotherm. Res. 1998, 84, 173–196. [Google Scholar] [CrossRef]
- Lau, Y.M.; Deen, N.G.; Kuipers, J.A.M. Development of an image measurement technique for size distribution in dense bubbly flows. Chem. Eng. Sci. 2013, 94, 20–29. [Google Scholar] [CrossRef]
- Lage, P.L.C.; Espósito, R.O. Experimental determination of bubble size distributions in bubble columns: Prediction of mean bubble diameter and gas hold up. Powder Technol. 1999, 101, 142–150. [Google Scholar] [CrossRef]
- Solsvik, J.; Jakobsen Hugo, A. Single Air Bubble Breakup Experiments in Stirred Water Tank. Int. J. Chem. React. Eng. 2015, 13, 477–497. [Google Scholar] [CrossRef]
- Honkanen, M.; Saarenrinne, P.; Stoor, T.; Niinimäki, J. Recognition of highly overlapping ellipse-like bubble images. Meas. Sci. Technol. 2005, 16, 1760–1770. [Google Scholar] [CrossRef]
- Rakoczy, R.; Masiuk, S. Experimental study of bubble size distribution in a liquid column exposed to a rotating magnetic field. Chem. Eng. Process. Process Intensif. 2009, 48, 1229–1240. [Google Scholar] [CrossRef]
- Hanselmann, W.; Windhab, E. Flow characteristics and modelling of foam generation in a continuous rotor/stator mixer. J. Food Eng. 1998, 38, 393–405. [Google Scholar] [CrossRef]
- Aloufi, F.M. An Investigation of Gas Void Fraction and Transition Conditions for Two-Phase Flow in an Annular Gap Bubble Column. Ph.D. Thesis, Loughborough University, Loughborough, UK, 2011. [Google Scholar]
- Hernandez-Alvarado, F.; Kleinbart, S.; Kalaga, D.V.; Banerjee, S.; Joshi, J.B.; Kawaji, M. Comparison of void fraction measurements using different techniques in two-phase flow bubble column reactors. Int. J. Multiph. Flow 2018, 102, 119–129. [Google Scholar] [CrossRef]
- Singh, B.K.; Quiyoom, A.; Buwa, V.V. Dynamics of gas–liquid flow in a cylindrical bubble column: Comparison of electrical resistance tomography and voidage probe measurements. Chem. Eng. Sci. 2017, 158, 124–139. [Google Scholar] [CrossRef]
- Chabot, J.; Farag, H.; de Lasa, H. Fluid dynamics of bubble columns at elevated temperature modelling and investigation with refractive fiber optic sensors. Chem. Eng. J. 1998, 70, 105–113. [Google Scholar] [CrossRef]
- Chaumat, H.; Billet-Duquenne, A.M.; Augier, F.; Mathieu, C.; Delmas, H. On the reliability of an optical fibre probe in bubble column under industrial relevant operating conditions. Exp. Therm. Fluid Sci. 2007, 31, 495–504. [Google Scholar] [CrossRef]
- Magaud, F.; Souhar, M.; Wild, G.; Boisson, N. Experimental study of bubble column hydrodynamics. Chem. Eng. Sci. 2001, 56, 4597–4607. [Google Scholar] [CrossRef]
- Moujaes, S.F. Testing of a spherical dual-tipped optical fiber probe for local measurements of void fraction and gas velocity in two-phase flows. Can. J. Chem. Eng. 1990, 68, 504–510. [Google Scholar] [CrossRef]
- Lichti, M.; Bart, H.-J. Bubble Size Distributions with a Shadowgraphic Optical Probe. Flow Meas. Instrum. 2018. [Google Scholar] [CrossRef]
- Tyagi, P.; Buwa, V.V. Experimental characterization of dense gas–liquid flow in a bubble column using voidage probes. Chem. Eng. J. 2017, 308, 912–928. [Google Scholar] [CrossRef]
- Vejražka, J.; Večeř, M.; Orvalho, S.; Sechet, P.; Ruzicka, M.C.; Cartellier, A. Measurement accuracy of a mono-fiber optical probe in a bubbly flow. Int. J. Multiph. Flow 2010, 36, 533–548. [Google Scholar] [CrossRef]
- Barrau, E.; Rivière, N.; Poupot, C.; Cartellier, A. Single and double optical probes in air-water two-phase flows: Real time signal processing and sensor performance. Int. J. Multiph. Flow 1999, 25, 229–256. [Google Scholar] [CrossRef]
- Chang, K.-A.; Lim, H.-J.; Su, C.B. Fiber optic reflectometer for velocity and fraction ratio measurements in multiphase flows. Rev. Sci. Instrum. 2003, 74, 3559–3565. [Google Scholar] [CrossRef]
- Lima Neto, I.; Zhu, D.; Rajaratnam, N. Air Injection in Water with Different Nozzles. J. Environ. Eng. 2008, 134, 283–294. [Google Scholar] [CrossRef]
- Kiambi, S.L.; Duquenne, A.-M.; Dupont, J.B.; Colin, C.; Risso, F.; Delmas, H. Measurements of Bubble Characteristics: Comparison Between Double Optical Probe and Imaging. Can. J. Chem. Eng. 2003, 81, 764–770. [Google Scholar] [CrossRef]
- Cartellier, A.; Barrau, E. Monofiber optical probes for gas detection and gas velocity measurements: Conical probes. Int. J. Multiph. Flow 1998, 24, 1265–1294. [Google Scholar] [CrossRef]
- Chaumat, H.; Billet-Duquenne, A.M.; Augier, F.; Mathieu, C.; Delmas, H. Application of the double optic probe technique to distorted tumbling bubbles in aqueous or organic liquid. Chem. Eng. Sci. 2005, 60, 6134–6145. [Google Scholar] [CrossRef]
- Liu, W.; Clark, N.N. Relationships between distributions of chord lengths and distributions of bubble sizes including their statistical parameters. Int. J. Multiph. Flow 1995, 21, 1073–1089. [Google Scholar] [CrossRef]
- Clark, N.N.; Turton, R. Chord length distributions related to bubble size distributions in multiphase flows. Int. J. Multiph. Flow 1988, 14, 413–424. [Google Scholar] [CrossRef]
- Hu, B.; Angeli, P.; Matar, O.K.; Lawrence, C.J.; Hewitt, G.F. Evaluation of drop size distribution from chord length measurements. AIChE J. 2006, 52, 931–939. [Google Scholar] [CrossRef]
- Carrara, M. Indagine Sperimentale su Flussi Bifase in Colonne Verticali. Master’s Thesis, Politecnico di Milano, Milan, Italy, 2014. [Google Scholar]
- Rüdisüli, M.; Schildhauer, T.J.; Biollaz, S.M.; Ommen, J.R.V. Monte Carlo simulation of the bubble size distribution in a fluidized bed with intrusive probes. Int. J. Multiph. Flow 2012, 44, 1–14. [Google Scholar] [CrossRef]
- Hoang, N.H.; Euh, D.J.; Yun, B.J.; Song, C.H. A new method of relating a chord length distribution to a bubble size distribution for vertical bubbly flows. Int. J. Multiph. Flow 2015, 71, 23–31. [Google Scholar] [CrossRef]
- Myers, K.; Duduković, M.; Ramachandran, P. Modelling churn-turbulent bubble columns—I. Liquid-phase mixing. Chem. Eng. Sci. 1987, 42, 2301–2311. [Google Scholar] [CrossRef]
- Anderson, K.G.; Rice, R.G. Local turbulence model for predicting circulation rates in bubble columns. AIChE J. 1989, 35, 514–518. [Google Scholar] [CrossRef]
- Burns, L.F.; Rice, R.G. Circulation in bubble columns. AIChE J. 1997, 43, 1390–1402. [Google Scholar] [CrossRef]
- Wilkinson, P.M.; Haringa, H.; Stokman, F.P.A.; Van Dierendonck, L.L. Liquid mixing in a bubble column under pressure. Chem. Eng. Sci. 1993, 48, 1785–1791. [Google Scholar] [CrossRef]
- Kantak, M.V.; Hesketh, R.P.; Kelkar, B.G. Effect of gas and liquid properties on gas phase dispersion in bubble columns. Chem. Eng. J. BioChem. Eng. J. 1995, 59, 91–100. [Google Scholar] [CrossRef]
- Dudukovic, M.P.; Toseland, B.A.; Bhatt, B.L. A Two-Compartment Convective-Diffusion Model for Slurry Bubble Column Reactors. Ind. Eng. Chem. Res. 1997, 36, 4670–4680. [Google Scholar] [CrossRef]
- Degaleesan, S.; Roy, S.; Kumar, S.B.; Duduković, M.P. Liquid mixing based on convection and turbulent dispersion in bubble columns. Chem. Eng. Sci. 1996, 51, 1967–1976. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, Z.; Qiu, C. Buoyancy-driven circulation in bubble columns: Alternative analysis. AIChE J. 1998, 44, 2561–2564. [Google Scholar] [CrossRef]
- Gupta, P.; Al-Dahhan, M.H.; Dudukovic, M.P.; Toseland, B.A. Comparison of single- and two-bubble class gas–liquid recirculation models—Application to pilot-plant radioactive tracer studies during methanol synthesis. Chem. Eng. Sci. 2001, 56, 1117–1125. [Google Scholar] [CrossRef]
- Shimizu, K.; Takada, S.; Minekawa, K.; Kawase, Y. Phenomenological model for bubble column reactors: Prediction of gas hold-ups and volumetric mass transfer coefficients. Chem. Eng. J. 2000, 78, 21–28. [Google Scholar] [CrossRef]
- Jakobsen, H.A.; Lindborg, H.; Dorao, C.A. Modeling of Bubble Column Reactors: Progress and Limitations. Ind. Eng. Chem. Res. 2005, 44, 5107–5151. [Google Scholar] [CrossRef]
- Delnoij, E.; Lammers, F.A.; Kuipers, J.A.M.; van Swaaij, W.P.M. Dynamic simulation of dispersed gas-liquid two-phase flow using a discrete bubble model. Chem. Eng. Sci. 1997, 52, 1429–1458. [Google Scholar] [CrossRef]
- Lapin, A.; Lübbert, A. Numerical simulation of the dynamics of two-phase gas—Liquid flows in bubble columns. Chem. Eng. Sci. 1994, 49, 3661–3674. [Google Scholar] [CrossRef]
- Buwa, V.V.; Deo, D.S.; Ranade, V.V. Eulerian–Lagrangian simulations of unsteady gas–liquid flows in bubble columns. Int. J. Multiph. Flow 2006, 32, 864–885. [Google Scholar] [CrossRef]
- Hu, G.; Celik, I. Eulerian–Lagrangian based large-eddy simulation of a partially aerated flat bubble column. Chem. Eng. Sci. 2008, 63, 253–271. [Google Scholar] [CrossRef]
- Besbes, S.; El Hajem, M.; Ben Aissia, H.; Champagne, J.Y.; Jay, J. PIV measurements and Eulerian–Lagrangian simulations of the unsteady gas–liquid flow in a needle sparger rectangular bubble column. Chem. Eng. Sci. 2015, 126, 560–572. [Google Scholar] [CrossRef]
- Jain, D.; Lau, Y.M.; Kuipers, J.A.M.; Deen, N.G. Discrete bubble modeling for a micro-structured bubble column. Chem. Eng. Sci. 2013, 100, 496–505. [Google Scholar] [CrossRef]
- Ishii, M. Thermo-fluid dynamic theory of two-phase flow. NASA STI/Recon Tech. Rep. A 1975, 75, 29657. [Google Scholar]
- Sokolichin, A.; Eigenberger, G. Gas—Liquid flow in bubble columns and loop reactors: Part I. Detailed modelling and numerical simulation. Chem. Eng. Sci. 1994, 49, 5735–5746. [Google Scholar] [CrossRef]
- Becker, S.; Sokolichin, A.; Eigenberger, G. Gas—Liquid flow in bubble columns and loop reactors: Part II. Comparison of detailed experiments and flow simulations. Chem. Eng. Sci. 1994, 49, 5747–5762. [Google Scholar] [CrossRef]
- Grevskott, S.; Sannæs, B.H.; Duduković, M.P.; Hjarbo, K.W.; Svendsen, H.F. Liquid circulation, bubble size distributions, and solids movement in two- and three-phase bubble columns. Chem. Eng. Sci. 1996, 51, 1703–1713. [Google Scholar] [CrossRef]
- Pan, Y.; Dudukovic, M.P.; Chang, M. Dynamic simulation of bubbly flow in bubble columns. Chem. Eng. Sci. 1999, 54, 2481–2489. [Google Scholar] [CrossRef]
- Hillmer, G. Experimentelle Untersuchung und Fluiddynamische Modellierung von Suspensionsblasensäulen; Der Technischen Fakultät der Universität Erlangen-Nürnberg: Erlangen, Germany, 1989. [Google Scholar]
- Gasche, H.-E. Modellierung von Blasensäulen; Der Technischen Fakultät der Universität Erlangen-Nürnberg: Erlangen, Germany, 1989. [Google Scholar]
- Menzel, T. Die Reynolds-Schubspannung als Wesentlicher Parameter zur Modellierungder Strömungsstruktur in Blasensäulen und Airlift-Schlaufenreaktoren; VDI-Verlag: Düsseldorf, Germany, 1990. [Google Scholar]
- Torvik. Investigations of 2-and 3-Phase Bubble Columns; The Norwegian Institute of technology: Trondheim, Norway, 1990. [Google Scholar]
- Grienberger, J. Untersuchung und Modellierung von Blasensäulen; Der Technischen Fakultät der Universität Erlangen-Nurnberg: Erlangen, Germany, 1992. [Google Scholar]
- Jakobsen Hugo, A. On the Modeling and Simulation of Bubble Column Reactors Using a Two-Fluid Model; Der Technischen Fakultät der Universität Erlangen-Nurnberg: Erlangen, Germany, 1993. [Google Scholar]
- Pfleger, D.; Gomes, S.; Gilbert, N.; Wagner, H.G. Hydrodynamic simulations of laboratory scale bubble columns fundamental studies of the Eulerian–Eulerian modelling approach. Chem. Eng. Sci. 1999, 54, 5091–5099. [Google Scholar] [CrossRef]
- Sokolichin, A.; Eigenberger, G. Applicability of the standard k–ε turbulence model to the dynamic simulation of bubble columns: Part I. Detailed numerical simulations. Chem. Eng. Sci. 1999, 54, 2273–2284. [Google Scholar] [CrossRef]
- Mudde, R.F.; Simonin, O. Two-and three-dimensional simulations of a bubble plume using a two-fluid model. Chem. Eng. Sci. 1999, 54, 5061–5069. [Google Scholar] [CrossRef]
- Ekambara, K.; Dhotre, M.T.; Joshi, J.B. CFD simulations of bubble column reactors: 1D, 2D and 3D approach. Chem. Eng. Sci. 2005, 60, 6733–6746. [Google Scholar] [CrossRef]
- Jakobsen, H.A.; Grevskott, S.; Svendsen, H.F. Modeling of Vertical Bubble-Driven Flows. Ind. Eng. Chem. Res. 1997, 36, 4052–4074. [Google Scholar] [CrossRef]
- Sokolichin, A.; Eigenberger, G.; Lapin, A.; Lübert, A. Dynamic numerical simulation of gas-liquid two-phase flows Euler/Euler versus Euler/Lagrange. Chem. Eng. Sci. 1997, 52, 611–626. [Google Scholar] [CrossRef]
- Jakobsen Hugo, A. Numerical Convection Algorithms and Their Role in Eulerian CFD Reactor Simulations. Int. J. Chem. React. Eng. 2002, 1. [Google Scholar] [CrossRef]
- Laborde-Boutet, C.; Larachi, F.; Dromard, N.; Delsart, O.; Schweich, D. CFD simulation of bubble column flows: Investigations on turbulence models in RANS approach. Chem. Eng. Sci. 2009, 64, 4399–4413. [Google Scholar] [CrossRef]
- Oey, R.S.; Mudde, R.F.; van den Akker, H.E.A. Sensitivity study on interfacial closure laws in two-fluid bubbly flow simulations. AIChE J. 2003, 49, 1621–1636. [Google Scholar] [CrossRef]
- Ma, T.; Lucas, D.; Ziegenhein, T.; Fröhlich, J.; Deen, N.G. Scale-Adaptive Simulation of a square cross-sectional bubble column. Chem. Eng. Sci. 2015, 131, 101–108. [Google Scholar] [CrossRef]
- Ma, T.; Ziegenhein, T.; Lucas, D.; Fröhlich, J. Large eddy simulations of the gas–liquid flow in a rectangular bubble column. Nucl. Eng. Des. Eng. Des. 2016. [Google Scholar] [CrossRef]
- Ma, T.; Ziegenhein, T.; Lucas, D.; Krepper, E.; Fröhlich, J. Euler–Euler large eddy simulations for dispersed turbulent bubbly flows. Int. J. Heat Fluid Flow 2015, 56, 51–59. [Google Scholar] [CrossRef]
- Liu, Z.; Li, B. Scale-adaptive analysis of Euler-Euler large eddy simulation for laboratory scale dispersed bubbly flows. Chem. Eng. J. 2018, 338, 465–477. [Google Scholar] [CrossRef]
- Milelli, M. A numerical analysis of confined turbulent bubble plumes. In Swiss Federal Institute of Technology Zurich; ETH Zurich: Zurich, Switzerland, 2002. [Google Scholar]
- Lakehal, D.; Smith, B.L.; Milelli, M. Large-eddy simulation of bubbly turbulent shear flows. J. Turbul. 2002, 3, N25. [Google Scholar] [CrossRef]
- Díaz, M.E.; Iranzo, A.; Cuadra, D.; Barbero, R.; Montes, F.J.; Galán, M.A. Numerical simulation of the gas–liquid flow in a laboratory scale bubble column: Influence of bubble size distribution and non-drag forces. Chem. Eng. J. 2008, 139, 363–379. [Google Scholar] [CrossRef]
- Krepper, E.; Reddy Vanga, B.N.; Zaruba, A.; Prasser, H.-M.; Lopez de Bertodano, M.A. Experimental and numerical studies of void fraction distribution in rectangular bubble columns. Nucl. Eng. Des. Eng. Des. 2007, 237, 399–408. [Google Scholar] [CrossRef]
- Frank, T.; Zwart, P.J.; Krepper, E.; Prasser, H.M.; Lucas, D. Validation of CFD models for mono- and polydisperse air–water two-phase flows in pipes. Nucl. Eng. Des. Eng. Des. 2008, 238, 647–659. [Google Scholar] [CrossRef]
- Khan, Z.; Bhusare, V.H.; Joshi, J.B. Comparison of turbulence models for bubble column reactors. Chem. Eng. Sci. 2017, 164, 34–52. [Google Scholar] [CrossRef]
- Borchers, O.; Busch, C.; Sokolichin, A.; Eigenberger, G. Applicability of the standard k–ε turbulence model to the dynamic simulation of bubble columns. Part II: Comparison of detailed experiments and flow simulations. Chem. Eng. Sci. 1999, 54, 5927–5935. [Google Scholar] [CrossRef]
- Buwa, V.V.; Ranade, V.V. Dynamics of gas–liquid flow in a rectangular bubble column: Experiments and single/multi-group CFD simulations. Chem. Eng. Sci. 2002, 57, 4715–4736. [Google Scholar] [CrossRef]
- Cachaza, E.M.; Díaz, M.E.; Montes, F.J.; Galán, M.A. Simultaneous Computational Fluid Dynamics (CFD) Simulation of the Hydrodynamics and Mass Transfer in a Partially Aerated Bubble Column. Ind. Eng. Chem. Res. 2009, 48, 8685–8696. [Google Scholar] [CrossRef]
- Guillen, D.P.; Grimmett, T.; Gandrik, A.M.; Antal, S.P. Development of a computational multiphase flow model for Fischer Tropsch synthesis in a slurry bubble column reactor. Chem. Eng. J. 2011, 176–177, 83–94. [Google Scholar] [CrossRef][Green Version]
- Dhotre, M.T.; Niceno, B.; Smith, B.L. Large eddy simulation of a bubble column using dynamic sub-grid scale model. Chem. Eng. J. 2008, 136, 337–348. [Google Scholar] [CrossRef]
- Zhang, D.; Deen, N.G.; Kuipers, J.A.M. Numerical simulation of the dynamic flow behavior in a bubble column: A study of closures for turbulence and interface forces. Chem. Eng. Sci. 2006, 61, 7593–7608. [Google Scholar] [CrossRef]
- Ekambara, K.; Dhotre, M.T. CFD simulation of bubble column. Nucl. Eng. Des. Eng. Des. 2010, 240, 963–969. [Google Scholar] [CrossRef]
- Tabib, M.V.; Roy, S.A.; Joshi, J.B. CFD simulation of bubble column—An analysis of interphase forces and turbulence models. Chem. Eng. J. 2008, 139, 589–614. [Google Scholar] [CrossRef]
- Cheung, S.C.P.; Yeoh, G.H.; Tu, J.Y. On the numerical study of isothermal vertical bubbly flow using two population balance approaches. Chem. Eng. Sci. 2007, 62, 4659–4674. [Google Scholar] [CrossRef][Green Version]
- Cheung, S.C.P.; Yeoh, G.H.; Tu, J.Y. On the modelling of population balance in isothermal vertical bubbly flows—Average bubble number density approach. Chem. Eng. Process. Process Intensif. 2007, 46, 742–756. [Google Scholar] [CrossRef]
- Duan, X.Y.; Cheung, S.C.P.; Yeoh, G.H.; Tu, J.Y.; Krepper, E.; Lucas, D. Gas–liquid flows in medium and large vertical pipes. Chem. Eng. Sci. 2011, 66, 872–883. [Google Scholar] [CrossRef]
- Rzehak, R.; Krepper, E. Closure models for turbulent bubbly flows: A CFD study. Nucl. Eng. Des. Eng. Des. 2013, 265, 701–711. [Google Scholar] [CrossRef]
- Rzehak, R.; Krepper, E.; Liao, Y.; Ziegenhein, T.; Kriebitzsch, S.; Lucas, D. Baseline Model for the Simulation of Bubbly Flows. Chem. Eng. Technol. 2015, 38, 1972–1978. [Google Scholar] [CrossRef]
- Rzehak, R.; Kriebitzsch, S. Multiphase CFD-simulation of bubbly pipe flow: A code comparison. Int. J. Multiph. Flow 2015, 68, 135–152. [Google Scholar] [CrossRef]
- Liao, Y.; Lucas, D.; Krepper, E. Application of new closure models for bubble coalescence and breakup to steam–water vertical pipe flow. Nucl. Eng. Des. Eng. Des. 2014, 279, 126–136. [Google Scholar] [CrossRef]
- Liao, Y.; Rzehak, R.; Lucas, D.; Krepper, E. Baseline closure model for dispersed bubbly flow: Bubble coalescence and breakup. Chem. Eng. Sci. 2015, 122, 336–349. [Google Scholar] [CrossRef]
- Shi, W.; Yang, N.; Yang, X. A kinetic inlet model for CFD simulation of large-scale bubble columns. Chem. Eng. Sci. 2017, 158, 108–116. [Google Scholar] [CrossRef]
- Masood, R.M.A.; Delgado, A. Numerical investigation of the interphase forces and turbulence closure in 3D square bubble columns. Chem. Eng. Sci. 2014, 108, 154–168. [Google Scholar] [CrossRef]
- Masood, R.M.A.; Rauh, C.; Delgado, A. CFD simulation of bubble column flows: An explicit algebraic Reynolds stress model approach. Int. J. Multiph. Flow 2014, 66, 11–25. [Google Scholar] [CrossRef]
- Colombo, M.; Fairweather, M. Multiphase turbulence in bubbly flows: RANS simulations. Int. J. Multiph. Flow 2015, 77, 222–243. [Google Scholar] [CrossRef]
- Pourtousi, M.; Sahu, J.N.; Ganesan, P. Effect of interfacial forces and turbulence models on predicting flow pattern inside the bubble column. Chem. Eng. Process. Process Intensif. 2014, 75, 38–47. [Google Scholar] [CrossRef]
- Parekh, J.; Rzehak, R. Euler–Euler multiphase CFD-simulation with full Reynolds stress model and anisotropic bubble-induced turbulence. Int. J. Multiph. Flow 2018, 99, 231–245. [Google Scholar] [CrossRef]
- Rzehak, R.; Krepper, E. CFD modeling of bubble-induced turbulence. Int. J. Multiph. Flow 2013, 55, 138–155. [Google Scholar] [CrossRef]
- Rzehak, R.; Krepper, E. Bubble-induced turbulence: Comparison of CFD models. Nucl. Eng. Des. Eng. Des. 2013, 258, 57–65. [Google Scholar] [CrossRef]
- Ma, T.; Santarelli, C.; Ziegenhein, T.; Lucas, D.; Fröhlich, J. Direct numerical simulation–based Reynolds-averaged closure for bubble-induced turbulence. Phys. Rev. Fluids 2017, 2, 034301. [Google Scholar] [CrossRef]
- Guan, X.; Yang, N. CFD simulation of pilot-scale bubble columns with internals: Influence of interfacial forces. Chem. Eng. Res. Des. 2017, 126, 109–122. [Google Scholar] [CrossRef]
- Lucas, D.; Krepper, E.; Prasser, H.M. Use of models for lift, wall and turbulent dispersion forces acting on bubbles for poly-disperse flows. Chem. Eng. Sci. 2007, 62, 4146–4157. [Google Scholar] [CrossRef]
- Rzehak, R.; Krepper, E.; Lifante, C. Comparative study of wall-force models for the simulation of bubbly flows. Nucl. Eng. Des. Eng. Des. 2012, 253, 41–49. [Google Scholar] [CrossRef]
- Deen, N.G.; Solberg, T.; Hjertager, B.H. Large eddy simulation of the Gas–Liquid flow in a square cross-sectioned bubble column. Chem. Eng. Sci. 2001, 56, 6341–6349. [Google Scholar] [CrossRef]
- Chen, P.; Sanyal, J.; Duduković, M.P. Numerical simulation of bubble columns flows: Effect of different breakup and coalescence closures. Chem. Eng. Sci. 2005, 60, 1085–1101. [Google Scholar] [CrossRef]
- Chen, P.; Sanyal, J.; Dudukovic, M.P. CFD modeling of bubble columns flows: Implementation of population balance. Chem. Eng. Sci. 2004, 59, 5201–5207. [Google Scholar] [CrossRef]
- Chen, P.; Duduković, M.P.; Sanyal, J. Three-dimensional simulation of bubble column flows with bubble coalescence and breakup. AIChE J. 2005, 51, 696–712. [Google Scholar] [CrossRef]
- Larachi, F.ç.; Desvigne, D.; Donnat, L.; Schweich, D. Simulating the effects of liquid circulation in bubble columns with internals. Chem. Eng. Sci. 2006, 61, 4195–4206. [Google Scholar] [CrossRef]
- Krepper, E.; Lucas, D.; Frank, T.; Prasser, H.-M.; Zwart, P.J. The inhomogeneous MUSIG model for the simulation of polydispersed flows. Nucl. Eng. Des. Eng. Des. 2008, 238, 1690–1702. [Google Scholar] [CrossRef]
- Díaz, E.M.; Montes, F.J.; Galán, M.A. Influence of the lift force closures on the numerical simulation of bubble plumes in a rectangular bubble column. Chem. Eng. Sci. 2009, 64, 930–944. [Google Scholar] [CrossRef]
- Masood, R.M.A.; Khalid, Y.; Delgado, A. Scale adaptive simulation of bubble column flows. Chem. Eng. J. 2015, 262, 1126–1136. [Google Scholar] [CrossRef]
- Pourtousi, M.; Zeinali, M.; Ganesan, P.; Sahu, J.N. Prediction of multiphase flow pattern inside a 3D bubble column reactor using a combination of CFD and ANFIS. RSC Adv. 2015, 5, 85652–85672. [Google Scholar] [CrossRef]
- Pourtousi, M.; Sahu, J.N.; Ganesan, P.; Shamshirband, S.; Redzwan, G. A combination of computational fluid dynamics (CFD) and adaptive neuro-fuzzy system (ANFIS) for prediction of the bubble column hydrodynamics. Powder Technol. 2015, 274, 466–481. [Google Scholar] [CrossRef]
- Ziegenhein, T.; Lucas, D.; Rzehak, R.; Krepper, E. Closure relations for CFD simulation of bubble columns. In Proceedings of the 8th International Conference on Multiphase Flow: ICMF 2013, Jeju, Korea, 26–31 May 2013. [Google Scholar]
- Liao, J.; Ziegenhein, T.; Rzehak, R. Bubbly flow in an airlift column: A CFD study. J. Chem. Technol. Biotechnol. 2016, 91, 2904–2915. [Google Scholar] [CrossRef]
- Rzehak, R.; Krauß, M.; Kováts, P.; Zähringer, K. Fluid dynamics in a bubble column: New experiments and simulations. Int. J. Multiph. Flow 2017, 89, 299–312. [Google Scholar] [CrossRef]
- Ziegenhein, T.; Rzehak, R.; Ma, T.; Lucas, D. Towards a unified approach for modelling uniform and non-uniform bubbly flows. Can. J. Chem. Eng. 2017, 95, 170–179. [Google Scholar] [CrossRef]
- Rzehak, R.; Ziegenhein, T.; Kriebitzsch, S.; Krepper, E.; Lucas, D. Unified modeling of bubbly flows in pipes, bubble columns, and airlift columns. Chem. Eng. Sci. 2017, 157, 147–158. [Google Scholar] [CrossRef]
- Lehr, F.; Mewes, D. A transport equation for the interfacial area density applied to bubble columns. Chem. Eng. Sci. 2001, 56, 1159–1166. [Google Scholar] [CrossRef]
- Adetunji, O.C.; Rawatlal, R. Prediction of bubble size and axial position distribution through hybridization of population balance modelling and dynamic gas disengagement. Flow Meas. Instrum. 2018, 59, 181–193. [Google Scholar] [CrossRef]
- Cheng, J.; Li, Q.; Yang, C.; Zhang, Y.; Mao, Z.-S. CFD-PBE simulation of a bubble column in OpenFOAM. Chin. J. Chem. Eng. 2017. [Google Scholar] [CrossRef]
- Yang, N.; Xiao, Q. A mesoscale approach for population balance modeling of bubble size distribution in bubble column reactors. Chem. Eng. Sci. 2017, 170, 241–250. [Google Scholar] [CrossRef]
- Guo, K.; Wang, T.; Liu, Y.; Wang, J. CFD-PBM simulations of a bubble column with different liquid properties. Chem. Eng. J. 2017, 329, 116–127. [Google Scholar] [CrossRef]
- Saleh, S.N.; Mohammed, A.A.; Al-Jubory, F.K.; Barghi, S. CFD assesment of uniform bubbly flow in a bubble column. J. Pet. Sci. Eng. 2018, 161, 96–107. [Google Scholar] [CrossRef]
- Besagni, G.; Inzoli, F.; Ziegenhein, T.; Lucas, D. Computational Fluid-Dynamic modeling of the pseudo-homogeneous flow regime in large-scale bubble columns. Chem. Eng. Sci. 2017, 160, 144–160. [Google Scholar] [CrossRef]
- Besagni, G.; Inzoli, F.; Ziegenhein, T.; Lucas, D. The pseudo-homogeneous flow regime in large-scale bubble columns: Experimental benchmark and computational fluid dynamics modeling. Petroleum 2017. [Google Scholar] [CrossRef]
- Xu, L.; Yuan, B.; Ni, H.; Chen, C. Numerical Simulation of Bubble Column Flows in Churn-Turbulent Regime: Comparison of Bubble Size Models. Ind. Eng. Chem. Res. 2013, 52, 6794–6802. [Google Scholar] [CrossRef]
- Krishna, R.; van Baten, J.M.; Urseanu, M.I. Three-phase Eulerian simulations of bubble column reactors operating in the churn-turbulent regime: A scale up strategy. Chem. Eng. Sci. 2000, 55, 3275–3286. [Google Scholar] [CrossRef]
- van Baten, J.M.; Krishna, R. Eulerian simulations for determination of the axial dispersion of liquid and gas phases in bubble columns operating in the churn-turbulent regime. Chem. Eng. Sci. 2001, 56, 503–512. [Google Scholar] [CrossRef]
- van Baten, J.M.; Krishna, R. CFD Simulations of a Bubble Column Operating in the Homogeneous and Heterogeneous Flow Regimes. Chem. Eng. Technol. 2002, 25, 1081–1086. [Google Scholar] [CrossRef]
- Krishna, R.; van Baten, J.M. Eulerian simulations of bubble columns operating at elevated pressures in the churn turbulent flow regime. Chem. Eng. Sci. 2001, 56, 6249–6258. [Google Scholar] [CrossRef]
- Krepper, E.; Lucas, D.; Prasser, H.-M. On the modelling of bubbly flow in vertical pipes. Nucl. Eng. Des. Eng. Des. 2005, 235, 597–611. [Google Scholar] [CrossRef]
- Lucas, D.; Tomiyama, A. On the role of the lateral lift force in poly-dispersed bubbly flows. Int. J. Multiph. Flow 2011, 37, 1178–1190. [Google Scholar] [CrossRef]
- Sporleder, F.; Dorao, C.A.; Jakobsen, H.A. Model based on population balance for the simulation of bubble columns using methods of the least-square type. Chem. Eng. Sci. 2011, 66, 3133–3144. [Google Scholar] [CrossRef]
- Colella, D.; Vinci, D.; Bagatin, R.; Masi, M.; Bakr, E.A. A study on coalescence and breakage mechanisms in three different bubble columns. Chem. Eng. Sci. 1999, 54, 4767–4777. [Google Scholar] [CrossRef]
- Ramkrishna, D.; Mahoney, A.W. Population balance modeling. Promise for the future. Chem. Eng. Sci. 2002, 57, 595–606. [Google Scholar] [CrossRef]
- Solsvik, J.; Jakobsen, H.A. A review of the statistical turbulence theory required extending the population balance closure models to the entire spectrum of turbulence. AIChE J. 2016, 62, 1795–1820. [Google Scholar] [CrossRef]
- Solsvik, J.; Jakobsen, H.A. Development of Fluid Particle Breakup and Coalescence Closure Models for the Complete Energy Spectrum of Isotropic Turbulence. Ind. Eng. Chem. Res. 2016, 55, 1449–1460. [Google Scholar] [CrossRef]
- Solsvik, J.; Jakobsen, H.A. Bubble Coalescence Modeling in the Population Balance Framework. J. Dispers. Sci. Technol. 2014, 35, 1626–1642. [Google Scholar] [CrossRef]
- Solsvik, J.; Tangen, S.; Jakobsen, H.A. On the Constitutive Equations for Fluid Particle Breakage. Rev. Chem. Eng. 2013, 29, 241. [Google Scholar] [CrossRef]
- Lehr, F.; Millies, M.; Mewes, D. Bubble-Size distributions and flow fields in bubble columns. AIChE J. 2002, 48, 2426–2443. [Google Scholar] [CrossRef]
- Howarth, W. Coalescence of drops in a turbulent flow field. Chem. Eng. Sci. 1964, 19, 33–38. [Google Scholar] [CrossRef]
- Shinnar, R.; Church, J.M. Statistical theories of turbulence in predicting particle size in agitated dispersions. Ind. Eng. Chem. 1960, 52, 253–256. [Google Scholar] [CrossRef]
- Ishii, M.; Kojasoy, G. Interfacial area transport equation and preliminary considerations for closure relations. In Technical Report, PU-NE-93/6; Nuclear Engineering Department, Purdue University West Lafayette: West Lafayette, IN, USA, 1993. [Google Scholar]
- Liao, Y. Development and Validation of Models for Bubble Coalescence and Breakup. Ph.D. Thesis, Technische University Dresden, Dresden, Germany, 2013. [Google Scholar]
- Solsvik, J.; Maaß, S.; Jakobsen, H.A. Definition of the Single Drop Breakup Event. Ind. Eng. Chem. Res. 2016, 55, 2872–2882. [Google Scholar] [CrossRef]
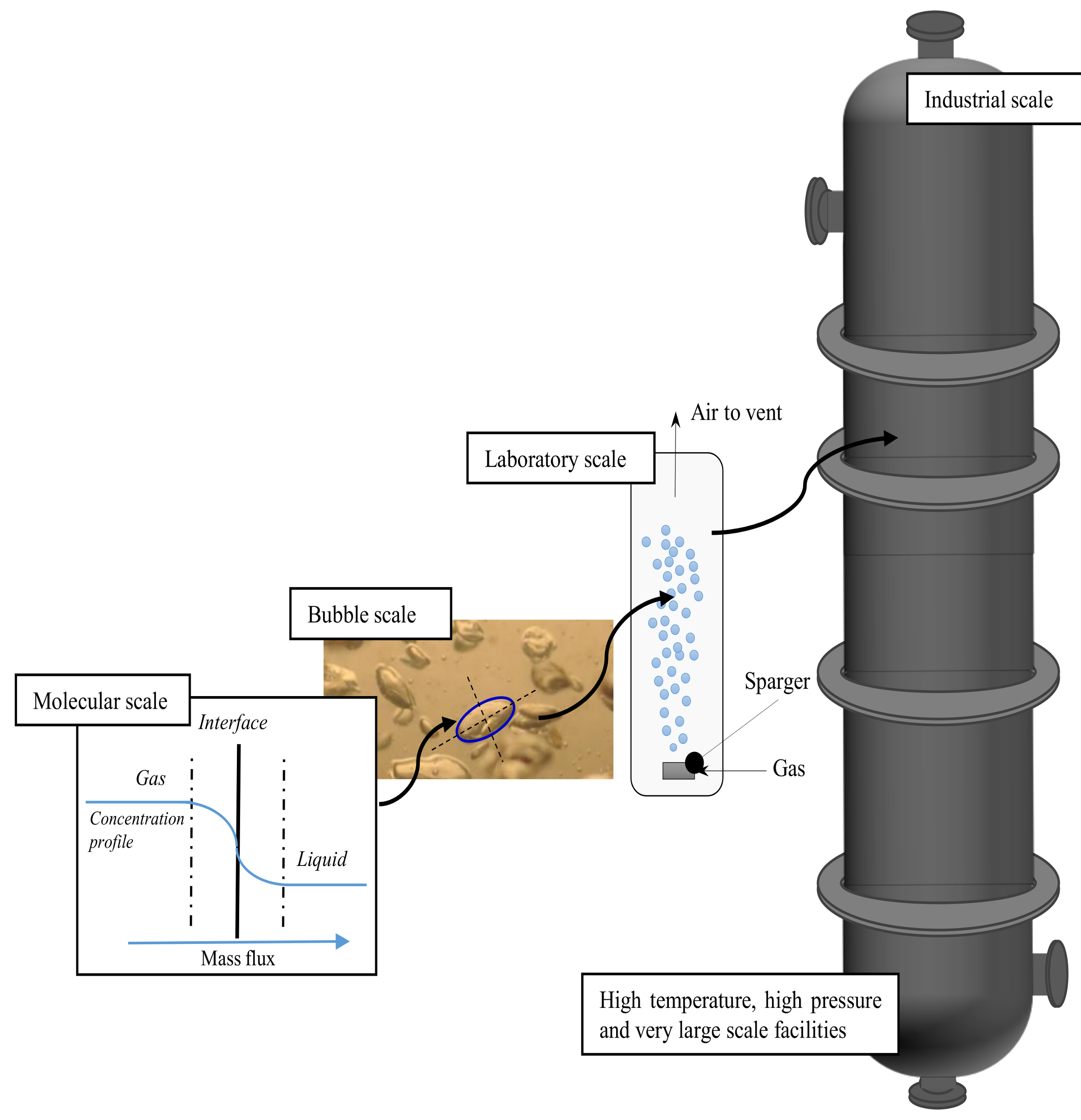
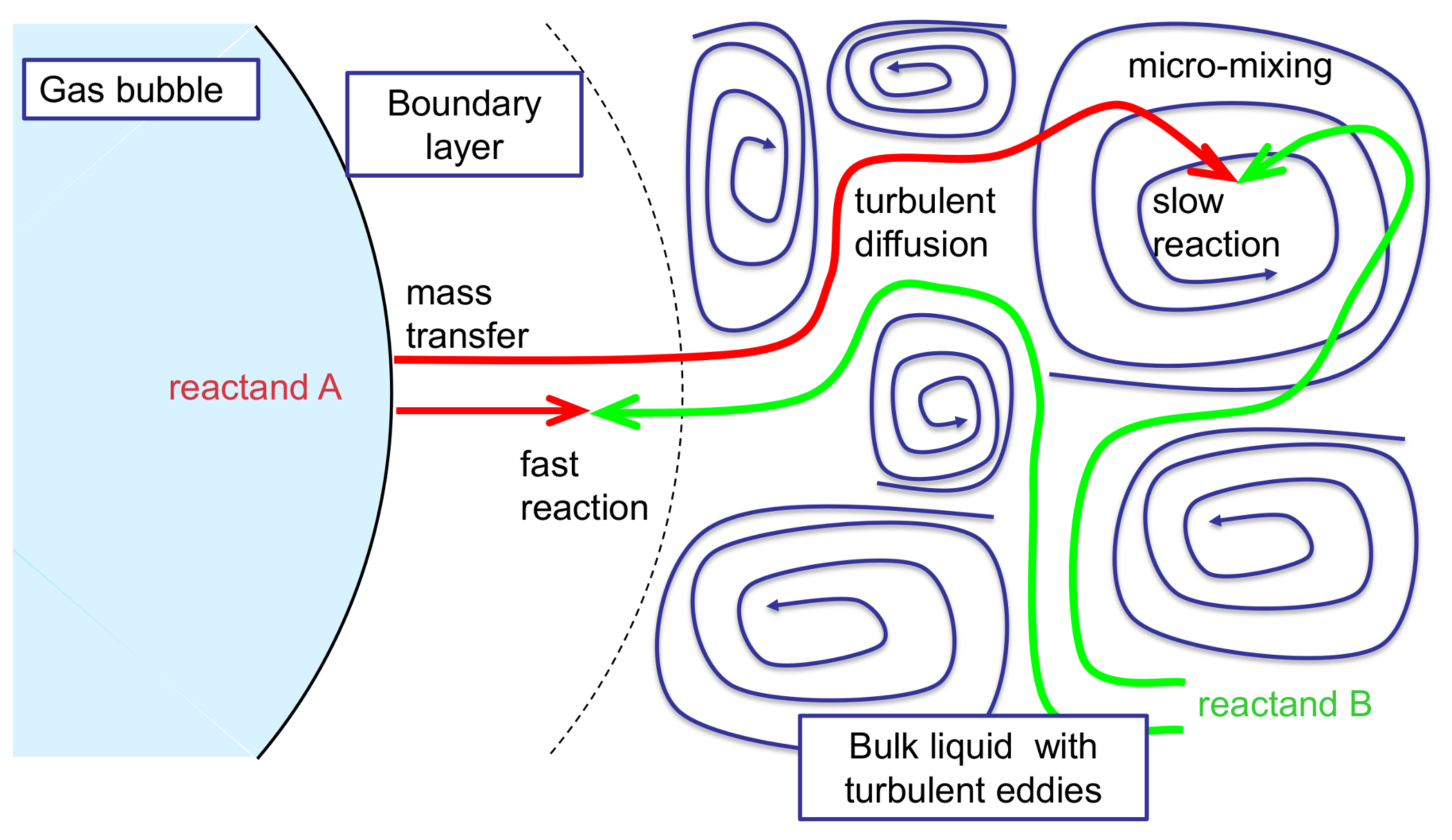
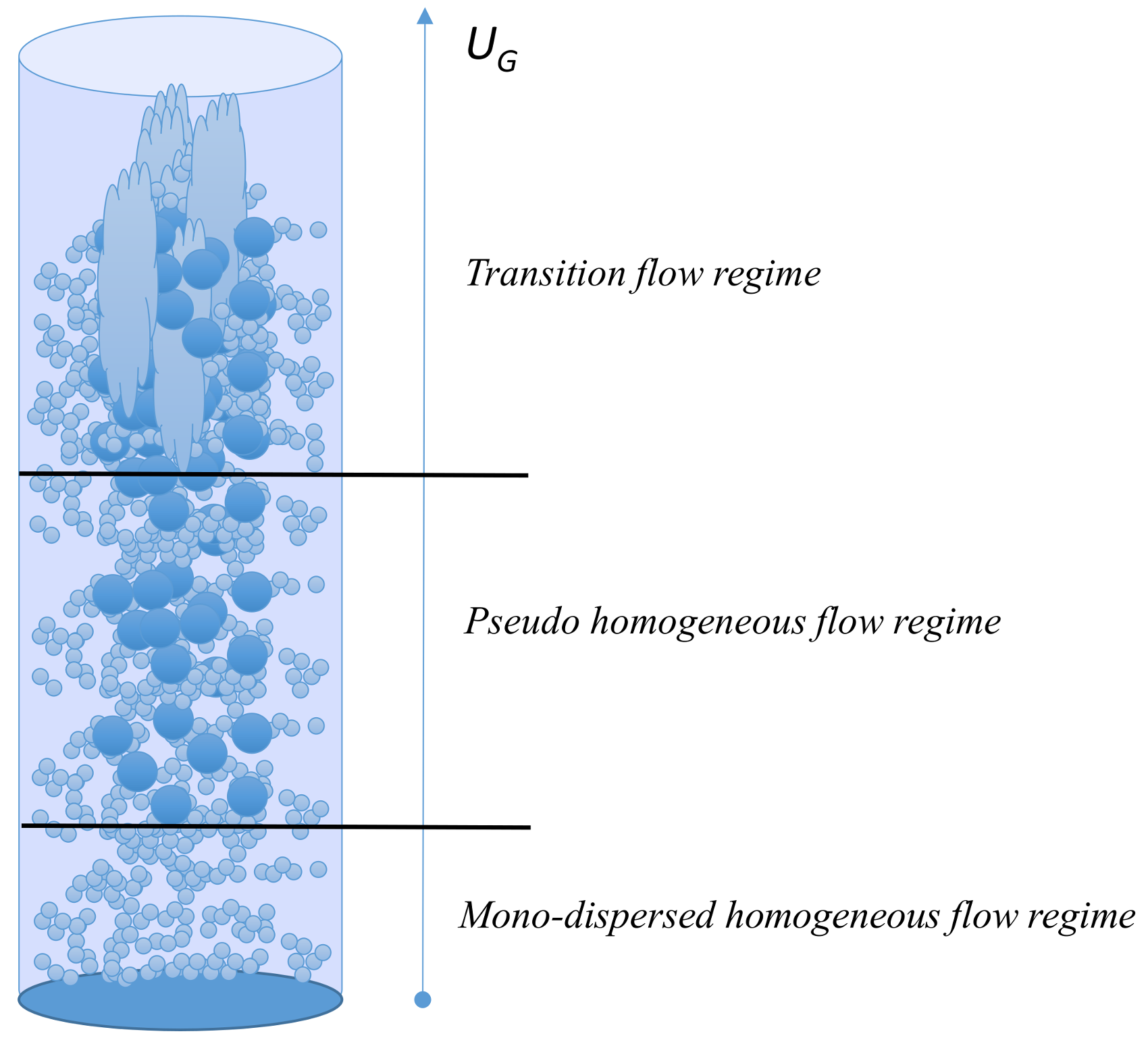
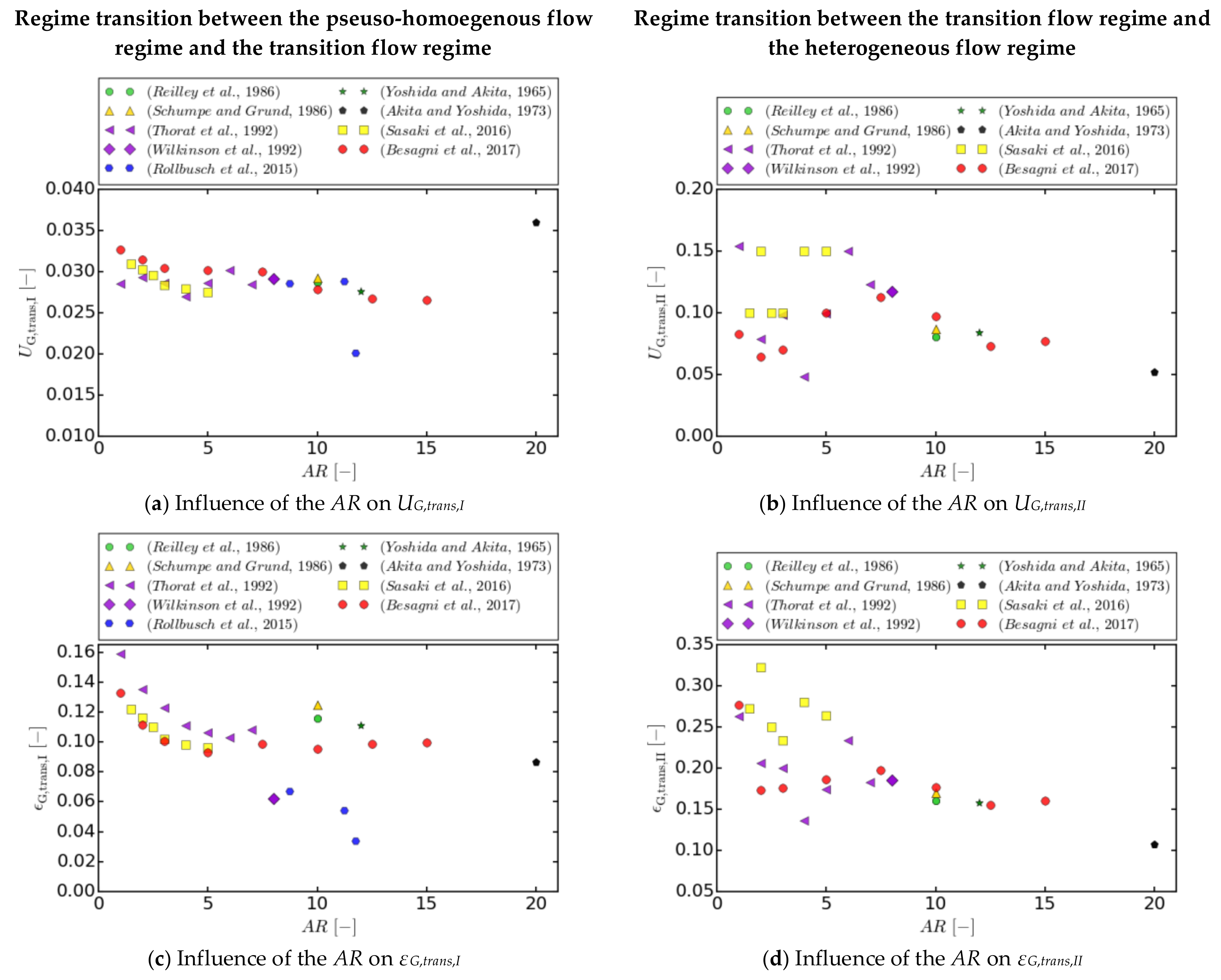


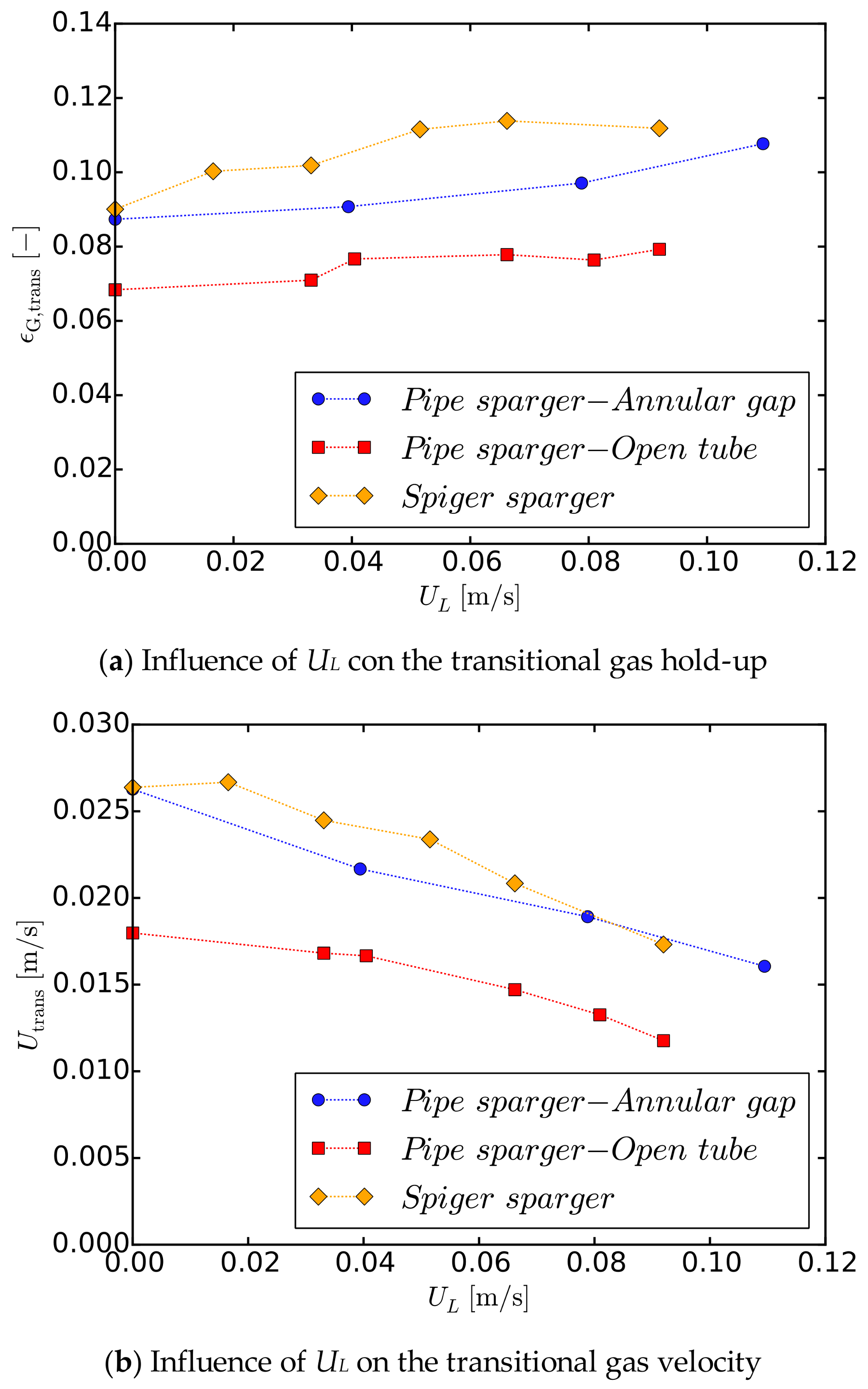
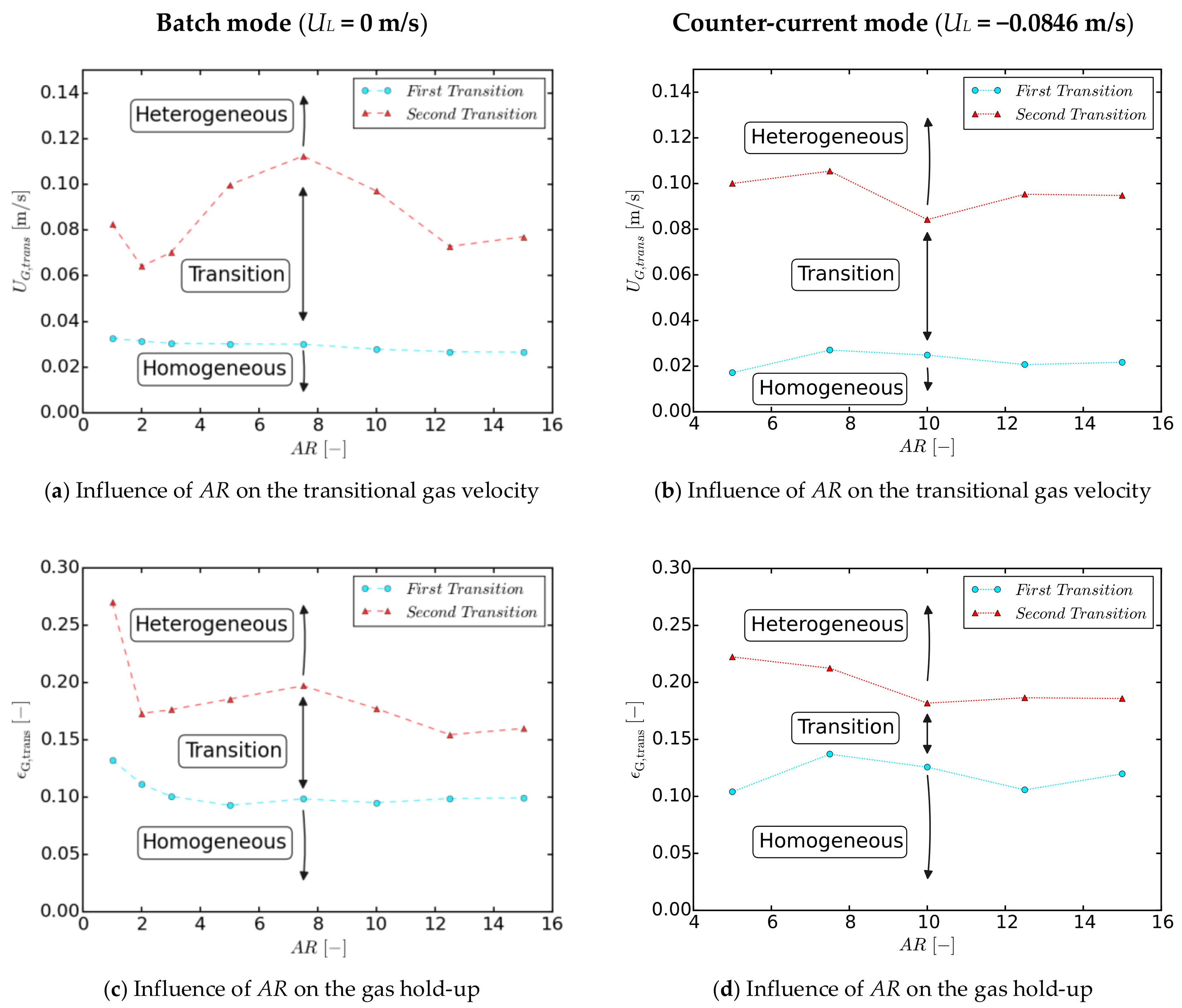
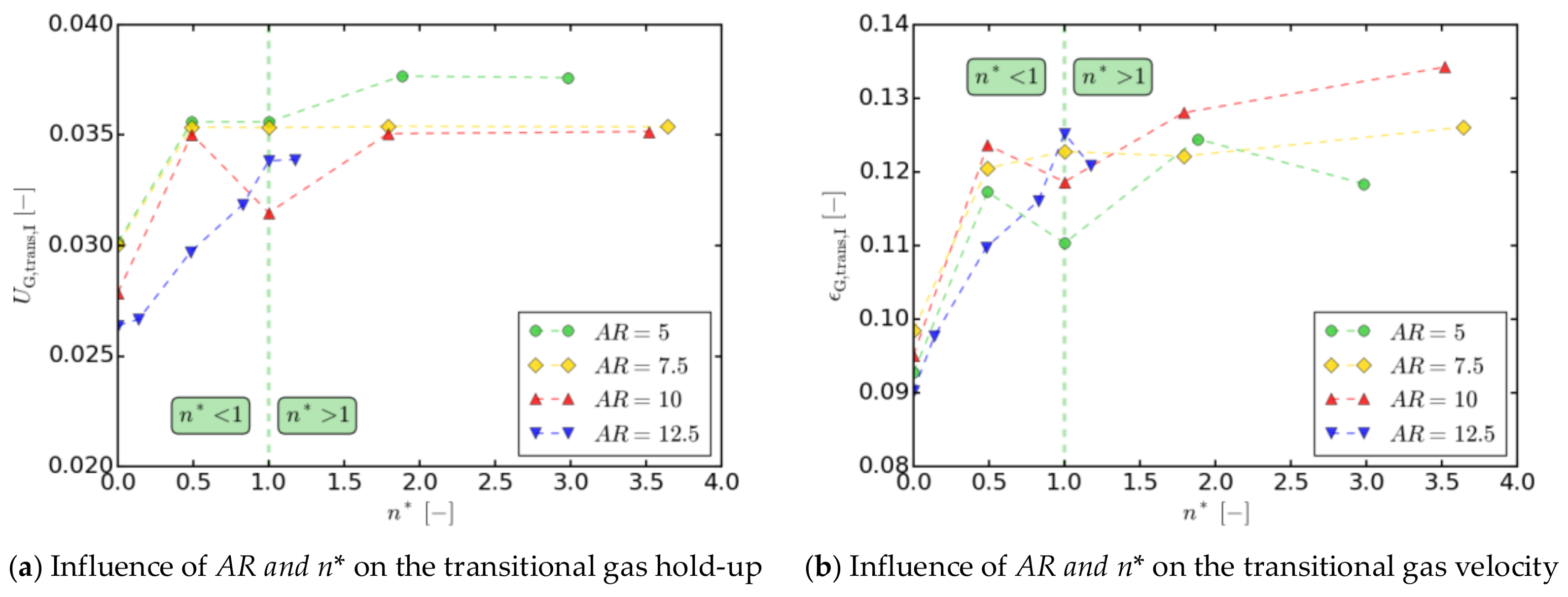
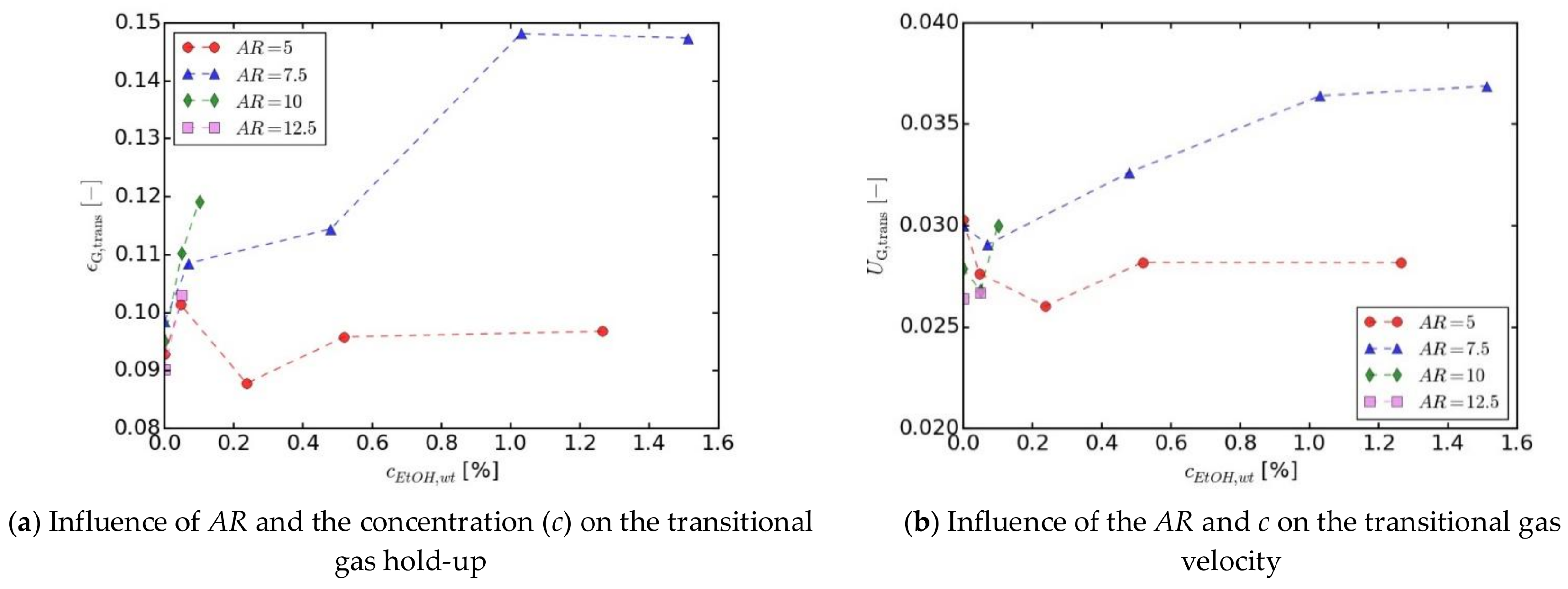
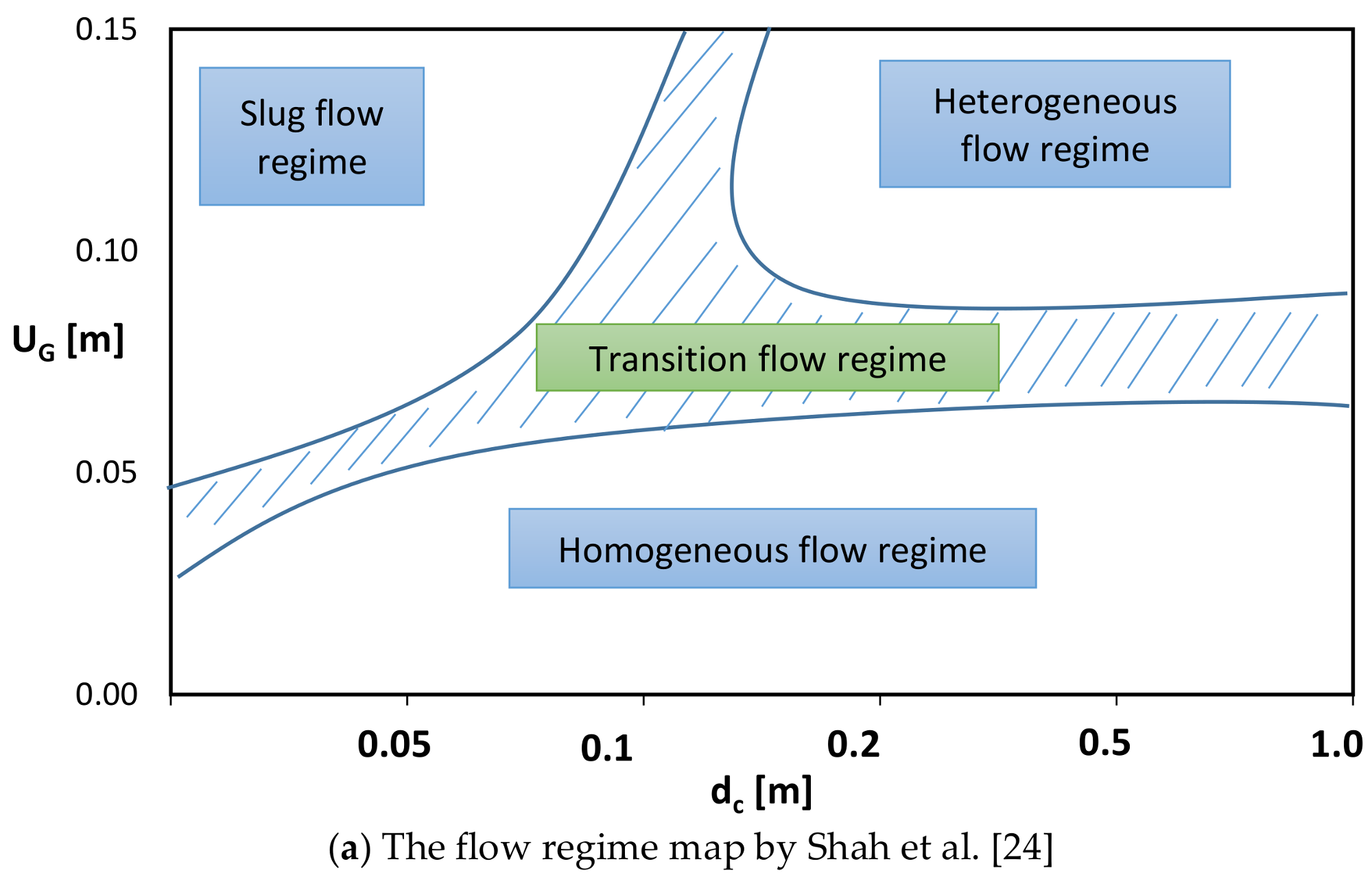
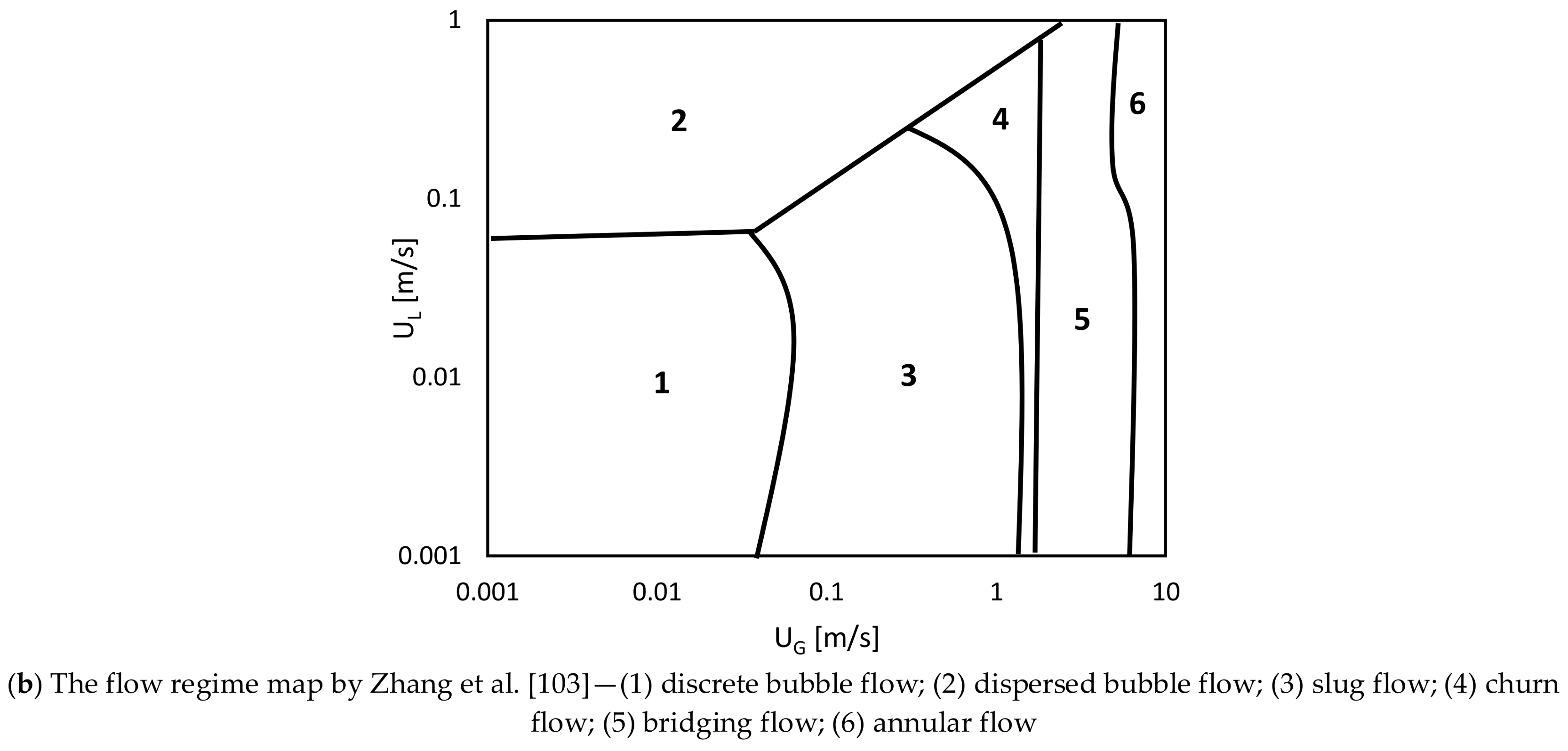
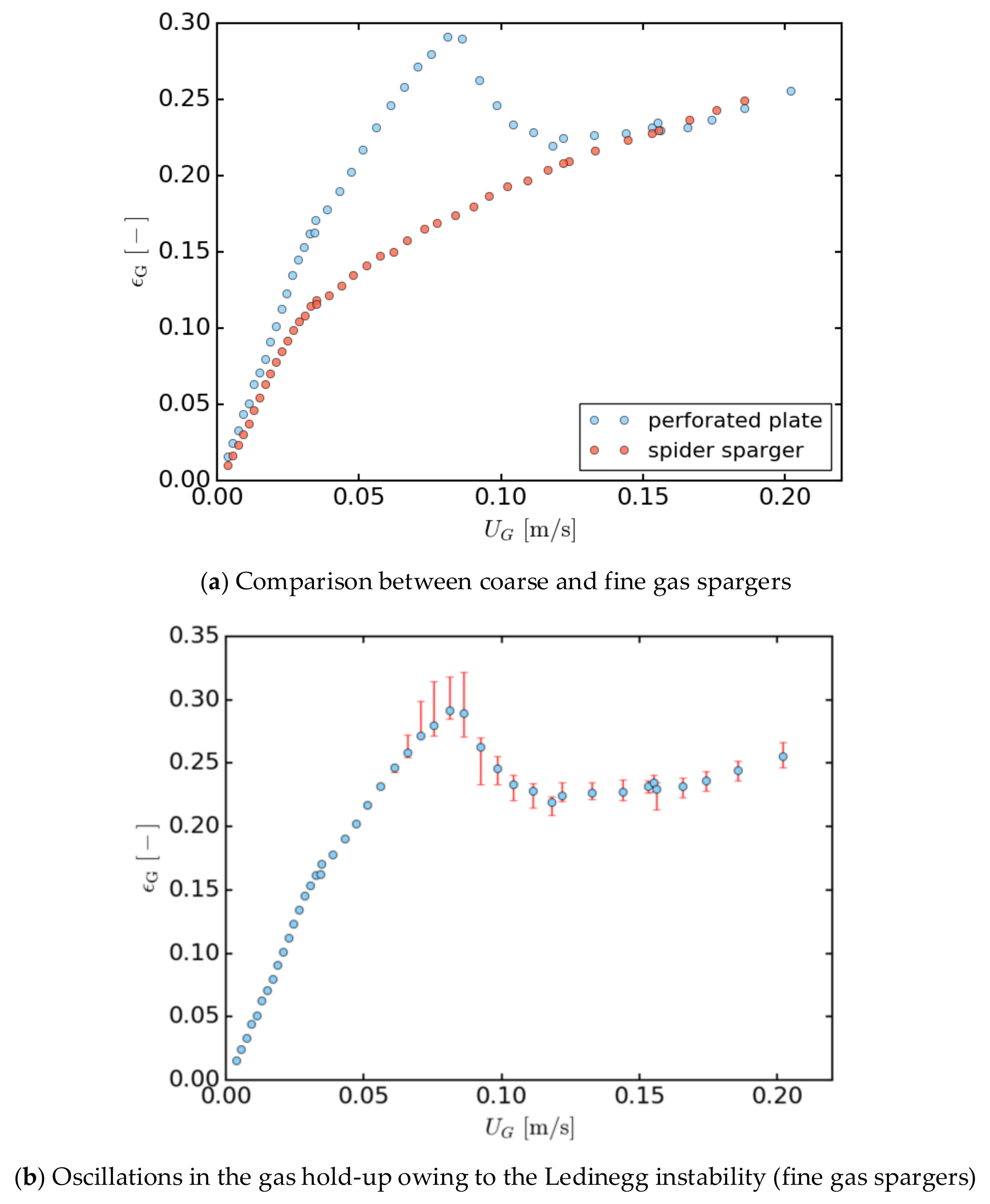
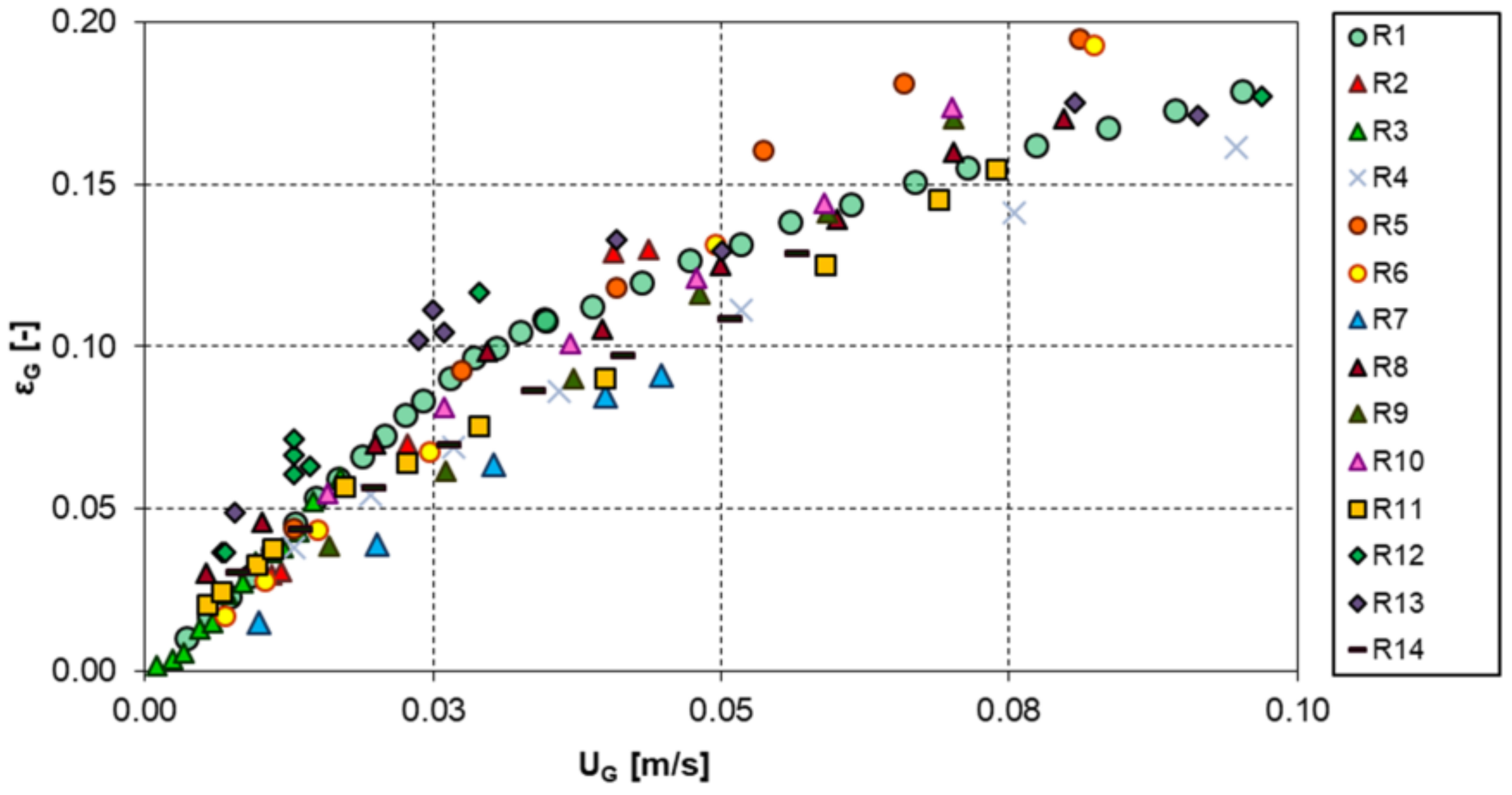
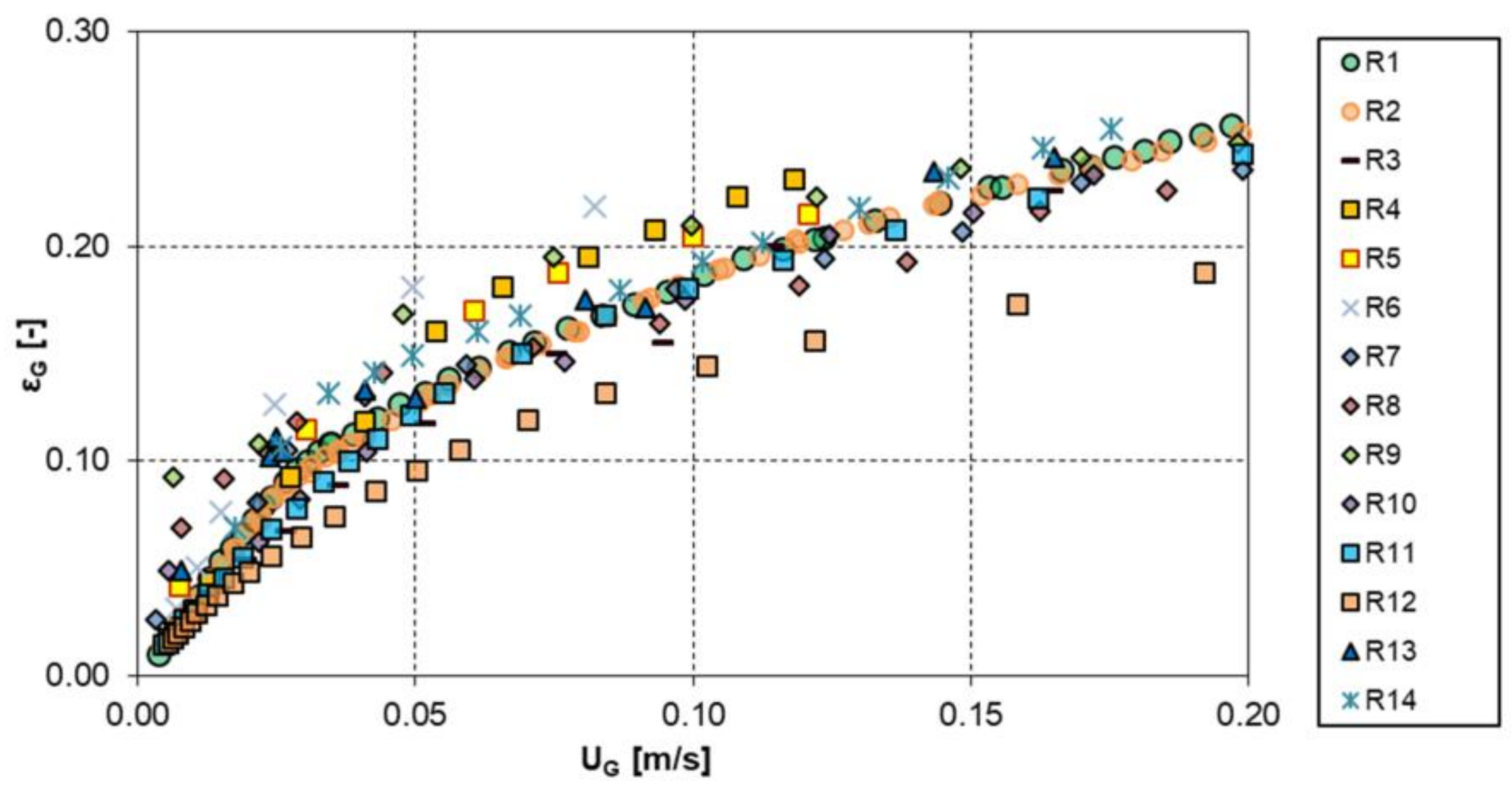
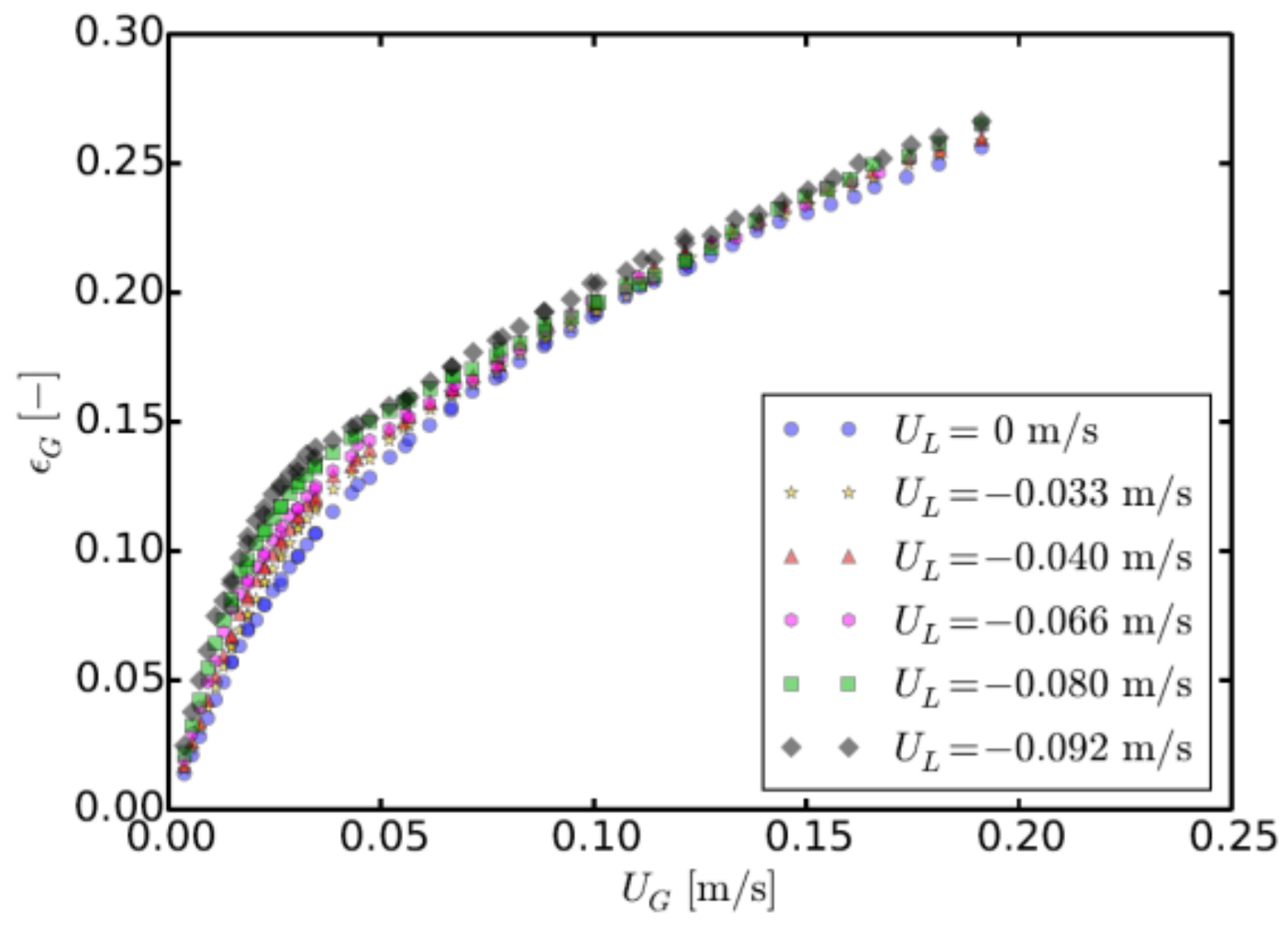
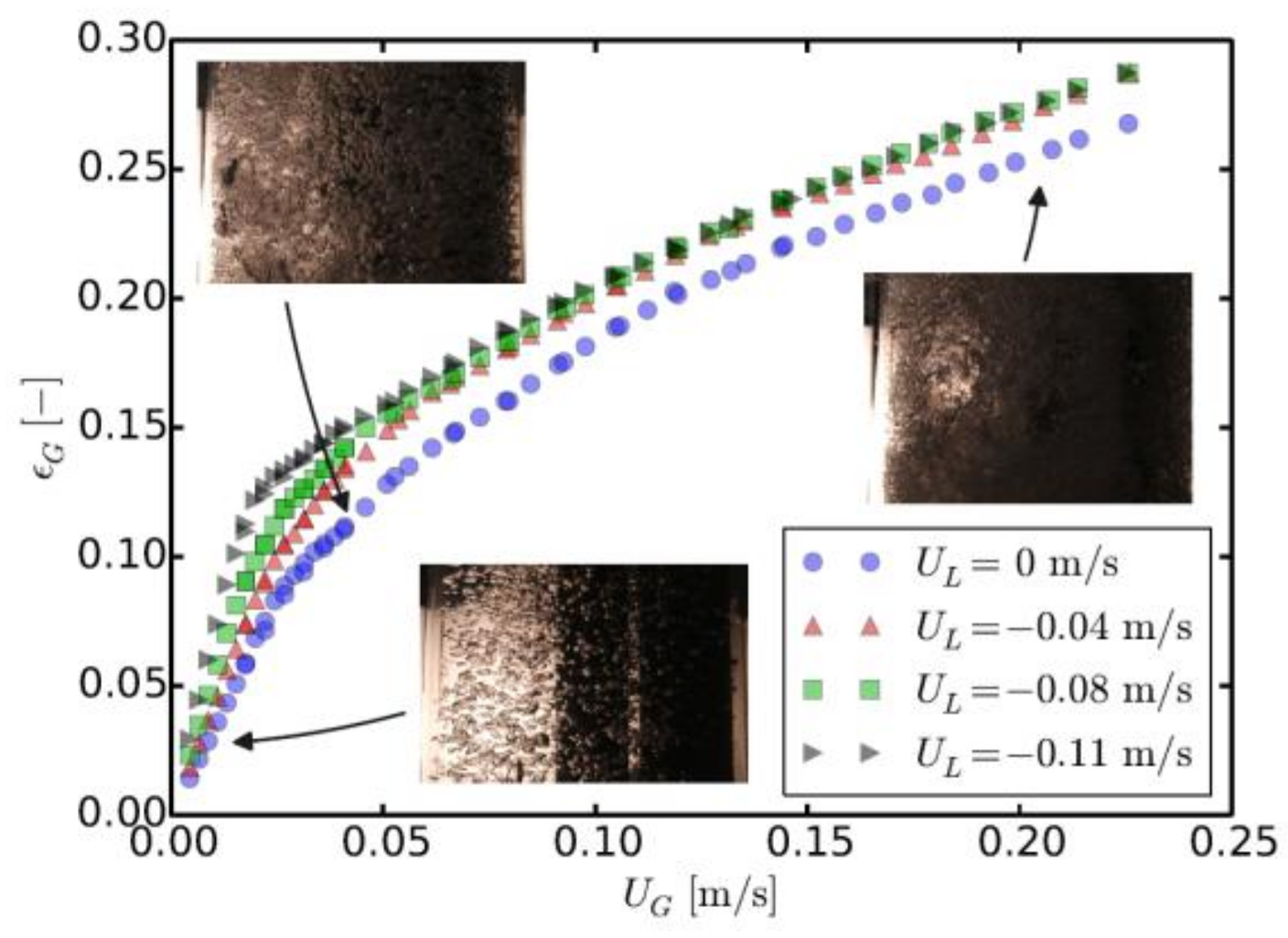
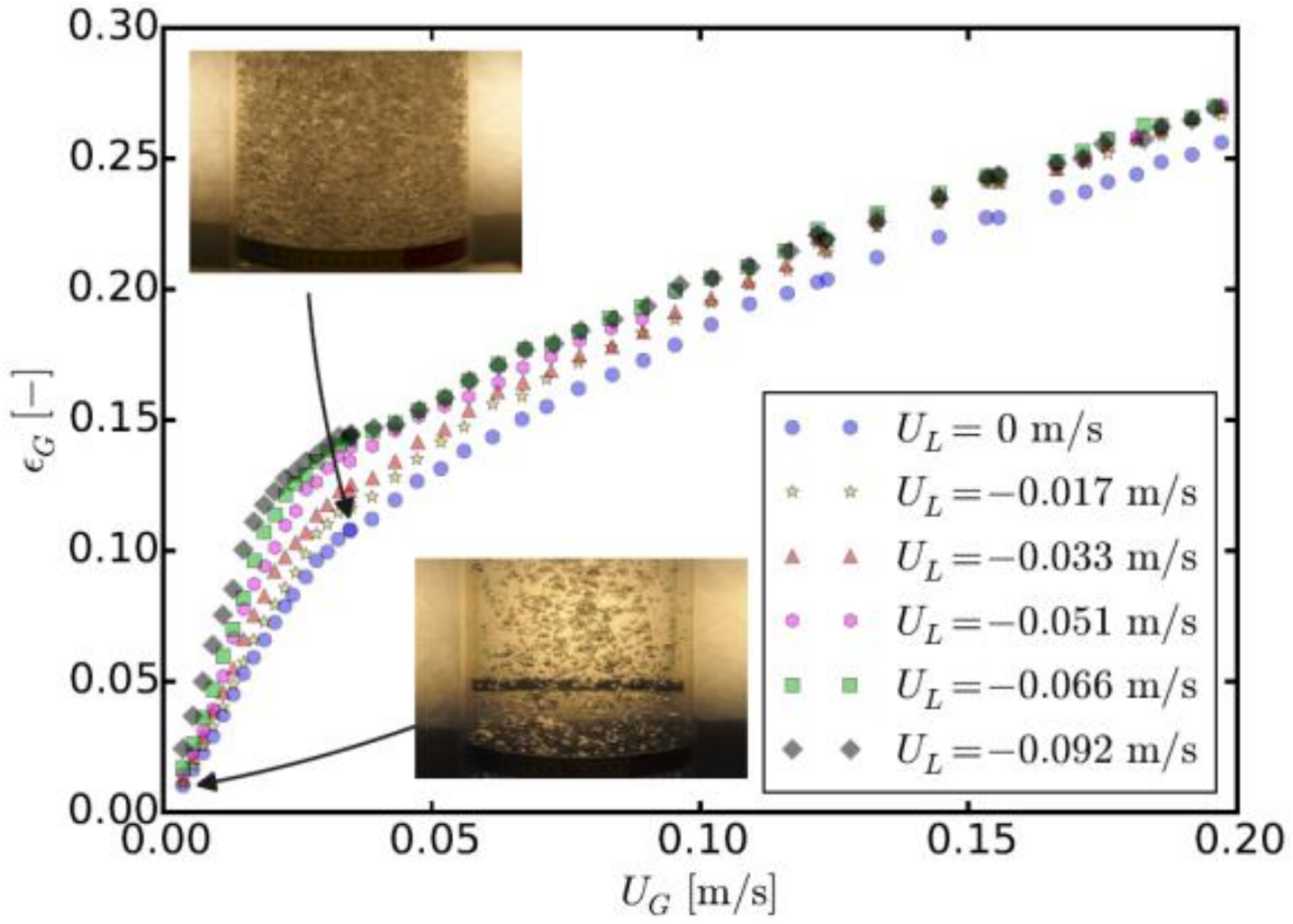
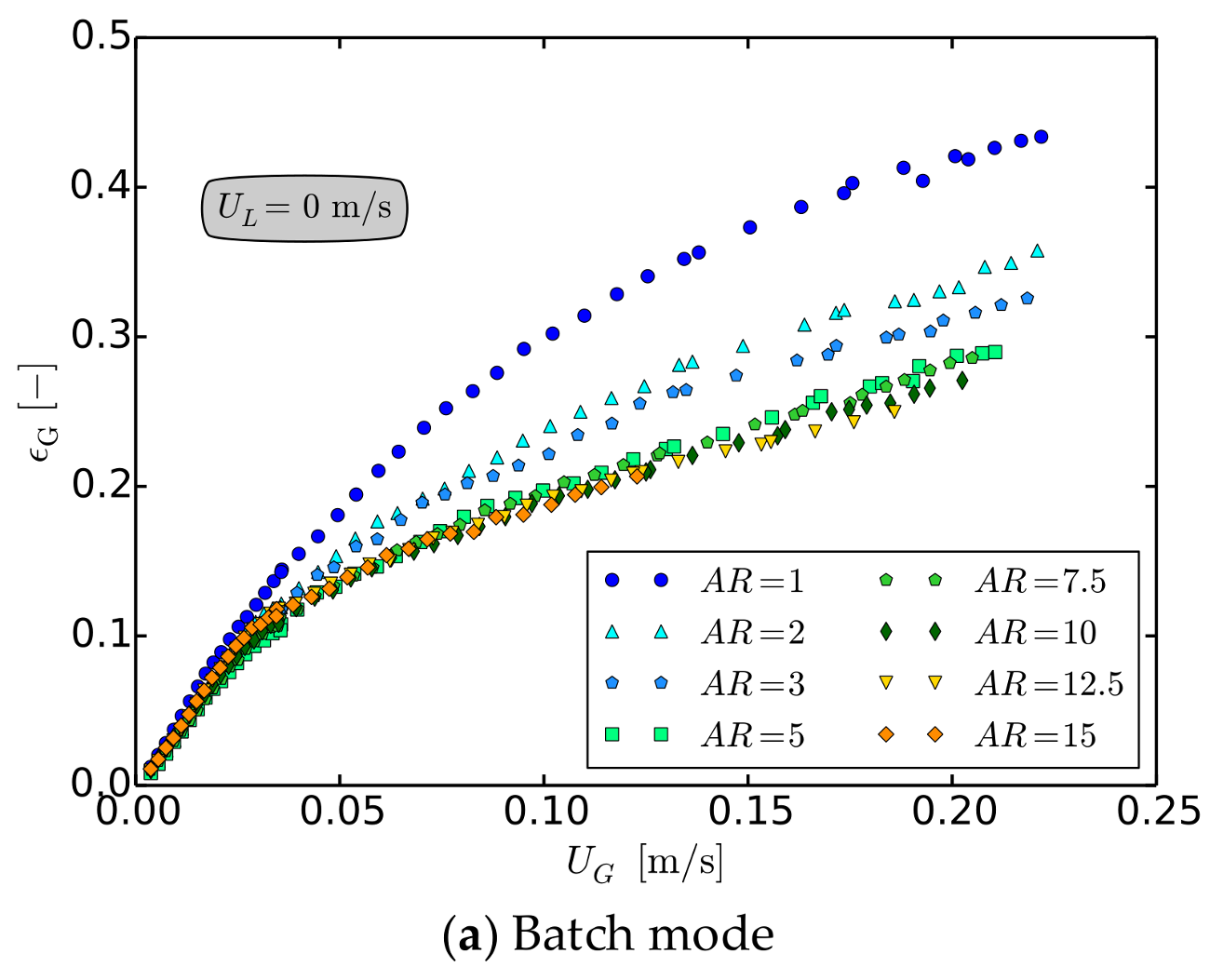
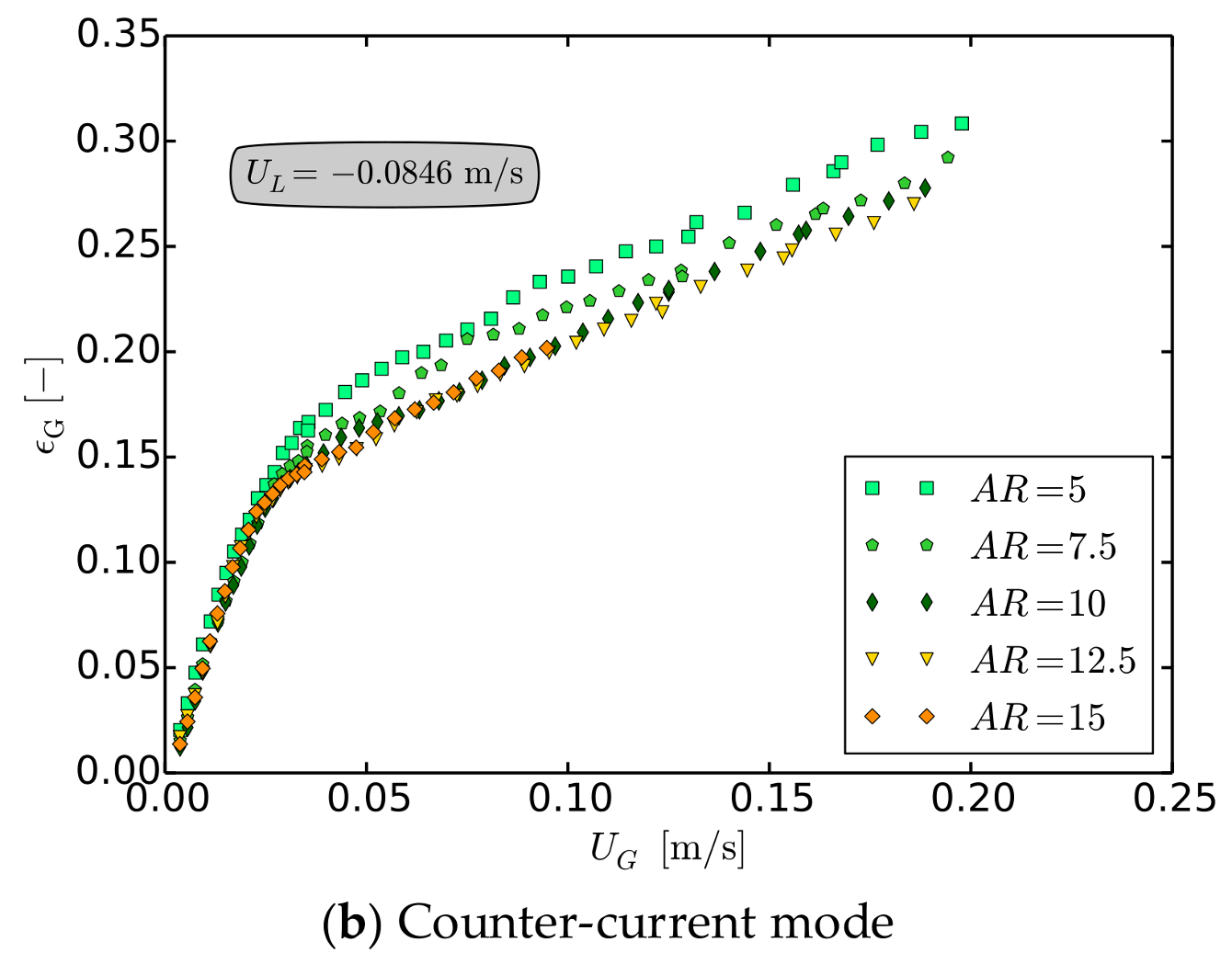

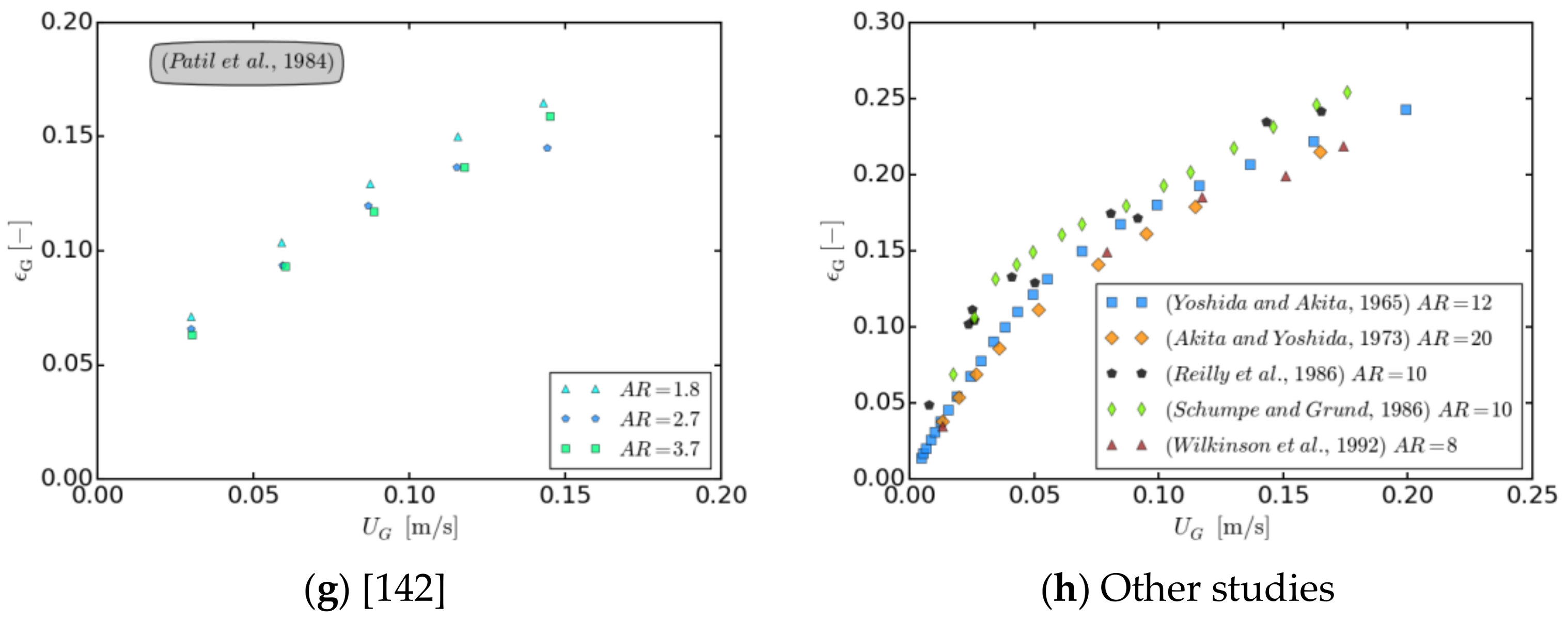

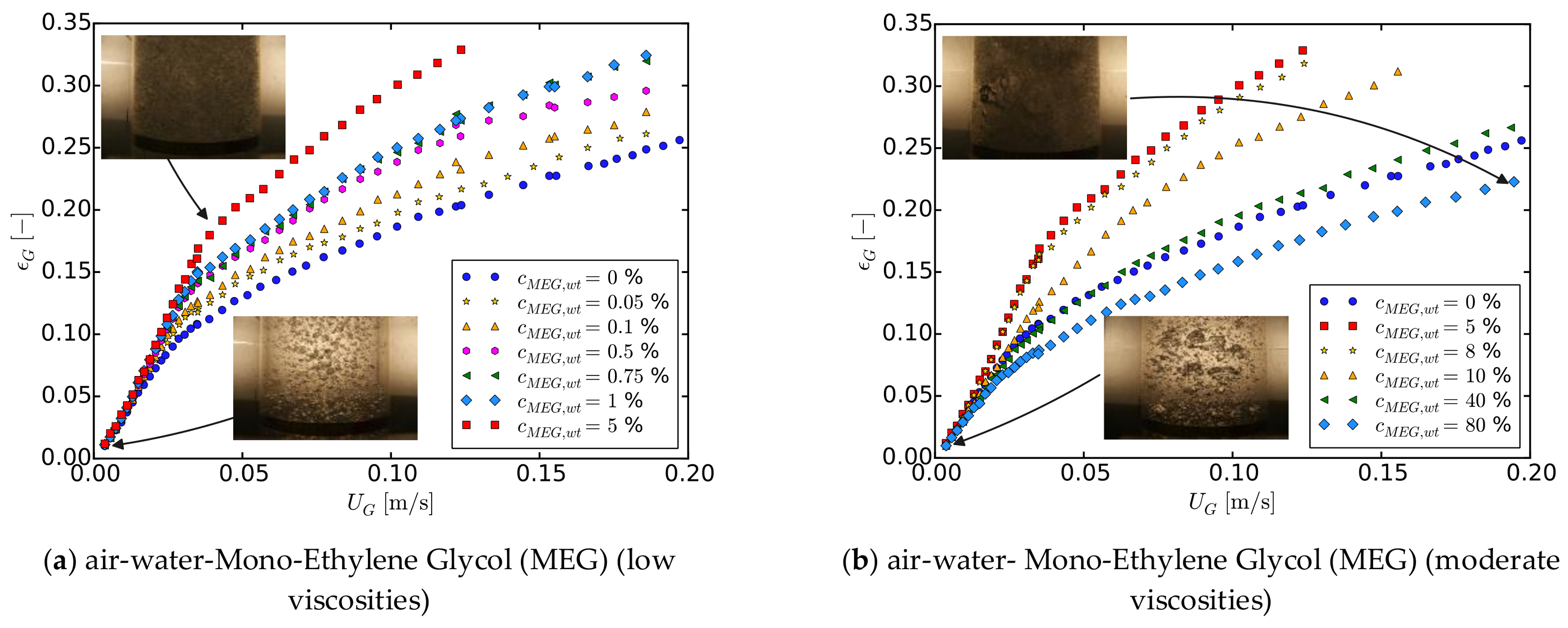
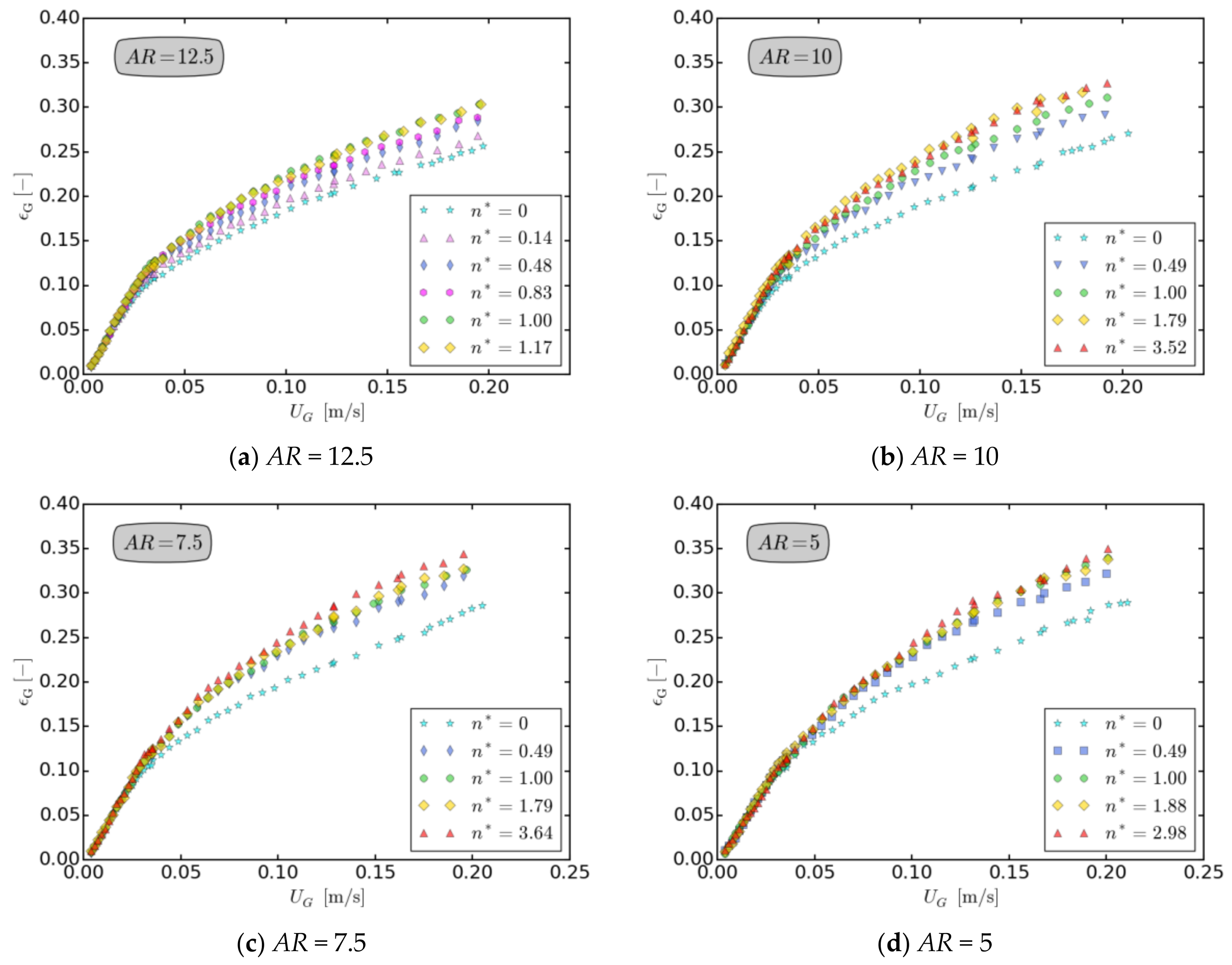

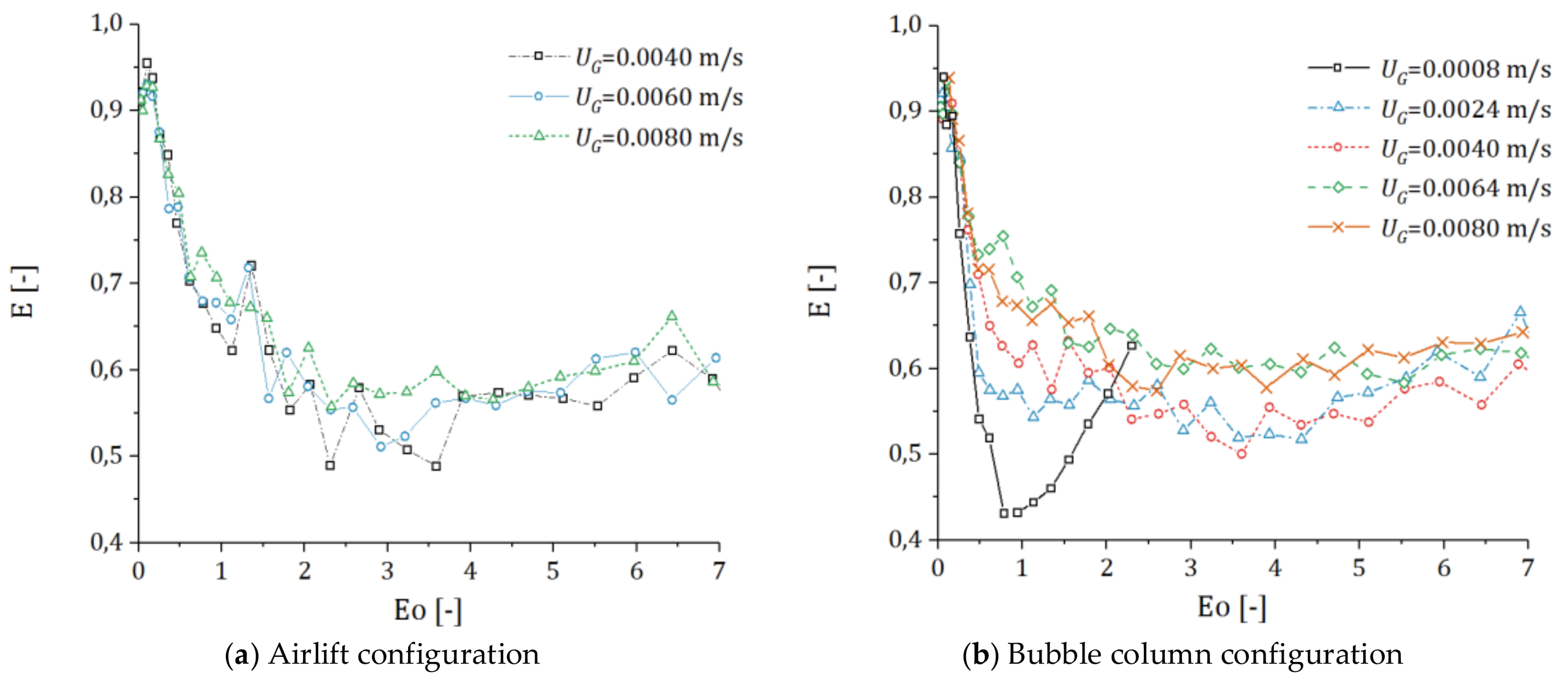
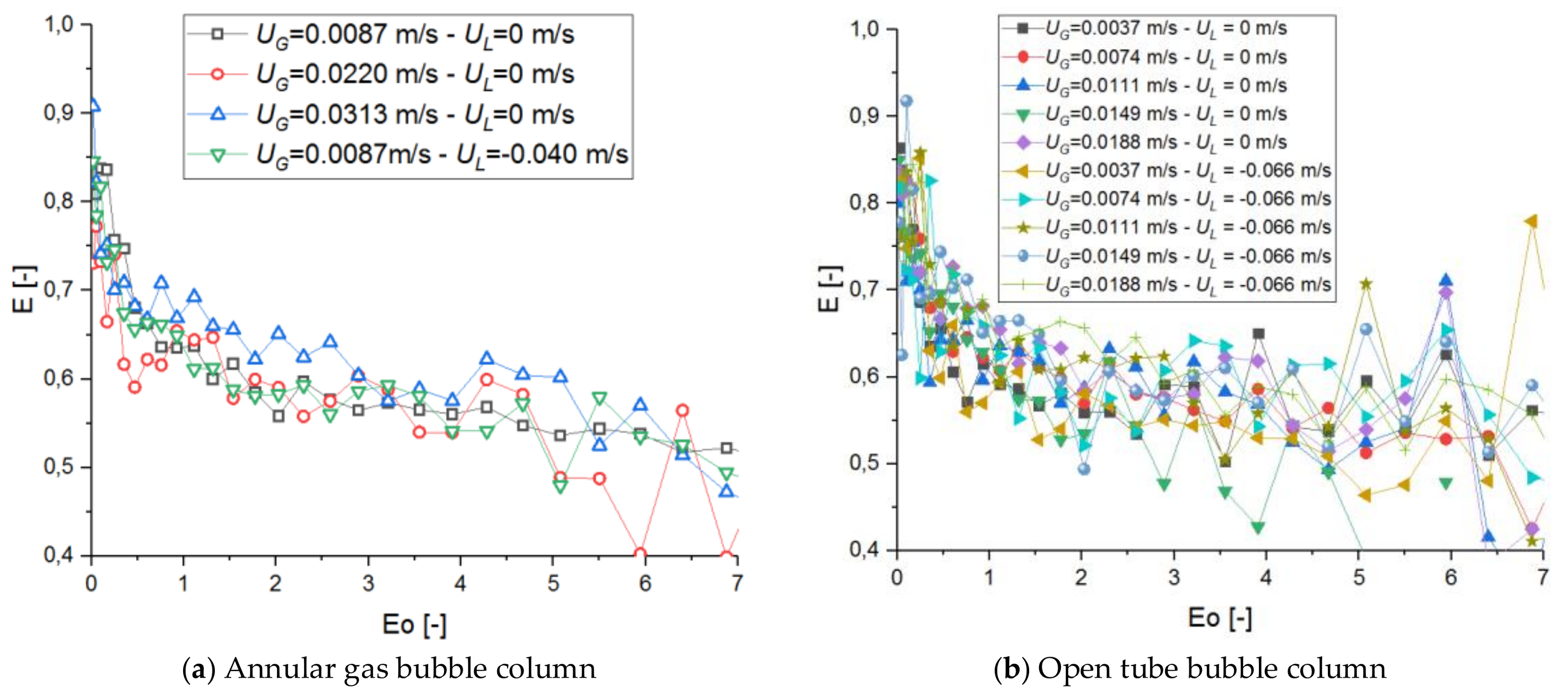
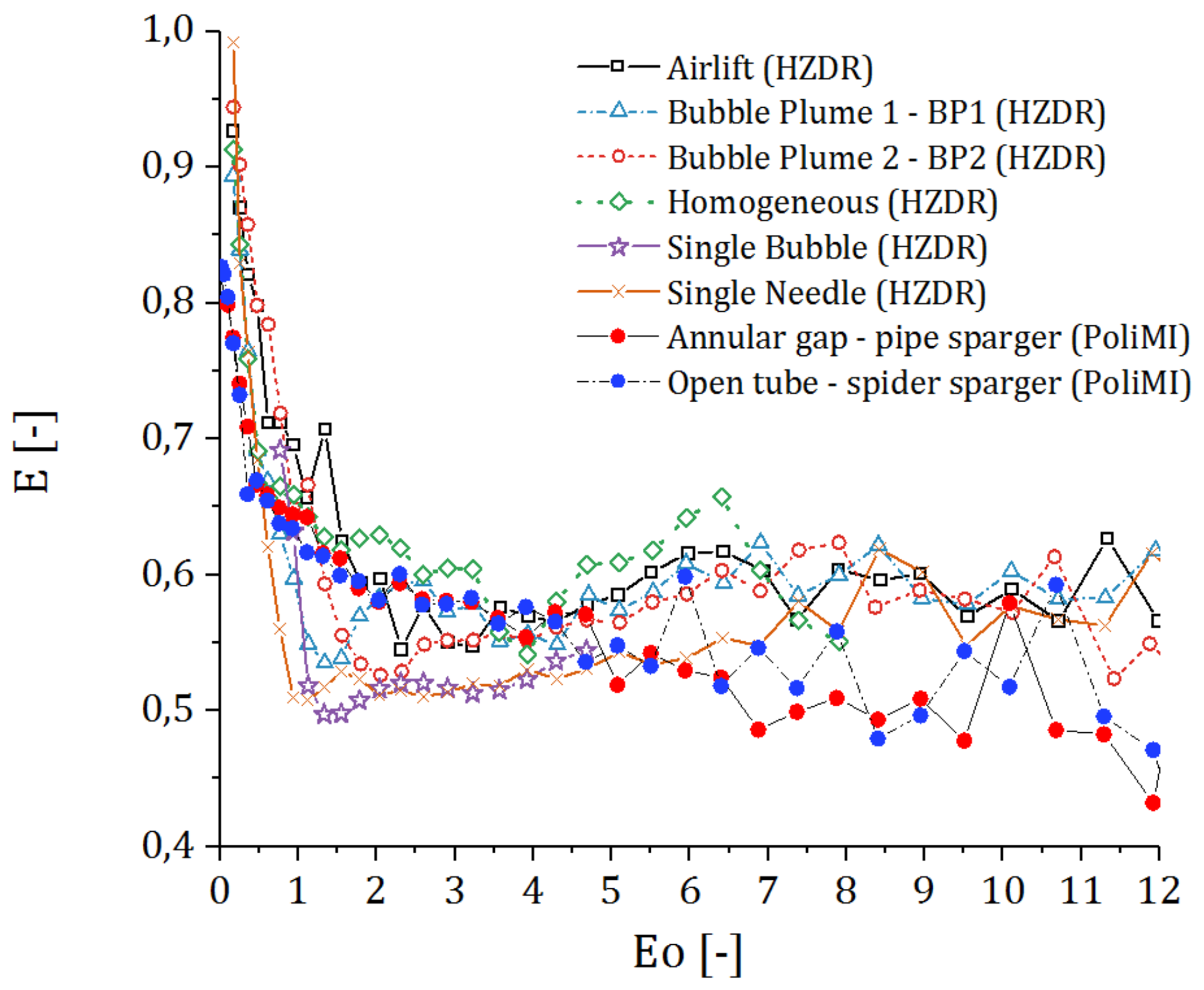
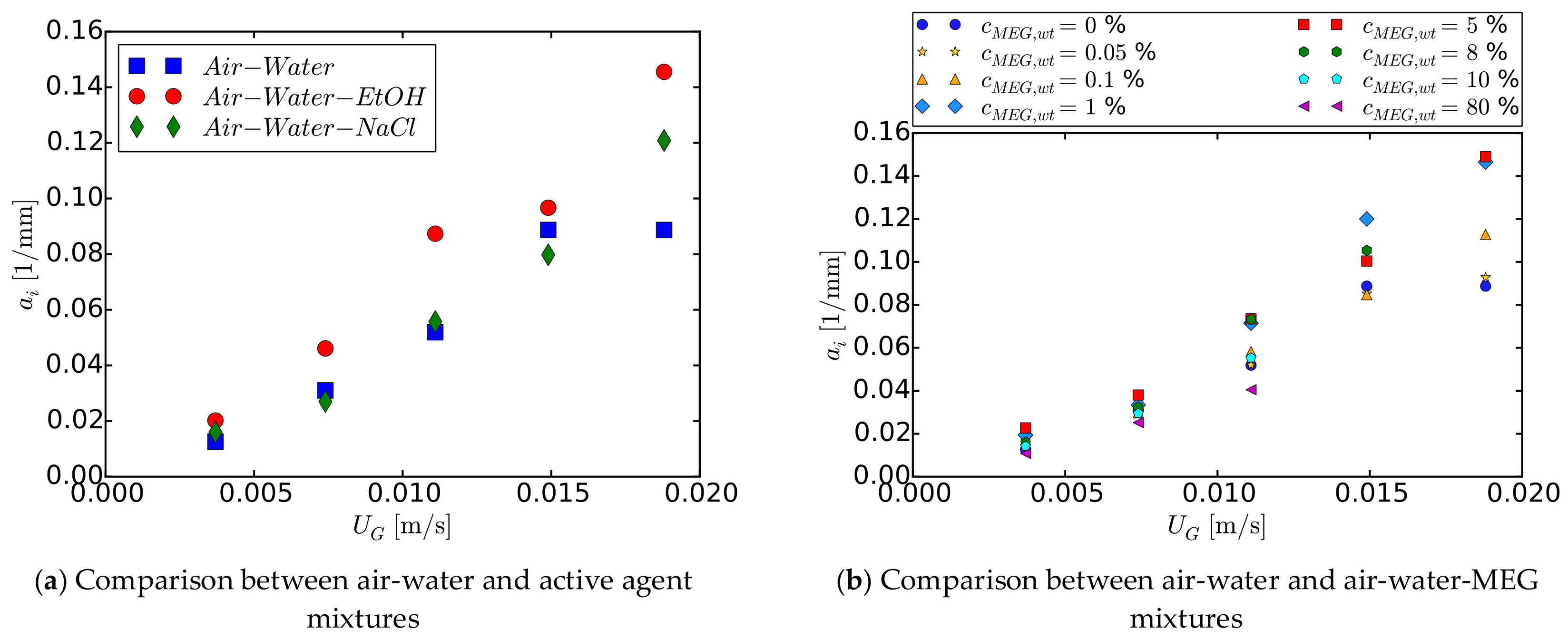
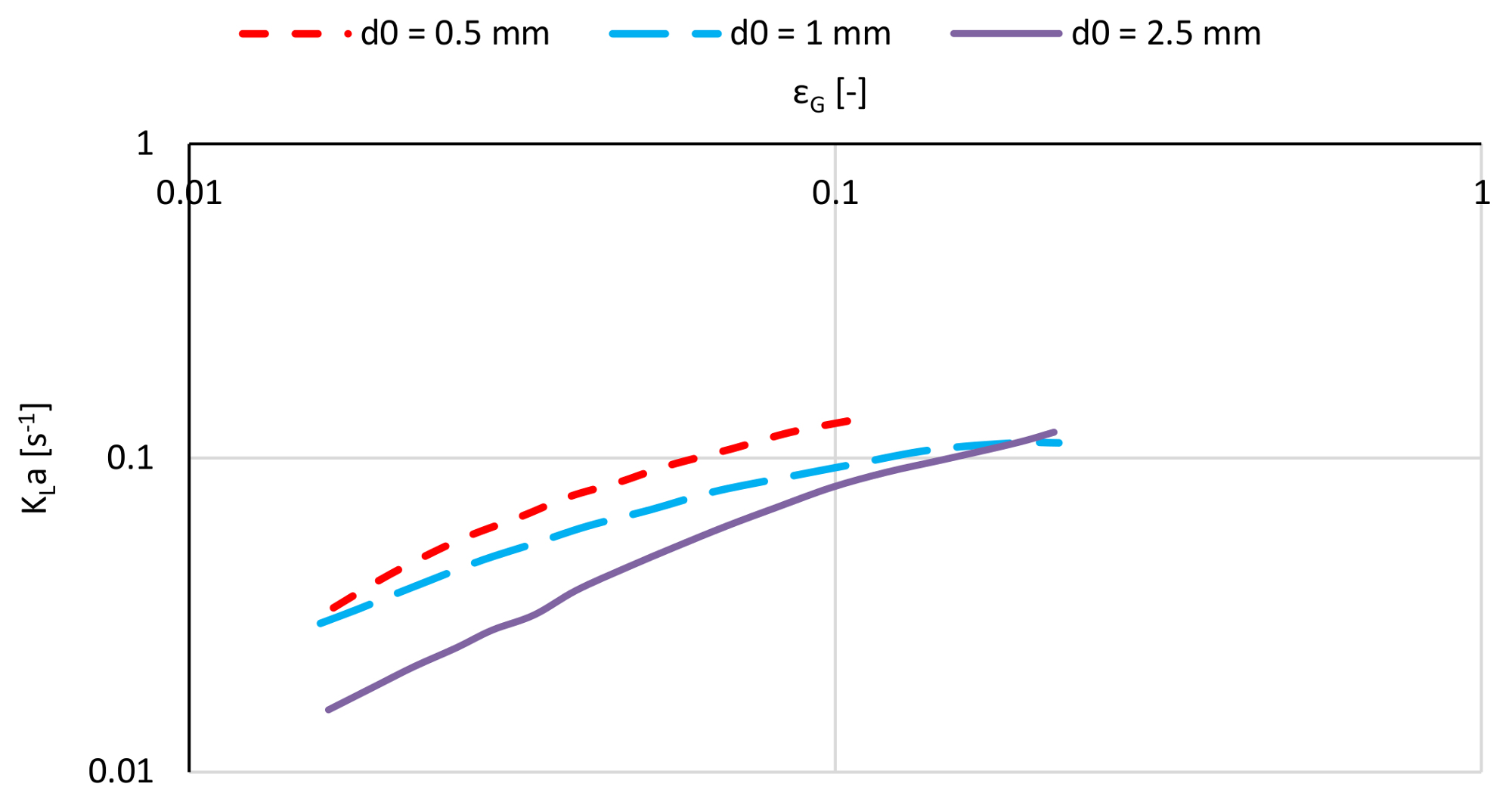
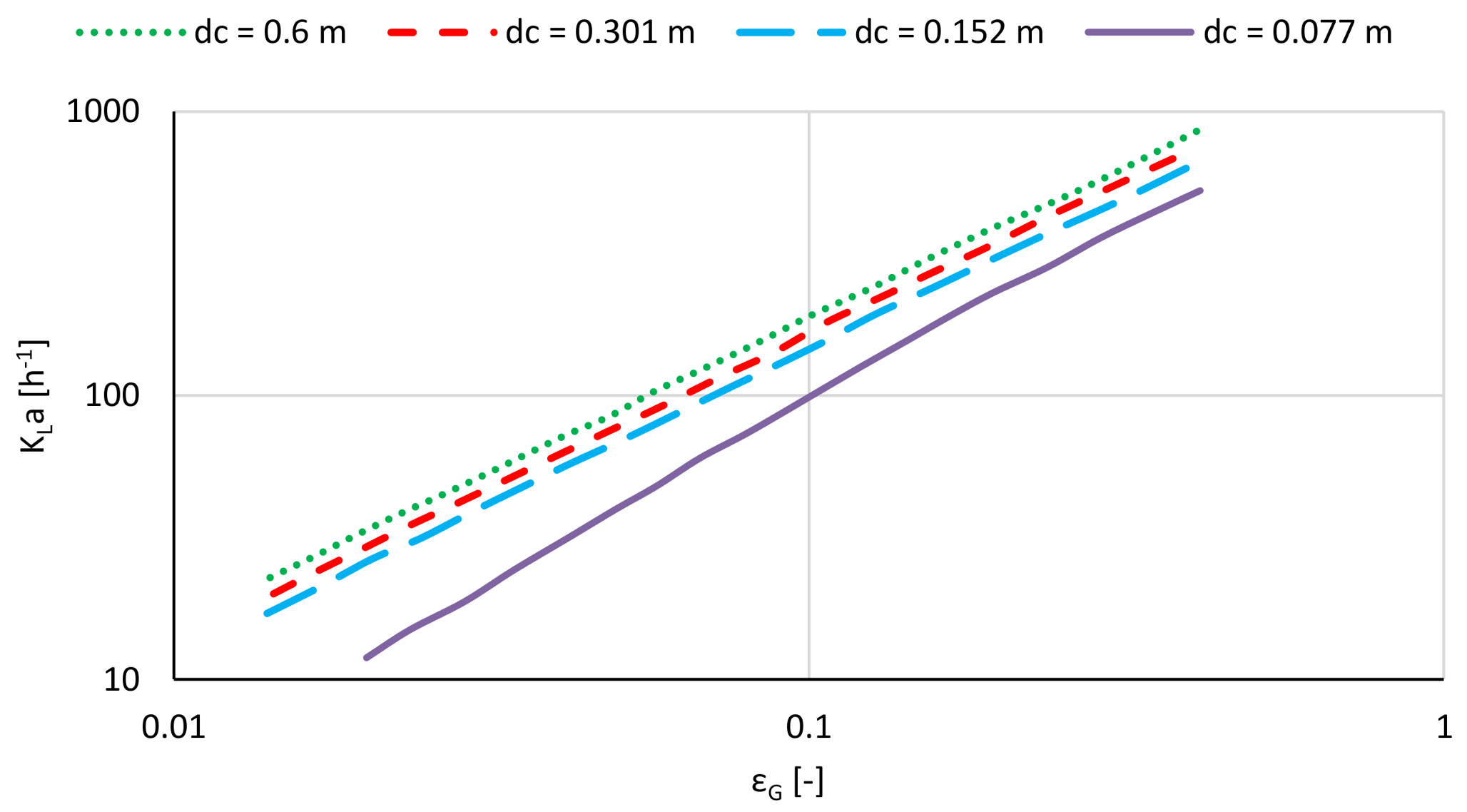
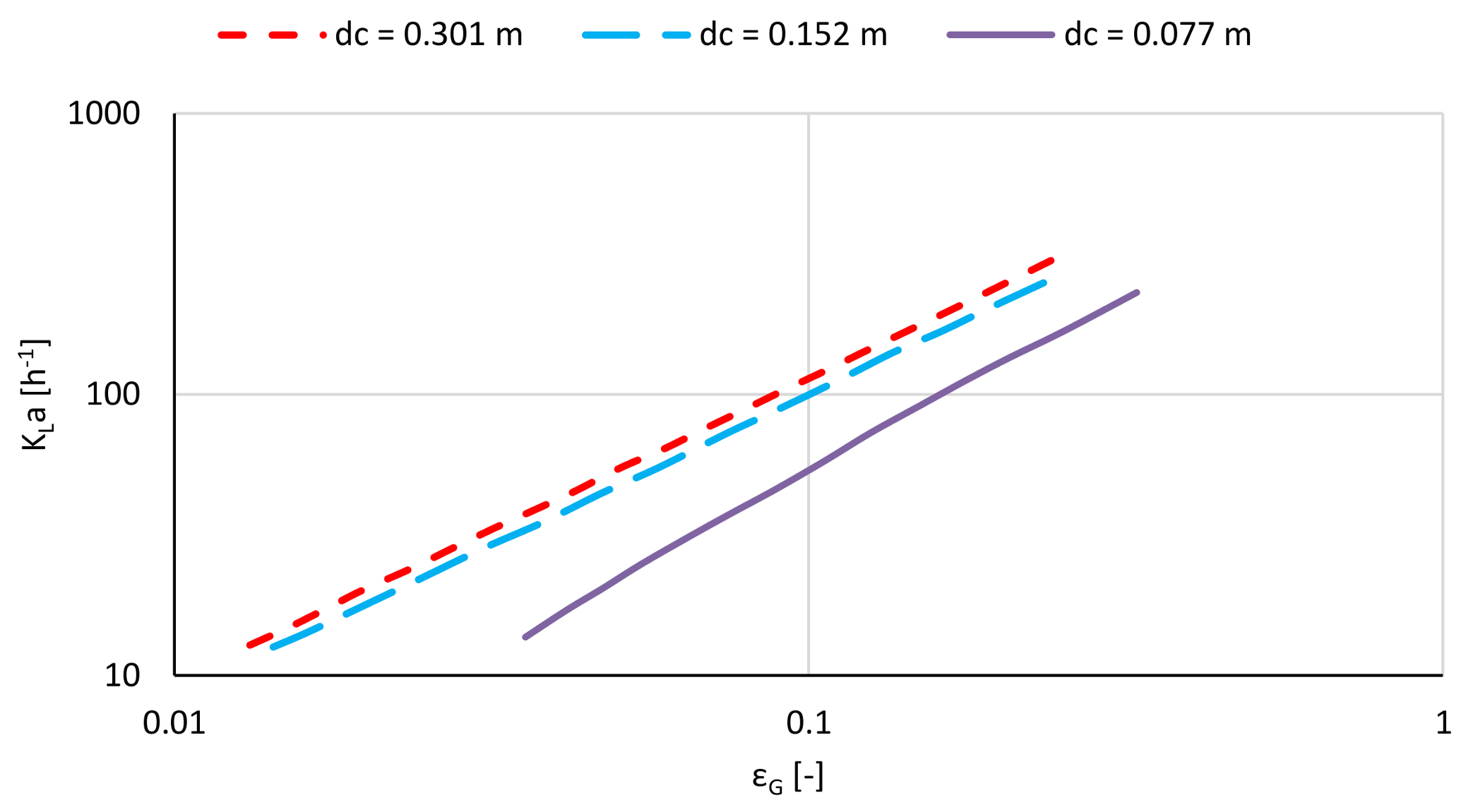
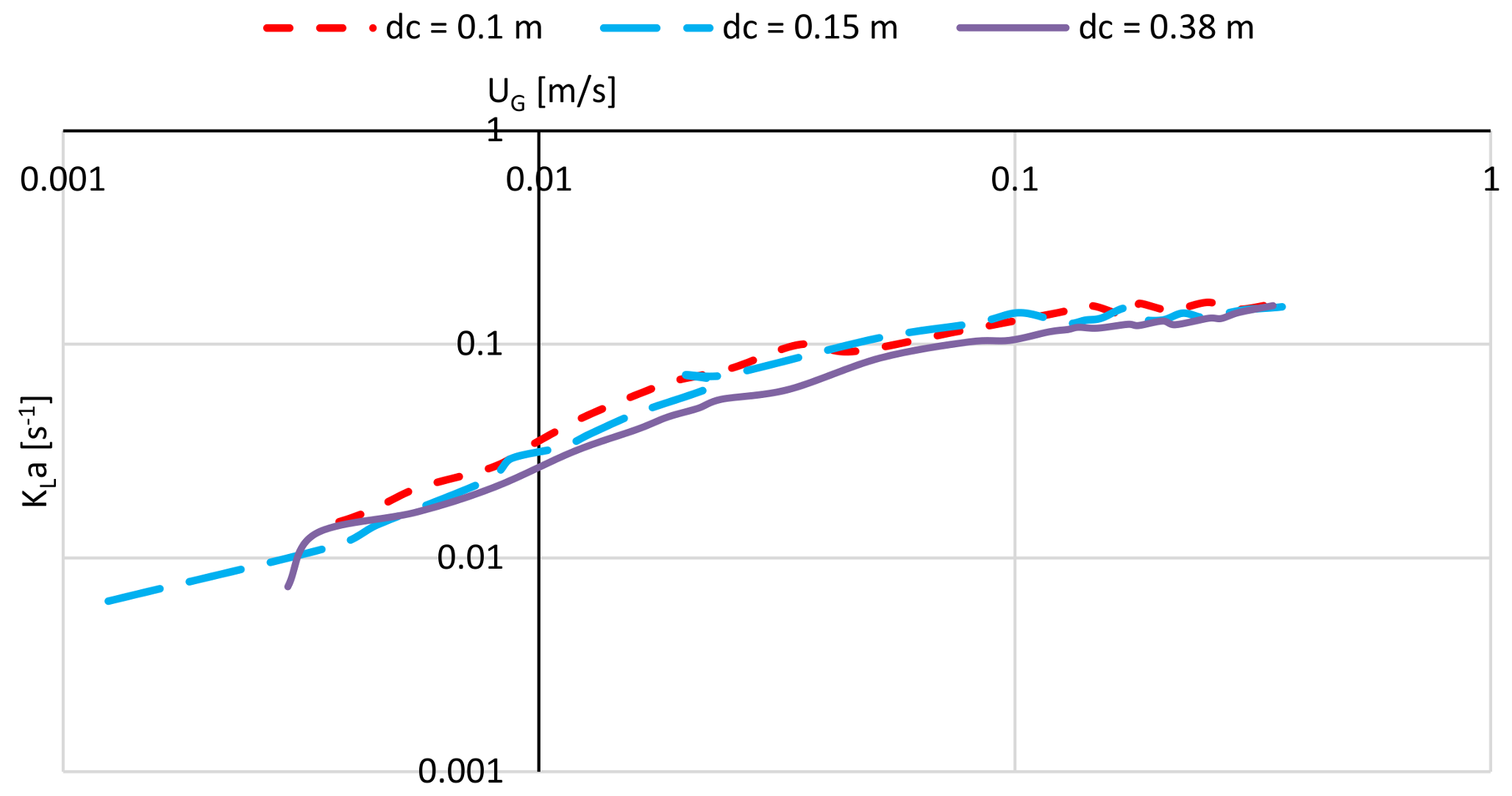
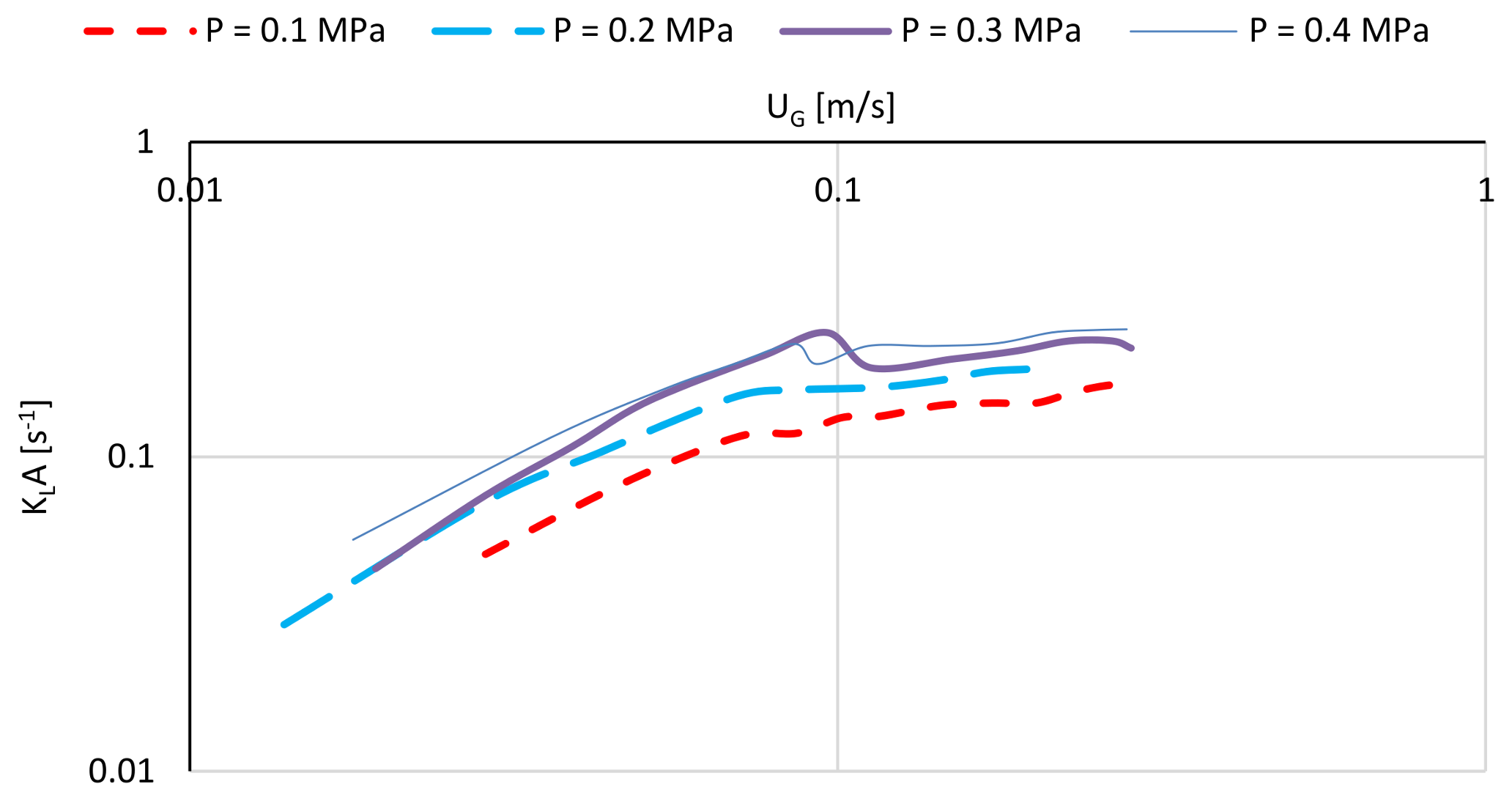
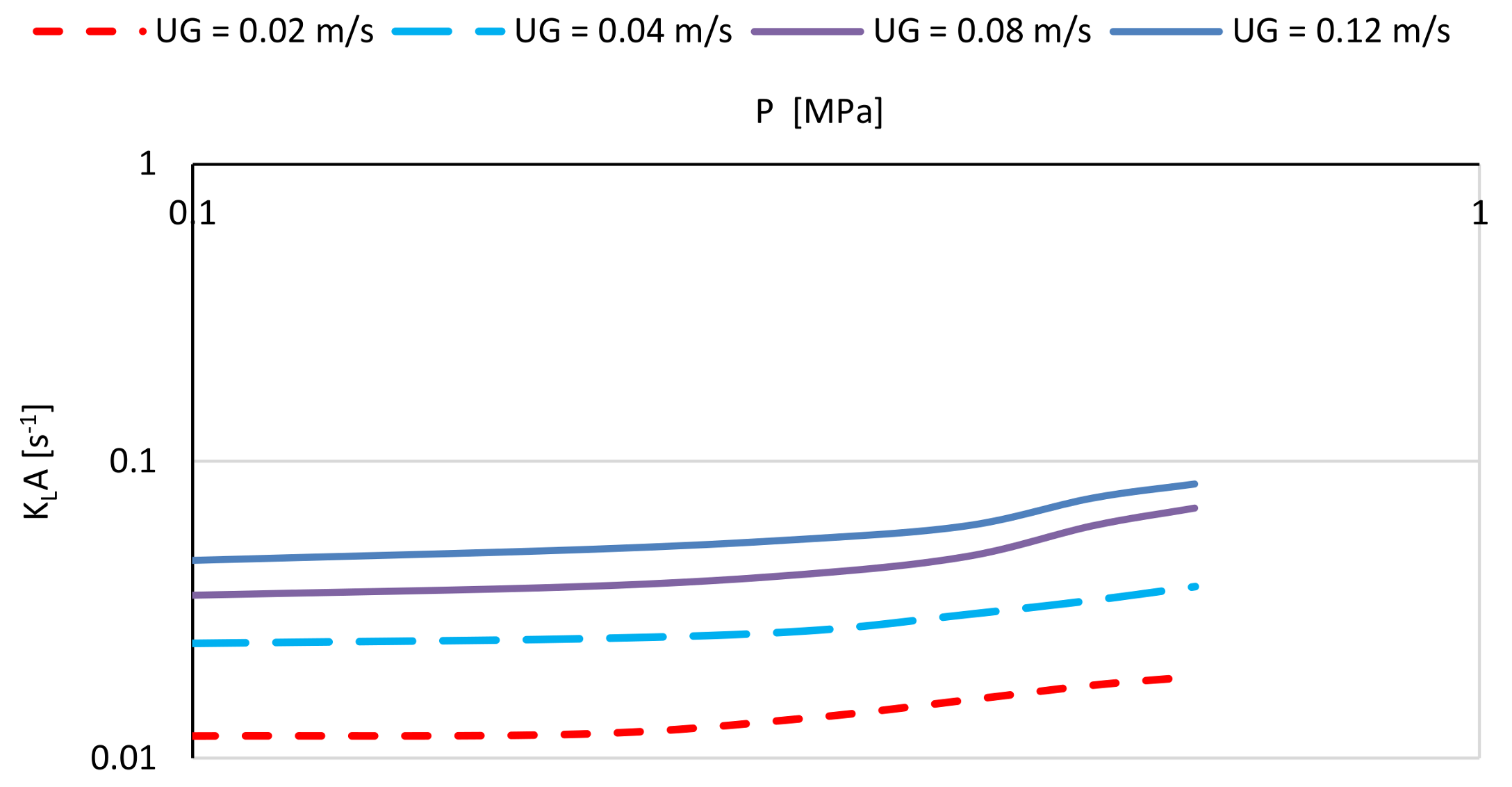
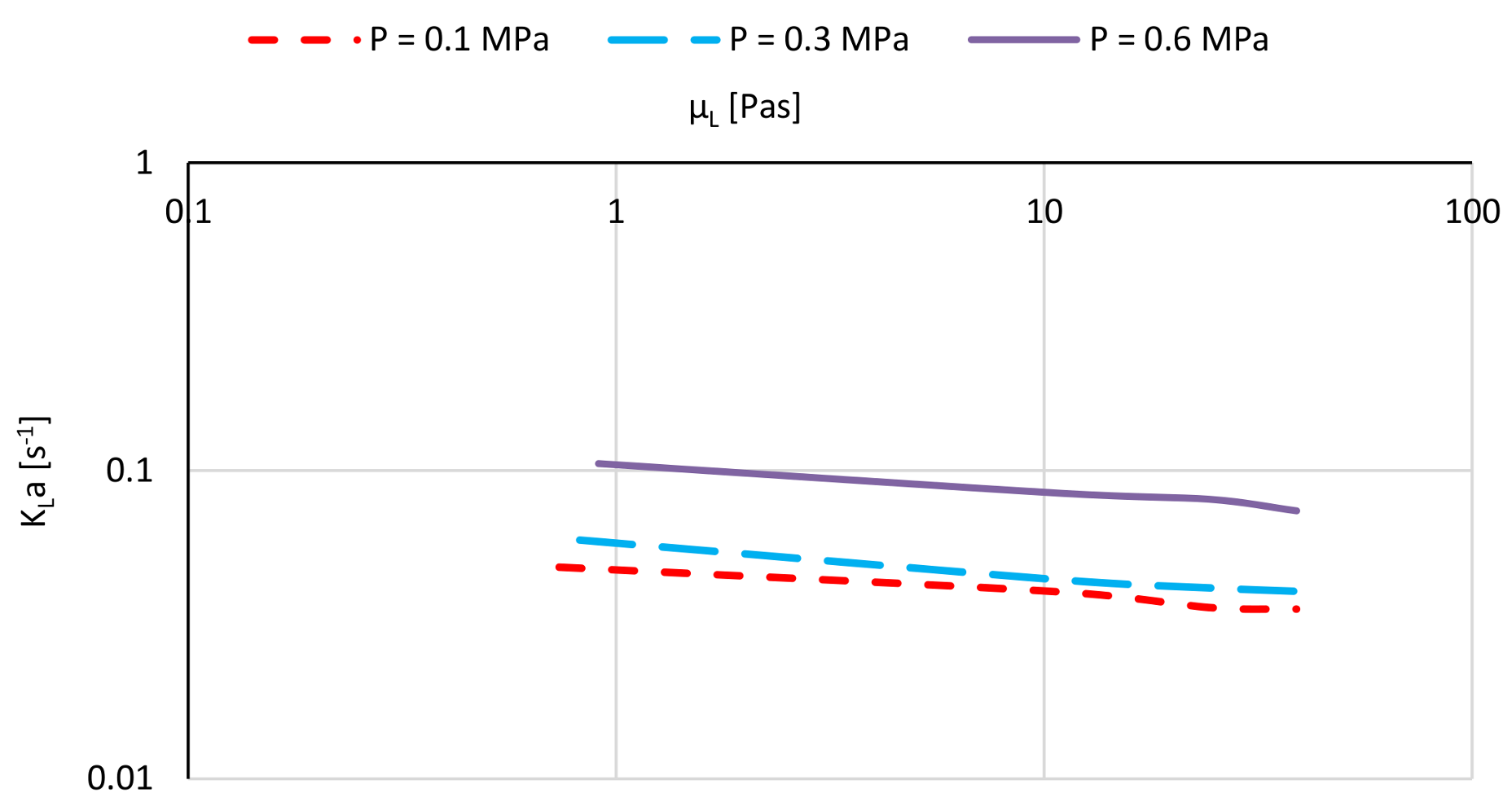
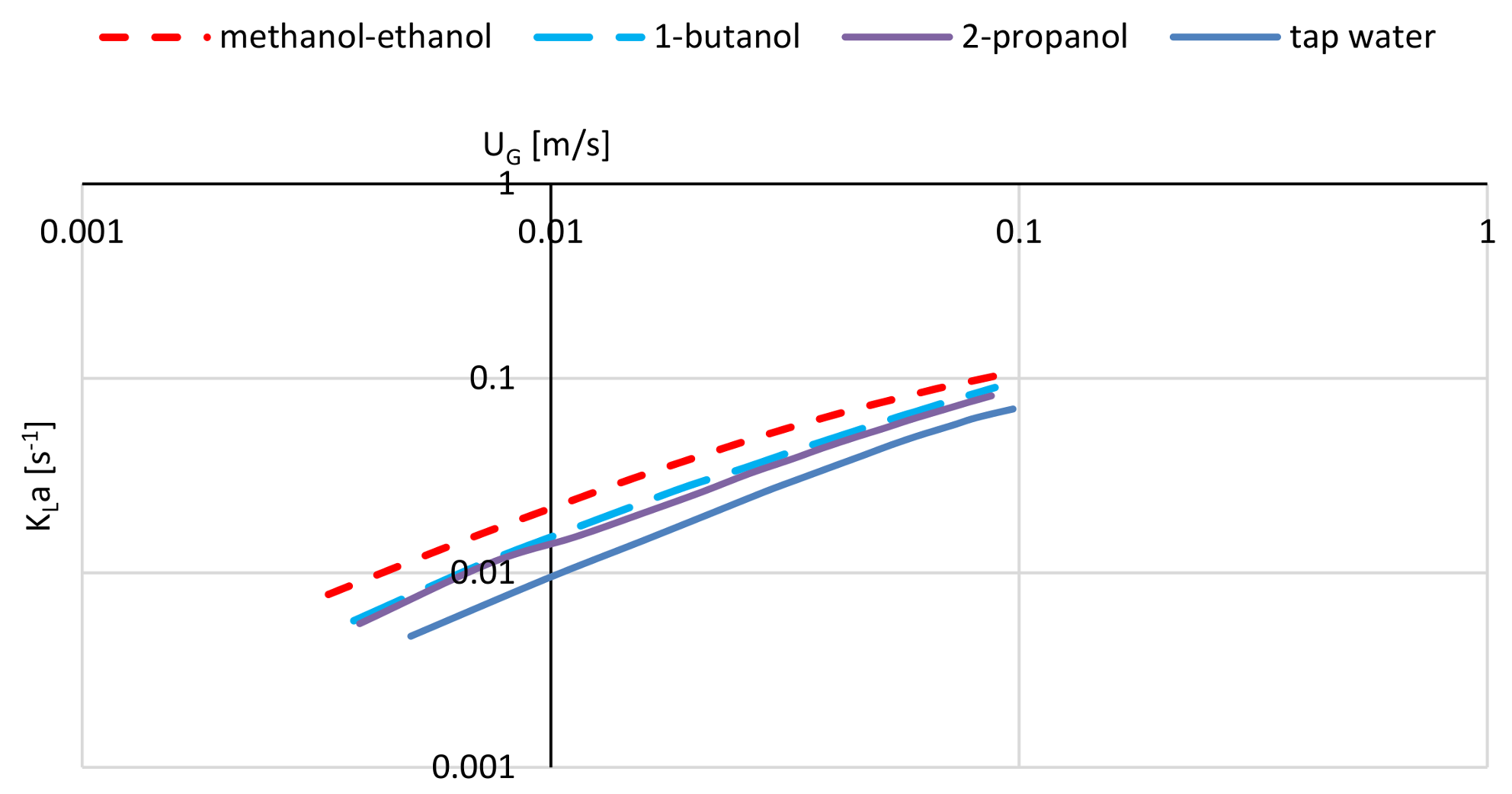
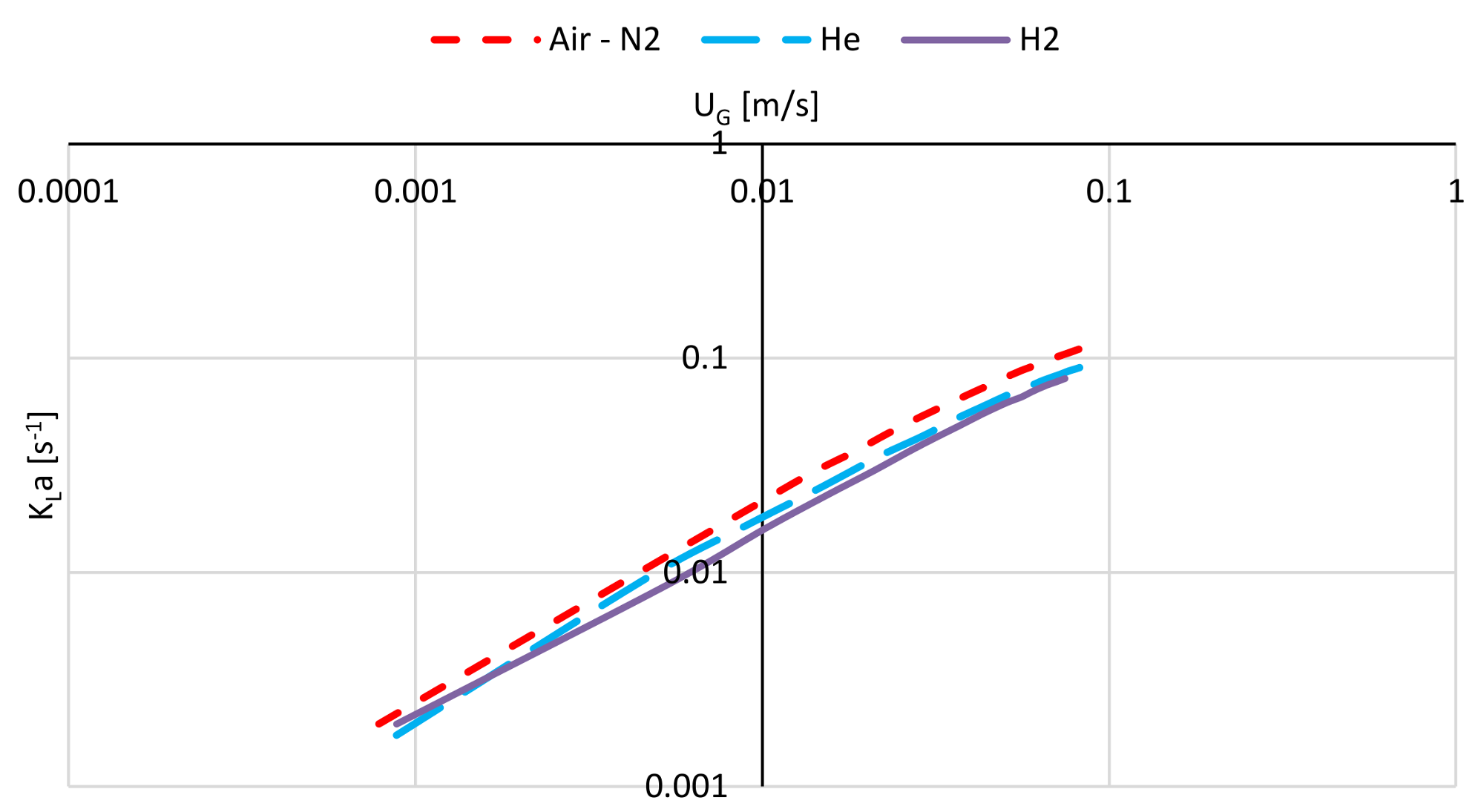
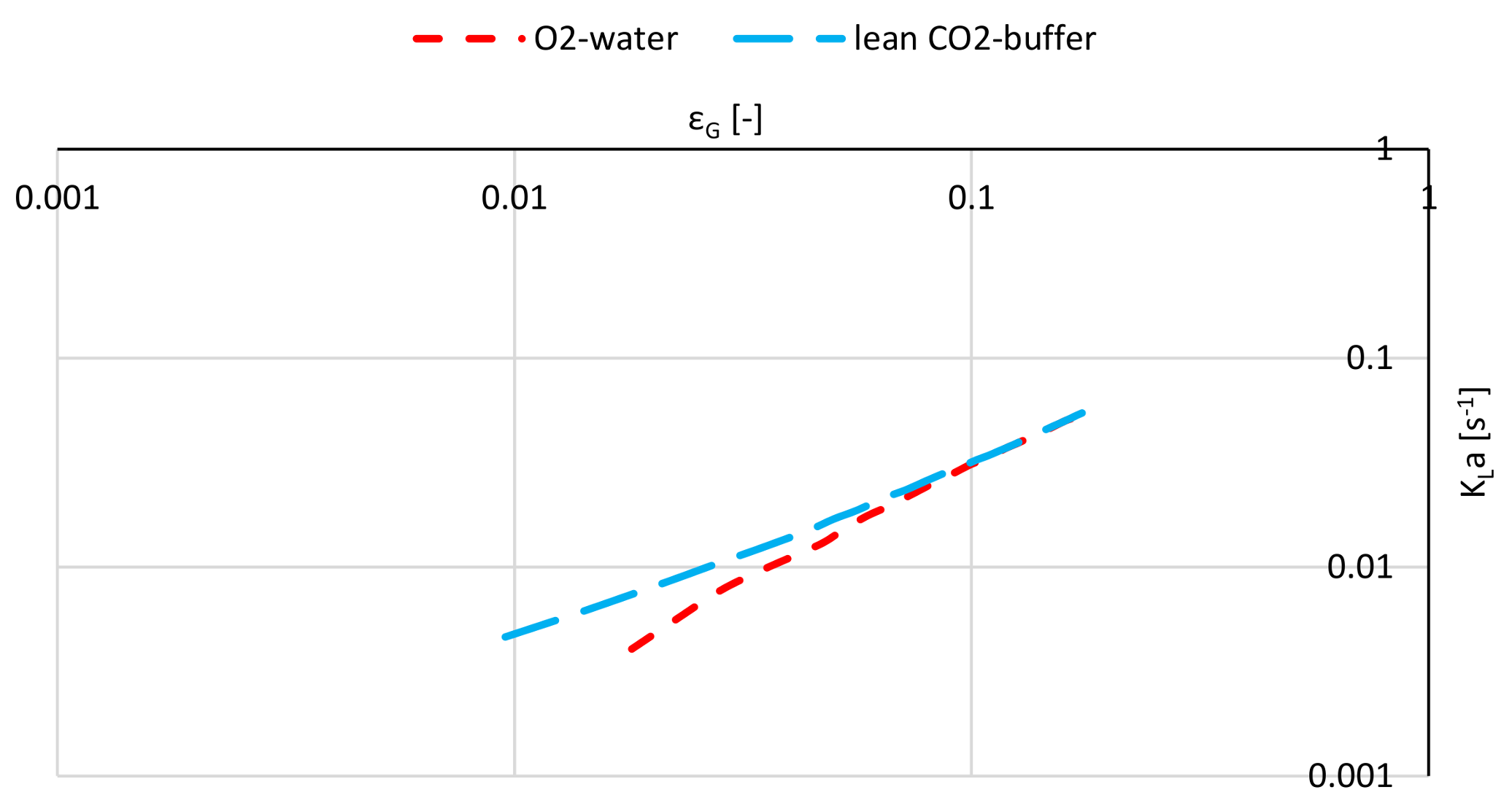
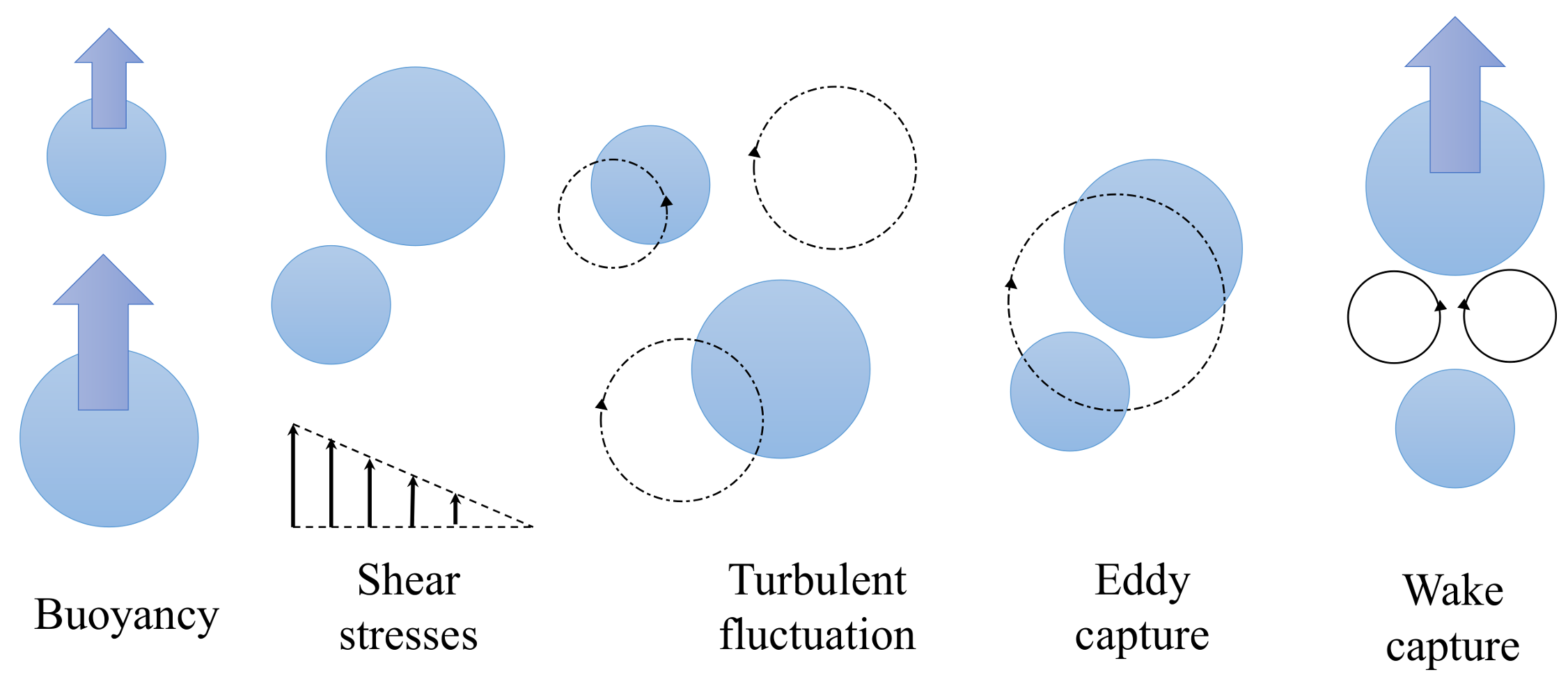

| Code | Reference | dc [m] | Aspect Ratio [-] | Sparger |
|---|---|---|---|---|
| R1 | [46] | 0.24 | 22.1 | Spider Sparger—d0 = 1–3.5 mm |
| R2 | [105] | 0.46 | 6.63 | Ring Sparger—d0 = 0.5 mm |
| R3 | [105] | 1.07 | 2.85 | Ring Sparger—d0 = 0.76 mm |
| R4 | [47] | 0.152 | 26.32 | Single Hole—d0 = 5 mm |
| R5 | [49] | 0.05 | 30 | Single Nozzle—d0 = 5 5 mm |
| R6 | [49] | 0.05 | 30 | Multiple Nozzle—d0 = 0.65 mm |
| R7 | [106] | 0.2 | 4 | Single Nozzle—d0 = 6 mm |
| R8 | [106] | 0.2 | 4 | Ring Sparger—d0 = 1 mm |
| R9 | [106] | 0.6 | 1 | Ring Sparger—d0 = 2 mm |
| R10 | [106] | 0.6 | 1 | Ring Sparger—d0 = 3 mm |
| R11 | [107] | 0.073 | 13 | Single Nozzle—d0 = 1.5–2.7–5.7 mm |
| R12 | [108] | 0.3 | 16.7 | Perforated Plate—d0 = 1.5 mm |
| R13 | [108] | 0.3 | 16.7 | Single Sparger—d0 = 25.4 mm |
| R14 | [109] | 0.23 | 5.3 | Multiple Nozzle—d0 = 1 mm |
| Code | Reference | dc [m] | Aspect Ratio [-] | Sparger |
|---|---|---|---|---|
| R1 | [46] | 0.24 | 22.1 | Spider Sparger—d0 = 1–3.5 mm |
| R2 | [52] | 0.24—Annular gap | 22.1 | Pipe Sparger—d0 = 3.5 mm |
| R3 | [47] | 0.152 | 26.32 | Single Hole—d0 = 5 mm |
| R4 | [110] | 0.305 | - | Single Hole—d0 = 1.66 mm |
| R5 | [110] | 0.127 | - | Single Hole—d0 = 1.66 mm |
| R6 | [49] | 0.05 | 30 | Single Nozzle—d0 = 5 5 mm |
| R7 | [111] | 0.385 | 7 | Sieve Plate—d0 = 1 mm |
| R8 | [111] | 0.385 | 7 | Sieve Plate—d0 = 1.5 mm |
| R9 | [111] | 0.385 | 7 | Sieve Plate—d0 = 3.0 mm |
| R10 | [111] | 0.385 | 7 | Sieve Plate—d0 = 6.0 mm |
| R11 | [112] | 0.0707 | 12–33 | Single Nozzle—d0 = 2.25–7 mm |
| R12 | [112] | 0.30 | 4–6.3 | Single Nozzle—d0 = 1.48–3.00 mm |
| R13 | [108] | 0.3 | 16.7 | Single Sparger—d0 = 25.4 mm |
| R14 | [18] | 0.3 | 12 | Single Sparger—d0 = 1 mm |
| Code | Description |
|---|---|
| R0 | cEtOH,wt = 0%—Air-water gas hold-up curve |
| R1 | cEtOH,wt = 0.3%—Gas hold-up curve measured after waiting 30 s for every gas hold-up measurement point from low to high gas flow rate: run 1. |
| R2 | cEtOH,wt = 0.3%—Gas hold-up curve measured after waiting 30 s for every gas hold-up measurement point from low to high gas flow rate: run 2. |
| R3 | cEtOH,wt = 0.3%—Gas hold-up curve measured after waiting 120 s for every gas hold-up measurement point from high to low gas flow rate. |
| R4 | cEtOH,wt = 0.3%—Gas holdup curve measured after waiting 120 s for every gas hold-up measurement point after each flow rate increase. |
| R5 | cEtOH,wt = 0.3%—Gas hold-up curve when foaming phenomenon was observed: run 1 |
| R6 | cEtOH,wt = 0.3%—Gas hold-up curve when foaming phenomenon was observed: run 2 |
| R7 | cEtOH,wt = 0.3%—Gas hold-up curve when foaming phenomenon was observed: run 3 |
| Reference | Bubble Column Design | Gas and Liquid Phases | Phase Properties |
|---|---|---|---|
| Hughmark, 1967 [133] | Multi-orifice gas sparger dc > 0.1 m UG = 0.004–0.450 m/s | Air-Water; Air-Na2CO3 aq. Soln.; Air-Kerosene; Air-Light oil; Ai-Glycerol aq. soln.; Air-ZnCl2 aq. soln.; Air-Na2SO3 aq. soln. | ρL = 0.78–1.7 [g/cm3] μL = 0.0009–0.152 [Pa∙s] σ = 0.025–0.076 [N/m] |
| Kato et al. 1972 [134] | dc = 0.066–0.214 m Hc = 2.01–4.05 m UG = 0–0.30 m/s UL = 0–0.015 m/s | Air-Water | |
| Kato and Nishiwaki, 1972 [193] | Single-hole gas sparger d0 = 0.005 m dc = 0.15–0.60 m UG = 0.005–0.42 m/s | Air-Water; Air-Glycol aq. soln.; Air-Methanol; Air-CCl4; Air-Na2SO3 aq. soln. (0.15 M); Air-NaCl aq. soln. (0.03 M, 0.07 M, 0.15 M, 0.6 M, 1 M): O2-Water; He-Water; CO2-Water | ρL = 0.79–1.59 [g/cm3] μL = 0.00058–0.0211 [Pa∙s] σ = 0.022–0.0742 [N/m] |
| Akita and Yoshida, 1973 [47] | d0 = 0.0013–0.00362 m dc = 0.10 and 0.19 m Hc = 1.5 and 2.4 m UG = 0.043–0.338 m/s | Air-Water; Air-8.0 wt% Methanol aq. soln.; Air-15.0 wt% Methanol aq. soln.; Air-53.0 wt% Methanol aq. soln.; Air-35.0 wt% Cane sugar aq. soln.; Air-50.0 wt% Cane sugar aq. soln. | ρL = 0.91–1.24 [g/cm3] μL = 0.001–0.0192 [Pa∙s] σ = 0.0382–0.0755 [N/m] |
| Hikita and Kikukawa, 1974 [194] (as reported by [24]). | Perforated plates and sintered plates d0 = 0.3 and 0.005 m dc = 0.0756–0.61 m Hc = 0.02–3.5 m UG = 0.01–0.08 m/s | Air used as gas. Liquids: water, methanol, iso- and n-propanol, iso- and n-butanol, carbon tetrachloride, dichloroethane, methyl ethyl ketone, ethyl acetate, ethylene glycol, benzene | ρL = 0.8–1.6 [g/cm3] μL = 0.00043–0.02 [Pa∙s] σ = 0.0214–0.0728 [N/m] K = 8×104–5×1010 |
| Gestrich and Rähse, 1975 [195] | Perforated plate d0 = 0.0087–0.0309 m dc = 0.05–0.10 m UG = 0.002–0.14 m/s | Air-Water; Air-Glycerol aq. soln. (40%); Air-Kerosene Reacting system: Air/CO2-aq. NaOH (2M) | ρL = 0.78–1.11 [g/cm3] μL = 0.00088–0.0115 [Pa∙s] σ = 0.0312–0.072 [N/m] |
| Kumar et al., 1976 [196] | Perforated plates d0 = 0.0005 and 0.001 m dc = 0.10 m Hc < 2 m UG = 0.01–0.20 m/s | Air used as gas; Liquids: n-octanol; tetrabromomethane, glycol; 1,3-butanediol. | ρL = 0.8–2.98 [g/cm3] μL = (20–100)∙10−3 [Pa∙s] σ = 21.7–72 [dyn/cm] |
| Mersmann,1978 [199] | Multi-nozzles d0 = 0.030 m dc = 5.50 m H0 = 7.0 m (liquid height) UG = 0.024–0.128 m/s | Air-Water | |
| Koide et al., 1979 [135] | Downflow bubble column | Gases: Air, Ar, H2, CCl2F2. Liquids: Water, CCl4, Glycerol aq. soln., CMC (Carboxymethyl cellulose). | I = 148–336 [kg/m2∙s] ε* = 0.003–0.24 ρL/ρG = 184–5340 μL/μG = 37–2220 σ = 0.055–0.07 [N/m] |
| Friedel et al., 1980 [197] | Single-nozzle gas sparger d0 = 0.011 m dc = 0.10 m Hc = 1.5 m UG = 0.042–0.38 m | Pure liquids or non-electrolyte solutions: Air-Water; Air-30 wt% Sucrose; Air-50 wt% Sucrose; Air-Methanol; Air-53 wt% Methanol; Air-nButanol; Air-Aniline; Air-7 wt% iButanol; H2–Water; CO2-Water; CH4-Water; C3H8-Water; H2+N2 (1:1)-Water; H2+N2 (5:1)-Water Electrolyte solutions: Air-(0.1–5.0 M) NaCl; Air-(0.1–1.5 M) Na2SO4; Air-(0.1–2.0 M) CaCl2; Air-0.4 M MgCl2; Air-(0.1–1.0 M) AlCl3; Air-(0.1–3.0 M) KCl; Air-0.5 M K2SO4; Air-(0.16 M, 0.5 M) K3PO4; Air-0.5 M KNO3 | Pure liquids or non-electrolyte solutions ρL = 0.794–1.24 [g/cm3] ρG = (0.0837–1.84) 10−3 [g/cm3] μL = (0.658–17.8)∙10−3 [Pa∙s] μG = (0.008–0.0181) ∙10−3 [Pa∙s] σ = 0.0229–0.0759 [N/m] Electrolyte solutions ρL = 1.01–1.17 [g/cm3] μL = 0.009–0.00187 [Pa∙s] σ = 0.0719–0.0796 [N/m] |
| Hikita et al., 1980 [80] | Porous plate dc = 0.153 m Hc = 2.5 m | Air-Distilled water | |
| Iordache and Muntean, 1981 [202] | Gas distributor: perforated plate (749 holes,) d0 = 0.00166 m dc = 0.305 m Hc = 2.44 m | Glycerine systems CMC solutions | Glycerine systems ρL = 1.010–1.249 [g/cm3] μL = 0.0013–0.246 [Pa∙s] CMC solutions K = 0.0018–2.570 n = 0.495–1.0 ρL = 0.996–1.008 [g/cm3] |
| Godbole et al., 1982 [152] | Single nozzle (d0 = 1.5, 2.7 and 5.7 [mm]) dc = 7.3 [cm] Hc = 0.95 [m] | Water-N2; Water-He; Water-CO2;; Methanol-N2; NaNO3-N2; NaNO3-He; LiCl-KCl-N2; LiCl-KCl-He | ρL = 0.788–1.888 [g/cm3] μL=(0.45–3.65)×10−3 [Pa∙s] σ = 0.0215–0.13 [N/m] |
| Sada et al., 1984 [107] | Sintered glass disc d0 = 0.10 m dc = 0.10 m Hc = 1.5 m UG = 0.001–0.045 m/s | Air-water; Air-NaCl-water (NaCl = 0.25 M); Air-CuCl2-water (CuCl2 = 0.25 M) T = 303–353 [K] | |
| Grover et al., 1986 [78] | dc = 0.30 m | Air-Wwater; Air-Varsol(*); Air-trichloroethylene (*) Varsol DX 3641 is a light hydrocarbon oil available from ESSO Chemicals. | ρL = 0.788–1.450 [g/cm3] μL = (0.552–1.452) × 10−3 [Pa∙s] σ = 0.0283–0.0720 [N/m] |
| Reilly et al., 1986 [108] | 40-L bubble column Perforated plate (20 holes) d0 = 0.001 m dc = 0.23 m Hc = 1.22 m 1000-L pilot plant fermenter Ring sparger (100 holes) d0 = 0.003 m dc = 0.76 m Hc = 3.21 m | Newtonian liquids: water, glycerine; dextrose aqueous solution; three fermentation media (glucose+mineral salt, molasses+mineral salt, Alpha-floc+mineral salt) Non-Newtonian fluids: Carboxy-methyl cellulose (CMC7H4, Hercules Inc.),; carboxypolymethylene (Carbopol 941, Goodrich Chemical Co.); and polyacrylamide (Separan NP10, Dow Chemical Co.) | Newtonian liquids ρL = 0.991–1.009 [g/cm3] Non-Newtonian fluids ρL = 0.991–0.993 [g/cm3] |
| Kawase and Moo-Young, 1987 [207] | Single tube (d0 = 0.003 m); ring gas sparger (29 holes, d0 = 0.002 m; ring gas sparger (56 holes, d0 = 0.002 m) dc = 0.06; 0.14; 0.30 m Hc = 1.8; 2.2; 2.0 m | Liquids: glycerol, CMC, PAA and Xanthan. | ρL = 0.999–1.248 [g/cm3] σ = 0.0495–0.0720 [N/m] K = 3.2–9780 n = 0.180–1 |
| Schumpe and Deckwer, 1987 [203] | Co-current and counter-current flow Single nozzle gas sparger d0 = 0.010 m d0 = 0.10 m Hc = 1.05 m UG = 0.01–0.16 m/s UL = 0.07 m/s | Air-Water; Air-Alcohol; Air-5%NaCl soln.T = 25–96.56 [°C] | ρL = 0.7483–1.0268 [g/cm3] μL = (0.2946–0.8937) × 10−3 [Pa∙s] σ = 0.01877–0.07197 [N/m] |
| Zou et al., 1988 [209] | Ejector gas sparger dc = 0.30 m Hc = 1.46 m | Coalescent batches: distilled water; distilled water & OCENOL; 3% SOKRAT & OCENOL (SOKRAT is a commercial thickener consisting of water and a soluble liquid polymer based on acrylonitrile and acrylic acid in a ratio of 2:1. OCEANOL is a foam breaker consisting of a mixture of saturated and unsaturated alcohol from the fraction C16–C18.) (*); 6% SOKRAT & OCENOL; 10% SOKRAT & OCENOL; 58% Sucrose Non-coalescent batches: 0.5% SOKRAT; 3% SOKRAT ; 6% SOKRAT; 10% SOKRAT | Coalescent batches ρL = 0.995–1.270 [g/cm3] μL = (0.7–25.6) × 10−3 [Pa∙s] σ = 0.0335–0.0654 [N/m] Non-coalescent batches ρL = 0.998–1.011 [g/cm3] μL = (1.5–24.4) × 10−3 [Pa∙s] σ = 0.0487–0.0645 [N/m] |
| Elgozali et al., 2002 [198] | Sieve plate gas sparger (25 holes, d0 = 0.005 m and 75 holes, d0 = 0.003 m) dc = 0.09 m Hc = 0.61 m | Air used as gas. Pure liquids: 2-propanol Binary mixtures: 2-propanol/methanol (20 mol% 2-propanol); 2-propanol/water (15 mol% 2-propanol); ethanol/water; ethylene glycol/water |
| Variable | All Batches | Coalescent Batches | Non-Coalescent Batches |
|---|---|---|---|
| K | (4.5 ± 5.9) × 109 | (1.92 ± 0.74) × 106 | (5.30 ± 11.70) × 106 |
| a | 0.67 ± 0.04 | 0.72 ± 0.01 | 0.44 ± 0.01 |
| b | 0.22 ± 0.02 | 0.14 ± 0.01 | 0.13 ± 0.02 |
| c | 1.95 ± 0.12 | 1.26 ± 0.04 | 1.41 ± 0.20 |
| T [°C] | 40 | 60 | 70 | 80 | 85 | 90 | 95 |
|---|---|---|---|---|---|---|---|
| f | 1.210 | 1.2468 | 1.1804 | 0.1607 | 0.1215 | 0.1505 | 0.2634 |
| cwt [%] | z1 | z2 | z3 | k1 | k2 | z4 | z5 |
|---|---|---|---|---|---|---|---|
| Air-Water | |||||||
| 0 | −0.657 | 0.001 | 1.00 | 0.690 | −0.251 | 0.750 | −0.300 |
| Air-Water-MEG | |||||||
| 0.05 | −0.570 | 0.001 | 1.00 | 0.691 | −0.300 | 0.670 | −0.280 |
| 0.1 | −0.550 | 0.001 | 1.00 | 0.701 | −0.294 | 0.692 | −0.280 |
| 0.5 | −0.666 | 0.001 | 1.00 | 0.674 | −0.308 | 0.666 | −0.300 |
| 1 | −0.560 | 0.001 | 1.00 | 0.689 | −0.321 | 0.667 | −0.300 |
| 5 | −0.420 | 0.001 | 1.00 | 0.730 | −0.295 | 0.735 | −0.300 |
| 8 | −0.340 | 0.001 | 1.00 | 0.744 | −0.300 | 0.745 | −0.300 |
| 10 | −0.625 | 0.001 | 1.00 | 0.693 | −0.385 | 0.710 | −0.300 |
| 80 | −0.340 | 0.001 | 1.00 | 0.730 | −0.237 | 0.703 | −0.300 |
| Air-Water-EtOH | |||||||
| 0.05 | −0.282 | 0.001 | 1.00 | 0.844 | −0.140 | 0.808 | −0.100 |
| Air-Water-NaCl | |||||||
| 0.4 (c/ct = 0.48) | −0.605 | 0.001 | 1.00 | 0.697 | −0.286 | 0.713 | −0.300 |
| 1 (c/ct = 1.17) | −0.485 | 0.001 | 1.00 | 0.722 | −0.284 | 0.738 | −0.300 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Besagni, G.; Inzoli, F.; Ziegenhein, T. Two-Phase Bubble Columns: A Comprehensive Review. ChemEngineering 2018, 2, 13. https://doi.org/10.3390/chemengineering2020013
Besagni G, Inzoli F, Ziegenhein T. Two-Phase Bubble Columns: A Comprehensive Review. ChemEngineering. 2018; 2(2):13. https://doi.org/10.3390/chemengineering2020013
Chicago/Turabian StyleBesagni, Giorgio, Fabio Inzoli, and Thomas Ziegenhein. 2018. "Two-Phase Bubble Columns: A Comprehensive Review" ChemEngineering 2, no. 2: 13. https://doi.org/10.3390/chemengineering2020013
APA StyleBesagni, G., Inzoli, F., & Ziegenhein, T. (2018). Two-Phase Bubble Columns: A Comprehensive Review. ChemEngineering, 2(2), 13. https://doi.org/10.3390/chemengineering2020013