Abstract
We present steady-state and time-resolved fluorescence spectroscopic data derived from coumarin 153 (C153) in a binary solution comprised of trihexyltetradecylphosphonium chloride ([P6,6,6,14]+Cl−) and supercritical CO2 (scCO2). Steady-state fluorescence of C153 was measured in neat scCO2 and ionic liquid (IL)-modified scCO2 solutions. The steady-state excitation and emission peak frequency data in neat scCO2 and IL/scCO2 diverge at low fluid density (ρr = ρ/ρc < 1). The prominent spectral differences at low fluid density provided clear evidence that C153 reports different microenvironments, and suggested that the IL is solubilized in the bulk scCO2 and heterogeneity of the C153 microenvironment is readily controlled by scCO2 density. C153 dimers have been reported in the literature, and this formed the basis of the hypothesis that dimerization is occurring in scCO2. Time-dependent density functional theory (TD-DFT) electronic structure calculations yielded transition energies that were consistent with excitation spectra and provided supporting evidence for the dimer hypothesis. Time-resolved fluorescence measurements yielded triple exponential decays with time constants that further supported dimer formation. The associated fractional contributions showed that the dominant contribution to the intensity decay was from C153 monomers, and that in high density scCO2 there was minimal contribution from C153 dimers.
1. Introduction
Room temperature ionic liquids (RTILs) are salts that consist of ions that are typically combinations of organic cations paired with inorganic anions that exist in the liquid state at room temperature. RTILs are also designer solvents in the sense that a wide variety of cations and anions can be combined to tailor ILs for task-specific processes or reactions [1,2]. RTILs have unique characteristics, such as low volatility, non-flammability and water miscibility, that make them candidates for use in many applications, and has given rise to their use as cosolvents [3,4,5,6] in numerous applications [1,3,4,5,6,7,8,9,10,11,12,13] that include electrochemistry [14,15,16], organic synthesis [17,18], gas separation/SLM’s [19,20] and catalysis [17,21]. The inherent polar and nonpolar nanodomains that form in ILs allow them to readily solvate polar and non-polar solutes, and this has given rise to a significant increase in their study over the last decade [8,14,15,17,19,20,21,22].
Supercritical fluids, carbon dioxide (scCO2) in particular, have been recognized as alternative, green solvents for use in industrial processes [1,23]. The interest stems from the ability to tune the solvent characteristics by simply adjusting the system pressure, and therefore, the fluid density [24]. However, one of the main drawbacks to wider implementation is their limited ability to solubilize polar media. One means of circumventing this problem has been to use small amounts (3–5 mol %) of a polar organic cosolvent, such as methanol or acetone, to modify the solvating power [25]. At least to some extent, this defeats the purpose of using an “environmentally friendly” alternative solvent in chemical processes. For almost two decades, many groups have studied CO2 interactions with ILs, which has led to IL applications such as CO2 capture [26,27], catalyst recycling [23,28] and nanomaterial processing [1]. Much of the work to date, both experimental and theoretical, has focused nearly exclusively on various 1-alkyl-3-methyl imidazolium cations in combination with a variety of anions, where the cation alkyl chains used have been typically from C2 to C6 [1,23,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42]. This body of literature can be summarized by two main goals: (1) the measurement of the phase behavior of CO2 dissolved in ILs; and (2) the quantitation of CO2 solubility in a bulk phase IL. As an example, in one recent study the solubility of CO2 gas in [C9-imidazolium][PF6] was shown to increase by ~22% over a [C4-imidazolium][PF6], as estimated from the liquid phase volume increase on going from low to high pressure at 298 K [43]. The main conclusion from all of this work is that CO2 is effectively captured in the bulk IL phase. It has also been reported that ILs are not appreciably soluble in a bulk scCO2 phase [44].
In contrast to the imidazolium work, only a few studies have used phosphonium cation ILs, such as the trihexyltetradecylphosphonium cation ([P6,6,6,14]+), Figure 1 [45,46,47]. To the best of our knowledge, we reported the first instance of a phosphonium IL that was shown to be soluble in a bulk scCO2 phase [47]. A variable volume view cell was used to demonstrate the phase behavior of trihexyltetradecylphosphonium chloride ([P6,6,6,14]+Cl−) dissolved in scCO2, and we showed that this IL was soluble up to about 7 mass % [47]. In that report, we also included an emission spectrum of the dye coumarin 153 (C153), Figure 1, in [P6,6,6,14]+Cl−/scCO2 that supported the assertion that the IL had a measurable effect on the probe’s emission. That preliminary spectroscopic data showed us that the C153 was able to report on the presence of IL in scCO2 and prompted us to investigate the [P6,6,6,14]+Cl−/scCO2 system in more detail given the general interest in ILs and scCO2. In this paper, we present a more complete spectroscopic study of the [P6,6,6,14]+Cl−/scCO2 system. Specifically, we report on the steady-state and time-resolved spectroscopy of C153 as a reporter of [P6,6,6,14]+Cl− dissolution in scCO2 at 323 K. C153 was chosen for these studies because it has a rich history of use as a probe of solvation and solvation dynamics in liquids and supercritical fluids [22,24,48,49,50], and represents a nearly ideal probe of solvation. The photophysics are simple and the S0 → S1 transition is not complicated by any nearby transitions [51,52]. Moreover, semiempirical quantum calculations show good agreement with experiments, suggesting that its spectroscopic properties can be accurately modeled [48,53,54].
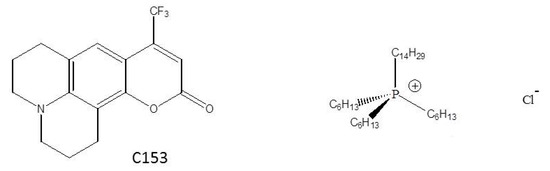
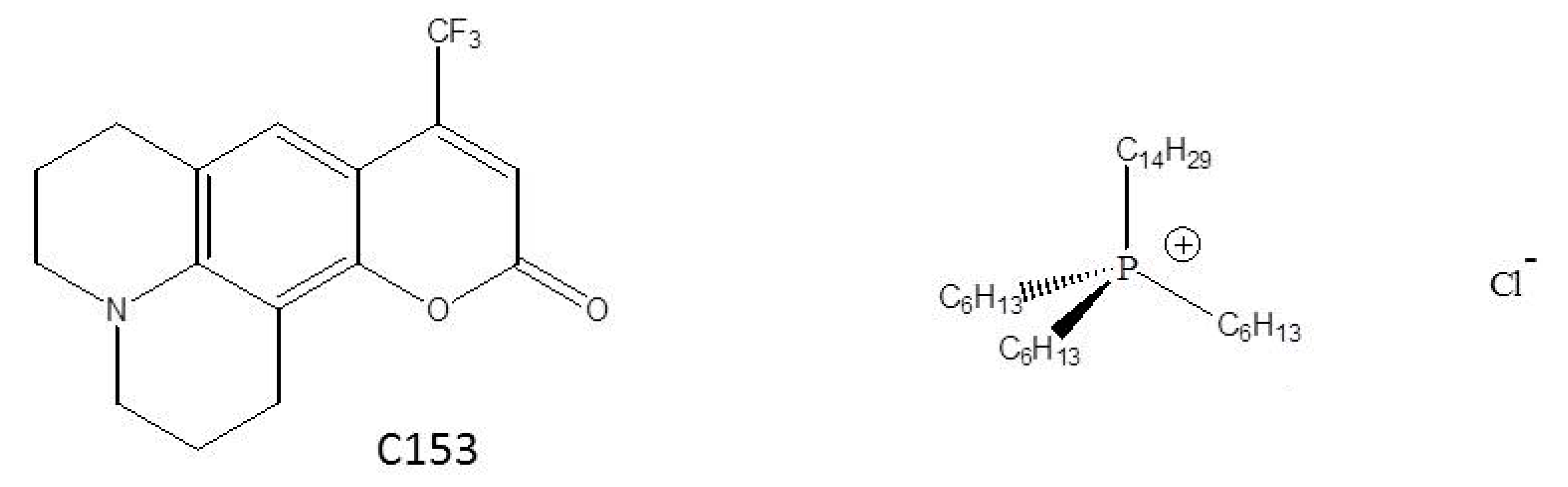
Figure 1.
Structures of coumarin 153 (C153) and the trihexyltetradecylphosphonium chloride ionic liquid, [P6,6,6,14]+Cl−.
2. Materials and Methods
Trihexyltetradecylphosphonium chloride (Cyphos® 101, [P6,6,6,14]+Cl−) was synthesized by Cytec Industries Inc. (Niagara Falls, ON, Canada) [55]. We have reported physicochemical properties of this IL both neat and in binary methanol solutions as a function of mole fraction and temperature [56]. Density varies only slightly from 897 kg·m3 at 298 K to 878 kg·m3 at 323 K whereas IL viscosity (η) changes from 2000 mPa·s at 298 K to 325 mPa·s at 323 K. The value of ln(η) showed a linear variation with inverse temperature. Initial water contamination was determined by Karl Fischer coulometric titration using a Mettler Toledo C20 titrator equipped with a DM 143-SC double platinum pin electrode at 295 K and replicate measurements showed that the [P6,6,6,14]+Cl− contained 0.11 ± 0.02 mass % water. We treated the IL by stirring in activated carbon for 7 days, after which the sample was filtered and dried by stirring under vacuum for 12 days at ~65 °C. The resulting IL was still slightly pale yellow. Water determinations on this treated sample showed a water content of 0.020 ± 0.003 mass % water. Carbon dioxide (99.99% purity) was from Scott Specialty Gases and used as received. Isothermal physical properties for CO2 were calculated for experimental temperatures and pressures using the NIST webbook [57]. The equation of state used to calculate CO2 densities was reported by Span and Wagner [58] and is incorporated into the NIST webbook. The CO2 critical parameters used in the equation of state are reported on the NIST website and include: critical temperature (Tc) = 304.1282 K, critical pressure (Pc) = 1070.0 psia, and critical density (ρc) = 0.467600 g·mL−1. Coumarin 153 (laser grade) was purchased from Exciton (West Chester, OH, USA), stored under desiccation, and used as received.
A stainless steel high-pressure cell was constructed using quartz windows and Teflon® O-rings as sealing devices. The internal volume was determined to be 3.9 mL. Measurements were performed at 323.3 K. Thermal control was accomplished using an Omega Engineering CN76133 controller with 2 CIR-1031 resistive cartridge heaters and a JMQSS-125G-6 thermocouple to monitor temperature in the cell. Temperature was maintained at the desired temperature to within ±0.5 K for data measured at 323 K. Pressure was generated using an Isco Model 260D microprocessor controlled syringe pump and measured using a Heise CC Dial pressure gauge. Uncertainty in pressure was ±2 psia. The pump’s thermal jacket allowed for warming the CO2 prior to injection into the cell, which helped speed solution equilibration.
All samples were prepared by first pipetting a 30 µL aliquot of C153 from a 1 mM stock C153/MeOH solution into the cell and then evaporating MeOH using a gentle stream of dry nitrogen gas. Final probe concentration in solution was not more than 8 µM, even at the highest pressure (density) measured where the C153 is most soluble. Addition of the IL to the cell was performed inside a nitrogen glove box, in which water was always maintained at less than 0.1 ppm and oxygen less than 2 ppm. The cell was sealed prior to removal from the glove box. Upon connection to the syringe pump gaseous CO2 was flowed through the cell as a final step to displace nitrogen prior to heating and pressuring the sample for measurement. A series of up to 15 fluorescence spectra were recorded as pressure was varied from low to high pressure, typically over a range of approximately 1000–4000 psia (ρr = ρ/ρc ~ 0.2–1.8) at 323.3 K. To begin a series, the cell was charged with CO2 and the pressure adjusted to the desired initial value and equilibrated overnight. In between each pressure adjustment, the contents of the cell were stirred thoroughly using a magnetic stirrer, with at least 5 min of equilibration time per pressure increment. Because of physical size limitations in the instrument sample compartment, stirring was discontinued just prior to measurement and the solution was equilibrated for an additional 5 min. Visual inspection of the cell contents showed that the resulting solution was optically transparent and there was no indication of a biphasic solution. Our previous work using a variable volume view cell for phase behavior studies was reported and mapped out the phase boundaries for this system [47].
Steady-state fluorescence excitation and emission data were collected using a Horiba Scientific (Spex) Fluorolog-3 fluorescence spectrometer (Horiba Scientific, Edison, NJ, USA) with single grating excitation and double grating emission monochromators. Instrument parameters were selected to provide 2 nm resolution. The instrument was calibrated using the water Raman signal and all spectra were blank subtracted and corrected for instrument response. Time-resolved emission intensity decays were measured using the Fluorolog-3 instrument, modified with time-correlated single photon counting (TCSPC) components from Horiba Scientific as described elsewhere [59]. In this work, all time-resolved measurements were excited with a 405 nm NanoLED (405-L) high output diode laser operating at a 1 MHz repetition rate, controlled through a FluoroHub controller that was run by DataStation (2.6) software. Excitation photons were passed through a vertically aligned polarizer prior to entering the sample. Emission was passed through a Glan-Thompson polarizer set at “magic” angle (54.7°) and spectrally resolved with the Fluorolog-3 double grating monochromator prior to detection with a cooled photocathode IBH TBX 850 detector (Horiba Scientific, Edison, NJ, USA). Instrument response was measured using an intensity matched scattering solution in a second, identically constructed stainless steel cell. Typical values for the instrument response of this system was routinely <200 ps per pulse. Emission intensity decays were measured over a 50-ns time window (~8000 channels) using a bin size of 14.1 ps per channel. Intensity decay data was measured at the steady-state emission peak, 450 nm. Taken together, the instrument response function and the intensity decay data were analyzed using the iterative reconvolution algorithm contained within the IBH DAS6 (6.6) software and decays were fit to a sum of exponentials models,
where Bi is the pre-exponential factor and τi is the lifetime of the ith component of the decay. The estimated effective time resolution was about 50–60 ps after deconvolution of the instrument response [60,61,62]. Quality of fit to a specific model was assessed using reduced chi-squared values (χr2) and a fit was judged to be acceptable if χr2 < 1.2 and the autocorrelation of residuals showed no systematic trend. When the data seemed to require a multi-exponential decay model we allowed the inclusion of an additional time constant only if there was at least a 10% improvement (decrease) in χr2 along with a discernable improvement in fit residuals and/or the fitted autocorrelation function. In multi-exponential models, fractional contributions of the individual lifetime components were calculated according to the following equation.
We used Spartan’16® Parallel Suite [63] to compute all C153 parameters reported in this work. Except for molecular mechanics and semi-empirical models, Spartan utilizes the Q-Chem ab-initio quantum chemistry code [64,65]. In the present work, initial geometry calculations were performed using the Hartree–Fock (H-F) 3-21G level of theory followed by a density-functional theory (DFT) geometry optimization using the B3LYP functional and 6-31G(d), 6-31+G(d,p) basis sets to be sure that we obtained the best geometry. Single point energy calculations were then performed using time-dependent DFT (TD-DFT) with the B3LYP functional and the 6-31+G(d,p) and 6-311G(d,p) basis sets to compute C153 transition energies. We did not observe a significant difference in energies using these basis sets so computational efficiency was the determining factor that was used to choose a basis set. The electronic absorption spectrum was obtained from calculation of the first six excited states using the optimized ground state geometry. For each excited state, the wavelength and intensity (oscillator strength) were calculated and these data were used to display the absorption spectra. The computed data were fitted to a Gaussian function in which the peak width (full width at half height, FWHH) is treated as a single parameter used to fit all 6 peaks; this fitting procedure was used to estimate spectral line broadening. Spectra shown in this work were visualized using a 40 nm FWHH and the accompanying discrete oscillator strengths were plotted by using 0 nm FWHH. The spectral intensity output for all results was plotted using the program’s default base-10 logarithmic scale that ranged from 1.0 × 10−6 to 1.0.
3. Results and Discussion
3.1. Steady-State Spectroscopy
Ionic liquids are often reported to contain a small fluorescence background, and our previous work with [P6,6,6,14]+Cl− is consistent with that observation [22,59,66], showing a broad, featureless emission spectrum with = 479 nm [59]. Excitation and emission scans of neat CO2 showed that it was free from any fluorescent impurities, however, there was measurable pressure-dependent emission when [P6,6,6,14]+Cl− was added to CO2. Compared to the neat [P6,6,6,14]+Cl− spectra, we observed a weak, blue-shifted emission at ~ 450 nm in [P6,6,6,14]+Cl−/CO2 at fluid densities greater than ρc (ρr > 1). For ρr < 1, the emission feature appeared only as an unresolved shoulder on the red edge of the Rayleigh scatter wavelength. Prior to addition of C153, the spectra of [P6,6,6,14]+Cl−/CO2 were measured using different excitation wavelengths (emission scans) and emission wavelengths (excitation scans) to determine what effect, if any, wavelength selection had on the observed spectral characteristics. To that end, we measured excitation scans using emission wavelengths of 480 nm and 525 nm, and emission scans were measured using excitation wavelengths at 365, 405 and 450 nm. The resulting spectra from these measurements showed no wavelength dependence.
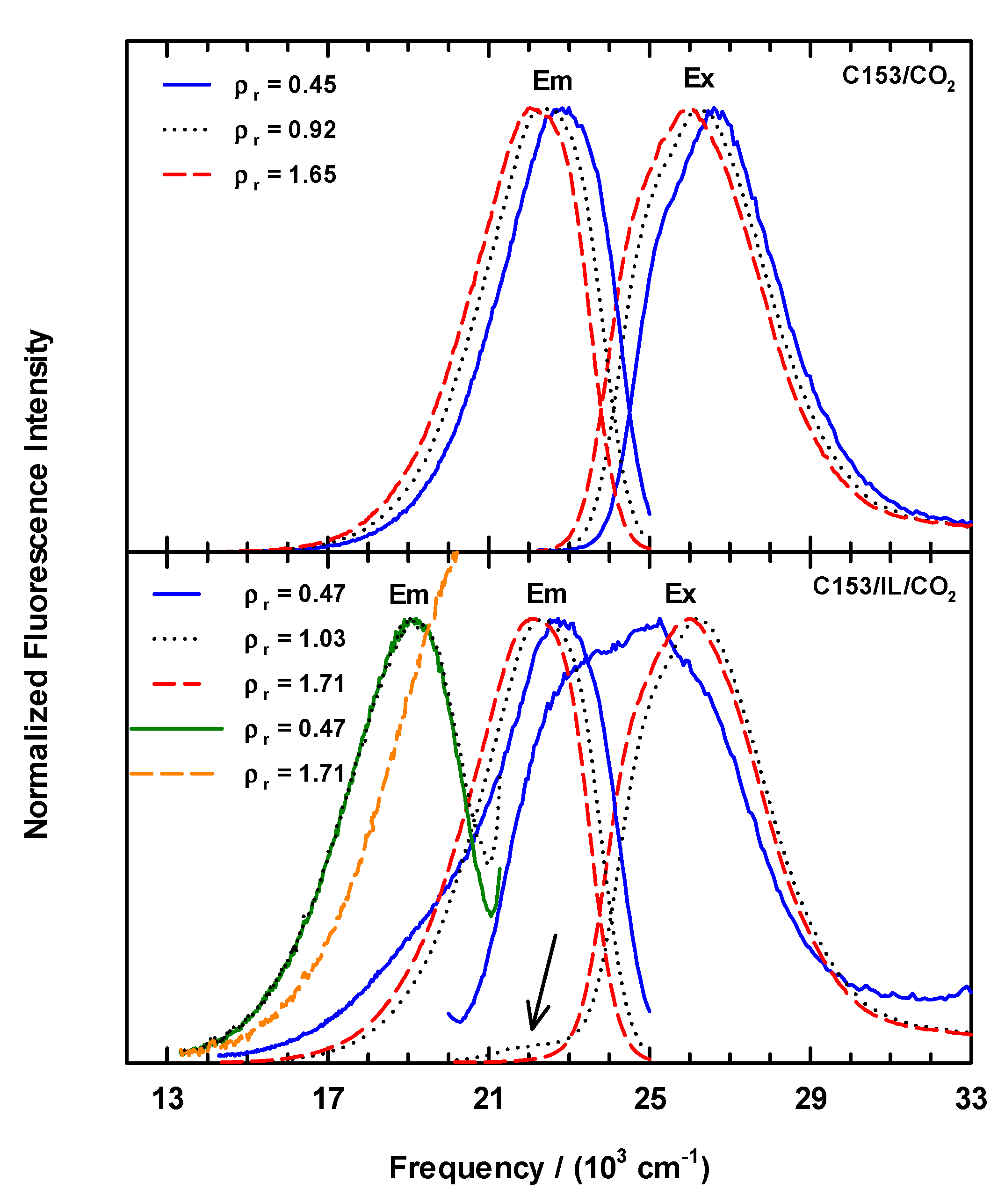
Representative normalized excitation and emission spectra of C153/scCO2 and C153/[P6,6,6,14]+Cl−/scCO2 at 323K are shown in Figure 2. In neat scCO2 (Figure 2, upper panel), the C153 excitation and emission spectra show a systematic red shift with increasing CO2 density. We also measured C153 excitation and emission in scCO2 at 308.3 K as a point of comparison to literature values of position and shift. The 308.3 K measurements showed excellent agreement with previous work at 309.3 K [24]. The C153 spectral shapes of our data in scCO2 at 308.3 K and 323 K are very similar to what one observes in liquid solvents with polarities that are comparable with CO2. The lower panel of Figure 2 shows examples of excitation and emission scans for scCO2 solutions containing ionic liquid that were recorded as a function of scCO2 density using the same scanning parameters as for C153 in neat scCO2, specifically using 27,400 cm−1 excitation (365 nm, for emission scans) and 19,040 cm−1 emission (525 nm, for excitation scans). Several features of these data are noteworthy. Excitation spectra measured at ρr < 1 showed a clearly different band shape. First, the entire envelope was shifted to much lower energy that was expected. Second, there was an additional component on the low energy side of the excitation spectrum that was not completely resolved and substantially broadened the spectrum. At the lowest density studied, the “extra feature” intensity was nearly 90% of the main peak’s intensity (Figure 2, lower panel, blue Ex line). As density increased up to ~ρr = 1, the intensity of the “extra feature” decreased and red-shifted by ~1000 cm−1 to ~22,000 cm−1, which can be seen as the low intensity peak in the ρr = 1.03 spectrum (arrow in Figure 2, lower panel). Excitation spectra of C153 in IL/scCO2 recorded at ρr > 1 are similar to the C153/scCO2 data in both shape and position, and the small shoulder at ~22,000 cm−1 was no longer observable. Similar to the excitation spectra at ρr > 1, the C153/IL/scCO2 emission spectra in Figure 2 behave similarly to the C153/scCO2 spectra with respect to peak shapes and positions. However, at ρr < 1 there are observable differences as can be seen in the emission spectrum at ρr = 0.47. At this density, the emission showed a broadened spectrum at ~19,000 cm−1 (see Figure 2, lower panel, blue Em line), where there appears to be an underlying, unresolved contribution to the emission band.
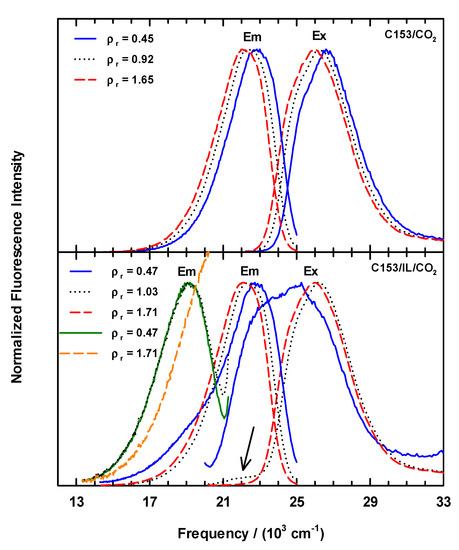
Figure 2.
Steady-state excitation and emission spectra for C153 observed at densities below (solid lines), near (dotted lines), and above (dashed lines) the critical density for CO2 (0.4676 g·mL−1) [57,58] at 323 K. Upper panel: emission and excitation spectra, respectively, for C153 in neat scCO2. Emission spectra were collected exciting at νex = 27,400 cm−1 (λex = 365 nm) and excitation spectra were measured using νem = 19,050 cm−1 (λem = 525 nm). Lower panel: observed spectra for C153 in [P6,6,6,14]+Cl−/scCO2. Emission spectra centered at ~19,000 cm−1 were measured using 22,220 cm−1 excitation (λex = 450 nm, orange and green lines) and those at ~23,000 cm−1 were excited using 27,400 cm−1 (λex = 365 nm, blue, dots and red lines) photons. Excitation spectra shown here at ~26,000 cm−1 were measured by monitoring the emission at 19,050 cm−1 (λem = 525 nm, blue, dots and red lines).
After noting the spectral effects from the low-density spectroscopy using 365 nm excitation, we measured the emission using excitation at 22,200 cm−1 (=405 nm) in an effort to move away from any potential IL contributions to the spectra. The analysis from this data indicated that the most intense emission occurred at 22,730 cm−1 with the expected red shift as density increased, but in addition for ρr < 1 the data displayed a second emission band at ~19,420 cm−1 that was most substantial at low density, and that rapidly disappeared as ρr → 1 to produce the typical unfeatured C153 emission spectrum. We further examined the emission at one final excitation wavelength, 22,220 cm−1 (=450 nm). Two emission spectra from this C153/IL/scCO2 series are included in Figure 2 and appear at ~19,000 cm−1 (orange and green lines). These spectra clearly illustrate the low energy contribution to the overall emission profile.
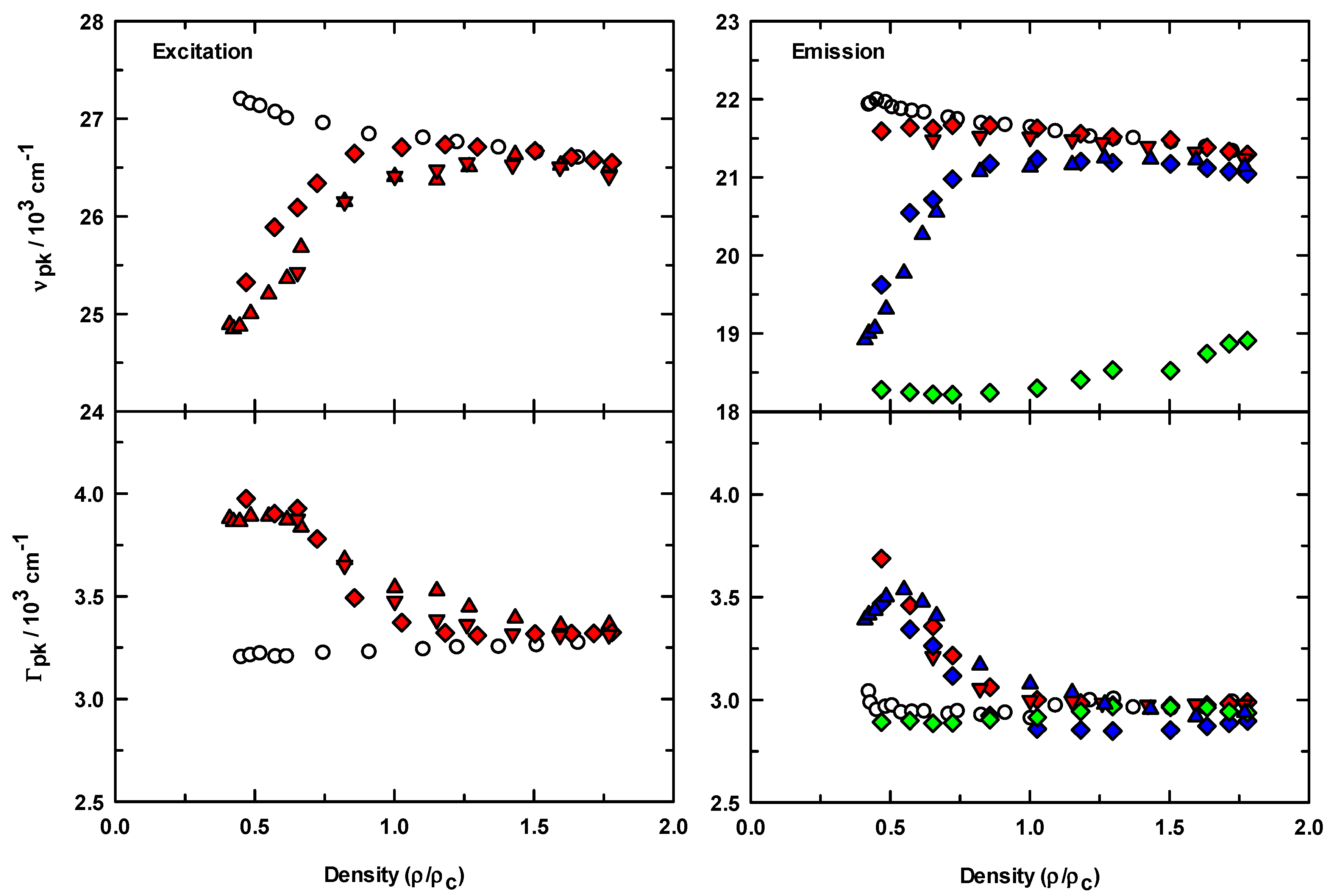
The steady-state spectroscopic results for all of the data acquired are summarized in terms of the average peak frequency (νpk, 1st moment) and full widths at the intensity half maximum (Γ) calculated from the spectra, and the reduced density dependence for this data is presented in Figure 3. The upper graphs show and for C153 in scCO2 (○) and in IL/scCO2 (filled symbols). In the absence of IL, both the excitation and emission frequencies of C153 show a systematic and smooth variation toward lower energy as CO2 density was increased. When IL was added to solution, was decreased by ~2500 cm−1 at the lowest scCO2 density compared to C153/scCO2. As density was increased, systematically increased to the value for C153 in neat scCO2. This behavior was observed independent of the purification process used (all filled symbols), but carbon filtering prior to drying under vacuum (diamonds) appeared to have a small influence on the absolute peak frequencies. The data for C153 emission in the presence of IL also showed similar energy reduction behavior at low density, but the extent of the shift was dependent on the excitation wavelength used. When excited with 365 nm photons (diamonds), the resulting emission spectra were most similar to the neat scCO2 data in both position and shift magnitude. The small difference in energy between ~22,000 cm−1 (for C153/scCO2, ○) and ~21,500 cm−1 on addition of IL (red symbols) at low density, compared to the changes in emission with 405 and 450 nm excitation, blue and green symbols respectively, is indicative of the degree to which we are able to isolate the effects of IL on the C153 spectroscopy. The increased intensity in the red edge tail of the ρr = 0.47 emission spectra (see Figure 2) contributed to the weighted spectrum such that the peak position at low density was at slightly less energy. By changing the excitation wavelength, we were able to better isolate the lower energy contributions to the C153/IL emission. For the IL solutions at high density, the excitation and emission peak positions eventually matched the values of C153/scCO2 to within experimental uncertainties, except for the emission data excited at 450 nm (Figure 3, green symbols). While we observed a small shift toward the neat CO2 peak value with increasing density, the peak position was still ~2200 cm−1 lower in energy. The reason for this lack of agreement stems from the scan ranges used when exciting with 450 nm photons, in that emission data was only available as high as 20,830 cm−1. Therefore, the weighted average reported in Figure 3 did not include any contribution from the higher energy, higher intensity emission.
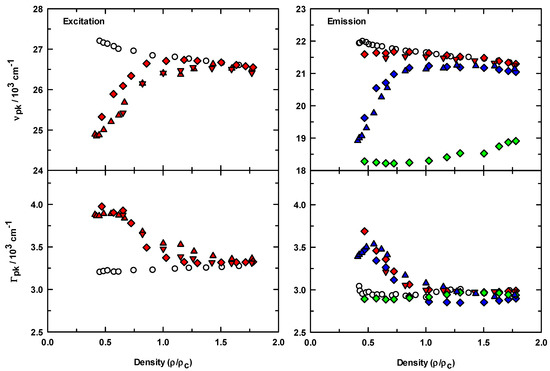
Figure 3.
Density dependence of the spectral parameters of C153 in the absence (open circles) and presence (filled symbols) of [P6,6,6,14]+Cl−. Diamond symbols are frequencies and widths from activated carbon treated IL samples whereas the triangle symbols were only treated by drying under vacuum (see experimental section for further details). Upper panels: excitation and emission frequencies calculated from first moments of the spectra. Emission spectra were acquired at several excitation wavelengths, λex = 365 nm (red symbols), λex = 405 nm (blue symbols), λex = 450 nm (green symbols). Lower panels: spectral bandwidths computed as full width at half maximum from the normalized spectra.
Figure 3 also depicts the variation in peak widths (Γ). Absorption (and/or excitation) spectral widths of C153 in liquid solvents are reported to be directly proportional to solvent polarity, whereas emission widths show an inverse proportionality [54]. In addition, the excitation widths are broader than emission widths by about 20%. Our width data for C153/scCO2 are in agreement with both of these points and are also consistent in magnitude with previous measurements [24]. Further, as CO2 density was increased the polarity increased and the spectral widths changed as expected [24] (based on liquid solvent data [54]), in that the excitation widths increased and emission widths decreased. In contrast, the widths in IL/scCO2 solutions showed a significant departure from the expected behavior, particularly at low density. While the excitation widths are still broader than the emission widths, the density dependence is unexpected.
In an effort to explain the observed spectral changes on adding IL into scCO2, we considered what role the IL might play. Choice of excitation (or emission) energy was important because measurement of the [P6,6,6,14]+Cl−/scCO2 blanks indicated that the IL absorbed photons above 25,000 cm−1 and it displayed a small emission background. Thus, one challenge arose from the spectral similarity that occurred between C153 and the [P6,6,6,14]+Cl− blank, both of which exhibited an excitation peak energy at about 26,100 ± 250 cm−1. However, the signal from [P6,6,6,14]+Cl− was always less than 1% of the total signal at any density and all data was blank corrected prior to processing to remove any small contribution to the signal by [P6,6,6,14]+Cl− and so [P6,6,6,14]+Cl− background signal cannot account for the low density C153 spectral changes. At the same time, the mere presence of IL in solution clearly influenced the signal and so we conclude that IL must be present in solution.
Taken together, the changes in peak frequencies and broadened widths for ρr < 1 showed that addition of [P6,6,6,14]+Cl− to a bulk scCO2 results in solubilization of this IL, consistent with our previous report [47]. More recently, we presented the C153 spectroscopy in binary solutions of [P6,6,6,14]+Cl−/MeOH [59]. Variation of xIL from 0 to 1 allowed us to examine the C153 response to the varying cosolvent microenvironment formed between MeOH and [P6,6,6,14]+Cl−. In that work, we observed that on going from neat MeOH to neat [P6,6,6,14]+Cl− , blue shifted by ~1100 cm−1 and the emission spectral width increased by 10% in response to decreased polarity of the C153 microenvironment. Based on that data, we would expect that if C153 is sensing an increasingly nonpolar environment through IL dissolution, then we should see a blue shift and broadening of the emission spectrum. However, the C153 data in IL/scCO2 are inconsistent with these expected changes, so apparently polarity change does not account for our observations. There are at least two other hypotheses that may help to explain the current results. A broadened spectrum could also result from increased solution heterogeneity, which is conceivable if C153 is partitioning into distinctly different solvent environments. Dissolution of amphiphilic molecules into a bulk supercritical fluid phase, including scCO2, has demonstrated the formation of a micellar environment in supercritical fluids [67,68,69,70,71,72]. While we are not suggesting micellization of [P6,6,6,14]+Cl−, these reports show that molecules similar to this IL have been solubilized in supercritical fluids. Therefore, it is plausible that dissolution of a small amount of IL into scCO2 could produce the solution heterogeneity to which C153 responds. While partitioning in a microheterogeneous solution might explain the Γ trends, and might also provide a rationale for the observed spectral shifts, it may not necessarily account completely for all of the spectral features. For example, while the spectral red shift in excitation and emission with increasing density at ρr > 1 is consistent with expected C153 behavior, the initial peak position and band shape of the excitation spectra at ρr = 0.47 coupled with the expectation that C153/IL interactions should result in a blue-shifted spectrum was inconsistent with the measured data. Therefore, we also considered the idea that C153 solute–solute interactions (dimerization) may contribute to the observed results, particularly at low density scCO2 where solubility is limited.
Several recent reports have discussed coumarin dye aggregation in liquid solvents, including work with C153 [73,74], C481 [75,76] and C343 [77,78]. Pal and co-workers observed a blue-shifted fluorescence emission for C153 in ethanol when the dye concentration approached 10−5 M [73], a concentration commonly used in solvation studies. They demonstrated that C153 undergoes H-aggregate formation under these conditions, whereas no spectral evidence for dimerization was observed in acetonitrile. The same authors also reported H-aggregate formation of C481 in ethanol and acetonitrile [76], as well as in acetonitrile–water binary mixtures [75]. In the context of Kasha’s molecular exciton coupling theory that describes molecular aggregation [79,80], the formation of a stacked molecular dimer (parallel transition dipole alignment, H-aggregate) should display a hypsochromic (blue) spectral shift with a concomitant diminution of intensity, whereas alignment of the J-aggregate type results in a bathochromic (red) spectral shift. If C153 aggregation is driven by IL dissolution in scCO2, then the spectral response should allow us to characterize this process. Our excitation spectra of C153/IL/scCO2 showed a red-shifted average peak at low density that was much broader than anticipated compared to C153/scCO2 (Figure 3). C153 dimer formation could explain these spectral observations. With increased density, the spectra narrowed and the average spectral peak increased in energy up to ρr = 1, after which it followed the expected red shift up to the highest densities measured. Increased solvating power of scCO2 is expected at high density and the dissolution of dimers back to monomers could be explained by improved solubility. Density-dependent behavior in supercritical fluids has been known for decades, and there are many reports that discuss density augmentation effects below the critical density (ρr = 1), which are then diminished by a sufficient increase in fluid density [24,81,82,83,84]. Limited solubility in supercritical fluids is expected below the critical density (ρr = 1), where the fluid density is more gas-like, and therefore, any potential aggregation would be expected at these lowest densities. Above the critical density, the physicochemical properties of the fluid become characteristically liquid-like and solubility is much improved. These effects coincide with the changes we see in C153/IL spectroscopy that showed a markedly different low-density behavior that became more similar to the neat scCO2 data at high density. A second indicator from our data that pointed toward aggregation effects as a plausible explanation was that we isolated a second emission band at 19,000 cm−1 that displayed weaker emission and diminished with increased density.
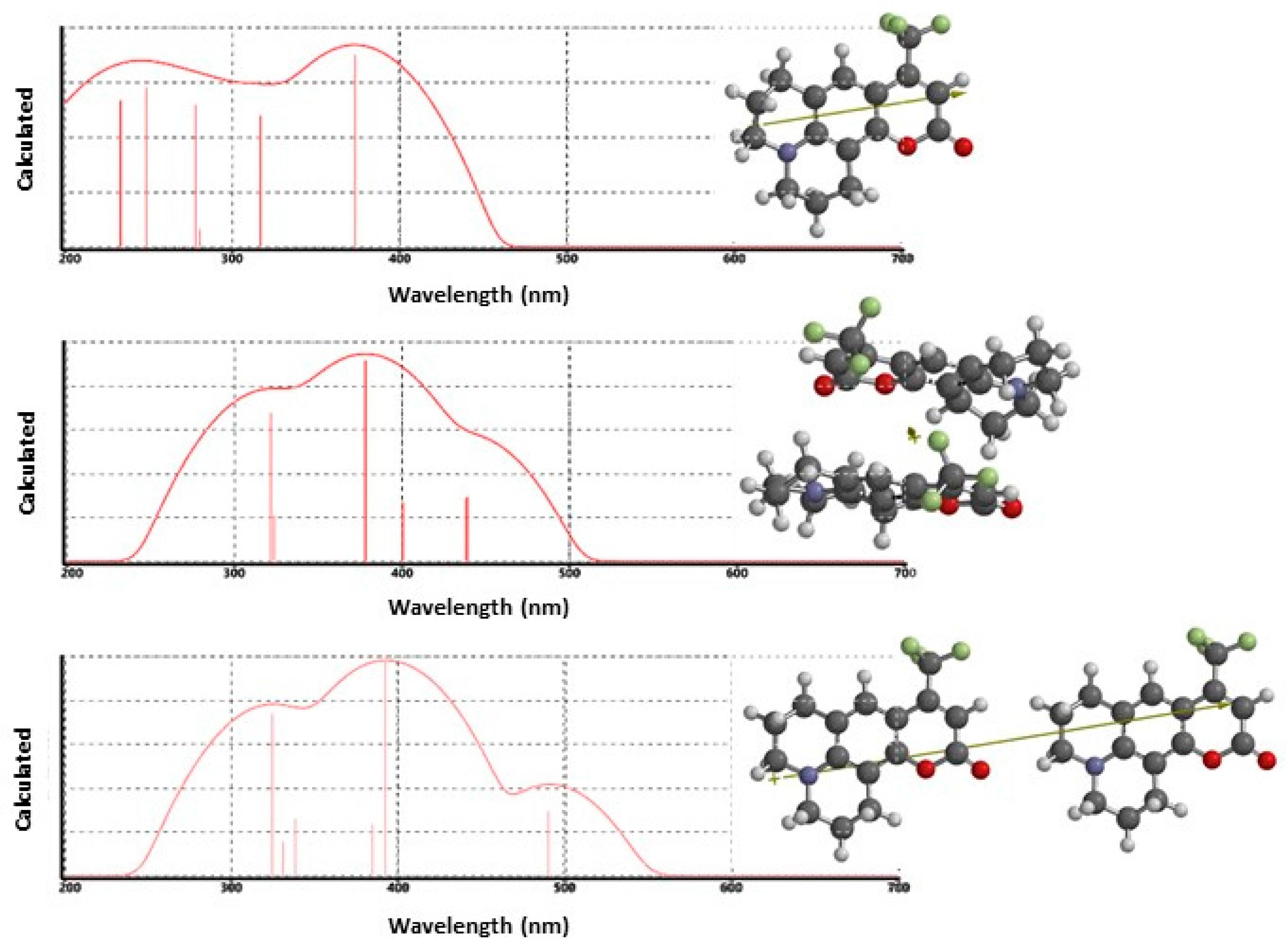
To further explore our dimer formation hypothesis, we performed a series of electronic structure calculations using Spartan’16® to compute dimer interactions. H- and J-aggregate structures were prepared, and initial gas phase geometries and orientations were calculated using the Hartree–Fock (H–F) method with the 3-21G basis set. The optimized H–F dimer geometries were re-computed with DFT by using the B3LYP/6-31G(d) functional and basis set to calculate a refined geometry. We performed geometry optimizations with higher level theories but observed no significant differences in the final geometries. To estimate the transition energies for gas-phase C153 and C153 dimers, TD-DFT calculations were performed at the B3LYP/6-31+G(d,p) level of theory, from which the excitation spectrum was computed. Figure 4 presents the results for C153 structures and dipole moments for the monomer (top), H-aggregate dimer (middle) and J-aggregate dimer (bottom). The strongest absorption in the calculated C153 monomer spectrum appeared at 373 nm and shows reasonable agreement with low density scCO2 experimental data, 376 nm, with the difference ascribed to solvation effects. The calculated H-aggregate spectrum showed that the strongest absorption was observed at 375 nm, which correlated well with the expected position of the monomer and a lower energy spectral feature at ~440 nm. This calculation also predicted the presence of a higher energy feature at about 320 nm but we saw no corresponding experimental evidence. The J-aggregate calculation also predicted a spectrum that was similar to the measured data. However, here the dominant contribution to the spectrum is observed at 393 nm accompanied by a lower energy contribution that was predicted at 491 nm. Unfortunately, the computational results only offer a limited amount of insight to differentiate between the two dimers, since both anticipated aggregate forms yield transition energies that show energies similar to the experimental data. However, it does appear that the calculated H-aggregate spectrum is more consistent with the measured data with respect to actual peak wavelengths. Although the Kasha model predicts that H-aggregates are non-fluorescent because of forbidden electronic transitions, fluorescent H-aggregates have been reported [73,76,77,85]. Pal and co-workers have discussed this at length for C153. They showed that C153 formed weakly fluorescent H-aggregates that were red-shifted in comparison to monomer emission [73]. They further pointed out that this may be explained through vibronic coupling and slight rotational twisting that misaligns the C153 molecular planes enough so that emission, albeit weak, is observed. In our present case, that model would appear to explain our steady-state data in low density scCO2.
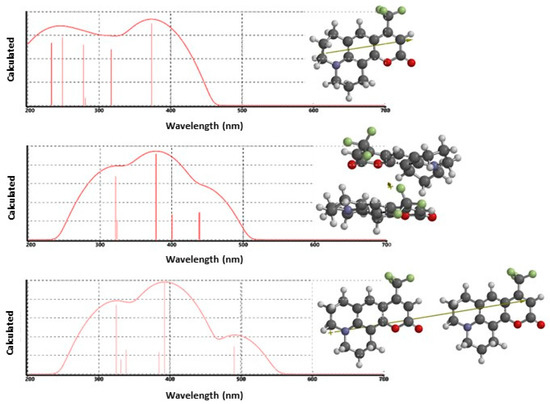
Figure 4.
Direct output of Spartan’16 electronic structure calculations showing the results of TD-DFT calculations using the B3LYP functional and 6-31+G(d,p) basis set for estimated solute-solute excitation spectra of C153 plotted as log(I) versus wavelength (nm). The top spectrum is the C153 monomer, the middle spectrum is the H-aggregate (stacked) dimer, and the bottom spectrum shows the head-to-tail C153 J-aggregate dimer. Vertical lines represent the positions and oscillator strengths of the first six excited states.
3.2. Time-Resolved Spectroscopy
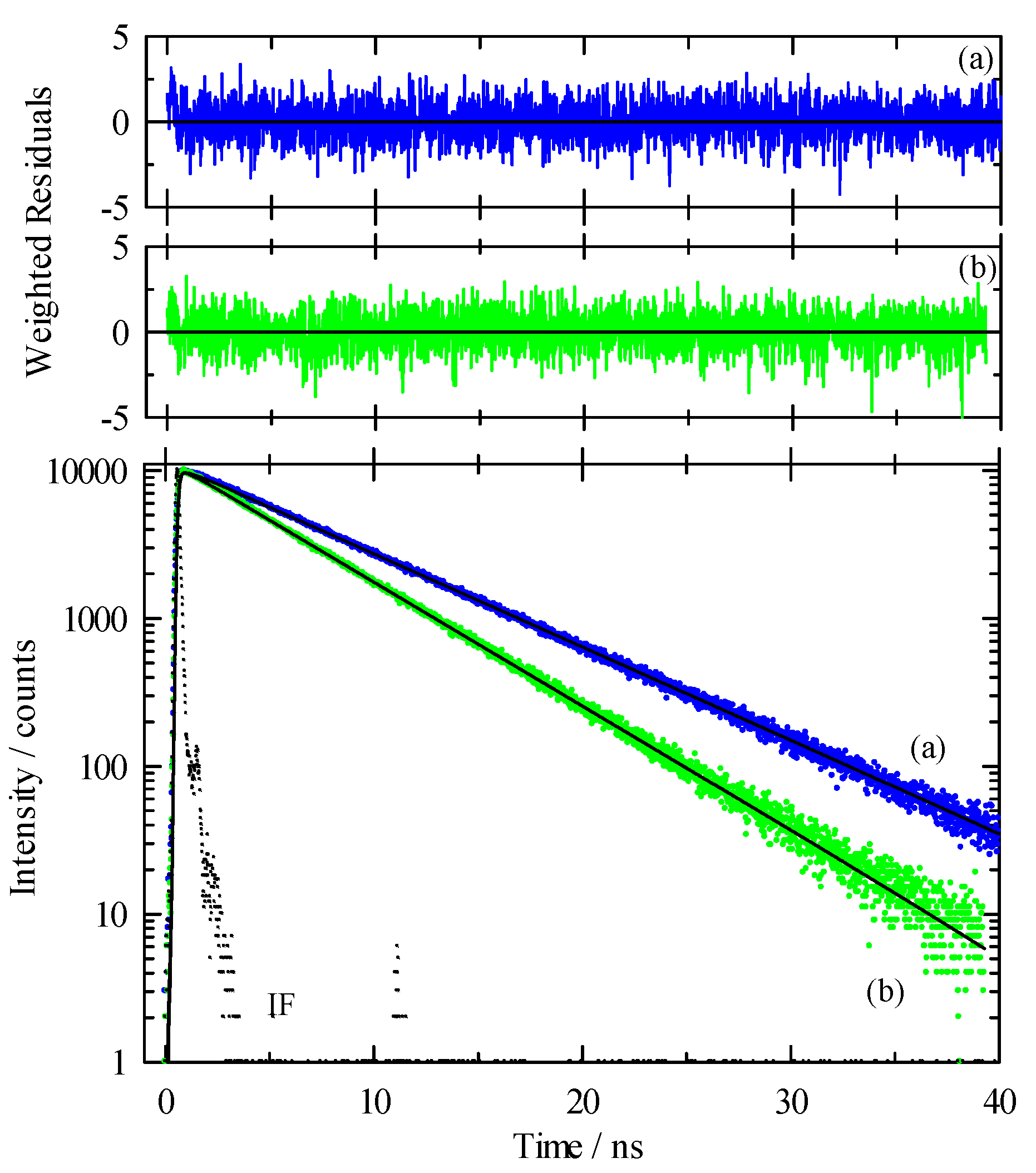
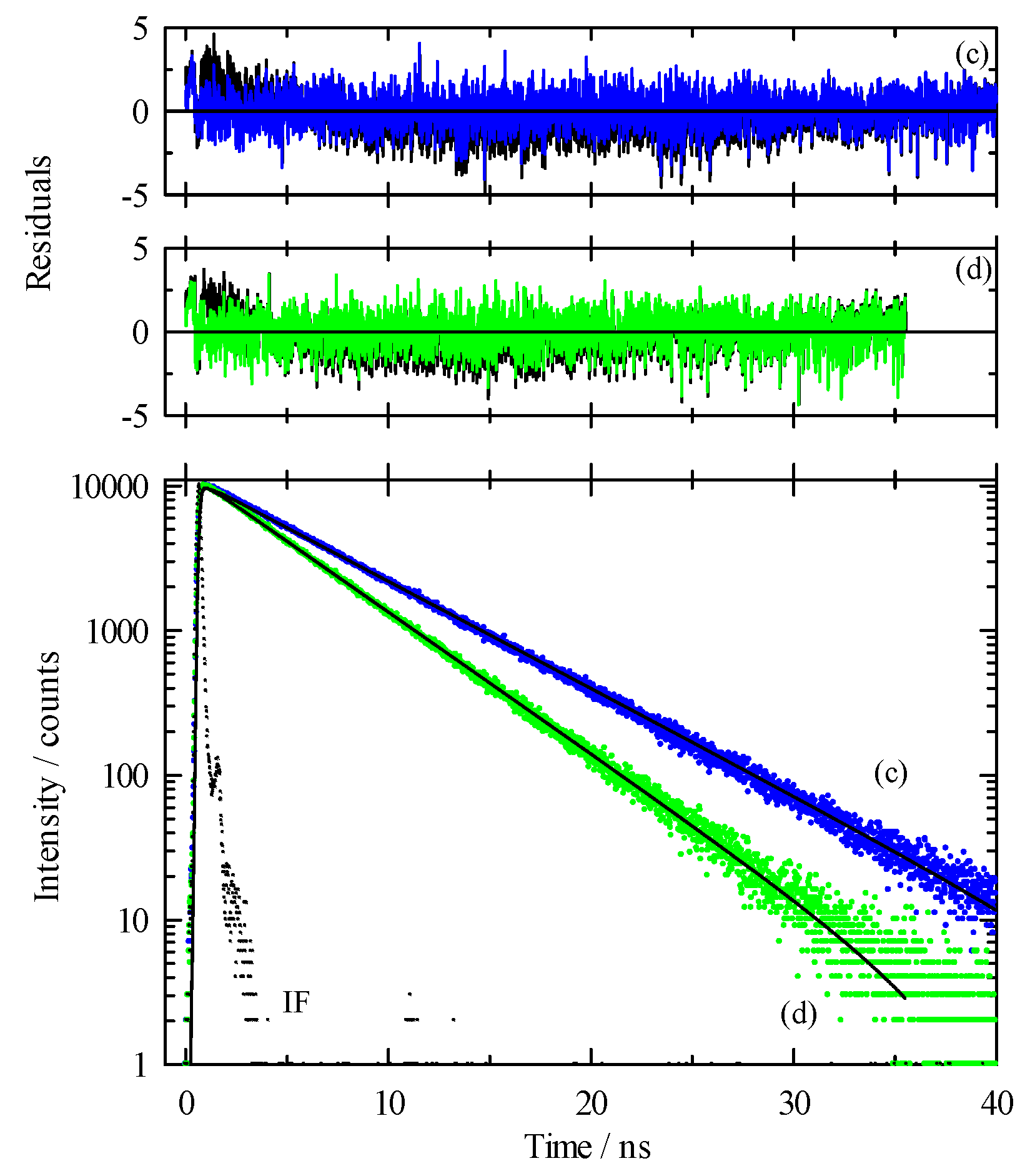
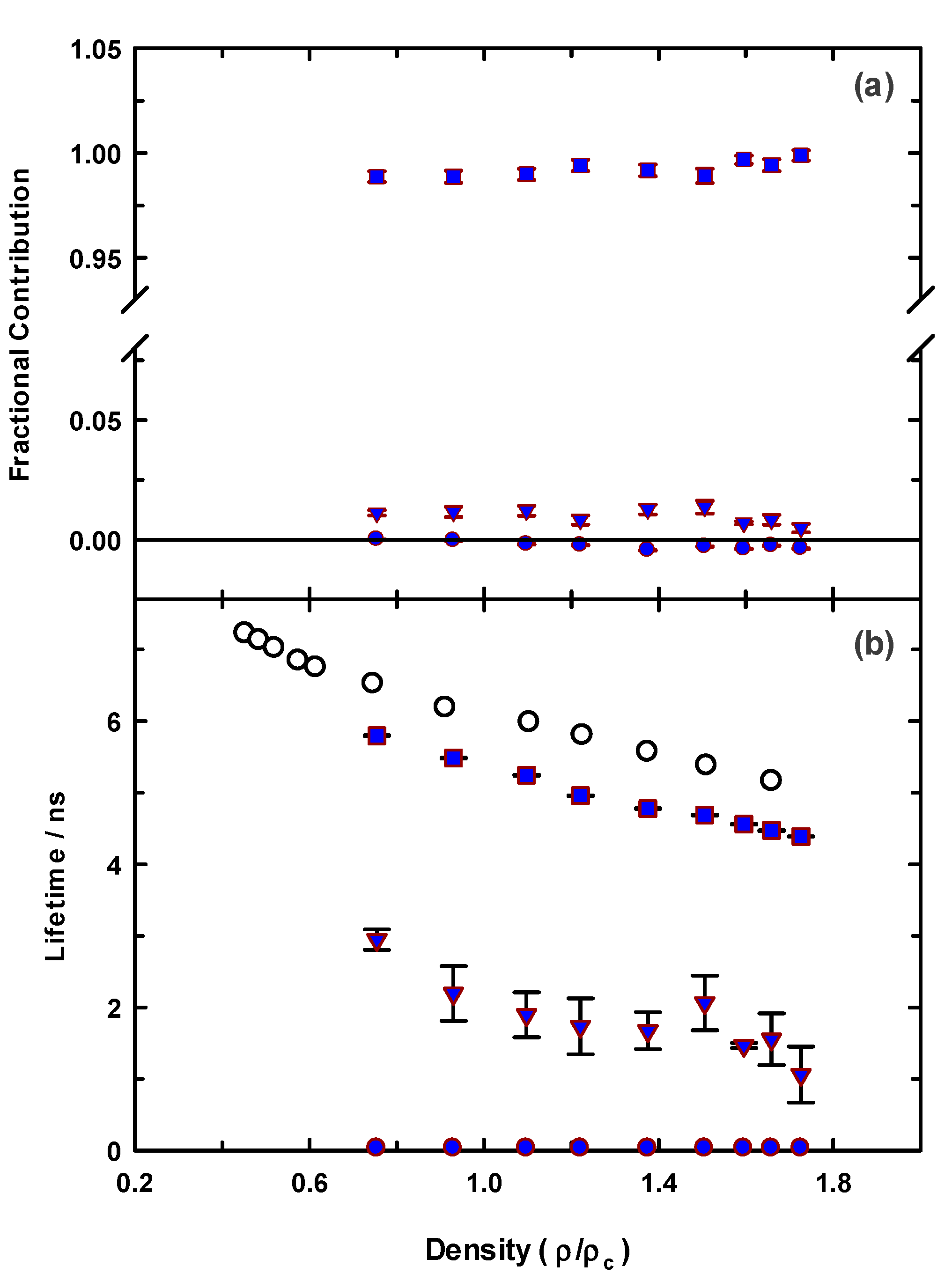
While our steady-state spectroscopy results suggest the presence of C153 aggregates, time-resolved intensity decay measurements are more sensitive to detecting multiple emitting species [60,61,62,86]. Figure 5 shows two C153/scCO2 intensity decays and corresponding residuals that were recorded at ρr = 0.571 (“a”, blue) and ρr = 1.659 (“b”, green). The best fits were described by a double exponential model. A significant improvement in the autocorrelation of the residuals (Figure S1) and reduction in χr2 values (e.g., 1.14 to 1.05 for trace “a” Figure 5) resulted when the second component was added to the fitting model. The additional time constant was always required to achieve the best fits as determined by residuals and autocorrelation of residuals, but its fractional contribution was negligibly small, <0.2%. We attributed this small contribution time constant (<70 ps) to photon scattering by the optical windows and stainless-steel cell interior. Thus, the data suggested a single exponential decay for C153 itself. The recovered lifetimes of the longer time constant for the data shown were 6.85 and 5.17 ns, and ρr = 0.571 and 1.659 respectively, which was typical of the magnitude across the density range. Example decays for C153 in [P6,6,6,14]+Cl−/scCO2 are shown in Figure 6 for data recorded at ρr = 0.754 (trace “c”, blue) and ρr = 1.726 (trace “d”, green). A triple exponential decay model was used to describe the intensity decays, again with one time constant used for scattered light. While the randomness in the double exponential model residuals for these decays (black lines in Figure 6) suggested that the decays might be adequately described by two time constants, significant improvement in the fit resulted by including a third time constant as judged by not only χr2, but more importantly, by randomness in the residual autocorrelations and fits to the decays (Figures S2 and S3, respectively). The complete set of fitting results for C153 in neat scCO2 and [P6,6,6,14]+Cl−/scCO2 are collected in Figure 7, which shows the recovered lifetimes and pre-exponential factors across the range of CO2 density. The smallest time constant was included to account for scattered light (Figure 7, blue circles on the x-axis) and the additional two-time constants described the lifetimes of monomeric and dimeric C153. The open symbols in the bottom panel of Figure 7 display the lifetimes for C153/scCO2 as a function of reduced density, and these results represent the benchmark for C153 monomer emission in neat scCO2. In the absence of solvent coupling, a 7 ns lifetime is a reasonable estimate for gas phase C153 [87]. The C153 intensity decay in low-density IL/scCO2 displayed a gas-like lifetime of 5.8 ns (squares), a difference only 0.7 ns less than the corresponding lifetime in neat scCO2. As density was increased, the C153 lifetime in IL/scCO2 decreased to 4.5 ns. The second time constant (triangles) showed a diminished C153 radiative rate, resulting in a lifetime of ~3 ns at the lowest density. A diminished lifetime is consistent with solute–solute interactions that quenched the fluorescence. The fractional contributions of the time constants indicated that the predominant form of C153 detected in solution (>98%) was monomeric at all densities. As the highest experimental density is approached, the contribution of C153 dimer decreased to nearly zero. Evidently, the high-density solubilizing capability of scCO2 is effective enough to minimize the tendency of C153 molecules to form dimers.
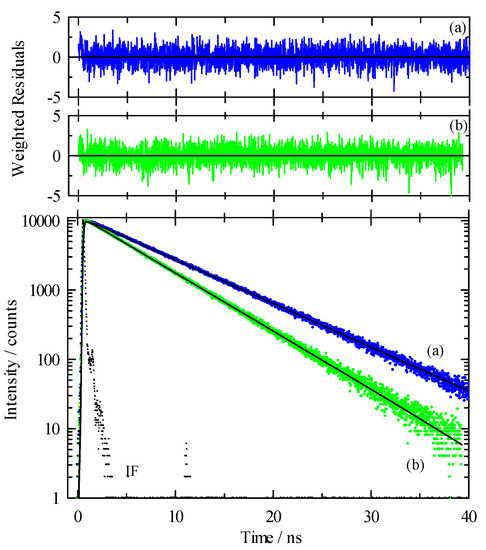
Figure 5.
Intensity decay data and fits for C153 in [P6,6,6,14]+Cl−/scCO2 at 323 K. Excitation was at 405 nm and emission at 450 nm for all traces. Lower panel: dots are measured data and solid lines are the multi-exponential fits to these data. “IF” is the instrument function. Trace “c” (blue) was recorded at ρr = 0.754 and trace “d” (green) was at ρr = 1.726. Upper panels: Residuals from the fits to a sum of exponentials model with the black lines showing fits to a double exponential decay whereas colored lines are fits to a triple exponential model.
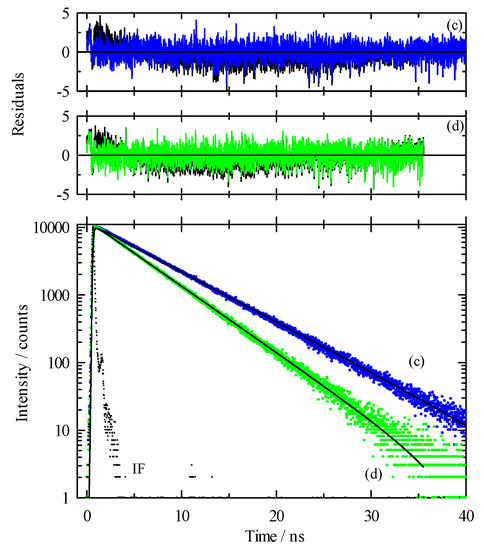
Figure 6.
Intensity decay data and fits for C153 in [P6,6,6,14]+Cl−/scCO2 at 323 K. Excitation was at 405 nm and emission at 450 nm for all traces. Lower panel: dots are measured data and solid lines are the multi-exponential fits to these data. “IF” is the instrument function. Trace “c” (blue) was recorded at ρr = 0.754 and trace “d” (green) was at ρr = 1.726. Upper panels: Residuals from the fits to a sum of exponentials model with the black lines showing fits to a double exponential decay whereas colored lines are fits to a triple exponential model.
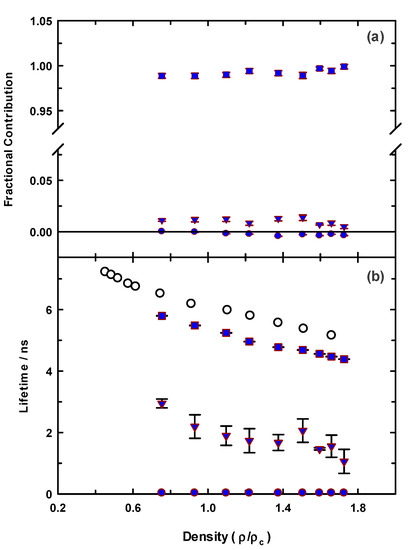
Figure 7.
Fitted decay parameters for C153 in [P6,6,6,14]+Cl−/scCO2 at 323 K (blue symbols). Open circles (lower panel) are for C153 in neat scCO2 at 323 K. All data was acquired using 405 nm excitation with 450 nm emission.
4. Conclusions
We have reported steady-state and time-resolved fluorescence data using C153. The data showed that the ionic liquid trihexyltetradecylphosphonium chloride, [P6,6,6,14]+Cl−, was dissolved into scCO2 at 323 K. Low density (ρr < 1) C153 excitation spectra in IL/scCO2 solutions showed markedly different behavior compared to that of C153/scCO2. Low-density C153/IL/scCO2 emission spectra also showed significant differences compared to the neat scCO2 that were strongly dependent on choice of excitation wavelength. Recent reports in the literature discussed the observation of C153 H-aggregate (dimer) formation [73,75,76], and we therefore hypothesized the presence of C153 dimers in scCO2. Electronic structure calculations were undertaken to study the effects of dimerization on C153 electronic transitions, and excitation spectra were computed. The calculated spectra for C153 dimers showed transition energies that were indeed consistent with experimental observations. Time-resolved fluorescence showed triple exponential behavior, with one component accounting for scattered light and two components associated with monomer and dimer lifetimes. Fractional contributions indicated that more than 98% of the intensity decay was due to C153 monomer emission and about 1% of the decay was contributed by C153 dimers.
The picture that emerges from the collective data presented here is that for low-density IL/scCO2 mixtures, small amounts of IL dissolve into the bulk scCO2 phase to form an optically transparent, single phase system. The hydrophobic nature of C153 drives association with the IL in solution, wherein C153 aggregates. As discussed, we (and others) observe no C153 aggregation in neat scCO2, and so it is clearly the IL that mediates aggregation. At high density, the propensity of C153 to aggregate diminishes and the solution behaves increasingly like neat scCO2. Our data demonstrate that IL/scCO2 mixtures can behave similar to supercritical fluids that have been modified by organic cosolvents, and therefore provide a potential alternative to using volatile organic cosolvents as modifiers of supercritical fluids.
Supplementary Materials
The following are available online at www.mdpi.com/2305-7084/1/2/12/s1, Figure S1: Autocorrelation of Residuals for C153/scCO2, Figure S2: Autocorrelation of Residuals for C153/IL/scCO2, Figure S3: Intensity Decays and Fits-Insets to Figure 6 for C153/IL/scCO2.
Acknowledgments
The authors would like to gratefully acknowledge Cytec Industries Inc., Ontario, Canada, for supplying the samples of the ionic liquid used in the studies. M.P. Heitz thanks Sean Ohlinger (Wavefunction, Inc.) for help with the electronic structure calculations, Mark Maroncelli and Markus M. Hoffmann for helpful discussions. The authors gratefully acknowledge support from the NSF-MRI program, grant award number CHE-0619320 for initial funding to acquire the time-resolved instrument. They would also like to acknowledge funding from the scholarly incentive grant program and Provost post-tenure fellowship program received from SUNY College at Brockport.
Author Contributions
Mark P. Heitz conceived and designed the experiments; Kristina L. Fuller and Kaitlin A. Ordiway performed the experiments; Mark P. Heitz performed all electronic structure calculations; all authors contributed to data analysis; Kristina L. Fuller and Kaitlin A. Ordiway contributed initial drafts and Mark P. Heitz wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Pollet, P.; Davey, E.A.; Urena-Benavides, E.E.; Eckert, C.A.; Liotta, C.L. Solvents for sustainable chemical processes. Green Chem. 2014, 16, 1034–1055. [Google Scholar] [CrossRef]
- Huang, Z.; Kawi, S.; Chiew, Y.C. Solubility of cholesterol and its esters in supercritical carbon dioxide with and without cosolvents. J. Supercrit. Fluids 2004, 30, 25–39. [Google Scholar] [CrossRef]
- Gao, L.; Jiang, T.; Zhao, G.; Mu, T.; Wu, W.; Hou, Z.; Han, B. Transesterification between isoamyl acetate and ethanol in supercritical CO2, ionic liquid, and their mixture. J. Supercrit. Fluids 2004, 29, 107–111. [Google Scholar] [CrossRef]
- Shariati, A.; Peters, C.J. High-pressure phase behavior of systems with ionic liquids: II. The binary system carbon dioxide+1-ethyl-3-methylimidazolium hexafluorophosphate. J. Supercrit. Fluids 2004, 29, 43–48. [Google Scholar] [CrossRef]
- Shariati, A.; Peters, C.J. High-pressure phase behavior of systems with ionic liquids: Part III. The binary system carbon dioxide+1-hexyl-3-methylimidazolium hexafluorophosphate. J. Supercrit. Fluids 2004, 30, 139–144. [Google Scholar] [CrossRef]
- Shariati, A.; Peters, C.J. High-pressure phase behavior of systems with ionic liquids: Measurements and modeling of the binary system fluoroform+1-ethyl-3-methylimidazolium hexafluorophosphate. J. Supercrit. Fluids 2003, 25, 109–117. [Google Scholar] [CrossRef]
- Batista, M.L.S.; Neves, C.M.S.S.; Carvalho, P.J.; Gani, R.; Coutinho, J.A.P. Chameleonic behavior of ionic liquids and its impact on the estimation of solubility parameters. J. Phys. Chem. B 2011, 115, 12879–12888. [Google Scholar] [CrossRef] [PubMed]
- Jodry, J.J.; Mikami, K. New chiral imidazolium ionic liquids: 3D-network of hydrogen bonding. Tetrahedron Lett. 2004, 45, 4429–4431. [Google Scholar] [CrossRef]
- Li, Z.; Xiao, Y.; Xue, W.; Yang, Q.; Zhong, C. Ionic liquid/metal–organic framework composites for H2S removal from natural gas: A computational exploration. J. Phys. Chem. C 2015, 119, 3674–3683. [Google Scholar] [CrossRef]
- Ahmed, O.U.; Mjalli, F.S.; Gujarathi, A.M.; Al-Wahaibi, T.; Al-Wahaibi, Y.; AlNashef, I.M. Feasibility of phosphonium-based ionic liquids as solvents for extractive desulfurization of liquid fuels. Fluid Phase Equilib. 2015, 401, 102–109. [Google Scholar] [CrossRef]
- Zhou, Y.; Dyck, J.; Graham, T.W.; Luo, H.; Leonard, D.N.; Qu, J. Ionic liquids composed of phosphonium cations and organophosphate, carboxylate, and sulfonate anions as lubricant antiwear additives. Langmuir 2014, 30, 13301–13311. [Google Scholar] [CrossRef] [PubMed]
- Zakrewsky, M.; Lovejoy, K.S.; Kern, T.L.; Miller, T.E.; Le, V.; Nagy, A.; Goumas, A.M.; Iyer, R.S.; Del Sesto, R.E.; Koppisch, A.T.; et al. Ionic liquids as a class of materials for transdermal delivery and pathogen neutralization. Proc. Natl. Acad. Sci. USA 2014, 111, 13313–13318. [Google Scholar] [CrossRef] [PubMed]
- Cieszynska, A.; Wisniewski, M. Extraction of palladium(Ⅱ) from chloride solutions with cyphos® IL 101/toluene mixtures as novel extractant. Sep. Purif. Technol. 2010, 73, 202–207. [Google Scholar] [CrossRef]
- Kawano, R.; Matsui, H.; Matsuyama, C.; Sato, A.; Susan, M.A.B.H.; Tanabe, N.; Watanabe, M. High performance dye-sensitized solar cells using ionic liquids as their electrolytes. J. Photochem. Photobiol. A 2004, 164, 87–92. [Google Scholar] [CrossRef]
- Sato, T.; Masuda, G.; Takagi, K. Electrochemical properties of novel ionic liquids for electric double layer capacitor applications. Electrochim. Acta 2004, 49, 3603–3611. [Google Scholar] [CrossRef]
- Zhao, G.; Jiang, T.; Han, B.; Li, Z.; Zhang, J.; Liu, Z.; He, J.; Wu, W. Electrochemical reduction of supercritical carbon dioxide in ionic liquid 1-N-butyl-3-methylimidazolium hexafluorophosphate. J. Supercrit. Fluids 2004, 32, 287–291. [Google Scholar] [CrossRef]
- Gui, J.; Cong, X.; Liu, D.; Zhang, X.; Hu, Z.; Sun, Z. Novel brønsted acidic ionic liquid as efficient and reusable catalyst system for esterification. Catal. Commun. 2004, 5, 473–477. [Google Scholar] [CrossRef]
- Ionic Liquids in Synthesis; Wasserscheid, P.; Welton, T. (Eds.) Wiley-VCH: Weinheim, Germany, 2003. [Google Scholar]
- Fortunato, R.; González-Muñoz, M.J.; Kubasiewicz, M.; Luque, S.; Alvarez, J.R.; Afonso, C.A.M.; Coelhoso, I.M.; Crespo, J.G. Liquid membranes using ionic liquids: The influence of water on solute transport. J. Membr. Sci. 2005, 249, 153–162. [Google Scholar] [CrossRef]
- Scovazzo, P.; Kieft, J.; Finan, D.A.; Koval, C.; DuBois, D.; Noble, R. Gas separations using non-hexafluorophosphate [PF6]− anion supported ionic liquid membranes. J. Membr. Sci. 2004, 238, 57–63. [Google Scholar] [CrossRef]
- Gruttadauria, M.; Riela, S.; Lo Meo, P.; D’Anna, F.; Noto, R. Supported ionic liquid asymmetric catalysis. A new method for chiral catalysts recycling. The case of proline-catalyzed aldol reaction. Tetrahedron Lett. 2004, 45, 6113–6116. [Google Scholar] [CrossRef]
- Ito, N.; Arzhantsev, S.; Heitz, M.; Maroncelli, M. Solvation dynamics and rotation of coumarin 153 in alkylphosphonium ionic liquids. J. Phys. Chem. B 2004, 108, 5771–5777. [Google Scholar] [CrossRef]
- Kroon, M.C.; Peters, C.J. Supercritical fluids in ionic liquids. In Ionic Liquids Further Uncoiled; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2014; pp. 39–57. [Google Scholar]
- Biswas, R.; Lewis, J.E.; Maroncelli, M. Electronic spectral shifts, reorganization energies, and local density augmentation of coumarin 153 in supercritical solvents. Chem. Phys. Lett. 1999, 310, 485–494. [Google Scholar] [CrossRef]
- Iwai, Y.; Nagano, H.; Lee, G.S.; Uno, M.; Arai, Y. Measurement of entrainer effects of water and ethanol on solubility of caffeine in supercritical carbon dioxide by FT-IR spectroscopy. J. Supercrit. Fluids 2006, 38, 312–318. [Google Scholar] [CrossRef]
- Li, A.; Tian, Z.; Yan, T.; Jiang, D.-E.; Dai, S. Anion-functionalized task-specific ionic liquids: Molecular origin of change in viscosity upon CO2 capture. J. Phys. Chem. B 2014, 118, 14880–14887. [Google Scholar] [CrossRef] [PubMed]
- Bates, E.D.; Mayton, R.D.; Ntai, I.; Davis, J.H., Jr. CO2 capture by a task-specific ionic liquid. J. Am. Chem. Soc. 2002, 124, 926–927. [Google Scholar] [CrossRef] [PubMed]
- Vesna, N.-V.; Ana, S.; José, M.S.S.E.; Henrique, J.R.G.; Luis, P.N.R.; da Manuel Nunes, P. Multiphase equilibrium in mixtures of [C4mim][PF6] with supercritical carbon dioxide, water, and ethanol: Applications in catalysis. In Ionic Liquids III A: Fundamentals, Progress, Challenges, and Opportunities; American Chemical Society: Washington, DC, USA, 2005; Volume 901, pp. 301–310. [Google Scholar]
- Shariati, A.; Peters, C.J. High-pressure phase equilibria of systems with ionic liquids. J. Supercrit. Fluids 2005, 34, 171–176. [Google Scholar] [CrossRef]
- Kumełan, J.; Tuma, D.; Maurer, G. Simultaneous solubility of carbon dioxide and hydrogen in the ionic liquid [hmim][Tf2N]: Experimental results and correlation. Fluid Phase Equilib. 2011, 311, 9–16. [Google Scholar] [CrossRef]
- Jang, S.; Cho, D.-W.; Im, T.; Kim, H. High-pressure phase behavior of CO2 + 1-butyl-3-methylimidazolium chloride system. Fluid Phase Equilib. 2010, 299, 216–221. [Google Scholar] [CrossRef]
- Gutkowski, K.I.; Shariati, A.; Peters, C.J. High-pressure phase behavior of the binary ionic liquid system 1-octyl-3-methylimidazolium tetrafluoroborate + carbon dioxide. J. Supercrit. Fluids 2006, 39, 187–191. [Google Scholar] [CrossRef]
- Kroon, M.C.; Florusse, L.J.; Kühne, E.; Witkamp, G.-J.; Peters, C.J. Achievement of a homogeneous phase in ternary ionic liquid/carbon dioxide/organic systems. Ind. Eng. Chem. Res. 2010, 49, 3474–3478. [Google Scholar] [CrossRef]
- Mena, M.; Shirai, K.; Tecante, A.; Bárzana, E.; Gimeno, M. Enzymatic syntheses of linear and hyperbranched poly-l-lactide using compressed r134a–ionic liquid media. J. Supercrit. Fluids 2015, 103, 77–82. [Google Scholar] [CrossRef]
- Timko, M.T.; Nicholson, B.F.; Steinfeld, J.I.; Smith, K.A.; Tester, J.W. Partition coefficients of organic solutes between supercritical carbon dioxide and water: Experimental measurements and empirical correlations. J. Chem. Eng. Data 2004, 49, 768–778. [Google Scholar] [CrossRef]
- Andanson, J.-M.; Jutz, F.; Baiker, A. Investigation of binary and ternary systems of ionic liquids with water and/or supercritical CO2 by in situ attenuated total reflection infrared spectroscopy. J. Phys. Chem. B 2010, 114, 2111–2117. [Google Scholar] [CrossRef] [PubMed]
- Tian, Q.; Li, R.; Sun, H.; Xue, Z.; Mu, T. Theoretical and experimental study on the interaction between 1-butyl-3-methylimidazolium acetate and CO2. J. Mol. Liq. 2015, 208, 259–268. [Google Scholar] [CrossRef]
- Bhargava, B.L.; Balasubramanian, S. Insights into the structure and dynamics of a room-temperature ionic liquid: Ab initio molecular dynamics simulation studies of 1-N-butyl-3-methylimidazolium hexafluorophosphate ([Bmim][PF6]) and the [Bmim][PF6]−CO2 mixture. J. Phys. Chem. B 2007, 111, 4477–4487. [Google Scholar] [CrossRef] [PubMed]
- Kanakubo, M.; Makino, T.; Umecky, T.; Sakurai, M. Effect of partial pressure on CO2 solubility in ionic liquid mixtures of 1-butyl-3-methylimidazolium acetate and 1-butyl-3-methylimidazolium bis(trifluoromethanesulfonyl)amide. Fluid Phase Equilib. 2016, 420, 74–82. [Google Scholar] [CrossRef]
- Koller, T.M.; Heller, A.; Rausch, M.H.; Wasserscheid, P.; Economou, I.G.; Fröba, A.P. Mutual and self-diffusivities in binary mixtures of [Emim][B(CN)4] with dissolved gases by using dynamic light scattering and molecular dynamics simulations. J. Phys. Chem. B 2015, 119, 8583–8592. [Google Scholar] [CrossRef] [PubMed]
- Lu, J.; Liotta, C.L.; Eckert, C.A. Spectroscopically probing microscopic solvent properties of room-temperature ionic liquids with the addition of carbon dioxide. J. Phys. Chem. A 2003, 107, 3995–4000. [Google Scholar] [CrossRef]
- Kumelan, J.; Tuma, D.; Maurer, G. Partial molar volumes of selected gases in some ionic liquids. Fluid Phase Equilib. 2009, 275, 132–144. [Google Scholar] [CrossRef]
- Kim, J.E.; Lim, J.S.; Kang, J.W. Measurement and correlation of solubility of carbon dioxide in 1-alkyl-3-methylimidazolium hexafluorophosphate ionic liquids. Fluid Phase Equilib. 2011, 306, 251–255. [Google Scholar] [CrossRef]
- Blanchard, L.A.; Gu, Z.; Brennecke, J.F. High-pressure phase behavior of ionic liquid/CO2 systems. J. Phys. Chem. B 2001, 105, 2437–2444. [Google Scholar] [CrossRef]
- Afzal, W.; Liu, X.; Prausnitz, J.M. High solubilities of carbon dioxide in tetraalkyl phosphonium-based ionic liquids and the effect of diluents on viscosity and solubility. J. Chem. Eng. Data 2014, 59, 954–960. [Google Scholar] [CrossRef]
- Carvalho, P.J.; Álvarez, V.H.; Marrucho, I.M.; Aznar, M.; Coutinho, J.A.P. High carbon dioxide solubilities in trihexyltetradecylphosphonium-based ionic liquids. J. Supercrit. Fluids 2010, 52, 258–265. [Google Scholar] [CrossRef]
- Hutchings, J.W.; Fuller, K.L.; Heitz, M.P.; Hoffmann, M.M. Surprisingly high solubility of the ionic liquid trihexyltetradecylphosphonium chloride in dense carbon dioxide. Green Chem. 2005, 7, 475–478. [Google Scholar] [CrossRef]
- Lewis, J.E.; Maroncelli, M. On the (uninteresting) dependence of the absorption and emission transition moments of coumarin 153 on solvent. Chem. Phys. Lett. 1998, 282, 197–203. [Google Scholar] [CrossRef]
- Maroncelli, M.; Fleming, G.R. Picosecond solvation dynamics of coumarin 153: The importance of molecular aspects of solvation. J. Chem. Phys. 1987, 86, 6221–6239. [Google Scholar] [CrossRef]
- Zhang, X.-X.; Breffke, J.; Ernsting, N.P.; Maroncelli, M. Observations of probe dependence of the solvation dynamics in ionic liquids. Phys. Chem. Chem. Phys. 2015, 17, 12949–12956. [Google Scholar] [CrossRef] [PubMed]
- Becker, R.S.; Chakravorti, S.; Gartner, C.A.; de Graca Miguel, M. Photosensitizers: Comprehensive photophysics/photochemistry and theory of coumarins, chromones, their homologues and thione analogues. J. Chem. Soc. Faraday Trans. 1993, 89, 1007–1019. [Google Scholar] [CrossRef]
- Kaliya, O.L. The photochemistry of coumarins. Rus. Chem. Rev. 1992, 61, 683. [Google Scholar]
- Reynolds, L.; Gardecki, J.A.; Frankland, S.J.V.; Horng, M.L.; Maroncelli, M. Dipole solvation in nondipolar solvents: Experimental studies of reorganization energies and solvation dynamics. J. Phys. Chem. 1996, 100, 10337–10354. [Google Scholar] [CrossRef]
- Horng, M.L.; Gardecki, J.A.; Papazyan, A.; Maroncelli, M. Subpicosecond measurements of polar solvation dynamics: Coumarin 153 revisited. J. Phys. Chem. 1995, 99, 17311–17337. [Google Scholar] [CrossRef]
- Bradaric, C.J.; Downard, A.; Kennedy, C.; Robertson, A.J.; Zhou, Y. Industrial preparation of phosphonium ionic liquids. Green Chem. 2003, 5, 143–152. [Google Scholar] [CrossRef]
- McAtee, Z.P.; Heitz, M.P. Density, viscosity and excess properties in the trihexyltetradecylphosphonium chloride ionic liquid/methanol cosolvent system. J. Chem. Thermodyn. 2016, 93, 34–44. [Google Scholar] [CrossRef]
- Lemmon, E.W.; McLinden, M.O.; Friend, D.G. Thermophysical properties of fluid systems. In NIST Chemistry Webbook; Linstrom, P.J., Mallard, W.G., Eds.; Nist Standard Reference Database Number 69; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2001. Available online: http://webbook.nist.gov (accessed on 18 April 2017).
- Span, R.; Wagner, W. A new equation of state for carbon dioxide covering the fluid region from the triple-point temperature to 1100 K at pressures up to 800 MPa. J. Phys. Chem. Ref. Data 1996, 25, 1509–1596. [Google Scholar] [CrossRef]
- Barra, K.M.; Sabatini, R.P.; McAtee, Z.P.; Heitz, M.P. Solvation and rotation dynamics in the trihexyl(tetradecyl)phosphonium chloride ionic liquid/methanol cosolvent system. J. Phys. Chem. B 2014, 118, 12979–12992. [Google Scholar] [CrossRef] [PubMed]
- O’Connor, D.V.; Phillips, D. Time-Correlated Single Photon Counting; Academic Press: Cambridge, MA, USA, 1984. [Google Scholar]
- Becker, W. Advanced Time-Correlated Single Photon Counting Techniques; Springer: Berlin, Germany, 2005. [Google Scholar]
- Lakowicz, J.R. Principles of Fluorescence Spectroscopy; Springer: New York, NY, USA, 2006. [Google Scholar]
- Spartan’16, version 16; Parallel Suite; Wavefunction Inc.: Irvine, CA, USA, 2016.
- Shao, Y.; Molnar, L.F.; Jung, Y.; Kussmann, J.; Ochsenfeld, C.; Brown, S.T.; Gilbert, A.T.B.; Slipchenko, L.V.; Levchenko, S.V.; O’Neill, D.P.; et al. Advances in methods and algorithms in a modern quantum chemistry program package. Phys. Chem. Chem. Phys. 2006, 8, 3172–3191. [Google Scholar] [CrossRef] [PubMed]
- Shao, Y.; Gan, Z.; Epifanovsky, E.; Gilbert, A.T.B.; Wormit, M.; Kussmann, J.; Lange, A.W.; Behn, A.; Deng, J.; Feng, X.; et al. Advances in molecular quantum chemistry contained in the Q-Chem 4 program package. Mol. Phys. 2015, 113, 184–215. [Google Scholar] [CrossRef]
- Arzhantsev, S.; Ito, N.; Heitz, M.; Maroncelli, M. Solvation dynamics of coumarin 153 in several classes of ionic liquids: Cation dependence of the ultrafast component. Chem. Phys. Lett. 2003, 381, 278–286. [Google Scholar] [CrossRef]
- Hoffmann, M.M.; Heitz, M.P.; Carr, J.B.; Tubbs, J.D. Surfactants in green solvent systems—Current and future research directions. J. Dispers. Sci. Technol. 2003, 24, 155–171. [Google Scholar] [CrossRef]
- Heitz, M.P.; Carlier, C.; deGrazia, J.; Harrison, K.L.; Johnston, K.P.; Randolph, T.W.; Bright, F.V. Water core within perfluoropolyether-based microemulsions formed in supercritical carbon dioxide. J. Phys. Chem. B 1997, 101, 6707–6714. [Google Scholar] [CrossRef]
- Johnston, K.P.; Harrison, K.L.; Clarke, M.J.; Howdle, S.M.; Heitz, M.P.; Bright, F.V.; Carlier, C.; Randolph, T.W. Water-in-carbon dioxide microemulsions: An environment for hydrophiles including proteins. Science 1996, 271, 624–626. [Google Scholar] [CrossRef]
- Holmes, J.D.; Ziegler, K.J.; Audriani, M.; Lee, C.T., Jr.; Bhargave, P.A.; Steytler, D.C.; Johnston, K.P. Buffering the aqueous phase ph in water-in- CO2 microemulsions. J. Phys. Chem. B 1999, 103, 5703–5711. [Google Scholar] [CrossRef]
- Lim, K.T.; Hwang, H.S.; Lee, M.S.; Lee, G.D.; Hong, S.S.; Johnston, K.P. Formation of TiO2 nanoparticles in water-in-CO2 microemulsions. Chem. Commun. 2002, 1528–1529. [Google Scholar] [CrossRef]
- Lim, K.T.; Hwang, H.S.; Ryoo, W.; Johnston, K.P. Synthesis of TiO2 nanoparticles utilizing hydrated reverse micelles in CO2. Langmuir 2004, 20, 2466–2471. [Google Scholar] [CrossRef] [PubMed]
- Verma, P.; Pal, H. Aggregation studies of dipolar coumarin-153 dye in polar solvents: A photophysical study. J. Phys. Chem. A 2014, 118, 6950–6964. [Google Scholar] [CrossRef] [PubMed]
- Sen, T.; Bhattacharyya, S.; Mandal, S.; Patra, A. Spectroscopic investigations on the h-type aggregation of coumarin 153 dye molecules: Role of au nanoparticles and γ-cyclodextrin. J. Fluoresc. 2012, 22, 303–310. [Google Scholar] [CrossRef] [PubMed]
- Verma, P.; Pal, H. Intriguing h-aggregate and h-dimer formation of coumarin-481 dye in aqueous solution as evidenced from photophysical studies. J. Phys. Chem. A 2012, 116, 4473–4484. [Google Scholar] [CrossRef] [PubMed]
- Verma, P.; Pal, H. Unusual h-type aggregation of coumarin-481 dye in polar organic solvents. J. Phys. Chem. A 2013, 117, 12409–12418. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.; Greenman, L.; Sarovar, M.; Whaley, K.B. Ab initio calculation of molecular aggregation effects: A coumarin-343 case study. J. Phys. Chem. A 2013, 117, 11072–11085. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Cole, J.M.; Low, K.S. Molecular origins of dye aggregation and complex formation effects in coumarin 343. J. Phys. Chem. C 2013, 117, 14723–14730. [Google Scholar] [CrossRef]
- Kasha, M.; Rawls, H.R.; El-Bayoumi, M.A. The exciton model in molecular spectroscopy. Pure Appl. Chem. 1965, 11, 371–392. [Google Scholar] [CrossRef]
- Kasha, M. Energy transfer mechanisms and the molecular exciton model for molecular aggregates. Radiat. Res. 1963, 20, 55–70. [Google Scholar] [CrossRef] [PubMed]
- Minami, K.; Aizawa, T.; Kanakubo, M.; Hiejima, Y.; Nanjo, H.; Smith, J.; Richard, L. Local density augmentation of excited 1-(dimethylamino)naphthalene in supercritical water. J. Supercrit. Fluids 2006, 39, 206–210. [Google Scholar] [CrossRef]
- Ruckenstein, E.; Shulgin, I.L. Why density augmentation occurs in dilute supercritical solutions. Chem. Phys. Lett. 2000, 330, 551–557. [Google Scholar] [CrossRef]
- Ingrosso, F.; Ladanyi, B.M.; Mennucci, B.; Scalmani, G. Solvation of coumarin 153 in supercritical fluoroform. J. Phys. Chem. B 2006, 110, 4953–4962. [Google Scholar] [CrossRef] [PubMed]
- Heitz, M.P.; Maroncelli, M. Rotation of aromatic solutes in supercritical CO2: Are rotation times anomalously slow in the near critical regime? J. Phys. Chem. A 1997, 101, 5852–5868. [Google Scholar] [CrossRef]
- Cigáň, M.; Donovalová, J.; Szöcs, V.; Gašpar, J.; Jakusová, K.; Gáplovský, A. 7-(dimethylamino)coumarin-3-carbaldehyde and its phenylsemicarbazone: Tict excited state modulation, fluorescent h-aggregates, and preferential solvation. J. Phys. Chem. A 2013, 117, 4870–4883. [Google Scholar] [CrossRef] [PubMed]
- Birks, J.B. Photophysics of Aromatic Molecules; Wiley-Interscience: Hoboken, NJ, USA, 1970. [Google Scholar]
- Jin, H.; Baker, G.A.; Arzhantsev, S.; Dong, J.; Maroncelli, M. Solvation and rotational dynamics of coumarin 153 in ionic liquids: Comparisons to conventional solvents. J. Phys. Chem. B 2007, 111, 7291–7302. [Google Scholar] [CrossRef] [PubMed]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).