Interpretable Machine Learning Models and Symbolic Regressions Reveal Transfer of Per- and Polyfluoroalkyl Substances (PFASs) in Plants: A New Small-Data Machine Learning Method to Augment Data and Obtain Predictive Equations
Abstract
1. Introduction
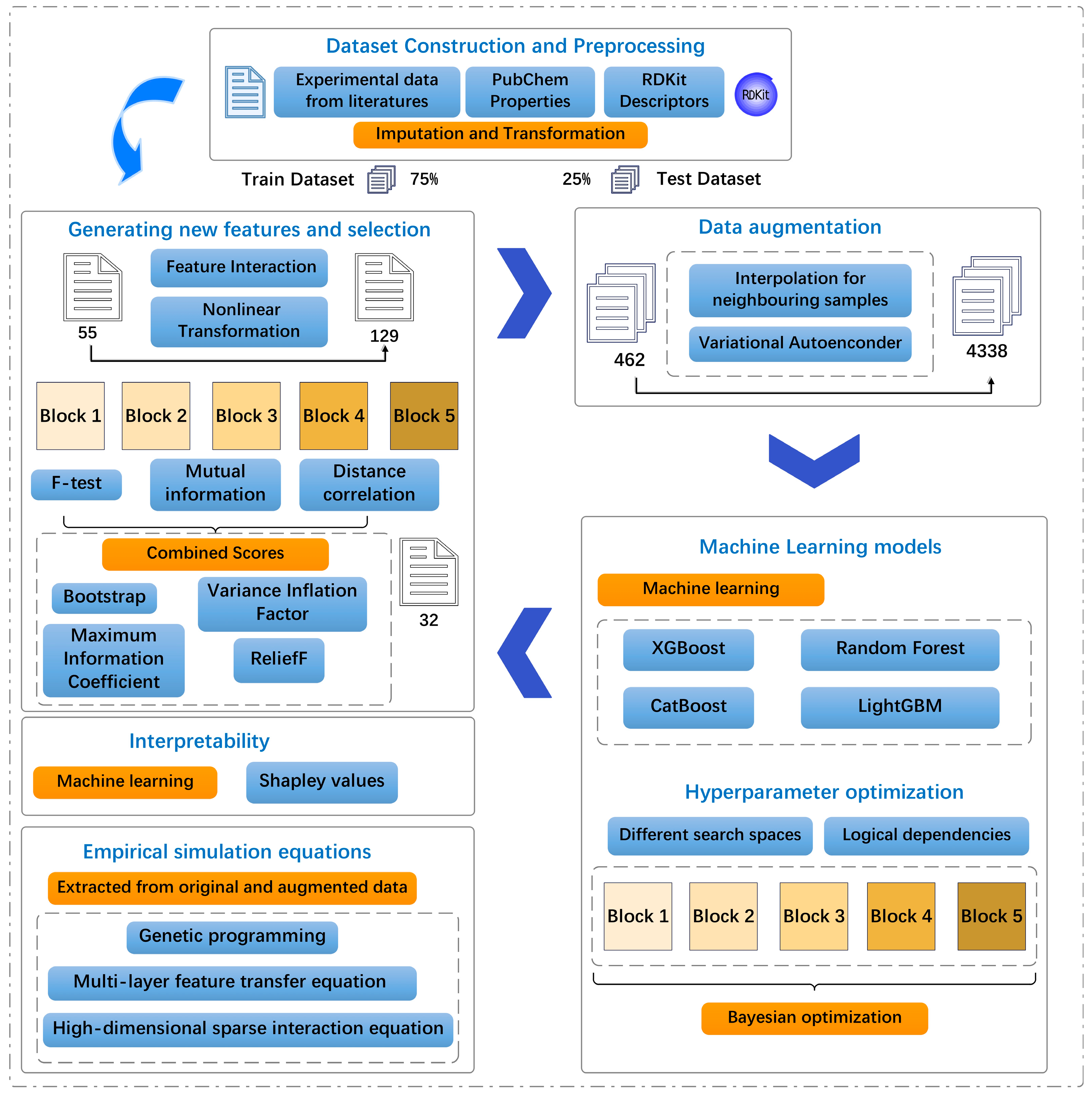
2. Materials and Methods
2.1. Data Preprocessing, Derived Feature Construction, and Selection for log RCF
2.1.1. Data Description and Preprocessing
2.1.2. Derived Feature Construction and Selection
2.2. Data Augmentation for log RCF Using Stratified Variational Regression
2.3. Development of ML Model for log RCF
2.3.1. ML Models
2.3.2. Hyperparameter Search Using Bayesian Search
2.4. Model Interpretability Using SHAP Analysis
2.5. Establishment of Empirical Simulation Equations for Predicting log RCF
2.5.1. Genetic Programming (GP) Symbolic Regression
2.5.2. Multilayer Feature Transfer Equation Construction (MFTEC)
2.5.3. High-Dimensional Sparse Interaction Equation (HSIE)
3. Results and Discussion
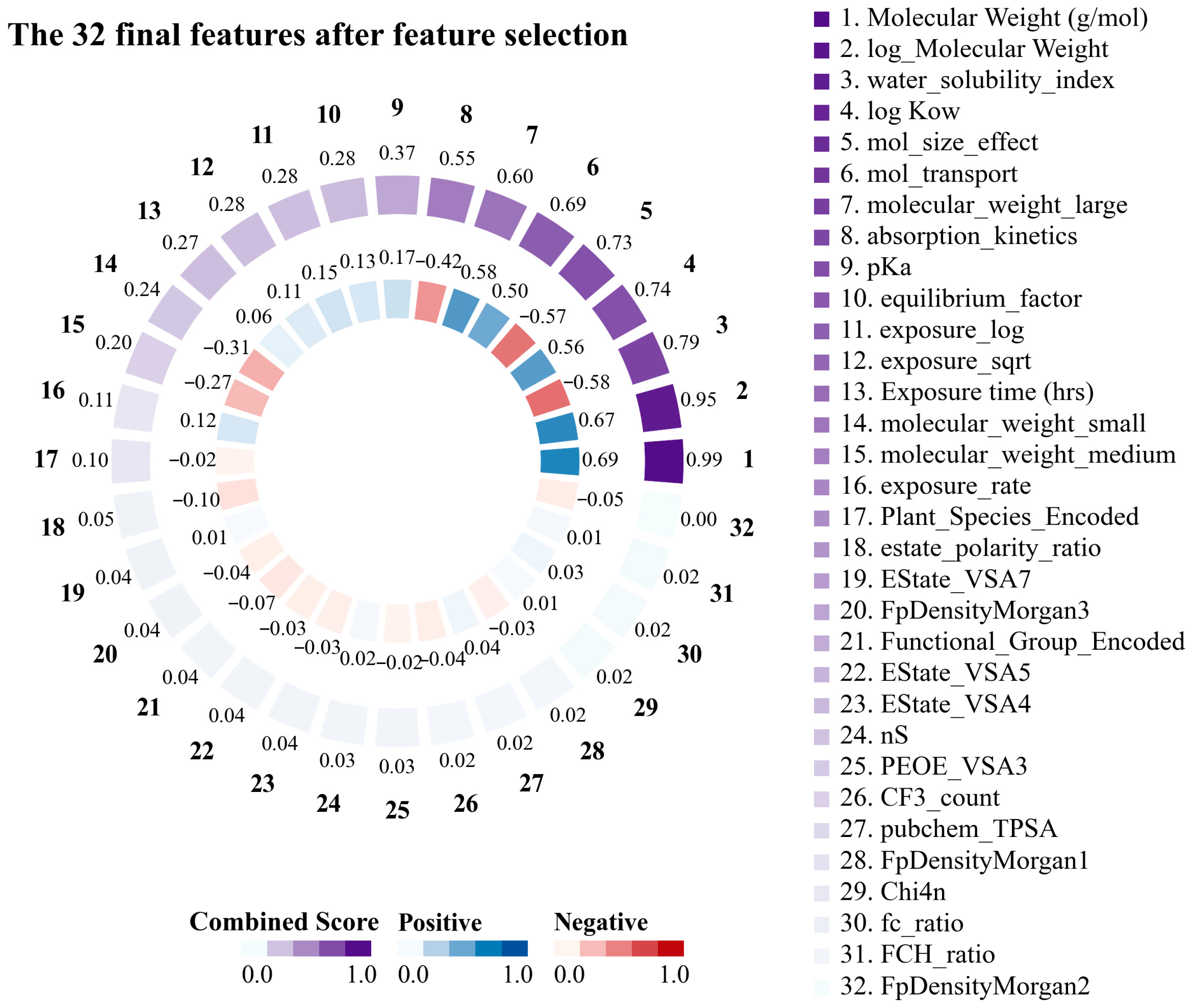
3.1. Based and Derived Features of PFASs Constructed Based on Empirical Formula Performance and Selection
3.2. Statistical Analysis Between Original and Augmented Data for the Training Set
3.3. Different Model Predictions for log RCF of PFASs in Plants
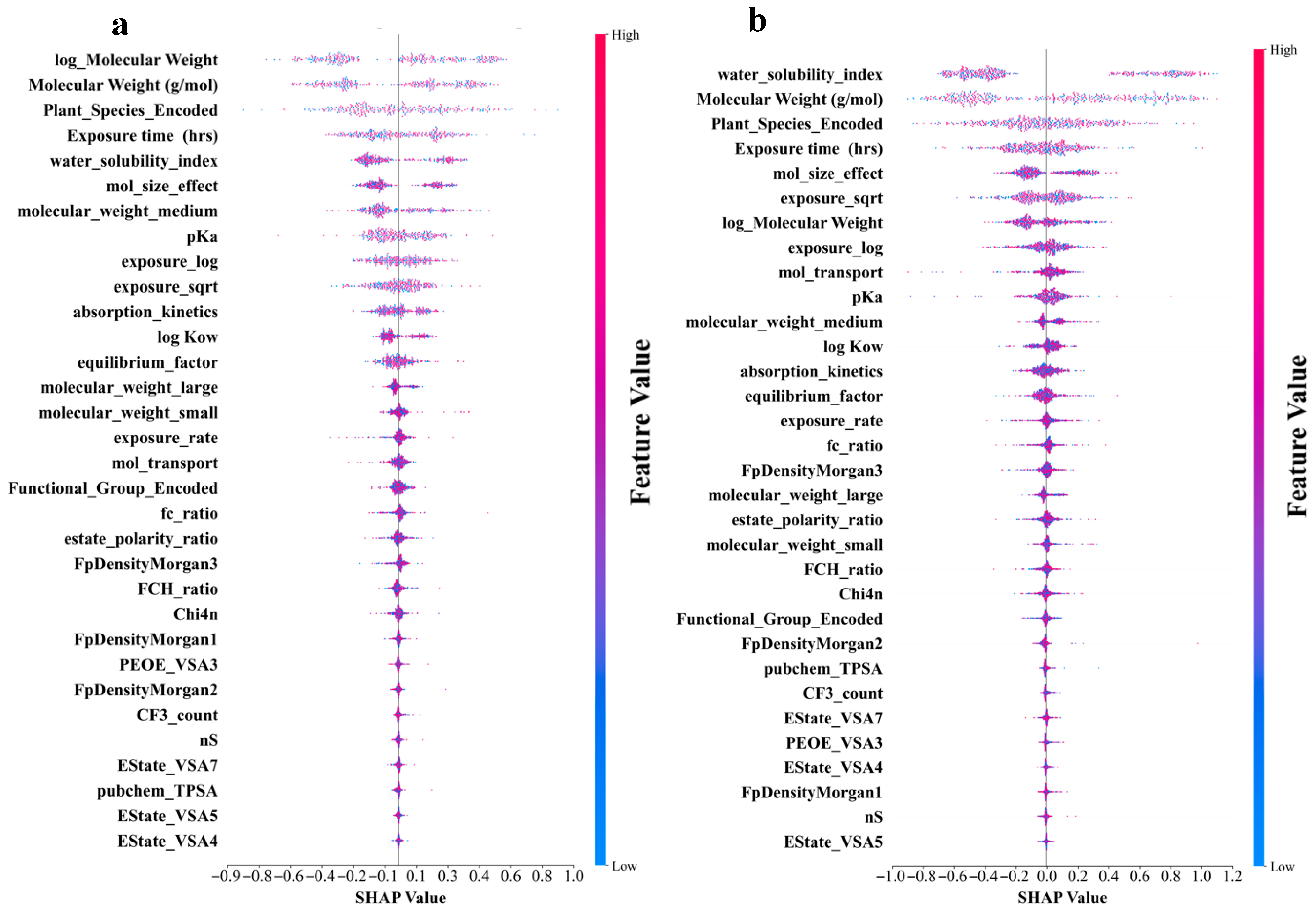
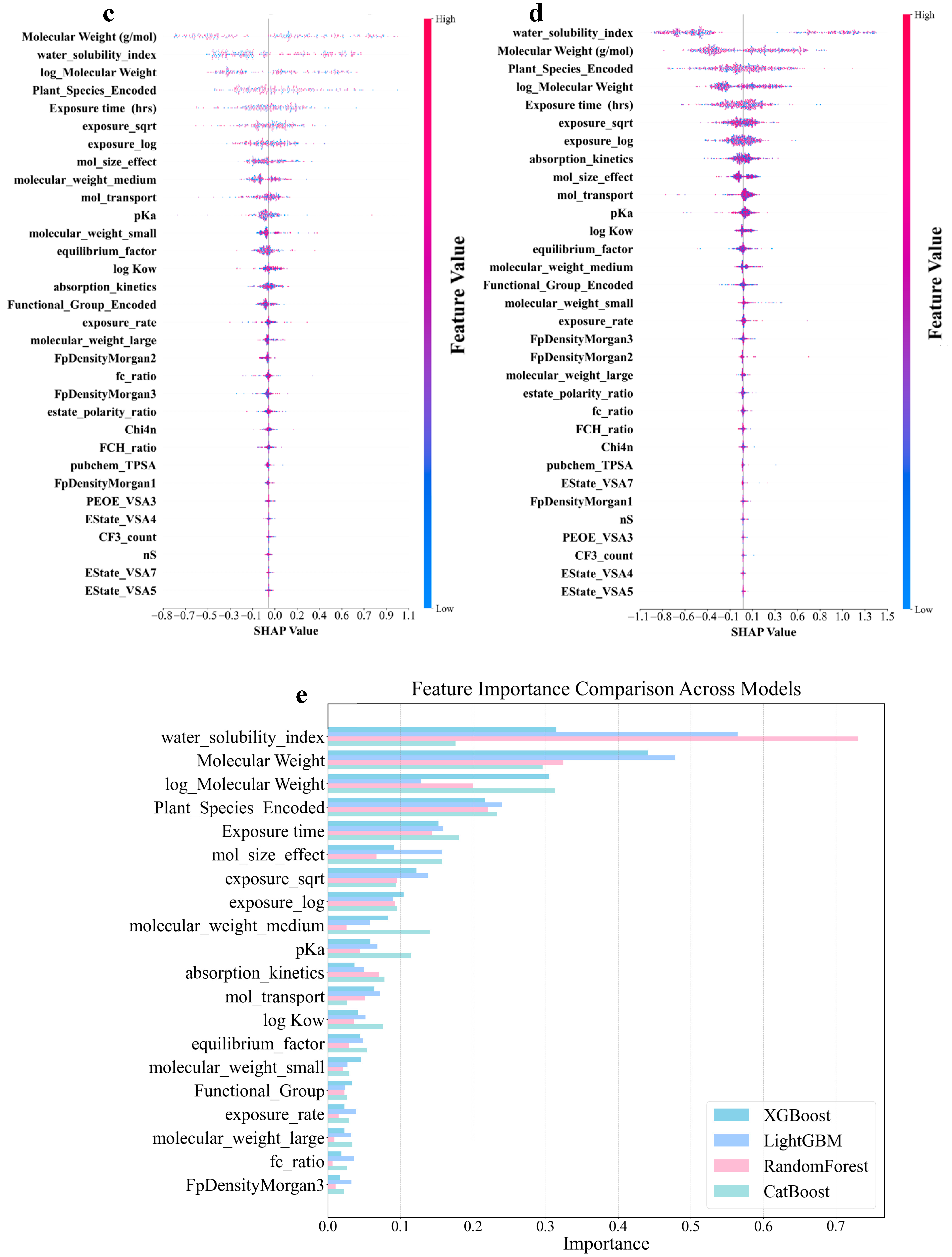
3.4. Identification of Different Important Features for Different Predictive Models of log RCF
3.5. Developing Mathematical Models to Estimate log RCF Values
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, X.; Shen, X.; Jiang, W.; Xi, Y.; Li, S. Comprehensive review of emerging contaminants: Detection technologies, environmental impact, and management strategies. Ecotoxicol. Environ. Saf. 2024, 278, 116420. [Google Scholar] [CrossRef]
- Ilango, A.K.; Zhang, W.; Liang, Y. Uptake of per- and polyfluoroalkyl substances by Conservation Reserve Program’s seed mix in biosolids-amended soil. Environ. Pollut. 2024, 363, 125235. [Google Scholar] [CrossRef] [PubMed]
- Li, Z. Plant Uptake Models of Pesticides: Advancing Integrated Pest Management, Food Safety, and Health Risk Assessment. Rev. Environ. Contam. Toxicol. 2025, 263, 3. [Google Scholar] [CrossRef]
- Trapp, S. Modelling uptake into roots and subsequent translocation of neutral and ionisable organic compounds. Pest Manag. Sci. 2000, 56, 767–778. [Google Scholar] [CrossRef]
- Li, Y.; Sallach, J.B.; Zhang, W.; Boyd, S.A.; Li, H. Characterization of Plant Accumulation of Pharmaceuticals from Soils with Their Concentration in Soil Pore Water. Environ. Sci. Technol. 2022, 56, 9346–9355. [Google Scholar] [CrossRef] [PubMed]
- Schymanski, E.L.; Zhang, J.; Thiessen, P.A.; Chirsir, P.; Kondic, T.; Bolton, E.E. Per- and Polyfluoroalkyl Substances (PFAS) in PubChem: 7 Million and Growing. Environ. Sci. Technol. 2023, 57, 16918–16928. [Google Scholar] [CrossRef]
- Evich, M.G.; Davis, M.J.B.; McCord, J.P.; Acrey, B.; Awkerman, J.A.; Knappe, D.R.U.; Lindstrom, A.B.; Speth, T.F.; Tebes-Stevens, C.; Strynar, M.J.; et al. Per- and polyfluoroalkyl substances in the environment. Science 2022, 375, eabg9065. [Google Scholar] [CrossRef]
- Ogunbiyi, O.D.; Ajiboye, T.O.; Omotola, E.O.; Oladoye, P.O.; Olanrewaju, C.A.; Quinete, N. Analytical approaches for screening of per- and poly fluoroalkyl substances in food items: A review of recent advances and improvements*. Environ. Pollut. 2023, 329, 121705. [Google Scholar] [CrossRef]
- Ji, Y.; Wang, X.; Wang, R.; Wang, J.; Zhao, X.; Wu, F. Toxicity prediction and risk assessment of per- and polyfluoroalkyl substances for threatened and endangered fishes. Environ. Pollut. 2024, 361, 124920. [Google Scholar] [CrossRef]
- Schriever, C.; Lamshoeft, M. Lipophilicity matters—A new look at experimental plant uptake data from literature. Sci. Total Environ. 2020, 713, 136667. [Google Scholar] [CrossRef]
- Yang, H.; Zhao, Y.; Chai, L.; Ma, F.; Yu, J.; Xiao, K.-Q.; Gu, Q. Bio-accumulation and health risk assessments of per- and polyfluoroalkyl substances in wheat grains. Environ. Pollut. 2024, 356, 124351. [Google Scholar] [CrossRef] [PubMed]
- Ismail, U.M.; Elnakar, H.; Khan, M.F. Sources, Fate, and Detection of Dust-Associated Perfluoroalkyl and Polyfluoroalkyl Substances (PFAS): A Review. Toxics 2023, 11, 335. [Google Scholar] [CrossRef] [PubMed]
- Nayak, S.; Sahoo, G.; Das, I.I.; Mohanty, A.K.; Kumar, R.; Sahoo, L.; Sundaray, J.K. Poly- and Perfluoroalkyl Substances (PFAS): Do They Matter to Aquatic Ecosystems? Toxics 2023, 11, 543. [Google Scholar] [CrossRef]
- Collins, C.D.; Finnegan, E. Modeling the Plant Uptake of Organic Chemicals, Including the Soil-Air-Plant Pathway. Environ. Sci. Technol. 2010, 44, 998–1003. [Google Scholar] [CrossRef] [PubMed]
- Qu, R.; Wang, J.X.; Li, X.J.; Zhang, Y.; Yin, T.L.; Yang, P. Per- and Polyfluoroalkyl Substances (PFAS) Affect Female Reproductive Health: Epidemiological Evidence and Underlying Mechanisms. Toxics 2024, 12, 678. [Google Scholar] [CrossRef]
- Alnaimat, S.; Mohsen, O.; Elnakar, H. Perfluorooctanoic Acids (PFOA) removal using electrochemical oxidation: A machine learning approach. J. Environ. Manag. 2024, 370, 122857. [Google Scholar] [CrossRef]
- Nie, Q.; Liu, T. Large language models: Tools for new environmental decision-making. J. Environ. Manag. 2025, 375, 124373. [Google Scholar] [CrossRef]
- Gao, F.; Shen, Y.; Sallach, B.; Li, H.; Zhang, W.; Li, Y.; Liu, C. Predicting crop root concentration factors of organic contaminants with machine learning models. J. Hazard. Mater. 2022, 424, 127437. [Google Scholar] [CrossRef]
- Wang, Y.; Dong, J.; Zhou, Y.; Cheng, Y.; Zhao, X.; Peijnenburg, W.J.G.M.; Vijver, M.G.; Leung, K.M.Y.; Fan, W.; Wu, F. Addressing the Data Scarcity Problem in Ecotoxicology via Small Data Machine Learning Methods. Environ. Sci. Technol. 2025, 59, 5867–5871. [Google Scholar] [CrossRef]
- Rao, K.M.; Saikrishna, G.; Supriya, K. Data preprocessing techniques: Emergence and selection towards machine learning models-a practical review using HPA dataset. Multimed. Tools Appl. 2023, 82, 37177–37196. [Google Scholar] [CrossRef]
- Reddy, G. A reinforcement-based mechanism for discontinuous learning. Proc. Natl. Acad. Sci. USA 2022, 119, e2215352119. [Google Scholar] [CrossRef] [PubMed]
- Moritz, P.; Nishihara, R.; Wang, S.; Tumanov, A.; Liaw, R.; Liang, E.; Elibol, M.; Yang, Z.; Paul, W.; Jordan, M.I.; et al. Ray: A Distributed Framework for Emerging AI Applications. arXiv 2018, arXiv:1712.05889. [Google Scholar]
- Liu, S.; Kappes, B.B.; Amin-ahmadi, B.; Benafan, O.; Zhang, X.; Stebner, A.P. Physics-informed machine learning for composition–process–property design: Shape memory alloy demonstration. Appl. Mater. Today 2021, 22, 100898. [Google Scholar] [CrossRef]
- Maeda, K.; Hirano, M.; Hayashi, T.; Iida, M.; Kurata, H.; Ishibashi, H. Elucidating Key Characteristics of PFAS Binding to Human Peroxisome Proliferator-Activated Receptor Alpha: An Explainable Machine Learning Approach. Environ. Sci. Technol. 2023, 58, 488–497. [Google Scholar] [CrossRef]
- Ileberi, E.; Sun, Y.; Wang, Z. A machine learning based credit card fraud detection using the GA algorithm for feature selection. J. Big Data 2022, 9, 24. [Google Scholar] [CrossRef]
- Song, W.C.; Xie, J. Group feature screening via the F statistic. Commun. Stat.-Simul. Comput. 2022, 51, 1921–1931. [Google Scholar] [CrossRef]
- Gonzalez, M.E.; Silva, J.F.; Videla, M.; Orchard, M.E. Data-Driven Representations for Testing Independence: Modeling, Analysis and Connection With Mutual Information Estimation. IEEE Trans. Signal Process. 2022, 70, 158–173. [Google Scholar] [CrossRef]
- Edelmann, D.; Mori, T.F.; Szekely, G.J. On relationships between the Pearson and the distance correlation coefficients. Stat. Probab. Lett. 2021, 169, 108960. [Google Scholar] [CrossRef]
- Xu, P.; Nian, M.; Xiang, J.; Zhang, X.; Cheng, P.; Xu, D.; Chen, Y.; Wang, X.; Chen, Z.; Lou, X.; et al. Emerging PFAS Exposure Is More Potent in Altering Childhood Lipid Levels Mediated by Mitochondrial DNA Copy Number. Environ. Sci. Technol. 2025, 59, 2484–2493. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, J.; Dai, Y.; Zhang, L.; Guo, J.; Xu, S.; Chang, X.; Wu, C.; Zhou, Z. Mediating effect of endocrine hormones on association between per- and polyfluoroalkyl substances exposure and birth size: Findings from sheyang mini birth cohort study. Environ. Res. 2023, 226, 115658. [Google Scholar] [CrossRef]
- Santibanez, N.; Vega, M.; Perez, T.; Enriquez, R.; Escalona, C.E.; Oliver, C.; Romero, A. In vitro effects of phytogenic feed additive on Piscirickettsia salmonisgrowth and biofilm formation. J. Fish Dis. 2024, 47, e13913. [Google Scholar] [CrossRef] [PubMed]
- Bolon-Canedo, V.; Sanchez-Marono, N.; Alonso-Betanzos, A. Recent advances and emerging challenges of feature selection in the context of big data. Knowl.-Based Syst. 2015, 86, 33–45. [Google Scholar] [CrossRef]
- Kovacs, K.D.; Haidu, I. Tracing out the effect of transportation infrastructure on NO2 concentration levels with Kernel Density Estimation by investigating successive COVID-19-induced lockdowns. Environ. Pollut. 2022, 309, 119719. [Google Scholar] [CrossRef]
- Dong, J.; Tsai, G.; Olivares, C.I. Prediction of 35 Target Per- and Polyfluoroalkyl Substances (PFASs) in California Groundwater Using Multilabel Semisupervised Machine Learning. ACS EST Water 2023, 4, 969–981. [Google Scholar] [CrossRef]
- Kang, J.-K.; Lee, D.; Muambo, K.E.; Choi, J.-w.; Oh, J.-E. Development of an embedded molecular structure-based model for prediction of micropollutant treatability in a drinking water treatment plant by machine learning from three years monitoring data. Water Res. 2023, 239, 120037. [Google Scholar] [CrossRef] [PubMed]
- Ng, K.; Alygizakis, N.; Androulakakis, A.; Galani, A.; Aalizadeh, R.; Thomaidis, N.S.; Slobodnik, J. Target and suspect screening of 4777 per- and polyfluoroalkyl substances (PFAS) in river water, wastewater, groundwater and biota samples in the Danube River Basin. J. Hazard. Mater. 2022, 436, 129276. [Google Scholar] [CrossRef]
- Lyu, H.; Xu, Z.; Zhong, J.; Gao, W.; Liu, J.; Duan, M. Machine learning-driven prediction of phosphorus adsorption capacity of biochar: Insights for adsorbent design and process optimization. J. Environ. Manag. 2024, 369, 122405. [Google Scholar] [CrossRef]
- Zheng, S.-S.; Guo, W.-Q.; Lu, H.; Si, Q.-S.; Liu, B.-H.; Wang, H.-Z.; Zhao, Q.; Jia, W.-R.; Yu, T.-P. Machine learning approaches to predict the apparent rate constants for aqueous organic compounds by ferrate. J. Environ. Manag. 2023, 329, 116904. [Google Scholar] [CrossRef]
- Lee, E.; You, Y.-W.; Jung, Y.-H.; Kam, J. Explainable AI-based risk assessment for pluvial floods over South Korea. J. Environ. Manag. 2025, 385, 125640. [Google Scholar] [CrossRef]
- Li, T.; Wu, Y.; Ren, F.; Li, M. Estimation of unrealized forest carbon potential in China using time-varying Boruta-SHAP-random forest model and climate vegetation productivity index. J. Environ. Manag. 2025, 377, 124649. [Google Scholar] [CrossRef]
- Ding, J.; Lee, S.-J.; Vlahos, L.; Yuki, K.; Rada, C.C.; van Unen, V.; Vuppalapaty, M.; Chen, H.; Sura, A.; McCormick, A.K.; et al. Therapeutic blood-brain barrier modulation and stroke treatment by a bioengineered FZD4-selective WNT surrogate in mice. Nat. Commun. 2023, 14, 2947. [Google Scholar] [CrossRef]
- Cao, H.; Peng, J.; Zhou, Z.; Sun, Y.; Wang, Y.; Liang, Y. Insight into the defluorination ability of per- and polyfluoroalkyl substances based on machine learning and quantum chemical computations. Sci. Total Environ. 2022, 807, 151018. [Google Scholar] [CrossRef] [PubMed]
- Schossler, R.T.; Ojo, S.; Yu, X.B. Optimizing Photodegradation Rate Prediction of Organic Contaminants: Models with Fine-Tuned Hyperparameters and SHAP Feature Analysis for Informed Decision Making. ACS EST Water 2023, 4, 1131–1145. [Google Scholar] [CrossRef]
- Sheik, A.G.; Krishna, S.B.N.; Patnaik, R.; Ambati, S.R.; Bux, F.; Kumari, S. Digitalization of phosphorous removal process in biological wastewater treatment systems: Challenges, and way forward. Environ. Res. 2024, 252, 119133. [Google Scholar] [CrossRef] [PubMed]
- Fabregat-Palau, J.; Ershadi, A.; Finkel, M.; Rigol, A.; Vidal, M.; Grathwohl, P. Modeling PFAS Sorption in Soils Using Machine Learning. Environ. Sci. Technol. 2025, 59, 7678–7687. [Google Scholar] [CrossRef] [PubMed]
- Lundberg, S.M.; Erion, G.; Chen, H.; DeGrave, A.; Prutkin, J.M.; Nair, B.; Katz, R.; Himmelfarb, J.; Bansal, N.; Lee, S.-I. From local explanations to global understanding with explainable AI for trees. Nat. Mach. Intell. 2020, 2, 56–67. [Google Scholar] [CrossRef]
- Xu, P.; Peng, J.; Yuan, T.; Chen, Z.; He, H.; Wu, Z.; Li, T.; Li, X.; Wang, L.; Gao, L.; et al. High-throughput mapping of single-neuron projection and molecular features by retrograde barcoded labeling. eLife 2024, 13, e85419. [Google Scholar] [CrossRef]
- Pak, W.; Hindges, R.; Lim, Y.S.; Pfaff, S.L.; O’Leary, D.D.M. Magnitude of binocular vision controlled by islet-2 repression of a genetic program that specifies laterality of retinal axon pathfinding. Cell 2004, 119, 567–578. [Google Scholar] [CrossRef]
- Adu, O.; Bryant, M.T.; Ma, X.; Sharma, V.K. A Machine Learning Approach for Predicting Plant Uptake and Translocation of Per- and Polyfluoroalkyl Substances (PFAS) from Hydroponics. ACS EST Eng. 2024, 4, 1884–1890. [Google Scholar] [CrossRef]
- Huang, D.; Xiao, R.; Du, L.; Zhang, G.; Yin, L.; Deng, R.; Wang, G. Phytoremediation of poly- and perfluoroalkyl substances: A review on aquatic plants, influencing factors, and phytotoxicity. J. Hazard. Mater. 2021, 418, 126314. [Google Scholar] [CrossRef]
- Linderman, G.C.; Rachh, M.; Hoskins, J.G.; Steinerberger, S.; Kluger, Y. Fast interpolation-based t-SNE for improved visualization of single-cell RNA-seq data. Nat. Methods 2019, 16, 243–245. [Google Scholar] [CrossRef] [PubMed]
- Chen, K.; Zhang, Z. Pedestrian Counting with Back-Propagated Information and Target Drift Remedy. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 639–647. [Google Scholar] [CrossRef]
- Nguyen, D.V.; Seo, M.; Chen, Y.; Wu, D. Enhancing hydrogen sulfide control in urban sewer systems using machine learning models: Development of a new predictive simulation approach by using boosting algorithm. J. Hazard. Mater. 2025, 491, 137906. [Google Scholar] [CrossRef] [PubMed]
- Li, F.; Duan, J.; Tian, S.; Ji, H.; Zhu, Y.; Wei, Z.; Zhao, D. Short-chain per- and polyfluoroalkyl substances in aquatic systems: Occurrence, impacts and treatment. Chem. Eng. J. 2020, 380, 122506. [Google Scholar] [CrossRef]
- Montal, M.; Mueller, P. Formation of bimolecular membranes from lipid monolayers and a study of their electrical properties. Proc. Natl. Acad. Sci. USA 1972, 69, 3561–3566. [Google Scholar] [CrossRef]
- Potts, D.S.; Bregante, D.T.; Adams, J.S.; Torres, C.; Flaherty, D.W. Influence of solvent structure and hydrogen bonding on catalysis at solid-liquid interfaces. Chem. Soc. Rev. 2021, 50, 12308–12337. [Google Scholar] [CrossRef]

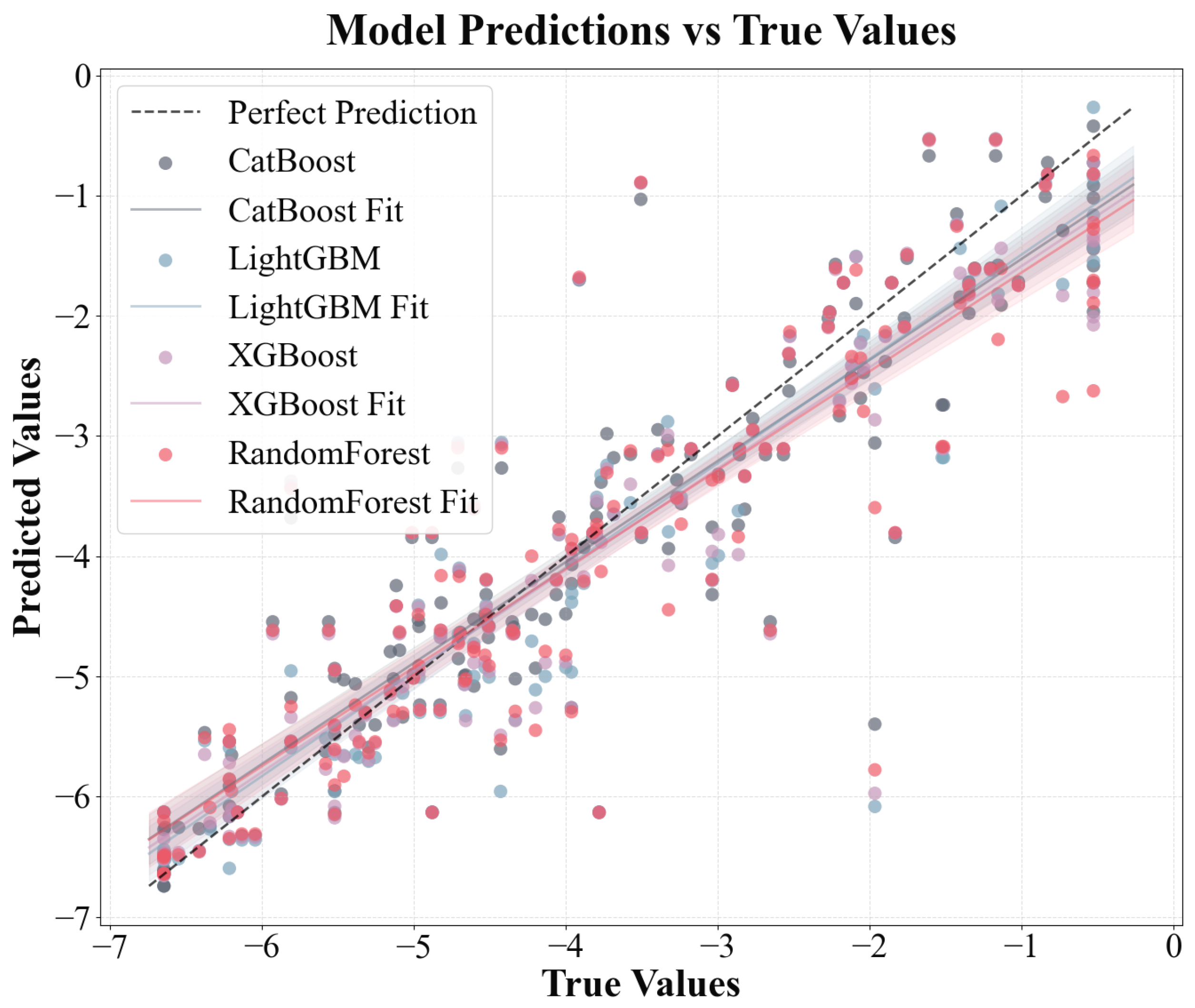

| Models | Dataset | R2 | RMSE | |
|---|---|---|---|---|
| CatBoost | Validation | Original | 0.8224 | 0.7401 |
| Augmented | 0.8564 | 0.6906 | ||
| Test | Original | 0.8012 | 0.8015 | |
| Augmented | 0.8300 | 0.7401 | ||
| LightGBM | Validation | Original | 0.8032 | 0.7793 |
| Augmented | 0.8449 | 0.7178 | ||
| Test | Original | 0.7851 | 0.8334 | |
| Augmented | 0.8249 | 0.7512 | ||
| XGBoost | Validation | Original | 0.7953 | 0.7902 |
| Augmented | 0.8503 | 0.7050 | ||
| Test | Original | 0.7827 | 0.8380 | |
| Augmented | 0.8147 | 0.7727 | ||
| RandomForest | Validation | Original | 0.7913 | 0.8029 |
| Augmented | 0.8386 | 0.7321 | ||
| Test | Original | 0.7713 | 0.8597 | |
| Augmented | 0.7790 | 0.8438 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Li, Y.; Li, Y.; Zhao, L.; Yang, Y. Interpretable Machine Learning Models and Symbolic Regressions Reveal Transfer of Per- and Polyfluoroalkyl Substances (PFASs) in Plants: A New Small-Data Machine Learning Method to Augment Data and Obtain Predictive Equations. Toxics 2025, 13, 579. https://doi.org/10.3390/toxics13070579
Zhang Y, Li Y, Li Y, Zhao L, Yang Y. Interpretable Machine Learning Models and Symbolic Regressions Reveal Transfer of Per- and Polyfluoroalkyl Substances (PFASs) in Plants: A New Small-Data Machine Learning Method to Augment Data and Obtain Predictive Equations. Toxics. 2025; 13(7):579. https://doi.org/10.3390/toxics13070579
Chicago/Turabian StyleZhang, Yuan, Yanting Li, Yang Li, Lin Zhao, and Yongkui Yang. 2025. "Interpretable Machine Learning Models and Symbolic Regressions Reveal Transfer of Per- and Polyfluoroalkyl Substances (PFASs) in Plants: A New Small-Data Machine Learning Method to Augment Data and Obtain Predictive Equations" Toxics 13, no. 7: 579. https://doi.org/10.3390/toxics13070579
APA StyleZhang, Y., Li, Y., Li, Y., Zhao, L., & Yang, Y. (2025). Interpretable Machine Learning Models and Symbolic Regressions Reveal Transfer of Per- and Polyfluoroalkyl Substances (PFASs) in Plants: A New Small-Data Machine Learning Method to Augment Data and Obtain Predictive Equations. Toxics, 13(7), 579. https://doi.org/10.3390/toxics13070579







