The System of Self-Consistent Models: QSAR Analysis of Drug-Induced Liver Toxicity
Abstract
1. Introduction
2. Materials and Methods
2.1. Optimal SMILES-Based Descriptors
2.2. Monte Carlo Optimization
2.3. The System of Self-Consistent Models
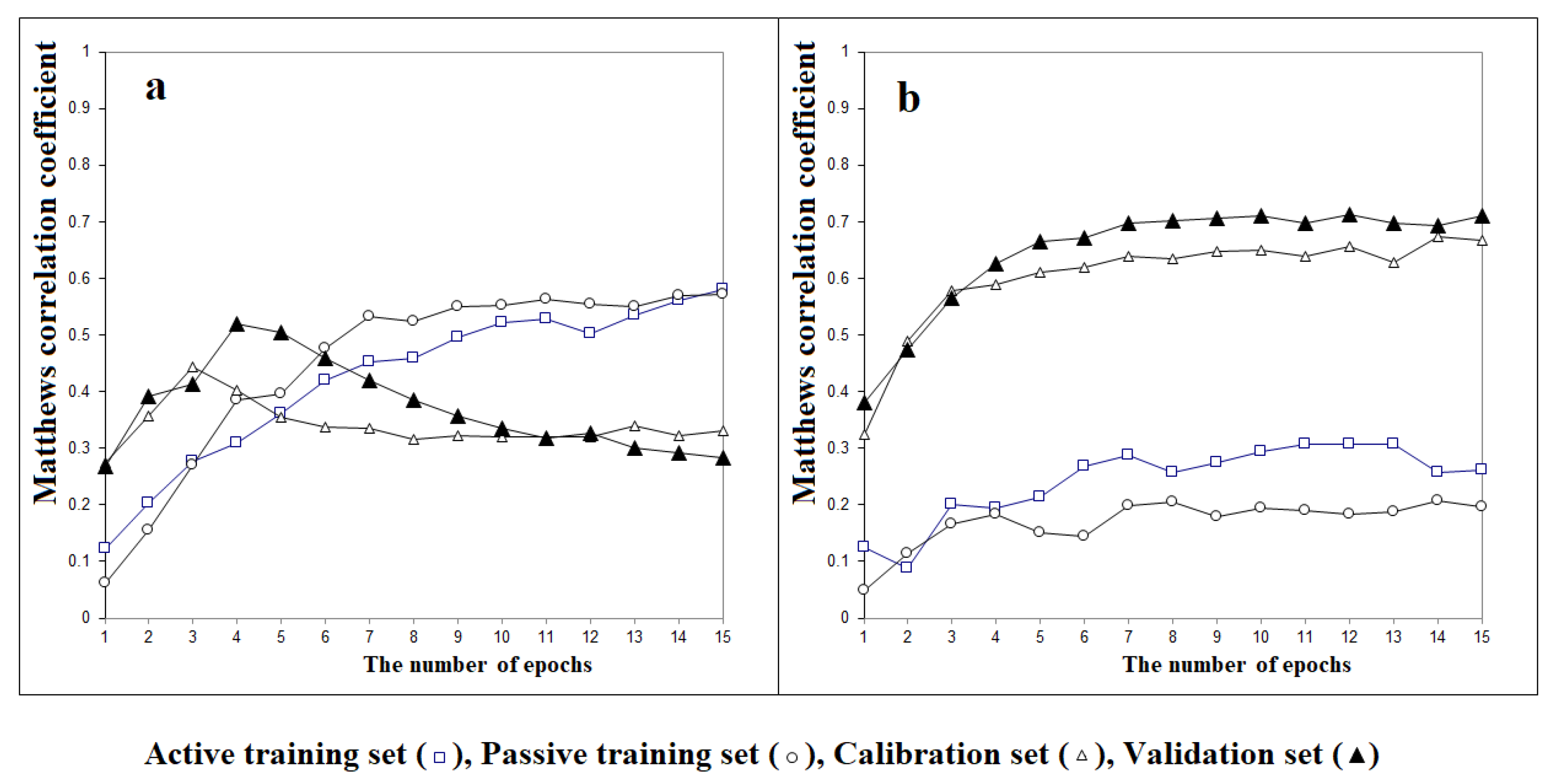
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liew, C.Y.; Lim, Y.C.; Yap, C.W. Mixed learning algorithms and features ensemble in hepatotoxicity prediction. J. Comput. Aided Mol. Des. 2011, 25, 855–871. [Google Scholar] [CrossRef] [PubMed]
- Zhu, X.; Kruhlak, N.L. Construction and analysis of a human hepatotoxicity database suitable for QSAR modeling using post-market safety data. Toxicology 2014, 321, 62–72. [Google Scholar] [CrossRef] [PubMed]
- Huang, S.-H.; Tung, C.-W.; Fülöp, F.; Li, J.-H. Developing a QSAR model for hepatotoxicity screening of the active compounds in traditional Chinese medicines. Food Chem. Toxicol. 2015, 78, 71–77. [Google Scholar] [CrossRef]
- Kim, M.T.; Huang, R.; Sedykh, A.; Wang, W.; Xia, M.; Zhu, H. Mechanism profiling of hepatotoxicity caused by oxidative stress using antioxidant response element reporter gene assay models and big data. Environ. Health Perspect. 2016, 124, 634–641. [Google Scholar] [CrossRef] [PubMed]
- He, S.; Ye, T.; Wang, R.; Zhang, C.; Zhang, X.; Sun, G.; Sun, X. An in silico model for predicting drug-induced hepatotoxicity. Int. J. Mol. Sci. 2019, 20, 1897. [Google Scholar] [CrossRef]
- Ancuceanu, R.; Hovanet, M.V.; Anghel, A.I.; Furtunescu, F.; Neagu, M.; Constantin, C.; Dinu, M. Computational models using multiple machine learning algorithms for predicting drug hepatotoxicity with the dilirank dataset. Int. J. Mol. Sci. 2020, 21, 2114. [Google Scholar] [CrossRef]
- Bajželj, B.; Drgan, V. Hepatotoxicity modeling using counter-propagation artificial neural networks: Handling an imbalanced classification problem. Molecules 2020, 25, 481. [Google Scholar] [CrossRef]
- Box, G.E.P. Science and statistics. J. Am. Stat. Assoc. 1976, 71, 791–799. [Google Scholar] [CrossRef]
- Curchoe, C.L. All Models Are Wrong, but Some Are Useful. J. Assist. Reprod. Genet. 2020, 37, 2389–2391. [Google Scholar] [CrossRef]
- Toropov, A.A.; Toropova, A.P.; Raitano, G.; Benfenati, E. CORAL: Building up QSAR models for the chromosome aberration test. Saudi J. Biol. Sci. 2019, 26, 1101–1106. [Google Scholar] [CrossRef]
- Toropova, A.P.; Toropov, A.A.; Benfenati, E. Semi-correlations as a tool to model for skin sensitization. Food Chem. Toxicol. 2021, 157, 112580. [Google Scholar] [CrossRef]
- Toropov, A.A.; Toropova, A.P.; Roncaglioni, A.; Benfenati, E. The system of self-consistent semi-correlations as one of the tools of cheminformatics for designing antiviral drugs. New J. Chem. 2021, 45, 20713–20720. [Google Scholar] [CrossRef]
- Toropov, A.A.; Toropova, A.P. The index of ideality of correlation: A criterion of predictive potential of QSPR/QSAR models? Mutat. Res. Genet. Toxicol. Environ. Mutagen. 2017, 819, 31–37. [Google Scholar] [CrossRef] [PubMed]
- Toropova, A.P.; Toropov, A.A.; Roncaglioni, A.; Benfenati, E. The system of self-consistent models for vapour pressure. Chem. Phys. Lett. 2022, 790, 139354. [Google Scholar] [CrossRef]
- Toropov, A.A.; Toropova, A.P.; Rasulev, B.F.; Benfenati, E.; Gini, G.; Leszczynska, D.; Leszczynski, J. CORAL: Binary classifications (active/inactive) for liver-related adverse effects of drugs. Curr. Drug. Saf. 2012, 7, 257–261. [Google Scholar] [CrossRef] [PubMed]
- Toropova, A.P.; Toropov, A.A. CORAL: Binary classifications (active/inactive) for drug-induced liver injury. Toxicol. Lett. 2017, 268, 51–57. [Google Scholar] [CrossRef] [PubMed]
- Toropov, A.A.; Toropova, A.P.; Benfenati, E.; Dorne, J.L. SAR for gastro-intestinal absorption and blood-brain barrier permeation of pesticides. Chem-Biol. Interact. 2018, 290, 1–5. [Google Scholar] [CrossRef]
- Toropova, A.P.; Toropov, A.A.; Benfenati, E.; Leszczynska, D.; Leszczynski, J. Prediction of antimicrobial activity of large pool of peptides using quasi-SMILES. BioSystems 2018, 169–170, 5–12. [Google Scholar] [CrossRef]
- Toropova, A.P.; Toropov, A.A.; Veselinović, A.M.; Veselinović, J.B.; Leszczynska, D.; Leszczynski, J. Semi-correlations combined with the index of ideality of correlation: A tool to build up model of mutagenic potential. Mol. Cell. Biochem. 2019, 452, 133–140. [Google Scholar] [CrossRef]
- Toropova, A.P.; Toropov, A.A.; Carnesecchi, E.; Benfenati, E.; Dorne, J.L. The index of ideality of correlation: Models for flammability of binary liquid mixtures. Chem. Pap. 2020, 74, 601–609. [Google Scholar] [CrossRef]
- Carnesecchi, E.; Toropov, A.A.; Toropova, A.P.; Kramer, N.; Svendsen, C.; Dorne, J.L.; Benfenati, E. Predicting acute contact toxicity of organic binary mixtures in honey bees (A. Mellifera) through innovative QSAR models. Sci. Total. Environ. 2020, 704, 135302. [Google Scholar] [CrossRef]
- Majumdar, S.; Basak, S.C. Beware of naïve q2, use true q2: Some comments on QSAR model building and cross validation. Curr. Comput. Aided Drug. Des. 2018, 14, 5–6. [Google Scholar] [CrossRef]
- Tuppurainen, K.; Korhonen, S.-P.; Ruuskanen, J. Performance of multicomponent self-organizing regression (MCSOR) in QSAR, QSPR, and multivariate calibration: Comparison with partial least-squares (PLS) and validation with large external data sets. SAR QSAR Environ. Res. 2006, 17, 549–561. [Google Scholar] [CrossRef]
- Toropov, A.A.; Toropova, A.P.; Benfenati, E.; Fanelli, R. QSAR as a random event: Selecting of the molecular structure for potential anti-tuberculosis agents. Anti-Infect. Agents 2016, 14, 3–10. [Google Scholar] [CrossRef]
- Toropova, A.P.; Meneses, J.; Alfaro-Moreno, E.; Toropov, A.A. The system of self-consistent models based on quasi-SMILES as a tool to predict the potential of nano-inhibitors of human lung carcinoma cell line A549 for different experimental conditions. Drug. Chem. Toxicol. 2023, in press. [Google Scholar] [CrossRef]
- Toropov, A.A.; Toropova, A.P.; Kudyshkin, V.O. The system of self-consistent QSPR-models for refractive index of polymers. Struct. Chem. 2022, 33, 617–624. [Google Scholar] [CrossRef]
- Toropov, A.A.; Toropova, A.P.; Achary, P.G.R.; Raškova, M.; Raška, I. The searching for agents for Alzheimer’s disease treatment via the system of self-consistent models. Toxicol. Mech. Methods 2022, 32, 549–557. [Google Scholar] [CrossRef]
- Toropova, A.P.; Toropov, A.A. The System of Self-Consistent of Models: A New Approach to Build Up and Validation of Predictive Models of the Octanol/Water Partition Coefficient for Gold Nanoparticles. Int. J. Environ. Res. 2021, 15, 709–722. [Google Scholar] [CrossRef]
- Toropov, A.A.; Toropova, A.P. The system of self-consistent models for the uptake of nanoparticles in PaCa2 cancer cells. Nanotoxicology 2021, 15, 995–1004. [Google Scholar] [CrossRef]
- Toropova, A.P.; Toropov, A.A.; Roncaglioni, A.; Benfenati, E. The index of ideality of correlation improves the predictive potential of models of the antioxidant activity of tripeptides from frog skin (Litoria rubella). Comput. Biol. Med. 2021, 133, 104370. [Google Scholar] [CrossRef]
- Ghiasi, T.; Ahmadi, S.; Ahmadi, E.; Talei Bavil Olyai, M.R.; Khodadadi, Z. The index of ideality of correlation: QSAR studies of hepatitis C virus NS3/4A protease inhibitors using SMILES descriptors. SAR QSAR Environ. Res. 2021, 32, 495–520. [Google Scholar] [CrossRef]
- Javidfar, M.; Ahmadi, S. QSAR modelling of larvicidal phytocompounds against Aedes aegypti using index of ideality of correlation. SAR QSAR Environ. Res. 2020, 31, 717–739. [Google Scholar] [CrossRef]
- Kumar, A.; Kumar, P. Prediction of power conversion efficiency of phenothiazine-based dye-sensitized solar cells using Monte Carlo method with index of ideality of correlation. SAR QSAR Environ. Res. 2021, 32, 817–834. [Google Scholar] [CrossRef]
- Kumar, A.; Kumar, P.; Singh, D. QSRR modelling for the investigation of gas chromatography retention indices of flavour and fragrance compounds on Carbowax 20 M glass capillary column with the index of ideality of correlation and the consensus modelling. Chemom. Intell. Lab. Syst. 2022, 224, 104552. [Google Scholar] [CrossRef]
- Jafari, K.; Fatemi, M.H.; Toropova, A.P.; Toropov, A.A. The development of nano-QSPR models for viscosity of nanofluids using the index of ideality of correlation and the correlation intensity index. Chemom. Intell. Lab. Syst. 2022, 222, 104500. [Google Scholar] [CrossRef]
- Toropova, A.P.; Toropov, A.A.; Viganò, E.L.; Colombo, E.; Roncaglioni, A.; Benfenati, E. Carcinogenicity prediction using the index of ideality of correlation. SAR QSAR Environ. Res. 2022, 33, 419–428. [Google Scholar] [CrossRef]
- Ahmadi, S.; Lotfi, S.; Kumar, P. Quantitative structure–toxicity relationship models for predication of toxicity of ionic liquids toward leukemia rat cell line IPC-81 based on index of ideality of correlation. Toxicol. Mech. Methods 2022, 32, 302–312. [Google Scholar] [CrossRef]
- Duhan, M.; Sindhu, J.; Kumar, P.; Devi, M.; Singh, R.; Kumar, R.; Lal, S.; Kumar, A.; Kumar, S.; Hussain, K. Quantitative structure activity relationship studies of novel hydrazone derivatives as α-amylase inhibitors with index of ideality of correlation. J. Biomol. Struct. Dyn. 2022, 40, 4933–4953. [Google Scholar] [CrossRef]
- Kumar, A.; Kumar, P. Cytotoxicity of quantum dots: Use of quasi SMILES in development of reliable models with index of ideality of correlation and the consensus modelling. J. Hazard. Mater. 2021, 402, 123777. [Google Scholar] [CrossRef]
- Kumar, P.; Kumar, A. Unswerving modeling of hepatotoxicity of cadmium containing quantum dots using amalgamation of quasi SMILES, index of ideality of correlation, and consensus modelling. Nanotoxicology 2021, 15, 1199–1214. [Google Scholar] [CrossRef]
| Set | Observed Classification Quality | Statistical Characteristics | |||||||
|---|---|---|---|---|---|---|---|---|---|
| TP | TN | FP | FN | N | Sensitivity | Specificity | Accuracy | MCC | |
| Active training | 119 | 99 | 49 | 47 | 314 | 0.7169 | 0.6689 | 0.6983 | 0.3861 |
| Passive training | 123 | 101 | 32 | 63 | 319 | 0.6613 | 0.7594 | 0.7022 | 0.4150 |
| Calibration | 160 | 100 | 28 | 31 | 319 | 0.8377 | 0.7813 | 0.8150 | 0.6167 |
| Validation | 181 | 86 | 20 | 35 | 322 | 0.8380 | 0.8113 | 0.8292 | 0.6300 |
| Total | 583 | 386 | 129 | 176 | 1274 | 0.7681 | 0.7495 | 0.7606 | 0.5116 |
| N | Sensitivity | Specificity | Accuracy | Sensitivity (Validation Set) | Specificity (Validation Set) | References |
|---|---|---|---|---|---|---|
| - | 0.73 | 0.73 | - | - | - | [2] |
| 6853 | 0.91 | 0.53 | 0.79 | - | - | [3] |
| 1550 | 0.76 | 0.71–0.92 | - | - | - | [4] |
| 1148 | - | - | - | 0.68–0.76 | 0.83–0.99 | [4] |
| 1254 | 0.82 | 0.75 | 0.78 | - | - | [5] |
| 83 | - | - | - | 0.818 | 0.748 | [5] |
| 1036 | 0.82–0.90 | 0.55–0.64 | 0.71–0.75 | - | - | [6] |
| 1274 | 0.77 | 0.75 | 0.76 | - | - | This work (split 1) |
| 322 | - | - | - | 0.838 | 0.8113 | This work (split 1) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Toropova, A.P.; Toropov, A.A.; Roncaglioni, A.; Benfenati, E. The System of Self-Consistent Models: QSAR Analysis of Drug-Induced Liver Toxicity. Toxics 2023, 11, 419. https://doi.org/10.3390/toxics11050419
Toropova AP, Toropov AA, Roncaglioni A, Benfenati E. The System of Self-Consistent Models: QSAR Analysis of Drug-Induced Liver Toxicity. Toxics. 2023; 11(5):419. https://doi.org/10.3390/toxics11050419
Chicago/Turabian StyleToropova, Alla P., Andrey A. Toropov, Alessandra Roncaglioni, and Emilio Benfenati. 2023. "The System of Self-Consistent Models: QSAR Analysis of Drug-Induced Liver Toxicity" Toxics 11, no. 5: 419. https://doi.org/10.3390/toxics11050419
APA StyleToropova, A. P., Toropov, A. A., Roncaglioni, A., & Benfenati, E. (2023). The System of Self-Consistent Models: QSAR Analysis of Drug-Induced Liver Toxicity. Toxics, 11(5), 419. https://doi.org/10.3390/toxics11050419









