Predicting of Daily PM2.5 Concentration Employing Wavelet Artificial Neural Networks Based on Meteorological Elements in Shanghai, China
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Location and Data Sources
2.2. Wavelet Transformation (WT)
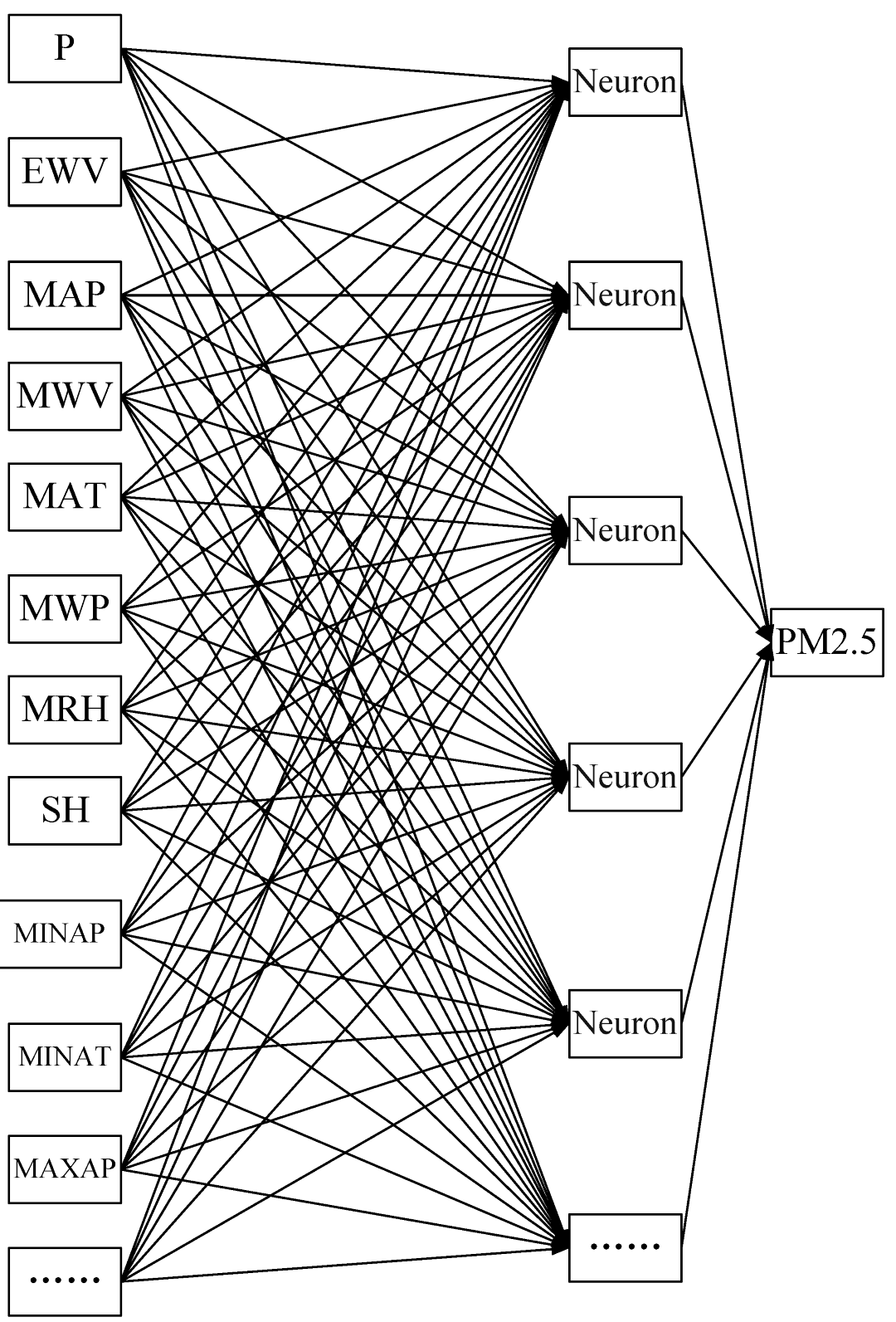
2.3. Artificial Neural Network (ANN)
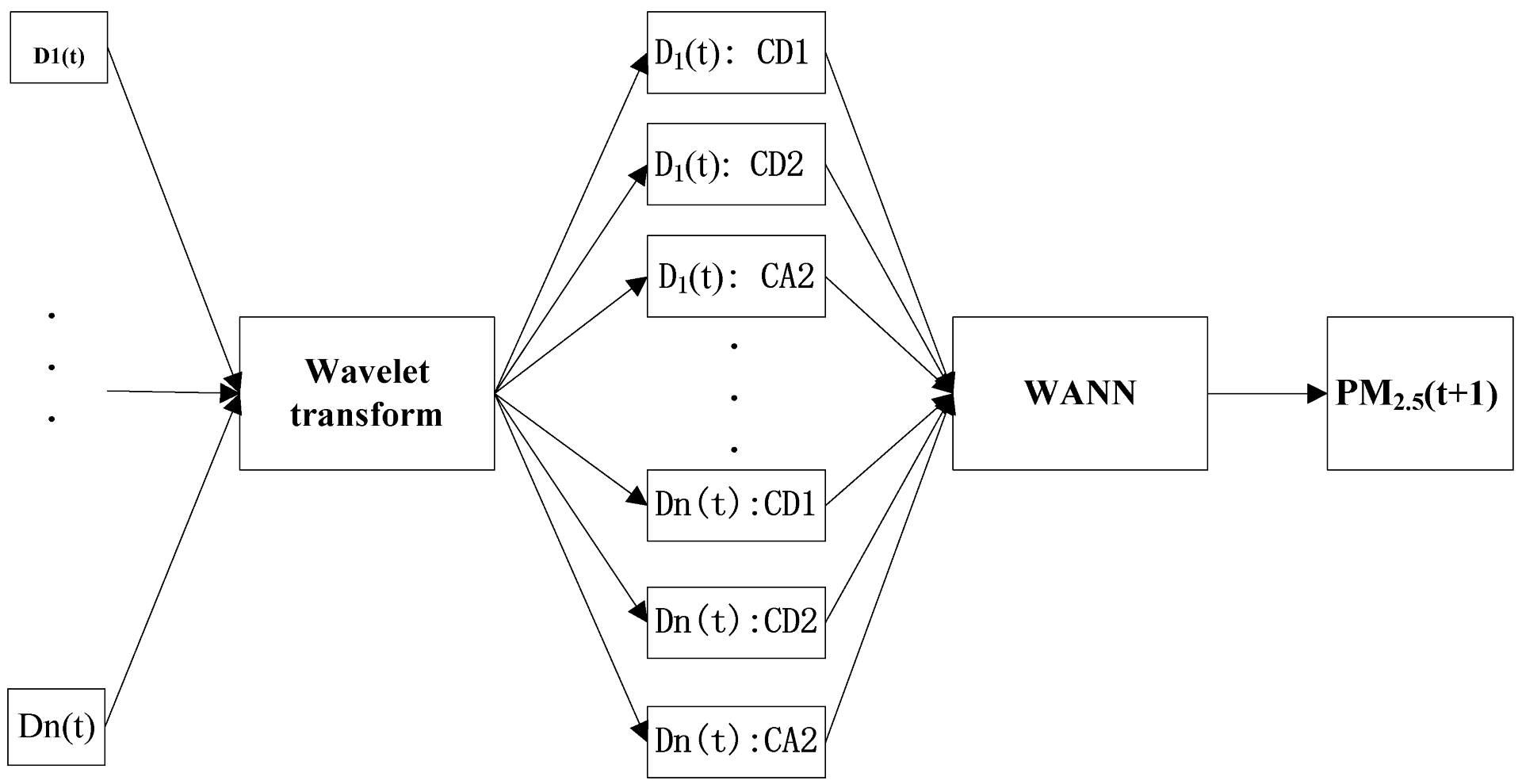
2.4. Wavelet Artificial Neural Network
2.5. Performance Criteria
3. Result and discussion
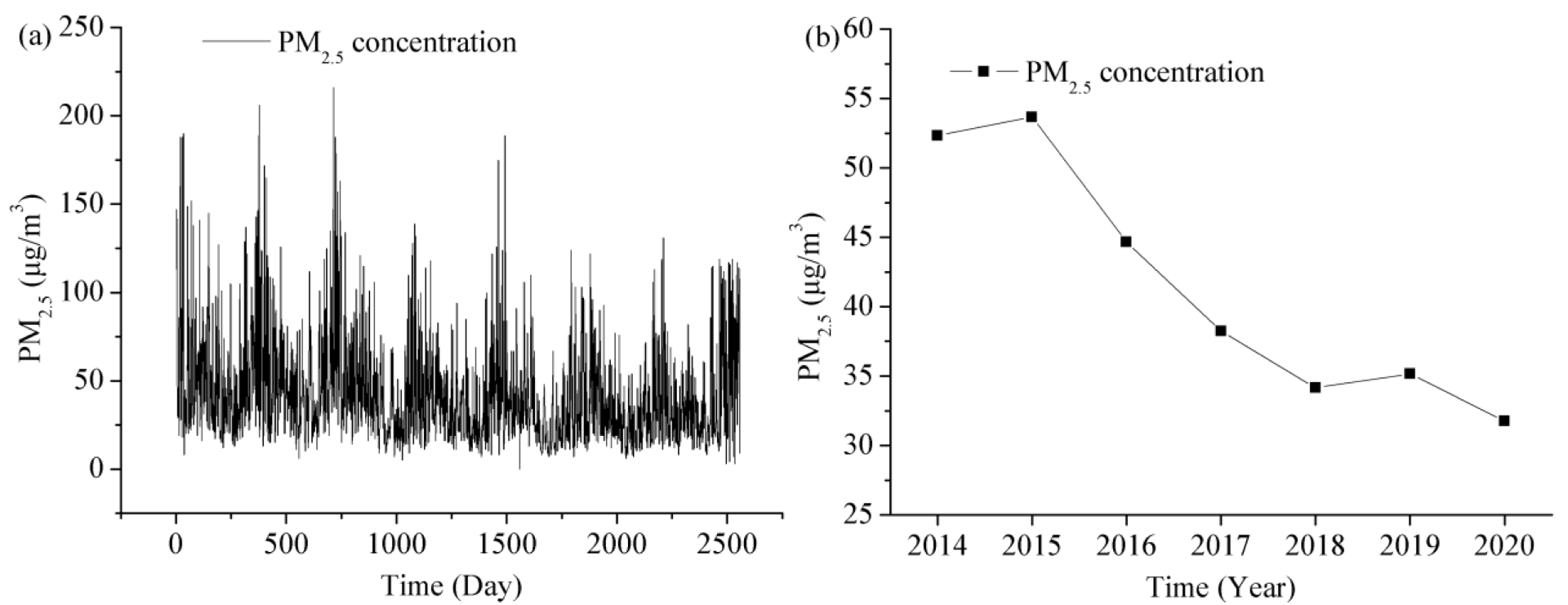
3.1. Long Term Change of PM2.5 Concentration in Shanghai
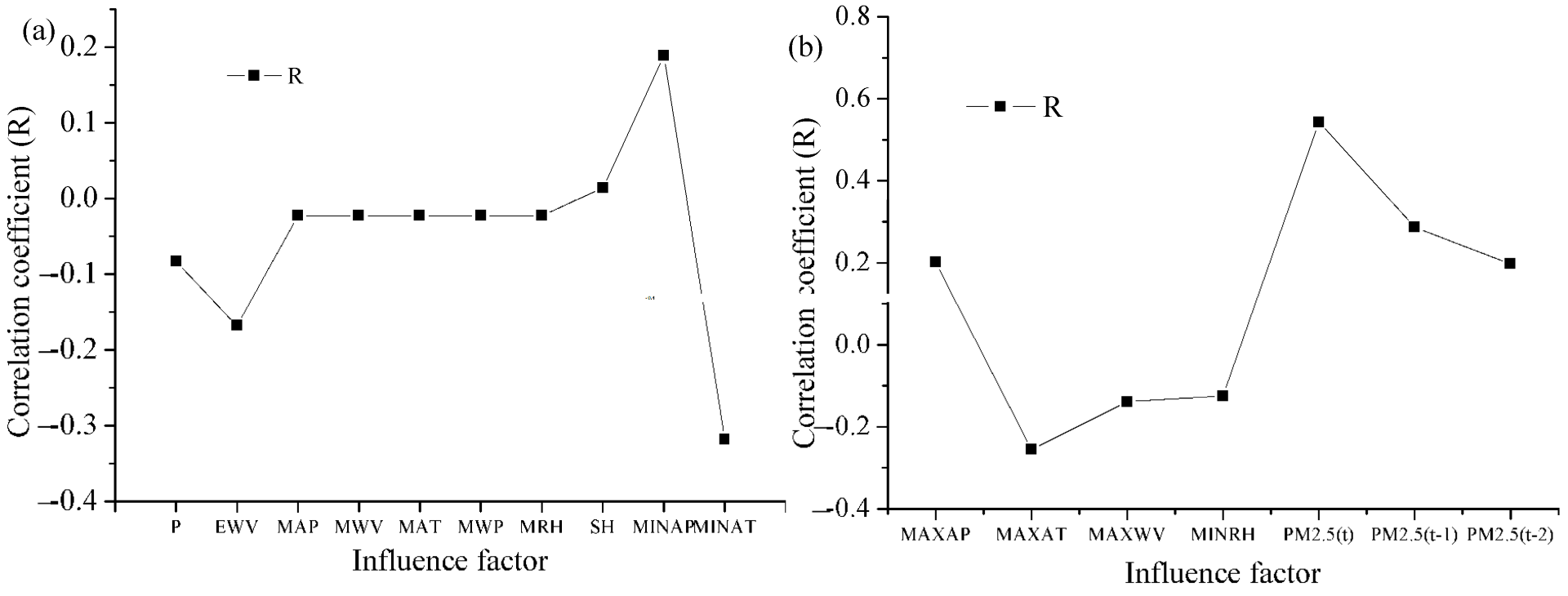
3.2. Relevance between Daily PM2.5 Concentration and Meteorological Factors in Shanghai
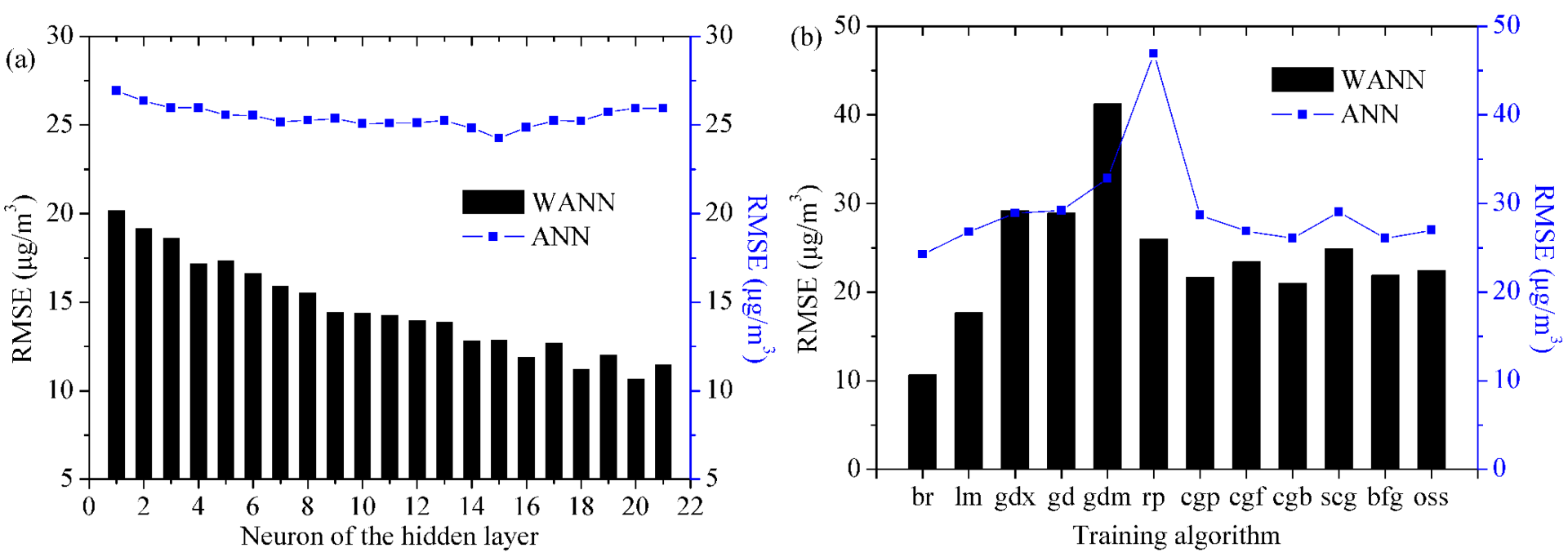
3.3. Determination of Model Structure and Parameters
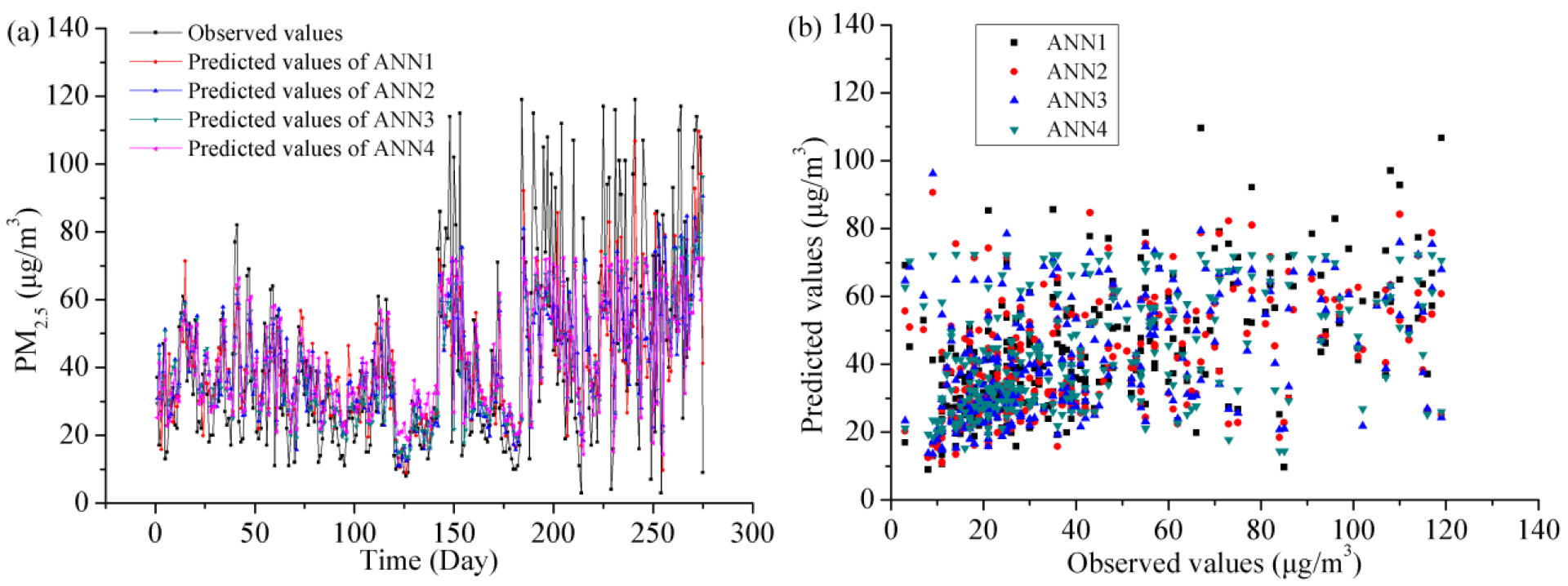
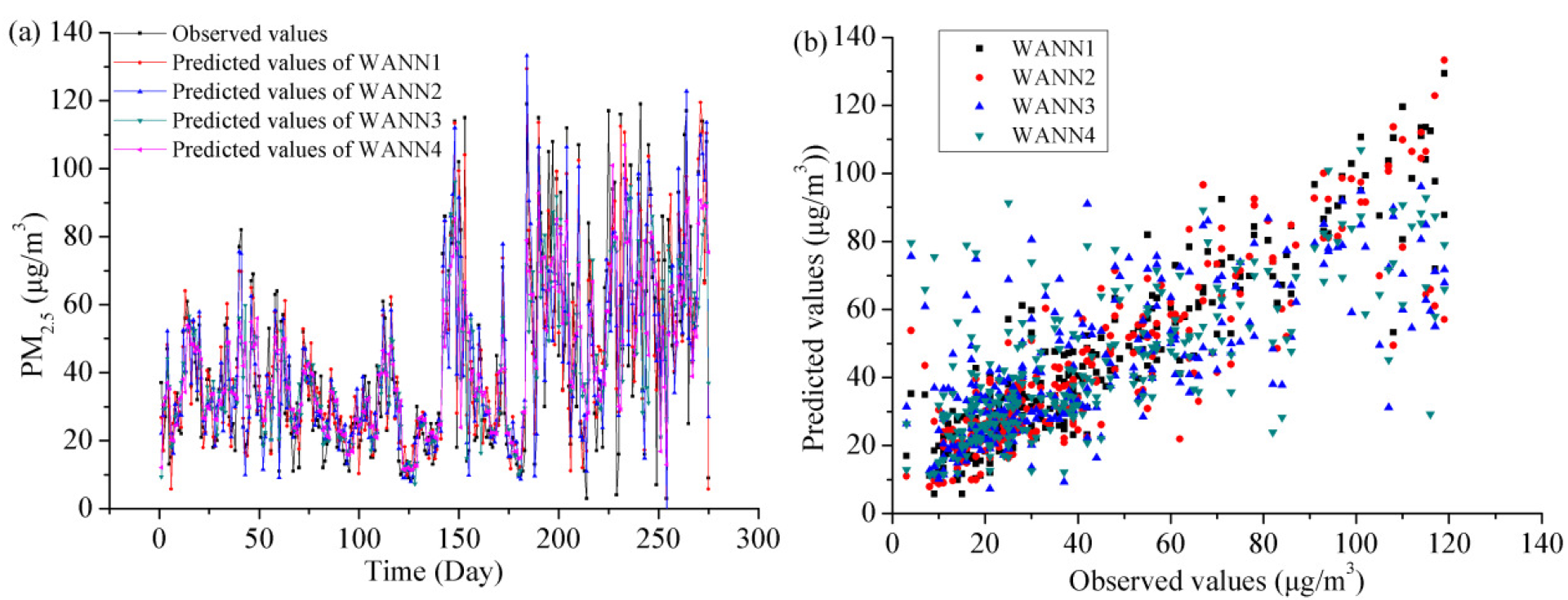
3.4. Comparative Analysis of the Different PM2.5 Predicting Models
3.5. Comparison with Other Existing PM2.5 Prediction Models
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Abbreviations | Full Name |
| AI | artificial intelligence |
| ANN | artificial neural network |
| AQGs | Global Air Quality Guidelines |
| ARIMA | autoregressive integrated moving average |
| bior | biorthogonal |
| BP | back propagation |
| BR | Bayesian regularization algorithm |
| CA | approximate composition |
| CD | detailed composition |
| CNN | convolutional neural network |
| coif | coiflet |
| CWT | continuous wavelet transform |
| DA-RNN | dual-stage attention-based recurrent neural network |
| db | Daubechies |
| DL | deep learning |
| DTR | decision tree regressor |
| DWT | discrete wavelet transform |
| EMD-GRU | gated recurrent unit neural network based on empirical mode decomposition |
| EWV | extreme wind velocity |
| GA-SVM | combined genetic algorithm and support vector machine |
| GBDT | gradient boosted decision trees |
| GBM | gradient boosting machine |
| GBRT | gradient boosting regression tree |
| GDP | gross domestic product |
| GRU | gated recurrent unit neural network |
| LM | Levenberg–Marquardt algorithm |
| LSTM | long short-term memory |
| MAE | mean absolute error |
| MAP | mean atmospheric pressure |
| MAT | mean atmospheric temperature |
| MAXAP | maximum atmospheric pressure |
| MAXAT | maximum atmospheric temperature |
| MAXWV | maximum wind velocity |
| MINAP | minimum atmospheric pressure |
| MINAT | minimum atmospheric temperature |
| MINRH | minimum relative humidity |
| ML | machine learning |
| MLR | multiple linear regression |
| MRH | mean relative humidity |
| MWP | mean water vapor pressure |
| MWV | mean wind velocity |
| P | precipitation |
| PM2.5 | fine particulate matter |
| R | correlation coefficient |
| RE | relative error |
| ReLU | rectified linear unit |
| RF | random forest |
| RMSE | root mean square error |
| RNN | recurrent neural network |
| SH | sunshine hours |
| SVM | support vector machine |
| SVR | support vector regression |
| sym | symlet |
| WANN | wavelet-ANN |
| W-GRU | wavelet-GRU |
| WHO | World Health Organization |
| W-LSTM | wavelet-LSTM |
| WT | wavelet transformation |
| XGBoost | extreme gradient boosting |
References
- Balogun, A.-L.; Tella, A.; Baloo, L.; Adebisi, N. A review of the inter-correlation of climate change, air pollution and urban sustainability using novel machine learning algorithms and spatial information science. Urban Clim. 2021, 40, 100989. [Google Scholar] [CrossRef]
- Ding, A.; Nie, W.; Huang, X.; Chi, X.; Sun, J.; Kerminen, V.M.; Xu, Z.; Guo, W.; Petäjä, T.; Yang, X.; et al. Long-term observation of air pollution-weather/climate interactions at the SORPES station: A review and outlook. Front. Environ. Sci. Eng. 2016, 10, 15. [Google Scholar] [CrossRef]
- Hu, F.; Guo, Y. Health impacts of air pollution in China. Front. Environ. Sci. Eng. 2021, 15, 74. [Google Scholar] [CrossRef]
- Zheng, Y.; Xue, T.; Zhao, H.; Lei, Y. Increasing life expectancy in China by achieving its 2025 air quality target. Environ. Sci. Ecotechnol. 2022, 12, 100203. [Google Scholar] [CrossRef] [PubMed]
- Guo, Q.; He, Z.; Wang, Z. Long-term projection of future climate change over the twenty-first century in the Sahara region in Africa under four Shared Socio-Economic Pathways scenarios. Environ. Sci. Pollut. Res. 2022. [Google Scholar] [CrossRef] [PubMed]
- Yin, H.; Brauer, M.; Zhang, J.; Cai, W.; Navrud, S.; Burnett, R.; Howard, C.; Deng, Z.; Kammen, D.M.; Schellnhuber, H.J.; et al. Population ageing and deaths attributable to ambient PM2.5 pollution: A global analysis of economic cost. Lancet Planet. Health 2021, 5, e356–e367. [Google Scholar] [CrossRef]
- Lelieveld, J.; Evans, J.S.; Fnais, M.; Giannadaki, D.; Pozzer, A. The contribution of outdoor air pollution sources to premature mortality on a global scale. Nature 2015, 525, 367. [Google Scholar] [CrossRef]
- Fowler, D.; Pyle, J.A.; Sutton, M.A.; Williams, M.L. Global Air Quality, past present and future: An introduction. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2020, 378, 20190323. [Google Scholar] [CrossRef]
- Murray, C.J.L.; Aravkin, A.Y.; Zheng, P.; Abbafati, C.; Abbas, K.M.; Abbasi-Kangevari, M.; Abd-Allah, F.; Abdelalim, A.; Abdollahi, M.; Abdollahpour, I.; et al. Global burden of 87 risk factors in 204 countries and territories, 1990–2019: A systematic analysis for the Global Burden of Disease Study 2019. Lancet 2020, 396, 1223–1249. [Google Scholar] [CrossRef]
- Wang, Y.; Shi, M.; Lv, Z.; Liu, H.; He, K. Local and regional contributions to PM2.5 in the Beijing 2022 Winter Olympics infrastructure areas during haze episodes. Front. Environ. Sci. Eng. 2021, 15, 140. [Google Scholar] [CrossRef]
- Geng, G.; Zheng, Y.; Zhang, Q.; Xue, T.; Zhao, H.; Tong, D.; Zheng, B.; Li, M.; Liu, F.; Hong, C.; et al. Drivers of PM2.5 air pollution deaths in China 2002–2017. Nat. Geosci. 2021, 14, 645–650. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, W.; Wang, S.; Song, T.; Gong, Z.; Ji, D.; Wang, L.; Liu, Z.; Tang, G.; Huo, Y.; et al. Contrasting trends of PM2.5 and surface-ozone concentrations in China from 2013 to 2017. Natl. Sci. Rev. 2020, 7, 1331–1339. [Google Scholar] [CrossRef]
- Zhong, J.; Zhang, X.; Gui, K.; Wang, Y.; Che, H.; Shen, X.; Zhang, L.; Zhang, Y.; Sun, J.; Zhang, W. Robust prediction of hourly PM2.5 from meteorological data using LightGBM. Natl. Sci. Rev. 2021, 8, nwaa307. [Google Scholar] [CrossRef]
- Xue, W.; Shi, X.; Yan, G.; Wang, J.; Xu, Y.; Tang, Q.; Wang, Y.; Zheng, Y.; Lei, Y. Impacts of meteorology and emission variations on the heavy air pollution episode in North China around the 2020 Spring Festival. Sci. China Earth Sci. 2021, 64, 329. [Google Scholar] [CrossRef]
- Zhang, H.; Jiang, Q.; Wang, J.; Li, K.; Wang, F. Analysis on the impact of two winter precipitation episodes on PM2.5 in Beijing. Environ. Sci. Ecotechnol. 2021, 5, 100080. [Google Scholar] [CrossRef]
- Hepburn, C.; Qi, Y.; Stern, N.; Ward, B.; Xie, C.; Zenghelis, D. Towards carbon neutrality and China’s 14th Five-Year Plan: Clean energy transition, sustainable urban development, and investment priorities. Environ. Sci. Ecotechnol. 2021, 8, 100130. [Google Scholar] [CrossRef]
- Yang, H.; Huang, X.; Hu, J.; Thompson, J.R.; Flower, R.J. Achievements, challenges and global implications of China’s carbon neutral pledge. Front. Environ. Sci. Eng. 2022, 16, 111. [Google Scholar] [CrossRef]
- Barua, S.; Nath, S.D. The impact of COVID-19 on air pollution: Evidence from global data. J. Clean. Prod. 2021, 298, 126755. [Google Scholar] [CrossRef]
- Wijnands, J.S.; Nice, K.A.; Seneviratne, S.; Thompson, J.; Stevenson, M. The impact of the COVID-19 pandemic on air pollution: A global assessment using machine learning techniques. Atmos. Pollut. Res. 2022, 13, 101438. [Google Scholar] [CrossRef]
- Habeebullah, T.M.; Munir, S.; Zeb, J.; Morsy, E.A. Modelling the Effect of COVID-19 Lockdown on Air Pollution in Makkah Saudi Arabia with a Supervised Machine Learning Approach. Toxics 2022, 10, 225. [Google Scholar] [CrossRef]
- Manoj, M.G.; Satheesh Kumar, M.K.; Valsaraj, K.T.; Vijayan, S.K.; Nishanth, T. Exacerbation of Fatality Rates Induced by Poor Air Quality Due to Open-Air Mass Funeral Pyre Cremation during the Second Wave of COVID-19. Toxics 2022, 10, 306. [Google Scholar] [CrossRef] [PubMed]
- Kaewrat, J.; Janta, R.; Sichum, S.; Rattikansukha, C.; Tala, W.; Kanabkaew, T. Human Health Risks and Air Quality Changes Following Restrictions for the Control of the COVID-19 Pandemic in Thailand. Toxics 2022, 10, 520. [Google Scholar] [CrossRef] [PubMed]
- Tyagi, B.; Vissa, N.K.; Ghude, S.D. Evolution of Pollution Levels from COVID-19 Lockdown to Post-Lockdown over India. Toxics 2022, 10, 653. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Ding, A.; Gao, J.; Zheng, B.; Zhou, D.; Qi, X.; Tang, R.; Wang, J.; Ren, C.; Nie, W.; et al. Enhanced secondary pollution offset reduction of primary emissions during COVID-19 lockdown in China. Natl. Sci. Rev. 2020, 8, nwaa137. [Google Scholar] [CrossRef] [PubMed]
- Guo, Q.; Wang, Z.; He, Z.; Li, X.; Meng, J.; Hou, Z.; Yang, J. Changes in Air Quality from the COVID to the Post-COVID Era in the Beijing-Tianjin-Tangshan Region in China. Aerosol Air Qual. Res. 2021, 21, 210270. [Google Scholar] [CrossRef]
- Cai, W.-J.; Wang, H.-W.; Wu, C.-L.; Lu, K.-F.; Peng, Z.-R.; He, H.-D. Characterizing the interruption-recovery patterns of urban air pollution under the COVID-19 lockdown in China. Build. Environ. 2021, 205, 108231. [Google Scholar] [CrossRef]
- Han, J.; Yin, J.; Wu, X.; Wang, D.; Li, C. Environment and COVID-19 incidence: A critical review. J. Environ. Sci. 2023, 124, 933–951. [Google Scholar] [CrossRef]
- Bao, R.; Zhang, A. Does lockdown reduce air pollution? Evidence from 44 cities in northern China. Sci. Total Environ. 2020, 731, 139052. [Google Scholar] [CrossRef]
- Jiang, X.; Wei, P.; Luo, Y.; Li, Y. Air Pollutant Concentration Prediction Based on a CEEMDAN-FE-BiLSTM Model. Atmosphere 2021, 12, 1452. [Google Scholar] [CrossRef]
- Su, X.; An, J.; Zhang, Y.; Zhu, P.; Zhu, B. Prediction of ozone hourly concentrations by support vector machine and kernel extreme learning machine using wavelet transformation and partial least squares methods. Atmos. Pollut. Res. 2020, 11, 51–60. [Google Scholar] [CrossRef]
- Kshirsagar, A.; Shah, M. Anatomization of air quality prediction using neural networks, regression and hybrid models. J. Clean. Prod. 2022, 369, 133383. [Google Scholar] [CrossRef]
- Masood, A.; Ahmad, K. A review on emerging artificial intelligence (AI) techniques for air pollution forecasting: Fundamentals, application and performance. J. Clean. Prod. 2021, 322, 129072. [Google Scholar] [CrossRef]
- Saldarriaga, J.F.; Cruz, Y.; Estiati, I.; Tellabide, M.; Olazar, M. Assessment of pressure drop in conical spouted beds of biomass by artificial neural networks and comparison with empirical correlations. Particuology 2022, 70, 1–9. [Google Scholar] [CrossRef]
- Karimi, M.; Vaferi, B.; Hosseini, S.H.; Olazar, M.; Rashidi, S. Smart computing approach for design and scale-up of conical spouted beds with open-sided draft tubes. Particuology 2021, 55, 179–190. [Google Scholar] [CrossRef]
- Ma, S.; Wu, T.; Chen, X.; Wang, Y.; Tang, H.; Yao, Y.; Wang, Y.; Zhu, Z.; Deng, J.; Wan, J.; et al. An artificial neural network chip based on two-dimensional semiconductor. Sci. Bull. 2022, 67, 270. [Google Scholar] [CrossRef]
- Wei, S.; Chen, Z.; Arumugasamy, S.K.; Chew, I.M.L. Data augmentation and machine learning techniques for control strategy development in bio-polymerization process. Environ. Sci. Ecotechnol. 2022, 11, 100172. [Google Scholar] [CrossRef]
- Cabaneros, S.M.; Calautit, J.K.; Hughes, B.R. A review of artificial neural network models for ambient air pollution prediction. Environ. Model. Softw. 2019, 119, 285–304. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, Q. An overview of multi-task learning. Natl. Sci. Rev. 2018, 5, 30–43. [Google Scholar] [CrossRef]
- Xing, J.; Zheng, S.; Ding, D.; Kelly, J.T.; Wang, S.; Li, S.; Qin, T.; Ma, M.; Dong, Z.; Jang, C.; et al. Deep Learning for Prediction of the Air Quality Response to Emission Changes. Environ. Sci. Technol. 2020, 54, 8589–8600. [Google Scholar] [CrossRef]
- Huang, G.; Ge, C.; Xiong, T.; Song, S.; Yang, L.; Liu, B.; Yin, W.; Wu, C. Large scale air pollution prediction with deep convolutional networks. Sci. China Inf. Sci. 2021, 64, 192107. [Google Scholar] [CrossRef]
- He, Z.; Zhang, Y.; Guo, Q.; Zhao, X. Comparative Study of Artificial Neural Networks and Wavelet Artificial Neural Networks for Groundwater Depth Data Forecasting with Various Curve Fractal Dimensions. Water Resour. Manag. 2014, 28, 5297–5317. [Google Scholar] [CrossRef]
- Guo, Q.; He, Z. Prediction of the confirmed cases and deaths of global COVID-19 using artificial intelligence. Environ. Sci. Pollut. Res. 2021, 28, 11672–11682. [Google Scholar] [CrossRef] [PubMed]
- Guo, Q.; He, Z.; Li, S.; Li, X.; Meng, J.; Hou, Z.; Liu, J.; Chen, Y. Air Pollution Forecasting Using Artificial and Wavelet Neural Networks with Meteorological Conditions. Aerosol Air Qual. Res. 2020, 20, 1429–1439. [Google Scholar] [CrossRef]
- He, Z.; Guo, Q.; Wang, Z.; Li, X. Prediction of Monthly PM2.5 Concentration in Liaocheng in China Employing Artificial Neural Network. Atmosphere 2022, 13, 1221. [Google Scholar] [CrossRef]
- Goudarzi, G.; Hopke, P.K.; Yazdani, M. Forecasting PM2.5 concentration using artificial neural network and its health effects in Ahvaz, Iran. Chemosphere 2021, 283, 131285. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Z.-H.; Feng, J. Deep forest. Natl. Sci. Rev. 2018, 6, 74–86. [Google Scholar] [CrossRef]
- Li, H. Deep learning for natural language processing: Advantages and challenges. Natl. Sci. Rev. 2017, 5, 24–26. [Google Scholar] [CrossRef]
- Iwabuchi, K.; Kato, K.; Watari, D.; Taniguchi, I.; Catthoor, F.; Shirazi, E.; Onoye, T. Flexible electricity price forecasting by switching mother wavelets based on wavelet transform and Long Short-Term Memory. Energy AI 2022, 10, 100192. [Google Scholar] [CrossRef]
- Wu, X.; He, S.; Guo, J.; Sun, W. A multi-scale periodic study of PM2.5 concentration in the Yangtze River Delta of China based on Empirical Mode Decomposition-Wavelet Analysis. J. Clean. Prod. 2021, 281, 124853. [Google Scholar] [CrossRef]
- Mallat, S.G. Multifrequency channel decompositions of images and wavelet models. IEEE Trans. Acoust. Speech Signal Process. 1989, 31, 2091–2110. [Google Scholar] [CrossRef]
- Rene, E.; Veiga, M.C.; Kennes, C. Neural network models for biological waste–Gas treatment systems. J. Biotechnol. 2010, 150, 41. [Google Scholar] [CrossRef]
- MacKay, D.J.C. Bayesian Interpolation. Neural Comput. 1992, 4, 415–447. [Google Scholar] [CrossRef]
- Sang, Y.F. A review on the applications of wavelet transform in hydrology time series analysis. Atmos. Res. 2013, 122, 8–15. [Google Scholar] [CrossRef]
- Moreno-Barón, L.; Cartas, R.; Merkoçi, A.; Alegret, S.; del Valle, M.; Leija, L.; Hernandez, P.R.; Muñoz, R. Application of the wavelet transform coupled with artificial neural networks for quantification purposes in a voltammetric electronic tongue. Sens. Actuators B Chem. 2006, 113, 487–499. [Google Scholar] [CrossRef]
- Agarwal, S.; Sharma, S.; Suresh, R.; Rahman, M.H.; Vranckx, S.; Maiheu, B.; Blyth, L.; Janssen, S.; Gargava, P.; Shukla, V.K.; et al. Air quality forecasting using artificial neural networks with real time dynamic error correction in highly polluted regions. Sci. Total Environ. 2020, 735, 139454. [Google Scholar] [CrossRef]
- Jida, S.N.; Hetet, J.-F.; Chesse, P.; Guadie, A. Roadside vehicle particulate matter concentration estimation using artificial neural network model in Addis Ababa, Ethiopia. J. Environ. Sci. 2021, 101, 428–439. [Google Scholar] [CrossRef]
- Wood, D.A. Trend decomposition aids forecasts of air particulate matter (PM2.5) assisted by machine and deep learning without recourse to exogenous data. Atmos. Pollut. Res. 2022, 13, 101352. [Google Scholar] [CrossRef]
- Gui, K.; Che, H.; Zeng, Z.; Wang, Y.; Zhai, S.; Wang, Z.; Luo, M.; Zhang, L.; Liao, T.; Zhao, H.; et al. Construction of a virtual PM2.5 observation network in China based on high-density surface meteorological observations using the Extreme Gradient Boosting model. Environ. Int. 2020, 141, 105801. [Google Scholar] [CrossRef]
- Kim, D.; Ho, C.-H.; Park, I.; Kim, J.; Chang, L.-S.; Choi, M.-H. Untangling the contribution of input parameters to an artificial intelligence PM2.5 forecast model using the layer-wise relevance propagation method. Atmos. Environ. 2022, 276, 119034. [Google Scholar] [CrossRef]
- Guo, X.; Wang, Y.; Mei, S.; Shi, C.; Liu, Y.; Pan, L.; Li, K.; Zhang, B.; Wang, J.; Zhong, Z.; et al. Monitoring and modelling of PM2.5 concentration at subway station construction based on IoT and LSTM algorithm optimization. J. Clean. Prod. 2022, 360, 132179. [Google Scholar] [CrossRef]
- Jiang, Z.; Zheng, T.; Bergin, M.; Carlson, D. Improving spatial variation of ground-level PM2.5 prediction with contrastive learning from satellite imagery. Sci. Remote Sens. 2022, 5, 100052. [Google Scholar] [CrossRef]
- Huang, G.; Li, X.; Zhang, B.; Ren, J. PM2.5 concentration forecasting at surface monitoring sites using GRU neural network based on empirical mode decomposition. Sci. Total Environ. 2021, 768, 144516. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.-J.; Kuo, P.-H. A Deep CNN-LSTM Model for Particulate Matter (PM2.5) Forecasting in Smart Cities. Sensors 2018, 18, 2220. [Google Scholar] [CrossRef] [PubMed]
- Faraji, M.; Nadi, S.; Ghaffarpasand, O.; Homayoni, S.; Downey, K. An integrated 3D CNN-GRU deep learning method for short-term prediction of PM2.5 concentration in urban environment. Sci. Total Environ. 2022, 834, 155324. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Long, Z.; Duan, Z.; Shi, H. A New Model Using Multiple Feature Clustering and Neural Networks for Forecasting Hourly PM2.5 Concentrations, and Its Applications in China. Engineering 2020, 6, 944–956. [Google Scholar] [CrossRef]
- Luo, Z.; Huang, F.; Liu, H. PM2.5 concentration estimation using convolutional neural network and gradient boosting machine. J. Environ. Sci. 2020, 98, 85–93. [Google Scholar] [CrossRef]
- Du, W.; Chen, L.; Wang, H.; Shan, Z.; Zhou, Z.; Li, W.; Wang, Y. Deciphering urban traffic impacts on air quality by deep learning and emission inventory. J. Environ. Sci. 2023, 124, 745–757. [Google Scholar] [CrossRef]
- Zhang, P.; Ma, W.; Wen, F.; Liu, L.; Yang, L.; Song, J.; Wang, N.; Liu, Q. Estimating PM2.5 concentration using the machine learning GA-SVM method to improve the land use regression model in Shaanxi, China. Ecotoxicol. Environ. Saf. 2021, 225, 112772. [Google Scholar] [CrossRef]
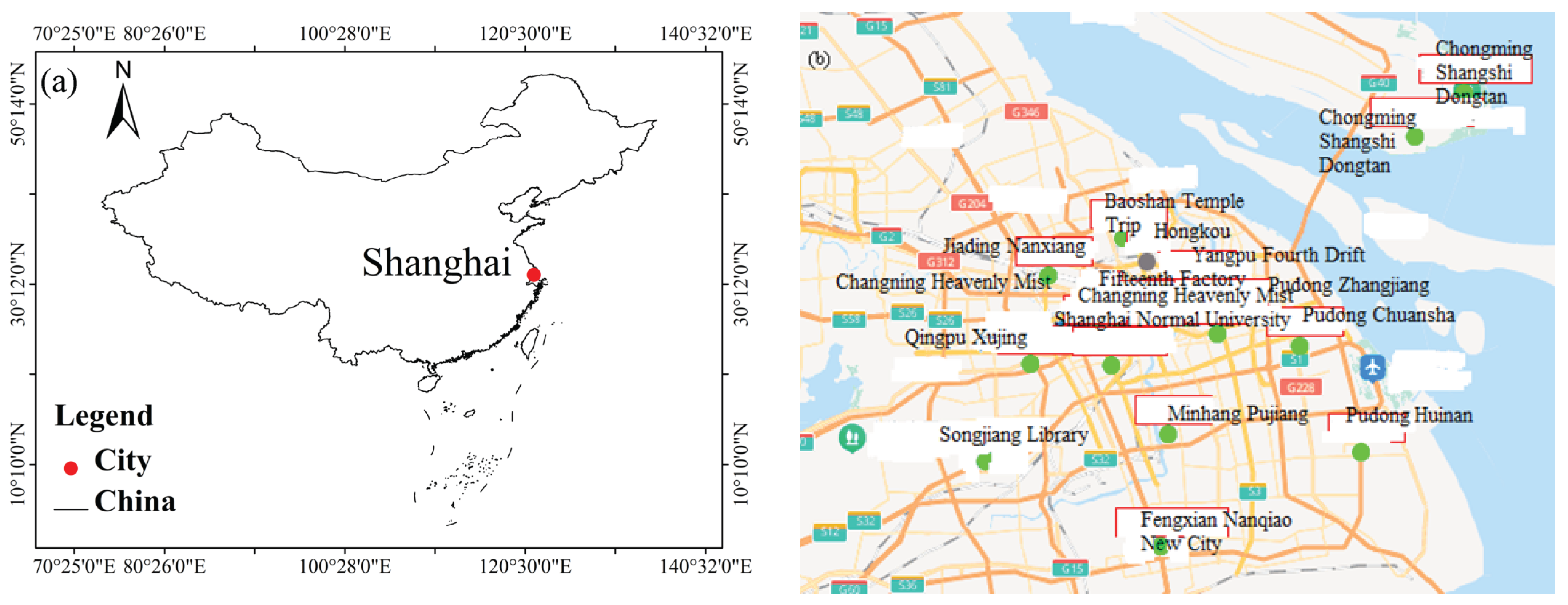



| Monitoring Sites | Monitoring Sites |
|---|---|
| Jinshan New City | Minhang Pujiang |
| Chongming Shangshi Dongtan | Qingpu Xujing |
| Chongming Shangshi Dongtan | Shanghai Normal University |
| Yangpu Fourth Drift | Pudong Zhangjiang |
| Fifteenth Factory | Baoshan Temple Trip |
| Jing’an Monitoring Station | Fengxian Nanqiao New City |
| Pudong Huinan | Jiading Nanxiang |
| Putuo | Songjiang Library |
| Pudong Chuansha | Changning Heavenly Mist |
| Pudong New Area Monitoring Station | Hongkou |
| Model ID | Input Variables | Structure |
|---|---|---|
| ANN1 ANN2 | P (t), EWV (t), MAP (t), MWV (t), MAT (t), MWP (t), MRH (t), SH (t), MINAP (t), MINAT (t), MAXAP (t), MAXAT (t), MAXWV (t), MINRH (t), PM2.5 (t), PM2.5 (t − 1), PM2.5 (t − 2) MINAT(t), MINAP(t), MAXAT(t), PM2.5 (t), PM2.5 (t − 1) | 17:15:1 5:19:1 |
| ANN3 | MINAT(t), PM2.5 (t) | 2:19:1 |
| ANN4 | PM2.5 (t) | 1:21:1 |
| WANN1 | P (t), EWV (t), MAP (t), MWV (t), MAT (t), MWP (t), MRH (t), SH (t), MINAP (t), MINAT (t), MAXAP (t), MAXAT (t), MAXWV (t), MINRH (t), PM2.5 (t), PM2.5 (t − 1), PM2.5 (t − 2) | 51:20:1 |
| WANN2 | MINAT(t), MINAP(t), MAXAT(t), PM2.5 (t), PM2.5 (t − 1) | 15:20:1 |
| WANN3 | MINAT(t), PM2.5 (t) | 6:17:1 |
| WANN4 | PM2.5 (t) | 3:19:1 |
| Model | R | RMSE (μg/m3) | MAE (μg/m3) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Training | Verification | Predicting | Training | Verification | Predicting | Training | Verification | Predicting | |
| ANN1 | 0.7061 | 0.6830 | 0.5618 | 20.7841 | 17.0006 | 24.2407 | 15.0825 | 13.1262 | 17.7867 |
| ANN2 | 0.6271 | 0.6258 | 0.4731 | 22.8559 | 18.1992 | 25.9092 | 16.3347 | 14.1125 | 18.9660 |
| ANN3 | 0.5947 | 0.5831 | 0.4454 | 23.5883 | 18.7088 | 26.4504 | 16.9128 | 14.5707 | 19.2679 |
| ANN4 | 0.5759 | 0.5450 | 0.4244 | 23.9847 | 18.9768 | 26.7117 | 17.2196 | 14.7856 | 19.7467 |
| WANN1 | 0.9416 | 0.8969 | 0.9316 | 9.8824 | 9.7850 | 10.6580 | 7.1153 | 6.8827 | 7.6918 |
| WANN2 | 0.9075 | 0.8424 | 0.8830 | 12.3243 | 11.9231 | 13.7228 | 8.4519 | 8.1825 | 9.1533 |
| WANN3 | 0.7952 | 0.6860 | 0.7213 | 17.7836 | 16.1466 | 20.2332 | 12.5331 | 11.1733 | 14.6255 |
| WANN4 | 0.7380 | 0.6404 | 0.7043 | 19.7903 | 17.0581 | 20.7106 | 13.5311 | 11.5643 | 14.7616 |
| Model | Area | R2 | RE | RMSE | MAE | Reference |
|---|---|---|---|---|---|---|
| ANN | Ahvaz, Iran | 0.74 | 0.91507 | 46.44 | [45] | |
| ANN | Delhi, India | 0.86 | 0.451 | [55] | ||
| ANN | Addis Ababa, Ethiopia | 0.943 | 0.12034 | 15.66 | 10.27 | [56] |
| SVR | Nottingham, United Kingdom | 0.88782 | 0.12224 | 2.45315 | 1.29443 | [57] |
| XGBoost | China | 0.8 | 0.36385 | 26.34 | 15.58 | [58] |
| RNN | Seoul metropolitan, Korea | 0.31 | 8.4 | [59] | ||
| LSTM | Tianjin, China | 0.94 | 0.4305 | 13.06 | 8.61 | [60] |
| CNN | Beijing, China | 0.7225 | 0.58843 | 40.83 | 25.32 | [61] |
| EMD-GRU | Beijing, China | 0.9706 | 0.14809 | 11.372 | 6.532 | [62] |
| CNN-LSTM | Beijing, China | 0.921573 | 0.1518 | 24.2287 | 14.63446 | [63] |
| 3D CNN-GRU | Tehran, Iran | 0.78 | 0.27781 | 6.44 | 8.89 | [64] |
| MCD-ESN-PSO | four cities, China | 0.9801 | 0.0167 | 1.18 | 0.88 | [65] |
| CNN-GBM | Shanghai, China | 0.85 | 0.07982 | 10.02 | [66] | |
| iDeepAir | Shanghai, China | 0.2227 | 15.587 | 12.373 | [67] | |
| GA-SVM | Shaanxi, China | 0.18773 | 12.1 | 10.07 | [68] | |
| WANN | Shanghai, China | 0.8679 | 0.1363 | 10.658 | 7.6918 | This article |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Q.; He, Z.; Wang, Z. Predicting of Daily PM2.5 Concentration Employing Wavelet Artificial Neural Networks Based on Meteorological Elements in Shanghai, China. Toxics 2023, 11, 51. https://doi.org/10.3390/toxics11010051
Guo Q, He Z, Wang Z. Predicting of Daily PM2.5 Concentration Employing Wavelet Artificial Neural Networks Based on Meteorological Elements in Shanghai, China. Toxics. 2023; 11(1):51. https://doi.org/10.3390/toxics11010051
Chicago/Turabian StyleGuo, Qingchun, Zhenfang He, and Zhaosheng Wang. 2023. "Predicting of Daily PM2.5 Concentration Employing Wavelet Artificial Neural Networks Based on Meteorological Elements in Shanghai, China" Toxics 11, no. 1: 51. https://doi.org/10.3390/toxics11010051
APA StyleGuo, Q., He, Z., & Wang, Z. (2023). Predicting of Daily PM2.5 Concentration Employing Wavelet Artificial Neural Networks Based on Meteorological Elements in Shanghai, China. Toxics, 11(1), 51. https://doi.org/10.3390/toxics11010051







