Neuro-Particle Swarm Optimization Based In-Situ Prediction Model for Heavy Metals Concentration in Groundwater and Surface Water
Abstract
1. Introduction
2. Materials and Methods
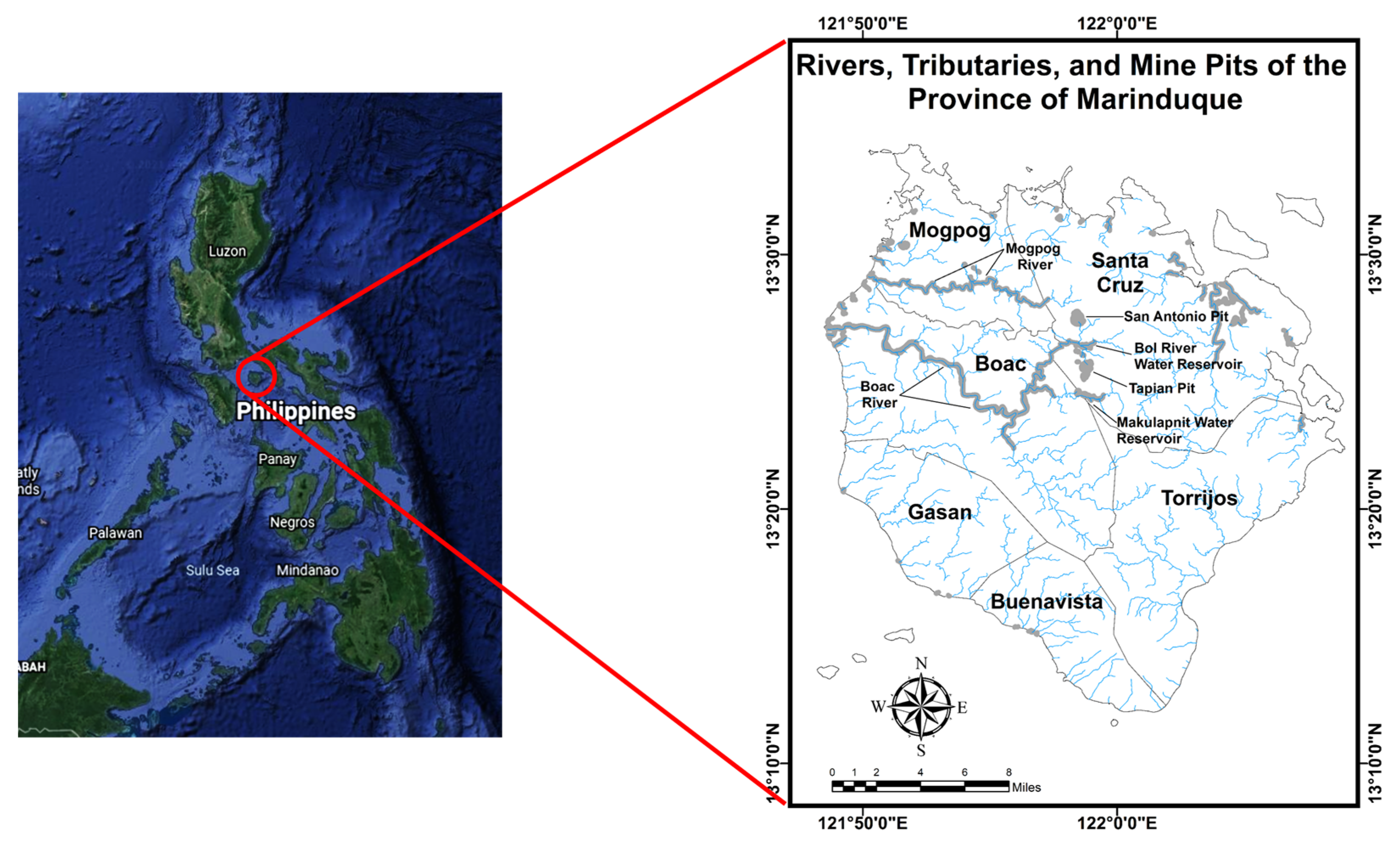
2.1. Location of the Study and Data Gathering
2.2. Analysis of Physicochemical Parameters and HM Concentrations
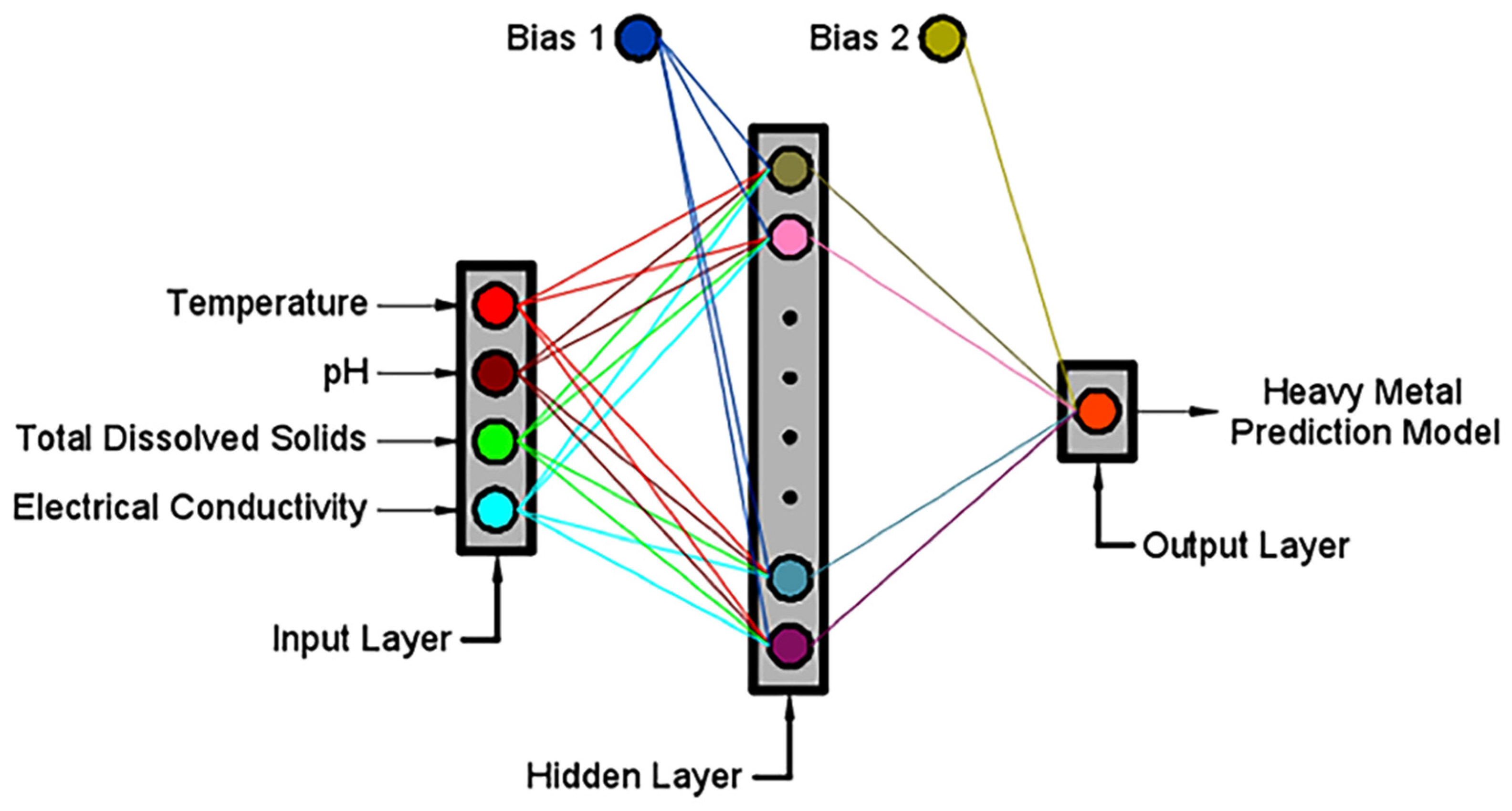
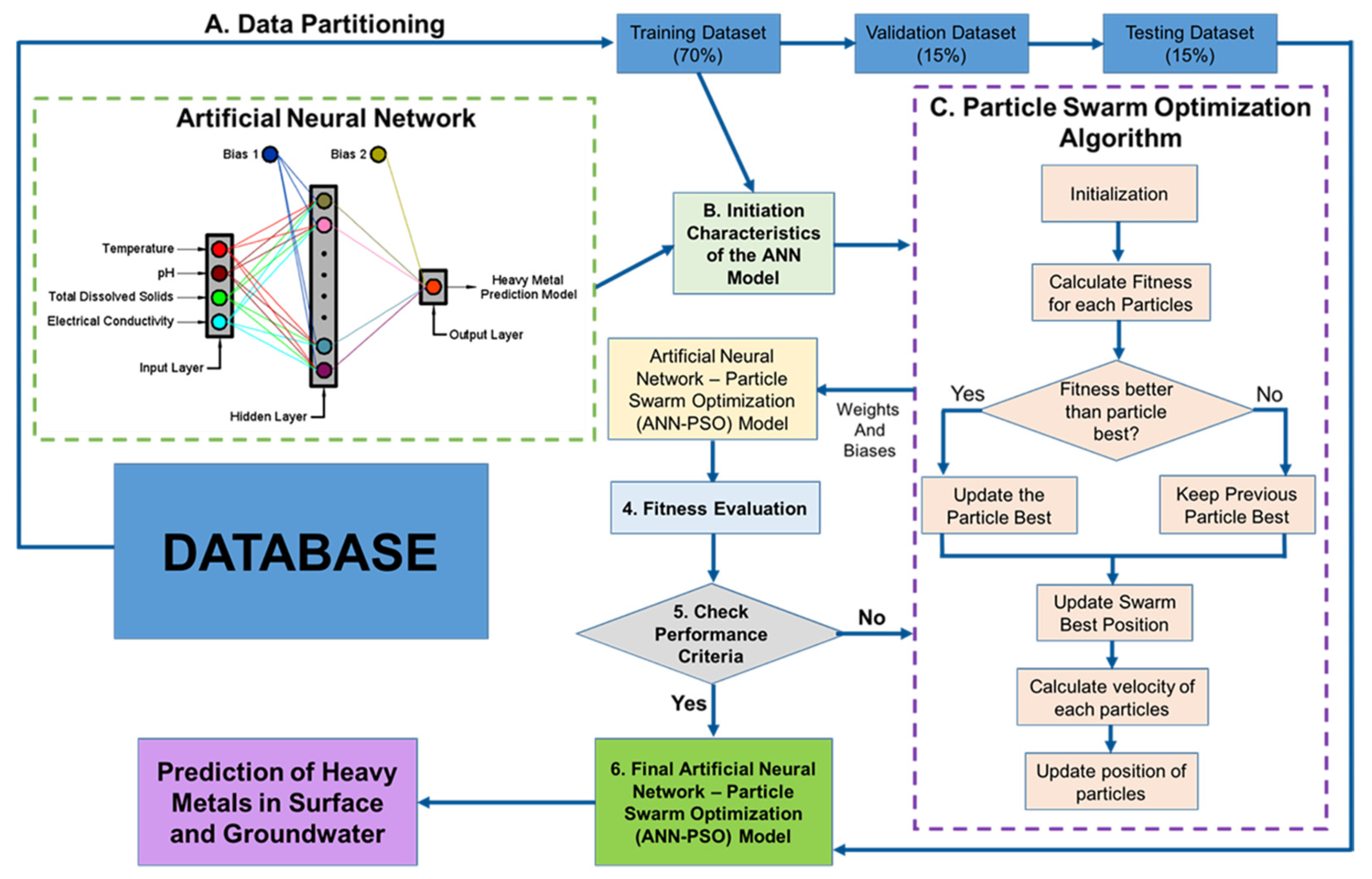
2.3. Neuro-Particle Swarm Optimization Modelling (NN-PSO)
2.3.1. Machine Learning Geostatistical Interpolation (MLGI) Mapping
2.3.2. Data Pre-Processing
2.3.3. Backpropagation Neural Network
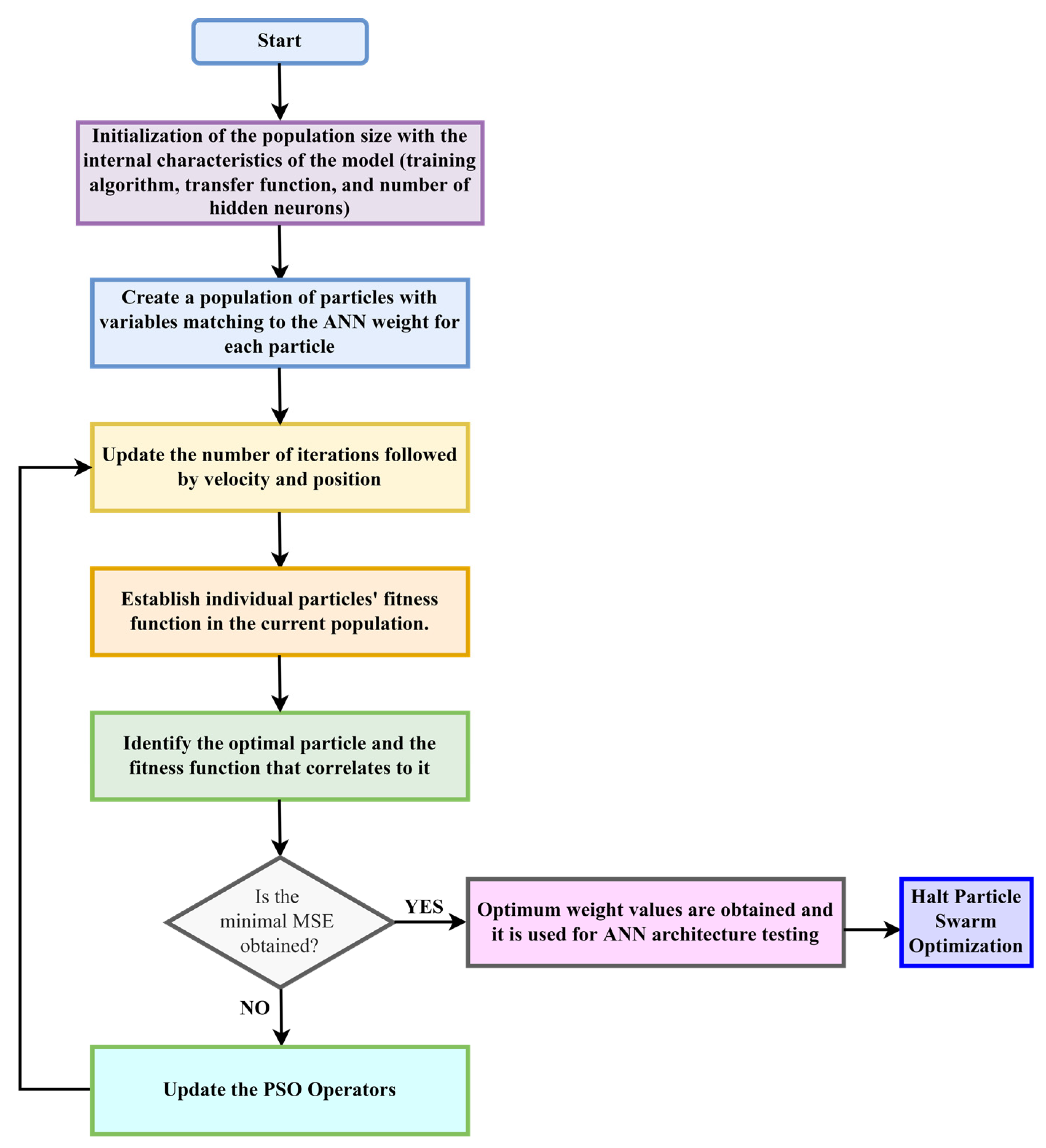
2.3.4. Particle Swarm Optimization
2.3.5. Hybrid NN-PSO (hN-PSO)
2.3.6. Performance Validation and Measurement
2.4. Comparison to Other Models
2.5. Sensitivity Analysis
3. Results
3.1. Heavy Metal Concentrations
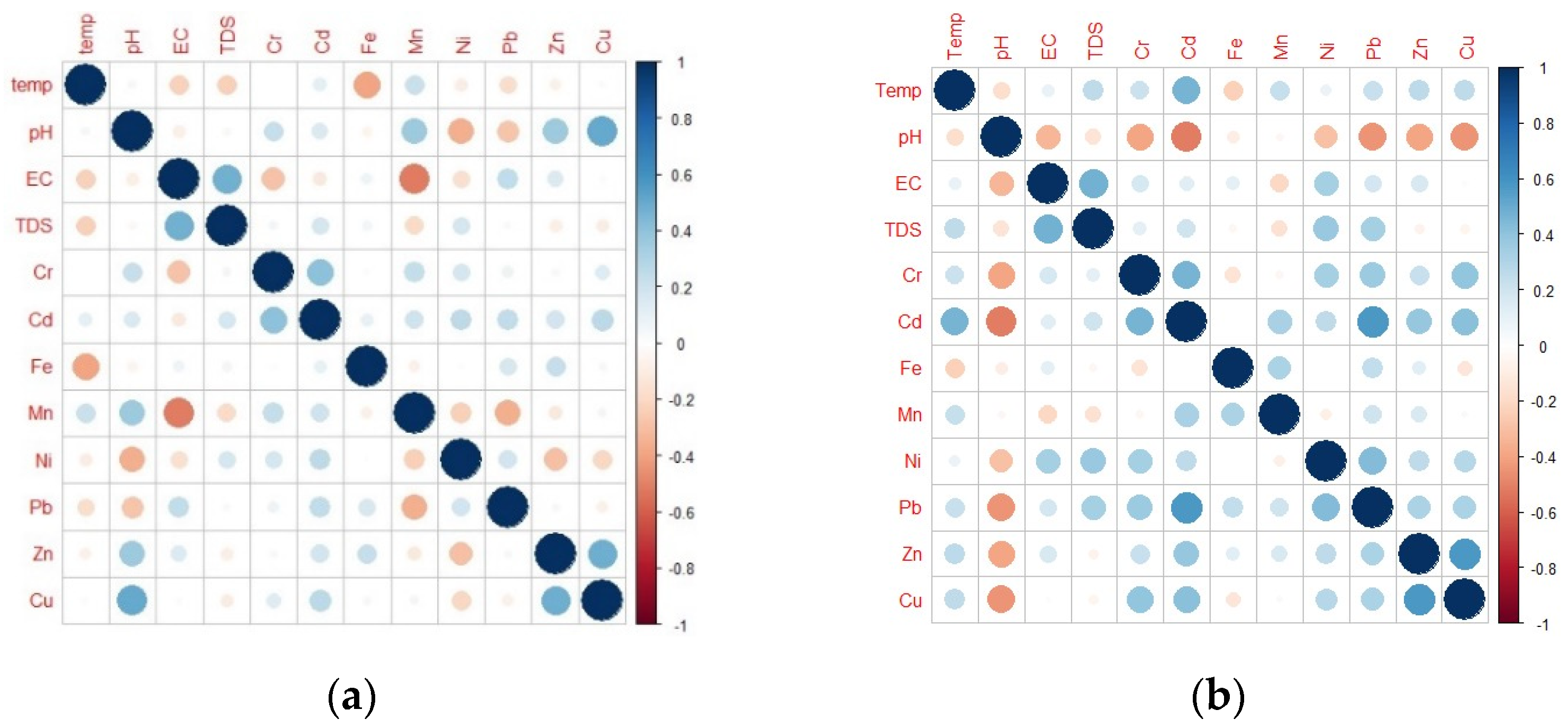
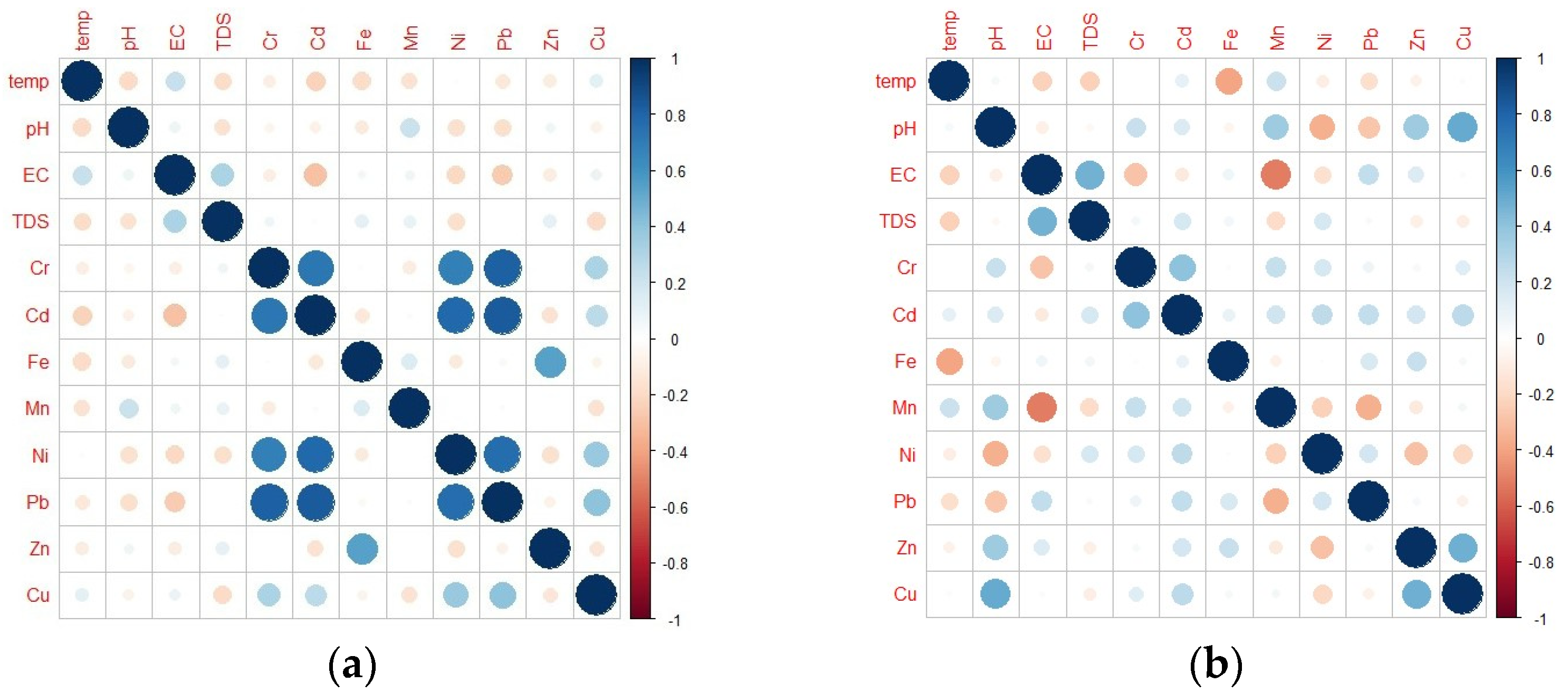
3.2. Correlation Analysis
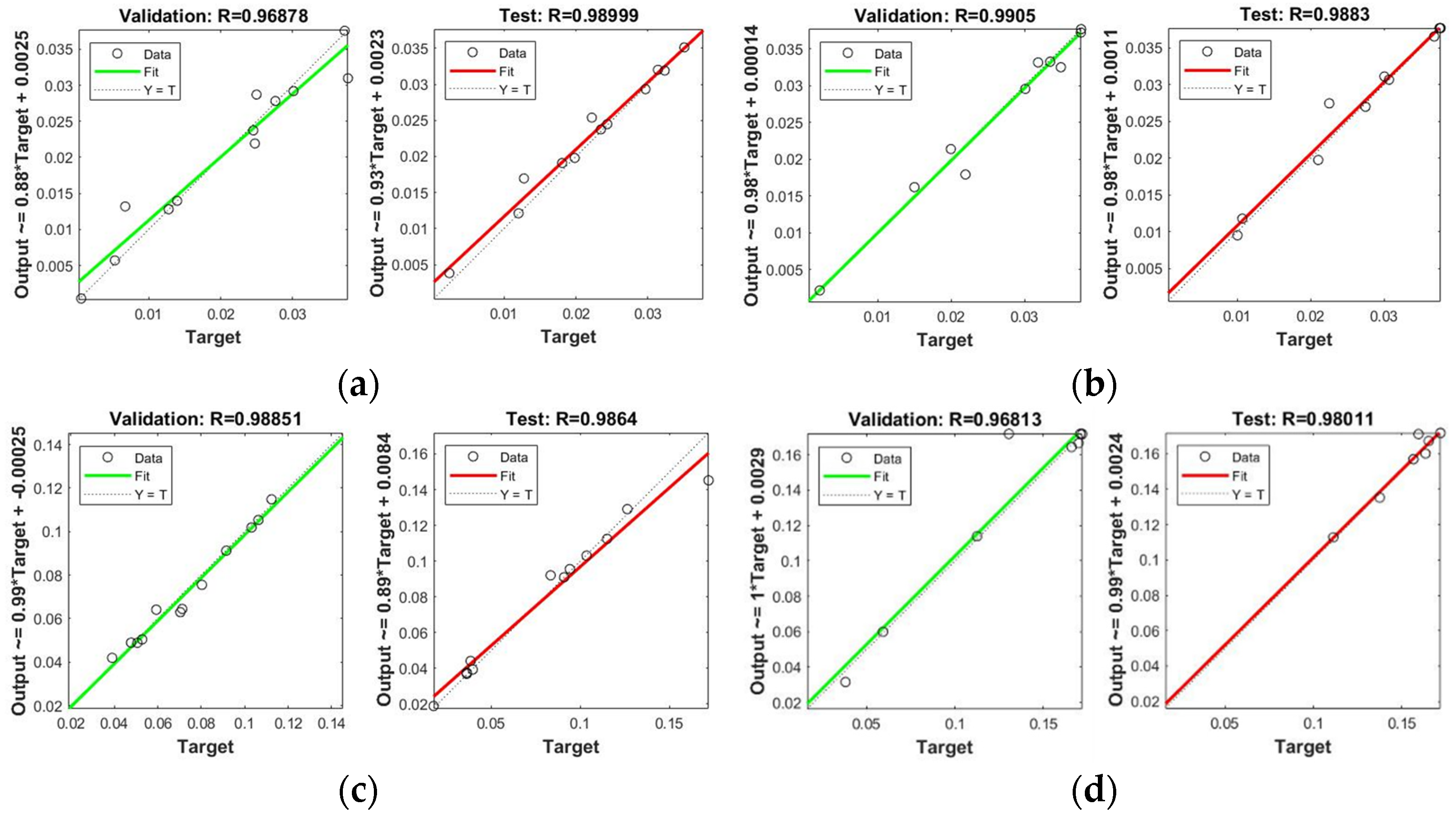
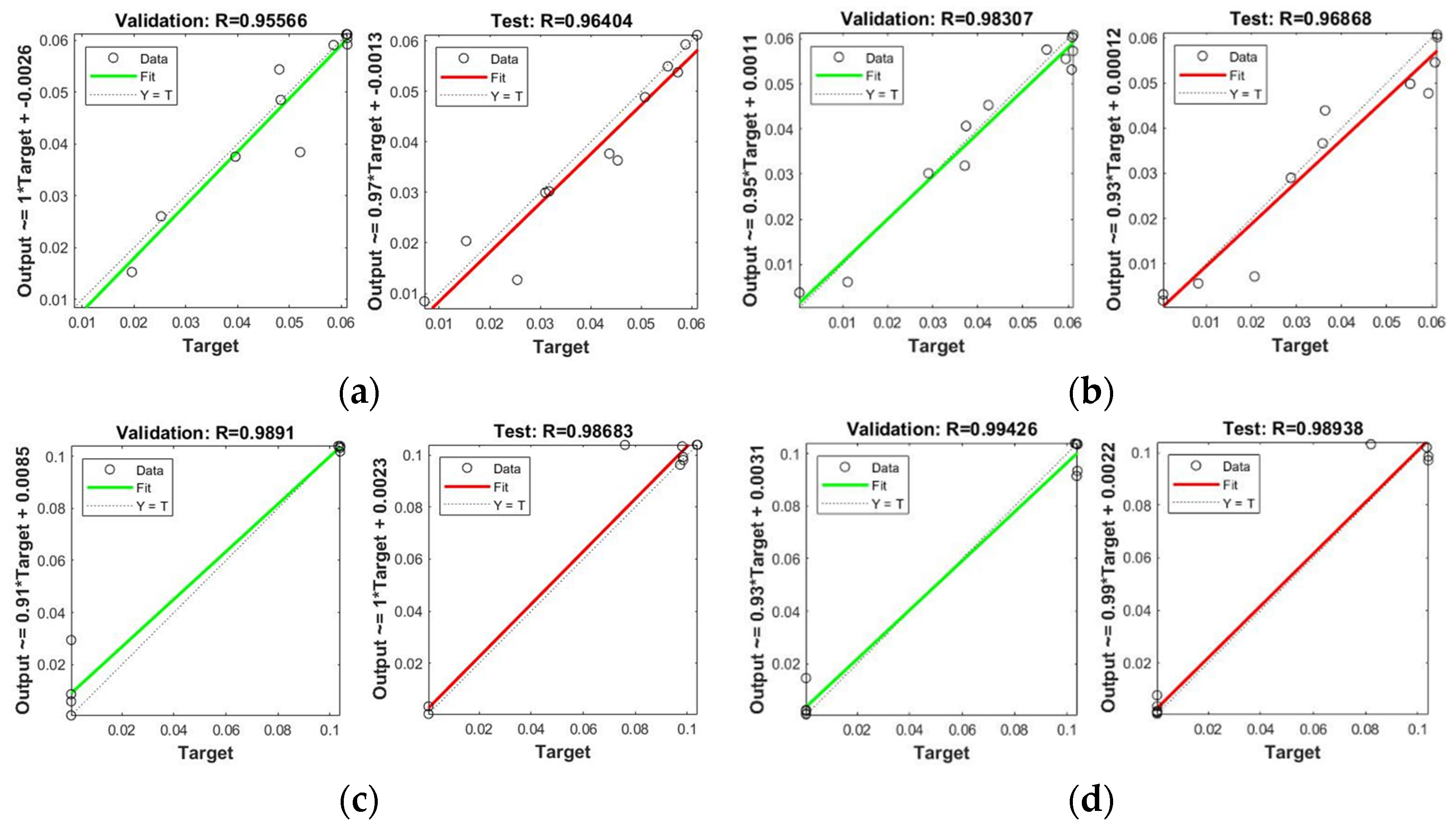
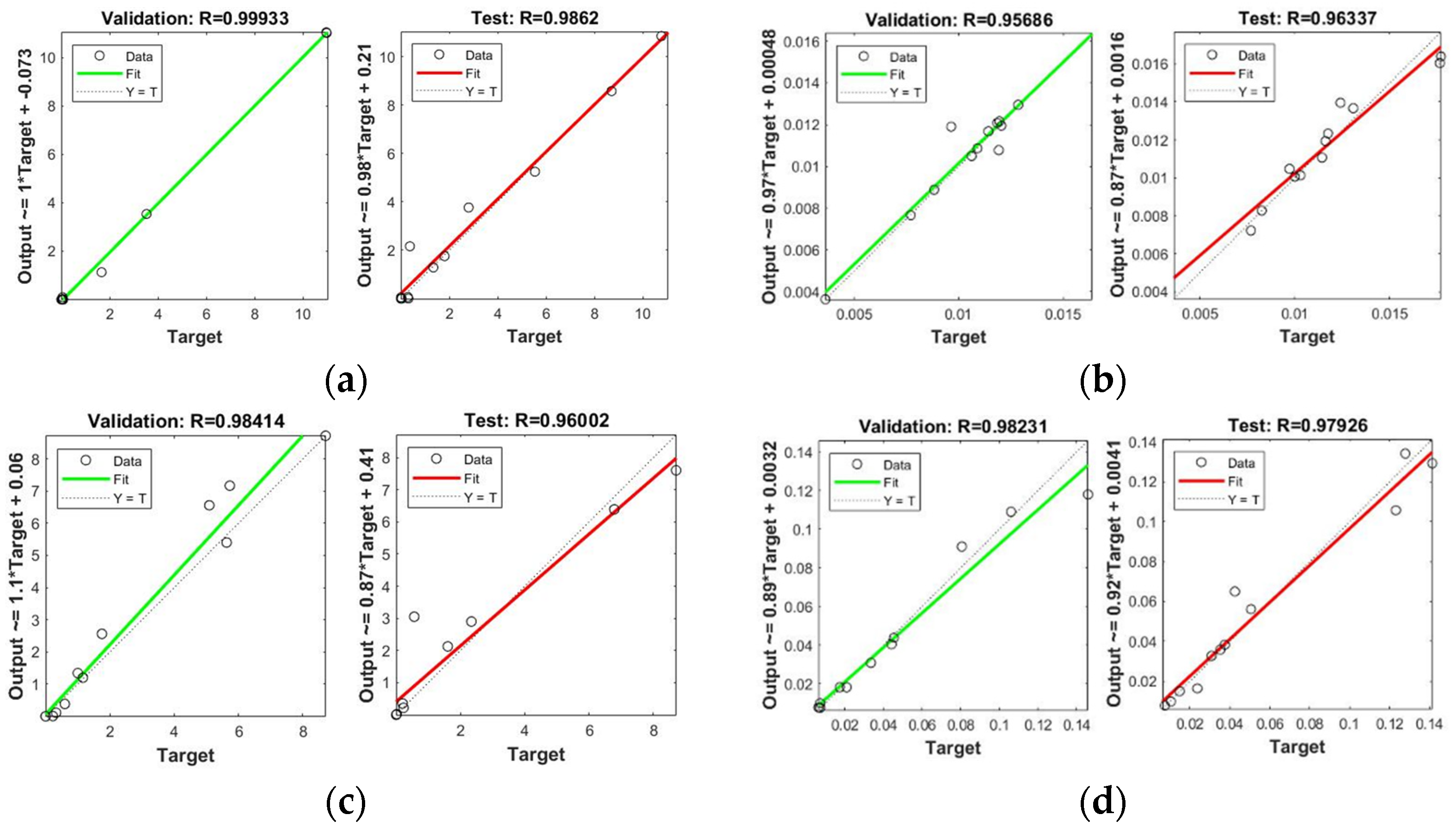
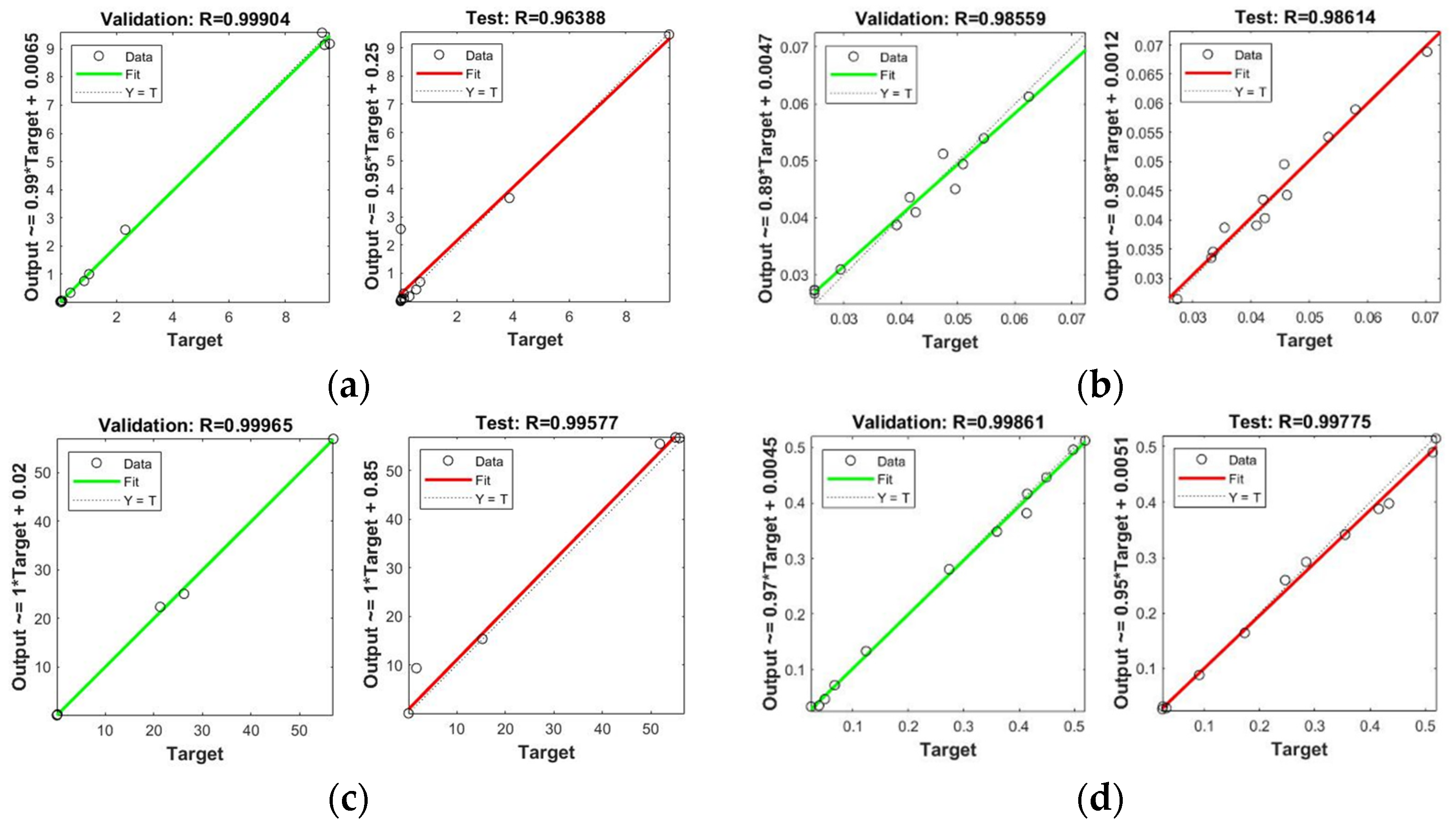
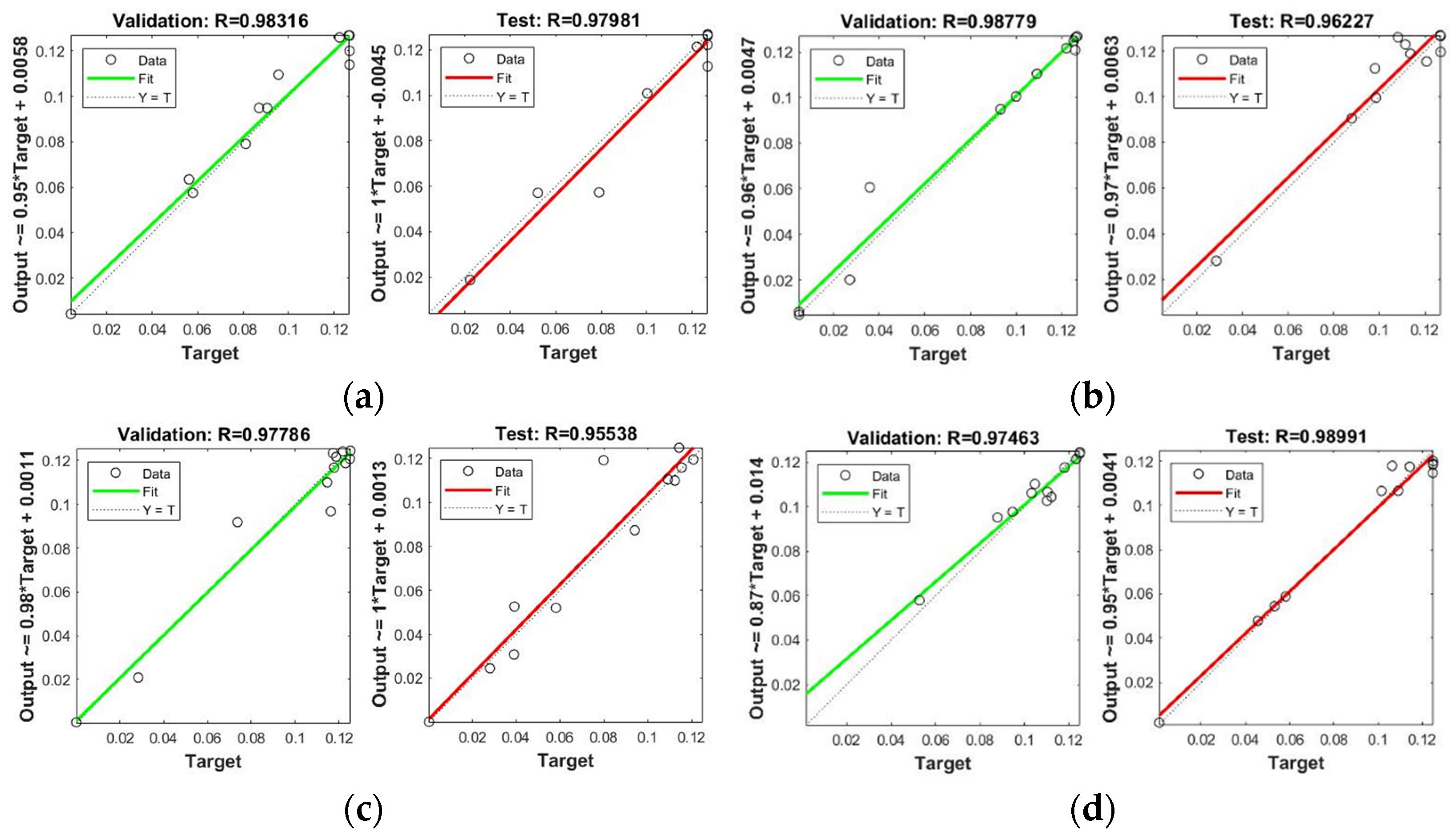
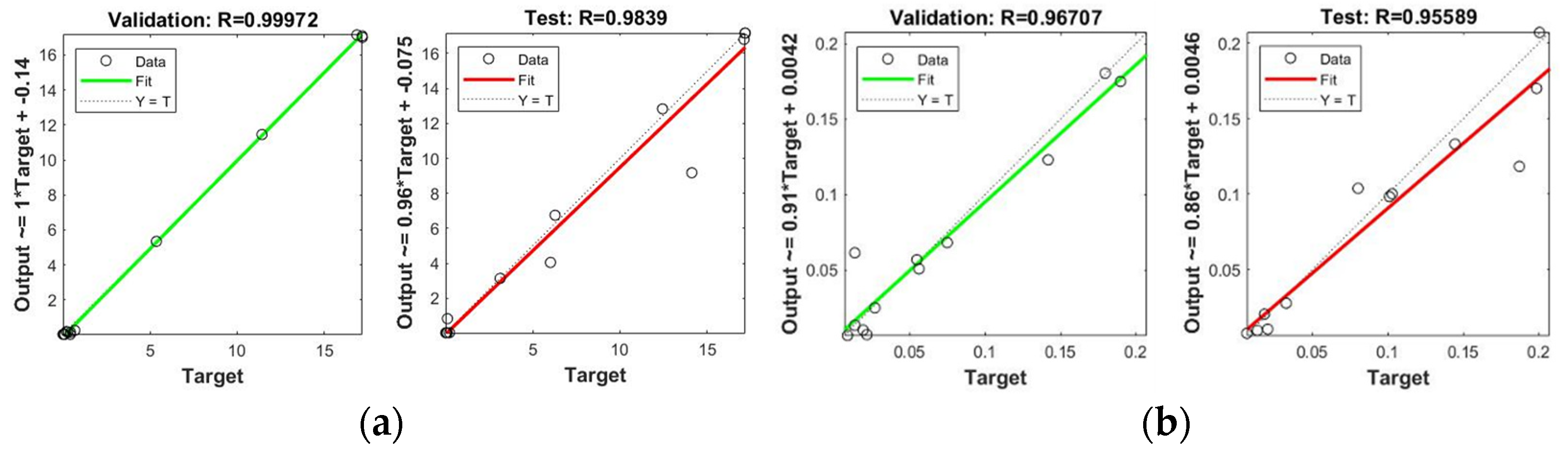
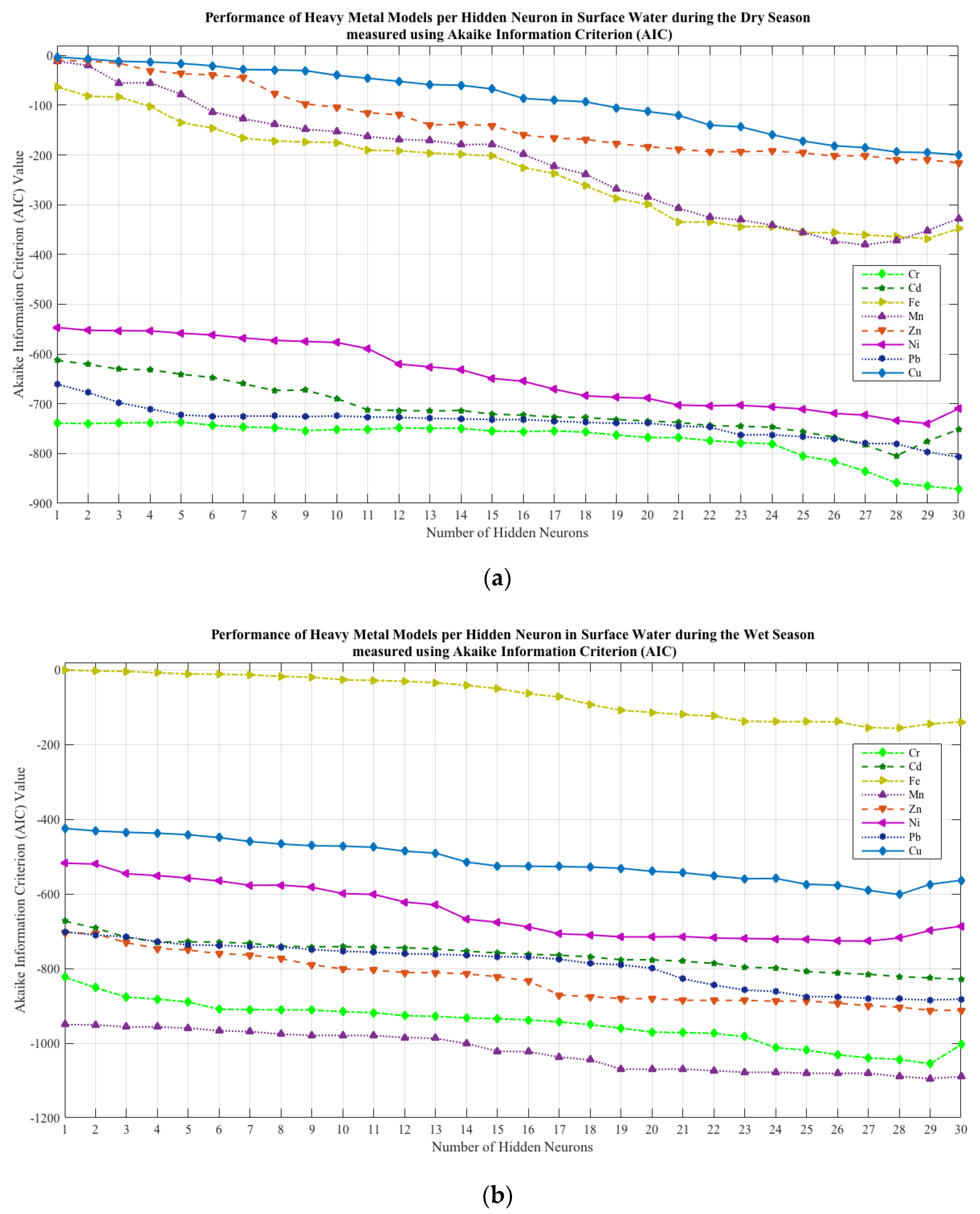
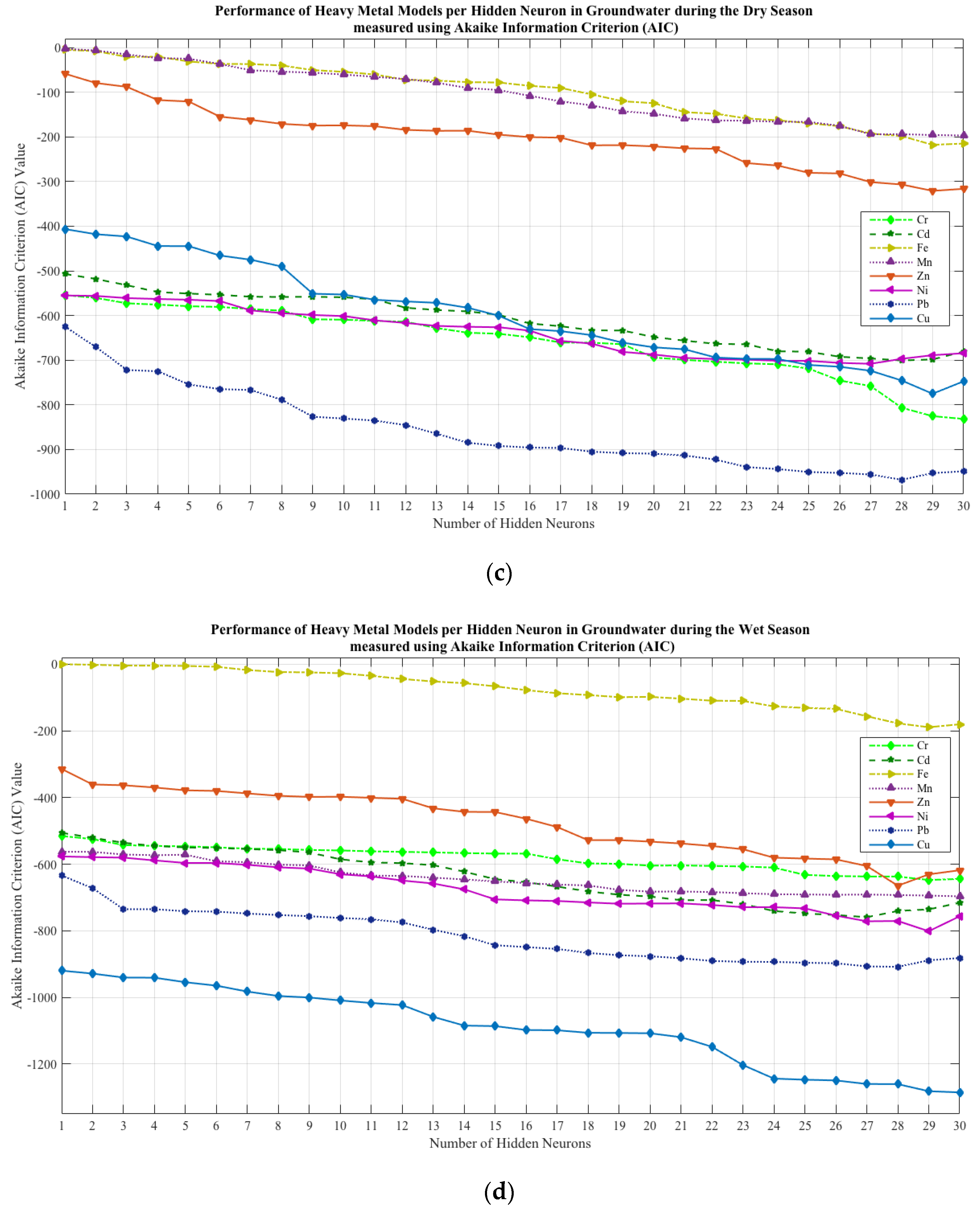
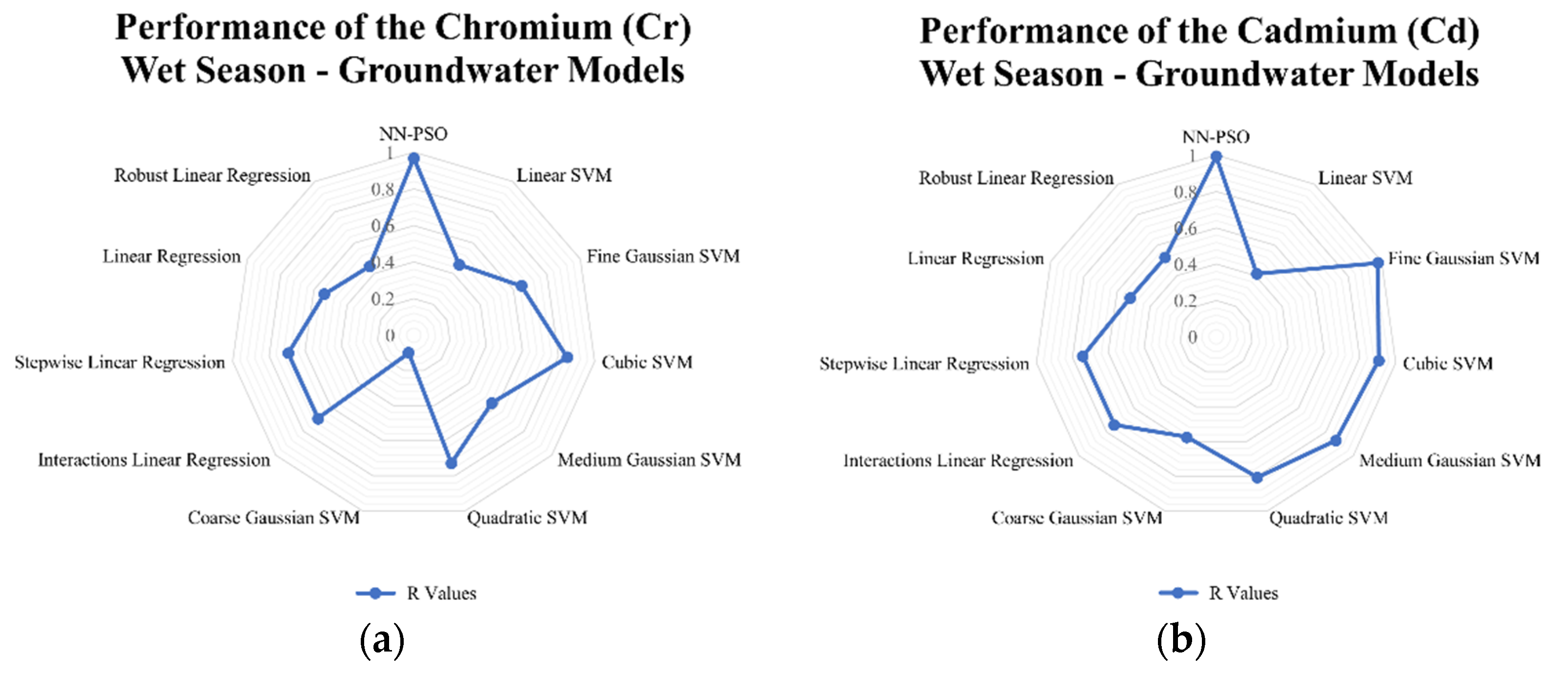
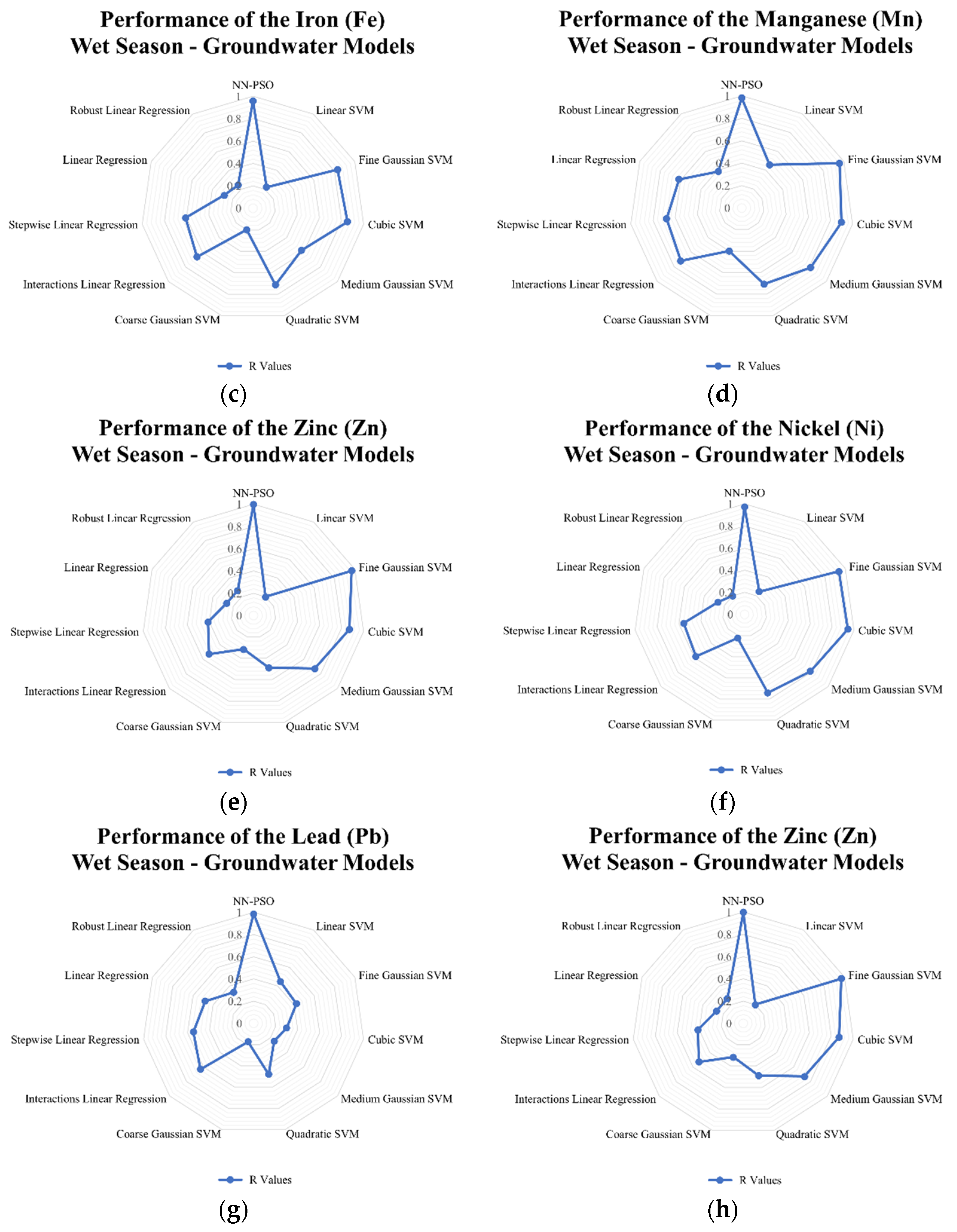
3.3. NN-PSO Modelling Results
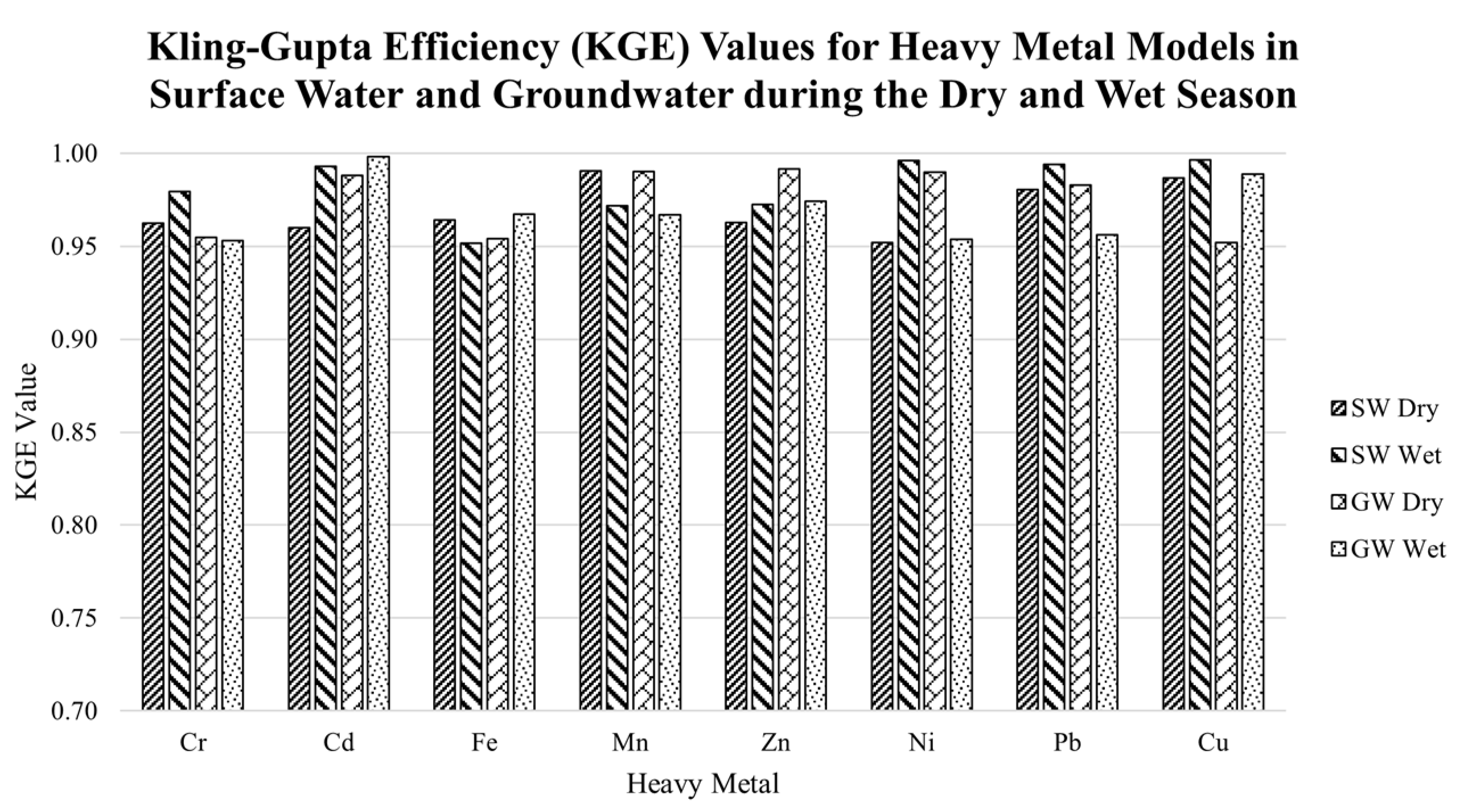
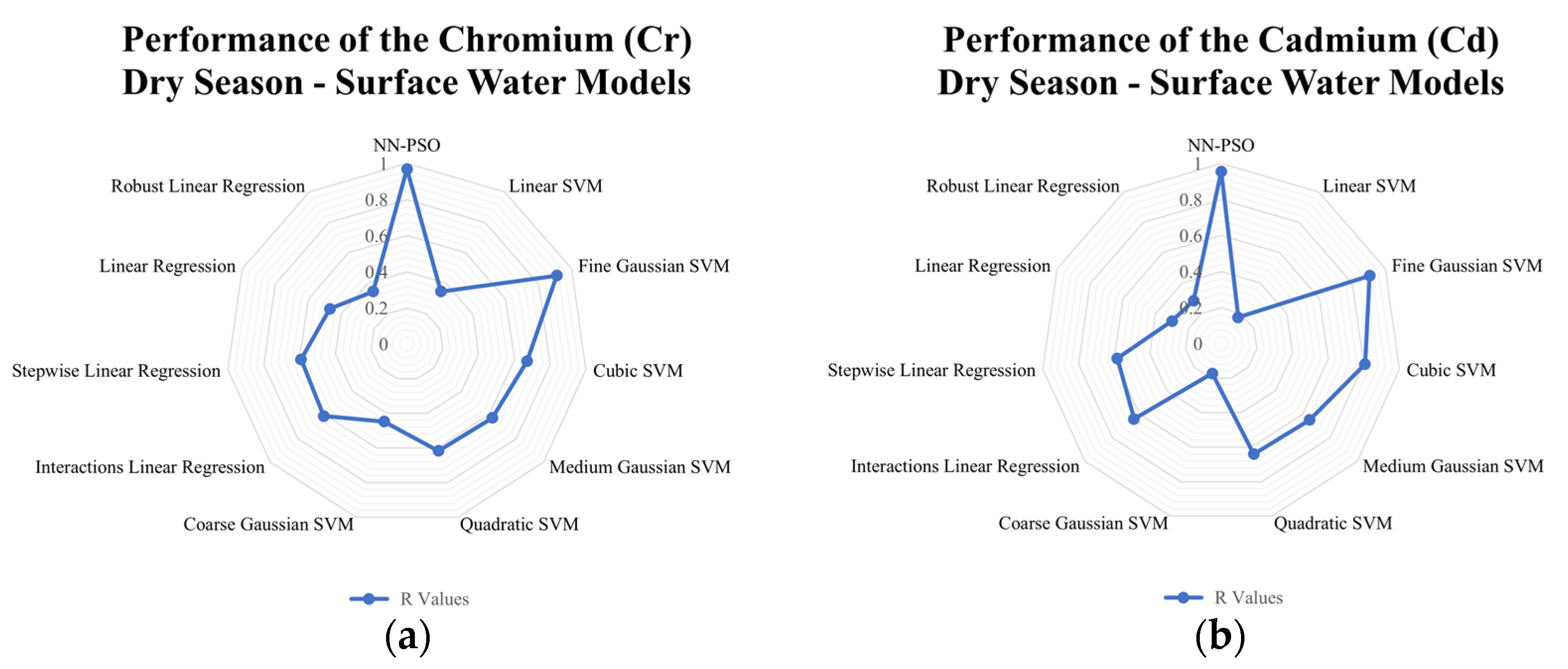
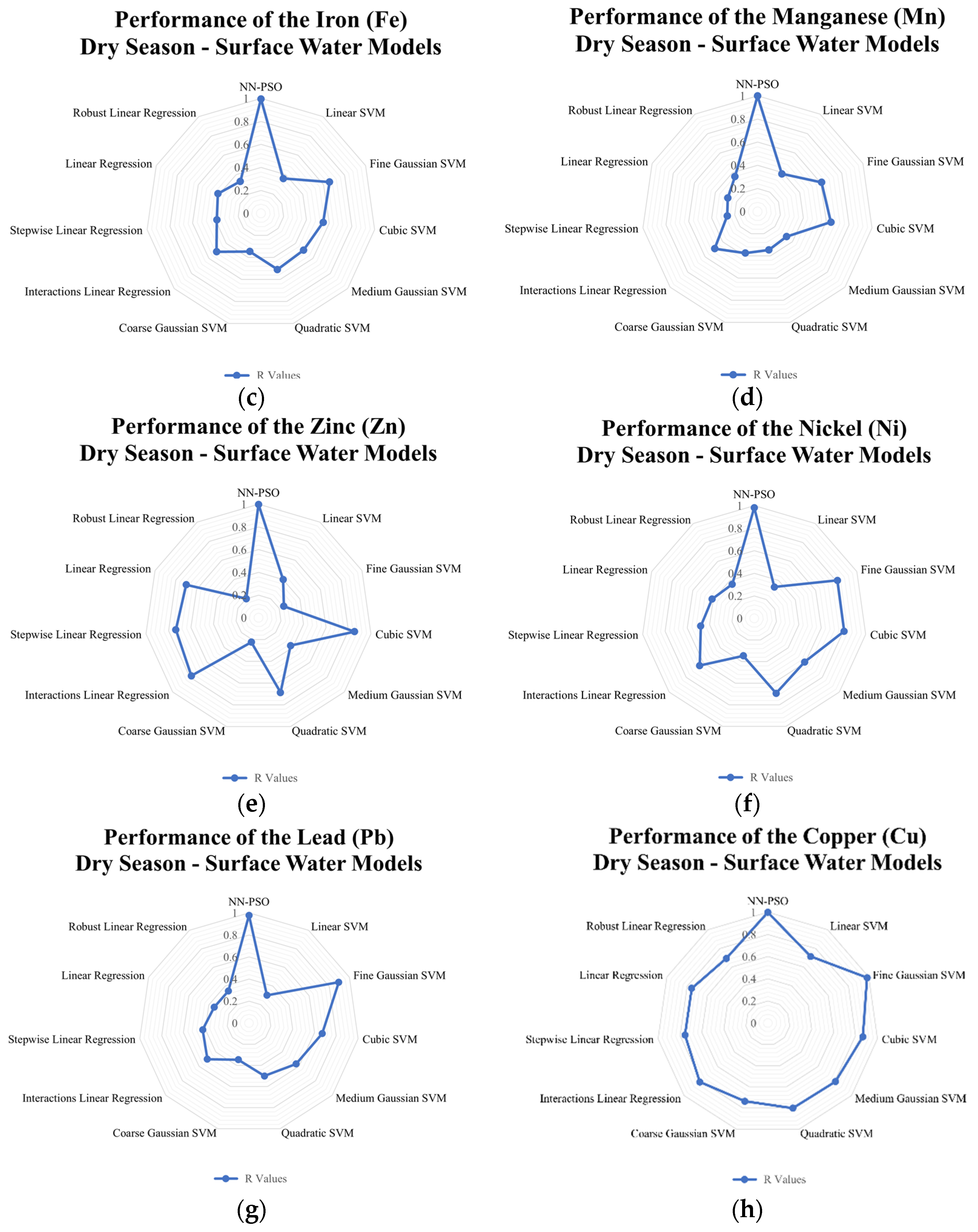
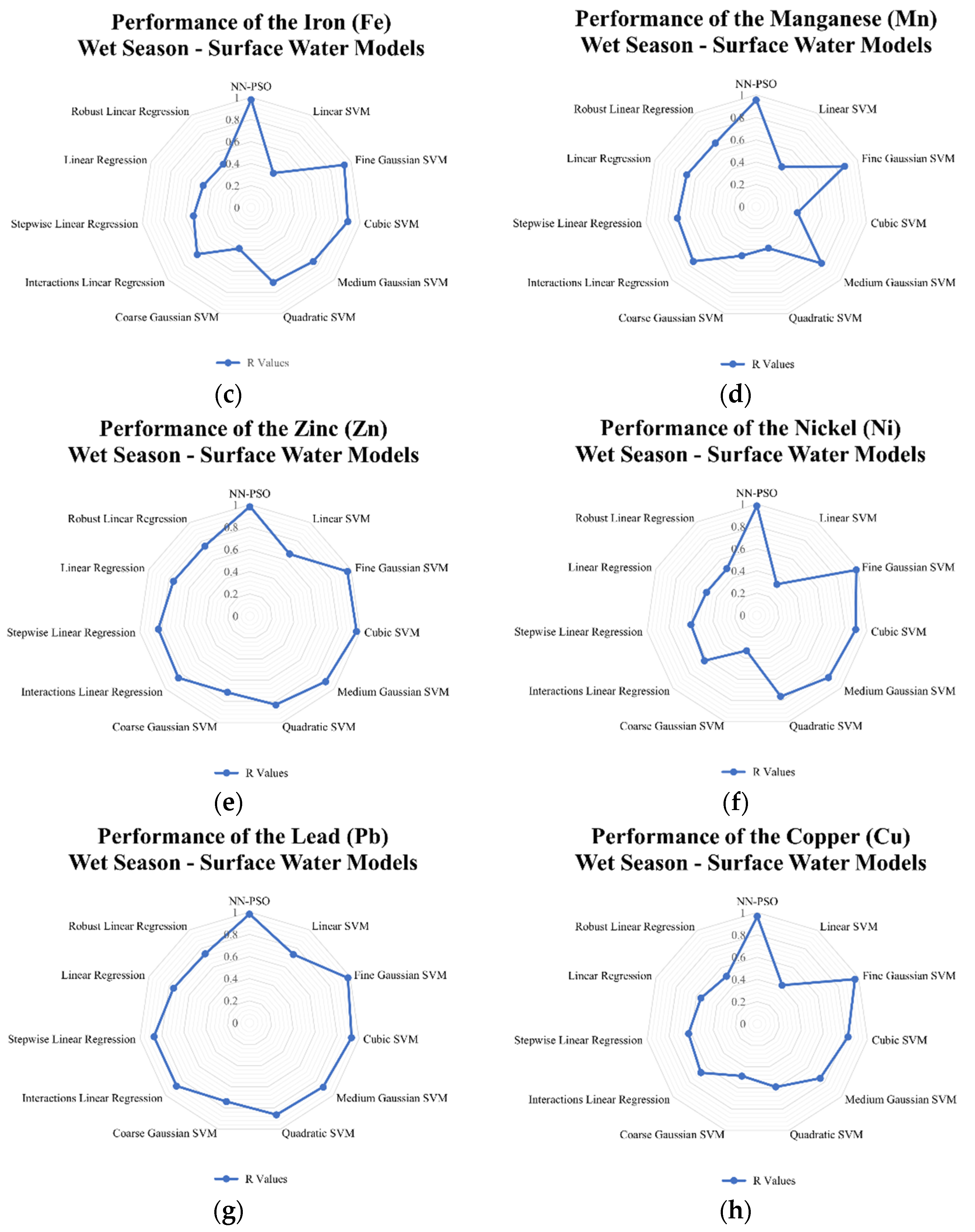
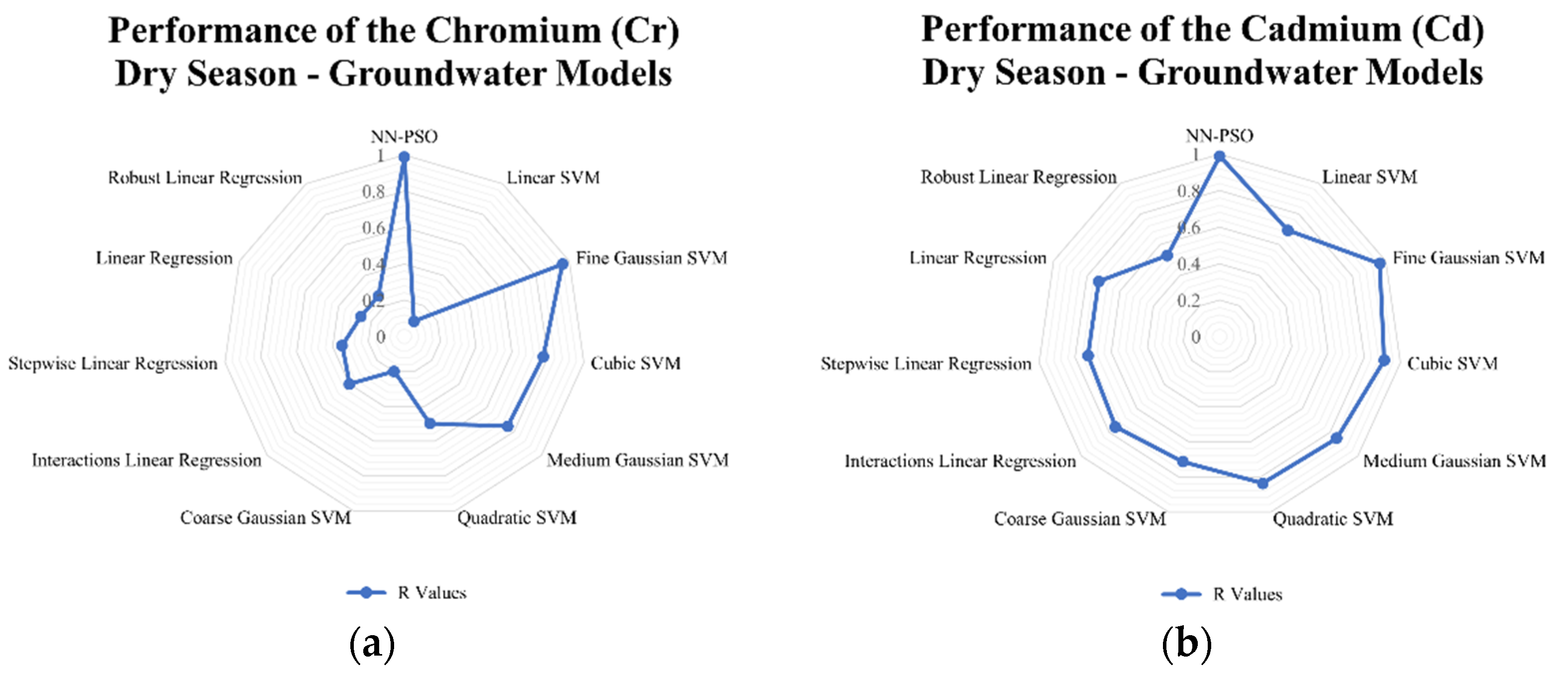
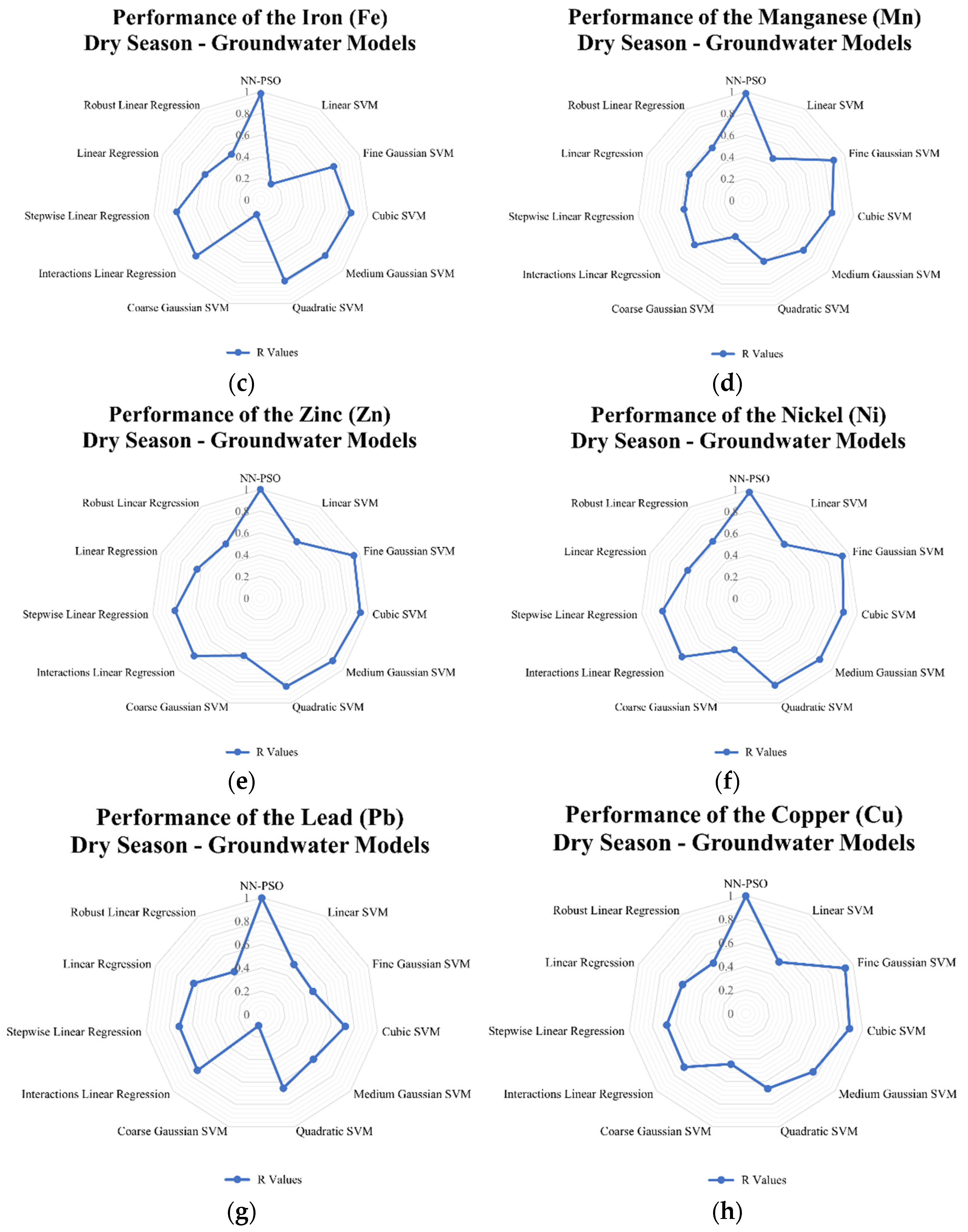
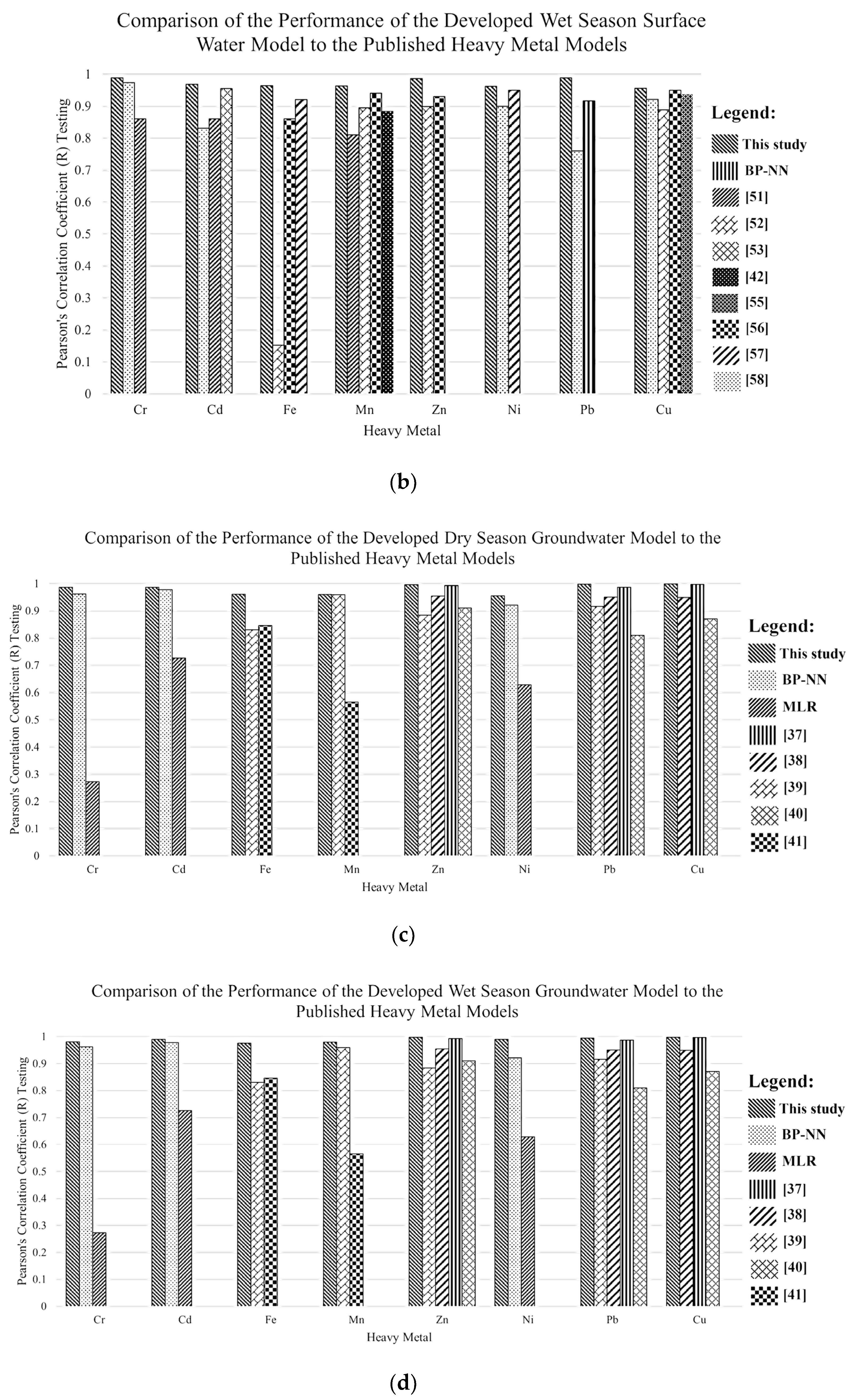
3.4. Comparison to Other Models
3.5. Sensitivity Analysis Using Olden’s Connection Weight Approach
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Location/Date | Cause of Release | Description of Release | Impact | Reference |
|---|---|---|---|---|
| Siocon, Zamboanga Del Norte/6 April and 11 July 2007 | Heavy rains eroded the clay soil and destroyed the concrete wall of the zinc extraction sulphide dam. | Contaminated water with detectable levels of cyanide and mercury ran down the Canatuan River and into the Siocon River, eventually reaching the sea. | Reports of siltation had reached up to 3 m thick, which caused frequent flash floods and obstructed irrigation flow from the river. The river mouth became brown and fish catches decreased. | [118] |
| Rapu–Rapu Island, Albay/ 11 and 31 October 2005 | The tailings pump failed, spilling tailings from the mill’s emergency pond into the gold processing facility and neighboring Alma and Pagcolbon creeks. | At least 20 cubic meters of slurry material (containing cyanide beyond the standard of 0.05 mg/L and other toxic heavy metals and chemicals) | Two kilograms of dead small fish and crustaceans at the shoreline collected on the same day at the location where the affected creeks exit into the sea. | [119] |
| San Marcelino, Zambales 27 August 27 and 11 September 2002 | The spillway of Bayarong tailings dam collapsed during heavy rain. | High concentrations of heavy metals and sulfide materials. | Low-lying settlements were inundated with mining waste, 250 residents were evacuated, and some tailings leaked into Mapanuepe Lake and later into the Sto. Tomas River. | [120] |
| Sipalay, Negros Occidental 8 December 1995 | At the Bulawan gold mine, the pressure of impounded tailings created a leakage in the decant tower of tailings pond no. 1. | Mine tailings caused the siltation of the Sipalay River. | Excessive quantities of dust covered a 5-square-kilometer region, affecting the air quality, and local inhabitants reported a rise in respiratory diseases. | [121] |
| Toledo City, Cebu 9 August 1999 | The outlet of an open pit’s drainage tunnel (from a closed copper mine) was obstructed, resulting in the loosening of accumulated silt and discharge into the Sapangdaku River toward the sea. | 5.7 million m3 of acidic water | Increased acidity in afflicted water bodies, resulting in fish mortality. | [122] |
| Placer, Surigao del Norte/ 26 April 1999 | Tailings pond No. 7 tailings discharged due to a broken concrete pipe. | 700,000 cubic meters of cyanide tailings | Seventeen homes buried, 40 heactares affected, including 20 hectares of agricultural land | [123] |
| Sibutad, Zamboanga del Norte 6 November 1997 | Two strong rain events resulted in mudflows and rockslides into a silt dam. | Sibutad gold project’s silt dam overflowed | Caused flash floods damaging the nearby houses and rice fields and fish kills. | [124] |
| Mankayan, Benguet 17 October 1986 | Tailings pond 3 collapsed as a result of a compromised dam embankment caused by excessive loading. | Mine tailings overflowed and huge amounts of Cu-contaminated mine wastes carried by the Comillas River | Caused siltation of the Abra River, affecting nine towns, and toxic contamination of the river, depriving the region of about 7.33 million kg of rice every year. | [125] |
| Marinduque Island 6 December 1993 | Maguilaguila siltation dam collapsed because of the siltation pressure at the dam wall. | Toxic mine tailings in silt and water | Flooding of the Mogpog River resulted in the death of two children, cattle, contamination of agricultural land, and flooding of downstream communities and Mogpog town. | [126,127] |
| Marinduque Island 24 March 1996 | According to the official explanation, the rock around the plug in the Tapian Pit drainage tunnel was cracked, resulting in the plug’s failure. However, in August 1995, the tunnel began to leak. Marcopper/Placer Dome began drilling 160 m down to the tube in September 1995. The drill struck the tube on 24 March 1996, releasing an air pocket that had been holding back tailings and initiating the leak. | The estimate based on the United Nations is between 2–3 million cubic meters over the first 4–5 days of discharge alone. | Approximately 1200 persons were evacuated, 26 km of the Makulapnit and Boac river systems were rendered impassable by tailings, flash floods cut off five communities, and 67,000 cubic meters of bagged tailings were gathered and placed on the banks of the Boac river since the cleaning started in 2000. | [126,127] |
Appendix B
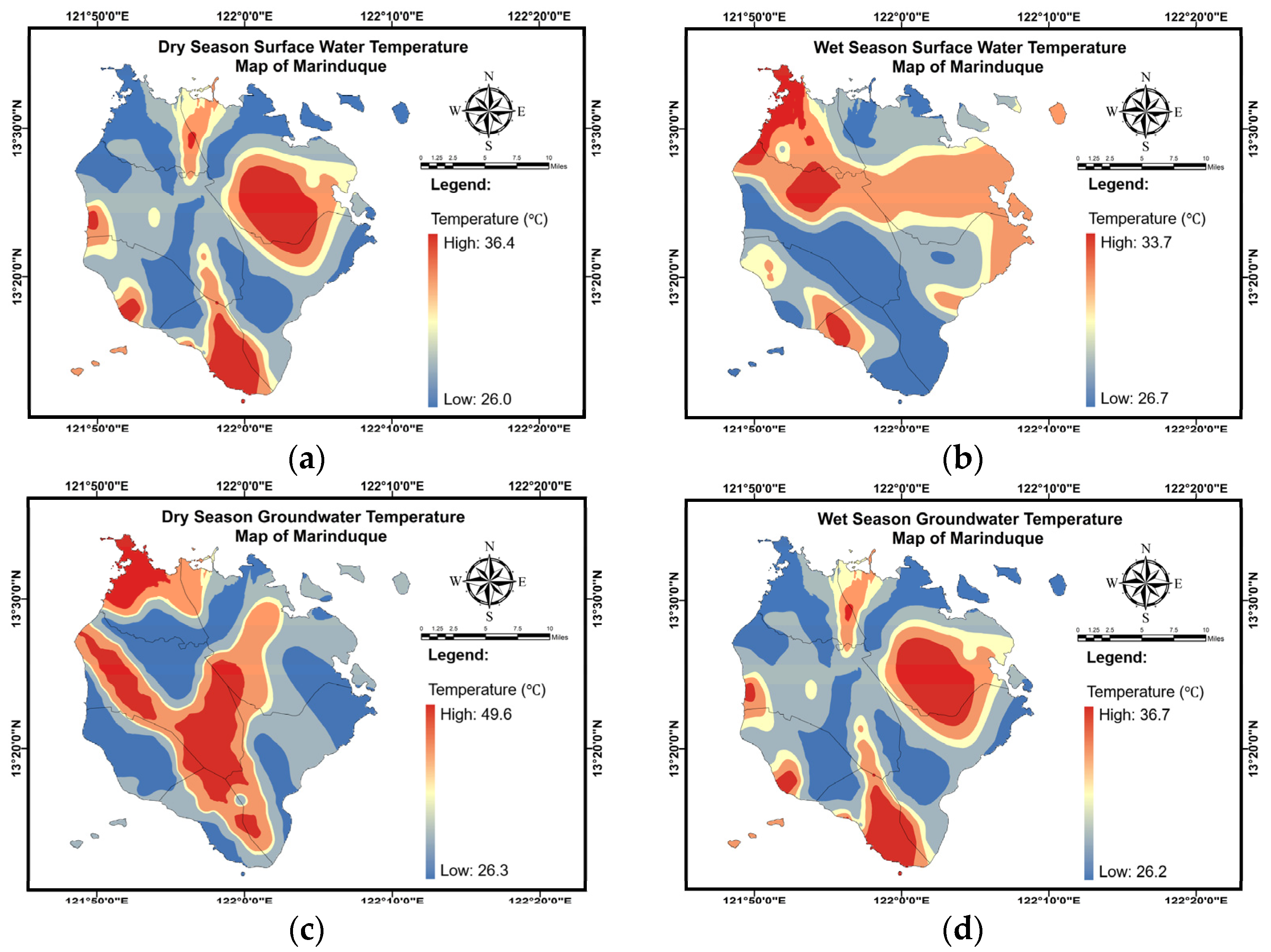



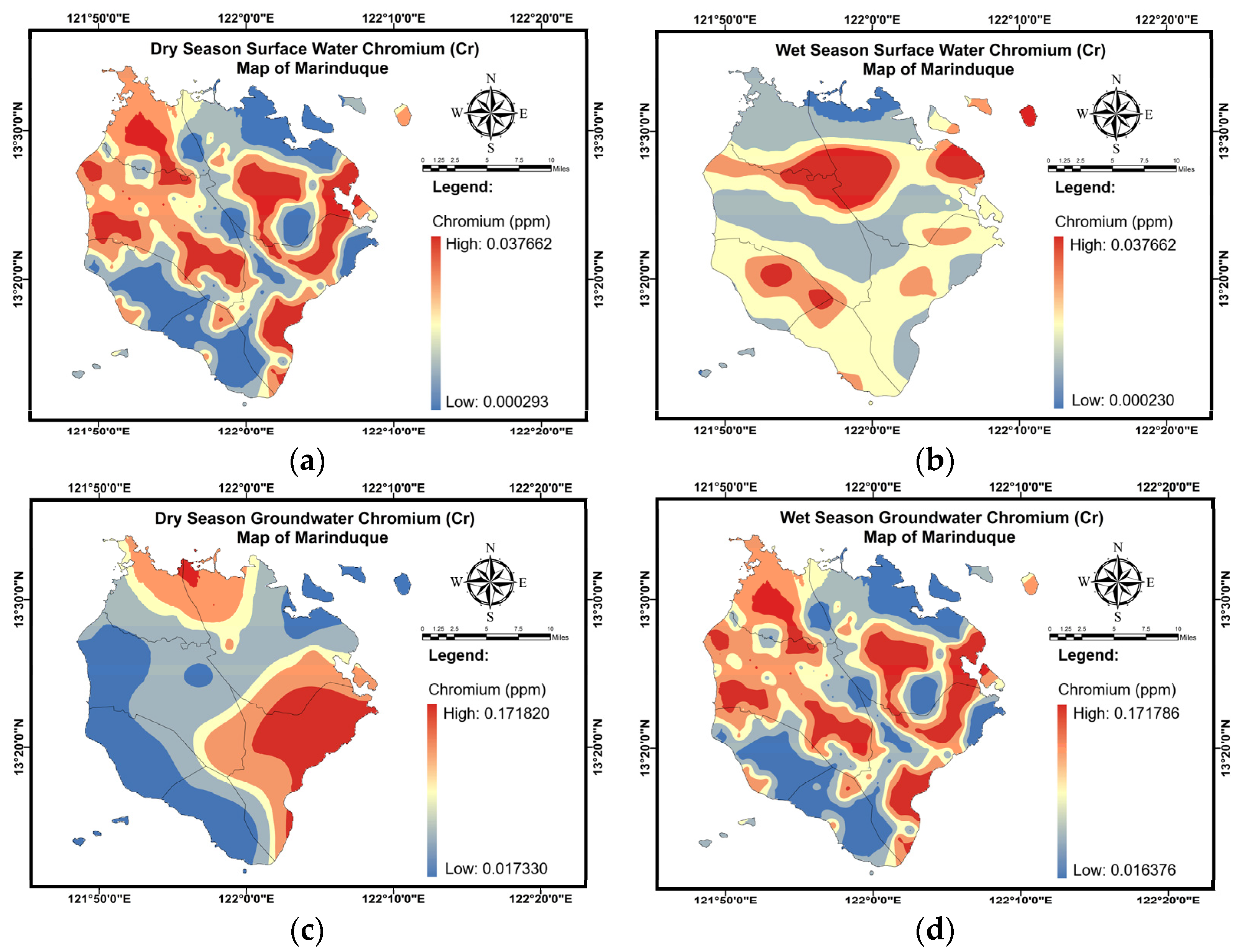
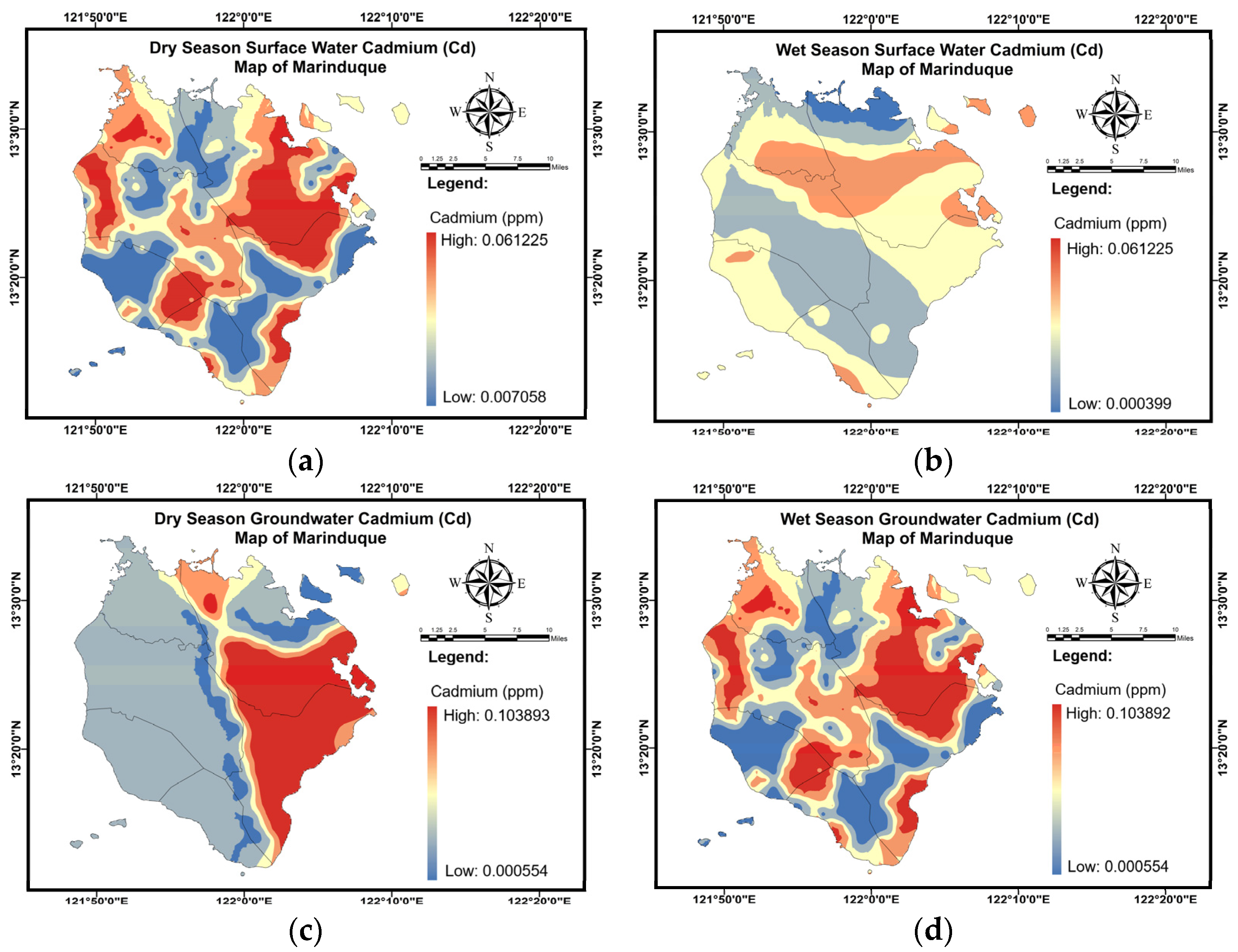
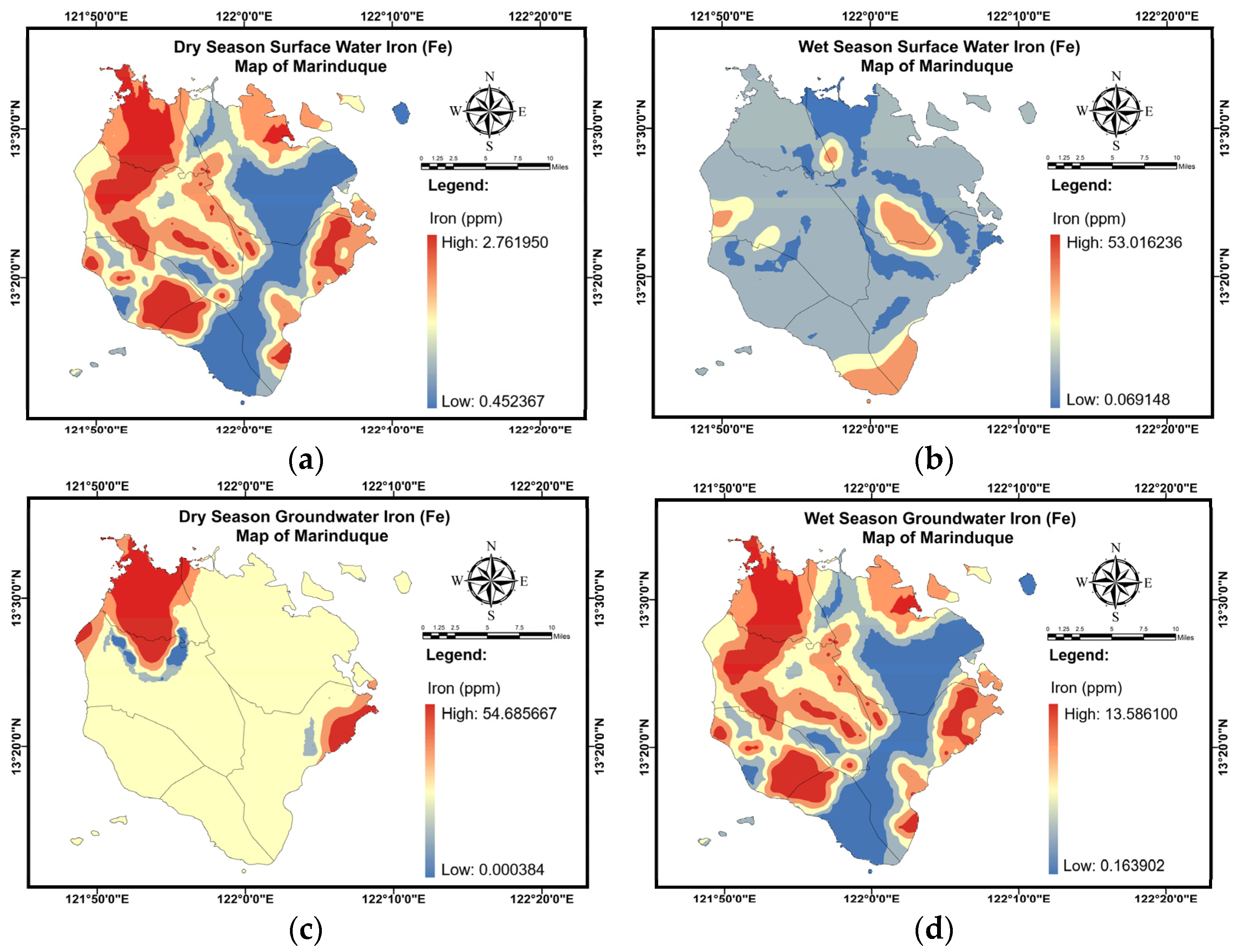

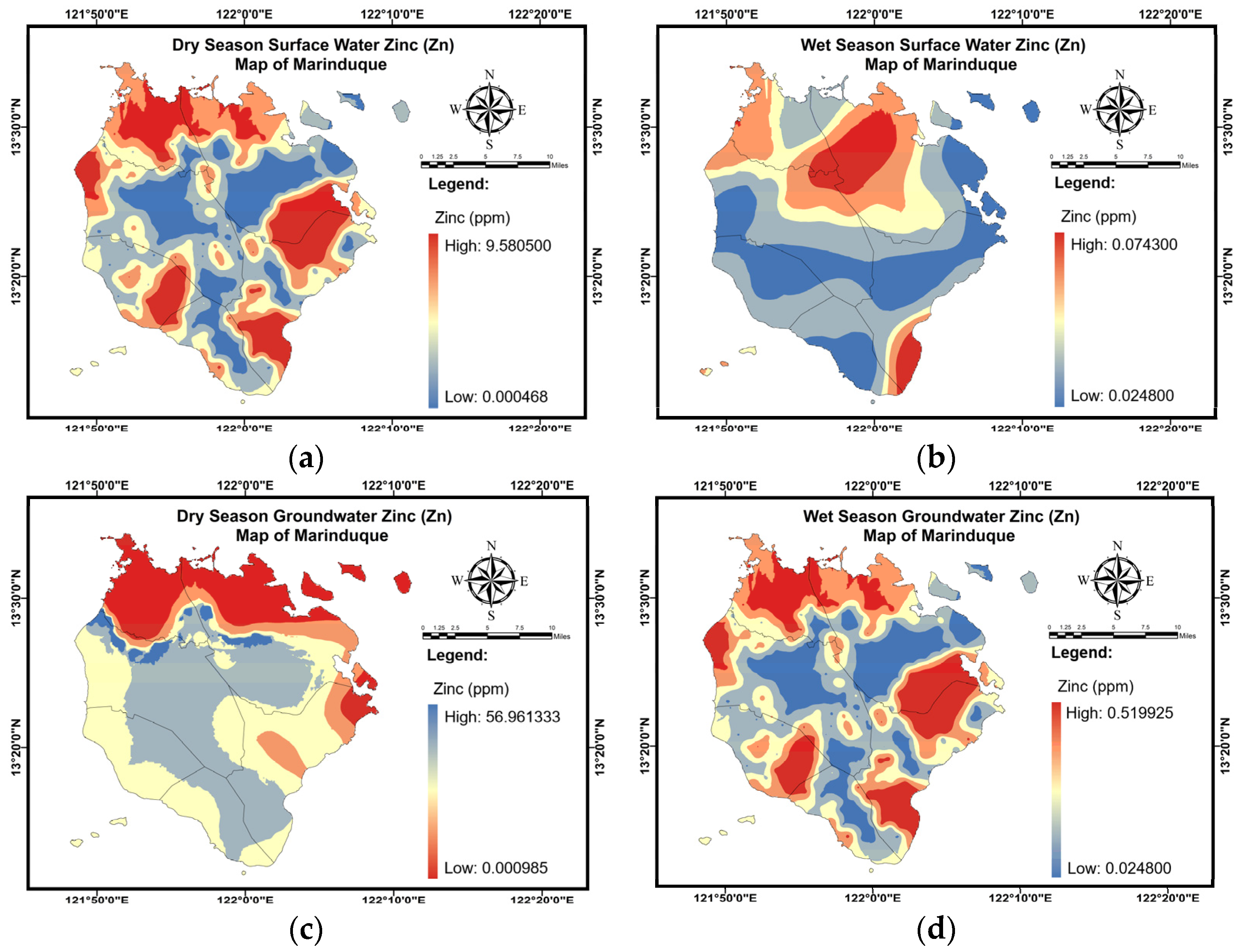
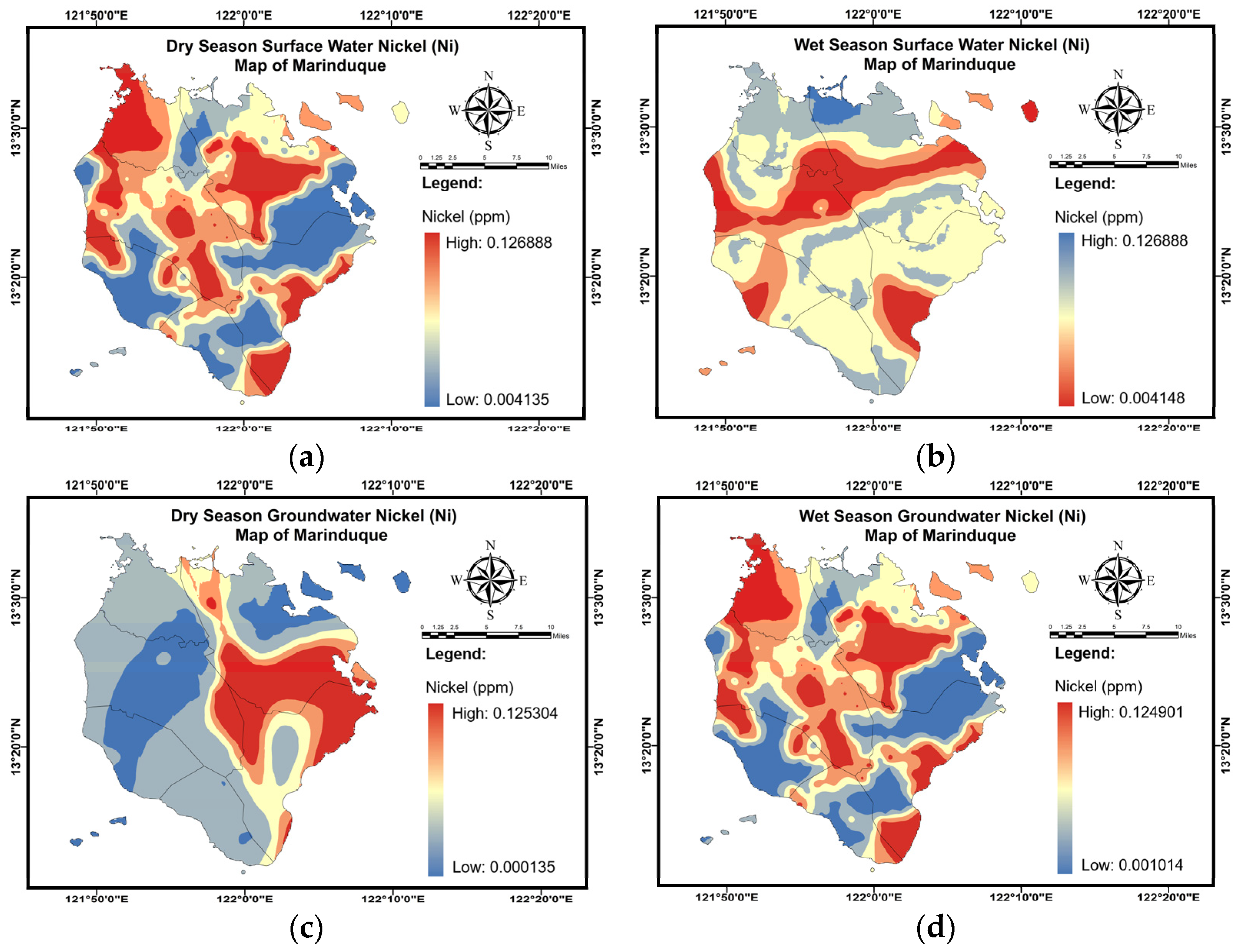
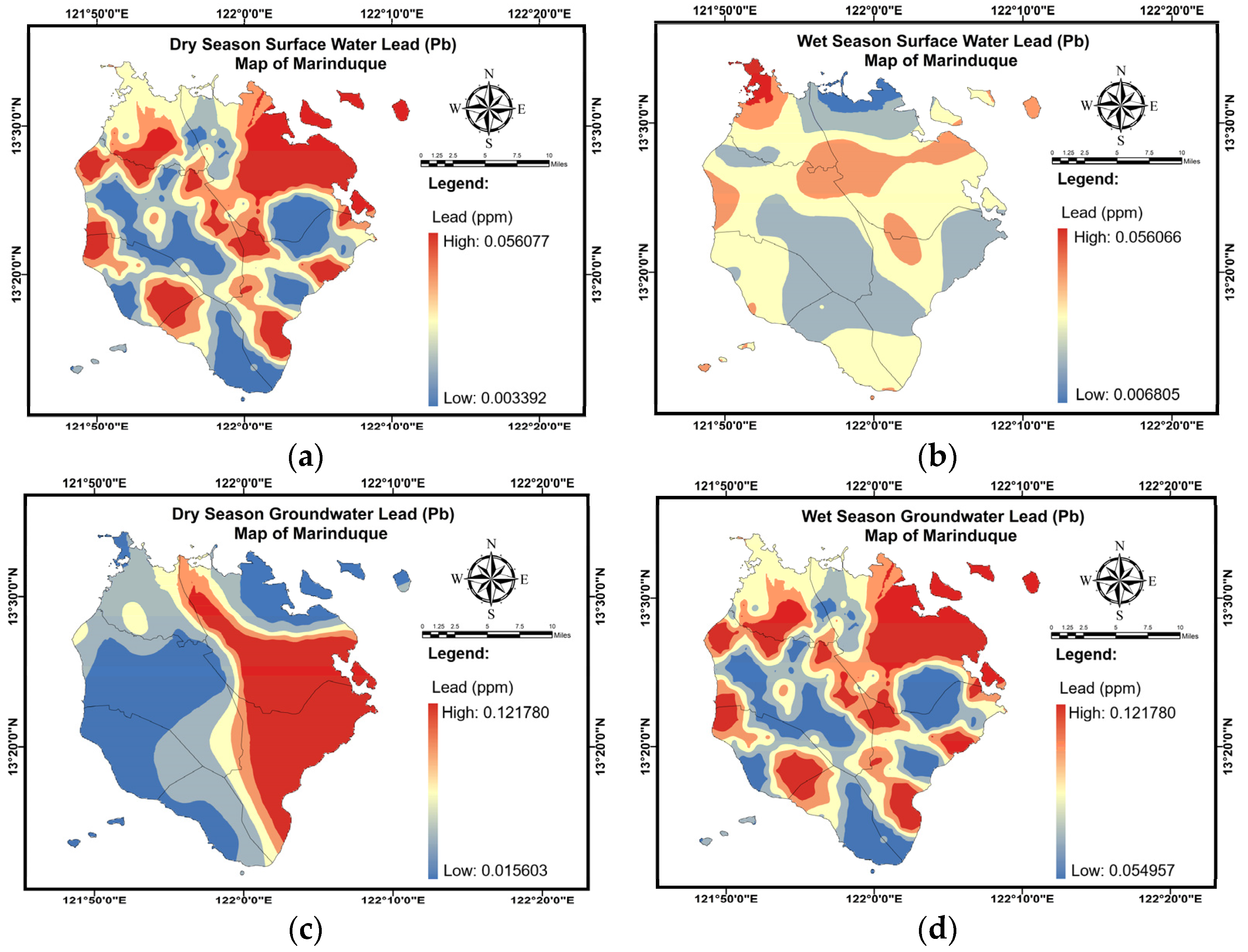
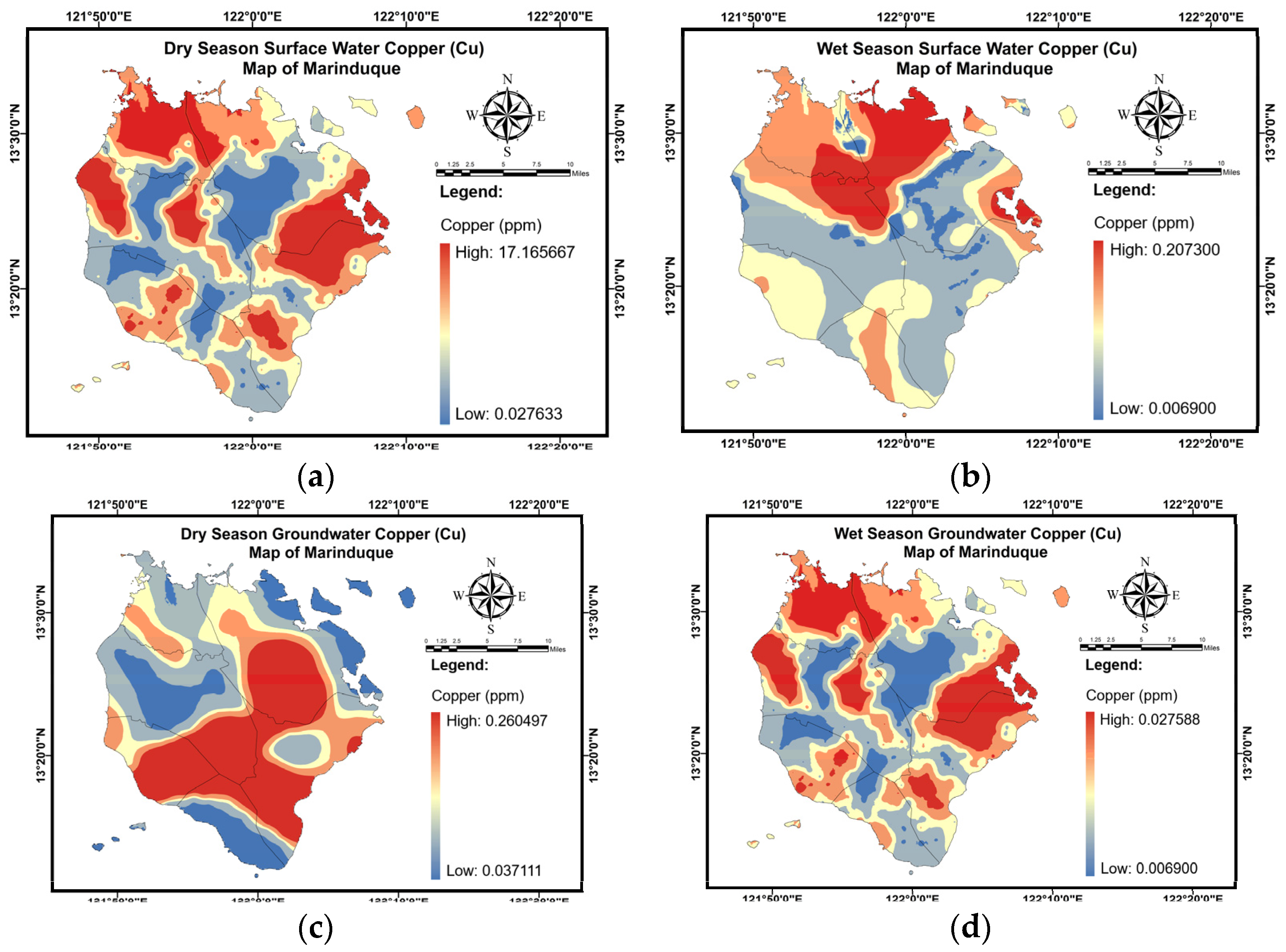
Appendix C




References
- Nem Singh, J.; Camba, A. The role of domestic policy coalitions in extractive industries’ governance: Disentangling the politics of “responsible mining” in the Philippines. Environ. Policy Gov. 2020, 30, 239–251. [Google Scholar] [CrossRef]
- Obasi, P.N.; Akudinobi, B.B. Potential health risk and levels of heavy metals in water resources of lead–zinc mining communities of Abakaliki, southeast Nigeria. Appl. Water Sci. 2020, 10, 184. [Google Scholar] [CrossRef]
- Carvalho, F.P. Mining industry and sustainable development: Time for change. Food Energy Secur. 2017, 6, 61–77. [Google Scholar] [CrossRef]
- Ali, H.; Khan, E.; Ilahi, I. Environmental chemistry and ecotoxicology of hazardous heavy metals: Environmental persistence, toxicity, and bioaccumulation. J. Chem. 2019, 2019, 6730305. [Google Scholar] [CrossRef]
- Gigantone, C.B.; Sobremisana, M.J.; Trinidad, L.C.; Migo, V.P. Impact of Abandoned Mining Facility Wastes on the Aquatic Ecosystem of the Mogpog River, Marinduque, Philippines. J. Health Pollut. 2020, 10, 200611. [Google Scholar] [CrossRef]
- Long, X.; Liu, F.; Zhou, X.; Pi, J.; Yin, W.; Li, F.; Huang, S.; Ma, F. Estimation of spatial distribution and health risk by arsenic and heavy metals in shallow groundwater around Dongting Lake plain using GIS mapping. Chemosphere 2021, 269, 128698. [Google Scholar] [CrossRef]
- Satarug, S. Cadmium sources and toxicity. Toxics 2019, 7, 25. [Google Scholar] [CrossRef]
- Wang, Y.; Su, H.; Gu, Y.; Song, X.; Zhao, J. Carcinogenicity of chromium and chemoprevention: A brief update. OncoTargets Ther. 2017, 10, 4065. [Google Scholar] [CrossRef]
- Boskabady, M.; Marefati, N.; Farkhondeh, T.; Shakeri, F.; Farshbaf, A.; Boskabady, M.H. The effect of environmental lead exposure on human health and the contribution of inflammatory mechanisms, a review. Environ. Int. 2018, 120, 404–420. [Google Scholar] [CrossRef]
- Alvarez-Bastida, C.; Martínez-Miranda, V.; Solache-Ríos, M.; Linares-Hernández, I.; Teutli-Sequeira, A.; Vázquez-Mejía, G. Drinking water characterization and removal of manganese. Removal of manganese from water. J. Environ. Chem. Eng. 2018, 6, 2119–2125. [Google Scholar] [CrossRef]
- Genchi, G.; Carocci, A.; Lauria, G.; Sinicropi, M.S.; Catalano, A. Nickel: Human health and environmental toxicology. Int. J. Environ. Res. Public Health 2020, 17, 679. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.J.; Kim, Y.S.; Kumar, V. Heavy metal toxicity: An update of chelating therapeutic strategies. J. Trace Elem. Med. Biol. 2019, 54, 226–231. [Google Scholar] [CrossRef] [PubMed]
- Ali, M.K.; Kim, R.Y.; Karim, R.; Mayall, J.R.; Martin, K.L.; Shahandeh, A.; Abbasian, F.; Starkey, M.R.; Loustaud-Ratti, V.; Johnstone, D.; et al. Role of iron in the pathogenesis of respiratory disease. Int. J. Biochem. Cell Biol. 2017, 88, 181–195. [Google Scholar] [CrossRef] [PubMed]
- Hussain, J.; Husain, I.; Arif, M.; Gupta, N. Studies on heavy metal contamination in Godavari river basin. Appl. Water Sci. 2017, 7, 4539–4548. [Google Scholar] [CrossRef]
- Şahan, T.; Erol, F.; Yılmaz, Ş. Mercury (II) adsorption by a novel adsorbent mercapto-modified bentonite using ICP-OES and use of response surface methodology for optimization. Microchem. J. 2018, 138, 360–368. [Google Scholar] [CrossRef]
- Diarra, I.; Kotra, K.K.; Prasad, S. Application of phytoremediation for heavy metal contaminated sites in the South Pacific: Strategies, current challenges and future prospects. Appl. Spectrosc. Rev. 2021. [Google Scholar] [CrossRef]
- Ahmed, A.N.; Othman, F.B.; Afan, H.A.; Ibrahim, R.K.; Fai, C.M.; Hossain, M.S.; Ehteram, M.; Elshafie, A. Machine learning methods for better water quality prediction. J. Hydrol. 2019, 578, 124084. [Google Scholar] [CrossRef]
- Myszczynska, M.A.; Ojamies, P.N.; Lacoste, A.; Neil, D.; Saffari, A.; Mead, R.; Hautbergue, G.M.; Holbrook, J.D.; Ferraiuolo, L. Applications of machine learning to diagnosis and treatment of neurodegenerative diseases. Nat. Rev. Neurol. 2020, 16, 440–456. [Google Scholar] [CrossRef]
- Hino, M.; Benami, E.; Brooks, N. Machine learning for environmental monitoring. Nat. Sustain. 2018, 1, 583–588. [Google Scholar] [CrossRef]
- Liu, J.; Sun, Y.; Li, Q. High-Resolution PM2.5 Estimation Based on the Distributed Perception Deep Neural Network Model. Sustainability 2021, 13, 13985. [Google Scholar] [CrossRef]
- Ding, X.; Zhao, Z.; Xing, Z.; Li, S.; Li, X.; Liu, Y. Comparison of Models for Spatial Distribution and Prediction of Cadmium in Subtropical Forest Soils, Guangdong, China. Land 2021, 10, 906. [Google Scholar] [CrossRef]
- Chen, S.; Fang, G.; Huang, X.; Zhang, Y. Water quality prediction model of a water diversion project based on the improved artificial bee colony–backpropagation neural network. Water 2018, 10, 806. [Google Scholar] [CrossRef]
- Jeon, J.P.; Kim, C.; Oh, B.D.; Kim, S.J.; Kim, Y.S. Prediction of persistent hemodynamic depression after carotid angioplasty and stenting using artificial neural network model. Clin. Neurol. Neurosurg. 2018, 164, 127–131. [Google Scholar] [CrossRef]
- Esmaeily, H.; Tayefi, M.; Ghayour-Mobarhan, M.; Amirabadizadeh, A. Comparing three data mining algorithms for identifying the associated risk factors of type 2 diabetes. Iran. Biomed. J. 2018, 22, 303. [Google Scholar] [CrossRef] [PubMed]
- Chiu, C.C.; Lee, K.T.; Lee, H.H.; Wang, J.J.; Sun, D.P.; Huang, C.C.; Shi, H.Y. Comparison of models for predicting quality of life after surgical resection of hepatocellular carcinoma: A prospective study. J. Gastrointest. Surg. 2018, 22, 1724–1731. [Google Scholar] [CrossRef] [PubMed]
- Bayat, H.; Ebrahimzadeh, G.; Mohanty, B.P. Investigating the capability of estimating soil thermal conductivity using topographical attributes for the Southern Great Plains, USA. Soil Tillage Res. 2021, 206, 104811. [Google Scholar] [CrossRef]
- Anifowose, F.; Ayadiuno, C.; Rashedan, F. Comparative Analysis of Machine Learning Based Feature Selection Approach for Carbonate Reservoir Cementation Factor Prediction. In Proceedings of the International Petroleum Technology Conference, Beijing, China, 26 March 2019; OnePetro: Richardson, TX, USA, 2019. [Google Scholar]
- Torabi-Kaveh, M.; Sarshari, B. Predicting convergence rate of Namaklan twin tunnels using machine learning methods. Arab. J. Sci. Eng. 2020, 45, 3761–3780. [Google Scholar] [CrossRef]
- Mohandes, S.R.; Zhang, X.; Mahdiyar, A. A comprehensive review on the application of artificial neural networks in building energy analysis. Neurocomputing 2019, 340, 55–75. [Google Scholar] [CrossRef]
- Abdallah, M.; Talib, M.A.; Feroz, S.; Nasir, Q.; Abdalla, H.; Mahfood, B. Artificial intelligence applications in solid waste management: A systematic research review. Waste Manag. 2020, 109, 231–246. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, J.; Li, G.; Wang, Y.; Sun, J.; Jiang, C. Optimized neural network using beetle antennae search for predicting the unconfined compressive strength of jet grouting coalcretes. Int. J. Numer. Anal. Methods Geomech. 2019, 43, 801–813. [Google Scholar] [CrossRef]
- Zhang, X.; Nguyen, H.; Bui, X.N.; Le, H.A.; Nguyen-Thoi, T.; Moayedi, H.; Mahesh, V. Evaluating and predicting the stability of roadways in tunnelling and underground space using artificial neural network-based particle swarm optimization. Tunn. Undergr. Space Technol. 2020, 103, 103517. [Google Scholar] [CrossRef]
- Bo, L.; Yi-Fan, Z.; Bei-Bei, Z.; Xian-Qing, W. A risk evaluation model for karst groundwater pollution based on geographic information system and artificial neural network applications. Environ. Earth Sci. 2018, 77, 344. [Google Scholar] [CrossRef]
- Islam, N.; Huang, W.; Zhuang, H.L. Machine learning for phase selection in multi-principal element alloys. Comput. Mater. Sci. 2018, 150, 230–235. [Google Scholar] [CrossRef]
- Shariati, M.; Mafipour, M.S.; Mehrabi, P.; Bahadori, A.; Zandi, Y.; Salih, M.N.; Nguyen, H.; Dou, J.; Song, X.; Poi-Ngian, S. Application of a hybrid artificial neural network-particle swarm optimization (ANN-PSO) model in behavior prediction of channel shear connectors embedded in normal and high-strength concrete. Appl. Sci. 2019, 9, 5534. [Google Scholar] [CrossRef]
- Zaman, H.R.R.; Gharehchopogh, F.S. An improved particle swarm optimization with backtracking search optimization algorithm for solving continuous optimization problems. Eng. Comput. 2021. [Google Scholar] [CrossRef]
- Alizamir, M.; Sobhanardakani, S. An Artificial Neural Network-Particle Swarm Optimization (ANN-PSO) approach to predict heavy metals contamination in groundwater resources. Jundishapur J. Health Sci. 2018, 10, e67544. [Google Scholar] [CrossRef]
- Alizamir, M.; Sobhanardakani, S. Predicting arsenic and heavy metals contamination in groundwater resources of Ghahavand plain based on an artificial neural network optimized by imperialist competitive algorithm. Environ. Health Eng. Manag. J. 2017, 4, 225–231. [Google Scholar] [CrossRef]
- Bayatzadeh Fard, Z.; Ghadimi, F.; Fattahi, H. Use of artificial intelligence techniques to predict distribution of heavy metals in groundwater of Lakan lead-zinc mine in Iran. J. Min. Environ. 2017, 8, 35–48. [Google Scholar]
- Ghadimi, F. Machine Learning Algorithm for Prediction of Heavy Metal Contamination in the Groundwater in the Arak Urban Area. J. Tethys 2017, 5, 115–127. [Google Scholar]
- Venkatramanan, S.; Chung, S.Y.; Selvam, S.; Son, J.H.; Kim, Y.J. Interrelationship between geochemical elements of sediment and groundwater at Samrak Park Delta of Nakdong River Basin in Korea: Multivariate statistical analyses and artificial neural network approaches. Environ. Earth Sci. 2017, 76, 456. [Google Scholar] [CrossRef]
- Ahangar, A.G.; Soltani, J.; Abdolmaleki, A.S. Predicting Mn concentration in water reservoir using Artificial neural network (Chahnimeh1 reservoir, Iran). Int. J. Agric. Crop Sci. 2013, 6, 1413. [Google Scholar]
- Khudair, B.H.; Jasim, M.M.; Alsaqqar, A.S. Artificial neural network model for the prediction of groundwater quality. Civ. Eng. J. 2018, 4, 2959–2970. [Google Scholar] [CrossRef]
- Egbueri, J.C.; Agbasi, J.C. Data-driven soft computing modeling of groundwater quality parameters in southeast Nigeria: Comparing the performances of different algorithms. Environ. Sci. Pollut. Res. 2022. [Google Scholar] [CrossRef] [PubMed]
- Singha, S.; Pasupuleti, S.; Singha, S.S.; Kumar, S. Effectiveness of groundwater heavy metal pollution indices studies by deep-learning. J. Contam. Hydrol. 2020, 235, 103718. [Google Scholar] [CrossRef] [PubMed]
- Boudaghpour, S.; Malekmohammadi, S. Modeling prediction of dispersal of heavy metals in plain using neural network. J. Appl. Water Eng. Res. 2020, 8, 28–43. [Google Scholar] [CrossRef]
- Kong, G.; Wang, Q.; Huang, Q. Evaluation of groundwater quality in Changping piedmont plain of Beijing based on BP neural network. Trans. Chin. Soc. Agric. Eng. 2017, 33, 150–156. [Google Scholar]
- Said, S.; Khan, S.A. Remote sensing-based water quality index estimation using data-driven approaches: A case study of the Kali River in Uttar Pradesh, India. Environ. Dev. Sustain. 2021, 23, 18252–18277. [Google Scholar] [CrossRef]
- Ayaz, M.; Khan, N.U. Forecasting of heavy metal contamination in coastal sea surface waters of the karachi harbour area by neural network approach. Nat. Environ. Pollut. Technol. 2019, 18, 719–733. [Google Scholar]
- Zhang, X.; Zhang, F.; Kung, H.T.; Shi, P.; Yushanjiang, A.; Zhu, S. Estimation of the Fe and Cu contents of the surface water in the Ebinur Lake basin based on LIBS and a machine learning algorithm. Int. J. Environ. Res. Public Health 2018, 15, 2390. [Google Scholar] [CrossRef]
- Lu, H.; Li, H.; Liu, T.; Fan, Y.; Yuan, Y.; Xie, M.; Qian, X. Simulating heavy metal concentrations in an aquatic environment using artificial intelligence models and physicochemical indexes. Sci. Total Environ. 2019, 694, 133591. [Google Scholar] [CrossRef]
- Fattahi, H.; Agah, A.; Soleimanpourmoghadam, N. Multi-Output Adaptive Neuro-Fuzzy Inference System for Prediction of Dissolved Metal Levels in Acid Rock Drainage: A Case Study. J. AI Data Min. 2018, 6, 121–132. [Google Scholar]
- Sonmez, A.Y.; Kale, S.; Ozdemir, R.C.; Kadak, A.E. An Adaptive Neuro-Fuzzy Inference System (ANFIS) to Predict of Cadmium (Cd) Concentrations in the Filyos River, Turkey. Turk. J. Fish. Aquat. Sci. 2018, 18, 1333–1343. [Google Scholar] [CrossRef]
- Betrie, G.D.; Tesfamariam, S.; Morin, K.A.; Sadiq, R. Predicting copper concentrations in acid mine drainage: A comparative analysis of five machine learning techniques. Environ. Monit. Assess. 2013, 185, 4171–4182. [Google Scholar] [CrossRef]
- Shakeri Abdolmaleki, A.; Gholamalizadeh Ahangar, A.; Soltani, J. Artificial Neural Network (ANN) Approach for Predicting Cu Concentration in Drinking Water of Chahnimeh1 Reservoir in Sistan-Balochistan, Iran. Health Scope 2013, 2, 31–38. [Google Scholar] [CrossRef]
- Aryafar, A.; Gholami, R.; Rooki, R.; Ardejani, F.D. Heavy metal pollution assessment using support vector machine in the Shur River, Sarcheshmeh copper mine, Iran. Environ. Earth Sci. 2012, 67, 1191–1199. [Google Scholar] [CrossRef]
- Gholami, R.; Kamkar-Rouhani, A.; Ardejani, F.D.; Maleki, S. Prediction of toxic metals concentration using artificial intelligence techniques. Appl. Water Sci. 2011, 1, 125–134. [Google Scholar] [CrossRef]
- Sharma, Y.C.; Mukherjee, A.K.; Srivastava, J.; Mahato, M.; Singh, T.N. Prediction of various parameters of a river for assessment of water quality by an intelligent technique. Chem. Prod. Process Model. 2008, 3. [Google Scholar] [CrossRef]
- Coumans, C. Into the deep: Science, politics and law in conflicts over marine dumping of mine waste. Int. Soc. Sci. J. 2018, 68, 303–323. [Google Scholar] [CrossRef]
- Senoro, D.B.; De Jesus, K.L.M.; Yanuaria, C.A.; Bonifacio, P.B.; Manuel, M.T.; Wang, B.N.; Kao, C.C.; Wu, T.N.; Ney, F.P.; Natal, P. Rapid site assessment in a small island of the Philippines contaminated with mine tailings using ground and areal technique: The environmental quality after twenty years. IOP Conf. Ser. Earth Environ. Sci. 2019, 351, 012022. [Google Scholar] [CrossRef]
- Abdel-Satar, A.M.; Ali, M.H.; Goher, M.E. Indices of water quality and metal pollution of Nile River, Egypt. Egypt. J. Aquat. Res. 2017, 43, 21–29. [Google Scholar] [CrossRef]
- Decker, C.; Simmons, K.; United States Environmental Protection Agency (U.S.E.P.A). Operating Procedure for In Situ Water Quality Monitoring (SESDPROC-111-R4). Available online: https://www.epa.gov/sites/default/files/2015-06/documents/Insitu-Water-Quality-Mon.pdf (accessed on 10 January 2022).
- Migo, V.P.; Mendoza, M.D.; Alfafara, C.G.; Pulhin, J.M. Industrial water use and the associated pollution and disposal problems in the Philippines. In Water Policy in the Philippines; Springer: Cham, Switzerland, 2018; pp. 87–116. [Google Scholar]
- Tolentino, P.L.M.; Poortinga, A.; Kanamaru, H.; Keesstra, S.; Maroulis, J.; David, C.P.C.; Ritsema, C.J. Projected impact of climate change on hydrological regimes in the Philippines. PLoS ONE 2016, 11, e0163941. [Google Scholar] [CrossRef] [PubMed]
- Moodley, R.; Mahlangeni, N.T.; Reddy, P. Determination of heavy metals in selected fish species and seawater from the South Durban Industrial Basin, KwaZulu-Natal, South Africa. Environ. Monit. Assess. 2021, 193, 206. [Google Scholar] [CrossRef] [PubMed]
- Reiman, J.H.; Xu, Y.J.; He, S.; DelDuco, E.M. Metals geochemistry and mass export from the Mississippi-Atchafalaya River system to the Northern Gulf of Mexico. Chemosphere 2018, 205, 559–569. [Google Scholar] [CrossRef]
- De Jesus, K.L.M.; Senoro, D.B.; Dela Cruz, J.C.; Chan, E.B. A Hybrid Neural Network–Particle Swarm Optimization Informed Spatial Interpolation Technique for Groundwater Quality Mapping in a Small Island Province of the Philippines. Toxics 2021, 9, 273. [Google Scholar] [CrossRef]
- Chen, Y.; Yu, G.; Long, Y.; Teng, J.; You, X.; Liao, B.Q.; Lin, H. Application of radial basis function artificial neural network to quantify interfacial energies related to membrane fouling in a membrane bioreactor. Bioresour. Technol. 2019, 293, 122103. [Google Scholar] [CrossRef]
- Ostad-Ali-Askari, K.; Shayannejad, M.; Ghorbanizadeh-Kharazi, H. Artificial neural network for modeling nitrate pollution of groundwater in marginal area of Zayandeh-rood River, Isfahan, Iran. KSCE J. Civ. Eng. 2017, 21, 134–140. [Google Scholar] [CrossRef]
- Okon, A.N.; Adewole, S.E.; Uguma, E.M. Artificial neural network model for reservoir petrophysical properties: Porosity, permeability and water saturation prediction. Model. Earth Syst. Environ. 2021, 7, 2373–2390. [Google Scholar] [CrossRef]
- Concha, N.; Oreta, A.W. A model for time-to-cracking of concrete due to chloride induced corrosion using artificial neural network. IOP Conf. Ser. Earth Environ. Sci. 2018, 431, 072009. [Google Scholar] [CrossRef]
- Mammadli, S. Financial time series prediction using artificial neural network based on Levenberg-Marquardt algorithm. Procedia Comput. Sci. 2017, 120, 602–607. [Google Scholar] [CrossRef]
- Rinchon, J.P.M. Strength durability-based design mix of self-compacting concrete with cementitious blend using hybrid neural network-genetic algorithm. IPTEK J. Proc. Ser. 2017, 3. [Google Scholar] [CrossRef][Green Version]
- Babu, D.; Thangarasu, V.; Ramanathan, A. Artificial neural network approach on forecasting diesel engine characteristics fuelled with waste frying oil biodiesel. Appl. Energy 2020, 263, 114612. [Google Scholar] [CrossRef]
- El-Gohary, K.M.; Aziz, R.F.; Abdel-Khalek, H.A. Engineering approach using ANN to improve and predict construction labor productivity under different influences. J. Const. Eng. Manag. 2017, 143, 04017045. [Google Scholar] [CrossRef]
- Abnisa, F.; Anuar Sharuddin, S.D.; bin Zanil, M.F.; Wan Daud, W.M.A.; Indra Mahlia, T.M. The yield prediction of synthetic fuel production from pyrolysis of plastic waste by levenberg–Marquardt approach in feedforward neural networks model. Polymers 2019, 11, 1853. [Google Scholar] [CrossRef]
- Alnaqi, A.A.; Moayedi, H.; Shahsavar, A.; Nguyen, T.K. Prediction of energetic performance of a building integrated photovoltaic/thermal system thorough artificial neural network and hybrid particle swarm optimization models. Energy Convers. Manag. 2019, 183, 137–148. [Google Scholar] [CrossRef]
- Nguyen, H.; Bui, H.B.; Bui, X.N. Rapid determination of gross calorific value of coal using artificial neural network and particle swarm optimization. Nat. Resour. Res. 2021, 30, 621–638. [Google Scholar] [CrossRef]
- Tufaner, F.; Demirci, Y. Prediction of biogas production rate from anaerobic hybrid reactor by artificial neural network and nonlinear regressions models. Clean Technol. Environ. Policy 2020, 22, 713–724. [Google Scholar] [CrossRef]
- Rukhaiyar, S.; Alam, M.N.; Samadhiya, N.K. A PSO-ANN hybrid model for predicting factor of safety of slope. Int. J. Geotech. Eng. 2018, 12, 556–566. [Google Scholar] [CrossRef]
- da Silva Veloso, Y.M.; de Almeida, M.M.; de Alsina, O.L.S.; Passos, M.L.; Mujumdar, A.S.; Leite, M.S. Hybrid phenomenological/ANN-PSO modelling of a deformable material in spouted bed drying process. Powder Technol. 2020, 366, 185–196. [Google Scholar] [CrossRef]
- Thio, Q.C.; Karhade, A.V.; Ogink, P.T.; Bramer, J.A.; Ferrone, M.L.; Calderón, S.L.; Raskin, K.A.; Schwab, J.H. Development and internal validation of machine learning algorithms for preoperative survival prediction of extremity metastatic disease. Clin. Orthop. Relat. Res. 2020, 478, 322. [Google Scholar] [CrossRef]
- Hannun, A.Y.; Rajpurkar, P.; Haghpanahi, M.; Tison, G.H.; Bourn, C.; Turakhia, M.P.; Ng, A.Y. Cardiologist-level arrhythmia detection and classification in ambulatory electrocardiograms using a deep neural network. Nat. Med. 2019, 25, 65–69. [Google Scholar] [CrossRef]
- Disse, E.; Ledoux, S.; Bétry, C.; Caussy, C.; Maitrepierre, C.; Coupaye, M.; Laville, M.; Simon, C. An artificial neural network to predict resting energy expenditure in obesity. Clin. Nutr. 2018, 37, 1661–1669. [Google Scholar] [CrossRef]
- Gao, Z.; Zhang, H.; Mao, G.; Ren, J.; Chen, Z.; Wu, C.; Gates, I.D.; Yang, W.; Ding, X.; Yao, J. Screening for lead-free inorganic double perovskites with suitable band gaps and high stability using combined machine learning and DFT calculation. Appl. Surf. Sci. 2021, 568, 150916. [Google Scholar] [CrossRef]
- Hou, J.; Yao, D.; Wu, F.; Shen, J.; Chao, X. Online vehicle velocity prediction using an adaptive radial basis function neural network. IEEE Trans. Veh. Technol. 2021, 70, 3113–3122. [Google Scholar] [CrossRef]
- Zhou, F.; Liu, B.; Duan, K. Coupling wavelet transform and artificial neural network for forecasting estuarine salinity. J. Hydrol. 2020, 588, 125127. [Google Scholar] [CrossRef]
- Hesamian, G.; Akbari, M.G. A robust varying coefficient approach to fuzzy multiple regression model. J. Comput. Appl. Math. 2020, 371, 112704. [Google Scholar] [CrossRef]
- Khademi, F.; Akbari, M.; Jamal, S.M.; Nikoo, M. Multiple linear regression, artificial neural network, and fuzzy logic prediction of 28 days compressive strength of concrete. Front. Struct. Civ. Eng. 2017, 11, 90–99. [Google Scholar] [CrossRef]
- Alnowami, M.; Abolaban, F.; Hijazi, H.; Nisbet, A. Regression Analysis of Rectal Cancer and Possible Application of Artificial Intelligence (AI) Utilization in Radiotherapy. Appl. Sci. 2022, 12, 725. [Google Scholar] [CrossRef]
- Garg, M.; Dhiman, G. A novel content-based image retrieval approach for classification using GLCM features and texture fused LBP variants. Neural Comput. Appl. 2021, 33, 1311–1328. [Google Scholar] [CrossRef]
- Bhati, B.S.; Rai, C.S. Analysis of support vector machine-based intrusion detection techniques. Arab. J. Sci. Eng. 2020, 45, 2371–2383. [Google Scholar] [CrossRef]
- Yap, K.Y.; Sarimuthu, C.R.; Lim, J.M.Y. Artificial intelligence based MPPT techniques for solar power system: A review. J. Mod. Power Syst. Clean Energy 2020, 8, 1043–1059. [Google Scholar]
- Jain, U.; Nathani, K.; Ruban, N.; Raj, A.N.J.; Zhuang, Z.; Mahesh, V.G. Cubic SVM classifier based feature extraction and emotion detection from speech signals. In Proceedings of the 2018 International Conference on Sensor Networks and Signal Processing (SNSP), Xi’an, China, 28–31 October 2018; IEEE: New York, NY, USA, 2018; pp. 386–391. [Google Scholar]
- Naicker, N.; Adeliyi, T.; Wing, J. Linear support vector machines for prediction of student performance in school-based education. Math. Probl. Eng. 2020, 2020. [Google Scholar] [CrossRef]
- Jimeno-Sáez, P.; Senent-Aparicio, J.; Pérez-Sánchez, J.; Pulido-Velazquez, D. A comparison of SWAT and ANN models for daily runoff simulation in different climatic zones of peninsular Spain. Water 2018, 10, 192. [Google Scholar] [CrossRef]
- Tenza-Abril, A.J.; Villacampa, Y.; Solak, A.M.; Baeza-Brotons, F. Prediction and sensitivity analysis of compressive strength in segregated lightweight concrete based on artificial neural network using ultrasonic pulse velocity. Constr. Build. Mater. 2018, 189, 1173–1183. [Google Scholar] [CrossRef]
- Hui, E.; Stafford, R.; Matthews, I.M.; Smith, V.A. Bayesian networks as a novel tool to enhance interpretability and predictive power of ecological models. Ecol. Inform. 2021, 68, 101539. [Google Scholar] [CrossRef]
- Alkadri, S.; Ledwos, N.; Mirchi, N.; Reich, A.; Yilmaz, R.; Driscoll, M.; Del Maestro, R.F. Utilizing a multilayer perceptron artificial neural network to assess a virtual reality surgical procedure. Comput. Biol. Med. 2021, 136, 104770. [Google Scholar] [CrossRef] [PubMed]
- DENR Administrative Order (DAO). No. 2016-08: Water Quality Guidelines and General Effluent Standards of 2016. Available online: https://emb.gov.ph/wp-content/uploads/2019/04/DAO-2016-08_WATER-QUALITY-GUIDELINES-AND-GENERAL-EFFLUENT-STANDARDS.pdf (accessed on 15 January 2022).
- Tiwari, A.K.; Singh, A.K.; Singh, A.K.; Singh, M.P. Hydrogeochemical analysis and evaluation of surface water quality of Pratapgarh district, Uttar Pradesh, India. Appl. Water Sci. 2017, 7, 1609–1623. [Google Scholar] [CrossRef]
- Huang, Z.; Zheng, S.; Liu, Y.; Zhao, X.; Qiao, X.; Liu, C.; Zheng, B.; Yin, D. Distribution, toxicity load, and risk assessment of dissolved metal in surface and overlying water at the Xiangjiang River in southern China. Sci. Rep. 2021, 11, 109. [Google Scholar] [CrossRef]
- Bhuyan, M.S.; Bakar, M.A.; Akhtar, A.; Hossain, M.B.; Ali, M.M.; Islam, M.S. Heavy metal contamination in surface water and sediment of the Meghna River, Bangladesh. Environ. Nanotechnol. Monit. Manag. 2017, 8, 273–279. [Google Scholar] [CrossRef]
- Wang, J.; Liu, G.; Liu, H.; Lam, P.K. Multivariate statistical evaluation of dissolved trace elements and a water quality assessment in the middle reaches of Huaihe River, Anhui, China. Sci. Total Environ. 2017, 583, 421–431. [Google Scholar] [CrossRef]
- Ukah, B.U.; Egbueri, J.C.; Unigwe, C.O.; Ubido, O.E. Extent of heavy metals pollution and health risk assessment of groundwater in a densely populated industrial area, Lagos, Nigeria. Int. J. Energy Water Resour. 2019, 3, 291–303. [Google Scholar] [CrossRef]
- Taylor, M.; Elliott, H.A.; Navitsky, L.O. Relationship between total dissolved solids and electrical conductivity in Marcellus hydraulic fracturing fluids. Water Sci. Technol. 2018, 77, 1998–2004. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, A.S.; Sultana, S.; Habib, A.; Ullah, H.; Musa, N.; Hossain, M.B.; Rahman, M.M.; Sarker, M.S.I. Bioaccumulation of heavy metals in some commercially important fishes from a tropical river estuary suggests higher potential health risk in children than adults. PLoS ONE 2019, 14, e0219336. [Google Scholar] [CrossRef] [PubMed]
- Magesh, N.S.; Chandrasekar, N.; Elango, L. Trace element concentrations in the groundwater of the Tamiraparani river basin, South India: Insights from human health risk and multivariate statistical techniques. Chemosphere 2017, 185, 468–479. [Google Scholar] [CrossRef] [PubMed]
- Rashid, A.; Ayub, M.; Javed, A.; Khan, S.; Gao, X.; Li, C.; Ullah, Z.; Sardar, T.; Muhammad, J.; Nazneen, S. Potentially harmful metals, and health risk evaluation in groundwater of Mardan, Pakistan: Application of geostatistical approach and geographic information system. Geosci. Front. 2021, 12, 101128. [Google Scholar] [CrossRef]
- Senoro, D.B.; de Jesus, K.L.M.; Mendoza, L.C.; Apostol, E.M.D.; Escalona, K.S.; Chan, E.B. Groundwater Quality Monitoring Using In-Situ Measurements and Hybrid Machine Learning with Empirical Bayesian Kriging Interpolation Method. Appl. Sci. 2022, 12, 132. [Google Scholar] [CrossRef]
- Wagh, V.M.; Panaskar, D.B.; Mukate, S.V.; Gaikwad, S.K.; Muley, A.A.; Varade, A.M. Health risk assessment of heavy metal contamination in groundwater of Kadava River Basin, Nashik, India. Model. Earth Syst. Environ. 2018, 4, 969–980. [Google Scholar] [CrossRef]
- Bhutiani, R.; Kulkarni, D.B.; Khanna, D.R.; Gautam, A. Water quality, pollution source apportionment and health risk assessment of heavy metals in groundwater of an industrial area in North India. Expo. Health 2016, 8, 3–18. [Google Scholar] [CrossRef]
- Hussein, A.A.; Chehade, A.A. Robust artificial neural network-based models for accurate surface temperature estimation of batteries. IEEE Trans. Ind. Appl. 2020, 56, 5269–5278. [Google Scholar] [CrossRef]
- Çolak, A.B. A novel comparative investigation of the effect of the number of neurons on the predictive performance of the artificial neural network: An experimental study on the thermal conductivity of ZrO2 nanofluid. Int. J. Energy Res. 2021, 45, 18944–18956. [Google Scholar] [CrossRef]
- Mathew, J.; Kshirsagar, R.; Zabeen, S.; Smyth, N.; Kanarachos, S.; Langer, K.; Fitzpatrick, M.E. Machine Learning-Based Prediction and Optimisation System for Laser Shock Peening. Appl. Sci. 2021, 11, 2888. [Google Scholar] [CrossRef]
- Aydoğdu, Ş. Predicting student final performance using artificial neural networks in online learning environments. Educ. Inf. Technol. 2020, 25, 1913–1927. [Google Scholar] [CrossRef]
- Morin, K.A.; Hutt, N.M. Prediction of minesite-drainage chemistry through closure using operational monitoring data. J. Geochem. Explor. 2001, 73, 123–130. [Google Scholar] [CrossRef]
- Kurita, H. Case Studies of Medium/large-scale Mines in the Philippines (2); Ehime Economic Review, Ehime University: Ehime, Japan, 2016. [Google Scholar]
- Cotter, J.; Brigden, K. Acid Mine Drainage: The Case of the Lafayette Mine, Rapu (Philippines); University of Exeter: Exeter, UK, 2006. [Google Scholar]
- Lee, J.U. Effect of sulfur concentration on microbial removal of arsenic and heavy metals from mine tailings using mixed culture of Acidithiobacillus spp. J. Geochem. Explor. 2015, 148, 241–248. [Google Scholar]
- Stark, J.; Li, J.; Terasawa, K. Environmental Safeguards and Community Benefits in Mining: Recent Lessons from the Philippines; Foundation for Environmental Security Sustainability: Falls Church, VA, USA, 2006. [Google Scholar]
- Ramos, H.C.; Cabalda, M.V.; Banaag, M.A. Tailings dam accidents and the use of chemicals in mining: Issues, policy response and lessons learned from the Philippines. In Proceedings of the International Workshop on Environmental Regulation for Accident Prevention in Mining, Tailings and Chemicals Management, Perth, Australia, 26–27 October 2000; pp. 25–27. [Google Scholar]
- Holden, W.N. Mining amid typhoons: Large-scale mining and typhoon vulnerability in the Philippines. Extr. Ind. Soc. 2015, 2, 445–461. [Google Scholar] [CrossRef]
- Balanay, R.M.; Halog, A. Promoting life cycle thinking for sustainability in the mining sector of the Philippines. Int. J. Life Cycle Assess. 2017, 22, 1864–1874. [Google Scholar] [CrossRef]
- Cuevas, V.C.; Orajay, J.I.; Lagman, C.A., Jr. Rice straw compost as amendment to reduce soil copper toxicity in lowland rice paddy field. Philipp. Sci. Lett. 2014, 7, 350–355. [Google Scholar]
- Coumans, C. Canadian Companies in the Philippines: Placer Dome. In Undermining the Forests: The Need to Control Transnational Mining Companies: A Canadian Case Study; Forest Peoples Programme: Moreton-in-Marsh, UK; Philippine Indigenous Peoples Links: Oxfordshire, UK; World Rainforest Movement: Montevideo, Uruguay, 2000; pp. 59–67. [Google Scholar]
- Regis, E.G. Assessment of the Effects of Acid Mine Drainage on Mogpog River Ecosystem, Marinduque, Phillippines, and Possible Impacts on Human Communities; Oxfam Australia: Melbourne, Australia, 2006. [Google Scholar]



| Abbreviation/ Symbol | Description | Abbreviation/ Symbol | Description |
|---|---|---|---|
| AAS | Atomic Absorption Spectroscopy | IoT | Internet of Things |
| AI | Artificial Intelligence | KGE | Kling-Gupta Efficiency |
| AIC | Akaike Information Criterion | KNN | K-Nearest Neighbor |
| AMD | Acid Mine Drainage | LM | Levenberg-Marquardt |
| ANN | Artificial Neural Network | LSTM | Long Short-Term Memory |
| BBO | Biogeography-Based Optimization | LSW | Lake Surface Water |
| BP | Back Propagation | M5P | Model Tree |
| BR | Bayesian Regularization | MANFIS | Multi-output Adaptive Neuro-Fuzzy Inference System |
| CA | Cluster Analysis | MHMI | Modified Heavy Metal Index |
| CI | Contamination Index | ML | Machine Learning |
| CSW | Coastal Surface Water | MLGI | Machine Learning Geostatistical Interpolation |
| EBK | Empirical Bayesian Kriging | MLR | Multiple Linear Regression |
| EHCI | Entropy Weight-based HM Conc. Index | NARX | Non-linear AutoRegressive eXogeneous |
| FCM | Fuzzy c-means Clustering Method | PLI | Pollution Load Index |
| GA | Genetic Algorithm | PMI | Principal Component Analysis-based Metal Index |
| GEP | Gene Expression Programming | PSO | Particle Swarm Optimization |
| GFF | Generalized Feed Forward | RBF | Radial Basis Function |
| GP | Grid Partitioning | RI | Relative Importance |
| GRNN | Generalized Regression Neural Network | SCM | Subtractive Clustering Method |
| HEI | Heavy Metal Evaluation Index | SPI | Synthetic Pollution Index |
| hN-PSO | Hybrid Neuro-Particle Swarm Optimization | SVM | Support Vector Machine |
| HPI | Heavy Metal Pollution Index | SVM-Poly | SVM with Polynomial |
| ICA | Imperialist Competitive Algorithm | WQG | Water Quality Guidelines |
| ICP-OES | Inductively Coupled Plasma-Optical Emission Spectrometry | WQI | Water Quality Index |
| Prediction Method | Sample Type | Target Output(s) of the Model | Reference |
|---|---|---|---|
| ANN–PSO, ANN- Bayesian Regularization (BR) | GW | As, Cu, Pb, Zn | [37] |
| ANN–Imperialist Competitive Algorithm (ICA), ANN–Levenberg–Marquardt (LM) | GW | As, Cu, Pb, Zn | [38] |
| ANN, ANN–Biogeography–Based Optimization (BBO) Algorithm, Multi-output Adaptive Neuro-Fuzzy Inference System (MANFIS)–Subtractive Clustering Method (SCM) | GW | Fe, Mn, Pb, Zn | [39] |
| SVM based Regression–Radial Basis Function (RBF) | GW | Pb, Zn, Cu | [40] |
| ANN | GW | Si, Al, Fe, K, Ca, Na, Mg, Cl, Mn, Sr, Br(Groundwater) | [41] |
| BP-NN, Nonlinear AutoRegressive eXogenous (NARX) | GW | As | [42] |
| ANN | GW | Water Quality Index | [43] |
| ANN, MLR | GW | pH, EC, TDS, TH, MHMI, PLI, SPI | [44] |
| ANN, Deep Learning | GW | HPI, HEI, CI, EHCI, HMI, PMI | [45] |
| MLP-NN, Elman-NN, GFF-NN | GW | Pb, Zn, As | [46] |
| BP-NN | GW | Turbidity, Fe, Cl, SO4, TDS, TH, Mn, Zn, KMnO4 Index, NO3-N, NO2-N, NH3-N, F | [47] |
| MLR, BP-NN, GEP | SW | WQI | [48] |
| NARX, BP-NN | CSW | Cr, Ni, Cu, Pb | [49] |
| K-Means CA, BP-NN | LSW | Fe, Cu | [50] |
| ANN, SVM | SW | Ti, Cu, Mn, Ni, As, Cd, Sb, Pb | [51] |
| MANFIS–Grid Partitioning (GP), MANFIS-SCM, MANFIS–Fuzzy c-means Clustering Method (FCM) | SW | Cu, Fe, Mn, Zn | [52] |
| Adaptive Neuro–Fuzzy Inference System (ANFIS) | SW | Cd | [53] |
| ANN–LM, ANN–ICA | SW | As, Cu, Pb, Zn | [38] |
| ANN | SW | Mn | [42] |
| ANN, SVM with Polynomial (SVM-Poly), SVM–RBF, Model Tree (M5P), K–Nearest Neighbor (K-NN) | SW | Cu | [54] |
| ANN | SW | Cu | [55] |
| SVM, Generalized Regression Neural Network (GRNN) | SW | Cu, Fe, Mn, Zn | [56] |
| SVM, ANN | SW | Ni, Fe | [57] |
| BP-LM | SW | Cd, Cr, Cu, | [58] |
| Parameter | N | Min | Max | Mean | Guidelines | |
|---|---|---|---|---|---|---|
| Philippine WQG [100] | WHO | |||||
| Temp (°C) | 80 | 26.0 | 36.4 | 30.58 | 25–31 | - |
| pH | 80 | 2.9 | 9.4 | 6.28 | 6.5–9.0 | 6.5–9.2 |
| EC (µS/cm) | 80 | 130.0 | 6000.0 | 2617.21 | - | 1500 |
| TDS (mg/L) | 80 | 60.0 | 3000.0 | 1377.66 | - | 1200 |
| Cr (mg/L) | 80 | 0.00029 | 0.03766 | 0.01820 | 0.010 | 0.050 |
| Cd (mg/L) | 80 | 0.00706 | 0.06122 | 0.04315 | 0.005 | 0.003 |
| Fe (mg/L) | 80 | 0.45237 | 2.76195 | 2.32390 | 1.500 | 0.300 |
| Mn (mg/L) | 80 | 0.00049 | 11.09783 | 2.07269 | 0.200 | 0.400 |
| Zn (mg/L) | 80 | 0.00047 | 9.58050 | 1.69057 | 2.000 | 3.000 |
| Ni (mg/L) | 80 | 0.00413 | 0.12689 | 0.10156 | 0.200 | 0.070 |
| Pb (mg/L) | 80 | 0.00339 | 0.05608 | 0.03851 | 0.050 | 0.010 |
| Cu (mg/L) | 80 | 0.02763 | 17.16567 | 7.67426 | - | 2.000 |
| Parameter | N | Min | Max | Mean | Guidelines | |
|---|---|---|---|---|---|---|
| Philippine WQG [100] | WHO | |||||
| Temp (°C) | 80 | 26.7 | 33.7 | 30.26 | 25–31 | - |
| pH | 80 | 3.1 | 8.4 | 5.94 | 6.5–9.0 | 6.5–9.2 |
| EC (µS/cm) | 80 | 90 | 5380.0 | 2211.00 | - | 1500.00 |
| TDS (mg/L) | 80 | 40 | 2670.0 | 1142.35 | - | 1200.00 |
| Cr (mg/L) | 80 | 0.00023 | 0.03766 | 0.02937 | 0.010 | 0.05 |
| Cd (mg/L) | 80 | 0.00040 | 0.06122 | 0.04459 | 0.005 | 0.003 |
| Fe (mg/L) | 80 | 0.06915 | 53.01624 | 21.74808 | 1.5 | 0.3 |
| Mn (mg/L) | 80 | 0.00361 | 0.01769 | 0.01027 | 0.2 | 0.4 |
| Zn (mg/L) | 80 | 0.02480 | 0.07430 | 0.03922 | 2.00 | 3.00 |
| Ni (mg/L) | 80 | 0.00415 | 0.12689 | 0.08820 | 0.20 | 0.07 |
| Pb (mg/L) | 80 | 0.00680 | 0.05607 | 0.03458 | 0.05 | 0.01 |
| Cu (mg/L) | 80 | 0.00690 | 0.20730 | 0.09144 | - | 2.00 |
| Parameter | N | Min | Max | Mean | Guidelines | |
|---|---|---|---|---|---|---|
| PNSDW 2017 [67] | WHO | |||||
| Temp (°C) | 80 | 26.3 | 49.6 | 37.72 | - | - |
| pH | 80 | 6.1 | 7.9 | 7.01 | 6.5–8.5 | 6.5–9.2 |
| EC (µS/cm) | 80 | 80.0 | 2350.0 | 1140.45 | - | 1500.000 |
| TDS (mg/L) | 80 | 30.0 | 1150.0 | 499.12 | 600.000 | 1200.000 |
| Cr (mg/L) | 80 | 0.01733 | 0.17182 | 0.07527 | 0.050 | 0.050 |
| Cd (mg/L) | 80 | 0.00055 | 0.10389 | 0.06879 | 0.003 | 0.003 |
| Fe (mg/L) | 80 | 0.00038 | 54.68567 | 11.50116 | 1.000 | 0.300 |
| Mn (mg/L) | 80 | 0.00009 | 8.71857 | 2.44137 | 0.400 | 0.400 |
| Zn (mg/L) | 80 | 0.00098 | 56.96133 | 13.95211 | 5.000 | 3.000 |
| Ni (mg/L) | 80 | 0.00013 | 0.12530 | 0.08955 | 0.070 | 0.070 |
| Pb (mg/L) | 80 | 0.01560 | 0.12178 | 0.10676 | 0.010 | 0.010 |
| Cu (mg/L) | 80 | 0.03711 | 0.26050 | 0.21542 | 1.000 | 2.000 |
| Parameter | N | Min | Max | Mean | Guidelines | |
|---|---|---|---|---|---|---|
| PNSDW 2017 [67] | WHO | |||||
| Temp (°C) | 80 | 26.2 | 36.7 | 30.25 | - | - |
| pH | 80 | 5.6 | 7.9 | 6.85 | 6.5–8.5 | 6.5–9.2 |
| EC (µS/cm) | 80 | 20.0 | 2840.0 | 1185.05 | - | 1500.000 |
| TDS (mg/L) | 80 | 10.0 | 1400.0 | 601.20 | 600.00 | 1200.000 |
| Cr (mg/L) | 80 | 0.01638 | 0.17179 | 0.14767 | 0.050 | 0.050 |
| Cd (mg/L) | 80 | 0.00055 | 0.10389 | 0.04458 | 0.003 | 0.003 |
| Fe (mg/L) | 80 | 0.16390 | 13.58610 | 9.82432 | 1.000 | 0.300 |
| Mn (mg/L) | 80 | 0.00405 | 0.14579 | 0.04089 | 0.400 | 0.400 |
| Zn (mg/L) | 80 | 0.02480 | 0.51992 | 0.26563 | 5.000 | 3.000 |
| Ni (mg/L) | 80 | 0.00101 | 0.12490 | 0.10005 | 0.070 | 0.070 |
| Pb (mg/L) | 80 | 0.05496 | 0.12178 | 0.11831 | 0.010 | 0.010 |
| Cu (mg/L) | 80 | 0.00690 | 0.02759 | 0.02257 | 1.000 | 2.000 |
| Hidden Neurons | No. of Particles | No. of Iterations | Elapsed Time (sec) | MSE | R | ||
|---|---|---|---|---|---|---|---|
| Validation | Testing | ||||||
| Cr | 30 | 7 | 2000 | 121.2884 | 0.000009 | 0.96878 | 0.98999 |
| Cd | 28 | 3 | 2000 | 153.1887 | 0.000021 | 0.95566 | 0.96404 |
| Fe | 29 | 9 | 2000 | 150.5006 | 0.004871 | 0.99585 | 0.97976 |
| Mn | 27 | 3 | 2000 | 151.0693 | 0.004364 | 0.99933 | 0.98620 |
| Zn | 30 | 6 | 2000 | 116.5287 | 0.031773 | 0.99904 | 0.96388 |
| Ni | 29 | 6 | 2000 | 115.7815 | 0.000047 | 0.98316 | 0.97981 |
| Pb | 30 | 4 | 2000 | 152.8467 | 0.000020 | 0.97832 | 0.96557 |
| Cu | 30 | 2 | 2000 | 153.2260 | 0.039010 | 0.99972 | 0.98390 |
| Hidden Neurons | No. of Particles | No. of Iterations | Elapsed Time (sec) | MSE | R | ||
|---|---|---|---|---|---|---|---|
| Validation | Testing | ||||||
| Cr | 29 | 2 | 2000 | 157.2246 | 0.0000009 | 0.99050 | 0.98830 |
| Cd | 30 | 8 | 2000 | 152.5088 | 0.0000150 | 0.98307 | 0.96868 |
| Fe | 28 | 10 | 2000 | 151.0597 | 0.0702760 | 0.98099 | 0.96368 |
| Mn | 29 | 10 | 2000 | 138.3126 | 0.0000006 | 0.95686 | 0.96337 |
| Zn | 30 | 3 | 2000 | 114.7199 | 0.000005 | 0.98559 | 0.98614 |
| Ni | 27 | 1 | 2000 | 120.5753 | 0.000058 | 0.98779 | 0.96227 |
| Pb | 29 | 1 | 2000 | 119.6443 | 0.000008 | 0.98377 | 0.98897 |
| Cu | 28 | 9 | 2000 | 153.6068 | 0.000269 | 0.96707 | 0.95589 |
| Hidden Neurons | No. of Particles | No. of Iterations | Elapsed Time (sec) | MSE | R | ||
|---|---|---|---|---|---|---|---|
| Validation | Testing | ||||||
| Cr | 30 | 8 | 2000 | 154.5653 | 0.000014 | 0.98851 | 0.98640 |
| Cd | 28 | 1 | 2000 | 156.7819 | 0.000078 | 0.98910 | 0.98683 |
| Fe | 29 | 9 | 2000 | 150.3615 | 0.031866 | 0.98414 | 0.96054 |
| Mn | 30 | 6 | 2000 | 158.4757 | 0.040315 | 0.98414 | 0.96002 |
| Zn | 29 | 4 | 2000 | 122.3900 | 0.008780 | 0.99965 | 0.99577 |
| Ni | 27 | 10 | 2000 | 155.5062 | 0.000073 | 0.97786 | 0.95538 |
| Pb | 28 | 9 | 2000 | 124.1062 | 0.000003 | 0.99641 | 0.99788 |
| Cu | 29 | 3 | 2000 | 122.3725 | 0.000030 | 0.99663 | 0.99835 |
| Hidden Neurons | No. of Particles | No. of Iterations | Elapsed Time (sec) | MSE | R | ||
|---|---|---|---|---|---|---|---|
| Validation | Testing | ||||||
| Cr | 29 | 2 | 2000 | 162.4754 | 0.00014800 | 0.96813 | 0.98011 |
| Cd | 27 | 4 | 2000 | 157.0324 | 0.00003800 | 0.99426 | 0.98938 |
| Fe | 29 | 8 | 2000 | 145.3954 | 0.04537300 | 0.96040 | 0.97544 |
| Mn | 30 | 8 | 2000 | 164.0052 | 0.00007800 | 0.98231 | 0.97926 |
| Zn | 28 | 5 | 2000 | 161.1227 | 0.00012300 | 0.99861 | 0.99775 |
| Ni | 29 | 7 | 2000 | 160.0693 | 0.00002200 | 0.97463 | 0.98991 |
| Pb | 28 | 10 | 2000 | 122.7119 | 0.00000600 | 0.98788 | 0.99495 |
| Cu | 30 | 5 | 2000 | 157.5830 | 0.00000005 | 0.99925 | 0.99815 |
| Model | Governing Network Structure | Model | Governing Network Structure |
|---|---|---|---|
| SW Dry Cr | 4-30-1 | GW Dry Cr | 4-30-1 |
| SW Dry Cd | 4-28-1 | GW Dry Cd | 4-28-1 |
| SW Dry Fe | 4-29-1 | GW Dry Fe | 4-29-1 |
| SW Dry Mn | 4-27-1 | GW Dry Mn | 4-30-1 |
| SW Dry Zn | 4-30-1 | GW Dry Zn | 4-29-1 |
| SW Dry Ni | 4-29-1 | GW Dry Ni | 4-27-1 |
| SW Dry Pb | 4-30-1 | GW Dry Pb | 4-28-1 |
| SW Dry Cu | 4-30-1 | GW Dry Cu | 4-29-1 |
| SW Wet Cr | 4-29-1 | GW Wet Cr | 4-29-1 |
| SW Wet Cd | 4-30-1 | GW Wet Cd | 4-27-1 |
| SW Wet Fe | 4-28-1 | GW Wet Fe | 4-29-1 |
| SW Wet Mn | 4-29-1 | GW Wet Mn | 4-30-1 |
| SW Wet Zn | 4-30-1 | GW Wet Zn | 4-28-1 |
| SW Wet Ni | 4-27-1 | GW Wet Ni | 4-29-1 |
| SW Wet Pb | 4-29-1 | GW Wet Pb | 4-28-1 |
| SW Wet Cu | 4-28-1 | GW Wet Cu | 4-30-1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Jesus, K.L.M.; Senoro, D.B.; Dela Cruz, J.C.; Chan, E.B. Neuro-Particle Swarm Optimization Based In-Situ Prediction Model for Heavy Metals Concentration in Groundwater and Surface Water. Toxics 2022, 10, 95. https://doi.org/10.3390/toxics10020095
De Jesus KLM, Senoro DB, Dela Cruz JC, Chan EB. Neuro-Particle Swarm Optimization Based In-Situ Prediction Model for Heavy Metals Concentration in Groundwater and Surface Water. Toxics. 2022; 10(2):95. https://doi.org/10.3390/toxics10020095
Chicago/Turabian StyleDe Jesus, Kevin Lawrence M., Delia B. Senoro, Jennifer C. Dela Cruz, and Eduardo B. Chan. 2022. "Neuro-Particle Swarm Optimization Based In-Situ Prediction Model for Heavy Metals Concentration in Groundwater and Surface Water" Toxics 10, no. 2: 95. https://doi.org/10.3390/toxics10020095
APA StyleDe Jesus, K. L. M., Senoro, D. B., Dela Cruz, J. C., & Chan, E. B. (2022). Neuro-Particle Swarm Optimization Based In-Situ Prediction Model for Heavy Metals Concentration in Groundwater and Surface Water. Toxics, 10(2), 95. https://doi.org/10.3390/toxics10020095







