Prioritization Model for the Location of Temporary Points of Distribution for Disaster Response

Abstract

Background: Disasters generate abrupt surges in humanitarian demand, requiring response strategies that balance operational performance with vulnerability considerations. This study examines how temporary Points of Distribution (PODs) can be planned and activated to support timely and equitable resource distribution after a high-magnitude earthquake. Methods: A two-stage framework is proposed. First, a modular p-median model identifies POD locations and allocates modular capacity to minimize population-weighted distance under capacity constraints; travel-distance percentiles guide the selection of p. Second, a SMART-based multi-criteria model ranks facilities using operational metrics and vulnerability indicators, including seismic and economic conditions and the presence of at-risk groups. Results: Evaluation of p values from 3 to 30 shows substantial reductions in travel distances as PODs increase, with an elbow at $p=12$, where 50% of the residents are within 500 m, 75% within 675 m, and 95% within 1200 m. The SMART analysis forms three priority clusters: facilities 24 and 9 as highest priority; 23, 4, 12, and 22 as medium priority; and the remaining sites as lower priority. Sensitivity analysis shows that rankings are responsive to vulnerability weights, although clusters remain stable. Conclusions: The framework integrates optimization and multi-criteria decision analysis without increasing model complexity, enabling meaningful decision-maker involvement throughout the modeling process.

1. Introduction

Every year, disasters cause a substantial loss of life, affect millions of people, and inflict severe economic damage throughout the globe [1,2]. Recent evidence indicates a growing trend in both the frequency and intensity of these events, a pattern closely linked to urban expansion, population growth in high-risk areas, and climate variability [3]. Among the different types of hazards, earthquakes stand out as some of the most devastating, producing large numbers of casualties and widespread destruction. Historical events, such as the 2004 Indian Ocean earthquake and tsunami [4], the 2010 Haitian earthquake [5], the 2011 Japan earthquake [1], and the 2015 Nepal earthquake [6], illustrate the catastrophic human and economic consequences that seismic disasters can entail.

In the aftermath of a disaster, logistics accounts for nearly 80% of all the relief efforts, making it a decisive factor that often determines the overall success or failure of humanitarian operations [7]. This underscores the central role of humanitarian logistics, defined as the “logistics and supply chain management focusing on the preparation for, response to, and recovery from a humanitarian crisis, with the aim of saving lives and alleviating the suffering of affected populations” [8]. The relevance of this field extends beyond operational efficiency, as it directly contributes to achieving Sustainable Development Goal 11.5, which aims to reduce the number of deaths and people affected by disasters and decrease the economic losses and vulnerabilities associated with them [9]. This is further accentuated by the growing yearly frequency and intensity of natural hazards observed in recent decades [10], emphasizing the need for more resilient, adaptive, and data-driven humanitarian logistics systems [11].

A critical operation in disaster response is humanitarian aid distribution [5,12]. Its efficient management is essential to ensure the survival of affected populations, particularly within the first 72 h, a period often referred to as the golden window of emergency response [13,14]. Moreover, in sudden-onset disasters, the magnitude and immediacy of demand surges can be substantial, posing severe logistical challenges for supply chain coordination and resource allocation [15,16]. In recent years, the study of temporary and modular facility location problems has gained increasing attention, particularly in contexts requiring rapid infrastructure deployment and flexibility under uncertainty [17]. In this approach, each facility is composed of independent units or modules that can be allocated or relocated to expand operational capacity according to evolving needs. These modular structures are designed for quick installation, removal, and redeployment, enabling a more agile and adaptive response to multiple affected areas [18].

Nevertheless, this type of problem involves a large number of variables and criteria that must be properly prioritized to achieve a balance between accuracy and practicality. An emerging and effective approach is thus to use classical facility location models as a mathematical foundation for identifying optimal spatial configurations [19], complemented by multi-criteria approaches that allow including qualitative or contextual factors without excessively increasing the model complexity [11]. This integration allows combining analytical rigor with decision-making flexibility, ensuring that both efficiency and equity relevance are properly reflected in the final solution.

Considering the information discussed in the previous paragraphs, there is a clear research gap in the current literature. While mathematical models are useful for identifying the locations of humanitarian facilities, they are insufficient to capture the full range of factors that influence humanitarian operations, particularly those related to vulnerability. Most existing approaches rely primarily on distance-based criteria, overlooking the need to prioritize which facilities should be activated first when resources are limited. This gap is particularly relevant in the context of earthquakes, which are among the most destructive types of disasters and make the decision of whom to assist first especially challenging. Moreover, this hazard was selected because, in the study area, it is the only disaster type for which block-level data are available.

For this reason, this paper proposes a two-stage framework that integrates mathematical modeling with a multi criteria prioritization approach to support the prioritization of point of distribution (POD) locations in the aftermath of an earthquake. In the first stage, a model based on the p median problem is formulated, incorporating modularization to identify the optimal locations of temporary PODs for disaster response, defined as “a site where humanitarian aid is delivered to the affected population” [20]. In the second stage, the Simple Multi Attribute Rating Technique (SMART) is applied to prioritize which locations should be activated first, taking into account both operational performance and vulnerability considerations.

The main contributions of this work can be summarized as follows:

• Development of a compact mixed-integer model that minimizes the total demand-weighted distance while respecting the modular capacity constraints that limit the demand served per facility.
• Integration of a two-stage decision-making process: the first stage optimizes the network design with the mathematical model, while the second stage applies the SMART method to complement the model results. This multi-criteria approach enables the inclusion of additional attributes that would otherwise make the mathematical formulation excessively complex.
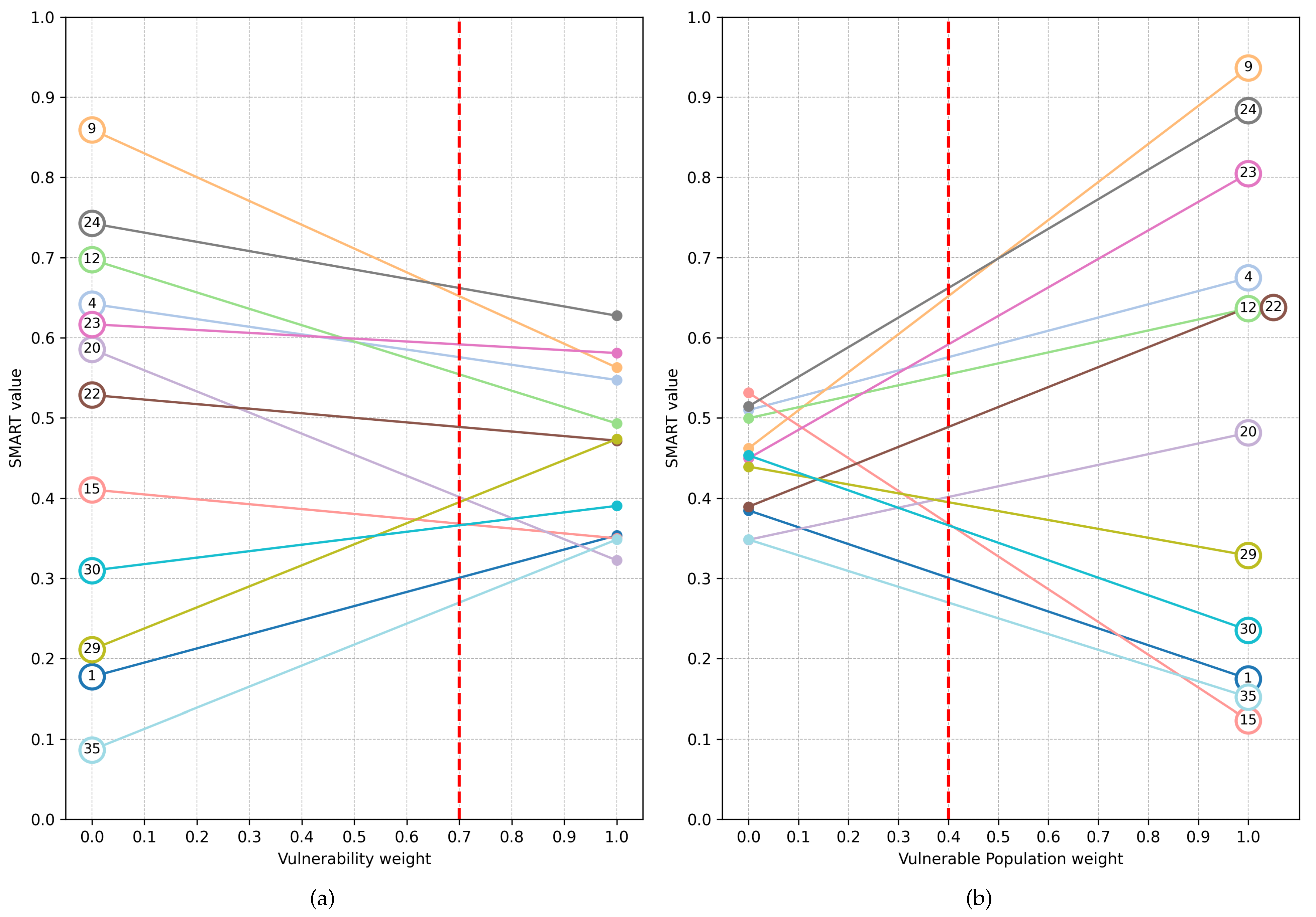
• Sensitivity analysis is a key component of multi criteria approaches, as it allows evaluating how changes in decision-makers’ preferences affect the results. This is particularly important given that decision-makers may change with the arrival of a new government.
• The application of the proposed two-stage framework to a real case study shows that combining modular facility allocation with a multi criteria approach that incorporates decision-maker preferences can enhance operational performance while also accounting for vulnerability considerations.

The remainder of the paper is organized as follows. Section 2 reviews the literature on temporary facility location in humanitarian logistics. Section 3 describes the case study that supports the prioritization analysis. Section 4 presents the prioritization framework, including the modular p median formulation and the SMART method. Section 5 reports and discusses the results from applying the framework to the case study. Finally, Section 6 presents the main conclusions and directions for future work.

2. Literature Review

In humanitarian logistics, the facility location problem generally seeks to identify the optimal placement of depots [14], points of distribution [21], and shelters [22] to ensure an efficient and timely response. Besides selecting suitable sites, this problem is often intertwined with a broader set of operational challenges, including evacuation planning [22], vehicle routing and transportation coordination [14], and the allocation and management of relief supplies [23]. This integration reflects the highly interconnected nature of humanitarian operations, in which facility location decisions influence, and are influenced by, multiple logistical processes that collectively shape the effectiveness of disaster response efforts.

The objective functions employed in humanitarian facility location models can generally be classified into four major categories: minimizing costs [24,25,26], minimizing operational or response time [24,27,28], maximizing the amount of demand satisfied [27], and minimizing unmet demand [14]. Although these objectives are essential, they largely mirror performance metrics commonly used in enterprise operations. Consequently, there is a need to complement them with additional criteria that capture the vulnerability of the population affected, ensuring that facility location decisions align with humanitarian priorities rather than purely operational efficiency.

Regarding the types of disasters studied, the literature has predominantly focused on natural and sudden onset events, particularly earthquakes [16,18,24,25,26,29,30,31], floods [14,23], and hurricanes [32]. This concentration on rapid onset hazards aligns with the urgent decision-making and high stakes contexts in which facility location models are most critically needed.

Humanitarian temporary facilities address different needs during disaster response; storage centers safeguard emergency inventories [16]; collection centers receive public donations [33]; processing centers sort, classify, and ensure the quality of donated goods [34]; and distribution centers deliver assistance to the communities affected [21]. Shelters provide temporary accommodation [35], medical centers offer urgent care [36], and logistics hubs function as strategic nodes that coordinate supply flows among facilities [37]. Within this spectrum, the literature focuses primarily on distribution centers, medical centers, and shelters, given their direct interaction with beneficiaries [17].

Identifying suitable sites for disaster response facilities is a complex task, since temporary installations must absorb abrupt increases in demand, especially during rapid onset events such as earthquakes. Location planning should explicitly account for both the opening and the subsequent closing of facilities, given their temporary character [38]. In parallel, response strategies benefit from modular capacity, which preserves system flexibility [18] and sustains service levels without requiring new infrastructure investments [39].

For example, [19] proposed to determine strategic sites for Mobile Logistics Hubs, combining a modified maximal covering location problem with stakeholder focus group discussions to merge quantitative optimization and qualitative expert judgment; optimization identifies the number and spatial placement of hubs, while deliberation narrows choices to five first-priority, city-level locations acceptable to diverse stakeholders.

Moreover, an optimization model for temporary depots in disaster response is proposed to integrate humanitarian operations management; it highlights the benefit of closing selected facilities in order to open others, reallocating scarce resources toward unmet demand, and thereby improving operational performance during and after emergencies [14].

Additionally, the Multi Period Modular Capacitated Maximal Covering Location Problem is introduced to address facility location, module assignment, and demand allocation across multiple periods; it is formulated as a mixed integer linear program, and the use of modules enables transfers over time, which improves service quality and cost management [18].

Furthermore, a two-stage multi-objective stochastic model for patient transfer and relief distribution under lockdown conditions illustrates the central role of temporary facilities during epidemic response; temporary distribution centers and temporary hospitals provide immediate relief and medical care, enable flexible adaptation to changing demands, and allow strategic siting as the outbreak evolves so that resources reach the areas with the highest need [29].

Similarly, a multi-period stochastic optimization model for post disaster emergency medical response integrates temporary medical center location, casualty allocation, and medical staff planning, capturing the dynamic evolution of the first 72 h after an earthquake by dividing the horizon into four periods and updating capacities and casualty health states [40]. Moreover, the model incorporates uncertainties in demand, road damage, and hospital capacity using scenario-based stochastic programming and chance constraints. This article only considers prioritization through triage categories.

In addition, a multi-period-integrated blood supply chain network model for disaster conditions seeks to minimize total cost and blood delivery time by coordinating four facility types, temporary collection centers, field hospitals, main processing centers, and medical centers, and integrating decisions across collection, processing, and distribution [41]. Despite this level of integration, the model does not incorporate vulnerability-related factors.

Finally, a robust multi-period blood supply chain network model addresses uncertainties in supply, demand and partial disruptions to donor groups, collection centers, blood banks and hospitals using a two-stage adaptive robust optimization approach [42]. The authors design an exact algorithm that combines column and constraint generation with Benders decomposition, underscoring the computational complexity required to obtain optimal solutions.

Based on the literature reviewed, many studies rely on mathematically sophisticated models that promise optimal solutions; however, these models are often not adopted in practice because decision-makers struggle to understand and communicate their underlying logic [19]. In emergency contexts, transparency and usability are essential. Simple mathematical models are therefore appealing, as they are easier to communicate and audit, but by design, they fail to capture several critical attributes. To address this limitation without compromising interpretability, simple location models can be complemented with multi-criteria approaches that incorporate additional factors [11]. In this study, we adopt a classical p median model to ensure spatial efficiency and couple it with a multi criteria layer based on the SMART method, allowing us to integrate operational performance metrics with vulnerability factors.

3. Case Study

We present a case study this section, emphasizing the geographical and administrative context to which the mathematical model will be applied.

Peru, situated within the Pacific Ring of Fire, is a geographic region susceptible to frequent seismic activity and volcanic activity. Nestled in the southwestern part of Peru, Arequipa City lies in close proximity to the converging Nazca and South American tectonic plates, thereby experiencing an elevated frequency of earthquakes. The 21st century witnessed one of the most severe earthquakes to impact Arequipa, occurring on 23 June 2001. This catastrophic event had a profound impact, with 74 reported fatalities, 2689 recorded injuries, 217,495 people displaced, 64 people reported missing, 35,601 dwellings affected, and 17,584 homes completely destroyed, as documented in [43].

In contrast to the seismic hazard map that encompasses the entire city of Arequipa, the seismic risk assessment for Alto Selva Alegre, one of its districts, offers a detailed block-level evaluation. This comprehensive analysis considers multiple parameters, including the vulnerability of urban occupation areas, predominant structural systems, construction materials, number of floors, and other relevant characteristics [44]. As of 2024, Alto Selva Alegre is projected to have approximately 93,730 inhabitants distributed over 1861 urban blocks [45].

Figure 1 presents a set of maps of the Alto Selva Alegre district, illustrating (a) the population distribution by block, (b) the seismic vulnerability levels, and (c) the socioeconomic classification. In panel (a), darker colors represent higher population density, showing that most of the inhabitants are concentrated in the southeastern region of the district. Panel (b) depicts the seismic vulnerability at the block level, where darker red areas indicate greater structural susceptibility, while green tones represent zones with minimal expected damage. Finally, panel (c) classifies each block according to its economic strata, where colors represent different income levels ranging from high to low.

Following an earthquake, the demand for humanitarian aid kits would sharply increase, potentially exceeding the current capacity to adequately respond to post-disaster needs [47]. In the case of high-intensity earthquakes, this demand could extend to the entire population. Consequently, strategic planning must include establishing PODs to ensure the efficient delivery of humanitarian assistance to affected individuals. According to the Sphere standards [48], it is essential that the population be served by facilities located within a maximum distance of 500 m. In the process of identifying potential PODs, a comprehensive assessment was conducted in various locations within Alto Selva Alegre. Sites such as schools, parks, churches, and municipal lands were examined to determine their suitability as PODs. Information about these PODs, including their names, categories, labels, and geographical coordinates (latitude and longitude), is summarized in

Table 1. Location of candidate points of distribution (PODs).

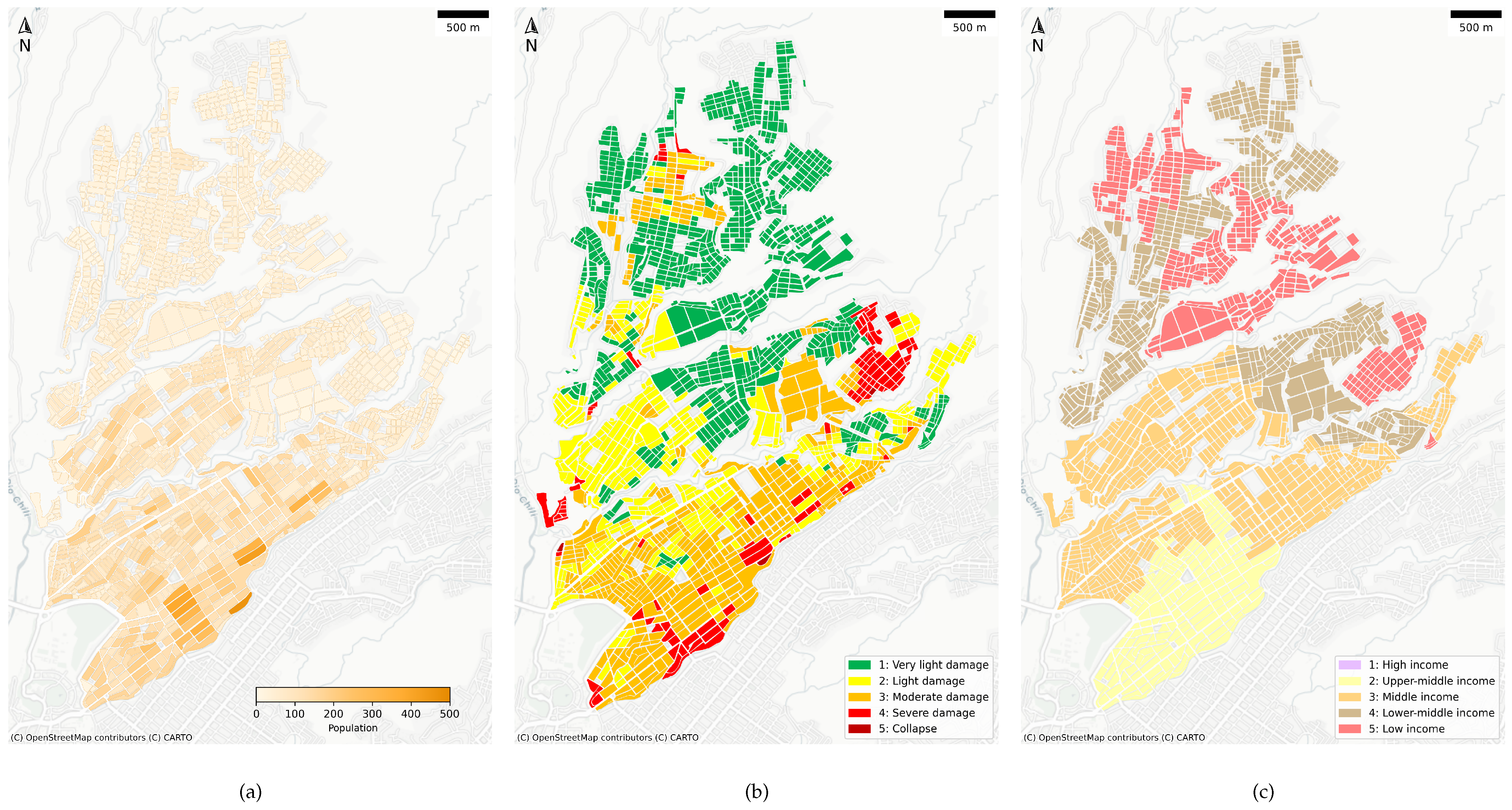
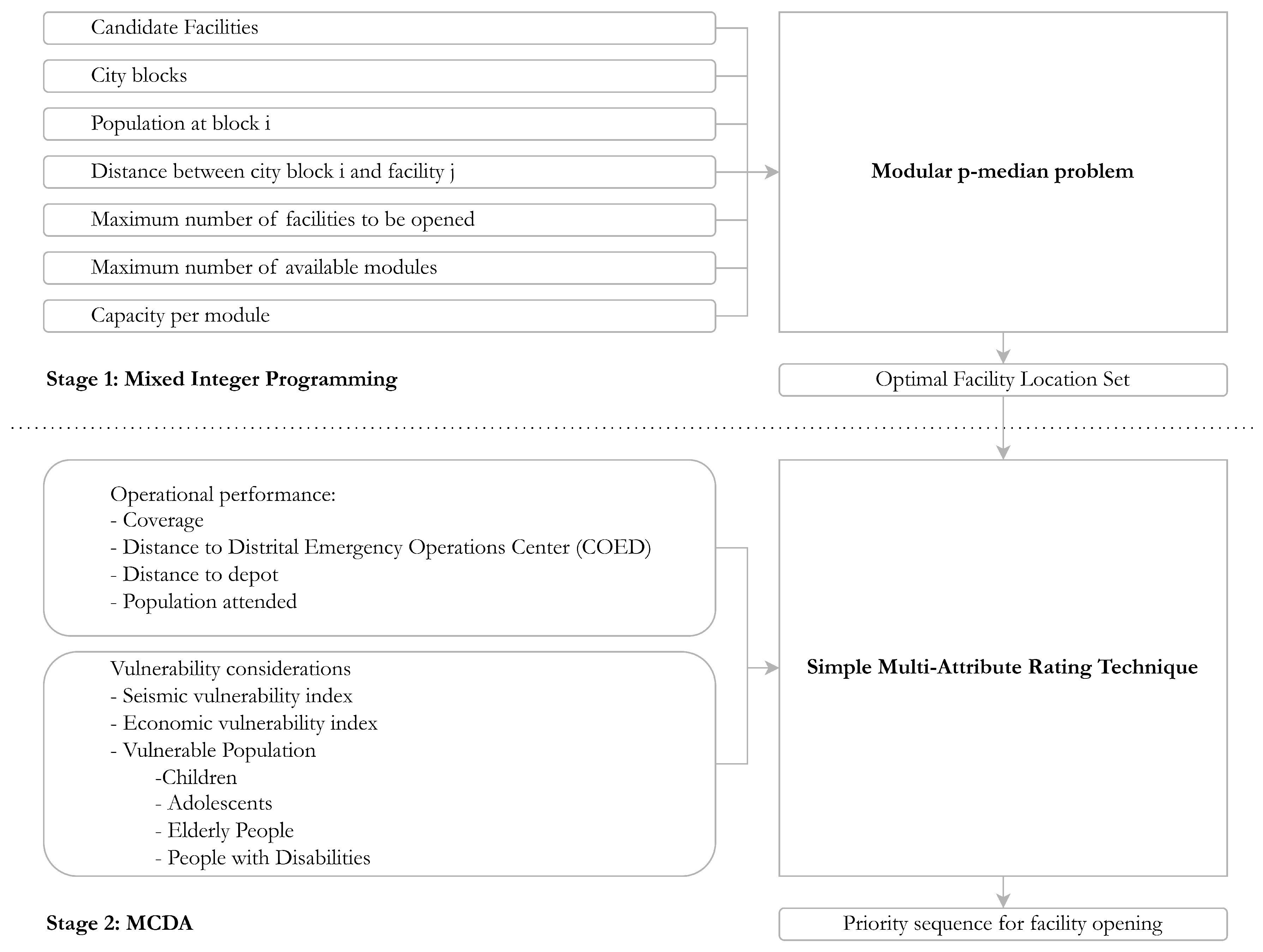
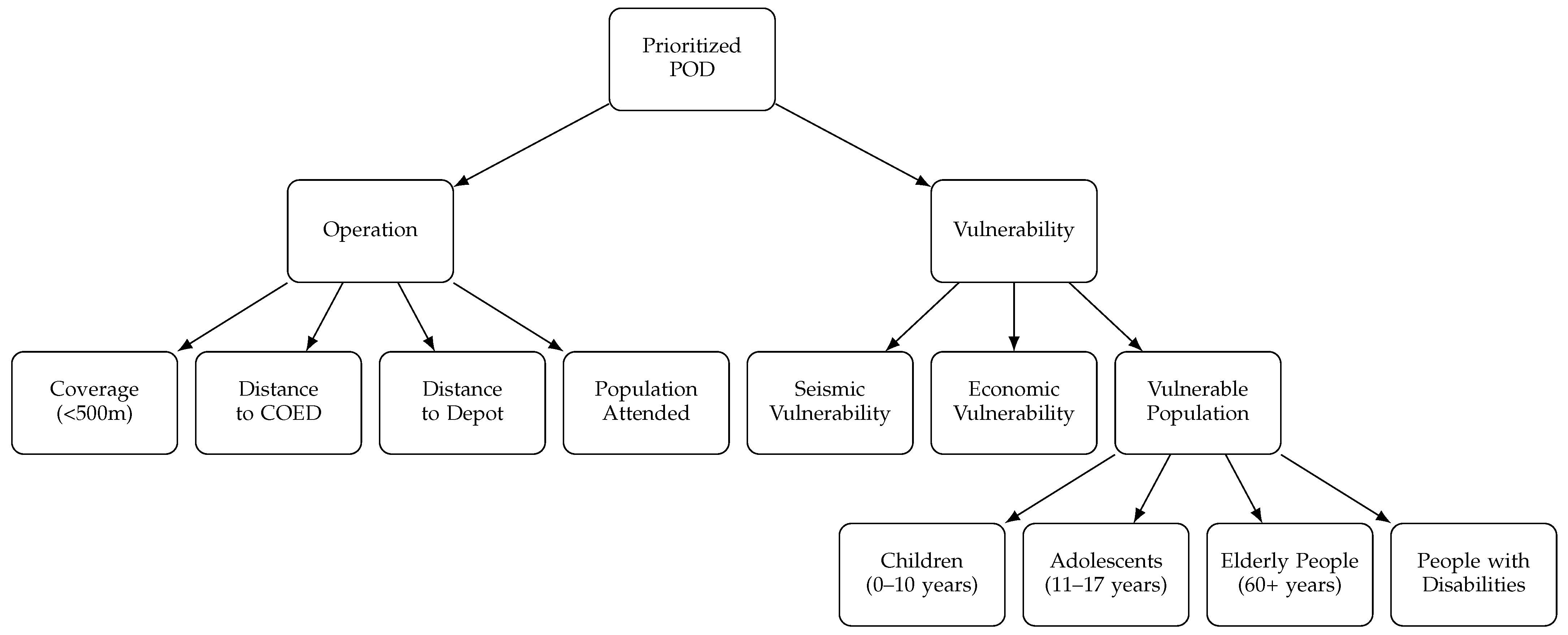
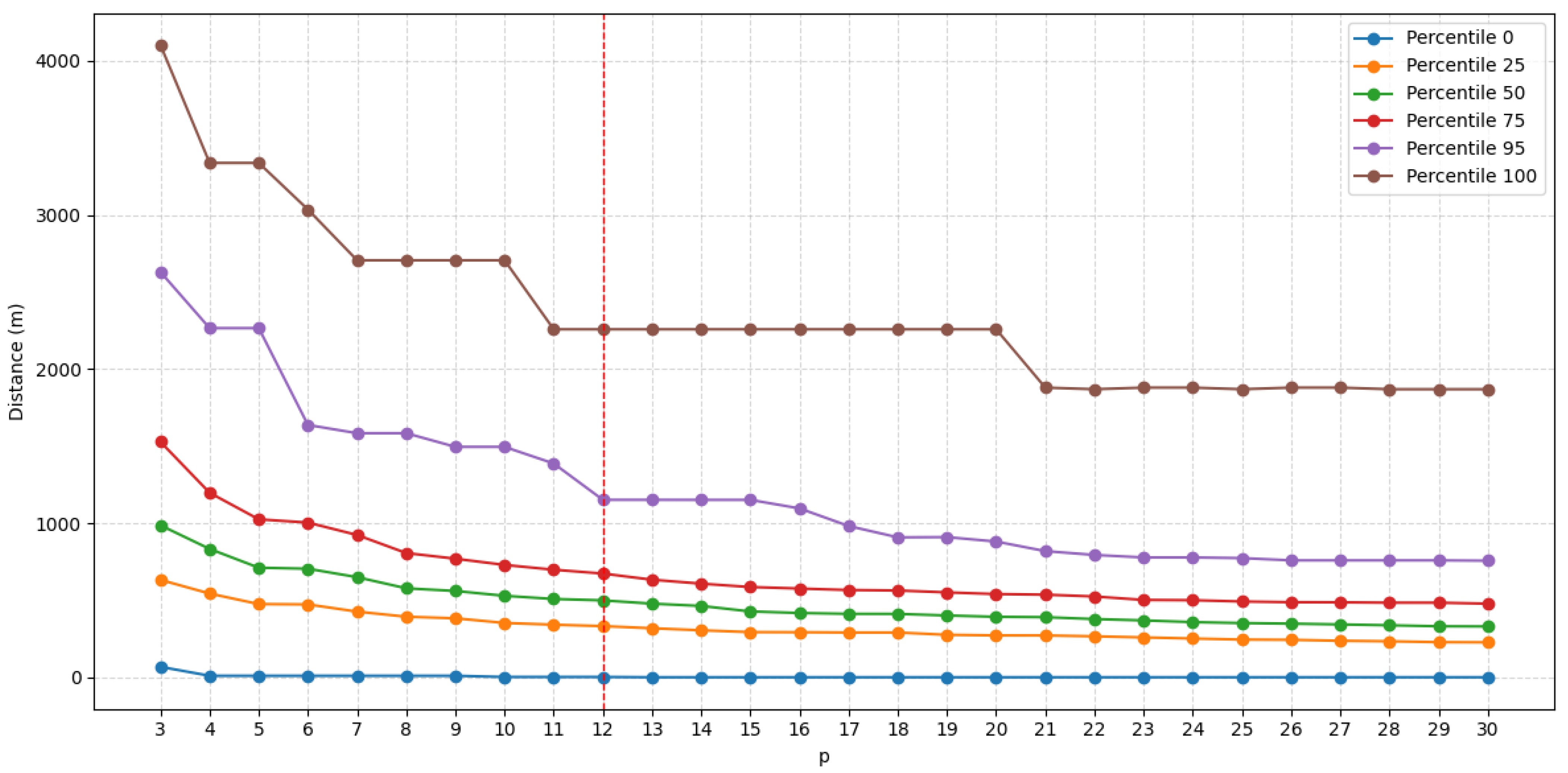
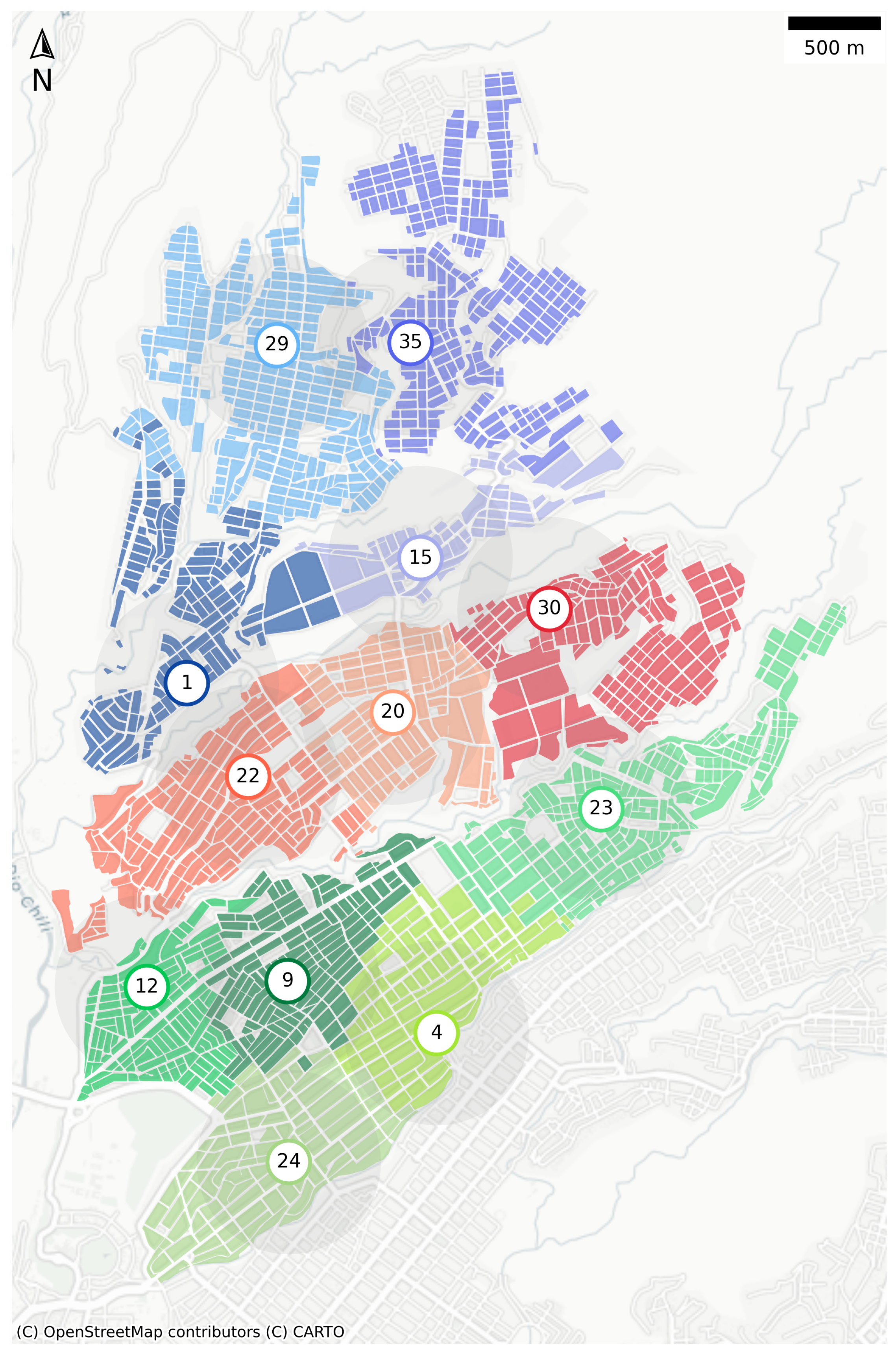
Facility	Category	Name	Latitude	Longitude
1	Stadium	Balcones Canchita Chilina	−16.3628	−71.5267
2	Stadium	Cancha Ampliación Villa Ecológica	−16.3496	−71.5177
3	Stadium	Cancha Romero	−16.3884	−71.5287
4	Stadium	Complejo Deportivo Alto Selva Alegre	−16.3792	−71.5146
5	Stadium	Complejo Deportivo Bella Esperanza	−16.3649	−71.4997
6	Stadium	Complejo Deportivo Roosvelt	−16.3821	−71.5235
7	Stadium	Complejo Deportivo Villa Asunción	−16.3623	−71.5158
8	Stadium	Complejo Pampa Chica	−16.3693	−71.5284
9	Stadium	Complejo Ramiro Prialé	−16.3767	−71.5218
10	Stadium	Complejo Rolando Jauregui	−16.3718	−71.5146
11	Stadium	Padre José Schmidpeter	−16.3761	−71.5171
12	Park	Parque Cruce Chilina	−16.3770	−71.5287
13	Park	Parque de la Juventud	−16.3739	−71.5169
14	Park	Parque del Trabajador	−16.3891	−71.5265
15	Park	Parque El Huarangal	−16.3570	−71.5153
16	Park	Parque Francisco Mostajo	−16.3626	−71.5195
17	Park	Parque La Familia	−16.3655	−71.5192
18	Park	Parque Leones del Misti	−16.3708	−71.5052
19	Park	Parque Los Eucaliptos	−16.3758	−71.5260
20	Park	Parque Los Eucaliptos 2	−16.3642	−71.5167
21	Park	Parque Municipal	−16.3796	−71.5205
22	Park	Parque Temático	−16.3672	−71.5237
23	Park	Parque Tripartito	−16.3687	−71.5065
24	Church	Parroquia Espíritu Santo	−16.3852	−71.5218
25	Park	Plaza Francisco Mostajo	−16.3639	−71.5219
26	Stadium	Polideportivo Juan Velasco Alvarado	−16.3751	−71.5222
27	School	San José Obrero Circa	−16.3771	−71.5187
28	Other	Plaza de Toros Villa Ecológica	−16.3537	−71.5231
29	School	Cuna Más Villa Ecológica	−16.3470	−71.5223
30	Stadium	Cancha El Mirador de Arequipa	−16.3594	−71.5091
31	Stadium	Losa Deportiva–El Gran Chaparral	−16.3654	−71.5094
32	Stadium	Losa Deportiva–Nueva Villa Ecológica Zona C	−16.3398	−71.5159
33	Stadium	Losa Deportiva–Los Enanitos	−16.3449	−71.5104
34	Stadium	Losa Deportiva APSIL	−16.3523	−71.5073
35	Stadium	Losa Deportiva–Nueva Villa Ecológica Zona B	−16.3469	−71.5158
36	Stadium	Losa Deportiva–El Mirador	−16.3605	−71.5242

.

To store goods and adequately serve the population affected, the installation of temporary modules in the facilities selected is necessary [17]. Note that each facility, depending on its physical dimensions, can accommodate only a limited number of modules. These modules can be disassembled and reinstalled at other suitable locations to support nearby populations. However, when a module is relocated, it becomes temporarily unavailable due to the time required for disassembly, transportation, and reassembly. Nevertheless, it is necessary to consider a broad set of criteria when deciding which PODs should be activated first under limited resource conditions. This decision should not be based solely on travel distance but it should also take into account the vulnerability of the population affected. Therefore, two complementary approaches are proposed: first, a mixed-integer programming model to optimize the allocation of resources, and second, a multi-criteria decision model to prioritize which facilities should be opened first, considering multiple attributes simultaneously.

4. Prioritization Model

The prioritization of humanitarian PODs requires not only determining where facilities should be installed but also deciding which should be activated first when resources are limited. These two decisions are inherently connected despite responding to different analytical needs.

The first stage involves a quantitative optimization model capable of identifying a feasible and efficient spatial configuration of potential distribution sites. This is achieved by the modular p-median formulation, which minimizes the travel distance between the populations affected and facilities available while accounting for service capacity and logistical constraints. The result of this stage is a set of candidate locations that can efficiently serve the population under normal operating conditions.

However, in real post-disaster scenarios, the simultaneous activation of all the feasible facilities is rarely possible due to restricted time, workforce, and equipment. Therefore, a second stage is required to establish priorities among the candidate sites based on their relative importance and impact. For this purpose, a multi-criteria decision analysis is integrated into the framework to evaluate each location according to accessibility and the vulnerability of the surrounding population.

Together, these two stages form a complementary decision-support framework: the mathematical model ensures spatial and operational efficiency, while the multi-criteria prioritization model ensures equity and humanitarian relevance in the final selection of facilities. The interaction between these two stages is shown in Figure 2.

4.1. Mathematical Model

Following the onset of a disaster, it is essential to take immediate action to deliver aid supplies to the population affected within the critical 72-h window [49], thereby ensuring their health and survival. To maximize the efficiency of distribution operations, temporary facilities must be activated to function as PODs, aiming at minimizing the distance that people must travel to receive assistance. However, due to administrative and logistical constraints, only a maximum of p facilities can be opened. At each POD, modular units are installed to store and facilitate the delivery of humanitarian aid. The goal is to deploy the minimum number of modules necessary to adequately serve the entire population.

Accordingly, this section presents the mathematical formulation of the modular p-median problem, designed to determine the optimal locations of PODs and the allocation of modular capacity units. Each module provides a fixed service capacity and can be reallocated to different facilities when required.

The sets, parameters, and decision variables used in the model are summarized in

Table 2. Sets, parameters, and decision variables of the modular p-median model.

Notation	Description
Sets
I	Set of city blocks (demand points).
J	Set of candidate facility locations.
Parameters
$h_i$	Population at city block i.
$d_{ij}$	Distance between city block i and facility j (km).
p	Maximum number of facilities to be opened.
r	Maximum total number of modules available.
c	Capacity of a single module.
Decision Variables
$X_{ij}$	Binary variable equal to 1 if demand point i is assigned to facility j; 0 otherwise.
$Y_j$	Binary variable equal to 1 if facility j is opened; 0 otherwise.
$Q_j$	Integer variable representing the number of modules installed at facility j.

.

Based on these definitions, the following mixed-integer programming model is formulated:

$$minZ=\sum _{i\in I}\sum _{j\in J}{h}_i·d_{ij}·X_{ij}.$$

(1)

The objective function (1) minimizes the total weighted distance between demand points and the facilities that serve them.

$$\sum _{j\in J}{X}_{ij}=1,\forall i\in I.$$

(2)

Constraint (2) ensures that each demand point is assigned to exactly one open facility.

$$X_{ij}\le Y_j,\forall i\in I,\forall j\in J.$$

(3)

Constraint (3) guarantees that a demand point can only be assigned to an open facility.

$$\sum _{j\in J}{Y}_j=p.$$

(4)

Constraint (4) enforces that exactly p facilities are opened.

$$\sum _{j\in J}{Q}_j=r.$$

(5)

Constraint (5) ensures that the total number of modules installed does not exceed the quantity available.

$$\sum _{i\in I}{h}_i·X_{ij}\le c·Q_j,\forall j\in J.$$

(6)

Constraint (6) limits the total demand served by each facility according to the modular capacity installed.

$$x_{ij}\in \{0,1\},y_j\in \{0,1\},q_j\in {\mathbb{Z}}_{+},\forall i\in I,\forall j\in J.$$

(7)

Constraint (7) defines the variable domains: assignment and opening decisions are binary, while the number of modules is a non-negative integer.

The model was evaluated for values of p ranging from 3 to 30 to explore different configurations of the modular p-median solution space. For each value of p, performance measures were computed and summarized using key statistical descriptors: the minimum (0th percentile), the first quartile (25th percentile, $Q1$), the median (50th percentile, $Q2$),the third quartile (75th percentile, $Q3$), the maximum, and the 95th percentile. These indicators were then analyzed using the elbow method, considering the second derivative, to identify the value of p that provides the best balance between solution quality and diminishing marginal improvements, allowing the selection of the most suitable number of facilities to activate.

4.2. Multi-Criteria Approach

Once the modular p-median model identified a feasible set of candidate PODs, a second stage was developed to determine the activation order of these facilities, considering that the modules available constitute the limiting resource. This stage employed the SMART method, a transparent and compensatory decision-making method that aggregates multiple normalized indicators through explicit weighting [50]. To guide the prioritization process, each candidate facility was evaluated using a combination of operational and vulnerability metrics.

The SMART procedure was applied following the step-by-step guidelines in [50], aiming mainly at prioritizing the PODs to be opened first. The decision-maker was identified as the Sub Gerencia de Gestión de Riesgo de Desastres of Alto Selva Alegre. Each alternative corresponded to one of the PODs under consideration resulting from the p-median model. A value tree was then constructed to specify the relevant attributes, encompassing both operational and vulnerability factors; this structure is shown in Figure 3. Each alternative was evaluated based on its performance on these attributes, and in consultation with the decision-maker, weights were assigned to represent their relative importance. A weighted average was subsequently computed for all the alternatives to enable direct comparison and establish a provisional ranking. Finally, a sensitivity analysis was performed to assess the robustness of the results under variations in attribute weights.

The prioritization model incorporated two main decision criteria: operational performance and vulnerability. The operational performance dimension comprised several attributes. The first was coverage, defined as the percentage of the population assigned to each POD that resides within 500 m of the site, based on walking distances obtained from Open Street Map [51]. A second attribute was the driving distance [51] to the District Emergency Operations Center (COED) of Alto Selva Alegre, which would function as the command point during an emergency. A third attribute captured the driving distance [51] to the main depot where essential supplies are stored before being dispatched to the PODs, stressing that the COED would also operate a temporary storage facility. Finally, the operational dimension included the total population served by each POD, with demographic data obtained from [46].

The second main dimension, vulnerability, consisted of three attributes. Seismic vulnerability was evaluated using information on housing structure, soil type, and related factors obtained from [44]. Economic vulnerability was assessed based on household income levels, using data from [45]. In addition, vulnerable population groups were identified using adjusted demographic data from [46], including children (0–10 years), adolescents (11–17 years), the elderly (60+ years), and individuals with disabilities affecting hearing, speech, vision, mobility, or cognition.

Normalization was applied to convert all the indicators to a comparable 0–1 scale. For coverage, a min–max normalization was used so that PODs with higher coverage obtain values closer to 1 and are therefore more highly prioritized, as shown in Equation (8).

$${\displaystyle \frac{Coverage-min\left(Coverage\right)}{max\left(Coverage\right)-min\left(Coverage\right)}}.$$

(8)

For the distance to the COED and the distance to the depot, an inverted min–max normalization was applied so that shorter distances receive higher scores, as shown in Equation (9).

$${\displaystyle \frac{max\left(Distance\right)-Distance}{max\left(Distance\right)-min\left(Distance\right)}}.$$

(9)

The same inverted normalization was used for the population attended and for each vulnerable population group, ensuring that alternatives serving larger populations receive higher scores, as shown in Equation (10).

$${\displaystyle \frac{max\left(Population\right)-Population}{max\left(Population\right)-min\left(Population\right)}}.$$

(10)

Finally, for the seismic vulnerability index and the economic vulnerability index—defined on qualitative scales from 1 (best) to 5 (worst)—normalization ensured that more vulnerable areas receive higher scores, as shown in Equation (11).

$${\displaystyle \frac{\mathrm{Vulnerability}\mathrm{Index}-1}{5-1}}.$$

(11)

For the operational factors, the decision-maker assigned the following weights: coverage ($Cov$) received 30%, as it reflects the proportion of the population able to reach a point od distribution within a reasonable walking distance; the distance to the COED ($Dist\_COED$) was assigned 20% due to its importance for command, control, and emergency coordination; the distance to the depot ($Dist\_Depot$) received 10%, reflecting its influence on supply delivery logistics; and the population attended ($Pop$) was weighted at 30%, emphasizing the need to prioritize PODs that serve a larger number of residents. The overall operational score ($O{S}_i$) for each POD was calculated using Equation (12).

$$O{S}_i=0.30Co{v}_i+0.20Dist\_COE{D}_i+0.10Dist\_Depo{t}_i+0.30Po{p}_i.$$

(12)

For the vulnerability factors, the decision-maker identified children ($Child$) and people with disabilities ($Disab$) as the most vulnerable groups, assigning each a weight of 30%. This reflects their strong dependence on caregivers, limited mobility, and heightened risk of severe outcomes when humanitarian assistance is not delivered promptly. Adolescents ($Adol$) were assigned a weight of 25%; although they possess greater physical resilience, they still rely on adult supervision during emergencies. The elderly ($Eld$) received the lowest weight (15%), as many are registered in social support programs that facilitate outreach and assistance; nevertheless, they remain susceptible to serious consequences if aid is delayed. The vulnerable people score ($VP{S}_i$) for each POD was calculated using Equation (13).

$$VP{S}_i=0.30Chil{d}_i+0.30Disa{b}_i+0.25Ado{l}_i+0.15El{d}_i.$$

(13)

The overall vulnerability score ($V{S}_i$) for each POD was determined by combining three components: the vulnerable population score ($VP{S}_i$), the seismic vulnerability index ($S{V}_i$), and the economic vulnerability index ($E{V}_i$). Following the decision-maker’s criteria, the vulnerable population component received the highest weight (40%) because the presence of at-risk groups directly reflects the potential human impact during an emergency. The seismic vulnerability index ($S{V}_i$) was assigned a weight of 25%, acknowledging that structural fragility and soil conditions influence expected physical damage but are less immediately linked to humanitarian access. The economic vulnerability index ($E{V}_i$) received a weight of 35%, as lower household income reduces the capacity to cope with and recover from disruptions. The vulnerability score was calculated using Equation (14).

$$V{S}_i=0.40VP{S}_i+0.25S{V}_i+0.35E{V}_i.$$

(14)

Finally, the SMART score for each POD was obtained by combining the two main criteria: the vulnerability score ($V{S}_i$) and the operational score ($O{S}_i$). In accordance with the decision-maker’s priorities, vulnerability was assigned a weight of 70%, reflecting the importance of directing humanitarian assistance toward areas with higher social, economic, and physical risk. The operational score received a weight of 30%, ensuring that logistical feasibility and accessibility remain relevant without overshadowing the needs of the most vulnerable populations. The SMART score was calculated using Equation (15).

$$SMAR{T}_i=0.70V{S}_i+0.30O{S}_i.$$

(15)

Facilities were ranked in descending order of $SMAR{T}_i$, with higher values indicating higher priority for activation. The model preserves monotonicity, ensuring that improvements in any individual criterion proportionally increase the overall score. Finally, a sensitivity analysis was conducted on two components: the vulnerability score and the vulnerable population score. The latter was examined in detail because it is directly linked to population size and can therefore shift the prioritization toward PODs located in more densely populated areas, where larger numbers of children, the elderly, and people with disabilities are concentrated.

5. Results

This section presents the main results from the two-stage prioritization framework. The analysis begins with the modular p-median optimization model, which determines the optimal spatial configuration of PODs and the allocation of modular units required to ensure adequate population coverage. The second part of the analysis applies a multi-criteria decision approach to rank these facilities according to operational and vulnerability metrics.

5.1. Mathematical Model

To examine the trade-off between the number of open facilities and the efficiency of service delivery, the model was evaluated for values of p ranging from 3 to 30. A maximum of 95 modular units was considered, representing the minimum number required to serve the entire target population in the study area. Setting this limit ensures that the capacity constraint remains active during the optimization process, forcing the model to allocate resources efficiently among the selected facilities.

Figure 4 shows how the average distance varies across the minimum (0th percentile), $Q1$ (25th percentile), $Q2$ (50th percentile), $Q3$ (75th percentile), the 95th percentile, and the maximum (100th percentile). As expected, the average distance decreases substantially as p increases. Using the elbow method based on the second derivative, the elbow for $Q1$ and $Q2$ occurs at $p=5$, for $Q3$ at $p=4$, and for the 95th percentile and the maximum at $p=7$.

However, the operational strategy aims to open additional PODs so that each site remains active until it fully serves its assigned demand before resources are moved to the next location. From this perspective, greater emphasis was placed on the upper percentiles, specifically the 95th percentile and the maximum distance, as these values capture the farthest households and therefore reflect the system most critical accessibility conditions. In this sense, a second elbow becomes apparent in 95th percentile at $p=12$. The value $p=12$ is particularly relevant, as it ensures that 95% of the population is served within a substantially reduced travel distance, improving accessibility for nearly all residents while maintaining feasible operational requirements. For this value of p, the model reports a minimum distance of 3.1 m, a first quartile (Q1) of 332.72 m, a median (Q2) of 499.73 m, a third quartile (Q3) of 673.65 m, a 95th-percentile distance of 1151.9 m, and a maximum distance of 2257.9 m. This ensures that at least 50% of the population can access humanitarian aid supply within 500 m, as recommended in [48]. The resulting network configuration is presented in Figure 5.

5.2. Multi-Criteria Approach

This section presents the results of the multi-criteria prioritization stage based on the SMART model. After the modular p-median optimization identified the feasible PODs, the SMART analysis was applied to rank these candidate facilities according to their relative urgency of activation, considering two main criteria: operational performance and vulnerability.

Table 3. Performance of operational score criterion.

Facility	Coverage	Distance COED	Distance Depot	Population	Operational Score
1	27.38%	3.77	3.33	3857	0.1774
4	47.12%	1.15	0.71	9997	0.6421
9	63.51%	0.89	0.52	12,994	0.8595
12	58.04%	0.81	1.28	8988	0.6973
15	67.68%	4.05	3.61	1999	0.4107
20	65.76%	3.12	2.68	6992	0.5857
22	46.44%	2.86	2.59	9741	0.5286
23	46.26%	2.43	1.99	11,994	0.6168
24	48.11%	0.64	0.96	12,887	0.7426
29	36.22%	5.34	4.90	6000	0.2114
30	46.62%	4.16	3.72	4281	0.3097
35	31.68%	5.98	5.54	4000	0.0866

provides a detailed summary of the performance of each attribute included in the operational criterion, together with the resulting operational score derived from Equation (12).

Table 4. Facility vulnerability metrics.

Fac.	Seismic Vuln.	Economic Vuln.	Children	Adolescents	Elderly	Disabilities	Vulnerability Score
1	1.36	4.05	852	365	392	359	0.3536
4	2.93	2.25	1774	848	1214	1060	0.5473
9	2.09	2.32	2419	1116	1526	1404	0.5628
12	2.14	2.90	1690	784	1015	938	0.4932
15	1.00	5.00	376	173	231	208	0.3500
20	1.06	3.20	1316	622	756	732	0.3225
22	1.64	3.00	1730	834	1253	1071	0.4717
23	1.65	3.24	2362	1062	1321	1235	0.5809
24	2.98	2.00	2202	1059	1857	1367	0.6275
29	1.12	4.63	1329	579	575	604	0.4737
30	1.29	4.34	951	412	371	379	0.3904
35	1.00	4.37	776	342	487	419	0.3484

presents a detailed summary of the performance of each attribute included in the vulnerability criterion, incorporating the calculations defined in Equations (13) and (14).

Finally,

Table 5. Prioritization of facilities based on Operation and Vulnerability metrics.

Priority	Facility	Op.	Vuln.	SMART
1	24: Parroquia Espíritu Santo	0.7426	0.6275	0.6620
2	9: Complejo Ramiro Prialé	0.8595	0.5628	0.6518
3	23: Parque Tripartito	0.6168	0.5809	0.5917
4	4: Complejo Deportivo Alto Selva Alegre	0.6421	0.5473	0.5758
5	12: Parque Cruce Chilina	0.6973	0.4932	0.5544
6	22: Parque Temático	0.5286	0.4717	0.4888
7	20: Parque Los Eucaliptos 2	0.5857	0.3225	0.4015
8	29: Cuna Más Villa Ecológica	0.2114	0.4737	0.3950
9	15: Parque El Huarangal	0.4107	0.3500	0.3682
10	30: Cancha El Mirador de Arequipa	0.3097	0.3904	0.3662
11	1: Balcones Canchita Chilina	0.1774	0.3536	0.3008
12	35: Losa Deportiva – Nueva Villa Ecológica Zona B	0.0866	0.3484	0.2699

presents the overall prioritization of the candidate facilities based on the operational score, the vulnerability score, and the combined SMART score computed using Equation (15). Since both the operational and vulnerability criteria include metrics that depend on population size and the presence of groups at risk, the resulting ranking tends to favor facilities located in areas with larger populations and in areas with higher concentrations of vulnerable residents.

The SMART results reveal three distinct priority clusters. The highest priority facilities are sites 24 and 9, with SMART scores of 0.6620 and 0.6518, respectively, reflecting a combination of strong operational performance and elevated vulnerability conditions that make early activation particularly impactful. A second priority cluster includes facilities 23, 4, 12, and 22, with scores ranging from 0.4888 to 0.5917; these locations exhibit balanced vulnerability levels and solid operational capacity, making them suitable for activation once the most urgent sites have been addressed. Finally, facilities 20, 29, 15, 30, 1, and 35 form the lowest priority cluster, with SMART values between 0.2699 and 0.4015, as their comparatively lower vulnerability metrics reduce the urgency of activation relative to the other sites.

Finally, a sensitivity analysis was conducted to examine how variations in the weighting scheme affect the SMART ranking. Figure 6a evaluates changes in the overall vulnerability weight, and Figure 6b focuses on changes in the weight assigned specifically to the vulnerable population component. In both figures, the red-dashed line marks the baseline weight used in the main analysis. The results show that the prioritization is highly sensitive to the weights selected: several facilities experience notable changes in their SMART values as the weights vary, and in many cases the relative ranking among facilities shifts considerably. This behavior reflects the strong influence that vulnerability and vulnerable population metrics exert on the final score, especially for facilities with intermediate baseline values. Consequently, the analysis confirms that decision-maker preferences regarding the importance of vulnerability criteria can meaningfully alter the activation order. Nevertheless, for weights equal to or greater than the selected baseline value, the previously priority clusters identified remain stable.

6. Conclusions

Mathematical optimization models are valuable tools for structuring humanitarian logistics problems and identifying efficient configurations for aid delivery. However, these models rely on simplified representations of reality, and their usefulness depends on finding an appropriate balance between analytical precision and interpretability. Each additional constraint or variable that introduces new dimensions increases computational complexity and reduces understanding among decision-makers. In practice, this can create a significant gap between model developers and those who must use the results, as decision-makers often require outputs that are not only accurate but also understandable and actionable. As a result, even well-designed models may be underutilized if they are perceived as inflexible, opaque, or disconnected from operational reality.

The results of this study show that mathematical optimization, albeit effective in defining spatially efficient configurations through the modular p-median formulation, is not sufficient to represent the full range of humanitarian priorities. Operational performance does not always coincide with vulnerability or perceived urgency after a disaster. For this reason, complementing the quantitative model with a multi-criteria approach, such as SMART, adds interpretive flexibility and strategic relevance. The multi-criteria stage makes it possible to include qualitative and contextual variables such as socioeconomic vulnerability and hazard exposure, which are difficult to represent as explicit constraints in a mathematical formulation.

This two-stage approach provides analytical rigor and decision transparency. The first stage ensures objective and reproducible allocation of resources according to spatial efficiency, while the second stage introduces a deliberative component that reflects vulnerability considerations and stakeholder perspectives. Efficiency is thus balanced with equity, and the results can be communicated more clearly to non-technical audiences. The explicit weighting of criteria and the use of normalized indicators contribute to transparency and allow the prioritization process to be reproduced and adapted in other contexts.

The methodological structure developed in this research is not exclusive to the case studied. The integration of a modular p-median model with a multi-criteria model can be applied to other problems that involve trade-offs between efficiency and equity, such as the location of health centers, vaccination hubs, evacuation shelters, or emergency supply depots. The same logic can also be adapted to different types of hazards and vulnerability indicators, maintaining quantitative coherence while preserving interpretability for decision-makers.

In summary, no single mathematical model can capture the full complexity of humanitarian logistics and disaster response. The value of this work lies in demonstrating that analytical precision and human judgment can be complementary. The integration of optimization and multi-criteria reasoning creates a more transparent, adaptable, and context-sensitive framework, capable of guiding humanitarian planners in prioritizing limited resources to achieve the greatest possible collective benefit.

The framework also has direct policy implications for municipalities and emergency management agencies. In this specific case, the relevant institution is the Subgerencia de Gestion de Riesgo de Desastres de la Municipalidad de Alto Selva Alegre (Disaster Risk Management Sub-Management), whose involvement is essential for guiding the decision process. By incorporating their participation in the selection of the best alternative, facilitating the exchange of information, and allowing them to express their preferences regarding the weights assigned to each attribute, the approach fosters stronger institutional engagement and enhances its potential for future implementation. Nevertheless, the frequent rotation of authorities may result in new personnel being unfamiliar with the model proposed, requiring additional calibration to reflect the preferences of incoming decision-makers.

This study presents several limitations that should be acknowledged. First, the availability of detailed block-level data constrained the analysis to earthquake scenarios, which limits the extent to which the model can be generalized to other types of hazards. Second, the applicability of the proposed framework to real emergency operations could not be evaluated, as no high-magnitude earthquake occurred during the study period that would allow for its practical implementation. Finally, frequent changes in local authorities can destabilize institutional priorities and preferences, thereby reducing the likelihood that the approach proposed will be consistently used during subsequent administrative periods.

Future work should advance the modeling in three main directions. First, as noted previously, complex models are rarely used by decision-makers; their usability could be enhanced through the development of flexible decision support systems that allow adjusting critical parameters according to stakeholder preferences. A multi-criteria approach remains highly relevant, as mathematical models increase substantially in complexity when multiple factors are incorporated, many of which can be more easily addressed through such an approach. Second, future research should explore the use of machine learning methods to obtain more accurate demand estimates for different disaster scenarios, allowing for more precise prioritization of the populations affected. Finally, the model should be expanded to include multiple disaster types, and its applicability to other geographic contexts should be examined by adapting it to locally available metrics and data conditions.