Abstract
Background: Over the past decade, the potential advantages of employing deep learning models and leveraging auxiliary data in data-driven end-to-end (E2E) frameworks to enhance inventory decision-making have gained recognition. However, current approaches predominantly rely on feed-forward networks, which may have difficulty capturing temporal correlations in time series data and identifying relevant features, resulting in less accurate predictions. Methods: Addressing this gap, we introduce novel E2E deep learning frameworks that combine Convolutional Neural Networks (CNN) and Long Short-Term Memory (LSTM) for resolving single-period inventory ordering decisions, also termed the Newsvendor Problem (NVP). This study investigates the performance drivers of hybrid CNN-LSTM architectures, coupled with an evolving algorithm for optimizing network configuration. Results: Empirical evaluation of real-world retail data demonstrates that our proposed models proficiently extract pertinent features and interpret sequential data characteristics, leading to more accurate and informed ordering decisions. Notably, results showcase substantial benefits, yielding up to an 85% reduction in costs compared to a univariate benchmark and up to 40% savings compared to a feed-forward E2E deep learning architecture. Conclusions: This confirms that, in practical scenarios, understanding the impact of features on demand empowers decision-makers to derive tailored, cost-effective ordering decisions for each store or product category.
1. Introduction
Companies have experienced a major shift from being operations-focused to becoming technology- and digitalization-oriented. In the operations management field, prescriptive analytics has become a noticeable hotspot of research that has been empowered by the latest developments in digital technologies with access to big data. Recent studies on the applications of data analytics in logistics and supply chain management confirmed the beginning of the big data era in operations management [1].
The conventional method to achieve ordering decisions, i.e., the model-based approach, assumes a known distribution for the demand. However, this approach does not conform to the current highly uncertain and rapidly fluctuating demand landscape. The surge in data availability and the rapid development of information gathering mechanisms have given rise to new data-driven methods, enabling more accurate and well-informed decisions. In this contribution, we focus on the development of data-driven approaches as prescriptive methods for achieving inventory ordering solutions, and we consider as data-driven the models in which the available data is the main interface adopted to achieve decisions [2].
The pivotal advantage of data-driven optimization over their traditional model-based counterparts lies in the use of high volume and good quality data to explore external factors, also called features, covariates, or contextual information, to identify patterns and relationships that affect demand, which is very useful to assortment planning and inventory management problems affected by frequent disruptions. The current challenge is how to best ponder this access to digitalization to optimize operational systems for better decisions and to discern the scenarios in which data-driven methods outperform conventional model-based approaches [3].
This study centers on the data-driven resolution of single-period inventory problems, commonly known as the Newsvendor Problem (NVP). These types of problems require precise decisions since they hinge on a delicate trade-off between ordering quantities for perishable goods and mismatching costs. If there is more demand than the predicted order quantity, stock-outs will occur, and customers will be unsatisfied. Conversely, if there are more products than the expected demand, the company must bear the overstocking costs.
Data-driven solutions for the NVP can be achieved by a two-step framework, also called separated estimation and optimization (SEO), that consists of first estimating the demand and then considering the overstocking and understocking costs in the subsequent optimization step. In this method, the prediction and the decision optimization problem are linked sequentially by two unrelated loss functions. This framework is more flexible since the loss function adopted is independent of the optimization problem. However, we have two separate optimization problems that are not congruent, which may lead to suboptimality [4]. Another way of achieving data-driven solutions is through a single-step framework, also named end-to-end approaches (E2E), which consists of a single optimization problem that integrates forecasting and optimization directly, considering the expected cost mismatch in inventory decisions. It has the strength of directly linking the features to a final decision. However, the framework must be tailored to a specific problem.
The existing body of research on data-driven E2E methods for the NVP is still in its infancy, with the prominent studies focusing on linear decision mapping for the ordering decisions, as in [5] with a linear programming approach and [6] with the development of a framework based on the Empirical Risk Minimization (ERM) principle. Additionally, machine and deep learning methods have proven to be powerful and flexible approaches to modeling single-step inventory problems, as shown in [7,8,9,10,11,12,13]. However, the studies that adopted neural networks as a data-driven solution for the NVP predominantly relied on Multi-Layer Perceptron (MLP) architectures. While effective in many contexts, MLP architectures may face challenges in accounting for the time correlation aspect of time series data, potentially leading to inventory decisions with lower accuracy and higher variance. Moreover, the adoption of evolving deep learning frameworks in the context of inventory optimization, especially those combining hybrid neural network architectures, remains understudied.
To address this gap, we turn to Long Short-Term Memory (LSTM) and Convolutional Neural Networks (CNN), which are better suited to model time series data that is attached to external features with different demand patterns across hundreds of products. These architectures have demonstrated promising results in passenger demand [14], finance [15], traffic prediction [16], price forecasting [17], e-commerce [18], and retail sales [19]. The challenge of efficiently modeling time series data with external features, however, remains understudied in the context of inventory optimization.
Furthermore, it remains an open question in which settings the data-driven approaches are more accurate and applicable than their model-based counterparts, and under what scenarios the single-step E2E solutions outperform the two-step methodologies. This study seeks to explore an operations research problem through the lens of integrating multiple features of information to reach solutions. For that, this contribution focuses on the development of evolving hybrid deep learning E2E solutions for the NVP. We delve into the performance drivers of hybrid CNN-LSTM architectures in conjunction with an evolving algorithm for determining the optimal neural network configuration.
Given the identified research gaps, this study aims to address the following research question: “Can evolving hybrid deep learning models, specifically the ones based in the CNN-LSTM architecture, effectively address the challenges of single-step inventory decision-making by efficiently utilizing time series data with external features and dynamically adapting network configurations?”.
To answer this question, we propose two hybrid deep neural network architectures based on CNN and LSTM that consider both temporal and external variables to reach the newsvendor decisions in a single E2E step. We design parallel (P-CNN-LSTM) and stacked (S-CNN-LSTM) architectures to make the best use of the data available in each module. In addition, our models adopt the principle of evolving networks by adopting a Grey Wolf Optimizer (GWO) algorithm to choose the best architecture configuration according to the input data and the cost settings. Our approaches were empirically tested on a dataset from a retail company and outperformed the model-based and data-driven benchmarks.
This work advances the literature in several key aspects: (1) It introduces a single-step E2E framework that automatically determines the best newsvendor order quantity for several products based on various demand characteristics. This is achieved through an innovative deep neural network design that captures the temporal sequence aspect of the time series and identifies the relevant external features and cross-product interactions that influence demand. (2) To the best of our knowledge, this is the first work in data-driven inventory optimization based on deep learning that adopts an evolving hybrid deep architecture for single-step newsvendor decisions, automatically configuring the best network based on the available data. (3) We study in which circumstances the data-driven approaches lead to better quality results when compared with the traditional model-based methods and explore the characteristics and performance drivers of the single and two-step methods to identify which is better replicable in a real-world setting and leads to better decisions. (4) Our E2E model streamlines the decision-making process for the supply chain industry, with potential applications extending beyond it as it adeptly generalizes various demand patterns and replenishment strategies.
The remainder of the paper is organized as follows: the related literature is detailed in Section 2. In Section 3, we introduce the deep neural network foundations that support the deployment of the proposed methods. Additionally, the big data-driven single-period inventory model is described, and details about the evolving CNN-LSTM architectures are presented. Section 4 evaluates the empirical results for the case study and compares them with a set of benchmark models. Lastly, the conclusions, managerial implications, and future research directions are highlighted in Section 5.
2. Related Literature
Single-period inventory problems are traditionally solved by assuming that the demand follows a specific probability distribution [20], which is unlikely to happen in realistic scenarios that have multiple products with complex time dependencies and external information attached to the demand data. Therefore, there are two large groups of approaches to solving inventory problems with unknown demand distribution: the parametric and nonparametric approaches [21].
In the first group, the Bayesian approach corresponds to the earliest solutions that were developed [22], which assumes that the unknown demand belongs to a parametric distribution family to reach the newsvendor solution in two separate steps for parameter estimation and inventory optimization. Operational statistics is another parametric approach that was designed to perform demand estimation and optimization simultaneously, as in previous literature [4,23,24,25]. The assumption that the decision-maker knows which distributional family the demand belongs to is still a limitation of this method.
Our focus is on the nonparametric approaches since they require no demand distribution assumptions and rely only on empirical information to achieve solutions. They are also referred to in the literature as data-driven. This study follows the big data terminology adopted in [6] that classifies multi-variate data-driven methods as big data, meaning that exogenous variables are directly considered in the decision model. Conversely, univariate data-driven methods only take into account the product demand information itself. In real-world scenarios, demand data is often dependable for a set of features, highlighting the need to evaluate if data-driven models based on feature data indeed improve accuracy in decision-making.
In the group of data-driven approaches that do not consider external information, Sample Average Approximation (SAA) is a method that replaces the demand assumptions with empirical data and was first studied to solve the NVP by [26]. Ref. [27] extends this by proposing a tighter bound on the probability that the regret exceeds a threshold.
In the group of data-driven approaches that do consider external information, there is a recent research stream that focuses on adopting machine learning (ML)-based methods to determine ordering policies in the NVP, where the policy that maps the feature space to the decision space can be treated as a hypothesis to be learned through a learning algorithm following the Empirical Risk Minimization (ERM) principle [28].
Following this line of work, ref. [5] designed the optimal inventory levels in the first study that proposed an integrated single-step procedure as the decision variables of linear programming. Ref. [29] extended this approach by studying censored demand and price-dependent scenarios. Ref. [6] proposed a linear hypothesis for the feature map based on the ERM with regularization and derived sample performance bounds for the out-of-sample costs.
Ref. [8] built a Multi-Layer Perceptron (MLP) neural network solution for the multi-feature NVP. The authors highlighted that the NVP-integrated solution is equivalent to quantile regression (QR). Ref. [10] presented a similar MLP architecture solution for the multi-feature NVP and a heuristic to solve a multi-item NVP with a capacity constraint. Ref. [30] proposed a double parallel feed-forward network as a single-step method for quantile forecasting and tested their model to solve the NVP.
Ref. [9] developed a multi-step local regression method based on a few ML methods and proposed a coefficient of prescriptiveness to measure the efficacy of an operations policy. Ref. [12] reproduced a kernel Hilbert space to propose a global ML method to predict the objective and optimizer.
Ref. [11] developed an end-to-end solution for the multi-item NVP by transforming the traditional NVP formulation into a loss function for a deep learning approach. The MLP-based model indeed outperformed other ML approaches, even with a small number of data points or high fluctuations in demand, which was a significant limitation in [8].
Ref. [7] also studied the NVP loss function for an end-to-end deep learning solution based on MLP. They highlighted the need to study how product demand relates to each other and how these relations evolve over time, characteristics that might be ignored due to the nature of MLP architectures that overlook the sequence aspect of time series data or have difficulty identifying and filtering relevant external information attached to the data. We intend to address this issue by proposing neural network architectures that are designed to simultaneously consider the time aspect of the data and capture the relevant features across different products and stores.
Recently, ref. [13] proposed an algorithm integrating neural networks and hidden Markov models to solve the data-driven NVP. Lastly, ref. [31] extended the [6] method to the non-linear case by maximizing the profit instead of minimizing the expected cost and conducted experiments with ARIMA models. Figure 1 presents an overview of the literature that was discussed in this section to correlate the mentioned studies and position our contribution.
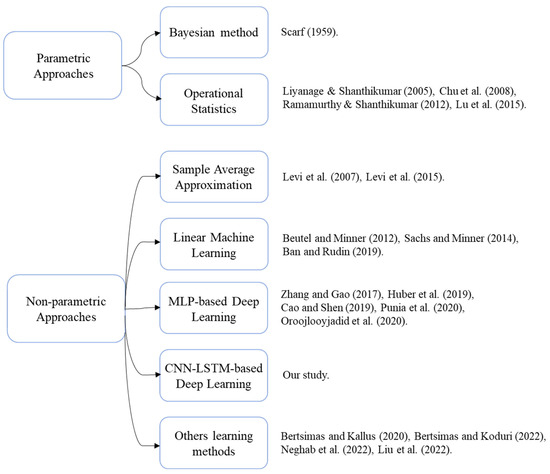
Figure 1.
Position of the proposed methods in the data-driven NVP inventory literature [4,5,6,7,8,9,10,11,12,13,22,23,24,25,26,27,29,30,31].
3. Methodology
The details of the big data-driven NVP are presented in Section 3.1; a brief explanation of deep neural networks is introduced in Section 3.2; and the proposed approaches are exhibited in Section 3.3.
3.1. Problem Description
Single-period inventory problems are designed to achieve ordering decisions for goods that have a limited selling season, such as dairy products, fashion and technology goods, newspapers, and airline tickets. The decision-maker purchases the goods at the beginning of the selling season and assumes that they will all be sold during this specific time window. A cost of overage per unit is incurred at the end of the selling season if there are excess goods remaining. On the other hand, a cost of underage per unit occurs if there is a stock-out of the product and the demand cannot be completely fulfilled. Therefore, the company aims to achieve ordering decisions that will minimize the expected sum of these costs, known as the mismatch cost. Readers are referred to [20,32] for further details. The optimal order quantity is obtained by solving an optimization problem where is the random demand, is the order quantity, and are the holding and stock-out costs per unit, respectively, and . This optimization problem is formulated in Equation (1).
It is well known that the solution for newsvendor-like problems is given by a particular quantile of the cumulative demand distribution, where is the optimal service level represented in Equation (2).
In traditional solutions to this problem, the demand distribution and its parameters are assumed to be known, but this approach does not reflect realistic, complex scenarios. This contribution studies the big data-driven NVP, meaning that no demand distribution assumptions are made and the data is attached to external features as represented below. There are historical observations about products with features, where and for and .
Therefore, in this paper, we train our proposed deep neural network models with a modified loss function that directly considers the operational costs of reaching inventory decisions in a single step, without demand distribution assumptions or the need to perform the point forecast estimation and inventory optimization steps separately. In the training phase, the demand observations () and their related features () are adopted to calculate the NVP costs and update the weights in the network in a direction to minimize the average costs. The modified loss function is expressed in Equation (3).
is the loss value of the -th observation, that minimizes the cost of the ordering quantities . Given that at least one of the two terms in the loss function must be zero, it can be rewritten as in Equation (4).
The order quantity is optimized in the training process based on the weights of the neural network being updated iteratively following the loss function that directly considers the trade-off between underage and overage costs instead of only predicting the demand as in the SEO method that first performs the forecasting step to then solve an optimization problem in the second step with two unrelated loss functions.
3.2. Deep Neural Networks
The proposed end-to-end inventory decision model consists of two main components: the hybrid CNN-LSTM network and the GWO method. CNNs were developed to identify and extract the most relevant features and correlations that impact the model outputs. For that, the convolution operation is responsible for detecting the feature maps by sliding filters over the input data [33]. The convolution kernels are then responsible for the matrix multiplications, and the selected feature maps are aggregated and compressed in the pooling layer. Each convolutional layer is responsible for extracting 1-D convolutional features from the time series of a product.
LSTM, which is a recurrent network variation, was developed to interpret long-term temporal dependencies. It is based on the principle of a gradient calculation structure that is updated at every step of the training process, which reduces the probability of vanishing [34]. This type of architecture is controlled by memory cells in the hidden layers that monitor the flow of information with three gates: forget, input, and output. The weights of the connections during the training process determine the operation of these gates [35]. These characteristics in the training process enable LSTM to learn long-term dependencies and effectively model sequences [36], making it the best suited for complex time series forecasting problems with external data. For comprehensive reviews of deep learning architectures, we refer readers to [37].
GWO is adopted to reduce the time-consuming and computationally expensive activity of manually engineering the parameters of the proposed neural network architectures for each cost combination and target service level. This technique is based on evolutionary algorithms to optimize the network configuration used to predict ordering decisions. GWO explores the parameter space of the hybrid CNN-LSTM architectures to determine the best configuration for each problem circumstance. GWO is a swarm intelligence algorithm proposed by [38] that acts based on the idea of social hierarchies and hunting habits of grey wolves. We refer the readers to [38] for the formulations and further technical details about GWO that are beyond the scope of this paper. This work is the first to adopt GWO as a search algorithm for the CNN-LSTM architecture in the context of inventory problem optimization.
3.3. The Proposed Evolving CNN-LSTM Models
In the proposed models, the CNN is combined with LSTM to construct accurate feature map representations while preserving the temporal aspects embedded in the time series data and removing irrelevant or redundant variations. A fully connected layer is adopted subsequently for the nonlinear transformations on the extracted features to produce the outcomes. In addition, an evolving process based on GWO is adopted to establish the optimal configurations of the hybrid network, i.e., the number of hidden nodes and kernel size. Then, the optimized CNN-LSTM chosen for a specific target service level is adopted to produce the ordering decisions.
We begin by determining two base architectures for the hybrid CNN-LSTM models that later will have their parameter configuration tailored by the GWO algorithm. The first one is a parallel organization of the layers, which separates the CNN and LSTM as two different pipelines that are concatenated at the end of the process to reach the outputs. The second architecture is stacked, with both pipelines being organized sequentially. Figure 2 and Figure 3 represent the parallel and stacked architectures, respectively.
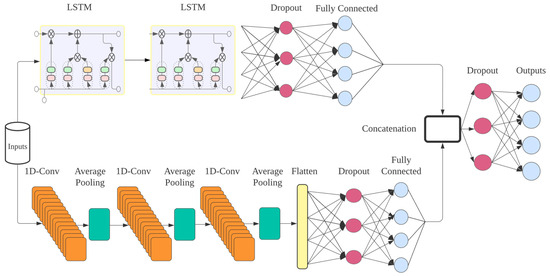
Figure 2.
Representation of the Parallel CNN-LSTM.

Figure 3.
Representation of the Stacked CNN-LSTM.
In the recurrent module of both architectures, two LSTM layers are followed by a dropout and a fully connected layer. Dropout [39] is a strategy adopted at the end of each module to prevent overfitting during training by removing a few units that will assist the model generalize better. In the convolutional module, there are three 1D convolutional layers that are followed by average pooling layers with padding. The selected feature maps are then flattened and applied to a dropout layer, followed by a fully connected layer. In the parallel architecture, the outputs of both modules are united by a concatenation layer to produce the final predictions.
Two different architectures are proposed to evaluate whether the parallel model makes better use of the data available in each pipeline when compared with the conventional stacking of layers. Ref. [16] empirically demonstrated that a parallel CNN-LSTM architecture outperforms its stacked counterpart in a model for metro ridership prediction. Since the research on hybrid deep learning approaches for inventory decisions is still in an early stage, we constructed a parallel model to evaluate its performance for the end-to-end NVP solution with a multi-feature time series dataset.
In stacked architectures, when adopting the strategy to begin the model with CNN layers to feed the LSTM with the selected features, such as in [40,41], we cannot ensure that both models are aligned, and relevant data for the LSTM might be discarded during the CNN process since their outputs may not represent the original temporal sequence from the time series. In other words, the focus of the CNN is to reduce the data dimensionality by choosing the most relevant features, which may impact the feature-temporal information in sequential types of data. Therefore, for the stacked architecture, we begin the model with two LSTM layers to then feed the CNN.
In comparison with pure deep learning architectures, our proposed hybrid architecture presents a more complex interaction between hyperparameters of the CNN and LSTM modules, therefore requiring a careful choice for the network structure that is automatically performed by the GWO algorithm. There is a range of hyperparameters that can be tuned by search algorithms, e.g., learning rate, dropout rate, pooling size, number of hidden nodes and filters in each layer, filter size, etc. However, the larger the number of parameters and their search range, the longer the training of the neural network. The decision-maker needs to consider this trade-off when building the models, since a search algorithm with too many parameters to be decided can become very computationally expensive, time-consuming, and infeasible for decision systems with hundreds or thousands of products.
The goal of this study is to propose a robust method that can be replicated in complex real-world settings. Therefore, we opt for adopting GWO to choose the best structure defined by the number of hidden nodes in each layer and kernel size, which will simplify the search process and reduce the training time while producing a network with very good results. Figure 4 depicts the overall ordering decision process.
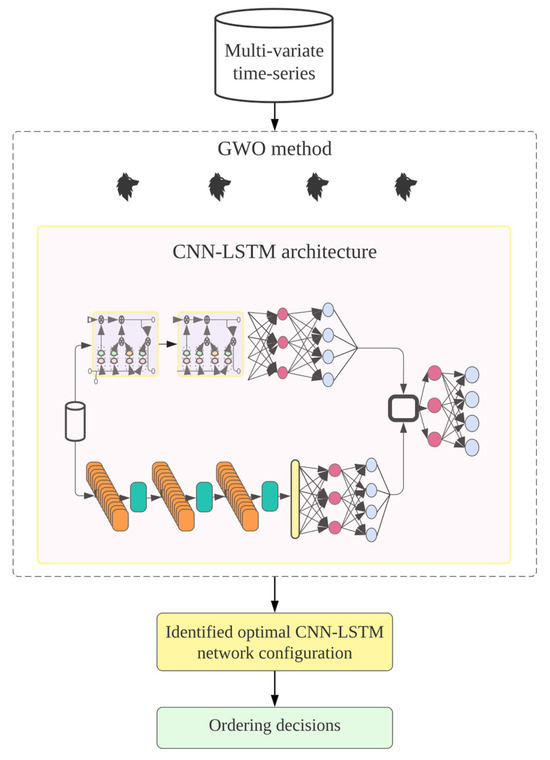
Figure 4.
Overview of the GWO-based CNN-LSTM model for inventory decisions.
The parameter search for the CNN-LSTM model occurs as follows: The GWO population is randomly initialized, with each individual (wolf) representing a possible configuration for the CNN-LSTM model. Each of these models is trained using the training dataset. With the validation set, the decision mismatch cost is computed by adopting the newsvendor loss function that directly considers the cost of underage and overage for the ordering quantity calculation. The three best-scoring solutions are employed to guide the wolf population toward global optimality. The optimal network configuration obtained is the final CNN-LSTM model. Lastly, the model is trained again, adopting the training and validation sets to be evaluated with the test set. The pseudo-code for the GWO-based CNN-LSTM model is detailed below in Algorithm 1. Section 4 empirically studies the performance of the parallel and stacked architectures tailored by GWO and compares them with benchmarks.
| Algorithm 1: GWO-based CNN-LSTM Training |
| Input: Train and validation datasets containing product sales information and external features with their respective labels |
| Output: Optimized model to be used for predicting ordering decisions |
| Initialization |
| 1: Start a grey wolf population with a specific CNN-LSTM structure being represented by each individual. |
| 2: Given training, validation, and test sets |
| 3: for each wolf in the population do |
| 4: decode into a CNN-LSTM model |
| 5: train the network with the training set |
| 6: evaluate the model’s performance based on the mismatch cost with the validation set |
| 7: end for |
| 8: Identify the three leader wolves () with the best performance |
| 9: while do |
| 10: evolve the wolf population following the mechanism described in lines 3–7 |
| 11: end while |
| 12: Output the solution with the best result () |
| 13: Decode () into its corresponding CNN-LSTM model |
| 14: Train the optimized network with the training and validation sets |
| 15: Evaluate the network with the test set |
| 16: Output the results |
| 17: end |
4. Experimental Design and Discussion of Results
In this section, the performance of the proposed hybrid GWO-based CNN-LSTM models is tested using a real-world retail dataset from the Kaggle platform [42]. Section 4.1 details the dataset used and its preparation. Section 4.2 describes the benchmarks that are adopted for comparison. Section 4.3 details the experimental setup for training the CNN-LSTM models and the different benchmarks. Section 4.4 presents the results and managerial implications.
4.1. Dataset Overview and Preparation
The public dataset was acquired from the Kaggle online platform, and it corresponds to daily point-of-sale information for 500 hundred products divided into 10 retail stores over a period between 2013 and 2017, comprising of 1826 data points for 500 time series. Figure 5 illustrates the point-of-sale data of product 1 from store 1 over one year to reflect the nature of the dataset.
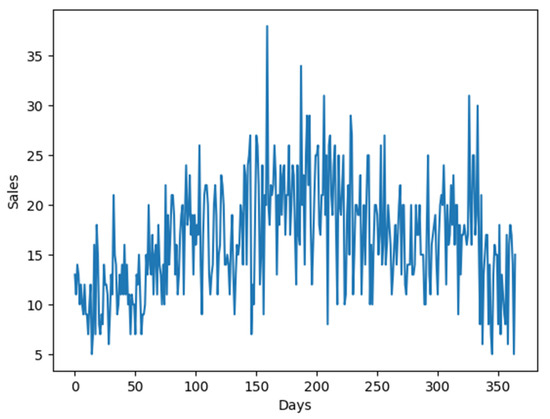
Figure 5.
Sales of product 1 in store 1 over a year.
The focus of this study is to evaluate the performance of the proposed hybrid architectures in a big data environment, which means that the data is attached to external features that may impact the learning process. Therefore, the dataset is enriched with categorical features in a one-hot-encoding format (each category is indicated by a binary variable) representing the day of the week, month of the year, and United States of America holiday calendar. In addition, the sales information is regrouped in such a way that the product information is combined per day, which will enable the model to evaluate if the daily sales have a relationship between products and stores. After, the dataset is divided into training, validation, and test sets and scaled to a 0 to 1 range, which will assist the models in deriving better results and reducing the training period.
4.2. Benchmark Methods
In addition to implementing our end-to-end deep learning models (P-CNN-LSTM and S-CNN-LSTM), several benchmarks are implemented for comparing the performance, as described next.
A key contribution of this paper is to study whether the integrated approaches are superior and better replicable than the traditional separated estimation and optimization (SEO) methods. In addition, we want to evaluate whether data-driven methods are indeed superior to their model-based counterparts. Therefore, to provide a fair analysis of the proposed integrated CNN-LSTM methods, we compare two variations of SEO methods: model-based and data-driven. In the model-based SEO method, once the point forecast is estimated with one of the CNN-LSTM architectures, we assume a normally distributed error distribution and solve the order quantity by estimating a specific quantile of the distribution. Consider as the mean forecast based on features, with and as the estimated parameters of the error distribution (.). The order quantity is calculated following Equation (5):
For data-driven SEO, once the point forecast is estimated with one of the CNN-LSTM architectures, the error distribution is determined by empirical forecast errors instead of assumptions. The newsvendor order quantity becomes as in Equation (6).
Another contribution of this study is to compare the hybrid CNN-LSTM architectures with the MLP architectures adopted in studies for end-to-end inventory decisions. In this aspect, a deep neural network MLP model similar to the ones proposed by [7,11] is adopted. We evaluate this architecture for the integrated method (MLP-E2E) and for both model-based (MLP-Normal) and data-driven (MLP-Empirical) SEO methods.
Moreover, we adopt a Naïve approach based on demand forecasting with Lasso regression to make demand predictions and directly adopt them as order quantities without considering the underage and overage costs to reach the decisions. This baseline method is valuable to analyze the effects of not considering demand uncertainty on inventory decision costs. Lastly, the Sample Average Approximation (SAA) proposed by [26] is implemented to evaluate the effects of not considering data features on big data-driven inventory problems.
4.3. Experimental Setup
The data preparation and deployment of the proposed models are executed in Python, adopting the Keras Framework [36] with a TensorFlow backend [43]. The neural network weights are optimized using Adaptive Moment Estimation-based algorithm (ADAM) [44] on an AMD Ryzen R5-3600 CPU at 3.6 GHz and 32 GB of RAM with an Nvidia RTX2060 GPU. The deep learning benchmarking models are also implemented with Keras. The Naïve and SAA methods are executed in Python, and the latter is solved with Gurobi Optimizer [45].
The main structure and the training procedure for the GWO-based CNN-LSTM models are explained with further details in Section 3. For the integrated end-to-end methods, the newsvendor loss function is adopted for training, as in Equation (3). In the separated estimation and optimization methods, the demand estimation models are trained adopting Mean Squared Error as the loss function, and the following NVP is solved either assuming a normal distribution or adopting the empirical error distribution as in Equations (5) and (6), respectively.
Once the dataset is prepared and the architectures’ main structure is defined, it is time to establish the hyperparameters. As mentioned in Section 3, the GWO algorithm was adopted to determine the best configuration in terms of the layer and kernel size, but other parameters are manually pre-determined with the aim of reducing the search space in the algorithm and training time. The values of dropout, batch size, learning rate, and weight initialization are strategically chosen for the models to generalize well and converge quickly. Table 1 describes the hypermeters and their range values considered. Table 2 details the search parameters in the GWO algorithm for the network structure.

Table 1.
Hyperparameters considered.

Table 2.
Search range for the GWO algorithm.
4.4. Empirical Results and Performance Analysis
To verify the robustness of our approach among different cost combinations, the experiments are conducted with different pairs of underage and overage costa that reflect a specific service level. Underage cost is assumed to be higher than overage cost in most of the settings to reflect real applications in which the opportunity cost and customer satisfaction are more valuable than the waste value. Table 3 displays the monthly average mismatch cost, reflecting the ordering decisions of the 500 products. The results are also displayed compared to the best-performing method for each and combination.

Table 3.
Inventory performance analysis.
The results show that the proposed end-to-end model based on the parallel architecture (P-CNN-LSTM-E2E) outperforms the other models for every and combination, with an average monthly mismatch cost of 5.09, 7.14, 18.49, and 14.56. The other proposed end-to-end model based on the stacked architecture (S-CNN-LSTM-E2E) does not perform as well, especially in circumstances with lower cost combinations, but still outperforms the MLP, SAA, and Naïve approaches. These outcomes corroborate the results in [16] that parallel neural network architectures are better suited to the problems in which the data corresponds to time series attached to external information. With a parallel model, there is no loss of information, and the CNN and LSTM modules run independently before being concatenated to provide the outputs, which in our application is fundamental to effectively interpreting the sequential aspect and possible correlations among products and stores. Additionally, these results confirm that MLP neural network architectures, as adopted in [7,8,10,11], underperform for problems that adopt time series data enriched with data features to solve the inventory problem.
The GWO-based CNN-LSTM architectures outperform the MLP architectures in most of the scenarios, confirming that it is outstanding to employ an appropriate deep learning architecture according to the type of data in consideration. In addition, the adoption of GWO is paramount to automatically choosing the best network configuration for each cost combination. Merging CNN and LSTM and empowering with GWO is ideal for this type of application with time series with external features.
Figure 6 illustrates the average cost of the decisions adopting the (2,1) combination of and . To facilitate understanding, the products in the picture are sorted by their respective decision costs. Figure 7 illustrates the order quantity decisions for the month and compares them with the real demand.
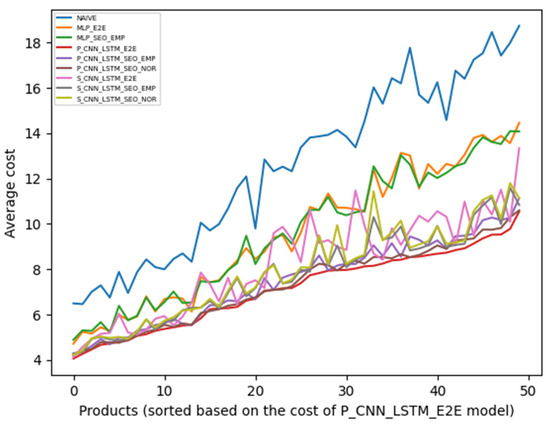
Figure 6.
Inventory decision average cost for (2,1).
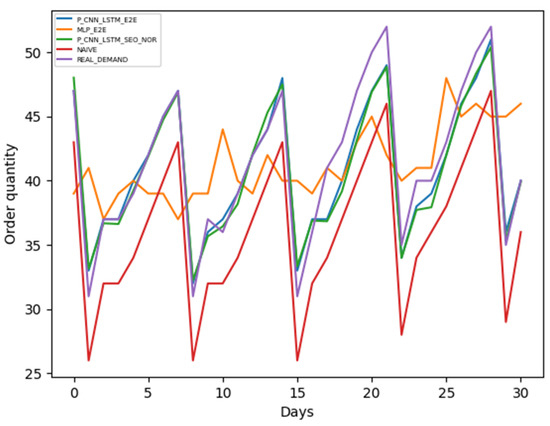
Figure 7.
Order quantity decisions for (2,1).
The Naïve results attest to the importance of considering underage and overage costs in inventory decisions since they only consider the point forecast to achieve the ordering decisions. Since this method tries to predict the mean of the data, it does not adapt well on days with large spikes in demand. The experiments with the (8,2) and (20,1) combinations of Cu and Co confirm this, given that when we heavily penalize stockouts, the decision cost becomes more than 300% higher than the proposed methods.
The largest benefit of end-to-end methods is that they directly achieve the solutions, which is a considerable advantage in settings with hundreds or thousands of products that require daily inventory decisions. In the SEO method, these two steps are performed separately, which may be time-consuming and computationally expensive in realistic applications. Corroborating the key takeaways in [11] about the better performance of integrated single-step inventory decisions, it can be observed that the strength of the proposed integrated approach comes from its end-to-end nature and not only due to the better performance of the deep learning architectures, given that all the variations of SEO adopting the CNN-LSTM architectures still cannot perform as well as the end-to-end approach.
The SEO methods show a very similar performance between assuming normally distributed errors or adopting the empirical error distribution. This is mainly due to the performance of the neural network architectures in the forecasting method. It can be noticed that when MLP architectures are used to forecast demand and input in the optimization problem, the MLP-Normal results are worse than the MLP-Empirical. For the cases where CNN-LSTM architectures are adopted as the forecast method, the outputs of the optimization problem are very similar, corroborating the findings in [6,8] that in SEO approaches, the forecasting method is the most relevant instrument that impacts the accuracy of the ordering decisions.
The effects of not considering data features in the decisions are also analyzed by executing the SAA method, as in [26]. This approach underperforms all the other data-driven methods, showing the importance of considering external information in decisions. If a company has access to multiple features, it is advisable to base the solutions on the full information available by adopting big data-driven models. Even simpler methods, such as MLP-Empirical, will result in an increase in prediction accuracy from the introduction of features in the analysis. In realistic scenarios, the supply chain manager of this retail chain may benefit from knowing how the features impact demand and derive tailored ordering decisions for each store or product category. Figure 8 brings insights about how each feature may impact the results in our case study, with the average order quantity being displayed in terms of each product in a store, per day of the week, and per store.
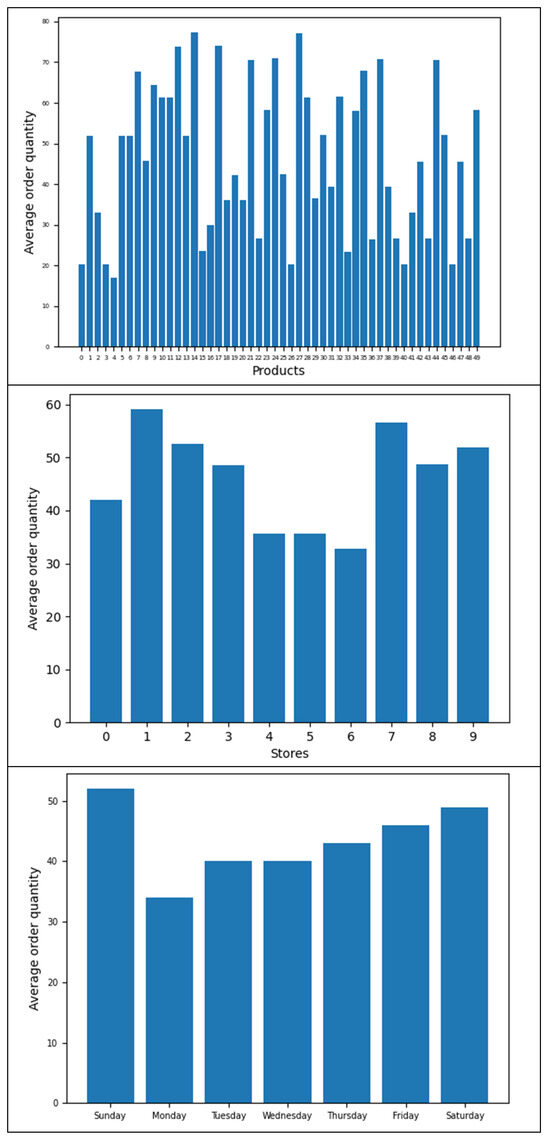
Figure 8.
The effects of different features in the order quantities for (8,2).
Lastly, we execute a Naïve method that adopts the point forecast as the ordering decision, ignoring the mismatch costs and demand uncertainty for the inventory solutions and, as expected, providing the worst results. This approach is still largely adopted in real-world settings due to its simplicity or the lack of data availability, computational power, or domain knowledge of the decision-maker. It is important to emphasize that although the proposed end-to-end methods indeed bring the best outcomes in all the circumstances studied, it is advisable to choose an appropriate data-driven model for a specific problem. For instance, if the main objective is to only estimate the relationship between the dependent variables and their features, simple neural networks can produce satisfactory outcomes. However, to solve a big data-driven operations research problem in which mismatch costs are also considered, it is required to use more complex models than the ones proposed in this study.
5. Conclusions
This contribution studied the different aspects of data-driven approaches to inventory decisions. In particular, evolving hybrid deep learning architectures were proposed as an end-to-end solution for the newsvendor problem. The results showed that indeed the GWO-based CNN-LSTM architectures, especially the parallel variation, outperform the other benchmarking methods, with up to an 85% reduction in costs compared to a univariate benchmark and up to 40% savings in contrast to an alternative end-to-end deep learning architecture.
The largest advantage of single-step models relies on the possibility of achieving inventory decisions directly from the available data, which is very useful in realistic scenarios with a large number of products that need to be simultaneously evaluated on a daily basis. The proposed single-step models reduce the complexity of manually tuning the neural network for each combination of product features, which is a limitation for decision-makers who do not pursue the required expertise or have to deal with hundreds or thousands of products together.
In addition, the use of GWO to automatically choose the best network configuration for each set of cost coefficients is another considerable benefit of the proposed approaches. The experimental results confirmed that it is outstanding to employ an appropriate deep learning architecture according to the type of data in consideration.
Our empirical results reiterate that if a company has access to data with multiple external features, it is advisable to base the solutions on the full information available by adopting big data-driven models. Even simpler neural network benchmark methods demonstrated an increase in prediction accuracy consequential to the introduction of features in the analysis. In realistic scenarios, the decision-maker may benefit from knowing how the features impact demand and design ordering decisions for each store or product category.
This contribution presents the natural limitation existing in neural networks of relying on data quality and availability. In cases where the organization does not have access to clean and complete datasets to train the models, their prediction performance might be affected. In addition, the methods executed in this study assumed a certain stability of external factors, such as consumer behavior and possible product substitution, and therefore variations in these factors that were not explicitly considered may influence the accuracy of the predictions. Lastly, this study concentrated on the single-period inventory problem. The performance of the proposed models in multi-period scenarios, which introduce additional temporal complexities, was not considered.
Therefore, an interesting extension to this study is to apply the GWO-based CNN-LSTM architectures to multi-period inventory problems. For that, a new loss function considering the inventory levels at the time of the decision needs to be developed. Another research direction would be to analyze the effects of product substitution on inventory decisions, adopting the proposed architectures as a learning framework. Lastly, since the case study is based on a retail dataset, it would be valuable to analyze the scalability of the proposed approaches for other supply chain problems with substantially different demand patterns or inventory management dynamics.
Author Contributions
Conceptualization, T.d.C.M.; Methodology, T.d.C.M.; Software, J.Q.; Validation, T.d.C.M.; Formal analysis, T.d.C.M.; Investigation, T.d.C.M.; Resources, T.d.C.M.; Data curation, T.d.C.M.; Writing—original draft, T.d.C.M.; Writing—review & editing, T.d.C.M. and X.-M.Y.; Visualization, T.d.C.M.; Supervision, X.-M.Y. and E.P.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Agency for Science, Technology and Research (A*STAR), under the SINGA Award.
Data Availability Statement
The data supporting the findings of this study are available in “Store Item Demand Forecasting Challenge” at [https://www.kaggle.com/competitions/demand-forecasting-kernels-only/data (accessed on 1 August 2021)].
Conflicts of Interest
The authors declare no conflict of interest.
References
- Maheshwari, S.; Gautam, P.; Jaggi, C.K. Role of Big Data Analytics in supply chain management: Current trends and future perspectives. Int. J. Prod. Res. 2021, 59, 1875–1900. [Google Scholar] [CrossRef]
- Erkip, N.K. Can accessing much data reshape the theory? Inventory theory under the challenge of data-driven systems. Eur. J. Oper. Res. 2023, 308, 949–959. [Google Scholar] [CrossRef]
- Clausen, J.B.B.; Li, H. Big data driven order-up-to level model: Application of machine learning. Comput. Oper. Res. 2022, 139, 105641. [Google Scholar] [CrossRef]
- Liyanage, L.H.; Shanthikumar, J.G. A practical inventory control policy using operational statistics. Oper. Res. Lett. 2005, 33, 341–348. [Google Scholar] [CrossRef]
- Beutel, A.-L.; Minner, S. Safety stock planning under causal demand forecasting. Int. J. Prod. Econ. 2012, 140, 637–645. [Google Scholar] [CrossRef]
- Ban, G.-Y.; Rudin, C. The Big Data Newsvendor: Practical Insights from Machine Learning. Oper. Res. 2019, 67, 90–108. [Google Scholar] [CrossRef]
- Zhang, Y.; Gao, J. Assessing the Performance of Deep Learning Algorithms for Newsvendor Problem. arXiv 2017, arXiv:1706.02899. Available online: https://www.proquest.com/publiccontent/docview/2075892090?parentSessionId=ovw5Sq5uahrO%2F2s479pwebNMZesJgwlhZSnj%2FrOC3V0%3D&pq-origsite=summon& (accessed on 27 June 2023).
- Huber, J.; Müller, S.; Fleischmann, M.; Stuckenschmidt, H. A data-driven newsvendor problem: From data to decision. Eur. J. Oper. Res. 2019, 278, 904–915. [Google Scholar] [CrossRef]
- Bertsimas, D.; Kallus, N. From Predictive to Prescriptive Analytics. Manag. Sci. 2020, 66, 1025–1044. [Google Scholar] [CrossRef]
- Punia, S.; Nikolopoulos, K.; Singh, S.P.; Madaan, J.K.; Litsiou, K. Deep learning with long short-term memory networks and random forests for demand forecasting in multi-channel retail. Int. J. Prod. Res. 2020, 58, 4964–4979. [Google Scholar] [CrossRef]
- Oroojlooyjadid, A.; Snyder, L.V.; Takáč, M. Applying deep learning to the newsvendor problem. IISE Trans. 2020, 52, 444–463. [Google Scholar] [CrossRef]
- Bertsimas, D.; Koduri, N. Data-Driven Optimization: A Reproducing Kernel Hilbert Space Approach. Oper. Res. 2022, 70, 454–471. [Google Scholar] [CrossRef]
- Neghab, D.P.; Khayyati, S.; Karaesmen, F. An integrated data-driven method using deep learning for a newsvendor problem with unobservable features. Eur. J. Oper. Res. 2022, 302, 482–496. [Google Scholar] [CrossRef]
- Ke, J.; Zheng, H.; Yang, H.; Chen, X. Short-term forecasting of passenger demand under on-demand ride services: A spatio-temporal deep learning approach. Transp. Res. Part C Emerg. Technol. 2017, 85, 591–608. [Google Scholar] [CrossRef]
- Fischer, T.; Krauss, C. Deep learning with long short-term memory networks for financial market predictions. Eur. J. Oper. Res. 2018, 270, 654–669. [Google Scholar] [CrossRef]
- Ma, X.; Zhang, J.; Du, B.; Ding, C.; Sun, L. Parallel Architecture of Convolutional Bi-Directional LSTM Neural Networks for Network-Wide Metro Ridership Prediction. IEEE Trans. Intell. Transp. Syst. 2019, 20, 2278–2288. [Google Scholar] [CrossRef]
- Livieris, I.E.; Pintelas, E.; Pintelas, P. A CNN–LSTM model for gold price time-series forecasting. Neural Comput. Appl. 2020, 32, 17351–17360. [Google Scholar] [CrossRef]
- Shao, S.; Xu, G.; Li, M.; Huang, G.Q. Synchronizing e-commerce city logistics with sliding time windows. Transp. Res. Part E Logist. Transp. Rev. 2019, 123, 17–28. [Google Scholar] [CrossRef]
- Ma, S.; Fildes, R. Retail sales forecasting with meta-learning. Eur. J. Oper. Res. 2021, 288, 111–128. [Google Scholar] [CrossRef]
- Zipkin, P.H. Foundations of inventory management. In Irwin Series in Quantitative Analysis for Business; McGraw-Hill: Boston, MA, USA, 2000. [Google Scholar]
- Moraes, T.C.; Yuan, X.-M. Data-Driven Solutions for the Newsvendor Problem: A Systematic Literature Review. In Advances in Production Management Systems, Artificial Intelligence for Sustainable and Resilient Production Systems; IFIP Advances in Information and Communication Technology, Nantes, France, 2021; Dolgui, A., Bernard, A., Lemoine, D., von Cieminski, G., Romero, D., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 149–158. [Google Scholar] [CrossRef]
- Scarf, H. Bayes Solutions of the Statistical Inventory Problem. Ann. Math. Stat. 1959, 30, 490–508. [Google Scholar] [CrossRef]
- Chu, L.Y.; Shanthikumar, J.G.; Shen, Z.-J.M. Solving operational statistics via a Bayesian analysis. Oper. Res. Lett. 2008, 36, 110–116. [Google Scholar] [CrossRef]
- Ramamurthy, V.; Shanthikumar, J.G.; Shen, Z.-J.M. Inventory Policy with Parametric Demand: Operational Statistics, Linear Correction, and Regression. Prod. Oper. Manag. 2012, 21, 291–308. [Google Scholar] [CrossRef]
- Lu, M.; Shanthikumar, J.G.; Shen, Z.-J.M. Technical note–operational statistics: Properties and the risk-averse case. Nav. Res. Logist. NRL 2015, 62, 206–214. [Google Scholar] [CrossRef]
- Levi, R.; Roundy, R.O.; Shmoys, D.B. Provably Near-Optimal Sampling-Based Policies for Stochastic Inventory Control Models. Math. Oper. Res. 2007, 32, 821–839. [Google Scholar] [CrossRef]
- Levi, R.; Perakis, G.; Uichanco, J. The Data-Driven Newsvendor Problem: New Bounds and Insights. Oper. Res. 2015, 63, 1294–1306. [Google Scholar] [CrossRef]
- Qi, M.; Mak, H.-Y.; Shen, Z.-J.M. Data-driven research in retail operations—A review. Nav. Res. Logist. NRL 2020, 67, 595–616. [Google Scholar] [CrossRef]
- Sachs, A.-L.; Minner, S. The data-driven newsvendor with censored demand observations. Int. J. Prod. Econ. 2014, 149, 28–36. [Google Scholar] [CrossRef]
- Cao, Y.; Shen, Z.-J.M. Quantile forecasting and data-driven inventory management under nonstationary demand. Oper. Res. Lett. 2019, 47, 465–472. [Google Scholar] [CrossRef]
- Liu, C.; Letchford, A.N.; Svetunkov, I. Newsvendor problems: An integrated method for estimation and optimisation. Eur. J. Oper. Res. 2022, 300, 590–601. [Google Scholar] [CrossRef]
- Porteus, E. Foundations of Stochastic Inventory Theory; Stanford University Press: Stanford, CA, USA, 2002. [Google Scholar]
- Rawat, W.; Wang, Z. Deep Convolutional Neural Networks for Image Classification: A Comprehensive Review. Neural Comput. 2017, 29, 2352–2449. [Google Scholar] [CrossRef]
- Hochreiter, S. The Vanishing Gradient Problem During Learning Recurrent Neural Nets and Problem Solutions. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 1998, 06, 107–116. [Google Scholar] [CrossRef]
- Schmidt, R.M. Recurrent Neural Networks (RNNs): A gentle Introduction and Overview. arXiv 2019, arXiv:1912.05911. Available online: http://arxiv.org/abs/1912.05911 (accessed on 14 July 2022).
- Chollet, F. Keras: Deep Learning for Humans. 2022. Available online: https://github.com/keras-team/keras (accessed on 14 July 2022).
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning. Available online: https://www.deeplearningbook.org/ (accessed on 14 July 2022).
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Donahue, J.; Anne Hendricks, L.; Guadarrama, S.; Rohrbach, M.; Venugopalan, S.; Saenko, K.; Darrell, T. Long-Term Recurrent Convolutional Networks for Visual Recognition and Description. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 677–691. [Google Scholar] [CrossRef]
- Yu, H.; Wu, Z.; Wang, S.; Wang, Y.; Ma, X. Spatiotemporal Recurrent Convolutional Networks for Traffic Prediction in Transportation Networks. Sensors 2017, 17, 1501. [Google Scholar] [CrossRef] [PubMed]
- Kaggle, Store Item Demand Forecasting Challenge. 2018. Available online: https://www.kaggle.com/competitions/demand-forecasting-kernels-only/data (accessed on 1 August 2021).
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. TensorFlow: A system for large-scale machine learning. arXiv 2016, arXiv:1605.08695. Available online: https://www.proquest.com/publiccontent/docview/2079694224?parentSessionId=6X%2BxA3ida%2Bjpq%2BtJ91ZM1qkh%2FNyWqV0bjZp8fQGMgQU%3D&pq-origsite=summon& (accessed on 27 June 2023).
- Kingma, D.P.; Ba, J.; Adam, J. A Method for Stochastic Optimization. arXiv 2017, arXiv:1412.6980. Available online: http://arxiv.org/abs/1412.6980 (accessed on 14 July 2022).
- Gurobi Optimization. Gurobi Optimizer Reference Manual. Available online: https://www.gurobi.com (accessed on 1 October 2022).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).