Production Inventory Optimization Considering Direct and Indirect Carbon Emissions under a Cap-and-Trade Regulation

Abstract

Background: The latest global agreement on net-zero emissions encourages new studies on production inventory optimization that promote carbon emissions reduction without harming a company’s profit performance, particularly because certain carbon-pricing regulations bind manufacturing companies. Methods: This study aims to develop a production inventory model that considers direct and indirect emissions in three emission scopes. It incorporates emissions from production, material handling, transportation, and waste disposal for further treatment under a carbon cap-and-trade regulation. With the help of Maple software, a convex total cost function was solved. Results: The results show that the optimum production quantity depends on the values of demand, setup cost, holding cost, fixed cost per delivery, fixed cost for waste disposal, and other parameters related to carbon prices. This study also found that the total cost was highly dependent on the values of the carbon cap, carbon price, and delivery distance. Meanwhile, changes in the delivery distance and fuel emissions standard significantly impacted total emissions. Conclusions: The proposed model can guide manufacturing companies in setting the optimum production quantity per cycle. Moreover, they must carefully manage the delivery and setting of the carbon cap and carbon price from the government.

1. Introduction

The latest global agreement on net-zero emissions requires the efforts of every country to limit greenhouse gas (GHG) emissions. Various initiatives have been implemented, such as converting to renewable energy and implementing carbon pricing. The World Bank reported that 70 carbon-pricing initiatives had been implemented in many national jurisdictions, covering around 23.17% of global GHG emissions [1]. This regulation binds industries. They have been recognized as one of the significant contributors to GHG emissions and, hence, are required to become more sustainable by optimizing their operations. Carbon emissions (e.g., CO₂ as one of the main GHG emissions) from companies are generally classified into direct and indirect emissions. Direct emissions come from company operations that they control directly, whereas indirect emissions are from sources that the company does not own or control [2]. Both must be included in the analysis and in reduction efforts [3].

Numerous researchers and practitioners have studied low-carbon logistics and supply chain systems to promote carbon emissions reduction because of increased concern for the environment [4,5]. The challenge is achieving this goal without harming a company’s profit performance [6,7]. The implementation of carbon-pricing regulations (e.g., carbon cap-and-trade system) by governments affects manufacturers because they tend to pay some additional costs. Responding to this situation, manufacturers need to adjust their operations, such as production and logistics decisions, so that they emit fewer emissions, which also means fewer costs [8]. Inventory optimization has been known as a function of its total cost. Hence, identifying the correct total cost structure guides managers to make the optimum inventory decisions [8,9].

In supply chains, production, transportation, and storage processes constitute a significant source of carbon emissions and can potentially contribute to global warming [9,10,11,12]. Accordingly, identifying and measuring supply chain carbon footprints are critical to mitigating supply chain risks [13]. It includes the direct and indirect emissions footprint of the industry. Direct emissions result from business operations involving forklifts, material handling equipment, boilers (generators), and other production-related machinery [2]. Indirect emissions are associated with the amount of purchased and used energy, such as electricity. Furthermore, these emission categories are divided into three scopes or tiers: scope 1 contains all direct emissions; scope 2 is comprised of indirect emissions from the generation of purchased electricity that the company uses; and scope 3 is composed of the additional indirect emissions of the system produced by external organizations [3]. Wangsa [2] proposed a low-carbon supply chain analysis method, considering direct and indirect emissions, including those from production and transportation. A freight transport company performs transportation; hence, transportation emissions are categorized as indirect emissions. Ong et al. [14] considered a similar carbon emission system but it was applied in a three-echelon supply chain. Recently, Wangsa et al. [15] incorporated the emissions from material handling activities for a complete analysis. A detailed analysis of emissions from forklift loading and unloading activities was also carried out to identify the emission footprint in the supply chain. Matthews et al. [16] highlighted the importance of a full carbon footprint analysis because direct emissions sometimes account for only a small part of a system’s total emissions. However, unfortunately, studies on low-carbon logistics systems that differentiate between direct and indirect emissions, especially those covering three emission scopes, are still limited.

Several researchers integrated environmental considerations into the inventory decision model in production systems and developed sustainable economic production quantity (sustainable EPQ) models. Mukhopadhyay and Goswami [17] considered pollution because of residual production, garbage, and waste from production activities. They included pollution control and maintenance costs in the total cost function. Datta [18] studied the effect of green technology investment on reducing carbon emissions in the EPQ model. Carbon emissions come from production setups, machine operations, product storage, and the disposal of defective products. Daryanto and Wee [19] solved a sustainable EPQ problem that considers solid waste disposal. Taleizadeh et al. [20] expanded on the traditional EPQ model for various shortage situations, considering emissions from production, the storage of goods, and disposal of obsolete goods. Daryanto and Wee [21] studied the EPQ model for products with a certain deterioration rate and imperfect product quality. Shen et al. [22] attempted to reduce the deterioration rate by investing in preservation technology and considering the emission level. Manna et al. [23] developed an EPQ model for products with a certain deterioration rate and the presence of an imperfect product with the possibility of rework. Priyamvada et al. [24] suggested an investment in preservation technology for similar problems. Priyan [25] developed an EPQ model involving a rework process for defective products under a carbon tax and cap regulation, while in their literature review on sustainable EPQ models, Karim and Nakade [6] suggested recycling processes for defective products and waste. Moon et al. [26] studied the reliability aspect of a production system to develop a sustainable system that reduces the number of defective products and waste. Recently, Mashud et al. [27] optimized the production cycle of a system and developed a sustainable production system by investing in green technology and preservation equipment to reduce waste and emissions. Overall, the EPQ models above did not classify the direct and indirect emissions of the system, did not differentiate the scope of emissions, and did not consider the emissions from material handling activities.

Generally, there are three common carbon-pricing regulations: the carbon tax, strict carbon limitation, and carbon cap-and-trade regulations [8,28]. Various studies on EPQ models have considered different regulations. Datta [18], Daryanto and Wee [19,21], Shen et al. [22], Mashud et al. [27], and Yassine [29] solved sustainable EPQ problems under a carbon tax system. Mukhopadhyay and Goswami [17] and Sinha and Modak [30] considered the costs of carbon emissions under a carbon cap-and-trade regulation to decide the production quantity per cycle. Recently, Entezaminia et al. [31] studied production quantity and carbon trade decisions using simulation. He et al. [32] compared the effects of carbon tax and cap-and-trade regulations on production decisions and the resulting emissions.

Companies must abide by the regulations implemented by the government where they operate. For example, the Indonesian government recently introduced a plan to implement carbon cap-and-trade and started it in several industrial sectors. From the above literature review, only a few previous EPQ studies considered a cap-and-trade regulation. Carbon emissions can be classified into direct and indirect emissions. The sources of carbon emissions considered in the previous studies vary. Emissions from production, transportation, and storage appear in most studies. Recently, emissions from material handling and disposal activities were incorporated [15,18,19,20,21,27]. In order to present an insight into the production inventory model by examining both direct and indirect emissions, such as those resulting from production processes, loading and unloading activities, as well as those from transportation for product delivery and waste disposal, this article has already adopted the approach used by Wangsa [2] and Wangsa et al. [15]. The objective function of the model is to minimize the total cost. This study can guide managers of manufacturing companies to determine the optimum production quantity and cycle time, considering various emission sources, and responding to the implemented carbon cap-and-trade regulation. A special case with an imperfect production system is also examined, particularly when defective products increase the amount of disposable waste.

Table 1. Literature overview.

Author(s)	Inventory Model	Direct-Indirect Emissions	Function of Emission Cost	Cap-and-Trade Regulation	Defective Products
Wangsa [2]	Two-echelon	Yes	Production, transportation	No	No
Huang et al. [11]	Two-echelon	No	Production, transportation, storage	Yes	No
Ong et al. [14]	Three-echelon	Yes	Production, transportation, storage	No	No
Wangsa et al. [15]	Two-echelon	Yes	Production, transportation, storage, material handling	No	No
Mukhopadhyay and Goswami [17]	EPQ	No	Production	Yes	Yes
Datta [18]	EPQ	No	Production, storage, disposal	No	Yes
Daryanto and Wee [19]	EPQ	No	Production, transportation, storage, disposal	No	No
Taleizadeh et al. [20]	EPQ	No	Production, storage, disposal	No	No
Daryanto and Wee [21]	EPQ	No	Production, transportation, storage, disposal	No	Yes
Shen et al. [22]	Two-echelon	No	Production, setup, storage, ordering	No	No
Manna et al. [23]	EPQ	No	Production, transportation	No	Yes
Priyamvada et al. [24]	EPQ	No	Production, storage, preservation	No	No
Priyan et al. [25]	EPQ	No	Production, transportation, storage	No	Yes
Moon et al. [26]	EPQ	No	Production, setup, storage	No	Yes
Mashud et al. [27]	EPQ	No	Transportation, disposal	No	No
Yassine [29]	EPQ	No	Ordering, transportation	No	Yes
Sinha and Modak [30]	EPQ	No	Production, storage	Yes	No
This study	EPQ	Yes	Production, material handling, storage, transportation, disposal	Yes	Yes

shows the research gap and this study’s contribution.

Our research differentiates itself from the existing production inventory studies in that it considers the direct and indirect emissions in three emission scopes. It incorporates the emissions from production, material handling, storage, transportation, and waste disposal for further treatment. It works under the carbon cap-and-trade regulation and based on this arrangement, offers some novel insights as to how managers’ optimal decisions can be obtained. In summary, the contributions of this research are:

• Develops a sustainable production inventory or EPQ model based on the direct and indirect emissions that classify them according to the three emission scopes.
• Studies the effect of the carbon cap, carbon price, and other environmental-related parameters on production inventory optimization under the carbon cap-and-trade system.
• Incorporates the effect of defective products in a sustainable EPQ model, considering direct and indirect emissions.

2. Method

This section provides the step-by-step research method for the modeling of a sustainable EPQ model considering direct and indirect emissions.

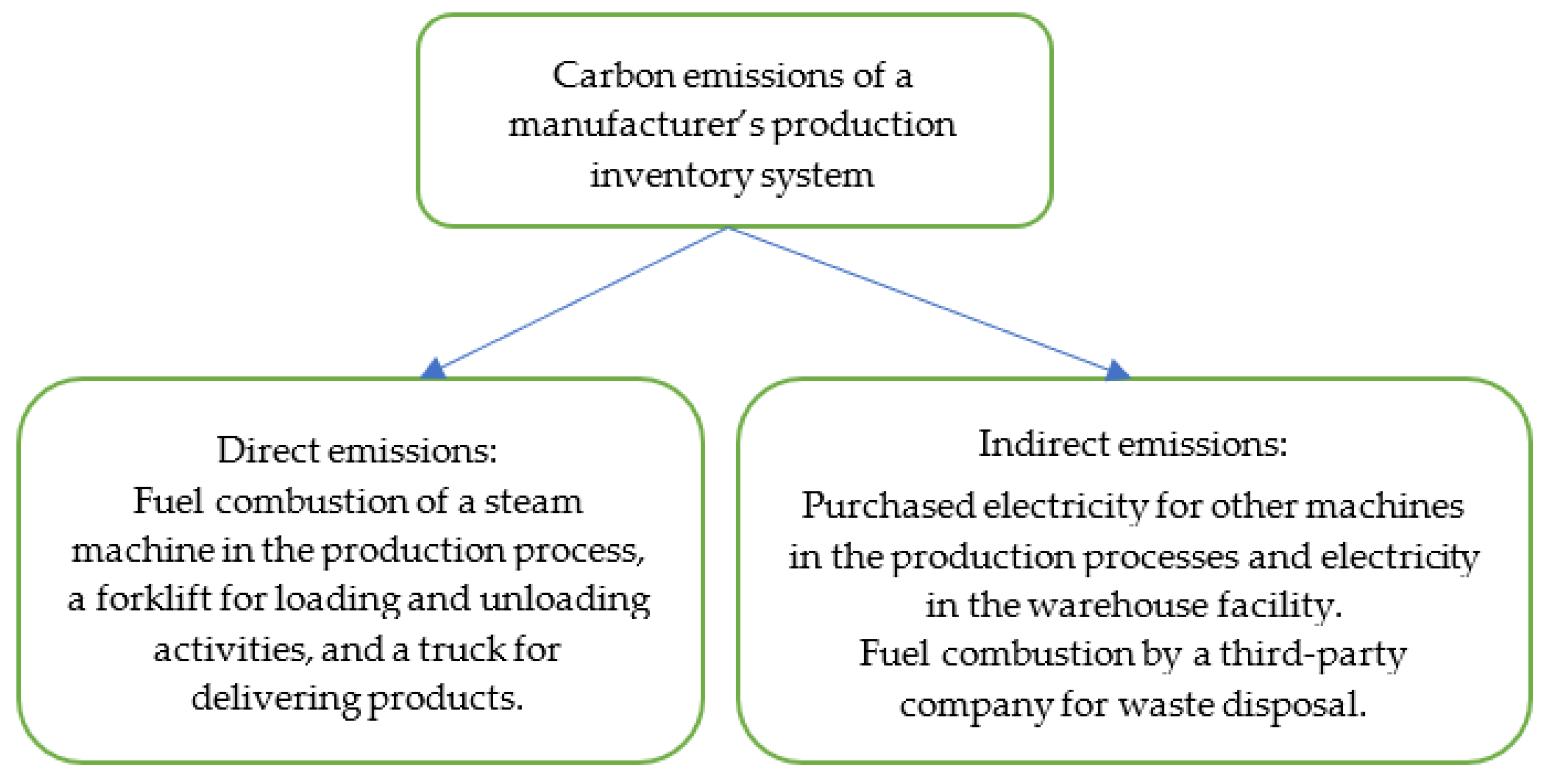
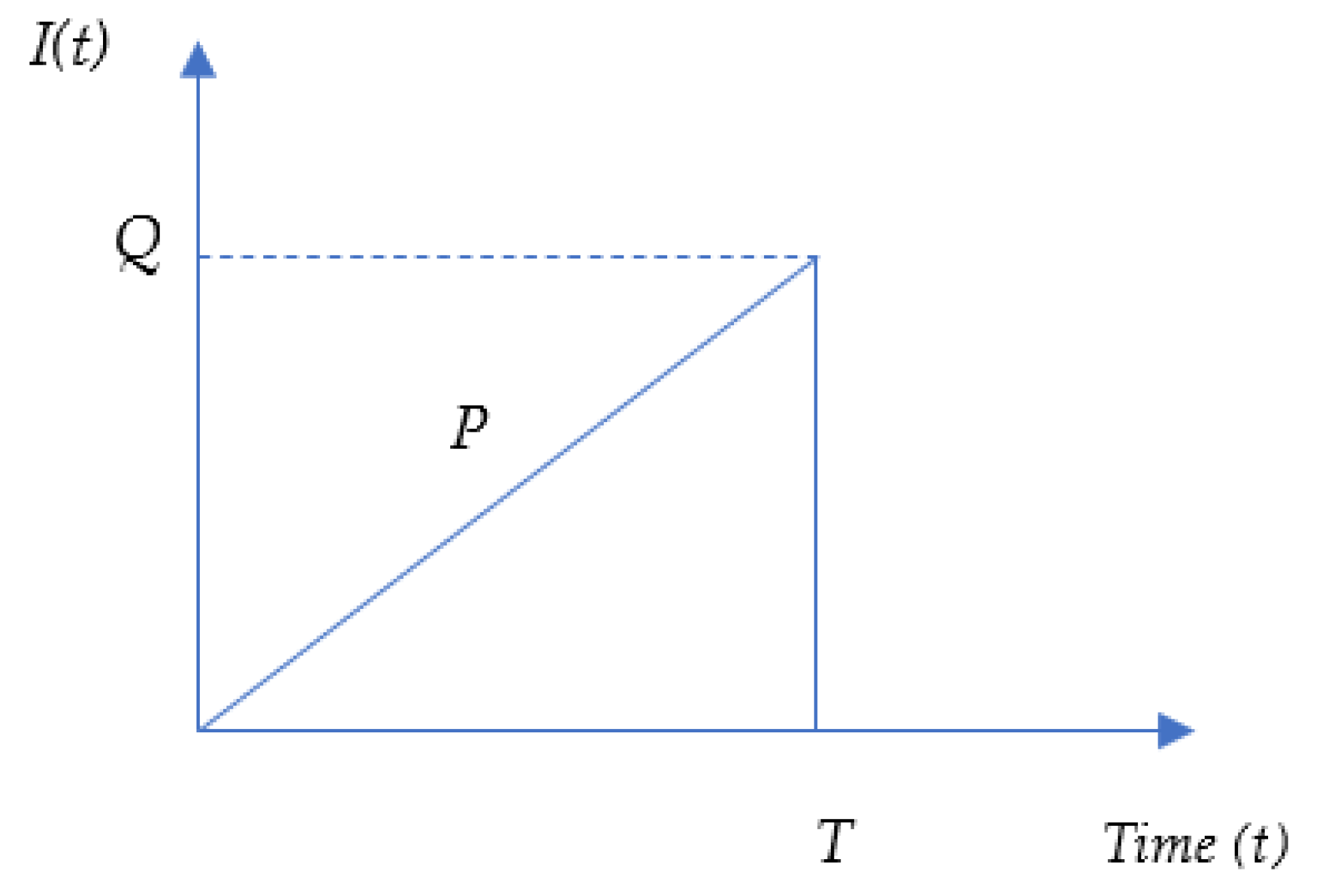
2.1. Problem Description

Several governments in developing and developed countries have begun to implement various measures, such as carbon taxes and pricing, to support the commitment to net-zero emissions. For example, the Indonesian government recently implemented carbon cap-and-trade regulations [33]. In this study, a manufacturing company works under the carbon cap-and-trade regulation. Carbon dioxide (CO₂), the main greenhouse gas, is directly generated from production, product delivery, and material handling activities, from the fuel for a steam machine, a forklift, and a truck (emissions scope 1). Electrical energy usage in production and product storage facilities has also been linked to indirect emissions (emissions scope 2). Disposing of solid waste carried out by a third-party company also contributes to indirect carbon emissions (emissions scope 3). The illustration of the direct and indirect emissions of the company is provided in Figure 1.

If the total emissions are larger than the cap, the company must buy additional emission quotas from the carbon market. In contrast, they can sell their extra quota to make more money if the emission level is below the limit. Because there are costs that arise, such as setup costs per production cycle, storage costs that are affected by inventory levels, emissions costs, and potential additional revenue from any excess quota, the company needs to determine the optimum production quantity and cycle time.

2.2. Assumptions

The following assumptions are applied in this research:

• A manufacturer produces one type of product based on a customer’s design. For example, a corrugated box manufacturer produces one type of box ordered by an FMCG manufacturer or an automotive component manufacturer produces one type of component for a car manufacturer.
• Demand from the customer is known and constant.
• Production rate is greater than the demand and is constant. The inventory is accumulated during the production period.
• Shortages are not allowed.
• At the end of the production cycle, a Q quantity of products is delivered to the customer (a single delivery model) as in Sinha and Modak [30] and Wee and Daryanto [34]. The production quantity per cycle is to be optimized by the manufacturer.
• The manufacturer performs delivery by truck. Transportation/logistics costs and direct CO₂ emissions are among the consequences [34,35].
• The truck’s fuel consumption is split into two categories—the fuel consumption of the truck when it is empty and the fuel consumption that is impacted by the weight of the truckload—to account for the effect of the number of truckloads [34,35,36].
• The manufacturer unloads the required material from the receiving dock to the production area. After the production, the manufacturer loads the finished products onto a truck at the shipping dock. Material handling costs and direct CO₂ emissions from a forklift are among the consequences, as in Wangsa et al. [15]. The distances from the receiving dock to the production area and from the production area to the shipping dock are the same.
• The holding cost considers the cost of warehousing and indirect CO₂ emissions from electricity usage, as in Daryanto and Wee [19].
• A certain amount of solid waste is produced and disposed of at the end of the production cycle by a third-party company. A fixed cost to dispose of and indirect CO₂ emissions are among the consequences [19].
• When total emissions exceed the carbon cap, extra carbon quotas are always available in the carbon market. Excess quotas can be sold when total emissions are less than the carbon cap.

2.3. Notations

Table 2. List of notations.

Notation	Description
D	Demand rate (units/year)
P	Production rate (units/year)
s	Setup cost ($/cycle)
Pc	Production cost ($/unit)
Ic	Inventory cost ($/unit/year)
cf	Forklift capacity (lbs/travel)
sf	Forklift speed (miles/h)
ff	Forklift fuel consumption (L/h)
df	Forklift traveling distances from the receiving dock to the production area and from the production area to the shipping dock (miles/travel)
tfix	Fixed cost ($/delivery)
Fp	Fuel price ($/L)
w1	Raw material weight, which is assumed to be 110% of product weight (lbs/unit)
w2	Product weight (lbs/unit)
pf	Production fuel consumption factor (L/unit)
Fe	Fuel emissions standard (tonCO2eq/L)
dc	Distance from manufacturer to customer site (miles)
c1	Fuel consumption of an empty truck (L/mile)
c2	Variable fuel consumption from truckload (L/mile/ton)
cd	Waste disposal fixed fees per cycle ($)
Pe	Production electricity consumption factor per cycle (kWh)
We	Warehouse electricity consumption factor per cycle (kWh)
Ee	Electricity emissions standard (tonCO2eq/kWh)
dt	Distance between the manufacturer and the third-party location (miles)
Te	Total emission quantity (tonCO2eq)
Tc	Total cost ($)
Ecap	Emission cap or limit (tonCO2eq)
CGHG	Carbon price ($/tonCO2eq)
Decision variables
Q	Optimum production quantity per cycle (unit products)
T	Cycle length (year)

lists all the notations used to represent the mathematical model.

2.4. Mathematical Modeling

A mathematical model was developed to minimize the system’s total cost. The total cost per year T_c is the sum of the setup cost, production cost, inventory holding cost, material handling cost, transportation cost, waste disposal cost, and carbon emission cost, as shown in Equation (1).

$$T_c=C_{st}+C_{pr}+C_{ih}+C_{mh}+C_{tr}+C_{wd}+C_{ce}$$

(1)

Note that due to the carbon cap-and-trade regulation, two situations may occur: (1) When the total emissions are larger than the cap (T_e > E_cap), the company must buy additional emission quotas; hence, $C_{ce}$ in Equation (1) exists; and (2) when the emission level is below the limit (E_cap > T_e), they can sell the extra quotas to gain additional revenue. $C_{ce}$ becomes negative and will reduce the total cost.

The detail of the costs are described as follows:

a.

Setup cost

Setup cost is all the expenses for production preparation, such as machine setup. If s is the setup cost per cycle, then the setup cost per year is s multiplied by the number of production cycles per year (D/Q), as shown in Equation (2).

$$C_{st}=s\frac{D}{Q}$$

(2)

b.

Production cost

All production process expenses are for materials, machines, and energy usage. If P_c is the production cost per unit item, then the production cost per year is P_c multiplied by the total production per year which is equal to the number of demands per year (D), as shown in Equation (3).

$$C_{pr}=P_{c}Q\left(\frac{D}{Q}\right)=P_{c}D$$

(3)

c.

Inventory holding cost

Figure 2 illustrates the accumulation of inventory per cycle until t = T. The production stops at T, which is equal to Q/P. Due to a single delivery, the whole lot, Q, then drops to 0.

Hence, the inventory holding cost per year generated from warehousing expenses is the inventory cost per unit product per year (I_c) multiplied by the total inventory per cycle multiplied by the number of production cycles per year (D/Q), as shown in Equation (4).

$$C_{ih}=I_c\left(\frac{1}{2}\frac{Q}{P}Q\right)\frac{D}{Q}=I_c\frac{QD}{2P}$$

(4)

d.

Material handling cost

This considers the material handling (unloading and loading) activities performed by a forklift (see Wangsa et al. [15]), in which c_f is forklift capacity (lbs), s_f is forklift speed (miles/h), f_f is forklift fuel consumption (L/h), d_f is forklift traveling distance from the receiving dock to the production area and from the production area to the shipping dock (miles), F_p is the fuel price ($/L), while w₁ and w₂ are raw material and product weight (lbs/unit), and then the material handling cost per year is

$$C_{mh}=\frac{D\left(w_1+w_2\right)}{c_f}\frac{f_f{d}_f{F}_p}{s_f}$$

(5)

e.

Transportation cost

Q product units are transported by truck from the manufacturer to the customer’s location within d_c (miles). Considering the fuel consumption of the truck when it is empty (c₁) and the fuel consumption that is impacted by the weight of the truckload (c₂), the transportation cost per year that accounts for the effect of the truckloads (Q.w₂) is presented in Equation (6).

$$C_{tr}=\frac{D}{Q}\left(t_{fix}+2d_c{c}_1{F}_p+d_{c}Q{w}_2{c}_2{F}_p\right)$$

(6)

f.

Waste disposal cost

A certain amount of solid waste arises, and the quantity is assumed as the deviation between the finished product and raw material weight. They are transported and disposed of at the end of the cycle at a third-party company’s treatment center; therefore, the cost of waste disposal is a function of the fixed fees charged (c_d). The waste disposal cost per year is

$$C_{wd}=\frac{D}{Q}{c}_d$$

(7)

g.

Emission cost

Following Wangsa [2] and Wangsa et al. [15], we consider the direct and indirect emissions of the production–inventory system. Furthermore, they can be classified into emissions scope 1, scope 2, and scope 3; hence, the total emission is T_e = S₁ + S₂ + S₃.

S₁ is all the direct emissions resulting from the fuel consumption for the steam machine in production, forklift, and truck. With a production fuel consumption factor p_f (L/unit) and fuel emissions standard F_e (tonCO₂eq/L), the direct emission quantity per year for the steam machine is formulated by

$$D{p}_f{F}_e$$

(8)

Based on Equation (5) and considering the fuel emissions standard f_e, the direct emission quantity per year for forklift operations is formulated by

$$\frac{D\left(w_1+w_2\right)}{c_f}\frac{f_f{d}_f{F}_e}{s_f}$$

(9)

Based on Equation (6) and considering the fuel emissions standard f_e, the direct emission quantity per year for truck operations is formulated by

$$\frac{D}{Q}\left(2d_c{c}_1{F}_e+d_{c}Q{w}_2{c}_2{F}_e\right)$$

(10)

Hence,

$$S_1=\left(D{p}_f{F}_e\right)+\left(\frac{D\left(w_1+w_2\right)}{c_f}\frac{f_f{d}_f{F}_e}{s_f}\right)+\left(\frac{D}{Q}\left(2d_c{c}_1{F}_e+d_{c}Q{w}_2{c}_2{F}_e\right)\right)$$

(11)

S₂ is the indirect emissions resulting from electricity consumption for production and storage. The production electricity consumption factor from various production processes is P_e (kWh). The warehouse electricity consumption factor for keeping the finished goods is W_e (kWh), and the electricity emissions standard is E_e (tonCO₂eq/kWh). Hence, the indirect emissions classified as S₂ per year are formulated by

$$S_2=\frac{D}{Q}\left(P_e+W_e\right)E_e$$

(12)

S₃ is the indirect emissions beyond the company’s control, resulting from the third-party company that transports the waste to their treatment facility. Considering the distance between the manufacturer and the third-party location d_t (miles) and the deviation between raw material and finished product weight (w₁ − w₂), the indirect emissions quantity classified as S₃ per year is formulated by

$$S_3=\frac{D}{Q}\left(2d_t{c}_1{F}_e+d_{t}Q\left(w_1-w_2\right)c_2{F}_e\right)$$

(13)

Therefore,

$$\begin{gathered} T_e=\left(D{p}_f{F}_e\right)+\left(\frac{D\left(w_1+w_2\right)}{c_f}\frac{f_f{d}_f{F}_e}{s_f}\right)+\left(\frac{D}{Q}\left(2d_c{c}_1{F}_e+d_{c}Q{w}_2{c}_2{F}_e\right)\right)+\frac{D}{Q}\left(P_e+W_e\right)E_e \\ +\frac{D}{Q}\left(2d_t{c}_1{F}_e+d_{t}Q\left(w_1-w_2\right)c_2{F}_e\right) \end{gathered}$$

(14)

The emission cost C_ce arises when T_e > E_cap. Considering the carbon price C_GHG, the emission cost is formulated by

$$C_{ce}=\left(T_e-E_{cap}\right)C_{GHG}$$

(15)

Note that when E_cap > T_e, C_ce becomes negative, it will reduce the total cost.

Substituting Equations (2)–(7), (14) and (15) into (1), we gain:

$$\begin{gathered} T_c=s\frac{D}{Q}+P_{c}D+I_c\frac{QD}{2P}+\frac{D\left(w_1+w_2\right)}{c_f}\frac{f_f{d}_f{F}_p}{s_f}+\frac{D}{Q}\left(t_{fix}+2d_c{c}_1{F}_p+d_{c}Q{w}_2{c}_2{F}_p\right)+\frac{D}{Q}{c}_d \\ +\left(\right(\left(D{p}_f{F}_e\right)+\left(\frac{D\left(w_1+w_2\right)}{c_f}\frac{f_f{d}_f{F}_e}{s_f}\right)+\left(\frac{D}{Q}\left(2d_c{c}_1{F}_e+d_{c}Q{w}_2{c}_2{F}_e\right)\right)+\frac{D}{Q}\left(P_e+W_e\right)E_e \\ +\frac{D}{Q}\left(2d_t{c}_1{F}_e+d_{t}Q\left(w_1-w_2\right)c_2{F}_e\right))-E_{cap})C_{GHG} \end{gathered}$$

(16)

The first derivative of T_c with respect to Q is

$$\begin{gathered} -\frac{sD}{Q^2}+\frac{I_{c}D}{2P}+\frac{D{d}_c{w}_2{c}_2{F}_p}{Q}-\frac{D}{Q^2}\left(t_{fix}+2d_c{c}_1{F}_p+d_{c}Q{w}_2{c}_2{F}_p\right)-\frac{D{c}_d}{Q^2} \\ +(\frac{D{d}_c{w}_2{c}_2{F}_e}{Q}-\frac{D}{Q^2}\left(2d_c{c}_1{F}_e+d_{c}Q{w}_2{c}_2{F}_e\right)-\frac{D}{Q^2}\left(P_e+W_e\right)E_e+\frac{D{d}_t\left(w_1-w_2\right)c_2{F}_e}{Q} \\ -\frac{D}{Q^2}\left(2d_t{c}_1{F}_e+d_{t}Q\left(w_1-w_2\right)c_2{F}_e\right))C_{GHG} \end{gathered}$$

(17)

The second derivative of T_c with respect to Q is

$$\begin{gathered} \frac{2sD}{Q^3}-\frac{2D{d}_c{w}_2{c}_2{F}_p}{Q^2}+\frac{2D}{Q^3}\left(t_{fix}+2d_c{c}_1{F}_p+d_{c}Q{w}_2{c}_2{F}_p\right)+\frac{2D{c}_d}{Q^3} \\ +(-\frac{2D{d}_c{w}_2{c}_2{F}_e}{Q^2}+\frac{2D}{Q^3}\left(2d_c{c}_1{F}_e+d_{c}Q{w}_2{c}_2{F}_e\right) \\ +\frac{2D}{Q^3}\left(P_e+W_e\right)E_e-\frac{2D{d}_t\left(w_1-w_2\right)c_2{F}_e}{Q^2}+\frac{2D}{Q^3}\left(2d_t{c}_1{F}_e+d_{t}Q\left(w_1-w_2\right)c_2{F}_e\right))C_{GHG} \end{gathered}$$

(18)

We can simplify Equation (18) and represent it in Equation (19) as follows:

$$\frac{2D}{Q^3}\left(s+t_{fix}+c_d+2d_c{c}_1{F}_p+\left(2c_1{F}_e(d_c+d_t\right)+\left(P_e+W_e\right)E_e)C_{GHG}\right)$$

(19)

When all the parameters and Q are positive, Equation (19) is always positive; hence, the cost function is strictly convex.

The optimal quantity of Q can be determined by setting Equation (17) equal to zero. Using the help of Maple software, the optimum production quantity Q is formulated as follows:

$$Q=\sqrt{\frac{2P\left(s+t_{fix}+c_d+2d_c{c}_1{F}_p+2d_c{c}_1{F}_e{C}_{GHG}+2d_t{c}_1{F}_e{C}_{GHG}+P_e{E}_e{C}_{GHG}+W_e{E}_e{C}_{GHG}\right)}{I_c}}$$

(20)

Finally, the production period T can be calculated by

$$T=\frac{Q}{P}$$

(21)

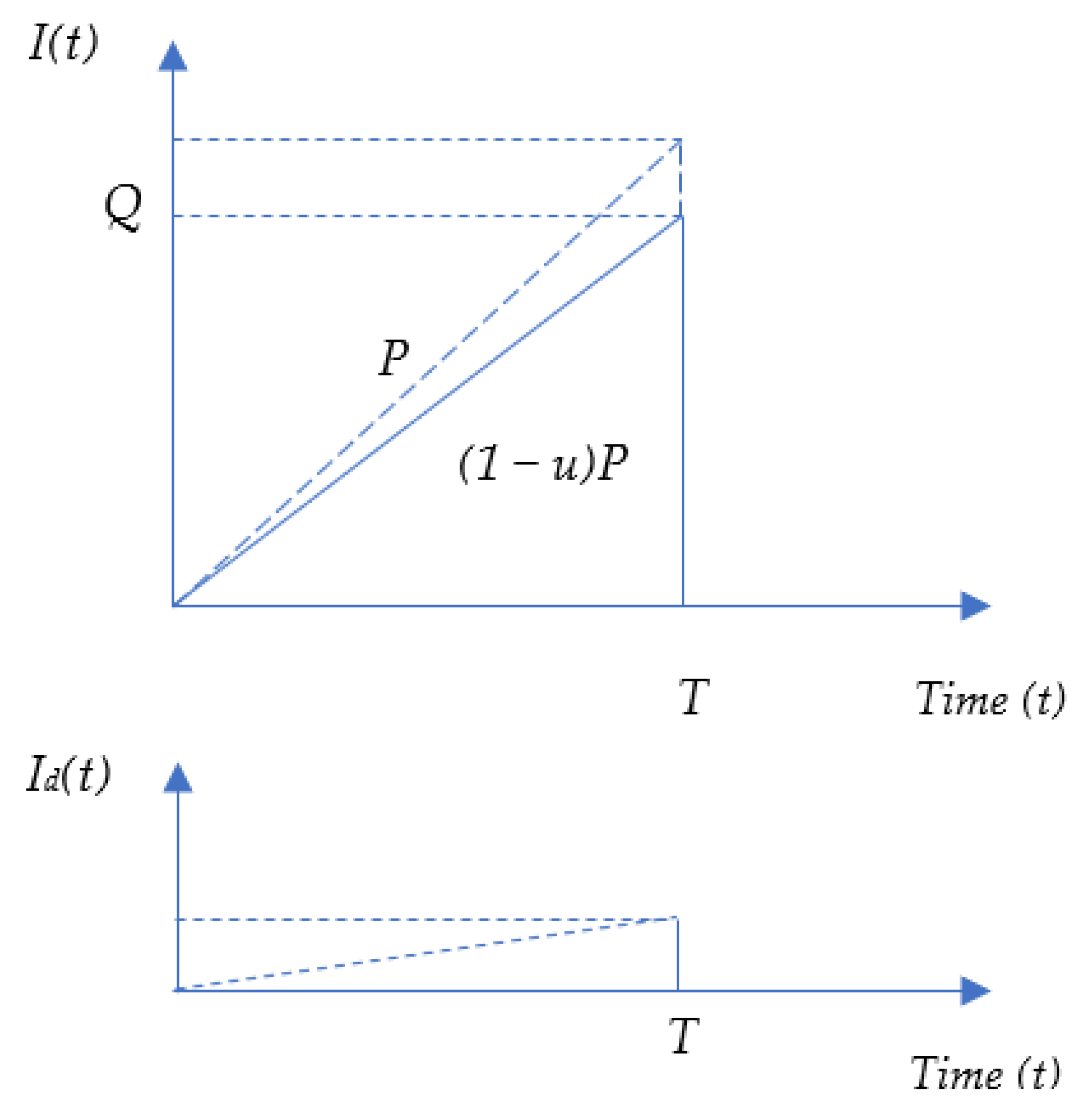
2.5. A Special Case of an Imperfect Production System

According to Datta [18], Manna et al. [23], Priyan et al. [25], Moon et al. [26], etc., certain manufacturers have an imperfect production system that produces undesirable defective products. In the special case of our proposed EPQ model, we assume that a manufacturer has an imperfect production system and performs a 100% quality check right after producing the product. Then, the defective products are separated and will be disposed of together with the solid waste (production scrap) by a third-party company at T.

Suppose u is the percentage of defective products. During the production cycle, the inventory of conforming products increases at a (1 − u)P rate, while the inventory (accumulation) of defective products increases at a uP rate. Figure 3 illustrates the inventory level of the conforming and defective products. The detail of the cost components are described as follows:

• Setup cost per year (C_st) remains the same as Equation (2).
• Production cost per year is the production cost per unit (P_c) multiplied by the production quantity per cycle (PT), multiplied by the number of production cycles per year (D/Q) as follows:

  $$C_{pr}=P_c\left(PT\right)\left(\frac{D}{Q}\right)$$

  (22)
  Because of the defective product percentage, the production cycle T is equal to Q/(1 − u)P. Hence, Equation (22) becomes

  $$C_{pr}=P_c\left(P\left(\frac{Q}{\left(1-u\right)P}\right)\right)\left(\frac{D}{Q}\right)=P_c\frac{D}{\left(1-u\right)}$$

  (23)
• Due to an imperfect production system, inspection costs arise to ensure that only conforming products are delivered to the customer. Inspection cost per year (C_i) is the inspection cost per unit (I_sp) multiplied by the production quantity per cycle (PT), multiplied by the number of production cycles per year (D/Q). As a result, C_i becomes

  $$C_i=I_{sp}\left(P\left(\frac{Q}{\left(1-u\right)P}\right)\right)\left(\frac{D}{Q}\right)=I_{sp}\frac{D}{\left(1-u\right)}$$

  (24)
• Inventory holding cost (C_ih) comes from the storage of conforming products (C_i1) and defective products (C_i2). The inventory cost per unit of the defective product (I_cd) could be much lower than the inventory cost per unit of the conforming product (I_c). Considering the length of the production cycle under the effect of defective products, we have

  $$C_{i1}=I_c\left(\frac{1}{2}\frac{Q}{\left(1-u\right)P}Q\right)\frac{D}{Q}=I_c\frac{QD}{2\left(1-u\right)P}$$

  (25)
  The expected number of defective products per cycle is

  $$\frac{Q}{\left(1-u\right)}-Q$$

  (26)
  Hence,

  $$C_{i2}=I_{cd}\left(\frac{1}{2}\left(\frac{Q}{\left(1-u\right)P}\right)\left(\frac{Q}{\left(1-u\right)}-Q\right)\right)\frac{D}{Q}=I_{cd}\frac{QuD}{2{\left(u-1\right)}^{2}P}$$

  (27)

  and

  $$C_{ih}=I_c\frac{QD}{2\left(1-u\right)P}+I_{cd}\frac{QuD}{2{\left(u-1\right)}^{2}P}$$

  (28)
• The cost of raw material handling is proportional to the number of products produced, so the total material handling costs are

  $$C_{mh}=\frac{\left(\frac{D}{\left(1-u\right)}{w}_1+D{w}_2\right)}{c_f}\frac{f_f{d}_f{F}_p}{s_f}$$

  (29)
• Because only the conforming products (Q) are delivered to the customer, the transportation cost is similar to Equation (6).
• The amount of waste that is disposed of receives an addition from the defective product. However, the cost of waste disposal still follows Equation (7), because it is only affected by a fixed disposal cost per cycle.
• Emission costs
  Again, considering the number of produced products as an effect of the defective products, the emission costs are as follows:

  $$S_1=\left(\frac{D}{\left(1-u\right)}{p}_f{F}_e\right)+\left(\frac{\left(\frac{D}{\left(1-u\right)}{w}_1+D{w}_2\right)}{c_f}\frac{f_f{d}_f{F}_p}{s_f}\right)+\left(\frac{D}{Q}\left(2d_c{c}_1{F}_e+d_{c}Q{w}_2{c}_2{F}_e\right)\right)$$

  (30)

  $$S_2=\frac{D}{Q}\left(P_e+W_e\right)E_e$$

  (31)

  $$S_3=\frac{D}{Q}\left(2d_t{c}_1{F}_e+d_t\left(\frac{Q}{\left(1-u\right)}\left(w_1-w_2\right)+\left(\frac{Q}{\left(1-u\right)}-Q\right)w_2\right)c_2{F}_e\right)$$

  (32)
  Therefore,

  $$\begin{gathered} T_e=\left(\frac{D}{\left(1-u\right)}{p}_f{F}_e\right)+\left(\frac{\left(\frac{D}{\left(1-u\right)}{w}_1+D{w}_2\right)}{c_f}\frac{f_f{d}_f{F}_p}{s_f}\right)+\left(\frac{D}{Q}\left(2d_c{c}_1{F}_e+d_{c}Q{w}_2{c}_2{F}_e\right)\right)+\frac{D}{Q}\left(P_e+W_e\right)E_e \\ +\frac{D}{Q}\left(2d_t{c}_1{F}_e+d_t\left(\frac{Q}{\left(1-u\right)}\left(w_1-w_2\right)+\left(\frac{Q}{\left(1-u\right)}-Q\right)w_2\right)c_2{F}_e\right) \end{gathered}$$

  (33)

  and

  $$\begin{gathered} T_c=s\frac{D}{Q}+P_c\frac{D}{\left(1-u\right)}+I_{sp}\frac{D}{\left(1-u\right)}+I_c\frac{QD}{2\left(1-u\right)P}+I_{cd}\frac{QuD}{2{\left(u-1\right)}^{2}P}+\frac{\left(\frac{D}{\left(1-u\right)}{w}_1+D{w}_2\right)}{c_f}\frac{f_f{d}_f{F}_p}{s_f} \\ +\frac{D}{Q}\left(t_{fix}+2d_c{c}_1{F}_p+d_{c}Q{w}_2{c}_2{F}_p\right)+\frac{D}{Q}{c}_d \\ +\left(\right((\frac{D}{\left(1-u\right)}{p}_f{F}_e)+\left(\frac{\left(\frac{D}{\left(1-u\right)}{w}_1+D{w}_2\right)}{c_f}\frac{f_f{d}_f{F}_p}{s_f}\right)+\left(\frac{D}{Q}\left(2d_c{c}_1{F}_e+d_{c}Q{w}_2{c}_2{F}_e\right)\right) \\ +\frac{D}{Q}\left(P_e+W_e\right)E_e+\frac{D}{Q}+\left(2d_t{c}_1{F}_e+d_t\left(\frac{Q}{\left(1-u\right)}\left(w_1-w_2\right)+\left(\frac{Q}{\left(1-u\right)}-Q\right)w_2\right)c_2{F}_e\right))-E_{cap})C_{GHG} \end{gathered}$$

  (34)

Setting the first derivative of T_c with respect to Q equal to zero, and solving it with the help of Maple software, we have

$$Q=\left(1-u\right)\sqrt{\frac{2P\left(s+t_{fix}+c_d+2d_c{c}_1{F}_p+2d_c{c}_1{F}_e{C}_{GHG}+2d_t{c}_1{F}_e{C}_{GHG}+P_e{E}_e{C}_{GHG}+W_e{E}_e{C}_{GHG}\right)}{\left(u-1\right)I_c-u{I}_{cd}}}$$

(35)

3. Results and Discussion

The result of the mathematical modeling in Equation (20) shows that the decision on the production quantity per cycle or production lot size (Q) depends on the values of the following variables: production rate, setup cost, holding cost, fixed cost per delivery, fixed cost for waste disposal, fuel price, and other parameters that relate to emission prices (C_GHG) such as distance to the customer and third-party company, fuel consumption rate of the truck, and average electricity consumption for production and storage. When the production system is imperfect, then the production lot size is also affected by the percentage and the inventory cost of the defective product.

To gain some insights from the proposed model, the next part of this section presents a case illustration, a numerical example, and the associated sensitivity analysis. Most of the numerical values were taken from Wangsa et al. [15].

3.1. Case Illustration

A corrugated carton box manufacturer can illustrate the case in this study. The company produces carton boxes for its buyer under a certain business contract [37]. The production facilities include a steam boiler that supplies steam used for conditioning and provides the heat necessary in the corrugated machine’s formation and bonding processes. The steam boiler, forklift in the production area, and truck for product delivery all consume fossil fuel. Other production machines, such as printing presses and cutting machines, are powered by electricity. Other facilities in the warehouse also consume electricity. Finally, solid waste, such as scrap material and defective products, will be recycled by a third-party company. The government implements a carbon cap-and-trade regulation and guides the carbon market, specifying the carbon price. Because this regulation binds the corrugated carton box company, they must align their production to ensure their operations remain good.

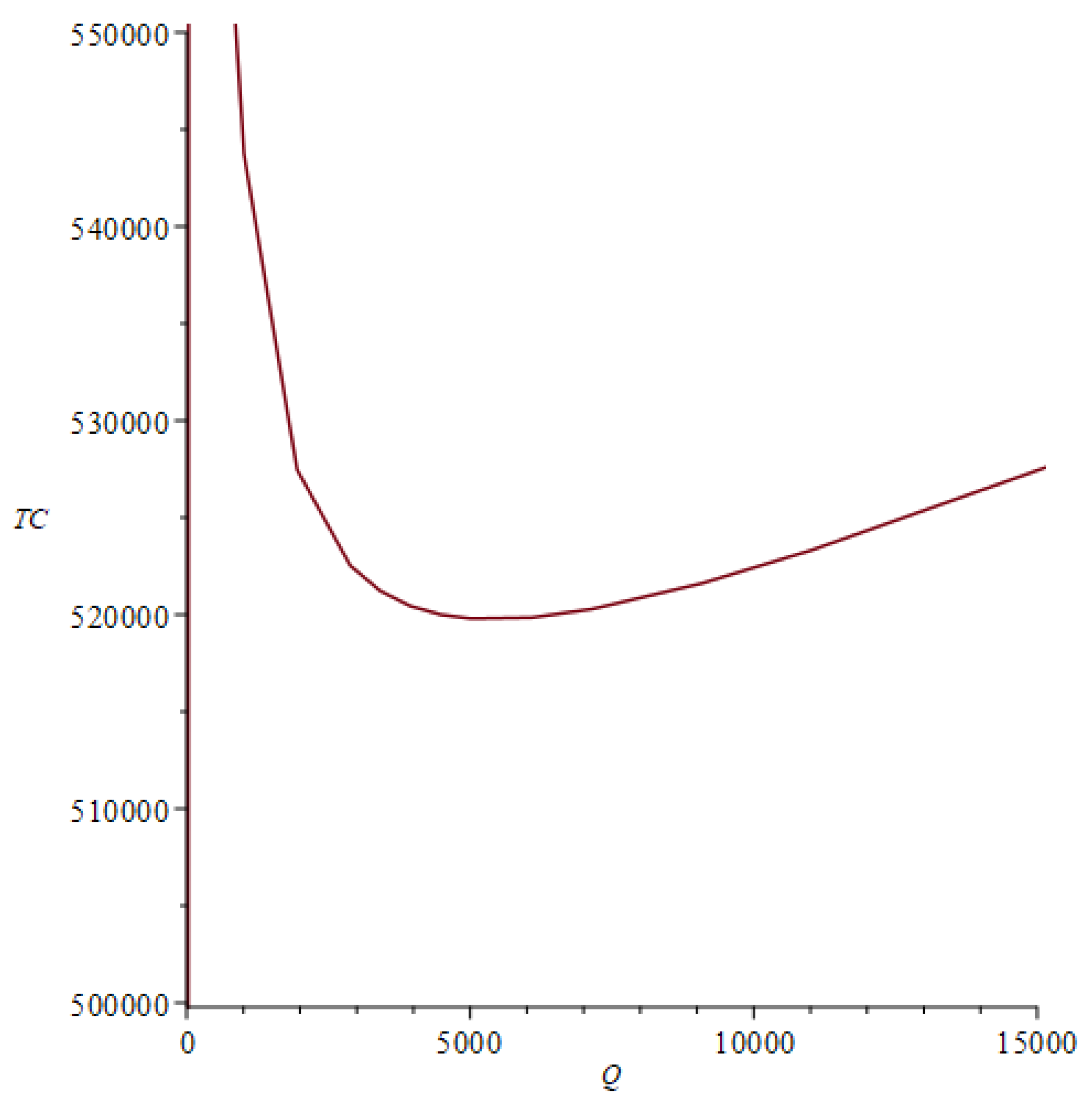
3.2. Numerical Example

Consider a manufacturer that produces one type of product to fulfill a customer’s demand. The demand rate D is 10,000 units per year, and the production rate P is 20,000 units per year. The associated costs of the production–inventory system includes a setup cost s = USD 1400 per cycle, a production cost of P_c = USD 50 per unit, and an inventory cost I_c = USD 5 per unit per year. The production process consumes (p_f) 0.00965 L of fuel per unit.

The material handling is performed by a forklift with a capacity c_f = 3300 lbs per trip, a traveling speed s_f = 6 miles per h, a standard fuel consumption f_f = 3 L per h, a traveling distance d_f = 0.015 miles per trip, and a fuel price F_p = USD 1.02 per L. The raw material weight w₁ = 22 lbs/unit, while the product weight w₂ = 20 lbs/unit.

The finished product is transported by a truck over a 50 miles distance (d_c), at a fixed cost t_fix = USD 1000 per delivery, an empty truck fuel consumption c₁ = 0.4345 L/mile, and a truckload fuel consumption c₂ = 0.0092 L/mile/ton. The waste is disposed of by a third-party logistics service with a fixed disposal cost c_d = USD 600 per cycle, and a distance to the disposal facility d_t = 30 miles.

To measure the emissions of the production–inventory system, we considered the fuel emission standard as F_e = 0.01268 tonCO₂eq/L, production electricity consumption per cycle as P_e = 1159 kWh, warehouse electricity consumption per cycle as W_e = 1545 kWh, and electricity emissions standard as E_e = 0.02264 tonCO₂eq/kWh. Additionally, we considered an emission cap E_cap = 10,000 tonCO₂eq and a carbon price C_GHG = USD 10 per tonCO₂eq.

Using Maple software, we solved Equations (14), (16), (20), and (21), respectively, and found that Q = 5415.0 units, T = 0.270 years, T_c = $ 519,756.4, and T_e = 1352.5 tonCO₂eq. The relationship between Q and T_c in Figure 4 illustrates the convexity of the total cost function.

3.3. Numerical Example of an Imperfect Production System

In a special case with an imperfect production system, some additional parameters were considered as follows: the percentage of defective products is 5%, the quality inspection cost I_sp = USD 0.1 per unit, and the inventory cost of defective products I_cd = USD 0.01 per unit per year.

Solving the problem using Maple software, we now found that Q = 5277.6 units, T = 0.2638 years, T_c = $547,883.2, and T_e = 1396.0 tonCO₂eq. These results show that due to some defective products, the total cost and total emissions increased. The production lot size and production cycle can be optimized and are smaller than in the absence of defective products.

3.4. Effects of Changes in Environmental Parameters

Further analysis and discussion were performed to study the model’s characteristics by changing the values of several environmental parameters. Compared to the original decisions, the %CTC and %CTE present the percentage of changes in the total cost and total emissions. The results are shown in

Table 3. Effects of changes in the cap-and-trade and environmental-related parameter values.

Parameters	Changes	Q	T	TC	%CTC	TE	%CTE
Ecap = 10,000	+50%	5415.0	0.2707	469,756.4	−9.62	1352.5	0
	+25%	5415.0	0.2707	494,756.4	−4.81	1352.5	0
	0	5415.0	0.2707	519,756.4	0	1352.5	0
	−25%	5415.0	0.2707	544,756.4	4.81	1352.5	0
	−50%	5415.0	0.2707	569.756.4	9.62	1352.5	0
CGHG = 10	+50%	5639.7	0.2820	476,507.1	−8.32	1347.9	−0.34
	+25%	5528.5	0.2764	498,134.6	−4.16	1350.1	−0.17
	0	5415.0	0.2707	519,756.4	0	1352.5	0
	−25%	5299.1	0.2649	541,372.2	4.16	1355.0	0.18
	−50%	5180.6	0.2590	562,981.4	8.32	1357.6	0.38
dc = 50	+50%	5433.4	0.2717	572,555.2	10.1	1935.9	43.1
	+25%	5424.2	0.2712	546,155.8	5.08	1644.2	21.6
	0	5415.0	0.2707	519,756.4	0	1352.5	0
	−25%	5405.8	0.2703	493,357.0	−5.08	1060.8	−21.6
	−50%	5396.6	0.2698	466,957.5	−10.1	769.1	−43.1
dt = 30	+50%	5416.2	0.2708	520,109.5	0.07	1387.7	2.61
	+25%	5415.6	0.2708	519,932.9	0.03	1370.1	1.30
	0	5415.0	0.2707	519,756.4	0	1352.5	0
	−25%	5414.4	0.2707	519,579.9	−0.03	1334.8	−1.30
	−50%	5413.8	0.2707	519,403.4	−0.07	1317.2	−2.61
c1 = 0.4345	+50%	5434.6	0.2713	519,805.4	0.009	1352.9	0.029
	+25%	5424.8	0.2712	519,780.9	0.005	1352.7	0.015
	0	5415.0	0.2707	519,756.4	0	1352.5	0
	−25%	5405.2	0.2703	519,731.9	−0.005	1352.3	−0.015
	−50%	5395.4	0.2698	519,707.3	−0.009	1352.1	−0.029
Fe = 0.01268	+50%	5418.3	0.2709	525,953.5	1.19	1972.1	45.8
	+25%	5416.7	0.2708	522,855.0	0.59	1662.3	22.9
	0	5415.0	0.2707	519,756.4	0	1352.5	0
	−25%	5413.4	0.2707	516,657.9	−0.59	1042.6	−22.9
	−50%	5411.8	0.2706	513,559.3	−1.19	732.8	−45.8
Ee = 0.02264	+50%	5636.6	0.2818	520,310.4	0.11	1402.3	3.68
	+25%	5526.9	0.2763	520,036.2	0.05	1377.8	1.87
	0	5415.0	0.2707	519,756.4	0	1352.5	0
	−25%	5300.8	0.2650	519,470.8	−0.05	1326.1	−1.95
	−50%	5184.0	0.2592	519,178.8	−0.11	1298.5	−3.99
Pe = 1159	+50%	5511.1	0.2755	519,996.6	0.05	1374.3	1.61
	+25%	5463.3	0.2731	519,877.0	0.02	1363.5	0.81
	0	5415.0	0.2707	519,756.4	0	1352.5	0
	−25%	5366.3	0.2683	519,634.7	−0.02	1341.3	−0.83
	−50%	5317.2	0.2659	519,511.9	−0.05	1329.9	−1.67
We = 1545	+50%	5542.7	0.2771	520,075.7	0.06	1381.4	2.14
	+25%	5479.2	0.2740	519,917.0	0.03	1367.1	1.08
	0	5415.0	0.2707	519,756.4	0	1352.5	0
	−25%	5350.0	0.2675	519,594.0	−0.03	1337.5	−1.11
	−50%	5284.3	0.2642	519,429.5	−0.06	1322.2	−2.24

.

Some insights can be obtained from the above results:

• The increase in the carbon cap (Ecap) does not change the decision on the optimal production quantity per cycle (Q); as a result, the total amount of emissions does not change either. Companies can buy additional carbon quotas from the market, so they are less concerned about the number of their emissions. However, as expected, the total cost decreases because the obligation to purchase additional carbon quotas has been reduced. This result follows the findings of Hasan et al. [28] and Sinha and Modak [30], even though they looked at it from a total profit perspective.
• Increased carbon prices (C_GHG) are anticipated by reducing the production quantity per cycle (Q). It causes a decrease in the number of emissions (T_e). This anticipation also provides a lower total cost (T_c). This result may seem unusual, but this reduction in total costs can only occur if there is part of the carbon quota left (E_cap > T_e). If a company’s total emissions are more significant than its quota (T_e > E_cap), an increase in carbon prices will burden them. To prove this, changes were made to the carbon cap and carbon price simultaneously. The result is that, when the carbon quota is exhausted, the increase in carbon price will also increase the total cost. This outcome is consistent with Sinha and Modak’s findings [30].
• Total expenses and emissions are significantly impacted by changes in the company’s proximity to the consumer (d_c). Hence, businesses must pay close attention to this factor and search for the best shipping option, particularly for long-distance goods. This result is in accordance with the findings of Wangsa [2] regarding the effect of distance on emissions and cost.
• The fuel emissions standard (F_e) also significantly affects total emissions, although it does not significantly change the total cost. Therefore, companies and the government need to consider the type of fuel with lower emissions to reduce emission levels. However, it should be noted that in this developed model, the price difference for a better type of fuel was not considered.
• Other parameters such as d_t, c₁, P_e, E_e, and W_e have no significant effect on the total cost or total emissions.

3.5. Effects of Cost Parameters

Further analyses were performed to study the model’s characteristics by changing the values of the cost parameters. The results are shown in

Table 4. Effects of changes in cost parameter values.

Parameters	Changes	Q	T	TC	%CTC	TE	%CTE
s = 1400	+50%	5909.5	0.2955	520,992.7	0.24	1342.9	−0.71
	+25%	5667.7	0.2834	520,388.0	0.12	1347.3	−0.38
	0	5415.0	0.2707	519,756.4	0	1352.5	0
	−25%	5150.0	0.2575	519,093.9	−0.13	1358.4	0.43
	−50%	4870.6	0.2435	518,395.3	−0.26	1365.3	0.94
Pc = 50	+50%	5415.0	0.2707	769,756.4	48.10	1352.5	0
	+25%	5415.0	0.2707	644,756.4	24.05	1352.5	0
	0	5415.0	0.2707	519,756.4	0	1352.5	0
	−25%	5415.0	0.2707	394,756.4	−24.05	1352.5	0
	−50%	5415.0	0.2707	269,756.4	−48.10	1352.5	0
Ic = 5	+50%	4421.3	0.2211	522,798.9	0.58	1378.2	1.90
	+25%	4843.3	0.2422	521,354.3	0.31	1366.0	1.00
	0	5415.0	0.2707	519,756.4	0	1352.5	0
	−25%	6252.7	0.3126	517,942.7	−0.35	1337.1	−1.14
	−50%	7658.0	0.3829	515,791.4	−0.76	1318.9	−2.48
Fp = 1.02	+50%	5431.4	0.2716	566,717.8	9.03	1352.1	−0.03
	+25%	5423.2	0.2712	543,237.1	4.52	1352.3	−0.01
	0	5415.0	0.2707	519,756.4	0	1352.5	0
	−25%	5406.8	0.2703	496,275.7	−4.51	1352.6	0.01
	−50%	5398.6	0.2699	472,795.0	−9.03	1352.8	0.02
tfix = 1000	+50%	5772.6	0.2886	520,650.3	0.17	1345.4	−0.53
	+25%	5596.6	0.2798	520,210.5	0.09	1348.7	−0.28
	0	5415.0	0.2707	519,756.4	0	1352.5	0
	−25%	5227.1	0.2613	519,286.6	−0.09	1356.6	0.30
	−50%	5032.1	0.2516	518,799.2	−0.18	1361.2	0.64

, with the following insights:

• The unit production cost (P_c) is the most sensitive parameter for the total cost. The increase in P_c is almost proportional to the increase in the total cost. Hence, the manager must carefully take care of this factor. However, it does not affect the total emissions, as they remain constant.
• Setup cost (s), fixed transportation cost (t_fix), and fuel price (F_p) have similar effects on the total cost and total emissions. The increases in s, t_fix, and F_p increase the total cost. In contrast, the total emission decreases, which is related to the increase in the production lot size Q.
• As expected, an increase in the inventory cost per unit (I_c) will increase total costs. In addition, the increase in I_c will be anticipated by lowering the production lot size Q to reduce inventory. This results in a shorter cycle time. However, the total emissions increase. Hence, the manager must carefully control the inventory cost (or reduce it if possible) because it is detrimental to the company and the environment.

4. Conclusions

In this study, we developed a production inventory model that considers direct and indirect emissions in three emission scopes. It incorporates the emissions from production processes, material handling, storage, transportation, and waste disposal for further treatment under a carbon cap-and-trade regulation. With the help of Maple software, a convex total cost function was solved. Then, a numerical example and sensitivity analysis was provided.

The proposed model guides manufacturing companies in setting the optimum production quantity per cycle. We found that the decision on the production quantity depends on the values of the production rate, setup cost, holding cost, fixed cost per delivery, fixed cost for waste disposal, fuel price, and other parameters that relate to emission prices, such as distance to a customer and a third-party company, the fuel consumption rate of the truck, and average electricity consumption for production and storage. The total cost is highly dependent on the values of the delivery distance, unit production cost, carbon cap, carbon price, and fuel price. Managers must carefully control the production cost per unit because it has a significant impact on total costs. In addition, managers must reduce inventory costs per unit because it is detrimental to the company and the environment.

This study found that the carbon cap has a significant effect on the total cost. However, when it is alone, the carbon cap has no effect on the optimum production lot size or total emissions. Hence, the government must carefully set the carbon price as it affects emission reduction. Delivery distance and the fuel emission standard are the two most significant factors that affect total emissions. Hence, businesses must pay close attention to these factors, for example, when searching for the best shipping option. The government also needs to consider the types of fuel and electricity sources that have better emission standards (lower emissions). However, the relationship between the fuel emission standard and its price needs further evaluation.

The study also presents a special case when the production system is imperfect and produces a percentage of defective products. In this setting, the production lot size and production cycle time are smaller than in the absence of defective products. It also results in higher total costs and total emissions.

This research assumes a disposable defective product, so further research can incorporate the possibility of reworking the defective product as in Manna et al. [23] and Priyan et al. [25], or improving the system reliability as in Moon et al. [26]. Another limitation of this study is that transportation costs and emissions are primarily determined by distance and fuel consumption, which is proportional to truckload. The effect of speed or transportation time can be considered in a future study. In future research, the existence of finished product recycling as well as green investment to reduce emissions levels can also be considered to increase the sustainability of the production system [6,11,27].