1. Introduction
As emphasized by many authors, tenderness is considered the most important qualitative characteristic of meat. Tenderness is also a highly variable characteristic, and this wide variability appears to be a significant reason for consumer dissatisfaction and reduction in beef consumption. Therefore, tenderness inconsistency is a priority issue for the meat industry [
1].
Tenderness can be evaluated by direct methods, such as instrumental or sensorial assessments, or by indirect methods, using muscular characteristics as tenderness predictors. Sensory methods are expensive, difficult to organize and time consuming [
2]. In addition, these methods are invasive, and cannot be performed early enough to allow carcasses to be adapted to markets according to their level of tenderness. Thus, there is a need for method that is available early post mortem to estimate the tenderness potential of each carcass, and among the possible methods, the abundance of certain proteins is of particular interest for predicting tenderness [
3,
4]. Previous works reviewed by Picard et al. [
5] made it possible to identify candidate biomarkers of tenderness. They belong to numerous biological pathways: heat shock proteins, oxidative and glycolytic metabolism, oxidative stress, muscle structure and contraction and proteolysis.
Predicting the overall tenderness of the whole carcass with a reduced number of indicators could be of interest for the beef meat chain. Indeed, with such information, retailers would be able to guide meat samples either to the traditional butchery circuits (if they are of good quality) or to the boning circuit (for those with a poor level of quality), thereby meeting consumer expectations. Therefore, it is interesting to investigate whether biomarkers of one muscle could predict the tenderness of another muscle of the carcass, and thus to evaluate the possibility of predicting the tenderness of a whole carcass by sampling only a reduced number of muscles.
Thus, the aim of the present work was to identify, from among a pool of 20 biomarkers of interest measured in five different muscles, whether a combination of biomarkers could predict the tenderness of each of the five muscles. Therefore, a specific statistical methodology adapted to a low number of samples with a large number of observations [
6,
7] was tested.
To investigate this question, we looked at five muscles that have been described in the literature as being muscles with different levels of tenderness. These were classified, according the Warner-Bratzler measurements, as tender (3.2 < Warner-Bratzler Shear Force < 3.9 kg;
Triceps brachii (TB) or intermediate (3.9 < Warner-Bratzler Shear Force < 4.6 kg;
gluteobiceps (GB)
, Vastus lateralis (VL),
semimembranosus (SM),
semitendinosus (ST)) according to [
8]. Indeed, data in the literature evaluating the correlations between the sensory tenderness of each of these five muscles and the “carcass sensory tenderness value” showed significant correlation coefficients (
p < 0.0001) going from 0.75 for the ST muscle, to 0.81 to the VL muscle [
9]. According to the literature, meat tenderness variation among muscles of the same carcass might be explained by animal genetics, feeding, handling or slaughter process [
10], but also by muscle characteristics. Indeed, muscle background toughness is mainly determined by its organization and amount of connective tissue. This property is also influenced by the level of intramuscular fat, which is known to be highly variable across the muscles [
11]. Then, the toughening and tenderization phases occur during postmortem storage of meat, as a result of sarcomere shortening during rigor development. The degree of contraction at which a muscle enters the state of rigor mortis is highly variable among different muscles within the carcass [
12]. Thus, it might be supposed that the five muscles studied represent a diversity of physicochemical and muscular characteristics, which could be considered to be representative of the whole carcass.
3. Results
3.1. Data Description
The five muscles were characterized by various slow oxidative MyHC I (
p = 0.007) and fast oxido-glycolytic MyHC IIA (
p < 0.001) proportions, whereas MyHC IIX (fast glycolytic) proportions were not significantly different among muscles (
p = 0.129;
Table 2).
The m. semimembranosus (SM) appeared to be the least slow oxidative muscle, with 10.5% of MyHC I, whereas the m. gluteobiceps (GB) and m. Triceps Brachii (TB), with proportions of MyHC I twice as large (20.4 and 22.5%, respectively), were the slowest oxidative muscles. The m. semitendinosus (ST) might be considered to be the most glycolytic muscle; even if the proportions of MyHC IIX were not significantly different among the five muscles, this muscle had low proportions of both MyHC I and MyHC IIA.
The TB muscle was the tenderest muscle, according the panelists. In accordance with this result, this muscle also had the lowest Warner-Bratzler shear force (
Table 2). At the same time, the GB, which was the toughest muscle according to the mechanical analysis, had the lowest scores for sensory tenderness. These data are related to the significant correlation between tenderness scores and shear force values observed in this study (correlation: −0.53 when considering the five muscles together;
p < 0.001). However, the correlation between tenderness and shear force is very muscle-dependent: for VL and ST muscles, the correlation is negative and significant (respectively −0.68 and 0.79), whereas for muscles GB, SM and TB, the correlation is non-significant.
Among the 20 analyzed biomarkers, three did not show a difference in relative abundances between the five muscles: αB-crystalin (
p = 0.179), prdx6 (
p = 0.293) and α-actin (
p = 0.323) (
Table 3).
The m. Vastus lateralis (VL) showed relative abundances significantly different from other muscles for many biomarkers. Indeed, it contained significantly less eno3, mylc1f, and Hsp40, and more m-calpain, pgm1, h2afx, and MyhcIIX than the other four muscles.
However, the VL muscle was close to the ST muscle for many biomarkers, especially Hsp70-1a, grp75 and mybph.
The SM muscle might be distinguished by a relatively high abundance of Hsp27, Hsp40, Hsp70-8, Dj1, sod1, mylc1f and µ-calpain.
The relative abundance of GB and TB muscle biomarkers was close, except for the Hsp20, which was lower in the TB muscle than in the GB muscle.
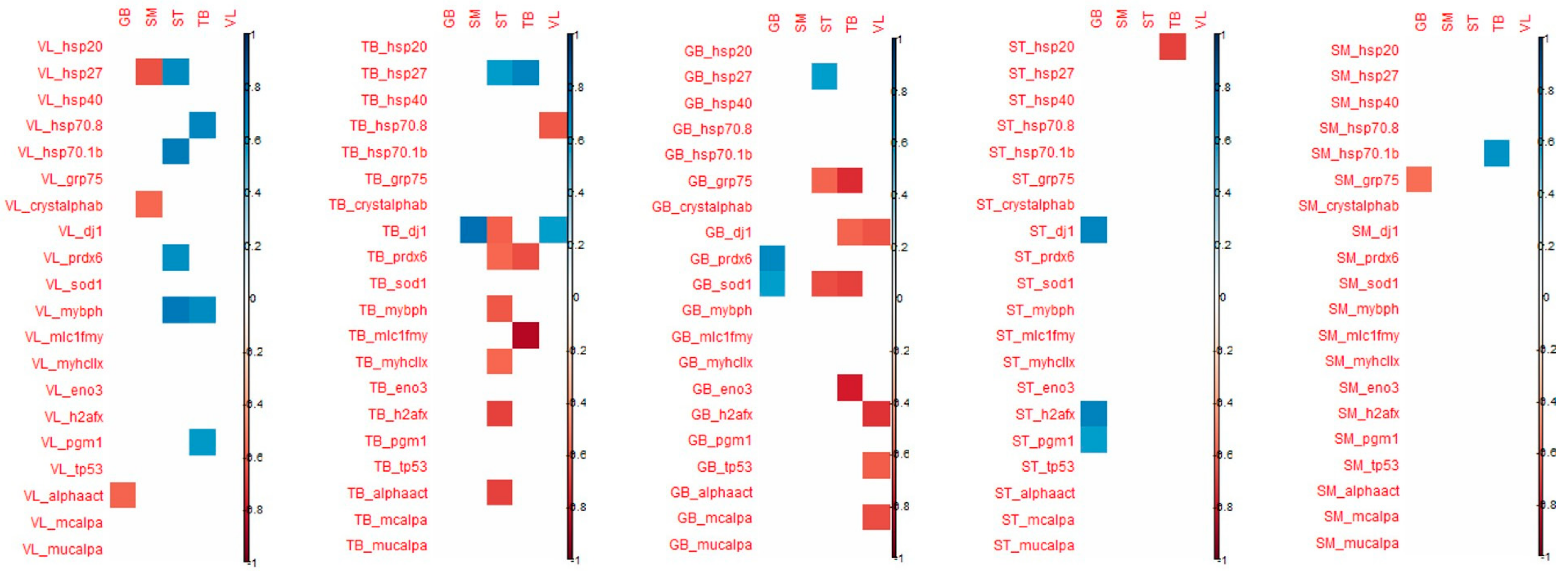
3.2. Links between Biomarkers and Tenderness Intra Muscles
When considering the tenderness of 1 muscle with associated biomarkers in the same muscle, Pearson correlations make it possible to highlight the following significant correlations (
Figure 3):
in the ST muscle, sensorial tenderness was negatively linked to Hsp40, Hsp27, pgm1
in the SM muscle, sensorial tenderness was negatively linked only to mylc1f
in the VL, GB and TB muscles, the sensorial tenderness was not significantly correlated with the abundance of any biomarkers (
Figure 3).
When considering the correlations between shear force and protein biomarkers in the same muscle, Pearson correlations make it possible to highlight the following significant correlations:
in the GB muscle, shear force was positively linked to prdx6
in the TB muscle, shear force was negatively linked to prdx6 and mylc1f, and positively to Hsp27;
in the other three muscles, the shear force was not significantly correlated with the abundance of an analyzed biomarker.
3.3. Links between Biomarkers and Tenderness among Muscles
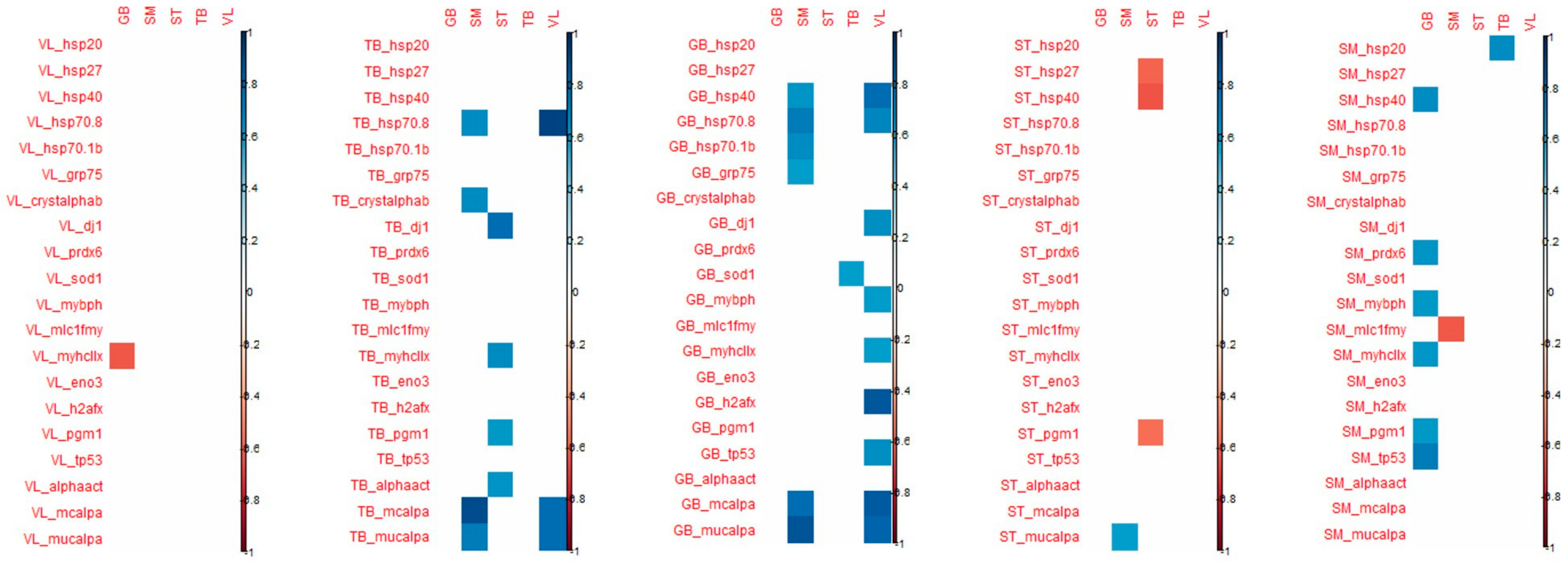
When considering the correlation that appeared between the tenderness of one muscle and the biomarker abundance of the 4 other muscles, the highest number of significant correlations were observed for VL and SM tenderness with biomarkers measured in GB and TB muscles (
Figure 4).
For biomarkers measured in GB muscle, the coefficient of correlation with VL tenderness were high particularly for h2afx (+0.85), m-calpain (+0.83), µ-calpain (+0.80), Hsp40 (+0.76), Hsp70-8 (+0.65) and for m-calpain (+0.77) and µ-calpain (+0.86), Hsp70-8 (+0.71) with SM tenderness.
For the biomarkers measured in TB muscle, high correlations were observed with VL tenderness for Hsp70-8 (+0.91), m-and µ- calpains (+0.77), as observed with biomarkers measured in GB muscle. For tenderness of SM muscle, high correlations were found with m- and µ-calpains (+0.89 and +0.71, respectively), Hsp70-8 (+0.63) as observed with VL tenderness, and with α-B crystalin (+0.63).
The tenderness of these two muscles VL and SM was especially correlated with biomarkers of GB and TB muscles.
Among these correlations, it might be noted that among biomarkers, µ-calpain, m-calpain, Hsp70-1a, Hsp70-8, tp53, pgm1 and mybph are always positively linked with tenderness, as opposed to MyhcIIx and Hsp40, which can be either positively or negatively linked to meat tenderness. Some biomarkers appeared to be more frequently correlated with tenderness: m-calpain, µ-calpain and Hsp70-8. These three biomarkers, evaluated in the TB and GB muscles, might be considered interesting biomarkers to predict meat tenderness.
Some coefficients of correlations were observed between biomarkers from TB muscle and tenderness of ST, SM and VL muscles (positively). However, biomarkers from TB muscles are mostly correlated with ST and TB shear force (negatively). It should be noted that many correlations can be observed with the tenderness of ST: dj1 (the highest; +0.76), MyhcIIx (in accordance with previous results in this muscle; +0.64), pgm1 (+0.58) and a-actin (+0.59) (
Figure 4).
Many correlations were noted between the proteins measured in SM muscle and GB tenderness, whereas for the other muscles, only a few correlations were significant. The highest number of correlations measured in ST muscle was observed for the tenderness of GB muscle (
Figure 4).
With regard to shear force, the muscle that is the most correlated with biomarkers is the ST muscle, the shear force of this muscle being especially correlated with biomarkers from VL, TB and GB muscles (
Figure 5). The biomarkers that are significantly correlated with shear force are quite different from those found for muscle tenderness even if shear force and tenderness are significantly correlated in ST and VL muscles.
The details of the correlations obtained between the either tenderness of shear force of each of the five muscles and the 20 biomarkers of each muscle have been annexed in
Figure 5.
3.4. Selection of Biomarkers the Most Predictive of Tenderness
To predict tenderness, the ddsPLS multi-block approach was used for five blocks of covariates (each one corresponding to the pool of 20 biomarkers for each of the 5 muscles) and for one block of response variables (corresponding to the five tenderness scores, one score for each muscle). Note that in the model, we entered a 6th block, , consisting of performance variables (age/weight). The covariates of were never selected in tenderness prediction, indicating that the protocol is well balanced, and that the variability of the tenderness is explained neither by weight or by age, nor by the combination of those factors.
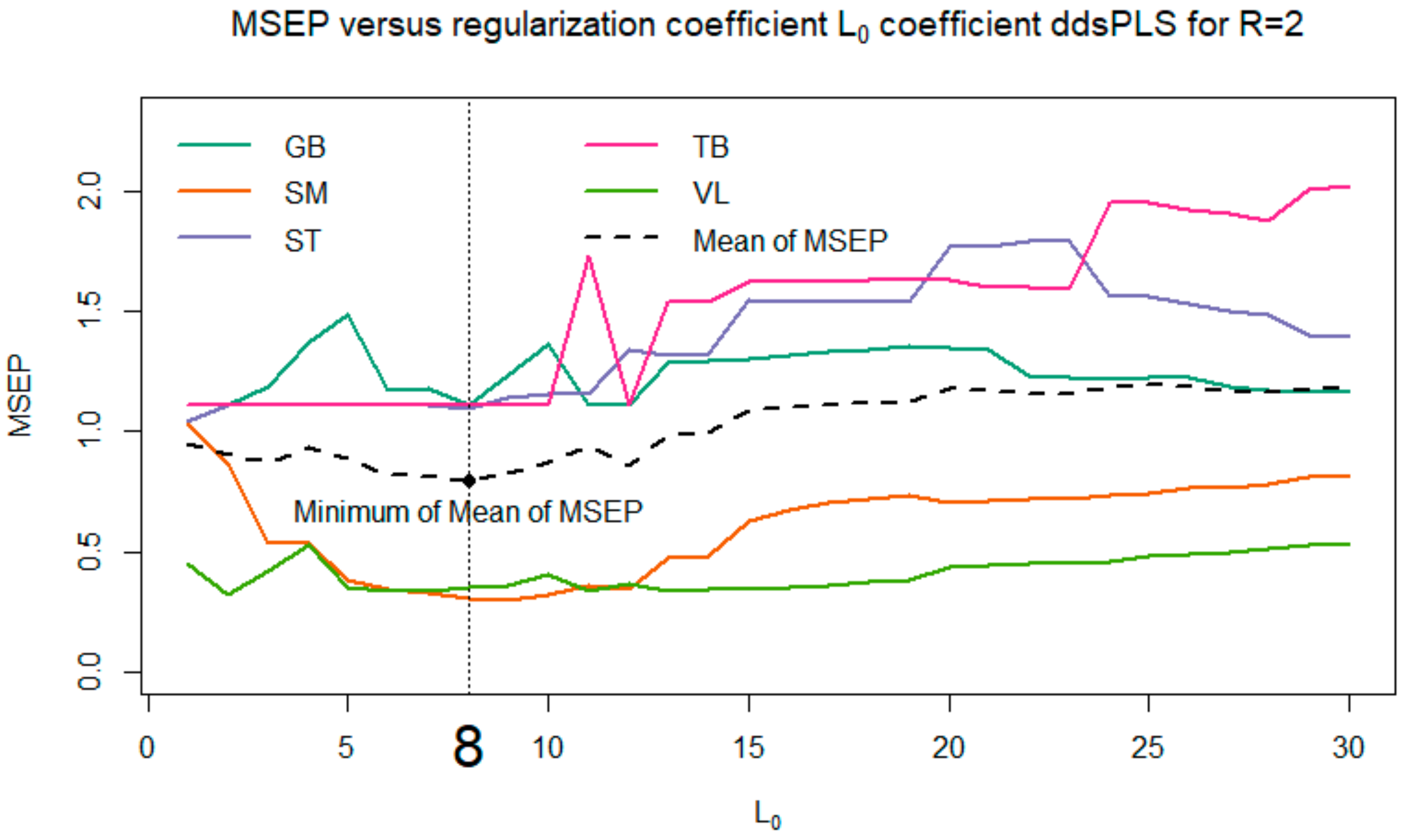
Among all the proposed models, we selected the one that minimizes the
MSEP (see
Figure 6). Thus, the model with
and
was selected.
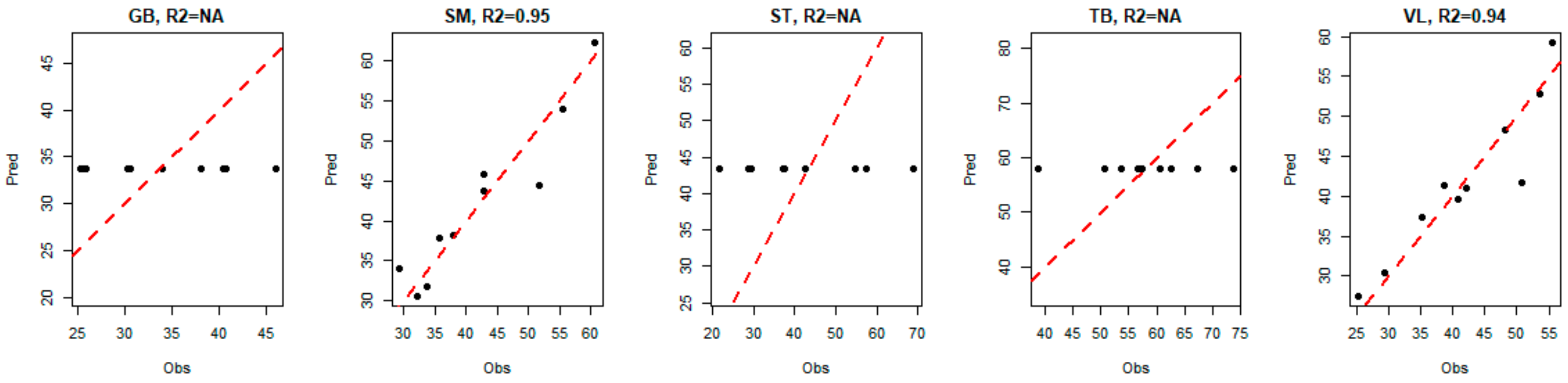
For the three muscles GB, ST and TB, the model indicated that the best way to predict tenderness is to predict the average value of the corresponding tenderness (i.e., the predicted values are equal to a constant, since there is no link with biomarkers). Hence, for these three muscles, we observe a horizontal alignment of the predicted values of tenderness, as shown in
Figure 7.
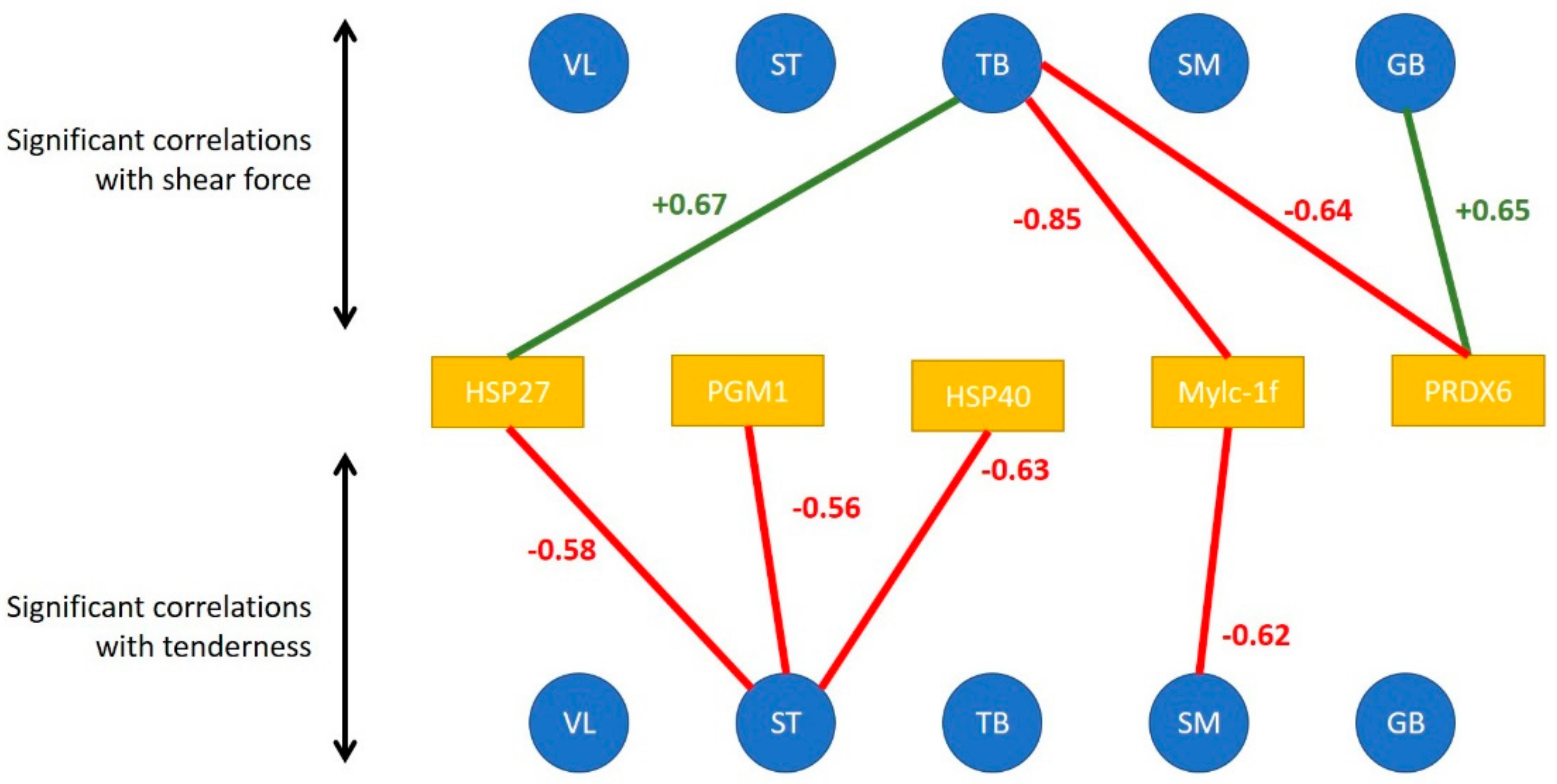
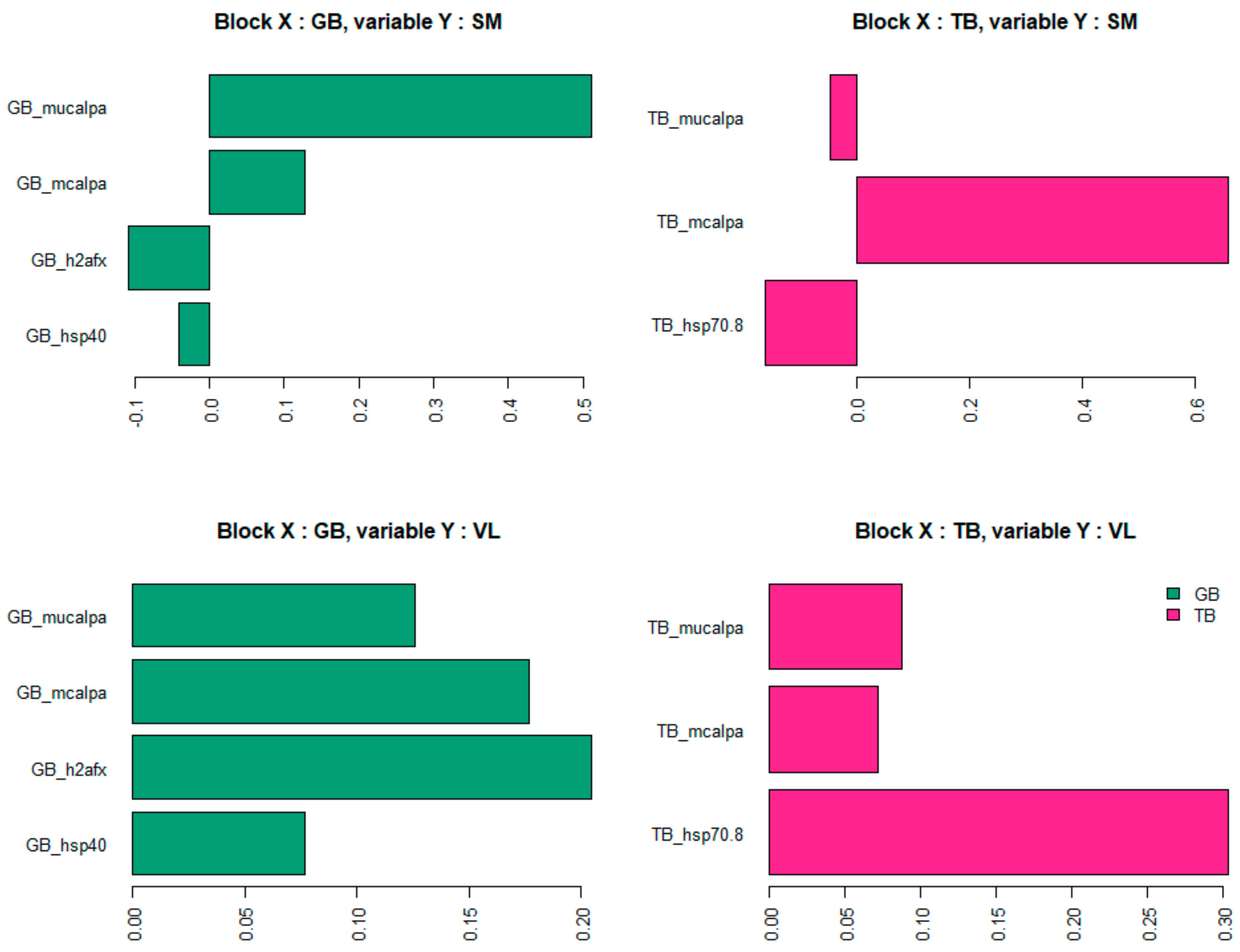
For VL and SM muscles, the seven biomarkers that were selected by the model to predict global tenderness were derived from two different muscles: GB and TB. However, none of the selected biomarkers came from the muscle for which tenderness was predicted (
Table 4). Among these seven biomarkers, two are derived from both GB muscle and TB muscle, leading to the number of distinct biomarkers solicited in the model being five.
The seven selected biomarkers measured in GB or TB muscles were the same for VL tenderness prediction and for SM tenderness prediction. These proteins belong to the heat shock protein family (Hsp40 and Hsp70-8) or were associated with the proteolysis (m-calpain and µ-calpain) and to the cellular response to DNA damage during oxidative stress (h2afx). Among the biomarkers selected in the model, two were selected in both the GB and the TB muscles: µ-calpain and m-calpain. The three other biomarkers are not the same; the model selected the h2afx and Hsp40 from the GB muscle and the Hsp70-8 from the TB muscle.
It is interesting to note that three biomarkers (see
Figure 8) enter with a positive impact on SM and VL tenderness prediction: µ-calpain and m-calpain of the GB muscle and m-calpain of the TB muscle. Whereas the other biomarkers are associated with tenderness prediction either positively (in the VL muscle) or negatively (in the SM muscle), depending on the muscle in which it was measured: h2afx and Hsp40 of the GB muscle, Hsp70-8 of the TB muscle.
Thus, the contribution of biomarkers in the prediction of tenderness seems to be modulated according to the muscle.
The same analysis was performed by replacing the tenderness score with the shear force value. It appears that none of the shear force values were correctly predicted by the muscular biomarkers, regardless of the origin of the biomarkers. The model explained no more than 20% of the shear force, except for the TB muscle, where 75% of the shear force could be explained by 2 proteins: the eno3 coming from the GB muscle, and the mylc1f coming from the TB muscle. However, due to the poor quality of the model, it was difficult to draw conclusions on the relevance of these two biomarkers in a definitive way.
4. Discussion
To complete the approach presented here, several models were evaluated for various values of the parameters
and
R; the corresponding results are not provided here. One can observe that these models show good stability. More precisely, if we focused in the present paper on the case
and
R = 2, which makes it possible to minimize the mean of MSEP, we also studied cases where
(corresponding to the flat area of the MSEP curves in
Figure 6). It appears that the biomarkers selected for
are successively supplemented with 1, 2, 3 (and so on) biomarkers when selecting a maximum of 5, 6, 7 (and so on) biomarkers. Moreover, we also tried to explore the models based on a multi-block model with a block of response variables
Y built only with the VL and SM tenderness, instead of the tenderness scores of the five muscles. The corresponding models selected the same biomarkers as previously indicated, and returned
R2 values close to the values indicated in
Figure 7. These different elements confirm the interest and relevance of the method, accurately predicting meat tenderness. The use of a multi-block model here (based on a linear relationship) allows us to highlight significant links between the tenderness and the abundance of certain biomarkers, even if they were not significantly correlated with tenderness. It is not inconsistent that the combination of several markers (individually little correlated with tenderness) can provide a relevant prediction of tenderness. It can also be noted that several biomarkers, significantly correlated with muscle tenderness, were not selected in the predictive models; this was certainly due to there being redundant information among different biomarkers. The two approaches, correlations and predictions, are thus fully complementary for resulting in relevant conclusions.
The highest number of significant correlations was observed for tenderness of VL and SM muscles with biomarkers measured in GB and TB muscles, mainly for VL tenderness with 12 proteins significantly correlated with tenderness, and 13 in SM muscle. Some coefficients of correlation were high both with SM and VL tenderness: for Hsp70-8, m-calpain and µ-calpain measured in GB and TB muscles. High correlations were found with VL tenderness for h2afx, and Hsp40 measured in GB and TB muscles. These proteins are the same that retained in the equations of prediction of the tenderness of these two muscles with the protein measured in GB muscle. Globally, the highest coefficients were found for VL and SM tenderness for most of the correlations: Hsp20, Hsp40, Hsp70-8, prdx6, dj1, MyBP-H, MyhcIIX, eno3, h2afx, pgm1, m- and µ-calpain. This suggests an important contribution of these proteins in the tenderness of these muscles.
Two models made it possible to predict the tenderness of a muscle (SM and VL) by the biomarkers of two other muscles of the carcasses (GB and TB). The selected proteins are the same in both predicted muscles, which testifies to the importance of these proteins in tenderness construction. Nevertheless, the coefficients associated with certain biomarkers highlight a different hierarchy in the selected biomarkers. Moreover, it might be noted that some coefficients might be reversed from one muscle to another. The fact that tenderness can be predicted only in the two muscles VL and SM can be explained by the fact that these two muscles are very different from the other three in terms of abundances of the analyzed proteins. The two muscles VL and SM are opposite for some proteins such as mylc1f and Hsp40, with the highest abundances being found in SM and the lowest in VL muscle. The abundances of m-calpain and µ-calpain are particular to these two muscles, in comparison to the three others, as m-calpain abundance was the highest in VL and µ-calpain abundance was the highest in SM muscle.
Both correlation and prediction analysis highlighted five proteins among the 20 putatively analyzed as interesting candidate biomarkers of tenderness: m-calpain, µ-calpain, Hsp40, Hsp70-8 and h2afx.
Among the selected biomarkers, the abundance of the m-calpain measured in GB and TB muscles enters the model with a positive coefficient in the prediction of the tenderness of the two muscles (VL and SM) and with a high effect. That highlights a major role of this protein in tenderness independent of the type of muscle. Meanwhile, the role of µ-calpain seems to be more muscle type-dependent.
Calpains (CAPN) are a large family of intracellular Ca
2+-dependent cysteine-neutral proteases. The CAPN system is one of the endogenous proteolysis systems, and it plays a major role in meat tenderization [
23]. Calpain’s actions are mainly due to having two major isoforms: μ-calpain and m-calpain. These two isoforms require different amounts of calcium in vitro, and their names suggest that they help promote the microscopic and milli-molar concentrations of intracellular Ca
2+ [
24]. Among CAPN enzymes responsible for meat tenderization, μ-calpain, which is encoded by the CAPN1 gene, plays a predominant role [
25]. As far as we know, calpains can cleave limited myofibrillar proteins such as titin, desmin and vinculin, and contribute to the improvement of tenderness, whereas, high levels of calpastatin are related to decreased proteolysis and increased meat toughness [
26,
27]. Furthermore, both proteases were found to interact with several proteins belonging to different pathways: homeostasis, structure, glucose metabolism, heat stress, mitochondria, apoptosis. The different implication of calpains in meat tenderness observed in the present study could be explained by a different role of each calpain in tenderization. In accordance with this hypothesis, it was shown in lamb m.
Biceps femoris that the autolysis of μ-calpain and loss of most of the activity occur within 7 days post-mortem whereas m-calpain activity did not decrease up to 56 days post-mortem. Moreover, very little post-mortem proteolysis is observed in the muscles of μ-calpain knockout mice suggesting its predominant effect on catalysis of proteins during postmortem aging.
Thus, we confirm that these proteases might be considered good biomarkers of beef tenderness, as already shown in the literature [
16,
28,
29]. Moreover, we also confirmed, as previously shown by Guillemin et al. [
16], that the contribution of proteolysis to tenderness might be different from one muscle to another. Indeed, these authors indicated that, in the LT muscle, m-calpain and µ-calpain are positively correlated with tenderness, whereas, in the ST muscle, tenderness appears to be positively correlated with µ-calpain, but negatively with m-calpain. These authors indicated that the inverse relation between tenderness and µ-calpain from one muscle to another is coherent with the inverse correlation between contractile and metabolic proteins and tenderness in ST and LT, and thus that muscular particularities might determine calpain contribution to tenderness. Thus, our results seem to confirm this hypothesis to the extent that the contribution of μ-calpain of TB in the construction of tenderness is positive in the VL and negative in the SM. Some studies analyzing a suppression of µ-calpain expression showed an increase in cell death through an activation of apoptotic caspases and an increase in Hsp27, Hsp70, and Hsp90 expressions. These data illustrate a link between the different biomarkers involved in tenderness prediction.
Heat Shock Proteins preserve cellular proteins against denaturation and possible loss of function [
30]. A large set of Hsp have been associated with meat tenderness. For example, Guillemin et al. [
28] proposed the ratio of Hsp70/small Hsps as a good predictor of muscle tenderness in charolais young bulls. The results of Bernard et al. [
31], on the same cattle, found Hsp40 (DNAJA1 gene) to be a positive marker of beef toughness in ST muscle. Hsp40s represent a large protein family that functions as a co-chaperone protein of Hsp70. These two families, Hsp70 and Hsp40, are often co-localized in the same subcellular compartment. Hsp40s function as ATP-independent chaperones that bind non-native polypeptides and protect cells from stress by preventing protein aggregation. The major function of Hsp40 proteins is to regulate ATP-dependent polypeptide binding by Hsp70 protein. Among the Hsp70 family, the Hsp70-8 is known to slow down the process of cellular death and to protect tissues against oxidative stress.
According to Picard et al. [
29], there is an inverse relationship between tenderness and proteins from the small Hsp family according to muscle type and breed. It is thus not astonishing that the influence of these proteins on tenderness might be reversed when considering two different muscles such as SM and VL. In accordance with these authors, the results of Guillemin et al. [
32] showed different relationships between proteins of the interactome of tenderness and tenderness in two different muscles such as ST and LT. The results of the present study confirm these observations.
The last protein involved in the prediction of VL and SM tenderness in the present study was h2afx. H2afx belongs to the histone h2a family involved in the cellular response to DNA damage, notably during oxidative stress [
33]. It has recently been shown that h2ax specifically controls the recruitment of DNA repair proteins to the sites of DNA damage [
34]. In eukaryotic cells, one of the first cellular response is the phosphorylation of h2afx within 1 to 3 min after damage. The number of H2AX phosphorylated molecules, γ-h2ax, increases linearly with the severity of the damage and is necessary for the recruitment of other factors to the sites of DNA damage [
35]. During stresses, h2afx recruits metabolism enzymes to activate energy generation, enhance protein synthesis, and recruit anti-stress proteins as hspa1a to protect cells from degradation. H2afx was proposed as a potential biomarker of beef tenderness by Guillemin et al. [
16], who showed that three proteins, h2afx, sumo4 and tp53, were situated at the crossroads between groups of proteins involved in tenderness, as metabolism, structure, cellular stress, oxidative stress, apoptosis, and calcium signaling proteins. As h2afx modulates different pathways and ensure genome integrity [
36], it could have a crucial role in meat tenderness, which is confirmed by the results of the present study. However, why its abundance only as measured in GB muscle is explicative of tenderness of SM and VL muscles, and why the relationships with tenderness are inverted in these two muscles, remain to be understood.
In conclusion, this study made it possible to propose an original statistical methodology well adapted to this type of multi-block data set with several covariates (biomarkers) larger than the number n of individuals (carcasses). Moreover, seven proteins could be proposed as candidate biomarkers of tenderness, but the understanding of the biological mechanisms involved according to the muscle considered, remain to be deeply analyzed.