Multiple Modeling Techniques for Assessing Sesame Oil Extraction under Various Operating Conditions and Solvents
Abstract
1. Introduction
2. Methodology
2.1. Modeling Techniques
2.1.1. Response Surface Methodology (RSM)
2.1.2. Linear and Multiquadric Radial Basis Function (LRBF and QRBF)
- Linear Radial Basis Function (LRBF): φ(r) = r.
- Gaussian: .
- Quadric Radial Basis Function (QRBF): .
- Inverse multiquadric: .
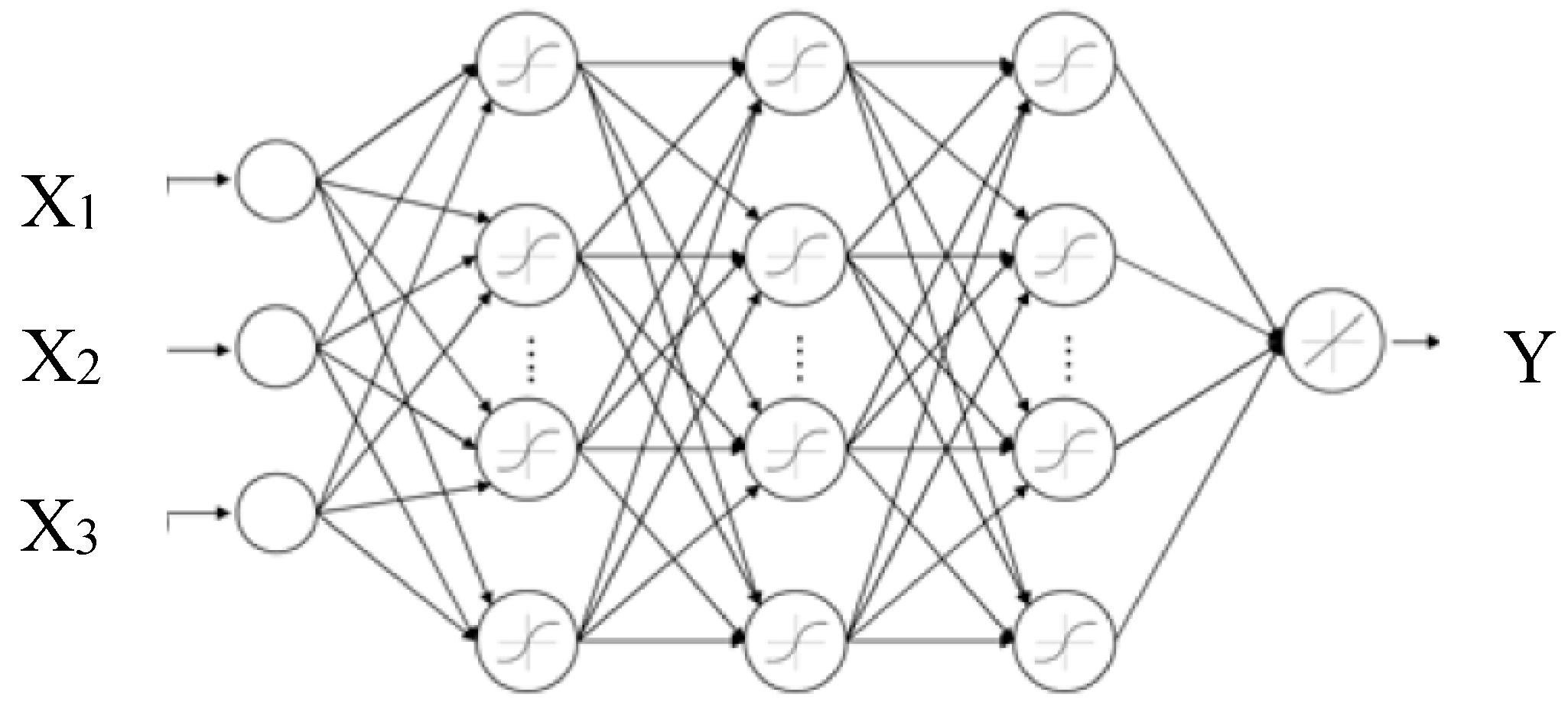
2.1.3. Artificial Neural Network (ANN)
2.2. Model Validation and Evaluation
2.2.1. Root Mean Square Error (RMSE)
2.2.2. R2 and R2adj
3. Results and Discussion
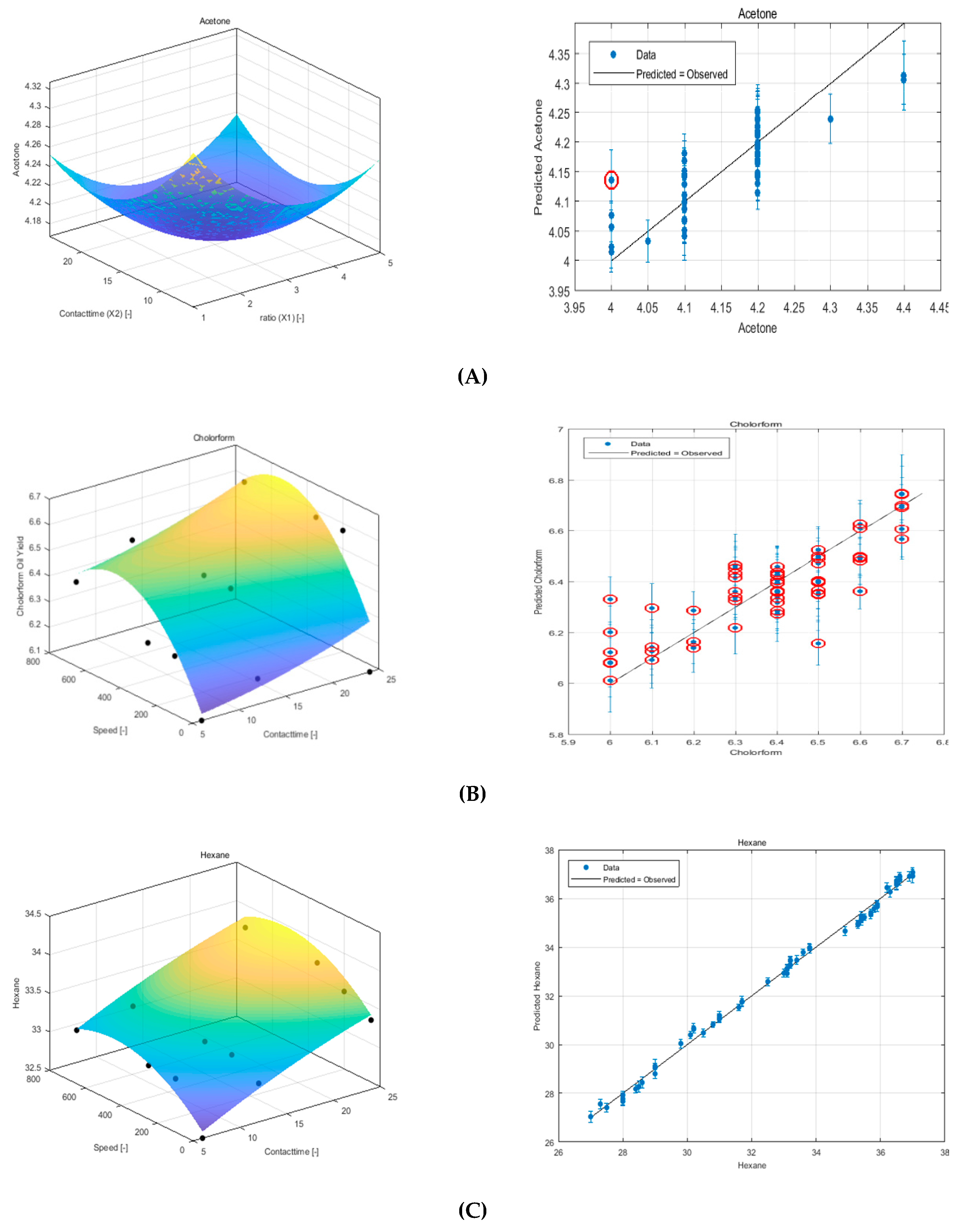
3.1. Modeling Experimental Data Using RSM
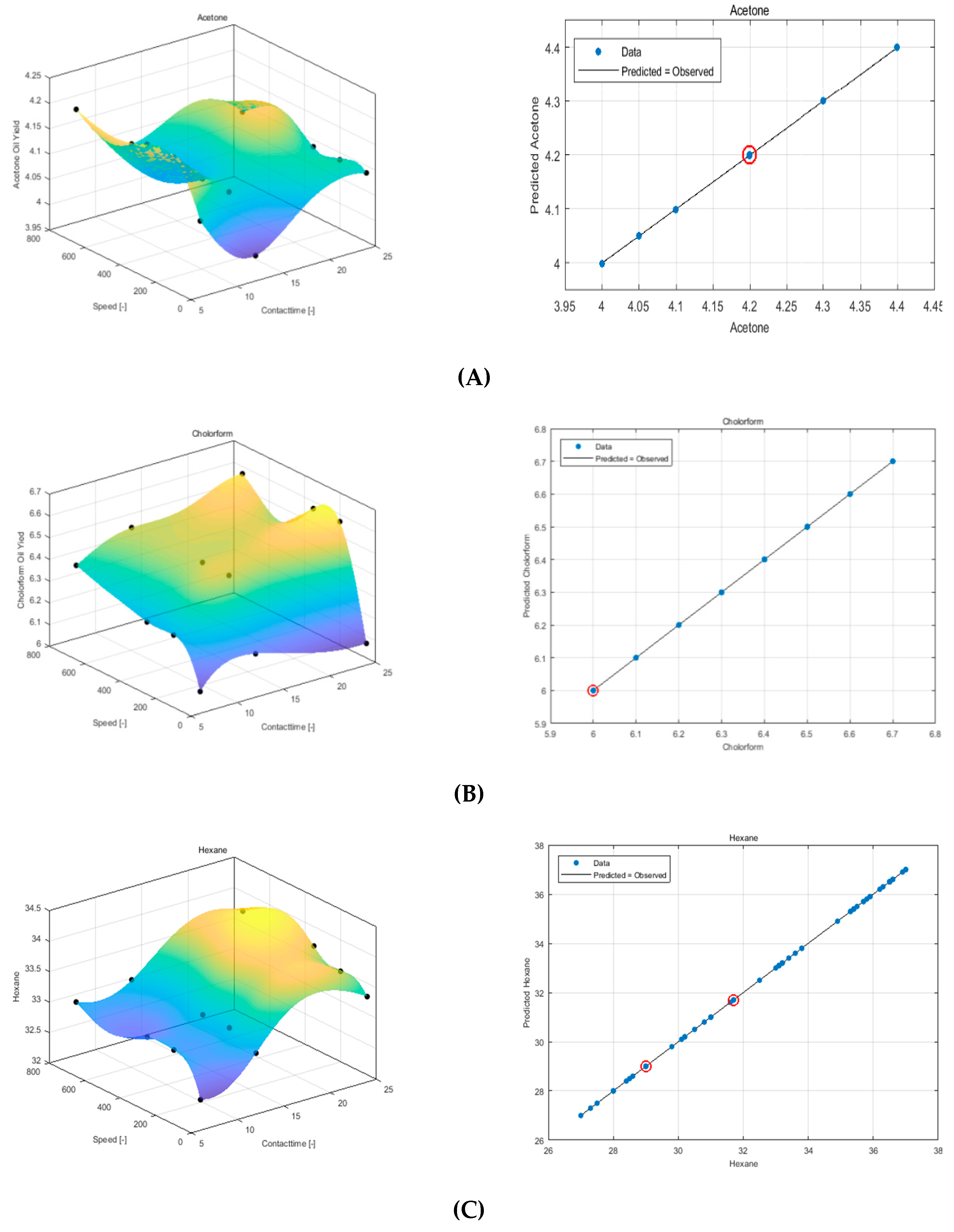
3.1.1. Acetone
3.1.2. Chloroform
3.1.3. Hexane
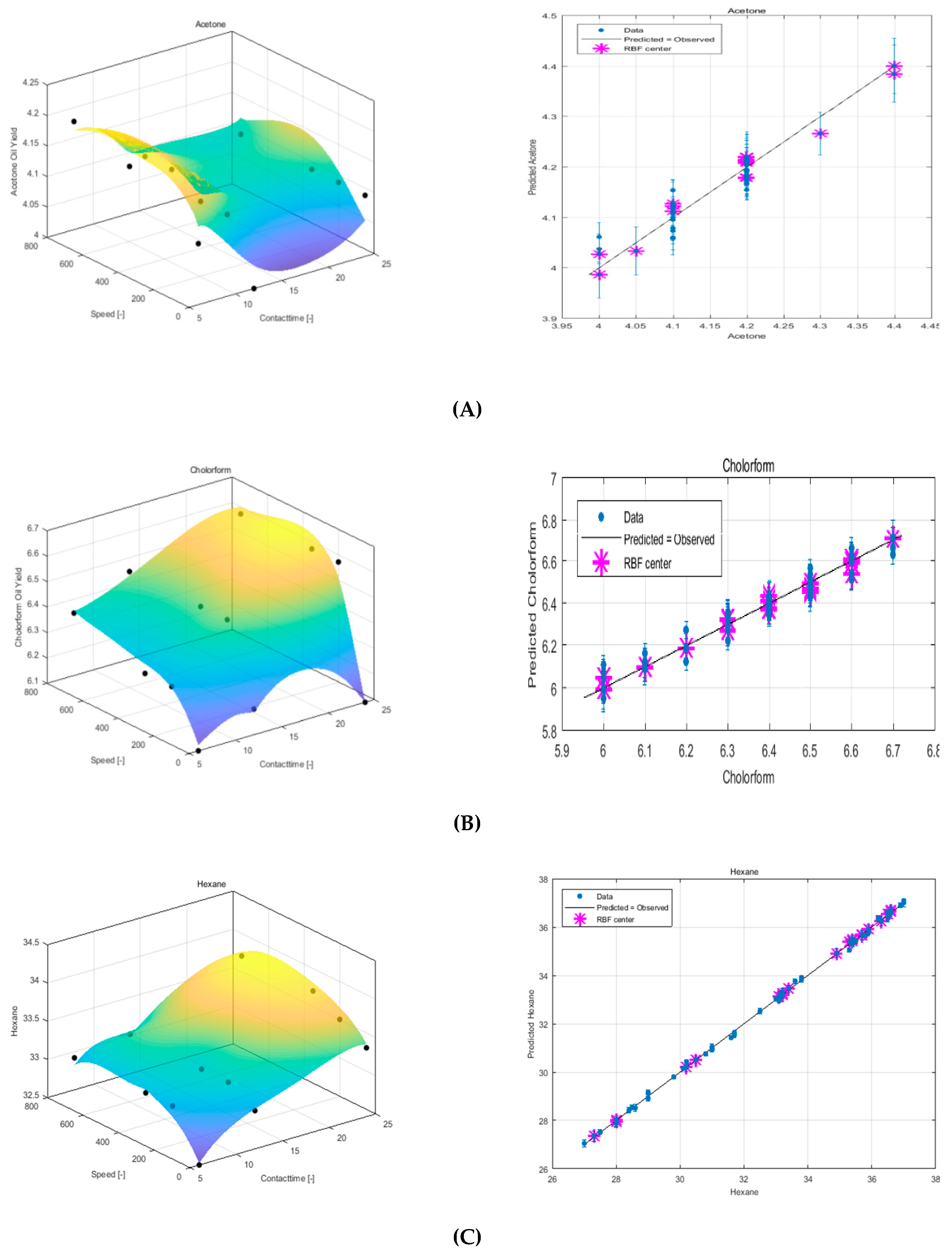
3.2. Modeling Experimental Data Using LRBF
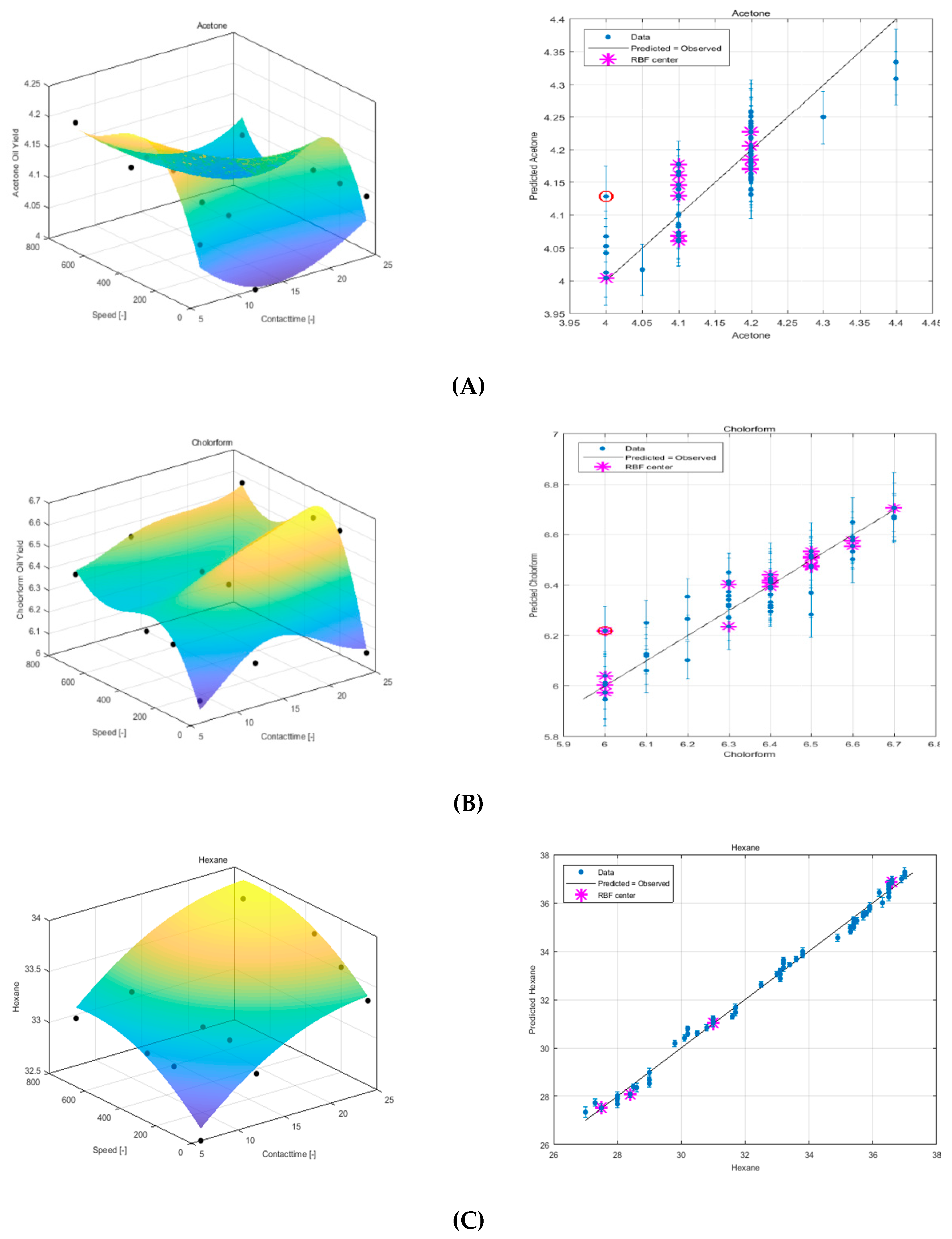
3.3. Modeling Experimental Data Using QRBF
3.4. Modeling Experimental Data Using ANN
4. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Seeds/Solvent Ratio | Contact Time (hour) | Stirring Speed (rpm) | Oil Yield % | ||
| By Chloroform | By Acetone | By Hexane | |||
| 1:1 | 6 | 0 | 6 | 4 | 27 |
| 1:1 | 6 | 150 | 6.3 | 4.3 | 27.5 |
| 1:1 | 6 | 300 | 6.5 | 4.4 | 28 |
| 1:1 | 6 | 700 | 6.5 | 4.4 | 28 |
| 1:1 | 12 | 0 | 6 | 4 | 27.3 |
| 1:1 | 12 | 150 | 6 | 4.2 | 28 |
| 1:1 | 12 | 300 | 6.3 | 4.2 | 28.4 |
| 1:1 | 12 | 700 | 6.3 | 4.2 | 28.5 |
| 1:1 | 24 | 0 | 6.5 | 4.1 | 28.6 |
| 1:1 | 24 | 150 | 6.7 | 4.2 | 29 |
| 1:1 | 24 | 300 | 6.7 | 4.2 | 29 |
| 1:1 | 24 | 700 | 6.7 | 4.2 | 29 |
| 1:2 | 6 | 0 | 6 | 4.1 | 29.8 |
| 1:2 | 6 | 150 | 6.2 | 4.2 | 30.1 |
| 1:2 | 6 | 300 | 6.3 | 4.2 | 30.2 |
| 1:2 | 6 | 700 | 6.5 | 4.2 | 30.2 |
| 1:2 | 12 | 0 | 6.5 | 4.05 | 30.5 |
| 1:2 | 12 | 150 | 6.6 | 4.2 | 30.8 |
| 1:2 | 12 | 300 | 6.6 | 4.2 | 31 |
| 1:2 | 12 | 700 | 6.6 | 4.2 | 31 |
| 1:2 | 24 | 0 | 6.3 | 4.1 | 31 |
| 1:2 | 24 | 150 | 6.7 | 4.2 | 31.6 |
| 1:2 | 24 | 300 | 6.7 | 4.2 | 31.7 |
| 1:2 | 24 | 700 | 6.7 | 4.2 | 31.7 |
| 1:3 | 6 | 0 | 6.1 | 4.1 | 32.5 |
| 1:3 | 6 | 150 | 6.3 | 4.2 | 33.1 |
| 1:3 | 6 | 300 | 6.3 | 4.2 | 33.1 |
| 1:3 | 6 | 700 | 6.4 | 4.2 | 33.1 |
| 1:3 | 12 | 0 | 6.2 | 4 | 33 |
| 1:3 | 12 | 150 | 6.5 | 4.1 | 33.2 |
| 1:3 | 12 | 300 | 6.5 | 4.1 | 33.2 |
| 1:3 | 12 | 700 | 6.5 | 4.1 | 33.2 |
| 1:3 | 24 | 0 | 6.1 | 4.1 | 33.4 |
| 1:3 | 24 | 150 | 6.6 | 4.1 | 33.6 |
| 1:3 | 24 | 300 | 6.6 | 4.1 | 33.8 |
| 1:3 | 24 | 700 | 6.6 | 4.1 | 33.8 |
| 1:4 | 6 | 0 | 6.2 | 4.1 | 34.9 |
| 1:4 | 6 | 150 | 6.4 | 4.2 | 35.3 |
| 1:4 | 6 | 300 | 6.4 | 4.2 | 35.4 |
| 1:4 | 6 | 700 | 6.4 | 4.2 | 35.4 |
| 1:4 | 12 | 0 | 6.1 | 4 | 35.3 |
| 1:4 | 12 | 150 | 6.3 | 4.2 | 35.5 |
| 1:4 | 12 | 300 | 6.3 | 4.2 | 35.7 |
| 1:4 | 12 | 700 | 6.3 | 4.2 | 35.7 |
| 1:4 | 24 | 0 | 6 | 4 | 35.4 |
| 1:4 | 24 | 150 | 6.5 | 4.1 | 35.8 |
| 1:4 | 24 | 300 | 6.5 | 4.2 | 35.9 |
| 1:4 | 24 | 700 | 6.5 | 4.2 | 35.9 |
| 1:5 | 6 | 0 | 6.1 | 4.1 | 36.3 |
| 1:5 | 6 | 150 | 6.4 | 4.2 | 36.5 |
| 1:5 | 6 | 300 | 6.4 | 4.2 | 36.5 |
| 1:5 | 6 | 700 | 6.4 | 4.2 | 36.5 |
| 1:5 | 12 | 0 | 6.1 | 4 | 36.2 |
| 1:5 | 12 | 150 | 6.4 | 4.2 | 36.5 |
| 1:5 | 12 | 300 | 6.4 | 4.2 | 36.6 |
| 1:5 | 12 | 700 | 6.4 | 4.2 | 36.6 |
| 1:5 | 24 | 0 | 6 | 4.1 | 36.5 |
| 1:5 | 24 | 150 | 6.4 | 4.2 | 36.9 |
| 1:5 | 24 | 300 | 6.4 | 4.2 | 37 |
| 1:5 | 24 | 700 | 6.4 | 4.2 | 37 |
References
- Hwang, L.S. Sesame oil. Bailey’s Ind. Oil Fat Prod. 2005, 2, 547–552. [Google Scholar]
- Dahlan, I.; Ahmad, Z.; Fadly, M.; Lee, K.T.; Kamaruddin, A.H.; Mohamed, A.R. Parameters optimization of rice husk ash (RHA)/CaO/CeO2 sorbent for predicting SO2/NO sorption capacity using response surface and neural network models. J. Hazard. Mater. 2010, 178, 249–257. [Google Scholar] [CrossRef]
- Elleuch, M.; Bedigian, D.; Zitoun, A.; Zouari, N. Sesame (Sesamum indicum L.) seeds in food, nutrition and health. Nuts Seeds Health Dis. Prev. 2011, 1029–1036. [Google Scholar]
- Kurt, C. Variation in oil content and fatty acid composition of sesame accessions from different origins. Grasas Y Aceites 2018, 69, 241. [Google Scholar] [CrossRef]
- Durmaz, G.; Gökmen, V. Impacts of roasting oily seeds and nuts on their extracted oils. Lipid Technol. 2010, 22, 179–182. [Google Scholar] [CrossRef]
- Elkhaleefa, A.; Shigidi, I. Optimization of sesame oil extraction process conditions. Adv. Chem. Eng. Sci. 2015, 5, 305–310. [Google Scholar] [CrossRef]
- Zhou, J.-C.; Feng, D.-W.; Zheng, G.-S. Extraction of sesamin from sesame oil using macroporous resin. J. Food Eng. 2010, 100, 289–293. [Google Scholar] [CrossRef]
- Elleuch, M.; Besbes, S.; Roiseux, O.; Blecker, C.; Attia, H. Quality characteristics of sesame seeds and by-products. Food Chem. 2007, 103, 641–650. [Google Scholar] [CrossRef]
- Corso, M.P.; Fagundes-Klen, M.R.; Silva, E.A.; Cardozo Filho, L.; Santos, J.N.; Freitas, L.S.; Dariva, C. Extraction of sesame seed (Sesamun indicum L.) oil using compressed propane and supercritical carbon dioxide. J. Supercrit. Fluids 2010, 52, 56–61. [Google Scholar] [CrossRef]
- Latif, S.; Anwar, F. Aqueous enzymatic sesame oil and protein extraction. Food Chem. 2011, 125, 679–684. [Google Scholar] [CrossRef]
- Ribeiro, S.A.O.; Nicacio, A.E.; Zanqui, A.B.; Biondo, P.B.F.; de Abreu-Filho, B.A.; Visentainer, J.V.; Gomes, S.T.M.; Matsushita, M. Improvements in the quality of sesame oil obtained by a green extraction method using enzymes. LWT-Food Sci. Technol. 2016, 65, 464–470. [Google Scholar] [CrossRef]
- Zhang, Y.-l.; Li, S.; Yin, C.-p.; Jiang, D.-h.; Yan, F.-f.; Xu, T. Response surface optimisation of aqueous enzymatic oil extraction from bayberry (Myrica rubra) kernels. Food Chem. 2012, 135, 304–308. [Google Scholar] [CrossRef]
- Casas, M.P.; González, H.D. Enzyme-assisted aqueous extraction processes. In Water Extraction of Bioactive Compounds; Elsevier: Amsterdam, The Netherlands, 2017; pp. 333–368. [Google Scholar]
- Anwar, F.; Zreen, Z.; Sultana, B.; Jamil, A. Enzyme-aided cold pressing of flaxseed (Linum usitatissimum L.): Enhancement in yield, quality and phenolics of the oil. Grasas Y Aceites 2013, 64, 463–471. [Google Scholar] [CrossRef]
- Shigidi, I.; Elkhaleefa, A. Parameters Optimization, Modelling and Kinetics of Balanites Aegyptiaca Kernel oil extraction. Int. J. Chem. Eng. Appl. Sci. 2015, 5, 1–4. [Google Scholar]
- Osman, H.; Shigidi, I.; Elkaleefa, A. Optimization Of Sesame Seeds Oil Extraction Operating Conditions Using The Response Surface Design Methodology. Sci. Study Res. Chem. Chem. Eng. Biotechnol. Food Ind. 2016, 17, 335–347. [Google Scholar]
- Maran, J.P.; Priya, B. Comparison of response surface methodology and artificial neural network approach towards efficient ultrasound-assisted biodiesel production from muskmelon oil. Ultrason. Sonochem. 2015, 23, 192–200. [Google Scholar] [CrossRef] [PubMed]
- Moghaddam, M.G.; Khajeh, M. Comparison of Response Surface Methodology and Artificial Neural Network in Predicting the Microwave-Assisted Extraction Procedure to Determine Zinc in Fish Muscles. Food Nutr. Sci. 2011, 2. [Google Scholar] [CrossRef]
- Bakhtiari, H.; Karimi, M.; Rezazadeh, S. Modeling, analysis and multi-objective optimization of twist extrusion process using predictive models and meta-heuristic approaches, based on finite element results. J. Intell. Manuf. 2016, 27, 463–473. [Google Scholar] [CrossRef]
- Speck, F.; Raja, S.; Ramesh, V.; Thivaharan, V. Modelling and optimization of homogenous photo-fenton degradation of rhodamine B by response surface methodology and artificial neural network. Int. J. Environ. Res. 2016, 10, 543–554. [Google Scholar]
- Osman, H. Optimizing Model Base Predictive Control for Combustion Boiler Process at High Model Uncertainty. Chem. Biochem. Eng. Q. 2017, 31, 313–324. [Google Scholar] [CrossRef]
- Osman, H. LQ evolution algorithm optimizer for model predictive control at model uncertainty. In Proceedings of the 2014 14th International Conference Control, Automation and Systems (ICCAS), Seoul, Korea, 22–25 October 2014; pp. 1272–1277. [Google Scholar]
- Sacks, J.; Welch, W.J.; Mitchell, T.J.; Wynn, H.P. Design and analysis of computer experiments. Stat. Sci. 1989, 409–423. [Google Scholar] [CrossRef]
- Box, G.E.; Wilson, K.B. On the experimental attainment of optimum conditions. J. R. Stat. Soc. Ser. B (Methodol.) 1951, 13, 1–38. [Google Scholar] [CrossRef]
- Hardy, R.L. Multiquadric equations of topography and other irregular surfaces. J. Geophys. Res. 1971, 76, 1905–1915. [Google Scholar] [CrossRef]
- Schölkopf, B.; Burges, C.; Vapnik, V. Incorporating invariances in support vector learning machines. In Proceedings of the International Conference on Artificial Neural Networks, Bochum, Germany, 16–19 July 1996; pp. 47–52. [Google Scholar]
- Haykin, S. Neural Networks: A Comprehensive Foundation; Prentice Hall PTR: Upper Saddle River, NJ, USA, 1994. [Google Scholar]
- Simpson, T.W.; Mauery, T.M.; Korte, J.J.; Mistree, F. Kriging models for global approximation in simulation-based multidisciplinary design optimization. AIAA J. 2001, 39, 2233–2241. [Google Scholar] [CrossRef]
- Forrester, A.I.; Keane, A.J. Recent advances in surrogate-based optimization. Prog. Aerosp. Sci. 2009, 45, 50–79. [Google Scholar] [CrossRef]
- Amouzgar, K.; Strömberg, N. Radial basis functions as surrogate models with a priori bias in comparison with a posteriori bias. Struct. Multidiscip. Optim. 2017, 55, 1453–1469. [Google Scholar] [CrossRef]
- Fang, H.; Rais-Rohani, M.; Liu, Z.; Horstemeyer, M. A comparative study of metamodeling methods for multiobjective crashworthiness optimization. Comput. Struct. 2005, 83, 2121–2136. [Google Scholar] [CrossRef]
- Rais-Rohani, M.; Singh, M. Comparison of global and local response surface techniques in reliability-based optimization of composite structures. Struct. Multidiscip. Optim. 2004, 26, 333–345. [Google Scholar] [CrossRef]
- Wang, G.; Dong, Z.; Aitchison, P. Adaptive response surface method-a global optimization scheme for approximation-based design problems. Eng. Optim. 2001, 33, 707–733. [Google Scholar] [CrossRef]
- Yang, B.S.; Yeun, Y.S.; Ruy, W.S. Managing approximation models in multiobjective optimization. Struct. Multidiscip. Optim. 2002, 24, 141. [Google Scholar] [CrossRef]
- Ayati, A.; Moghaddam, A.Z.; Tanhaei, B.; Deymeh, F.; Sillanpaa, M. Response surface methodology approach for optimization of methyl orange adsorptive removal by magnetic chitosan nanocomposite. Maced. J. Chem. Chem. Eng. 2017, 36, 143–151. [Google Scholar] [CrossRef]
- Gendy, T.S.; El-Temtamy, S.A.; El-Salamony, R.A.; Ghoneim, S.A. Comparative assessment of response surface methodology quadratic models and artificial neural network method for dry reforming of natural gas. Energy Sourcespart A Recoveryutilizationand Environ. Effect 2018, 40, 1573–1582. [Google Scholar] [CrossRef]
- Wendland, H. On the smoothness of positive definite and radial functions. J. Comput. Appl. Math. 1999, 101, 177. [Google Scholar] [CrossRef]
- Krishnamurthy, T. Response surface approximation with augmented and compactly supported radial basis functions. In Proceedings of the 44th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Norfolk, VA, USA, 9 April 2003; p. 1748. [Google Scholar]
- Zaouk, A.; Marzougui, D.; Bedewi, N. Development of a detailed vehicle finite element model part I: Methodology. Int. J. Crashworthiness 2000, 5, 25–36. [Google Scholar] [CrossRef]
| Independent Variables Xn | Coded Levels | |||
|---|---|---|---|---|
| −1 | 0 | 1 | ||
| X1: Seeds to solvent ratio (%) | A | 1 | 3 | 5 |
| X2: Contact Time (hr) | B | 6 | 12 | 24 |
| X3: Stirring speed (rpm) | C | 0 | 350 | 700 |
| Solvents | Model | Centers | Width | Regularization Parameter λ |
|---|---|---|---|---|
| Acetone | Linear RBF | 20 | 0.0593 | 0.0487 |
| Multi-quadric RBF | 11 | 2.718 | 2.471 | |
| Chloroform | Linear RBF | 20 | 0.055952 | 0.03144 |
| Multi-quadric RBF | 19 | 1.432 | 2.13 × 10−5 | |
| Hexane | Linear RBF | 20 | 0.0683 | 0.03375 |
| Multi-quadric RBF | 4 | 4.75 | 4.399 × 10−5 |
| Parameter | Value |
|---|---|
| Number of input variables | 3 |
| Number of first layer neurons | 10 |
| Number of output neurons | 5 |
| Learning rule | Levenberg–Marquardt |
| Number of iteration | 1000 |
| Error goal | 0.0001 |
| Mu | 0.0005 |
| Solvents | Model Name | Observations | RMSE | R2 | R2adj |
|---|---|---|---|---|---|
| Hexane | RSM Quadratic | 60 | 0.225 | 0.996 | 0.995 |
| ANN [5,10] | 60 | 2.23 × 10−3 | 1 | 1 | |
| LRBF | 60 | 0.116 | 0.998 | 0.999 | |
| QRBF | 60 | 0.263 | 1 | 1 | |
| Chloroform | RSM Quadratic | 60 | 0.123 | 0.693 | 0.638 |
| ANN [5,10] | 60 | 3.3757 × 10−5 | 1 | 1 | |
| LRBF | 60 | 0.053 | 0.912 | 0.933 | |
| QRBF | 60 | 0.086 | 1 | 1 | |
| Acetone | RSM Quadratic | 60 | 0.05 | 0.692 | 0.636 |
| ANN [5,10] | 60 | 3.7 × 10−5 | 1 | 1 | |
| LRBF | 60 | 0.03 | 0.852 | 0.871 | |
| QRBF | 60 | 0.047 | 1 | 1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Osman, H.; Shigidi, I.; Arabi, A. Multiple Modeling Techniques for Assessing Sesame Oil Extraction under Various Operating Conditions and Solvents. Foods 2019, 8, 142. https://doi.org/10.3390/foods8040142
Osman H, Shigidi I, Arabi A. Multiple Modeling Techniques for Assessing Sesame Oil Extraction under Various Operating Conditions and Solvents. Foods. 2019; 8(4):142. https://doi.org/10.3390/foods8040142
Chicago/Turabian StyleOsman, Haitham, Ihab Shigidi, and Amir Arabi. 2019. "Multiple Modeling Techniques for Assessing Sesame Oil Extraction under Various Operating Conditions and Solvents" Foods 8, no. 4: 142. https://doi.org/10.3390/foods8040142
APA StyleOsman, H., Shigidi, I., & Arabi, A. (2019). Multiple Modeling Techniques for Assessing Sesame Oil Extraction under Various Operating Conditions and Solvents. Foods, 8(4), 142. https://doi.org/10.3390/foods8040142





