Improved Shell Color Index for Chicken Eggs with Blue-green Shells Based on Machine Learning Analysis
Abstract
1. Introduction
2. Materials and Methods
2.1. Egg Samples
2.2. Eggshell Color Measurement and Visual Classification
2.3. Data Analyses
2.3.1. Batch Correction
2.3.2. Corrected Data Statistics
2.3.3. Machine Learning Comparisons
2.3.4. Optimal Model Analysis and Simple Color Index Construction
3. Results
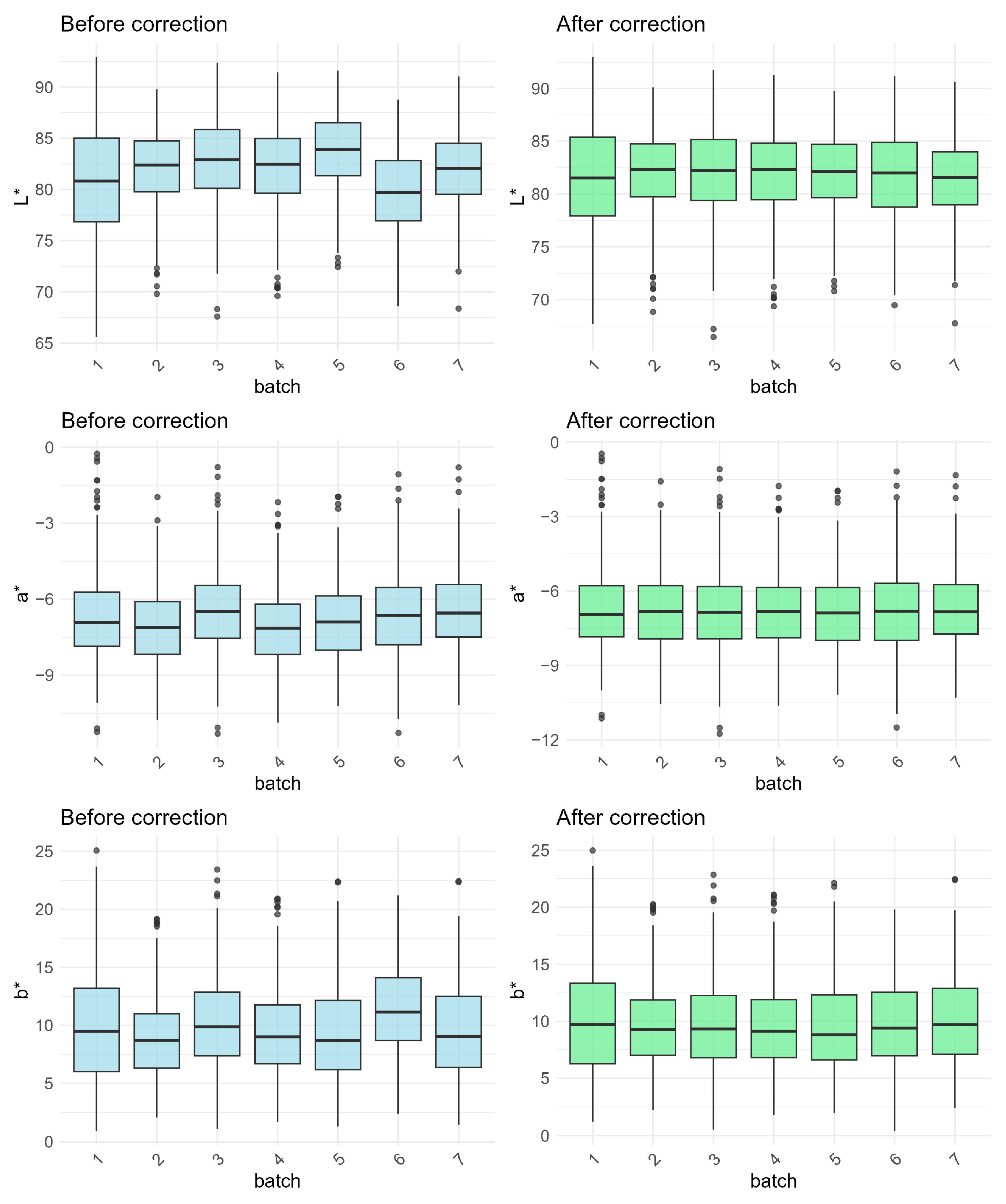
3.1. Effects of Batch Correction
3.2. Statistical Results of Corrected Data
3.3. Classification Results of Machine Learning Algorithms
3.4. Analyzed Results of the Optimal Model
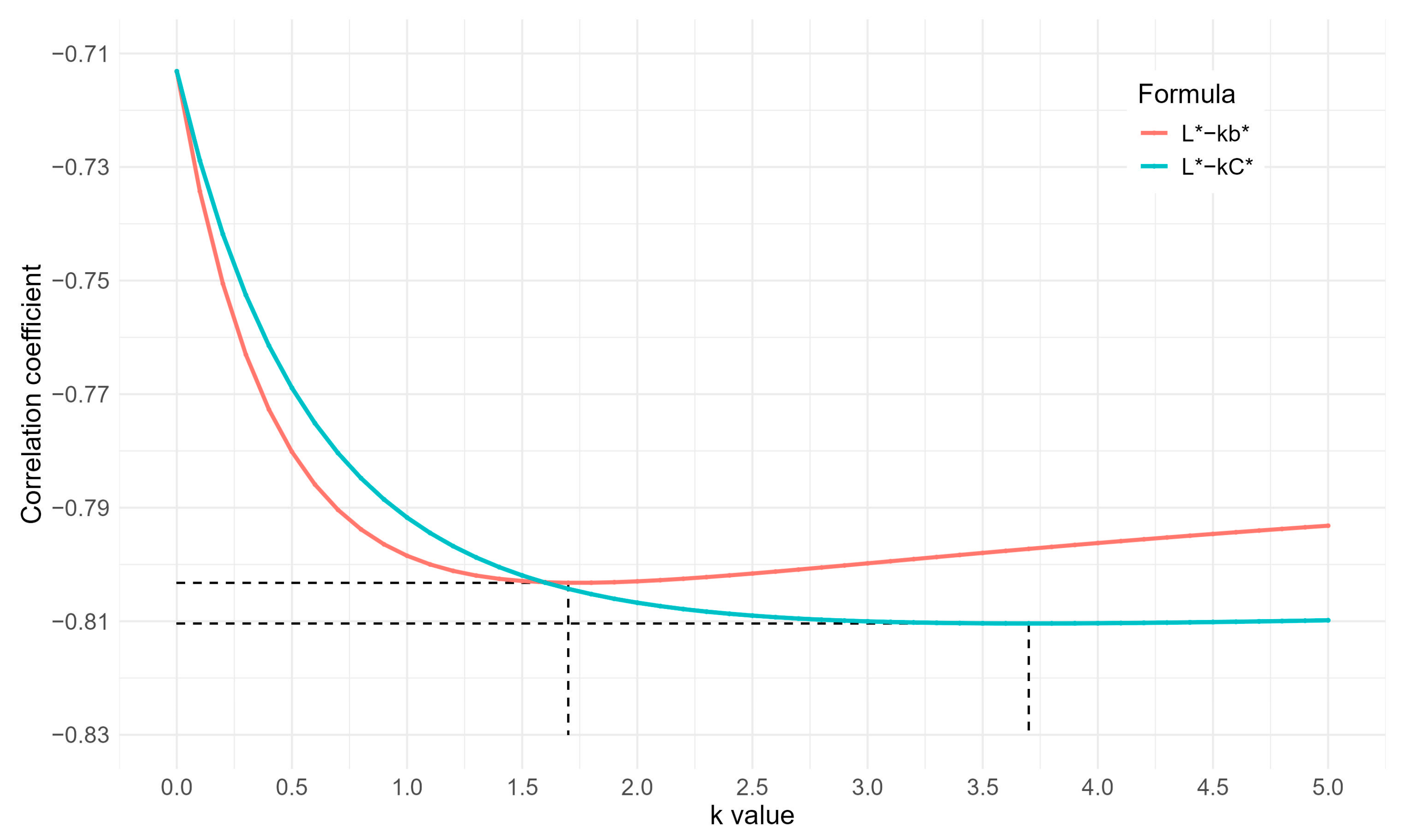
3.5. Optimized Results of Simple Color Indices
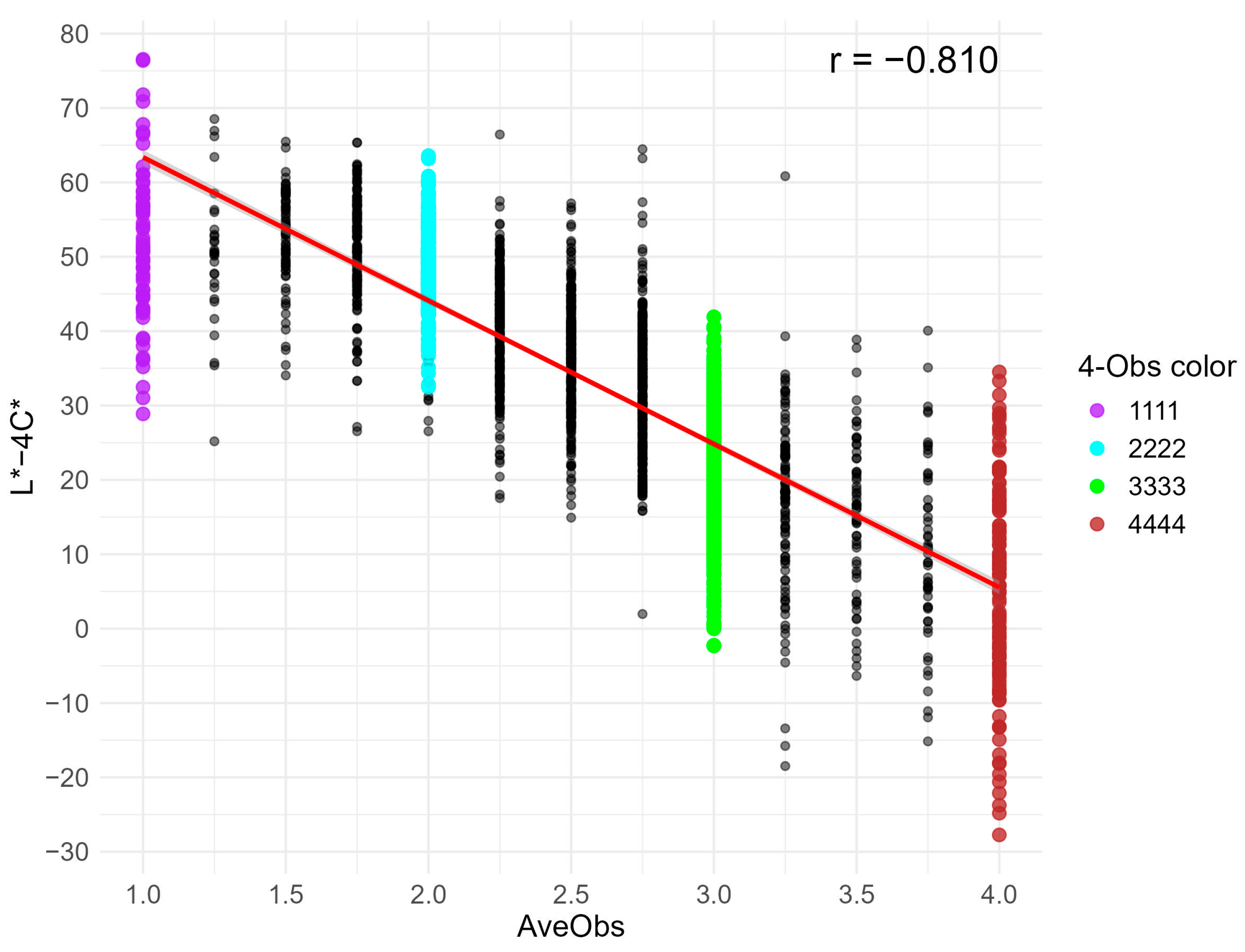
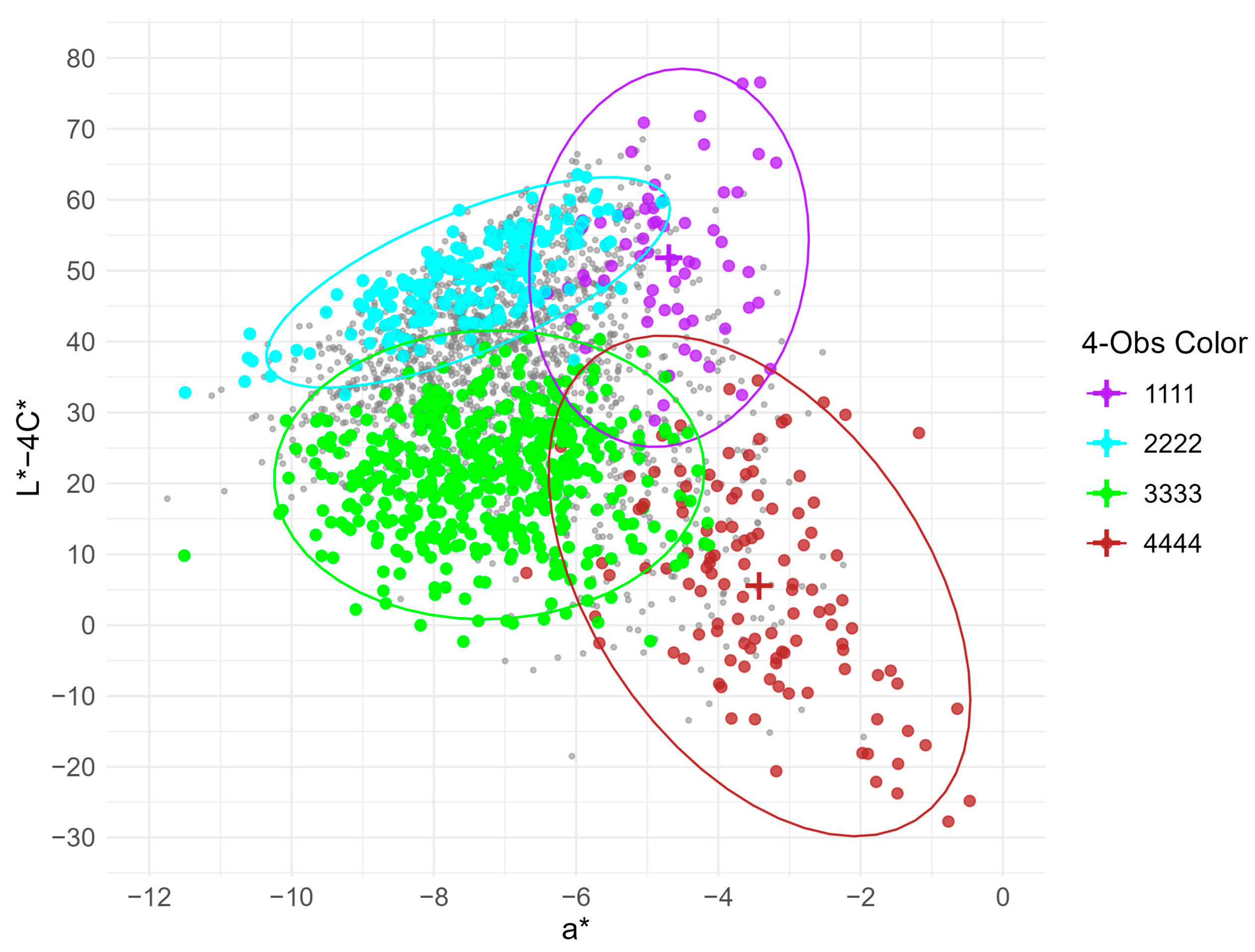
3.6. Practical Distribution with Superior Color Index (L* − 4C*)
4. Discussion
4.1. Batch Correction for Measurement of Eggshell Color
4.2. Machine Learning for Shell Color Classification
4.3. Shell Color Indices for Blue-green Eggs
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lahti, D.C. Population differentiation and rapid evolution of egg color in accordance with solar radiation. Auk 2008, 125, 796–802. [Google Scholar] [CrossRef]
- Soler, J.J.; Navarro, C.; Contreras, T.P.; Avilés, J.M.; Cuervo, J.J. Sexually selected egg coloration in spotless starlings. Am. Nat. 2008, 171, 183–194. [Google Scholar] [CrossRef]
- Ingram, D.R.; Hatten, L.F.; Homan, K.D. A study on the relationship between eggshell color and eggshell quality in commercial broiler breeders. Inter. J. Poult. Sci. 2008, 7, 700–703. [Google Scholar] [CrossRef]
- Drabik, K.; Karwowska, M.; Wengerska, K.; Prochniak, T.; Adamczuk, A.; Batkowska, J. The variability of quality traits of table eggs and eggshell mineral composition depending on hens’ breed and eggshell color. Animals 2021, 11, 1204. [Google Scholar] [CrossRef]
- Zhao, R.; Xu, G.Y.; Liu, Z.Z.; Li, J.Y.; Yang, N. A study on eggshell pigmentation: Biliverdin in blue-shelled chickens. Poult. Sci. 2006, 85, 546–549. [Google Scholar] [CrossRef]
- Wang, X.T.; Zhao, C.J.; Li, J.Y.; Xu, G.Y.; Lian, L.S.; Wu, C.X.; Deng, X.M. Comparison of the total amount of eggshell pigments in Dongxiang brown-shelled eggs and Dongxiang blue-shelled eggs. Poult. Sci. 2009, 88, 1735–1739. [Google Scholar] [CrossRef]
- Liu, H.C.; Cheng, W.T.K. Eggshell pigmentation: A review. J. Chin. Soc. Anim. Sci. 2010, 39, 75–89. [Google Scholar]
- Lu, M.Y.; Xu, L.; Qi, G.H.; Zhang, H.J.; Qiu, K.; Wang, J.; Wu, S.G. Mechanisms associated with the depigmentation of brown eggshells: A review. Poult. Sci. 2021, 100, 101273. [Google Scholar] [CrossRef]
- Guyonnet, V. Does eggshell color really matter? WATT Poult. Int. 2022, 61, 22–23. [Google Scholar]
- Braak, V.T. Eggshell Color Eggsplained. Hendrix Genetics. 2023. Available online: https://layinghens.hendrix-genetics.com/en/articles/eggshell-color-eggsplained/ (accessed on 6 May 2025).
- Samiullah, S.; Roberts, J.R.; Chousalkar, K. Eggshell color in brown-egg laying hens—A review. Poult. Sci. 2015, 94, 2566–2575. [Google Scholar] [CrossRef]
- Cavero, D.; Schmutz, M.; Icken, W.; Preisinger, R. Attractive eggshell color as a breeding goal. Lohmann Inf. 2012, 47, 15–21. [Google Scholar]
- Mulder, H.A.; Visscher, J.; Fablet, J. Estimating the purebred-crossbred genetic correlation for uniformity of eggshell color in laying hens. Genet. Sel. Evol. 2016, 48, 39. [Google Scholar] [CrossRef]
- Dalirsefat, S.B. Analysis of Eggshell Pigmentation in the Chinese Indigenous Blue-Shelled Chickens. Ph.D. Thesis, China Agricultural University, Beijing, China, 2015. (In Chinese with English Abstract). [Google Scholar]
- Xu, J.M. Breeding Study of Changshun Blue-Eggshell Chicken. Master’s Thesis, Foshan University, Foshan, China, 2018. (In Chinese with English Abstract). [Google Scholar]
- Wang, H.H.; Cahaner, A.; Lou, L.F.; Zhang, L.; Ge, Y.; Li, Q.H.; Zhang, X.D. Genetics and breeding of a black-bone and blue eggshell chicken line. 3. Visual eggshell color and colorimeter parameters in 3 consecutive generations. Poult. Sci. 2023, 102, 103052. [Google Scholar] [CrossRef]
- Young, K.W.; Whittle, K.J. Colour measurement of fish minces using Hunter L, a, b values. J. Sci. Food Agric. 1985, 36, 383–392. [Google Scholar] [CrossRef]
- Kim, S.; Park, J.B.; Hwang, I.K. Quality attributes of various varieties of Korean red pepper powders (Capsicum annuum L.) and color stability during sunlight exposure. J. Food Sci. 2002, 67, 2957–2961. [Google Scholar] [CrossRef]
- Xu, L.; Li, Q.; Yu, H.; Kong, L. Estimates of heritability for growth and shell color traits and their genetic correlations in the black shell strain of pacific oyster Crassostrea gigas. Mar. Biotechnol. 2017, 19, 421–429. [Google Scholar] [CrossRef]
- Zeng, L.S.; Xu, G.Y.; Jiang, C.Y.; Li, J.Y.; Zheng, J.X. Research note: L*a*b* color space for prediction of eggshell pigment content in differently colored eggs. Poult. Sci. 2022, 101, 101942. [Google Scholar] [CrossRef]
- Konica Minolta. Precise Color Communication, Part I, Let’s Look at Some Color Spaces. 2007. Available online: https://www.konicaminolta.com/instruments/knowledge/color/part1/07.html (accessed on 6 May 2025).
- Moreno, J.; Osorno, J.L.; Morales, J.; Merino, S.; Tomás, G. Egg colouration and male parental effort in the pied flycatcher Ficedula hypoleuca. J. Avian Biol. 2004, 35, 300–304. [Google Scholar] [CrossRef]
- Maroco, J.; Silva, D.; Rodrigues, A.; Guerreiro, M.; Santana, I.; Mendonça, A. Data mining methods in the prediction of Dementia: A real-data comparison of the accuracy, sensitivity and specificity of linear discriminant analysis, logistic regression, neural networks, support vector machines, classification trees and random forests. BMC Res. Notes 2011, 4, 299. [Google Scholar] [CrossRef]
- Osisanwo, F.Y.; Akinsola, J.E.T.; Awodele, O.; Hinmikaiye, J.O.; Olakanmi, O.; Akinjobi, J. Supervised machine learning algorithms: Classification and comparison. Int. J. Comput. Trend. Technol. 2017, 48, 128–138. [Google Scholar]
- Sen, P.C.; Hajra, M.; Ghosh, M. Supervised classification algorithms in machine learning: A survey and review. In Emerging Technology in Modelling and Graphics: Proc. IEM Graph; Springer: Singapore, 2020; pp. 99–111. [Google Scholar]
- Wang, H.H.; Cahaner, A.; Lou, L.F.; Zhang, L.; Ge, Y.; Li, Q.H.; Zhang, X.D. Genetics and breeding of a black-bone and blue eggshell chicken line. 1. Body weight, skin color, and their combined selection. Poult. Sci. 2021, 100, 101035. [Google Scholar] [CrossRef]
- Chen, Q.; Wang, Z.P. A new molecular mechanism supports that blue-greenish egg color evolved independently across chicken breeds. Poult. Sci. 2022, 101, 102223. [Google Scholar] [CrossRef]
- Yang, Z.Q.; Chen, Y.J.; Jin, C.F.; Ding, H.R.; Shi, K.; Chen, C.K. Study on the evaluation on eggshell color of black feather chicken in different laying period by Lab color system. J. Anhui Agric. Sci. 2013, 22, 9316–9318, (In Chinese with English Abstract). [Google Scholar]
- Zhou, Y.; Fu, S.Y.; Ren, T.H.; Song, Y.Y.; Jiang, R.R.; Tian, Y.D.; Kang, X.T.; Li, Z.J. Analysis on color change rule of green-shell eggs in different weeks of age of Lushi chickens. China Poult. 2016, 38, 15–18, (In Chinese with English Abstract). [Google Scholar]
- Zhao, H.B.; Zhou, X.H. Egg freshness recognition based on a fuzzy radial-basis-function neural network technology. In Proceedings of the 5th International Conference on Agricultural and Biological Sciences (ABS), IOP Conference Series: Earth and Environmental Science, Macau, China, 21–24 July 2019; Volume 346, p. 012084. [Google Scholar]
- Maimunah, R.; Handayanto, T.; Rokhman, T. Support vector machine for classifying the quality of the eggs based on the color. In Proceedings of the 1st International Conference on Recent Innovations, Jakarta, Indonesia, 26–28 September 2018; pp. 3092–3098. [Google Scholar]
- Morales, J.; Kim, S.Y.; Lobato, E.; Merino, S.; Tomás, G.; Puente, J.M.; Moreno, J. On the heritability of blue-green eggshell coloration. J. Evol. Biol. 2010, 23, 1783–1791. [Google Scholar] [CrossRef]
- Lukanov, H.; Genchev, A.; Pavlov, A. Colour traits of chicken eggs with different eggshell pigmentation. Trakia J. Sci. 2015, 2, 149–158. [Google Scholar] [CrossRef]
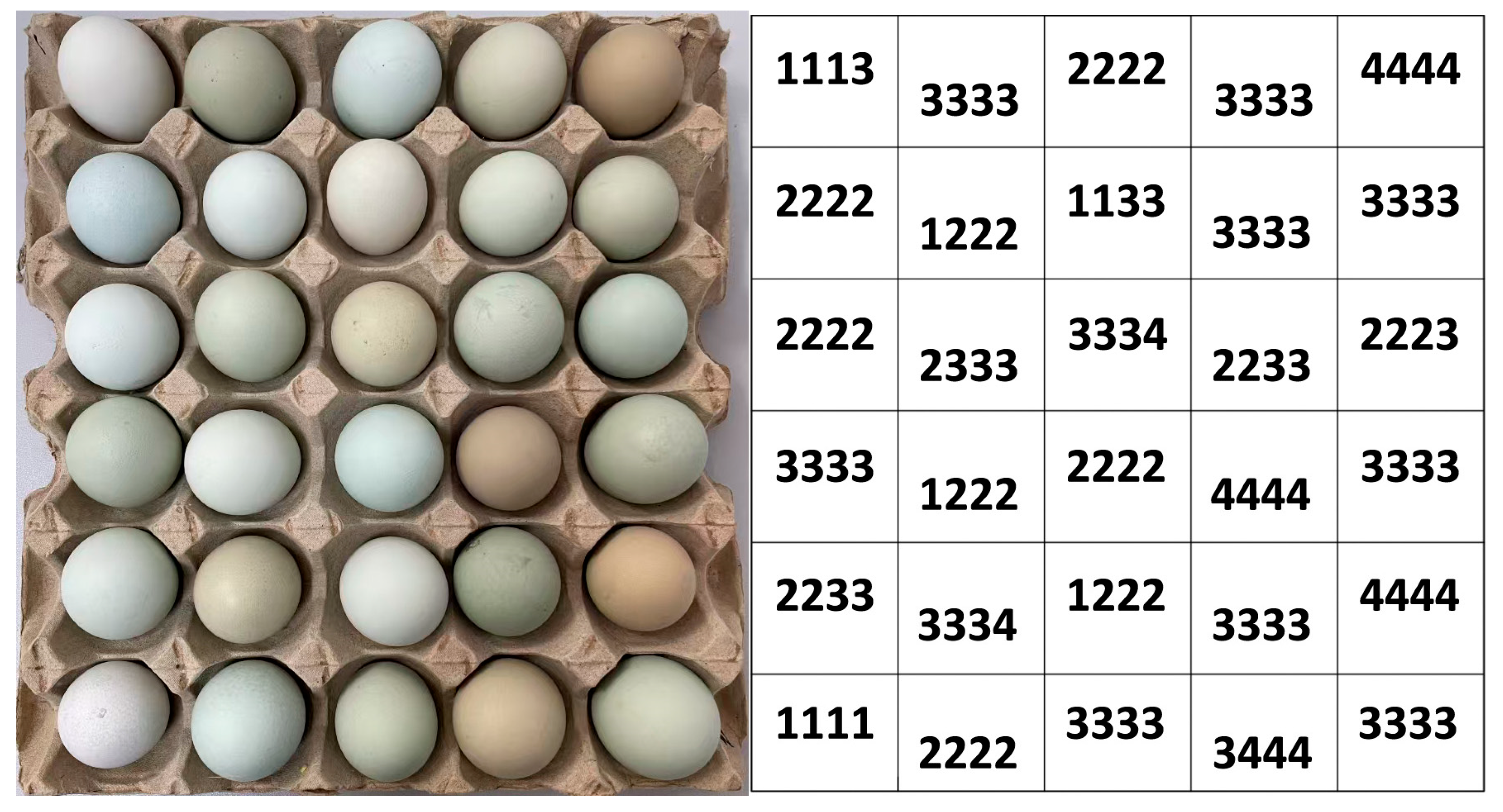
| Generation | G5 | G6 | G7 | G8 | |||
|---|---|---|---|---|---|---|---|
| Days of Age | 250 d | 200 d | 300 d | 200 d | 300 d | 200 d | 300 d |
| Batch | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Egg number | 484 | 458 | 398 | 320 | 196 | 242 | 176 |
| No. | AveObs | 4-Obs | N (Cons.) | N (Incons.) | N (All) | % of Total |
|---|---|---|---|---|---|---|
| 1 | 1.00 | 1111 1 | 63 | 0 | 63 | 2.8 |
| 2 | 1.25 | 1112 | 0 | 29 | 29 | 1.3 |
| 3 | 1.50 | 1113, 1122 | 0 | 69 | 69 | 3.0 |
| 4 | 1.75 | 1114, 1123, 1222 | 0 | 135 | 135 | 5.9 |
| 5 | 2.00 | 1124, 1133, 1223, 2123, 2222 1 | 199 | 80 | 279 | 12.3 |
| 6 | 2.25 | 1134, 1224, 1233, 2223 | 0 | 260 | 260 | 11.4 |
| 7 | 2.50 | 1144, 1234, 1333, 2233 | 0 | 287 | 287 | 12.6 |
| 8 | 2.75 | 1334, 2234, 2333 | 0 | 337 | 337 | 14.8 |
| 9 | 3.00 | 1344, 2334, 3333 1 | 484 | 9 | 493 | 21.7 |
| 10 | 3.25 | 1444, 2344, 3334 | 0 | 95 | 95 | 4.2 |
| 11 | 3.50 | 2444, 3344 | 0 | 59 | 59 | 2.6 |
| 12 | 3.75 | 3444 | 0 | 54 | 54 | 2.4 |
| 13 | 4.00 | 4444 1 | 114 | 0 | 114 | 5.0 |
| Before Corr. CV (%) | After Corr. CV (%) | Reduction Rate (%) | |
|---|---|---|---|
| L* | 1.55 | 0.35 | 77.4 |
| a* | 4.42 | 0.71 | 83.9 |
| b* | 8.40 | 2.70 | 67.9 |
| L* | a* | b* | |
|---|---|---|---|
| Mean ± SD, CV% | 81.82 ± 4.24, 5.19% | −6.74 ± 1.65, 24.51% | 9.76 ± 3.99, 40.84% |
| a* | −0.088 | ||
| b* | −0.722 | 0.451 | |
| AveObs | −0.713 | 0.218 | 0.771 |
| Sample | Model | Accuracy | F1-Score | Kappa | Noise Sensitivity | Prediction Efficiency |
|---|---|---|---|---|---|---|
| All | LDA | 0.450 | 0.391 | 0.357 | 0.284 | 172,803 |
| RF | 0.395 | 0.320 | 0.305 | 0.461 | 848 | |
| SVM | 0.439 | 0.472 | 0.341 | 0.287 | 2352 | |
| NNET | 0.408 | 0.390 | 0.306 | 0.261 | 157,423 | |
| Cons. | LDA | 0.941 | 0.914 | 0.903 | 0.018 | 129,695 |
| RF | 0.934 | 0.889 | 0.889 | 0.038 | 37,059 | |
| SVM | 0.941 | 0.911 | 0.902 | 0.017 | 23,885 | |
| NNET | 0.934 | 0.896 | 0.889 | 0.024 | 72,194 | |
| Incons. | LDA | 0.448 | 0.388 | 0.335 | 0.098 | 140,334 |
| RF | 0.348 | 0.343 | 0.220 | 0.332 | 14,681 | |
| SVM | 0.436 | 0.482 | 0.314 | 0.095 | 3580 | |
| NNET | 0.386 | 0.341 | 0.261 | 0.117 | 115,515 |
| SCI | C* | L* − 2b* | L* − 4C* | |
|---|---|---|---|---|
| r | −0.782 | 0.797 | −0.803 | −0.810 |
| SCI | 0.179 | 0.057 | 0.010 * | |
| C* | 0.574 | 0.216 | ||
| L* − 2b* | 0.500 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Wei, Y.; Zhang, L.; Ge, Y.; Liu, H.; Zhang, X. Improved Shell Color Index for Chicken Eggs with Blue-green Shells Based on Machine Learning Analysis. Foods 2025, 14, 3027. https://doi.org/10.3390/foods14173027
Wang H, Wei Y, Zhang L, Ge Y, Liu H, Zhang X. Improved Shell Color Index for Chicken Eggs with Blue-green Shells Based on Machine Learning Analysis. Foods. 2025; 14(17):3027. https://doi.org/10.3390/foods14173027
Chicago/Turabian StyleWang, Huanhuan, Yinghui Wei, Lei Zhang, Ying Ge, Hang Liu, and Xuedong Zhang. 2025. "Improved Shell Color Index for Chicken Eggs with Blue-green Shells Based on Machine Learning Analysis" Foods 14, no. 17: 3027. https://doi.org/10.3390/foods14173027
APA StyleWang, H., Wei, Y., Zhang, L., Ge, Y., Liu, H., & Zhang, X. (2025). Improved Shell Color Index for Chicken Eggs with Blue-green Shells Based on Machine Learning Analysis. Foods, 14(17), 3027. https://doi.org/10.3390/foods14173027






