Optimizing Cold Food Supply Chains for Enhanced Food Availability Under Climate Variability
Abstract
1. Introduction
1.1. Literature Review
1.2. Research Gap and Contributions
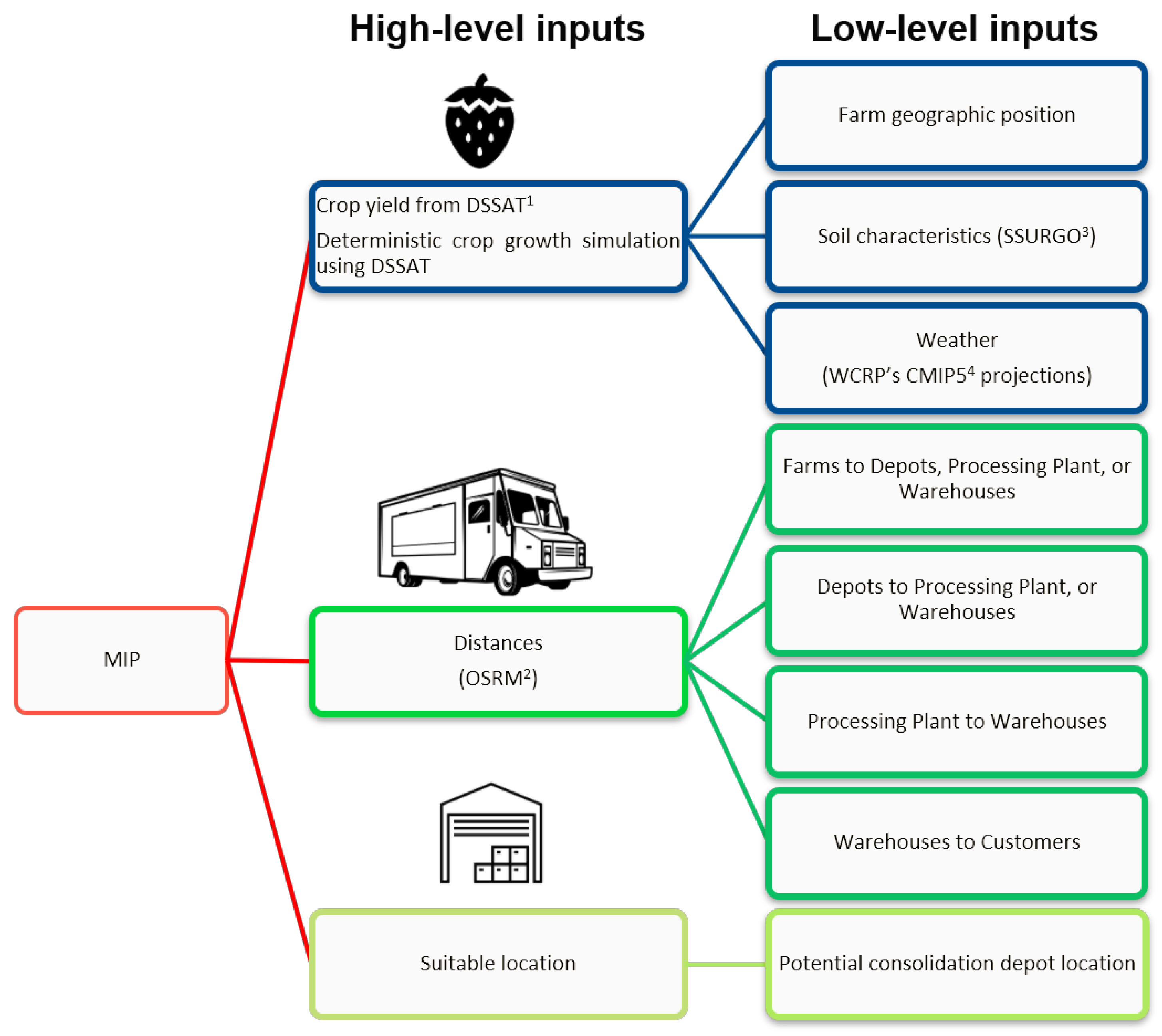
2. Methodology
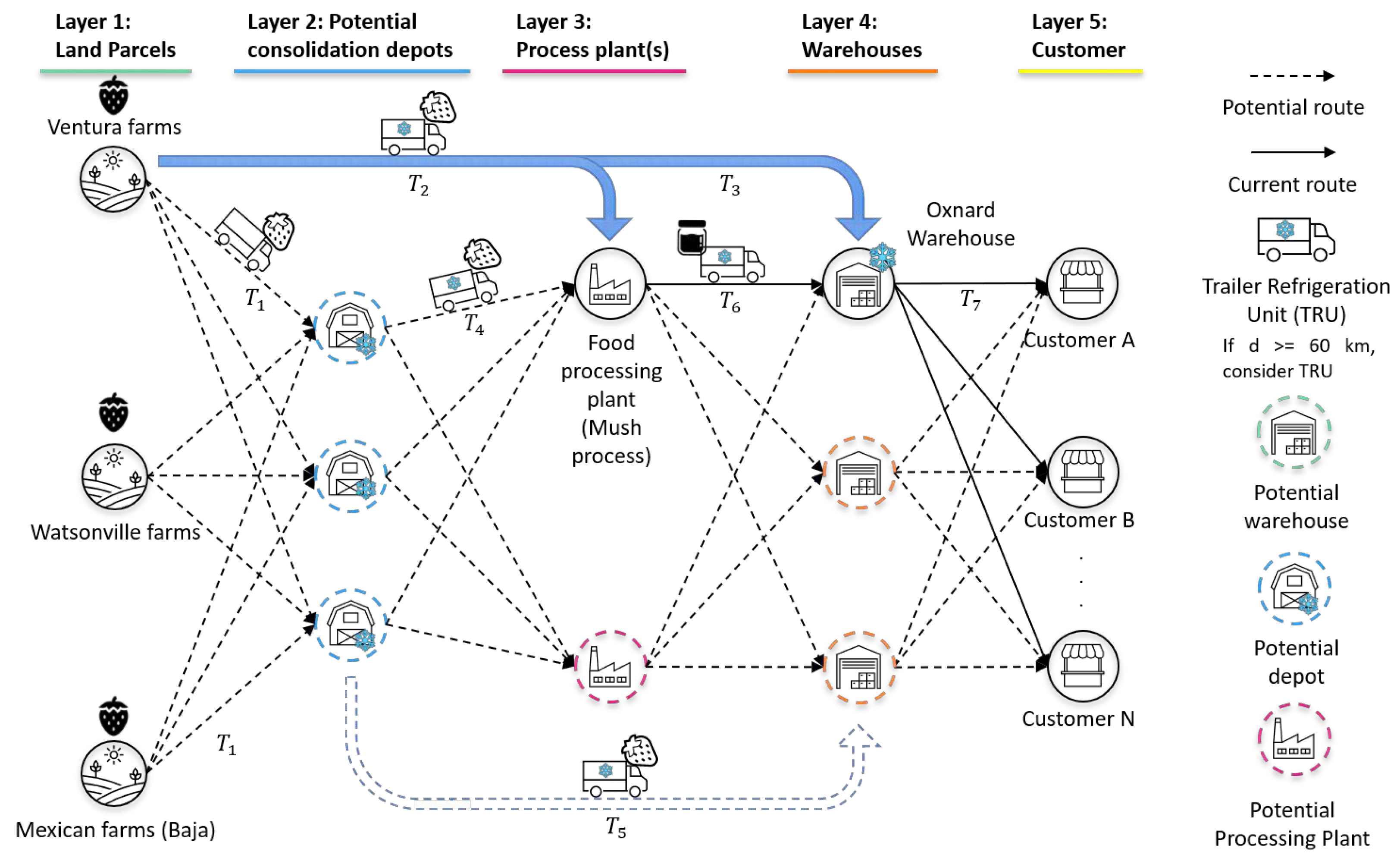
3. Mathematical Model
- Sets
- P Set of parcels/farms;
- D Set of potential locations for depots;
- W Set of warehouses;
- C Set of customers;
- Set of arcs that connect parcels/farms to the processing plant for all ;
- Set of arcs that connect parcels/farms to potential depot locations for all ;
- Set of arcs that connect parcels/farms to centralized warehouses for all ;
- Set of arcs that connect potential depot locations to the processing plant for all ;
- Set of arcs that connect potential depot locations to centralized warehouses for all ;
- Set of arcs that connect the processing plant to centralized warehouses for all ;
- Set of arcs that connect centralized warehouses to customers for all .
- Design variables
- Flow along arc ;
- Flow along arc ;
- Flow along arc ;
- Flow along arc ;
- Flow along arc ;
- Flow along arc ;
- Flow along arc ;
- A binary variable that takes the value of 1 if is used as a depot, otherwise 0.
- A binary variable that takes the value of 1 if is used as a warehouse, otherwise 0.
- Problem parameters
- Unit cost per metric ton shipped along ;
- Unit cost per metric ton shipped along ;
- Unit cost per metric ton shipped along ;
- Unit cost per metric ton shipped along ;
- Unit cost per metric ton shipped along ;
- Unit cost per metric ton shipped along ;
- Unit cost per metric ton shipped along ;
- Storage capacity of depot ;
- Storage capacity of warehouse ;
- Storage capacity of the processing plant;
- Fixed investment cost to open a depot at node ;
- Fixed rental cost to store product in a warehouse at node ;
- Supply of strawberries at parcel location ;
- Demand for whole strawberry from each customer location ;
- Demand for strawberry mush from each customer location ;
- Total demand for strawberries from each customer location ;
- Losses during the peeling process.
4. Case Study
4.1. Types of Products
4.2. Crop Yield Simulations
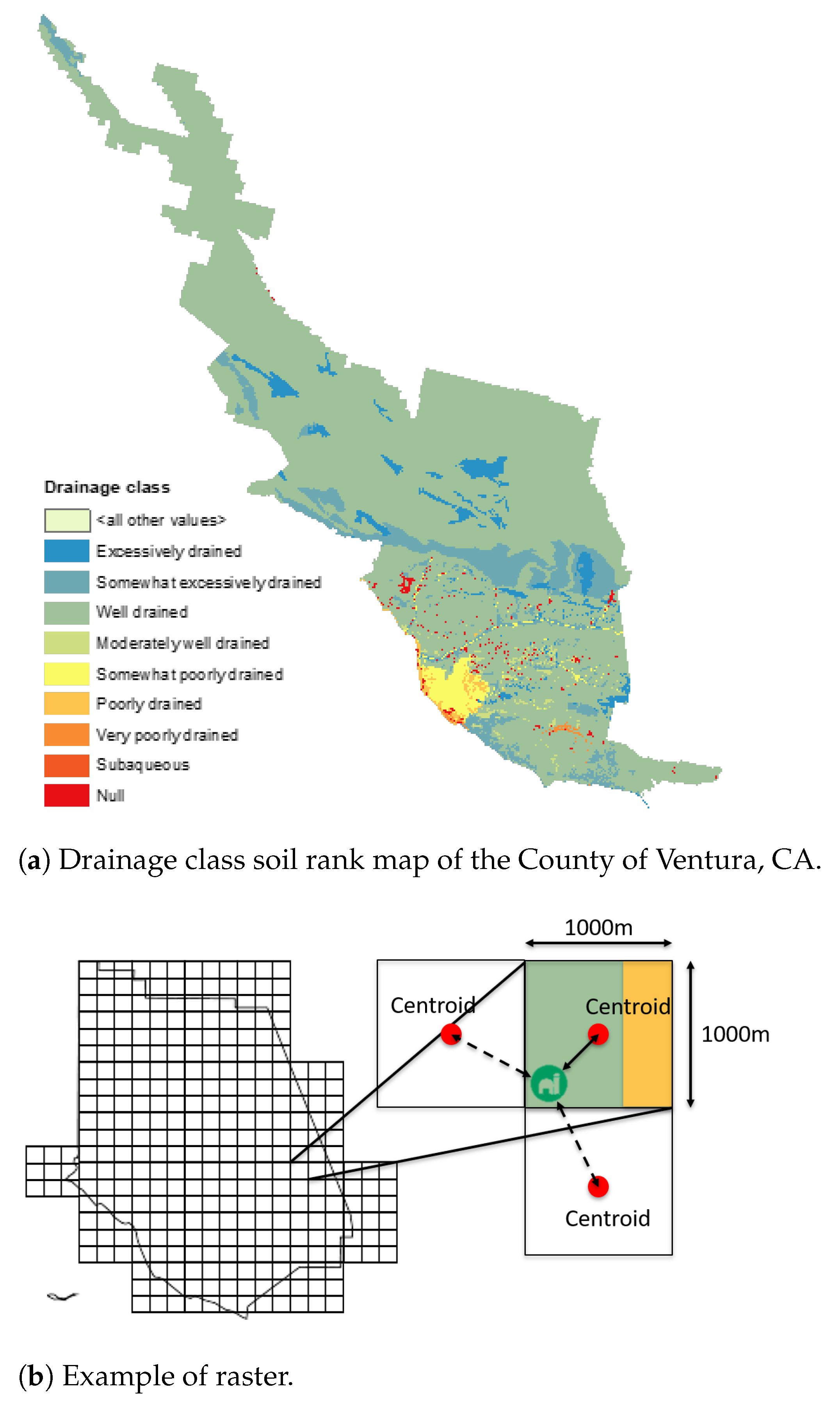
4.2.1. Soil Surface and Profile Information
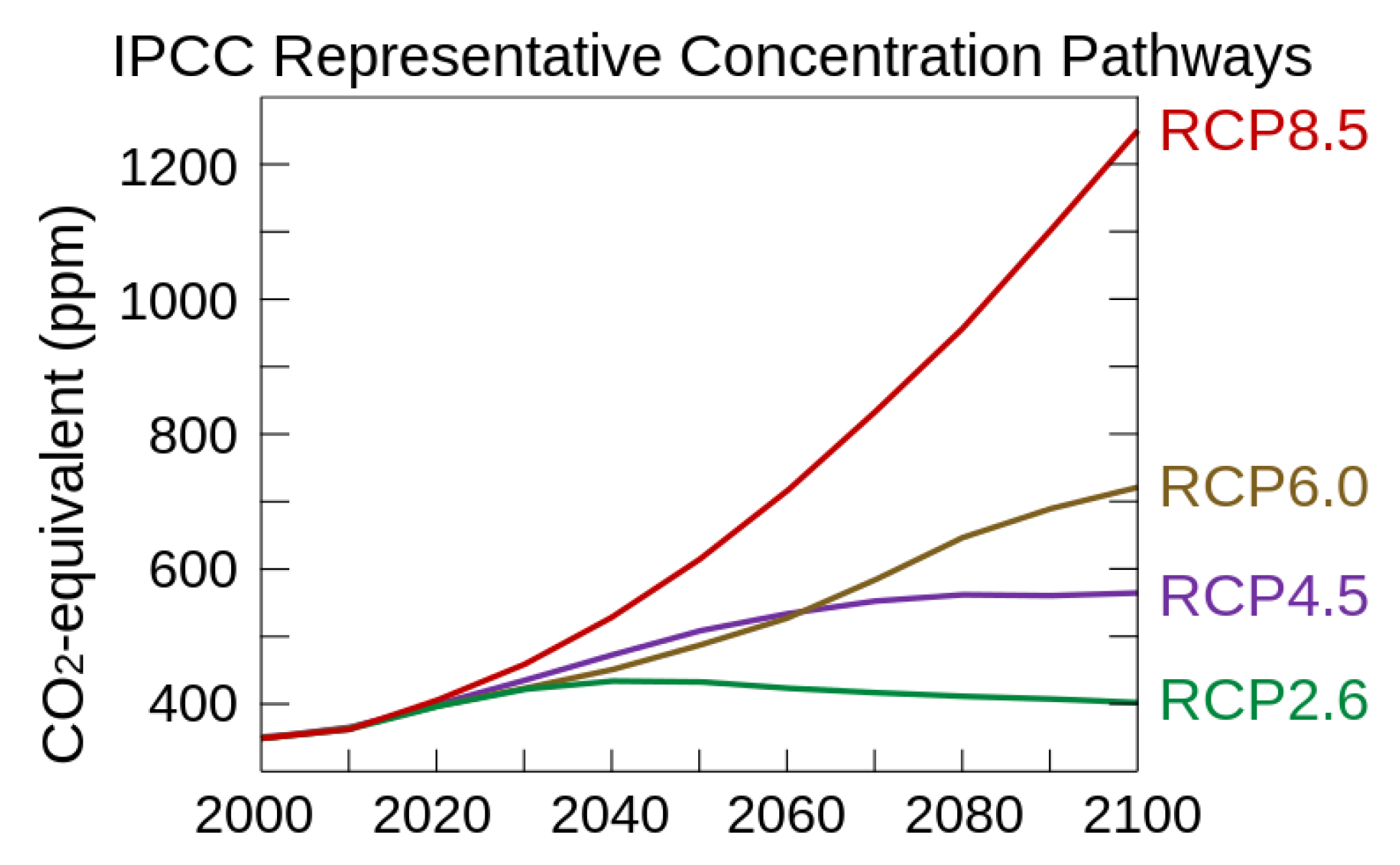
4.2.2. Climate Scenarios
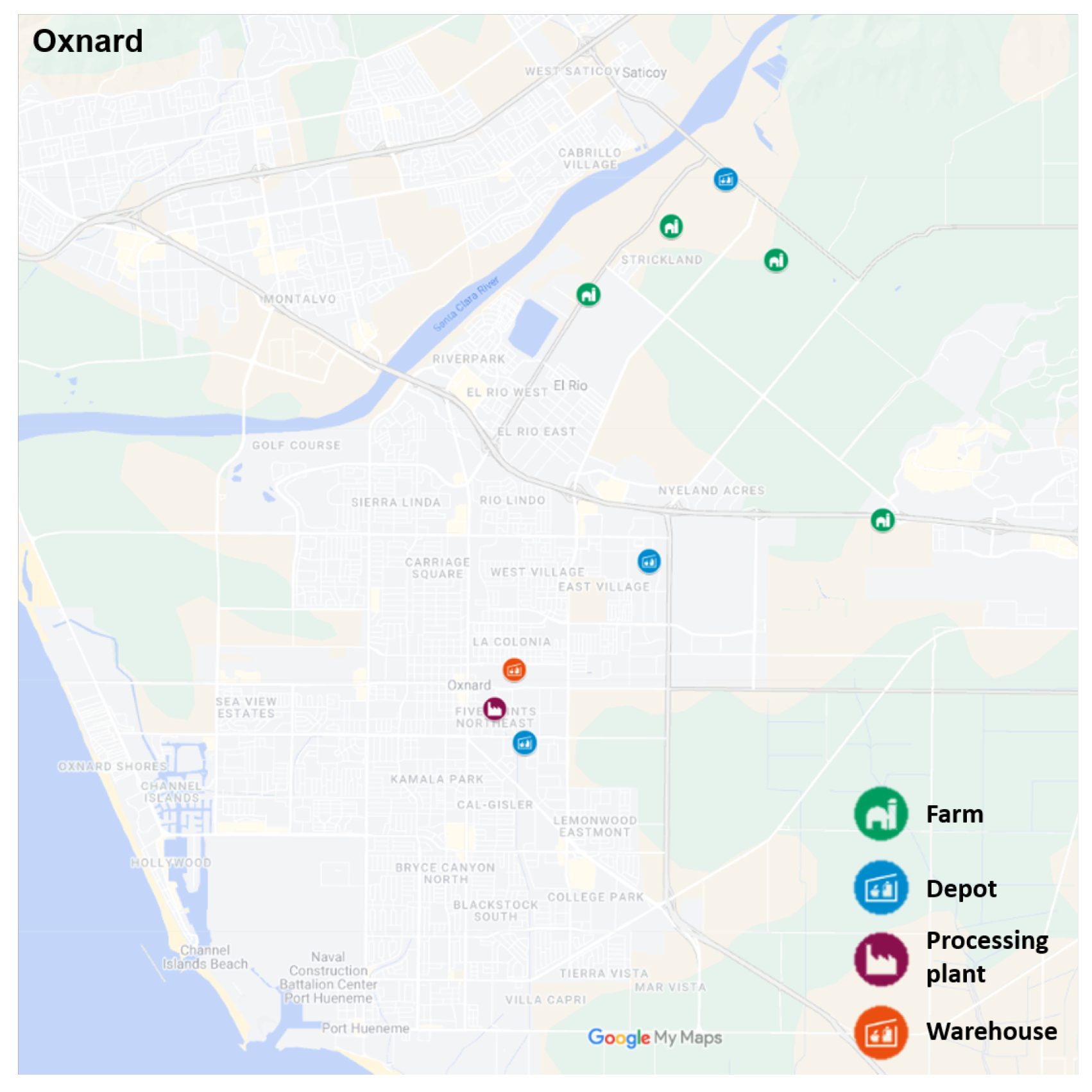
4.3. Geospatial Parameters
Potential Depot Locations
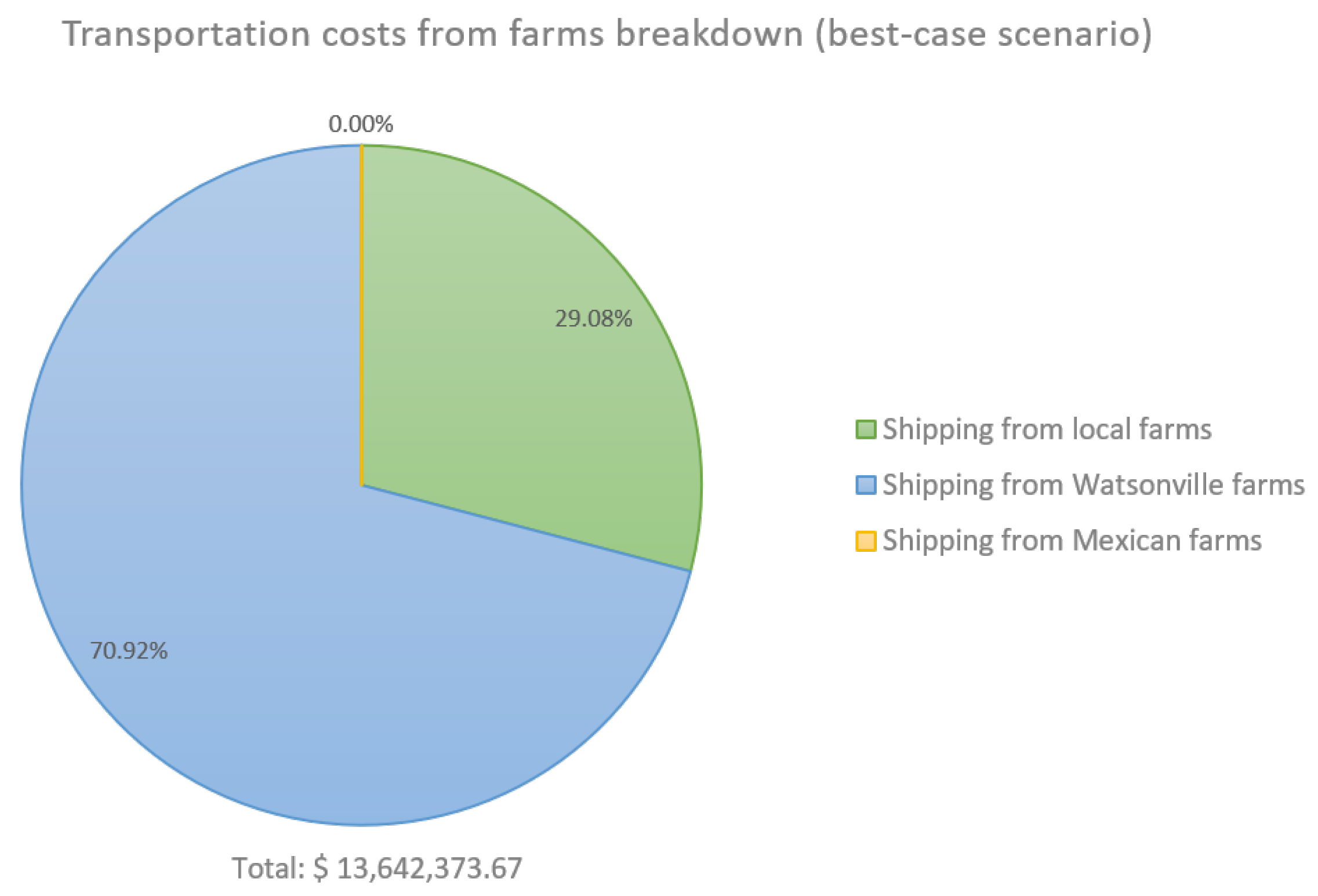
4.4. Transportation Costs: Costs Along Arcs T
5. Results and Discussion
5.1. Numerical Results
5.2. Sensitivity Analysis
6. Concluding Remarks
6.1. Summary of Contributions
6.2. Practical Implications
6.3. Limitations of the Study and Future Directions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Maskey, M.L.; Pathak, T.B.; Dara, S.K. Weather based strawberry yield forecasts at field scale using statistical and machine learning models. Atmosphere 2019, 10, 378. [Google Scholar] [CrossRef]
- Nguyen, T.D.; Nguyen-Quang, T.; Venkatadri, U.; Diallo, C.; Adams, M. Mathematical Programming Models for Fresh Fruit Supply Chain Optimization: A Review of the Literature and Emerging Trends. AgriEngineering 2021, 3, 519–541. [Google Scholar] [CrossRef]
- Food and Agriculture Organization of the United Nations. FAOSTAT: Crops and Livestock Products. 2023. Available online: https://www.fao.org/faostat/en/#data/QCL (accessed on 13 January 2025).
- United States Department of Agriculture. National Agricultural Statistics Service-Strawberry Production. 2023. Available online: https://www.nass.usda.gov/Data_and_Statistics/ (accessed on 13 January 2025).
- USDA Economic Research Service. Fruit and Tree Nut Yearbook Tables. 2023. Available online: https://www.ers.usda.gov/data-products/fruit-and-tree-nuts-data/fruit-and-tree-nuts-yearbook-tables (accessed on 11 February 2025).
- Masini, G.L.; Blanco, A.M.; Petracci, N.; Bandoni, J.A. Supply chain tactical optimization in the fruit industry. Process Syst. Eng. Supply Chain. Optim. 2007, 4, 121–172. [Google Scholar]
- Rong, A.; Akkerman, R.; Grunow, M. An optimization approach for managing fresh food quality throughout the supply chain. Int. J. Prod. Econ. 2011, 131, 421–429. [Google Scholar] [CrossRef]
- Etemadnia, H.; Goetz, S.J.; Canning, P.; Tavallali, M.S. Optimal wholesale facilities location within the fruit and vegetables supply chain with bimodal transportation options: An LP-MIP heuristic approach. Eur. J. Oper. Res. 2015, 244, 648–661. [Google Scholar] [CrossRef]
- Rocco, C.D.; Morabito, R. Production and logistics planning in the tomato processing industry: A conceptual scheme and mathematical model. Comput. Electron. Agric. 2016, 127, 763–774. [Google Scholar] [CrossRef]
- Soto-Silva, W.E.; González-Araya, M.C.; Oliva-Fernández, M.A.; Plà-Aragonés, L.M. Optimizing fresh food logistics for processing: Application for a large Chilean apple supply chain. Comput. Electron. Agric. 2017, 136, 42–57. [Google Scholar] [CrossRef]
- Musavi, M.; Bozorgi-Amiri, A. A multi-objective sustainable hub location-scheduling problem for perishable food supply chain. Comput. Ind. Eng. 2017, 113, 766–778. [Google Scholar] [CrossRef]
- Bottani, E.; Murino, T.; Schiavo, M.; Akkerman, R. Resilient food supply chain design: Modelling framework and metaheuristic solution approach. Comput. Ind. Eng. 2019, 135, 177–198. [Google Scholar] [CrossRef]
- Maia, L.O.A.; Lago, R.A.; Qassim, R.Y. Selection of postharvest technology routes by mixed-integer linear programming. Int. J. Prod. Econ. 1997, 49, 85–90. [Google Scholar] [CrossRef]
- Kazaz, B.; Webster, S. The impact of yield-dependent trading costs on pricing and production planning under supply uncertainty. Manuf. Serv. Oper. Manag. 2011, 13, 404–417. [Google Scholar] [CrossRef]
- Mirzapour Al-E-Hashem, S.; Malekly, H.; Aryanezhad, M.B. A multi-objective robust optimization model for multi-product multi-site aggregate production planning in a supply chain under uncertainty. Int. J. Prod. Econ. 2011, 134, 28–42. [Google Scholar] [CrossRef]
- Baghalian, A.; Rezapour, S.; Farahani, R.Z. Robust supply chain network design with service level against disruptions and demand uncertainties: A real-life case. Eur. J. Oper. Res. 2013, 227, 199–215. [Google Scholar] [CrossRef]
- Ahumada, O.; Villalobos, J.R.; Mason, A.N. Tactical planning of the production and distribution of fresh agricultural products under uncertainty. Agric. Syst. 2012, 112, 17–26. [Google Scholar] [CrossRef]
- Aranguren, M.; Castillo-Villar, K. Bi-objective stochastic model for the design of large-scale carbon footprint conscious co-firing biomass supply chains. Comput. Ind. Eng. 2022, 171, 108352. [Google Scholar] [CrossRef]
- Baghizadeh, K.; Cheikhrouhou, N.; Govindan, K.; Ziyarati, M. Sustainable agriculture supply chain network design considering water-energy-food nexus using queuing system: A hybrid robust possibilistic programming. Nat. Resour. Model. 2022, 35, e12337. [Google Scholar] [CrossRef]
- Hernandez-Cuellar, D. An Stochastic Cold Food Supply Chain (CFSC) Design. In Proceedings of the Cyber-Physical Systems and Internet of Things Week 2023, San Antonio, TX, USA, 9–12 May 2023; CPS-IoT Week ’23. Association for Computing Machinery: New York, NY, USA, 2023; pp. 391–394. [Google Scholar] [CrossRef]
- Hoogenboom, G.; Porter, C.; Shelia, V.; Boote, K.; Singh, U.; White, J.; Hunt, L.; Ogoshi, R.; Lizaso, J.; Koo, J.; et al. Decision Support System for Agrotechnology Transfer (DSSAT) Version 4.7; DSSAT Foundation: Gainesville, FL, USA, 2017. [Google Scholar]
- Luxen, D.; Vetter, C. Real-time routing with OpenStreetMap data. In Proceedings of the 19th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems (GIS ’11), Chicago, IL, USA, 1–4 November 2011; ACM: New York, NY, USA, 2011; pp. 513–516. Available online: https://project-osrm.org/ (accessed on 1 July 2025).
- Soil Survey Staff. Gridded Soil Survey Geographic (gSSURGO) Database. United States Department of Agriculture, Natural Resources Conservation Service. Available online: https://gdg.sc.egov.usda.gov/ (accessed on 1 July 2025).
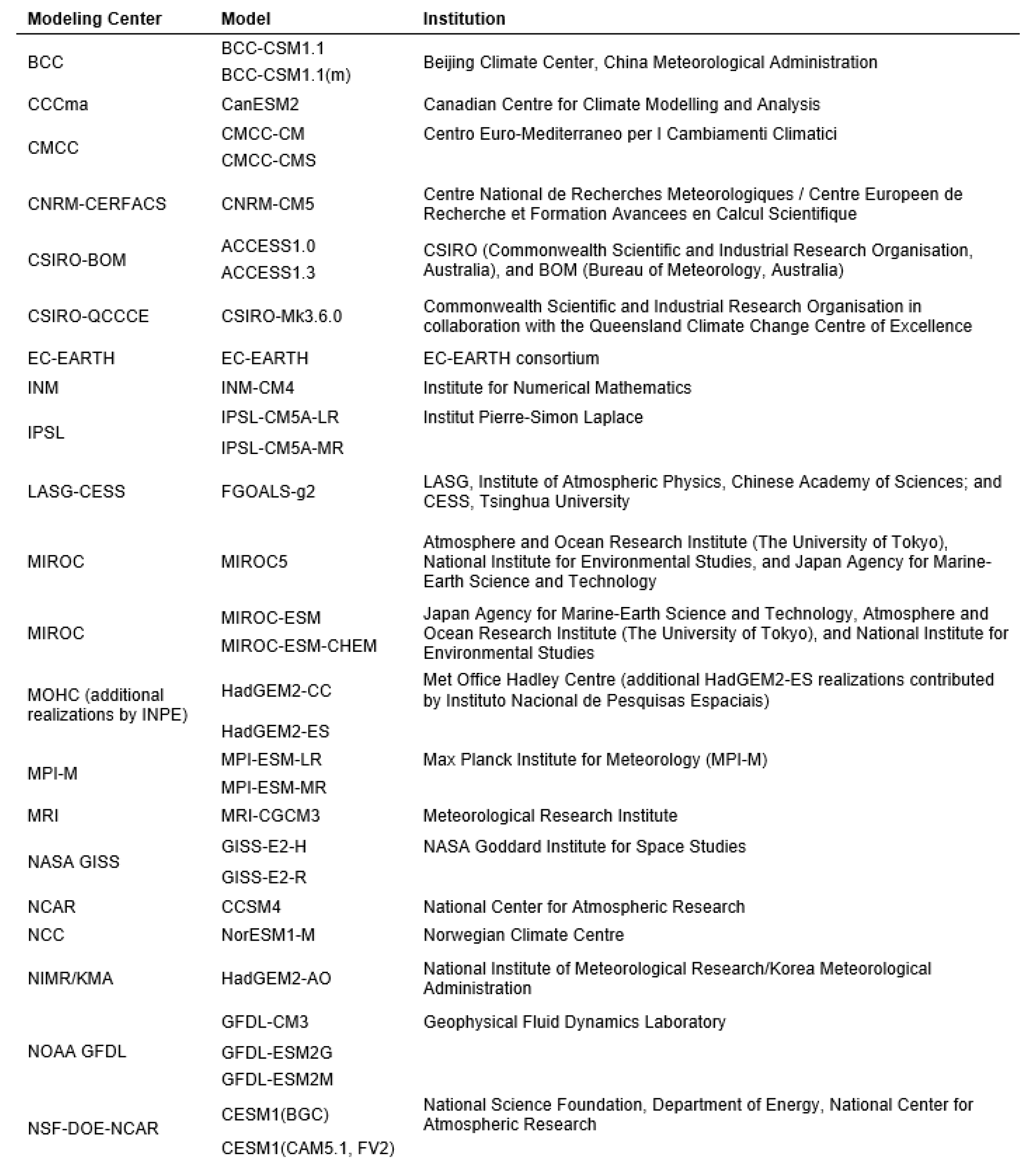
- WCRP, W.C.R.P. CMIP Phase 5 (CMIP5). 2020. Available online: https://pcmdi.llnl.gov/mips/cmip5/availability.html (accessed on 1 July 2025).
- Hopf, A.; Boote, K.J.; Oh, J.; Guan, Z.; Agehara, S.; Shelia, V.; Whitaker, V.M.; Asseng, S.; Zhao, X.; Hoogenboom, G. Development and improvement of the CROPGRO-Strawberry model. Sci. Hortic. 2022, 291, 110538. [Google Scholar] [CrossRef]
- ESRI. ArcGIS Desktop: ArcMap. Available online: https://desktop.arcgis.com/en/arcmap/ (accessed on 1 July 2025).
- Aranguren, M.F. Stochastic Programming Models to Design Biomass Supply Chains for Co-Firing in Coal-Fired Power Plants. Ph.D. Thesis, The University of Texas at San Antonio, San Antonio, TX, USA, 2021. [Google Scholar]
- Collaborators. Downscaled CMIP3 and CMIP5 Climate and Hydrology Projections. Available online: https://gdo-dcp.ucllnl.org/downscaled_cmip_projections/ (accessed on 1 July 2025).
- RCP Database. RCP Database (Version 2.0). Available online: https://tntcat.iiasa.ac.at/RcpDb (accessed on 1 August 2025).
- Wikipedia. Representative Concentration Pathway. The Original Author of the Graph is the International Institute for Applied Systems Analysis (IIASA). 2023. Available online: http://www.iiasa.ac.at/web-apps/tnt/RcpDb (accessed on 1 August 2025).
- City of Omaha. Planning and Zoning Search. Available online: https://planning.cityofomaha.org/planning-zoning (accessed on 1 August 2025).
- Lamers, P.; Roni, M.S.; Tumuluru, J.S.; Jacobson, J.J.; Cafferty, K.G.; Hansen, J.K.; Kenney, K.; Teymouri, F.; Bals, B. Techno-economic analysis of decentralized biomass processing depots. Bioresour. Technol. 2015, 194, 205–213. [Google Scholar] [CrossRef] [PubMed]
- Syam, M.M.; Cabrera-Calderon, S.; Vijayan, K.A.; Balaji, V.; Phelan, P.E.; Villalobos, J.R. Mini Containers to Improve the Cold Chain Energy Efficiency and Carbon Footprint. Climate 2022, 10, 76. [Google Scholar] [CrossRef]
- IBM Corporation. Meet the Python API. Available online: https://www.ibm.com/docs/en/icos/22.1.2 (accessed on 1 August 2025).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2022. [Google Scholar]

| Supply Uncertainty | |||||
|---|---|---|---|---|---|
| References | Methods/Approach | Type | Objective | Probability Dist. | Weather Projections |
| Masini et al. (2007) [6] | LP 1 + MCS 2 | Deterministic | Single | ||
| Rong et al. (2011) [7] | MILP 3 | Deterministic | Single | ||
| Etemadnia et al. (2015) [8] | MIP 4 + Heuristics | Deterministic | Single | ||
| Rocco and Morabito (2016) [9] | LP 1 | Deterministic | Single | ||
| Soto-Silva et al. (2017) [10] | MIP 4 | Deterministic | Single | ||
| Musavi and Bozorgi-Amiri (2017) [11] | MIP 4 + Meta-Heuristic (NSGA-II 5) | Deterministic | Multiple | ||
| Bottani et al. (2019) [12] | MINLP 6 + Meta-Heuristic (ACO 7) | Deterministic | Multiple | ✓ | |
| Maia et al. (1997) [13] | MIP 4 | Stochastic | Single | ✓ | |
| Kazaz and Webster (2011) [14] | Newsvendor | Stochastic | Single | ✓ | |
| Mirzapour Al-E-Hashem et al. (2011) [15] | MILP + RO + LP Metrics | Stochastic | Multiple | ✓ | |
| Ahumada et al. (2012) [17] | MIP 4 | Stochastic | Multiple | ||
| Baghalian et al. (2013) [16] | MINLP 6 + RO 8 + Piece-wise Linearization | Stochastic | Single | ✓ | |
| Aranguren and Castillo-Villar (2022) [18] | Hybrid: Yield Simulations + MILP 3 + Meta-Heuristic (SA and PSO) | Stochastic | Multiple | ✓ | |
| Baghizadeh et al. (2022) [19] | MINLP 6 + HRPP 9 + LR 10 | Fuzzy sets | Multiple | ✓ | |
| This paper | Hybrid: Yield Simulations + MIP 4 | Stochastic | Single | ✓ | |
| Item | Value ∗ | Unit |
|---|---|---|
| Avg. truck speed (v) | 60 | Km/h |
| Truck operational cost () | 48.4 | USD/h |
| Loading cost (L) | 3.59 | USD/MTon |
| Unloading cost (U) | 3.58 | USD/MTon |
| Stacking cost () | 0.44 | USD/MTon |
| Truck capacity () | 21.76 | MTon |
| Round trip factor () | 2 | - |
| Δ Yield | Percentile | Farms Used | Depots | Warehouses | Avg. Supply (mt) | Cost |
|---|---|---|---|---|---|---|
| −10% | 25th | 17 | 0 | 11 | 56,670.67 | USD 1,194,608,386.58 |
| 0% | 25th | 17 | 0 | 11 | 56,670.67 | USD 1,190,332,227.52 |
| +10% | 25th | 16 | 0 | 11 | 60,212.59 | USD 1,186,607,165.33 |
| −10% | 50th | 8 | 0 | 11 | 120,425.18 | USD 1,168,407,595.64 |
| 0% | 50th | 6 | 0 | 11 | 160,566.90 | USD 1,168,394,944.64 |
| +10% | 50th | 6 | 0 | 11 | 160,566.90 | USD 1,168,388,566.68 |
| −10% | 75th | 6 | 0 | 11 | 160,566.90 | USD 1,168,346,008.80 |
| 0% | 75th | 5 | 0 | 11 | 192,680.29 | USD 1,168,336,253.85 |
| +10% | 75th | 4 | 0 | 11 | 240,850.36 | USD 1,168,334,088.73 |
| Δ Yield | Percentile | Farms Used | Depots | Warehouses | Avg. Supply (mt) | Cost |
|---|---|---|---|---|---|---|
| −10% | 25th | 16 | 0 | 11 | 60,212.59 | USD 1,186,898,725.03 |
| 0% | 25th | 15 | 0 | 11 | 64,226.76 | USD 1,182,436,538.05 |
| +10% | 25th | 14 | 0 | 11 | 68,814.39 | USD 1,180,608,885.81 |
| −10% | 50th | 6 | 0 | 11 | 160,566.90 | USD 1,168,394,783.53 |
| 0% | 50th | 6 | 0 | 11 | 160,566.90 | USD 1,168,387,679.00 |
| +10% | 50th | 6 | 0 | 11 | 160,566.90 | USD 1,168,380,574.47 |
| −10% | 75th | 6 | 0 | 11 | 160,566.90 | USD 1,168,340,993.58 |
| 0% | 75th | 4 | 0 | 11 | 240,850.36 | USD 1,168,335,097.63 |
| +10% | 75th | 4 | 0 | 11 | 240,850.36 | USD 1,168,333,199.09 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hernandez-Cuellar, D.; Castillo-Villar, K.K.; Castillo-Villar, F.R. Optimizing Cold Food Supply Chains for Enhanced Food Availability Under Climate Variability. Foods 2025, 14, 2725. https://doi.org/10.3390/foods14152725
Hernandez-Cuellar D, Castillo-Villar KK, Castillo-Villar FR. Optimizing Cold Food Supply Chains for Enhanced Food Availability Under Climate Variability. Foods. 2025; 14(15):2725. https://doi.org/10.3390/foods14152725
Chicago/Turabian StyleHernandez-Cuellar, David, Krystel K. Castillo-Villar, and Fernando Rey Castillo-Villar. 2025. "Optimizing Cold Food Supply Chains for Enhanced Food Availability Under Climate Variability" Foods 14, no. 15: 2725. https://doi.org/10.3390/foods14152725
APA StyleHernandez-Cuellar, D., Castillo-Villar, K. K., & Castillo-Villar, F. R. (2025). Optimizing Cold Food Supply Chains for Enhanced Food Availability Under Climate Variability. Foods, 14(15), 2725. https://doi.org/10.3390/foods14152725






