Phenolic Acid–β-Cyclodextrin Complexation Study to Mask Bitterness in Wheat Bran: A Machine Learning-Based QSAR Study
Abstract
1. Introduction
2. Materials and Methods
2.1. Dataset Preparation
2.2. Binding Constant Calculations
2.3. Docking Procedures
2.4. Molecular Descriptors Generation
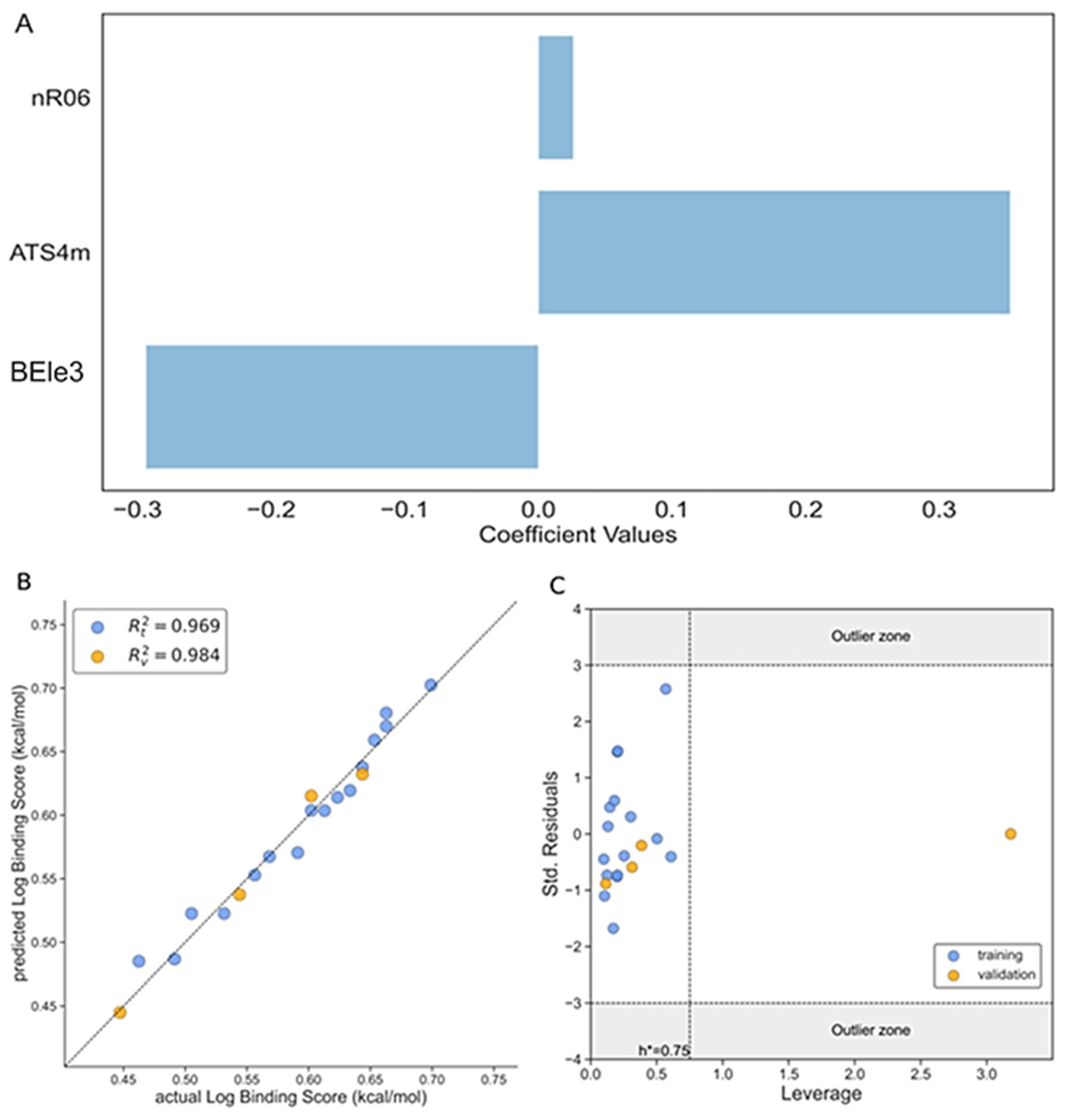
2.5. Variable Selection and QSAR Modeling
2.6. Applicability Domain
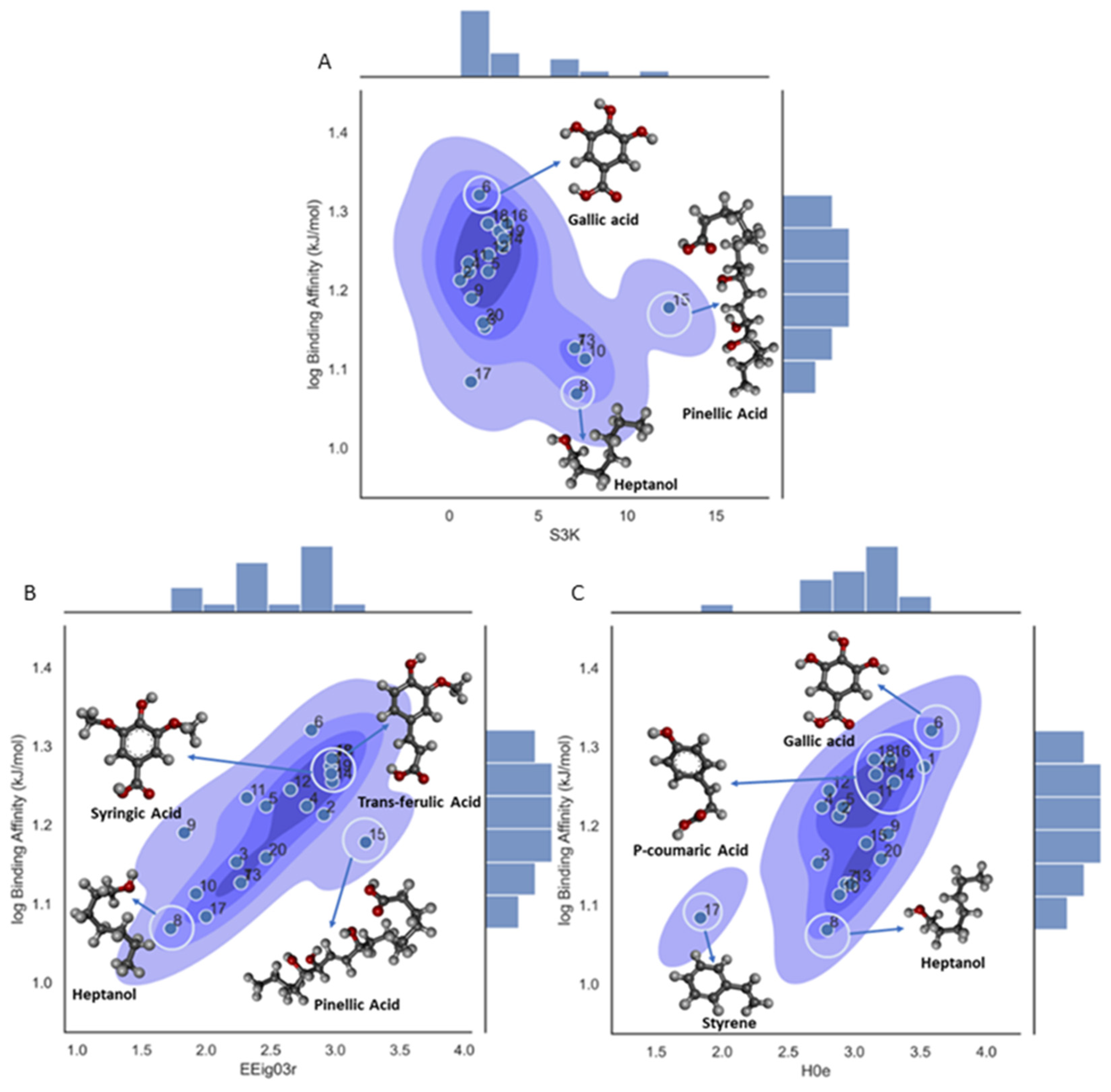
2.7. Descriptor Significance Plot
3. Results and Discussion
3.1. Binding Score Affinity (Model 1)
3.2. Binding Affinity (Model 2)
3.3. Binding Energy
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Khan, A.S.; Murtaza, B.; Hichami, A.; Khan, N.A. A cross-talk between fat and bitter taste modalities. Biochimie 2019, 159, 3–8. [Google Scholar] [CrossRef]
- Ardoin, R.; Smith, B.; Lea, J.; Boue, S.; Smolensky, D.; Santana, A.L.; Peterson, J. Consumer perceptions and antioxidant profiling of acidified cold-brewed sorghum bran beverages. J. Food Sci. 2023, 88, 2301–2312. [Google Scholar] [CrossRef] [PubMed]
- Vuolo, M.M.; Lima, V.S.; Maróstica Junior, M.R. Chapter 2—Phenolic Compounds: Structure, Classification, and Antioxidant Power. In Bioactive Compounds; Campos, M.R.S., Ed.; Woodhead Publishing, Elsevier: Sawston, UK, 2019; pp. 33–50. [Google Scholar]
- Taofiq, O.; González-Paramás, A.M.; Barreiro, M.F.; Ferreira, I.C.F.R. Hydroxycinnamic Acids and Their Derivatives: Cosmeceutical Significance, Challenges and Future Perspectives, a Review. Molecules 2017, 22, 281. [Google Scholar] [CrossRef] [PubMed]
- Heleno, S.A.; Martins, A.; Queiroz, M.J.R.P.; Ferreira, I.C.F.R. Bioactivity of phenolic acids: Metabolites versus parent compounds: A review. Food Chem. 2015, 173, 501–513. [Google Scholar] [CrossRef]
- Luna-Guevara, M.L.; Luna-Guevara, J.J.; Hernández-Carranza, P.; Ruíz-Espinosa, H.; Ochoa-Velasco, C.E. Chapter 3—Phenolic Compounds: A Good Choice Against Chronic Degenerative Diseases. In Studies in Natural Products Chemistry; Atta-ur-Rahman, Ed.; Elsevier: Amsterdam, The Netherlands, 2018; Volume 59, pp. 79–108. [Google Scholar]
- Rosa, L.A.; Moreno-Escamilla, J.O.; Rodrigo-Gracia, J.; Haard, N.F. Phenolic Compounds, Chapter 12. In Postharvest Physiology and Biochemistry of Fruits and Vegetables; Woodhead Publishing: Sawston, UK, 2019; pp. 253–271. [Google Scholar]
- Combes, J.; Clavijo Rivera, E.; Clément, T.; Fojcik, C.; Athès, V.; Moussa, M.; Allais, F. Solvent selection strategy for an ISPR (In Situ/In stream product recovery) process: The case of microbial production of p-coumaric acid coupled with a liquid-liquid extraction. Sep. Purif. Technol. 2021, 259, 118170. [Google Scholar] [CrossRef]
- Furia, E.; Beneduci, A.; Malacaria, L.; Fazio, A.; La Torre, C.; Plastina, P. Modeling the Solubility of Phenolic Acids in Aqueous Media at 37 °C. Molecules 2021, 26, 6500. [Google Scholar] [CrossRef]
- Rodrigues, J.F.; Soares, C.; Moreira, M.M.; Ramalhosa, M.J.; Duarte, N.F.; Delerue-Matos, C.; Grosso, C. Moringa oleifera Lam. Commercial Beverages: A Multifaceted Investigation of Consumer Perceptions, Sensory Analysis, and Bioactive Properties. Foods 2023, 12, 2253. [Google Scholar] [CrossRef]
- Zhang, S.; Shan, X.; Niu, L.; Chen, L.; Wang, J.; Zhou, Q.; Yuan, H.; Li, J.; Wu, T. The Integration of Metabolomics, Electronic Tongue, and Chromatic Difference Reveals the Correlations between the Critical Compounds and Flavor Characteristics of Two Grades of High-Quality Dianhong Congou Black Tea. Metabolites 2023, 13, 864. [Google Scholar] [CrossRef]
- Issaoui, M.; Delgado, A.M.; Caruso, G.; Micali, M.; Barbera, M.; Atrous, H.; Ouslati, A.; Chammem, N. Phenols, Flavors, and the Mediterranean Diet. J. AOAC Int. 2020, 103, 915–924. [Google Scholar] [CrossRef]
- Kim, J.S. Synthesis and Characterization of Phenolic Acid/Hydroxypropyl-β-Cyclodextrin Inclusion Complexes. Prev. Nutr. Food Sci. 2020, 25, 440–448. [Google Scholar] [CrossRef]
- Cid-Samamed, A.; Rakmai, J.; Mejuto, J.C.; Simal-Gandara, J.; Astray, G. Cyclodextrins inclusion complex: Preparation methods, analytical techniques and food industry applications. Food Chem. 2022, 384, 132467. [Google Scholar] [CrossRef] [PubMed]
- Gramage-Doria, R.; Armspach, D.; Matt, D. Metallated cavitands (calixarenes, resorcinarenes, cyclodextrins) with internal coordination sites. Coord. Chem. Rev. 2013, 257, 776–816. [Google Scholar] [CrossRef]
- Faisal, Z.; Fliszár-Nyúl, E.; Dellafiora, L.; Galaverna, G.; Dall’Asta, C.; Lemli, B.; Kunsági-Máté, S.; Szente, L.; Poór, M. Cyclodextrins Can Entrap Zearalenone-14-Glucoside: Interaction of the Masked Mycotoxin with Cyclodextrins and Cyclodextrin Bead Polymer. Biomolecules 2019, 9, 354. [Google Scholar] [CrossRef] [PubMed]
- Mathivet, T.; Méliet, C.; Castanet, Y.; Mortreux, A.; Caron, L.; Tilloy, S.; Monflier, E. Rhodium catalyzed hydroformylation of water insoluble olefins in the presence of chemically modified β-cyclodextrins: Evidence for ligand-cyclodextrin interactions and effect of various parameters on the activity and the aldehydes selectivity. J. Mol. Catal. A Chem. 2001, 176, 105–116. [Google Scholar] [CrossRef]
- Sandilya, A.A.; Natarajan, U.; Priya, M.H. Molecular View into the Cyclodextrin Cavity: Structure and Hydration. ACS Omega 2020, 5, 25655–25667. [Google Scholar] [CrossRef] [PubMed]
- da Rocha Neto, A.C.; de Oliveira da Rocha, A.B.; Maraschin, M.; Di Piero, R.M.; Almenar, E. Factors affecting the entrapment efficiency of β-cyclodextrins and their effects on the formation of inclusion complexes containing essential oils. Food Hydrocoll. 2018, 77, 509–523. [Google Scholar] [CrossRef]
- Chodankar, D.; Vora, A.; Kanhed, A. β-cyclodextrin and its derivatives: Application in wastewater treatment. Environ. Sci. Pollut. Res. 2022, 29, 1585–1604. [Google Scholar] [CrossRef] [PubMed]
- Tajbakhsh, M.; Naimi-Jamal, M.R. Copper-doped functionalized β-cyclodextrin as an efficient green nanocatalyst for synthesis of 1,2,3-triazoles in water. Sci. Rep. 2022, 12, 4948. [Google Scholar] [CrossRef]
- Hedges, A. Chapter 22—Cyclodextrins: Properties and Applications. In Starch, 3rd ed.; BeMiller, J., Whistler, R., Eds.; Academic Press: San Diego, CA, USA, 2009; pp. 833–851. [Google Scholar]
- Crini, G.; Fourmentin, S.; Fenyvesi, É.; Torri, G.; Fourmentin, M.; Morin-Crini, N. Cyclodextrins, from molecules to applications. Environ. Chem. Lett. 2018, 16, 1361–1375. [Google Scholar] [CrossRef]
- Braga, S.S.; Barbosa, J.S.; Santos, N.E.; El-Saleh, F.; Paz, F.A.A. Cyclodextrins in Antiviral Therapeutics and Vaccines. Pharmaceutics 2021, 13, 409. [Google Scholar] [CrossRef]
- Jiayue, L.; Tian, B. Selective modifications at the different positions of cyclodextrins: A review of strategies. Turk. J. Chem. 2020, 44, 261–278. [Google Scholar] [CrossRef]
- Stella, V.J.; He, Q. Cyclodextrins. Toxicol. Pathol. 2008, 36, 30–42. [Google Scholar] [CrossRef] [PubMed]
- Toropov, A.; Toropova, A.; Rasulev, B.; Benfenati, E.; Gini, G.; Leszczynska, D.; Leszczynski, J. CORAL: Binary Classifications (Active/Inactive) for Liver-Related Adverse Effects of Drugs. Curr. Drug Saf. 2012, 7, 257–261. [Google Scholar] [CrossRef] [PubMed]
- Karuth, A.; Alesadi, A.; Xia, W.; Rasulev, B. Predicting Glass Transition of Amorphous Polymers by Application of Cheminformatics and Molecular Dynamics Simulations. Polymer 2021, 218, 123495. [Google Scholar] [CrossRef]
- Chen, M.; Jabeen, F.; Rasulev, B.; Ossowski, M.; Boudjouk, P. A computational structure-property relationship study of glass transition temperatures for a diverse set of polymers. J. Polym. Sci. Part B Polym. Phys. 2018, 56, 877–885. [Google Scholar] [CrossRef]
- Rasulev, B.; Jabeen, F.; Stafslien, S.; Chisholm, B.; Bahr, J.; Ossowski, M.; Boudjouk, P. Polymer Coating Materials and Their Fouling Release Activity: A Cheminformatics Approach to Predict Properties. ACS Appl. Mater. Interfaces 2016, 9, 1781–1792. [Google Scholar] [CrossRef] [PubMed]
- Toropova, A.; Toropov, A.; Rasulev, B.; Benfenati, E.; Gini, G.; Leszczynska, D.; Leszczynski, J. QSAR models for ACE-inhibitor activity of tri-peptides based on representation of the molecular structure by graph of atomic orbitals and SMILES. Struct. Chem. 2012, 23, 1873–1878. [Google Scholar] [CrossRef]
- Rasulev, B.; Kusic, H.; Leszczynska, D.; Leszczynski, J.; Koprivanac, N. QSAR modeling of acute toxicity on mammals caused by aromatic compounds: The case study using oral LD50 for rats. J. Environ. Monit. 2010, 12, 1037–1044. [Google Scholar] [CrossRef]
- Gooch, A.; Sizochenko, N.; Rasulev, B.; Gorb, L.; Leszczynski, J. In vivo toxicity of nitroaromatics: A comprehensive quantitative structure–activity relationship study. Environ. Toxicol. Chem. 2017, 36, 2227–2233. [Google Scholar] [CrossRef]
- Golmohammadi, M.; Aryanpour, M. Analysis and evaluation of machine learning applications in materials design and discovery. Mater. Today Commun. 2023, 35, 105494. [Google Scholar] [CrossRef]
- Ji, H.; Pu, D.; Yan, W.; Zhang, Q.; Zuo, M.; Zhang, Y. Recent advances and application of machine learning in food flavor prediction and regulation. Trends Food Sci. Technol. 2023, 138, 738–751. [Google Scholar] [CrossRef]
- Kou, X.; Shi, P.; Gao, C.; Ma, P.; Xing, H.; Ke, Q.; Zhang, D. Data-Driven Elucidation of Flavor Chemistry. J. Agric. Food Chem. 2023, 71, 6789–6802. [Google Scholar] [CrossRef] [PubMed]
- Mirrahimi, F.; Salahinejad, M.; Ghasemi, J.B. QSPR approaches to elucidate the stability constants between β-cyclodextrin and some organic compounds: Docking based 3D conformer. J. Mol. Liq. 2016, 219, 1036–1043. [Google Scholar] [CrossRef]
- Rescifina, A.; Chiacchio, U.; Iannazzo, D.; Piperno, A.; Romeo, G. β-Cyclodextrin and Caffeine Complexes with Natural Polyphenols from Olive and Olive Oils: NMR, Thermodynamic, and Molecular Modeling Studies. J. Agric. Food Chem. 2010, 58, 11876–11882. [Google Scholar] [CrossRef]
- Simsek, T.; Rasulev, B.; Mayer, C.; Simsek, S. Preparation and Characterization of Inclusion Complexes of β-Cyclodextrin and Phenolics from Wheat Bran by Combination of Experimental and Computational Techniques. Molecules 2020, 25, 4275. [Google Scholar] [CrossRef] [PubMed]
- Chemaxon MarvinView, 16.3.14.0-Master-4840. 2016. Available online: www.chemaxon.com (accessed on 15 June 2020).
- Hanwell, M.D.; Curtis, D.E.; Lonie, D.C.; Vandermeersch, T.; Zurek, E.; Hutchison, G.R. Avogadro: An advanced semantic chemical editor, visualization, and analysis platform. J. Cheminforma. 2012, 4, 17. [Google Scholar] [CrossRef]
- HyperChem(TM) Professional, version 8.0; Hypercube Inc., N.t.S.: Gainesville, FL, USA, 2019.
- Vanommeslaeghe, K.; Hatcher, E.; Acharya, C.; Kundu, S.; Zhong, S.; Shim, J.; Darian, E.; Guvench, O.; Lopes, P.; Vorobyov, I.; et al. CHARMM general force field: A force field for drug-like molecules compatible with the CHARMM all-atom additive biological force fields. J. Comput. Chem. 2010, 31, 671–690. [Google Scholar] [CrossRef]
- Eberhardt, J.; Santos-Martins, D.; Tillack, A.F.; Forli, S. AutoDock Vina 1.2.0: New Docking Methods, Expanded Force Field, and Python Bindings. J. Chem. Inf. Model. 2021, 61, 3891–3898. [Google Scholar] [CrossRef]
- Górnas, P.; Neunert, G.; Baczyński, K.; Polewski, K. Beta-cyclodextrin complexes with chlorogenic and caffeic acids from coffee brew: Spectroscopic, thermodynamic and molecular modelling study. Food Chem. 2009, 114, 190–196. [Google Scholar] [CrossRef]
- Santos, C.; Buera, P.; Mazzobre, M. Phase solubility studies and stability of cholesterol/β-cyclodextrin inclusion complexes. J. Sci. Food Agric. 2011, 91, 2551–2557. [Google Scholar] [CrossRef]
- Pinho, E.; Soares, G.; Henriques, M. Cyclodextrin modulation of gallic acid in vitro antibacterial activity. J. Incl. Phenom. Macrocycl. Chem. 2015, 81, 205–214. [Google Scholar] [CrossRef]
- Karathanos, V.; Mourtzinos, I.; Yannakopoulou, K.; Andrikopoulos, N. Study of the solubility, antioxidant activity and structure of inclusion complex of vanillin with β-cyclodextrin. Food Chem. 2007, 101, 652–658. [Google Scholar] [CrossRef]
- Rajendiran, N.; Mohandoss, T.; Thulasidhasan, J. Photophysics of Caffeic, Ferulic and Sinapic Acids with α- and β-Cyclodextrins: Spectral and Molecular Modeling Studies. Int. Lett. Chem. Phys. Astron. 2017, 72, 37–51. [Google Scholar] [CrossRef]
- Liu, B.; Zeng, J.; Chen, C.; Liu, Y.; Ma, H.; Mo, H.; Liang, G. Interaction of cinnamic acid derivatives with β-cyclodextrin in water: Experimental and molecular modeling studies. Food Chem. 2016, 194, 1156–1163. [Google Scholar] [CrossRef]
- Lukasiewicz, M.; Jakubowski, P. Determination of Complexation Parameters for β-Cyclodextrin and Randomly Methylated β-Cyclodextrin Inclusion Complexes of p-Cumaric Acid Using Reversed-Phase Liquid Chromatography. In Proceedings of the 18th International Electronic Conference on Synthetic Organic Chemistry session Bioorganic, Medicinal and Natural Products Chemistry, Online, 1–30 November 2014. [Google Scholar] [CrossRef]
- Stewart, J. Optimization of parameters for semiempirical methods VI: More modifications to the NDDO approximations and re-optimization of parameters. J. Mol. Model. 2012, 19, 1–32. [Google Scholar] [CrossRef] [PubMed]
- Stewart, J.J.P. Optimization of parameters for semiempirical methods V: Modification of NDDO approximations and application to 70 elements. J. Mol. Model. 2007, 13, 1173–1213. [Google Scholar] [CrossRef] [PubMed]
- Hanson, R.M. Jmol SMILES and Jmol SMARTS: Specifications and applications. J. Cheminformatics 2016, 8, 50. [Google Scholar] [CrossRef]
- Schrodinger, L. The PyMOL Molecular Graphics System, 1.3r1; 2010. Available online: https://www.schrodinger.com/platform/products/pymol/ (accessed on 1 June 2024).
- Toddeschini, R.; Consonni, V.; Mauri, A.; Pavan, M. Dragon Software for the Calculation of Molecular Descriptors, Version 6 for Windows; Talete SRL: Milan, Italy, 2014. [Google Scholar]
- Cassani, S.; Kovarich, S.; Papa, E.; Roy, P.P.; van der Wal, L.; Gramatica, P. Daphnia and fish toxicity of (benzo)triazoles: Validated QSAR models, and interspecies quantitative activity-activity modelling. J. Hazard. Mater. 2013, 258–259, 50–60. [Google Scholar] [CrossRef] [PubMed]
- Gramatica, P.; Chirico, N.; Papa, E.; Cassani, S.; Kovarich, S. QSARINS: A new software for the development, analysis, and validation of QSAR MLR models. J. Comput. Chem. 2013, 34, 2121–2132. [Google Scholar] [CrossRef]
- Gramatica, P.; Cassani, S.; Chirico, N. QSARINS-chem: Insubria datasets and new QSAR/QSPR models for environmental pollutants in QSARINS. J. Comput. Chem. 2014, 35, 1036–1044. [Google Scholar] [CrossRef]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef] [PubMed]
- Najafi, A.; Ardakani, S.S.; Marjani, M. Quantitative Structure-Activity Relationship Analysis of the Anticonvulsant Activity of Some Benzylacetamides Based on Genetic Algorithm-Based Multiple Linear Regression. Trop. J. Pharm. Res. 2011, 10, 483–490. [Google Scholar] [CrossRef]
- MathWorks, I. MATLAB: The Language of Technical Computing: Computation, Visualization, Programming: Installation Guide for UNIX Version 5; Math Works Inc.: Natick, MA, USA, 1996. [Google Scholar]
- Hunter, J.D. Matplotlib: A 2D graphics environment. Comput. Sci. Eng. 2007, 9, 99–104. [Google Scholar] [CrossRef]
- Tropsha, A. Best practices for QSAR model development, validation, and exploitation. Mol. Inform. 2010, 29, 476–488. [Google Scholar] [CrossRef] [PubMed]
- Dieguez-Santana, K.; Pham-The, H.; Villegas-Aguilar, P.J.; Le-Thi-Thu, H.; Castillo-Garit, J.A.; Casañola-Martin, G.M. Prediction of acute toxicity of phenol derivatives using multiple linear regression approach for Tetrahymena pyriformis contaminant identification in a median-size database. Chemosphere 2016, 165, 434–441. [Google Scholar] [CrossRef] [PubMed]
- dos Passos Menezes, P.; Dória, G.A.A.; de Souza Araújo, A.A.; Sousa, B.M.H.; Quintans-Júnior, L.J.; Lima, R.N.; Alves, P.B.; Carvalho, F.M.S.; Bezerra, D.P.; Mendonça-Júnior, F.J.B.; et al. Docking and physico-chemical properties of α- and β-cyclodextrin complex containing isopulegol: A comparative study. J. Incl. Phenom. Macrocycl. Chem. 2016, 85, 341–354. [Google Scholar] [CrossRef]
- Talhout, R.; Villa, A.; Mark, A.E.; Engberts, J.B.F.N. Understanding Binding Affinity: A Combined Isothermal Titration Calorimetry/Molecular Dynamics Study of the Binding of a Series of Hydrophobically Modified Benzamidinium Chloride Inhibitors to Trypsin. J. Am. Chem. Soc. 2003, 125, 10570–10579. [Google Scholar] [CrossRef]
- Ertl, P.; Rohde, B.; Selzer, P. Fast calculation of molecular polar surface area as a sum of fragment-based contributions and its application to the prediction of drug transport properties. J. Med. Chem. 2000, 43, 3714–3717. [Google Scholar] [CrossRef]




| ID | β-CD-Ligand Complex | HOMO a (eV) | LUMO b (eV) | Gap (eV) | Binding Score (kJ/mol) | Binding Affinity (kJ/mol) |
|---|---|---|---|---|---|---|
| 1 | Caffeic acid-in | −9.1890 | −1.0514 | −8.1376 | −4.5 | −51.1831 |
| 2 | Camphor-in | −10.1147 | 0.0704 | −10.1851 | −3.9 | −34.4419 |
| 3 | D-Limonene-in | −9.3119 | 0.0092 | −9.3211 | −3.5 | −44.2580 |
| 4 | Eucalyptol-in | −9.9785 | 0.1605 | −10.139 | −4.0 | −52.1555 |
| 5 | Eugenol-up | −8.9658 | −0.1518 | −8.8140 | −4.0 | −35.1691 |
| 6 | Gallic acid-up | −9.5087 | −1.2760 | −8.2327 | −5.0 | −35.6459 |
| 7 | Geranial-up | −9.5651 | −0.2514 | −9.3137 | −3.2 | −58.3673 |
| 8 | Heptanol-up | −10.2024 | −0.1426 | −10.0598 | −2.8 | −26.6948 |
| 9 | Hydroxy Methyl Furfural-up | −9.2240 | −0.4026 | −8.8214 | −3.7 | −64.9081 |
| 10 | Isoamyl acetate-up | −10.1978 | −0.3113 | −9.8865 | −3.1 | −66.5904 |
| 11 | Maltol-up | −9.8792 | −1.3000 | −8.5792 | −4.1 | −64.6218 |
| 12 | Menthol-in | −10.1733 | −0.0167 | −10.1566 | −4.2 | −57.9313 |
| 13 | Neral-up | −9.7932 | −0.4443 | −9.3489 | −3.4 | −66.7781 |
| 14 | P-Coumaric acid-in | −9.3920 | −0.3048 | −9.0872 | −4.3 | −63.3347 |
| 15 | Pinellic acid-in | −9.8072 | 0.0819 | −9.8891 | −3.6 | −63.3198 |
| 16 | Sinapic acid-up | −9.1111 | −1.1979 | −7.9132 | −4.6 | −90.6849 |
| 17 | Styrene-up | −9.4684 | −0.4950 | −8.9734 | −2.9 | −45.7564 |
| 18 | Syringic acid-up | −9.2231 | −0.9025 | −8.3206 | −4.6 | −76.8800 |
| 19 | Trans Ferulic acid-up | −9.0647 | −1.4466 | −7.6181 | −4.4 | −64.1563 |
| 20 | Vanillic acid-in | −9.1477 | −0.9277 | −8.2200 | −4.4 | −76.3647 |
| Parameters | Log BSA | Log BA | Log BE |
|---|---|---|---|
| Model # Number of variables | 1 (Equation (3)) 3 | 2 (Equation (4)) 3 | 3 (Equation (5)) 3 |
| R2 (training set) | 0.969 | 0.859 | 0.779 |
| RMSE (training set) | 0.0116 | 0.0256 | 0.0631 |
| MAE (training set) | 0.0095 | 0.0192 | 0.0527 |
| CCC (training set) | 0.985 | 0.924 | 0.876 |
| F | 126.902 | 24.349 | 14.117 |
| R2 (cross-validation) | 0.925 | 0.805 | 0.634 |
| RMSE (cross-validation) | 0.0182 | 0.0302 | 0.0812 |
| MAE (cross-validation) | 0.0135 | 0.0236 | 0.0698 |
| CCC (cross-validation) | 0.961 | 0.897 | 0.790 |
| R2 (external test) | 0.984 | 0.956 | 0.663 |
| RMSE (external test) | 0.0093 | 0.0156 | 0.0685 |
| MAE (external test) | 0.0082 | 0.0146 | 0.0563 |
| Descriptor | Description | Class |
|---|---|---|
| Model 1—Binding Score Affinity | ||
| nR06 | Number of 6-membered rings | Ring descriptors |
| ATS4m | Broto–Moreau autocorrelation of lag 4 (log function) weighted by mass | 2D Autocorrelations |
| BEle3 | Lowest eigenvalue No. 3 of Burden matrix/weighted by atomic Sanderson electronegativities | BCUT descriptors |
| Model 2—Binding Affinity | ||
| S3K | 3-path Kier alpha-modified shape index | Topological Indices |
| EEig03r | Eigenvalues | Edge adjacency indices |
| H0e | H autocorrelation of lag 0/weighted by Sanderson electronegativity | GETAWAY descriptors |
| Model 3—Binding Energy | ||
| GATS8e | Geary autocorrelation of lag 8 weighted by mass | 2D Autocorrelations |
| Mor10u | Signal 10/unweighted | 3D-MoRSE descriptors |
| TPSA | Topological polar surface area using N,O polar contributions | Molecular properties |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iduoku, K.; Ngongang, M.; Kulathunga, J.; Daghighi, A.; Casanola-Martin, G.; Simsek, S.; Rasulev, B. Phenolic Acid–β-Cyclodextrin Complexation Study to Mask Bitterness in Wheat Bran: A Machine Learning-Based QSAR Study. Foods 2024, 13, 2147. https://doi.org/10.3390/foods13132147
Iduoku K, Ngongang M, Kulathunga J, Daghighi A, Casanola-Martin G, Simsek S, Rasulev B. Phenolic Acid–β-Cyclodextrin Complexation Study to Mask Bitterness in Wheat Bran: A Machine Learning-Based QSAR Study. Foods. 2024; 13(13):2147. https://doi.org/10.3390/foods13132147
Chicago/Turabian StyleIduoku, Kweeni, Marvellous Ngongang, Jayani Kulathunga, Amirreza Daghighi, Gerardo Casanola-Martin, Senay Simsek, and Bakhtiyor Rasulev. 2024. "Phenolic Acid–β-Cyclodextrin Complexation Study to Mask Bitterness in Wheat Bran: A Machine Learning-Based QSAR Study" Foods 13, no. 13: 2147. https://doi.org/10.3390/foods13132147
APA StyleIduoku, K., Ngongang, M., Kulathunga, J., Daghighi, A., Casanola-Martin, G., Simsek, S., & Rasulev, B. (2024). Phenolic Acid–β-Cyclodextrin Complexation Study to Mask Bitterness in Wheat Bran: A Machine Learning-Based QSAR Study. Foods, 13(13), 2147. https://doi.org/10.3390/foods13132147








