Detection of the Spatio-Temporal Differentiation Patterns and Influencing Factors of Wheat Production in Huang-Huai-Hai Region
Abstract
:1. Introduction
2. Materials and Methods
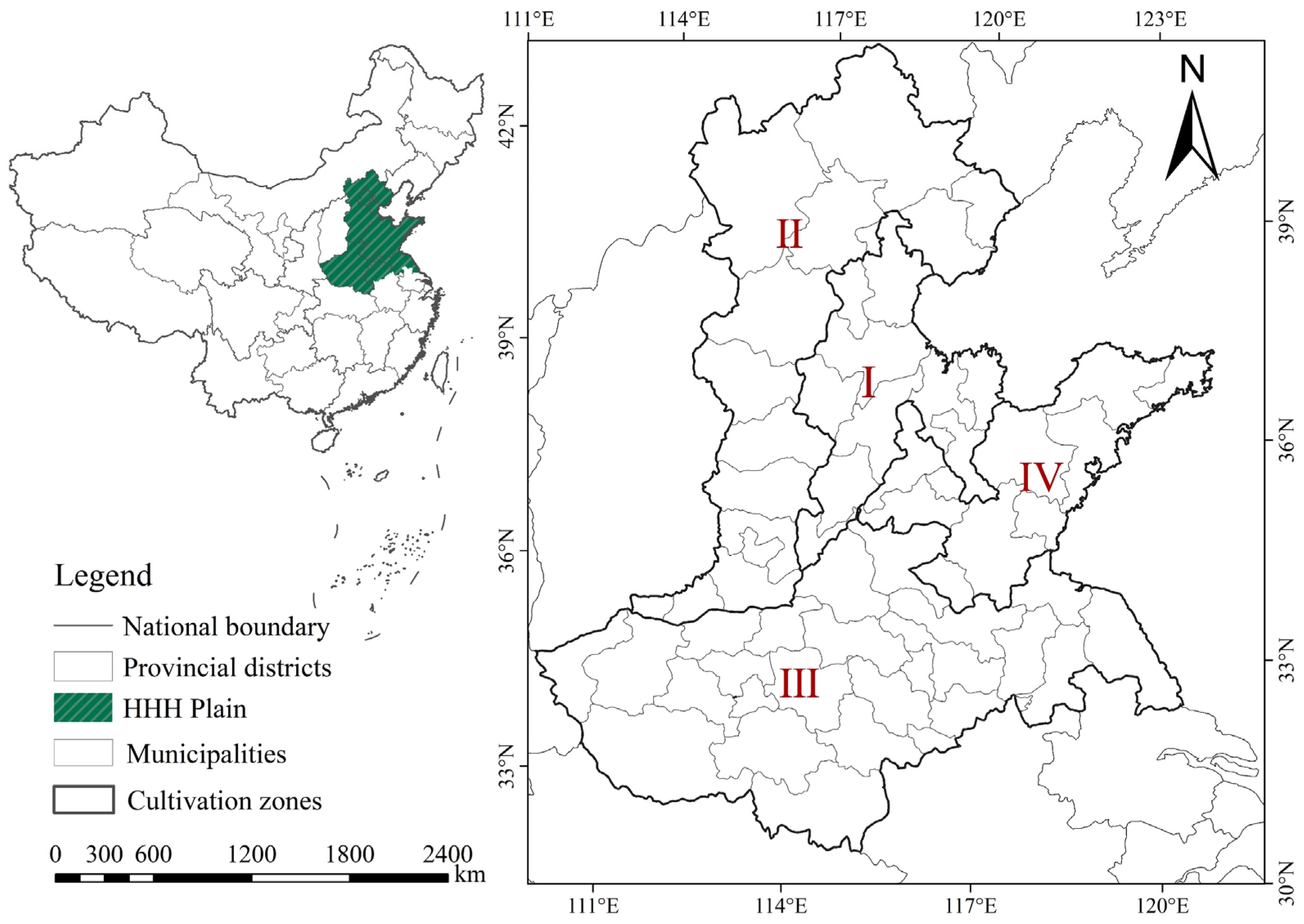
2.1. Overview of the Study Area
2.2. Data Sources and Processing
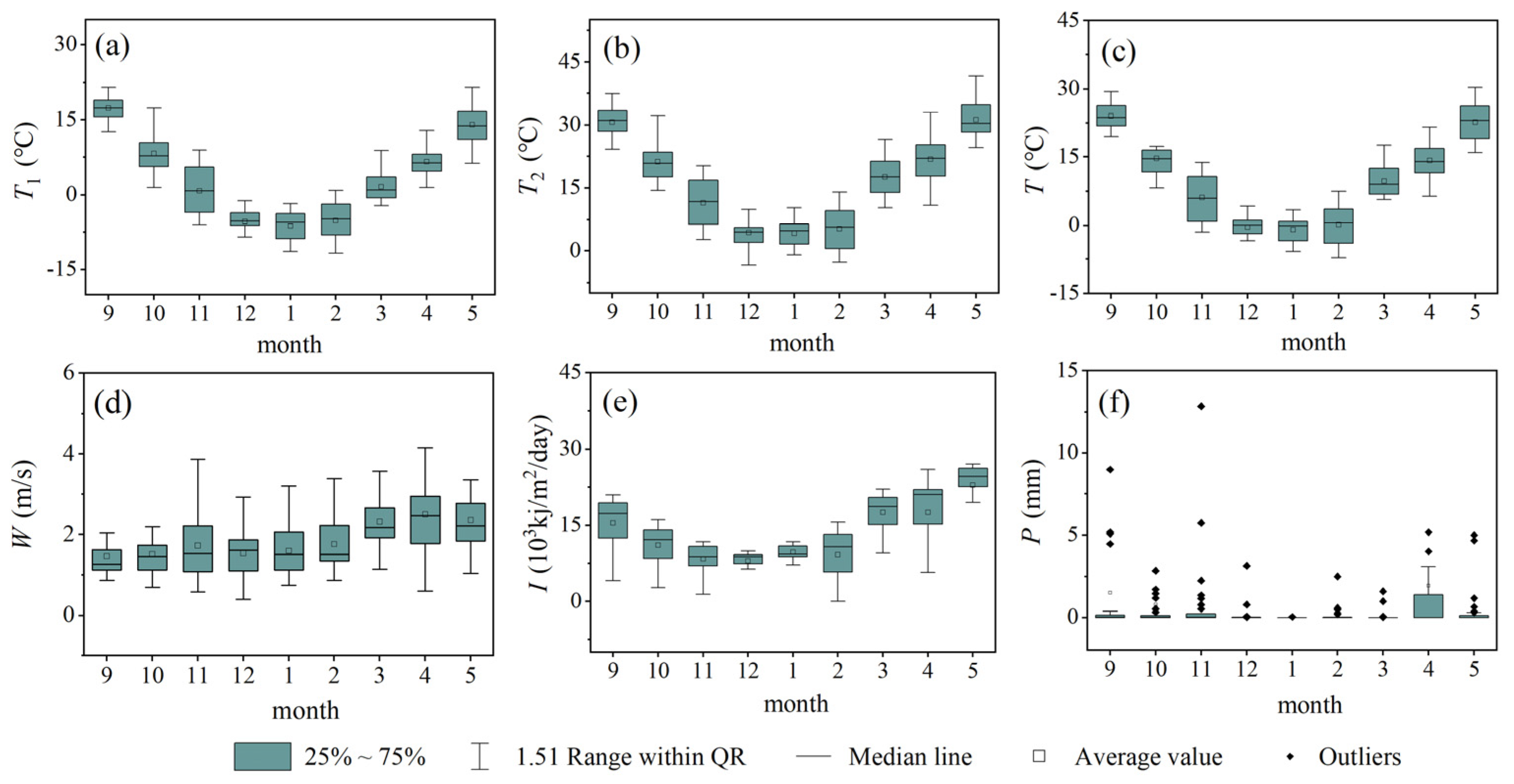
2.2.1. Natural Attribute Data
2.2.2. Social Attribute Data
2.3. Research Methods
2.3.1. Theil Index
2.3.2. ESDA
2.3.3. SCA-GWR
- Step 1. Screen variables from the SCA.
- Step 2. Establish the GWR model.
- Step 3. Estimate the parameters.
- Step 4. Inspect accuracy.
3. Results
3.1. Temporal and Spatial Differentiation of Wheat Production in the HHH
3.1.1. Time Distribution
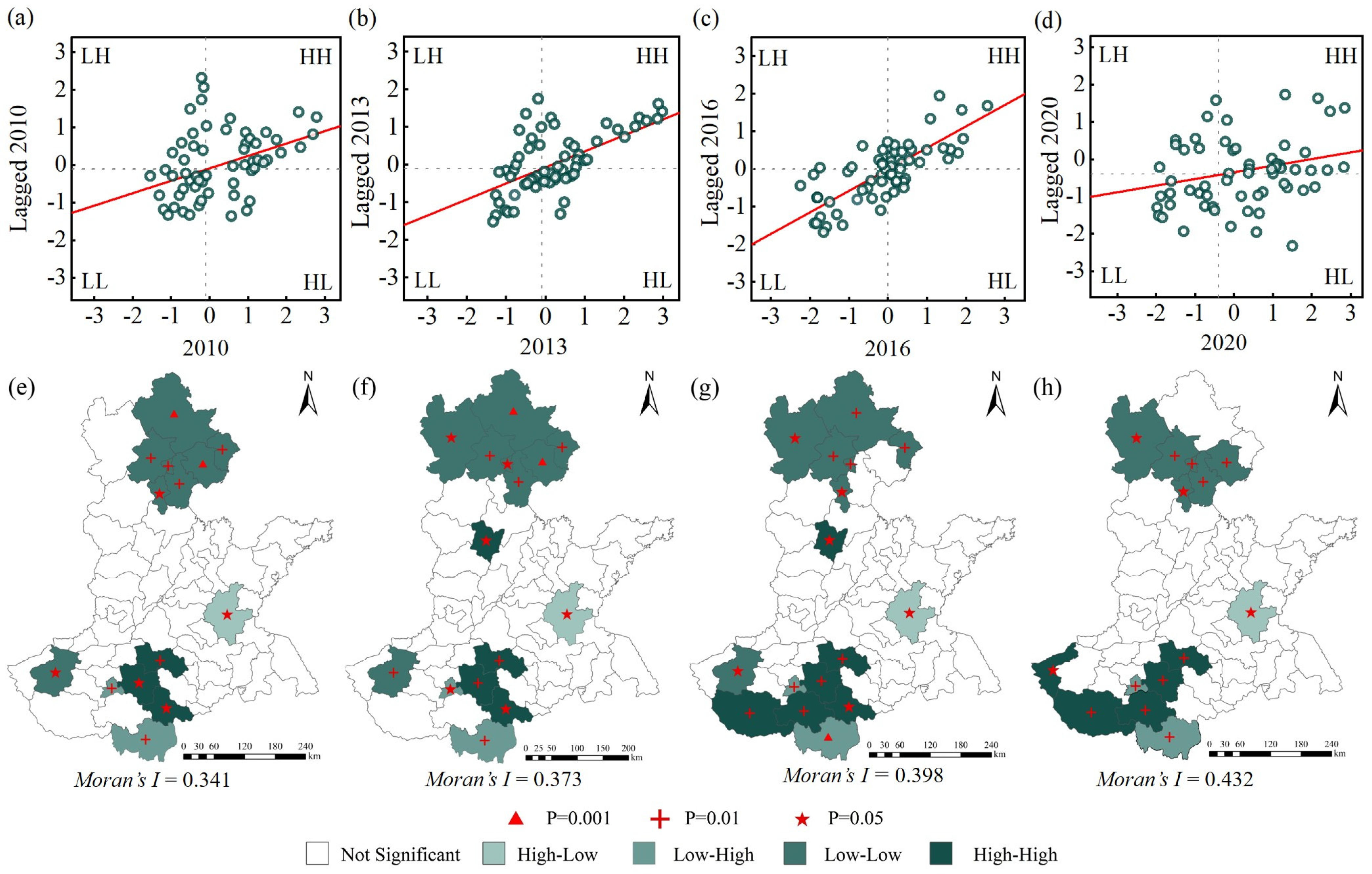
3.1.2. Spatial Distribution
3.2. HHH Wheat Production Factor Model Establishment
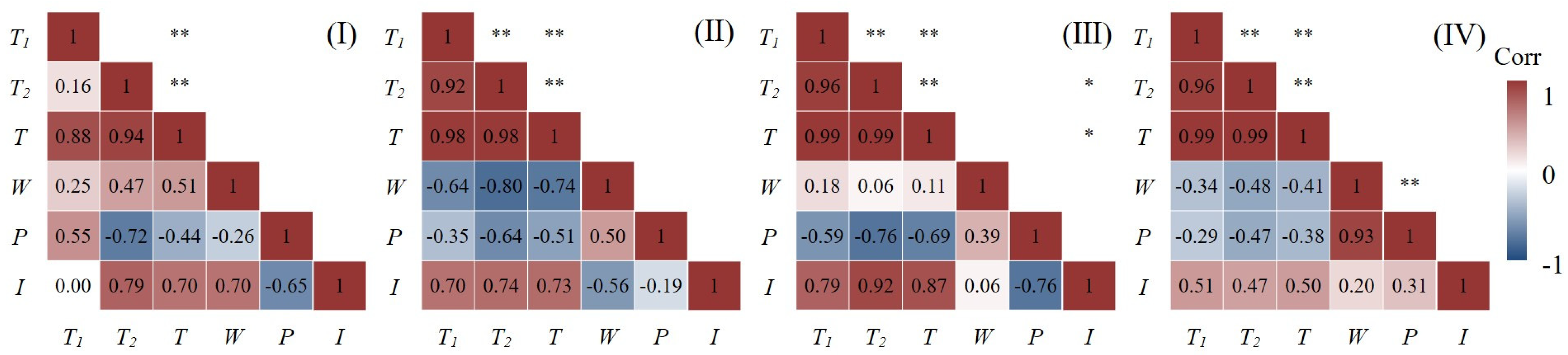
3.2.1. Variable Filtering
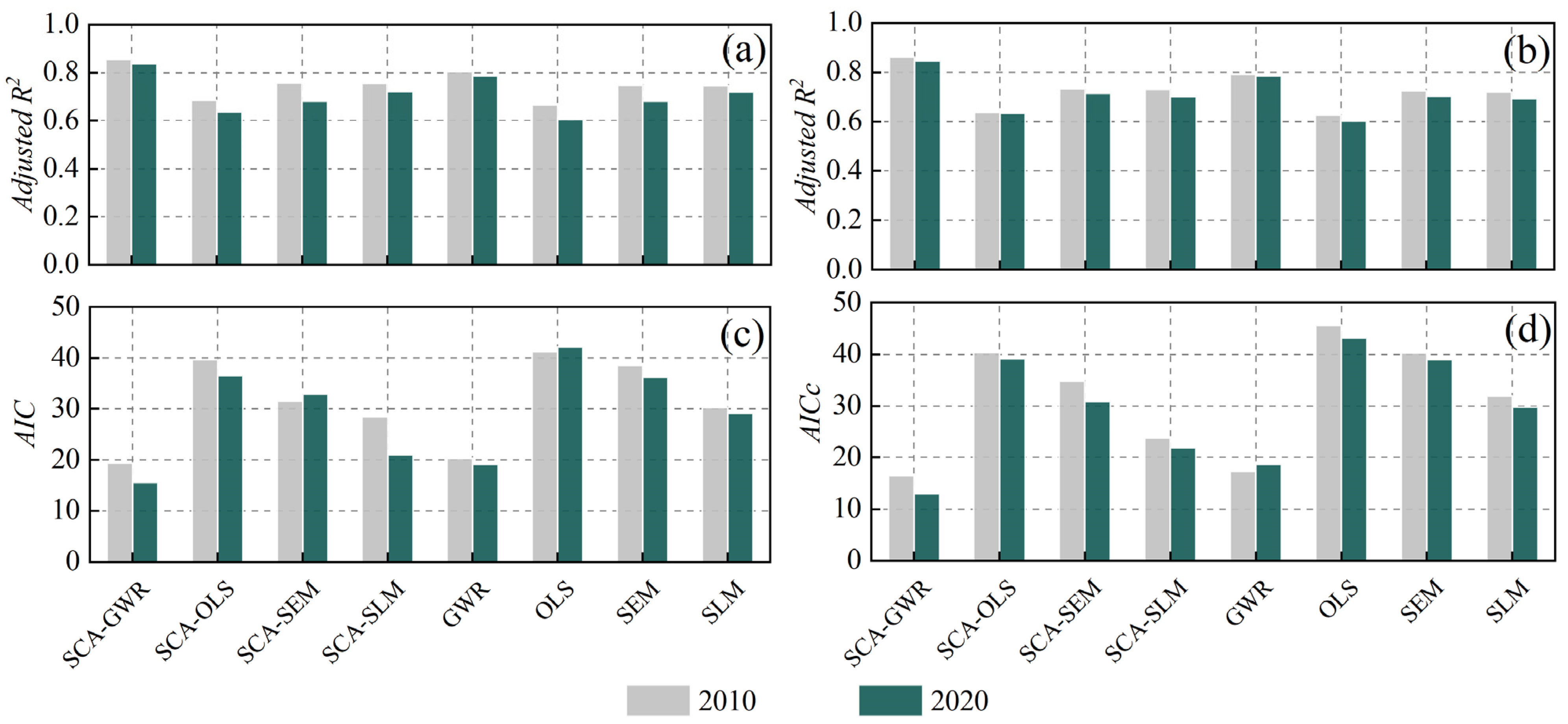
3.2.2. Model Filtering
3.3. Detection of Influencing Factors for Wheat Production in the HHH Based on the SCA-GWR Model
4. Discussion
- (1)
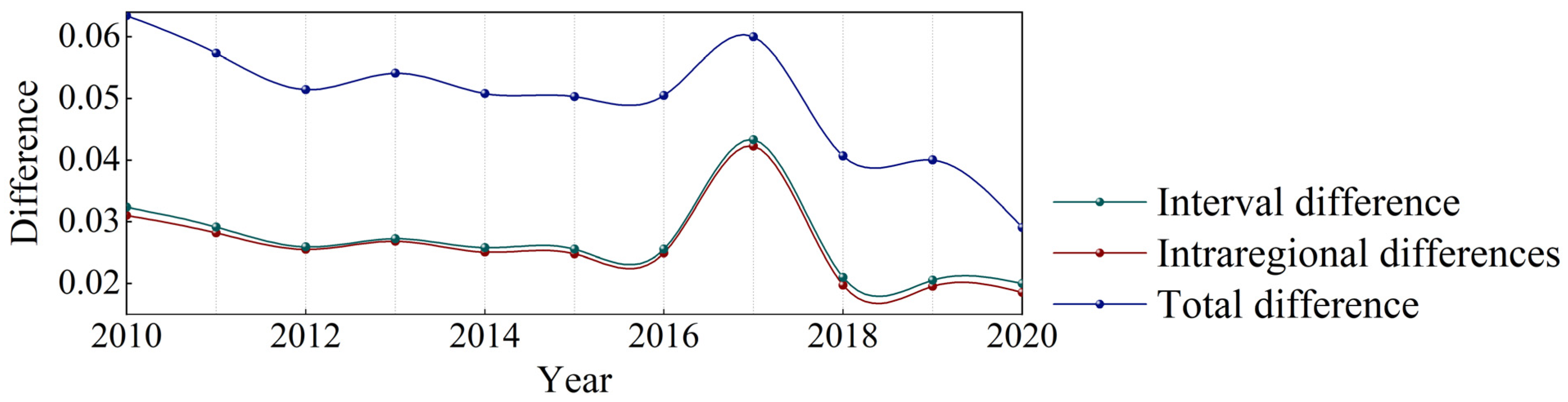
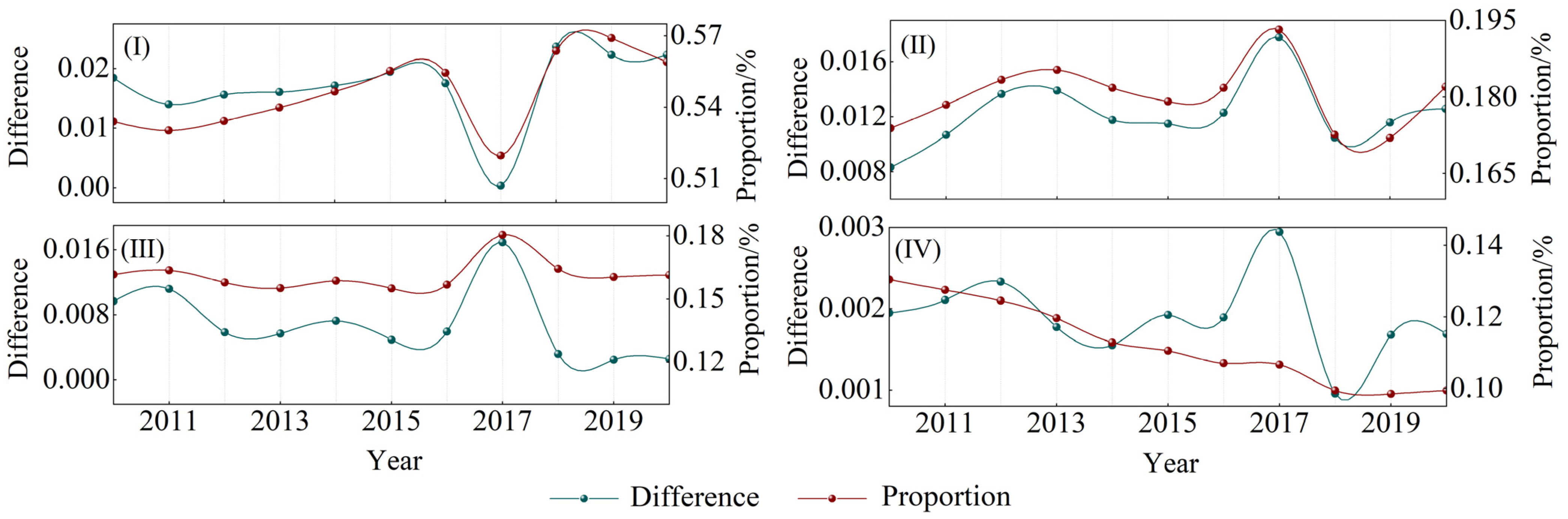
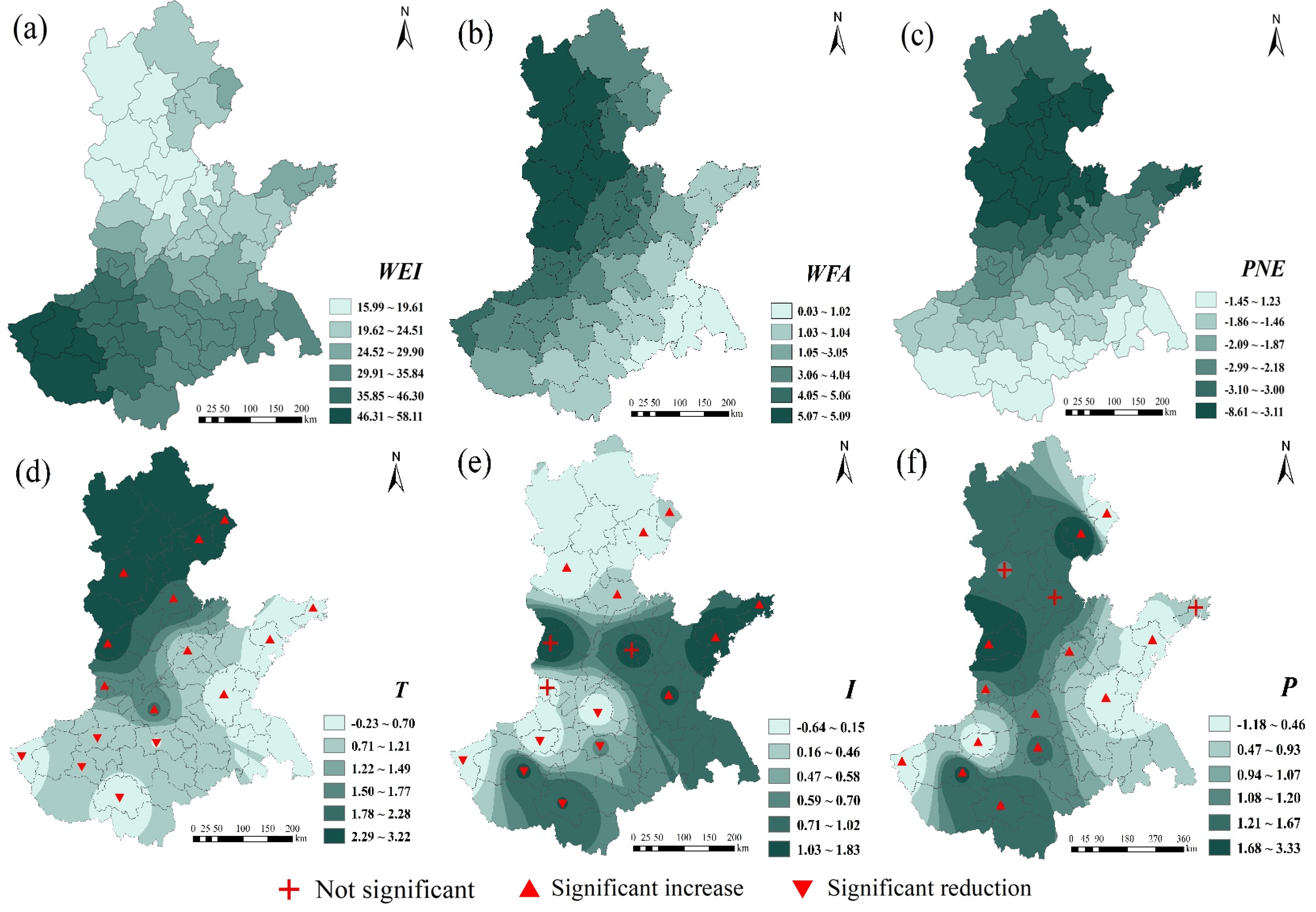
- Zones I, II, and III were were the main contributors to the overall differences in HHH wheat. For wheat production, attention should be paid to the control of these regional differences, and measures should be taken according to local conditions, while strengthening the management of water and fertilizer to control and ultimately prevent agricultural endogenous pollution. The spatial agglomeration of wheat production is relatively strong (Figure 6). It is necessary to give full play to the learning and imitation abilities of farmers in neighboring regions, improve the technical efficiency of wheat production, and give full play to the planting advantages of different regions.
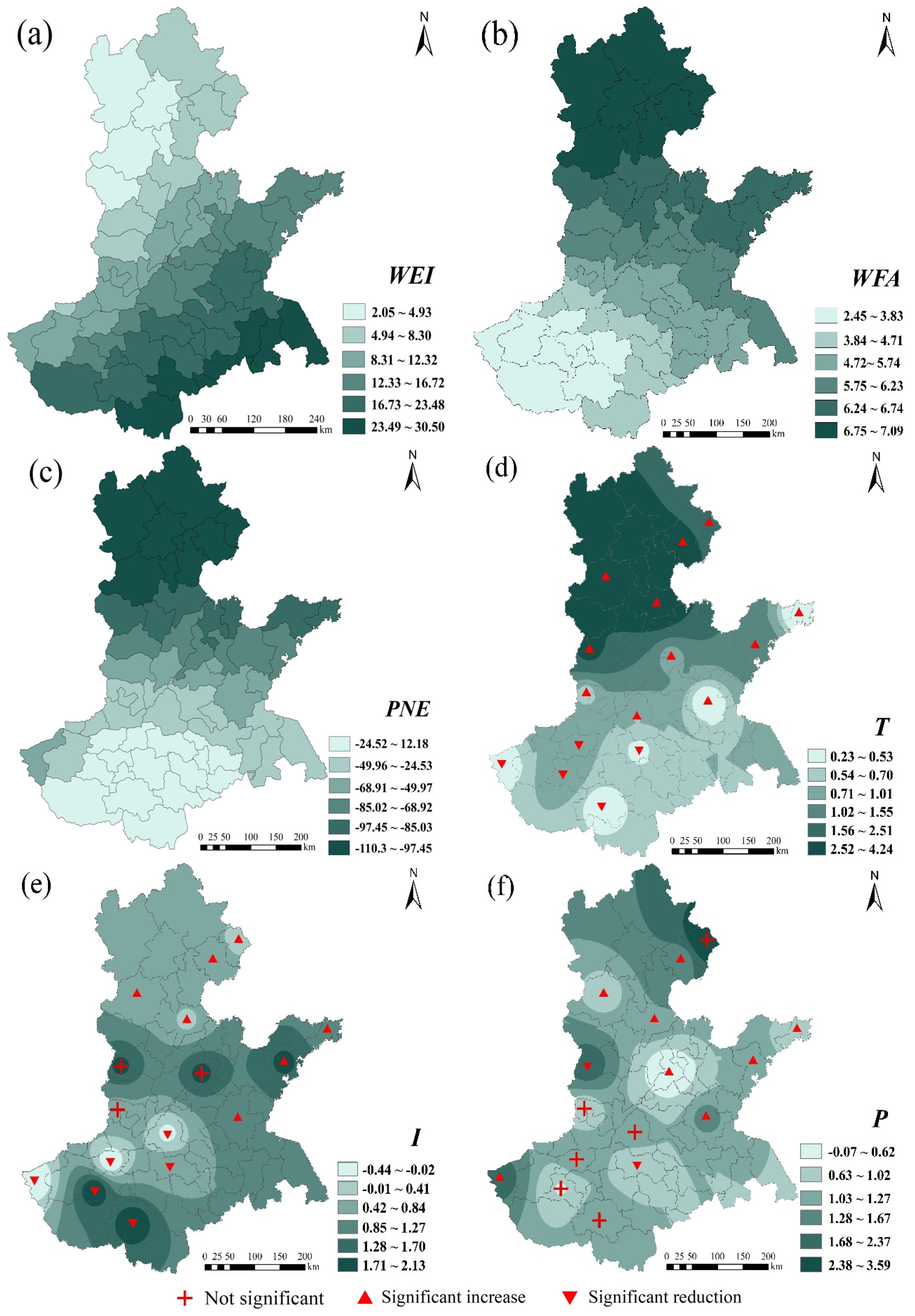
- (2)
- Since PNE has an inhibitory effect on wheat in most areas (Figure 11), attention should be paid to the fluctuation in wheat planting areas caused by the transfer of agricultural labor in wheat production so as to effectively protect farmers’ income. According to the different effects of T, I, and P in the same area (Table 3), when optimizing the layout of wheat production, the spatial interaction of factors such as economic development and factor input should be fully utilized according to natural climatic conditions.
- (3)
- Compared with 2010, wheat still relies heavily on WEI in 2020, while the demand for WFA is gradually weakening (Figure 10 and Figure 11). The rational use of water and fertilizer is the key factor in improving the utilization rate of water and fertilizer, which is related to the sustainable development of agriculture. Relevant management departments need to increase investment in agricultural infrastructure and high-standard farmland construction and promote the efficient and sustainable use of water and fertilizer resources. The scope of influence for PNE is gradually expanding. Against the background of continuous improvement in the nonagricultural labor force, the shortage of labor supply caused by the transfer of rural labor can be effectively dealt through the acceleration of agricultural mechanization and intelligent development.
- (4)
- Over time, T has an inhibitory effect in some areas. With the gradual warming of the climate, it can delay the sowing time of wheat and slow down the growth and development rate before winter. In response to the problem of insufficient I, scientific and technological departments can vigorously develop radiation breeding technology based on environmental factors and wheat varieties to ensure the smooth progress of wheat photosynthesis. The previous analysis shows that P is only a part of the water supply for wheat, and irrigation is still needed to ensure the smooth growth of wheat. It is necessary to grasp the best irrigation period and amount of irrigation for wheat, improve the water use efficiency of wheat, and achieve sustainable development of high-yield, high-efficiency wheat.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, H.J.; Murray, D.; McIntosh, A.; Zhou, Y. Breeding new cultivars for sustainable wheat production. Crop J. 2019, 7, 715–717. [Google Scholar] [CrossRef]
- Zhou, B.Y.; Ge, J.Z.; Sun, X.F.; Han, Y.L.; Ma, W.; Ding, Z.S.; Li, C.F.; Zhao, M. Research advance on optimizing annual distribution of solar and heat resources for double cropping system in the Yellow-Huaihe-Haihe Rivers plain. Acta Agron. Sin. 2021, 47, 1843–1853. [Google Scholar] [CrossRef]
- De Sousa, T.; Ribeiro, M.; Sabença, C.; Igrejas, G. The 10,000-Year success story of wheat! Foods 2021, 10, 2124. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.; Zhang, Y.; Hong, Y.; He, L.; Chen, Y. Experiences and lessons from Agri-Food system transformation for sustainable food security: A review of China’s practices. Foods 2022, 11, 137. [Google Scholar] [CrossRef] [PubMed]
- Pan, J.W.; Chen, Y.Y.; Zhang, Y.; Chen, M.; Fennell, S.; Luan, B.; Wang, F.; Meng, D.; Liu, Y.L.; Jiao, L.M.; et al. Spatial-temporal dynamics of grain yield and the potential driving factors at the county level in China. J. Clean. Prod. 2020, 255, 120312. [Google Scholar] [CrossRef]
- Yao, C.S.; He, Y.B.; Cao, Z.Y. Spatial-temporal evolution and driving mechanism of mechanization level of staple food grain production in China. J. China Agric. Univ. 2021, 26, 208–220. [Google Scholar]
- Yu, X.; Sun, J.X.; Sun, S.K.; Yang, F.; Lu, Y.J.; Wang, Y.B.; Wu, F.J.; Liu, P. A comprehensive analysis of regional grain production characteristics in China from the scale and efficiency perspectives. J. Clean. Prod. 2019, 212, 610–621. [Google Scholar]
- Wu, S.; Mu, Y.Y.; Nie, F.Y. Influencing factors and forecast of China’s wheat production fluctuations. Agric. Outlook 2020, 16, 40–47, 58. [Google Scholar]
- Feng, Z.M.; Sun, T.; Yang, Y.Z. Study on the spatiotemporal patterns and contribution factors of China’s grain output increase during 2003–2013. J. Nat. Resour. 2016, 31, 895–907. [Google Scholar]
- Li, H.S.; Hu, C.P.; Qu, C.H. Spatio-temporal feature of wheat production efficiency in main producing provinces of China. Chin. J. Agric. Resour. Reg. Plan. 2018, 39, 91–99. [Google Scholar]
- Guo, D.Y.; Wang, G.R.; Li, M.; Wang, X.; Zhang, X.S.; Cui, Y.F. Analysis on regional distribution and influencing factors of wheat yield in Hebei Province. Manag. Agric. Sci. Technol. 2021, 40, 54–58. [Google Scholar]
- Cai, R.; Tao, S.M. Evolution characteristics of grain production distribution and spatial mechanism decomposition in China from 1978 to 2018. J. Arid. Land Resour. Environ. 2021, 35, 1–7. [Google Scholar]
- Zhang, Y.J.; Zhao, J.; Yan, Y.X.; Shi, Y.; Yu, Q. Relationship of population migration, crop production pattern, and socioeconomic development: Evidence from the early 21st century. Environ. Res. Lett. 2021, 16, 074045. [Google Scholar] [CrossRef]
- Zhao, X.Y.; An, Z.C.; Chen, M.Y.; Wang, C.H.; Guo, X.W.; Cui, Z.L. Analysis of yield gaps and limiting factors of winter wheat in Quzhou County. J. Triticeae Crops 2019, 39, 1368–1376. [Google Scholar]
- Yu, D.; Hu, S.G.; Tong, L.Y.; Xia, C.; Ran, P.L. Dynamics and determinants of the grain yield gap in major grain-producing areas: A case study in Hunan Province, China. Foods 2022, 11, 1122. [Google Scholar] [CrossRef]
- Twizerimana, A.; Niyigaba, E.; Mugenzi, I.; Ngnadong, W.A.; Li, C.; Hao, T.Q.; Shio, B.J.; Hai, J.B. The combined effect of different sowing methods and seed rates on the quality features and yield of winter wheat. Agriculture 2020, 10, 153. [Google Scholar] [CrossRef]
- Wu, F.; Xu, P.; Guo, H.Q.; Zhang, Z.B. Advances in research regarding the yield gap and resource use efficiency of winter wheat cultivation and the related regulatory approaches. Chin. J. Eco-Agric. 2020, 28, 1551–1567. [Google Scholar]
- Lin, Y.; Shao, H.Y. Study on optimal time and influencing factors for winter wheat yield prediction in Henan based on random forest algorithm. J. Triticeae Crops 2020, 40, 874–880. [Google Scholar]
- Yang, Y.J.; Tong, X.Q.; Zhu, J.H. A geographically weighted model of the regression between grain production and typical factors for the Yellow River Delta. Math. Comput. Model. 2013, 58, 582–587. [Google Scholar] [CrossRef]
- Wang, J.; Xiao, H.F. The Spatial-temporal pattern changes and driving factors of grain production in Xinjiang Province. Chin. J. Agric. Resour. Reg. Plan. 2018, 39, 58–66. [Google Scholar]
- Hao, X.Y.; Zhang, Y.; Han, Y.J. Study on wheat spatial distribution variation and influencing factors in China. Chin. J. Agric. Resour. Reg. Plan. 2018, 39, 40–48. [Google Scholar]
- Li, W. Spatiotemporal evolution Characteristics and influencing factors of wheat production in China. Chin. J. Agric. Resour. Reg. Plan. 2019, 40, 49–57. [Google Scholar]
- Zhang, L.L.; Feng, H.; Dong, Q.G. Spatial-temporal distribution characteristics of winter wheat potential yields and its influencing factors in the Loess Plateau. Agric. Res. Arid. Areas 2019, 37, 267–274. [Google Scholar]
- Fang, W.; Huang, H.L.; Yang, B.X.; Hu, Q. Factors on spatial heterogeneity of the grain production capacity in the major grain sales area in southeast China: Evidence from 530 Counties in Guangdong Province. Land 2021, 10, 206. [Google Scholar] [CrossRef]
- He, X.D.; Mai, X.M.; Shen, G.Q. Poverty and physical geographic factors: An empirical analysis of Sichuan Province using the GWR model. Sustainability 2021, 13, 100. [Google Scholar] [CrossRef]
- Zhang, Q.N.; Zhang, F.F.; Wu, G.Y.; Mai, Q. Spatial spillover effects of grain production efficiency in China: Measurement and scope. J. Clean. Prod. 2021, 278, 121062. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Y.F.; Pan, J.W.; Zhang, Y.; Liu, D.F.; Chen, H.T.; Wei, J.Q.; Zhang, Z.Y.; Liu, Y.L. Exploring spatially non-stationary and scale-dependent responses of ecosystem services to urbanization in Wuhan, China. Int. J. Environ. Res. Public Health 2020, 17, 2989. [Google Scholar] [CrossRef]
- Liu, Y.W.; Liu, C.W.; He, Z.Y.; Zhou, X.; Han, B.H.; Hao, H.Z. Spatial-temporal evolution of ecological land and influence factors in Wuhan urban agglomeration based on geographically weighted regression model. Chin. J. Appl. Ecol. 2020, 31, 987–998. [Google Scholar]
- Wang, C.X.; Du, S.Q.; Wen, J.H.; Zhang, M.; Gu, H.H.; Shi, Y.; Xu, H. Analyzing explanatory factors of urban pluvial floods in Shanghai using geographically weighted regression. Stoch. Environ. Res. Risk Assess. 2017, 31, 1777–1790. [Google Scholar] [CrossRef]
- Li, Y.F.; Zhao, B.C.; Huang, A.; Xiong, B.Y.; Cong, C.F. Characteristics and driving forces of non-grain production of cultivated land from the perspective of food security. Sustainability 2021, 13, 14047. [Google Scholar] [CrossRef]
- Han, X.C.; Ming, Y.F.; Ji, Z.L.; Wang, K. Habitat suitability for wheat yellow mosaic disease in Huang-Huai-Hai region based on the maximum entropy model. J. Agric. Sci. Technol. 2020, 22, 111–119. [Google Scholar]
- Yang, Q.L.; Zheng, F.X.; Jia, X.C.; Liu, P.; Dong, S.T.; Zhang, J.W.; Zhao, B. The combined application of organic and inorganic fertilizers increases soil organic matter and improves soil microenvironment in wheat-maize field. J. Soils Sediments 2020, 20, 2395–2404. [Google Scholar] [CrossRef]
- Ren, S.J.; Guo, B.; Wu, X.; Zhang, L.G.; Ji, M.; Wang, J. Winter wheat planted area monitoring and yield modeling using MODIS data in the Huang-Huai-Hai Plain, China. Comput. Electron. Agric. 2021, 182, 106049. [Google Scholar] [CrossRef]
- Grovermann, C.; Umesh, K.B.; Quiédeville, S.; Kumar, B.G.; Srinivasaiah, S.; Moakes, S. The economic reality of underutilised crops for climate resilience, food security and nutrition: Assessing finger millet productivity in India. Agriculture 2018, 8, 131. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Sarkar, A.; Ma, L.; Wu, Q.; Wei, F. Measurement of investment potential and spatial distribution of arable land among countries within the “Belt and Road Initiative”. Agriculture 2021, 11, 848. [Google Scholar] [CrossRef]
- Liu, Y.W.; Zhou, X.; He, Z.Y.; Hao, H.Z.; He, G.S. Quantitative evolution and marginal effect analysis of spatial factors of cultivated land based on logistic regression. Trans. Chin. Soc. Agric. Eng. 2020, 36, 267–276. [Google Scholar]
- Zhu, Z.Y.; Li, B.B.; Zhao, Y.G.; Zhao, Z.Y.; Chen, L.H. Socio-Economic impact mechanism of ecosystem services value, a PCA-GWR approach. Pol. J. Environ. Stud. 2020, 30, 977–986. [Google Scholar] [CrossRef]
- Wu, D.C. Spatially and temporally varying relationships between ecological footprint and influencing factors in China’s provinces using geographically weighted regression (GWR). J. Clean. Prod. 2020, 261, 121089. [Google Scholar] [CrossRef]
- Sun, Y.; Chang, Y.Y.; Liu, J.N.; Ge, X.P.; Liu, G.J.; Chen, F. Spatial differentiation of non-grain production on cultivated land and its driving factors in coastal China. Sustainability 2021, 13, 13064. [Google Scholar] [CrossRef]
- Oshan, T.M.; Smith, J.P.; Fotheringham, A.S. Targeting the spatial context of obesity determinants via multiscale geographically weighted regression. Int. J. Health Geogr. 2020, 19, 11. [Google Scholar] [CrossRef]
- Hou, M.Y.; Deng, Y.J.; Yao, S.B. Spatial agglomeration pattern and driving factors of grain production in China since the reform and opening up. Land 2020, 10, 10. [Google Scholar] [CrossRef]
- Wang, S.J.; Wang, Y.; Zhao, Y.B. Spatial spillover effects and multi-mechanism for regional development in Guangdong province since 1990s. Acta Geogr. Sin. 2015, 70, 965–979. [Google Scholar]
- Chu, L.; Huang, C.; Liu, Q.S.; Cai, C.F.; Liu, G.H. Spatial heterogeneity of winter wheat yield and its determinants in the Yellow River Delta, China. Sustainability 2020, 12, 135. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Wang, E.L.; Liu, D.L. Modelling the impacts of climate change on wheat yield and field water balance over the murray–darling basin in Australia. Theor. Appl. Climatol. 2011, 104, 285–300. [Google Scholar] [CrossRef]
- Li, M.; Bu, R.Y.; Han, S.; Chen, Y.; Yu, Z.; Wang, H.; Cheng, W.L.; Wu, J. Current status of fertilizer application and utilization efficiency of winter wheat in Anhui Province, China. Ying Yong Sheng Tai Xue Bao = J. Appl. Ecol. 2020, 31, 3051–3059. [Google Scholar]
- Zhao, J.W.; Wang, X.P.; Du, X.Y.; Shang, Z.Y. Spatial structure and control factors of winter wheat production in Hebei Province. Chin. J. Eco-Agric. 2016, 24, 1683–1692. [Google Scholar]
- Zhang, L.L.; Zhang, Y.G.; Liu, R.Q.; Xu, H.; Chen, Y.H. Spatial disparity and dynamic evolution of grain yield per unit area and its driving factors in Hebei Province. Res. Soil Water Conserv. 2011, 18, 192–197. [Google Scholar] [CrossRef]
- Zhang, L.; Luo, B.L. How can small farmers be incorporated into modern agricultural development? Evidence from Wheat-producing areas of China. Econ. Res. J. 2018, 53, 144–160. [Google Scholar]
- Li, B.J.; Zhang, Y.F.; Zhang, S.H.; Li, W.Y. Prediction of grain yield in Henan Province based on grey BP neural network model. Discret. Dyn. Nat. Soc. 2021, 2021, 9919332. [Google Scholar] [CrossRef]
- Ji, Z.X.; Wang, X.L.; Li, L.; Guan, X.K.; Yu, L.; Xu, Y.Q. The evolution of cultivated land utilization efficiency and its influencing factors in Nanyang Basin. J. Nat. Resour. 2021, 36, 688–701. [Google Scholar] [CrossRef]
- Jing, Y.G.; Fan, J.Z.; Gao, M.S. Influences of the climate warming on developmental stages of winter wheat in Shaanxi. J. Triticeae Crops 2013, 33, 389–396. [Google Scholar]
- Luan, Q.; Guo, J.P.; Ma, Y.L.; Zhang, L.M.; Wang, J.X.; Li, W.W. Comparison of model’s stability about integrated temperature based on linear hypotheses. Chin. J. Agrometeorol. 2020, 41, 695–706. [Google Scholar]
- Cheng, L.; Li, T.X.; Liu, R.H. Effect of climate change on growth and yield of winter wheat in Henan Province. Chin. J. Eco-Agric. 2017, 25, 931–940. [Google Scholar]
- Xiao, D.P.; Tao, F.L.; Shen, Y.J.; Liu, J.F.; Wang, R.D. Sensitivity of response of winter wheat to climate change in the North China Plain in the last three decades. Chin. J. Eco-Agric. 2014, 22, 430–438. [Google Scholar]
- Zhao, Y.X.; Xiao, D.P.; Tang, J.Z.; Bai, H.Z. Effects of climate change on the yield of major grain crops and its adaptation measures in China. Res. Soil Water Conserv. 2019, 26, 317–326. [Google Scholar]
- Ding, B.B.; Zhang, X.L.; Zhao, Z.T.; Hou, Y.H. Change in winter wheat yield and its water use efficiency as affected by limited irrigation in North China plain: A Meta-analysis. J. Irrig. Drain. 2021, 40, 7–17. [Google Scholar]
- Chen, H.; Cao, C.F.; Kong, L.C.; Zhang, C.L.; Li, W.; Qiao, Y.Q.; Du, S.Z.; Zhao, Z. Study on wheat yield stability in Huaibei lime concretion black soil area based on long-term fertilization experiment. Sci. Agric. Sin. 2014, 47, 2580–2590. [Google Scholar]


| Year | Variable | Unit | Average | Maximum | Minimum | Upper Quartile | Lower Quartile | Median |
|---|---|---|---|---|---|---|---|---|
| 2010 | TWY | 104 ton | 155.20 | 1098.46 | 107.04 | 221.68 | 66.52 | 131.85 |
| WTP | 104 kw | 33,561.61 | 143,419.54 | 1987.59 | 44,264.45 | 15,090.82 | 27,522.41 | |
| WEI | 107 m2 | 15,672.03 | 45,851.22 | 694.89 | 22,451.03 | 6730.75 | 12,639.72 | |
| WFA | 104 ton | 1528.18 | 4207.60 | 70.23 | 2202.16 | 713.55 | 1204.01 | |
| NRL | 104 | 70.68 | 319.98 | 1.08 | 113.87 | 9.90 | 27.47 | |
| GDPP | yuan | 40,072.60 | 155,892.37 | 3648.24 | 49,575.96 | 17,799.53 | 33,679.70 | |
| ECO | / | 1.50 | 34.86 | 0.25 | 10.35 | 0.30 | 2.33 | |
| PNO | % | 84.14 | 160.40 | 84.30 | 95.30 | 96.15 | 120.30 | |
| PNE | % | 81.37 | 119.90 | 50.80 | 101.75 | 60.65 | 61.03 | |
| 2020 | TWY | 104 ton | 190.98 | 1289.12 | 202.00 | 255.77 | 70.24 | 159.10 |
| WTP | 104 kw | 33,881.96 | 121,197.22 | 1259.43 | 47,352.48 | 15,726.14 | 32,028.60 | |
| WEI | 107 m2 | 18,812.90 | 54,031.37 | 1052.95 | 26,056.74 | 8197.97 | 15,171.26 | |
| WFA | 104 ton | 1628.59 | 3676.66 | 80.19 | 2502.11 | 763.71 | 1343.38 | |
| NRL | 104 | 90.35 | 880.81 | 1.41 | 115.97 | 10.10 | 61.30 | |
| GDPP | yuan | 46,550.22 | 19,1173.06 | 894.77 | 66,501.80 | 4234.95 | 43,065.25 | |
| ECO | / | 1.18 | 29.60 | 0.14 | 0.30 | 0.24 | 0.27 | |
| PNO | % | 81.38 | 102.76 | 20.38 | 93.42 | 83.23 | 90.57 | |
| PNE | % | 77.20 | 126.64 | 53.19 | 89.39 | 64.16 | 70.67 |
| Model Parameters | 2010 | 2020 |
|---|---|---|
| Bandwidth | 41.665 | 10.867 |
| Residual Squares | 50.44 | 66.12 |
| Effective Number | 16.297 | 17.021 |
| Sigma | 0.573 | 0.624 |
| Degree of freedom | 291.113 | 282.998 |
| 0.217 * | 0.113 * |
| Factor | Average | Maximum | Minimum | Upper Quartile | Lower Quartile | Median | |
|---|---|---|---|---|---|---|---|
| 2010 | WEI | 14.38 | 30.50 | 2.05 | 18.73 | 8.69 | 14.10 |
| WFA | 4.17 | 7.09 | 2.45 | 6.65 | 3.85 | 5.25 | |
| PNE | −68.14 | 12.18 | −110.35 | −39.64 | −97.81 | −85.32 | |
| T | 2.01 | 3.21 | −0.24 | 2.35 | 0.62 | 1.48 | |
| P | 0.41 | 0.83 | −1.78 | 0.18 | −1.12 | −0.47 | |
| I | 0.39 | 2.23 | −2.48 | 2.05 | −1.30 | −0.125 | |
| 2020 | WEI | 30.01 | 58.11 | 16.00 | 34.97 | 21.58 | 29.04 |
| WFA | 0.06 | 5.09 | 0.03 | 0.07 | 0.05 | 0.06 | |
| PNE | 8.09 | 19.04 | −3.11 | 3.12 | −3.42 | 2.00 | |
| T | 1.35 | 3.22 | −0.23 | 2.33 | 0.39 | 0.86 | |
| P | 0.48 | 1.83 | −0.64 | 1.10 | −0.24 | 0.48 | |
| I | 0.97 | 3.33 | −1.18 | 1.55 | −0.03 | 1.10 |
| SCA-OLS | ||||||||
|---|---|---|---|---|---|---|---|---|
| 2010 | 2020 | |||||||
| Variable | Coefficient | Standard Deviation | t/z Value | p-Value | Coefficient | Standard Deviation | t/z Value | p-Value |
| intercept | −8.476 | 5.976 | −1.419 | 0.162 | −4.659 | 9.946 | −0.468 | 0.641 |
| WEI | 2.976 | 21.319 | 0.139 | 0.889 | 71.940 | 43.701 | 1.646 | 0.006 |
| WFA | 0.063 | 0.017 | 3.577 | 0.000 | 0.074 | 0.044 | 1.670 | 0.001 |
| PNE | 48.810 | 52.445 | 1.898 | 0.043 | 50.910 | 55.460 | 0.034 | 0.072 |
| T | 3.001 | 23.363 | 4.832 | 0.000 | 20.070 | 60.888 | 0.770 | 0.444 |
| P | 1.677 | 17.187 | 0.938 | 0.352 | 7.281 | 73.314 | 1.009 | 0.317 |
| I | 4.556 | 66.953 | 0.966 | 0.038 | 8.802 | 41.648 | 0.160 | 0.873 |
| 2010—F Statistics: 31.675, p-value: 0.023; 2020—F Statistics: 23.876, p-value: 0.876. | ||||||||
| SCA-SEM | ||||||||
| intercept | −8.587 | 5.336 | −1.610 | 0.107 | −7.291 | 7.266 | −1.004 | 0.314 |
| WEI | 3.570 | 19.363 | 0.184 | 0.853 | 69.755 | 34.236 | 2.037 | 0.041 |
| WFA | 0.063 | 0.016 | 3.956 | 0.000 | 0.084 | 0.033 | 2.517 | 0.011 |
| PNE | 19.87 | 46.566 | 2.134 | 0.032 | −22.193 | 42.458 | −0.544 | 0.586 |
| T | 9.578 | 59.767 | 5.530 | 0.000 | 23.564 | 61.471 | 1.694 | 0.000 |
| P | 4.274 | 72.241 | 1.080 | 0.279 | 9.351 | 56.112 | 1.811 | 0.070 |
| I | 3.366 | 29.339 | 1.100 | 0.271 | 2.230 | 48.950 | 0.483 | 0.028 |
| 2010—Lambda: −0.045, Lagrange multiplier test: 10.987; 2020—Lambda: −0.675, Lagrange multiplier test: 19.013. | ||||||||
| SCA-SLM | ||||||||
| intercept | −7.356 | 5.606 | −1.313 | 0.188 | −5.129 | 8.950 | −0.572 | 0.567 |
| WEI | 1.582 | 19.248 | 0.082 | 0.934 | 76.857 | 39.676 | 1.937 | 0.052 |
| WFA | 0.064 | 0.016 | 4.017 | 0.000 | 0.072 | 10.039 | 1.811 | 0.070 |
| PNE | 17.73 | 99.227 | 2.038 | 0.001 | −52.761 | 18.150 | −0.040 | 0.007 |
| T | 80.404 | 91.783 | 3.895 | 0.000 | 4.280 | 29.138 | 1.021 | 0.307 |
| P | 35.078 | 77.415 | 0.940 | 0.346 | 4.113 | 68.385 | 1.237 | 0.215 |
| I | 3.063 | 38.180 | 0.887 | 0.374 | 2.215 | 86.861 | 0.170 | 0.864 |
| 2010—Rho: 0.062, Lagrange multiplier test: 21.987; 2020—Rho: 0.591, Lagrange multiplier test: 30.013. | ||||||||
| 2010 | 2020 | |||||||
|---|---|---|---|---|---|---|---|---|
| Factor | Moran’s I | Z Value | p-Value | Spatial Correlation | Moran’s I | Z Value | p-Value | Spatial Correlation |
| WEI | 0.222 | 9.001 | 0.000 | + | 0.232 | 9.897 | 0.000 | + |
| WFA | 0.155 | 6.145 | 0.003 | + | 0.183 | 7.563 | 0.001 | + |
| PNE | 0.214 | 8.675 | 0.000 | + | 0.201 | 8.564 | 0.000 | + |
| T | 0.109 | 4.768 | 0.007 | + | 0.229 | 9.023 | 0.000 | + |
| P | 0.008 | 0.758 | 0.167 | / | 0.013 | 1.003 | 0.134 | / |
| I | 0.164 | 6.453 | 0.001 | + | 0.198 | 7.980 | 0.001 | + |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Li, B. Detection of the Spatio-Temporal Differentiation Patterns and Influencing Factors of Wheat Production in Huang-Huai-Hai Region. Foods 2022, 11, 1617. https://doi.org/10.3390/foods11111617
Zhang Y, Li B. Detection of the Spatio-Temporal Differentiation Patterns and Influencing Factors of Wheat Production in Huang-Huai-Hai Region. Foods. 2022; 11(11):1617. https://doi.org/10.3390/foods11111617
Chicago/Turabian StyleZhang, Yifan, and Bingjun Li. 2022. "Detection of the Spatio-Temporal Differentiation Patterns and Influencing Factors of Wheat Production in Huang-Huai-Hai Region" Foods 11, no. 11: 1617. https://doi.org/10.3390/foods11111617
APA StyleZhang, Y., & Li, B. (2022). Detection of the Spatio-Temporal Differentiation Patterns and Influencing Factors of Wheat Production in Huang-Huai-Hai Region. Foods, 11(11), 1617. https://doi.org/10.3390/foods11111617






