Determination of a Representative and 3D-Printable Root Canal Geometry for Endodontic Investigations and Pre-Clinical Endodontic Training—An Ex Vivo Study
Abstract
1. Introduction
2. Materials and Methods
2.1. Artificial Root Canal Models and Purpose of Use in Endodontics

| Author(s), Ref. | Purpose of Use | Material | Canal Shape | ||||
|---|---|---|---|---|---|---|---|
| Endodontic Training | Dentin Removal | Activation Irrigants | Fatigue Instruments | Dental Tissue Regeneration | |||
| Al-Sudani and Basudan [12] | x | Transparent or colored resin, such as acrylic resin | c | ||||
| Bitter et al. [11] | x | c | |||||
| Bürklein et al. [52] | x | c | |||||
| Cassim and van der Vyver [51] | x | c | |||||
| Christofzik et al. [50] | x | c | |||||
| Gu et al. [54] | x | c | |||||
| Hasselgren et al. [10] | x | c | |||||
| Hasselgren and Tronstad [9] | x | c | |||||
| Huang et al. [47] | x | c | |||||
| Khalilak et al. [45] | x | c | |||||
| Kim et al. [56] | x | c | |||||
| Luz et al. [8] | x | c | |||||
| Reymus et al. [7] | x | c | |||||
| Reymus et al. [6] | x | c | |||||
| Reymus et al. [5] | x | c | |||||
| Shi et al. [42] | x | c | |||||
| Silva et al. [55] | x | c | |||||
| Sonntag et al. [41] | x | c | |||||
| Spenst and Kahn [3] | x | s, c | |||||
| Tchorz et al. [2] | x | c | |||||
| Yekta-Michael et al. [1] | x | c | |||||
| Alghamdi et al. [53] | x | Natural tooth | c | ||||
| Al-Sudani and Basudan [12] | x | c | |||||
| Bitter et al. [11] | x | c | |||||
| Castagna et al. [15] | x | c | |||||
| Eggmann et al. [17] | x | c | |||||
| Gümüş and Delikan [19] | x | c | |||||
| Hartmann et al. [49] | x | c | |||||
| Hilaly Eid and Wanees Amin [48] | x | c | |||||
| Loroño et al. [24] | x | c | |||||
| Malentacca et al. [26] | x | c | |||||
| Ni et al. [61] | x | c | |||||
| Pawar et al. [60] | x | c | |||||
| Peters et al. [44] | x | c | |||||
| Retsas et al. [43] | x | c | |||||
| Rodrigues et al. [28] | x | x | c | ||||
| Yekta-Michael et al. [1] | x | c | |||||
| Al-Obaida et al. [37] | x | Stainless steel | c | ||||
| Boutsioukis et al. [14] | x | s | |||||
| Chi et al. [36] | x | c | |||||
| Gündoğar and Özyürek [35] | x | c | |||||
| Kirsch et al. [34] | x | c | |||||
| Conde et al. [16] | x | Manufactured dental hard tissue | s | ||||
| Jiang et al. [70] | x | s | |||||
| Jiang et al. [20] | x | s | |||||
| Jiang et al. [21] | x | s | |||||
| Jiang et al. [22] | x | s | |||||
| Betancourt et al. [13] | x | Glass | s | ||||
| Jiang et al. [22] | x | s | |||||
| Swimberghe et al. [29] | x | Polymethylmethacrylate | s | ||||
| Swimberghe et al. [30] | x | c | |||||
| Macedo et al. [25] | x | Polydimethylsiloxane | s | ||||
| Nagahashi et al. [27] | x | Porcine tooth | s | ||||
| Neunzehn et al. [62] | x | Bovine tooth | s | ||||
| Robberecht et al. [4] | x | Ceramic | s | ||||
2.2. Teeth Selection and Preparation
2.3. Computed Tomographic Imaging Technique for the Determination of Root Canal Geometry
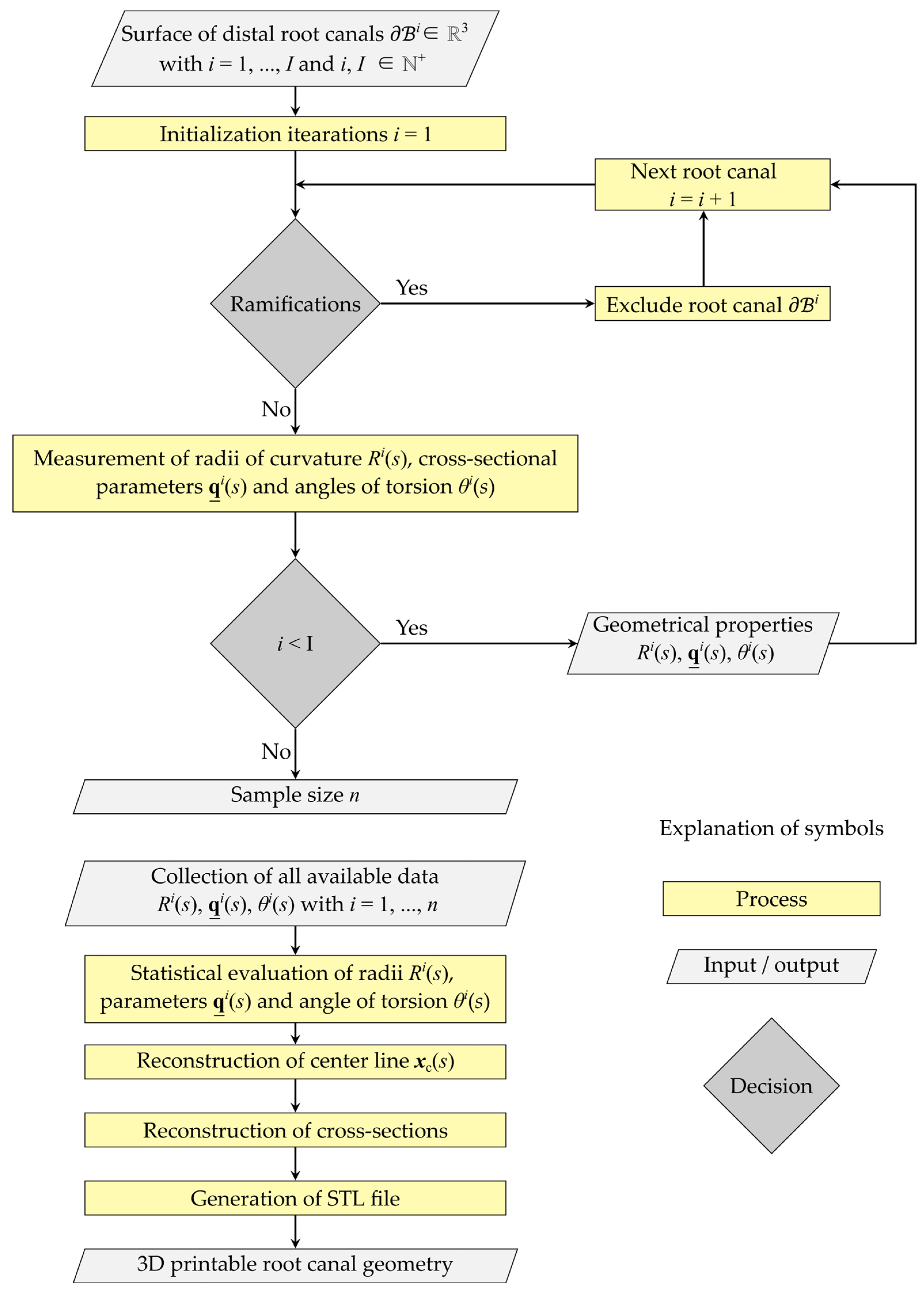
2.4. Approach for Determining the Root Canal Model
2.5. Determination of Representative Center Line and Approximation of Cross-Sectional Dimensions
2.6. Statistical Evaluation of Curvature and Cross-Sectional Measures
2.7. Determination of the Root Canal’s Angle of Torsion
2.8. Reconstruction of Geometry-Based Center Line and Cross-Sections
2.9. Generation of STL File for 3D Printing
3. Results
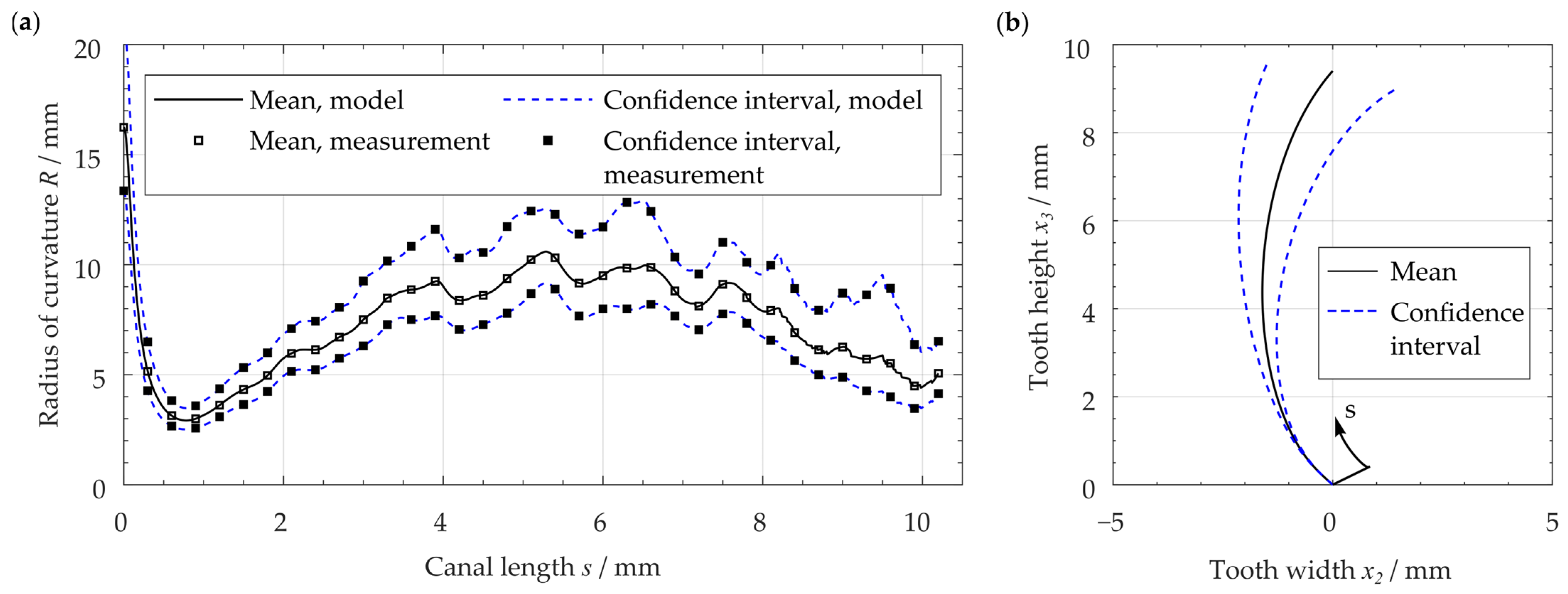
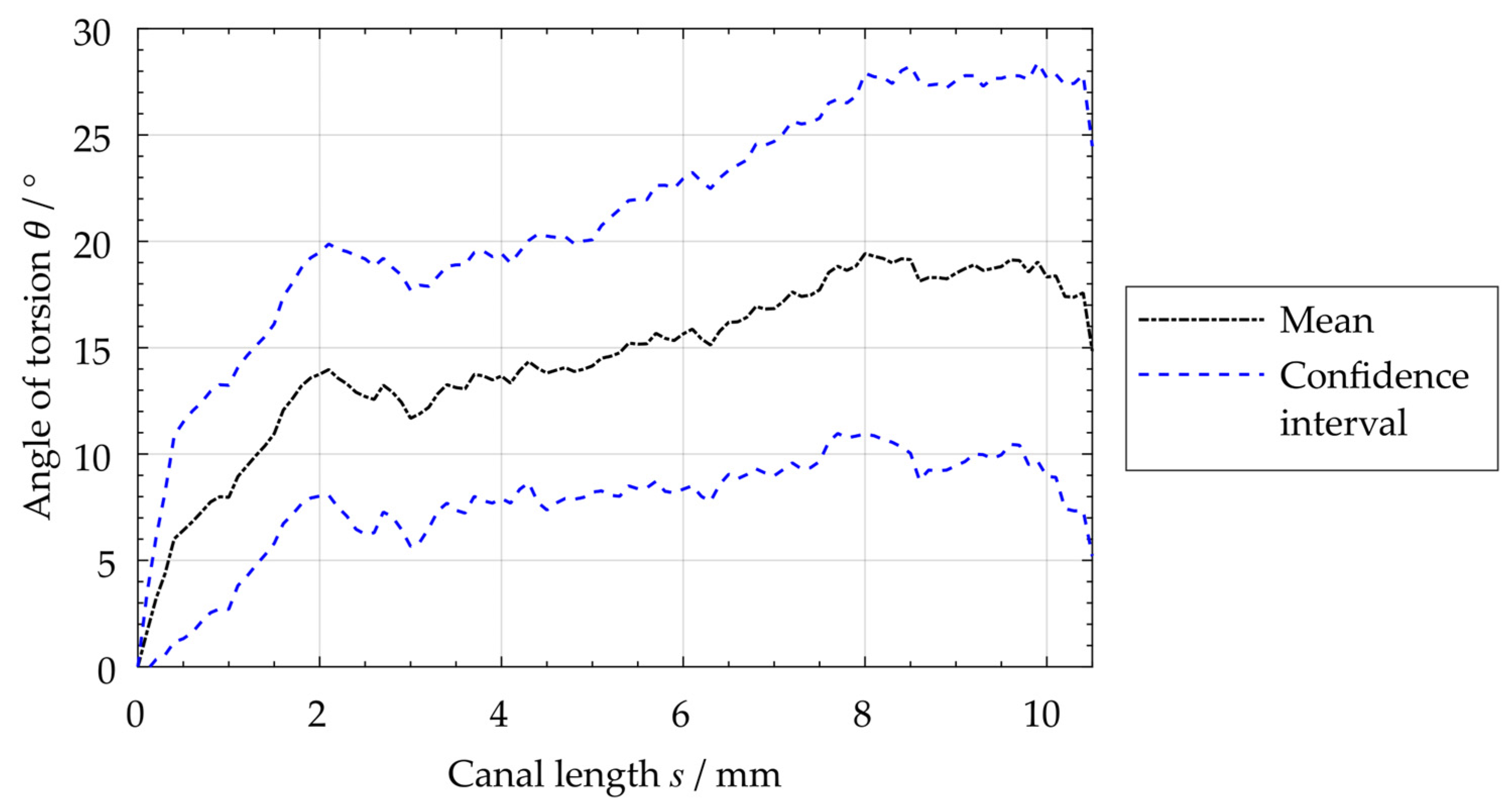
3.1. Resulting Reconstructed Center Line and Root Canal’s Angle of Torsion
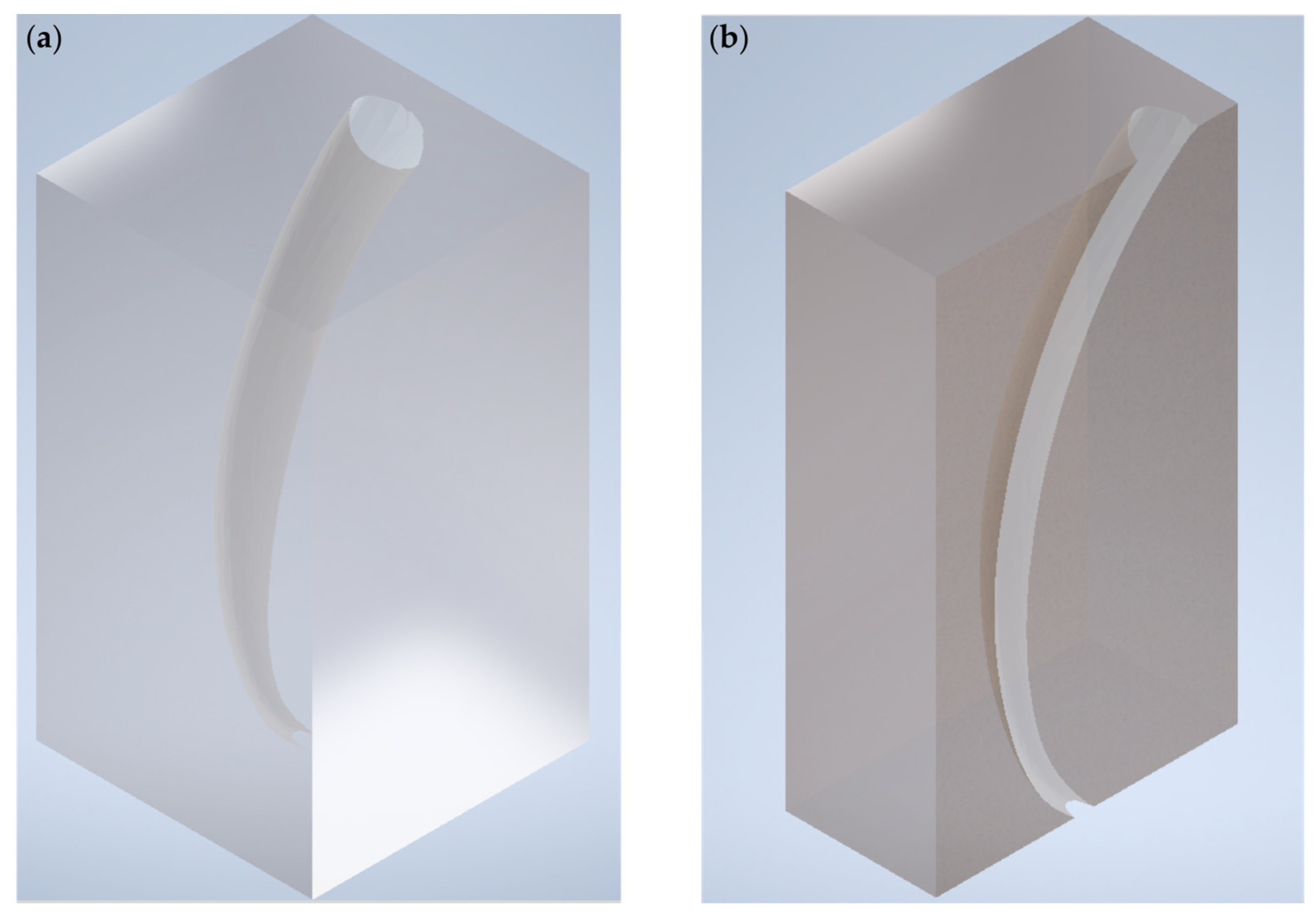
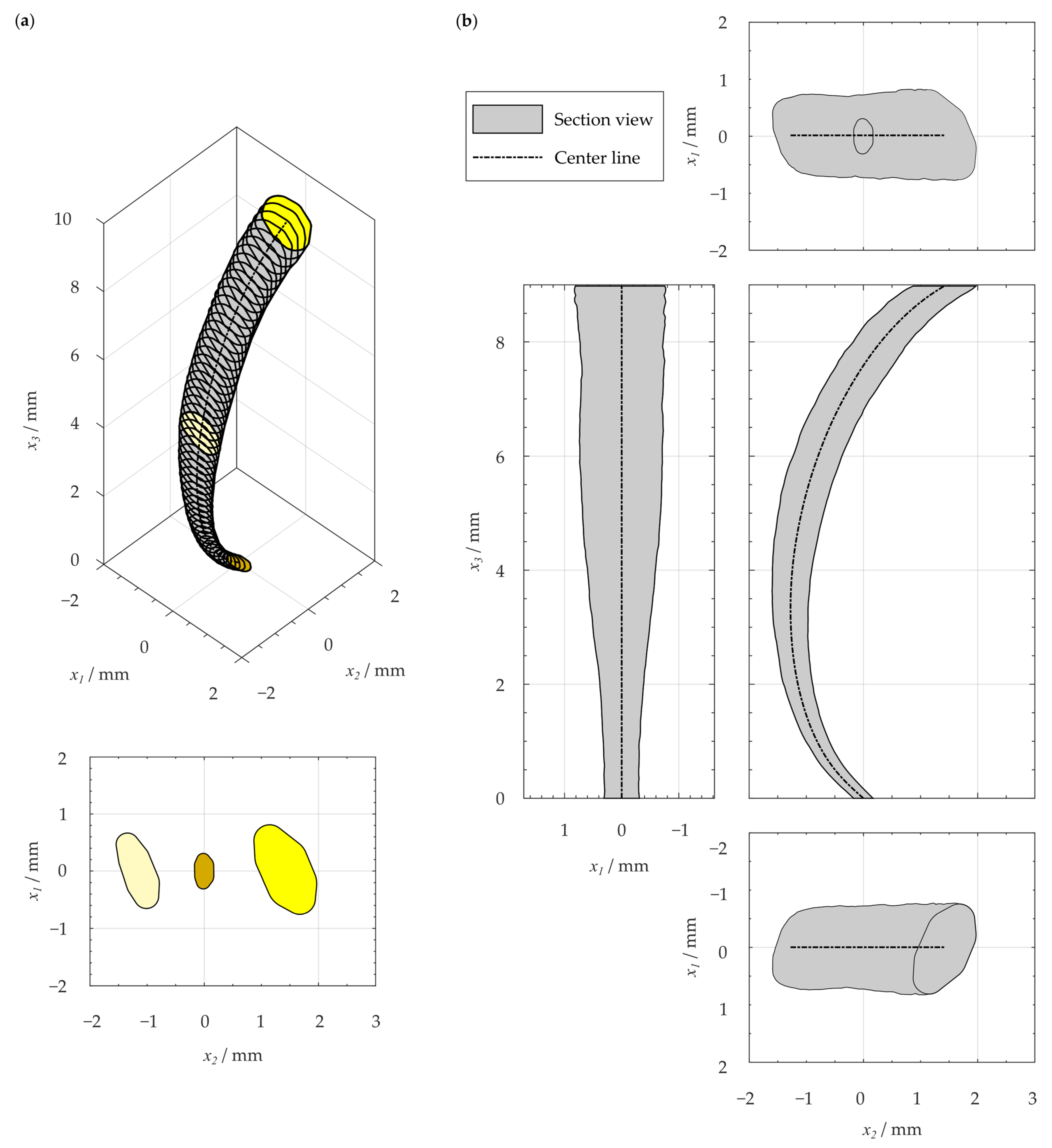
3.2. Resulting Geometry-Based Artificial Root Canal Model
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Yekta-Michael, S.S.; Färber, C.M.; Heinzel, A. Evaluation of new endodontic tooth models in clinical education from the perspective of students and demonstrators. BMC Med. Educ. 2021, 21, 447. [Google Scholar] [CrossRef] [PubMed]
- Tchorz, J.P.; Brandl, M.; Ganter, P.A.; Karygianni, L.; Polydorou, O.; Vach, K.; Hellwig, E.; Altenburger, M.J. Pre-clinical endodontic training with artificial instead of extracted human teeth: Does the type of exercise have an influence on clinical endodontic outcomes? Int. Endod. J. 2015, 48, 888–893. [Google Scholar] [CrossRef] [PubMed]
- Spenst, A.; Kahn, H. The use of a plastic block for teaching root canal instrumentation and obturation. J. Endod. 1979, 5, 282–284. [Google Scholar] [CrossRef] [PubMed]
- Robberecht, L.; Chai, F.; Dehurtevent, M.; Marchandise, P.; Bécavin, T.; Hornez, J.-C.; Deveaux, E. A novel anatomical ceramic root canal simulator for endodontic training. Eur. J. Dent. Educ. 2017, 21, e1–e6. [Google Scholar] [CrossRef] [PubMed]
- Reymus, M.; Liebermann, A.; Diegritz, C.; Keßler, A. Development and evaluation of an interdisciplinary teaching model via 3D printing. Clin. Exp. Dent. Res. 2021, 7, 3–10. [Google Scholar] [CrossRef]
- Reymus, M.; Stawarczyk, B.; Winkler, A.; Ludwig, J.; Kess, S.; Krastl, G.; Krug, R. A critical evaluation of the material properties and clinical suitability of in-house printed and commercial tooth replicas for endodontic training. Int. Endod. J. 2020, 53, 1446–1454. [Google Scholar] [CrossRef]
- Reymus, M.; Fotiadou, C.; Kessler, A.; Heck, K.; Hickel, R.; Diegritz, C. 3D printed replicas for endodontic education. Int. Endod. J. 2019, 52, 123–130. [Google Scholar] [CrossRef]
- Luz, D.d.S.; Ourique, F.d.S.; Scarparo, R.K.; Vier-Pelisser, F.V.; Morgental, R.D.; Waltrick, S.B.; des Figueiredo, J.A. Preparation Time and Perceptions of Brazilian Specialists and Dental Students Regarding Simulated Root Canals for Endodontic Teaching: A Preliminary Study. J. Dent. Educ. 2015, 79, 56–63. [Google Scholar] [CrossRef]
- Hasselgren, G.; Tronstad, L. The use of transparent teeth in the teaching of preclinical endodontics. J. Endod. 1975, 1, 278–280. [Google Scholar] [CrossRef]
- Hasselgren, G.; Nellestam, P.; Bynum-Hasselgren, R.M. Teeth with transparent roots--an improved teaching aid for preclinical endodontics. J. Endod. 1987, 13, 126–127. [Google Scholar] [CrossRef]
- Bitter, K.; Gruner, D.; Wolf, O.; Schwendicke, F. Artificial Versus Natural Teeth for Preclinical Endodontic Training: A Randomized Controlled Trial. J. Endod. 2016, 42, 1212–1217. [Google Scholar] [CrossRef]
- Al-Sudani, D.I.; Basudan, S.O. Students’ perceptions of pre-clinical endodontic training with artificial teeth compared to extracted human teeth. Eur. J. Dent. Educ. 2017, 21, e72–e75. [Google Scholar] [CrossRef] [PubMed]
- Betancourt, P.; Merlos, A.; Sierra, J.M.; Camps-Font, O.; Arnabat-Dominguez, J.; Viñas, M. Effectiveness of low concentration of sodium hypochlorite activated by Er,Cr:YSGG laser against Enterococcus faecalis biofilm. Lasers Med. Sci. 2019, 34, 247–254. [Google Scholar] [CrossRef] [PubMed]
- Boutsioukis, C.; Verhaagen, B.; Walmsley, A.D.; Versluis, M.; van der Sluis, L.W.M. Measurement and visualization of file-to-wall contact during ultrasonically activated irrigation in simulated canals. Int. Endod. J. 2013, 46, 1046–1055. [Google Scholar] [CrossRef] [PubMed]
- Castagna, F.; Rizzon, P.; da Rosa, R.A.; Santini, M.F.; Barreto, M.S.; Duarte, M.A.H.; Só, M.V.R. Effect of passive ultrassonic instrumentation as a final irrigation protocol on debris and smear layer removal—A SEM analysis. Microsc. Res. Tech. 2013, 76, 496–502. [Google Scholar] [CrossRef] [PubMed]
- Conde, A.J.; Estevez, R.; Loroño, G.; Valencia de Pablo, Ó.; Rossi-Fedele, G.; Cisneros, R. Effect of sonic and ultrasonic activation on organic tissue dissolution from simulated grooves in root canals using sodium hypochlorite and EDTA. Int. Endod. J. 2017, 50, 976–982. [Google Scholar] [CrossRef]
- Eggmann, F.; Vokac, Y.; Eick, S.; Neuhaus, K.W. Sonic irrigant activation for root canal disinfection: Power modes matter! BMC Oral Health 2020, 20, 102. [Google Scholar] [CrossRef] [PubMed]
- Gulabivala, K.; Ng, Y.-L.; Gilbertson, M.; Eames, I. The fluid mechanics of root canal irrigation. Physiol. Meas. 2010, 31, R49–R84. [Google Scholar] [CrossRef]
- Gümüş, H.; Delikan, E. The effect of sonic activation of irrigant on postoperative pain after root canal treatment in primary molar teeth: A randomized, clinical study. Clin. Oral Investig. 2021, 25, 363–370. [Google Scholar] [CrossRef]
- Jiang, L.-M.; Lak, B.; Eijsvogels, L.M.; Wesselink, P.; van der Sluis, L.W.M. Comparison of the cleaning efficacy of different final irrigation techniques. J. Endod. 2012, 38, 838–841. [Google Scholar] [CrossRef]
- Jiang, L.-M.; Verhaagen, B.; Versluis, M.; Langedijk, J.; Wesselink, P.; van der Sluis, L.W.M. The influence of the ultrasonic intensity on the cleaning efficacy of passive ultrasonic irrigation. J. Endod. 2011, 37, 688–692. [Google Scholar] [CrossRef]
- Jiang, L.-M.; Verhaagen, B.; Versluis, M.; van der Sluis, L.W.M. Evaluation of a sonic device designed to activate irrigant in the root canal. J. Endod. 2010, 36, 143–146. [Google Scholar] [CrossRef]
- Kucher, M. Hochfrequent Beanspruchte Polymerstrukturen für den Einsatz als Endodontische Instrumente. Doctoral Thesis, Technische Universität Dresden, Dresden, Germany, 2023. [Google Scholar]
- Loroño, G.; Zaldivar, J.R.; Arias, A.; Cisneros, R.; Dorado, S.; Jimenez-Octavio, J.R. Positive and negative pressure irrigation in oval root canals with apical ramifications: A computational fluid dynamics evaluation in micro-CT scanned real teeth. Int. Endod. J. 2020, 53, 671–679. [Google Scholar] [CrossRef] [PubMed]
- Macedo, R.; Verhaagen, B.; Rivas, D.F.; Versluis, M.; Wesselink, P.; van der Sluis, L. Cavitation measurement during sonic and ultrasonic activated irrigation. J. Endod. 2014, 40, 580–583. [Google Scholar] [CrossRef]
- Malentacca, A.; Uccioli, U.; Mannocci, F.; Bhuva, B.; Zangari, D.; Pulella, C.; Lajolo, C. The comparative effectiveness and safety of three activated irrigation techniques in the isthmus area using a transparent tooth model. Int. Endod. J. 2018, 51 (Suppl. S1), e35–e41. [Google Scholar] [CrossRef]
- Nagahashi, T.; Yahata, Y.; Handa, K.; Nakano, M.; Suzuki, S.; Kakiuchi, Y.; Tanaka, T.; Kanehira, M.; Suresh Venkataiah, V.; Saito, M. Er:YAG laser-induced cavitation can activate irrigation for the removal of intraradicular biofilm. Sci. Rep. 2022, 12, 4897. [Google Scholar] [CrossRef]
- Rodrigues, C.T.; EzEldeen, M.; Jacobs, R.; Lambrechts, P.; Alcalde, M.P.; Hungaro Duarte, M.A. Cleaning efficacy and uncontrolled removal of dentin of two methods of irrigant activation in curved canals connected by an isthmus. Aust. Endod. J. 2021, 47, 631–638. [Google Scholar] [CrossRef]
- Swimberghe, R.C.D.; de Clercq, A.; de Moor, R.J.G.; Meire, M.A. Efficacy of sonically, ultrasonically and laser-activated irrigation in removing a biofilm-mimicking hydrogel from an isthmus model. Int. Endod. J. 2019, 52, 515–523. [Google Scholar] [CrossRef] [PubMed]
- Swimberghe, R.C.D.; Buyse, R.; Meire, M.A.; de Moor, R.J.G. Efficacy of different irrigation technique in simulated curved root canals. Lasers Med. Sci. 2021, 36, 1317–1322. [Google Scholar] [CrossRef]
- Wang, Y.; Guo, L.-Y.; Fang, H.-Z.; Zou, W.-L.; Yang, Y.-M.; Gao, Y.; Yang, H.; Hu, T. An in vitro study on the efficacy of removing calcium hydroxide from curved root canal systems in root canal therapy. Int. J. Oral Sci. 2017, 9, 110–116. [Google Scholar] [CrossRef]
- Zhou, N.; Huang, Z.; Yu, M.; Deng, S.; Fu, B.; Jin, H. Influence of needle working length and root canal curvature on irrigation: A computational fluid dynamics analysis based on a real tooth. BMC Oral Health 2022, 22, 179. [Google Scholar] [CrossRef] [PubMed]
- Roda-Casanova, V.; Pérez-González, A.; Zubizarreta-Macho, Á.; Faus-Matoses, V. Fatigue Analysis of NiTi Rotary Endodontic Files through Finite Element Simulation: Effect of Root Canal Geometry on Fatigue Life. J. Clin. Med. 2021, 10, 5692. [Google Scholar] [CrossRef] [PubMed]
- Kirsch, J.; Reinauer, K.S.; Meissner, H.; Dannemann, M.; Kucher, M.; Modler, N.; Hannig, C.; Weber, M.-T. Ultrasonic and sonic irrigant activation in endodontics: A fractographic examination. Dtsch. Zahnärztl. Z. Int. 2019, 1, 209–221. [Google Scholar] [CrossRef]
- Gündoğar, M.; Özyürek, T. Cyclic Fatigue Resistance of OneShape, HyFlex EDM, WaveOne Gold, and Reciproc Blue Nickel-titanium Instruments. J. Endod. 2017, 43, 1192–1196. [Google Scholar] [CrossRef]
- Chi, C.-W.; Li, C.-C.; Lin, C.-P.; Shin, C.-S. Cyclic fatigue behavior of nickel-titanium dental rotary files in clinical simulated root canals. J. Formos. Med. Assoc. 2017, 116, 306–312. [Google Scholar] [CrossRef]
- Al-Obaida, M.I.; Alzuwayer, A.A.; Alanazi, S.S.; Balhaddad, A.A. In Vitro Analysis of the Fatigue Resistance of Four Single File Canal Preparation Instruments. Materials 2022, 15, 688. [Google Scholar] [CrossRef]
- Dede, M.; Basche, S.; Neunzehn, J.; Dannemann, M.; Hannig, C.; Kühne, M.-T. Efficacy of Endodontic Disinfection Protocols in an E. faecalis Biofilm Model—Using DAPI Staining and SEM. J. Funct. Biomater. 2023, 14, 176. [Google Scholar] [CrossRef]
- Sterzenbach, T.; Pioch, A.; Dannemann, M.; Hannig, C.; Weber, M.-T. Quantification of Bacterial Colonization in Dental Hard Tissues Using Optimized Molecular Biological Methods. Front. Genet. 2020, 11, 599137. [Google Scholar] [CrossRef]
- Weber, M.-T.; Alkhafaji, Y.; Pioch, A.; Trips, E.; Basche, S.; Dannemann, M.; Kilistoff, A.; Hannig, C.; Sterzenbach, T. Quantification of Bacterial DNA from Infected Human Root Canals Using qPCR and DAPI after Disinfection with Established and Novel Irrigation Protocols. Materials 2022, 15, 1911. [Google Scholar] [CrossRef]
- Sonntag, D.; Guntermann, A.; Kim, S.K.; Stachniss, V. Root canal shaping with manual stainless steel files and rotary Ni-Ti files performed by students. Int. Endod. J. 2003, 36, 246–255. [Google Scholar] [CrossRef]
- Shi, L.; Zhou, J.; Wan, J.; Yang, Y. Shaping ability of ProTaper Gold and WaveOne Gold nickel-titanium rotary instruments in simulated S-shaped root canals. J. Dent. Sci. 2022, 17, 430–437. [Google Scholar] [CrossRef] [PubMed]
- Retsas, A.; Koursoumis, A.; Tzimpoulas, N.; Boutsioukis, C. Uncontrolled Removal of Dentin during In Vitro Ultrasonic Irrigant Activation in Curved Root Canals. J. Endod. 2016, 42, 1545–1549. [Google Scholar] [CrossRef]
- Peters, O.A.; Peters, C.I.; Schönenberger, K.; Barbakow, F. ProTaper rotary root canal preparation: Effects of canal anatomy on final shape analysed by micro CT. Int. Endod. J. 2003, 36, 86–92. [Google Scholar] [CrossRef]
- Khalilak, Z.; Fallahdoost, A.; Dadresanfar, B.; Rezvani, G. Comparison of extracted teeth and simulated resin blocks on apical canal transportation. Iran. Endod. J. 2008, 3, 109–112. [Google Scholar]
- Hülsmann, M. A critical appraisal of research methods and experimental models for studies on root canal preparation. Int. Endod. J. 2022, 55 (Suppl. S1), 95–118. [Google Scholar] [CrossRef]
- Huang, Z.; Quan, J.; Liu, J.; Zhang, W.; Zhang, X.; Hu, X. A microcomputed tomography evaluation of the shaping ability of three thermally-treated nickel-titanium rotary file systems in curved canals. J. Int. Med. Res. 2019, 47, 325–334. [Google Scholar] [CrossRef] [PubMed]
- Hilaly Eid, G.E.; Wanees Amin, S.A. Changes in diameter, cross-sectional area, and extent of canal-wall touching on using 3 instrumentation techniques in long-oval canals. Oral Surg. Oral Med. Oral Pathol. Oral Radiol. Endod. 2011, 112, 688–695. [Google Scholar] [CrossRef] [PubMed]
- Hartmann, M.S.M.; Barletta, F.B.; Camargo Fontanella, V.R.; Vanni, J.R. Canal transportation after root canal instrumentation: A comparative study with computed tomography. J. Endod. 2007, 33, 962–965. [Google Scholar] [CrossRef]
- Christofzik, D.; Bartols, A.; Faheem, M.K.; Schroeter, D.; Groessner-Schreiber, B.; Doerfer, C.E. Shaping ability of four root canal instrumentation systems in simulated 3D-printed root canal models. PLoS ONE 2018, 13, e0201129. [Google Scholar] [CrossRef]
- Cassim, I.; van der Vyver, P. An in vitro comparison of different techniques for glide path preparation. S. Afr. Dent. J. 2015, 70, 452–456. [Google Scholar]
- Bürklein, S.; Poschmann, T.; Schäfer, E. Shaping ability of different nickel-titanium systems in simulated S-shaped canals with and without glide path. J. Endod. 2014, 40, 1231–1234. [Google Scholar] [CrossRef] [PubMed]
- Alghamdi, A.; Alsofi, L.; Balto, K. Effects of a Novel NiTi Thermomechanical Treatment on the Geometric Features of the Prepared Root Canal System. Materials 2020, 13, 5546. [Google Scholar] [CrossRef] [PubMed]
- Gu, Y.; Kum, K.-Y.; Perinpanayagam, H.; Kim, C.; Kum, D.J.; Lim, S.-M.; Chang, S.-W.; Baek, S.-H.; Zhu, Q.; Yoo, Y.-J. Various heat-treated nickel-titanium rotary instruments evaluated in S-shaped simulated resin canals. J. Dent. Sci. 2017, 12, 14–20. [Google Scholar] [CrossRef] [PubMed]
- Silva, E.J.N.L.; Tameirão, M.D.N.; Belladonna, F.G.; Neves, A.A.; Souza, E.M.; De-Deus, G. Quantitative Transportation Assessment in Simulated Curved Canals Prepared with an Adaptive Movement System. J. Endod. 2015, 41, 1125–1129. [Google Scholar] [CrossRef]
- Kim, H.; Jeon, S.-J.; Seo, M.-S. Comparison of the canal transportation of ProTaper GOLD, WaveOne GOLD, and TruNatomy in simulated double-curved canals. BMC Oral Health 2021, 21, 533. [Google Scholar] [CrossRef]
- Kirsch, J.; Basche, S.; Neunzehn, J.; Dede, M.; Dannemann, M.; Hannig, C.; Weber, M.-T. Is it really penetration? Locomotion of devitalized Enterococcus faecalis cells within dentinal tubules of bovine teeth. Arch. Oral Biol. 2017, 83, 289–296. [Google Scholar] [CrossRef] [PubMed]
- Kirsch, J.; Basche, S.; Neunzehn, J.; Dede, M.; Dannemann, M.; Hannig, C.; Weber, M.-T. Is it really penetration? Part 2. Locomotion of Enterococcus faecalis cells within dentinal tubules of bovine teeth. Clin. Oral Investig. 2019, 23, 4325–4334. [Google Scholar] [CrossRef]
- Ghorpade, R.; Sundaram, K.; Hegde, V. Mechanical factors influencing success in root canal obturation. In Proceedings of the 2017 2nd International Conference for Convergence in Technology (I2CT), Mumbai, India, 7–9 April 2017; Kharate, G.K., Ed.; IEEE: Piscataway, NJ, USA, 2017; pp. 1085–1088. [Google Scholar]
- Pawar, A.M.; Kfir, A.; Metzger, Z.; Bhardwaj, A.; Yohana, Y.; Wahjuningrun, D.A.; Luke, A.M.; Pawar, B.A. Can Type of Instrumentation and Activation of the Final Irrigant Improve the Obturation Quality in Oval Root Canals? A Push-Out Bond Strength Study. Biology 2022, 11, 59. [Google Scholar] [CrossRef]
- Ni, N.; Ye, J.; Wang, L.; Shen, S.; Han, L.; Wang, Y. Stress distribution in a mandibular premolar after separated nickel-titanium instrument removal and root canal preparation: A three-dimensional finite element analysis. J. Int. Med. Res. 2019, 47, 1555–1564. [Google Scholar] [CrossRef]
- Neunzehn, J.; Weber, M.-T.; Wittenburg, G.; Lauer, G.; Hannig, C.; Wiesmann, H.-P. Dentin-like tissue formation and biomineralization by multicellular human pulp cell spheres in vitro. Head Face Med. 2014, 10, 25. [Google Scholar] [CrossRef]
- Kolling, M.; Backhaus, J.; Hofmann, N.; Keß, S.; Krastl, G.; Soliman, S.; König, S. Students’ perception of three-dimensionally printed teeth in endodontic training. Eur. J. Dent. Educ. 2022, 26, 653–661. [Google Scholar] [CrossRef] [PubMed]
- Kucher, M.; Dannemann, M.; Modler, N.; Haim, D.; Hannig, C.; Weber, M.-T. Continuous Measurement of Three-Dimensional Root Canal Curvature Using Cone-Beam Computed and Micro-Computed Tomography: A Comparative Study. Dent. J. 2020, 8, 16. [Google Scholar] [CrossRef] [PubMed]
- Kucher, M.; Dannemann, M.; Modler, N.; Hannig, C.; Weber, M.-T. An Automated Measurement Method for the Endodontic Working Width of Lower Molars by Means of Parametric Models Using Cone-beam Computed Tomographcy and Micro-Computed Tomography. J. Endod. 2021, 47, 1790–1795. [Google Scholar] [CrossRef]
- Peters, O.A.; Laib, A.; Rüegsegger, P.; Barbakow, F. Three-dimensional Analysis of Root Canal Geometry by High-resolution Computed Tomography. J. Dent. Res. 2000, 79, 1405–1409. [Google Scholar] [CrossRef]
- Dong, J.; Hong, S.Y.; Hasselgren, G. Theories and algorithms for 3-D root canal model construction. Comput. Aided Des. 2005, 37, 1177–1189. [Google Scholar] [CrossRef]
- Dannemann, M.; Kucher, M.; Kirsch, J.; Binkowski, A.; Modler, N.; Hannig, C.; Weber, M.-T. An Approach for a Mathematical Description of Human Root Canals by Means of Elementary Parameters. J. Endod. 2017, 43, 536–543. [Google Scholar] [CrossRef]
- Kucher, M.; Dannemann, M.; Modler, N.; Bernhard, M.R.; Hannig, C.; Weber, M.-T. Mapping of the Micro-Mechanical Properties of Human Root Dentin by Means of Microindentation. Materials 2021, 14, 505. [Google Scholar] [CrossRef]
- Jiang, L.-M.; Verhaagen, B.; Versluis, M.; van der Sluis, L.W.M. Influence of the oscillation direction of an ultrasonic file on the cleaning efficacy of passive ultrasonic irrigation. J. Endod. 2010, 36, 1372–1376. [Google Scholar] [CrossRef] [PubMed]
- Pachpore, S.S.; Jadhav, P.V.; Ghorpade, R.R. Analyzing Relation of Canal Operating Force and Canal Curvature in RCT: A Mathematical Overview. Mater. Today Proc. 2021, 47, 5690–5696. [Google Scholar] [CrossRef]
- Technisches Zeichnen: Grundlagen, Normen, Beispiele, Darstellende Geometrie; Lehr-, Übungs- und Nachschlagewerk für Schule, Fortbildung, Studium und Praxis, mit Mehr als 100 Tabellen und weit über 1.000 Zeichnungen; Hesser, W., Hoischen, H., Eds.; Überarb. und Aktualisierte Auflage; Cornelsen: Berlin, Germany, 2009; Volume 32, ISBN 978-3-589-24132-3. [Google Scholar]
- Ahmed, H.M.A.; Versiani, M.A.; De-Deus, G.; Dummer, P.M.H. A new system for classifying root and root canal morphology. Int. Endod. J. 2017, 50, 761–770. [Google Scholar] [CrossRef]

| Property | Unit | Value |
|---|---|---|
| Mean value | mm | 6.1 |
| Minimum | mm | 2.5 |
| Maximum | mm | 13.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kucher, M.; Dannemann, M.; Modler, N.; Böhm, R.; Hannig, C.; Kühne, M.-T. Determination of a Representative and 3D-Printable Root Canal Geometry for Endodontic Investigations and Pre-Clinical Endodontic Training—An Ex Vivo Study. Dent. J. 2023, 11, 133. https://doi.org/10.3390/dj11050133
Kucher M, Dannemann M, Modler N, Böhm R, Hannig C, Kühne M-T. Determination of a Representative and 3D-Printable Root Canal Geometry for Endodontic Investigations and Pre-Clinical Endodontic Training—An Ex Vivo Study. Dentistry Journal. 2023; 11(5):133. https://doi.org/10.3390/dj11050133
Chicago/Turabian StyleKucher, Michael, Martin Dannemann, Niels Modler, Robert Böhm, Christian Hannig, and Marie-Theres Kühne. 2023. "Determination of a Representative and 3D-Printable Root Canal Geometry for Endodontic Investigations and Pre-Clinical Endodontic Training—An Ex Vivo Study" Dentistry Journal 11, no. 5: 133. https://doi.org/10.3390/dj11050133
APA StyleKucher, M., Dannemann, M., Modler, N., Böhm, R., Hannig, C., & Kühne, M.-T. (2023). Determination of a Representative and 3D-Printable Root Canal Geometry for Endodontic Investigations and Pre-Clinical Endodontic Training—An Ex Vivo Study. Dentistry Journal, 11(5), 133. https://doi.org/10.3390/dj11050133








