Determination of pKa Values via ab initio Molecular Dynamics and its Application to Transition Metal-Based Water Oxidation Catalysts
Abstract
1. Introduction
2. Methodology
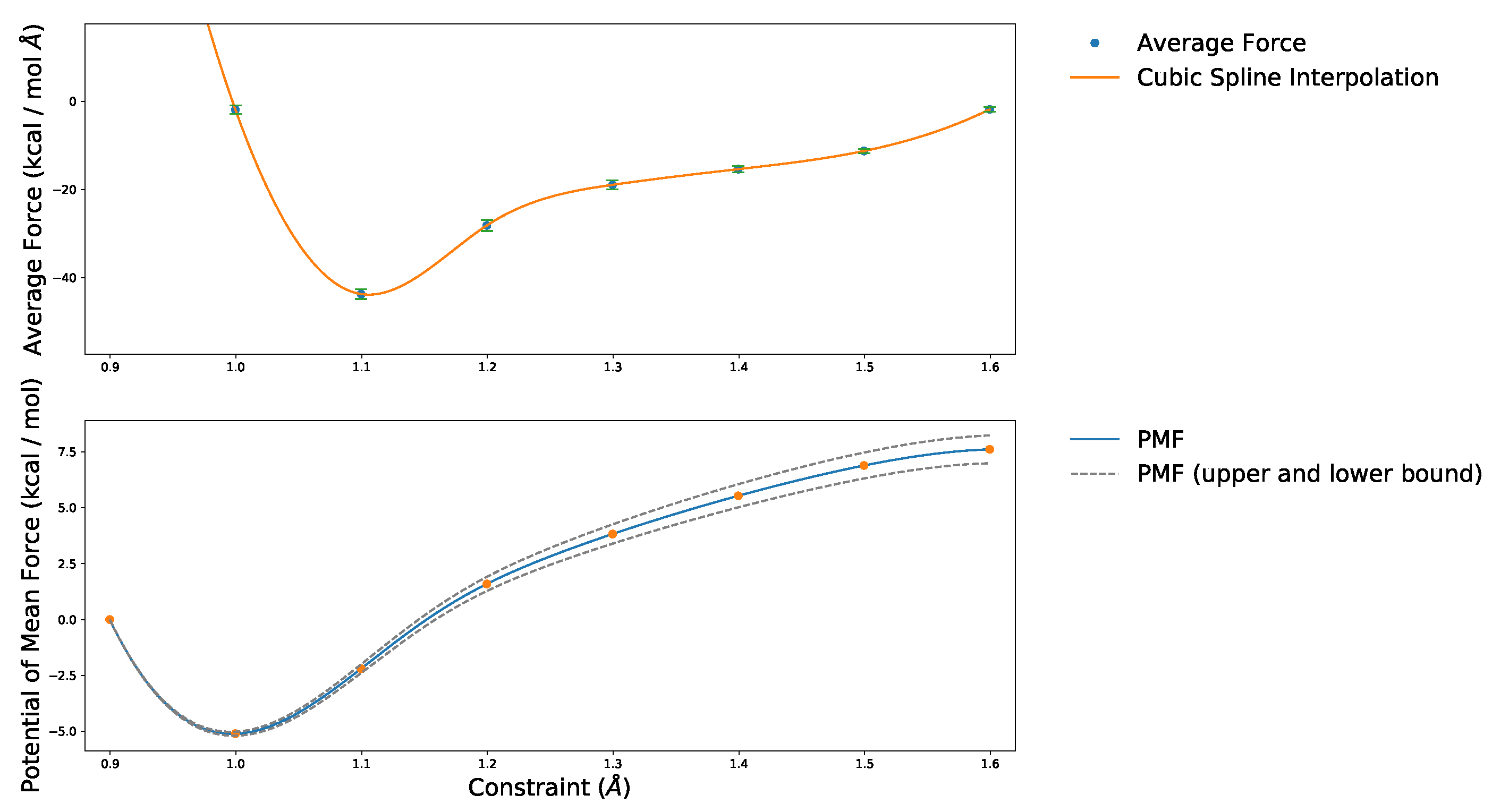
2.1. Choice of Constraint
2.2. Estimation of Values from the Free Energy Differences
2.2.1. Absolute
2.2.2. Relative
2.2.3. Probabilistic
3. Computational Settings
3.1. Model Systems
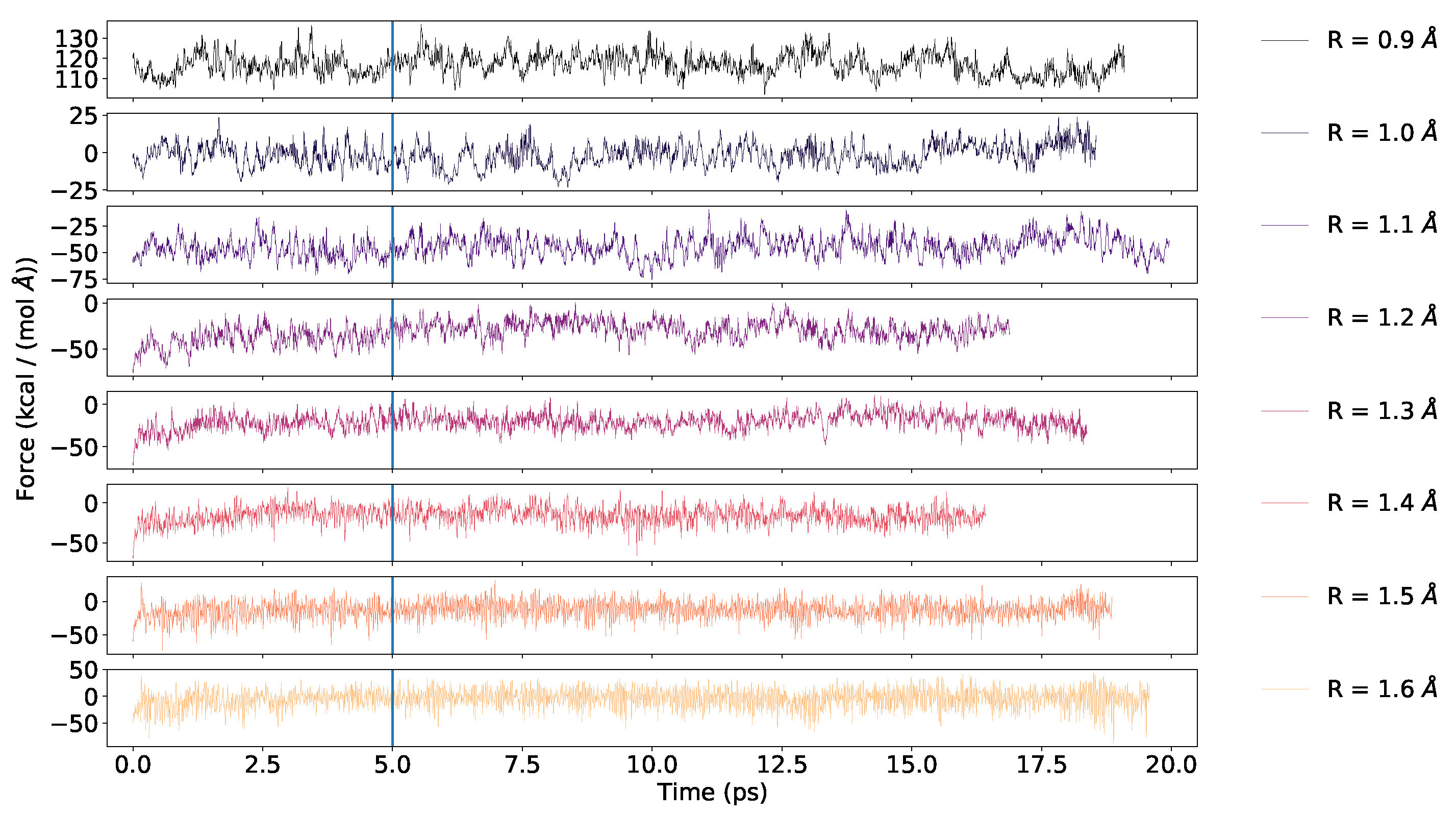
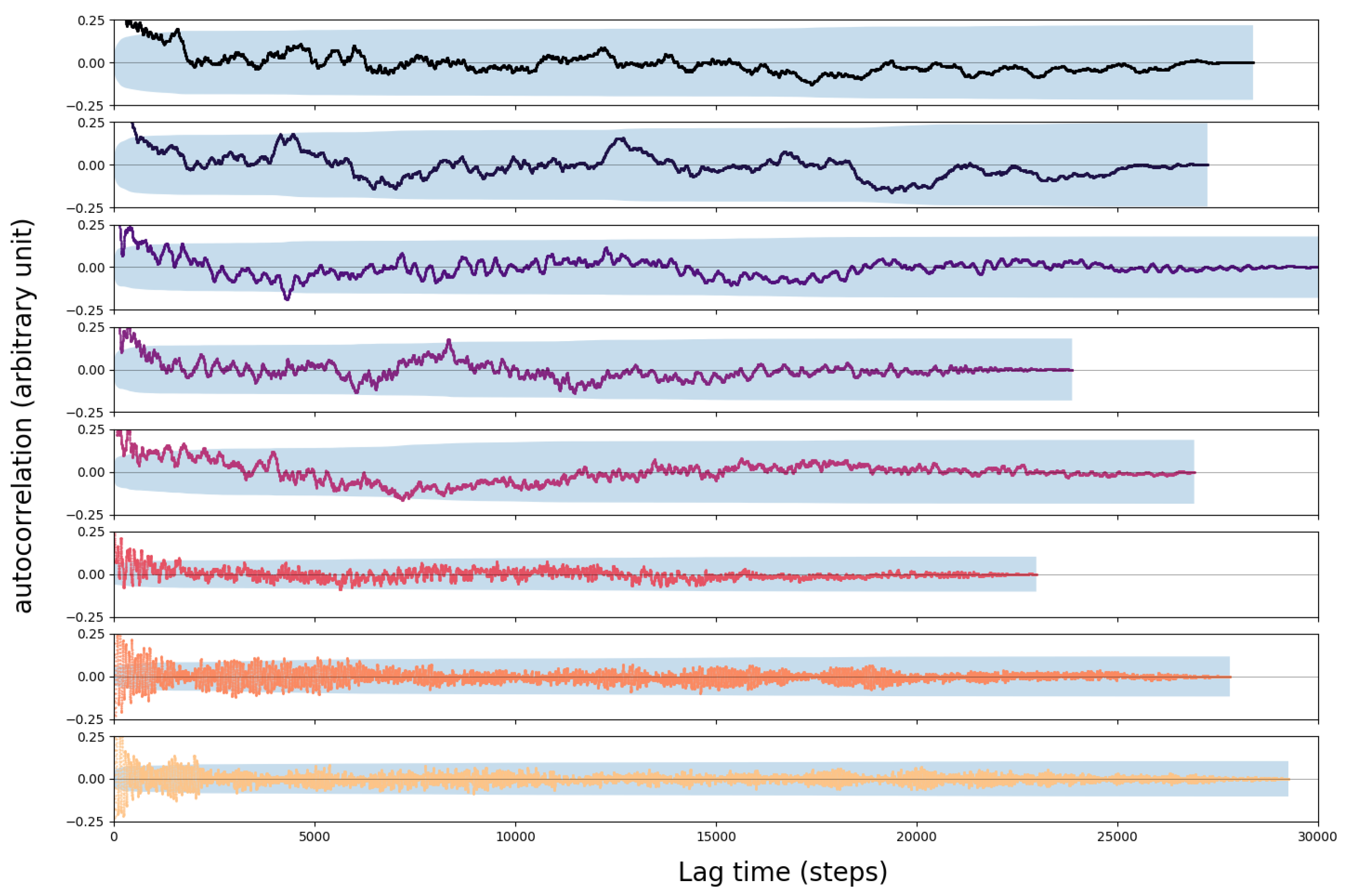
3.2. Error Analysis
4. Results and Discussion
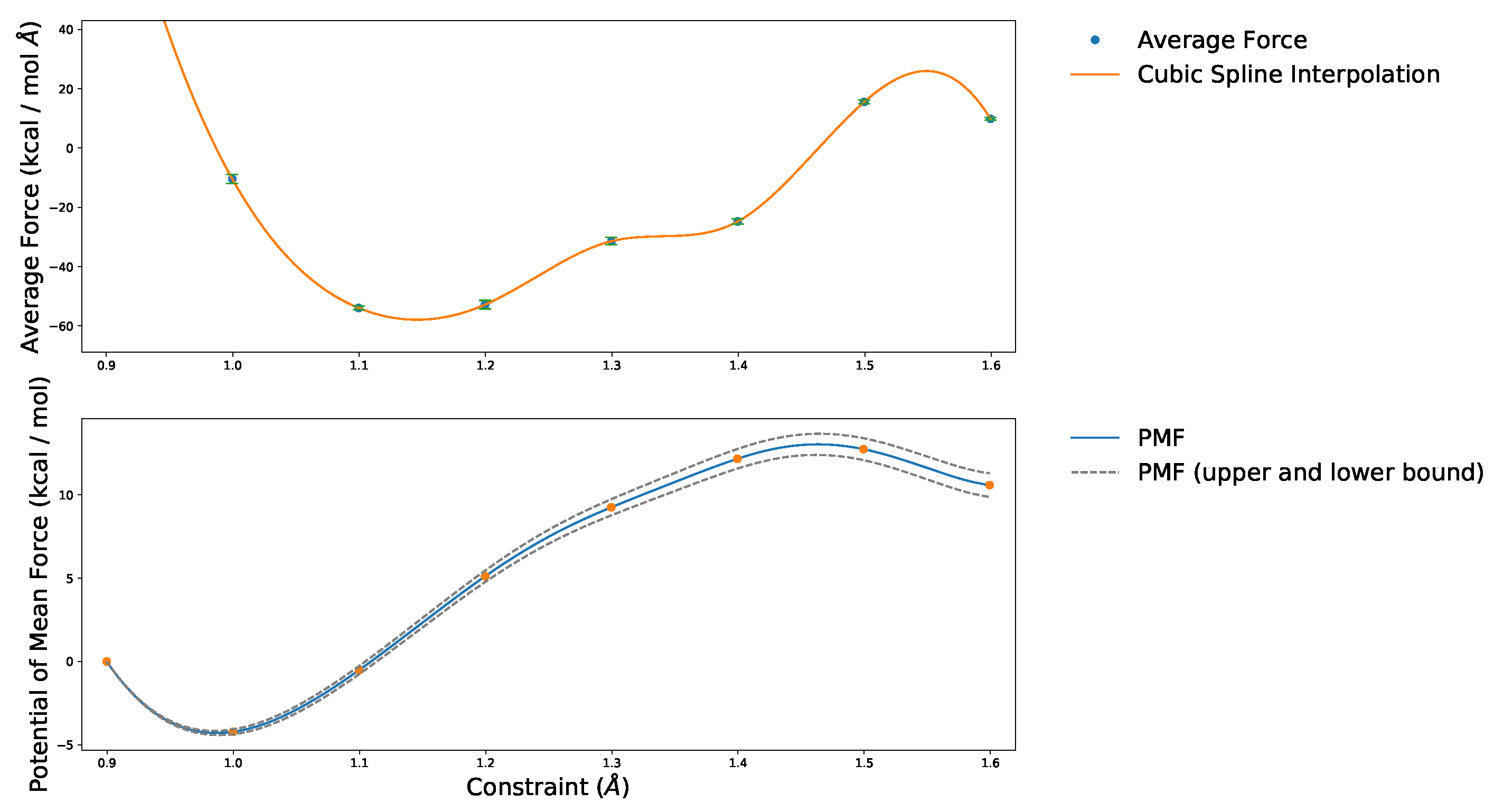
4.1. Convergence of the AIMD Simulations
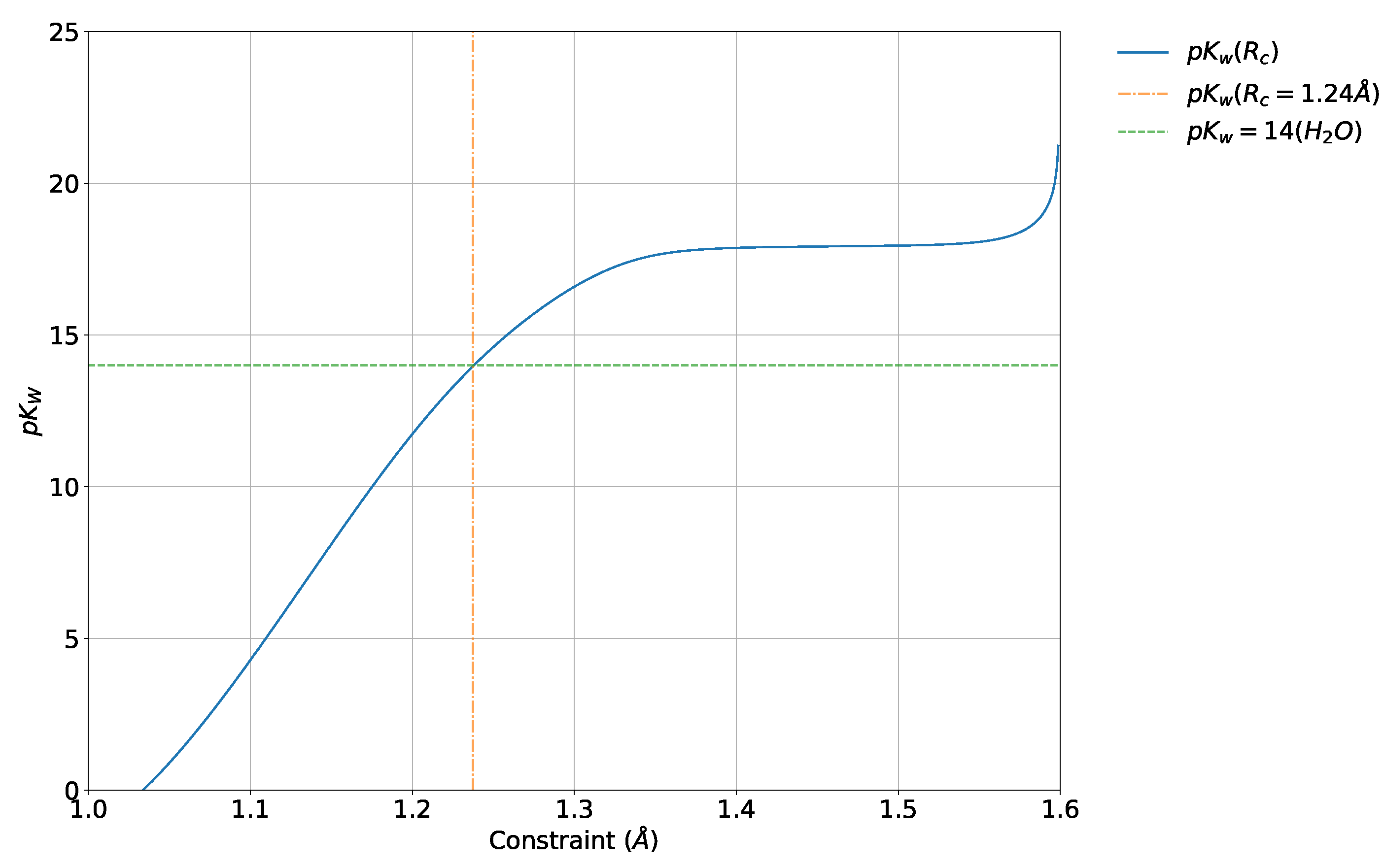
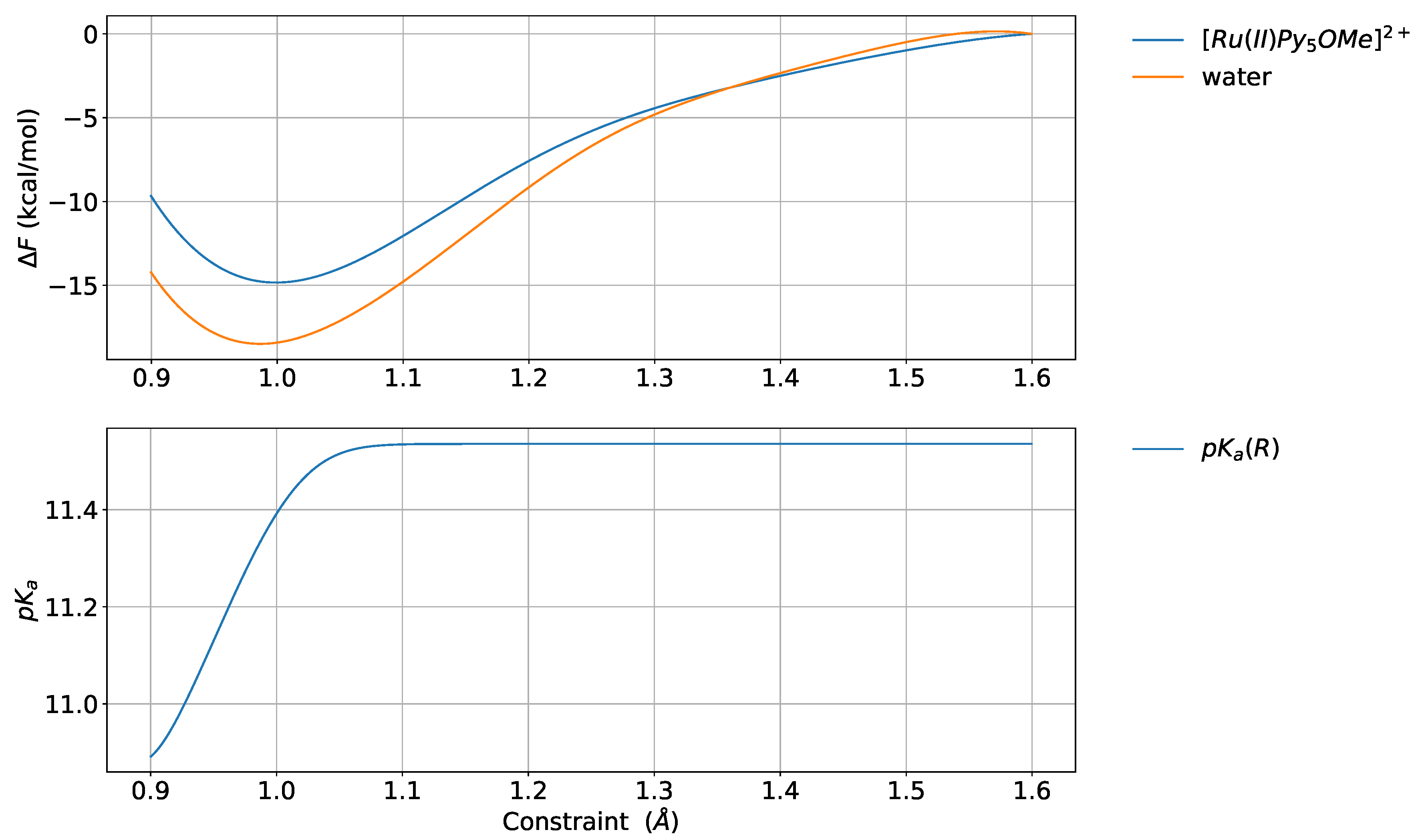
4.2. Reference System
4.3. Overview of Calculated Values
4.4. Deuterated Solvent
4.5. Absolute and Probabilistic —Dependence on
4.6. Relative
5. Summary and Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| DOAJ | Directory of open access journals |
| TLA | Three letter acronym |
| LD | Linear dichroism |
References
- Chen, Y.L.; Doltsinis, N.L.; Hider, R.C.; Barlow, D.J. Prediction of Absolute Hydroxyl pKa Values for 3-Hydroxypyridin-4-ones. J. Phys. Chem. Lett. 2012, 3, 2980–2985. [Google Scholar] [CrossRef]
- Kiliç, M.; Ensing, B. Acidity constants of lumiflavin from first principles molecular dynamics simulations. Phys. Chem. Chem. Phys. 2014, 16, 18993–19000. [Google Scholar] [CrossRef] [PubMed]
- De Meyer, T.; Ensing, B.; Rogge, S.M.J.; De Clerck, K.; Meijer, E.J.; Van Speybroeck, V. Acidity Constant (pKa) Calculation of Large Solvated Dye Molecules: Evaluation of Two Advanced Molecular Dynamics Methods. ChemPlusChem 2016, 17, 3447–3459. [Google Scholar] [CrossRef]
- Ivanov, I.; Chen, B.; Raugei, S.; Klein, M.L. Relative pKa Values from First-Principles Molecular Dynamics: The Case of Histidine Deprotonation. J. Phys. Chem. B 2006, 110, 6365–6371. [Google Scholar] [CrossRef] [PubMed]
- Bankura, A.; Klein, M.L.; Carnevale, V. Proton affinity of the histidine-tryptophan cluster motif from the influenza A virus from ab initio molecular dynamics. Chem. Phys. 2013, 422, 156–164. [Google Scholar] [CrossRef][Green Version]
- Bernasconi, L.; Baerends, E.J.; Sprik, M. Long-Range Solvent Effects on the Orbital Interaction Mechanism of Water Acidity Enhancement in Metal Ion Solutions: A Comparative Study of the Electronic Structure of Aqueous Mg and Zn Dications. J. Phys. Chem. B 2006, 110, 11444–11453. [Google Scholar] [CrossRef] [PubMed]
- Gil-Sepulcre, M.; Böhler, M.; Schilling, M.; Bozoglian, F.; Bachmann, C.; Scherrer, D.; Fox, T.; Spingler, B.; Gimbert-Suriñach, C.; Alberto, R.; et al. Ruthenium Water Oxidation Catalysts based on Pentapyridyl Ligands. ChemSusChem 2017, 10, 4517–4525. [Google Scholar] [CrossRef]
- Schilling, M.; Böhler, M.; Luber, S. Towards the rational design of the Py5-ligand framework for ruthenium-based water oxidation catalysts. Dalton Trans. 2018, 47, 10480–10490. [Google Scholar] [CrossRef]
- Shields, G.S.; Seybold, P.G. CRC Handbook of Chemistry and Physics; CRC Press: Boca Raton, FL, USA; Taylor & Francis Group: Abingdon, UK, 2014. [Google Scholar]
- Tomasi, J. Thirty years of continuum solvation chemistry: A review, and prospects for the near future. Theor. Chem. Acc. 2004, 112, 184–203. [Google Scholar] [CrossRef]
- Tomasi, J.; Cancès, E.; Pomelli, C.S.; Caricato, M.; Scalmani, G.; Frisch, M.J.; Cammi, R.; Basilevsky, M.V.; Chuev, G.N.; Mennucci, B. Modern Theories of Continuum Models; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2007. [Google Scholar]
- Bayly, C.I.; Cieplak, P.; Cornell, W.; Kollman, P.A. A well-behaved electrostatic potential based method using charge restraints for deriving atomic charges: The RESP model. J. Chem. Phys. 1993, 97, 10269–10280. [Google Scholar] [CrossRef]
- Am Busch, M.S.; Knapp, E.W. Accurate pKa Determination for a Heterogeneous Group of Organic Molecules. ChemPlusChem 2004, 5, 1513–1522. [Google Scholar] [CrossRef]
- Galstyan, G.; Knapp, E.W. Computing pKa Values of Hexa-Aqua Transition Metal Complexes. J. Comput. Chem. 2015, 36, 69–78. [Google Scholar] [CrossRef] [PubMed]
- Simonson, T.; Carlsson, J.; Case, D.A. Proton Binding to Proteins: pKa Calculations with Explicit and Implicit Solvent Models. J. Am. Chem. Soc. 2004, 126, 4167–4180. [Google Scholar] [CrossRef] [PubMed]
- Meyer, T.; Kieseritzky, G.; Knapp, E.W. Electrostatic pKa computations in proteins: Role of internal cavities. Proteins 2011, 79, 3320–3332. [Google Scholar] [CrossRef] [PubMed]
- Cramer, C.J.; Truhlar, D.G. Implicit Solvation Models: Equilibria, Structure, Spectra, and Dynamics. Chem. Rev. 1999, 99, 2161–2200. [Google Scholar] [CrossRef] [PubMed]
- Ho, J.; Coote, M.L. A universal approach for continuum solvent pKa calculations: Are we there yet? Theor. Chem. Acc. 2009, 125, 3. [Google Scholar] [CrossRef]
- Zhan, C.G.; Dixon, D.A. Absolute Hydration Free Energy of the Proton from First-Principles Electronic Structure Calculations. J. Phys. Chem. A 2001, 105, 11534–11540. [Google Scholar] [CrossRef]
- Klamt, A.; Eckert, F.; Diedenhofen, M.; Beck, M.E. First Principles Calculations of Aqueous pKa Values for Organic and Inorganic Acids Using COSMO-RS Reveal an Inconsistency in the Slope of the pKa Scale. J. Phys. Chem. A 2003, 107, 9380–9386. [Google Scholar] [CrossRef]
- Nielsen, J.E.; Gunner, M.R.; García-Moreno, E.B. The pKa Cooperative: A collaborative effort to advance structure-based calculations of pKa values and electrostatic effects in proteins. Proteins 2011, 79, 3249–3259. [Google Scholar] [CrossRef]
- Alexov, E.; Mehler, E.L.; Baker, N.M.; Baptista, A.; Huang, Y.; Milletti, F.; Erik Nielsen, J.; Farrell, D.; Carstensen, T.; Olsson, M.H.M.; et al. Progress in the prediction of pKa values in proteins. Proteins 2011, 79, 3260–3275. [Google Scholar] [CrossRef]
- Marenich, A.V.; Ho, J.; Coote, M.L.; Cramer, C.J.; Truhlar, D.G. Computational electrochemistry: Prediction of liquid-phase reduction potentials. Phys. Chem. Chem. Phys. 2014, 16, 15068–15106. [Google Scholar] [CrossRef] [PubMed]
- Ho, J. Are thermodynamic cycles necessary for continuum solvent calculation of pKas and reduction potentials? Phys. Chem. Chem. Phys. 2015, 17, 2859–2868. [Google Scholar] [CrossRef] [PubMed]
- Gunner, M.; Baker, N. Chapter One—Continuum Electrostatics Approaches to Calculating pKas and Ems in Proteins. In Computational Approaches for Studying Enzyme Mechanism Part B; Voth, G.A., Ed.; Academic Press: Cambridge, MA, USA, 2016; Volume 578, pp. 1–20. [Google Scholar] [CrossRef]
- Sulpizi, M.; Sprik, M. Acidity constants from vertical energy gaps: Density functional theory based molecular dynamics implementation. Phys. Chem. Chem. Phys. 2008, 10, 5238–5249. [Google Scholar] [CrossRef] [PubMed]
- Cheng, J.; Sulpizi, M.; Sprik, M. Redox potentials and pKa for benzoquinone from density functional theory based molecular dynamics. J. Chem. Phys. 2009, 131, 154504. [Google Scholar] [CrossRef] [PubMed]
- Sulpizi, M.; Sprik, M. Acidity constants from DFT-based molecular dynamics simulations. J. Phys. Condens. Matter. 2010, 22, 284116. [Google Scholar] [CrossRef] [PubMed]
- Cheng, J.; Liu, X.; VandeVondele, J.; Sulpizi, M.; Sprik, M. Redox Potentials and Acidity Constants from Density Functional Theory Based Molecular Dynamics. Acc. Chem. Res. 2014, 47, 3522–3529. [Google Scholar] [CrossRef]
- Sprik, M. Computation of the pK of liquid water using coordination constraints. Chem. Phys. 2000, 258, 139–150. [Google Scholar] [CrossRef]
- Davies, J.E.; Doltsinis, N.L.; Kirby, A.J.; Roussev, C.D.; Sprik, M. Estimating pKa Values for Pentaoxyphosphoranes. J. Am. Chem. Soc. 2002, 124, 6594–6599. [Google Scholar] [CrossRef]
- Doltsinis, N.L.; Sprik, M. Theoretical pKa estimates for solvated P(OH)5 from coordination constrained Car-Parrinello molecular dynamics. Phys. Chem. Chem. Phys. 2003, 5, 2612–2618. [Google Scholar] [CrossRef]
- Sprik, M.; Ciccotti, G. Free energy from constrained molecular dynamics. J. Chem. Phys. 1998, 109, 7737–7744. [Google Scholar] [CrossRef]
- Ciccotti, G.; Ferrario, M. Blue Moon Approach to Rare Events. Mol. Sim. 2004, 30, 787–793. [Google Scholar] [CrossRef]
- Ciccotti, G.; Kapral, R.; Vanden-Eijnden, E. Blue Moon Sampling, Vectorial Reaction Coordinates, and Unbiased Constrained Dynamics. ChemPlusChem 2005, 6, 1809–1814. [Google Scholar] [CrossRef]
- Brüssel, M.; Di Dio, P.J.; Muñiz, K.; Kirchner, B. Comparison of Free Energy Surfaces Calculations from Ab Initio Molecular Dynamic Simulations at the Example of Two Transition Metal Catalyzed Reactions. Int. J. Mol. Sci. 2011, 12, 1389–1409. [Google Scholar] [CrossRef] [PubMed]
- Sprik, M. Coordination numbers as reaction coordinates in constrained molecular dynamics. Faraday Discuss. 1998, 110, 437–445. [Google Scholar] [CrossRef]
- Liu, X.; Lu, X.; Wang, R.; Zhou, H. In Silico Calculation of Acidity Constants of Carbonic Acid Conformers. J. Phys. Chem. A 2010, 114, 12914–12917. [Google Scholar] [CrossRef] [PubMed]
- Sinha, V.; Govindarajan, N.; de Bruin, B.; Meijer, E.J. How Solvent Affects C–H Activation and Hydrogen Production Pathways in Homogeneous Ru-Catalyzed Methanol Dehydrogenation Reactions. ACS Catal. 2018, 8, 6908–6913. [Google Scholar] [CrossRef]
- Chandler, D. Introduction to Modern Statistical Mechanics; Oxford University Press, Inc.: Oxford, UK, 1987. [Google Scholar]
- CP2K Developers Group. CP2K Program Package. Available online: https://www.cp2k.org/ (accessed on 11 June 2019).
- VandeVondele, J.; Hutter, J. Gaussian basis sets for accurate calculations on molecular systems in gas and condensed phases. J. Chem. Phys. 2007, 127, 114105. [Google Scholar] [CrossRef]
- Goedecker, S.; Teter, M.; Hutter, J. Separable dual-space Gaussian pseudopotentials. Phys. Rev. B 1996, 54, 1703–1710. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H–Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
- Mahoney, M.W.; Jorgensen, W.L. A five-site model for liquid water and the reproduction of the density anomaly by rigid, nonpolarizable potential functions. J. Chem. Phys. 2000, 112, 8910–8922. [Google Scholar] [CrossRef]
- Nosé, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511–519. [Google Scholar] [CrossRef]
- Nosé, S. A molecular dynamics method for simulations in the canonical ensemble. Mol. Phys. 1984, 52, 255–268. [Google Scholar] [CrossRef]
- VandeVondele, J.; Mohamed, F.; Krack, M.; Hutter, J.; Sprik, M.; Parrinello, M. The influence of temperature and density functional models in ab initio molecular dynamics simulation of liquid water. J. Chem. Phys. 2005, 122, 014515. [Google Scholar] [CrossRef] [PubMed]
- Gil-Sepulcre, M.; Axelson, J.C.; Aguiló, J.; Solà-Hernández, L.; Francàs, L.; Poater, A.; Blancafort, L.; Benet-Buchholz, J.; Guirado, G.; Escriche, L.; et al. Synthesis and Isomeric Analysis of Ru(II) Complexes Bearing Pentadentate Scaffolds. Inorg. Chem. 2016, 55, 11216–11229. [Google Scholar] [CrossRef] [PubMed]
- Braude, A.E.; Nachod, F.C. Determination of Organic Structures by Physical Methods; Academic Press., Inc.: Cambridge, MA, USA, 1955; Volume 1. [Google Scholar]
- Schilling, M.; Luber, S. Computational Modeling of Cobalt-Based Water Oxidation: Current Status and Future Challenges. Front Chem. 2018, 6, 100. [Google Scholar] [CrossRef]
- Flyvbjerg, H.; Petersen, H.G. Error estimates on averages of correlated data. J. Chem. Phys. 1989, 91, 461–466. [Google Scholar] [CrossRef]
- Robinson, R.A.; Paabo, M.; Bates, R.G. Deuterium Isotope Effect on the Dissociation of Weak Acids in Water and Deuterium Oxide. J. Res. Natl. Bur. Stand. 1969, 73A, 299–308. [Google Scholar] [CrossRef]
- Delgado, R.; Silva, J.D.; Amorim, M.; Cabral, M.; Chaves, S.; Costa, J. Dissociation constants of Brønsted acids in D2O and H2O: Studies on polyaza and polyoxa-polyaza macrocycles and a general correlation. Anal. Chim. Acta 1991, 245, 271–282. [Google Scholar] [CrossRef]
- Krȩżel, A.; Bal, W. A formula for correlating pKa values determined in D2O and H2O. J. Inorg. Biochem. 2004, 98, 161–166. [Google Scholar] [CrossRef] [PubMed]
- Lide, D.R. CRC Handbook of Chemistry and Physics; Number 8–85; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
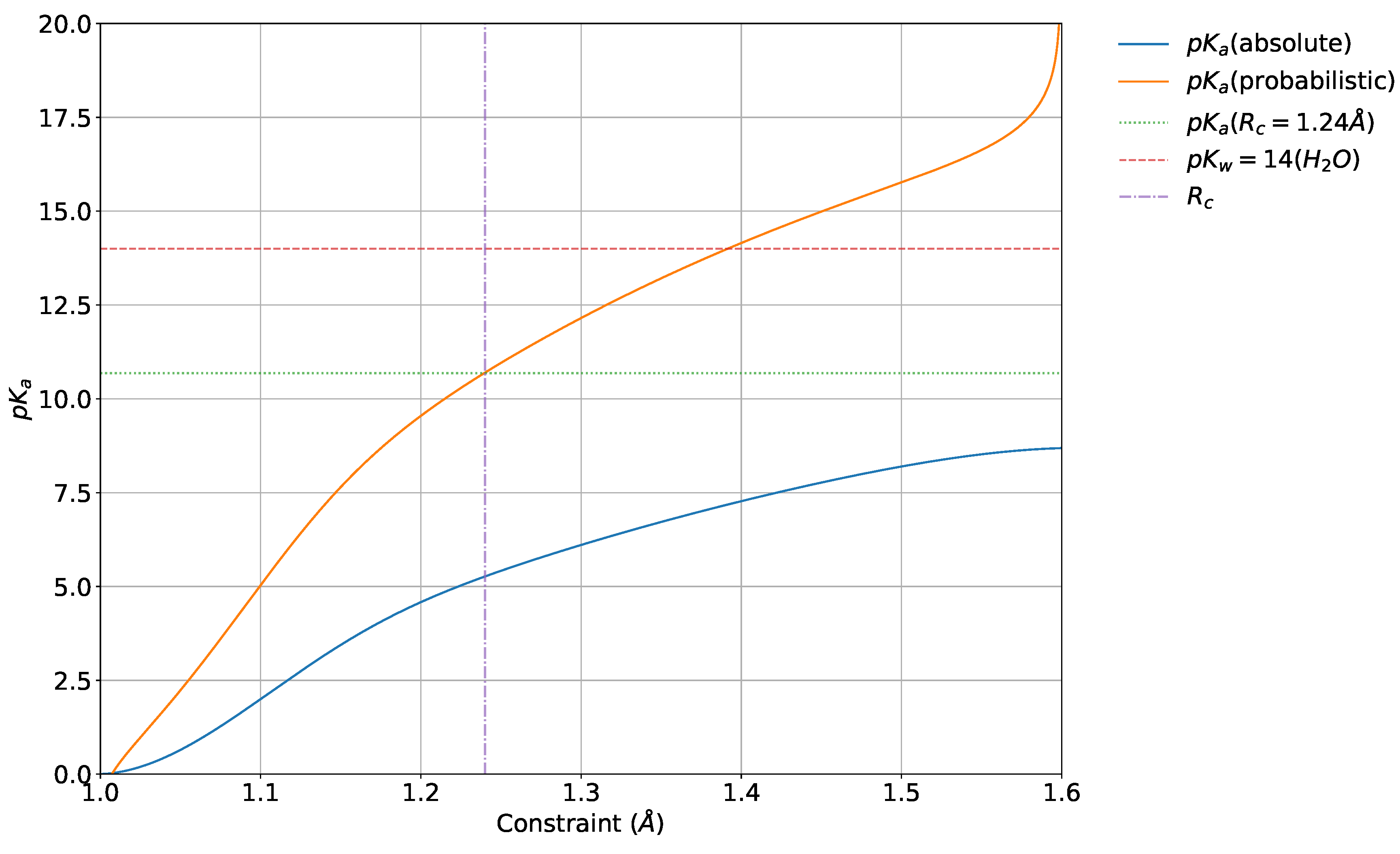
| Molecule | Side-Length [Å] | (exp.) | (calc.) | |
|---|---|---|---|---|
| H2O | 128 | 15.6 | 14.0 | – |
| H2O | 256 | 19.7 | 14.0 | – |
| HCOOH | 126 | 15.6 | 3.8 [52] | – |
| PhOH | 123 | 15.6 | 10.0 [52] | 9.7 [3] |
| [Ru(II)Py5Me(H2O)]2+ | 112 | 15.6 | ∼11 [7] | – |
| [Ru(II)Py5OMe(H2O)]2+ | 112 | 15.6 | ∼11 [7] * | – |
| [Ru(II)Py5OMe(H2O)]2+ | 234 | 19.7 | ∼11 [7] * | – |
| [Ru(II)Py5OMe(H2O)]3+ | 112 | 15.6 | ∼3 [7] * | – |
| [Ru(II)Py5OMe(H2O)]3+ | 234 | 19.7 | ∼3 [7] * | – |
| Molecule | (exp.) | |||
|---|---|---|---|---|
| H2O | 14.0 | – | – | |
| HCOOH | 3.8 [52] | |||
| PhOH | 10.0 [52] | |||
| [Ru(II)Py5Me(H2O)]2+ | ∼11 [51] | |||
| [Ru(II)Py5OMe(H2O)]2+ | ∼11 [51] | |||
| [Ru(III)Py5OMe(H2O)]3+ | ∼2.5 [51] |
| Molecule | (exp.) | |||
|---|---|---|---|---|
| H2O | 14.0 | – | – | |
| [Ru(II)Py5OMe(H2O)]2+ | ∼11 [51] | |||
| [Ru(III)Py5OMe(H2O)]3+ | ∼2.5 [51] |
| Molecule | (exp.) | (a) | (b) | (c) | |
|---|---|---|---|---|---|
| H2O | 14.0 | – | – | – | – |
| HCOOH | 3.8 [52] | 4.2 | 4.3 | 3.8 | 4.0 |
| PhOH | 10.0 [52] | 10.7 | 11.2 | 10.4 | 10.5 |
| [Ru(II)Py5Me(H2O)]2+ | ∼11 [51] | 11.2 | 12.0 | 11.2 | 11.2 |
| [Ru(II)Py5OMe(H2O)]2+ | ∼11 [51] | 11.1 | 11.8 | 11.0 | 11.0 |
| [Ru(III)Py5OMe(H2O)]3+ | ∼2.5 [51] | 4.5 | 4.6 | 4.1 | 4.3 |
| Molecule | (exp.) | (a) | (b) | (c) | |
|---|---|---|---|---|---|
| H2O | 14.0 | - | - | - | - |
| [Ru(II)Py5OMe(H2O)]2+ | ∼11 [51] | 12.7 | 13.1 | 12.2 | 12.2 |
| [Ru(III)Py5OMe(H2O)]3+ | ∼2.5 [51] | 4.3 | 4.4 | 3.9 | 4.1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schilling, M.; Luber, S. Determination of pKa Values via ab initio Molecular Dynamics and its Application to Transition Metal-Based Water Oxidation Catalysts. Inorganics 2019, 7, 73. https://doi.org/10.3390/inorganics7060073
Schilling M, Luber S. Determination of pKa Values via ab initio Molecular Dynamics and its Application to Transition Metal-Based Water Oxidation Catalysts. Inorganics. 2019; 7(6):73. https://doi.org/10.3390/inorganics7060073
Chicago/Turabian StyleSchilling, Mauro, and Sandra Luber. 2019. "Determination of pKa Values via ab initio Molecular Dynamics and its Application to Transition Metal-Based Water Oxidation Catalysts" Inorganics 7, no. 6: 73. https://doi.org/10.3390/inorganics7060073
APA StyleSchilling, M., & Luber, S. (2019). Determination of pKa Values via ab initio Molecular Dynamics and its Application to Transition Metal-Based Water Oxidation Catalysts. Inorganics, 7(6), 73. https://doi.org/10.3390/inorganics7060073






