Modeling the Catalyst Activation Step in a Metal–Ligand Radical Mechanism Based Water Oxidation System
Abstract
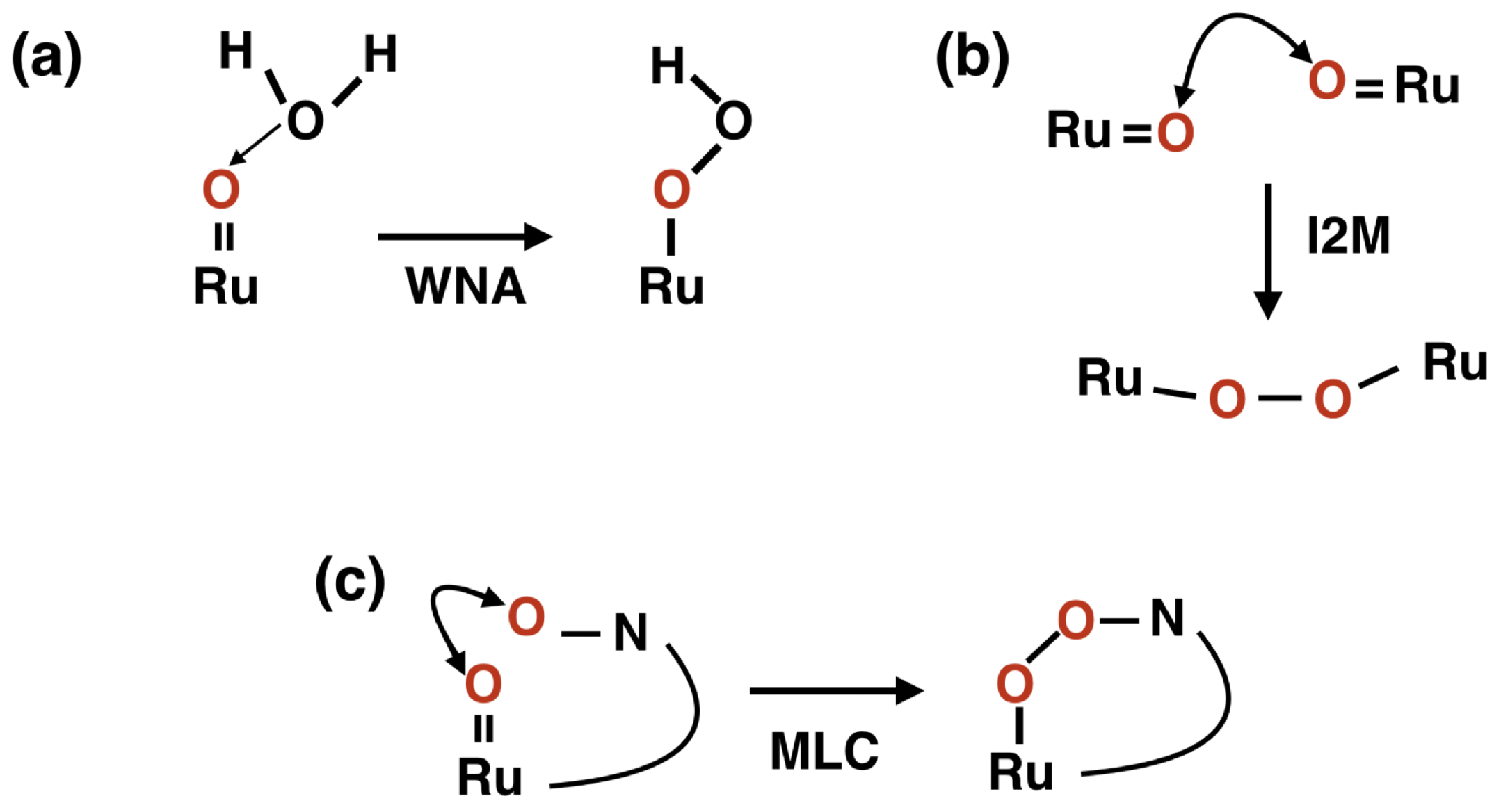
1. Introduction
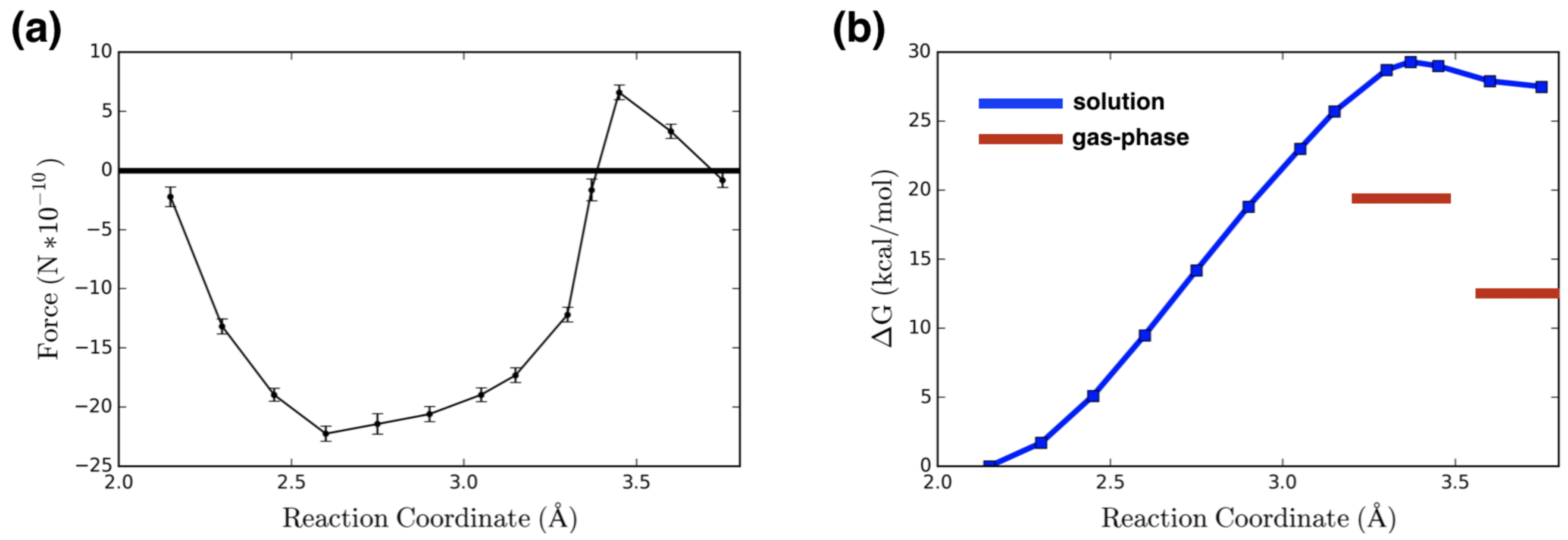
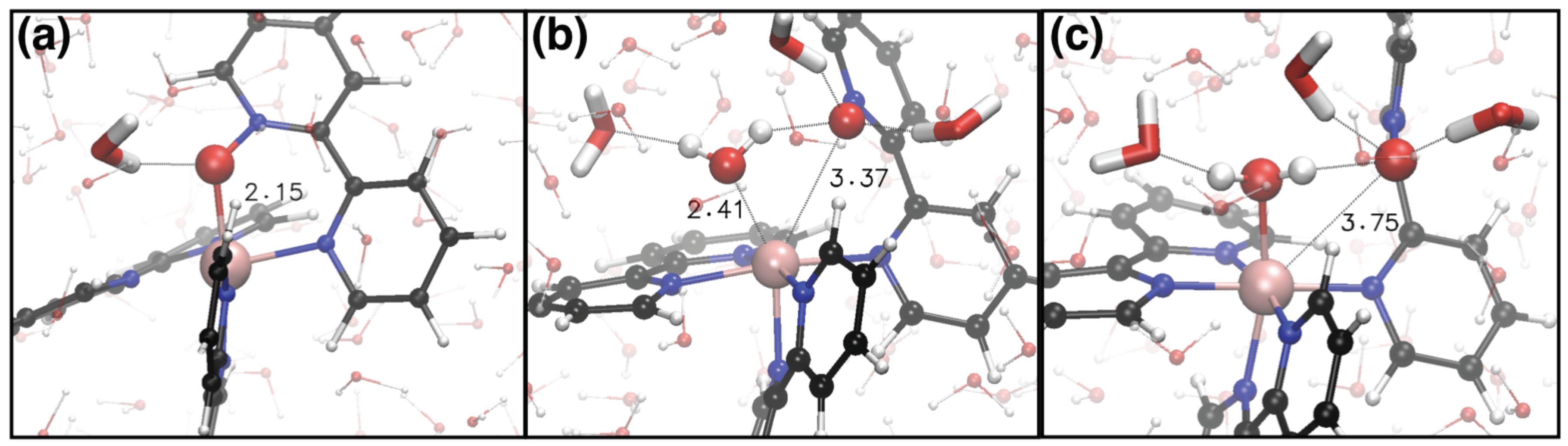
2. Results and Discussion
3. Materials and Methods
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Detz, R.J.; Reek, J.N.H.; van der Zwaan, B.C.C. The future of solar fuels: When could they become competitive? Energy Environ. Sci. 2018, 11, 1653–1669. [Google Scholar] [CrossRef]
- Song, F.; Bai, L.; Moysiadou, A.; Lee, S.; Hu, C.; Liardet, L.; Hu, X. Transition Metal Oxides as Electrocatalysts for the Oxygen Evolution Reaction in Alkaline Solutions: An Application-Inspired Renaissance. J. Am. Chem. Soc. 2018, 140, 7748–7759. [Google Scholar] [CrossRef] [PubMed]
- Man, I.C.; Su, H.Y.; Calle-Vallejo, F.; Hansen, H.A.; Martinez, J.I.; Inoglu, N.G.; Kitchin, J.; Jaramillo, T.F.; Norskov, J.K.; Rossmeisl, J. Universality in Oxygen Evolution Electrocatalysis on Oxide Surfaces. ChemCatChem 2011, 3, 1159–1165. [Google Scholar] [CrossRef]
- Hessels, J.; Detz, R.J.; Koper, M.T.M.; Reek, J.N.H. Rational Design Rules for Molecular Water Oxidation Catalysts based on Scaling Relationships. Chem. Eur. J. 2017, 23, 16413–16418. [Google Scholar] [CrossRef] [PubMed]
- Vojvodic, A.; Nørskov, J.K. New design paradigm for heterogeneous catalysts. Natl. Sci. Rev. 2015, 2, 140–143. [Google Scholar] [CrossRef]
- Govindarajan, N.; Garcia-Lastra, J.M.; Meijer, E.J.; Calle-Vallejo, F. Does the breaking of adsorption-energy scaling relations guarantee enhanced electrocatalysis? Curr. Opin. Electrochem. 2018, 8, 110–117. [Google Scholar] [CrossRef]
- Fabbri, E.; Schmidt, T.J. Oxygen Evolution Reaction: The Enigma in Water Electrolysis. ACS Catal. 2018, 8, 9765–9774. [Google Scholar] [CrossRef]
- Duan, L.; Wang, L.; Li, F.; Li, F.; Sun, L. Highly Efficient Bioinspired Molecular Ru Water Oxidation Catalysts with Negatively Charged Backbone Ligands. Acc. Chem. Res. 2015, 48, 2084–2096. [Google Scholar] [CrossRef]
- Duan, L.; Araujo, C.M.; Ahlquist, M.S.; Sun, L. Highly efficient and robust molecular ruthenium catalysts for water oxidation. Proc. Natl. Acad. Sci. USA 2012, 109, 15584–15588. [Google Scholar] [CrossRef]
- Blakemore, J.D.; Crabtree, R.H.; Brudvig, G.W. Molecular Catalysts for Water Oxidation. Chem. Rev. 2015, 115, 12974–13005. [Google Scholar] [CrossRef]
- Concepcion, J.J.; Jurss, J.W.; Templeton, J.L.; Meyer, T.J. One Site is Enough. Catalytic Water Oxidation by [Ru(tpy)(bpm)(OH2)]2+ and [Ru(tpy)(bpz)(OH2)]2+. J. Am. Chem. Soc. 2008, 130, 16462–16463. [Google Scholar] [CrossRef]
- Matheu, R.; Ertem, M.Z.; Benet-Buchholz, J.; Coronado, E.; Batista, V.S.; Sala, X.; Llobet, A. Intramolecular Proton Transfer Boosts Water Oxidation Catalyzed by a Ru Complex. J. Am. Chem. Soc. 2015, 137, 10786–10795. [Google Scholar] [CrossRef]
- Nyhlan, J.; Duan, L.; Akermark, B.; Sun, L.; Privalov, T. Evolution of O2 in a Seven-Coordinate RuIV Dimer Complex with a [HOHOH] Bridge: A Computational Study. Angew. Chem. Int. Ed. 2010, 49, 1773–1777. [Google Scholar] [CrossRef]
- Shaffer, D.W.; Xie, Y.; Concepcion, J.J. O–O bond formation in ruthenium-catalyzed water oxidation: Single-site nucleophilic attack vs. O–O radical coupling. Chem. Soc. Rev. 2017, 46, 6170–6193. [Google Scholar] [CrossRef]
- Xie, Y.; Shaffer, D.W.; Concepcion, J.J. O–O Radical Coupling: From Detailed Mechanistic Understanding to Enhanced Water Oxidation Catalysis. Inorg. Chem. 2018, 57, 10533–10542. [Google Scholar] [CrossRef]
- Erdman, D.; Pineda-Galvan, Y.; Pushkar, Y. Mechanistic Analysis of Water Oxidation Catalyst cis-[Ru(bpy)2(H2O)2]2+: Effect of Dimerization. Catalysts 2017, 7, 39. [Google Scholar] [CrossRef]
- Wang, L.; Duan, L.; Stewart, B.; Pu, M.; Liu, J.; Privalov, T.; Sun, L. Toward Controlling Water Oxidation Catalysis: Tunable Activity of Ruthenium Complexes with Axial Imidazole/DMSO Ligands. J. Am. Chem. Soc. 2012, 134, 18868–18880. [Google Scholar] [CrossRef]
- Zhan, S.; Zou, R.; Ahlquist, M.S.G. Dynamics with Explicit Solvation Reveals Formation of the Prereactive Dimer as Sole Determining Factor for the Efficiency of Ru(bda)L2 Catalysts. ACS Catal. 2018, 8, 8642–8648. [Google Scholar] [CrossRef]
- Pushkar, Y.; Pineda-Galvan, Y.; Ravari, A.K.; Otroshchenko, T.; Hartzler, D.A. Mechanism for O–O Bond Formation via Radical Coupling of Metal and Ligand Based Radicals: A New Pathway. J. Am. Chem. Soc. 2018, 140, 13538–13541. [Google Scholar] [CrossRef]
- Handgraaf, J.W.; Meijer, E.J. Realistic Modeling of Ruthenium-Catalyzed Transfer Hydrogenation. J. Am. Chem. Soc. 2007, 129, 3099–3103. [Google Scholar] [CrossRef]
- Pavlova, A.; Meijer, E.J. Understanding the Role of Water in Aqueous Ruthenium-Catalyzed Transfer Hydrogenation of Ketones. ChemPhysChem 2012, 13, 3492–3496. [Google Scholar] [CrossRef]
- Pavlova, A.; Rösler, E.; Meijer, E.J. Mechanistic Aspects of Using Formate as a Hydrogen Donor in Aqueous Transfer Hydrogenation. ACS Catal. 2016, 6, 5350–5358. [Google Scholar] [CrossRef]
- Sinha, V.; Govindarajan, N.; de Bruin, B.; Meijer, E.J. How Solvent Affects C–H Activation and Hydrogen Production Pathways in Homogeneous Ru-Catalyzed Methanol Dehydrogenation Reactions. ACS Catal. 2018, 8, 6908–6913. [Google Scholar] [CrossRef]
- Vidossich, P.; Lledos, A.; Ujaque, G. First-Principles Molecular Dynamics Studies of Organometallic Complexes and Homogeneous Catalytic Processes. Acc. Chem. Res. 2016, 49, 1271–1278. [Google Scholar] [CrossRef]
- Ma, C.; Piccinin, S.; Fabris, S. Reaction Mechanisms of Water Splitting and H2 Evolution by a Ru(II)–Pincer Complex Identified with Ab Initio Metadynamics Simulations. ACS Catal. 2012, 2, 1500–1506. [Google Scholar] [CrossRef]
- Hodel, F.H.; Luber, S. What Influences the Water Oxidation Activity of a Bioinspired Molecular CoII4O4 Cubane? An In-Depth Exploration of Catalytic Pathways. ACS Catal. 2016, 6, 1505–1517. [Google Scholar] [CrossRef]
- Narzi, D.; Bovi, D.; Guidoni, L. Pathway for Mn-cluster oxidation by tyrosine-Z in the S2 state of photosystem II. Proc. Natl. Acad. Sci. USA 2014, 111, 8723–8728. [Google Scholar] [CrossRef]
- Vallés-Pardo, J.L.; Guijt, M.C.; Iannuzzi, M.; Joya, K.S.; de Groot, H.J.M.; Buda, F. Ab Initio Molecular Dynamics Study of Water Oxidation Reaction Pathways in Mono-Ru Catalysts. ChemPhysChem 2012, 13, 140–146. [Google Scholar] [CrossRef]
- Govindarajan, N.; Tiwari, A.; Ensing, B.; Meijer, E.J. Impact of the Ligand Flexibility and Solvent on the O–O Bond Formation Step in a Highly Active Ruthenium Water Oxidation Catalyst. Inorg. Chem. 2018, 57, 13063–13066. [Google Scholar] [CrossRef]
- Hodel, F.H.; Luber, S. Redox-Inert Cations Enhancing Water Oxidation Activity: The Crucial Role of Flexibility. ACS Catal. 2016, 6, 6750–6761. [Google Scholar] [CrossRef]
- de Ruiter, J.M.; de Groot, H.J.M.; Buda, F. Energetic Effects of a Closed System Approach Including Explicit Proton and Electron Acceptors as Demonstrated by a Mononuclear Ruthenium Water Oxidation Catalyst. ChemCatChem 2018, 10, 4594–4601. [Google Scholar] [CrossRef]
- Meyer, B.; Sawatlon, B.; Heinen, S.; von Lilienfeld, O.A.; Corminboeuf, C. Machine learning meets volcano plots: Computational discovery of cross-coupling catalysts. Chem. Sci. 2018, 9, 7069–7077. [Google Scholar] [CrossRef]
- VandeVondele, J.; Krack, M.; Mohamed, F.; Parrinello, M.; Chassaing, T.; Hutter, J. Quickstep: Fast and accurate density functional calculations using a mixed Gaussian and plane waves approach. Comput. Phys. Commun. 2005, 167, 103–128. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H–Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Goedecker, S.; Teter, M.; Hutter, J. Separable Dual-Space Gaussian Pseudopotentials. Phys. Rev. B 1996, 54, 1703–1710. [Google Scholar] [CrossRef]
- Hartwigsen, C.; Goedecker, S.; Hutter, J. Relativistic Separable Dual-Space Gaussian Pseudopotentials From H to Rn. Phys. Rev. B 1998, 58, 3641–3662. [Google Scholar] [CrossRef]
- Bussi, G.; Donadio, D.; Parrinello, M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007, 126, 1–7. [Google Scholar] [CrossRef]
- Carter, E.; Ciccotti, G.; Hynes, J.T.; Kapral, R. Constrained reaction coordinate dynamics for the simulation of rare events. Chem. Phys. Lett. 1989, 156, 472–477. [Google Scholar] [CrossRef]
- Sprik, M.; Ciccotti, G. Free energy from constrained molecular dynamics. J. Chem. Phys. 1998, 109, 7737. [Google Scholar] [CrossRef]
- Neese, F. The ORCA program system. Wiley Comput. Mol. Sci. 2011, 2, 73–78. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Govindarajan, N.; Meijer, E.J. Modeling the Catalyst Activation Step in a Metal–Ligand Radical Mechanism Based Water Oxidation System. Inorganics 2019, 7, 62. https://doi.org/10.3390/inorganics7050062
Govindarajan N, Meijer EJ. Modeling the Catalyst Activation Step in a Metal–Ligand Radical Mechanism Based Water Oxidation System. Inorganics. 2019; 7(5):62. https://doi.org/10.3390/inorganics7050062
Chicago/Turabian StyleGovindarajan, Nitish, and Evert Jan Meijer. 2019. "Modeling the Catalyst Activation Step in a Metal–Ligand Radical Mechanism Based Water Oxidation System" Inorganics 7, no. 5: 62. https://doi.org/10.3390/inorganics7050062
APA StyleGovindarajan, N., & Meijer, E. J. (2019). Modeling the Catalyst Activation Step in a Metal–Ligand Radical Mechanism Based Water Oxidation System. Inorganics, 7(5), 62. https://doi.org/10.3390/inorganics7050062




