First Principles Study of the Vibrational and Thermal Properties of Sn-Based Type II Clathrates, Cs_xSn₁₃₆ (0 ≤ x ≤ 24) and Rb₂₄Ga₂₄Sn₁₁₂

Abstract

After performing first-principles calculations of structural and vibrational properties of the semiconducting clathrates Rb₂₄Ga₂₄Sn₁₁₂ along with binary Cs_xSn₁₃₆ (0 ≤ x ≤ 24), we obtained equilibrium geometries and harmonic phonon modes. For the filled clathrate Rb₂₄Ga₂₄Sn₁₁₂, the phonon dispersion relation predicts an upshift of the low-lying rattling modes (~25 cm⁻¹) for the Rb (“rattler”) compared to Cs vibration in Cs_xSn₁₃₆. It is also found that the large isotropic atomic displacement parameter (U_iso) exists when Rb occupies the “over-sized” cage (28 atom cage) rather than the 20 atom counterpart. These guest modes are expected to contribute significantly to minimizing the lattice’s thermal conductivity (κ_L). Our calculation of the vibrational contribution to the specific heat and our evaluation on κ_L are quantitatively presented and discussed. Specifically, the heat capacity diagram regarding C_V/T³ vs. T exhibits the Einstein-peak-like hump that is mainly attributable to the guest oscillator in a 28 atom cage, with a characteristic temperature 36.82 K for Rb₂₄Ga₂₄Sn₁₁₂. Our calculated rattling modes are around 25 cm⁻¹ for the Rb trapped in a 28 atom cage, and 65.4 cm⁻¹ for the Rb encapsulated in a 20 atom cage. These results are utilized to predict the lattice’s thermal conductivity (approximately 0.62 W/m/K) in Rb₂₄Ga₂₄Sn₁₁₂ within the kinetic theory approximation.

1. Introduction

At present, the shortage of energy resources and air pollution have become more and more crucial around the globe. Therefore, seeking clean energy rather than old-fashioned fossil fuel has attracted attention, both from the viewpoint of theoretical investigation and experimental synthesis work. Utilizing themoelectric (TE) materials based on the clathrate phase provides an efficient way of converting waste heat to usable electric energy [1,2], according to the Seeback effect [3]. This novel technology has several advantages, such as low cost, long lifetime, as well as pollution-free properties. Motivated by these potential developments that benefit our society by exploring energy resources, growing research interest has given to clathrate, whose TE performance is evaluated by the dimensionless figure of merit (ZT) value: ZT = TS²σ/κ. Here Z denotes the figure of merit while T represents the absolute temperature. The electrical conductivity and thermal conductivity are given by σ and κ, respectively. S is the Seeback coefficient. It is noted that an efficient TE device [4,5] with prominent performance is manifested by a large value of ZT. To our knowledge, the best ZT value for TE material synthesized from a clathrate compound is around 1.0 [4].

Recently, much focus has been placed on “cage-structured” clathrate materials [5,6,7] whose empty frameworks are capable of encapsulating “rattling” guests arising from alkaline or alkaline-earth atoms. This is due to the fact that this kind of material satisfies the “phonon glass electron crystal” (PGEC) concept proposed by G. A. Slack [8,9]. In this work, we employ the term “guest” to describe the atom (e.g., Rb of Cs) that enters into the cage polyhedron made of Sn (or a mixture of Ga and Sn). Furthermore, the characteristics of the PGEC material can be connected to glass-like thermal conductivity along with the electronic performance found in the crystal. Previous calculations [10,11,12,13] have shown that the guest, acting as a “rattler”, can vibrate resonantly with the framework cage in order to effectively minimize the lattice’s thermal conductivity, thereby contributing efficiently to the enhancement of the ZT value of these TE materials.

Specifically, inorganic clathrates based on Group-IV elements, such as Si, Ge, and Sn, have so far received considerable attention [14,15,16,17], owing to their potential role of serving as thermoelectric candidate materials. Compared to silicon and germanium, the relatively large atomic weight of tin causes its cage size to stay comparably greater than its Si and Ge counterparts, leading to a reduced lattice thermal conductivity, while the “rattler” atom remains fixed in the entire compound system [18,19]. Consequently, research on Sn-based clathrate has become popular. It was reported that low thermal conductivity can be found in the Sn-based clathrate whose polyhedron building block (cage) incorporates an Sr atom as a “guest filler”, causing the material to exhibit prominent thermoelectric performance [20].

Lattice structures of the Sn-based clathrate framework are built from face-shared polyhedron cages, offering a series of ways to host encapsulated “guest” impurities. In particular, tuning the guest atom (or substitutional framework atom) type and number can produce unexpected electronic, vibrational, thermal, and transport properties for these “cage-structured” clathrate compounds. Accordingly, a rich variety of lab-synthesized clathrates, whose frameworks are made of Sn, can be normally classified as either Type-I or Type-II structures [21,22,23,24], in spite of little understanding on the Type-VIII configuration [25,26]. It is anticipated that the Type-VIII Sn-based clathrate might be one of the most efficient TE materials due to its promising transport behavior.

In this paper, we mainly explore the structural, vibrational, and thermal properties of the Type-II binary clathrate A_xSn₁₃₆ (0 < x ≤ 24; A = Na, K, Cs) and ternary semiconducting compound Rb₂₄Ga₂₄Sn₁₁₂. It is necessary to mention that the framework of the Type-II clathrate comprises 20 atom (dodecahedron) cages and 28 atom (hexakeidacahedron) cages which are connected with a ratio of 4:2 in the context of a unit cell involving 136 atoms. Unlike A_xSi₁₃₆ (0 < x ≤ 24), A_xSn₁₃₆ possesses a tuned framework whose host atom varies from silicon to tin, making it impossible to have lattice contraction when x is elevated from 4 to 16 in an ascending order. Regarding the composition-dependent structural response, we always assumed that the “over-sized” cages (e.g., 28 atom tin cages or Sn₂₈) are partially or completely filled with preferred priority. The vibrational modes with Cs vibration in the Sn₂₈ cage, as well as Rb rattling modes in 28 atom (and 20 atom) cages, are also examined. The obtained results show that frequency of Cs vibration in the Sn₂₈ cage of Cs_xSn₁₃₆ (x = 12, 16, 20) is almost half as much as that of the Rb in the 28 atom cage of Rb₂₄Ga₂₄Sn₁₁₂. Meanwhile, Rb vibration in a dodecahedron cage induces smaller atomic displacement parameters (ADPs) than that of Rb vibration in the hexakeidacahedron cage, leading to discrepant rattling frequency and different characteristic temperature of the Einstein oscillator, which pertains to specific heat investigation.

2. Results and Discussion

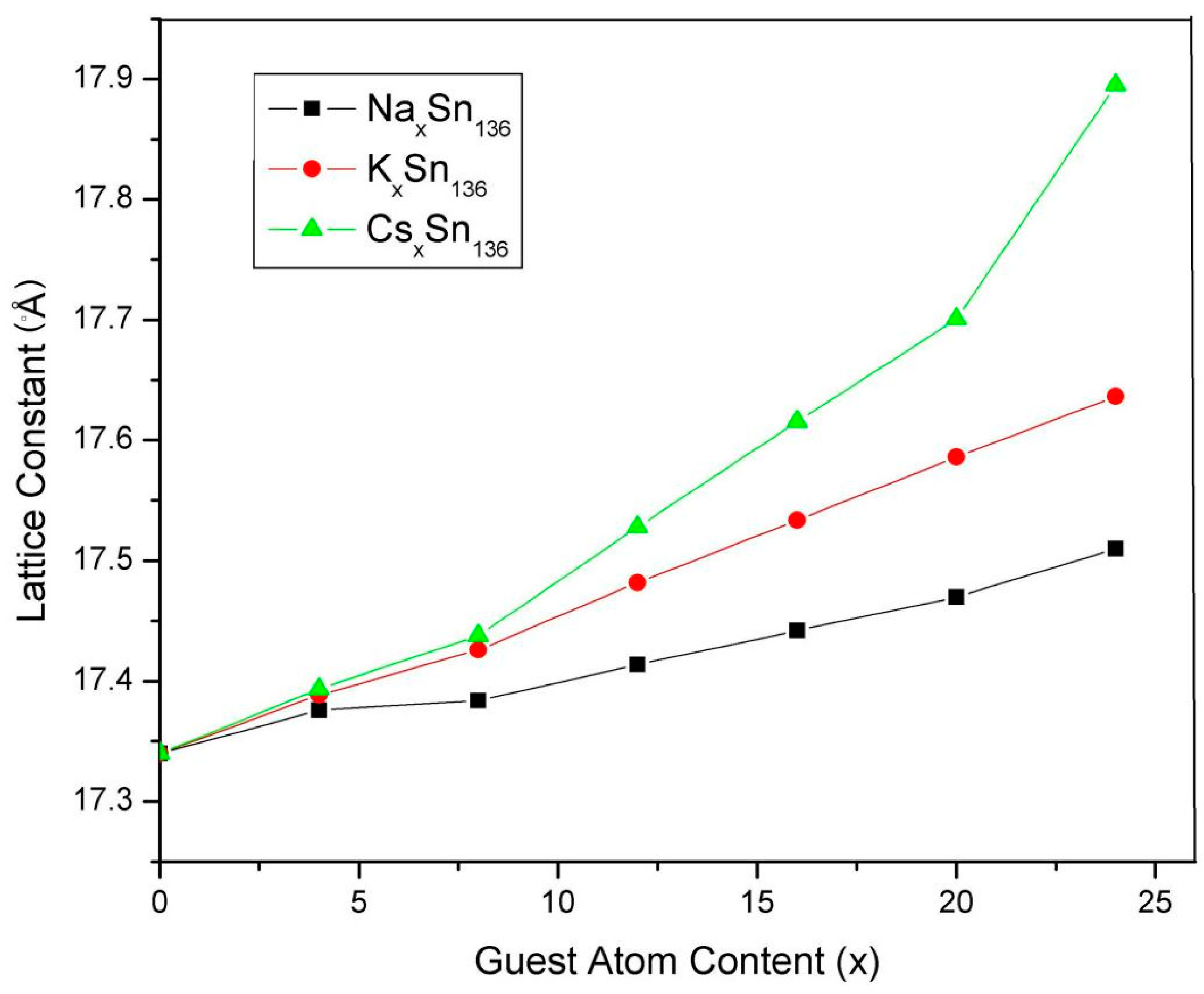
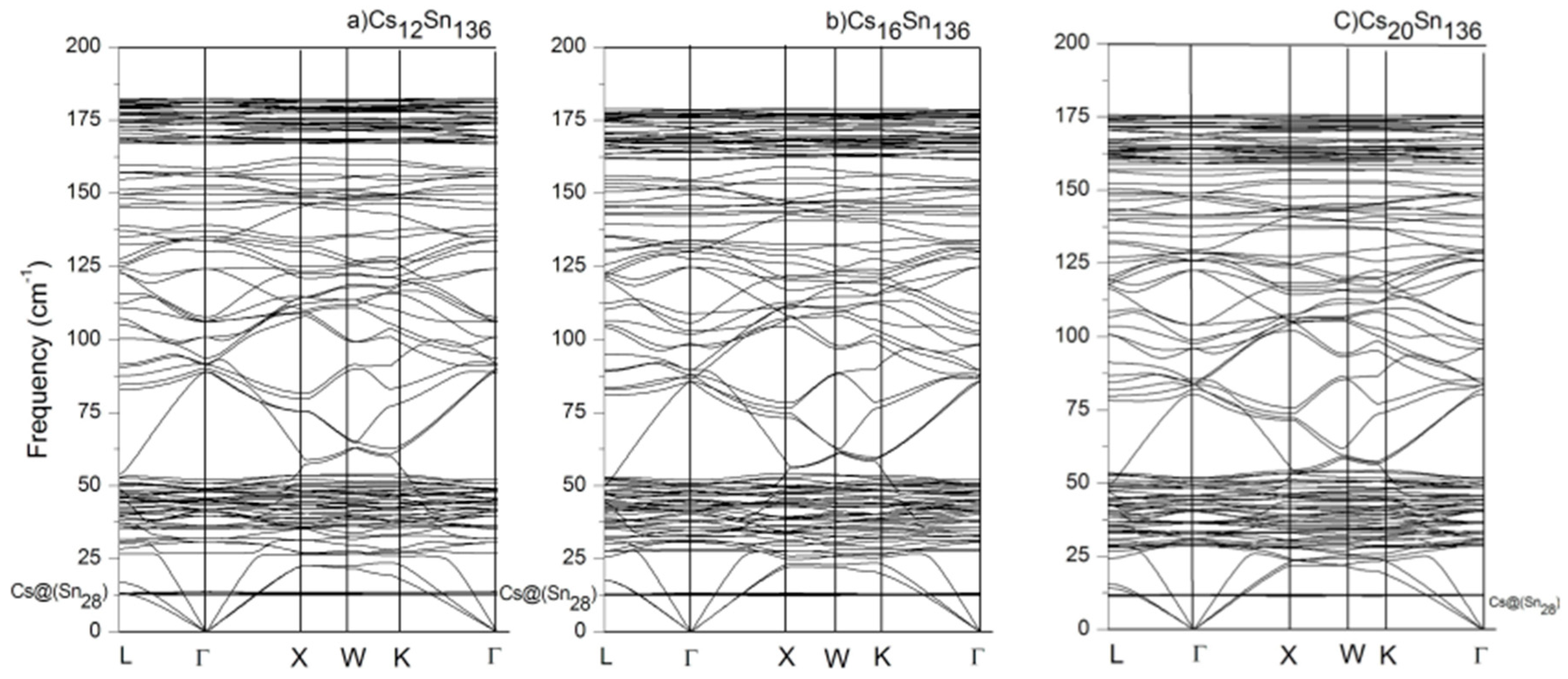
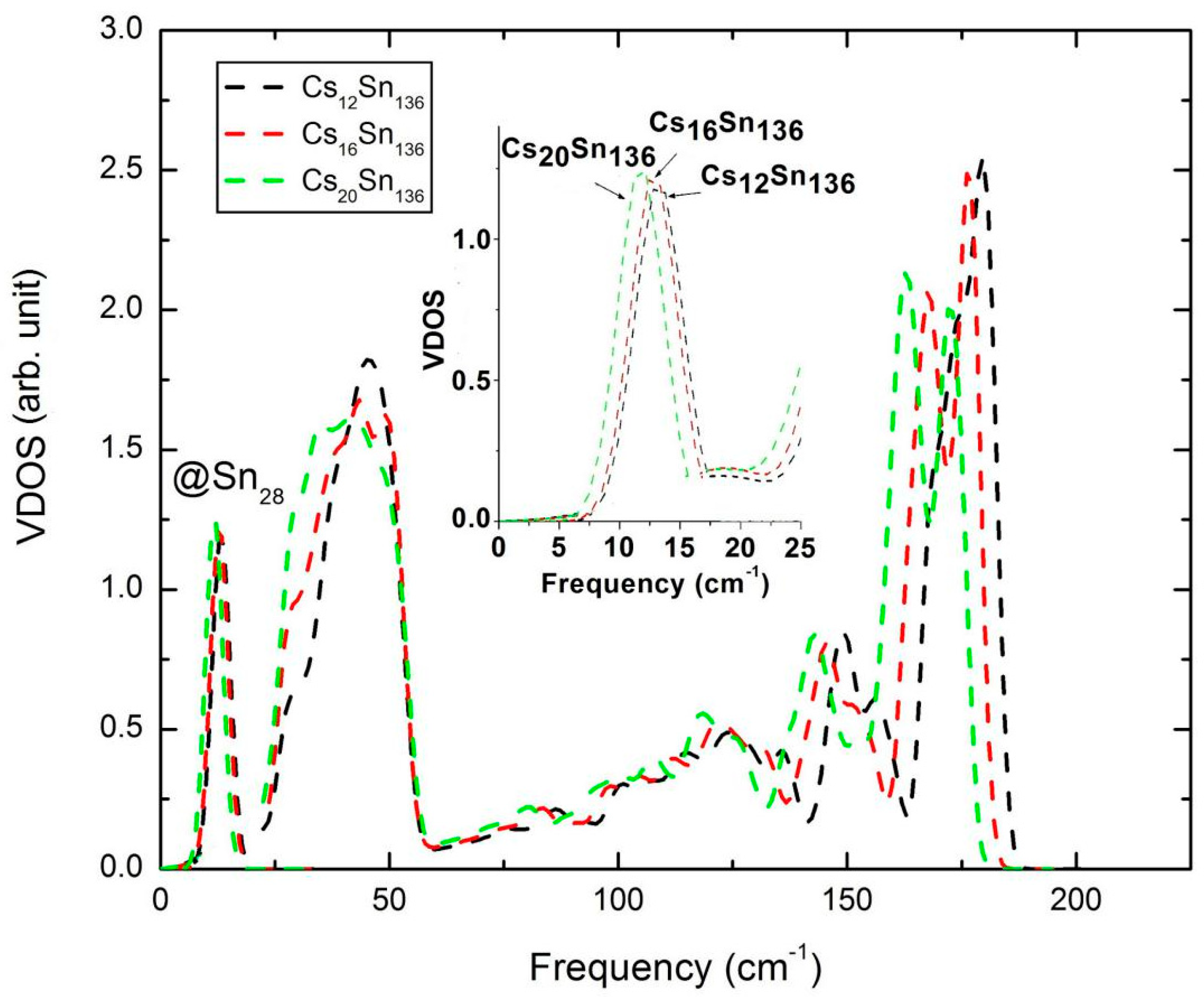
2.1. Structural Property of A_xSn₁₃₆ (0 ≤ x ≤ 24; A = Na, K, Cs) and Vibrational Property of Cs_xSn₁₃₆ (x = 12, 16, 20)

It is necessary to point out that the binary clathrate system studied here possesses a face centered cubic (FCC) Type-II structure, for which the group notation reads No. 227, Fd3m. Accordingly, the chemical stoichiometry of the framework sites, along with the guest impurity, is manifested by the notation A_xSn₁₃₆. Two classes of polyhedron cages form the building blocks inside the Sn136 framework: Sn₂₈ and Sn₂₀ cages, whose voids are connected periodically with a 2:4 ratio. These two different sized cages that contain 28 and 20 atoms are also termed hexakaidecahedron and dodecahedron cages, respectively. For the geometry optimization process, we need to point out that the starting atomic coordinate for each atom in the primitive unit cell is a specified “guess”, indicating that it is not identical, but very close, to the perfect value, according to the definition of “Ab initio” first-principle computation. Thus, we chose the atomic coordinates that were derived from our previous research work coping with Sn₁₃₆ [17]. Furthermore, on the basis of pure Sn₁₃₆ framework coordinates, we make sure that the added Cs guest impurities go to the specified Wyckoff sites—for instance, 8b and 16c, in a given integer amount. In other words, it depends on how many integer numbers of Cs atoms occupy either the small cage (16c site) or the oversized cage (8b site). It seems necessary to mention that the large cages are always filled in the very high priority, meaning that the small cage begins to accommodate the Cs guest until all of the 28 atom cages are completely occupied.

Previous X-ray diffraction (XRD) work along with our VASP calculation [27] on A_xSi₁₃₆ reported that, as x increases, the lattice contracts for 0 < x < 8 and expands for 8 < x < 24. However, changing all silicon framework atoms into tin in A_xSi₁₃₆ results in no lattice contraction, according to our calculations. In other words, the lattice configuration for Sn-based clathrates experiences monotonically increasing behavior if the composition x, which spans over the range of 0 and 24, is elevated from the lower limit. The following figure illustrates our theoretical predictions on the composition-dependent lattice constant, in the context of the fact that the rattler is tuned from Na to K to Cs.

As seen from the numerical results in Figure 1, our predicted lattice constant, as a function of composition x, is 17.38 Å for Na₈Sn₁₃₆, 17.43 Å for K₈Sn₁₃₆, and 17.44 Å for Cs₈Sn₁₃₆. Considering the case x = 24 where all cages are completely occupied by guest impurities, the predicted lattice constants are distinct and given by 17.51 Å for Na₂₄Sn₁₃₆, 17.64 Å for K₂₄Sn₁₃₆, and 17.90 Å for Cs₂₄Sn₁₃₆. The result of the pure Sn₁₃₆ gives rise to 17.34 Å for the lattice constant when x equals zero. Figure 2 shows the predicted vibrational spectrum of the Cs_xSn₁₃₆ (x = 12, 16, 20) clathrate materials.

It is clearly seen from Figure 2 that the low-lying vibrational modes, with respect to Cs motion in Sn₂₈ cages (written as “Cs@Sn₂₈” in the figure), remain in the range of 11.5–12.5 cm⁻¹ for the three clathrates. The frequency of the tops of these optic bands relating to the Cs guest seems to decrease in a slight manner, as composition x is increased from 12 to 16 to 20. Besides this, the acoustic bands are located within the range of 0–25 cm⁻¹ while exhibiting little variation. In other words, the acoustic bandwidths in Cs_xSn₁₃₆ (x = 12, 16, 20) are nearly unchanged, leading them to be independent of their guest concentration x.

The vibrational density of states (VDOS) obtained below (Figure 3) is shown to demonstrate the interesting features of the “rattling” modes (the top of entire optic band and the densely flat optic modes (right above the acoustic bands) in Figure 2). As seen from the low-frequency (about 5–20 cm⁻¹) picture of VDOS, the compounds Cs_xSn₁₃₆ are intriguing because of the existence of “rattler” vibrational modes (shown by the peaks), due to the Cs motion in the “over-sized” cage. More precisely, introducing the Cs impurities into the 28 atom framework cages can produce the “rattling” vibrational modes. These predicted VDOS curves are presented with respect to Cs_xSn₁₃₆, for x = 12, 16, and 20. The inset figure intricately illustrates how these Cs “rattling” modes are remarkably identified by the thin peaks centered around 12 cm⁻¹. An extremely slight decreasing behavior subjected to the Cs mode frequency (peak value) can be captured, as the number of guests who occupy Sn₂₀ cages is elevated from 4 to 8 to 12. This result is gained on the basis of enlarged unit cell geometry (containing 136 atoms), assuming all Sn₂₈ cages are completely occupied. Furthermore, the “red-shift” of phonon vibrational frequency is clearly illustrated when paying attention to the top of the densely flat optic band (within the range of 25 and 50 cm⁻¹). Accordingly, there appears to be a reduction of the entire optic band’s maximum (located right below about 190 cm⁻¹) with the elevated composition x. Specifically, the “red-shift” of the top of the entire optic band occurring at about 180 cm⁻¹ is obtained for Cs₂₀Sn₁₃₆, in contrast to that of Cs₁₆Sn₁₃₆ (at about 183 cm⁻¹) and Cs₁₂Sn₁₃₆ (at about 186 cm⁻¹).

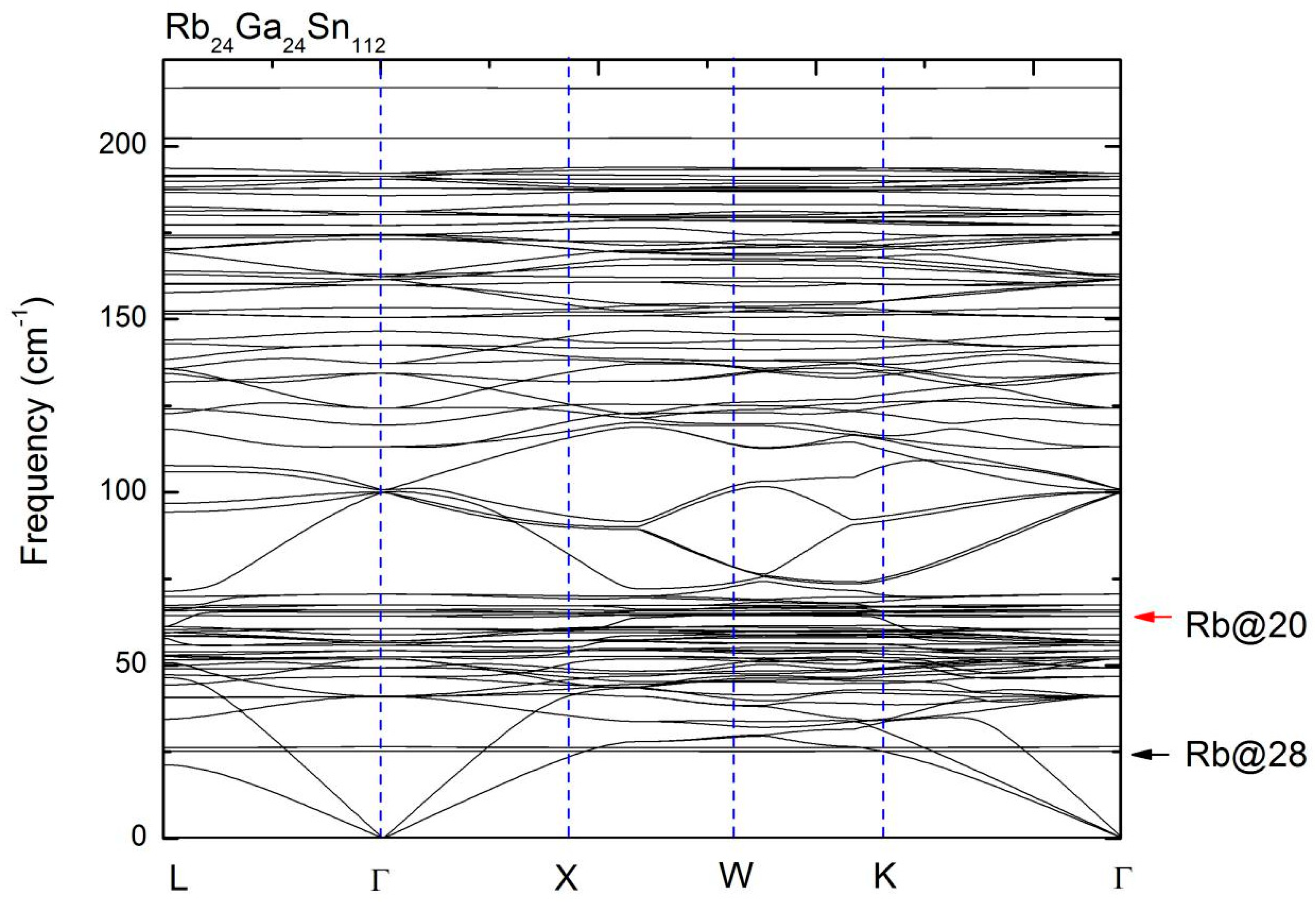
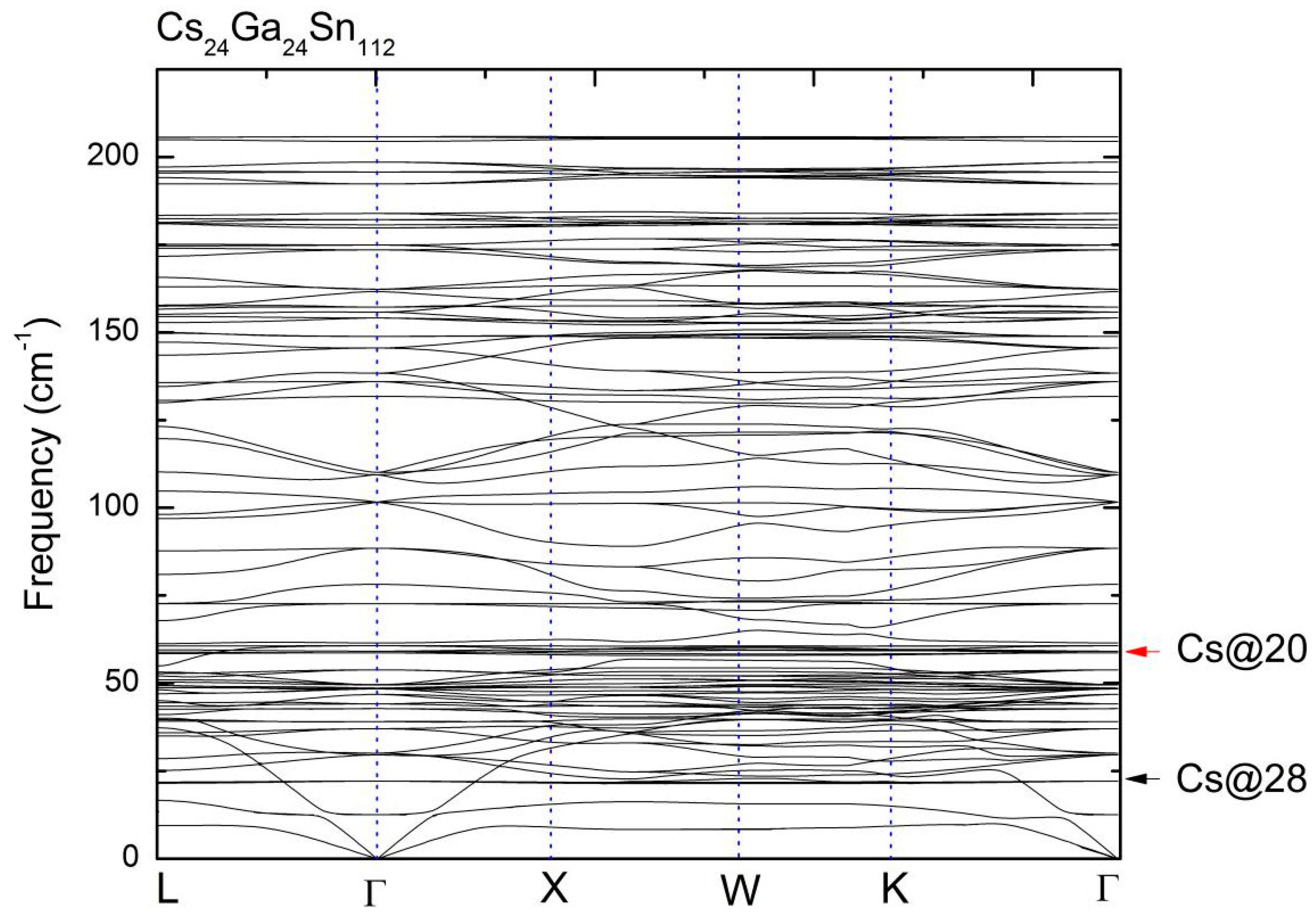
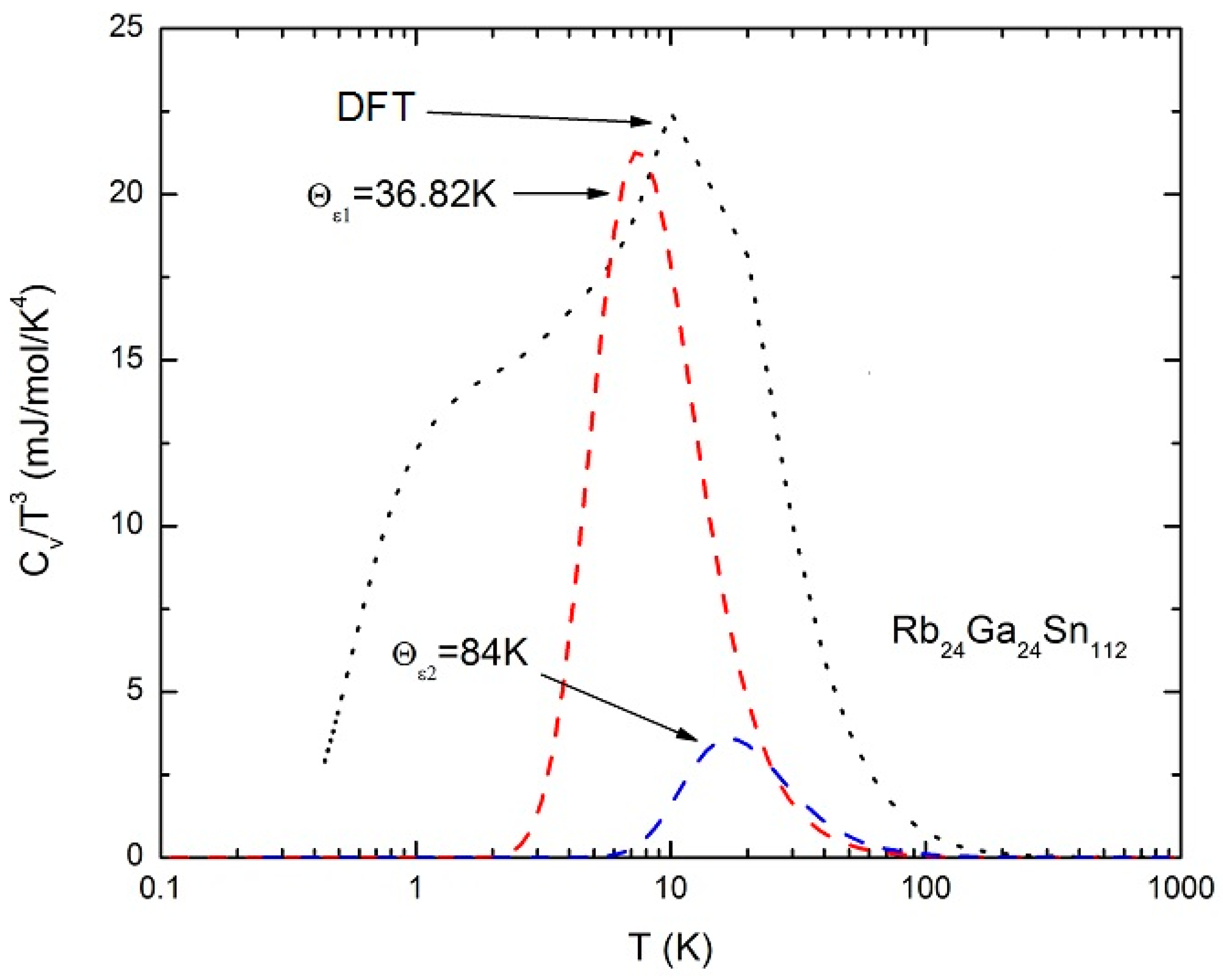
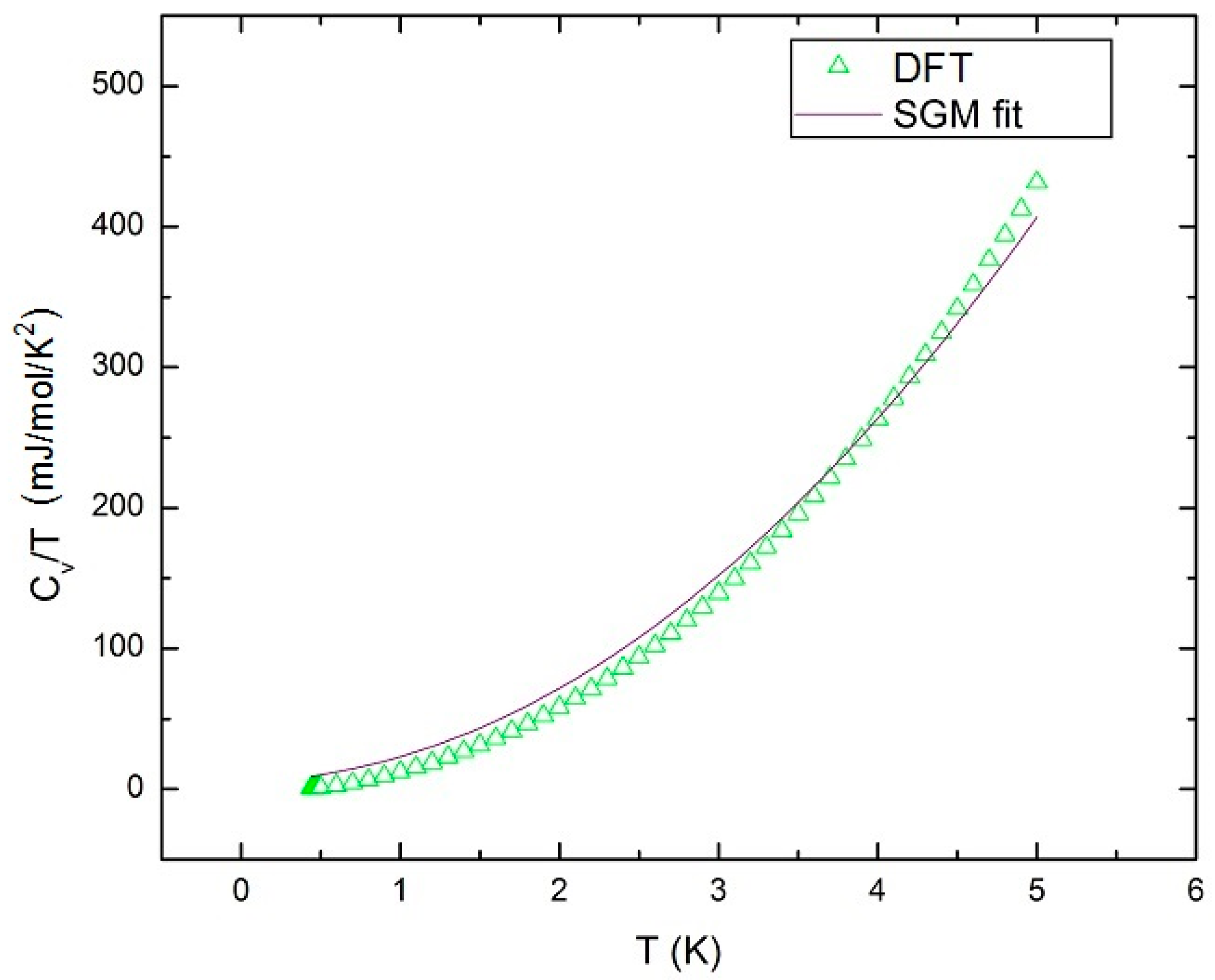
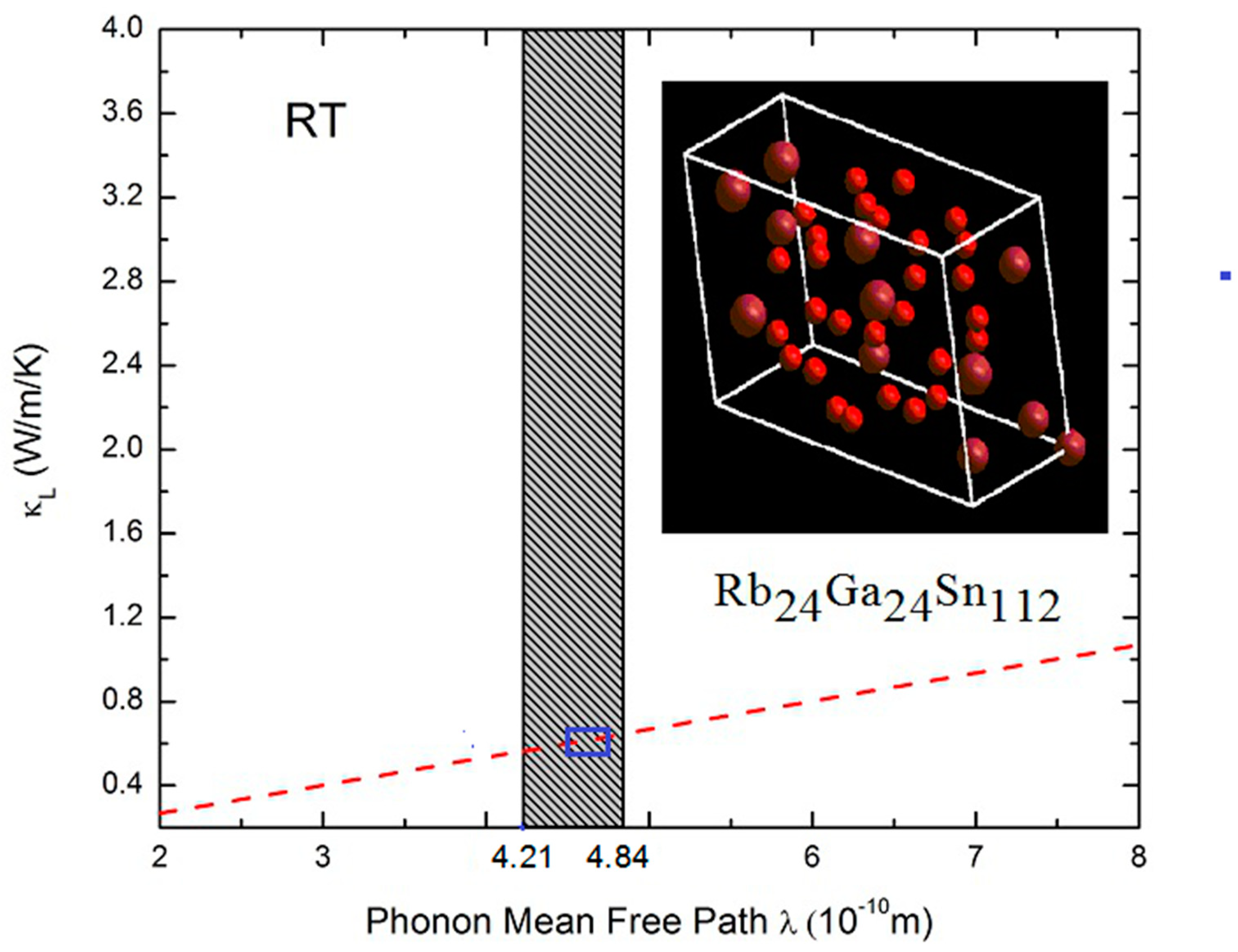
2.2. Vibrtional and Thermal Properties of Rb₂₄Ga₂₄Sn₁₁₂ and Cs₂₄Ga₂₄Sn₁₁₂

The crystal structure for the framework of the clathrate-II system is explained in the way that the [512614] and [512] polyhedron cages alternate with a 1:2 ratio, generally. For our studied material, Rb₂₄Ga₂₄Sn₁₁₂, its stoichiometry can be associated with Type-II semiconducting clathrate due to the “Zintl-phase” concept, which was named after Edward Zintl who pioneered their investigation on the classical NaTl material [28]. It is theoretically noted that each constituent of this ternary compound attains a closed s³p¹ valence shell by establishing a required charge transfer with covalent bonds. The charge compensation is achieved between the substitutional cage atoms (Ga) and guest impurities (Rb). In other words, the Rb atoms donate twenty-four electrons to the host so that the octet rule for the twenty-four Ga atoms is satisfied in terms of Rb₂₄Ga₂₄Sn₁₁₂. All framework bonds are, therefore, saturated. Additionally, the covalent configuration demonstrating sp³ coordination makes it possible to form zeolite-like expanded volume phases in an open framework given by Ga₂₄Sn₁₁₂. This four-fold-coordinated system possesses a local bonding picture, which remains similar to that of the diamond phase structure (e.g., α-Sn).

In order to explore the effect of the encapsulated Rb rattler on the cages of the open framework Ga₂₄Sn₁₁₂ in our study, we show the vibrational dispersion curves for Rb₂₄Ga₂₄Sn₁₁₂ and Cs₂₄Ga₂₄Sn₁₁₂ in Figure 4 and Figure 5. Our eigenvector analysis shows that the acoustic phonon region (below about 45 cm⁻¹) contains flat Rb-associated phonon bands lying around 25 cm⁻¹. Accordingly, the optic mode region ranges from about 45 cm⁻¹ to about 220 cm⁻¹. The average value of the “localized”, flat, vibrational modes of Rb is used to characterize the guest, which is loosely confined in a 28 atom cage (“over-sized” cage), leading to a comparably small effective force constant (ϕ). Here, the vibrational frequency ω is given by ω = (ϕ/m)^1/2, where m can be numerically replaced by the atomic mass of Rb (85.47 a.u). Contrary to this, the Rb guest, which is strongly bound to the small 20 atom cage, results in a vibrational frequency that is labeled by the red arrow (showing about 65.4 cm⁻¹ in Figure 4). The discussed modes of Rb in the 28 and 20 atom cages are indicated by the notation “Rb@28” along with “Rb@20”. The downshift of the labeled frequency is expected to arise from the comparably large cage size of the 28 atom cage, in contrast to that of the 20 atom cage.

In contrast to vibrational property found in Figure 4, we illustrate the dispersion relation of Cs₂₄Ga₂₄Sn₁₁₂ in the following figure after conducting the DFT calculation. As seen from Figure 5, the Cs-associated phonon bands lying around 22 cm⁻¹ denote the localized, flat, optic phonons. This means that the Cs guest vibration restricted within the 28 atom cage produces a slightly smaller “rattling” frequency than that of Rb guest mode in Rb₂₄Ga₂₄Sn₁₁₂. Similar to the result in Figure 4, the Cs guest, which is strongly bound in the 20 atom cage, relates to the vibrational mode, leading to a value of about 55 cm⁻¹, labeled by the red arrow. Considering the relation ω = (ϕ/m)^1/2 while taking the Rb mass (85.47 a.u) and Cs mass (132.91 a.u.) into account, the calculated force constant ratio of Rb to Cs yields (85.47² × 25)/(132.91² × 22) ≈ 0.47. Therefore, the Rb seems to be loosely bound with respect to the 28 atom cage when compared to the Cs resonant vibration with the 28 atom cage in Cs₂₄Ga₂₄Sn₁₁₂.

In Figure 6, we present our calculated isotropic atomic displacement parameters (ADPs) for the Rb “rattler”, which is localized to vibrate in the 20 and 28 atom cages. This work is done after we have theoretically determined the vibration mode of Rb from lattice dynamics computation, using the LDA scheme. Our work was originally motivated by the temperature-dependent isotropic mean-square displacement (U_iso), defined as U_iso = (h/(8π²mv))coth(hv/(2k_BT)). This defined parameter evaluates displaced distance for an atom that deviates from its equilibrium position. From the numerical definition, v denotes the vibrational frequency, m represents the reduced mass of the oscillator, h is Plank’s constant, and k_B is Boltzmann’s constant. Combined with the high-temperature approximation (hω/2π << k_BT; ω ≡ 2πv), we use k_BT/ϕ to estimate U_iso according to the relation ϕ ≡ mω². In Figure 6, the temperature variable is restricted to the range of 0 and 400 K. Meanwhile, the notations Rb(1) and Rb(2) represent the guest rattlers confined in the 28 atom and 20 atom cages, respectively. The results show that U_iso parameters for the Rb atoms in the 28 atom cages are larger than those for the same “rattlers” confined within the Sn₂₀ polyhedron cages. These calculations can be compared, to some extent, to the old investigations on U_iso of Rb in Na₁₆Rb₈Ge₁₃₆ [29], as well as U_iso of Rb in Na₁₆Rb₈Si₁₃₆ [30].

In addition, the slope of each curve of ADPs vs. T predicts a different magnitude of the “rattler”’s oscillator strength. Weak bonding gives rise to a small ϕ, as found in the inverse of the slope of curve (with notation “Rb(1)”) in Figure 6. The Rb impurity vibrating inside the 28 atom cage induces the smallest ϕ compared to the same “rattler”’s motion in the 20 atom cage. Similar results can be linked to the powder XRD and single-crystal XRD data regarding the calculated ϕ at room temperature (RT) in the case of Na₂₄Si₁₃₆ [31]. Other similar results reported elsewhere relate to the Type-I clathrates [32,33,34] and skutterudites [35,36].

Before determining the heat capacity within the framework of harmonic approximation (HA), the temperature-dependent Helmholtz free energy F is identified as F(T) = k_BT∑_q∑_j In {2sinh(hω_j(q)/4πk_BT)}, where k_B is Boltzmann’s constant and h is Planck’s constant. ω_j(q) remains to be the jth-phonon mode frequency. It was realized that we should ignore the volume-dependent static contribution to the internal energy acquired by LDA because we solely care about the temperature derivative with respect to free energy. Consequently, using the same HA scheme, we theoretically obtain the specific heat at a constant volume of C_v = −T(ə²F(T)/ə²T)_V, in the context of the first-principles determination on the eigenenergy of each phonon mode. According to this introduced method to compute the specific heat, the following Figure 7 gives rise to our predicted Cv(T) for Rb₂₄Ga₂₄Sn₁₁₂ and Cs₂₄Ga₂₄Sn₁₁₂. Values for the heat capacity of Rb₂₄Ga₂₄Sn₁₁₂ are always smaller than those of Cs₂₄Ga₂₄Sn₁₁₂, when the temperature roughly satisfies the condition 100 K < T ≤ 1000 K.

The atomic vibrations of guest atoms produce glass-like low-lying modes, accounting for the “hump” found in the temperature-dependent specific heat profile. Typically, such excess specific heats due to guest “rattling” can be associated with the peak occurring in a temperature range whose center is normally 10–100 times smaller than the Debye temperature [37]. Previous reports identified the characteristic humps that were determined around T ~ 5 K, in the case of Type-I β-Rb₈Ga₁₆Sn₃₀ (β-RGS) and Type-I Sr₈Ga₁₆Ge₃₀ [38,39,40,41,42,43] compounds. Our computational work presents this form of hump in the Type-II Rb₂₄Ga₂₄Sn₁₁₂ clathrate, owing primarily to two sorts of isotropic Einstein oscillators that originate from the 28 atom and 20 atom cages, respectively. Making use of the definition of specific heat regarding the Einstein solid, we realize that the characteristic temperature of the Rb oscillator encapsulated in the 28 atom cage is calculated to be θ_E1 = 36.82 K, while the characteristic temperature of the Rb oscillator trapped in the 20 atom cage is θ_E2 = 84.00 K.

Besides the isotropic ADP study in Figure 6, we have found that excess specific heat results can be attributed to the introduced isotropic Einstein oscillators. Consequently, three characteristic temperature regions in Figure 8 might be of great interest. Initially, the low-T (<6 K) behavior of C_V(T) is numerically governed by the relation [44,45,46]: C_V(T) ≈ αT^1+δ + βT³. The usage of the three coefficients, α, β, δ, will be discussed later. Second, excess specific heat at about T ~ 10 K is thought to correlate with the “rattling” modes in the presence of guest vibration in Sn₂₀ and Sn₂₈ cages. This excess hump in the C_V/T³ curve is characterized to remain nearly identical to the Einstein peaks. The third temperature-regime is the one for which C_V(T) approaches a vanishingly small magnitude above about 70 K. Additional intriguing thermal properties involving inspection of the lattice dynamics quantity C_P(T) − C_V(T) = KTVα² agree with the previous work [47,48], while C_P(T) pertains to the heat capacity at a constant pressure. Here, K is the bulk modulus and α denotes the volume coefficient of thermal expansion.

It is necessary to point out that the thermal influence of C_V(T) arising from conduction electrons is neglected for Rb₂₄Ga₂₄Sn₁₁₂ in our computation. In Figure 8, DFT data (black dotted line) plotted as C_V(T)/T³ vs. T show a remarkable hump appearing around T ~ 10 K. This observed unusual peak was simulated by displaying the C_V(T) calculated from encapsulated “rattlers”, according to the theory of the isotropic Einstein oscillator. Therefore, our work, shown by the red dashed and blue dashed curves, was deduced via the fitting parameters given by the characteristic temperature of the Einstein oscillator (θ_E1, θ_E2) and the number of oscillators (N_E1, N_E2)). Here, the obtained parameters were N_E1 = 2 guest oscillators in 28 atom cages and N_E2 = 4 rattler oscillators inside 20 atom cages of primitive unit cells (consisting of 34 atoms). Apparently, such excess specific heat is shown to be more heavily dependent on Rb vibration in the hexakaidecahedron, rather than dodecahedron, cage.

Figure 9 shows the low-T (<6 K) specific heat (green triangle from DFT calculation) fitted by the theoretical relation: C_V(T) ≈ αT^1+δ + βT³. This scaled form of C_V(T) was initially proposed by Zeller and Pohl [44], who focused on silica glass. Here, we note that the deviation from a linear dependence on temperature of the first term (αT^1+δ) is given by a power exponent increment, δ. However, αT^1+δ has no connection with the specific heat contributed by the conduction electron, γT. Therefore, our first-principle generated C_V(T) was fitted by taking the pristine silica glass model (SGM) into account. Then, the fitting process lead to α ≈ 7.075 mJ·mol⁻¹·K⁻², β ≈ 15.886 mJ·mol⁻¹·K⁻⁴ along with the small exponential factor determined as δ ≈ 0.21. As a whole, our predicted values (α, β parameters) were relatively small when compared to the measurement of Type-I Ba₆Ga₁₆Sn₃₀ (β-BGS) showing α ≈ 30 mJ·mol⁻¹·K⁻², β ≈ 50 mJ·mol⁻¹·K⁻⁴ and δ ≈ 0.20 [41,42].

Figure 10 displays the evaluated lattice’s thermal conductivity κ_L for Rb₂₄Ga₂₄Sn₁₁₂ in terms of the guest–host distance, which is approximated as the phonon’s mean free path. Using the average value for a range of mean free paths, our computation was guided by the simple kinetic model κ_L = (1/3)C_Vv_sλ, which yields 0.25 W/m/K ≤ κ_L ≤ 1.08 W/m/K in the vicinity of room temperature when the mean free path spans over the range of 2 and 8 Å. It is mentioned that λ is the average mean free path while vs. manifests the sound speed of acoustic phonon bands. On the other hand, previous work predicted a κ_L of the Type-I tin-containing compound K₈Al₈Sn₃₈, which turned out to be 1.2 W/m/K [49]. In our work, λ has been approximated as a covalent-like Rb–Sn bond whose length ranges from 4.56 Å to 4.76 Å in terms of the DFT computation. The small box (formed by blue solid lines) in the shaded area of Figure 10 represents the coverage of the possible bond length range (4.56 Å < λ < 4.76 Å). Therefore, the correct range of lattice thermal conductivity should be κ_L(λ = 4.56 Å) ≈ 0.60 W/m/K < κ_L < κ_L(λ = 4.76 Å) ≈ 0.64 W/m/K. It is also expected that the formation of those covalent-like Rb–Sn bonds links to the coupling of the Rb “rattling” modes with host framework vibrations. On the whole, our predicted κ_L at RT seems to be around 0.62 W/m/K for Rb₂₄Ga₂₄Sn₁₁₂. Previous work reports the figure of merit of Type-I β-Ba₈Ga₁₆Sn₃₀ (abbreviated as β-BGS) to be smaller than 0.6 [41]. Meanwhile, the lattice thermal conductivity of this β-BGS remains between 0.6 and 0.7 W/K/m at T = 150 K, approximately. According to our DFT-calculated heat capacity in Figure 7, we found that the C_V at T = 150 K for Rb₂₄Ga₂₄Sn₁₁₂ is about half as much as the value at T = 300 K. Assuming the existence of a temperature-independent phonon mean free path and the sound velocity of acoustic phonons, we concluded that the lattice thermal conductivity at T = 150 K is nearly half as much as the value at T = 300 K, in the context of Rb₂₄Ga₂₄Sn₁₁₂. Therefore, our predicted κ_L at T = 150 K is about equal to 0.31 W/K·m. Considering that the figure of merit is approximately proportional to the inverse of the lattice’s thermal conductivity while taking the negligible impact from the Seeback coefficient, electrical conductivity, and electronic thermal conductivity into account, the lower lattice thermal conductivity always indicates a larger ZT value. Consequently, Rb₂₄Ga₂₄Sn₁₁₂ shows better thermoelectric performance when compared to the β-Ba₈Ga₁₆Sn₃₀ and several other Sn-based clathrate compounds, including Type-VIII Ba₈Ga₁₆Sn₃₀, or Type-I n-type (or p-type) Ba₈Ga₁₆Sn₃₀ [40,41,50].

3. Computational Approach

Utilizing first-principles code named the Vienna ab initio simulation package (VASP) [51], we performed our research work to study the structural and vibrational properties of Sn-based Type-II clathrate compounds. Normally, the entire computation process makes use of ultra-soft pesudopotential (US-PP) [52,53] or generalized gradient approximation (GGA) PW91 to describe the correlation found between electron and ion cores, as well as the functional exchange-correlation, with respect to electrons. In contrast to these formalisms, our study is based on an ab initio density functional planewave method, which relies on local density approximation (LDA) and density functional theory (DFT). Additionally, the Celperly-Alder functional [54] is used to explain electron correlation effects and the electron exchange-correlation energy. This technique has been tested a few times on various clathrate systems [30,55,56,57], in order to ensure the accuracy of computational results while achieving a reduced time load for calculation. The cutoff-energy of the plane-wave basis is selected to be 300 eV, when the 4 × 4 × 4 Monkhorst-pack k-point grid [58] confined within the first Brillouin zone (BZ) is used to establish the cutting grid for acquiring the structural features. The detailed pseudopotential contains information on the valence electrons of the tin framework atom (denoted by 5s²5p²), while the rest of the electrons in the Sn atom are treated as core electrons. Similarly, the valence electron configurations of Cs and Rb, as well as the Ga atom, read 5p⁶6s¹, 4p⁶5s¹, and 4s²4p¹.

To determine the optimized configuration, a fixed unit cell volume is selected at the beginning. Next, optimizing the ionic positions is done by minimizing the total binding energy with a conjugate gradient (CG) algorithm that uses atomic forces. This energy minimization process is repeated for a range of unit cell volumes, from which an equation of state (EOS) [59] and an equilibrium state configuration possessing the least energy can be established. Then, the internal coordinates are optimized at the minimum energy configuration. Once the equilibrium geometry has been fully gained, knowledge of the structural parameters corresponding to the minimum energy state can guide us to continuously explore the volume-dependent binding energy, the lattice constant, the dispersion relationships, and the heat capacity trends in a quantitative manner. For binary Cs_xSn₁₃₆ (0 ≤ x ≤ 24) and ternary Rb₂₄Ga₂₄Sn₁₁₂, the LDA-determined energy vs. volume curve, which arises from the above procedure, has been fit with the Birch-Murnaghan EOS. This fitting process determines the minimum binding energy E₀, the volume V₀ at optimized geometry, the equilibrium bulk modulus K₀, and the pressure (P) derivative of K₀ written as dK₀/dP.

It is noticed that three inequilibrium sites exist for framework atoms that seek stable locations, namely, 8a, 32e and 96g. It is also known that selecting a different number of Group-III atom (e.g., Ga) that occupy some places in these Wyckoff positions may have an impact on tuning the physical properties of those Sn-based ternary clathrates. Generally, the balance between the number of excess electrons resulting from alkaline atoms and the number of compensation donors arising from Ga atoms needs to be carefully considered, when taking the “semiconducting compound” idea into account.

According to harmonic approximation, the diagonalization process applied to the wavevector (q)-dependent dynamic matrix D(q) produces eigenvalues for vibrational modes, including acoustic phonons and optic ones. Determination of the dynamic matrix needs a second derivative of the LDA-binding energy with respect to atomic displacement. Normally, we utilize the finite atomic displacement parameter U₀ to compute these forces, which linearly scale with the displacements. Both +U₀ and −U₀ variables are used to calculate D(q). Two wavevector-dependent phonon modes are examined before gaining a complete D(q) in the vicinity of the Γ point confined within the q-space. Firstly, D(q) is constructed at the gamma (Γ) point [q = (0,0,0)]. On the other hand, D(q) can still be calculated for nonzero wavevectors if we assumed that the matrix elements of D(q) vanish for atoms separated by a distance greater than the third nearest neighbor distance [60,61]. Additionally, group theory [17] has been used to reduce the computational effort when determining the energies and forces during structural optimization. It also reduces the effort of examining vibrational dispersion relationships. Considering the symmetries found with the 102 (3 × 34) Γ-point modes that exist in the Ga_xSn_136−x framework (x = 0, 24), 42 distinct frequencies that possess symmetries among them are of crucial importance.

4. Conclusions

Previously, theoretical investigations of the properties of the Type-II clathrate Cs_xSi₁₃₆ (0 < x ≤ 24) have found that, as the composition x increases, the Si₁₃₆ lattice exhibits framework contraction upon filling (0 < x ≤ 8), followed by an expansion of the unit cell volume (9 < x ≤ 24). However, tuning all the host atoms from Si to Sn cause no lattice contraction to occur according to our determination on composition-dependent lattice parameters in Cs_xSn₁₃₆ (0 < x ≤ 24). In addition to these geometry characteristics, the calculated behavior of the guest’s “rattling” phonon modes, along with the vibrational density of states in these materials, are also presented. Specifically, the determined frequency describing “localized” flat optic bands emerging from Cs guest seems to decrease in a slight manner as composition x is elevated from 12 to 16 to 20 from the viewpoint of dispersion relations. Meanwhile, an extremely slight decreasing behavior relating to the VDOS peak of Cs rattling modes is also captured as the number of guests who occupy Sn₂₀ cages is elevated from 4 to 8 to 12 in the presence of enlarged unit cell (136 atoms) geometry, assuming all Sn₂₈ cages are completely filled. In contrast to the predicted low-lying modes of guests appearing in a 28 atom cage of the Cs_xSn₁₃₆ (x = 12, 16, 20) system, an upshift of the low-lying optic modes (centered around 25 cm⁻¹) is found for vibration of the light guest (“rattler”) Rb in a 28 atom cage of Rb₂₄Ga₂₄Sn₁₁₂. It is also expected that the guest vibration in the “over-sized” cage is mainly responsible for effectively lowering the lattice’s thermal conductivity. This is due to the fact that the Einstein-peak-like hump arising from the C_V/T³ vs. T relation is shown to originate mainly from the contribution of the guest oscillator in a 28 atom cage rather than that in the 20 atom cage of Rb₂₄Ga₂₄Sn₁₁₂. Within the kinetic theory approximation, our lattice’s predicted thermal conductivity in Rb₂₄Ga₂₄Sn₁₁₂ is approximately equal to 0.62 W/m/K at room temperature.