Hydrogen-Bonding Assembly of Coordination Polymers Showing Reversible Dynamic Solid-State Structural Transformations
Abstract
1. Introduction
2. Results and Discussion
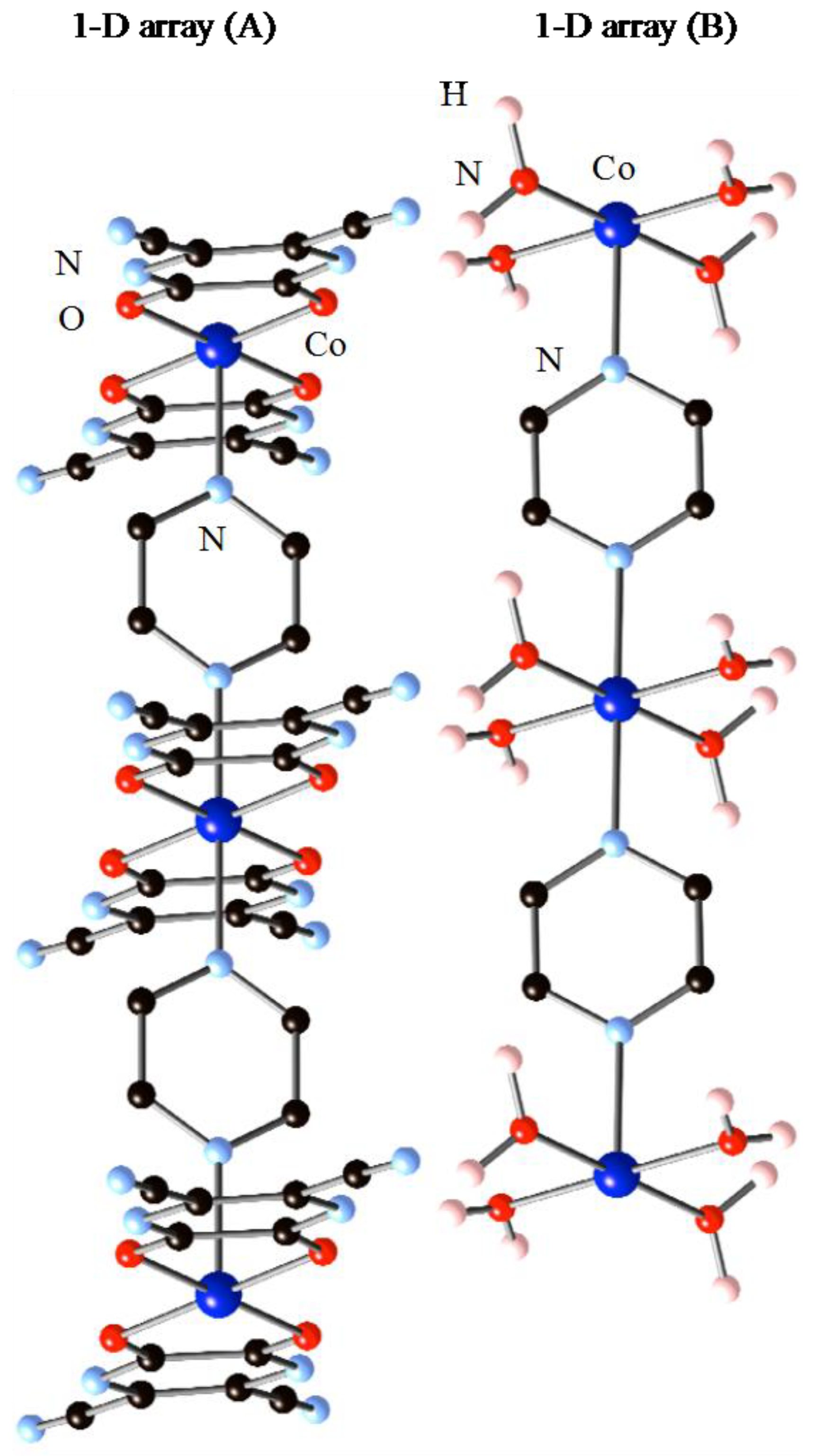
2.1. X-Ray Structures
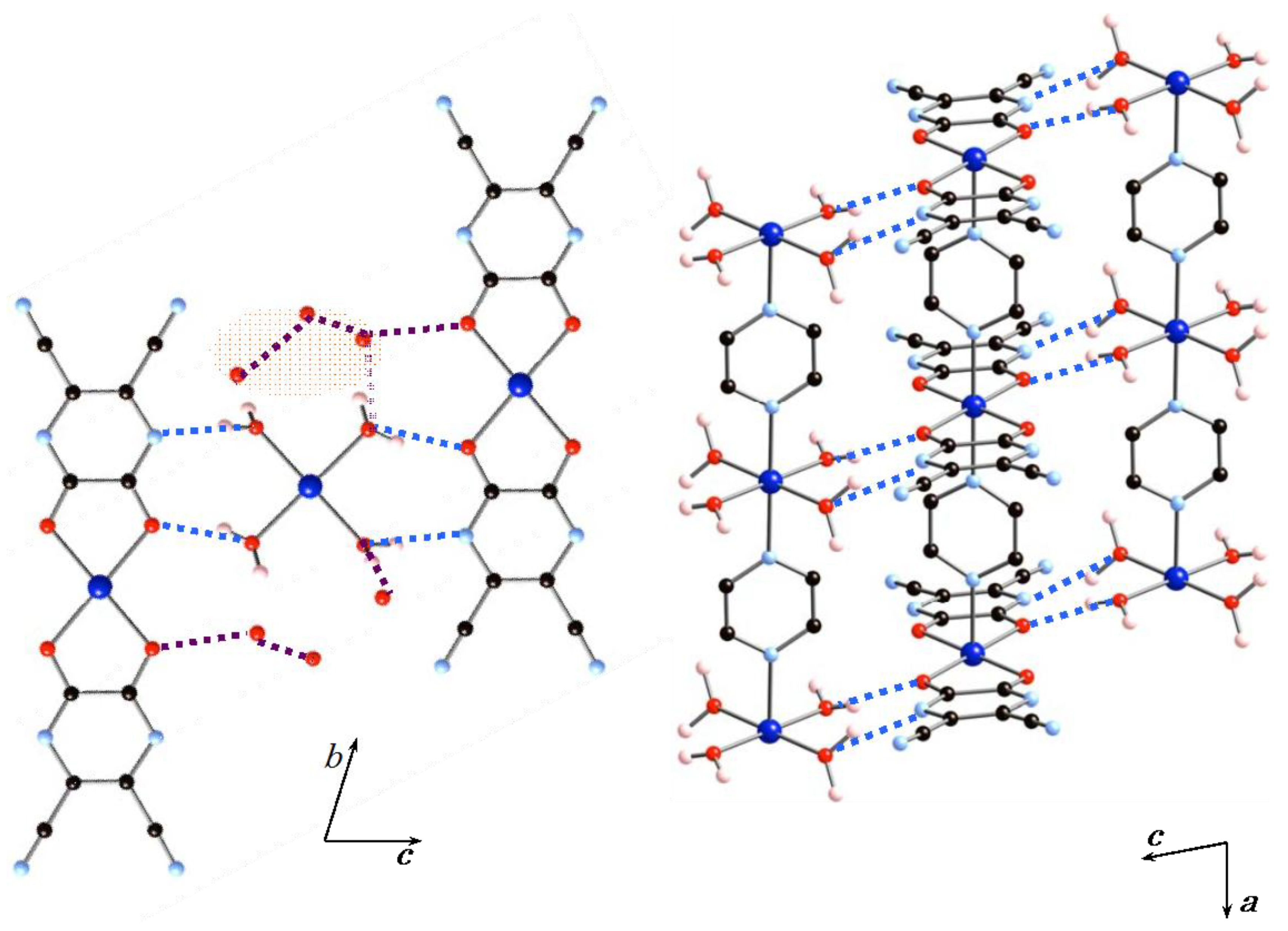
2.1.1. Structures of 1·10H2O and 2·10H2O
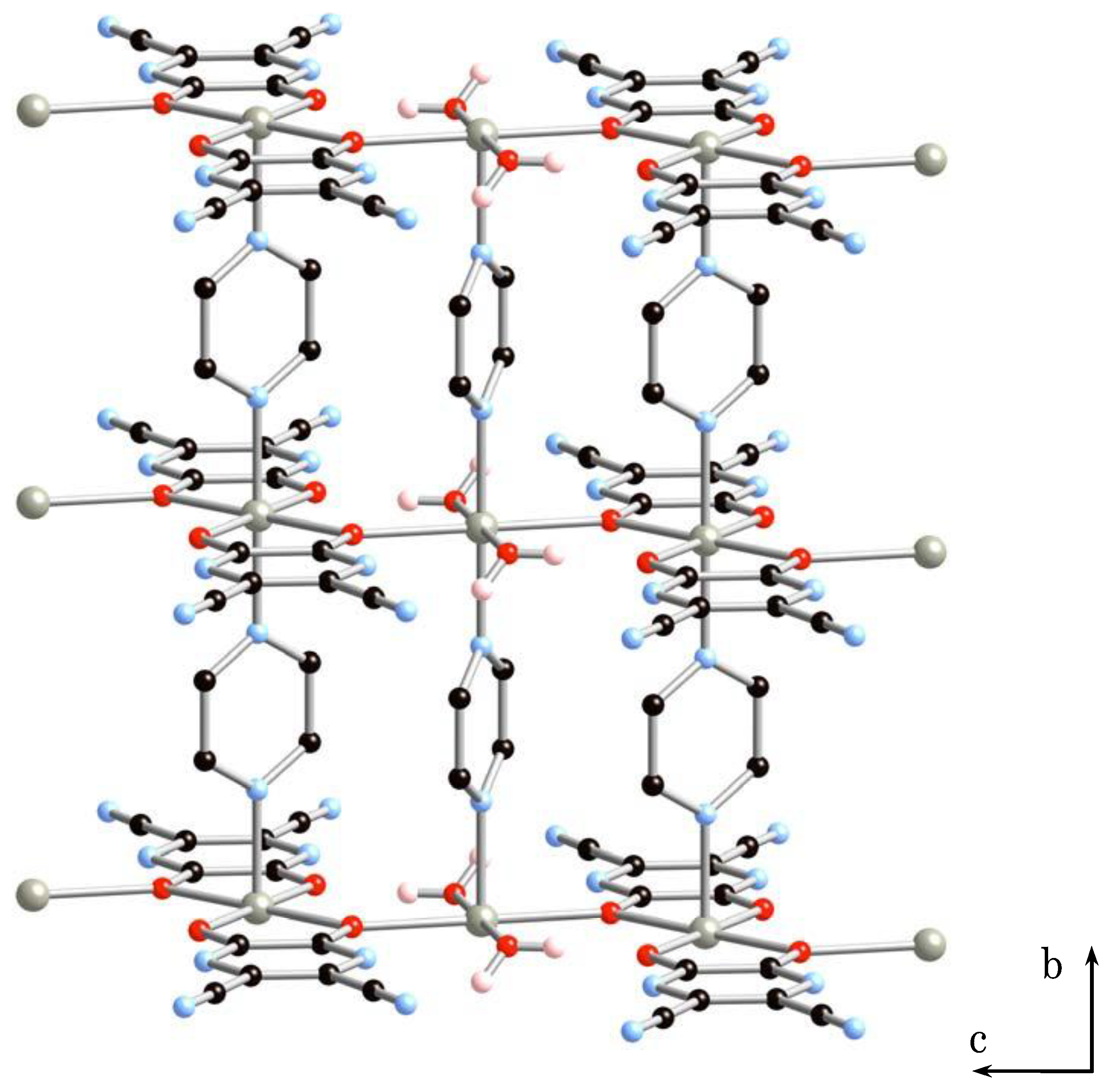
2.1.2. Structure of 2·2H2O
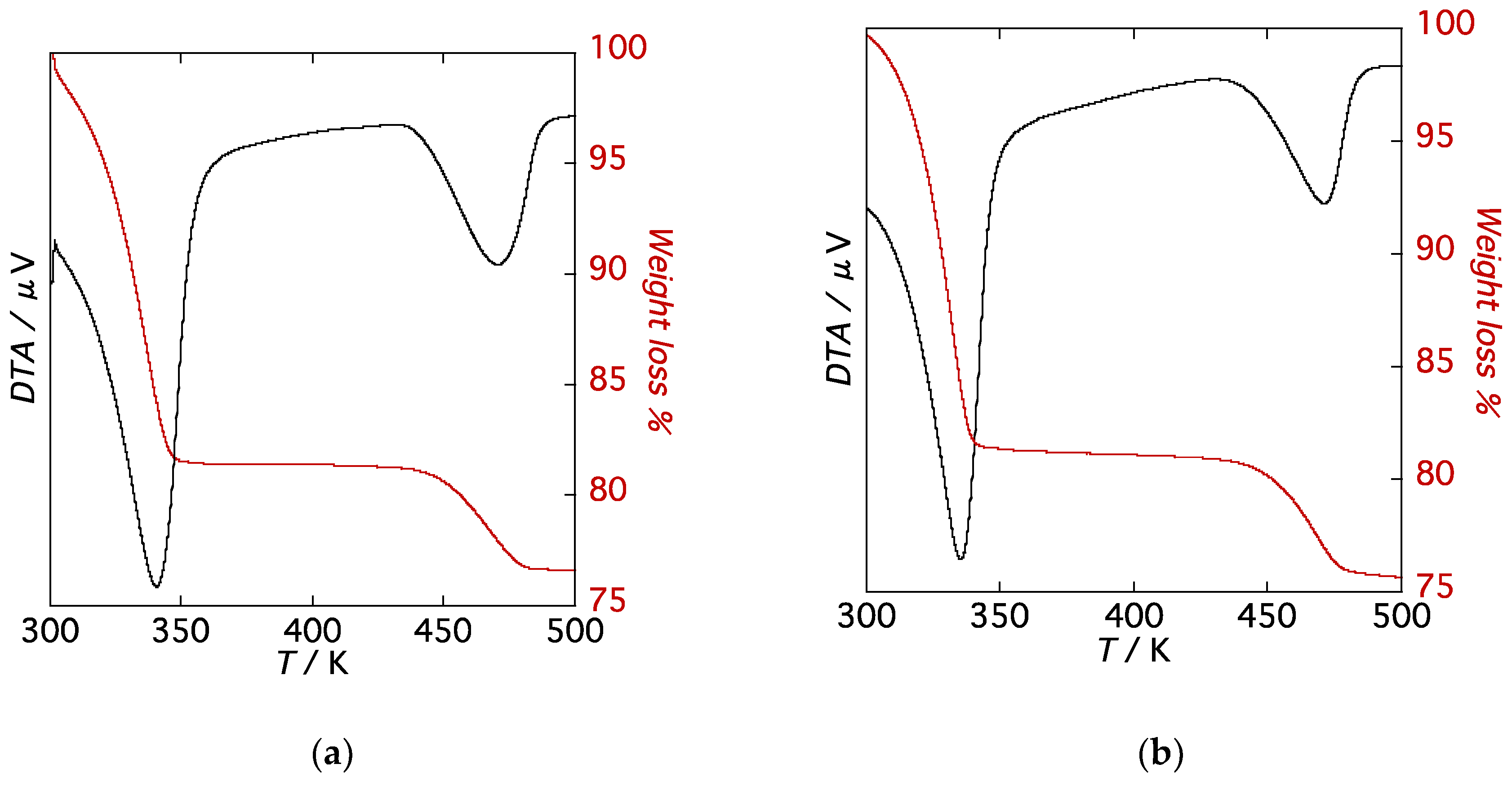
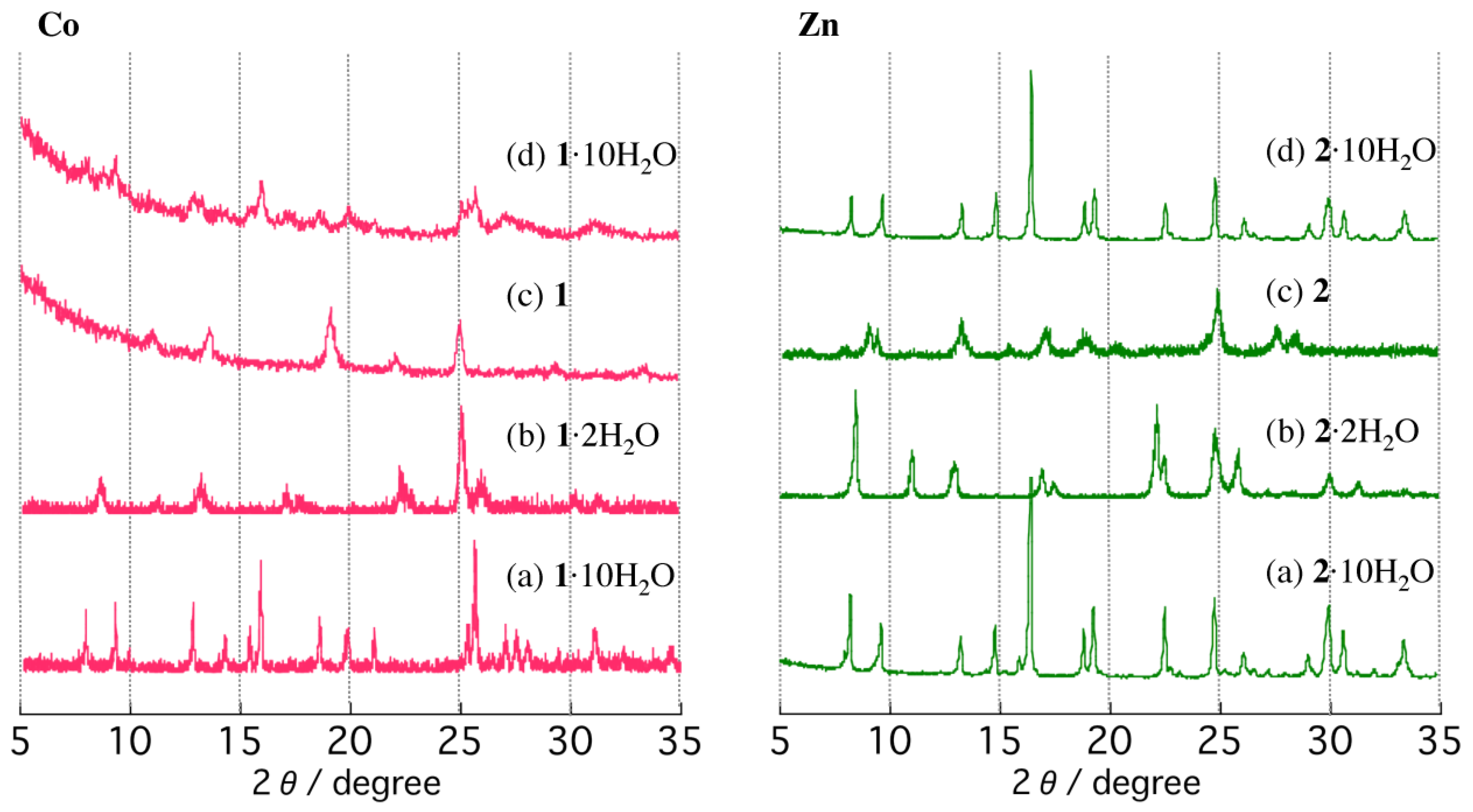
2.2. TGA and PXRD Measurements
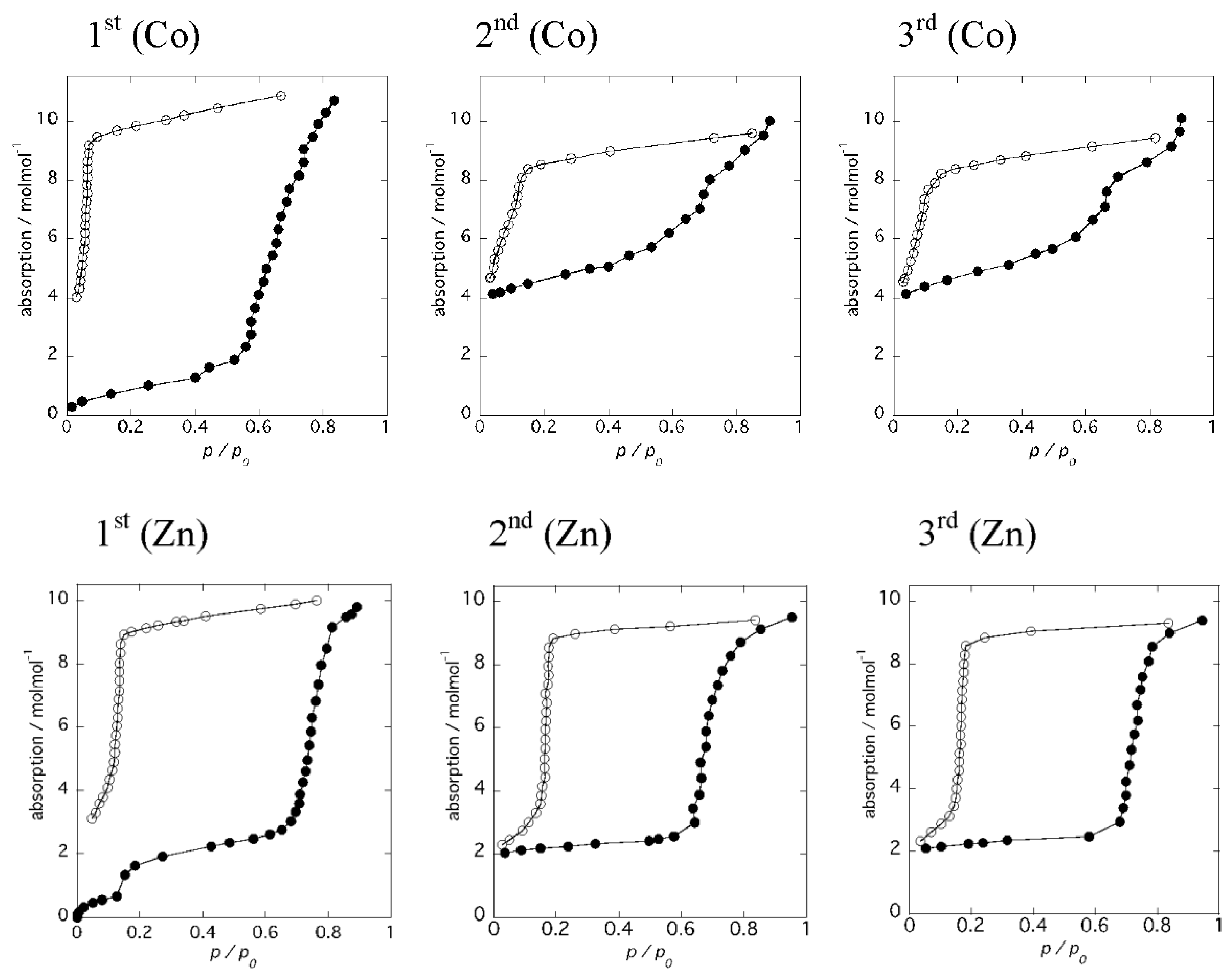
2.3. Reversible Dehydration-Rehydration and Structural Transformation
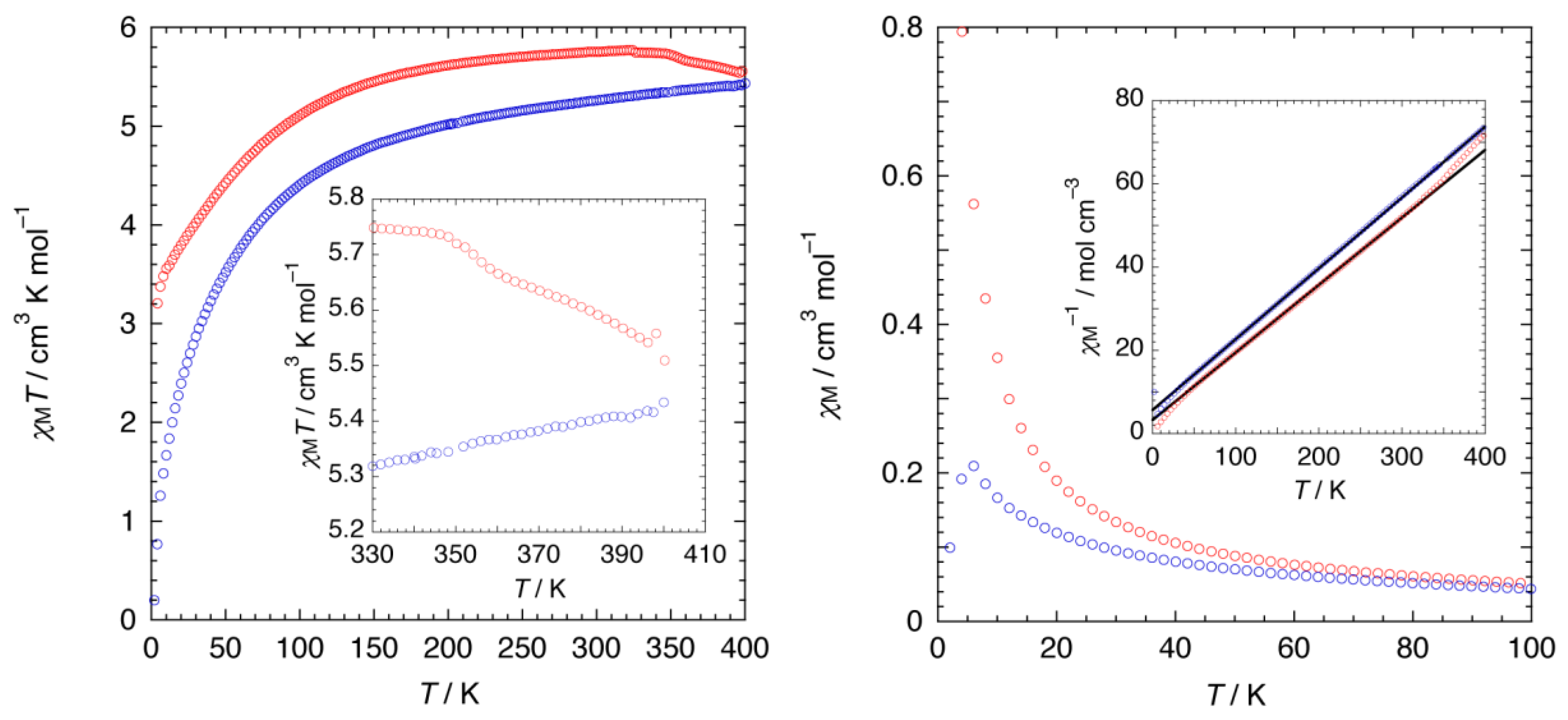
2.4. Magnetic Property
3. Experimental Section
3.1. Materials and Methods
3.2. Preparation of {[Co(H2O)4(pyz)][Co(tdpd)2(pyz)]·6(H2O)}n (1·10H2O)
3.3. Preparation of {[Zn(H2O)4(pyz)][Zn(tdpd)2(pyz)]·6(H2O)}n (2·10H2O) and Transformation to [Zn2(tdpd)2(H2O)2(pyz)]n (2·2H2O)
3.4. Single-Crystal X-Ray Diffraction Measurement and Structure Determination
3.5. Powder X-Ray Measurement and Structure Determination
3.6. Physical Measurements
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Wu, W.-P.; Li, Z.-S.; Liu, B.; Liu, P.; Xi, Z.-P.; Wang, Y.-Y. Double-Step CO2 Sorption and Guest-Induced Single-Crystal-to-Single-Crystal Transformation in a Flexible Porous Framework. Dalton Trans. 2015, 44, 10141–10145. [Google Scholar] [CrossRef] [PubMed]
- Ling, S.; Slater, B. Unusually Large Band Gap Changes in Breathing Metal–Organic Framework Materials. J. Phys. Chem. C 2015, 119, 16667–16677. [Google Scholar] [CrossRef]
- Han, J.; Nishihara, S.; Inoue, K.; Kurmoo, M. High Magnetic Hardness for the Canted Antiferromagnetic, Ferroelectric, and Ferroelastic Layered Perovskite-like (C2H5NH3)2[FeIICl4]. Inorg. Chem. 2015, 54, 2866–2874. [Google Scholar] [CrossRef] [PubMed]
- Kataoka, S.; Banerjee, S.; Kawai, A.; Kamimura, Y.; Choi, J.-C.; Kodaira, T.; Sato, K.; Endo, A. Layered Hybrid Perovskites with Micropores Created by Alkylammonium Functional Silsesquioxane Interlayers. J. Am. Chem. Soc. 2015, 137, 4158–4163. [Google Scholar] [CrossRef] [PubMed]
- DeCoste, J.B.; Peterson, G.W. Metal–Organic Frameworks for Air Purification of Toxic Chemicals. Chem. Rev. 2014, 114, 5695–5727. [Google Scholar] [CrossRef] [PubMed]
- Karttunen, A.J.; Tynell, T.; Karppinen, M. Atomic-Level Structural and Electronic Properties of Hybrid Inorganic–Organic ZnO:Hydroquinone Superlattices Fabricated by ALD/MLD. J. Phys. Chem. C 2015, 119, 13105–13114. [Google Scholar] [CrossRef]
- Sadakiyo, M.; Yamada, T.; Honda, K.; Matsui, H.; Kitagawa, H. Control of Crystalline Proton-Conducting Pathways by Water-Induced Transformations of Hydrogen-Bonding Networks in a Metal–Organic Framework. J. Am. Chem. Soc. 2014, 136, 7701–7707. [Google Scholar] [CrossRef] [PubMed]
- Luo, L.; Zeng, Y.; Li, L.; Luo, Z.; Smirnova, T.I.; Maggard, P.A. Manganese–Vanadate Hybrids: Impact of Organic Ligands on Their Structures, Thermal Stabilities, Optical Properties, and Photocatalytic Activities. Inorg. Chem. 2015, 54, 7388–7401. [Google Scholar] [CrossRef] [PubMed]
- Jiang, J.; Yaghi, O.M. Brønsted Acidity in Metal–Organic Frameworks. Chem. Rev. 2015, 115, 6966–6997. [Google Scholar] [CrossRef] [PubMed]
- Oburn, S.M.; Bowling, N.P.; Bosch, E. Formation of Self-Complementary Halogen-Bonded Dimers. Cryst. Growth Des. 2015, 15, 1112–1118. [Google Scholar] [CrossRef]
- Fan, H.; Shi, Q.; Yan, H.; Ji, S.; Dong, J.; Zhang, G. Simultaneous Spray Self-Assembly of Highly Loaded ZIF-8–PDMS Nanohybrid Membranes Exhibiting Exceptionally High Biobutanol-Permselective Pervaporation. Angew. Chem. Int. Ed. Engl. 2014, 53, 5578–5582. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.; Cui, Y.; Wu, C.-D.; Yang, Y.; Chen, B.; Qian, G. Two-Photon Responsive Metal–Organic Framework. J. Am. Chem. Soc. 2015, 137, 4026–4029. [Google Scholar] [CrossRef] [PubMed]
- Podgajny, R.; Choraży, S.; Nitek, W.; Budziak, A.; Rams, M.; Gómez-García, C.J.; Oszajca, M.; Łasocha, W.; Sieklucka, B. Humidity-Driven Reversible Transformation and Guest Inclusion in a Two-Dimensional Coordination Framework Tailored by Organic Polyamine Cation. Cryst. Growth Des. 2011, 11, 3866–3876. [Google Scholar] [CrossRef]
- Manna, B.; Desai, A.V.; Ghosh, S.K. Neutral N-Donor Ligand Based Flexible Metal–Organic Frameworks. Dalton Trans. 2016, 45, 4060–4072. [Google Scholar] [CrossRef] [PubMed]
- Nagarkar, S.S.; Das, R.; Poddar, P.; Ghosh, S.K. Bistable Dynamic Coordination Polymer Showing Reversible Structural and Functional Transformations. Inorg. Chem. 2012, 51, 8317–8321. [Google Scholar] [CrossRef] [PubMed]
- Couck, S.; Van Assche, T.R.C.; Liu, Y.-Y.; Baron, G.V.; Van Der Voort, P.; Denayer, J.F.M. Adsorption and Separation of Small Hydrocarbons on the Flexible, Vanadium-Containing MOF, COMOC-2. Langmuir 2015, 31, 5063–5070. [Google Scholar] [CrossRef] [PubMed]
- Guerri, A.; Taddei, M.; Bataille, T.; Moneti, S.; Boulon, M.-E.; Sangregorio, C.; Costantino, F.; Ienco, A. Same Not the Same: Thermally Driven Transformation of Nickel Phosphinate-Bipyridine One-Dimensional Chains into Three-Dimensional Coordination Polymers. Cryst. Growth Des. 2018, 18, 2234–2242. [Google Scholar] [CrossRef]
- Meng, X.-R.; Zhong, D.-C.; Jiang, L.; Li, H.-Y.; Lu, T.-B. Unprecedented Tuning of Structures and Gas Sorption Properties of Two 2D Nickel Metal−Organic Frameworks via Altering the Positions of Fluorine Atoms in Azamacrocyclic Ligands. Cryst. Growth Des. 2011, 11, 2020–2025. [Google Scholar] [CrossRef]
- Douvali, A.; Tsipis, A.C.; Eliseeva, S.V.; Petoud, S.; Papaefstathiou, G.S.; Malliakas, C.D.; Papadas, I.; Armatas, G.S.; Margiolaki, I.; Kanatzidis, M.G.; et al. Turn-On Luminescence Sensing and Real-Time Detection of Traces of Water in Organic Solvents by a Flexible Metal–Organic Framework. Angew. Chem. Int. Ed. Engl. 2015, 54, 1651–1656. [Google Scholar] [CrossRef] [PubMed]
- Li, P.; Arman, H.D.; Wang, H.; Weng, L.; Alfooty, K.; Angawi, R.F.; Chen, B. Solvent Dependent Structures of Melamine: Porous or Nonporous? Cryst. Growth Des. 2015, 15, 1871–1875. [Google Scholar] [CrossRef]
- Wang, H.; Li, B.; Wu, H.; Hu, T.-L.; Yao, Z.; Zhou, W.; Xiang, S.; Chen, B. A Flexible Microporous Hydrogen-Bonded Organic Framework for Gas Sorption and Separation. J. Am. Chem. Soc. 2015, 137, 9963–9970. [Google Scholar] [CrossRef] [PubMed]
- Yamamura, Y.; Shimoi, H.; Sumita, M.; Yasuzuka, S.; Adachi, K.; Fuyuhiro, A.; Kawata, S.; Saito, K. Calorimetric Study of Correlated Disordering in [Hdamel]2[CuII(tdpd)2]·2THF Crystal. J. Phys. Chem. A 2008, 112, 4465–4469. [Google Scholar] [CrossRef] [PubMed]
- Kawata, S.; Kumagai, H.; Adachi, K.; Kitagawa, S. Novel Layered Structures Constructed from Metal(II)–Chloranilate Monomer Compounds. J. Chem. Soc. Dalton Trans. 2000, 2409–2417. [Google Scholar] [CrossRef]
- Chuang, Y.-C.; Ho, W.-L.; Sheu, C.-F.; Lee, G.-H.; Wang, Y. Crystal Engineering from a 1D Chain to a 3D Coordination Polymer Accompanied by a Dramatic Change in Magnetic Properties. Chem. Commun. 2012, 48, 10769–10771. [Google Scholar] [CrossRef] [PubMed]
- Adachi, K.; Sugiyama, Y.; Kumagai, H.; Inoue, K. Crystal Structures and Magnetic Properties of Novel Coordination Polymers with Rectangular Lattice Constructed from Pyrazine Derivative. Polyhedron 2001, 20, 1411–1415. [Google Scholar] [CrossRef]
| Compound | 1·10H2O | 2·10H2O | 2·2H2O |
| Formula | C20H28Co2N12O14 | C20H28Zn2N12O14 | C20H12Zn2N12O6 |
| Crystal system | Triclinic | Monoclinic | Monoclinic |
| Space group | P-1 | P2/n | C2/m |
| a/Å | 7.0728(9) | 12.0699(3) | 21.0743(11) |
| b/Å | 10.3625(13) | 7.11859(17) | 7.1528(3) |
| c/Å | 12.0604(16) | 18.4918(5) | 8.0963(5) |
| α/Å | 67.284(4) | 90 | 90 |
| β/Å | 81.212(4) | 98.7958(9) | 98.773(2) |
| γ/Å | 77.056(4) | 90 | 90 |
| V/Å3 | 792.48(18) | 1570.14(7) | 1206.17(11) |
| Z | 1 | 2 | 2 |
| R1 1 | 0.0977 | 0.0213 | 0.0766 |
| wR2 1 | 0.1893 | 0.0583 | 0.1014 |
| S(GOF) 1 | 1.109 | 1.131 | 1.5331 |
| Compound | 1·10H2O | 2·10H2O | 2·2H2O | |||
| (A) | (B) | (A) | (B) | |||
| M–N | 2.102(5) | 2.096(5) | 2.1781(15) | 2.1668(15) | 2.149(8) | |
| 2.1652(15) | 2.1599(15) | 2.161(7) | ||||
| M–O | 2.080(3) | 2.059(4) | 2.0878(9) | 2.0888(9) | 2.186(7) | 2.340(6) |
| 2.092(3) | 2.094(4) | 2.0862(9) | 2.0996(9) | 1.964(3) | 1.961(11) | |
| N–M–N | 180.0 | 180.0 | 180.0 | 180.0 | 180.0 | 180.0 |
| O–M–N | 88.89(19) | 90.6(2) | 90.35(2) | 92.11(3) | 90.0(2) | |
| 91.11(19) | 89.4(2) | 89.65(2) | 87.89(3) | 90.00(17) | ||
| 87.3(2) | 89.9(2) | 89.27(2) | 87.54(3) | |||
| 92.7(2) | 90.1(2) | 90.73(2) | 92.46(2) | |||
| O–M–O | 180.0 | 91.42(15) | 80.58(3) | 86.98(4) | 80.8(2) | 89.0(4) |
| 100.11 (13) | 88.58(15) | 99.43(3) | 93.20(4) | 99.2(3) | 180.0 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumagai, H.; Yagishita, S.; Kanazashi, K.; Ishii, M.; Hayami, S.; Konaka, H.; Ishikawa, R.; Kawata, S. Hydrogen-Bonding Assembly of Coordination Polymers Showing Reversible Dynamic Solid-State Structural Transformations. Inorganics 2018, 6, 115. https://doi.org/10.3390/inorganics6040115
Kumagai H, Yagishita S, Kanazashi K, Ishii M, Hayami S, Konaka H, Ishikawa R, Kawata S. Hydrogen-Bonding Assembly of Coordination Polymers Showing Reversible Dynamic Solid-State Structural Transformations. Inorganics. 2018; 6(4):115. https://doi.org/10.3390/inorganics6040115
Chicago/Turabian StyleKumagai, Hitoshi, Sadahiro Yagishita, Ken Kanazashi, Mariko Ishii, Shinya Hayami, Hisashi Konaka, Ryuta Ishikawa, and Satoshi Kawata. 2018. "Hydrogen-Bonding Assembly of Coordination Polymers Showing Reversible Dynamic Solid-State Structural Transformations" Inorganics 6, no. 4: 115. https://doi.org/10.3390/inorganics6040115
APA StyleKumagai, H., Yagishita, S., Kanazashi, K., Ishii, M., Hayami, S., Konaka, H., Ishikawa, R., & Kawata, S. (2018). Hydrogen-Bonding Assembly of Coordination Polymers Showing Reversible Dynamic Solid-State Structural Transformations. Inorganics, 6(4), 115. https://doi.org/10.3390/inorganics6040115








