Regium-π vs Cation-π Interactions in M2 and MCl (M = Cu, Ag and Au) Complexes with Small Aromatic Systems: An ab Initio Study
Abstract
1. Introduction
2. Results and Discussion
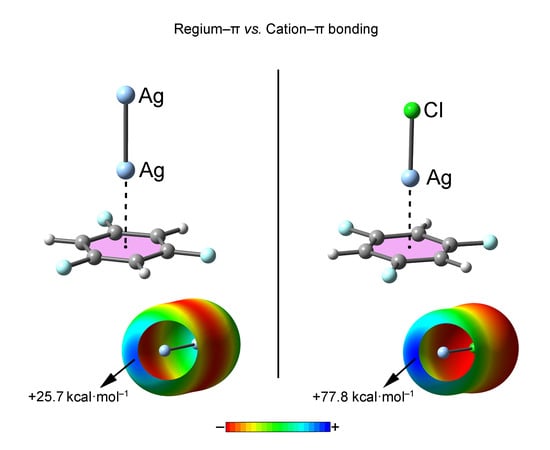
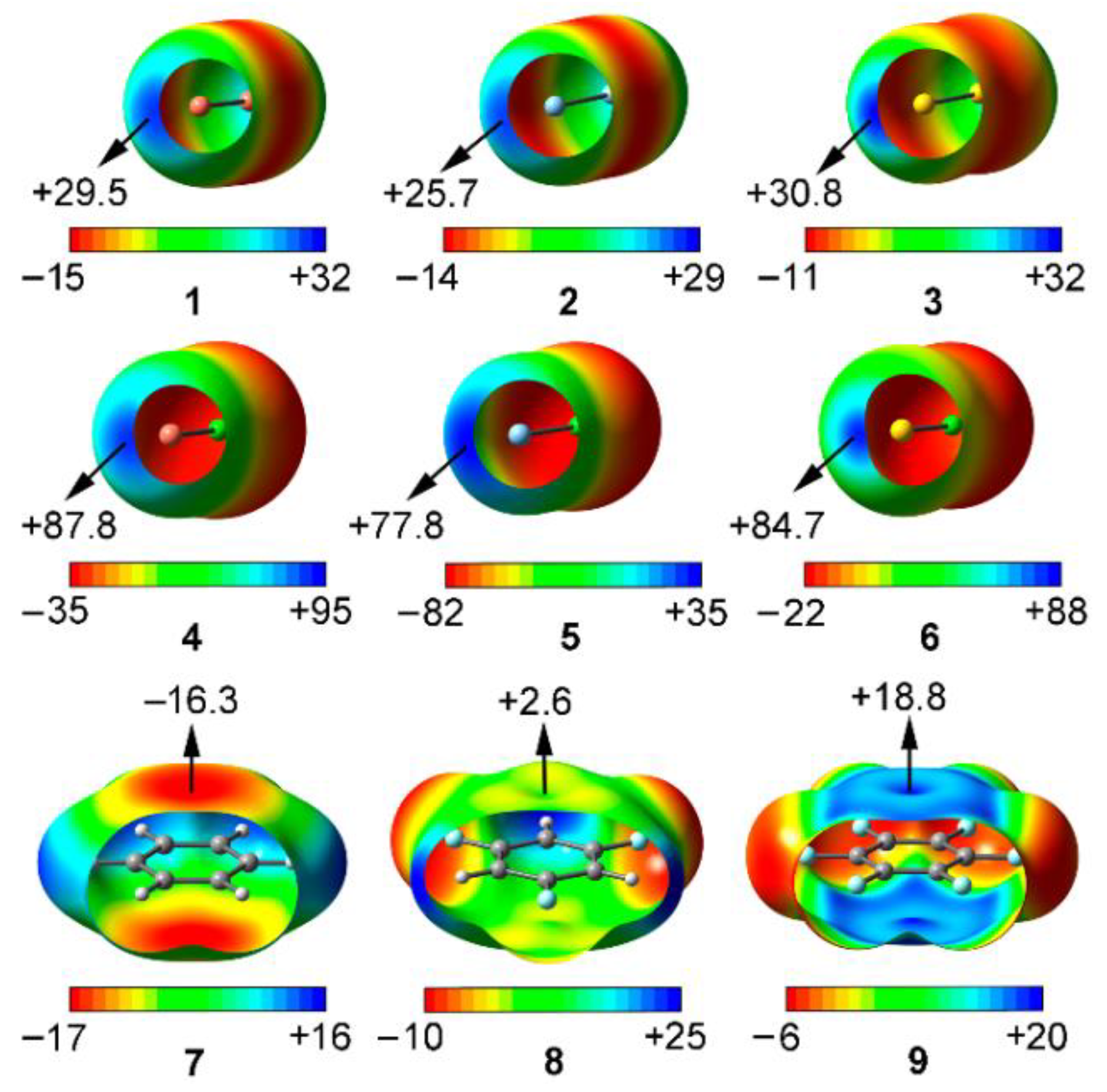
2.1. Preliminary MEP Analysis
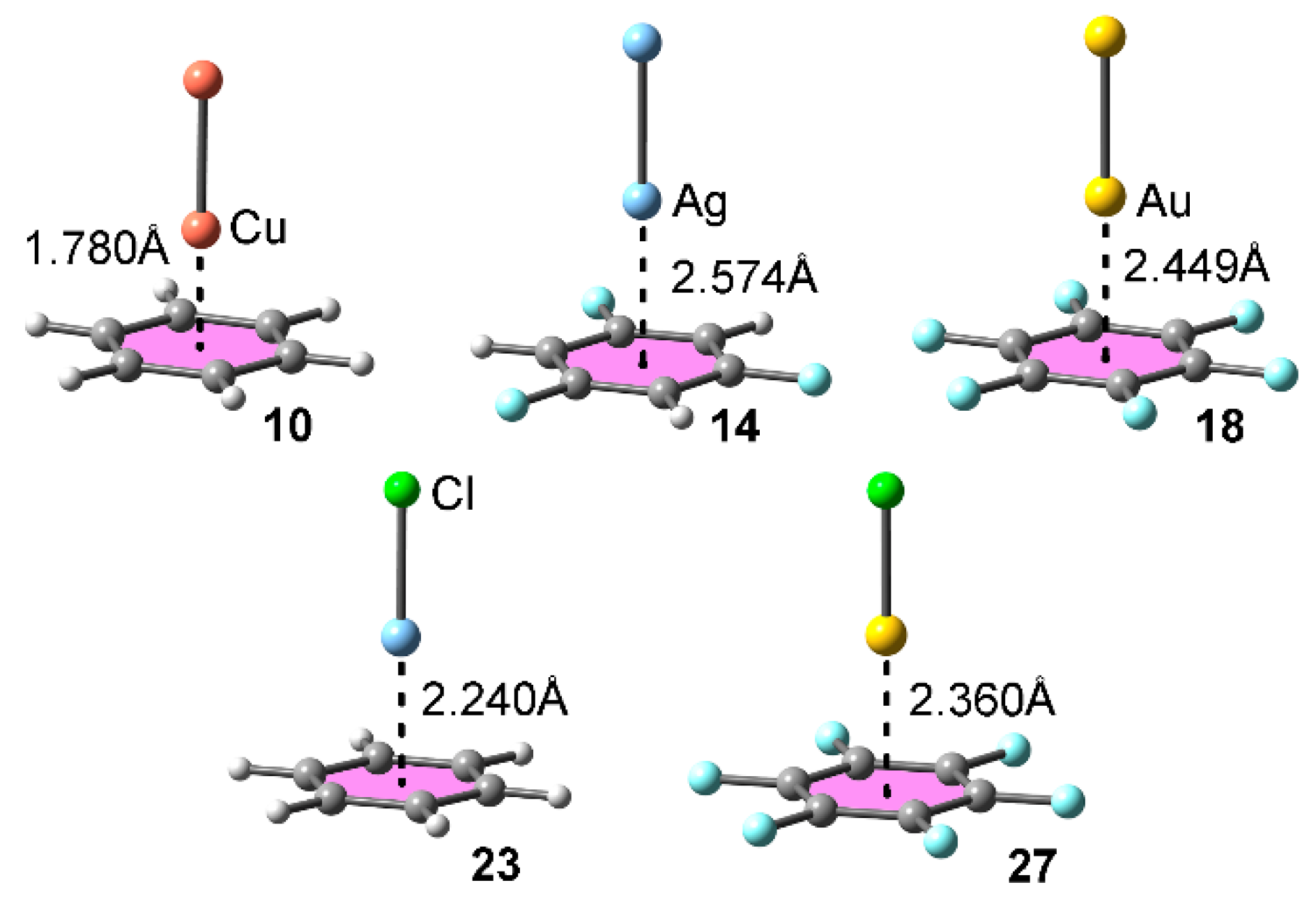
2.2. Energetic Study
2.3. AIM and NBO Analyses
2.4. SAPT Analysis of Ag Complexes
3. Theoretical Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| DOAJ | Directory of open access journals |
| AIM | Atoms in molecules |
| MEP | Molecular electrostatic potential |
| MP2 | Second order Moller-Plesset |
| BSSE | Basis Set Superposition Error |
| NBO | Natural Bonding Orbital |
| CP | Critical point |
| MINECO | Ministerio de Economía y Competitividad |
| AEI | Agencia Española de Investigación |
| NP | Nanoparticle |
| OS | Oxidation State |
| ECP | Efective Core Potential |
| CSD | Cambridge Structural Database |
| CTI | Centre de Tecnologies de la Informació |
| SAPT | Symmetry Adapted Perturbation Theory |
References
- Schneider, H.J. Binding mechanisms in supramolecular complexes. Angew. Chem. Int. Ed. 2009, 48, 3924–3977. [Google Scholar] [CrossRef] [PubMed]
- Maharramov, A.M.; Mahmudov, K.T.; Kopylovich, M.N.; Pombeiro, A.J.L. Non-Covalent Interactions in the Synthesis and Design of New Compounds; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Vickaryous, W.J.; Herges, R.; Jonhson, D.W. Arsenic–π interactions stabilize a self-assembled As2L3 supramolecular complex. Angew. Chem. Int. Ed. 2004, 43, 5831–5833. [Google Scholar] [CrossRef] [PubMed]
- Grabowski, S.J. What is the covalency of hydrogen bonding? Chem. Rev. 2011, 111, 2597–2625. [Google Scholar] [CrossRef] [PubMed]
- Murrayrust, P.; Motherwell, W.D.S. Computer retrieval and analysis of molecular geometry. 4. Intermolecular interactions. J. Am. Chem. Soc. 1979, 101, 4374–4376. [Google Scholar] [CrossRef]
- Bai, Y.; Sosnick, T.R.; Mayne, L.; Englander, S.W. Protein folding intermediates: Native-state hydrogen exchange. Science 1995, 269, 192–197. [Google Scholar] [CrossRef] [PubMed]
- Bauzá, A.; Mooibroek, T.J.; Frontera, A. The bright future of unconventional σ/π-hole interactions. ChemPhysChem 2015, 16, 2496–2517. [Google Scholar] [CrossRef] [PubMed]
- Bauzá, A.; Frontera, A. Aerogen bonding interaction: A new supramolecular force? Angew. Chem. Int. Ed. 2015, 54, 7340–7343. [Google Scholar] [CrossRef] [PubMed]
- Politzer, P.; Murray, J.S.; Clark, T. Halogen bonding: An electrostatically-driven highly directional noncovalent interaction. Phys. Chem. Chem. Phys. 2010, 12, 7748–7757. [Google Scholar] [CrossRef] [PubMed]
- Grabowski, S.J. Triel bonds-complexes of boron and aluminum trihalides and trihydrides with benzene. Struct. Chem. 2017, 28, 1163–1171. [Google Scholar] [CrossRef]
- Scheiner, S. The pnicogen bond: Its relation to hydrogen, halogen, and other noncovalent bonds. Acc. Chem. Res. 2013, 46, 280–288. [Google Scholar] [CrossRef] [PubMed]
- Marín-Luna, M.; Alkorta, I.; Elguero, J. Cooperativity in Tetrel Bonds. J. Phys. Chem. A 2016, 120, 648–656. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Ji, B.; Zhang, Y. Chalcogen bond: A sister noncovalent bond to halogen bond. J. Phys. Chem. A 2009, 113, 8132–8135. [Google Scholar] [CrossRef] [PubMed]
- Bauzá, A.; Frontera, A. π-hole aerogen bonding interactions. Phys. Chem. Chem. Phys. 2015, 17, 24748–24753. [Google Scholar] [CrossRef] [PubMed]
- Politzer, P.; Murray, J.S. Halogen bonding: An interim discussion. ChemPhysChem 2013, 14, 278–294. [Google Scholar] [CrossRef] [PubMed]
- Fanfrlík, J.; Přáda, A.; Padělková, Z.; Pecina, A.; Macháček, J.; Lepšík, M.; Holub, J.; Růžička, A.; Hnyk, D.; Hobza, P. The dominant role of chalcogen bonding in the crystal packing of 2D/3D aromatics. Angew. Chem. Int. Ed. 2014, 53, 10139–10142. [Google Scholar] [CrossRef] [PubMed]
- Müller, G.; Brand, J.; Jetter, S.E. Donor-acceptor complexes between organoamines and phosphorus tribromide. Z. Naturforsch. 2001, 56, 1163–1171. [Google Scholar] [CrossRef]
- Dai, X.; Schulz, D.L.; Braun, C.W.; Ugrinov, A.; Boudjouk, P. “Inverse sandwich” complexes of perhalogenated cyclohexasilane. Organometallics 2010, 29, 2203–2205. [Google Scholar] [CrossRef]
- Goettel, J.T.; Haensch, V.G.; Schrobilgen, J.G. Stable chloro- and bromoxenate cage anions; [X3(XeO3)3]3– and [X4(XeO3)4]4– (X = Cl or Br). J. Am. Chem. Soc. 2017, 139, 8725–8733. [Google Scholar] [CrossRef] [PubMed]
- Grasberger, B.L.; Lu, T.; Schubert, C.; Parks, D.J.; Carver, T.E.; Koblish, H.K.; Cummings, M.D.; LaFrance, L.V.; Milkiewicz, K.L.; Calvo, R.R.; et al. Discovery and cocrystal structure of benzodiazepinedione HDM2 antagonists that activate p53 in cells. J. Med. Chem. 2005, 48, 909–912. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.; Liu, Z.; Chen, T.; Chen, T.; Wang, Z.; Tian, G.; Shi, J.; Wang, X.; Lu, Y.; Yan, X.; et al. Utilization of halogen bond in lead optimization: A case study of rational design of potent phosphodiesterase type 5 (PDE5) inhibitors. J. Med. Chem. 2011, 54, 5607–5611. [Google Scholar] [CrossRef] [PubMed]
- Bauzá, A.; Frontera, A. RCH3···O interactions in biological systems: Are they trifurcated H-bonds or noncovalent carbon bonds? Crystals 2016, 6, 26. [Google Scholar] [CrossRef]
- García-Llinás, X.; Bauzá, A.; Seth, S.K.; Frontera, A. Importance of R–CF3···O tetrel bonding interactions in biological systems. J. Chem. Phys. A 2017, 121, 5371–5376. [Google Scholar] [CrossRef] [PubMed]
- Iwaoka, M.; Isozumi, N. Possible roles of S···O and S···N interactions in the functions and evolution of phospholipase A2. Biophysics 2006, 2, 23–34. [Google Scholar] [CrossRef] [PubMed]
- Meyer, F.; Dubois, P. Halogen bonding at work: Recent applications in synthetic chemistry and materials science. CrystEngComm 2013, 15, 3058–3071. [Google Scholar] [CrossRef]
- Britvin, S.N.; Kashtanov, S.A.; Krivovichev, S.V.; Chukanov, N.V. Xenon in rigid oxide frameworks: Structure, bonding and explosive properties of layered perovskite K4Xe3O12. J. Am. Chem. Soc. 2016, 138, 13838–13841. [Google Scholar] [CrossRef] [PubMed]
- Bruckmann, A.; Pena, M.A.; Bolm, C. Organocatalysis through halogen-bond activation. Synlett 2008, 900–902. [Google Scholar] [CrossRef]
- Benz, S.; Macchione, M.; Verolet, Q.; Mareda, J.; Sakai, N.; Matile, S. Anion transport with chalcogen bonds. J. Am. Chem. Soc. 2016, 138, 9093–9096. [Google Scholar] [CrossRef] [PubMed]
- Robinson, E.R.T.; Walden, D.M.; Fallan, C.; Greenhalgh, M.D.; Cheong, P.H.-Y.; Smith, A.D. Non-bonding 1,5-S···O interactions govern chemo- and enantioselectivity in isothiourea-catalyzed annulations of benzazoles. Chem. Sci. 2016, 7, 6919–6927. [Google Scholar] [CrossRef] [PubMed]
- Aakeroy, C.B.; Rajbanshi, A.; Metrangolo, P.; Resnati, G.; Parisi, M.F.; Desper, J.; Pilati, T. The quest for a molecular capsule assembled via halogen bonds. CrystEngComm 2012, 14, 6366–6368. [Google Scholar] [CrossRef]
- Yang, X. Synthesis and crystal structure of tetramethylammonium fluoride octadecasil. Mater. Res. Bull. 2006, 41, 54–66. [Google Scholar] [CrossRef]
- Stenlid, J.H.; Brinck, T. Extending the σ-hole concept to metals: An electrostatic interpretation of the effects of nanostructure in gold and platinum catalysis. J. Am. Chem. Soc. 2017, 139, 11012–11015. [Google Scholar] [CrossRef] [PubMed]
- Stenlid, H.; Johansson, A.J.; Brinck, T. σ-Holes and σ-lumps direct the Lewis basic and acidic interactions of noble metal nanoparticles: Introducing regium bonds. Phys. Chem. Chem. Phys. 2018, 20, 2676–2692. [Google Scholar] [CrossRef] [PubMed]
- Joy, J.; Jemmis, E.D. Contrasting behavior of the Z bonds in X–Z···Y weak interactions: Z = main group elements versus the transition metals. Inorg. Chem. 2017, 56, 1132–1143. [Google Scholar] [CrossRef] [PubMed]
- Gautam, S.; De Sarkar, A. A systematic investigation of acetylene activation and hydracyanation of the activated acetylene on Aun (n = 3–10) clusters via density functional theory. Phys. Chem. Chem. Phys. 2016, 18, 13830–13843. [Google Scholar] [CrossRef] [PubMed]
- Ziegler, T.; Rauk, A. A theoretical study of the ethylene-metal bond in complexes between copper(1+), silver(1+), gold(1+), platinum(0) or platinum(2+) and ethylene, based on the Hartree-Fock-Slater transition-state method. Inorg. Chem. 1979, 18, 1558–1565. [Google Scholar] [CrossRef]
- Grabowski, S.J.; Ruipérez, F. π⋅⋅⋅H+ ⋅⋅⋅π Hydrogen bonds and their lithium and gold analogues: MP2 and CASPT2 calculations. ChemPhysChem 2017, 18, 2409–2417. [Google Scholar] [CrossRef] [PubMed]
- Grabowski, S.J.; Ruipérez, F. Dihydrogen bond interactions as a result of H2 cleavage at Cu, Ag and Au centres. Phys. Chem. Chem. Phys. 2016, 18, 12810–12818. [Google Scholar] [CrossRef] [PubMed]
- Frontera, A.; Bauzá, A. Regium–π bonds: An unexplored link between noble metal nanoparticles and aromatic surfaces. Chem. Eur. J. 2018, 24, 7228–7234. [Google Scholar] [CrossRef] [PubMed]
- Grabowski, S.J. Tetrel bond–σ-hole bond as a preliminary stage of the SN2 reaction. Phys. Chem. Chem. Phys. 2014, 16, 1824–1834. [Google Scholar] [CrossRef] [PubMed]
- Astruc, D.; Lu, F.; Aranzaes, J.R. Nanoparticles as recyclable catalysts: The frontier between homogeneous and heterogeneous catalysis. Angew. Chem. Int. Ed. 2005, 44, 7852–7872. [Google Scholar] [CrossRef] [PubMed]
- Daniel, M.-C.; Astruc, D. Gold nanoparticles: assembly, supramolecular chemistry, quantum-size-related properties, and applications toward biology, catalysis, and nanotechnology. Chem. Rev. 2004, 104, 293–346. [Google Scholar] [CrossRef] [PubMed]
- Haruda, M.; Yamada, N.; Kobayashi, T.; Iijima, S. Gold catalysts prepared by coprecipitation for low-temperature oxidation of hydrogen and of carbon monoxide. J. Catal. 1989, 115, 301–309. [Google Scholar] [CrossRef]
- Ali, Z.I.; Ghazy, O.A.; Meligi, G.; Saleh, H.H.; Bekhit, M. Copper nanoparticles: Synthesis, characterization and its application as catalyst for p-nitrophenol reduction. J. Inorg. Organomet. Polym. Mater. 2018, 28, 1195–1205. [Google Scholar] [CrossRef]
- Venkatesha, N.J.; Rameh, S. Citric acid-assisted synthesis of nanoparticle copper catalyst supported on an oxide system for the reduction of furfural to furfuryl alcohol in the vapor phase. Ind. Eng. Chem. Res. 2018, 57, 1506–1515. [Google Scholar] [CrossRef]
- Zhang, W.; Sun, Y.; Zhang, L. Fabrication of high efficient silver nanoparticle catalyst supported on poly(glycidyl methacrylate)–polyacrylamide. Ind. Eng. Chem. Res. 2016, 55, 12398–12406. [Google Scholar] [CrossRef]
- Schroder, F.; Sharma, U.K.; Mertens, M.; Devred, F.; Debecker, D.P.; Luque, R.; Van der Eycken, E.V. Silver-nanoparticle-catalyzed dearomatization of indoles toward 3-spiroindolenines via a 5-exo-dig spirocyclization. ACS Catal. 2016, 6, 8156–8161. [Google Scholar] [CrossRef]
- Stratakis, M.; García, H. Catalysis by supported gold nanoparticles: Beyond aerobic oxidative processes. Chem. Rev. 2012, 112, 4469–4506. [Google Scholar] [CrossRef] [PubMed]
- Di Pietro, P.; Strano, G.; Zuccarello, L.; Satriano, C. Gold and silver nanoparticles for applications in theranostics. Curr. Top. Med. Chem. 2016, 16, 3069–3102. [Google Scholar] [CrossRef]
- Kar, S.; Bagchi, B.; Kundu, B.; Bhandary, S.; Basu, R.; Nandy, P.; Das, S. Synthesis and characterization of Cu/Ag nanoparticle loaded mullite nanocomposite system: A potential candidate for antimicrobial and therapeutic applications. Biochim. Biophys. Acta 2014, 1840, 3264–3276. [Google Scholar] [CrossRef] [PubMed]
- Zhou, N.; López-Puente, V.; Wang, Q.; Polavarapu, L.; Pastoriza-Santos, I.; Xu, Q.-H. Plasmon-enhanced light harvesting: Applications in enhanced photocatalysis, photodynamic therapy and photovoltaics. RSC Adv. 2015, 5, 29076–29097. [Google Scholar] [CrossRef]
- Jung, H.-Y.; Yeo, I.-S.; Kim, T.-U.; Ki, H.-C.; Gu, H.-B. Surface plasmon resonance effect of silver nanoparticles on a TiO2 electrode for dye-sensitized solar cells. Appl. Surf. Sci. 2018, 432, 266–271. [Google Scholar] [CrossRef]
- Shen, P.; Liu, Y.; Long, Y.; Shen, L.; Kang, B. High-performance polymer solar cells enabled by copper nanoparticles-induced plasmon resonance enhancement. J. Phys. Chem. C 2016, 120, 8900–8906. [Google Scholar] [CrossRef]
- Frontera, A.; Gamez, P.; Mascal, M.; Mooibroek, T.J.; Reedijk, J. Putting anion–π interactions into perspective. Angew. Chem. Int. Ed. 2011, 50, 9564–9583. [Google Scholar] [CrossRef] [PubMed]
- Weinhold, F.; Landis, C.R. Valency and Bonding: A Natural Bond Orbital Donor-Acceptor Perspective; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef] [PubMed]
- Ahlrichs, R.; Bär, M.; Hacer, M.; Horn, H.; Kömel, C. Electronic structure calculations on workstation computers: The program system turbomole. Chem. Phys. Lett. 1989, 162, 165–169. [Google Scholar] [CrossRef]
- Keith, T.A. AIMAll (Version 13.05.06), TK Gristmill Software: Overland Park, KS, USA, 2013.
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision B.01; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Heβelmann, A.; Jansen, G. The helium dimer potential from a combined density functional theory and symmetry-adapted perturbation theory approach using an exact exchange-correlation potential. Phys. Chem. Chem. Phys. 2003, 5, 5010–5014. [Google Scholar] [CrossRef]
- Werner, H.-J.; Knowles, P.J.; Knizia, G.; Manby, F.R.; Schütz, M. Molpro: A general-purpose quantum chemistry program package. WIREs Comput. Mol. Sci. 2012, 2, 242–253. [Google Scholar] [CrossRef]
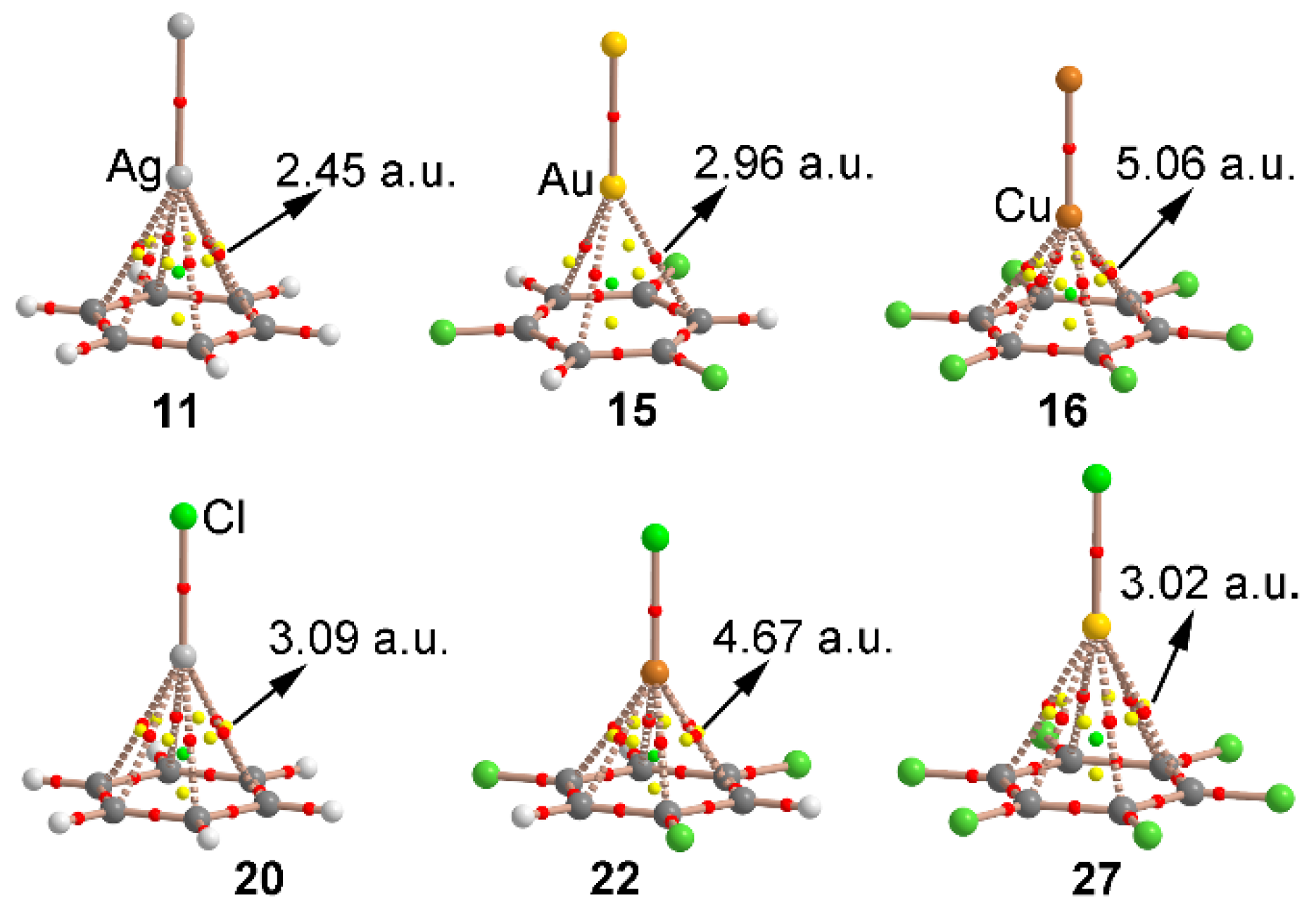
| Complex | ΔEBSSE | Re a | 102 × ρ |
|---|---|---|---|
| 10 | −9.7 | 1.780 | 4.91 |
| 11 | −6.8 | 2.381 | 2.45 |
| 12 | −12.7 | 2.244 | 3.57 |
| 13 | −3.5 | 1.849 | 4.48 |
| 14 | −3.7 | 2.574 | 1.83 |
| 15 | −7.8 | 2.374 | 2.96 |
| 16 | +0.5 (−0.1) b | 1.785 | 5.06 |
| 17 | −2.2 | 2.674 | 1.56 |
| 18 | −5.2 | 2.449 | 2.64 |
| 19 | −21.0 | 1.767 | 5.01 |
| 20 | −15.1 | 2.240 | 3.09 |
| 21 | −20.1 | 2.230 | 3.64 |
| 22 | −11.9 | 1.829 | 4.63 |
| 33 | −7.9 | 2.349 | 2.65 |
| 24 | −12.9 | 2.316 | 3.22 |
| 25 | −5.4 | 1.813 | 4.83 |
| 26 | −2.4 | 2.416 | 2.37 |
| 27 | −8.1 | 2.360 | 3.02 |
| Complex | Donor a | Acceptor | E(2) |
|---|---|---|---|
| 10 | BD C–C | BD* Cu–Cu | 6.96 |
| 11 | BD C–C | BD* Ag–Ag | 1.50 |
| 12 | BD C–C | BD* Au–Au | 5.46 |
| 13 | BD C–C | BD* Cu–Cu | 6.75 |
| 14 | BD C–C | BD* Ag–Ag | 1.74 |
| 15 | BD C–C | BD* Au–Au | 4.59 |
| 16 | BD C–C | BD* Cu–Cu | 0.39 |
| 17 | BD C–C | BD* Ag–Ag | 3.09 |
| 18 | BD C–C | BD* Au–Au | 6.09 |
| 19 | BD C–C | Ry* Cu | 9.18 |
| 20 | BD C–C | Ry* Ag | 7.0 |
| 21 | BD C–C | Ry* Au | 13.46 |
| 22 | BD C–C | Ry* Cu | 2.79 |
| 23 | BD C–C | Ry* Ag | 3.52 |
| 24 | BD C–C | Ry* Au | 5.97 |
| 25 | BD C–C | Ry* Cu | 5.54 |
| 26 | BD C–C | Ry* Ag | 4.04 |
| 27 | BD C–C | Ry* Au | 5.93 |
| Complex | Epol | Eex | Eind + Eind_exc | Edisp + Edisp_exc | Etotal |
|---|---|---|---|---|---|
| 11 | −36.4 | 55.5 | −23.3 | −13.7 | −17.8 |
| 14 | −21.3 | 35.2 | −11.7 | −10.4 | −8.2 |
| 17 | −15.1 | 28.0 | −8.4 | −9.0 | −4.5 |
| 20 | −39.4 | 59.4 | −34.2 | −13.3 | −27.4 |
| 23 | −24.8 | 44.7 | −24.8 | −11.3 | −16.2 |
| 26 | −15.8 | 37.4 | −20.6 | −10.2 | −9.2 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bauzá, A.; Frontera, A. Regium-π vs Cation-π Interactions in M2 and MCl (M = Cu, Ag and Au) Complexes with Small Aromatic Systems: An ab Initio Study. Inorganics 2018, 6, 64. https://doi.org/10.3390/inorganics6030064
Bauzá A, Frontera A. Regium-π vs Cation-π Interactions in M2 and MCl (M = Cu, Ag and Au) Complexes with Small Aromatic Systems: An ab Initio Study. Inorganics. 2018; 6(3):64. https://doi.org/10.3390/inorganics6030064
Chicago/Turabian StyleBauzá, Antonio, and Antonio Frontera. 2018. "Regium-π vs Cation-π Interactions in M2 and MCl (M = Cu, Ag and Au) Complexes with Small Aromatic Systems: An ab Initio Study" Inorganics 6, no. 3: 64. https://doi.org/10.3390/inorganics6030064
APA StyleBauzá, A., & Frontera, A. (2018). Regium-π vs Cation-π Interactions in M2 and MCl (M = Cu, Ag and Au) Complexes with Small Aromatic Systems: An ab Initio Study. Inorganics, 6(3), 64. https://doi.org/10.3390/inorganics6030064