1. Introduction
Nanoparticles are halfway between atomic world and bulk world. A whole new and non-trivial variety of effects arise whenever a system is pushed towards the atomic scale. Material’s properties change significantly when system size becomes comparable to a characteristic length scale, such as the mean free path of particles or excitations that carry charges, energy and momentum. The high density of interfaces confers to nano-systems unique physical and chemical properties, and promotes their chemical reactivity. The thermodynamics of nano-scaled systems is strongly altered with respect to bulk material and size-dependent effects [
1,
2], becoming more and more complicated when dealing with compounds and heterogeneous ones [
3]. Far from putting a limit to the exploitation of nanoparticles, this fascinating behavior allows for the tailoring of material properties by designing unique functional devices at nanoscale. This work aims to discuss hydride formation in composite nanomaterials, relating peculiar H-sorption properties to confinement effects [
4] and to the physical properties of interfaces [
5].
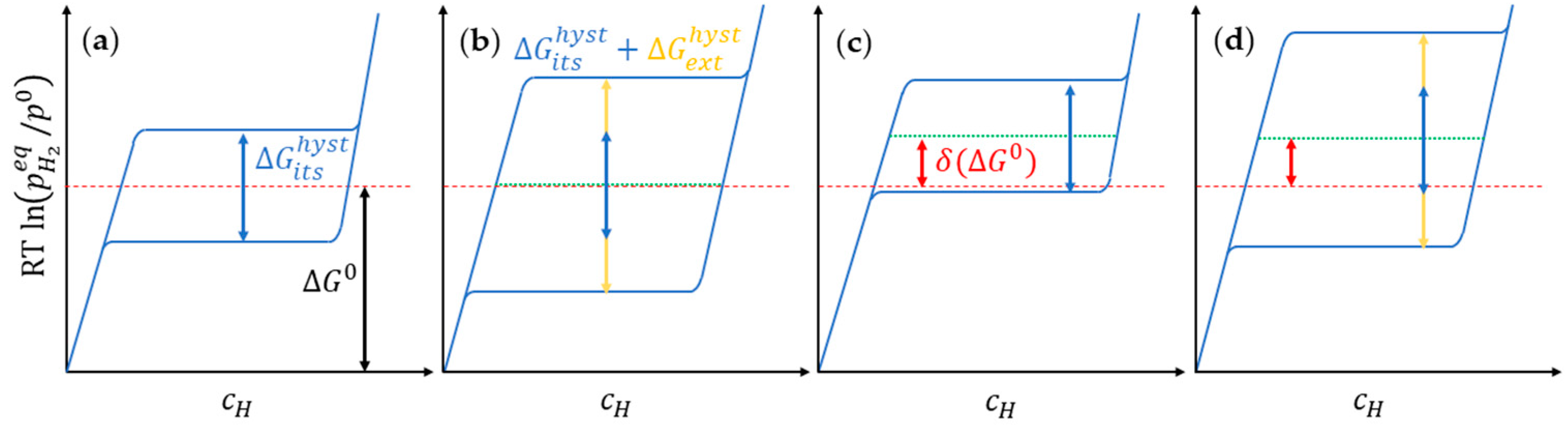
Before going into details with the effects of nanosizing, we recall some general concepts about the thermochemical equilibrium of hydride formation. The Van’t Hoff equation relates the equilibrium pressure
and temperature
T to the reaction’s free energy
at standard conditions:
where
and
are, respectively, the enthalpy and the entropy at standard conditions. The workhorse for the characterization of the thermodynamics of hydride formation are the pressure-composition isotherms (PCI). All real systems exhibit some hysteresis, i.e., a pressure shift between the absorption and desorption branches of a PCI cycle, due to coherency strains [
6,
7]. This is called intrinsic hysteresis and is represented in
Figure 1a. In presence of hysteresis, the equilibrium pressure
is calculated as the geometric average of the absorption (
) and desorption (
) plateau pressures. The hysteresis is usually quantified by the ratio:
Additional sources of strain, such as the presence of defects or interfaces in the material, can lead to a wider extrinsic hysteresis, as shown in
Figure 1b, where the equilibrium pressure is not altered because of the symmetrical shift of both absorption and desorption plateau. A simple relation between
and plateau pressures holds:
A true thermodynamical bias, i.e., a change
in the free energy, corresponds to a rigid shift of both PCI branches as schematized in
Figure 1c.
Many efforts have been made to design and grow nano-sized materials with more favorable hydrogen sorption thermodynamics than their bulk counterparts by inducing a thermodynamical bias in the right direction. For instance, if the material is too stable, an upward shift of the PCI branches, i.e., a positive thermodynamical bias, is desired. There are two main contributions to the thermodynamical bias when a material is refined to the nanoscale. The first one originates with the interface free energy [
5,
7] according to the following equation:
where
and
are the interface free energy for unit area for metal hydride and metal, respectively, while
and
are the corresponding interface areas.
This contribution clearly scales with the volume fraction occupied by interfaces (or surfaces), and is roughly inversely proportional to the material’s length scale. In this sense, the effect of the interfaces is short-ranged, i.e., it vanishes rapidly as the spatial separation between interfaces increases above a few nanometers.
The second contribution can arise in case of elastic confinement, i.e., if the material is prevented to freely expand upon hydride formation [
4]. The hydride formation enthalpy of core-shell nanoparticles (NPs) subjected to elastic constraints,
, is less negative with respect to
of the corresponding free NPs [
6]. The thermodynamical bias in this case is proportional to the volume strain
in the constrained hydride NPs:
where
B is the bulk modulus and
is the volume strain. In Equation (5), we have assumed that
. Elastic strain engineering has the potential to induce a significant bias up to length scales of a few tens of nanometers. The main problem is that the onset of plastic deformation strongly suppresses the effect and induces an unwanted extrinsic hysteresis [
5].
Comparing Equations (1), (4) and (5), one obtains:
and the total thermodynamical bias
can be estimated from the ratio between the equilibrium pressures in the nanomaterial and in the bulk material.
In a real nano-system there may be a combination of extrinsic hysteresis and thermodynamical bias, leading to an asymmetric shift of PCI branches as sketched in
Figure 1d. The comprehension of these separate contributions to the difference in thermodynamics and kinetics of hydrogen sorption is of paramount importance in the perspective of specifically designed multifunctional materials. We will here analyze and compare our results in the framework of these guidelines.
2. Results
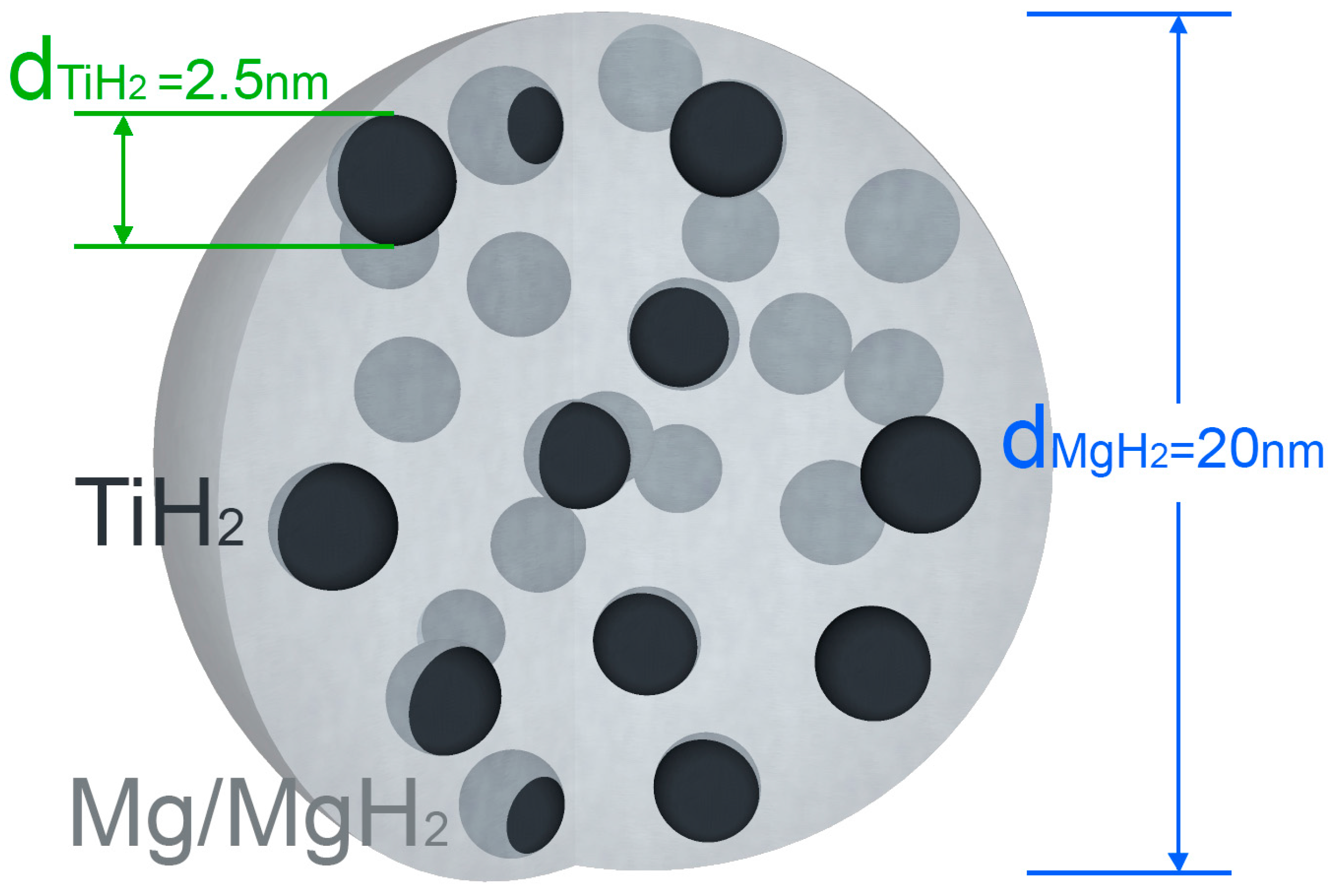
The materials analyzed in this work are composite Mg–Ti–H nanoparticles (NPs) synthetized by gas phase condensation, as previously reported [
8]. A broader description of the NPs growth technique is given in the Methods and Material section of this work. The combination of scanning transmission electron microscopy and X-ray diffraction suggested that the composite NPs are MgH
2 single crystals, in which ultrafine TiH
2 crystallites are dispersed. A schematic representation of the composite NPs is shown in
Figure 2. They will be compared to the results obtained on multilayered, nanoconfined Mg/Ti/Pd nanodots (NDs) [
5] sketched in
Figure 3.
H-sorption thermodynamics and kinetics were measured in-situ in an ultra-high-vacuum (UHV) chamber directly connected to the NPs deposition chamber. The hydrogen sorption properties were investigated in the low temperature regime (340 K <
T < 425 K) to determine
and
.
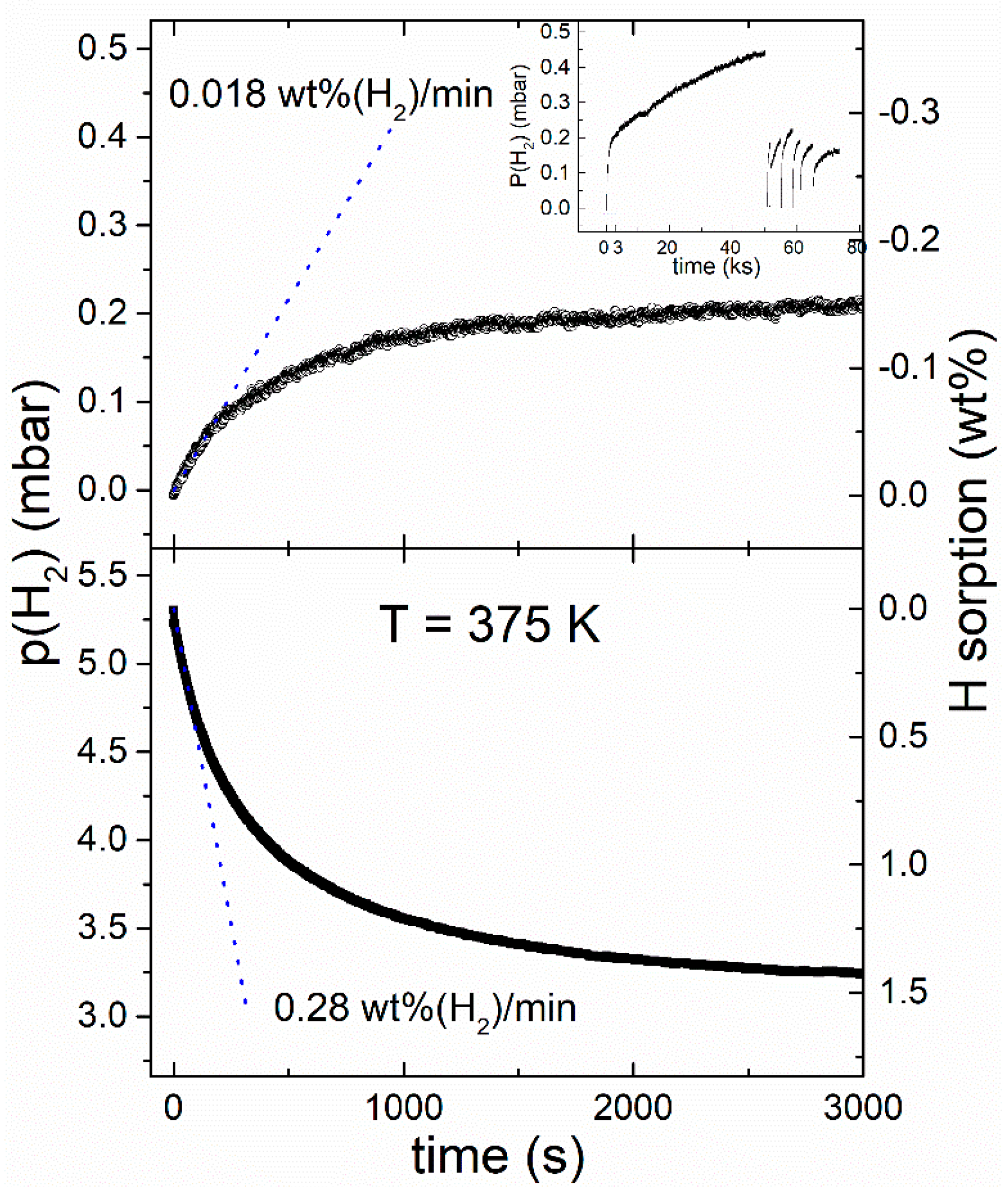
Figure 4 shows sorption pseudo-kinetics obtained at 375 K. The hydrogen absorption and desorption rates were calculated from the initial slope of the kinetics, resulting in 0.28 wt % H
2/min in absorption and 0.018 wt % H
2/min. These values are roughly one order of magnitude lower than observed at 423 K [
8], but are remarkable for MgH
2 at such low temperature and mild pressure, especially for hydrogen desorption.
Figure 4 also suggests that the sorption rates rapidly decrease when
approaches unity because the thermodynamic driving force tends to zero in this limit. Even if the chamber volume is large, the pressure approaches the low equilibrium values after a relatively small mass loss (<0.5%) for a Mg-based material. Therefore, several steps are needed in order to complete the desorption, as reported in the inset of
Figure 4. These steps altogether make it possible to construct a PCI curve and to determine the plateau pressure
for desorption. A similar argument applies to the determination of the absorption plateau pressure
.
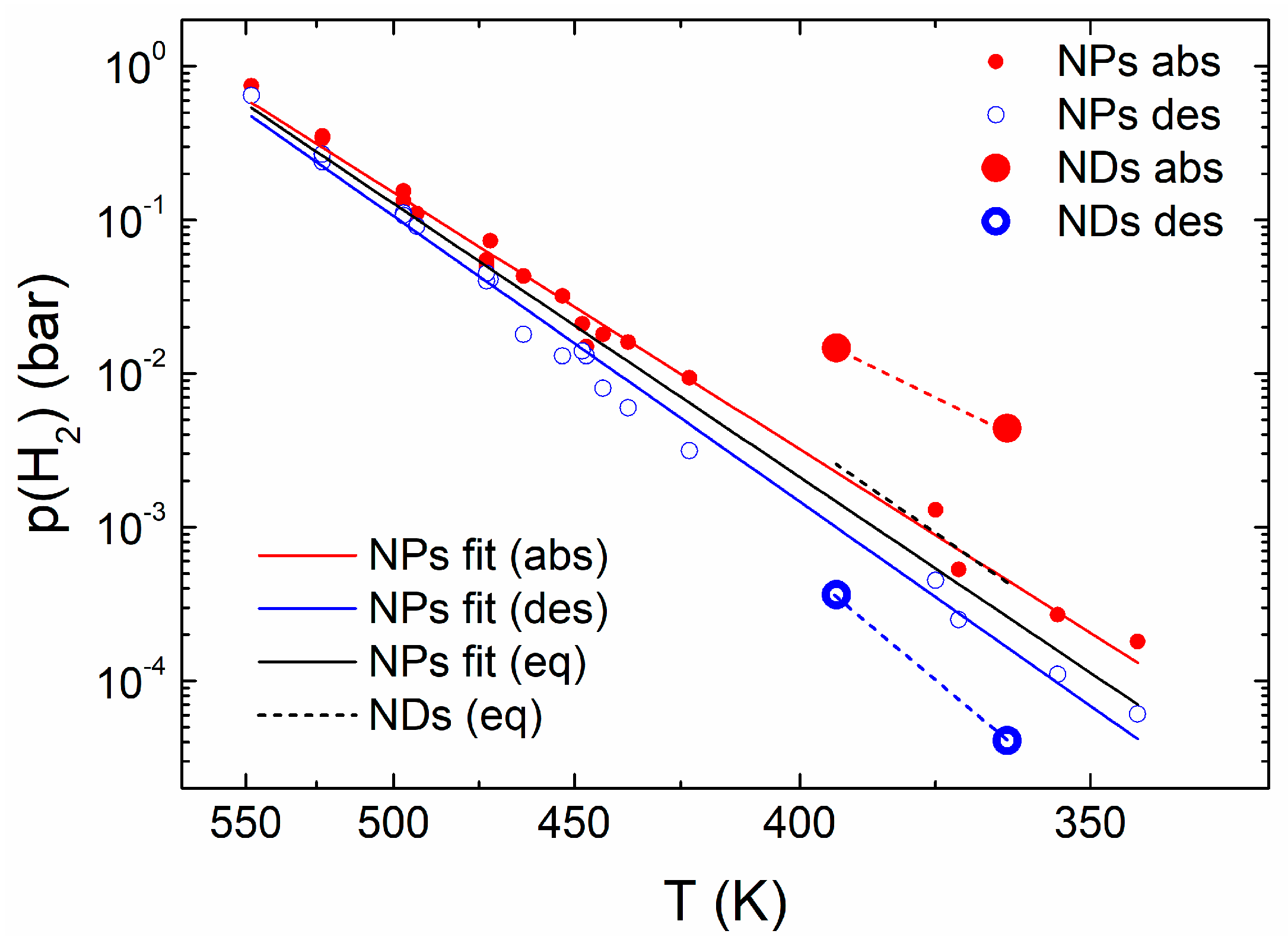
The fast kinetics at low temperature make it possible to measure absorption and desorption plateau pressures and to calculate the equilibrium values down to 355 K. In
Figure 5, the
and
values for a collection of NPs with varying Ti content (
XTi =
Ti/(
Mg +
Ti) = 6, 15, 30 atom %) are shown along with those measured on NDs. The corresponding enthalpy and entropy values are collected in
Table 1. The discrepancy between absorption and desorption is due to hysteresis. In general, the determination of thermodynamic parameters from only absorption (or desorption) pressures is prone to large errors. This is particularly evident for the NDs that, due to strong hysteretic behavior, show remarkably different slopes and intercepts in absorption and desorption, resulting in unrealistic enthalpy/entropy values (see
Table 1). The correct results are retrieved by fitting the equilibrium pressure. Looking at the equilibrium data in
Table 1, we notice that the formation enthalpy for both NPs and NDs is slightly less negative than for bulk Mg (although the error on the NDs is quite large). For the NPs, the entropy is also less negative (by about 10%) compared to the bulk, whereas for the NDs, the difference is smaller (about 3%) and well within the uncertainty. In
Figure 5, we also notice that the equilibrium pressure of the NDs (dotted black line) is larger than that of the NPs (solid black line) and of bulk Mg [
8] by a factor of two. The NDs, therefore, realize the picture outlined
Figure 1d, showing both an upward shift of the equilibrium pressure (thermodynamical bias) and a large extrinsic hysteresis.
The combination of these two effects does not result in a true destabilization of the NDs, that can only be claimed if
is higher than the bulk equilibrium value [
10].
The pressure hysteresis values measured on NPs and NDs are collected in
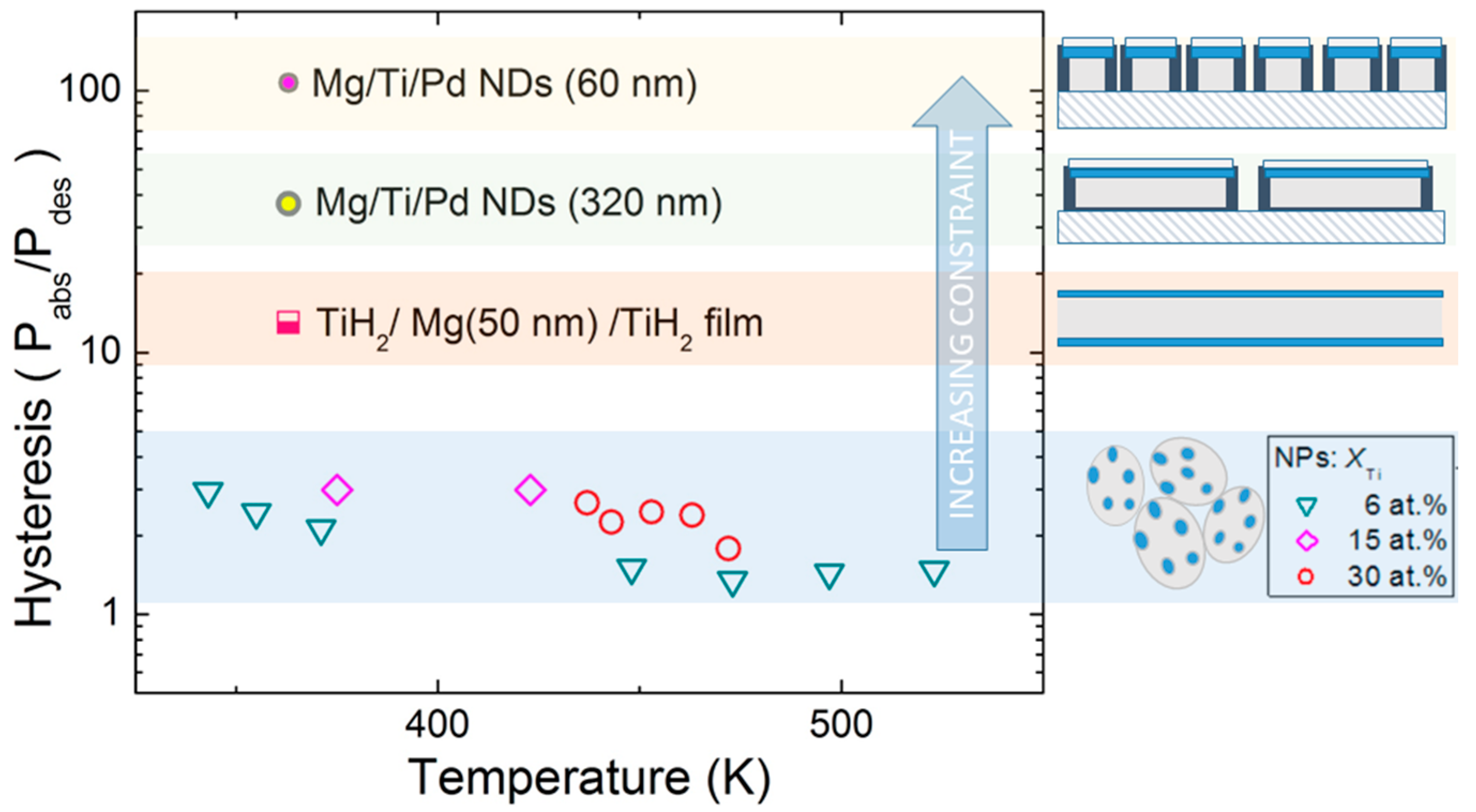
Figure 6. The NPs, which are relatively free to expand and contract upon hydrogen sorption, exhibit a small hysteresis, from ~3 at low temperature to ~1.5 at high temperature. The NDs show a huge hysteresis of ~100 at low temperature. The observation of a high hysteresis is quite common in constrained systems such as thin films clamped on a rigid substrate [
10,
11,
12].
Figure 6 suggests, qualitatively, that the hysteresis rises with increasing dimensionality of the constraint (1D for thin films and 3D for NDs) and with decreasing confinement length (decreasing ND diameter).
A brief comment to the temperature extent of Van’t Hoff plot is due. Mg NPs are subjected to severe coarsening when the temperature rises above 475 K. As shown in our precedent work [
8], NPs remain stable upon cycling in the 340 K <
T < 425 K range, while the nanostructure coarsens dramatically upon cycling at higher temperatures, where Mg sublimation from the clean Mg surface occurs and diffusion is faster. This establishes an upper temperature limit. On the other side, the exploration of significantly lower temperatures is hindered by the rapidly decreasing sorption rates and by the fact that the equilibrium pressure enters the high vacuum regime. Nevertheless, to the best of our knowledge, these composite NPs are the only system, with the exception of thin films coated by a Pd catalyst layer, in which the Mg to MgH
2 reversible transformation can be observed at such low temperature.
3. Discussion
Starting from the model presented in
Figure 2, if we assume that all the contributions to the thermodynamical bias come from an interface region of thickness
between
M (metal) or
MH (hydride) and a second phase (here indicated with
α) dispersed as spherical nanocrystals inside the M-matrix, Equation (4) turns into
where
, and the function
F ≤ 1 takes into account a possible decrease of the interface area due to coalescence of the
α-phase crystallites.
F ≈ 1 when the
α-phase crystallites are separated, a condition reasonably satisfied in the limit of low
α-phase content. For high
, e.g., close to the percolative threshold, the α-phase crystallites will start merging, leading to a collapse of the interface area. Equation (7) is completely general in the limit
, i.e., when the
M ↔
MH transformation is complete and
α-phase morphology is unchanged upon phase transformation.
Assuming
F ≈ 1 in the NPs, where the
α-phase is TiH
2 and
M = Mg, Equation (7) becomes:
where
is the molar volume of Mg,
and
are the volumes occupied by TiH
2 and Mg, respectively, and
is the average TiH
2 grain size inside the Mg matrix. Exploiting the enthalpic end entropic contribution to the interface free energy, i.e.,:
we can separately evaluate these contributions to the thermodynamical bias since they are simply multiplied by a geometrical term and Equation (8) becomes
Hao et al. reported density functional theory calculations of the Mg|TiH
2 and MgH
2|TiH
2 interface energy, yielding
= 0.59 ÷ 0.69 J/m
2 [
13].
Unfortunately, it is more difficult either to calculate the interfacial entropy or to extract it from experiments. The entropy has both a configurational and a vibrational term. The configurational term is due to the fraction of atom in the small (about 1 nm thick) interfacial region that accommodates the crystalline mismatch between different phases. According to literature [
14], a rather generous estimation for this value is the one associated with the glass transition entropy,
. The vibrational entropy term is even more challenging to assess and depends critically on the nature of the interfaces. For nanocrystalline materials, an increased vibrational entropy at interfaces
seems a realistic estimate [
14]. It therefore appears reasonable to consider an overall entropy per interface H atom of
.
The interface-induced entropy variation per unit area,
, can then be calculated with the approximation that the volume of H atoms at the interface is the average 〈
〉 = 1.7 cm
3/mol of the corresponding volumes in MgH
2 (2.08 cm
3/mol) and in TiH
2 (1.32 cm
3/mol):
where
is the interface volume. Assuming
= 1 nm, we obtain
≈ 0.9 × 10
−3 J/K·m
2.
Now we can further manipulate Equation (10) to make explicit the dependence on the parameter
(atomic fraction Ti/(Mg + Ti)), yielding:
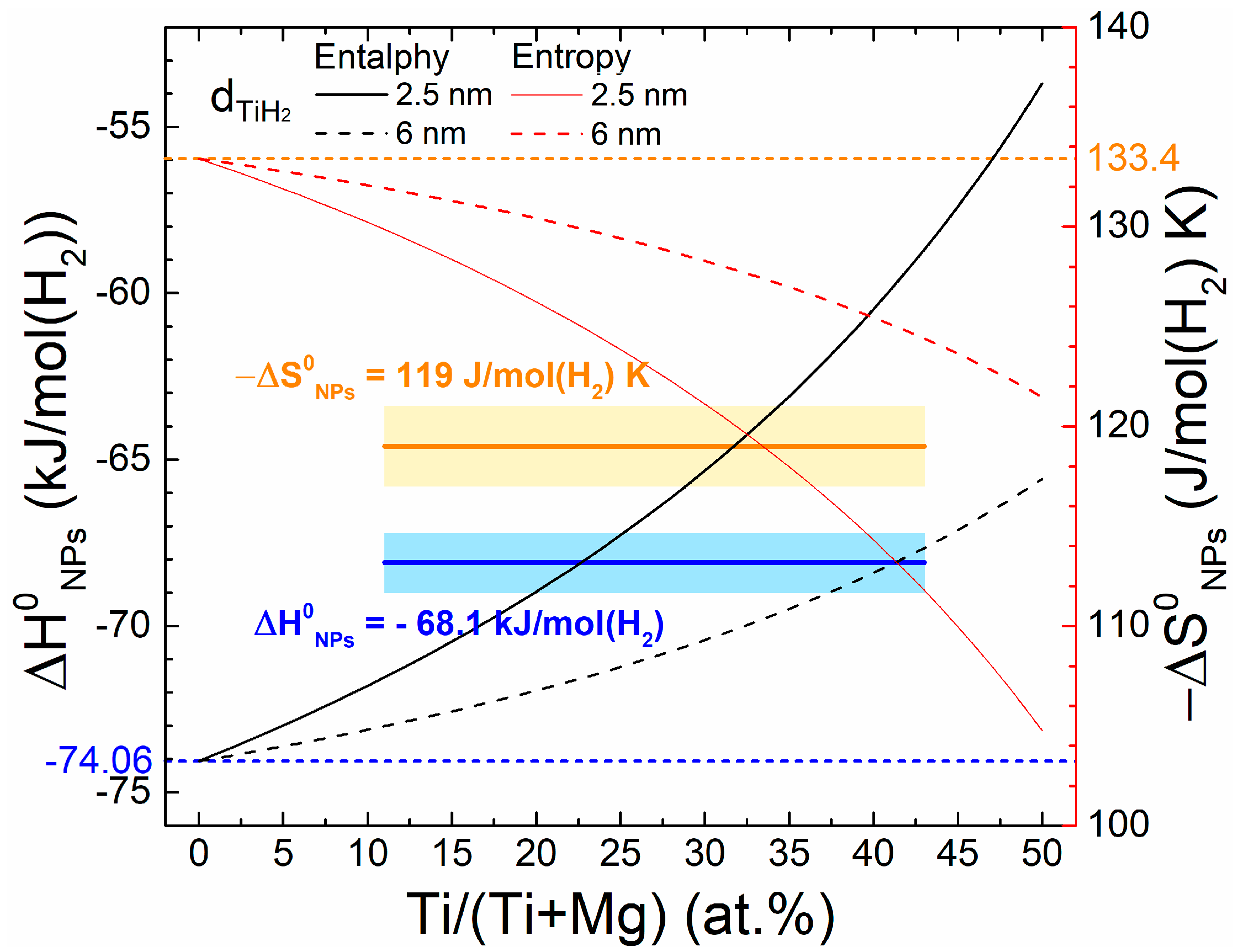
Values calculated with Equation (10), where no percolation effects are considered, are reported in
Figure 7 for the composite NPs as a function of
XTi and for different TiH
2 mean crystallite sizes. We assumed
= 0.64 J/m
2 = 0.9 × 10
−3 J/K·m
2 and used
= 13.26 cm
3/mol. Experimental values for NPs are also displayed with error bands in the explored range of compositions. The experimental range shown is not relative to nominal
XTi = 6, 15, 30 atom %, but refers to
= 11, 20, 43 atom % values calculated only considering MgH
2 and TiH
2 crystallites and neglecting the MgO phase that is not participating to H
2 sorption process [
8]. The experimentally determined
≈ 6 kJ/mol (H
2) is compatible with
= 20 and 43 atom % for
= 2.5 and 6 nm, respectively. However, for
= 11 atom %, the calculations only partially explain the enthalpy change, unless the existence of very small TiH
2 domains (about 1 nm diameter) is invoked.
The calculated entropy critically depends on the chosen
, for which we have just done a simple guess. A more detailed analysis of vibrational and configurational entropy per interface atom would help in refining the parameters for this model. The entropy curves in
Figure 7 account only for a fraction of the experimental bias
≈ 14 J/mol (H
2). Therefore, the experiments suggest that the interface entropy in the composite NPs may be significantly larger than our guessed value
. However, the experimental error could also be larger than the statistical error obtained from the best fitting procedure, due to coarsening of Mg and TiH
2 upon high temperature cycling.
Equations (8)–(10) have interesting implications on the possible presence of a unique enthalpy-entropy compensation temperature in nanomaterials that does not depend on microstructural parameters. This is a non-trivial issue which has stimulated discussions and controversies, since in many cases, the apparent enthalpy-entropy correlation is a phantom statistical phenomenon [
15,
10]. Starting from (10) and enthalpy and entropy being proportional to the same geometrical factor, as evident in the shapes of the curves in
Figure 7, the temperature
, at which entropy and enthalpy compensate each other, depends neither on Ti content nor on TiH
2 crystallite size and is simply given by
We stress again that this result is valid only if the average
and
are independent or weakly dependent on system size. This assumption is corroborated by measurements on MgH
2 thin films of varying thickness and on MgH
2 nanoclusters embedded in TiH
2 [
7,
16].
A slightly different expression holds for Mg-based NDs where one has also to take into account the presence of the Mg|MgO lateral interface and of the SiO2 substrate. With the assumption of a cylindrical ND, it is straightforward from Equation (4) that
Comparing this result with the corresponding Equation (10) one can see that the geometry of the system does not enter simply as a multiplicative term. Therefore, by changing thickness or diameter independently, one can make a determined specific free energy more relevant. Then, in principle, the possibility to tailor the geometry of the system makes it possible to tune the formation enthalpy and entropy and to change .
To the best of our knowledge, there are no literature data on
and
. A rather crude simplification consists in taking the same interfacial free energy for every interface, turning Equation (14) into the simple:
Here, similarly to NPs, one has a free energy term multiplied by the molar volume and by a geometrical factor, which is the surface-to-volume ratio of the nanosized object. Therefore, for a ND embedded in a homogeneous matrix the compensation temperature is independent on the number and extension of interfaces and can again be calculated using Equation (13).
The application of the simple Equation (15) to the NDs sketched in
Figure 3 yields a thermodynamical bias of ~0.6 kJ/mol H
2. This small value is consistent with the low fraction of interfaces in a ND, which is 30 nm thick and 60 nm in diameter. Despite this, the equilibrium pressure of the NDs lies distinctly above those measured in NPs, suggesting that the elastic strain plays a role in the thermodynamics of NDs. The clamping provided by the surrounding phases, which do not expand upon hydrogen absorption, results in a compressive strain that makes the hydride slightly less stable. We believe that this argument does not apply to the NPs, which are relatively free to expand. Even though the effect of elastic strain seems detectable in NDs, it does not provide a significant destabilization of MgH
2, because the pressure change is too small for practical applications. Even worse, the high extrinsic hysteresis in the constrained ND system counterbalances the destabilizing elastic strains during desorption, resulting in an overall reduction of the desorption pressure. We can argue that the hysteresis could be reduced and a true destabilization achieved if it were possible to avoid the onset of plastic deformation. However, the volume changes induced by hydrogen sorption in Mg are so high (~32%) that the resulting stresses exceed by far the yield stress of almost all involved phases.
Finally, we remark that Equation (15) well explains the thermodynamical bias observed in ultra-small Mg clusters (
r ≈ 1 nm) immersed in a TiH
2 matrix, for which the interface free energy becomes relevant [
16,
17].
5. Conclusions
Interface free energy and elastic confinement have the potential to induce a thermodynamical bias in nanoscale hydrides. The independent evaluation of interface enthalpy and entropy is important, in order to assess the temperature dependence and magnitude of the bias. In general, the enthalpy-entropy compensation temperature depends on various microstructural and compositional parameters. However, it can be shown that the compensation temperature is unchanged if the following conditions hold: (i) the specific interface enthalpy and entropy (or their average) is the same for all the interfaces, and (ii) the interface free energy is the sole source of a bias (i.e., absence of elastic constraints).
We have applied these arguments to interpret experimental results obtained on a biphasic nanocomposite, in which ultrafine TiH
2 crystallites are dispersed in a Mg (or MgH
2) NP [
8]. The calculations of the enthalpy change, based on DFT data for the interface enthalpy, are in reasonable agreement with the experiments, although they tend to underestimate the enthalpy change at low TiH
2 content. The experimental calculations comparison is much more difficult in the case of entropy, because there are no useful literature data on the interface entropy. An improved understanding and calculation of vibrational and configurational interface entropy appears to be of great importance in order to estimate the entropy change in nano-hydrides, which may be the key to tailoring their thermodynamics.
In the case of constrained systems, such as Mg NDs surrounded by rigid interfaces, an additional positive (i.e., destabilizing) contribution to the bias arises from elastic strains. However, the concomitant development of plastic deformation upon hydrogen sorption reduces the bias and brings about a large hysteresis, which results in a lower desorption pressure compared to the bulk counterparts.