96Zr Tracer Diffusion in AZrO3 (A = Ca, Sr, Ba)
Abstract
:1. Introduction
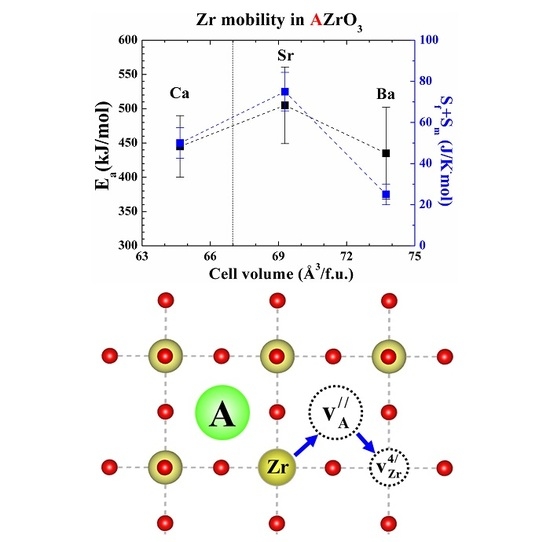
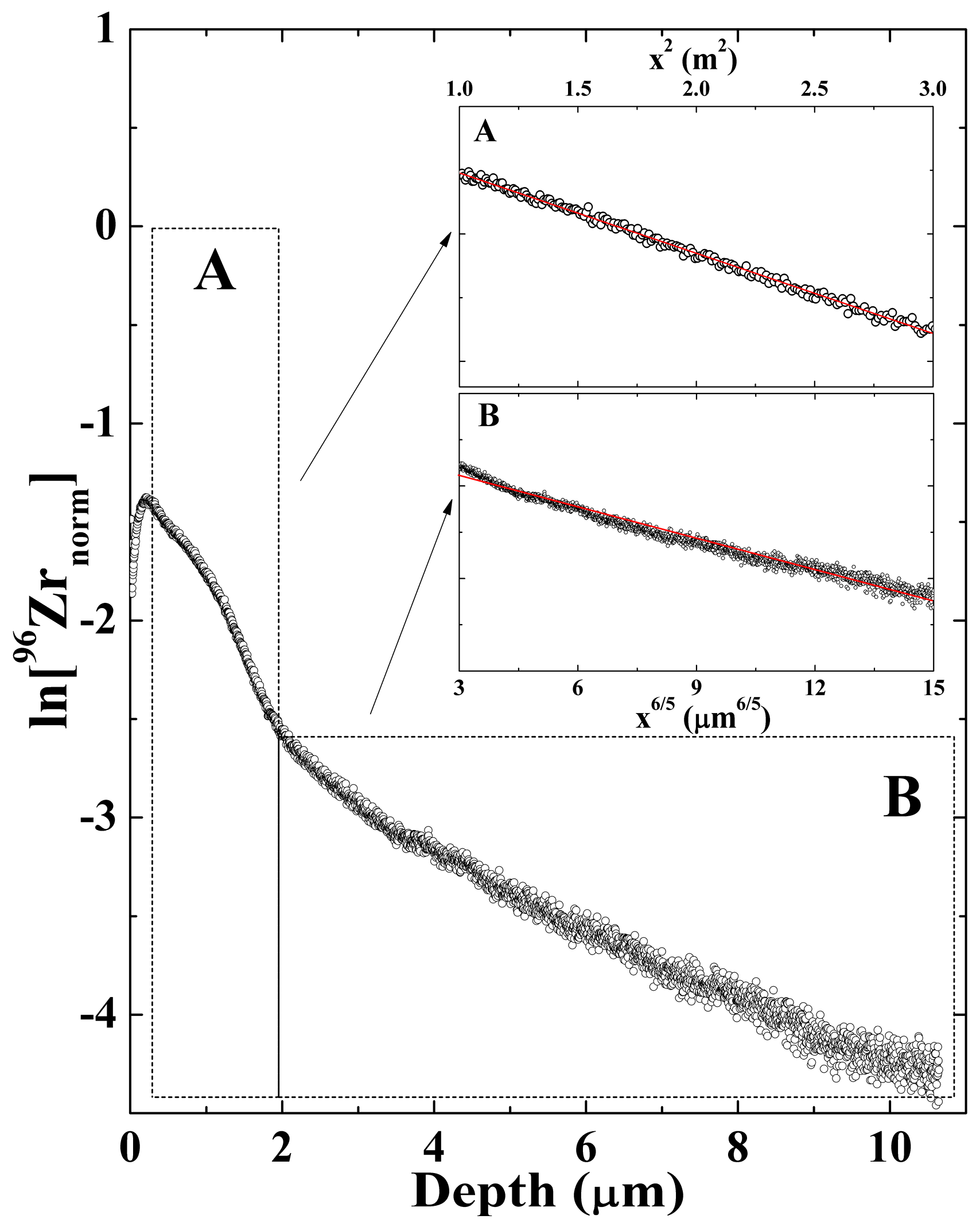
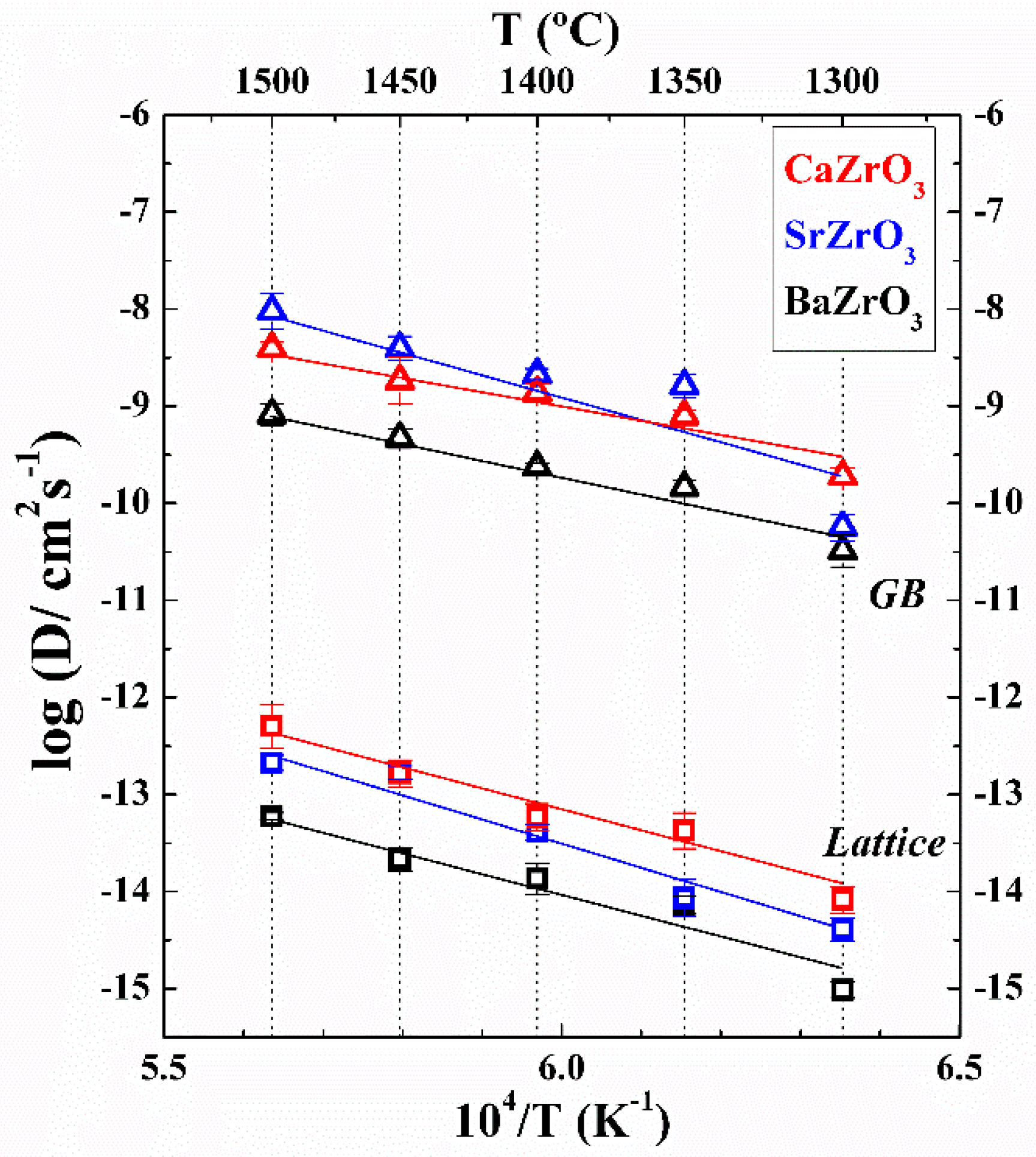
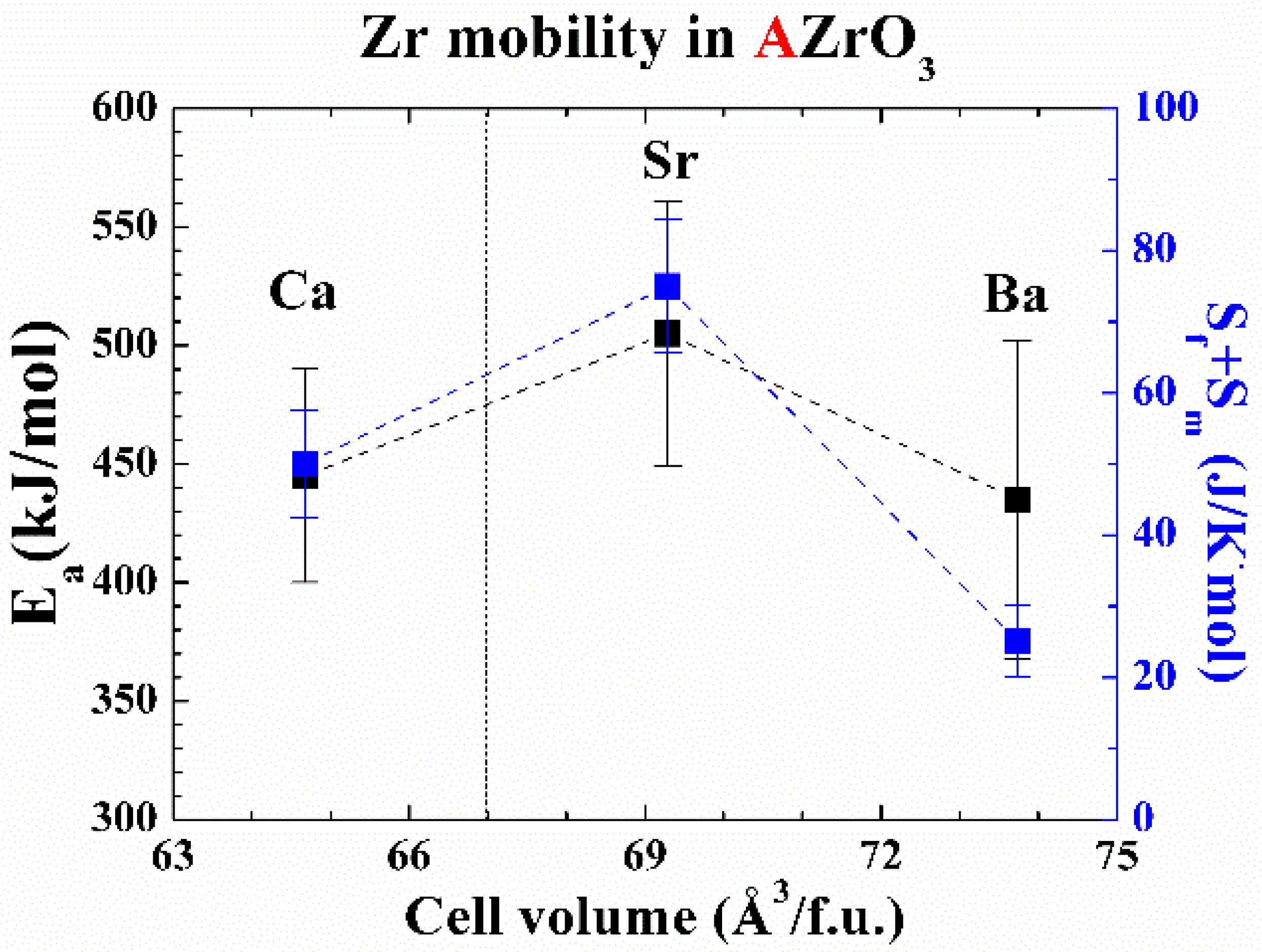
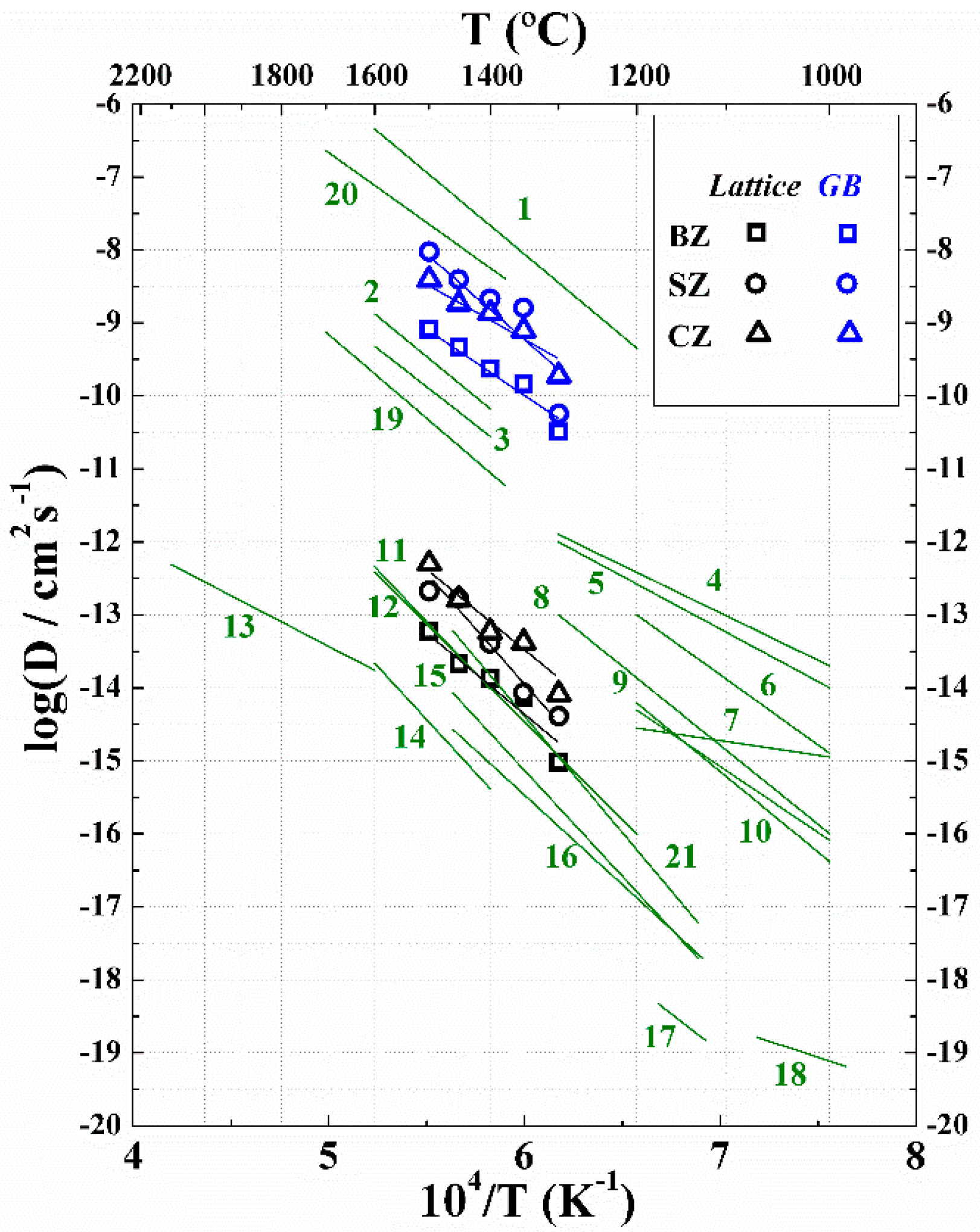
2. Results
3. Discussion
4. Materials and Methods
4.1. Sample Preparation
4.2. Secondary Ion Mass Spectrometry
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- De Souza, E.C.C.; Muccillo, R. Properties and applications of perovskite proton conductors. Mater. Res. 2010, 13, 385–394. [Google Scholar] [CrossRef]
- Phair, J.W.; Badwal, S.P.S. Materials for separation membranes in hydrogen and oxygen production and future power generation. Sci. Technol. Adv. Mater. 2016, 7, 792–805. [Google Scholar] [CrossRef]
- Malavasi, L.; Fisher, C.A.; Islam, M.S. Oxide-ion and proton conducting electrolyte materials for clean energy applications: Structural and mechanistic features. Chem. Soc. Rev. 2010, 39, 4370–4387. [Google Scholar] [CrossRef] [PubMed]
- Kochetova, N.; Animitsa, I.; Medvedev, D.; Demin, A.; Tsiakaras, P. Recent activity in the development of proton-conducting oxides for high-temperature applications. RSC Adv. 2016, 6, 73222–73268. [Google Scholar] [CrossRef]
- Kreuer, K.D. Proton-Conducting Oxides. Ann. Rev. Mater. Res. 2003, 33, 333–359. [Google Scholar] [CrossRef]
- Kreuer, K.D. Aspects of the formation and mobility of protonic charge carriers and the stability of perovskite-type oxides. Solid State Ion. 1997, 125, 285–302. [Google Scholar] [CrossRef]
- Hibino, T.; Mizutani, K.; Yajima, T.; Iwahara, H. Evaluation of proton conductivity in SrCeO3, BaCeO3, CaZrO3 and SrZrO3 by temperature programmed desorption method. Solid State Ion. 1992, 57, 303–306. [Google Scholar] [CrossRef]
- Sažinas, R.; Bernuy-López, C.; Einarsrud, M.-A.; Grande, T. Effect of CO2 exposure on the chemical stability and mechanical properties of BaZrO3-ceramics. J. Am. Ceram. Soc. 2016, 99, 3685–3695. [Google Scholar] [CrossRef]
- Bera, J.; Rout, S.K. On the formation mechanism of BaTiO3–BaZrO3 solid solution through solid-oxide reaction. Mater. Lett. 2005, 59, 135–138. [Google Scholar] [CrossRef]
- Itoh, J.-I.; Yashima, I.; Ohashi, N.; Sakaguchi, I.; Haneda, H.; Tanaka, J. Ni ion diffusion in barium titanate perovskite. J. Ceram. Soc. Jpn. 2001, 109, 955–959. [Google Scholar] [CrossRef]
- Itoh, J.-I.; Haneda, H.; Hishita, S.; Sakaguchi, I.; Ohashi, N.; Park, D.-C.; Yashima, I. Diffusion and solubility of holmium ions in barium titanate ceramics. J. Mater. Res. 2004, 19, 3512–3520. [Google Scholar] [CrossRef]
- Koerfer, S.; De Souza, R.A.; Yoo, H.-I.; Martin, M. Diffusion of Sr and Zr in BaTiO3 single crystals. Solid State Sci. 2008, 10, 725–734. [Google Scholar] [CrossRef]
- Yoo, H.-I.; Lee, C.-E.; De Souza, R.A.; Martin, M. Equal mobility of constituent cations in BaTiO3. Appl. Phys. Lett. 2008, 92, 252103. [Google Scholar] [CrossRef]
- Lewis, G.V.; Catlow, C.R.A. Computer modelling of barium titanate. Radiat. Eff. 1983, 73, 307–314. [Google Scholar] [CrossRef]
- Mizoguchi, T.; Takahashi, N.; Lee, H.-S. First-principles study on migration mechanism in SrTiO3. Appl. Phys. Lett. 2011, 98, 091909. [Google Scholar] [CrossRef]
- Gömann, K.; Borchardt, G.; Schulz, M.; Gömann, A.; Maus-Friedrichs, W.; Lesage, B.; Kaïtasov, O.; Hoffmann-Eifert, S.; Schneller, T. Sr diffusion in undoped and La-doped SrTiO3 single crystals under oxidizing conditions. Phys. Chem. Chem. Phys. 2005, 7, 2053–2060. [Google Scholar] [CrossRef] [PubMed]
- Sažinas, R.; Sakaguchi, I.; Hasle, I.; Polfus, J.M.; Haugsrud, R.; Einarsrud, M.-A.; Grande, T. Tracer diffusion of 96Zr and 134Ba in polycrystalline BaZrO3. Phys. Chem. Chem. Phys. 2017, 19, 21878–21886. [Google Scholar] [CrossRef] [PubMed]
- Sažinas, R.; Sakaguchi, I.; Einarsrud, M.-A.; Grande, T. 134Ba tracer diffusion in polycrystalline BaMO3 (M = Ti, Zr, Ce). AIP Adv. 2017, 7, 115024. [Google Scholar] [CrossRef]
- Martin, M. Materials in thermodynamic potential gradients. J. Chem. Thermodyn. 2003, 35, 1291–1308. [Google Scholar] [CrossRef]
- Kharton, V.V. Solid State Electrochemistry II, 1st ed.; Wiley-VCH: Weinheim, Germany, 2011. [Google Scholar]
- Yamanaka, S.; Fujikane, M.; Hamaguchi, T.; Muta, H.; Oyama, T.; Matsuda, T.; Kobayashi, S.-I.; Kurosaki, K. Thermophysical properties of BaZrO3 and BaCeO3. J. Alloys Compd. 2003, 359, 109–113. [Google Scholar] [CrossRef]
- Yamanaka, S.; Kurosaki, K.; Oyama, T.; Muta, H.; Uno, M.; Matsuda, T.; Kobayashi, S.-I. Thermophysical properties of perovskite-type strontium cerate and zirconate. J. Am. Ceram. Soc. 2005, 88, 1496–1499. [Google Scholar] [CrossRef]
- Szczerba, J.; Pdzich, Z.; Madej, D. Synthesis of spinel-calcium zirconate materials. Mater. Ceram. 2011, 63, 27–33. [Google Scholar]
- Gryaznov, D.; Fleig, J.; Maier, J. An improved procedure for determining grain boundary diffusion coefficients from averaged concentration profiles. J. Appl. Phys. 2008, 103, 063717. [Google Scholar] [CrossRef]
- Gömann, K.; Borchardt, G.; Gunhold, A.; Maus-Friedrichs, W.; Baumann, H. Ti diffusion in La-doped SrTiO3 single crystals. Phys. Chem. Chem. Phys. 2004, 6, 3639–3644. [Google Scholar] [CrossRef]
- Kennedy, B.J.; Howard, C.J.; Chakoumakos, B.C. High-temperature phase transitions in SrZrO3. Phys. Rev. B 1999, 59, 4023–4027. [Google Scholar] [CrossRef]
- Wang, K.; Li, C.H.; Gao, Y.H.; Lu, X.G.; Ding, W.Z. Thermodynamic reassessment of ZrO2–CaO System. J. Am. Ceram. Soc. 2009, 92, 1098–1104. [Google Scholar] [CrossRef]
- Mathews, M.D.; Mirza, E.B.; Momin, A.C. High-temperature X-ray diffractometric studies of CaZrO3, SrZrO3 and BaZrO3. J. Mater. Sci. Lett. 1991, 10, 305–306. [Google Scholar] [CrossRef]
- Grande, T.; Tolchard, J.R.; Selbach, S.M. Anisotropic thermal and chemical expansion in Sr-substituted LaMnO3+δ: Implications for chemical strain relaxation. Chem. Mater. 2012, 24, 338–345. [Google Scholar] [CrossRef]
- Stokes, S.J.; Islam, M.S. Defect chemistry and proton-dopant association in BaZrO3 and BaPrO3. J. Mater. Chem. 2010, 20, 6258–6264. [Google Scholar] [CrossRef]
- Klyukin, K.; Alexandrov, V. Effect of intrinsic point defects on ferroelectric polarization behavior of SrTiO3. Phys. Rev. B 2017, 95, 035301. [Google Scholar] [CrossRef]
- Davies, R.A.; Islam, M.S.; Gale, J.D. Dopant and proton incorporation in perovskite-type zirconates. Solid State Ion. 1999, 126, 323–335. [Google Scholar] [CrossRef]
- Yamazaki, Y.; Yang, C.-K.; Haile, S.M. Unraveling the defect chemistry and proton uptake of yttrium-doped barium zirconate. Scri. Mater. 2011, 65, 102–106. [Google Scholar] [CrossRef]
- Shannon, R.D. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Cryst. A 1976, 32, 751–767. [Google Scholar] [CrossRef]
- Crank, J. The Mathematics of Diffusion; Oxford University Press: Oxford, UK, 1975. [Google Scholar]
- Taylor, M.A.; Kilo, M.; Borchardt, G.; Weber, S.; Scherrer, H. 96Zr diffusion in polycrystalline scandia stabilized zirconia. J. Eur. Ceram. Soc. 2005, 25, 1591–1595. [Google Scholar] [CrossRef]
- Dobson, T.W.; Wager, J.F.; Van Vechten, J.A. Entropy of migration for atomic hopping. Phys. Rev. B 1989, 40, 2962–2967. [Google Scholar] [CrossRef]
- Smith, D.W. An acidity scale for binary oxides. J. Chem. Educ. 1987, 64, 480–481. [Google Scholar] [CrossRef]
- Xu, J.; Yamazaki, D.; Katsura, T.; Wu, X.; Remmert, P.; Yurimoto, H.; Chakraborty, S. Silicon and magnesium diffusion in a single crystal of MgSiO3 perovskite. J. Geophys. Res. 2011, 116, 1–8. [Google Scholar] [CrossRef]
- Palcut, M.; Christensen, J.S.; Wiik, K.; Grande, T. Impurity diffusion of 141Pr in LaMnO3, LaCoO3 and LaFeO3 material. Phys. Chem. Chem. Phys. 2008, 10, 6544–6552. [Google Scholar] [CrossRef] [PubMed]
- Palcut, M.; Wiik, K.; Grande, T. Cation self-diffusion in LaCoO3 and La2CoO4 studied by diffusion couple experiments. J. Phys. Chem. B 2007, 111, 2299–2308. [Google Scholar] [CrossRef] [PubMed]
- Miyoshi, S.; Martin, M. B-Site cation diffusivity of Mn and Cr in perovskite-type LaMnO3 with cation-deficit nonstoichiometry. Phys. Chem. Chem. Phys. 2009, 11, 3063–3070. [Google Scholar] [CrossRef] [PubMed]
- Palcut, M.; Knibbe, R.; Wiik, K.; Grande, T. Cation inter-diffusion between LaMnO3 and LaCoO3 materials. Solid State Ion. 2011, 202, 6–13. [Google Scholar] [CrossRef]
- Petrov, A.N.; Rabinovich, L.Y.; Zhukovskii, V.M.; Zhukovskaia, A.S. Diffusion of the metallic components in sintered lanthanoid orthocobaltites LnCoO3 (Ln = La, Pr, Nd, Sm, Eu, Gd). Dokl. Chem. 1987, 292, 18–21. [Google Scholar]
- Sakai, N.; Yamaji, K.; Horita, T.; Negishi, H.; Yokokawa, H. Chromium diffusion in lanthanum chromites. Solid State Ion. 2000, 135, 469–474. [Google Scholar] [CrossRef]
- Smith, J.; Norby, T. Cation self-diffusion in LaFeO3 measured by the solid state reaction method. Solid State Ion. 2006, 177, 639–646. [Google Scholar] [CrossRef]
- Pavlyuchenko, M.M.; Filonov, B.O.; Shimanovich, I.E.; Produkina, S.A. Fe diffusion in NdFeO3. Dokl. Akad. Nauk BSSR 1970, 14, 328–350. [Google Scholar]
- Kishimoto, H.; Sakai, N.; Horita, T.; Yamaji, K.; Brito, M.; Yokokawa, H. Cation transport behavior in SOFC cathode materials of La0.8Sr0.2CoO3 and La0.8Sr0.2FeO3 with perovskite structure. Solid State Ion. 2007, 178, 1317–1325. [Google Scholar] [CrossRef]
- Swaroop, S.; Kilo, M.; Argirusis, C.; Borchardt, G.; Chokshi, A.H. Lattice and grain boundary diffusion of cations in 3YTZ analyzed using SIMS. Acta Mater. 2005, 53, 4975–4985. [Google Scholar] [CrossRef]
- Sakai, N.; Kishimoto, H.; Yamaji, K.; Horita, T.; Brito, M.E.; Yokokawa, H. Interface stability of perovskite cathodes and rare-earth. Doped ceria interlayer in SOFCs. J. Electrochem. Soc. 2007, 154, B1331–B1337. [Google Scholar] [CrossRef]
- Chen, P.-L.; Chen, I.W. Role of defect interaction in boundary mobility and cation diffusivity of CeO2. J. Am. Ceram. Soc. 1994, 77, 2289–2297. [Google Scholar] [CrossRef]
- Izuki, M.; Brito, M.E.; Yamaji, K.; Kishimoto, H.; Cho, D.-H.; Shimonosono, T.; Horita, T.; Yokokawa, H. Interfacial stability and cation diffusion across the LSCF/GDC interface. J. Power Sources 2011, 196, 7232–7236. [Google Scholar] [CrossRef]
- Freer, R. Self-diffusion and impurity diffusion in oxides. J. Mater. Sci. 1980, 15, 803–824. [Google Scholar] [CrossRef]
- Kilo, M.; Taylor, M.A.; Argirusis, C.; Borchardt, G.; Lesage, B.; Weber, S.; Scherrer, S.; Scherrer, H.; Schroeder, M.; Martin, M. Lanthanide transport in stabilized zirconias: Interrelation between ionic radius and diffusion coefficient. J. Appl. Phys. 2003, 94, 7547–7552. [Google Scholar] [CrossRef]
- Rockenhäuser, C.; Butz, B.; Schichtel, N.; Janek, J.; Oberacker, R.; Hoffmann, M.J.; Gerthsen, D. Microstructure evolution and cation interdiffusion in thin Gd2O3 films on CeO2 substrates. J. Eur. Ceram. Soc. 2014, 34, 1235–1242. [Google Scholar] [CrossRef]
- Tarrida, M.; Larguem, H.; Madon, M. Structural investigations of (Ca,Sr)ZrO3 and Ca(Sn,Zr)O3 perovskite compounds. Phys. Chem. Miner. 2009, 36, 403–413. [Google Scholar] [CrossRef]
- Vocke, R.D. Atomic weights of the elements 1997. Pure Appl. Chem. 1999, 71, 1593–1607. [Google Scholar] [CrossRef]

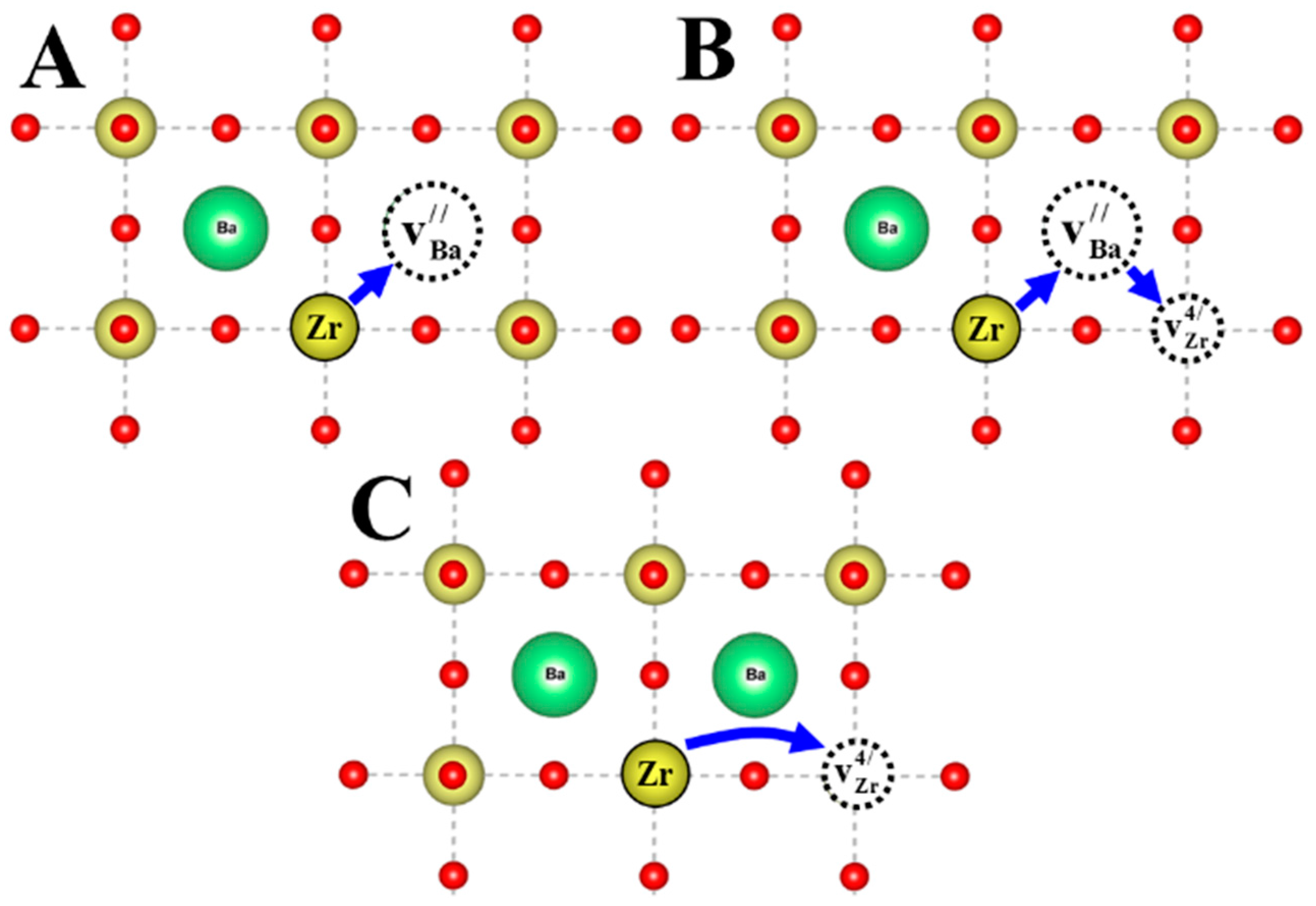

| Material | Crystal Structure | Unit Cell Parameters (Å) | Grain Size (μm) | Relative Density (%) |
|---|---|---|---|---|
| BaZrO3 | Cubic | a = 4.193 | 0.1 | 97 ± 1 |
| SrZrO3 | Orthorhombic | a = 5.797 b = 5.824 c = 8.209 | 5.2 ± 0.1 | 96 ± 2 |
| CaZrO3 | Orthorhombic | a = 5.763 b = 8.023 c = 5.596 | 10.5 ± 0.2 | 98 ± 1 |
| Material | Do (cm2/s) | Ea, lattice (kJ/mol) | Ea, GB (kJ/mol) |
|---|---|---|---|
| BaZrO3 | 0.4 ± 0.1 | 435 ± 67 | 356 ± 40 |
| SrZrO3 | 220 ± 90 | 505 ± 56 | 523 ± 134 |
| CaZrO3 | 6.3 ± 1.4 | 445 ± 45 | 322 ± 46 |
| Material | Cation Sublattice | Cation Size [34] (Å) | Partly Schottky Defect (eV/Defect) | Schottky Defect (eV/Defect) | Reference |
|---|---|---|---|---|---|
| BaZrO3 | Zr | 0.72 | 3.75 | 3.20 | [30] |
| Ba | 1.61 | 2.80 | |||
| SrZrO3 | Zr | 0.72 | 4.45 | 3.51 | [32] |
| Sr | 1.44 | 2.68 | |||
| CaZrO3 | Zr | 0.72 | 3.09 | 2.22 | |
| Ca | 1.34 | 1.26 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sažinas, R.; Sakaguchi, I.; Einarsrud, M.-A.; Grande, T. 96Zr Tracer Diffusion in AZrO3 (A = Ca, Sr, Ba). Inorganics 2018, 6, 14. https://doi.org/10.3390/inorganics6010014
Sažinas R, Sakaguchi I, Einarsrud M-A, Grande T. 96Zr Tracer Diffusion in AZrO3 (A = Ca, Sr, Ba). Inorganics. 2018; 6(1):14. https://doi.org/10.3390/inorganics6010014
Chicago/Turabian StyleSažinas, Rokas, Isao Sakaguchi, Mari-Ann Einarsrud, and Tor Grande. 2018. "96Zr Tracer Diffusion in AZrO3 (A = Ca, Sr, Ba)" Inorganics 6, no. 1: 14. https://doi.org/10.3390/inorganics6010014
APA StyleSažinas, R., Sakaguchi, I., Einarsrud, M.-A., & Grande, T. (2018). 96Zr Tracer Diffusion in AZrO3 (A = Ca, Sr, Ba). Inorganics, 6(1), 14. https://doi.org/10.3390/inorganics6010014